Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x).
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон
А1:В22. - Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон
A1:V22. - Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
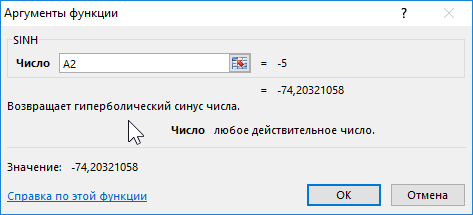
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
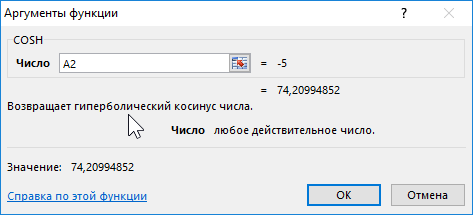
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
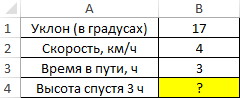
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
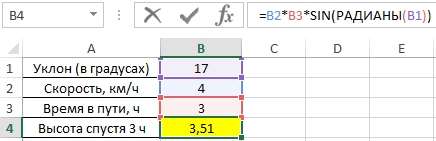
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
Таблица синусов и косинусов в Excel
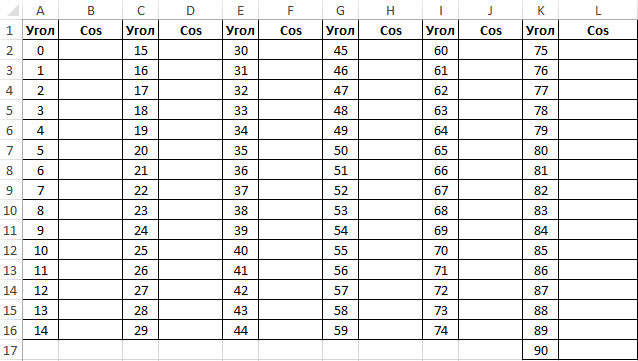
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
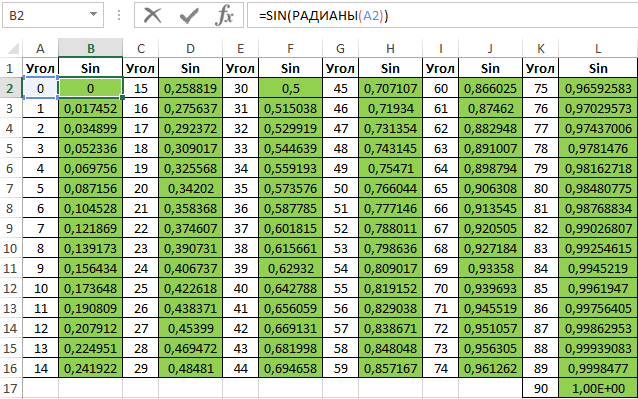
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
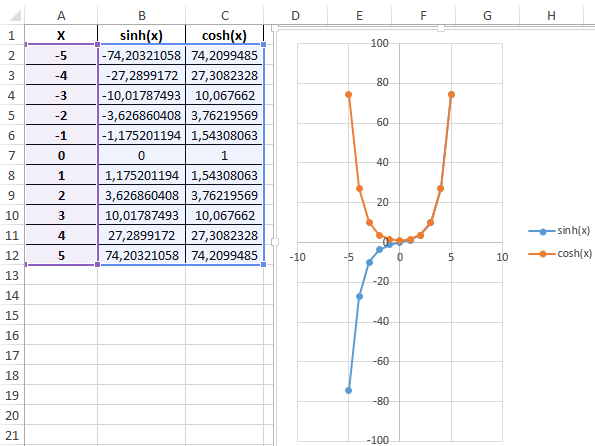
Построение графика функций SINH и COSH в Excel
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
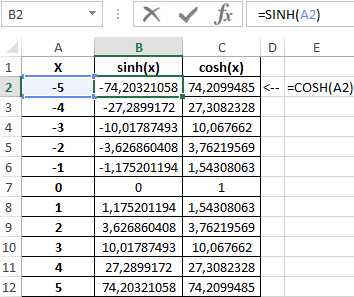
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Содержание
- Microsoft Excel
- Построение в Excel графиков математических и тригонометрических функций
- Построение графиков математических функций с одной переменной
- Построение графиков математических функций с двумя переменными
- Как построить график функции в Excel
- Как в экселе построить график косинуса?
- Видео
- Варианты построения графика функции в Microsoft Excel
- Вариант 1: График функции X^2
- Вариант 2: График функции y=sin(x)
Microsoft Excel
трюки • приёмы • решения
Построение в Excel графиков математических и тригонометрических функций
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x) .
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон А1:В22 .
- Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон A1:V22 .
- Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Источник
Как построить график функции в Excel
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .
Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .
В поле «Элементы легенды» кликаем на кнопочку «Добавить» .
Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .
Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Источник
Как в экселе построить график косинуса?
Построить график косинуса в программе эксель несложна задача, которую нужно сделать в несколько этапов, рассмотрим каждый по отдельности:
Первый этап. Построим график косинуса от нуля до ста восьмидесяти градусов, шаг точки возьмем пятнадцать градусов.
Второй этап. Переведем градусы в радианы, для этого воспользуемся функцией «РАДИАНЫ(Х)», где «Х» — это значение в градусах, которое необходимо перевести в радианы. Сначала в ячейке «В2» пишем формулу: =РАДИАНЫ(A2), потом копируем эту формулу на другие ячейки.
Третий этап. Посчитаем значение косинуса для каждого значения, для этого сначала пропишем в ячейке «С2» формулу: =COS(B2). После снова нужно скопировать эту формулу на остальные ячейки. В итоге все готово, чтобы начать строить график косинуса.
Четвертый этап. Выделим область ячеек с «В2» по «С14». На верхней панели настроек, активируем панель «Вставка», в ней отыскиваете блок «Диаграммы» и выбираете «Точечная», после нажатия на данную иконку, отразиться выбор графиков, нужно выбрать в первой строке вторую картинку.
В итоге получаем небольшой участок графика косинуса, дальше можно его строить в обоих направления, используя вышеописанный алгоритм.
Видео
Источник
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
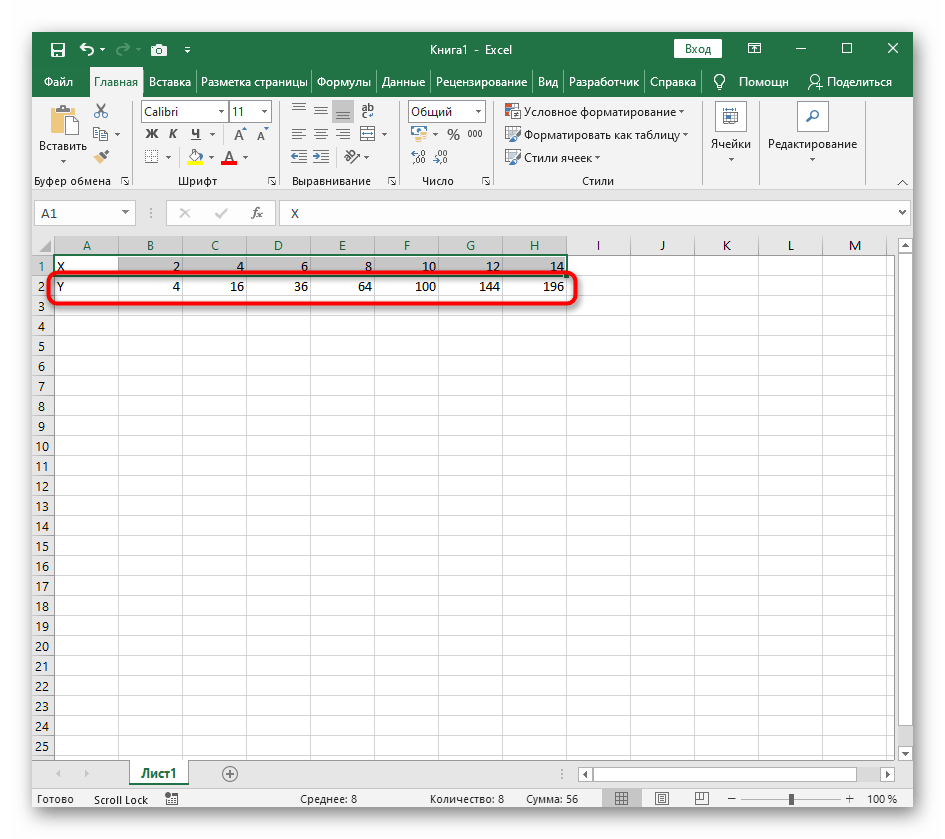
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
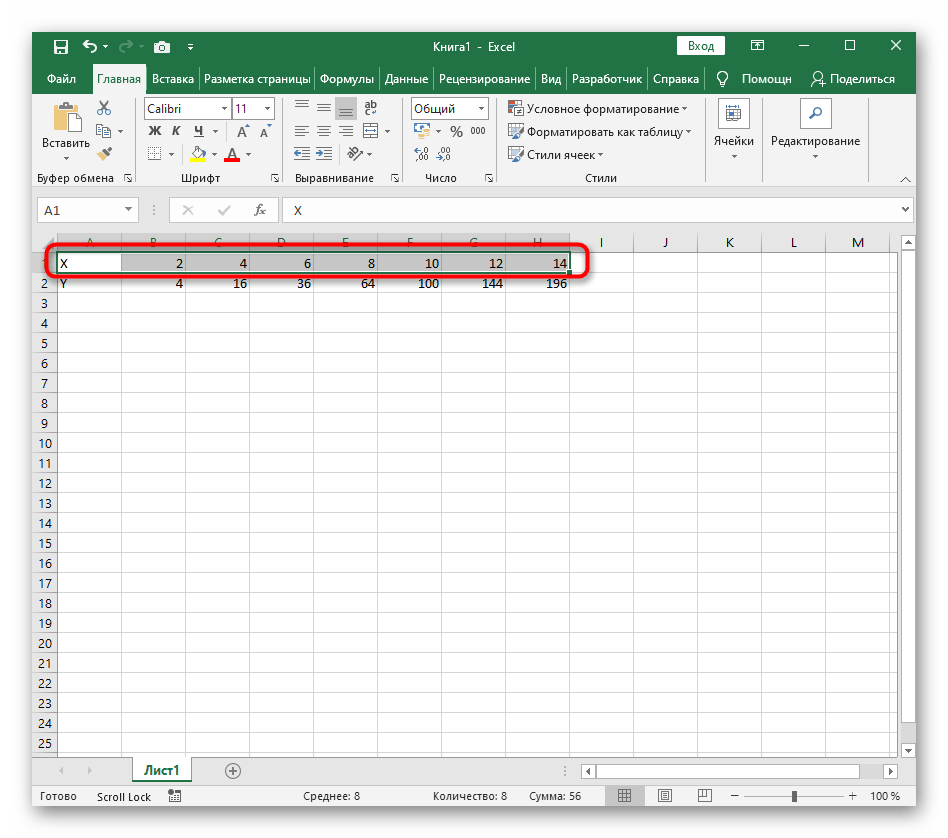
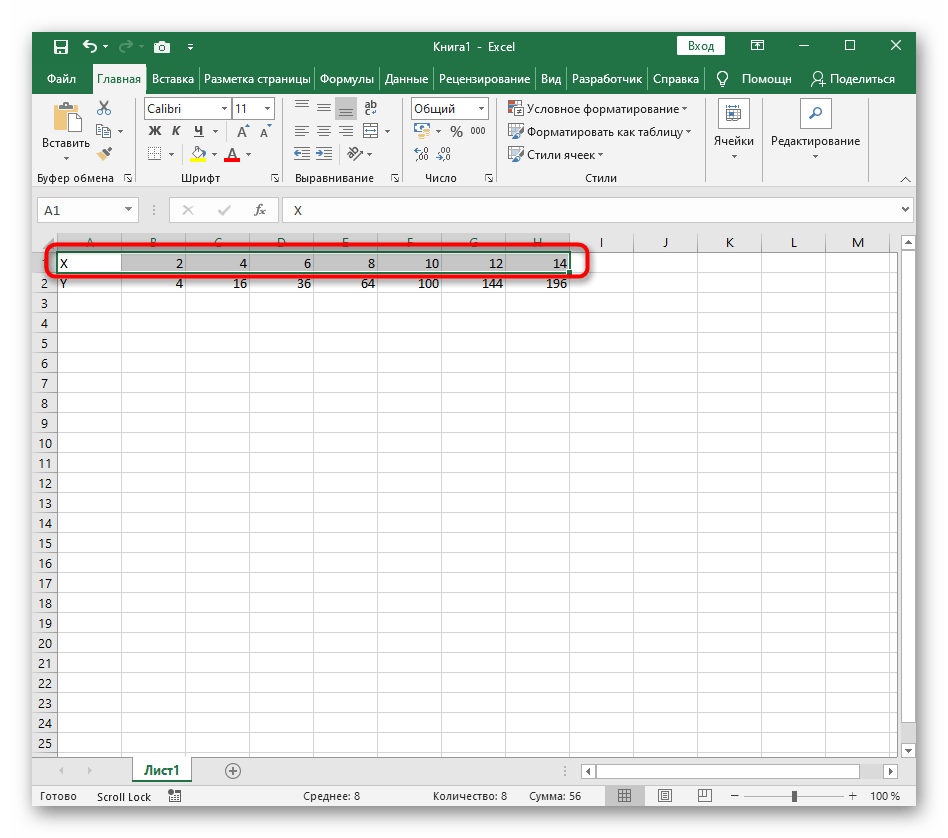
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
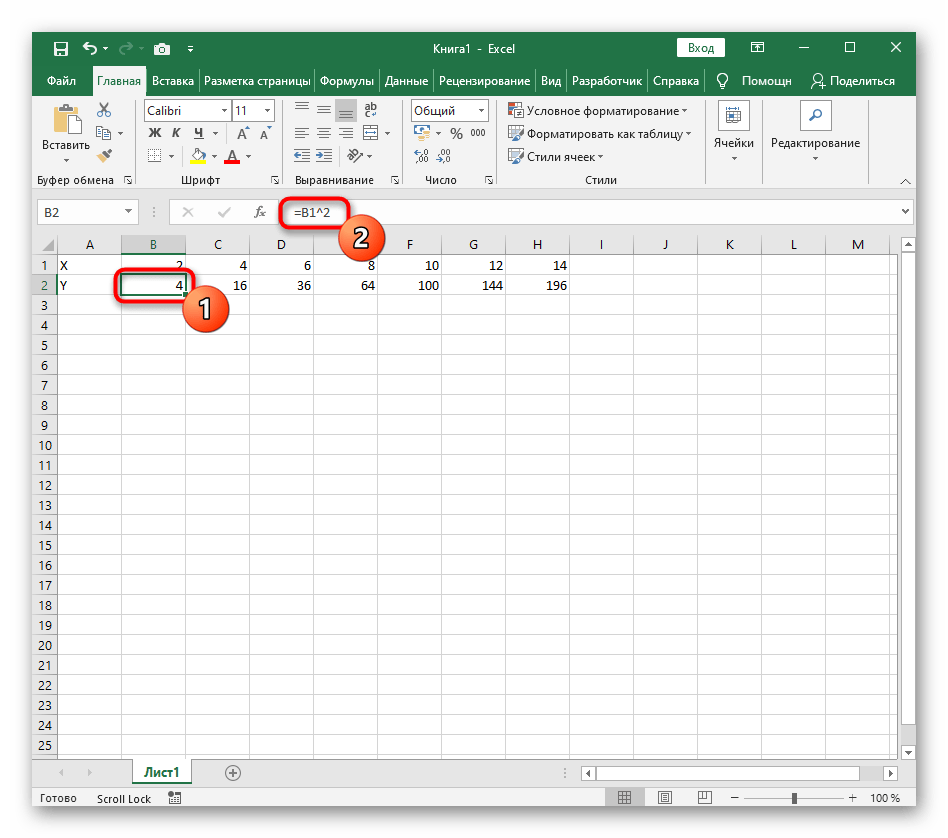
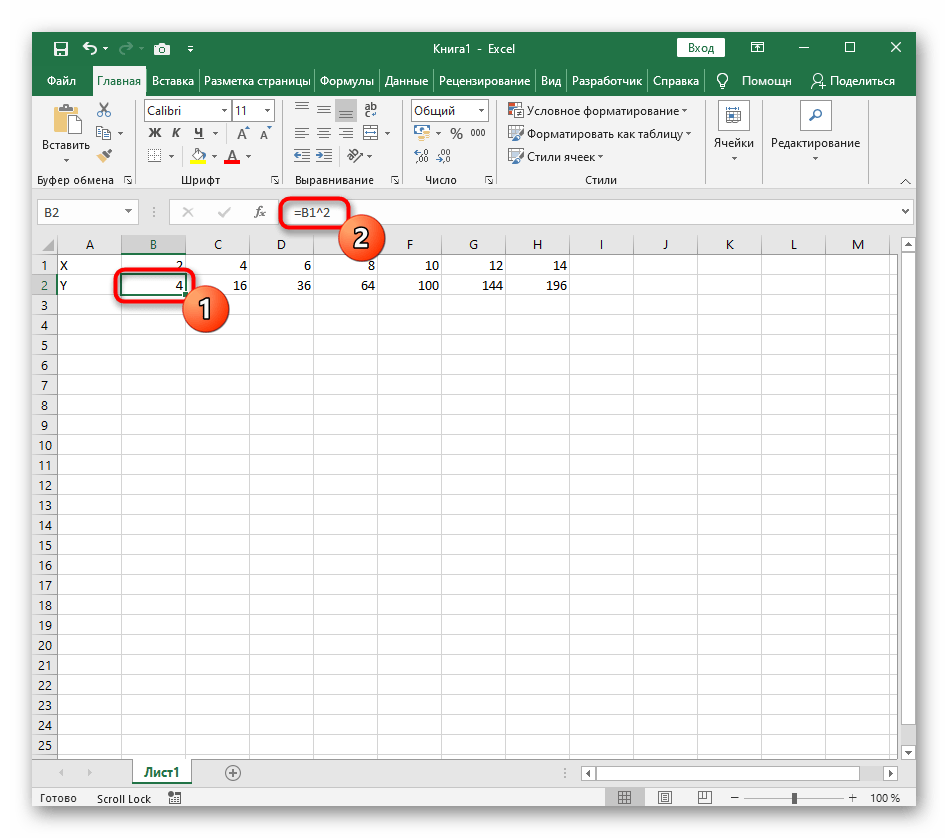
- Нажмите по первой ячейке и впишите =B1^2 , что значит автоматическое возведение указанной ячейки в квадрат.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.











Источник
Тип урока: урок обобщения и
систематизации знаний
Цели:
- научить строить графики тригонометрических
функций средствами MS Excel - закрепить навыки работы в электронных таблицах,
- углубить представления учащихся о взаимосвязи
предметов и прикладной ориентации курса
информатики.
ХОД УРОКА
Если вычислений много, а времени мало,
то доверьтесь электронным таблицам
1. Сообщение целей и задач урока
– Ребята, сегодня мы продолжим знакомиться с
возможностями электронных таблиц Excel. Давайте
вспомним, для чего предназначены электронные
таблицы? (Автоматизация расчетов).
– Что вы уже умеете делать в электронных
таблицах? (Создавать и форматировать таблицу,
работать с типами данных, решать задачи
используя относительную и абсолютную ссылки,
строить диаграммы).
– На уроках математики вы изучили
тригонометрические функции и их графики. При
построении графиков тригонометрических функций
необходимо учесть множество нюансов. Начертить
синусоиду или косинусоиду красиво – это уже
искусство, а если необходимо график растянуть,
сжать или симметрично отобразить относительно
какой-либо оси – это может вызвать затруднения. И
здесь нам на помощь нам придут электронные
таблицы MS Excel. Вы узнаете как с их помощью быстро и
красиво построить график.
Сегодня на уроке мы познакомимся с алгоритмом
построения графика тригонометрической функции.
Эпиграфом к уроку я взяла слова «Если
вычислений много, а времени мало, то доверьтесь
электронным таблицам»
2. Актуализация знаний
Фронтальный опрос (за правильный ответ даем
красную карточку)
- С чего начинается ввод формулы в ячейку? (Со
знака равенства) - На каком языке набирается формула в MS Excel? (Английском)
- Как скопировать формулу в другие ячейки?(С
помощью маркера автозаполнения) - Как изменить число десятичных знаков после
запятой в отображаемом числе? (Выделить,
Формат, Ячейки, вкладка Число, Числовой формат,
…..) - Что означает запись ###### в ячейке? (Длина
водимых данных превышает ширину ячейки) - Каким образом набирается формула, содержащая
какую-либо функцию? (Выделить ячейку, в которую
нужно вставить первое значение функции;Вставка,
Функция, выбрать Категорию и саму функцию) - Каким образом набирается формула, содержащая
сложную функцию, например, y = |x2|? (Вставляется
внешняя функция с пустым аргументом, затем левее
строки редактирования формул из раскрывающегося
списка выбирается внутренняя функция) - Как вставить какой-либо символ, например,
математический в ячейку? (Вставка, Символ, в
появившемся диалоговом окне выбрать шрифт Symbol и
нужный символ)
На прошлом уроке вы строили графики
элементарных функций. Давайте повторим алгоритм
построения графика (Учащиеся называют шаги
построения графика функции, а учитель показывает
соответствующий пункт алгоритма на доске
(используется проектор) и если необходимо
дополняет ответ учеников) (см. Приложение
1).
3. Изучение нового
С использованием презентации (см. Приложение
2) учитель рассказывает, как строится
график тригонометрической функций, а затем
выполняет его построение в электронных таблицах.
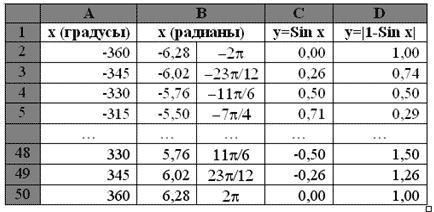
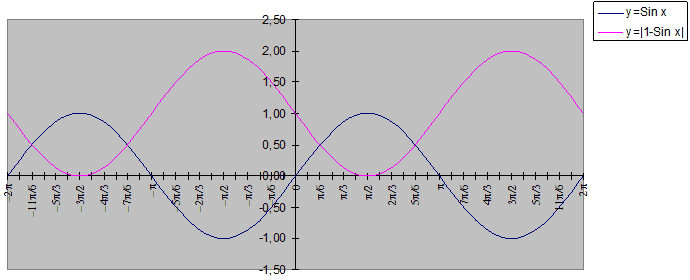
Задание. Построить в MS Excel графики
функций y = Sin x и y = |1 – sin x| на
промежутке [–360о; 360о] с шагом 15о.
Построенные графики смотри в Приложении
3
4. Закрепление полученных знаний
Каждому ученику даётся карточка с заданием и
оценочный лист, который после выполнения задания
отдается учителю (Каждый пункт в оценочном
листе является шагом построения графика
тригонометрической функции с использованием
MSExcel). Презентация находится в
сетевой папке, и любой ученик может ею
воспользоваться при выполнении своего задания.
Задание. Построить в MS Excel графики
функций на промежутке [–36о;36о] с
шагом 15о.
5. Проверка построенных графиков и разбор
нюансов
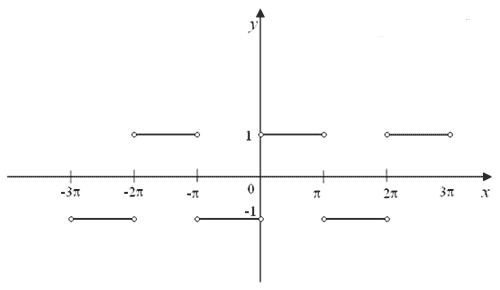
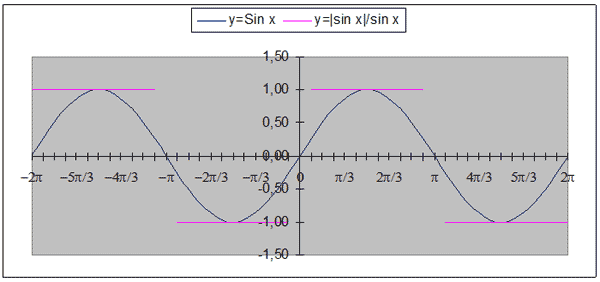
Один из учеников строил график y = |Sin x|
/ Sin x на промежутке [–360о;360о] с
шагом 15о. На доске демонстрируется этот
график и график, построенный традиционным
алгебраическим способом.
С помощью этого примера обращается внимание
учащихся, что существуют функции, графики
которых в электронных таблицах строятся неточно.
Учащихся можно попросить найти неточности в
графике, построенном с помощью MS Excel и попросить
объяснить их.
График, построенный традиционным
алгебраическим
График, построенный с использованием МS
Exel
6. Подведение итогов
Учеников просят ответить на вопросы:
- В чем достоинства и недостатки алгебраического
метода построения графиков функций и построения
графиков с использованием электронных таблиц? - Каким образом можно использовать полученные на
уроке знания в учебе?
Вывод. MS Excel облегчает построение
графиков функций, но без глубоких математических
знаний построить точные графики сложных функций
(тригонометрических функций, функций с модулем,
функций имеющих точки разрыва) невозможно.
Математика – это царица всех наук!
7. Постановка Д/З.
Построить график функции y= 1 + 0,5*ctg(X–П/4) на
промежутке [–360о;360о] с шагом 15о.
8. Рефлексия
Оцени свое настроение на уроке
Оценочный лист
|
Фамилия, имя |
Количество баллов |
| Создание заголовка таблицы |
0,2 |
| Заполнение ряда значений аргумента х в градусах |
0,1 |
| Заполнение ряда значений аргумента х в радианах (перевод градусов в радианы) |
0,5 |
| Запись формулы для вычисления значений сложной функции |
1 |
| Запись формулы для вычисления значений элементарной функции |
0,5 |
| Заполнение рядов значений функций (для обеих функций) |
0,1 |
| Установка числового формата данных |
0,2 |
| Построение графиков функций |
1 |
| Перенос оси |
0,2 |
| Подпись значений х на оси абсцисс (в градусах) |
0,2 |
| Создание ряда значений аргумента х (в радианах, например П/3) |
0,7 |
| Подпись значений х на оси абсцисс (в радианах, например П/3) |
0,5 |
|
ИТОГО |
5 |
| Если вы обращаетесь к учителю, то ставится 0 баллов |
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
- Нажмите по первой ячейке и впишите
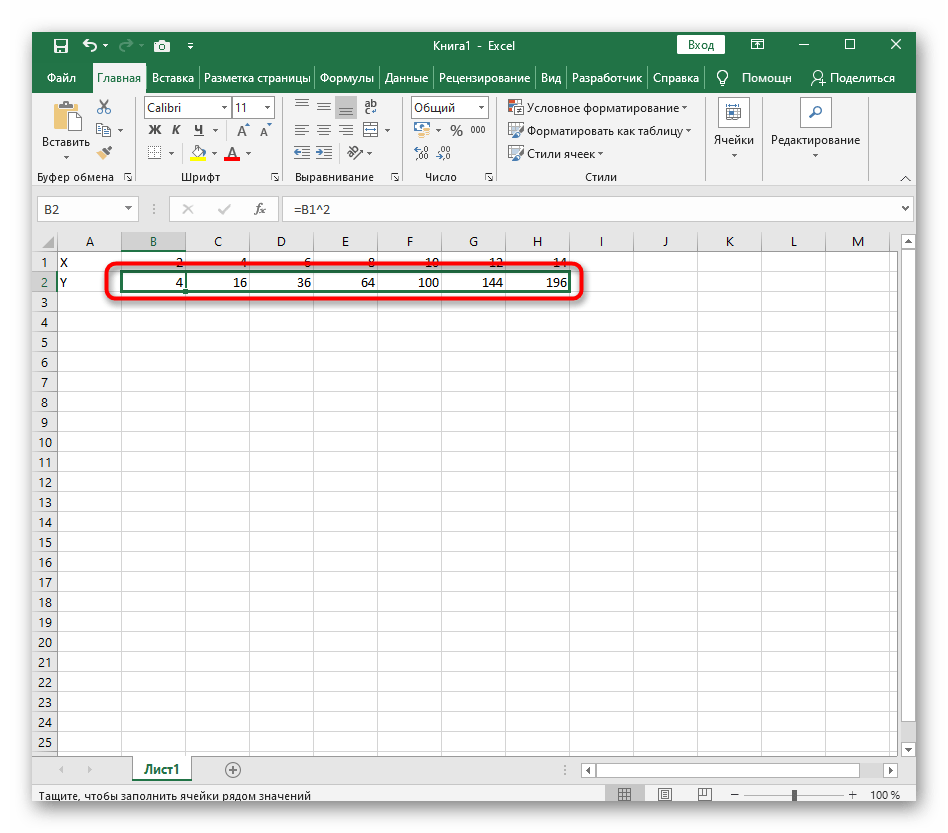
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
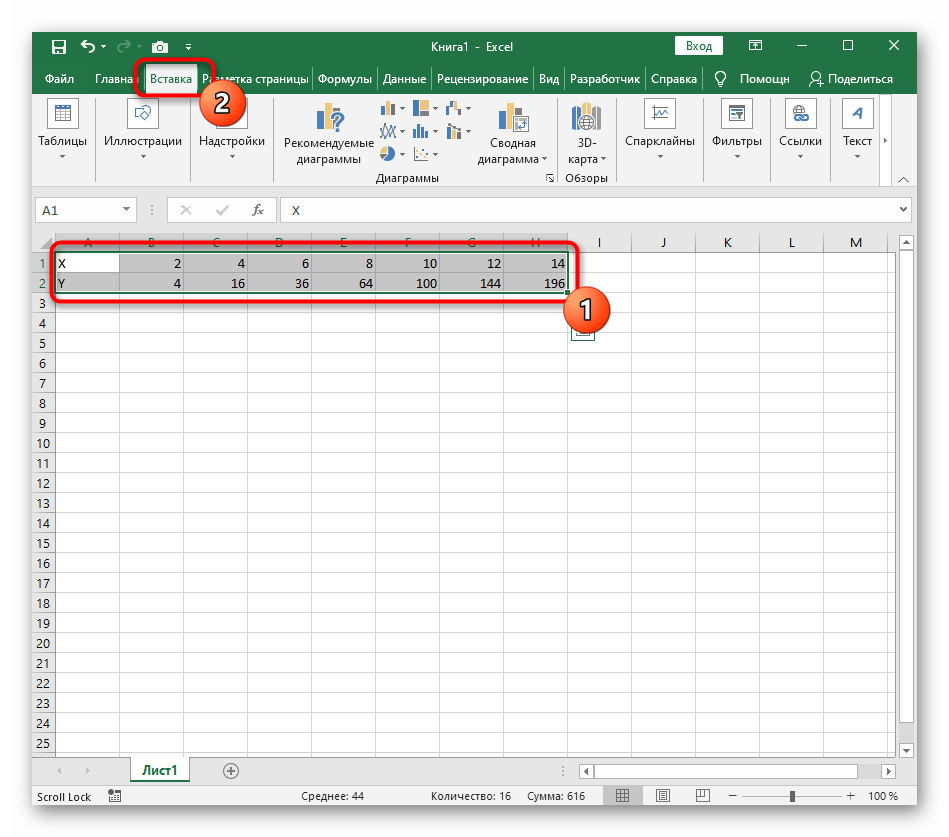
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
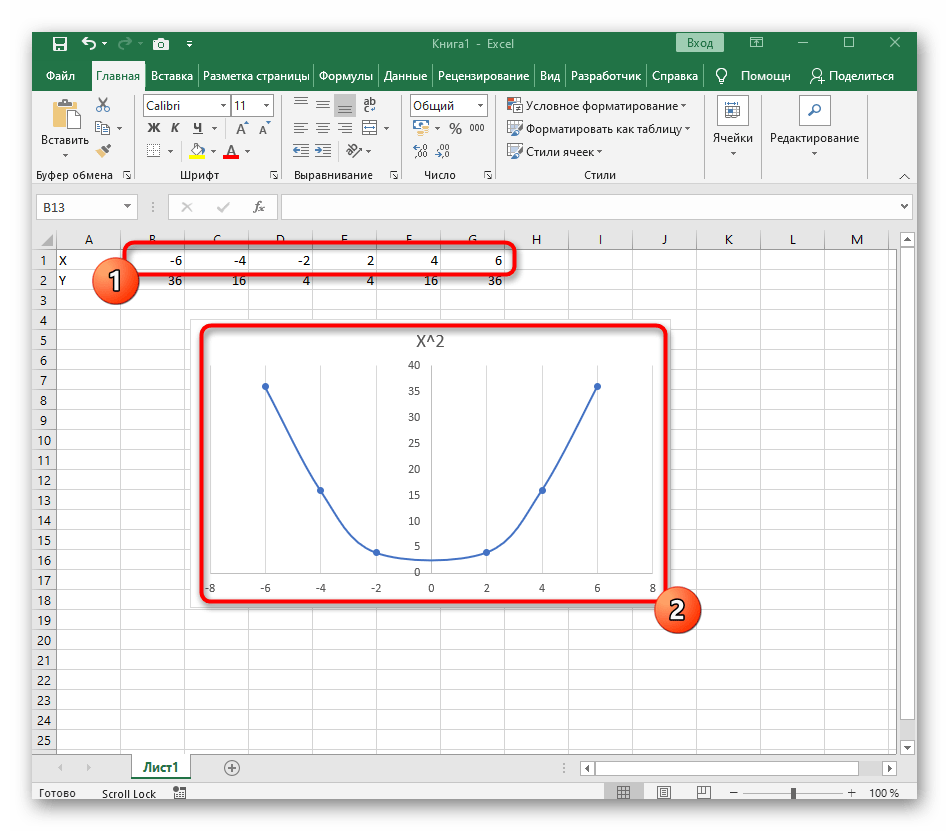
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
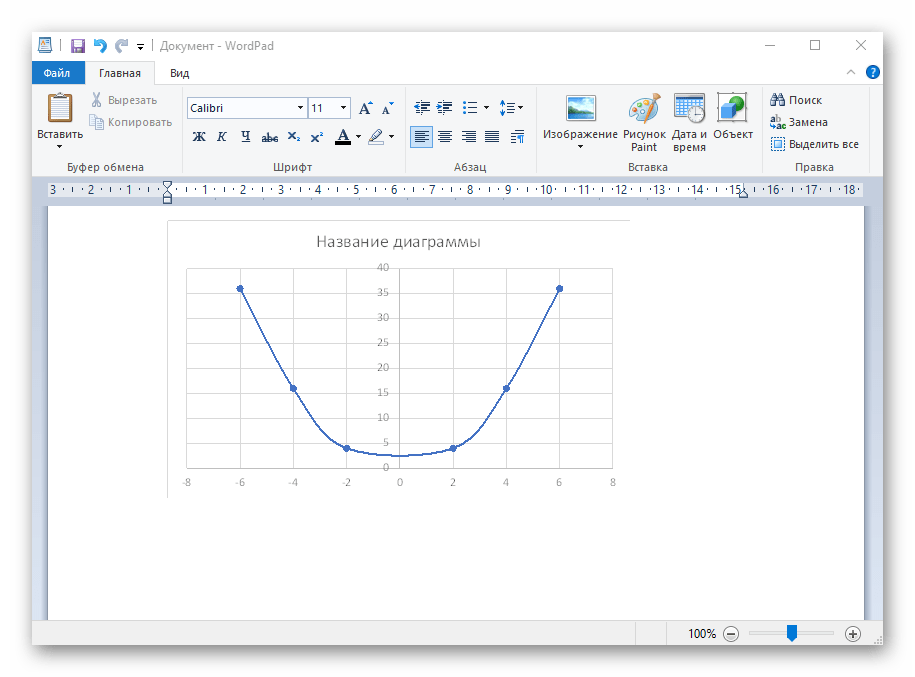
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме: