Построение графиков функций
1. Построить в разных системах координат при x [− 2, 2] графики функций
|
1 + x2 |
3 |
|||||||||||||||||
|
1 + x |
2 |
, x < 0 |
||||||||||||||||
|
, x ≤ 0 |
||||||||||||||||||
|
1 + x |
1 + x |
4 |
||||||||||||||||
|
2 |
−2x |
|||||||||||||||||
|
y = sin |
(x) + |
, |
g = |
, z |
= 2e |
, |
x [0;1] |
|||||||||||
|
1 + cos2 (x) |
||||||||||||||||||
|
2x |
x >1 |
|||||||||||||||||
|
1 + |
, x > 0 |
2sin(3x), |
||||||||||||||||
|
2 |
||||||||||||||||||
|
1 |
+ x |
|||||||||||||||||
|
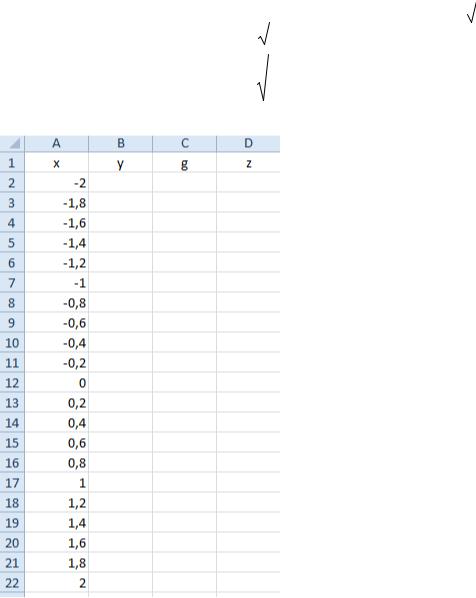
В ячейки A1:D1 записываем заголовки |
||||||||||||||||||
|
таблицы x, y, g ,z. |
||||||||||||||||||
|
Графики нужно |
построить |
в пределах |
||||||||||||||||
|
x [− 2, 2], возьмём шаг 0,2. |
Тогда x будет принимать значения -2, -1,8, -1,6, -1,4 и так далее до 2
В ячейку A2 введем первое значение -2, в ячейку A3 введем следующее значение — 1,8. Выделим эти две ячейки и протянем их до значения 2.
Вячейку B2 введем формулу для вычисления y(x) =SIN(A2)^2+(1+A2)/(1+COS(A2)^2)
Вячейку C2 введем формулу для вычисления g(x) =ЕСЛИ(A2<=0;(1+A2^2)/(1+A2^4)^(1/2);(1+2*A2/(1+A2^2))^(1/2))
Вячейку D2 введем формулу для вычисления z(x) =ЕСЛИ(A2<0;(1+A2^2)^(1/3);ЕСЛИ(A2<=1;2*EXP(-2*A2);2*SIN(3*A2)))
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
1 |
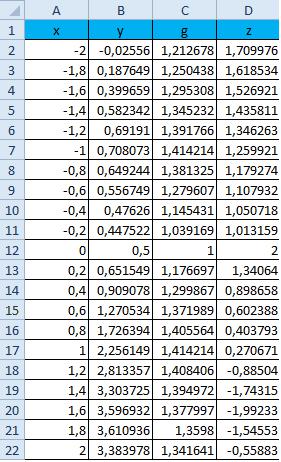
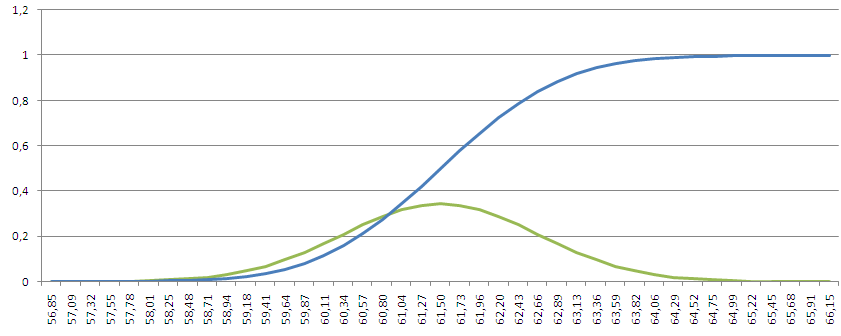
Ячейки B2, C2, D2 протянем вниз до значения x равного 2, в данном случае до 22 строчки. В результате, получим
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
2 |
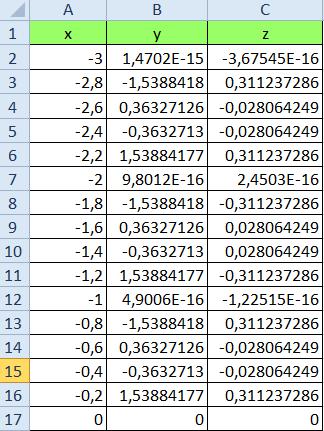
2. Построить в одной системе координат при x [− 3;0] графики функции
Y =2sin(2πx)cos(4πx) Z =cos3 (4πx)sin(πx)
На новом листе Excel в столбце A, протабулируем значения x в пределах от -3 до 0 с шагом 0,2.
В ячейку B2 введем формулу =2*SIN(2*ПИ()*A2)*COS(4*ПИ()*A2)
В ячейку C2 введем формулу =COS(4*ПИ()*A2)^3*SIN(ПИ()*A2)
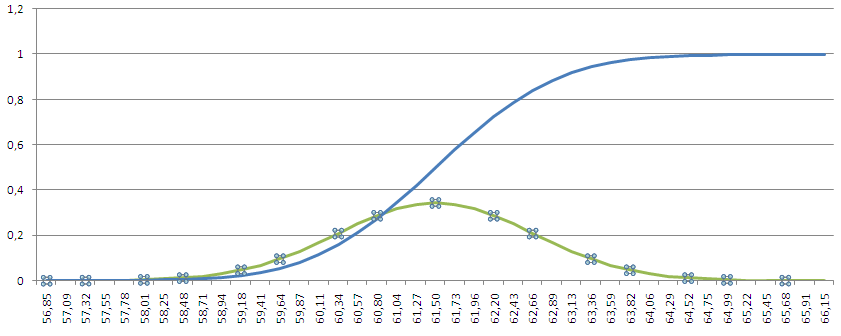
Ячейки B2, C2 протянем вниз до значения x равного 0, в данном случае до 17 строчки.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
3 |
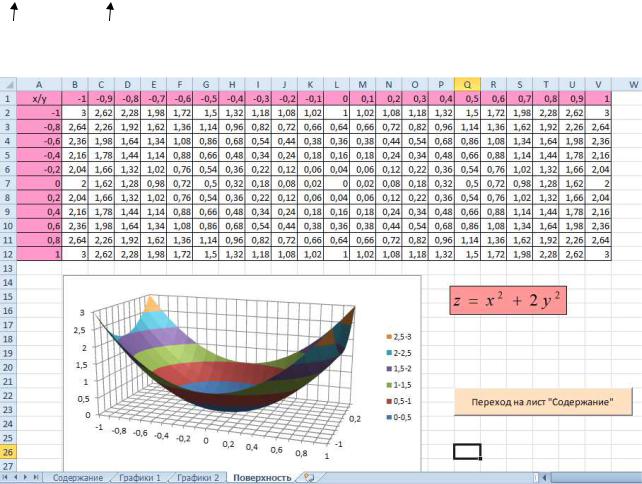
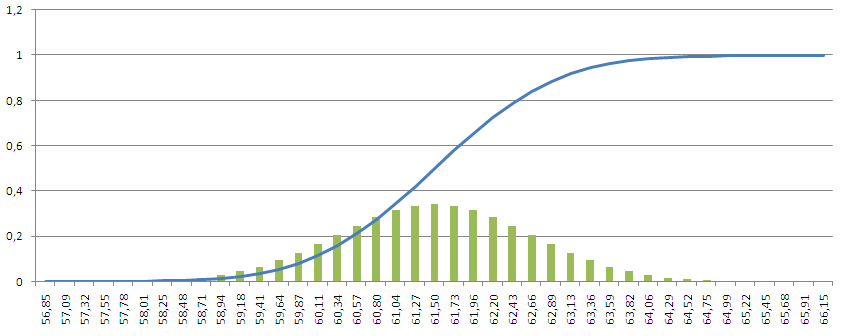
3. Построить поверхность z = x2 + 2y 2 при x [−1;1] В ячейку B2 введем формулу
=$A2^2+2*B$1^2
|
фиксируем |
фиксируем |
|
номер столбца |
номер строки |
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
4 |

Пользовательские функции.
Сохранить файл в формате *.xlsm (тип файла Книга Excel с поддержкой макросов)
Открыть редактор Visual Basic (Alt+F11) Добавить модуль Insert → Module
|
sin 2 (x) + |
1 + x |
||||||||||
|
1 + cos2 (x) |
|||||||||||
|
1 + x |
2 |
x ≤ 0 |
|||||||||
|
, |
|||||||||||
|
1 + x4 |
|||||||||||
|
1 + |
2x |
, x > 0 |
|||||||||
|
2 |
|||||||||||
|
1 + x |
|||||||||||
|
3 |
|||||||||||
|
1 + x |
2 , |
x < 0 |
|||||||||
|
2e−2x, |
x [0;1] |
||||||||||
|
x >1 |
|||||||||||
|
2sin(3x), |
|||||||||||
Y =2sin(2πx)cos(4πx)
Z =cos3 (4πx)sin(πx)
z = x2 + 2y 2
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
5 |
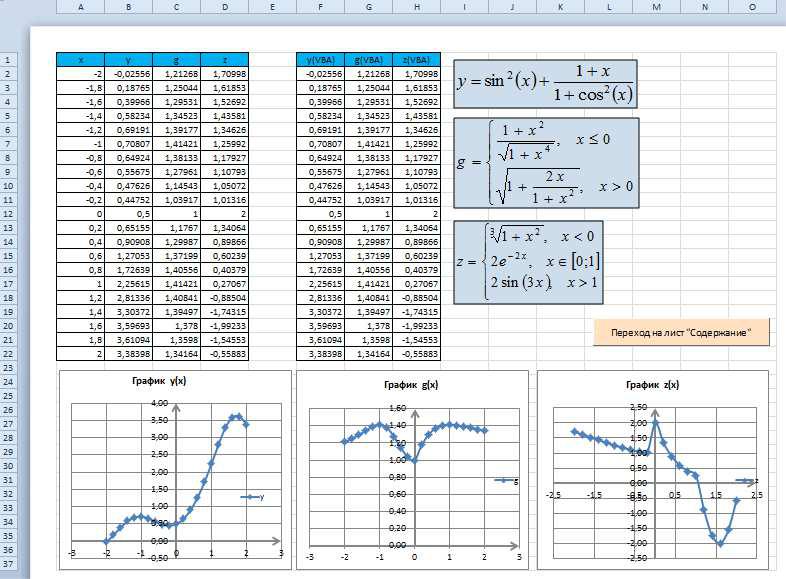
Построение графиков функций y(x), g(x), z(x) в разных системах координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
6 |
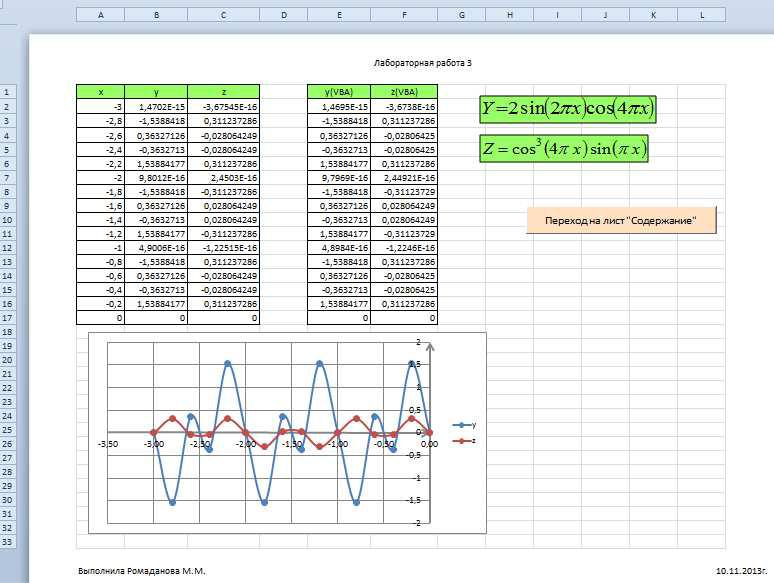
Построение графиков функций y(x), z(x) в одной системе координат
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
7 |
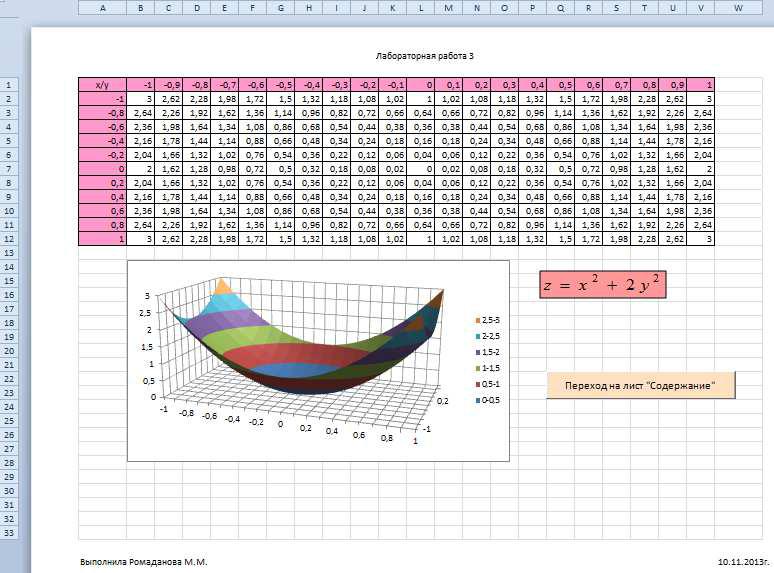
Построение поверхности z(x,y)
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
8 |
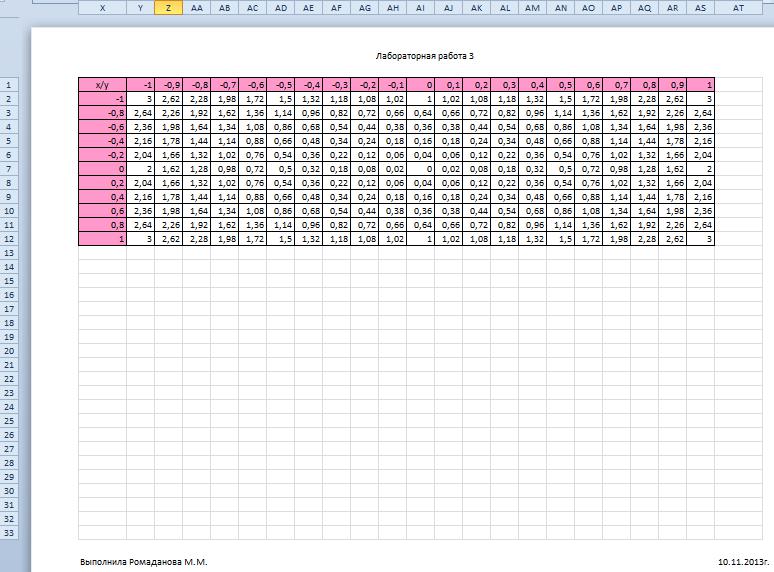
Поверхность z(x,y), построенная с помощью пользовательских функций. Должны получиться такие же значения, как и в предыдущей таблице.
|
Ромаданова М.М. |
|
|
Кафедра Прикладной математики и информатики СПбГАСУ |
9 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.03.2015511.29 Кб43.pdf
- #
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
|
1 / 1 / 1 Регистрация: 27.09.2016 Сообщений: 48 |
|
|
1 |
|
Построить в разных системах координат графики функций23.10.2016, 19:58. Показов 15017. Ответов 20
Построить в разных системах координат при х ϵ [-2; 2] графики функций. Помогите, заранее спасибо! Миниатюры
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
24.10.2016, 09:02 |
2 |
|
1. =(1+A2^2)/(1+2*A2^2)
2 |
|
2 / 2 / 0 Регистрация: 09.11.2015 Сообщений: 16 |
|
|
24.10.2016, 17:14 |
3 |
|
Почему бы не использовать маткад к примеру для построения графиков?) мне кажется что атм попроще это сделать. Хотя, кто как привык.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 10:49 |
4 |
|
Всем добрый день, уважаемые форумчане, со всеми новогодними праздниками! , может кто сталкивался, направьте на верный ход мыслей, пожалуйста.
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
08.01.2017, 11:34 |
5 |
|
Код y=(1+EXP(3*A2))^(1/4) g=ЕСЛИ(A2>0;2*A2^2*COS(A2)^2;(3+SIN(A2))/(1+A2^2)) с третим пробуем сами разобраться по аналогии второго. про построение смотрит похожие темы в форуме не раз обсуждалось. как вариант построение смотрим видео в теме в шапке (не полное совпадение).
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 13:05 |
6 |
|
нет, подобное не воспроизведу. .
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 13:43 |
7 |
|
графики построю сама, помощь нужна со значениями.
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
08.01.2017, 15:14 |
8 |
|
помощь нужна со значениями. для первых (задание «а») не дано значит берете произвольно. Добавлено через 5 минут Код 1,3 =ЕСЛИ(A2<0;ABS(A2)^(1/3);ЕСЛИ(A2<1;-2*A2+A2/(1+A2);ABS(3-A2)/(1+A2))) п.с. в 1,3 ошибка т.к. по условию получается 1 принадлежит двум условиям (второму и третьему). Добавлено через 3 минуты Код =2*SIN(ПИ()*A2)*COS(ПИ()*A2) =COS(ПИ()*A2)^2*SIN(3*ПИ()*A2) Добавлено через 3 минуты Код =2*$A6^2*COS($A6)^2-2*B$5^2
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
08.01.2017, 16:19 |
9 |
|
Огромное Вам спасибо.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
11.01.2017, 20:24 |
10 |
|
Vlad999, Вот что получилось, есть сомнения. Если не затруднит, посмотрите, пожалуйста.1.xls 2.xls 3
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
12.01.2017, 09:39 |
11 |
|
как то так. поверхность не настраивал.
1 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
12.01.2017, 19:08 |
12 |
|
Vlad999, спасибо Вам большое, очень помогли.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:43 |
13 |
|
Всем доброй ночи, уважаемые форумчане, как добавить вспомогательную ось в гистограмму в ексель 2003, смотрю, читаю примеры приведены в поисковике на более поздних версиях, у меня такого функционала нет.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:50 |
14 |
|
Вот как здесь, справа.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 22:52 |
15 |
|
И еще график, как добавит с данными, как на диаграмме.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 23:05 |
16 |
|
Вот что получилось у меня, нужно добавить график с данными и вспомогательную ось, затрудняюсь.
0 |
|
1 / 1 / 0 Регистрация: 07.01.2017 Сообщений: 11 |
|
|
13.01.2017, 23:07 |
17 |
|
Извините закачемтво фото.
0 |
|
0 / 0 / 0 Регистрация: 10.10.2019 Сообщений: 1 |
|
|
10.10.2019, 15:48 |
18 |
|
Буду благодарен, если решите) Миниатюры
0 |
|
2632 / 1637 / 745 Регистрация: 23.03.2015 Сообщений: 5,149 |
|
|
10.10.2019, 16:04 |
19 |
|
волололо, Вы хоть на верх этой темы заглядывали?
0 |
|
0 / 0 / 0 Регистрация: 28.01.2020 Сообщений: 4 |
|
|
30.11.2020, 12:47 |
20 |
|
Vlad999, Вы мне можете помочь с одним заданием?
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
30.11.2020, 12:47 |
|
Помогаю со студенческими работами здесь Построить в разных системах координат графики следующих функций Построить в разных системах координат при х ϵ [-1.8; 1.8] графики функций Построить в разных системах координат при x принадлежит [-1,7. 1,5] графики функций: построить в разных системах координат при x[-1,5;1,5] графики следующих функций с использо-ванием пользовательских функций
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 20 |
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2× 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
В дополнение привожу видео — где показан порядок действий, описанный выше.
Как совместить два графика в excel с разными координатами
Построение графиков в Excel стало очень простым занятием в Excel 2010 и Excel 2013 – для этого достаточно сделать 3 движения мышкой. Но при построении двух графиков в одной координатной оси может возникнуть сложность, если значения для графиков сильно отличаются.
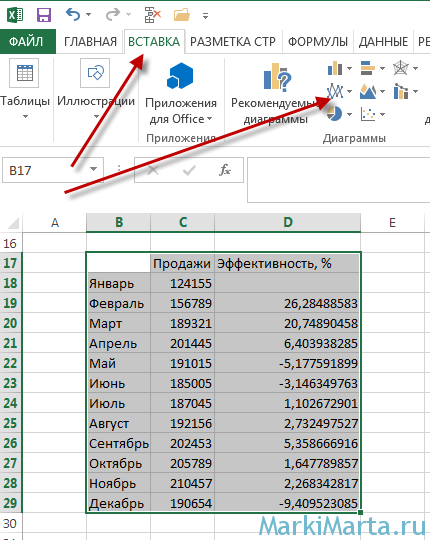
Для примера возьмем таблицу с показателями продаж и эффективностью и создадим для них график.
Как создать график в Excel?
Выделяете область, для которой хотите построить график, заходите в риббоне в закладку «Вставка», выбираете понравившийся график (Рис.1)
Рис.1. Как построить график в Excel
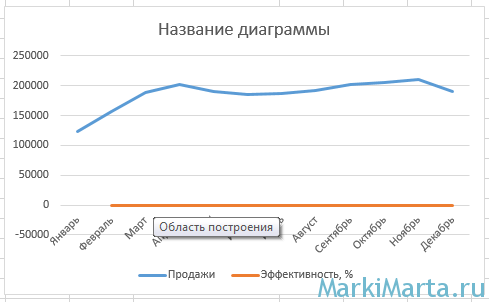
Если этим ограничиться, то результат вряд ли вас удовлетворит (Рис.2), т.к. график эффективности получился прямой линией. Это не удивительно, поскольку значения колонок «Продажи» и «Эффективность» отличаются на несколько порядков.
Рис.2. Неудовлетворительный вид графика
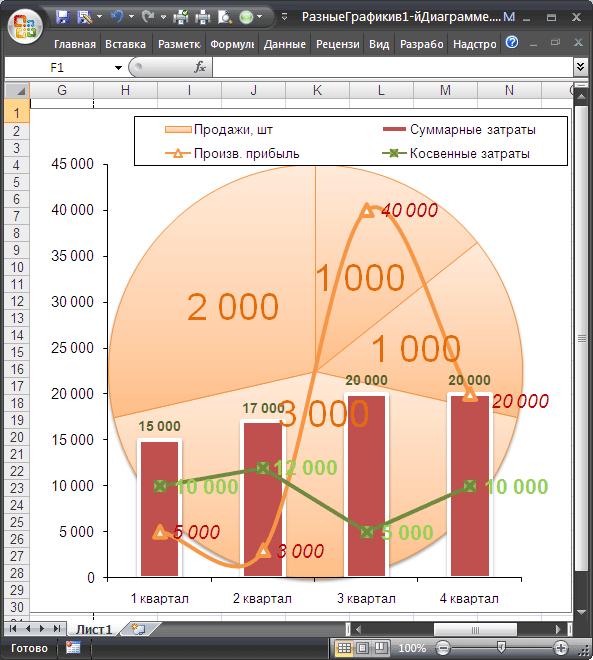
Чтобы в одной координатной плоскости Excel было отображено 2 графика с принципиально разными значениями, нужно добавить для одного из графиков так называемую «вспомогательную ось». Для этого нажмите правой кнопкой мыши на прямой график (на рисунке 2 – оранжевый график), в выпадающем меню выберите пункт «Формат ряда данных» и в открывшейся справа боковой колонке установите галочку около пункта «По вспомогательной оси» (см. анимацию ниже).
Совмещаем разные типы диаграмм в EXCEL
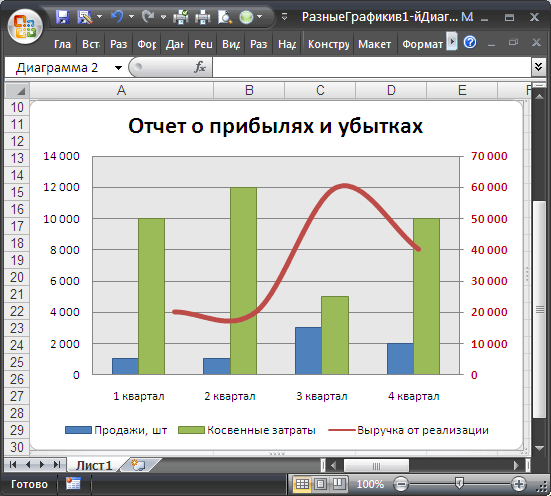
Иногда требуется на одной диаграмме совместить разные типы диаграмм, например гистограмму и обычную кривую:
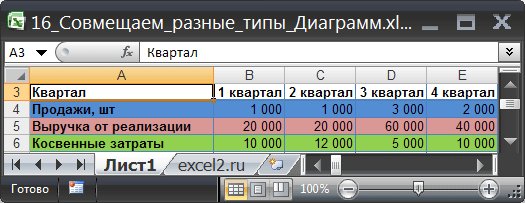
Исходные данные для диаграммы представлены в таблице (см. файл примера ):
Для наглядности цвет строки в таблице совпадает с цветом соответствующей диаграммы. Например, строка 5 «Выручка от реализации» (выделена бордовым цветом) соответствует бордовой кривой на диаграмме (см. самый верхний рисунок).
Алгоритм построения совмещенных диаграмм следующий:
- выделяем все данные, которые должны попасть в диаграмму (ячейки A3:E6 );
- в меню Вставка/ Диаграммы/ Гистограммы выбираем, например, Гистограмма с группировкой; в Конструкторе диаграмм меняем местами столбцы и строки ( Работа с диаграммами/ Конструктор/ Данные/ Строка-Столбец );
- на диаграмме выделяем столбцы, которые соответствует Выручке от реализации (эти столбцы будут иметь другой тип графика — отличный от гистограммы);
- через меню Работа с диаграммами/ Конструктор/ Тип/ Изменить тип диаграммы выбрать нужный тип.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Другой пример. Пусть на диаграмме имеется 2 графика:
Требуется из зеленого графика сделать гистограмму. Для этого выделите зеленый график.
Через меню Работа с диаграммами/ Конструктор/ Тип/ Изменить тип диаграммы выберите тип Гистограмма с группировкой , нажмите ОК.
Некоторые типы диаграмм могут не сочетаться — EXCEL предупредит Вас об этом.
Более сложный вариант совмещения разных типов диаграмм содержится в файле примера и представлен на рисунке ниже:
Совет : Т.к. для совмещения различных типов диаграмм требуется несколько рядов данных, то для углубленного изучения диаграмм полезно прочитеть статью Построение диаграмм с несколькими рядами данных в MS EXCEL
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.
Что показывает лепестковая диаграмма
Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).
В каких ситуациях полезна именно лепестковая диаграмма:
- нужна максимальная наглядность;
- необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
- важно показать на одном графике зависимость переменных величин от набора стабильных значений.
График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.
- На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
- Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
- После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.
* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.
Получаем такой рисунок:
* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.
Построение графика в полярной системе координат с помощью Excel
В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.
Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:
- для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
- значение ряда данных – расстояние от центра до маркера – величина радиуса;
- категория – угловая координата точки – наклон радиуса.
Известны следующие значения точек:
| π /8 | π /6 | π /4 | π /3 | 3π/8 | 5π/12 | π/2 | 7 π/12 |
| 5 π/8 | 4 π/6 | 3 π/4 | 5 π/6 | 7 π*8 | 11 π/12 | π |
Уравнение функции:
r = 3 * sin (6 * φ)/
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.
Формулы для заполнения первого столбца берем из таблицы значений точек:
В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:
На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке . Называем столбец «х», пишем первое значение «-3», второе – «-2,5». Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у», для удобства можно вписать всю формулу. Выделяем ячейку В2, ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6». Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х», в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у», переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная». Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси».
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений», поставьте маркер в пункте «фиксированное» и впишите значение «0,5».
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор», «Макет», «Формат».
Построить график функции в Эксель можно и с помощью «Графика». О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х».
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные».
В поле «Элементы легенды» кликаем на кнопочку «Добавить».
Появится окно «Изменение ряда». Поставьте курсор в поле «Имя ряда» и выделите ячейку С1. Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК».
Чтобы для первого графика в Легенде не было написано «Ряд 1», выделите его и нажмите на кнопку «Изменить».
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК».
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1, подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1».
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Поделитесь статьёй с друзьями:
Добрый день. А есть возможность в Excele создать график с тремя переменными, но на одном графике? 2 параметра как обычно, координаты х и у, а третий параметр чтоб отражался размером метки? Вот как пример, такой график —
Рубрика Excel
Также статьи о графиках в Экселе:
- Как сделать диаграмму в Эксель?
- Как сделать круговую диаграмму в Экселе?
- Как построить график в Экселе?
- Построение точечной диаграммы в Excel
В Экселе можно результаты расчетов отобразить в виде диаграммы или графика, придавая им большую наглядность, а для сравнения иногда нужно построить два графика рядом. Как построить два графика в Excel на одном поле мы далее и рассмотрим.
Начнем с того, что не каждый тип диаграмм в Экселе сможет отобразить именно тот результат, который мы ожидаем. К примеру, имеются результаты расчетов для нескольких функций на основе одинаковых исходных данных. Если по этим данным строить обычную гистограмму или график, то исходные данные не будут учитываться при построении, а лишь их количество, между которыми будут задаваться одинаковые интервалы.
Выделяем два столбца результатов расчетов и строим обычную гистограмму.
Теперь попробуем добавить еще одну гистограмму к имеющимся с таким же количеством результатов расчетов. Для добавления графика в Экселе делаем активным имеющийся график, выделив его, и на появившейся вкладке «Конструктор» выбираем «Выбрать данные». В появившемся окошке в разделе «Элементы легенды» нажимаем добавить, и указываем ячейки «Имя ряда:» и «Значения:» на листе, в качестве которых будут значения расчета функции «j».
Теперь посмотрим, как будет выглядеть наша диаграмма, если мы к имеющимся гистограммам добавим еще одну, у которой количество значений почти в два раза больше. Добавим к графику значения функции «k».
Как видно, последних добавленных значений гораздо больше, и они настолько малы, что их на гистограмме практически не видно.
Если изменить тип диаграммы с гистограммы на обычный график, результат получится в нашем случае более наглядным.
Если использовать для построения графиков в Экселе точечную диаграмму, то на полученных графиках будет учитываться не только результат расчетов, но и исходные данные, т.е. будет прослеживаться четкая зависимость между величинами.
Для создания точеного графика выделим столбец начальных значений, и пару столбцов результатов для двух разных функций. На вкладке «Вставка» выбираем точечную диаграмму с гладкими кривыми.
Для добавления еще одного графика выделяем имеющиеся, и на вкладке «Конструктор» нажимаем «Выбрать данные».
В новом окошке в графе «Элементы легенды» нажимаем «Добавить», и указываем ячейки для «Имя ряда:», «Значения X:» и «Значения Y:». Добавим таким образом функцию «j» на график.
Теперь добавим функцию «k», у которой совершенно другие исходные данные и их количество.
Как видно, на точечном графике функция «k» практически незаметна, но зато построена с учетом значений по обеим осям.
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества













 Построить в разных системах координат при х ∈[-1,8,1,8] графики следующих функций
Построить в разных системах координат при х ∈[-1,8,1,8] графики следующих функций