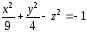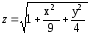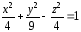Практическая
работа
Тема:
Построение диаграмм и графиков в электронных таблицах MS Excel.
Цель:
закрепление практических навыков по теме «Построение диаграмм и графиков в электронных
таблицах MS Excel».
Задачи:
Образовательная: формирование глубоких и прочных знаний по построению диаграмм и
графиков, формирование умений и навыков, носящих в современных условиях общенаучный
и общекультурный характер;
Развивающая:
развитие у школьников
теоретического, творческого мышления; формирования операционного мышления,
направленного на выбор оптимальных решений; развить навыки мыслительной
деятельности, включая каждого учащегося в учебно – познавательный процесс и
создание условия для работы каждого в индивидуальном темпе;
Воспитательная:
развитие
познавательной активности и интереса к предмету, воспитание информационной
культуры.
Программное
обеспечение: Windows, Microsoft Office.
Ход
работы:
Задание
1.
Представить данные
в виде круговой диаграммы:
 |
|||
 |
|||
Задание
2.

гистограммы:
Задание
3. Построить
графики функций: у = х3, у = 2х для х в диапазоне
[-4;4] с шагом 1и у = -2х2-2х+5 для х в диапазоне [-4;3] с шагом
0,5.

данные в виде двухрядной линейчатой диаграммы:
Задание
5. Построение
рисунка «Зонтик»
Приведены
функции, графики которых участвуют в этом изображении:
у1=
-1/18х2 + 12, хÎ[-12;12]
y2= -1/8х2
+6, хÎ[-4;4]
y3= -1/8(x+8)2
+ 6, хÎ[-12; -4]
y4= -1/8(x-8)2
+ 6, хÎ[4; 12]
y5=
2(x+3)2
– 9, хÎ[-4;0]
y6=1.5(x+3)2
– 10, хÎ[-4;0]
Порядок
выполнения действий:
1. Запустить
MS EXCEL
2. В ячейке А1
внести обозначение переменной х
3. Заполнить
диапазон ячеек А2:А26 числами от -12 до 12 с шагом 1, используя меню
(ЗАПОЛНИТЬ-ПРОГРЕССИЯ-ПО СТОЛБЦАМ).
4. Последовательно
для каждого графика функции будем вводить формулы.
Для у1= -1/18х2
+ 12, хÎ[-12;12]
5. Устанавливаем
курсор в ячейку В1 и вводим у1
6. В ячейку В2
вводим формулу
7. 
Enter
на
клавиатуре
8. Автоматически
происходит подсчет значения функции.
9. Растягиваем
формулу до ячейки В26
10. Аналогично
в ячейку С10 (т.к значение функции находим только на отрезке хÎ[-4;4]) вводим
формулу для графика функции y2= -1/8х2 +6.
и.т.д.
В
результате должна получиться следующая ЭТ
После
того, как все значения функций подсчитаны, можно строить графики этих функций.
1. Выделяем
диапазон ячеек А1:G26
2. На панели
инструментов выбираем меню Вставка → Диаграмма.
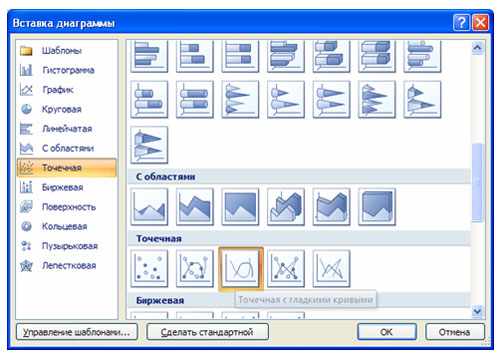
3. В окне
Мастера диаграмм выберите Точечная → Выбрать нужный вид→ Нажать Ok.
В
результате должен получиться следующий рисунок:
Выполнение
проекта:
Выберите себе один
из вариантов заданий на карточках и выполните проект по образцу, описав ход
выполнения работы по алгоритму, похожему на алгоритм выполнения Проекта
«Зонтик». Карточки с заданиями проектов для самостоятельного выполнения (обучающимся
таблица с решением не видна, доступны только уравнения функций, и изображение,
которое должно получиться в ходе выполнения работы, построения графиков фукций).
Домашнее
задание:
 |
Итог
урока:
Укажите в ВЫВОДЕ
после практической работы, достигли ли вы целей и задач нашего урока, получили
ли результат, удовлетворены ли вы результатом своей работы?
Список
литературы:
1.
И.Семакин, Е.К. Хеннер.
Задачник – практикум. Информатика и ИКТ в двух томах — М.: БИНОМ. Лаборатория
знаний, 2012;
2.
И.Семакин, Е.К. Хеннер.
Информатика, 11 класс-М.: БИНОМ. Лаборатория знаний, 2015
ВАРИАНТ№1
Задание
. Выполнить Проект «Очки» по образцу
1. y=-116(x+5)*(x+5)+2,
xЄ [-9;-1];
2. y=-116(x-5)*(x-5)+2,
xЄ [1;9];
3. y=-14(x+5)*(x+5)-3,xЄ[-9;-1];
4. y=-14(x-5)*(x-5)-3,xЄ[1;9];
5. y=–(x+9)*(x+9)+1,
xЄ[-9;-6];
6. y=–(x-9)*(x-9)+1,
xЄ[6;9];
7. y=-0,5*x*x+1,5,xЄ[-1;1];
|
x |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
|
-9 |
1 |
1 |
1 |
||||
|
-8 |
1,4375 |
-0,75 |
0 |
||||
|
-7 |
1,75 |
-2 |
-3 |
||||
|
-6 |
1,9375 |
-2,75 |
-8 |
||||
|
-5 |
2 |
-3 |
|||||
|
-4 |
1,9375 |
-2,75 |
|||||
|
-3 |
1,75 |
-2 |
|||||
|
-2 |
1,4375 |
-0,75 |
|||||
|
-1 |
1 |
1 |
1 |
||||
|
0 |
1,5 |
||||||
|
1 |
1 |
1 |
1 |
||||
|
2 |
1,4375 |
-0,75 |
|||||
|
3 |
1,75 |
-2 |
|||||
|
4 |
1,9375 |
-2,75 |
|||||
|
5 |
2 |
-3 |
|||||
|
6 |
1,9375 |
-2,75 |
-8 |
||||
|
7 |
1,75 |
-2 |
-3 |
||||
|
8 |
1,4375 |
-0,75 |
0 |
||||
|
9 |
1 |
1 |
1 |
ВАРИАНТ
№2
Задание
. Выполнить Проект «Лицо» по образцу
1. y=0,25*x*x-5,xЄ
[-6;6];
2. y=0,25*x*x-3,xЄ[-2;2];
3. y=-x*x+2,xЄ[-1;1];
4. y=0,33333*(x+3)*(x+3)+2,
хЄ[-5;-1];
5. y=0,2*(x-3)*(x-3)+2,хЄ[1;5];
6. y=-0,2*(x+3)*(x+3)+4,хЄ[-5;-1];
7. y=-0,2*(x-3)*(x-3)+4,хЄ[1;5];
8. y=-0,2*(x+3)*(x+3)+5,хЄ[-5;-1];
9. y=-0,2*(x-3)*(x-3)+5,хЄ[1;5];
10. y=-0,2*x*x+10,xЄ[-6;6];
|
x |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y9 |
y10 |
|
-6 |
4 |
2,8 |
||||||||
|
-5 |
1,25 |
3,333333 |
3,2 |
4,2 |
5 |
|||||
|
-4 |
-1 |
2,333333 |
3,8 |
4,8 |
6,8 |
|||||
|
-3 |
-2,75 |
2 |
4 |
5 |
8,2 |
|||||
|
-2 |
-4 |
-2 |
2,333333 |
3,8 |
4,8 |
9,2 |
||||
|
-1 |
-4,75 |
-4,75 |
1 |
3,333333 |
3,2 |
4,2 |
9,8 |
|||
|
0 |
-5 |
-3 |
2 |
10 |
||||||
|
1 |
-4,75 |
-4,75 |
1 |
2,8 |
3,2 |
4,2 |
9,8 |
|||
|
2 |
-4 |
-2 |
2,2 |
3,8 |
4,8 |
9,2 |
||||
|
3 |
-2,75 |
2 |
4 |
5 |
8,2 |
|||||
|
4 |
-1 |
2,2 |
3,8 |
4,8 |
6,8 |
|||||
|
5 |
1,25 |
2,8 |
3,2 |
4,2 |
5 |
|||||
|
6 |
4 |
2,2 |
3,2 |
2,8 |
ВАРИАНТ№3
Цель работы:
- научиться строить графики в Excel;
- развить самостоятельность;
- развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;
Оборудование:
- ПЭВМ, сеть, проектор;
- опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.
| Этапы | План урока + опорный конспект | Средства обучения |
| I | Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока. |
— |
| II | Повторение.
Фронтальный опрос изученного материала. Вопросы:
|
проектор |
| III | Объяснение нового материала и подготовка к практической работе:
|
Проектор, раздаточный материал |
| IV | Выполнение проектной практической работы:
|
Компьютер |
| V | Итоги:
|
Проектор, раздаточный материал, компьютер |
Опорный конспект
Построение совмещенных графиков в Microsoft Office Excel -2007.
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
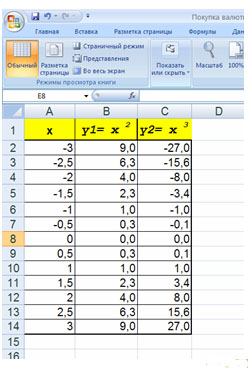
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
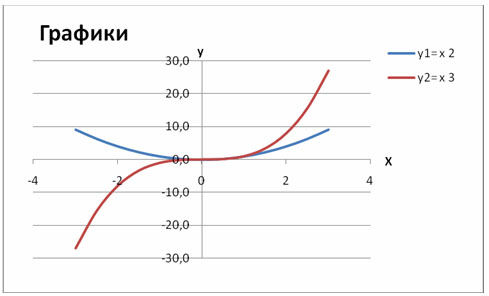
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
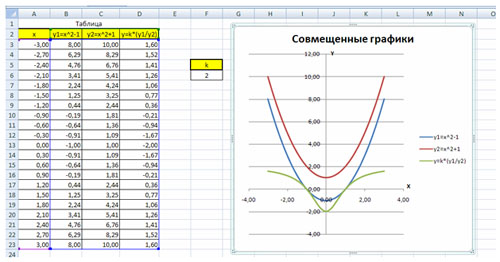
Построить графики функций y1= x 2 -1, y2= x 2+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
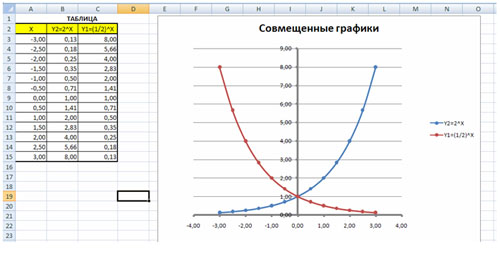
Построить графики функций y1= и y2= 2х на интервале [- 3 ; 3] с шагом 0,5.
ВАРИАНТ 3
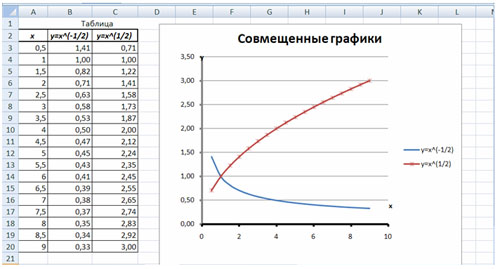
Построить графики функций y1= , y2=
на интервале [- 0,5 ; 9] с шагом 0,5.
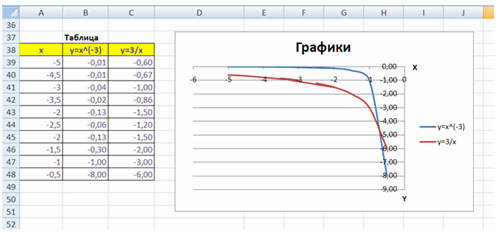
ВАРИАНТ 4
Построить графики функций y1=, y2=
на интервале [- 5 ; -0,5] с шагом 0,5.
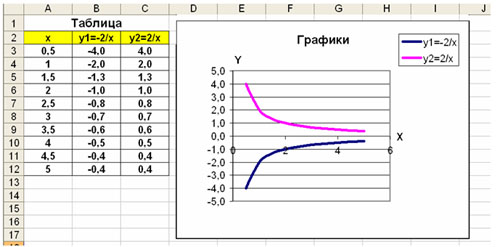
ВАРИАНТ 5
Построить графики функций y1= , y2=
на интервале [0,5 ; 5] с шагом 0,5.
Лабораторная работа
№2
Тема:
«Вычисление
функций одной переменной в Excel»
Цель
занятия:
получить практические навыки вычисления
функций одной переменной у=f(x)
и построения их графиков в Excel
Отрабатываемые
вопросы:
1.Создание
формул для вычисления функций одной
переменной.
2.Построение
графиков функций.
Организационно
– методические указания
В Excel
удобно осуществлять построение различных
функций на плоскости и поверхностей в
пространстве.
1.Построение
прямой.
Рассмотрим построение данной функции
в Excel
на примере уравнения у=2х+1
в диапазоне
: х[0; 3]
с шагом х=0,25. Решение
задачи
включает следующие этапы.
1.1. Ввод данных.
Для этого
значения аргумента Х
и функции У
следует
представить в таблице, первый
столбец
которой будет заполнен значениями Х ,
а второй
– функцией У.
Для этого в
ячейку А1 вводим заголовок Аргумент,
а в ячейку В1
– заголовок Прямая.
В ячейку А2 вводится
первое значение аргумента 0,
а в ячейку A3
вводится второе значение аргумента с
учетом шага построения (0,25).
Затем, выделив
блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее вводим
уравнение прямой: в ячейку В2 вводим
формулу: =2*A2+1,
затем копируем
эту формулу в ячейки В2:В14. В результате
должна быть получена следующая таблица
исходных данных и результатов (рис.1.) .
Рис.1.Построение
прямой
1.2. Построение
графика функции. Выделите диаграмму и,
используя вкладку Вставка
График, постройте
график
функции у=2х+1
(рис.2.).
Рис.2. График прямой
1.3.
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
2.Решение
уравнения второго порядка.
Примерами уравнений второго порядка
являются: парабола,
гипербола, окружность,
эллипс и другие.
В качестве
примера рассмотрим построение параболы
вида: у =х2
в диапазоне
х[–3;
+3] с шагом х=0,5.
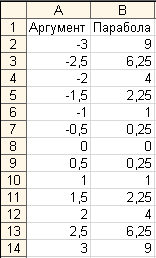
2.1. Ввод данных.
В ячейку А2
вводится первое значение аргумента
(-3), в
ячейку A3 вводится второе значение
аргумента (–2,5),
а затем, выделив
блок ячеек А2:АЗ,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее в ячейку В2
вводим уравнение =А2*А2,
а затем копируем
эту формулу в диапазон В2:В14. В результате
должна быть получена следующая таблица
исходных данных.
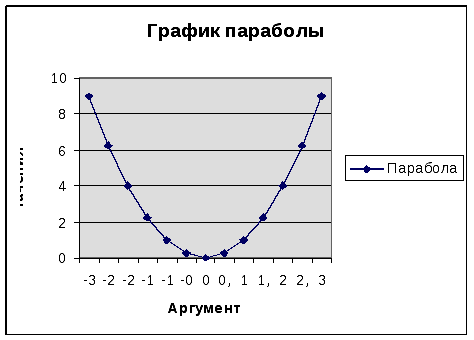
2.2.Построение
графика функции. Используя вкладку
Вставка
ДИАГРАММА, постройте
график
функции у=х^2
(РИС.4).
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
Рис.3. Построение
параболы
Рис.4.График параболы
Рис.5. График
гиперболы
3.Построение
гиперболы.
В простейшем
случае уравнение гиперболы имеет вид
y=k/x.
Задача построения гиперболы аналогична
построению параболы.
Рассмотрим
построение гиперболы y=1/x
в диапазоне х[0,1:
10,1] с шагом х=0,5. Выполните
все вышеуказанные действия самостоятельно
(рис.5).
Задания для
самостоятельного выполнения
-
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции Зх–5у+15=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции У=е2х в диапазоне х[0.1;
2] с шагом =0,2. -
Построить график
функции У=2х в диапазоне х[–2;
2] с шагом =0,5. -
Построить график
функции У=lnx в диапазоне х[0.5;
10] с шагом =0,5. -
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции y=2cos3x в диапазоне х[0.1;
1.8] с шагом =0,1. -
Построить график
функции y=x2 в диапазоне х[–3;
3] с шагом =0,25. -
Построить график
функции y=1/2x в диапазоне х[0.1;
10] с шагом =0,25. -
Построить верхнюю
часть параболы у2=х в диапазоне x[0;
4] с шагом =0,25. -
Построить гиперболу
y =1/2х в диапазоне х
[0,1; 5,1] с шагом =0,25 -
Построить верхнюю
полуокружность эллипса x4/4+у2=1 в диапазоне
х
[–2,25; 2,25] с шагом =0,25. -
Постройте параболу:
у2=6х в диапазоне х
[0; 4] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы. -
Постройте параболу:
х2=8у в диапазоне x
[–2,25; 2,25] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы.
ЛАБОРАТОРНАЯ
РАБОТА №3
Тема:
Вычисление сложных функций в Excel
Цель
занятия:
получить практические навыки вычисления
сложных функций от двух переменных z
= f(x,у)
и построения их графиков в Excel.
Отрабатываемые
вопросы.
1.Создание
формул для вычисления функций от двух
переменных.
2.Построение
графиков типа поверхностей в трехмерном
пространстве.
Организационно
– методические указания
В качестве примера
рассмотрим построение поверхностей
второго порядка таких как: эллипсоид,
гиперболоид, параболоид и т.п.
1.
Рассмотрим
построение эллипсоида в Excel
в соответствии с уравнением:
Пусть необходимо
построить верхнюю часть эллипсоида,
лежащую в диапазонах: х[–3;
3], у[–2;
2] с шагом =0,5
для обеих переменных.
Решение данной
задачи включает следующие этапы.
1.1.Вначале необходимо
разрешить уравнение относительно
переменной z:
1.2.Ввести значения
переменных х
(по вертикали)
, начиная с
ячейки А2
и у (по
горизонтали) , начиная с ячейки B1:
-
в ячейку А2
вводится первое значение аргумента (х
= –3),
затем в ячейку A3
вводится второе значение аргумента (х
= –2,5)
и,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента х
(за правый нижний угол блока протягиваем
до ячейки А14). -
значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
(у = –2),
в ячейку С1
вводится второе значение переменной
( у = –1,5)
, а затем,
выделив блок ячеек В1:С1,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки J1).
1.3.Вычисление
значений функции z.
Для этого
курсор необходимо поместить в ячейку
В2
и вызвать Мастер
функций. В
появившемся диалоговом окне Мастер
функций — шаг 1 из 2
слева в поле Категория
выбираем Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В диалоговом окне Корень
в рабочем
поле вводим подкоренное выражение: 1
— $А2^2/9 — В$1^2/4.
Обратите
внимание, что символы $
предназначены для фиксации адреса
столбца А
— переменной х
и
строки 1
— переменной у.
Нажимаем
кнопку ОК
и в ячейке В2
появляется « #ЧИСЛО!»,
так как при значениях х
= –3 и у
= –2 точек
рассматриваемого эллипсоида не существует
(рис 1.).
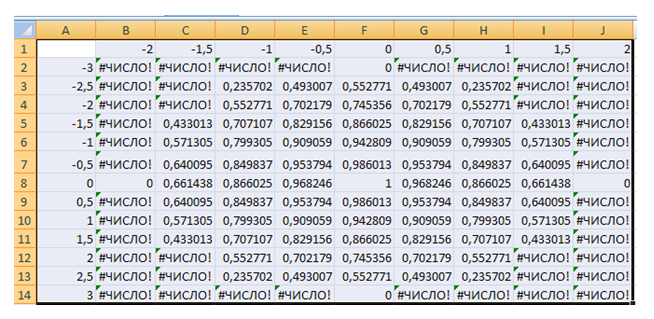
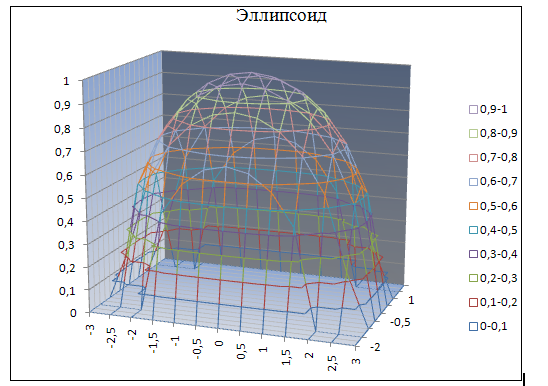
Рис.1. Построение
эллипсоида
1.4.Копирование
значений функции из ячейки В2,
для чего автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
а затем протягиванием вниз копируем в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица всех точек
эллипсоида (рис.1).
1.5.Построение
диаграммы. Выделяем полученную таблицу
(A1:
J14),
вызываем вкладку Вставка
и в группе
Диаграммы
выбираем
График
Все типы диаграмм
окно
Вставка диаграмм. В
данном окне выбираем Поверхность
тип
Проволочная поверхность и
нажимаем ОК,
в результате
получаем поверхность эллипсоида (рис.2).
Далее,
используя
средства
Работа с диаграммами , оформляем
полученную поверхность. Например,
вкладки Стенка
и Основание диаграммы
позволяют определить их цвета. Для этого
выберите опцию Дополнительные параметры
стенок и вид заливки, название диаграммы
и т.п. Выполните данные действия
самостоятельно.
2.
Рассмотрим
построение гиперболоида следующего
вида:
Пусть необходимо
построить верхнюю часть гиперболоида,
лежащую в диапазонах:
х[–3;
3], у[–2;
2] с шагом
=0,5
для обеих переменных.
2.1.Вначале необходимо
преобразовать уравнение относительно
переменной Z:
Рис.2. Поверхность
эллипсоида
2.2.Введем значения
переменной х
в столбец
А.
Для этого в ячейку А1
вводим символ x,
в ячейку А2
вводится первое значение аргумента х
= –3, а в
ячейку A3
— второе значение аргумента х = –2,5
. Затем,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки А14).
Значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
у= –2,
в ячейку С1
— второе значение переменной у
= –1,5,
а затем, выделив
блок ячеек В1:С1,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки J1).
2.3.Вычисление
значения переменной Z.
Для этого
табличный курсор необходимо поместить
в ячейку В2
, вызвать Мастер
функций, в
поле Категория
выбрать Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В рабочее поле вводим подкоренное
выражение: 1
+ $А2^2/9 + В$1^2/4 и
нажимаем
кнопку ОК.
В ячейке В2
появляется
1,732051.
Теперь необходимо
скопировать функцию из ячейки В2.
Для этого автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
после чего протягиванием вниз — в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица точек гиперболоида
(рис.3.):
Рис.3. Построение
гиперболоида
Построение диаграммы
гиперболоида выполните самостоятельно
по аналогии с эллипсоидом. Ниже на рис.4
приведен вариант диаграммы гиперболоида
, построенного на основании данной
таблицы.
Рис.4.
Диаграмма гиперболоида
Задания для
самостоятельного выполнения
1.Построить верхнюю
часть эллипсоида:
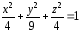
Диапазоны изменения
переменных х
и у: х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
2.Построить верхнюю
часть однополостного гиперболоида:
Диапазоны изменения
переменных х
и у:
х[–3;
3] с шагом =0,5,
у[–4;
4] с шагом =1.
3.Построить
эллиптический параболоид:

Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
4.Построить верхнюю
часть конуса
Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у [–3;
3] с шагом =1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Был в сети 07.04.2023 09:00

Куликовский Максим Юрьевич
преподаватель
10 546
2 245
13.12.2018 08:46
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»
-
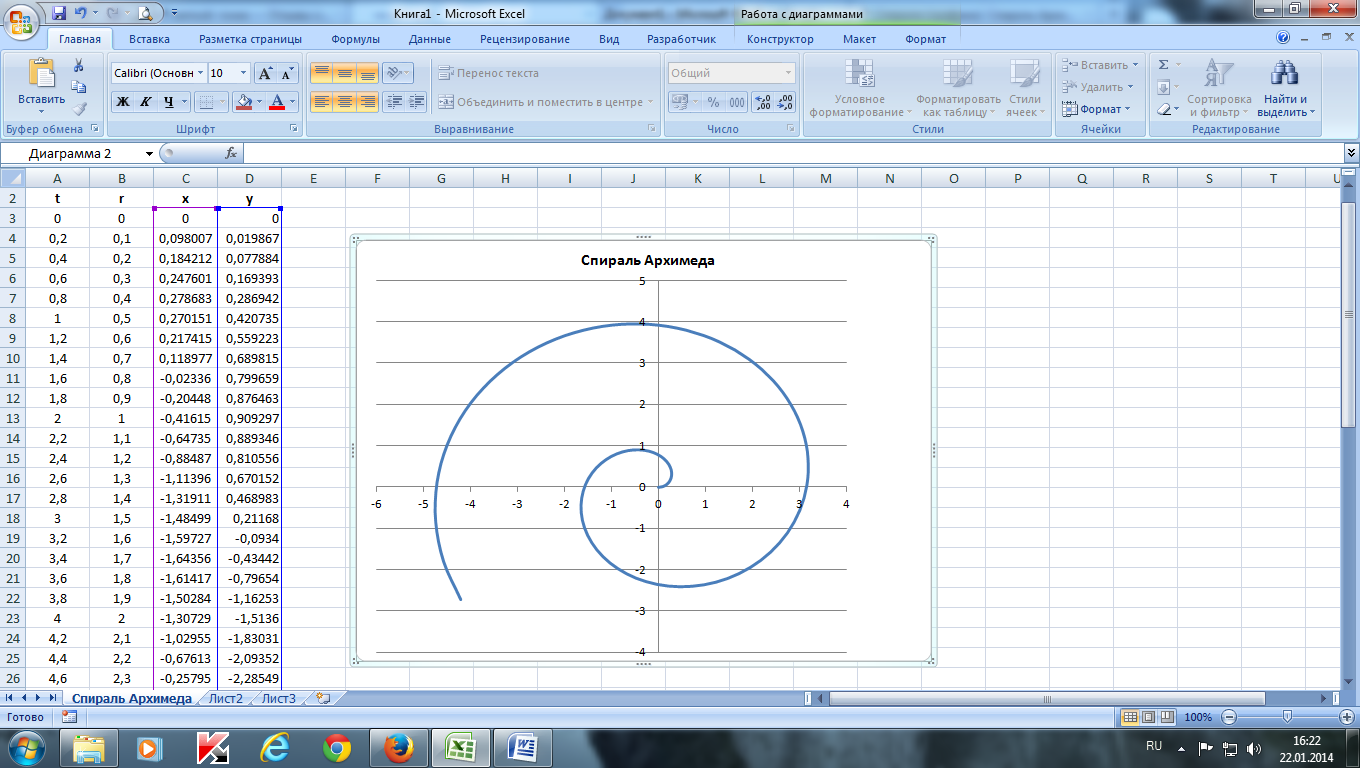
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
-
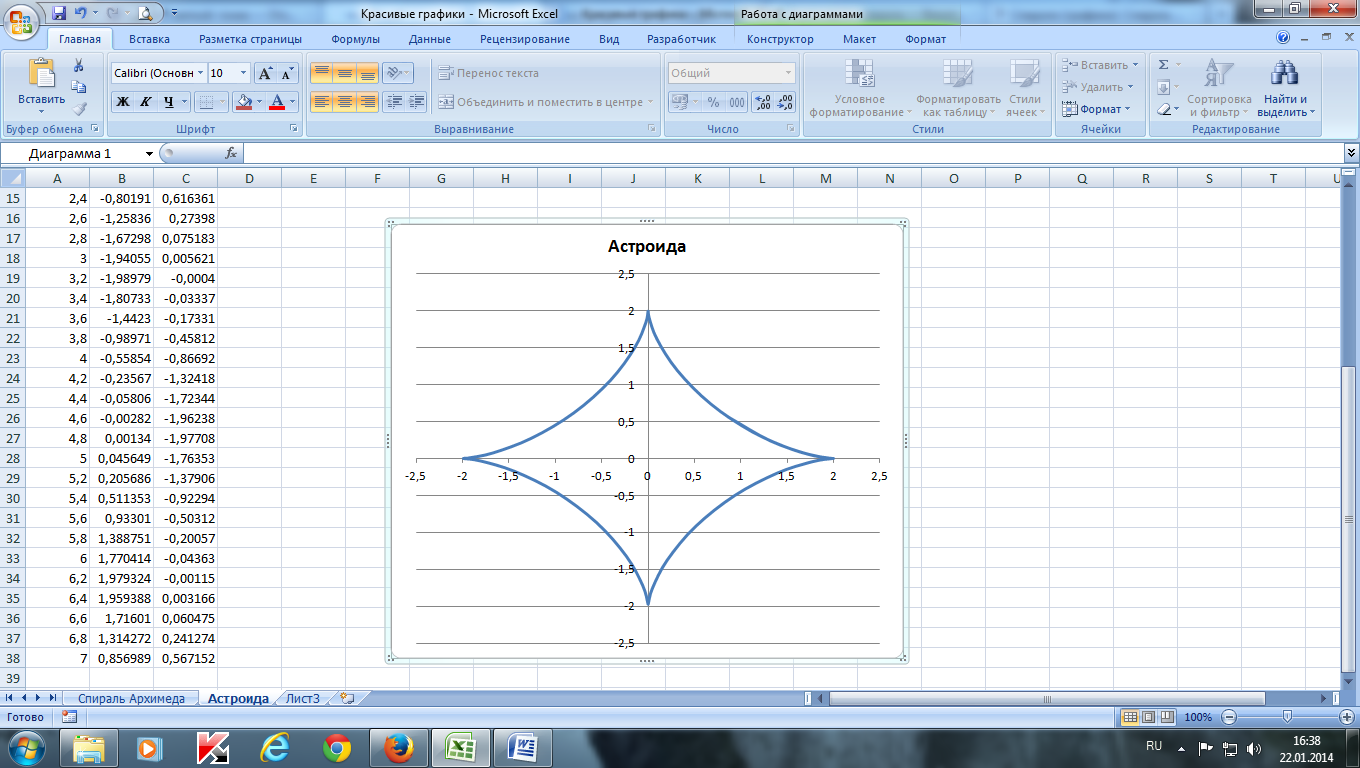
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t))3
— в столбце С – значения y = 2*(sin (t))3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
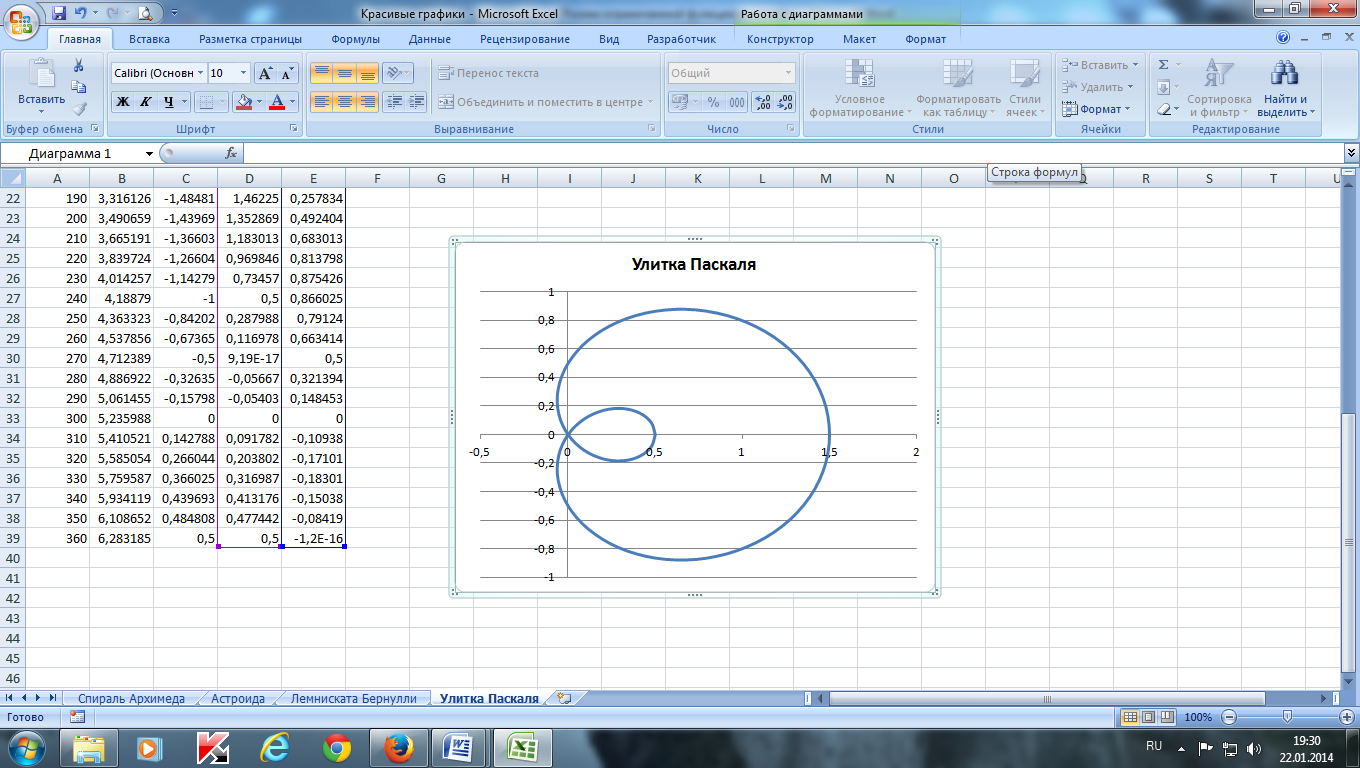
-
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми) -
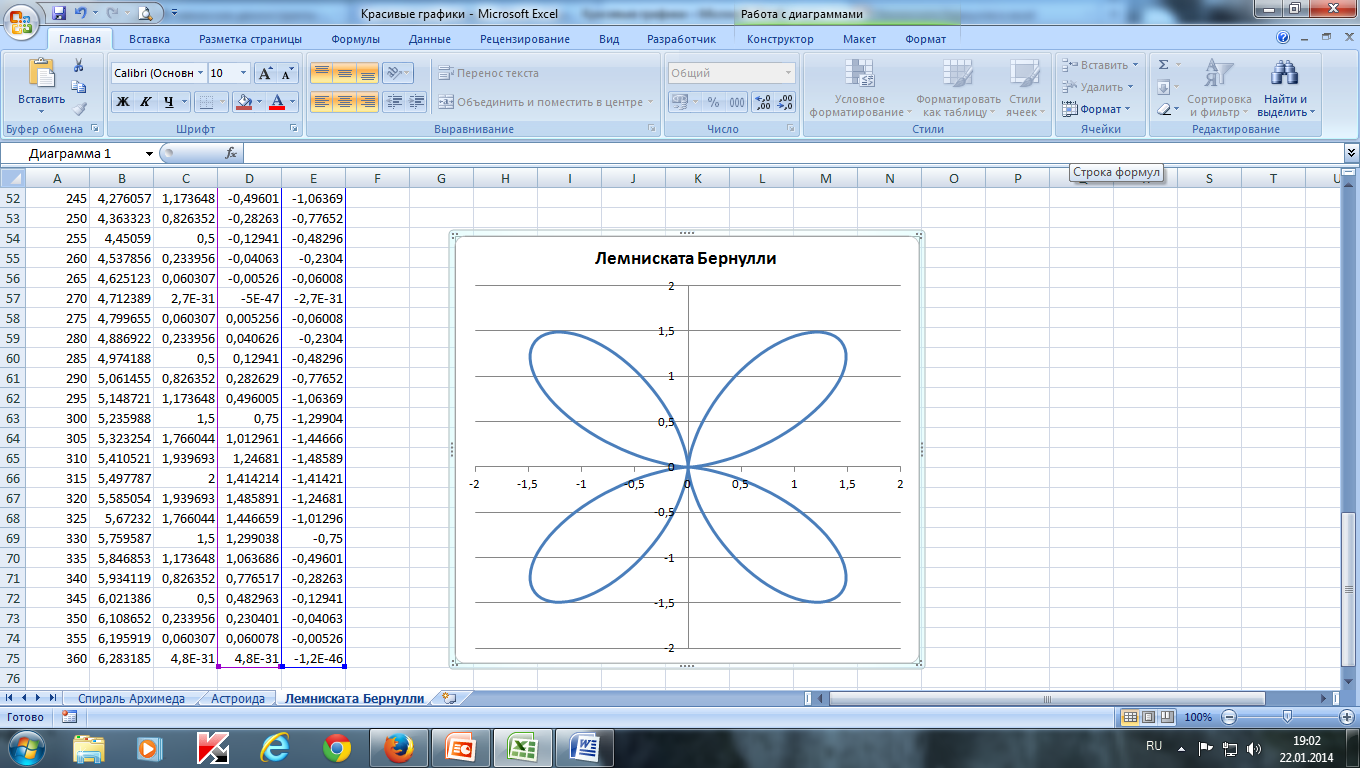
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t)2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
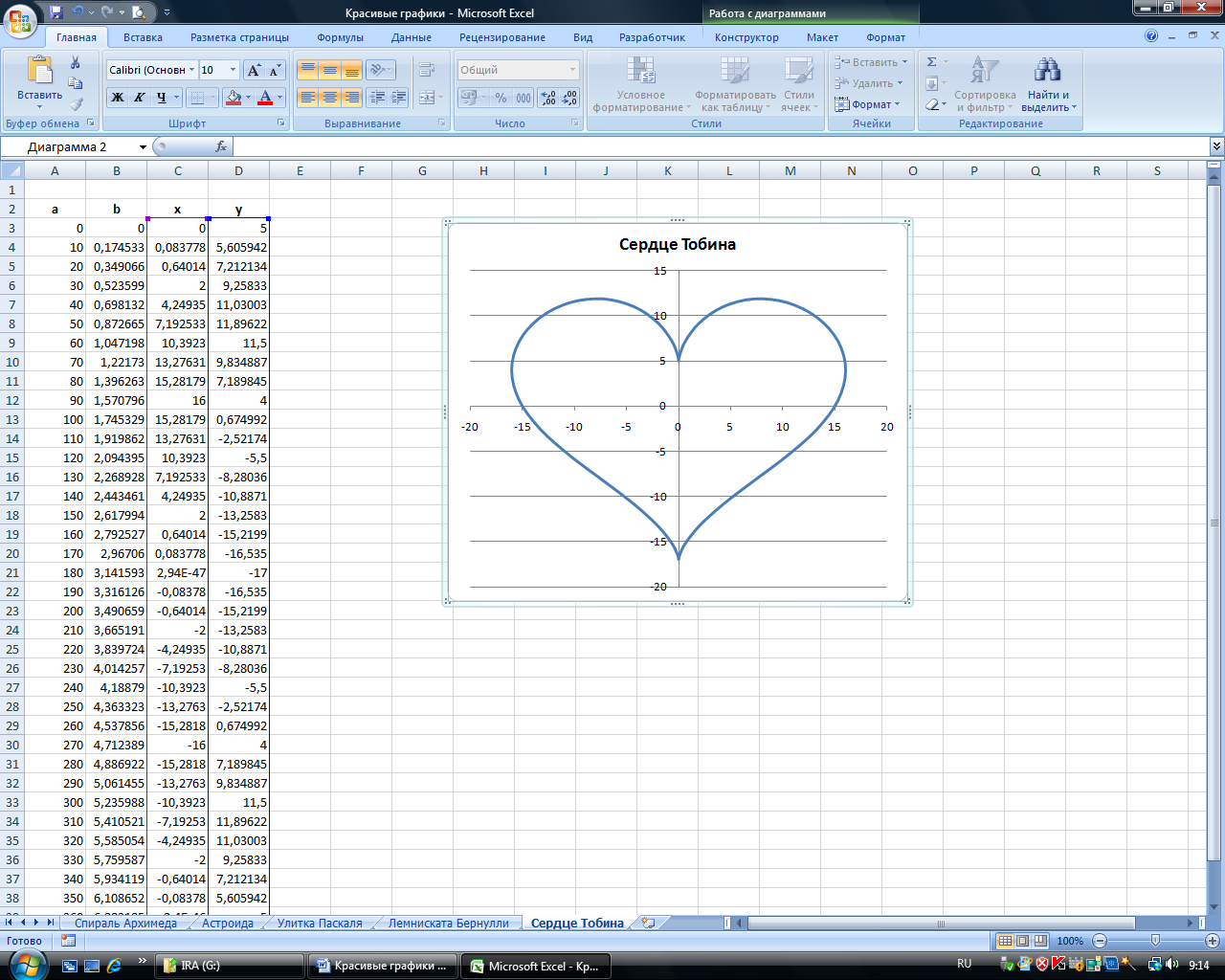
-
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t))3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
По теме: методические разработки, презентации и конспекты
Практическая работа «Взаимное расположение графиков линейных функций»
Построить в одной системе координат графики функций у=3х и у=3х-4, заполнить таблицу 1. Построить в одной системе координатграфики функций у=-2х и у=3х-4, заполнить таблицу 2. Сделать выводы о взаимно…
Материалы открытого урока «Построение графиков функций в MS Excel 2007»
Разработан урок построения графиков сложных функций в пакете MS Excel 2007, лабраторная работа, дополнительные методические элементы. На уроке необходимо использовать эвристические методы обучения и м…
Практическая работа по теме «Финансовые функции Excel»
Дидактический материал практическая работа по теме «Финансовые функции Excel» предназначена для студентов 2 курса колледжа .Для выполнения работы используется программа Microsoft Excel ….
Урок «Условная функция в Microsoft Excel»
Урок «Условная функция в Microsoft Excel»…
Презентация «Условная функция в Microsoft Excel»
Презентация «Условная функция в Microsoft Excel»Цель урока: научить учащихся применять условную функцию в Microsoft Excel. Отработать умения использования условной функции при реше…
Построение графиков функций в Microsoft Excel
Ознакомление с возможностями табличного процессора Excel, построение графиков функций в MS Excel….
ПРАКТИЧЕСКАЯ РАБОТА ПО ТЕМЕ «ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЁ ГРАФИК»
Цель работы: Отработать на практике построение графика линейной функции y=kx+b….