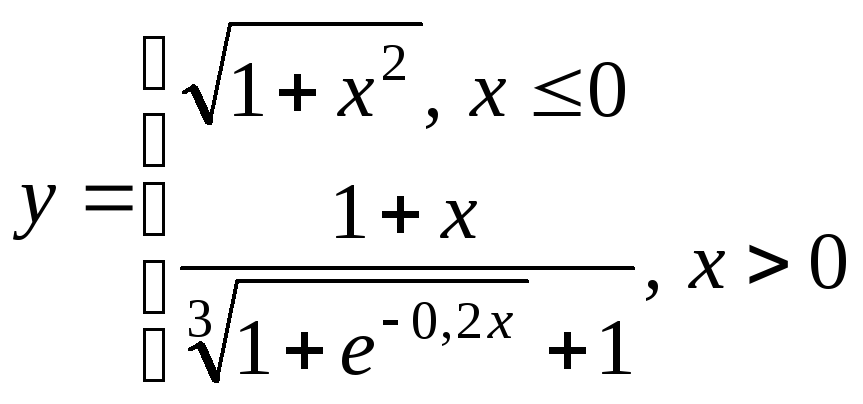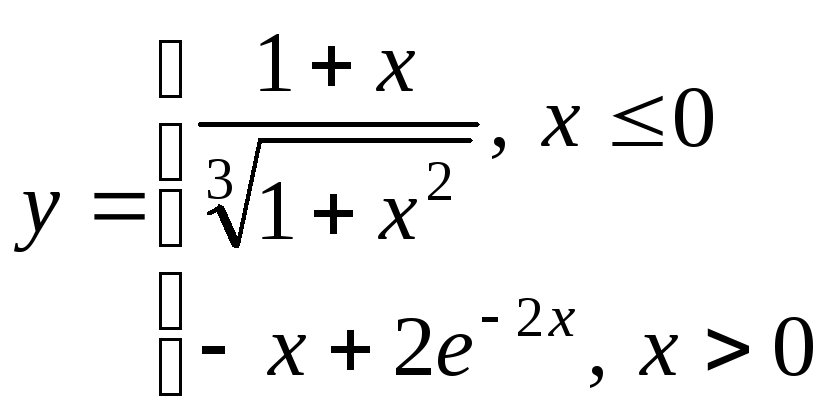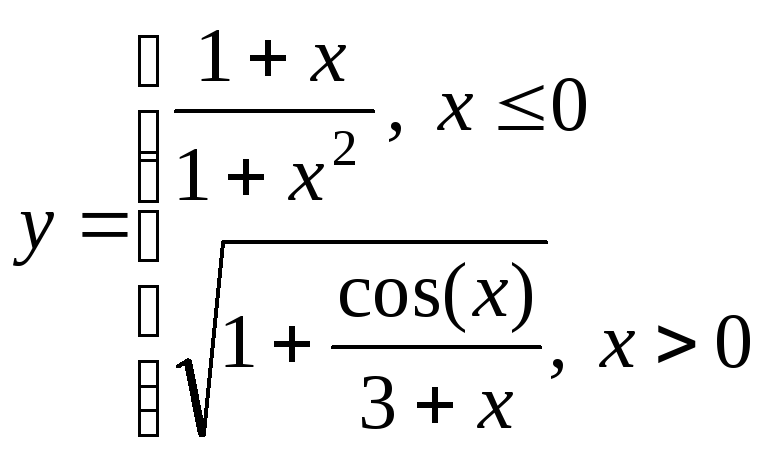Построить график функции с двумя переменными в excel - Word и Excel

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x).

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).

Чтобы создать эту диаграмму, выполните следующие действия.

Выделите диапазон А1:В22.
Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22.
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Источник

Содержание

Как в офисе.
Построение графиков математических функций с одной переменной
Построение графиков математических функций с двумя переменными
Как построить график функции от двух переменных?
Microsoft Excel
Построение в Excel графиков математических и тригонометрических функций
Построение графиков математических функций с одной переменной
Построение графиков математических функций с двумя переменными
Пример №17 ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Как в офисе.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от −5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

Выделите диапазон А1:В22 .
Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от −3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22 .
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Источник

Как построить график функции от двух переменных?

Графики в Excel

Как построить график функции от одной переменной?

Пусть дана таблица 1 зависимости цены единицы некоторого товара от объема его продаж (известная в экономике «кривая спроса D-D»). Сразу отметим: если функция задана аналитической зависимостью y=f(x), то нужно предварительно ее протабулировать, то есть построить таблицу <x_i , y_i>, где x_i=x₀ + i×h, h = (x_n – x₀)/n; i = 0…n, а y_i=f(x_i). Для заполнения ряда x используется режим автозаполнения.

Объем продаж, тыс. шт.

Цена, руб.

Порядок построения графика следующий.

1. Выделяем всю таблицу и вызываем Мастер диаграмм.

2. На первом шаге выбираем Тип: Точечная и Вид: Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Обращаем ваше внимание на то, что Тип: График не пригоден в данном случае, так как показывает тенденции изменения данных за равные промежутки времени; при этом обе группы данных (х и у) отображаются в виде графиков.

3. На втором шаге в окне предварительного просмотра проверяем, правильно ли построен график. Обратите внимание: первая строка (или первый столбец, если данные расположены столбцом) воспринимается как данные оси Х , а вторая строка (столбец) или строки (столбцы), если они имеются, как данные оси Y.

4. Следующие шаги выполняются так же, как описано выше.

Результат приведен на рис. 1.

Как построить график функции от двух переменных?

Построим график производственной функции Кобба-Дугласа Y=A×K a L b , где А, a, b – константы, K – объем фондов , L – объем трудовых ресурсов, Y – выпуск продукции предприятием или отраслью. Эти переменные могут выражаться либо в стоимостном выражении, либо в натуральном количестве.

Пусть функция имеет вид:

где K=100 . 200 тыс. руб.; L=30 . 50 тыс. руб.

Графическое представление функции двух переменных – поверхность в трехмерном пространстве.

Табулируем функцию, располагая значения K по горизонтали, а L – по вертикали; тогда на пересечении столбца со значением K_i и строки со значением L_i будет находиться значение функции Y_i .

При наборе формулы необходимо зафиксировать знаком $ номер строки переменной, изменяющейся по горизонтали (т.е. K), и номер столбца переменной, изменяющейся по вертикали (т.е. L).

Например, в таблице 2 в ячейке В21 находится формула вида

Тогда при копировании формулы на все ячейки таблицы смена адресов для переменных будет проведена корректно (проверьте!).

Элемент листа Excel с табулированием функции двух переменных

A	B	C	D	E
.	Значения L	Значения К
.
21063,1	22091,2	23073,5	.
21890,7	22959,2	23980,1	.
22633,8	23738,5	24794,1	.
.	.	.	.	.

Результаты построения приведены на рисунке 2.

Порядок построения этой поверхности следующий.

1. Выделяем всю таблицу: и значения аргументов, и значения функции. Обратите внимание: левая верхняя ячейка выделенной области таблицы (у нас это ячейка А20) должна быть пустая.

2. Вызываем Мастер диаграмм.

3. На первом шаге выбираем Вид: Поверхность, Тип: Поверхность

4. На втором шаге можем предварительно посмотреть построенную поверхность и, при необходимости, изменить ряды данных.

5. На третьем шаге пишем название диаграммы, название оси Х (категорий) — это горизонтальный ряд данных, т.е. K, название оси Y (рядов данных) — это вертикальный ряд данных, т.е. L, и название оси Z (значений) – это наша функция Y.

6. На четвертом шаге размещаем построенную диаграмму на выбранном листе.

Обычно после построения требуется отредактировать диаграмму: сменить размер шрифта, фон стенок, размещение надписей и т.д. Для этого надо подвести стрелку к соответствующему объекту, щелкнуть правой клавишей мыши и из контекстно-зависимого меню выбрать соответствующую опцию. Пробуйте, экспериментируйте. Excel предоставляет для этого массу возможностей!

Отметим еще, что, подведя курсор к какому-нибудь углу стенок области построения графика (появится надпись «Углы») и «схватив» мышью этот угол (появится тонкий крестик), можно двигать область диаграммы, рассматривая график в различных ракурсах.

Дата добавления: 2015-08-13 ; просмотров: 1919 | Нарушение авторских прав

Источник

Microsoft Excel

трюки • приёмы • решения

Построение в Excel графиков математических и тригонометрических функций

Построение графиков математических функций с одной переменной

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

Выделите диапазон А1:В22 .
Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Построение графиков математических функций с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

Выделите диапазон A1:V22 .
Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)

Источник

Пример №17 ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Чуть ранее мы научились строить график функции одной переменной. В
построении графика функции двух переменных также нет ничего сложного.
Для этого нужно создать таблицу сродни таблицы умножения. Сверху
горизонтально и слева вертикально должны располагаться, соответственно,
подставляемые значения одного и другого параметров, а на пересечении —
значение функции ( рисунок 18.). Таблицу необходимо заполнить с помощью Автоматического заполнения таблицы (растягиванием формулы по вертикали и по горизонтали). Затем необходимо выделить весь массив вычисленных значений функции (B3:Q23) и построить диаграмму типа Поверхность (см. пример №16). Получим диаграмму, полученную на рисунке 19.

Рисунок 18. Таблица с данными из условия примера №17

Задание: выбрать для построенной диаграммы стиль с чёрным фоном (Конструктор->Стили диаграмм)

Рисунок 19. График функции двух переменных

Заключение

Подведём краткий итог рассмотренного материала. Excel 2010 обладает потрясающимся по функциональности и простоте функциями построения

графиков и диаграмм. С его помощью вы можете построить графики/
диаграммы для анализа данных любой сложности. Для быстрого построения
графика/диаграммы вам достаточно указать данные для построения и
выбрать макет графика/диаграммы.

Так же просто, как и построить график/диаграмму, настроить его в
соответствии с вашими потребностями. Вы можете настроить каждый
элемент графика/диаграммы. А если еще принять во внимание то, что
количество настроек для каждого элемента очень велико, можно смело
сказать, что для каждого конкретного случая анализа данных вы можете
построить неограниченное число диаграмм.

Напоследок, отметим случаи, когда и какие графики/диаграммы лучше
строить.

· Если вы хотите сравнить между собой доходы нескольких предпри-
ятий или проанализировать одно предприятие по нескольким пара-
метрам, вы можете построить гистограмму, линейчатую диаграмму,
кольцевую диаграмму или лепестковую диаграмму;

· Гистограммы и линейчатые диаграммы подойдут для анализа в тех
случаях, когда вы сравниваете деятельность одного предприятия по
нескольким параметрам за 2,3 или 4 периода;

· В случае, когда вы оцениваете отрасль или предприятие по несколь-
ким параметрам, вы можете построить круговую диаграмму;

· Если вы хотите показать деятельность предприятия как часть всей
отрасли, вам подойдет вторичная круговая диаграмма или вторич-
ная гистограмма;

· Если вы сравниваете предприятие по нескольким параметрам со
всей отраслью, вы можете построить двойную диаграмму, т.е. факти-
чески построить две диаграммы, которые будут выглядеть, как одна;

· Для анализа данных по трем параметрам вам подойдет пузырьковая
диаграмма;

· Если вы хотите просмотреть динамику развития предприятия, вы
можете построить график. Также вы можете сделать прогноз раз-
вития вашего предприятия, добавив линию тренда. А показав ко-
эффициент корреляции и функцию (предполагаемую), по которой
распределены ваши данные, вы можете установить принадлежность
распределения ваших данных тому или иному закону. Также для
анализа динамики развития подойдут точечные диаграммы.

И еще несколько советов непосредственно по построению диаграмм:

· Для каждого случая, когда вам необходимо проанализировать дан-
ные, стройте несколько типов графиков/диаграмм. Это позволит
вам взглянуть на оцениваемый объект с нескольких сторон;

· Для каждого графика/диаграммы экспериментируйте с настрой-
ками, пока не добьетесь желаемого результата. В некоторых слу-
чаях ручная настройка дает гораздо лучший результат, чем в слу-
чае, когда диаграмма/график построена с использованием настроек
по умолчанию (или настроек, выставляемых автоматически) Ехсе1 2010

1. Что такое адрес ячейки и как он обозначается?

2. Как исправить содержимое ячейки?

3. Как дать понять программе, что ввод данных в ячейку закончен?

4. Каково назначение функции автозаполнения?

5. Как выполнить выравнивание данных в ячейках электронной таблицы?

6. В каком случае вместо числа в ячейке отображаются символы #?

7. Как обозначаются строки и столбцы в электронной таблице?

8. С какими основными объектами работает Excel?

9. Как перейти с одного листа на другой?

10. Как создать новый лист?

11. Какие основные типы диаграмм используются в Excel?

12. Как задать исходные данные для построения диаграммы?

13. Что представляет собой легенда на диаграмме и как разместить легенду на диаграмме?

14. Каким образом вводится название диаграммы?

15. Опишите алгоритм построения диаграмм

Список литературы

1. Косовцева Т.Р., Петров В.Ю. MS EXCEL в расчетных задачах; Учебное пособие. — СПб: СПГУ ИТМО, 2010. — с.82.

2. Наглядно – убедительно, доходчиво. М., Панорама, 1990.-48с.

3. Анеликова Л.А. Лабораторные работы по Excel. –М.: СОЛОН-ПРЕСС, 2006. –128 с.

4. Лавренов С.М. Excel: Сборник примеров и задач. –М.: Финансы и статистика, 2003. –336 с

5. Информатика: Базовый курс: учебник для студентов / под ред. С. В. Симоновича. СПб.: Питер, 2002.

6. Карлберг, К. Бизнес-анализ с помощью Microsoft Excel.— 2-е испр. изд. — М.: Вильямс, 2007 .— 464 с.

7. Левин А. Ш. Самоучитель работы на компьютере/А. Ш. Левин. 8-е изд. СПб.: Питер, 2004.

8. Леонтьев В. П. Новейшая энциклопедия персонального компьютера 2003 / В. П. Леонтьев. М.: ОЛМА-Пресс, 2003.

9. Могилев А. В. Информатика: учеб. пособие для студентов/ А. В. Могилев, Н. И. Пак, Е. К. Хеннер; под ред. Е. К. Хеннера. М.: Академия, 2001.

Источник

Содержание

Процедура создания графика
- Способ 1: создание графика зависимости на основе данных таблицы
- Способ 2: создание графика зависимости с несколькими линиями
- Способ 3: построение графика при использовании различных единиц измерения
- Способ 4: создание графика зависимости на основе алгебраической функции
Вопросы и ответы

Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.

Процедура создания графика

Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.

Способ 1: создание графика зависимости на основе данных таблицы

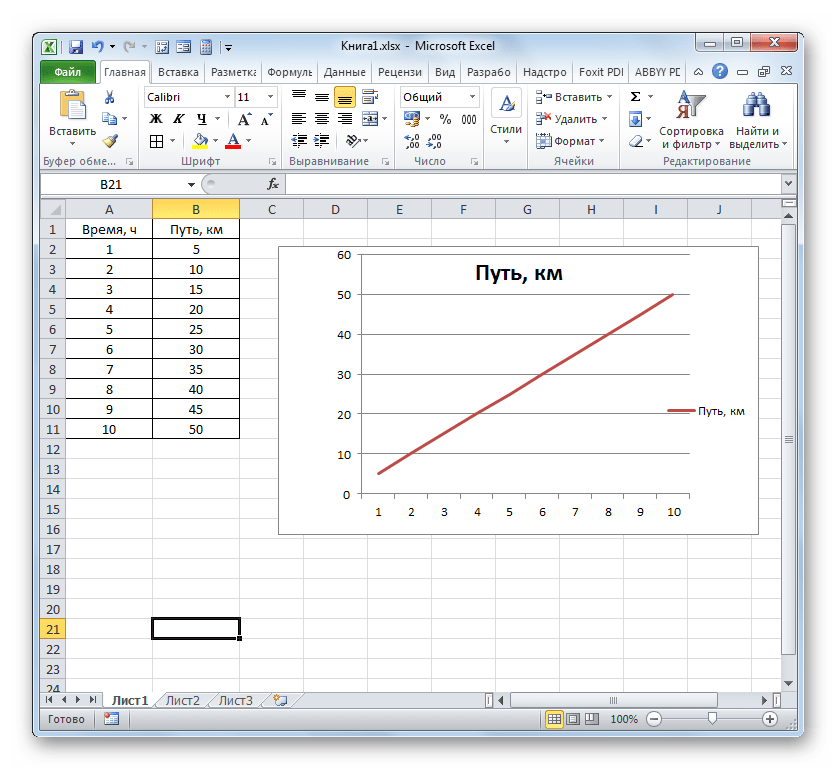
Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).

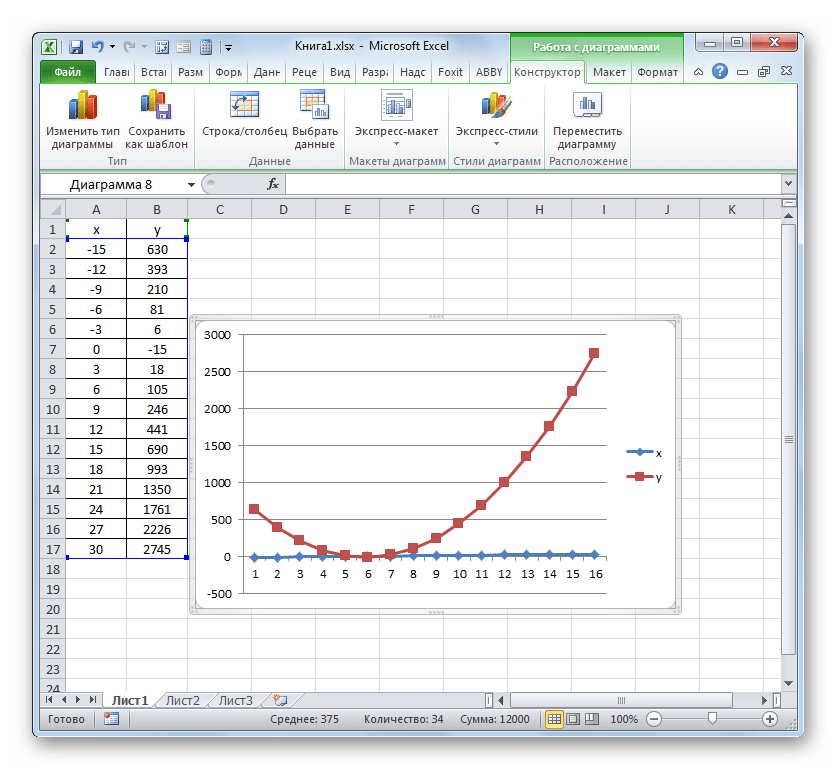
Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.

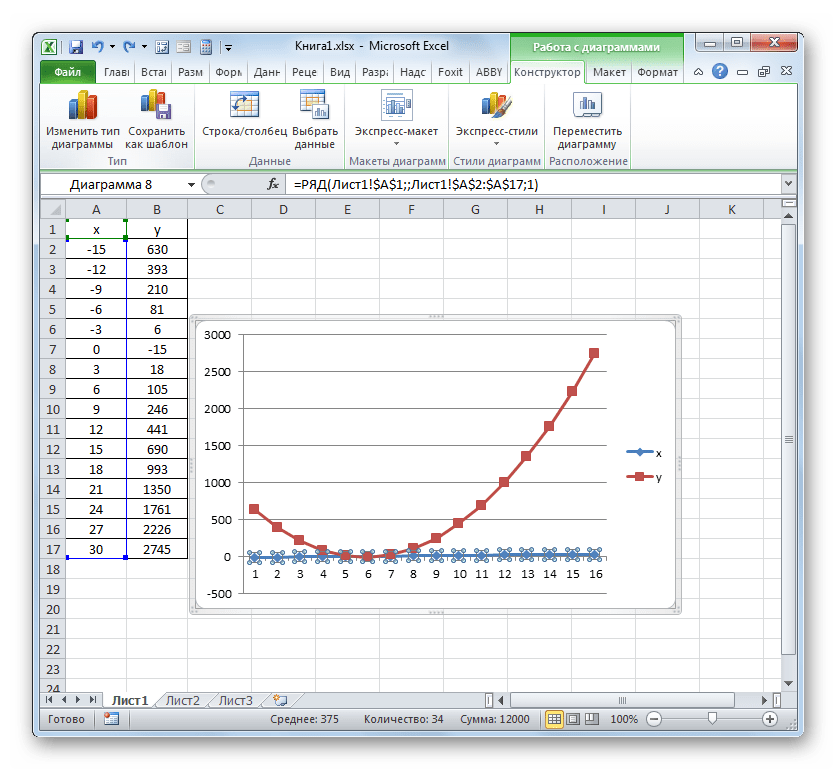
Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.

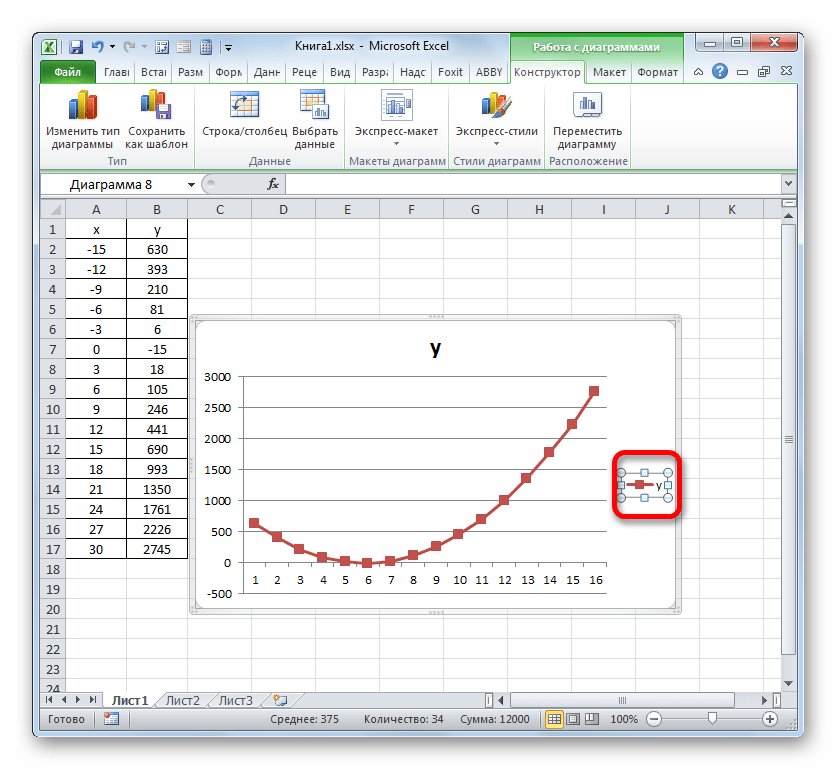
Выделенная линия будет удалена.

Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.

Урок: Как сделать график в Экселе

Способ 2: создание графика зависимости с несколькими линиями

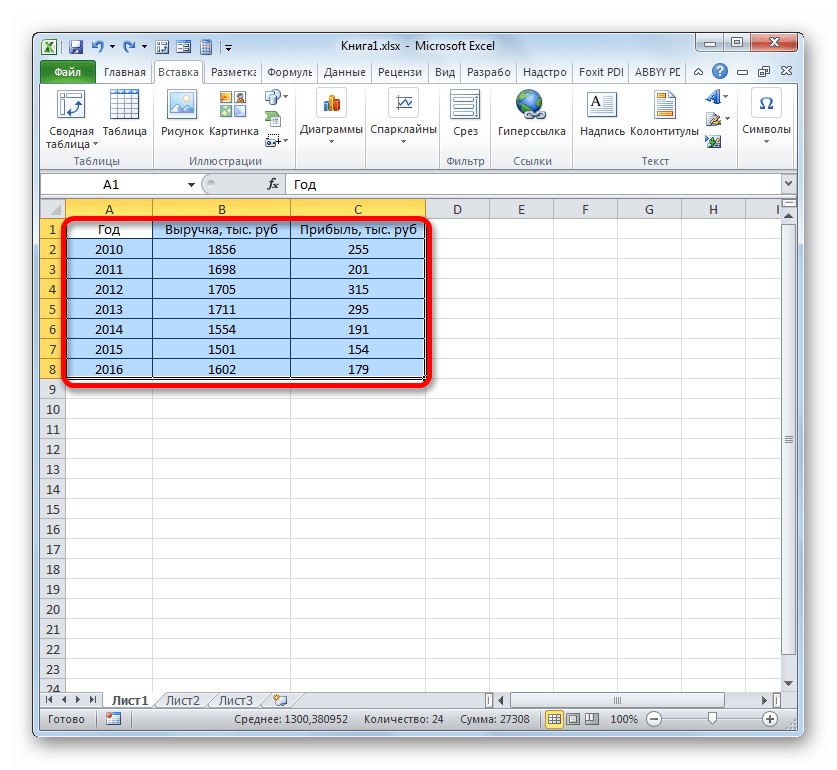
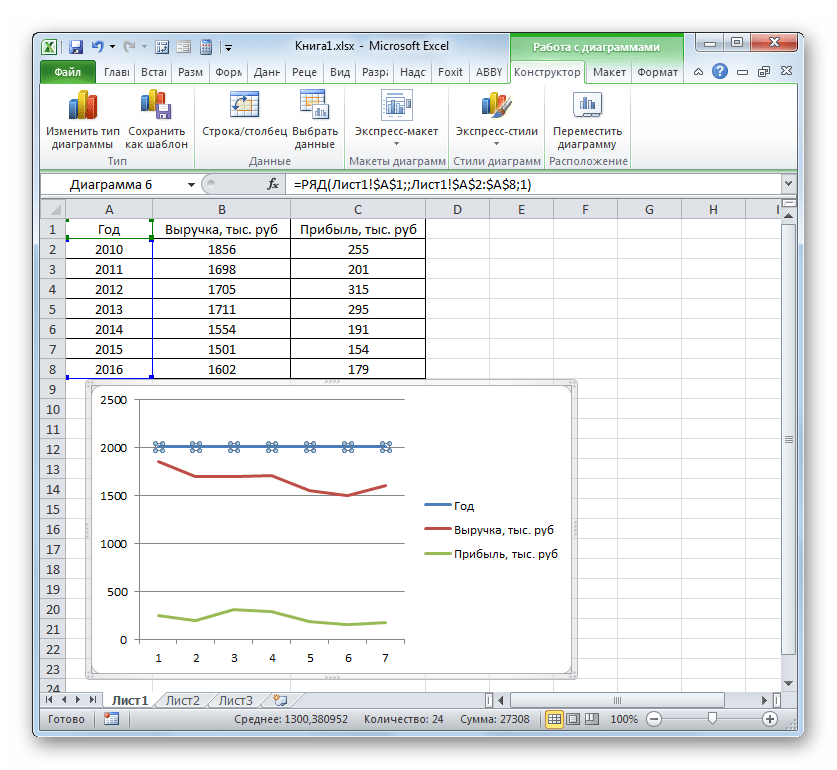
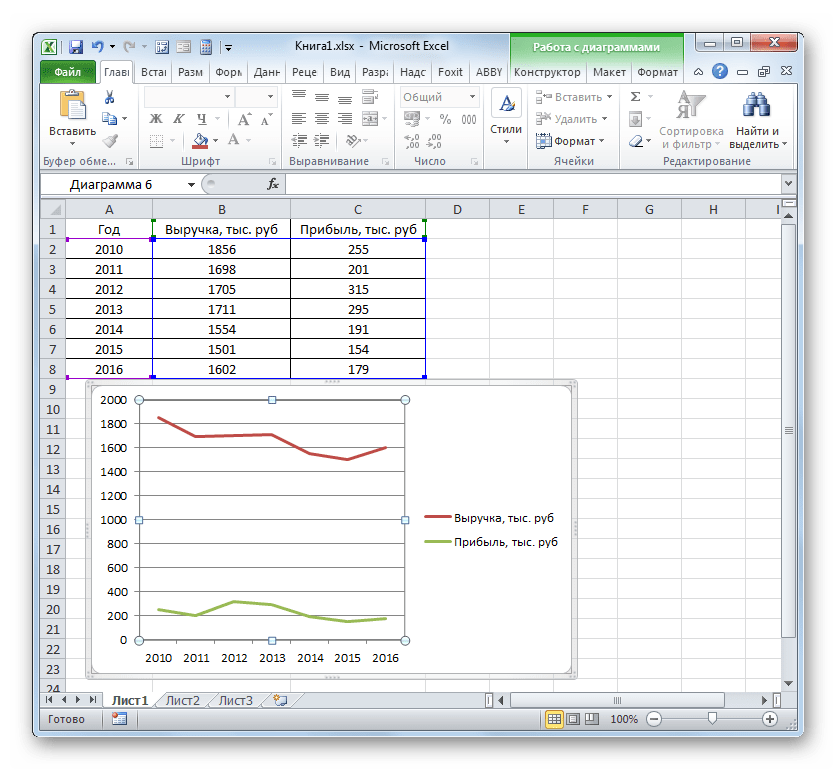
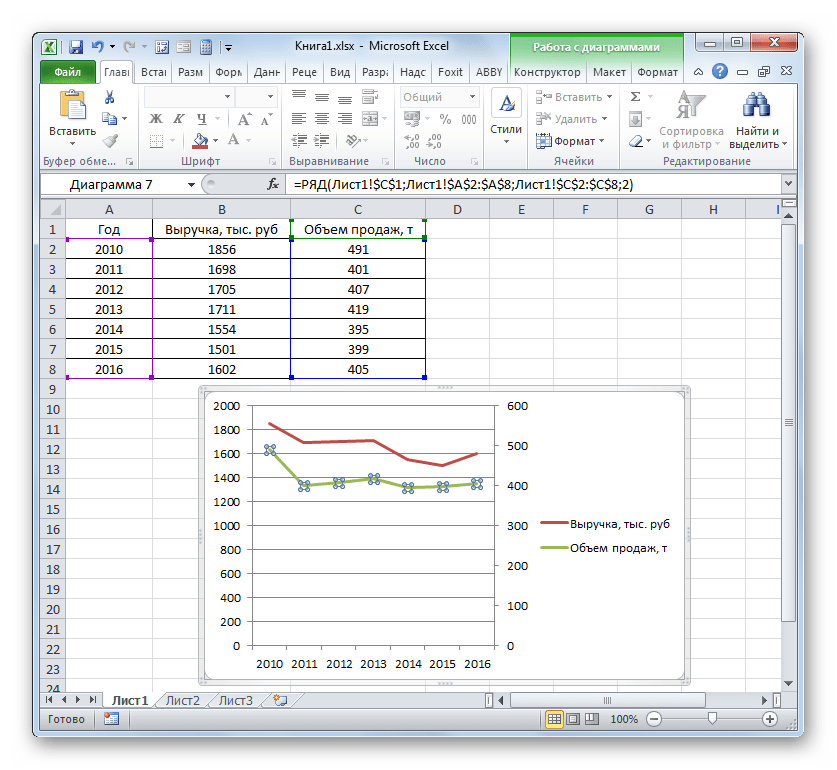
Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.

Выделяем всю таблицу вместе с шапкой.

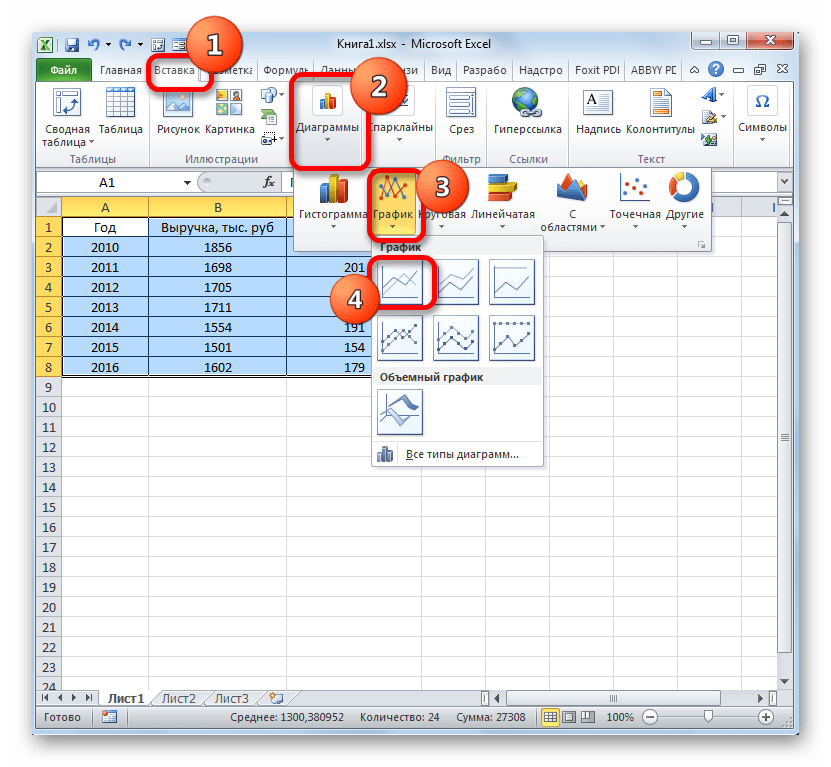
Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.

Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.
Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.

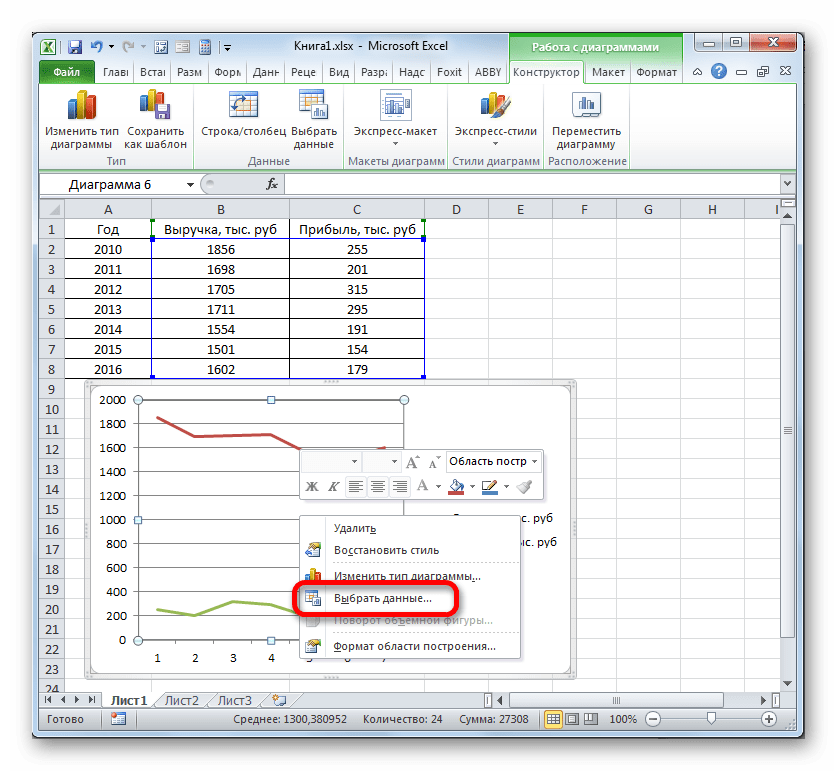
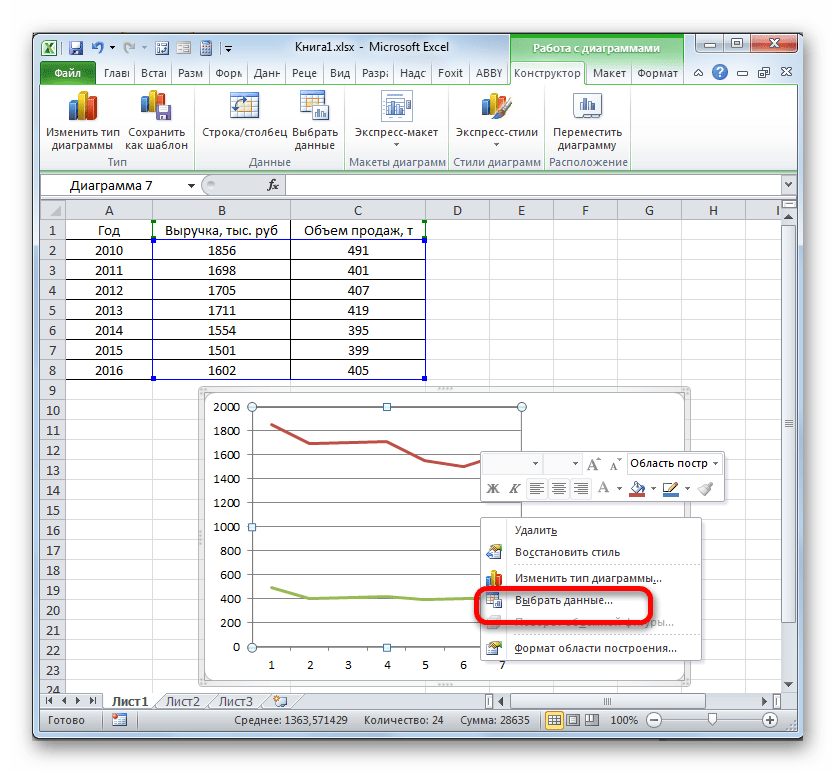
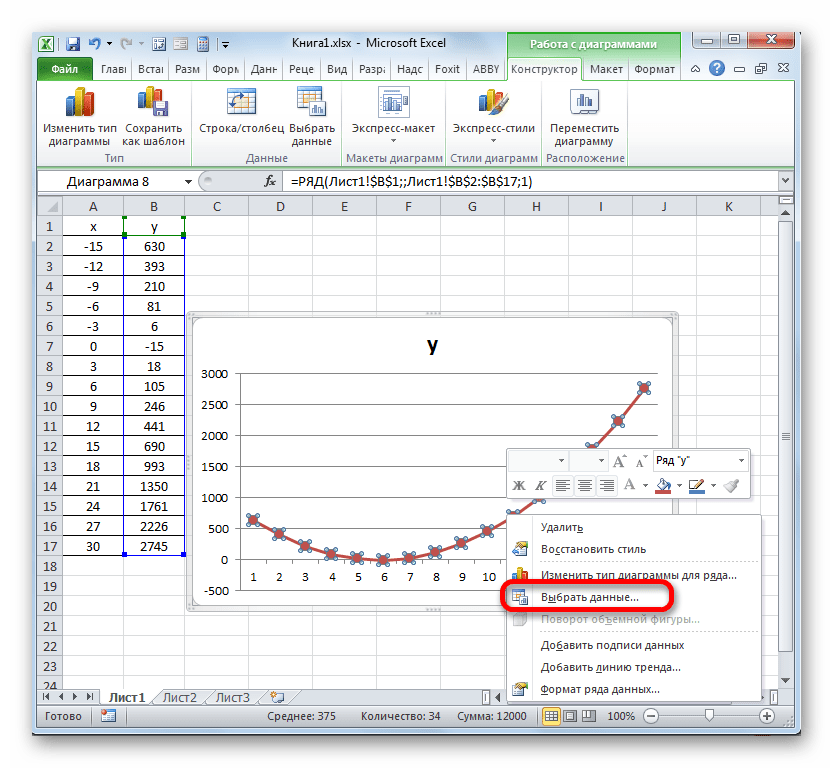
Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».

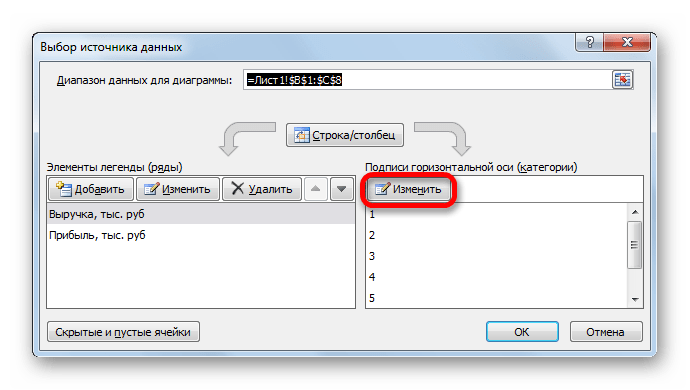
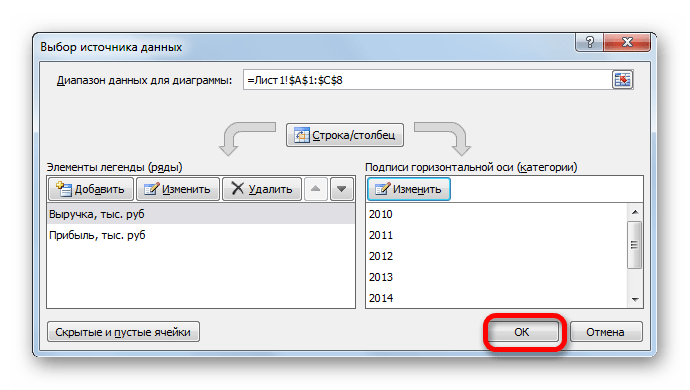
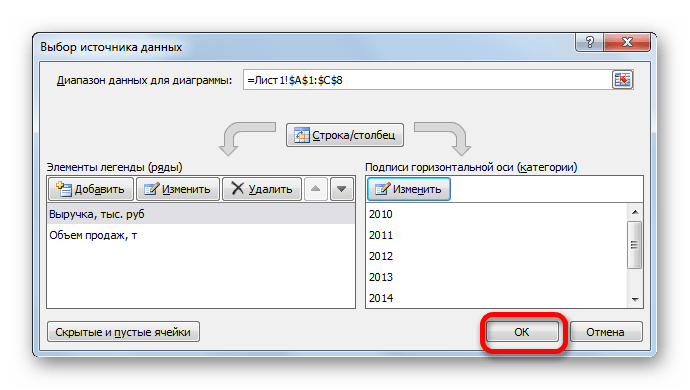
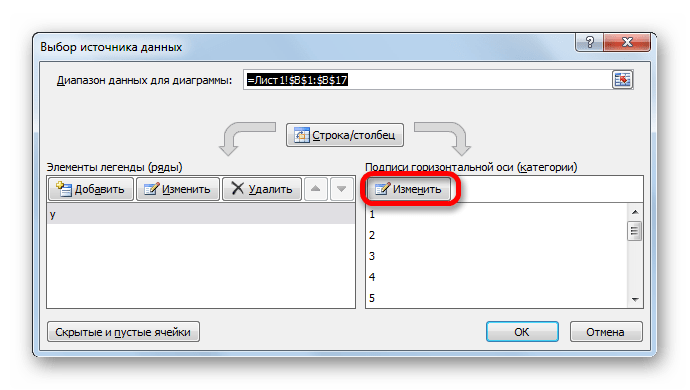
Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».

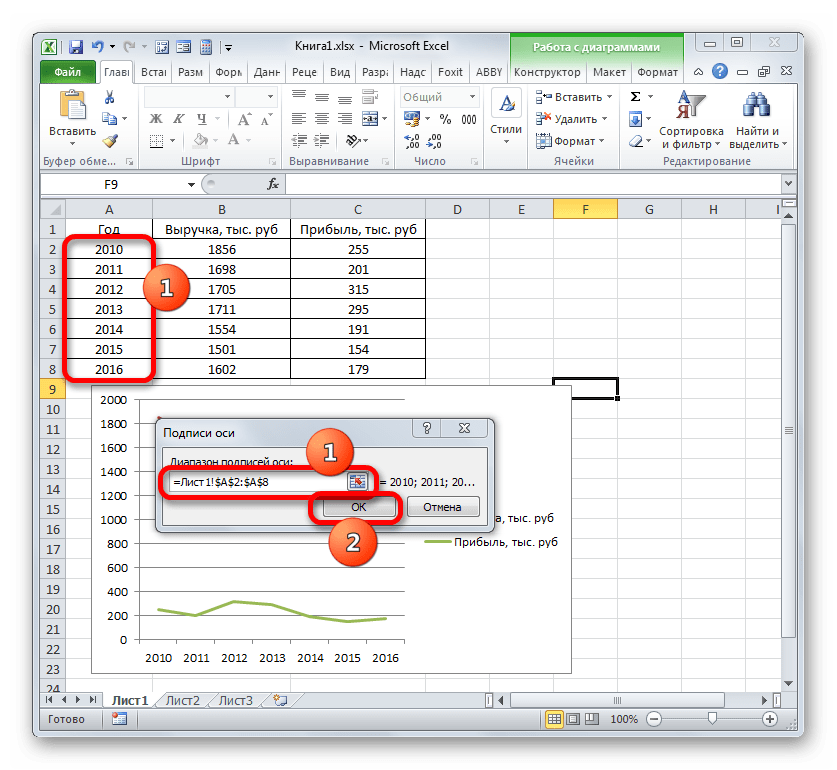
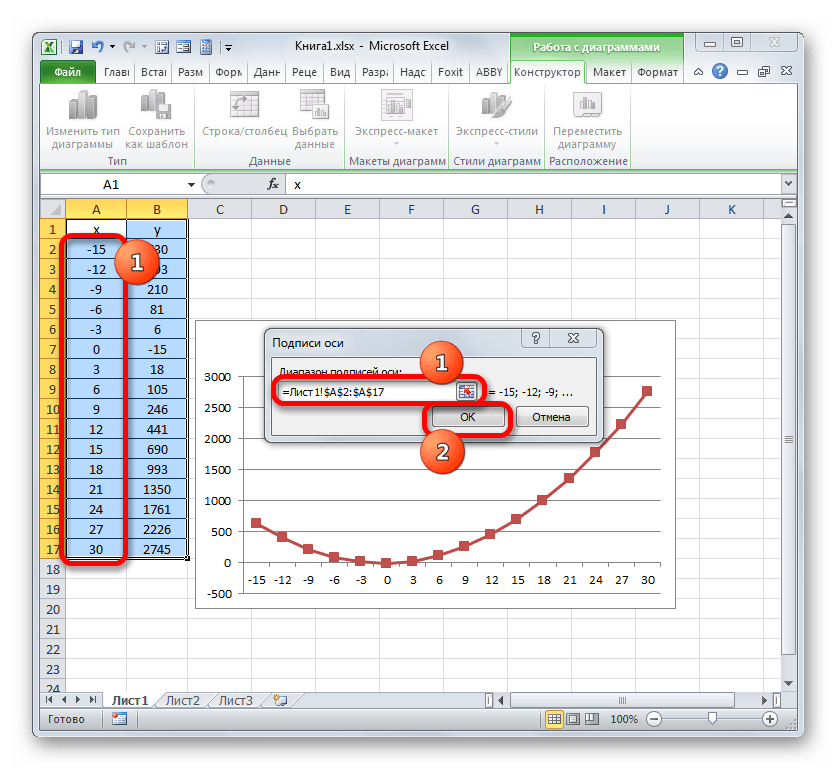
Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».

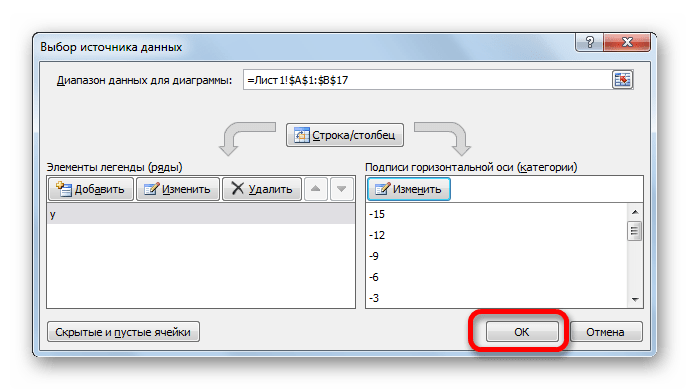
Вернувшись в окно выбора источника данных, тоже щелкаем «OK».

После этого оба графика, размещенные на листе, отображаются корректно.

Способ 3: построение графика при использовании различных единиц измерения

В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.

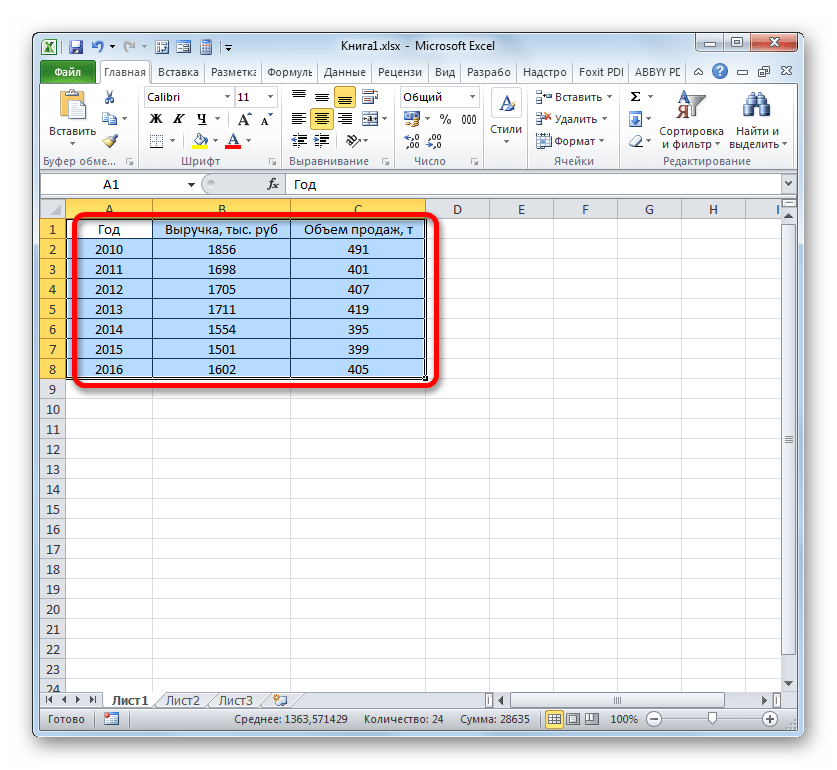
Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.

Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.

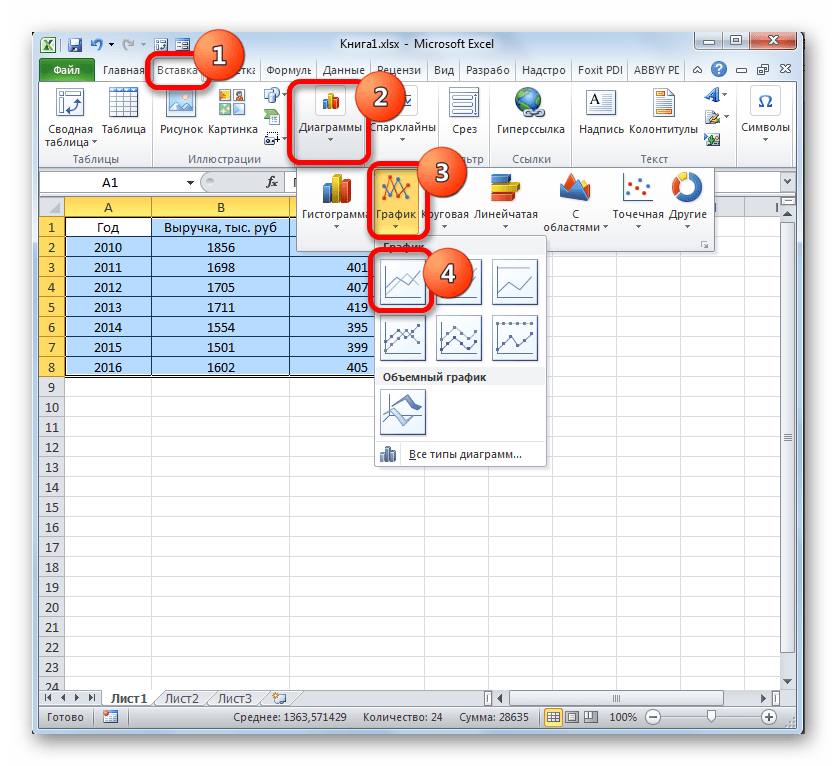
Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.

Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».

Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».

В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.

В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».

При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».

Теперь нам следует решить проблему, с которой ещё не встречались в предыдущих случаях построения, а именно, проблему несоответствия единиц величин. Ведь, согласитесь, не могут располагаться на одной панели координат деления, которые одновременно обозначают и денежную сумму (тыс. рублей) и массу (тонны). Для решения данной проблемы нам потребуется произвести построение дополнительной вертикальной оси координат.
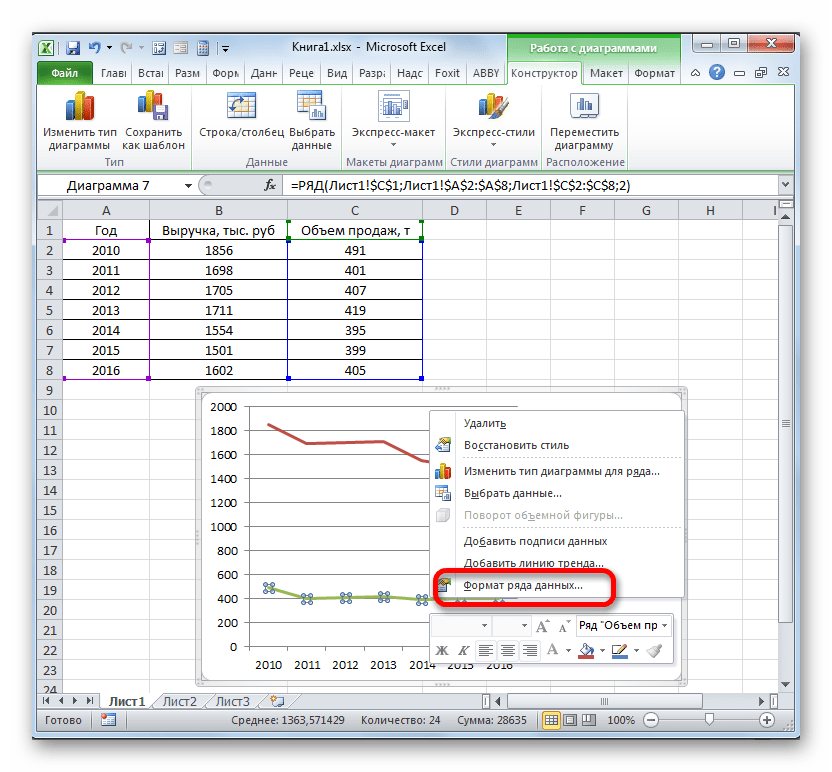
В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».

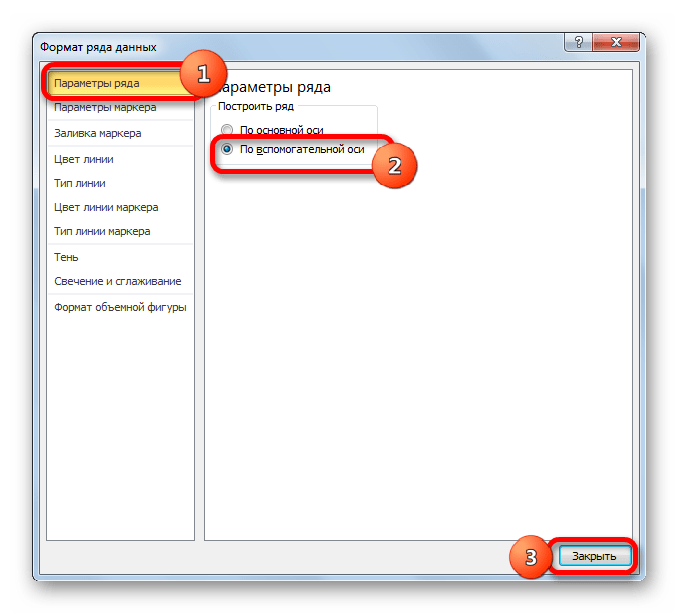
Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».

После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.

Способ 4: создание графика зависимости на основе алгебраической функции

Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.

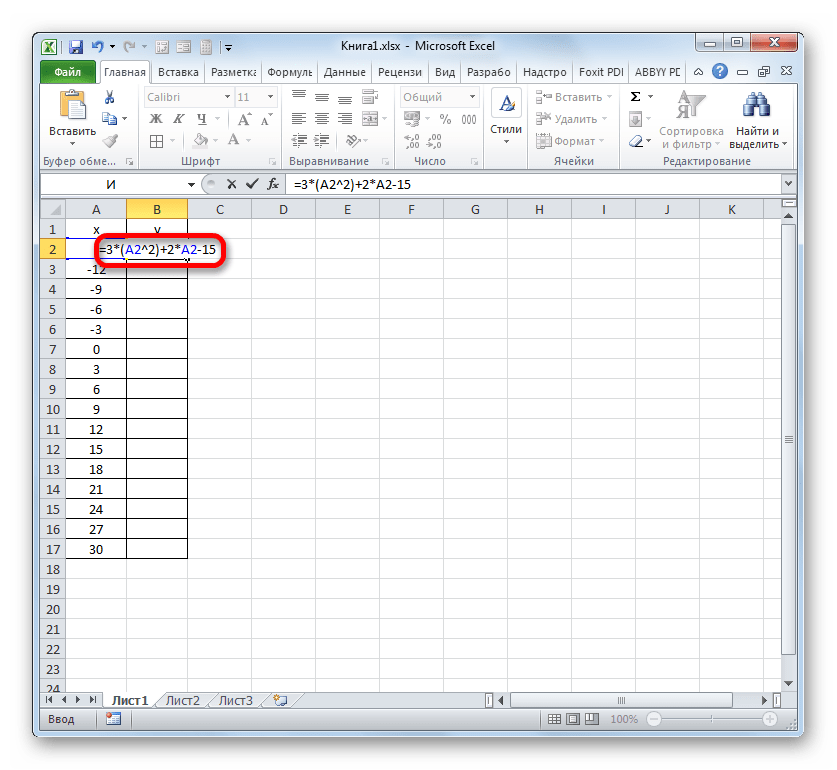
У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.

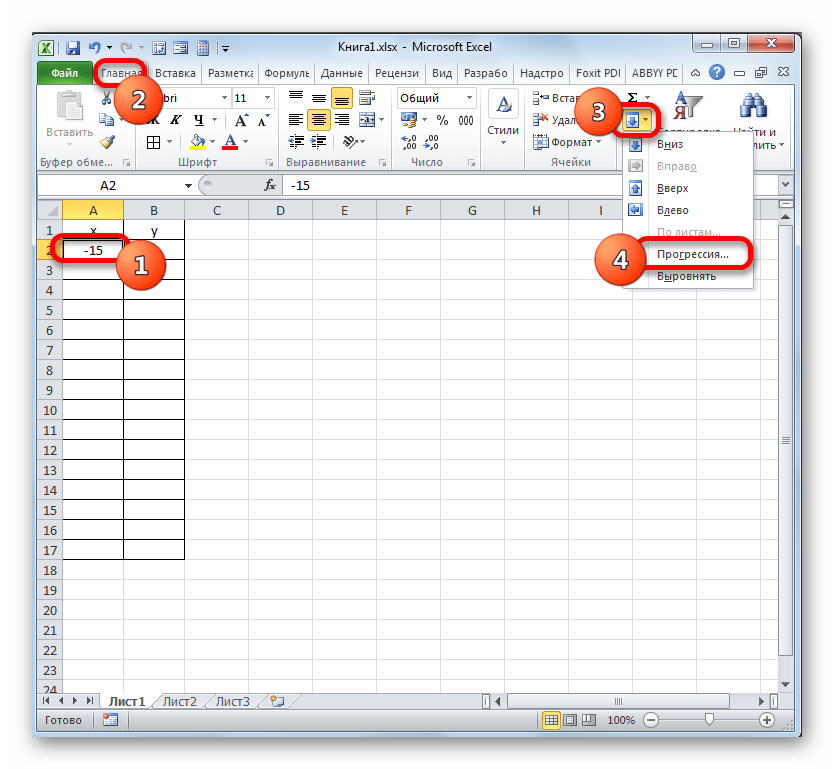
Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».
Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».

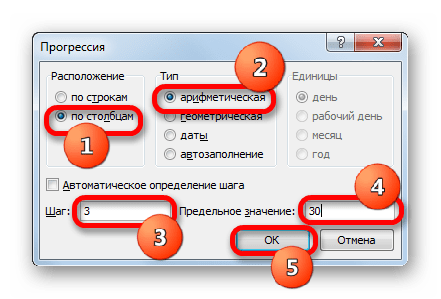
Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».

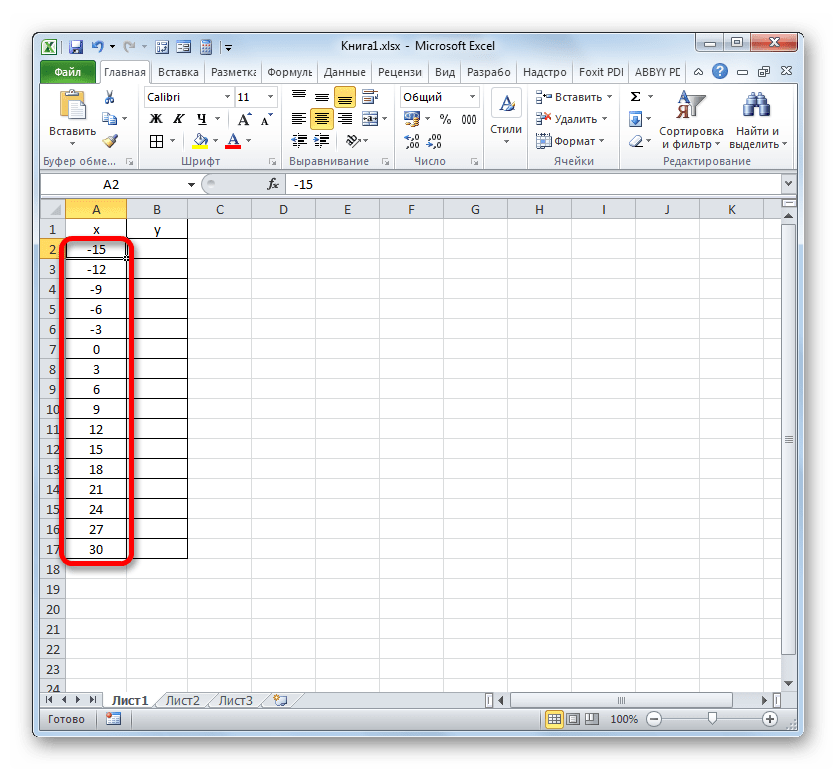
После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.

Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.
Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:

=3*(A2^2)+2*A2-15

Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.

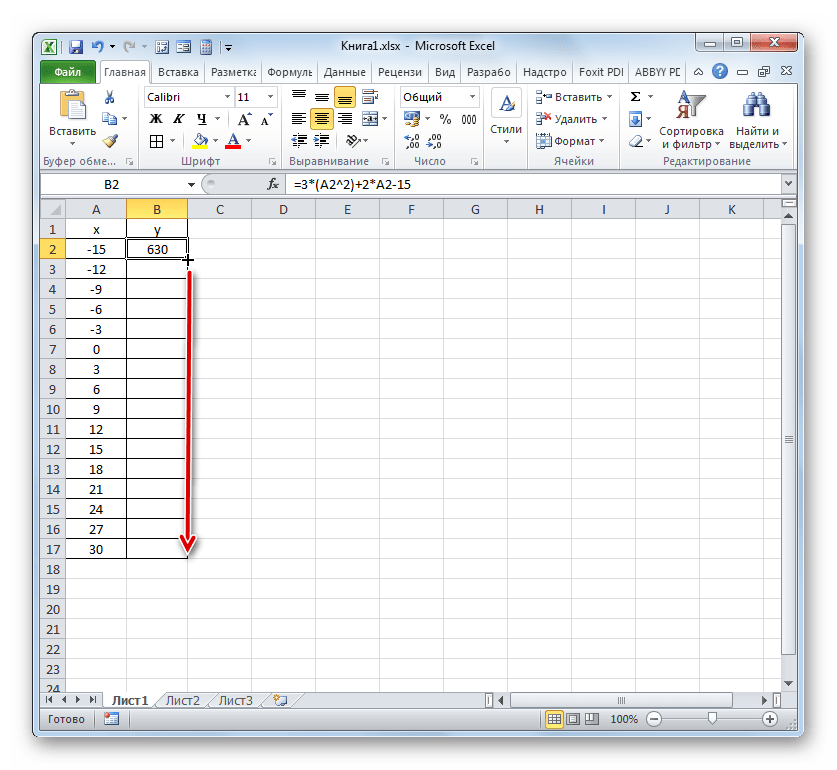
Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.
Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».

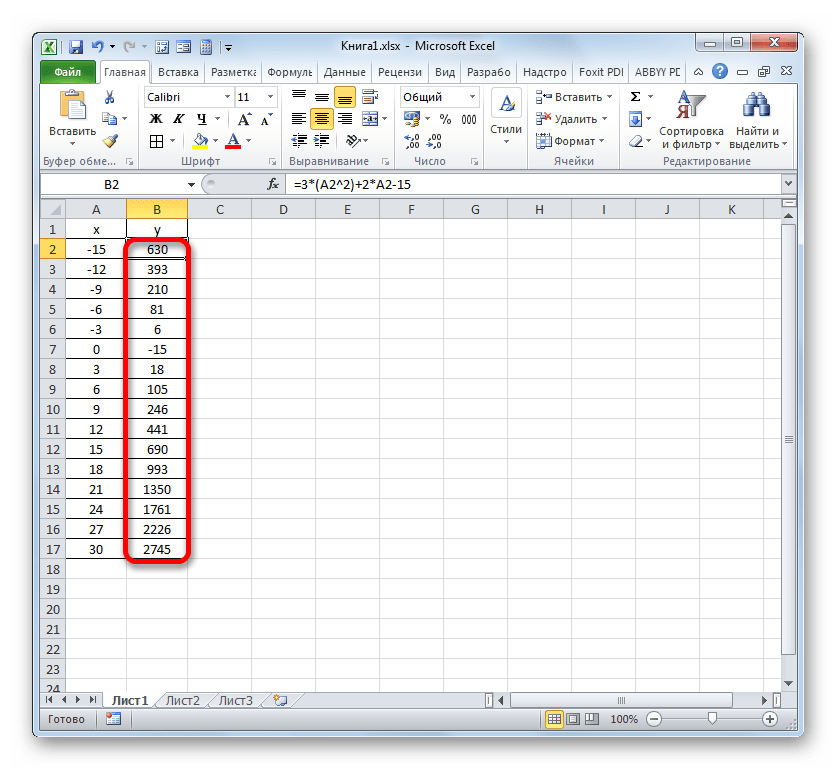
Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.

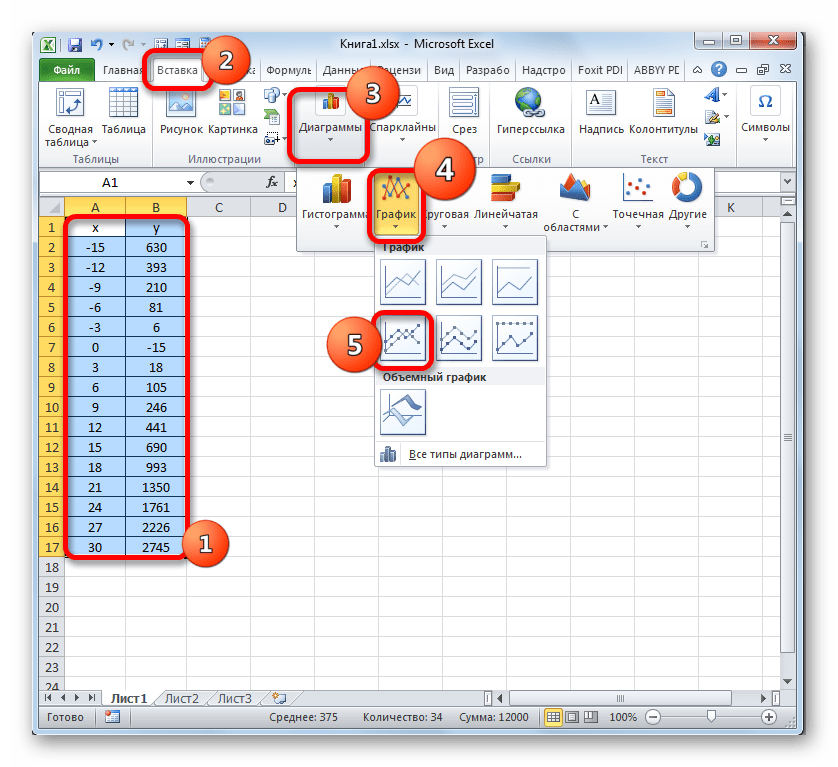
Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».

Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.

Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.

Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.

Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.
Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».

В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».

Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».

Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.

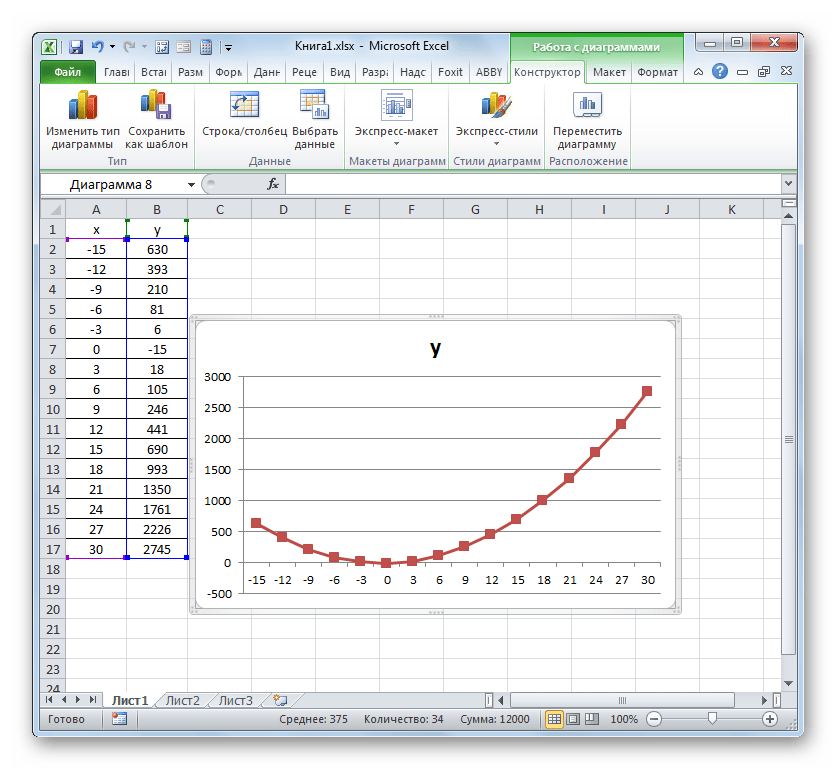
После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.

Урок: Как сделать автозаполнение в Майкрософт Эксель

Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Цель
работы: научиться табулировать функции
одного и двух переменных, строить графики
и поверхности, освоить работу с функцией
Excel
ЕСЛИ и логическими функциями И, ИЛИ.

С
помощью Excel можно превращать сухие и
абстрактные строки и столбцы чисел в
привлекательные и информативные графики
и диаграммы. Визуальное представление
информации облегчает ее восприятие,
помогает лучше представить поведение
функциональных зависимостей.

Построение
графиков и диаграмм осуществляется с
помощью Мастера
диаграмм.
Его вызов производится либо с помощью
команды Вставка
| Диаграмма,
либо щелчком по кнопке Мастер
диаграмм
в панели инструментов Стандартная.

Как построить
диаграмму?

Рассмотрим
таблицу 2.1, показывающую рост штатного
состава подразделений фирмы. Порядок
действий следующий.

Таблица 2.1 – Штат
фирмы «Шмидт и сыновья»

Подразделение	Период
Январь	Октябрь
Офис 1	2	5
Офис 2	7	9

Выделяем
необходимые табличные данные вместе
с подписями строк и столбцов. В
рассматриваемом примере можно выделить
всю таблицу, но чаще иллюстрируют лишь
некоторые строки или столбцы, содержащие
группы
данных одной размерности
(например, руб., или кг, или %).
Нажимаем
кнопку Мастер
диаграмм
и шаг за шагом проходим все этапы
построения диаграммы.

Шаг
1.
Выбираем тип диаграммы Гистограмма
и вид диаграммы Объемная
(рис. 2.1).

Шаг
2.
Здесь указывается диапазон ячеек,
содержащих данные (рис. 2.2). Так как
таблица была заранее выделена, диапазон
уже установлен. Проверьте в окне
предварительного просмотра, как выглядит
диаграмма. Если она не соответствует
желаемому, укажите другой диапазон.

Отметьте,
как расположены данные – в столбцах
или строках. Если в строках, то подписями
оси Х
будут
Январь,
Октябрь,
а категории Офис
1
и Офис
2
уйдут в легенду диаграммы, если в
столбцах, то наоборот.

На
вкладке Ряд
можно указать другие данные для диаграммы,
а также удалить или добавить ряды.

Шаг
3.
В этом окне находится шесть вкладок
(рис. 2.3), на которых можно изменить
параметры выбранного типа диаграммы,
например, написать название диаграммы,
задать сетку, написать значения (или
проценты, доли) над столбцами диаграммы
и т.д.

Шаг
4.
Здесь указывается место размещения
новой диаграммы: либо на имеющемся
листе, либо на новом листе (рис. 2.4).

После
построения диаграммы имеется возможность
изменить ее параметры. Для этого
достаточно щелкнуть правой клавишей
мыши по области построения диаграммы
и выбрать в появившемся контекстно-зависимом
меню необходимую опцию (обратите
внимание, что меню будет иметь разный
вид в зависимости от того, по какому
месту щелкнуть: или по легенде, или по
оси, или по области диаграммы и т.д.).

Существует
также удобный способ добавления новых
данных к диаграмме: выделить новые
данные в таблице и перетащить их на
диаграмму. В соответствующем виде они
появятся на поле диаграммы.

Как построить
график зависимости функции одного
переменного?

Пусть
дана таблица 2.2 зависимости цены единицы
некоторого товара от объема его продаж
(известная в экономике «кривая спроса
D-D»).
Сразу отметим: если функция задана
аналитической зависимостью y=f(x),
то нужно предварительно ее протабулировать,
то есть построить таблицу {x_i
, y_i},
где x_i=x₀
+ ih
–
узловые точки;
h
= (x_n
– x₀)/n
– шаг
табуляции;
i
= 0…n,
а
y_i=f(x_i).
Для заполнения ряда x
можно использовать режим автозаполнения
или формулу увеличения значения х
на один шаг.

Таблица 2.2 – Спрос

Объем продаж, тыс. шт.	8	10	18	20	32	40	50
Цена, руб.	510	430	350	280	200	100	80

Порядок построения
графика следующий.

Выделяем
всю таблицу и вызываем Мастер
диаграмм.
На
первом шаге выбираем Тип:
Точечная
и Вид:
Точечная
диаграмма со значениями, соединенными
сглаживающими линиями без маркеров.
Обращаем ваше внимание на то, что Тип:
График
не пригоден в данном случае, так как
показывает тенденции изменения данных
за равные
промежутки времени; при этом обе
группы данных (х
и у)
отображаются в виде графиков.
На
втором шаге в окне предварительного
просмотра проверяем, правильно ли
построен график. Обратите внимание:
первая строка (или первый столбец, если
данные расположены столбцом) воспринимается
как данные оси Х,
а вторая строка (столбец) или строки
(столбцы), если они имеются, как данные
оси Y.
Следующие
шаги
выполняются
так
же,
как
описано
выше.

Результат
приведен на рисунке 2.5.

Как
построить график зависимости функции
двух переменных?

Построим
график производственной функции
Кобба-Дугласа Y=AK^L^,
где А,
,

– константы, K
– объем фондов , L
–
объем трудовых ресурсов, Y
– выпуск продукции предприятием или
отраслью. Эти переменные могут выражаться
либо в стоимостном выражении, либо в
натуральном количестве.

Пусть функция
имеет вид:

Y=900K^0,5L^0,25
( тыс. руб.),

где
K=100
… 200 тыс. руб.;
L=30
… 50 тыс. руб.

Графическое
представление функции двух переменных
– поверхность в трехмерном пространстве.

Табулируем
функцию, располагая значения K
по горизонтали, а L
– по вертикали; тогда на пересечении
столбца со значением K_i
и строки со значением L_i
будет находиться значение функции Y_i
(табл. 2.3).

При
наборе формулы необходимо зафиксировать
знаком $ номер строки переменной,
изменяющейся по горизонтали (т.е. K),
и номер столбца переменной, изменяющейся
по вертикали (т.е. L).

Таблица
2.3 – Элемент листа Excel
с табулированием функции двух переменных

	A	B	C	D	E
…	Значения L	Значения К
20		100	110	120	…
21	30	21063,1	22091,2	23073,5	…
22	35	21890,7	22959,2	23980,1	…
23	40	22633,8	23738,5	24794,1	…
24	…	…	…	…	…

Например, в таблице
2.3 в ячейке В21 находится формула вида

=
900*B$20^0,5*$A21^0,25

Тогда
при копировании формулы на все ячейки
таблицы смена адресов для переменных
будет проведена корректно (проверьте!).

Порядок построения
этой поверхности следующий.

Выделяем
всю таблицу: и значения аргументов, и
значения функции. Обратите внимание:
левая верхняя ячейка выделенной области
таблицы (у нас это ячейка А20) должна
быть пустая.
Вызываем
Мастера
диаграмм.
На
первом шаге выбираем Вид:
Поверхность, Тип: Поверхность.
На
втором шаге можем предварительно
посмотреть построенную поверхность
и, при необходимости, изменить ряды
данных.
На
третьем шаге пишем название диаграммы,
название оси Х
(категорий) 
это горизонтальный ряд данных, т.е. K,
название оси Y
(рядов данных) 
это вертикальный ряд данных, т.е. L,
и название оси Z
(значений) – это наша функция Y.
На
четвертом шаге размещаем построенную
диаграмму на выбранном листе.

Обычно
после построения требуется отредактировать
диаграмму: сменить размер шрифта, фон
стенок, размещение надписей и т.д. Для
этого надо подвести стрелку к
соответствующему объекту, щелкнуть
правой клавишей мыши и из контекстно-зависимого
меню выбрать соответствующую опцию.
Пробуйте, экспериментируйте. Excel
предоставляет для этого массу возможностей!

Результаты
построения приведены на рисунке 2.6.

Отметим
также, что, подведя курсор к какому-нибудь
углу стенок области построения графика
(появится надпись «Углы») и «схватив»
мышью этот угол (появится тонкий крестик),
можно двигать область диаграммы,
рассматривая поверхность в различных
ракурсах.

Задания

Задание
1.
Построить диаграммы, иллюстрирующие
табличные данные из лабораторной работы
1. Тип диаграммы выбрать исходя из степени
наглядности представления информации.
Обязательно включить название, подписи
рядов данных, легенду. Поместить диаграмму
на отдельном листе.

Задание
2.
Построить графики функции одного
переменного на отрезке х[2;
2] для одного из выбранных вариантов,
приведенных ниже, при разных шагах
табуляции: 0,5; 0,2; 0,1. Сравнить вид графиков,
сделать выводы.

1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26
27		28
29		30

При
записи формулы использовать функцию
ЕСЛИ. Она возвращает одно значение, если
заданное условие при вычислении дает
значение ИСТИНА, и другое значение, если
ЛОЖЬ.

Синтаксис
этой функции (рис. 2.7):

ЕСЛИ(условие;значение_если_истина;значение_если_ложь).

В
условии для сравнения двух значений
используются операторы сравнения: =
(равно); > (больше); < (меньше); >= (не
меньше); <= (не больше); <> (не равно).

Например, формула

=ЕСЛИ(А1>=0;КОРЕНЬ(A1);”число
отрицательное!”),

записанная
в какой-либо ячейке, помещает в нее
значение квадратного корня из числа,
находящегося в ячейке А1, при его
неотрицательном значении, и выдает
предупредительный текст в случае
отрицательного значения.

Сравнивать
можно как арифметические, так и текстовые
выражения.

Примечание.
Если
после набора формулы в одном из полей
(рис. 2.7), она вдруг окажется охваченной
двойными кавычками, т.е. интерпретирована
как текст – ищите ошибку. Это может быть
несоответствие скобок, неверно записанное
или использованное имя функции, адрес
ячейки, содержащий русские буквы,
пропущенный знак умножения и т.п.

Задание
3.
Существует гипотеза, что параметры
физической активности человека, его
умственных способностей и эмоционального
состояния можно описать периодическими
функциями вида:

где
t
– время (дни, отсчитываемые со дня
рождения
t₀);

T_i
– периоды: Т₁=23
дня для физического цикла; Т₂=28
дней для эмоционального цикла; Т₃=33
дня для интеллектуального цикла.

1. Построить
таблицу биоритмов на текущий месяц,
задав информацию о дате рождения, дате
начала построения графика (взяв, например,
первый день месяца), дате конца построения
графика (последний день месяца).

Для
ячеек, где будут располагаться даты,
установить формат Дата
(Формат
| Ячейки | Число | Дата).
Для подсчета прожитых лет использовать
функцию Год.

Синтаксис функции:

ГОД(дата)

Дата
– это дата, год которой необходимо
найти. Даты вводятся как текстовые
строки в двойных кавычках, например,
“31.12.03”, “7.12.2003”^¹.

Вариант расположения
информации на листе показан на рис. 2.8.

2. Построить
графики биоритмов.

3. Определить
«положительные и отрицательные
критические дни», т.е. точки совпадения
графиков (двойные и тройные) в положительной
или отрицательной области изменения
соответствующих функций.

Для
этого предлагается с помощью вложенных
функций ЕСЛИ
преобразовать значения функций биоритмов
в условные значки (см. рис. 2.8, столбцы
Визуальное
представление):

+ – если значения
функции положительные;

– – если значения
функции отрицательные;

*
– при совпадении двух любых функций
(можно усложнить задачу, введя разные
значки для разных комбинаций совпадений);

+!!!
– при совпадении значений всех трех
функций в положительной области;

–!!!
– при совпадении значений всех трех
функций в отрицательной области.

Сравнивать
значения рекомендуется по одному или
двум знакам после запятой (т.е. решать
задачу в некотором приближении) с
использованием функции ОТБР,
назначение которой – отсечение дробной
части числа до указанного количества
разрядов.

Формирование
условий для функций ЕСЛИ
потребует применения логических функций
И
и ИЛИ.

Функция
И
возвращает значение ИСТИНА, если все
аргументы имеют значение ИСТИНА, и
возвращает значение ЛОЖЬ, если хотя бы
один аргумент имеет значение ЛОЖЬ.

Синтаксис функции:

И(условие1;
условие2;
…).

Функция
ИЛИ
возвращает значение ИСТИНА, если хотя
бы один из аргументов имеет значение
ИСТИНА, и возвращает значение ЛОЖЬ, если
все аргументы имеют значение ЛОЖЬ.

Синтаксис функции:

ИЛИ(условие1;
условие2;
…).

В
рассматриваемой задаче условие
– это сравнение типа «равенство».

Примечание.
Задания на построение поверхности будут
предложены в лабораторных работах 3 и
4.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
#
11.05.2015211.06 Кб22mss_labN5.docx

Источник

График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.

Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.

Построение графиков в Excel по данным таблицы

В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д. В этом уроке мы разберем, для чего применяют графики. И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики. Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить. a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.). b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением) c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени. Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

Создайте сразу два столбца — X и Y, куда будете записывать данные.

Запишите самостоятельно первые два или три значения с указанным шагом.

Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.

Сама функция автоматически высчитает синус заданного числа.
Растяните столбец точно так же, как это было показано ранее.

Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

Выделите столбец с Y и перейдите на вкладку «Вставка».

Создайте стандартный график, развернув выпадающее меню.

График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Мы рады, что смогли помочь Вам в решении проблемы. Помимо этой статьи, на сайте еще 12419 инструкций. Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам. Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Простая диаграмма

Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.

Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху). В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.

Выбираем график слева, т.к. он показывает изменение прибыли во времени. Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:

Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг. Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.

После этого появится такое окошко:

Изменяем подписи горизонтальной оси. Должно открыться такое окошко:

Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:

Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:

Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:

Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:

В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак , который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

График с накоплением

Строим по этим же данным график с накоплением. Повторяем все те же самые действия, как и в п.1. Поэтому мы покажем начало, на котором видно, какой график выбираем, и конец, на котором виден результат работы.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Объемный график

Объемный график похож на первый с той лишь разницей, что выполнен в объеме.

В этой работе были рассмотрены различные варианты построения такой разновидности диаграмм, как графики. А также случаи их применения. Для изучения построения диаграмм в программе Эксель заходите читать статьи на Справочнике!

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Добавление второй оси

Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.

Сначала строим график так, будто у нас одинаковые единицы измерения.

Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».

Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.

Это один из способов. Есть и другой – изменение типа диаграммы.

Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».

Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.

Всего несколько нажатий – дополнительная ось для другого типа измерений готова.

Как добавить название в график Эксель

На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:

Нажать на графике левой клавишей мыши;
Нажать на “зеленый крестик” в правом верхнем углу графика;
Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:

Над графиком появится поле с названием графика. Кликните по нему левой клавишей мыши и внесите свое название:

( 1 оценка, среднее 5 из 5 )

Источник