Построить астроиду в excel

Пример построения графика астроиды (кубоциклоида/звездообразной кривой) в Excel.

Для построения графика использованы параметрические уравнения x = R*cos3t и y = R*sin3t. 

Также посчитана площадь фигуры.

Скачать пример — Astroida.xlsx

То же в Python:

import matplotlib.pyplot as plt
import math
x=[]
y=[]
for i in range (1,1000):
    x.append((math.sin(i))**3)
    y.append((math.cos(i))**3)

plt.scatter(x,y)
plt.show()

Источник

Инфоурок

›

Информатика

›Другие методич. материалы›Практическая работа в MS EXCEL «Красивые графики»



Скачать материал



Скачать материал

  • Сейчас обучается 36 человек из 26 регионов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 211 896 материалов в базе

  • Выберите категорию:

  • Выберите учебник и тему

  • Выберите класс:

  • Тип материала:

    • Все материалы

    • Статьи

    • Научные работы

    • Видеоуроки

    • Презентации

    • Конспекты

    • Тесты

    • Рабочие программы

    • Другие методич. материалы

Найти материалы

Другие материалы

  • 28.02.2017
  • 1261
  • 14
  • 28.02.2017
  • 701
  • 4
  • 28.02.2017
  • 532
  • 0
  • 28.02.2017
  • 476
  • 0
  • 28.02.2017
  • 476
  • 0
  • 28.02.2017
  • 1354
  • 15
  • 28.02.2017
  • 434
  • 6

Вам будут интересны эти курсы:

  • Курс повышения квалификации «Информационные технологии в деятельности учителя физики»

  • Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

  • Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»

  • Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

  • Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»

  • Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

  • Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»



  • Скачать материал


    • 28.02.2017


      22412
    • DOCX
      1.1 мбайт
    • 452
      скачивания
    • Рейтинг:
      3 из 5
    • Оцените материал:





  • Настоящий материал опубликован пользователем Zilowski Max Jurievich. Инфоурок является
    информационным посредником и предоставляет пользователям возможность размещать на сайте
    методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
    сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

    Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
    сайта, Вы можете оставить жалобу на материал.

    Удалить материал

  • Zilowski Max Jurievich

    • На сайте: 2 года и 6 месяцев
    • Подписчики: 0
    • Всего просмотров: 435217
    • Всего материалов:

      49

  • Файлы

Файлы

Рабочий лист подходит для учеников 7 класса, работающих по учебнику «Информатика. ФГОС», автор Л….

Источник

Построение
графиков 3-х видов в электронной таблице
Excel

1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .

№

Название

кривой

Вид
графика

Параметри­ческие
уравнения

Диапазон

аргумента

Кол-во

граф.

Значения
констант

1

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

5

a = 1;
1.25;
1.5; 1.75; 2

2

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

6

a = 2

 = 0.4;
0.7; 1.0;
1.3; 1.6; 2.0

3

Трохоида

x = at — bsin
t

y = a — bcos
t

t  0  10

шаг
0,1

5

a = -1

b
= 0.1; 1; 2; 3; 4

4

Эпитрохоида

x = acos
(t)
— bcos
(t + t)

y = asin
(t)
— bsin
(t + t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

5

Гипотрохоида

x = acos
(t)
— bcos
(t — t)

y = asin
(t)
— bsin
(t — t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

6

Декартов

лист

x = at   / (1 + t3)

y = a
t2 / (1 + t3)

t  -6  6

шаг
0,3

6

a = 1;
2; 3; 4; 5; 6

7

Циссоида
Диоклеса

x = a
t2 / (1 + t2)

y = a
t3 / (1 + t2)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

8

Строфоида

x = a
 (t2 — 1) / (t2 + 1)

y = at(t2 — 1) / (t2 + 1)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

9

Конхоида

Никомеда

x = a + bcos
t

y = atg
t + bsin
t

t  0

10

шаг
0,2

5

a = 2

b
= 1; 10; 30; 50; 90

10

Улитка

Паскаля

x = acos2
t + bcos
t

y = a
cos
t sin
t + bsin
t

t  0  2

шаг
0,1

6

a = 1;
2; 3; 4; 5; 6

b
= 3

11

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a sin[(a + b)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1;
2; 3; 4; 5; 6

12

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  10

Шаг
0,2

6

a = 3;
b = 4

 = 0.5;
0.7; 1;
1.5; 2; 3

13

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 4; 6

14

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 7;
b = 4

 = 0.5;
1; 2; 4; 6; 8

15

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1.5;
2.5; 3;
3.5; 4; 5

16

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  6

Шаг
0,5

6

a
= 1.5; 2; 2.5;
3; 3,5; 4

b = 1

17

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 3; 4

18

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  10

Шаг
0,2

6

a = 5;
b = 2

 = 0.2;
0.5; 0.7;
1; 1.5; 2

19

Спираль

x = atcos
t

y = btsin
t

t  0  10

Шаг
0,5

6

a
= 2

b = -2;
-1; 1; 2; 3; 4

20

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  -6  6

Шаг
0,3

5

a = 2

b = 1;
2; 3; 4; 5

21

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  0.5  20

Шаг
0,5

5

a = 3

b = 1;
2; 3; 4; 5

22

Астроида

x = acos3
(t / 4)

y = b
sin3
(t / 4)

t  0  8

Шаг
0,1

5

a
= 2

b = 1;
2;
3;
4;
5

23

Астроида

x = acos3
(t – b)

y = a
sin3
t

t  0  8

Шаг
0,2

5

a
= 2

b = 0;
1; 2; 3; 4

24

Астроида

x = acos3
(bt
)

y = a
sin3
t

t  0  8

Шаг
0,1

5

a
= 2

b = 0.5;
1; 1.5; 3; 3.5

25

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  -10 10

Шаг
0,5

4

a
= -2;
-1; 1; 2

26

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  0 20

Шаг
0,5

4

a
= -2;
-1; 1; 2

27

Эллипс

x = acos
t

y = b
sin
t

t  0  2

Шаг
0,5

5

a
= 7

b = 1;
4; 7; 10; 13

28

Эллипс

x = acos(c
+ t)

y = b
sin(c
— t)

t  0  2

Шаг
0,11

5

a
= 3 b = 2

b = 1;
2; 3; 4; 5

29

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Формула Бернулли в Excel

В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!

Схема независимых испытаний

В общем виде схема повторных независимых испытаний записывается в виде задачи:

Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.

Эта вероятность вычисляется по формуле Бернулли:

$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$

Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:

  • Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
  • Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
  • События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.

Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.

Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.

Формула Бернулли в Эксель

Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.

Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .

Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).

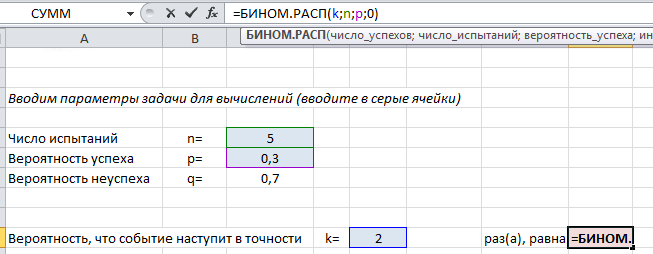
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:

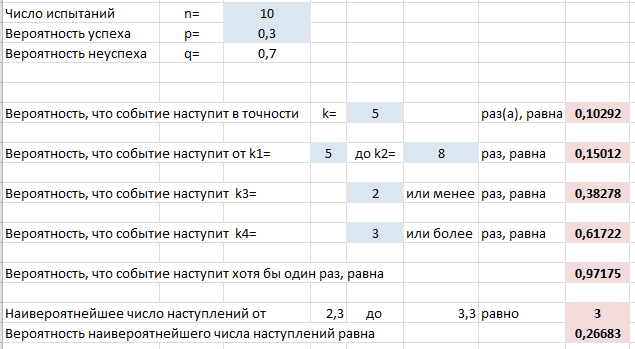
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):

  • Событие произойдет в точности $k$ раз из $n$:
    =БИНОМ.РАСП(k;n;p;0)
    $$P_n(k)=C_n^k cdot p^k cdot q^$$
  • Событие произойдет от $k_1$ до $k_2$ раз:
    =БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
    $$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$
  • Событие произойдет не более $k_3$ раз:
    =БИНОМ.РАСП(k_3;n;p;1)
    $$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$
  • Событие произойдет не менее $k_4$ раз:
    =1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
    $$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$
  • Событие произойдет хотя бы один раз:
    =1-БИНОМ.РАСП(0;n;p;0)
    $$P_n( X ge 1)=1-P_n(0)=1-q^$$
  • Наивероятнейшее число наступлений события $m$:
    =ОКРУГЛВВЕРХ(n*p-q;0)
    $$np-q le m le np+p$$

Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.

Примеры решений задач

Рассмотрим решение типовых задач.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.

Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:

$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$

Для вероятности 6 или 7 попаданий суммируем:

$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$

А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?

Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:

$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$

Наивероятнейшее число мальчиков найдем из неравенства:

$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$

Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).

Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.

Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?

Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!

Плоские алгебраические кривые в EXCEL

history 16 апреля 2015 г.
    Группы статей

  • Диаграммы и графики

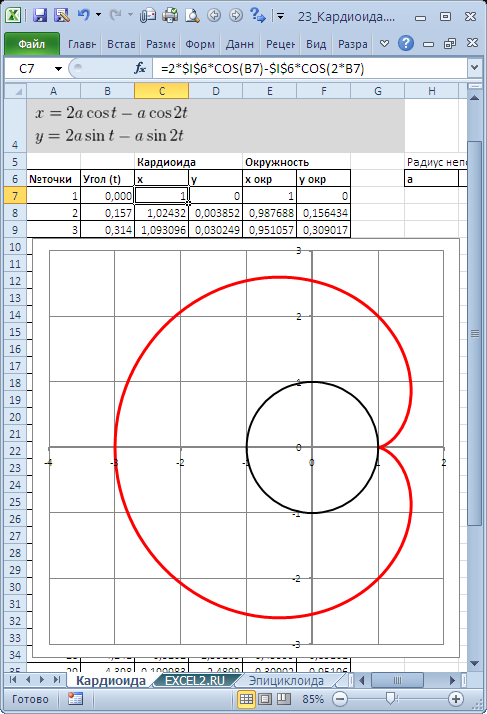
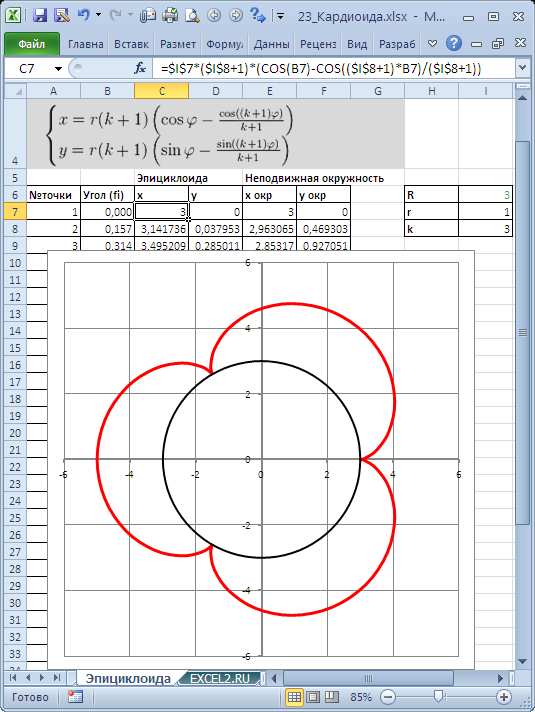
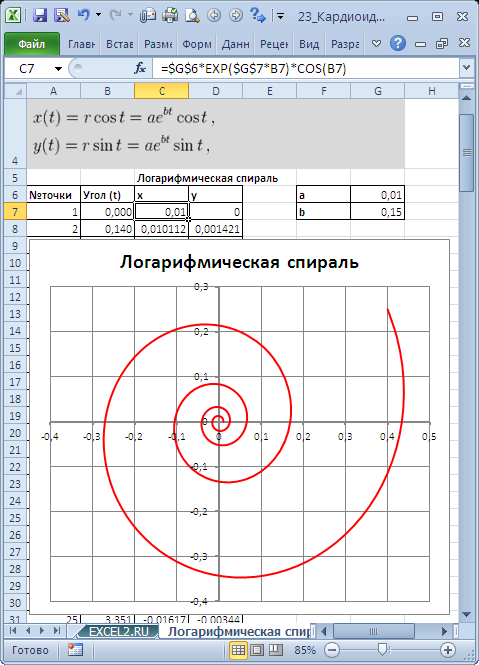
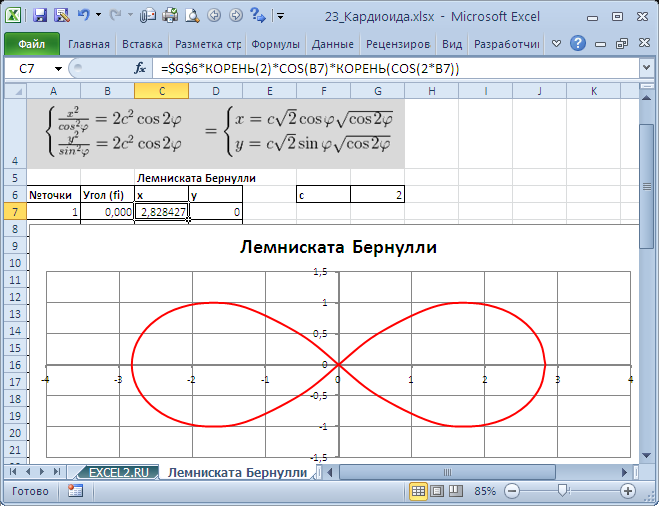
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.

Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):

Для построения использован тип диаграммы Точечная с гладкими кривыми.

В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.

СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .

Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»

Практическая работа «Красивые графики функций»

Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )

П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )

П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )

источники:

http://excel2.ru/articles/ploskie-algebraicheskie-krivye-v-ms-excel

http://pedsovet.su/excel/48255_krasivye_grafiki_v_excel

Источник

Егорова Елена 5.0

Отзыв о товаре ША PRO Анализ техники чтения по классам
и четвертям

Хочу выразить большую благодарность от лица педагогов начальных классов гимназии
«Пущино» программистам, создавшим эту замечательную программу! То, что раньше мы
делали «врукопашную», теперь можно оформить в таблицу и получить анализ по каждому
ученику и отчёт по классу. Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.

Наговицина Ольга Витальевна 5.0

учитель химии и биологии, СОШ с. Чапаевка, Новоорский район, Оренбургская область
Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ
по ХИМИИ

Спасибо, аналитическая справка замечательная получается, ОГЭ химия и биология.
Очень облегчило аналитическую работу, выявляются узкие места в подготовке к
экзамену. Нагрузка у меня, как и у всех учителей большая. Ваш шаблон экономит
время, своим коллегам я Ваш шаблон показала, они так же его приобрели. Спасибо.

Чазова Александра 5.0

Отзыв о товаре ША Шаблон Excel Анализатор результатов ОГЭ по
МАТЕМАТИКЕ

Очень хороший шаблон, удобен в использовании, анализ пробного тестирования
занял считанные минуты. Возникли проблемы с распечаткой отчёта, но надо ещё раз
разобраться. Большое спасибо за качественный анализатор.

Лосеева Татьяна Борисовна 5.0

учитель начальных классов, МБОУ СОШ №1, г. Красновишерск, Пермский край
Отзыв о товаре Изготовление сертификата или свидетельства конкурса

Большое спасибо за оперативное изготовление сертификатов! Все очень красиво.
Мой ученик доволен, свой сертификат он вложил в портфолио.
Обязательно продолжим с Вами сотрудничество!

Язенина Ольга Анатольевна 4.0

учитель начальных классов, ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Отзыв о товаре Вебинар Как создать интересный урок:
инструменты и приемы

Я посмотрела вебинар! Осталась очень довольна полученной
информацией. Всё очень чётко, без «воды». Всё, что сказано, показано, очень
пригодится в практике любого педагога. И я тоже обязательно воспользуюсь
полезными материалами вебинара. Спасибо большое лектору за то, что она
поделилась своим опытом!

Арапханова Ашат 5.0

ША Табель посещаемости + Сводная для ДОУ ОКУД

Хотела бы поблагодарить Вас за такую помощь. Разобралась сразу же, всё очень
аккуратно и оперативно. Нет ни одного недостатка. Я не пожалела, что доверилась и
приобрела у вас этот табель. Благодаря Вам сэкономила время, сейчас же
составляю табель для работников. Удачи и успехов Вам в дальнейшем!

Дамбаа Айсуу 5.0

Отзыв о товаре ША Шаблон Excel Анализатор результатов ЕГЭ по
РУССКОМУ ЯЗЫКУ

Спасибо огромное, очень много экономит времени, т.к. анализ уже готовый, и
особенно радует, что есть варианты с сочинением, без сочинения, только анализ
сочинения! Превосходно!

Источник

Понравилась статья? Поделить с друзьями:
  • Построить график систем уравнений в excel
  • Построитель формул в excel как открыть
  • Построить график с заданным шагом в excel как
  • Построитель формул в excel если
  • Построить график разброса в excel