Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x).
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон
А1:В22. - Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон
A1:V22. - Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Тип урока: урок обобщения и
систематизации знаний
Цели:
- научить строить графики тригонометрических
функций средствами MS Excel - закрепить навыки работы в электронных таблицах,
- углубить представления учащихся о взаимосвязи
предметов и прикладной ориентации курса
информатики.
ХОД УРОКА
Если вычислений много, а времени мало,
то доверьтесь электронным таблицам
1. Сообщение целей и задач урока
– Ребята, сегодня мы продолжим знакомиться с
возможностями электронных таблиц Excel. Давайте
вспомним, для чего предназначены электронные
таблицы? (Автоматизация расчетов).
– Что вы уже умеете делать в электронных
таблицах? (Создавать и форматировать таблицу,
работать с типами данных, решать задачи
используя относительную и абсолютную ссылки,
строить диаграммы).
– На уроках математики вы изучили
тригонометрические функции и их графики. При
построении графиков тригонометрических функций
необходимо учесть множество нюансов. Начертить
синусоиду или косинусоиду красиво – это уже
искусство, а если необходимо график растянуть,
сжать или симметрично отобразить относительно
какой-либо оси – это может вызвать затруднения. И
здесь нам на помощь нам придут электронные
таблицы MS Excel. Вы узнаете как с их помощью быстро и
красиво построить график.
Сегодня на уроке мы познакомимся с алгоритмом
построения графика тригонометрической функции.
Эпиграфом к уроку я взяла слова «Если
вычислений много, а времени мало, то доверьтесь
электронным таблицам»
2. Актуализация знаний
Фронтальный опрос (за правильный ответ даем
красную карточку)
- С чего начинается ввод формулы в ячейку? (Со
знака равенства) - На каком языке набирается формула в MS Excel? (Английском)
- Как скопировать формулу в другие ячейки?(С
помощью маркера автозаполнения) - Как изменить число десятичных знаков после
запятой в отображаемом числе? (Выделить,
Формат, Ячейки, вкладка Число, Числовой формат,
…..) - Что означает запись ###### в ячейке? (Длина
водимых данных превышает ширину ячейки) - Каким образом набирается формула, содержащая
какую-либо функцию? (Выделить ячейку, в которую
нужно вставить первое значение функции;Вставка,
Функция, выбрать Категорию и саму функцию) - Каким образом набирается формула, содержащая
сложную функцию, например, y = |x2|? (Вставляется
внешняя функция с пустым аргументом, затем левее
строки редактирования формул из раскрывающегося
списка выбирается внутренняя функция) - Как вставить какой-либо символ, например,
математический в ячейку? (Вставка, Символ, в
появившемся диалоговом окне выбрать шрифт Symbol и
нужный символ)
На прошлом уроке вы строили графики
элементарных функций. Давайте повторим алгоритм
построения графика (Учащиеся называют шаги
построения графика функции, а учитель показывает
соответствующий пункт алгоритма на доске
(используется проектор) и если необходимо
дополняет ответ учеников) (см. Приложение
1).
3. Изучение нового
С использованием презентации (см. Приложение
2) учитель рассказывает, как строится
график тригонометрической функций, а затем
выполняет его построение в электронных таблицах.
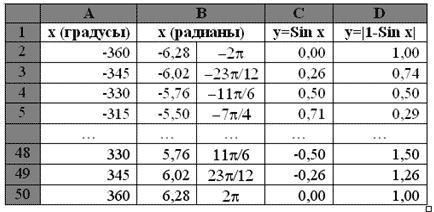
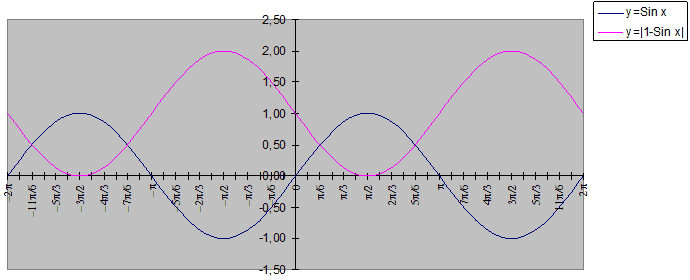
Задание. Построить в MS Excel графики
функций y = Sin x и y = |1 – sin x| на
промежутке [–360о; 360о] с шагом 15о.
Построенные графики смотри в Приложении
3
4. Закрепление полученных знаний
Каждому ученику даётся карточка с заданием и
оценочный лист, который после выполнения задания
отдается учителю (Каждый пункт в оценочном
листе является шагом построения графика
тригонометрической функции с использованием
MSExcel). Презентация находится в
сетевой папке, и любой ученик может ею
воспользоваться при выполнении своего задания.
Задание. Построить в MS Excel графики
функций на промежутке [–36о;36о] с
шагом 15о.
5. Проверка построенных графиков и разбор
нюансов
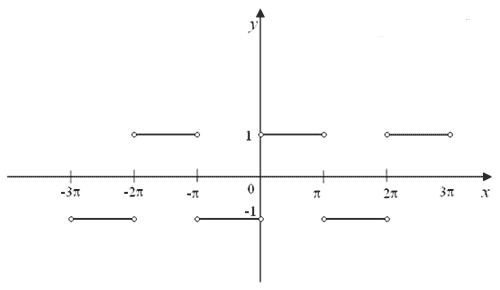
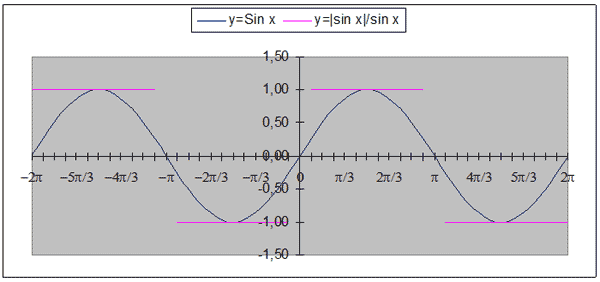
Один из учеников строил график y = |Sin x|
/ Sin x на промежутке [–360о;360о] с
шагом 15о. На доске демонстрируется этот
график и график, построенный традиционным
алгебраическим способом.
С помощью этого примера обращается внимание
учащихся, что существуют функции, графики
которых в электронных таблицах строятся неточно.
Учащихся можно попросить найти неточности в
графике, построенном с помощью MS Excel и попросить
объяснить их.
График, построенный традиционным
алгебраическим
График, построенный с использованием МS
Exel
6. Подведение итогов
Учеников просят ответить на вопросы:
- В чем достоинства и недостатки алгебраического
метода построения графиков функций и построения
графиков с использованием электронных таблиц? - Каким образом можно использовать полученные на
уроке знания в учебе?
Вывод. MS Excel облегчает построение
графиков функций, но без глубоких математических
знаний построить точные графики сложных функций
(тригонометрических функций, функций с модулем,
функций имеющих точки разрыва) невозможно.
Математика – это царица всех наук!
7. Постановка Д/З.
Построить график функции y= 1 + 0,5*ctg(X–П/4) на
промежутке [–360о;360о] с шагом 15о.
8. Рефлексия
Оцени свое настроение на уроке
Оценочный лист
|
Фамилия, имя |
Количество баллов |
| Создание заголовка таблицы |
0,2 |
| Заполнение ряда значений аргумента х в градусах |
0,1 |
| Заполнение ряда значений аргумента х в радианах (перевод градусов в радианы) |
0,5 |
| Запись формулы для вычисления значений сложной функции |
1 |
| Запись формулы для вычисления значений элементарной функции |
0,5 |
| Заполнение рядов значений функций (для обеих функций) |
0,1 |
| Установка числового формата данных |
0,2 |
| Построение графиков функций |
1 |
| Перенос оси |
0,2 |
| Подпись значений х на оси абсцисс (в градусах) |
0,2 |
| Создание ряда значений аргумента х (в радианах, например П/3) |
0,7 |
| Подпись значений х на оси абсцисс (в радианах, например П/3) |
0,5 |
|
ИТОГО |
5 |
| Если вы обращаетесь к учителю, то ставится 0 баллов |
Содержание
- Microsoft Excel
- Построение в Excel графиков математических и тригонометрических функций
- Построение графиков математических функций с одной переменной
- Построение графиков математических функций с двумя переменными
- Как построить график функции в Excel
- Как в экселе построить график косинуса?
- Видео
- Варианты построения графика функции в Microsoft Excel
- Вариант 1: График функции X^2
- Вариант 2: График функции y=sin(x)
Microsoft Excel
трюки • приёмы • решения
Построение в Excel графиков математических и тригонометрических функций
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x) .
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон А1:В22 .
- Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон A1:V22 .
- Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Источник
Как построить график функции в Excel
Построение графиков функции в Excel – тема не сложная и Эксель с ней может справиться без проблем. Главное правильно задать параметры и выбрать подходящую диаграмму. В данном примере будем строить точечную диаграмму в Excel.
Учитывая, что функция – зависимость одного параметра от другого, зададим значения для оси абсцисс с шагом 0,5. Строить график будем на отрезке [-3;3]. Называем столбец «х» , пишем первое значение «-3» , второе – «-2,5» . Выделяем их и тянем вниз за черный крестик в правом нижнем углу ячейки.
Будем строить график функции вида y=х^3+2х^2+2. В ячейке В1 пишем «у» , для удобства можно вписать всю формулу. Выделяем ячейку В2 , ставим «=» и в «Строке формул» пишем формулу: вместо «х» ставим ссылку на нужную ячейку, чтобы возвести число в степень, нажмите «Shift+6» . Когда закончите, нажмите «Enter» и растяните формулу вниз.
У нас получилась таблица, в одном столбце которой записаны значения аргумента – «х» , в другом – рассчитаны значения для заданной функции.
Перейдем к построению графика функции в Excel. Выделяем значения для «х» и для «у» , переходим на вкладку «Вставка» и в группе «Диаграммы» нажимаем на кнопочку «Точечная» . Выберите одну из предложенных видов.
График функции выглядит следующим образом.
Теперь покажем, что по оси «х» установлен шаг 0,5. Выделите ее и кликните по ней правой кнопкой мши. Из контекстного меню выберите пункт «Формат оси» .
Откроется соответствующее диалоговое окно. На вкладке «Параметры оси» в поле «цена основных делений» , поставьте маркер в пункте «фиксированное» и впишите значение «0,5» .
Чтобы добавить название диаграммы и название для осей, отключить легенду, добавить сетку, залить ее или выбрать контур, поклацайте по вкладкам «Конструктор» , «Макет» , «Формат» .
Построить график функции в Эксель можно и с помощью «Графика» . О том, как построить график в Эксель, Вы можете прочесть, перейдя по ссылке.
Давайте добавим еще один график на данную диаграмму. На этот раз функция будет иметь вид: у1=2*х+5. Называем столбец и рассчитываем формулу для различных значений «х» .
Выделяем диаграмму, кликаем по ней правой кнопкой мыши и выбираем из контекстного меню «Выбрать данные» .
В поле «Элементы легенды» кликаем на кнопочку «Добавить» .
Появится окно «Изменение ряда» . Поставьте курсор в поле «Имя ряда» и выделите ячейку С1 . Для полей «Значения Х» и «Значения У» выделяем данные из соответствующих столбцов. Нажмите «ОК» .
Чтобы для первого графика в Легенде не было написано «Ряд 1» , выделите его и нажмите на кнопку «Изменить» .
Ставим курсор в поле «Имя ряда» и выделяем мышкой нужную ячейку. Нажмите «ОК» .
Ввести данные можно и с клавиатуры, но в этом случае, если Вы измените данные в ячейке В1 , подпись на диаграмме не поменяется.
В результате получилась следующая диаграмма, на которой построены два графика: для «у» и «у1» .
Думаю теперь, Вы сможете построить график функции в Excel, и при необходимости добавлять на диаграмму нужные графики.
Источник
Как в экселе построить график косинуса?
Построить график косинуса в программе эксель несложна задача, которую нужно сделать в несколько этапов, рассмотрим каждый по отдельности:
Первый этап. Построим график косинуса от нуля до ста восьмидесяти градусов, шаг точки возьмем пятнадцать градусов.
Второй этап. Переведем градусы в радианы, для этого воспользуемся функцией «РАДИАНЫ(Х)», где «Х» — это значение в градусах, которое необходимо перевести в радианы. Сначала в ячейке «В2» пишем формулу: =РАДИАНЫ(A2), потом копируем эту формулу на другие ячейки.
Третий этап. Посчитаем значение косинуса для каждого значения, для этого сначала пропишем в ячейке «С2» формулу: =COS(B2). После снова нужно скопировать эту формулу на остальные ячейки. В итоге все готово, чтобы начать строить график косинуса.
Четвертый этап. Выделим область ячеек с «В2» по «С14». На верхней панели настроек, активируем панель «Вставка», в ней отыскиваете блок «Диаграммы» и выбираете «Точечная», после нажатия на данную иконку, отразиться выбор графиков, нужно выбрать в первой строке вторую картинку.
В итоге получаем небольшой участок графика косинуса, дальше можно его строить в обоих направления, используя вышеописанный алгоритм.
Видео
Источник
Варианты построения графика функции в Microsoft Excel
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
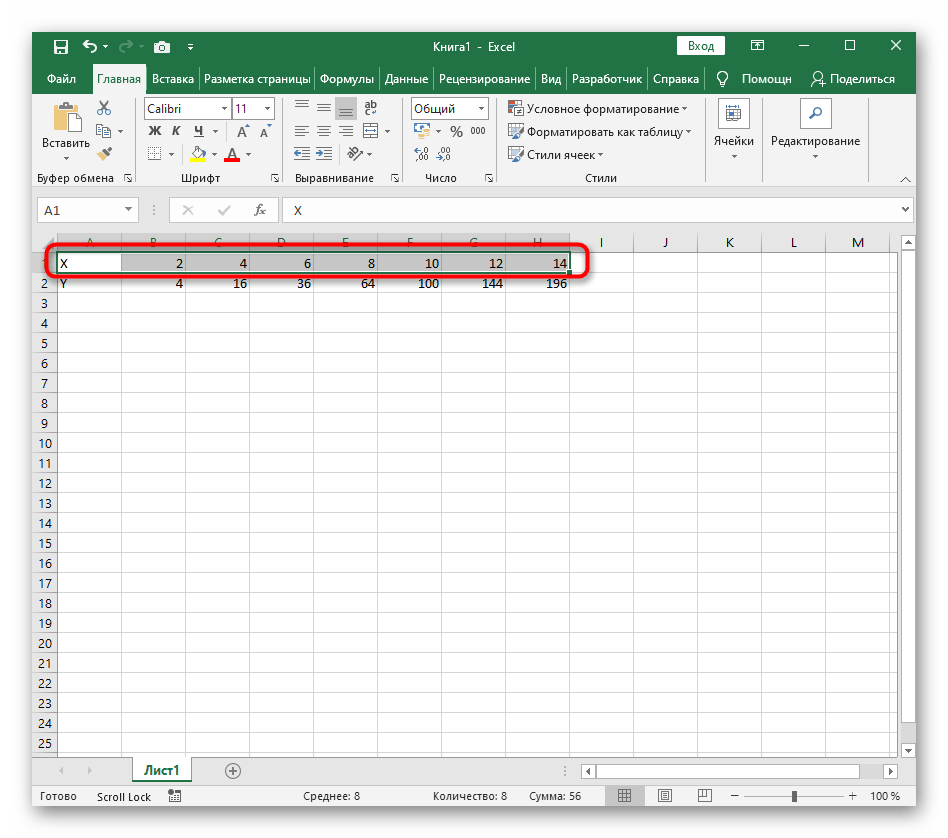
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
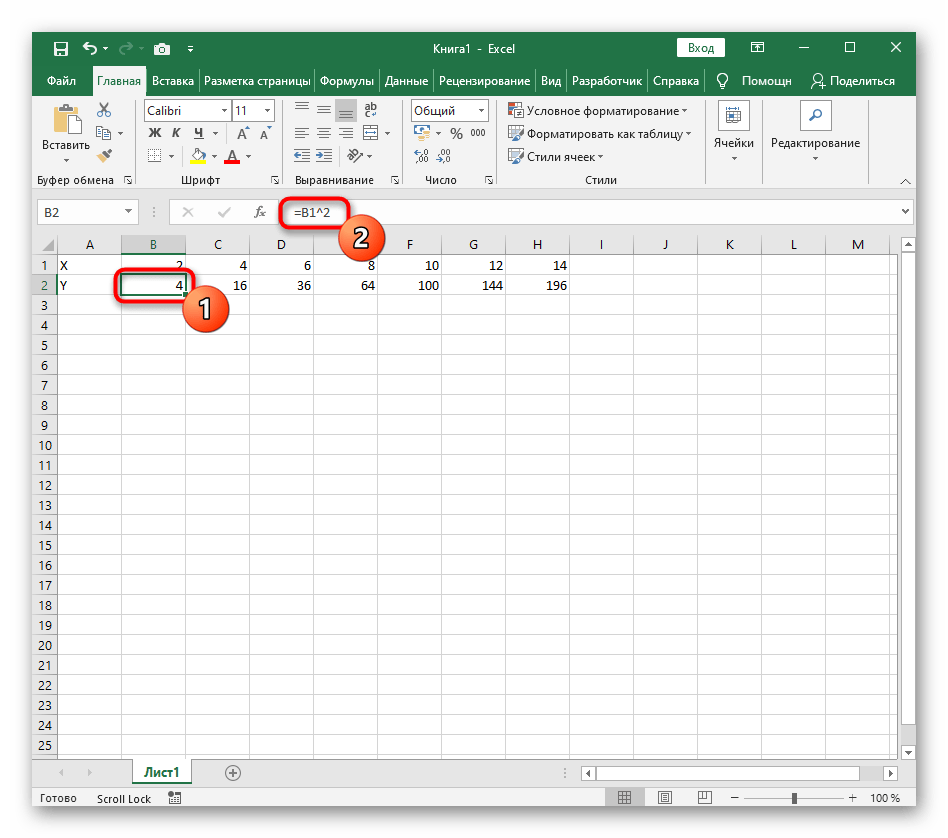
- Нажмите по первой ячейке и впишите =B1^2 , что значит автоматическое возведение указанной ячейки в квадрат.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.











Источник
Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.
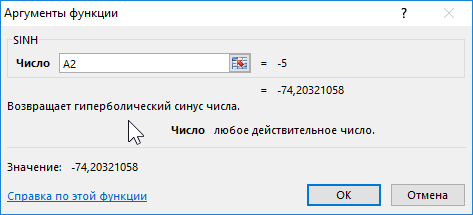
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.
Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.
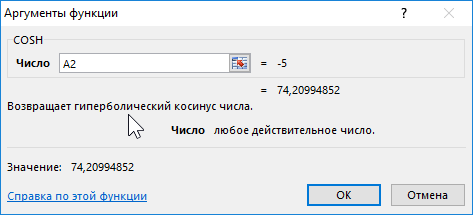
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.
Примеры использования функций SIN, SINH, COS и COSH в Excel
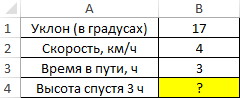
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.
Таблица данных:
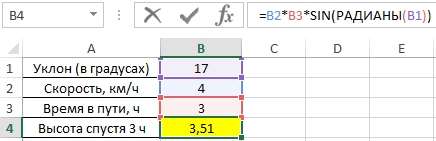
Для решения используем формулу:
=B2*B3*SIN(РАДИАНЫ(B1))
Описание аргументов:
- B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
- SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.
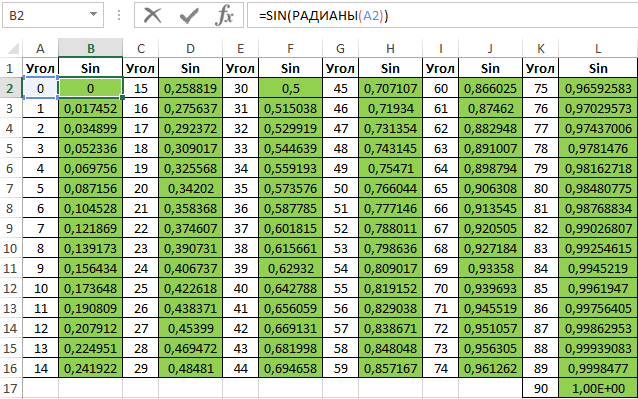
Таблица синусов и косинусов в Excel
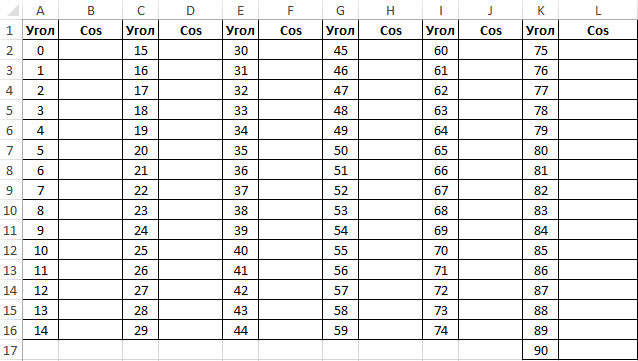
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?
Заполним столбцы значениями углов в градусах:
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:
=COS(РАДИАНЫ(A2:A16))
Вычислим значения для всех значений углов. Полученный результат:
Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.
Аналогичным способом создадим таблицу синусов в Excel:
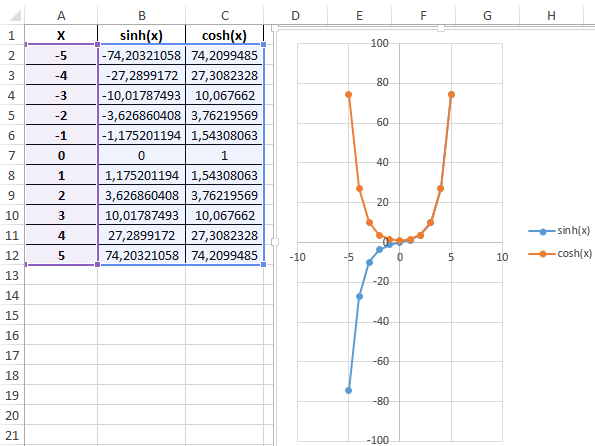
Построение графика функций SINH и COSH в Excel
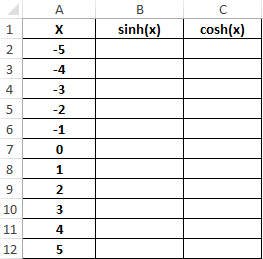
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.
Исходные данные:
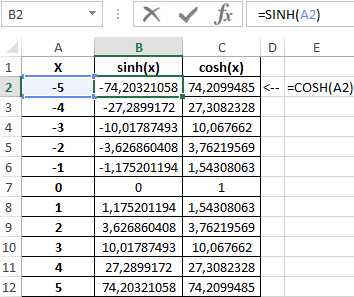
Формула для нахождения синусов гиперболических:
=SINH(A2:A12)
Формула для нахождения косинусов гиперболических:
=COSH(A2:A12)
Таблица полученных значений:
Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:
Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.
Особенности использования тригонометрических функций в Excel
Синтаксис функции SIN:
=SIN(число)
Синтаксис функции SINH:
=SINH(число)
Синтаксис функции COS:
=COS(число)
Синтаксис функции COSH:
>=COSH(число)
Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).
Примечания 1:
- Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
- В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
- Все рассматриваемые функции могут быть использованы в качестве формул массива.
Примечения 2:
- Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
- Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
- При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:
Скачать примеры тригонометрических функций SIN и COS
- Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
- Выражение ПИ()*угол_в_градусах/180.
Want to graph trigonometric equations, but don’t know where to start? Here’s how to do it in Excel like a pro.
Visualizing trigonometric equations is an important step in understanding the relationship between the X and Y axis. Without a graph, guessing a complex trigonometric equation’s behavior can become quite a challenge. Fortunately, Microsoft Excel is an excellent tool for graphing and visualizing data, including trigonometric equations.
Visualizing an equation makes it easier to grasp, and once you’ve got the hang of graphing trigonometric equations with Excel, you’ll have a better time understanding trigonometry. In this article, we’ll explain how to use Excel to graph trigonometric equations and provide a step-by-step example to help you get started.
How to Graph Trigonometric Equations With Excel
To graph an equation with Excel, you’ll need to create a chart for the X and Y values. The good news is that you don’t have to manually calculate the Y values, as Excel has an arsenal of trigonometric functions built into it.
All you need to do is create a data table with the X values, and then write an Excel formula to automatically calculate the Y values. With your data table ready, you can create an Excel chart to graph the equation.
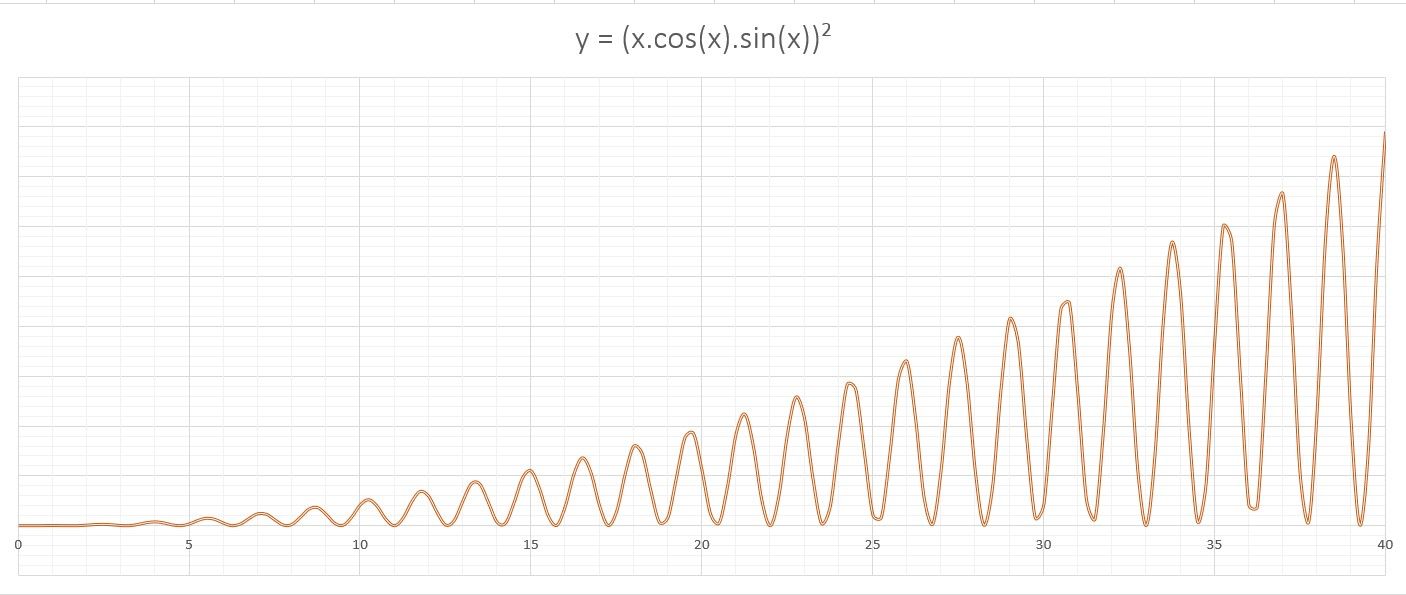
Now let’s put this outline to use and graph the y = (x.cos(x).sin(x))² equation. This equation is tough to imagine just by looking at it, but you can save yourself the burden by quickly graphing the equation with Excel.
1. Input the X Values
A graph needs X and Y values. You can enter the domain you want to graph in the X values, and then calculate the Y values with a formula in the next step. It’s a good idea to create a table for your data, as it will enable Excel’s autofill feature.
The smaller the increment between your X values is, the more accurate your graph will be. We’re going to have each X value increase by 1/4 in this table. Here’s how you can automatically input the X values:
- Type in the first value in a cell. In this example, we’re going to type -3 in cell A3.
- Select the cell below. That’s A4 in our case.
- In the formula bar, enter the formula below:
=A3+1/4 - Press Enter.
- Grab the fill handle and drop it into the cells below.
Excel will now fill in all the other X values. The advantage of using a formula to input the values is that you can now quickly change the values by editing the first value or altering the formula.
2. Create a Formula to Calculate the Y Values
With the X values in place, it’s time to calculate the Y values. You can calculate the Y values by translating the trigonometric equation into Excel’s language. It’s essential that you have an understanding of the trigonometric functions in Excel to proceed with this step.
When creating your formula, you can use a circumflex (^) to specify the power. Use parentheses where needed to indicate the order of operations.
- Select the first cell where you want to calculate the Y value. That’s B3 in our case.
- Go to the formula bar and enter the formula below:
=(A3*COS(A3)*SIN(A3))^2 - Press Enter.
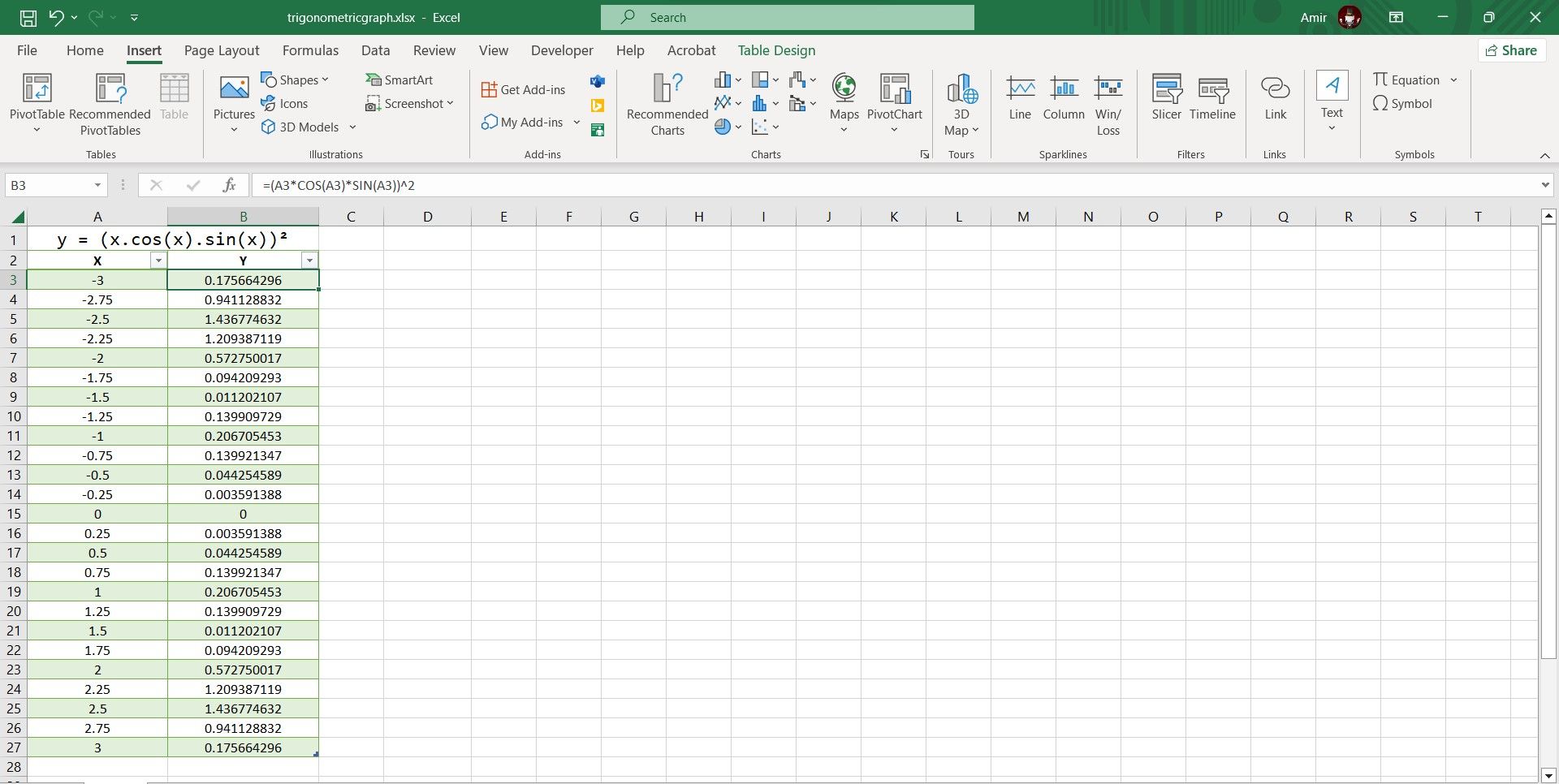
Excel will now calculate all Y values in the table. Excel’s trigonometric functions use radians, so this formula will perceive the X values as radians as well. If you want your X-axis to be on a pi-radian scale rather than a radian scale, you can multiply the cell reference by pi using the PI function in Excel.
=(A3*PI()*COS(A3*PI())*SIN(A3*PI()))^2
The formula above will output the Y values for the same trigonometric equation, but the values will be on a pi-radian scale instead.
3. Create a Scatter Plot Chart
A scatter plot is the best way to graph a trigonometric equation in Excel. Since you’ve got your X and Y values ready, you can graph your equation with a single click:
- Select the table containing the X and Y values.
- Go to the Insert tab.
- In the Charts section, click on Scatter and then select Scatter with Smooth Lines.
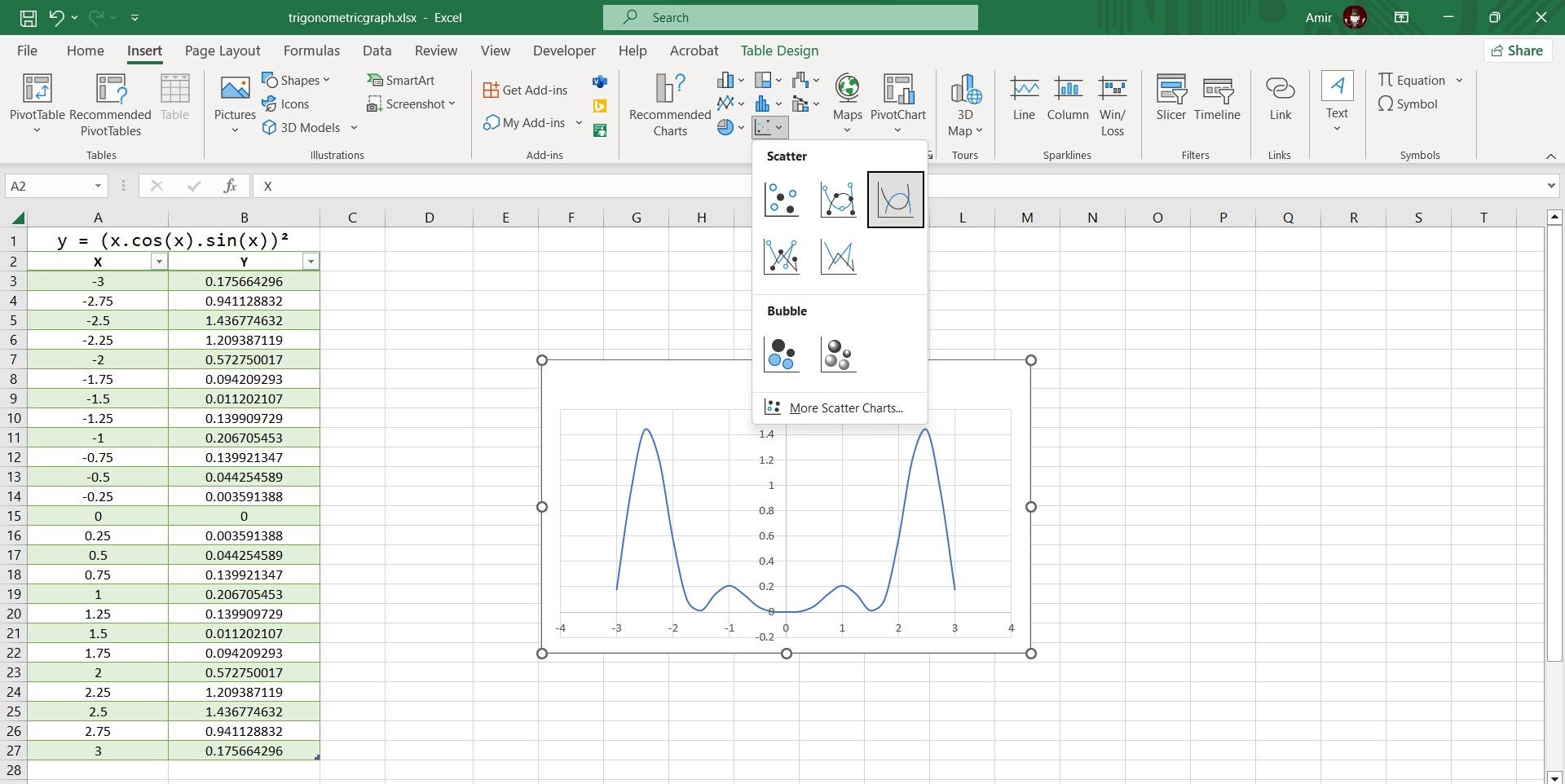
There you have it! You can now inspect the graph to better understand the equation’s behavior. This is the last step if you’re looking for a quick visualization, but if you want to present the graph, you can fully customize the Excel chart to properly graph the trigonometric equation.
4. Modify the Excel Chart
Although the chart does display the graph, you can make some changes to improve the chart’s readability and make it more presentable. There are lots of things you can customize to improve the chart, and in the end, it’s a matter of personal preference. Still, here are some adjustments that can always improve your trigonometric graph.
I. Set the Axis Units and Add Tick Marks
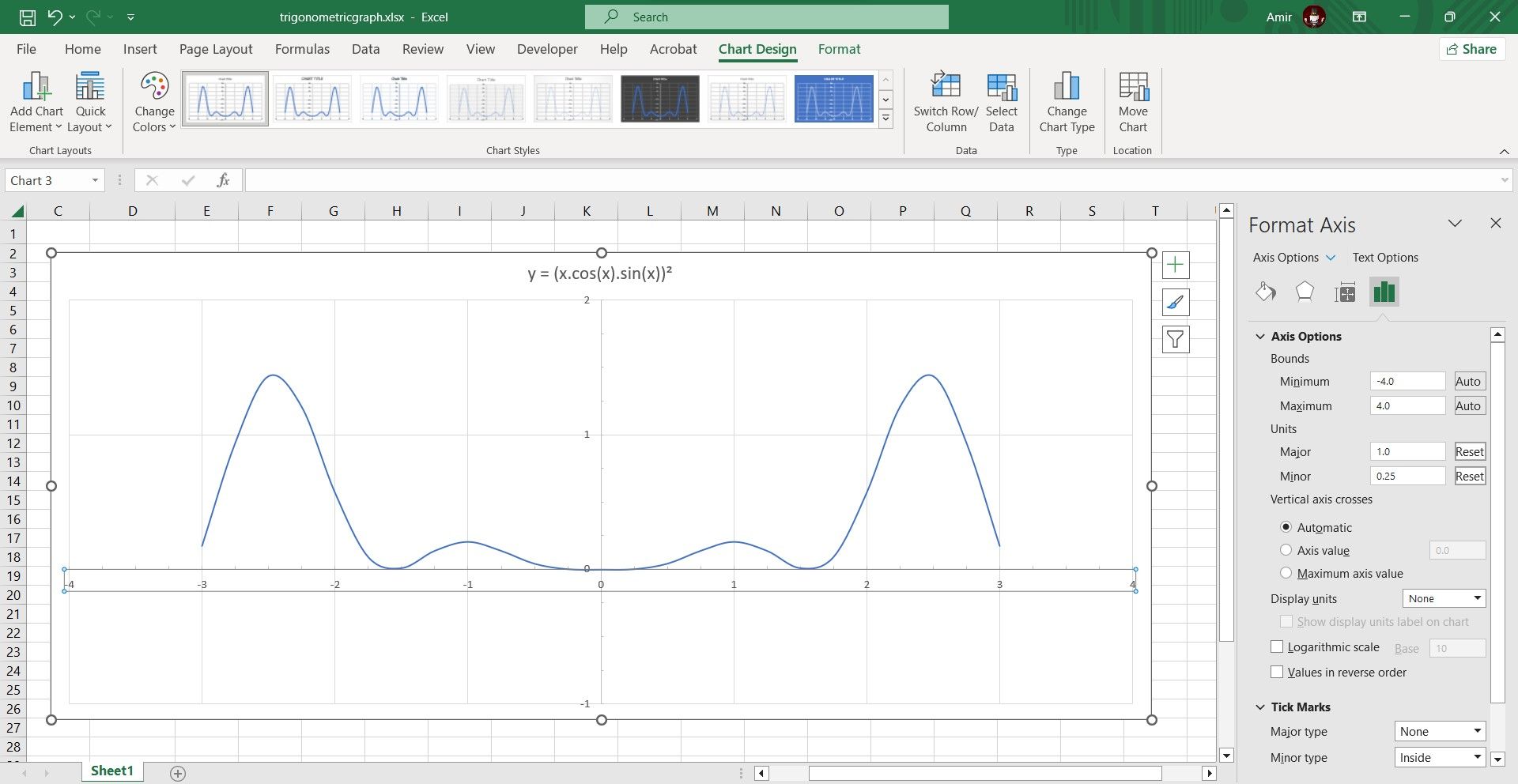
If you take a closer look at your chart, you’ll see that the horizontal and vertical grid lines aren’t the same unit. Here’s how you can fix that:
- Click on the chart to select it.
- Double-click the axis. This will bring up Format Axis on the right.
- In Format Axis, find Units under Axis Options and change Major and Minor.
- Go to Tick Marks and change Minor type to what you want.
Repeat the same process for the other axis, and make sure that you use the same major and minor units for both. Your graph should look tidier now.
II. Add Minor Gridlines
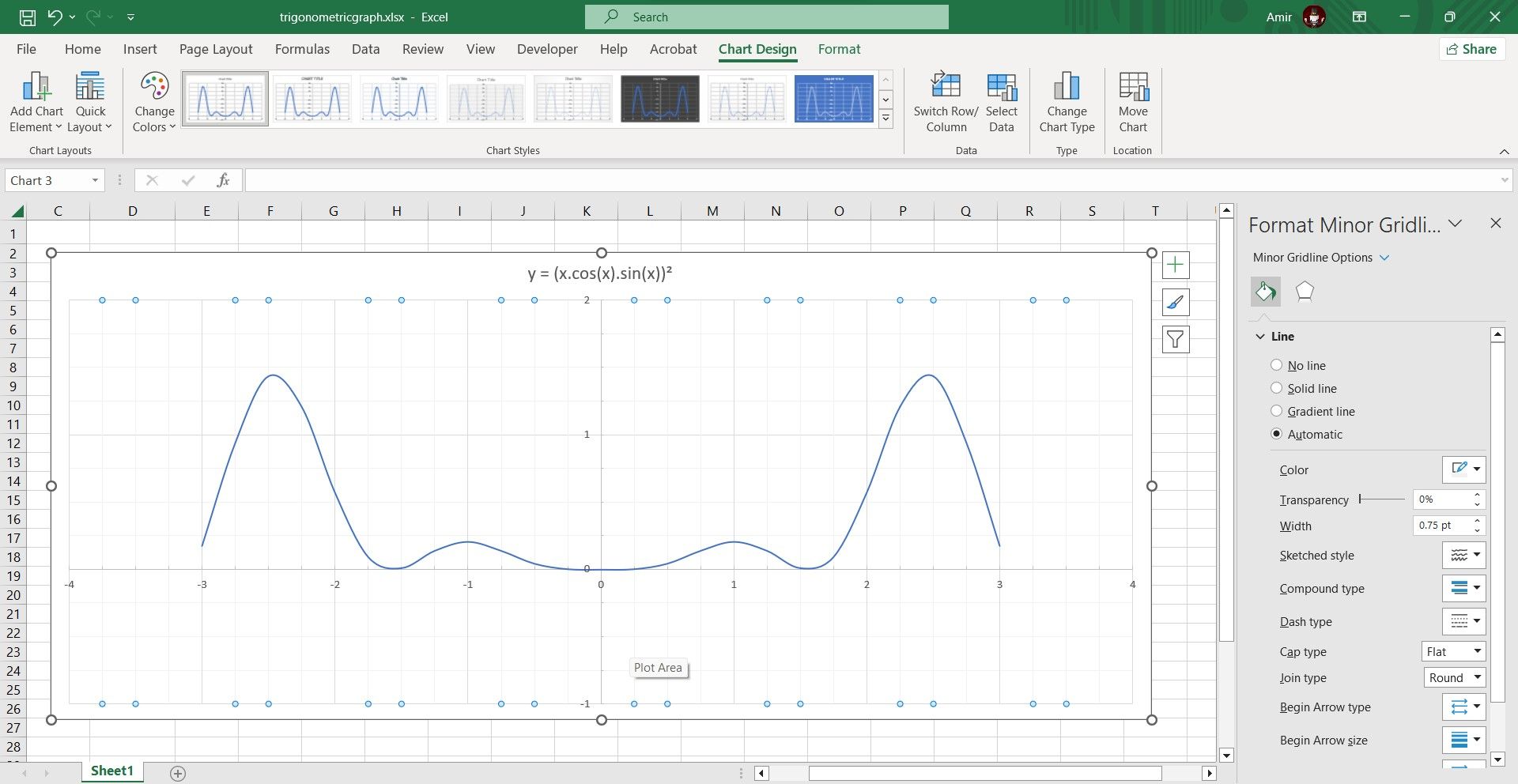
You can add minor gridlines to make the graph easier to read. To do this, simply right-click on the axis and then select Add Minor Gridlines. Repeat the process for the other axis to add gridlines there as well. You can then right-click the axis and select Format Minor Gridlines to change their appearance.
III. Add Axis Titles
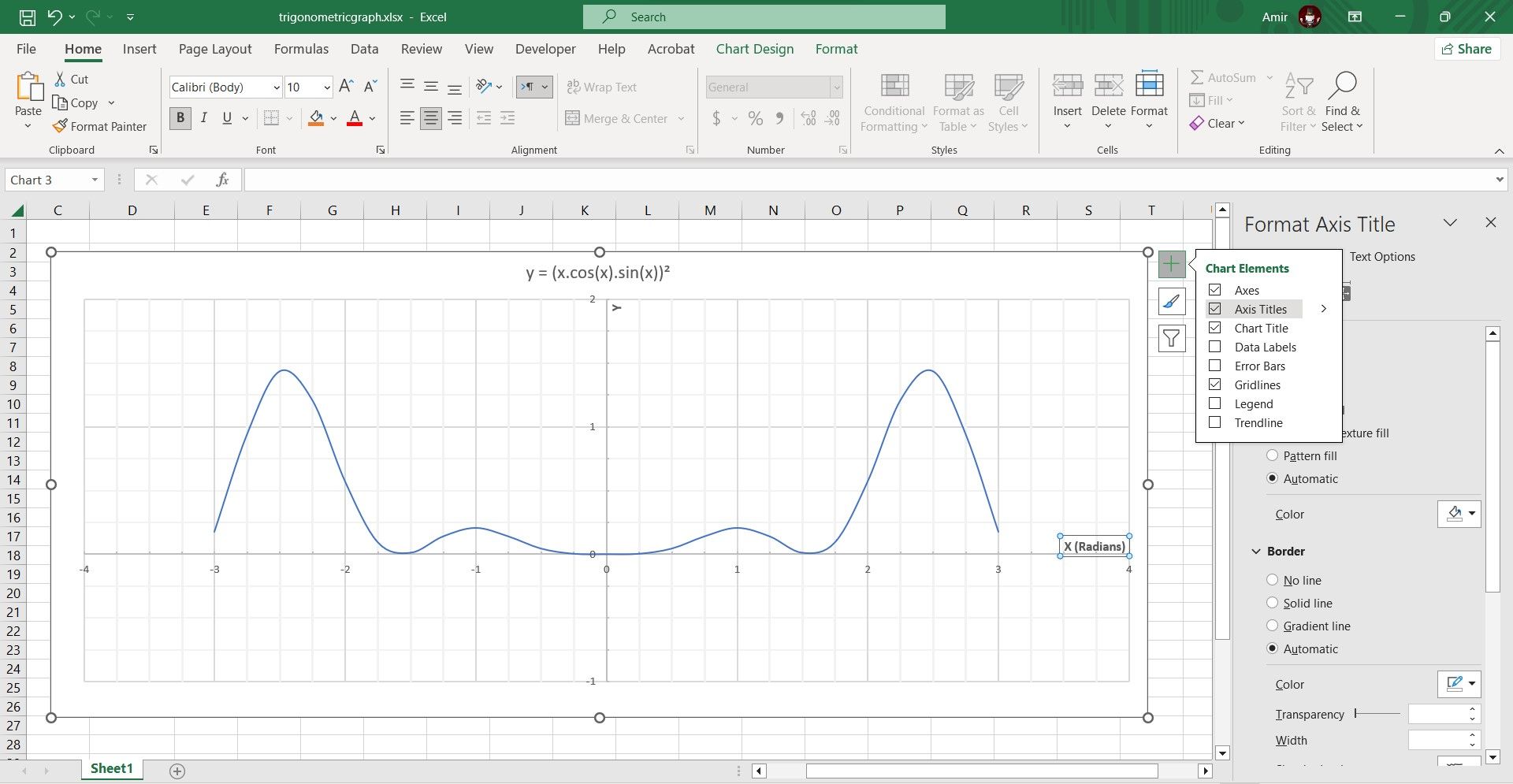
Although it’s obvious that the horizontal axis is displaying the X values, you can add a title to specify that the values are in radians. This prevents confusion with pi-radians.
- Select the chart.
- Click on Chart Elements on the top right. This is marked with a + sign.
- Select Axis Titles.
- Double-click the axis titles and edit the text.
IV. Add Data Callouts
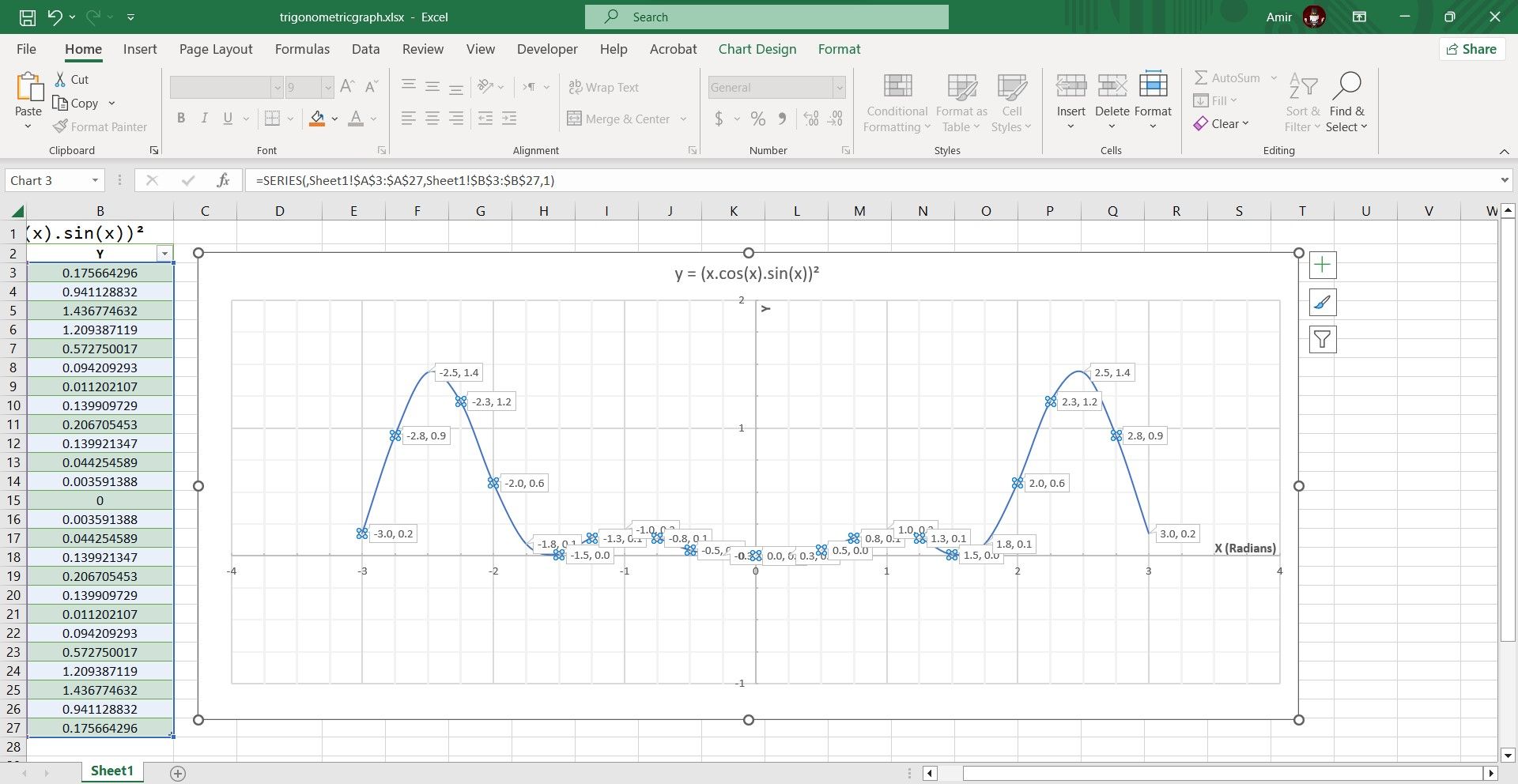
Finally, you can add callouts to identify the minimum and maximum points on your graph. Here’s how you can do that:
- Select the chart.
- Right-click the series line.
- Go to Add Data Labels and then select Add Data Callouts.
If some of the callouts seem unnecessary to you, you can individually select them and then press Del on your keyboard to delete the callout.
Graph It Properly With Excel
Visualizing an equation is vital to understanding it. This is especially true when you’re dealing with complex trigonometric equations and can’t quickly guess the values. Well, there’s no need to tax your brain to get a mental image of an equation. You can use Excel to efficiently graph a trigonometric function.
The only elements that you need to manually input are the starting X value and the increment. From there, you can have Excel automatically fill in the X values. Thanks to its array of trigonometric functions, you can easily turn your equation into an Excel formula and calculate the Y values as well.
With both the X and Y values set out in a table, graphing the equation is only a matter of selecting the data and creating a scatter plot to visualize it.