Фев 04 2021
Вроде простая вещь — нужно вычислить результат для нескольких булевых переменных
Читаем основную статью
Компьютер
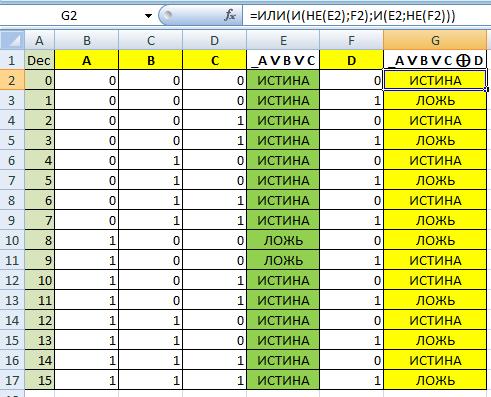
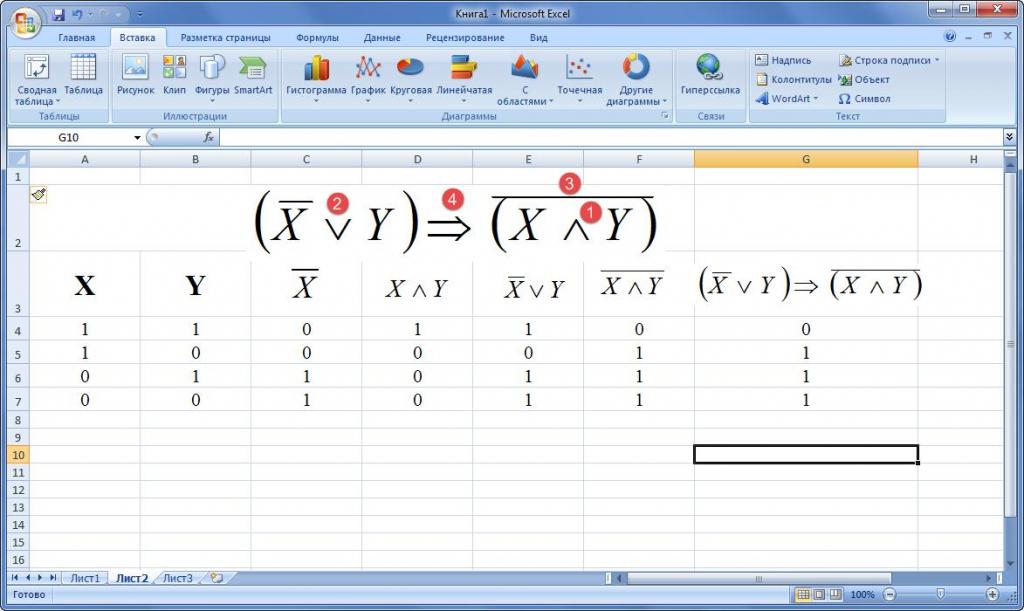
Вроде всё просто. Но вот такой пример вида _A ∨ B ∨ C ⊕ D
Переводим на русский язык (с математического языка) — нужно сделать таблицу истинности для выражения
не A или B или C иск.или D
для всех вариантов переменных A,B.C.D, которые могут принимать значения «Истина» / «Ложь»
Или на английском (для программирования) = not.A.or.B.or.C.xor.D
Задача на булеву алгебру не сложная — но у нас четыре переменных и 16 строк в таблице (да, 24 = 16). А если таких переменных будет 5, то в таблице будет 32 строки.
Но у нас есть Excel (Execute Cell), который прекрасно понимает формулы логики. Достаточно правильно написать формулу для одной строки — и потом мышкой перетащить эту формулу на остальные строки. Готово!
Итак по частям.
Логическая операция это операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логическая связка это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
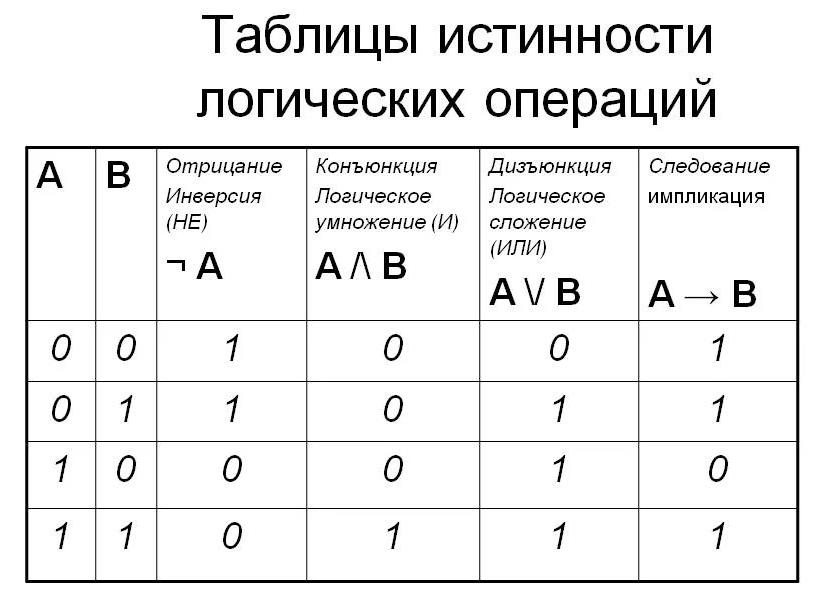
Логические операции
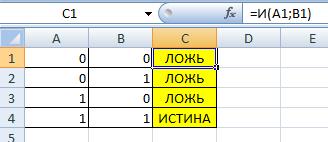
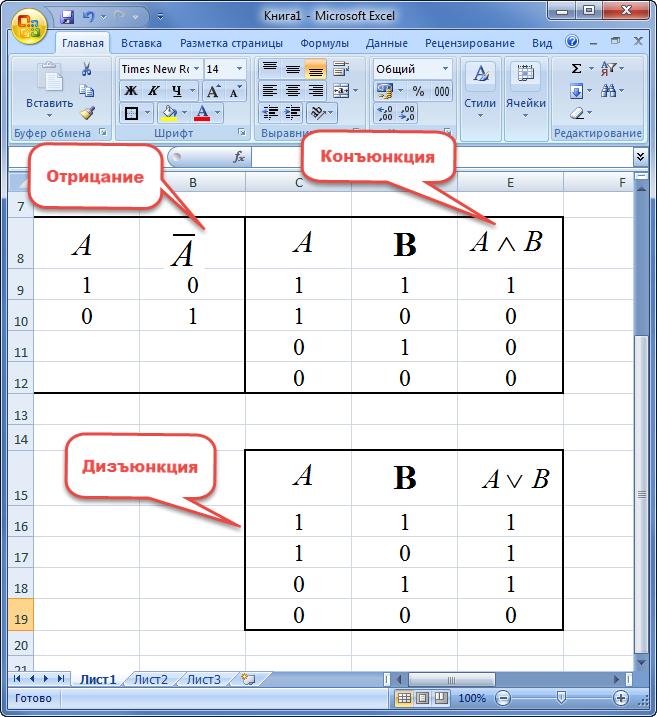
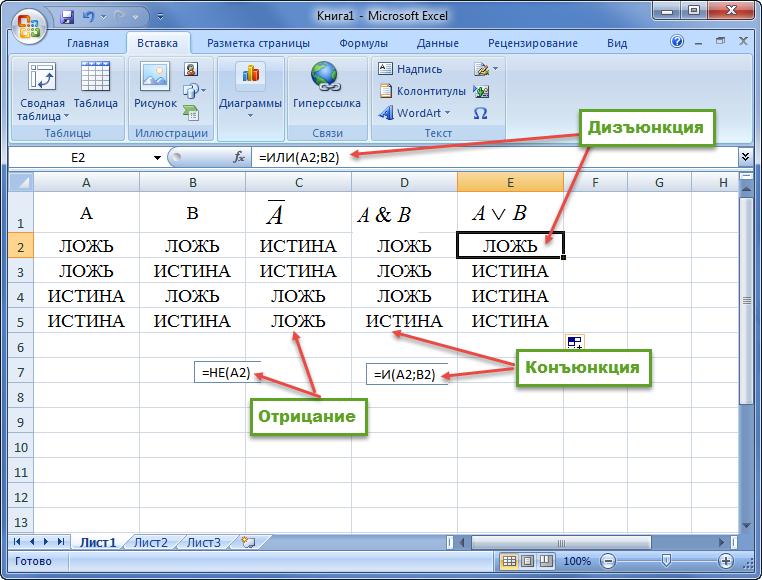
Логическая операция И (Конъюнкция)
Конъюнкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логическое «И», логическое умножение, иногда просто «И»
И таблица истинности (AND таблица истинности)
=И(A1;B1)
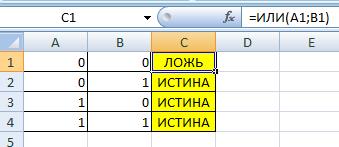
Логическая операция ИЛИ (Дизъюнкция)
Дизъюнкция (от лат. disjunctio — «разобщение») — логическое сложение, логическое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»
ИЛИ таблица истинности (OR таблица истинности)
=ИЛИ(A1;B1)
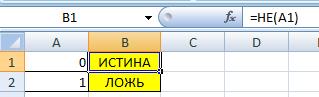
Логическая операция отрицания (Инверсия)
Инверсия (от лат. inversio «переворачивание; перестановка») — отрицание — переворачивание смысла, замена «белого» «чёрным»
НЕ таблица истинности (NOT таблица истинности)
=НЕ(A1)
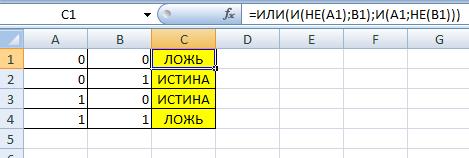
Логическая операция XOR (исключающее ИЛИ)
XOR таблица истинности
В Excel 2007 её нет.
В более современных версиях она есть. Но мы её можем собрать самостоятельно.
=ИЛИ(И(НЕ(A1);B1);И(A1;НЕ(B1)))
Логические связки
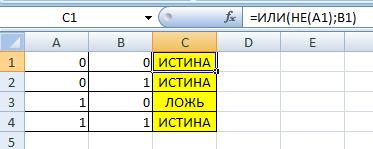
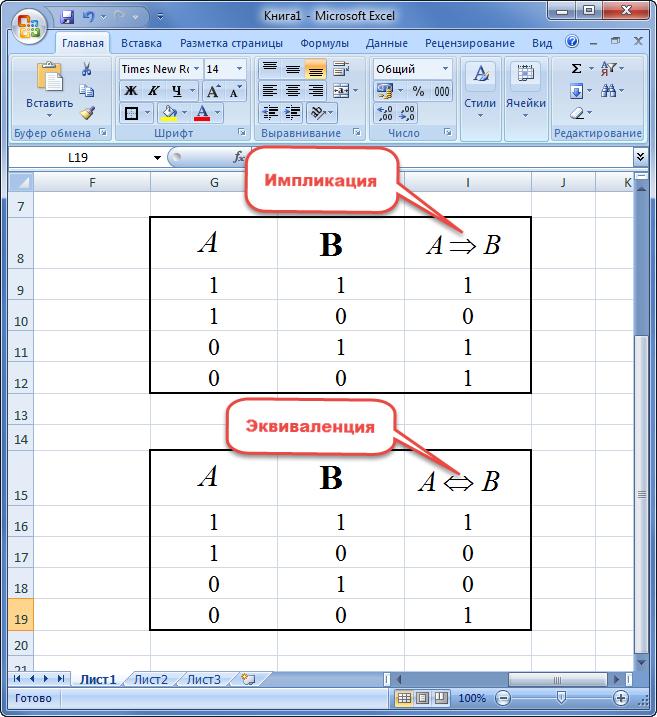
Логическая связка Импликация (прямая)
Логическая связка как A → B
используем аналог _A V B
=ИЛИ(НЕ(A1);B1)
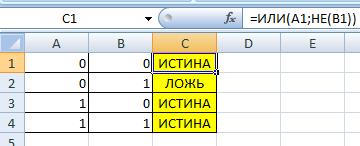
Логическая связка Импликация (обратная)
Логическая связка как A ← B
используем аналог A V _B
=ИЛИ(A1;НЕ(B1))
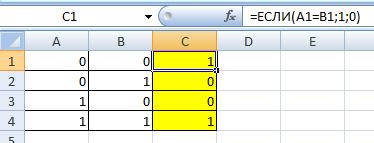
Логическая связка ТОЖДЕСТВО
Используем ЕСЛИ, чтобы логическая связка получилась
=ЕСЛИ(A1=B1;1;0)
или вывод текстом
=ЕСЛИ(A1=B1;"ИСТИНА";"ЛОЖЬ")
Собираем таблицу истинности
Не обязательно собирать всё в одной ячейке. Можно сделать столбцы для промежуточных вычислений.
Для нашего примера _A ∨ B ∨ C ⊕ D
Удобно.
Последние публикации
- Статьи от: Автор
- Рубрика: Блог
- Сортировка: дата публикации по убыванию
Классический вход Windows 7
Публикация 2 года назад
Как это было в Windows XP Для входа в систему нужно указать: пользователь (login)
пароль В Windows 7 сделали по умолчанию стандартный вход в систему Мышкой выбираем пользователя и вводим только пароль (если он установлен). Как вернуть классический вход в систему Windows 7 и зачем это нужно? Для работы на локальной машине — конечно удобнее стандартный вход. А вот если Вы подключаетесь к удаленной машине через RDP — то ввода только пароля недостаточно. Читаем статью RDP — удаленный рабочий стол Большое количество ботов со всего мира подберет Ваш пароль достаточно быстро (в логах будет по 5-10 попыток в секунду). Читаем статью Включаем шифрование…
(Читать полностью…)
Процессоры AMD FX и их «ядра»

Публикация 2 года назад
Немного маркетинга в тему — ядра процессоров AMD FX и ядра процессоров Intel AMD FX (AM3+) — хорошие были процессоры. Но есть нюанс. AMD использовала хитрую терминологию — «ядра» и «модули». Это была вершина маркетинга 
Одно…
(Читать полностью…)
Загадочная «маска подсети» — это просто
Публикация 2 года назад
Многие видели в Windows свойства адаптера сети при ручной настройке Многие даже понимают, что IP-адрес 192.168.1.1 — это запись в десятичной форме 32-х бит адреса IP v4 с разбивкой на оксеты (по 8 бит). Что такое «маска подсети»?
Которая 255.255.255.0. И зачем она нужна? Посмотрим в таком же двоичном виде — легко видеть, что это 24 единицы подряд Это просто так айтишники шутят 
(Читать полностью…)
Вычисляем большие числа

Публикация 2 года назад
Самое известное большое число googol — отсюда собственно название Google 10100 = это 1 единица и 100 нулей Хорошо. А например, 2512 — это сколько? Калькулятор Windows говорит, что это 1,3 * 10154 Тоже неплохо, да и больше чем googol на 54 порядка 
(Читать полностью…)
Как соединить два роутера проводом?
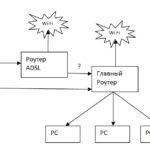
Публикация 3 года назад
Предположим, у нас есть «Главный роутер», который управляем всеми нашими устройствами PC. И еще есть: у «Главного роутера» второй WAN-порт
бесхозный ADSL роутер Простой вопрос — как сделать резервирование интернета? Что бы при отсутствии основного интернета можно было подключить и использовать «Роутер ADSL»? Основная статья про сеть здесь Варианты в лоб: использовать только «Роутер ADSL» — но это придется к нему переподключать все конечные ПК
и сетку Wi-Fi придется перестраивать для переподключения мобильных устройств Нехорошо 
(Читать полностью…)
Как не надо устанавливать SSD M.2

Публикация 3 года назад
Иногда вот такая жесть бывает при установке SSD M.2. Небольшой изгиб, так сказать. Основная статья про M.2 тут Интерфейс NVMe и разъемы M.2 и U.2 Как это получилось? Обычно так бывает при самостоятельной сборке ПК из новых комплектующих. SSD M.2 устанавливается под 45% в разъем на плате и потом прижимается винтиком, которые вкручивается в другой винтик на материнской плате. Но почему этот основной винтик «пенек» может отсутствовать на материнской плате? Вот тут хорошо видно проблему 
или кладет все…
(Читать полностью…)
Как набрать немецкие умляуты (umlaut) на обычной клавиатуре в России?

Публикация 3 года назад
Будем разбираться с немецкими умляутами Делаем свой набор горячих клавиш (hotkey) для умляутов
Самый удобный вариант 
R Alt A
Ä
ä O
Ö
ö U
Ü
ü S
ẞ
ß Здесь символы A, O, U и S — это не буквы, а кнопки на клавиатуре. Как это сделать? Используем программу QuickTextPaste — в ней можно завязать не только отдельные буквы, и целые части текста. Настройки хранятся в C:UsersNameAppDataRoamingQuickTextPasteQuickTextPaste.ini Использование простое: добавляем комбинацию клавиш
…
(Читать полностью…)
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.

Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
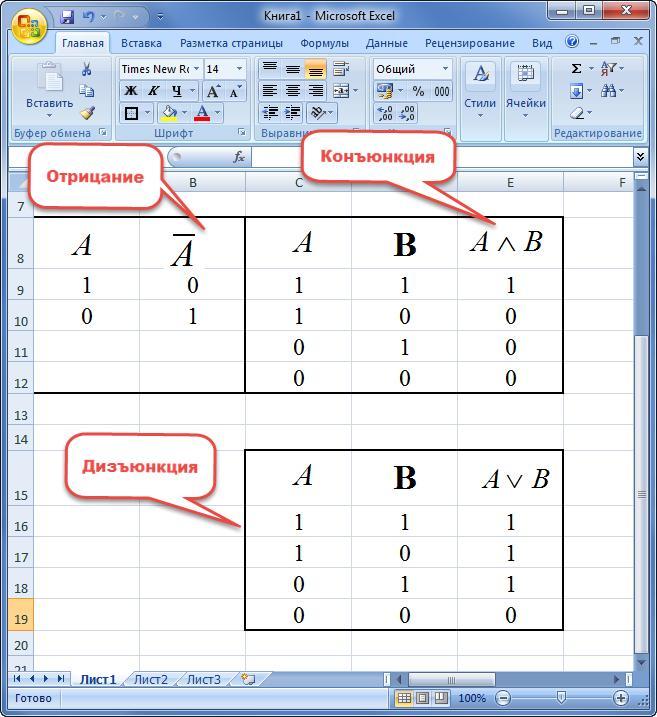
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
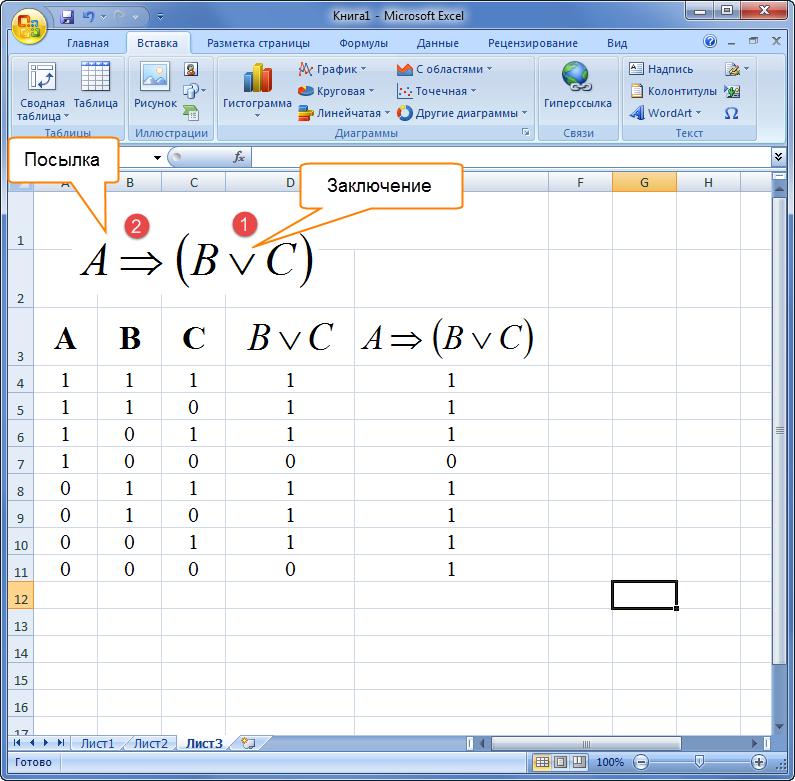
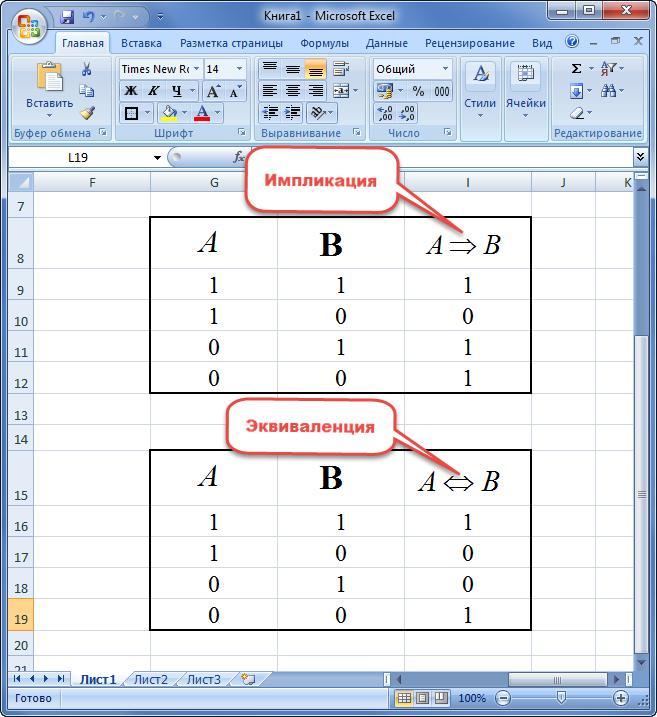
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
- штрих Шеффера;
- стрелка Пирса.
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
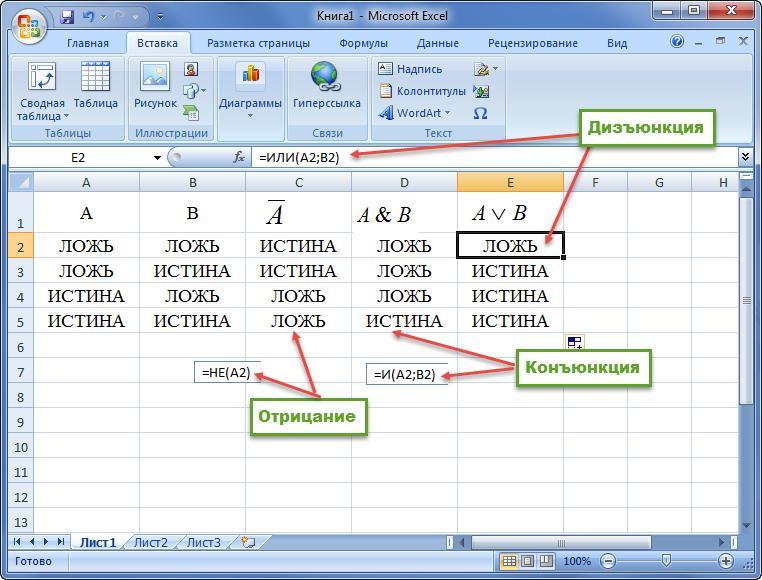
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
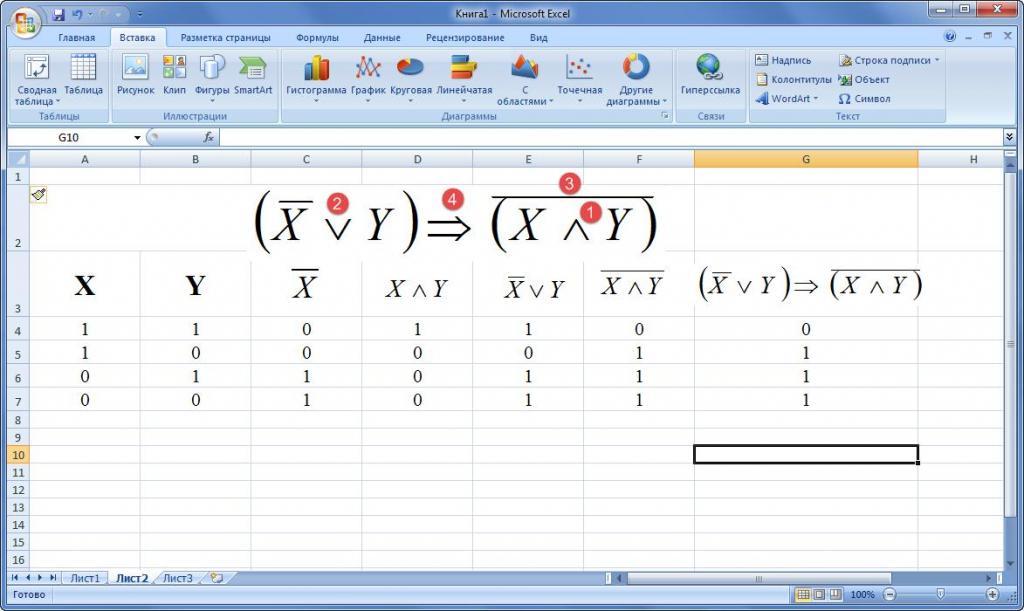
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
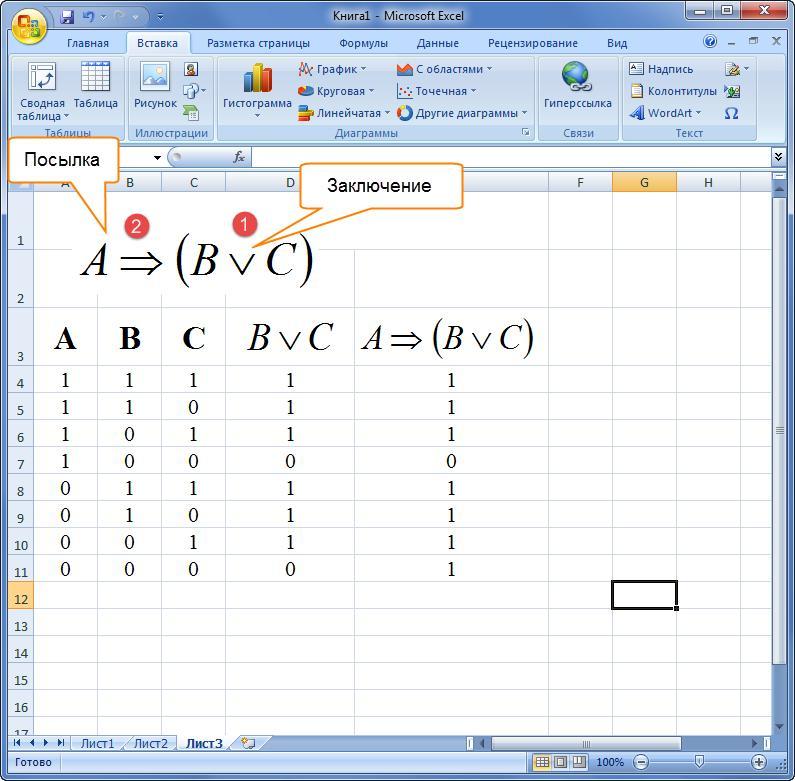
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Автор:
03-12-2018 21:56
Жду ваши вопросы и мнения в комментариях
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
- если посылка истинна, а следствие ложно, то выражение равняется «0»;
- высказывание равняется «1» в остальных случаях.
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
- инверсия (отрицание);
- конъюнкция (логическая функция в Excel «И»);
- дизъюнкция (булев оператор в Excel «ИЛИ»);
- импликация (следствие);
- эквиваленция.
Существуют еще две операции, но для них приоритет не определен:
- штрих Шеффера;
- стрелка Пирса.
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
- Первая часть выражения: А = «треугольник равносторонний».
- Вторая: В = «все стороны фигуры равны».
- Третья: С = «все углы треугольника равны».
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Содержание
- 1 Примеры использования логических функций ИСТИНА, ЛОЖЬ и НЕ в Excel
- 2 Как посчитать среднее значение по условию в Excel
- 3 Как получить значение по модулю числа без использования функции ABS
- 4 Таблицы истинности для основных двоичных логических функций
- 5 Порядок выполнения логических операций
- 6 Примеры решения задач
Функция ИСТИНА в Excel предназначена для указания логического истинного значения и возвращает его в результате вычислений.
Функция ЛОЖЬ в Excel используется для указания логического ложного значения и возвращает его соответственно.
Функция НЕ в Excel возвращает противоположное указанному логическому значению. Например, запись =НЕ(ИСТИНА) вернет результат ЛОЖЬ.
Пример 1. В таблице Excel хранятся телефонные номера различных организаций. Звонки на некоторые из них являются бесплатными (с кодом 8800), на остальные – платные по тарифу 1,5 руб/мин. Определить стоимость совершенных звонков.
Таблица данных:
В столбце «Бесплатный» отобразим логические значения ИСТИНА или ЛОЖЬ по следующему условию: является ли код номера телефона равным «8800»? Введем в ячейку C3 формулу:
Описание аргументов:
- ЛЕВСИМВ(B3;4)=»8800″ – условие проверки равенства первых четырех символов строки указанному значению («8800»).
- Если условие выполняется, функция ИСТИНА() вернет истинное логическое значение;
- Если условие не выполнено, функция ЛОЖЬ() вернет ложное логическое значение.
Аналогично определим является ли звонок бесплатным для остальных номеров. Результат:
Для расчета стоимости используем следующую формулу:
Описание аргументов:
- C3=ИСТИНА() – проверка условия «является ли значение, хранящееся в ячейке C3 равным значению, возвращаемым функцией (логическое истина)?».
- 0- стоимость звонка, если условие выполнено.
- D3*1,5 – стоимость звонка, если условие не выполнено.
Результаты расчетов:
Мы получили суммарную стоимость вех совершенных звонков по всем организациям.
Как посчитать среднее значение по условию в Excel
Пример 2. Определить средний балл за экзамен для группы студентов, в составе которой есть студенты, которые его провалили. Так же необходимо получить среднюю оценку успеваемости только лишь для тех студентов, которые сдали экзамен. Оценка студента, не сдавшего экзамен, должна учитываться как 0 (нуль) в формуле для расчета.
Таблица данных:
Для заполнения столбца «Сдал» используем формулу:
Результат вычислений:
Создадим новый столбец, в который перезапишем оценки при условии, что оценка 2 интерпретируется как 0 с использованием формулы:
Результат вычислений:
Определим средний балл по формуле:
=СРЗНАЧ(D3:D14)
Результат:
Теперь получим средний балл успеваемости, для студентов, которые допущены к следующим экзаменам. Для этого воспользуемся еще одной логической функцией СРЗНАЧЕСЛИ:
Как получить значение по модулю числа без использования функции ABS
Пример 3. Реализовать алгоритм определения значения модуля числа (абсолютную величину), то есть альтернативный вариант для функции ABS.
Таблица данных:
Для решения используем формулу массива:
=ЕСЛИ(НЕ(A3:A100, функция НЕ будет возвращать ЛОЖЬ.
Если единственным аргументом функции НЕ является текстовая строка, функция вернет код ошибки #ЗНАЧ!. В вычислительной технике используется специальный логический тип данных (в программировании имеет название «булев» тип или Boolean в честь известного математика Джорджа Буля). Этот тип данных оперирует всего двумя значениями: 1 и 0 (ИСТИНА, ЛОЖЬ). В Excel истинному логическому значению также соответствует число 1, а ложному логическому значению – также числовое значение 0 (нуль). Функции ИСТИНА() и ЛОЖЬ() могут быть введены в любую ячейку или использоваться в формуле и будут интерпретированы в качестве логических значений соответственно. Обе рассмотренные выше функции необходимы для обеспечения совместимости с другими программными продуктами, предназначенными для работы с таблицами. Функция НЕ позволяет расширить возможности функций, предназначенных для выполнения логической проверки. Например, при использовании данной функции в качестве аргумента лог_выражение функции ЕСЛИ, можно обеспечить проверку сразу нескольких условий.
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.
Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквиваленция
- Штрих Шеффера
- Стрелка Пирса
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
Лабораторная работа
по теме «Построение таблиц истинности с помощью электронных таблиц Excel»
Цель работы: познакомиться с логическими функциями Excel, научиться строить таблицы истинности сложных высказываний.
Порядок выполнения работы.
1.Найдите обозначения логических функций, которые имеются в Excel
2.Используя Мастер функций , начните заполнять таблицу:
|
A |
B |
C |
D |
E |
|
|
A |
B |
Не А |
A&B |
А или В |
|
|
ложь |
ложь |
||||
|
ложь |
истина |
||||
|
истина |
ложь |
||||
|
истина |
истина |
3. Используя Мастер функций , продолжите заполнение таблицы.
А) В ячейку С2 занесите формулу : =НЕ(А2).
В ячейку D2 занесите формулу : =И(А2;В2).
В ячейку Е2 занесите формулу : =ИЛИ(А2;В2).
Б) Выделяйте ячейки С2:Е2.
В) Скопируйте выделенный блок в ячейки С3:Е5.
4. Проверьте полученную таблицу.
5. Перейдите на лист 2.
6. Используя Мастер функций, постройте таблицу истинности функций
А v A v A v A, A & A & A & A вида:
|
A |
B |
А или А или А или А |
А и А и А и А |
|
ЛОЖЬ |
ЛОЖЬ |
= ИЛИ(А2;A2;A2;A2) |
= И(A2;A2;A2;A2;) |
|
ЛОЖЬ |
ИСТИНА |
||
|
ИСТИНА |
ЛОЖЬ |
||
|
ИСТИНА |
ИСТИНА |
7. Перейдите на лист 3.
8. Используя Мастер функций, постройте таблицу истинности функций
А&A, AA вида:
|
А |
НЕ А |
А И НЕ А |
А ИЛИ НЕ А |
|
ЛОЖЬ |
= НЕ (А2) |
= И(А2; НЕ (А2)) |
=ИЛИ(А2; НЕ(А2)) |
|
ИСТИНА |
9. Перейдите на лист 4.
Используя Мастер функций, постройте таблицу истинности функций
(AB), (A&B), A B, A& B
Подсказка: формулы в ячейках будут таковы:
Я
Найдите среди этих функций эквивалентные.
чейка С2: =HE(ИЛИ(А2;В2))
Ячейка D2 =HE(И(А2;В2))
Ячейка Е2: =ИЛИ(НЕ(А2);НЕ(В2))
Ячейка F2: =И(НЕ(А2);НЕ(В2))
10. Перейдите на лист 5. Используя Мастер функций, постройте таблицы истинности функций A B, A B, AB.
П
Найдите функции, эквивалентные функциям В→А, А→В.
одсказка: формулы в ячейках будут таковы:
Ячейка С2: =ИЛИ(НЕ(А2);В2)
Ячейка D2: =ИЛИ(А2;НЕ(В2))
Ячейка Е2: =ИЛИ(НЕ(А2);НЕ(В2))
11. Выделите информацию на листах 1, 2, 3, 4, 5 и удалите её, нажав клавишу Delete.
Дата публикации:
03.04.2023
Описание:
Данная разработка содержит практическую работу «Построение таблиц истинности для логических выражений в MS Excel» и файл Таблицы Истинности в Excel .xlsx, в котором учащиеся непосредственно выполняют эту работу, а так же презентацию к данному уроку.
Цель данного урока: научиться использовать логические функции MS Exsel для построения таблиц истинности.
Задачи урока:
— познакомится с синтаксисом основных логических функцийMS Exsel ;
-научиться строить таблицы истинности, используя логические функции MS Exsel
Прикрепленные файлы:
9556f1060172a748e1fea8c852487e71.rar