Практическая работа №15 «Получение
регрессионных моделей». Регрессионная модель
Цель
урока:
1.
Образовательные: освоение способов построения по экспериментальным данным
регрессионной модели и тренда средствами Ms Excel.
2.
Познавательные:
––
формирование умений применять имеющиеся математические знания и знания из курса
информатики к решению практических задач;
–
развитие внимания, познавательной активности, творческих способностей,
логического мышления.
3.
Воспитательные:
–
воспитание интереса к предмету;
–
самостоятельности в принятии решения;
Используемые
программные средства: табличный процессор Ms Excel.
Тип
урока : Комбинированный.
План урока.
1. Организационная часть.
2. Постановка цели урока
Анализ данных — область информатики, занимающаяся
построением и исследованием наиболее общих математических методов и
вычислительных алгоритмов извлечения знаний из экспериментальных (в широком
смысле) данных.
Вопросы ученикам: 1) Как Вы думаете, какое программное
обеспечение имеет средства анализа данных? (табличный процессор Excel)
2) Какие именно возможности табличного процессора
можно отнести к средствам анализа данных?
К средствам анализа относятся:
• Обработка списка с помощью различных формул и функций;
• Построение диаграмм и использование карт Ms Excel;
• Проверка данных рабочих листов и рабочих книг на
наличие ошибок;
• Структуризация рабочих листов;
• Автоматическое подведение итогов (включая мастер
частичных сумм);
• Консолидация данных;
• Сводные таблицы;
• Специальные средства анализа выборочных записей и
данных — подбор параметра, поиск решения, сценарии и др.
3) В каких областях могут найти практическое
применение средства анализа табличного процессора Excel?
Цель нашего урока: научиться строить регрессионные модели средствами Excel..
3. Актуализация знаний
В состав Microsoft
Excel входит набор средств анализа данных (так называемый пакет анализа),
предназначенный для решения сложных статистических и инженерных задач. Для
проведения анализа данных с помощью этих инструментов следует указать входные
данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической
или инженерной макрофункции, а результат будет помещен в выходной диапазон.
Другие средства позволяют представить результаты анализа в графическом виде.
Статистические
данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает
весьма трудно обнаружить в них имеющиеся неточности и ошибки.
Графическое же
представление статистических данных помогает легко и быстро выявить ничем не
оправданные пики и впадины, явно не соответствующие изображаемым статистическим
данным, аномалии и отклонения.
4. Теоретическая часть. Объяснение нового материала.
Объяснение нового
материала происходит с использованием презентации. В управлении и
планировании существует целый ряд типовых задач, которые можно переложить на
плечи компьютера
Ms Excel – это не просто
электронная таблица с данными и формулами для вычислений. Это универсальная
система обработки данных, которая может использоваться для анализа и
представления данных в наглядной форме.
Мы уже с вами говорили о
том, что решение задач планирования и управления постоянно требует учета
зависимостей одних факторов от других. Таких примеров мы приводили очень много.
Один из таких примеров:
определение зависимости время падения тела на землю от первоначальной высоты.
Зависимость эта очевидна. Для её проверки можно провести эксперимент, сбрасывая
предметы с разных этажей многоэтажного здания, данные занести в таблицу. Таким
образом мы легко создадим табличную модель, на основе её построим график. Кроме
этого нам не составит особого труда и составление функциональной зависимости,
так как падение тел происходит согласно всем нам известному физическому закону.
Тем самым у нас будет и математическая модель по которой мы легко рассчитаем
время падения тел даже с очень большой высоты.
|
Н (м) |
t (сек) |
|
6 9 12 15 18 21 24 27 30 |
1,1 1,4 1,6 1,7 1,9 2,1 2,2 2,3 2,5 |
,
Но не все зависимости
так просты.
|
С, мг/куб.м |
Р, бол./тыс. |
|
2 |
19 |
|
2,5 |
20 |
|
2,9 |
32 |
|
3,2 |
34 |
|
3,6 |
51 |
|
3,9 |
55 |
|
4,2 |
90 |
|
4,6 |
108 |
|
5 |
171 |
Например, нам необходимо
найти зависимость частоты заболеваемости жителей города бронхиальной астмой от
качества воздуха.
Любому человеку понятно,
что такая зависимость существует. Очевидно, что чем хуже воздух, тем больше
больных астмой. Но это качественное заключение. Его недостаточно для того,
чтобы управлять этим процессом, нам потребуются более конкретные знания. Нужно
установить, какие именно примеси сильнее всего влияют на здоровье людей, как
связаны концентрация этих примесей в воздухе с числом заболеваний. Такую
зависимость можно установить только путем сбора многочисленных данных, их
анализа и обобщения.
В таких ситуациях на
помощь приходит статистика: наука о сборе, изменении и анализе массовых
количественных данных.
Специалисты по медицинской статистике
проводят сбор данных. Они собирают сведения из разных городов о средней
концентрации угарного газа в атмосфере и о заболеваемости астмой (число
хронических больных на тысячу жителей). Полученные данные можно свести в
таблицу, а также представить в виде точечной диаграммы .
При этом необходимо
помнить, что статистические данные всегда являются приближенными, усредненными.
Поэтому они носят оценочный характер. Однако, они верно отражают характер
зависимости величин. И еще одно важное замечание: для достоверности
результатов, полученных путем анализа статистических данных, этих данных должно
быть много.
Из полученных данных
можно сделать вывод, что при концентрации угарного газа до 3 мг/куб.м его
влияние на заболеваемость астмой несильное. С дальнейшим ростом концентрации
наступает резкий рост заболеваемости.
Построить табличную
модель и графическую по экспериментальным данным
Но нужно ещё и получить
формулу, отражающую эту зависимость. На языке математики это называется
функцией зависимости Р от С: Р(С). Вид такой функции неизвестен, её следует
искать методом подбора по экспериментальным данным. Понятно, что график
искомой функции должен проходить близко к точкам диаграммы экспериментальных
данных. Строить функцию так, чтобы ёе график точно проходил через все данные
точки (рисунок 2), не имеет смысла. Во-первых, математический вид такой функции
может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные
значения являются приближенными.
Отсюда следуют основные
требования к искомой функции:
·
она должна быть достаточно простой для
использования её в дальнейших вычислениях;
·

проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от
графика были минимальны и равномерны
Полученную функцию,
график которой приведен на рисунке, принято называть в статистике регрессионной
моделью. Регрессионная модель – это функция, описывающая
зависимость между количественными характеристиками сложных систем.
Получение регрессионной
модели происходит в два этапа:
1.
подбор
вида функции;
2.
вычисление
параметров функции.
Чаще всего выбор
производится среди следующих функций:
y=ax+b – линейная
функция;
y=ax2+bx+c
– квадратичная функция;
y=aln(x)+b –
логарифмическая функция;
y=aebx —
экспоненциальная функция;
y=axb —
степенная функция.
Если Вы выбрали
(сознательно или наугад) одну из предлагаемых функций, то следующим шагом нужно
подобрать параметры (a,b,c и пр.) так, чтобы функция располагалась как можно
ближе к экспериментальным точкам. Для этого подходит метод наименьших квадратов
(МНК). Суть его заключается в следующем: искомая функция должна быть построена
так, чтобы сумма квадратов отклонений у – координат всех экспериментальных
точек от у – координат графика функции была бы минимальной.

понимать следующее: методом наименьших квадратов по данному набору
экспериментальных точек можно построить любую функцию. А вот будет ли она нас
удовлетворять, это уже другой вопрос – вопрос критерия соответствия. На рисунке
4 изображены 3 функции, построенные методом наименьших квадратов.

Данные рисунки получены
с помощью Ms Excel. График регрессионной модели называется трендом (trend
– направление, тенденция).

линейной функции – это прямая. Полученная по методу МНК прямая отражает факт
роста заболеваемости от концентрации угарного газа, но по этому графику трудно
что – либо сказать о характере этого роста. А вот квадратичный и
экспоненциальный тренды – ведут себя очень правдоподобно.
На графиках присутствует
ещё одна величина, полученная в результате построения трендов. Она обозначена
как R2. В статистике эта величина называется коэффициентом
детерминированности. Именно она определяет, насколько удачной получится
регрессионная модель. Коэффициент детерминированности всегда заключен в
диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные
значения, если 0, то выбранный вид регрессионной модели неудачен. Чем R2 ближе
к 1, тем удачнее регрессионная модель.
Метод наименьших
квадратов используется для вычисления параметров регрессионной модели. Этот
метод содержится в математическом арсенале электронных таблиц.
5. Практическая часть.
Выполнение лабораторной работы. По предложенной инструкции
выполнить практическую работу, оформить отчет
Задание 1
1. Ввести табличные данные зависимости
заболеваемости бронхиальной астмой от концентрации угарного газа в атмосфере
(см. рисунок).
2. Представить зависимость в виде точечной диаграммы (см.
рисунок).
Задание 2

Требуется получить три варианта регрессионных моделей (три графических
тренда) зависимости заболеваемости бронхиальной астмой от концентрации угарного
газа в атмосфере.
1. Для получения линейного тренда выполнить
следующий алгоритм:
=> щелкнуть ПКМ на поле диаграммы «Заболеваемость
астмой», построенной в предыдущем задании;
=> выполнить команду Вставить линию тренда;
=> в открывшемся окне на вкладке Тип
выбрать Линейный тренд;
=> установить галочки на флажках: показывать
уравнения на диаграмме и поместить на диаграмму величину достоверности
аппроксимации R^2;
=> щелкнуть на кнопке ОК. Полученная
диаграмма представлена на рисунке:
2. Получить экспоненциальный тренд. Алгоритм
аналогичен предыдущему. На закладке Тип выбрать Экспоненциальный
тренд. Результат представлен на рисунке:
3. Получить степенной тренд. Алгоритм аналогичен
предыдущему. На закладке Тип выбрать Степенной тренд.
Результат представлен на рисунке:
6. Домашнее задание:
Конспект
(тема “ Регрессионная модель ”); заполнить лист Отчета полностью (ответить на вопросы).
7. Подведение итогов. Рефлексия
Отчет
по практической работе
«Построение
регрессионных моделей с помощью табличный процессор Ms Excel»
Практическую работу
выполнял:_________________
|
Тип |
Уравнение |
R2 |
|
Линейный |
||
|
Квадратичный |
||
|
Логарифмический |
||
|
Степенной |
||
|
Экспоненциальный |
||
|
Полином третей |
Вывод: для
графика, полученного по экспериментальным точкам больше всего подходит
регрессионная модель, построенная с помощью _______________________________
____________________________________________________
Ёе формула имеет вид
_________________________________
R2 равен
____________________________________________
По полученной
формуле рассчитайте предполагаемую на 15 число.
________________________________________________________________________________________________________
Вывод по работе:
____________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________
Построение регрессионных моделей с помощью табличного процессора
Опишем алгоритм получения с помощью MS
Excel регрессионных моделей по МНК с
построением тренда.
Сначала следует ввести табличные данные
и построить точечную диаграмму, как это
показано на рис. 2.12 (можно игнорировать
все лишние детали — надписи, легенду,
— чтобы получилось так, как на рис. 2.14
а, в качестве подписи к оси ОХ выбрать
текст «Линейный тренд»). Далее следует:
=> щелкнуть мышью по полю диаграммы
(по одной из точек диаграммы); => выполнить
команду => Диаграмма => Добавить линию
тренда;
:=> в открывшемся окне на закладке «Тип»
выбрать «Линейный тренд»;
=> перейти к закладке «Параметры»;
установить галочки на флажках «показывать
уравнения на диаграмме» и «поместить
на диаграмму величину достоверности
аппроксимации R2», щелкнуть по
кнопке ОК.
Диаграмма готова. Она будет точно такой,
как на рис. 2.14 а. Аналогично можно получить
и другие типы трендов. Квадратичный
тренд получается путем выбора
полиномиального типа функции с
указанием степени 2.
Заметим, что MS Excel дает возможность
пользователю самому задавать тип
регрессионной модели, а не ограничиваться
предлагаемым меню из шести функций.
Однако для большого числа практических
ситуаций этих функций бывает вполне
достаточно.
Продолжение линии тренда за границы
области данных, приведенных в исходной
таблице, называется экстраполяцией.
Для получения такого рисунка нужно
добавить в описанный в описанный
выше алгоритм еще одно действие: => на
вкладке «Параметры» в области «Прогноз»
в строке «вперед на» установить 2 единицы.
Здесь имеются в виду единицы используемого
масштаба по горизонтальной оси.
Задание для самостоятельного выполнения
-
По данным из следующей таблицы постройте
с помощью MS Excel линейную, квадратичную,
экспоненциальную и логарифмическую
регрессионные модели. Определите
параметры, выберите лучшую модель.
Произвести прогнозирование по полученной
модели: получить значение Y
для Х=1, 17, 19, 29.
|
X |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
|
Y |
44 |
32 |
35 |
40 |
30 |
27 |
21 |
25 |
20 |
23 |
18 |
19 |
20 |
16 |
-
В следующей таблице приводится прогноз
средней дневной температуры на последнюю
неделю мая в различных городах европейской
части России. Города упорядочены по
алфавиту. Указана также географическая
широта этих городов. Построить несколько
вариантов регрессионных моделей (не
менее трех), отражающих зависимость
температуры от широты города. Выбрать
наиболее подходящую функцию. Произвести
прогнозирование по полученной модели:
рассчитать прогноз средней температуры
для следующих городов: Сочи — 43,5 гр. с.
ш., Москва — 55,7 гр. с. ш., Санкт-Петербург
— 60 гр. с. ш., Мурманск — 69 гр. с. ш.
|
Город |
Широта, гр. с. ш. |
Температура |
|
Воронеж |
51,5 |
16 |
|
Краснодар |
45 |
24 |
|
Липецк |
52,6 |
12 |
|
Новороссийск |
44,8 |
25 |
|
Ростов на Дону |
47,3 |
19 |
|
Рязань |
54,5 |
11 |
|
Северодвинск |
64,8 |
5 |
|
Череповец |
59,4 |
7 |
|
Ярославль |
57,7 |
10 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.
Пример: простая линейная регрессия в Excel
Предположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.
Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести простую линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:
Шаг 2: Визуализируйте данные.
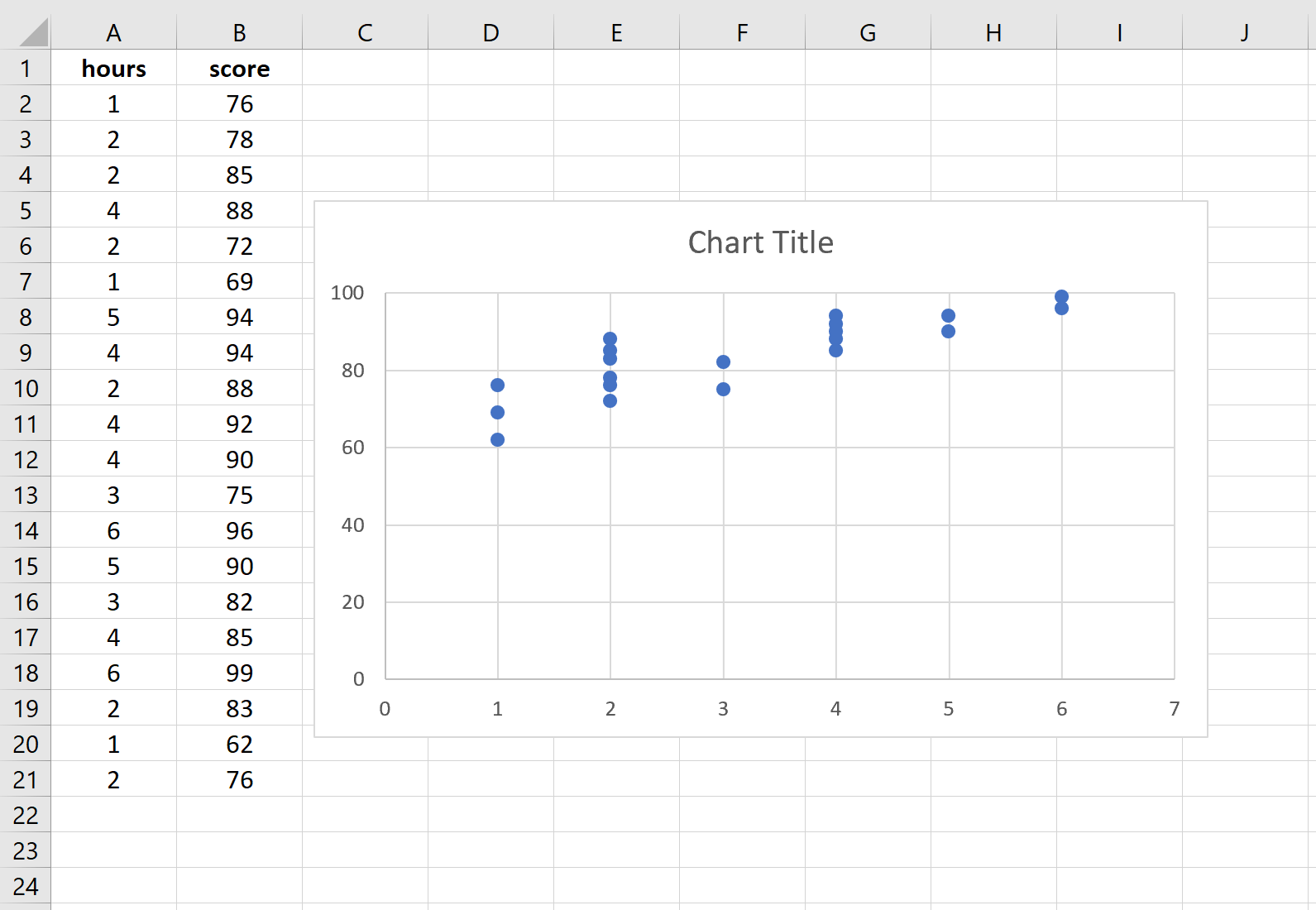
Прежде чем мы выполним простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что действительно существует линейная зависимость между отработанными часами и экзаменационным баллом.
Выделите данные в столбцах A и B. В верхней ленте Excel перейдите на вкладку « Вставка ». В группе « Диаграммы » нажмите « Вставить разброс» (X, Y) и выберите первый вариант под названием « Разброс ». Это автоматически создаст следующую диаграмму рассеяния:
Количество часов обучения показано на оси x, а баллы за экзамены показаны на оси y. Мы видим, что между двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими баллами на экзаменах.
Чтобы количественно оценить взаимосвязь между этими двумя переменными, мы можем выполнить простую линейную регрессию.
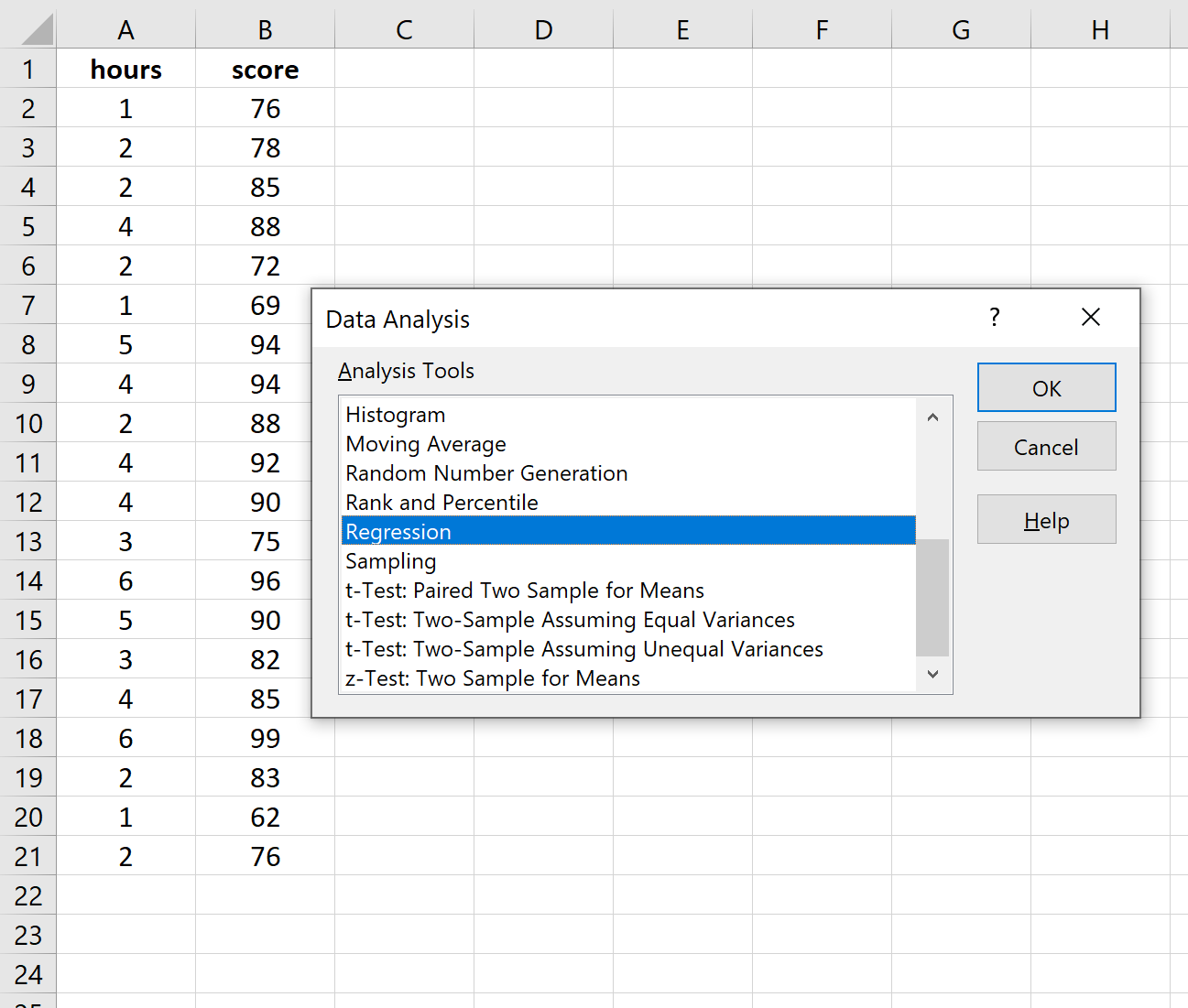
Шаг 3: Выполните простую линейную регрессию.
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
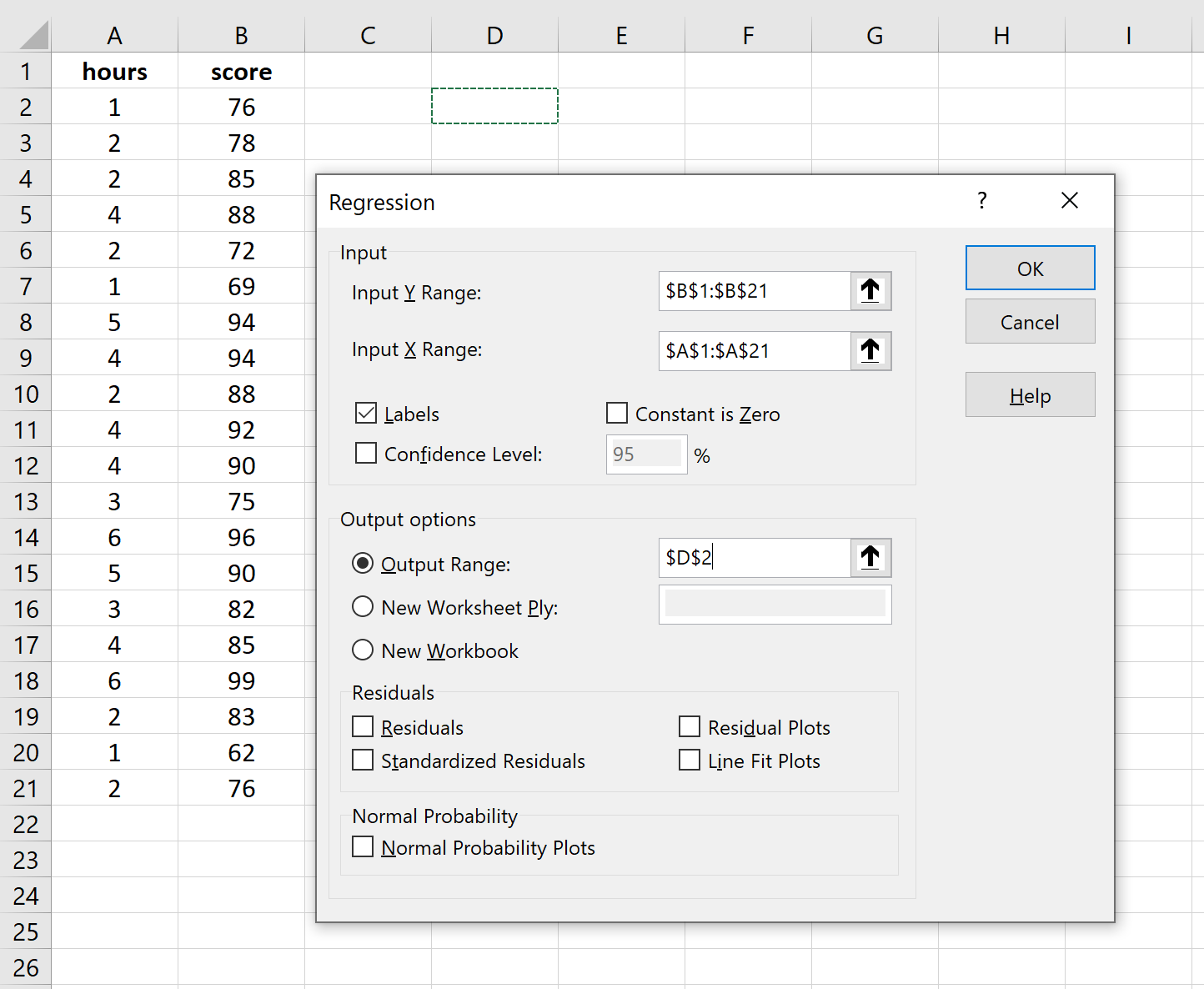
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для независимой переменной.
Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны.
В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии.
Затем нажмите ОК .
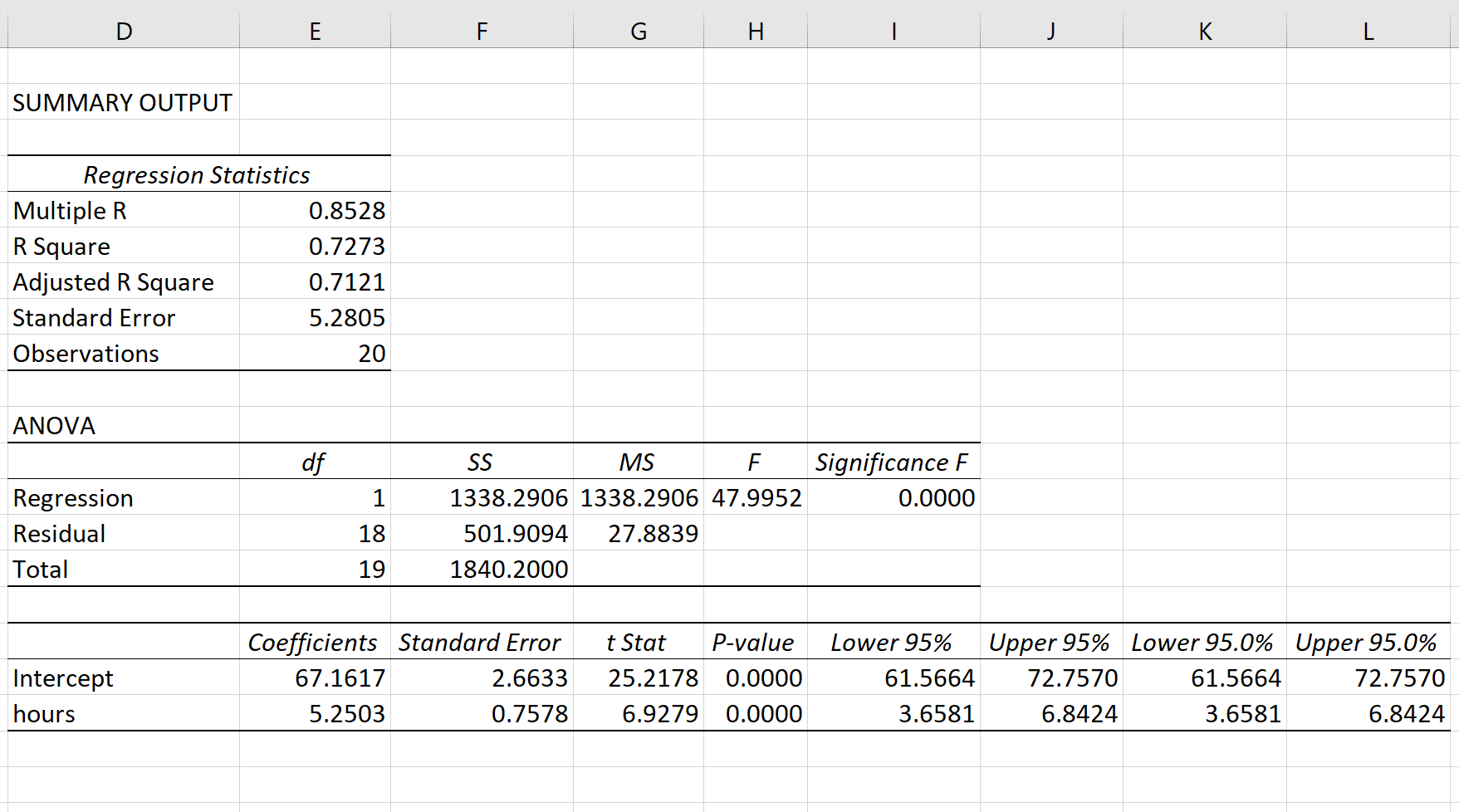
Автоматически появится следующий вывод:
Шаг 4: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,7273.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.
Стандартная ошибка: 5.2805.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,2805 единиц.
Ф: 47,9952.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель статистически значимой. Другими словами, он говорит нам, имеет ли независимая переменная статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на наличие статистически значимой связи между отработанными часами и полученными экзаменационными баллами.
Коэффициенты: коэффициенты дают нам числа, необходимые для написания оценочного уравнения регрессии. В этом примере оцененное уравнение регрессии:
экзаменационный балл = 67,16 + 5,2503*(часов)
Мы интерпретируем коэффициент для часов как означающий, что за каждый дополнительный час обучения ожидается увеличение экзаменационного балла в среднем на 5,2503.Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится без часов, составляет 67,16 .
Мы можем использовать это оценочное уравнение регрессии для расчета ожидаемого экзаменационного балла для учащегося на основе количества часов, которые он изучает.
Например, ожидается, что студент, который занимается три часа, получит на экзамене 82,91 балла:
экзаменационный балл = 67,16 + 5,2503*(3) = 82,91
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать остаточный график в Excel
Как построить интервал прогнозирования в Excel
Как создать график QQ в Excel