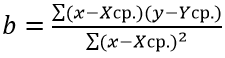Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Еще…Меньше
Если у вас есть статистические данные с зависимостью от времени, вы можете создать прогноз на их основе. При этом в Excel создается новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. С помощью прогноза вы можете предсказывать такие показатели, как будущий объем продаж, потребность в складских запасах или потребительские тенденции.
Сведения о том, как вычисляется прогноз и какие параметры можно изменить, приведены ниже в этой статье.
Создание прогноза
-
На листе введите два ряда данных, которые соответствуют друг другу:
-
ряд значений даты или времени для временной шкалы;
-
ряд соответствующих значений показателя.
Эти значения будут предсказаны для дат в будущем.
Примечание: Для временной шкалы требуются одинаковые интервалы между точками данных. Например, это могут быть месячные интервалы со значениями на первое число каждого месяца, годичные или числовые интервалы. Если на временной шкале не хватает до 30 % точек данных или есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет точным. Но для повышения точности прогноза желательно перед его созданием обобщить данные.
-
-
Выделите оба ряда данных.
Совет: Если выделить ячейку в одном из рядов, Excel автоматически выделит остальные данные.
-
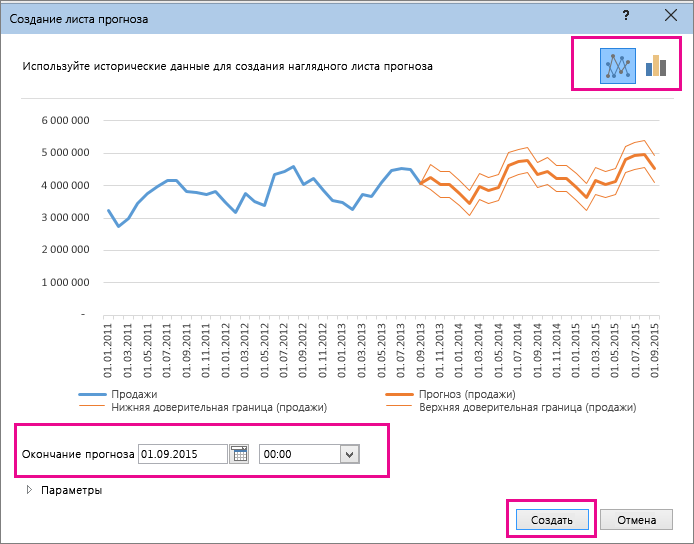
На вкладке Данные в группе Прогноз нажмите кнопку Лист прогноза.
-
В окне Создание прогноза выберите график или гограмму для визуального представления прогноза.
-
В поле Завершение прогноза выберите дату окончания, а затем нажмите кнопку Создать.
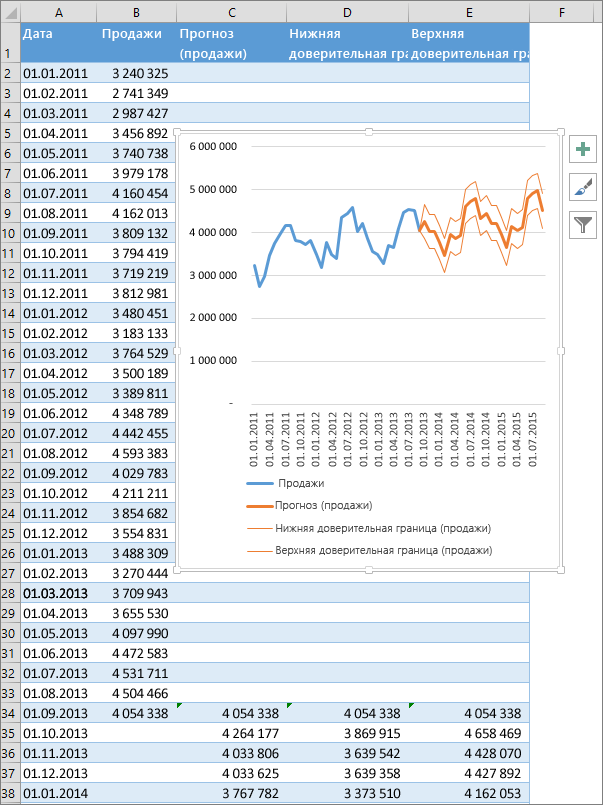
В Excel будет создан новый лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.
Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (то есть перед ним).
Настройка прогноза
Если вы хотите изменить дополнительные параметры прогноза, нажмите кнопку Параметры.
Сведения о каждом из вариантов можно найти в таблице ниже.
|
Параметры прогноза |
Описание |
|
Начало прогноза |
Выберите дату, с которой должен начинаться прогноз. При выборе даты начала, которая наступает раньше, чем заканчиваются статистические данные, для построения прогноза используются только данные, предшествующие ей (это называется «ретроспективным прогнозированием»). Советы:
|
|
Доверительный интервал |
Установите или снимите флажок Доверительный интервал, чтобы показать или скрыть его. Доверительный интервал — это диапазон вокруг каждого предсказанного значения, в который в соответствии с прогнозом (при нормальном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает определить точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по умолчанию определяется для 95 % точек, но это значение можно изменить с помощью стрелок вверх или вниз. |
|
Сезонность |
Сезонность — это число для длины (количества точек) сезонного шаблона и автоматически обнаруживается. Например, в ежегодном цикле продаж, каждый из которых представляет месяц, сезонность составляет 12. Автоматическое обнаружение можно переопрепредидить, выбрав установить вручную и выбрав число. Примечание: Если вы хотите задать сезонность вручную, не используйте значения, которые меньше двух циклов статистических данных. При таких значениях этого параметра приложению Excel не удастся определить сезонные компоненты. Если же сезонные колебания недостаточно велики и алгоритму не удается их выявить, прогноз примет вид линейного тренда. |
|
Диапазон временной шкалы |
Здесь можно изменить диапазон, используемый для временной шкалы. Этот диапазон должен соответствовать параметру Диапазон значений. |
|
Диапазон значений |
Здесь можно изменить диапазон, используемый для рядов значений. Этот диапазон должен совпадать со значением параметра Диапазон временной шкалы. |
|
Заполнить отсутствующие точки с помощью |
Для обработки отсутствующих точек в Excel используется интерполяция, то есть отсутствующие точки будут заполнены в качестве взвешенного среднего значения соседних точек, если отсутствует менее 30 % точек. Чтобы нули в списке не были пропущены, выберите в списке пункт Нули. |
|
Использование агрегатных дубликатов |
Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтобы использовать другой метод вычисления, например Медиана илиКоличество,выберите нужный способ вычисления из списка. |
|
Включить статистические данные прогноза |
Установите этот флажок, если хотите поместить на новом листе дополнительную статистическую информацию о прогнозе. При этом добавляется таблица статистики, созданная с помощью прогноза. Ets. Функция СТАТ и показатели, такие как коэффициенты сглаживания («Альфа», «Бета», «Гамма») и метрики ошибок (MASE, SMAPE, MAE, RMSE). |
Формулы, используемые при прогнозировании
При использовании формулы для создания прогноза возвращаются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предсказывает будущие значения на основе имеющихся данных, зависящих от времени, и алгоритма экспоненциального сглаживания (ETS) версии AAA.
Таблицы могут содержать следующие столбцы, три из которых являются вычисляемыми:
-
столбец статистических значений времени (ваш ряд данных, содержащий значения времени);
-
столбец статистических значений (ряд данных, содержащий соответствующие значения);
-
столбец прогнозируемых значений (вычисленных с помощью функции ПРЕДСКАЗ.ЕTS);
-
два столбца, представляющие доверительный интервал (вычисленные с помощью функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы отображаются только при проверке доверительный интервал в разделе Параметры.
Скачивание образца книги
Щелкните эту ссылку, чтобы скачать книгу с Excel FORECAST. Примеры функции ETS
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Статьи по теме
Функции прогнозирования
Нужна дополнительная помощь?
Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
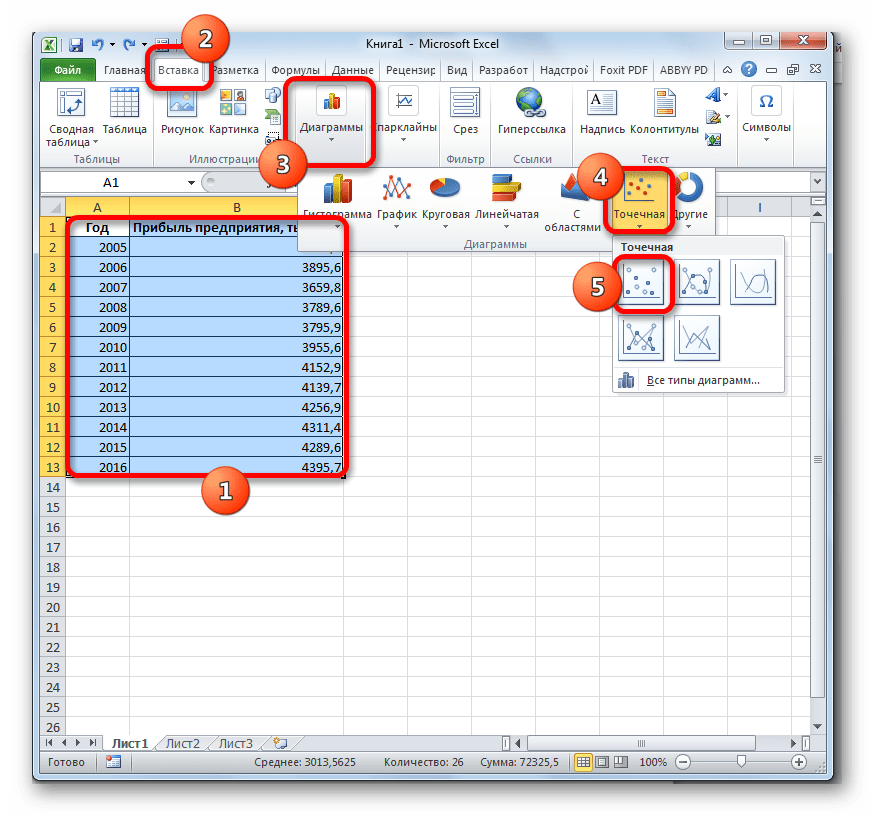
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
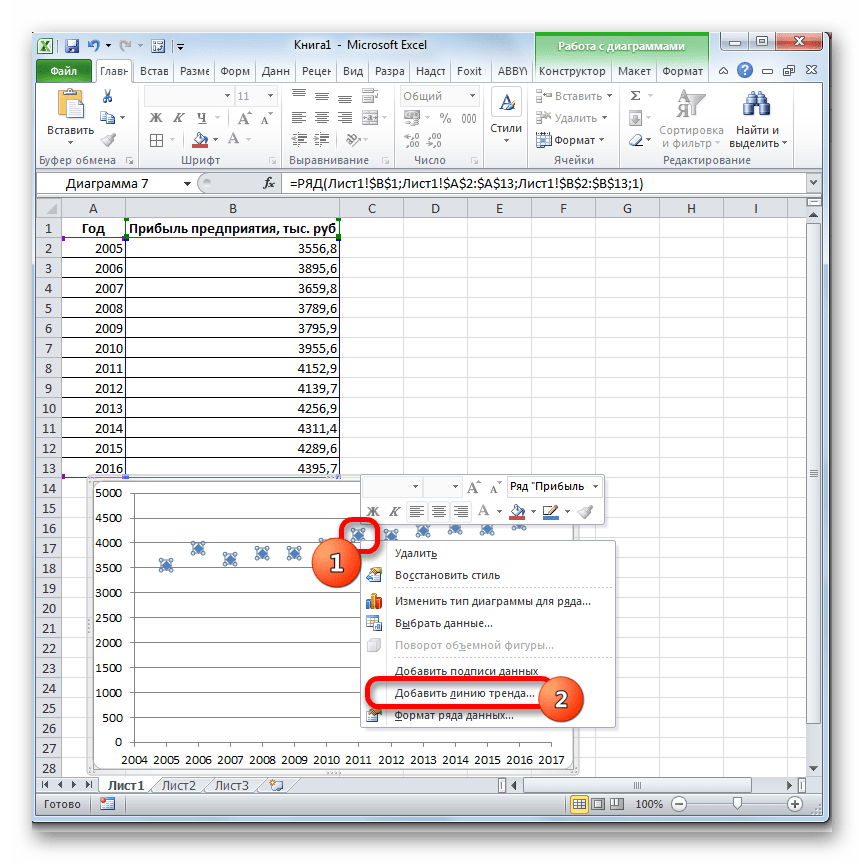
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
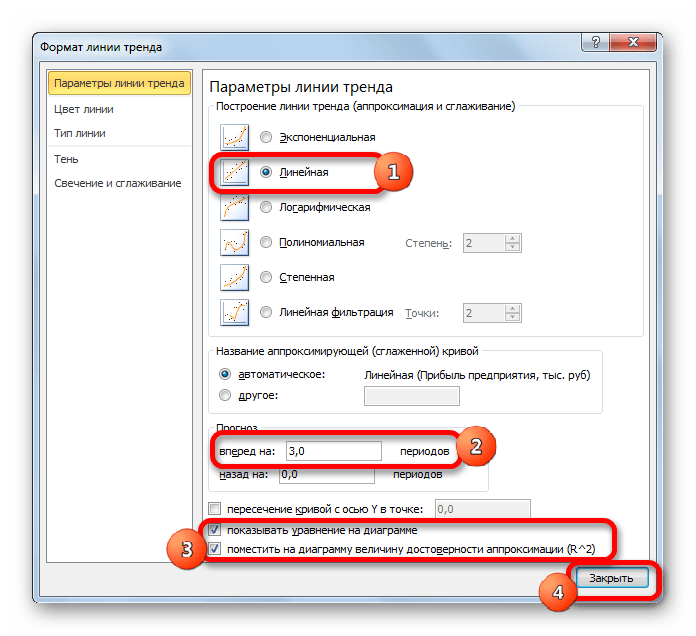
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
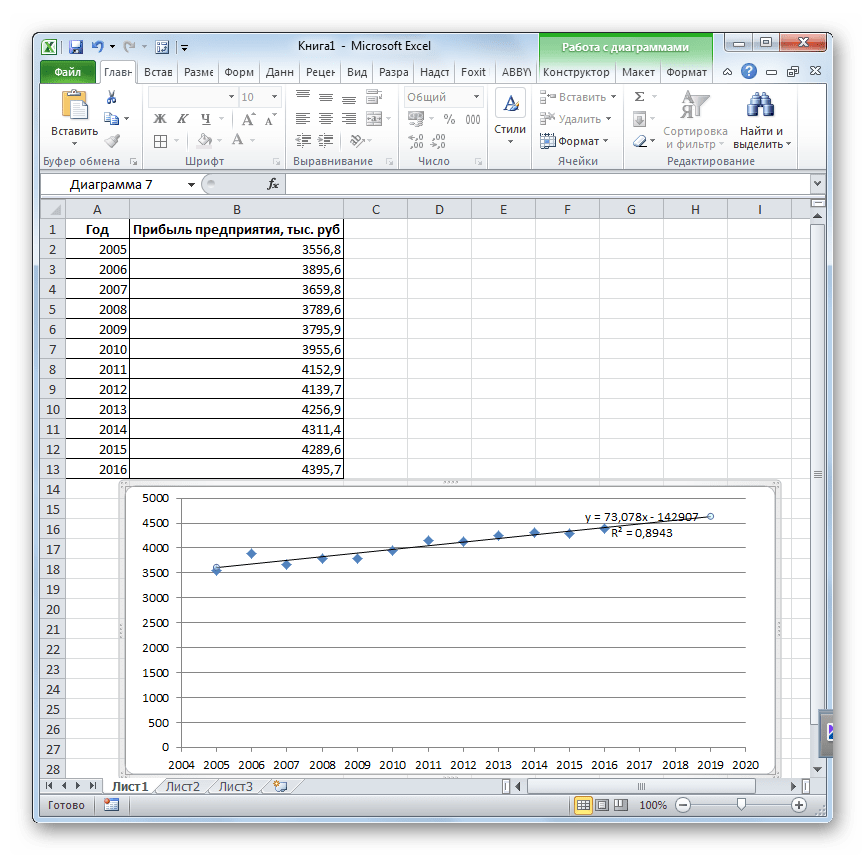
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
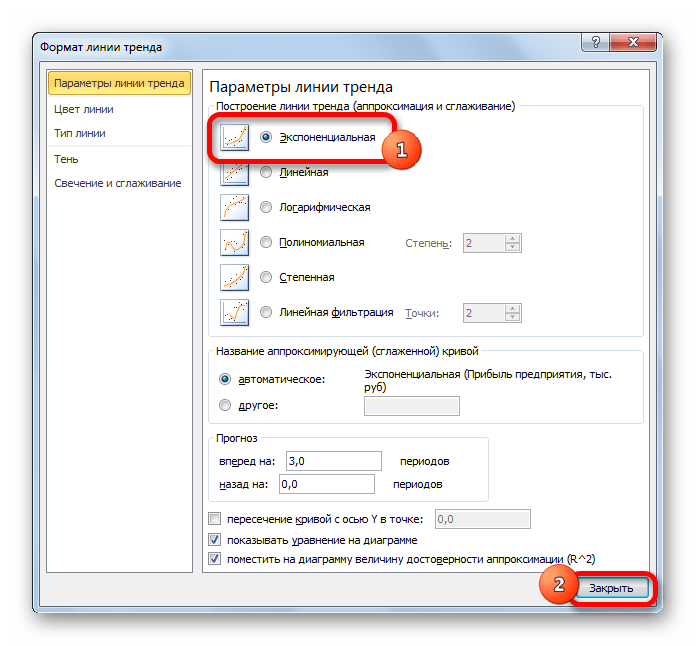
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
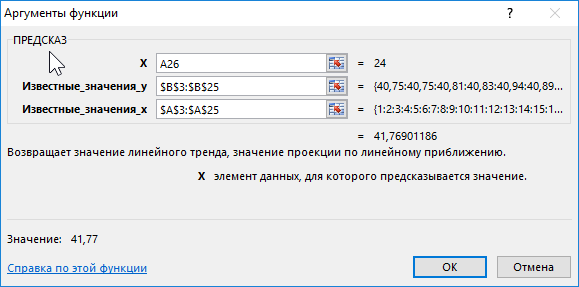
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
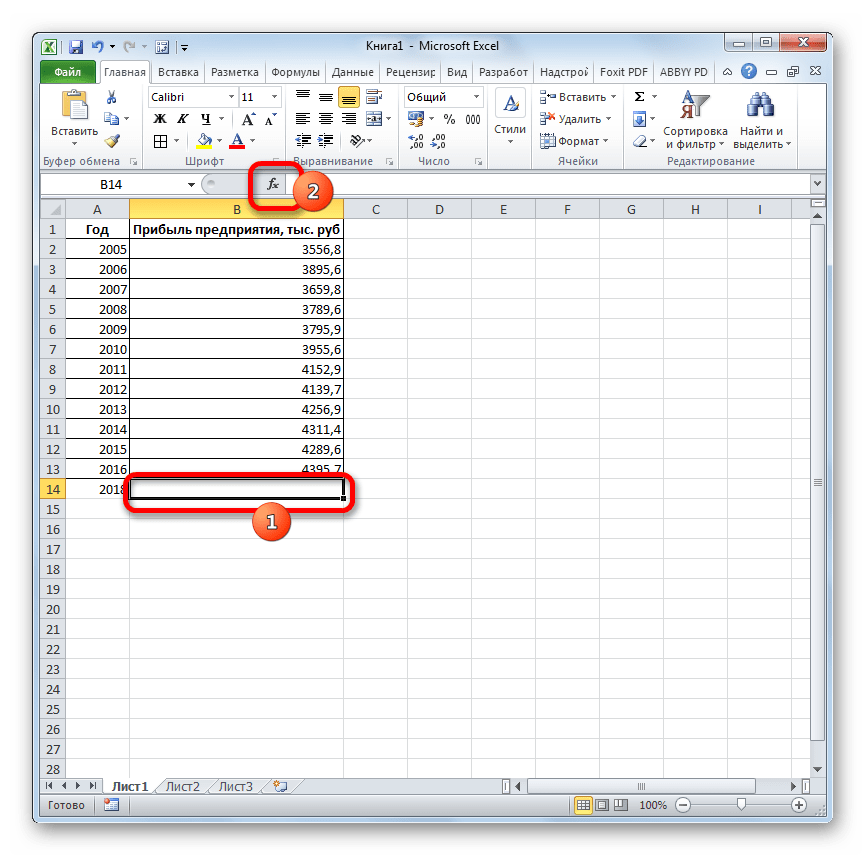
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
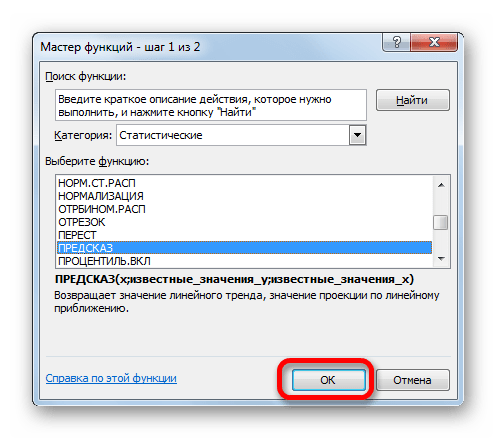
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
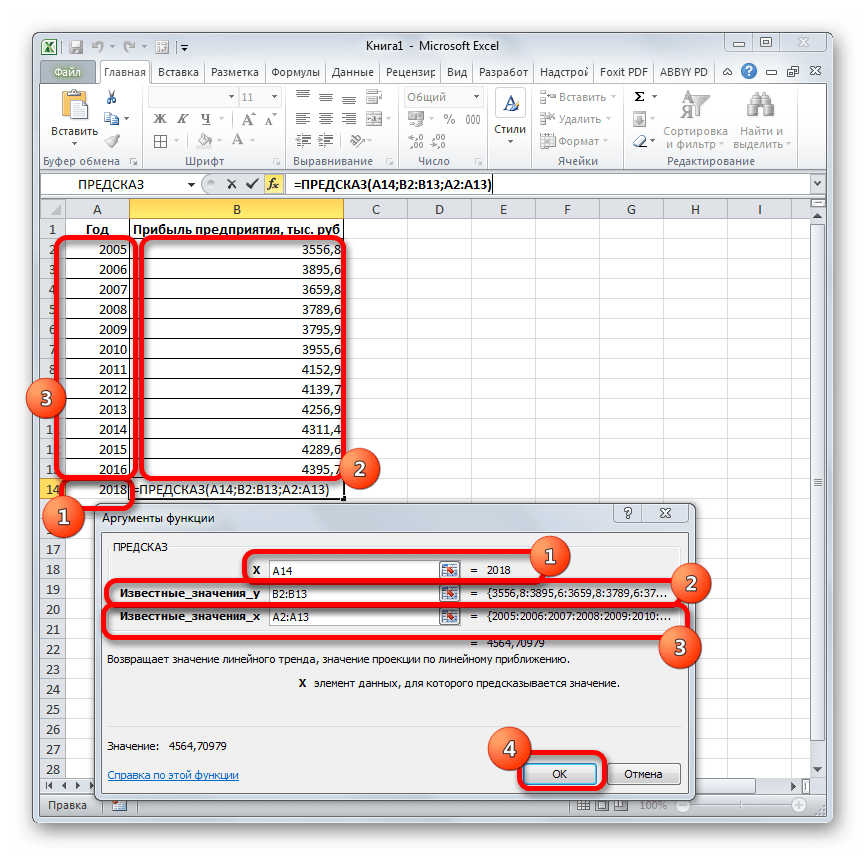
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
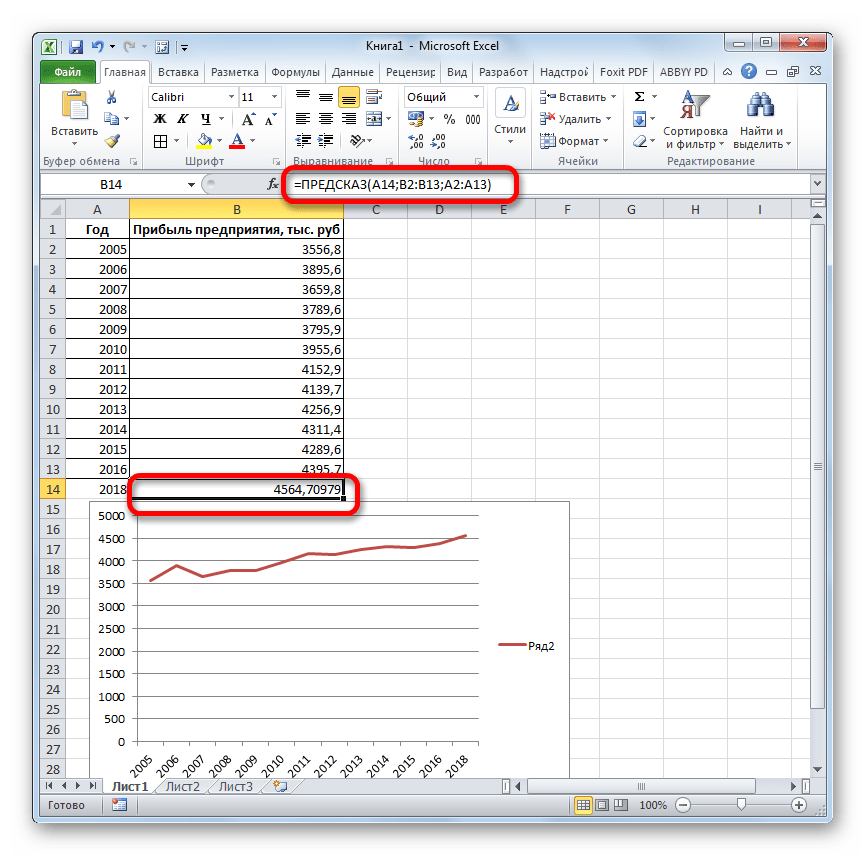
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
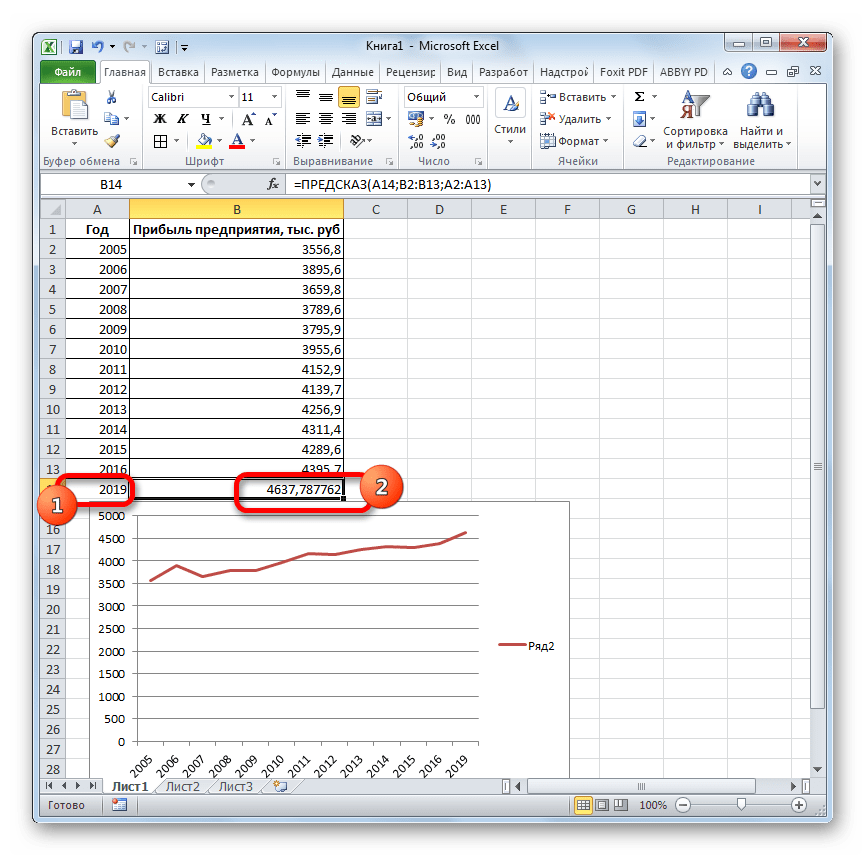
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
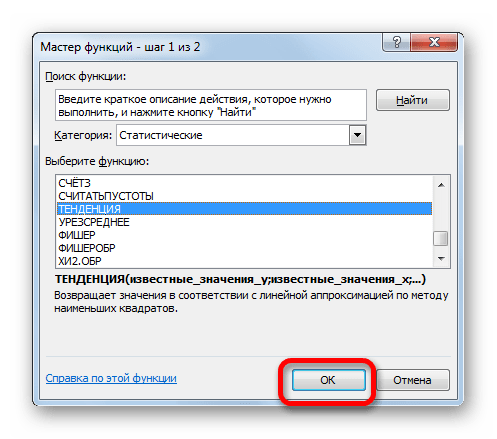
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
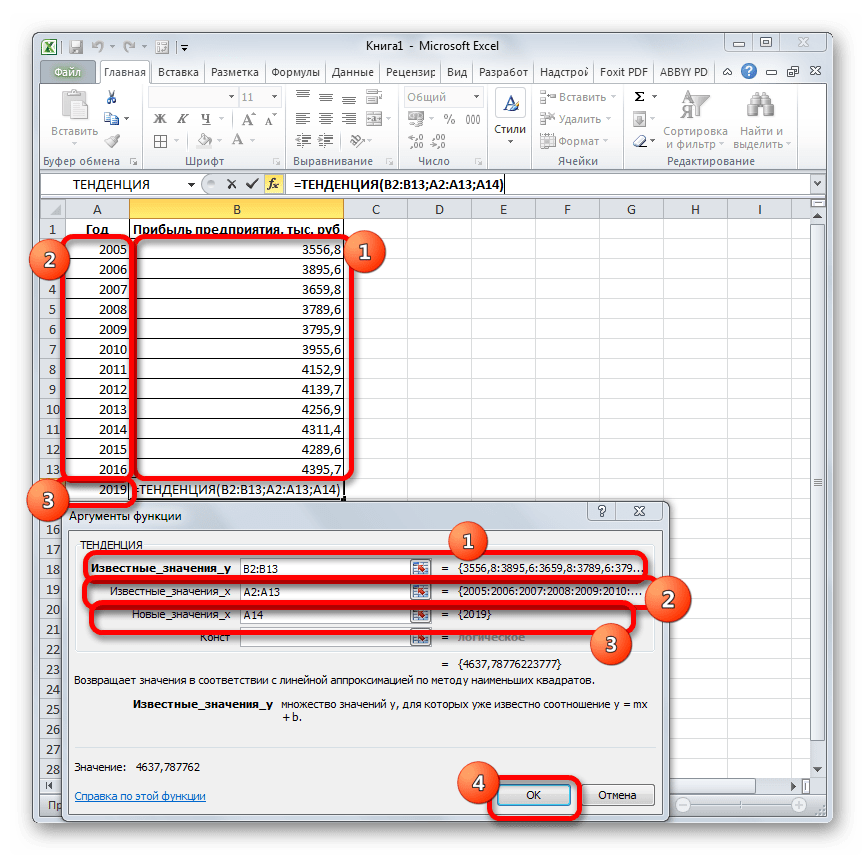
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
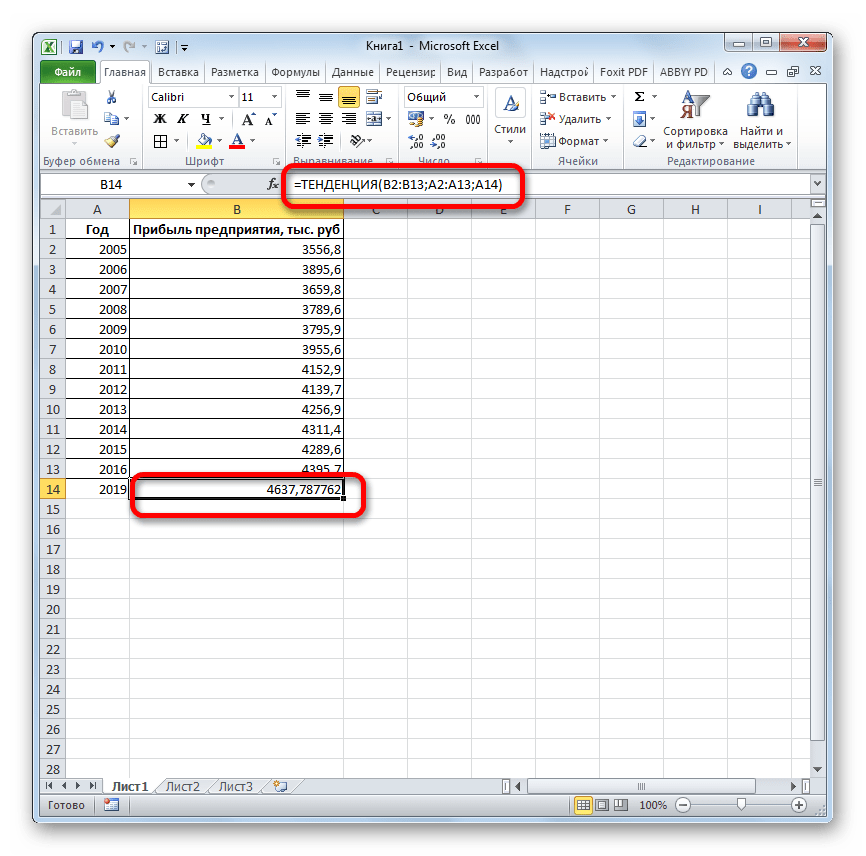
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
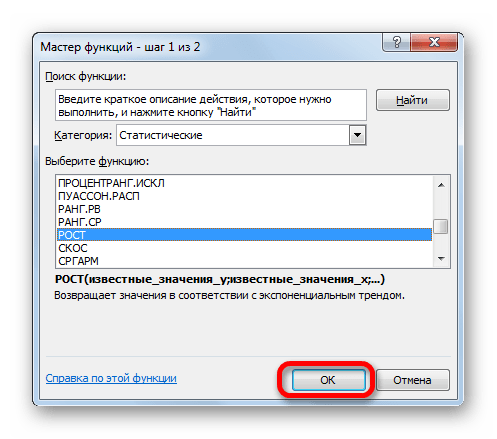
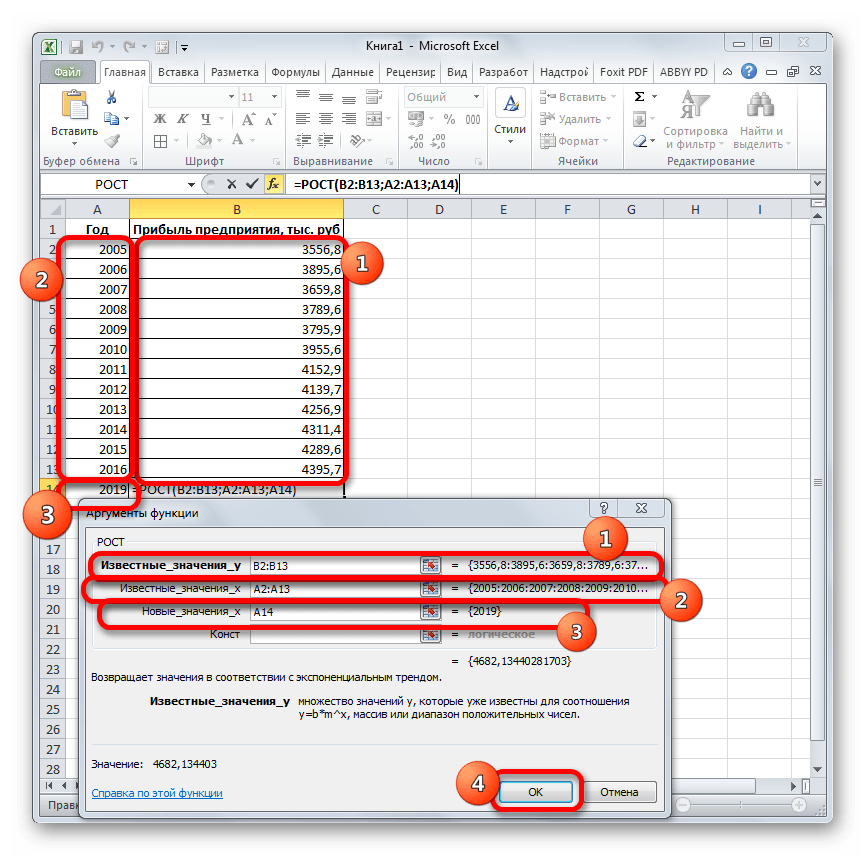
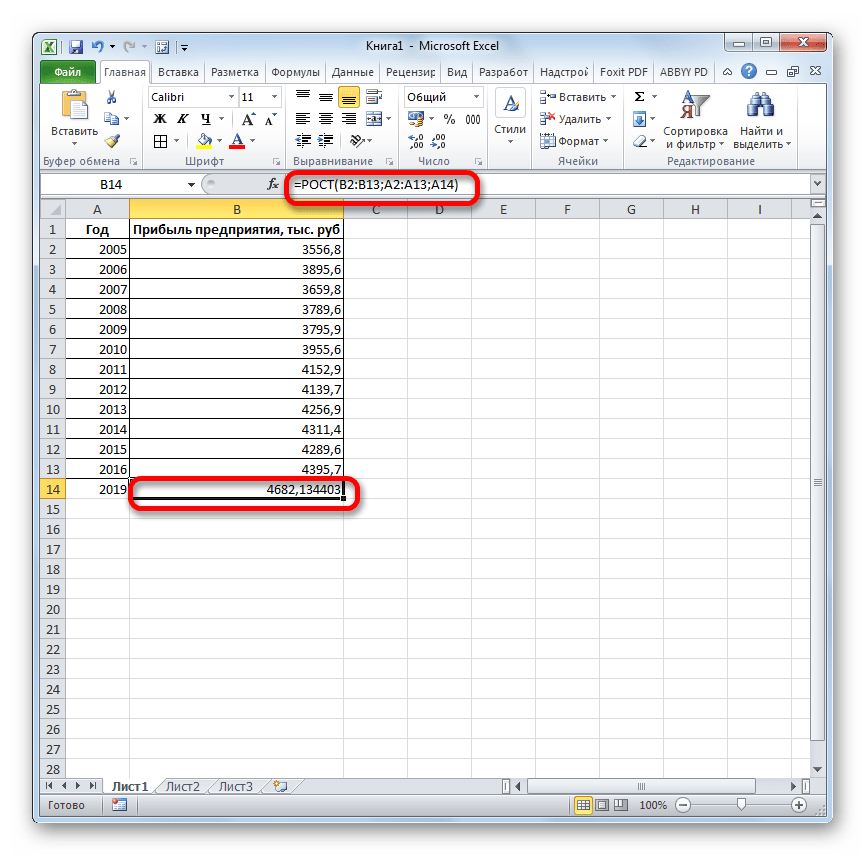
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
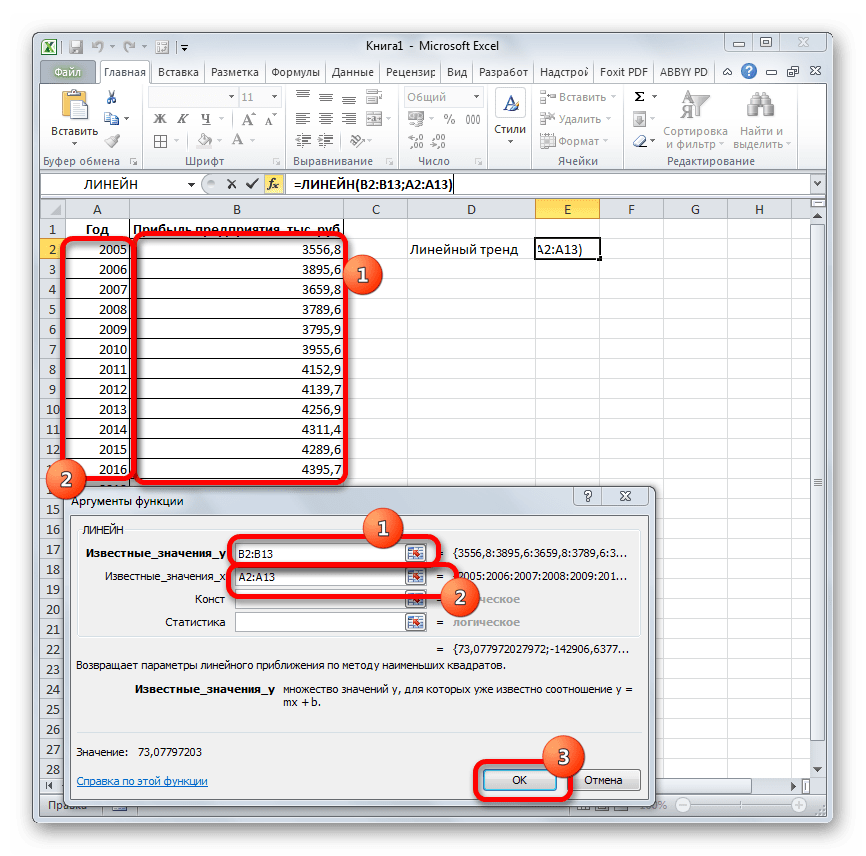
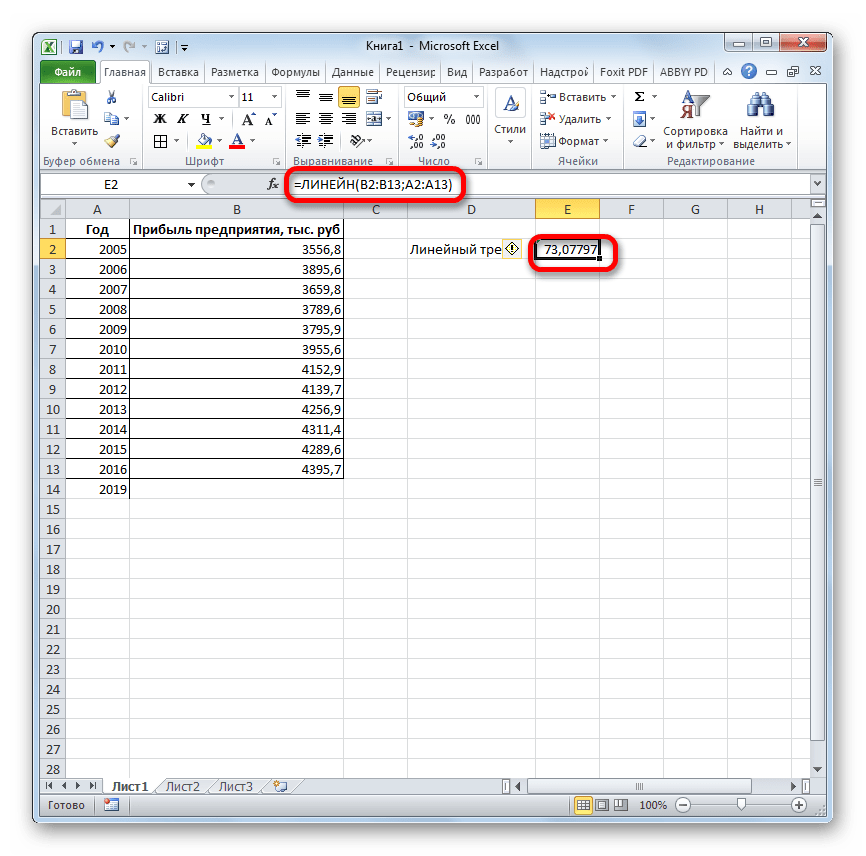
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
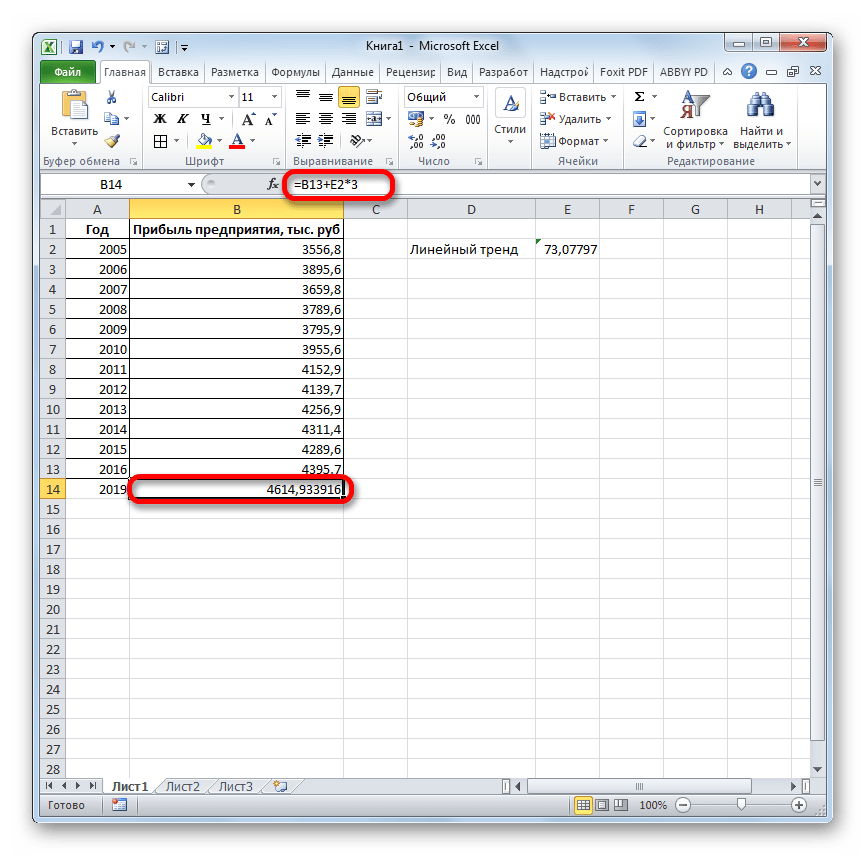
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
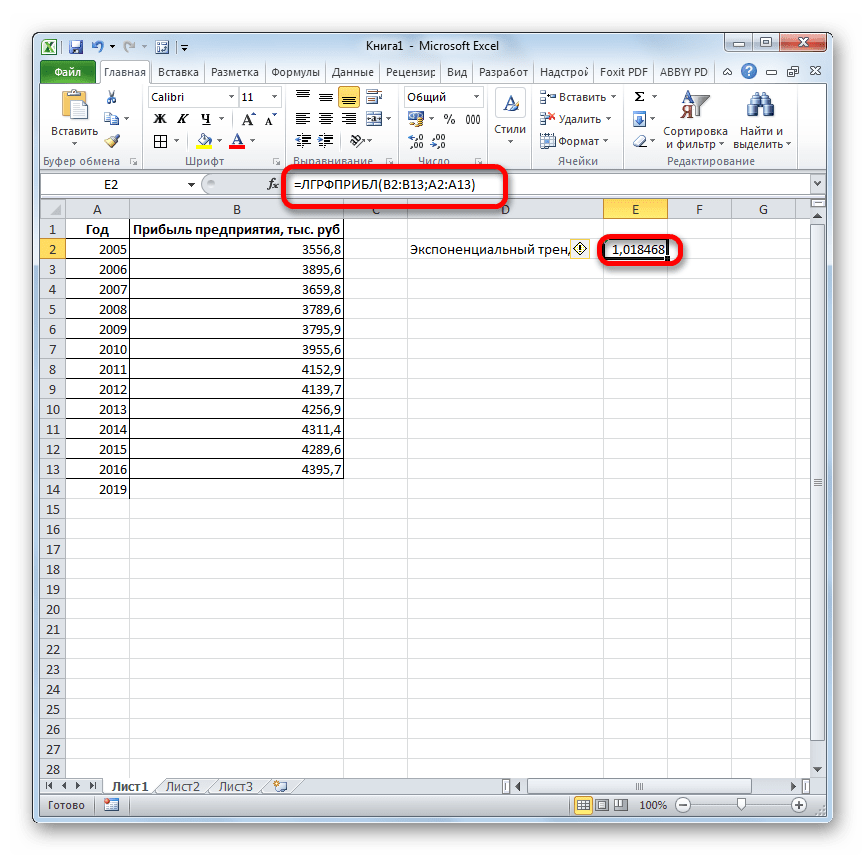
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
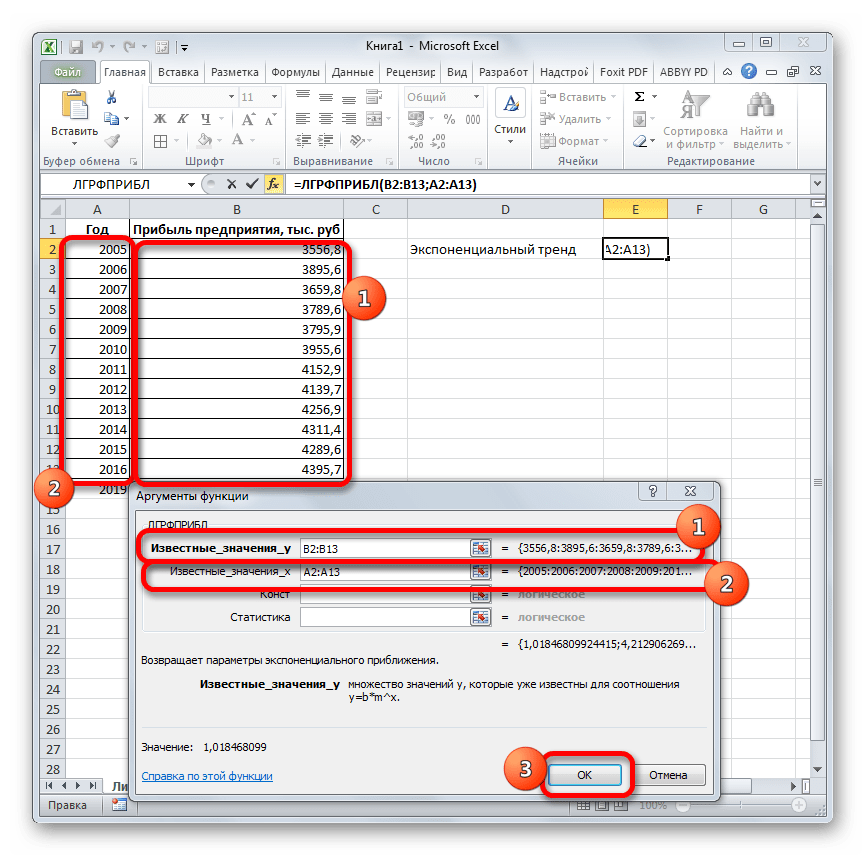
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
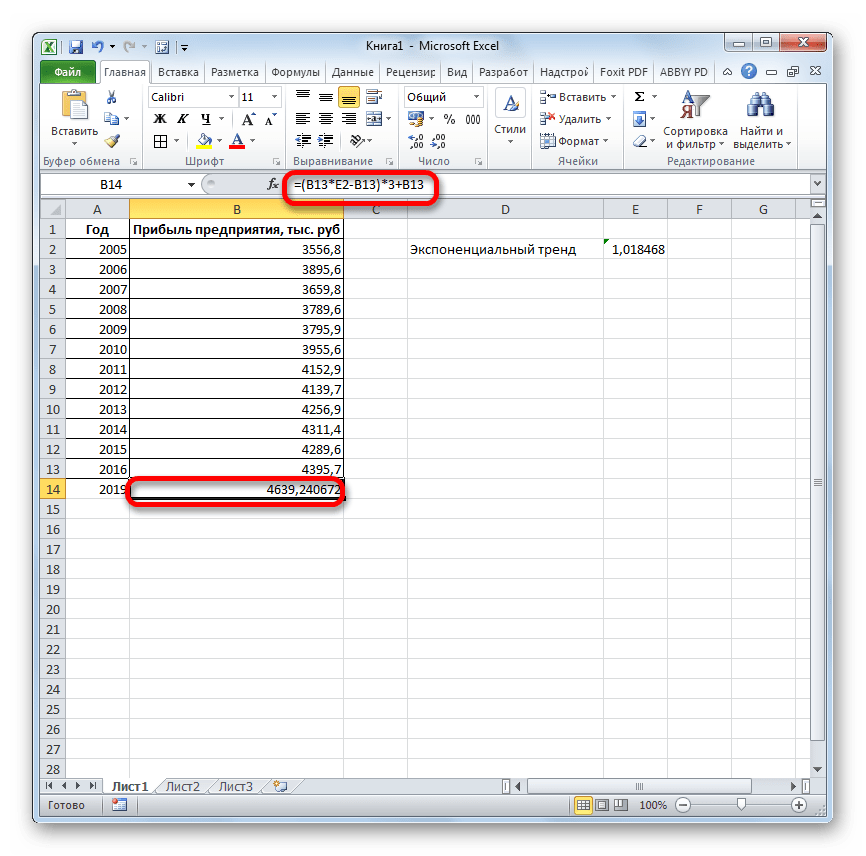
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Прогнозирование — хоть и неблагодарное, но необходимое дело и для решения таких задач в Microsoft Excel есть весьма приличный инструментарий — от простейших функций линейного тренда до навороченных статистических инструментов из надстройки Пакет Анализа (Analysis Toolpak). Одними из самых простых в реализации и при этом весьма эффективных являются функции прогнозирования по методу экспоненциального сглаживания.
Суть этого метода (если не вдаваться в математические подробности) можно объяснить относительно легко. Если бы мы, например, делали прогноз совсем примитивным способом по среднему арифметическому, то все исторические данные брались бы с одинаковым весом (в статистике этот метод «средней температуры по больнице» имеет, кстати, даже официальное название — «наивный прогноз»). При прогнозировании же по методу экспоненциального сглаживания принимается идея, что старые данные должны иметь вес меньше, чем новые. Изменение этого веса в зависимости от новизны или старости наших данных происходит по лавинообразной экспоненциальной кривой — отсюда и название методики.
В Microsoft Excel для её реализации есть две основные функции, появившиеся начиная с 2016-й версии Excel:
- ПРЕДСКАЗ.ETS (FORECAST.ETS) — вычисляет будущие спрогнозированные значения на основе исторических данных.
- ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ (FORECAST.ETS.CONFINT) — вычисляет размах доверительного интервала — коридора погрешности, в пределах которого с заданной вероятностью наш прогноз должен сбыться.
Особенно приятно, что вводить вручную эти функции и их многочисленные аргументы совершенно не требуется — в Microsoft Excel для этого есть гораздо более удобный инструмент, получивший название Лист прогноза (Forecast Sheet). Давайте рассмотрим работу с ним на следующем примере.
В качестве исходных исторических данных возьмем с сайта AutoVercity реальную статистику по продажам автомобилей в России за 2019-2020 годы (все марки суммарно):
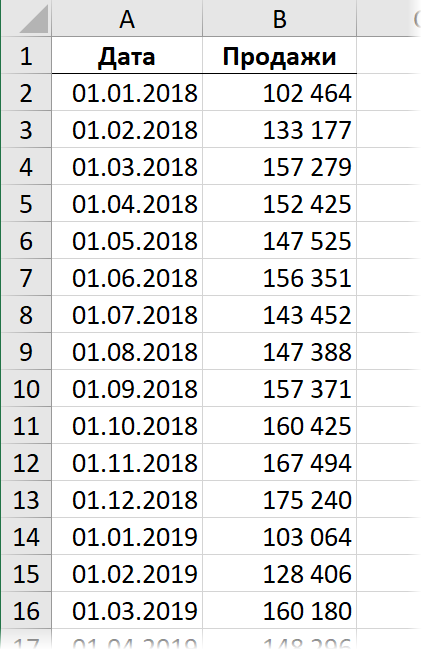
Представим на минуту, что сейчас конец 2020 года и мы хотим, используя эти данные, сделать помесячный прогноз продаж автомобилей на следующие полтора года. Выделим всю нашу таблицу и на вкладке Данные воспользуемся кнопкой Лист прогноза (Data — Forecast Sheet).
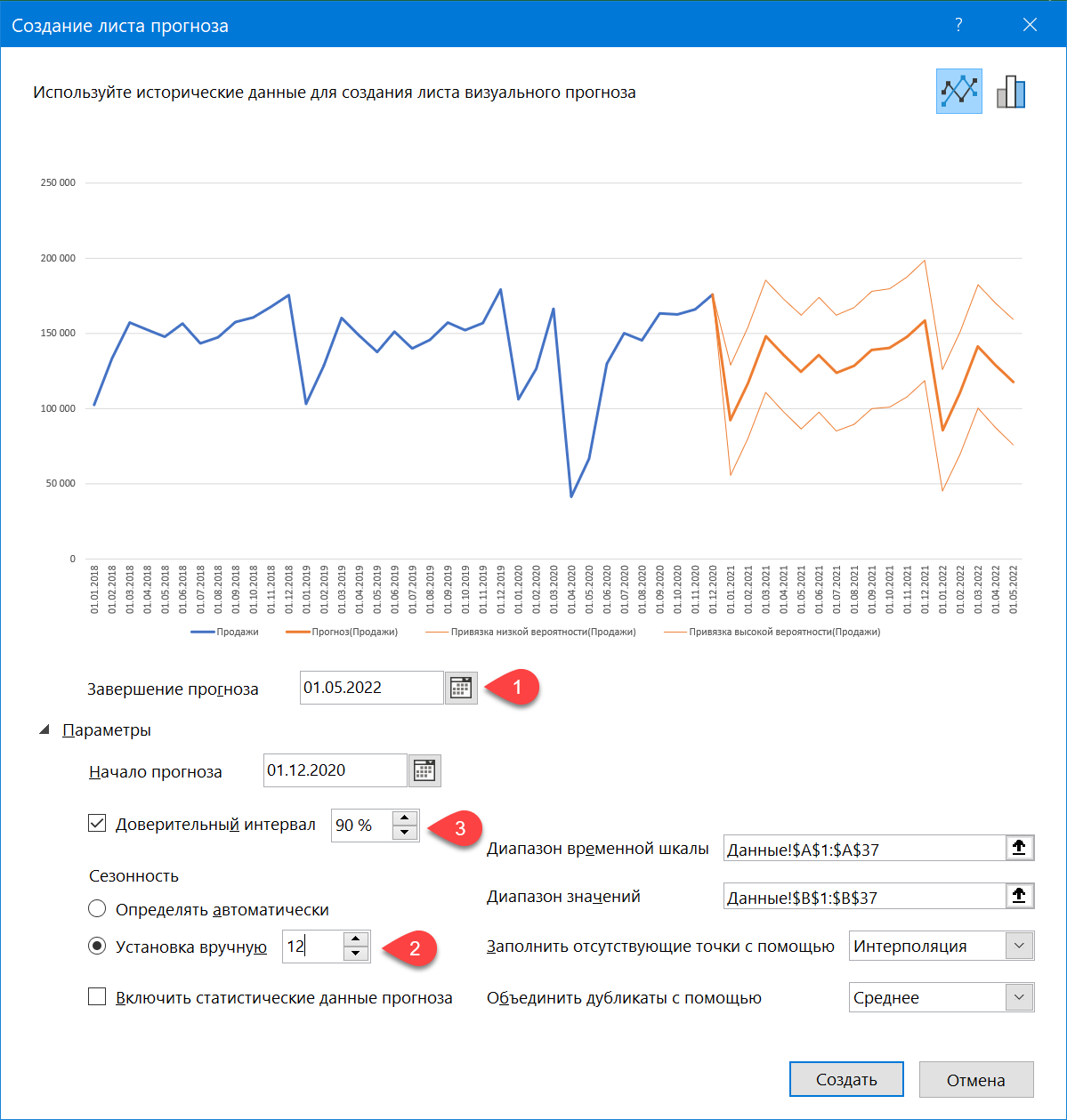
В открывшемся окне зададим следующие настройки:
- Дату завершения прогноза
- Сезонность — почти никогда корректно не определяется автоматически, к сожалению, так что лучше задать её вручную. В большинстве бизнесов она годовая (т.е. «узор» колебаний похожим образом повторяется из года в год), так что установим её равной 12 месяцам.
- Вероятность, с которой мы требуем попадания будущих фактических значений в коридор доверительного интервала. Чем больше эта вероятность, тем шире интервал (т.е. более размыт прогноз). Обычно используют значения 90-95%.
- В правом нижнем углу окна можно дополнительно выбрать реакцию на пустые ячейки (их можно заполнить нулями или средним соседних значений — интерполяцией) и на дубликаты (обычно их усредняют). Однако же, по возможности, лучше заранее подготовить исходные исторические данные, чтобы таких пробелов или дублей в них не было.
После нажатия на кнопку Создать будет сформирован новый лист с прогнозной таблицей и диаграммой, которая по ней построена:
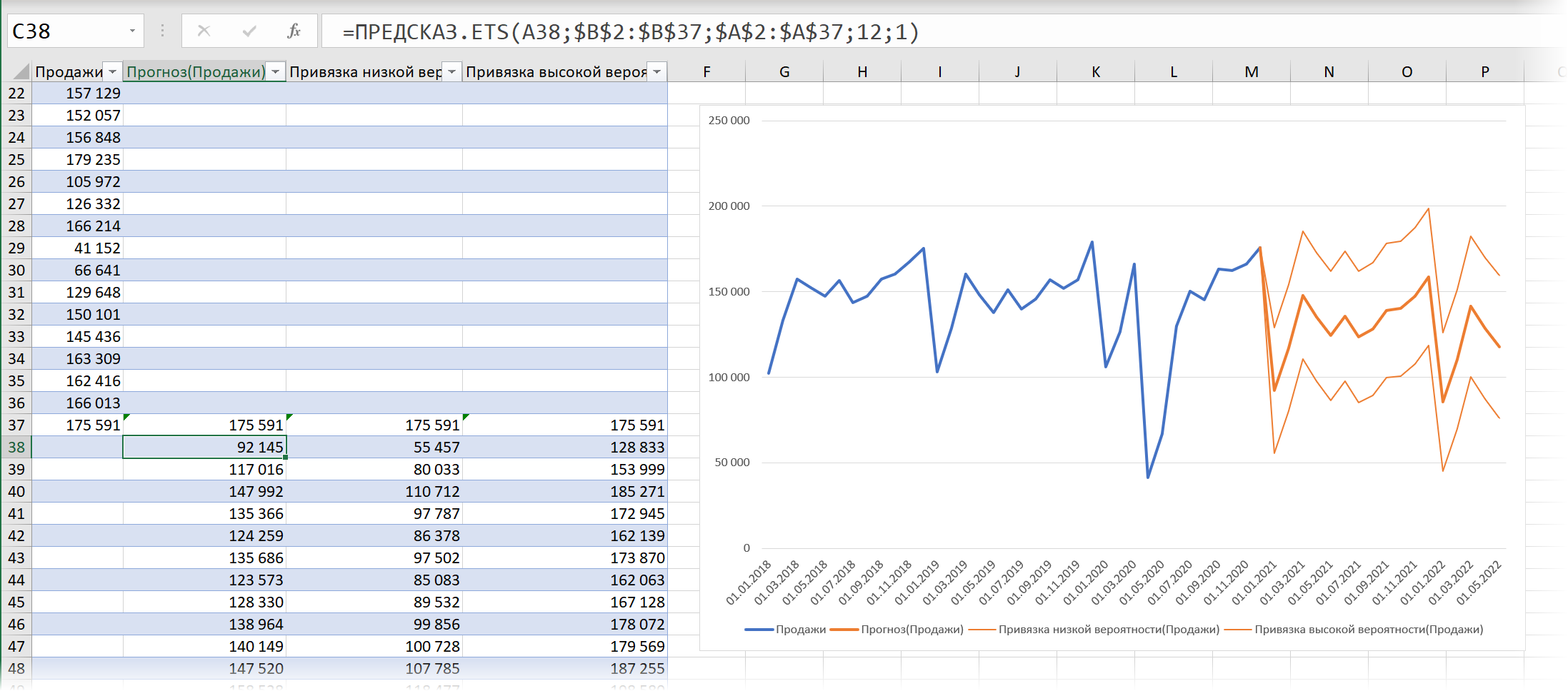
В верхней части таблицы будут идти строки с историческими данными (синяя линия), а в момент их окончания произойдет переключение на три новых столбца с прогнозом функцией ПРЕДСКАЗ.ETS и верхней и нижней границами доверительного интервала, вычисленного с помощью функции ПРЕДСКАЗ.ETS.ДОВИНТЕРВАЛ.
Ссылки по теме
- Моделирование и оценка вероятности выигрыша в лотерею
- Оптимизация доставки в Excel с помощью Поиска решения (Solver)
- Быстрое добавление новых данных в диаграмму
Функция ПРЕДСКАЗ в Excel позволяет с некоторой степенью точности предсказать будущие значения на основе существующих числовых значений, и возвращает соответствующие величины. Например, некоторый объект характеризуется свойством, значение которого изменяется с течением времени. Такие изменения могут быть зафиксированы опытным путем, в результате чего будет составлена таблица известных значений x и соответствующих им значений y, где x – единица измерения времени, а y – количественная характеристика свойства. С помощью функции ПРЕДСКАЗ можно предположить последующие значения y для новых значений x.
Примеры использования функции ПРЕДСКАЗ в Excel
Функция ПРЕДСКАЗ использует метод линейной регрессии, а ее уравнение имеет вид y=ax+b, где:
- Коэффициент a рассчитывается как Yср.-bXср. (Yср. и Xср. – среднее арифметическое чисел из выборок известных значений y и x соответственно).
- Коэффициент b определяется по формуле:
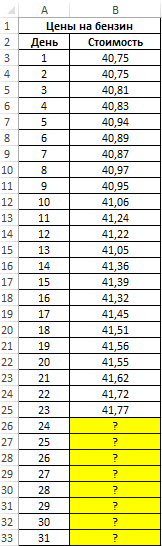
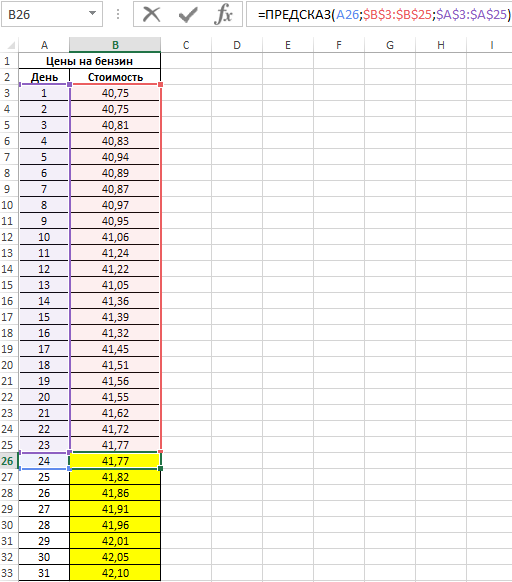
Пример 1. В таблице приведены данные о ценах на бензин за 23 дня текущего месяца. Согласно прогнозам специалистов, средняя стоимость 1 л бензина в текущем месяце не превысит 41,5 рубля. Спрогнозировать стоимость бензина на оставшиеся дни месяца, сравнить рассчитанное среднее значение с предсказанным специалистами.
Вид исходной таблицы данных:
Чтобы определить предполагаемую стоимость бензина на оставшиеся дни используем следующую функцию (как формулу массива):
Описание аргументов:
- A26:A33 – диапазон ячеек с номерами дней месяца, для которых данные о стоимости бензина еще не определены;
- B3:B25 – диапазон ячеек, содержащих данные о стоимости бензина за последние 23 дня;
- A3:A25 – диапазон ячеек с номерами дней, для которых уже известна стоимость бензина.
Результат расчетов:
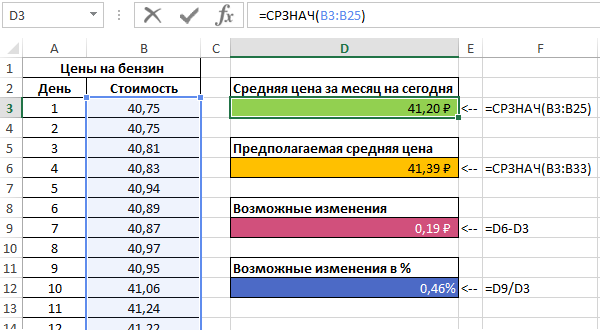
Рассчитаем среднюю стоимость 1 л бензина на основании имеющихся и расчетных данных с помощью функции:
=СРЗНАЧ(B3:B33)
Результат:
Можно сделать вывод о том, что если тенденция изменения цен на бензин сохранится, предсказания специалистов относительно средней стоимости сбудутся.
Анализ прогноза спроса продукции в Excel по функции ПРЕДСКАЗ
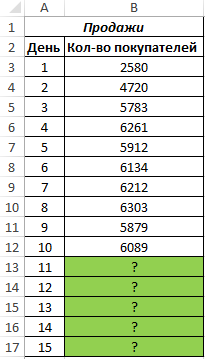
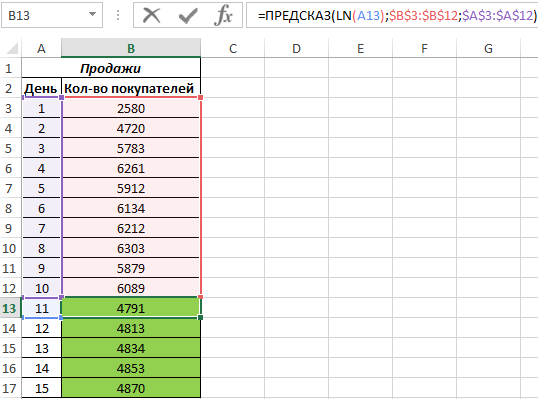
Пример 2. Компания недавно представила новый продукт. С момента вывода на рынок ежедневно ведется учет количества клиентов, купивших этот продукт. Предположить, каким будет спрос на протяжении 5 последующих дней.
Вид исходной таблицы данных:
Как видно, в первые дни спрос был небольшим, затем он рос достаточно большими темпами, а на протяжении последних трех дней изменялся незначительно. Это свидетельствует о том, что основным фактором роста продаж на данный момент является не расширение базы клиентов, а развитие продаж с постоянными клиентами. В таких случаях рекомендуют использовать не линейную регрессию, а логарифмический тренд, чтобы результаты прогнозов были более точными.
Рассчитаем значения логарифмического тренда с помощью функции ПРЕДСКАЗ следующим способом:
Как видно, в качестве первого аргумента представлен массив натуральных логарифмов последующих номеров дней. Таким образом получаем функцию логарифмического тренда, которая записывается как y=aln(x)+b.
Результат расчетов:
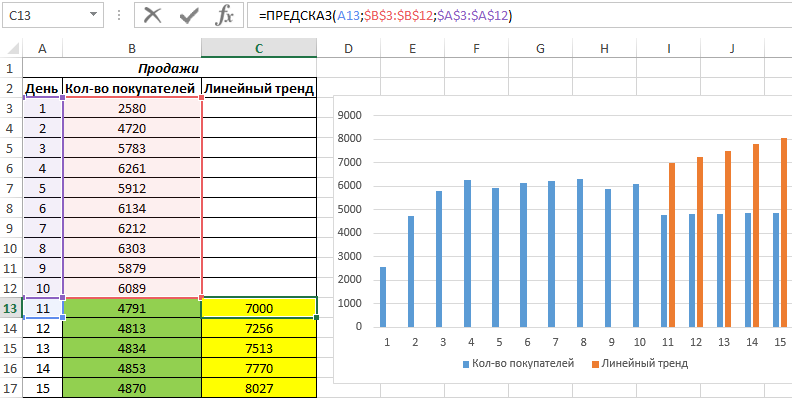
Для сравнения, произведем расчет с использованием функции линейного тренда:
И для визуального сравнительного анализа построим простой график.
Полученные результаты:
Как видно, функцию линейной регрессии следует использовать в тех случаях, когда наблюдается постоянный рост какой-либо величины. В данном случае функция логарифмического тренда позволяет получить более правдоподобные данные (более наглядно при большем количестве данных).
Прогнозирование будущих значений в Excel по условию
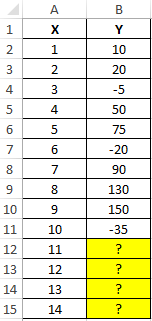
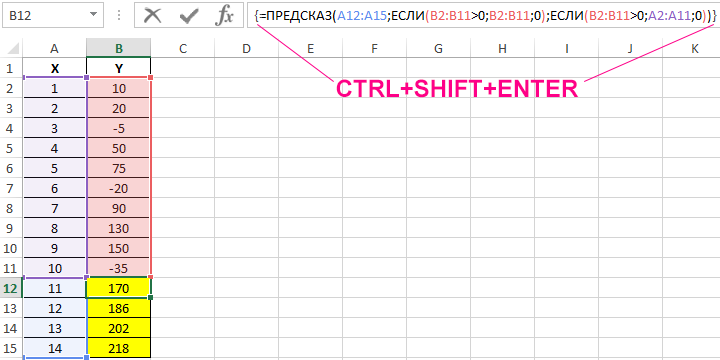
Пример 3. В таблице Excel указаны значения независимой и зависимой переменных. Некоторые значения зависимой переменной указаны в виде отрицательных чисел. Спрогнозировать несколько последующих значений зависимой переменной, исключив из расчетов отрицательные числа.
Вид таблицы данных:
Для расчета будущих значений Y без учета отрицательных значений (-5, -20 и -35) используем формулу:
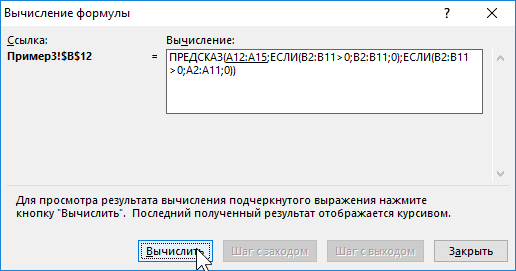
C помощью функций ЕСЛИ выполняется перебор элементов диапазона B2:B11 и отброс отрицательных чисел. Так, получаем прогнозные данные на основании значений в строках с номерами 2,3,5,6,8-10. Для детального анализа формулы выберите инструмент «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу». Один из этапов вычислений формулы:
Полученные результаты:
Особенности использования функции ПРЕДСКАЗ в Excel
Функция имеет следующую синтаксическую запись:
=ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x)
Описание аргументов:
- x – обязательный для заполнения аргумент, характеризующий одно или несколько новых значений независимой переменной, для которых требуется предсказать значения y (зависимой переменной). Может принимать числовое значение, массив чисел, ссылку на одну ячейку или диапазон;
- известные_значения_y – обязательный аргумент, характеризующий уже известные числовые значения зависимой переменной y. Может быть указан в виде массива чисел или ссылки на диапазон ячеек с числами;
- известные_значения_x – обязательный аргумент, который характеризует уже известные значения независимой переменной x, для которой определены значения зависимой переменной y.
Примечания:
- Второй и третий аргументы рассматриваемой функции должны принимать ссылки на непустые диапазоны ячеек или такие диапазоны, в которых число ячеек совпадает. Иначе функция ПРЕДСКАЗ вернет код ошибки #Н/Д.
- Если одна или несколько ячеек из диапазона, ссылка на который передана в качестве аргумента x, содержит нечисловые данные или текстовую строку, которая не может быть преобразована в число, результатом выполнения функции ПРЕДСКАЗ для данных значений x будет код ошибки #ЗНАЧ!.
- Статистическая дисперсия величин (можно рассчитать с помощью формул ДИСП.Г, ДИСП.В и др.), передаваемых в качестве аргумента известные_значения_x, не должна равняться 0 (нулю), иначе функция ПРЕДСКАЗ вернет код ошибки #ДЕЛ/0!.
- Рассматриваемая функция игнорирует ячейки с нечисловыми данными, содержащиеся в диапазонах, которые переданы в качестве второго и третьего аргументов.
- Функция ПРЕДСКАЗ была заменена функцией ПРЕДСКАЗ.ЛИНЕЙН в Excel версии 2016, но была оставлена для обеспечения совместимости с Excel 2013 и более старыми версиями.
- Для предсказания только одного будущего значения на основании известного значения независимой переменной функция ПРЕДСКАЗ используется как обычная формула. Если требуется предсказать сразу несколько значений, в качестве первого аргумента следует передать массив или ссылку на диапазон ячеек со значениями независимой переменной, а функцию ПРЕДСКАЗ использовать в качестве формулы массива.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:

Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
Модель с полиномиальным трендом
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…