Построение графиков в полярной системе координат в excel

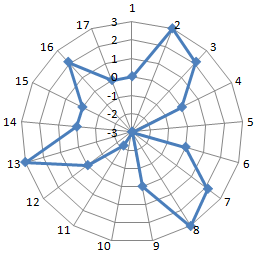
Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.

Что показывает лепестковая диаграмма

Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).

В каких ситуациях полезна именно лепестковая диаграмма:

• нужна максимальная наглядность;
• необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
• важно показать на одном графике зависимость переменных величин от набора стабильных значений.

График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.



Как построить лепестковую диаграмму в Excel

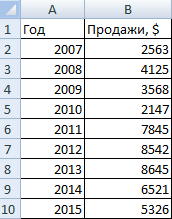
1. На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.



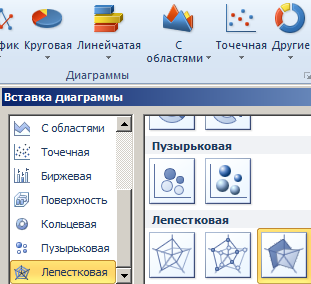
2. Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».



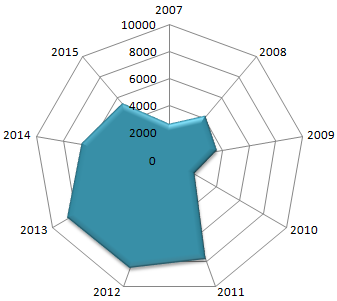
3. После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.

* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.

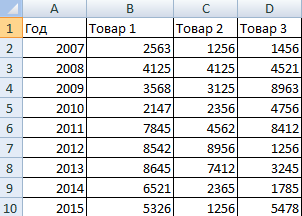
В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:

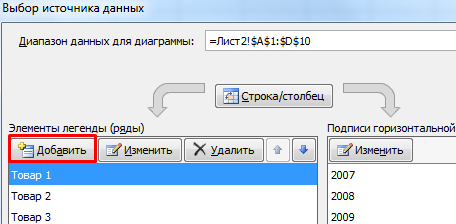
Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.

Получаем такой рисунок:

* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.

Построение графика в полярной системе координат с помощью Excel

В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.

Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:

1. для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
2. значение ряда данных – расстояние от центра до маркера – величина радиуса;
3. категория – угловая координата точки – наклон радиуса.

Известны следующие значения точек:

π /8	π /6	π /4	π /3	3π/8	5π/12	π/2	7 π/12
5 π/8	4 π/6	3 π/4	5 π/6	7 π*8	11 π/12	π

Уравнение функции:

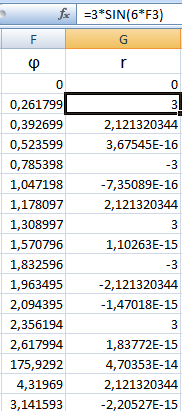
r = 3 * sin (6 * ^φ)/

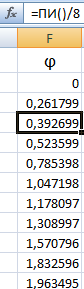
Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.

Формулы для заполнения первого столбца берем из таблицы значений точек:

В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:

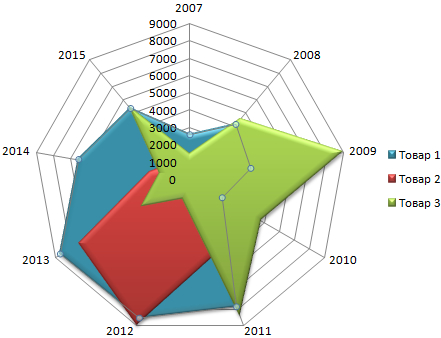
Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:

На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.

В этом руководстве будет показано, как создать полярный график во всех версиях Excel: 2007, 2010, 2013, 2016 и 2022.

Полярный график используется для определения точки в пространстве в так называемой полярной системе координат, где вместо использования стандартных координат x и y каждая точка на полярной плоскости выражается с использованием этих двух значений:

• Радиус (р) — Расстояние от центра участка
• Тета (θ) — Угол от опорного угла

Сама плоскость состоит из концентрических кругов, расширяющихся наружу от начала координат или полюса — отсюда и название. Полярный график пригодится, когда анализируемые данные имеют циклический характер.

В качестве примера на диаграмме ниже сравниваются оценки удовлетворенности клиентов (CSAT) — метрика, которая иллюстрирует удовлетворенность потребителя брендом или продуктом, двух организаций на протяжении 2022 года: Simpson Ltd и Griffin Ltd.

Сюжет позволяет быстро оценить хорошие и плохие месяцы для каждой компании, что способствует принятию более правильных решений.

Однако вот в чем проблема:

Excel не поддерживает этот тип диаграмм — на самом деле, он даже не может считывать полярные координаты, а это значит, что вам придется создавать его с нуля. Также не забудьте попробовать надстройку Chart Creator, мощный инструмент для создания умопомрачительных расширенных диаграмм и графиков Excel всего за несколько кликов.

В этом подробном пошаговом руководстве вы узнаете, как с нуля преобразовать необработанные данные в полярный график в Excel. Для справки, эта статья основана на учебнике, созданном Джоном Пелтье.

Начиная

Поскольку оценки CSAT обычно выражаются в виде процентной шкалы, рассмотрите следующую таблицу:

Шаг № 1: Настройте вспомогательную таблицу.

Сразу же наметьте вспомогательную таблицу, в которой будут выполняться все вычисления для вашей диаграммы. Чтобы построить график, вам необходимо сначала вычислить полярные координаты, а затем преобразовать их в значения осей x и y, используемые Excel для создания диаграммы.

Настройте отдельную фиктивную таблицу следующим образом:

Обратите внимание, как вспомогательная таблица начинается с фиктивной строки (E2: H2) — определяет опорный угол. Давайте подробнее поговорим о каждом элементе таблицы:

• Месяц — Этот столбец содержит качественные категории, полученные из ваших исходных данных. Введите «Старт» в первую ячейку (E2) и скопируйте категории (в нашем случае месяцы) прямо под ними (E3: E14).
• Угол (Тета) — Этот столбец содержит тета-значения, отвечающие за рисование спиц, в которые будут помещены фактические значения. Вы всегда должны вводить «0» в первую ячейку (F2) этого столбца.
• CSAT Simpson LTD (Радиус) и CSAT Griffin LTD (Радиус) — Эти столбцы содержат значения радиуса, иллюстрирующие производительность каждой компании в течение года.

Шаг № 2: Вычислить значения угла (тета).

Если у вас уже есть значения r и theta, пропустите эту часть и прокрутите вниз до Шаг # 4.

На этом этапе наша цель — равномерно отобразить спицы в зависимости от количества категорий в наборе данных. Поскольку один полный круговой оборот равен 360 градусам, чтобы выполнить задачу, вам нужно разделить 360 на количество категорий в вашем наборе данных (в нашем случае — двенадцать месяцев).

Затем складывайте это число по мере продвижения от нуля до 360. И здесь в игру вступает функция СЧЁТ. По сути, он подсчитывает количество непустых ячеек в указанном диапазоне.

Скопируйте эту формулу в ячейку F3:

1	= 360 / COUNTA (3 австралийских доллара: 14 австралийских долларов)

С этой формулой в ячейке F3, используйте эту другую формулу в ячейке F4 чтобы добавить заданное значение угла к сумме всех значений тета, которые идут перед ним в столбце:

1	= F3 + 360 / COUNTA (3 австралийских доллара: 14 австралийских долларов)

Важно заблокировать диапазон ячеек (A3: A14), чтобы легко скопировать формулу в оставшиеся ячейки.

Теперь выполните формулу для остальных ячеек в столбце (F5: F14), выбрав F4 и перетащите маркер заполнения вниз.

Шаг № 3: Вычислите значения радиуса.

Полярный график будет состоять из 10 колец данных, каждая радиальная точка (расстояние между внутренним и внешним краем кольца) представляет собой десятипроцентное приращение по шкале от 0 до 100.

Поскольку оценки CSAT также измеряются по процентной шкале, просто разделите каждую таблицу оценок CSAT на 10.

Вот как это сделать быстро и легко. Чтобы найти значения радиуса для первой компании (Simpson Ltd), введите эту крошечную формулу в ячейку G3 и скопируем в остальные ячейки (G4: G14):

Теперь точно так же вычислим радиусы для второй компании (Griffin Ltd):

В этот момент вы можете подумать: «Что, если мой тип данных отличается? Как вы корректируете, сравнивая, например, доход, полученный компаниями, с оценками CSAT? »

Проще говоря, вы должны проанализировать свои фактические данные, определить эквивалент одной радиальной точки (скажем, 50 000 долларов США) и разделить все значения в вашем наборе данных на это число. Предположим, что в мае какая-то компания заработала 250 000 долларов. Чтобы найти радиус, разделите 250 000 долларов на 50 000. Так просто.

Шаг №4: Скопируйте последние значения радиуса во вспомогательную строку.

Заполните таблицу, скопировав значения r в самом низу (G14: H14) каждого столбца в соответствующие фиктивные ячейки (G2: H2).

Шаг № 5: Рассчитайте значения по осям x и y для каждой компании.

Пришло время перейти к преобразованию полярных координат в соответствующие значения по осям x и y. Благодаря тригонометрии вы можете осуществить переход, используя две специальные формулы, которые вы выучите за несколько секунд.

Начнем сначала со значений оси X. В ячейке рядом со вспомогательной таблицей (I2) введите следующую формулу:

1	= G2 * SIN (F2 / 180 * PI ())

Скопируйте эту формулу в остальные ячейки под ней (I3: I14).

Точно так же вставьте эту формулу в ячейку J2 чтобы найти значения оси Y и выполнить его для остальных ячеек (J3: J14) также:

1	= G2 * COS (F2 / 180 * PI ())

Важная заметка: Помните, что ячейка строки заголовка (J1) столбца со значениями оси Y (столбец J) будет действовать как имя серии, то есть значение в этой ячейке перейдет в легенду диаграммы.

Повторите тот же процесс, чтобы вычислить значения X и Y для второй компании, корректируя формулу для использования данных в столбце Griffin Ltd:

1	= H2 * SIN (F2 / 180 * PI ())

1	= H2 * COS (F2 / 180 * PI ())

Шаг № 6: Настройте вторую вспомогательную таблицу для сетки полярных графиков.

Да, вы не ослышались. Вам нужна еще одна вспомогательная таблица. К счастью, худшее уже позади, так как не требуется единой формулы, чтобы составить таблицу.

Взгляните на это:

По сути, таблица состоит из трех элементов:

• Качественная шкала (желтая область или N2: N11) — Это отражает интервалы значений на основе ваших фактических данных. Заполните ячейки процентами, как показано на скриншоте. В качестве примера альтернативных данных, если бы мы проанализировали доход, упомянутый ранее, этот столбец увеличился бы с 50 000 до 500 000 долларов США.
• Строка заголовка (красная область или O1: Z1) — Он содержит все имена категорий, полученные из исходной таблицы данных, только что размещенные вертикально.
• Значения сетки (зеленая зона или O2: Z11) — Эти значения разделят будущие кольца данных на равные части, очерчивая сетку графика. Просто выберите число из ничего и скопируйте его во все ячейки в пределах диапазона.

Шаг № 7: Создайте набор кольцевых диаграмм.

Наконец-то вы собрали все необходимые данные для графиков — это было довольно интенсивно. Попрощайтесь с функциями и формулами, потому что теперь вы можете приступить к построению самого полярного графика.

Начните с настройки полярной плоскости, создав 10 кольцевых диаграмм, наложенных друг на друга:

1. Выделите все значения сетки из второй вспомогательной таблицы (O2: Z11).
2. Перейти к Вставлять таб.
3. Щелкните значок «Вставить круговую или кольцевую диаграмму» кнопка.
4. Выбирать «Пончик.”

В результате Excel должен дать вам набор из 10 колец.

Иногда Excel не может правильно прочитать ваши данные. Чтобы обойти проблему, если это произойдет с вами, следуйте нескольким простым инструкциям, чтобы сложить диаграммы вручную. В целях иллюстрации предположим, что вместо этого вы собираетесь анализировать данные за восемь месяцев.

Сначала выберите любую пустую ячейку и постройте пустую кольцевую диаграмму, выполнив действия, описанные выше.

Затем щелкните правой кнопкой мыши график и выберите «Выберите данные.”

После этого в Выберите источник данных диалоговом окне щелкните значок «Добавлять» кнопка.

в Редактировать серию выберите все значения сетки в первой строке (O2: V2) и нажмите «Ok.”

Как вы, возможно, догадались, промойте и повторите для каждого ряда, чтобы получить те же 10 колец, нанесенных на диаграмму.

Шаг № 8: Уменьшите размер отверстия для пончика.

Как видите, все кольца сжаты вместе от центра. Давайте изменим это, уменьшив размер отверстия для пончика.

1. Щелкните правой кнопкой мыши любое кольцо данных.
2. Выбирать «Форматировать ряд данных.”

Во всплывающей панели задач измените значение размера отверстия пончика по умолчанию, чтобы волшебство произошло:

1. Переключитесь на Варианты серий таб.
2. Установить Размер отверстия для пончика к «10%.”

Шаг № 9: Настройте сетку диаграммы.

На той же панели задач преобразуйте кольца в сетку, выполнив следующие простые шаги:

1. Перейти к Заливка и линия таб.
2. Под «Наполнять,» выбирать «Без заливки.”
3. Под «Граница,» Выбрать «Сплошная линия.”
4. Щелкните значок «Цвет контура», Чтобы открыть цветовую палитру и выбрать светло-серый.
5. Установить Ширина к «5 пт.”

Промыть и повторить для остальных колец.

Шаг № 10: Добавьте данные диаграммы.

Теперь, когда основа заложена, добавьте в диаграмму значения x и y из первой вспомогательной таблицы.

1. Выделите все значения по осям x и y, показывающие оценки CSAT первой компании (Simpson Ltd), а также ячейки строки заголовка (I1: J14) и скопируйте данные (щелкните правой кнопкой мыши и выберите Копировать).
2. Выберите область диаграммы.
3. Перейдите к Дом таб.
4. Щелкните значок «Вставить» кнопка.
5. Выбирать «Специальная вставка.”

В крошечном Специальная вставка В появившемся диалоговом окне выполните следующие действия:

1. Под «Добавить ячейки как,» выбирать «Новая серия.”
2. Под «Значения (Y) в,» Выбрать «Колонны.”
3. Проверить «Имена серий в первой строке» а также «Категории (метки X) в первом столбце»Коробки.
4. Нажмите «OK.”

Повторите процесс, чтобы добавить данные диаграммы, связанные со второй компанией (Griffin Ltd).

Шаг № 11: Измените тип диаграммы для вставленного ряда данных.

Теперь измените тип диаграммы для обеих вновь добавленных серий, представляющих фактические значения.

1. Щелкните правой кнопкой мыши любую из серий, представляющих фактические значения (либо Серия «Симпсон Лтд» или Серия «Гриффин Лтд.»).
2. Выбирать «Изменить тип диаграммы серии.”

Оказавшись там, измените тип диаграммы для Серия «Симпсон Лтд.» а также Серия «Гриффин Лтд.» к «Разброс с гладкими линиями и маркерами».

Шаг № 12: Измените масштабы горизонтальной и вертикальной оси.

Как только оси диаграммы появятся, измените диапазоны шкалы горизонтальной и вертикальной оси для диаграммы, чтобы точно отразить данные, нанесенные на нее.

1. Щелкните правой кнопкой мыши вертикальную ось.
2. Выбирать «Ось формата.”

Когда появится панель задач, определите новые диапазоны шкалы оси:

1. Перейти к Параметры оси таб.
2. Установить Минимальные границы ценность для “-10.”
3. Изменить Максимальные границы ценность для “10.”

После этого перейдите к горизонтальной оси и проделайте то же самое.

Шаг № 13: Удалите линии сетки, оси и нерелевантные элементы легенды.

Очистите график, удалив элементы диаграммы, которые не имеют никакого практического значения: линии сетки, оси, а также все элементы легенды — за исключением двух, которые вам действительно нужны (отметка информации о компании).

Для этого дважды щелкните каждый элемент, затем снова щелкните его правой кнопкой мыши и выберите «Удалить.”

Шаг № 14: Добавьте метки данных.

Поскольку мы постепенно приближаемся к концу нашего грандиозного приключения в Excel, пришло время добавить метки данных, представляющие каждую качественную категорию в вашем наборе данных.

Щелкните правой кнопкой мыши на внешнее кольцо (Серия «10») и выберите «Добавьте метки данных.”

Шаг № 15: Настройте метки данных.

По сути, все, что вам нужно сделать здесь, это заменить метки данных по умолчанию на имена категорий из таблицы, содержащей ваши фактические данные.

Щелкните правой кнопкой мыши любую метку данных и выберите «Отформатируйте метки данных.”

Когда откроется панель задач, замените значения, выполнив следующие действия:

1. Перейти к Параметры метки таб.
2. Проверить «Значение из ячеек» коробка.
3. Выделите значения категорий из исходной таблицы данных (A3: A14).
4. Нажмите «OK.”
5. Снимите флажок «Ценить» коробка.
6. Снимите флажок «Показать линии выноски» коробка.

Шаг №16: переставьте этикетки.

Теперь немного сместите метки, разместив их по краю внешнего кольца в порядке, показанном на скриншоте ниже. Это нужно будет сделать вручную, перетащив каждый заголовок в нужное место.

Наконец, измените название диаграммы, и все готово!

1


Полярные координаты. Построение графиков кривых в программе Microsoft Office Еxcel

2


В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O — полюс и ось OP, которая называется полярной осью. В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O — полюс и ось OP, которая называется полярной осью. Если M — произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r — ее расстояния от полюса, выраженного в единицах масштаба, и — угла φ, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и φ называются полярными координатами точки M. Если M — произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r — ее расстояния от полюса, выраженного в единицах масштаба, и — угла φ, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и φ называются полярными координатами точки M. Полярные координаты M O P φ r

3


Переход из полярной системы координат в декартовую систему координат. Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол φ, то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол φ, то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул

4


Пример 1 Построить кривую, заданную уравнением r=4cos3 φ Внесем данные и получим следующее распределение по столбцам электронной таблицы: где аргумент F (угол в радианах) будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 12,6; 18,9; 25,2 и т.д.

5


Далее выделим те данные, которые получились в столбцах «Х» и «У», нажмём кнопку «Мастер диаграмм» на панели инструментов и выберем тип диаграммы «Точечная диаграмма со значениями, соединёнными сглаживающими линиями без маркеров» Получим кривую: r = a cos k φ r = a sin kφ Данная кривая является частным случаем семейства кривых, имеющих общее уравнение r = a cos k φ или r = a sin kφ и называемых «Розами Гранди»

6


РОЗЫ ГРАНДИ РОЗЫ ГРАНДИ Гвидо Гранди ( ) – итальянский математик, историк и священник В уравнении «роз» параметр а отвечает за радиус лепестков, а параметр k – за их количество k=2 k=7 k=7 k=3 k=4 k=2 k=10 k=5

7


Вариации роз

8


k=59 k=15 k=13,97 k=9,5 k=9,5 k=74 k=10,4

9


Пример 2 Спираль Архимеда r = a φ

10


Пример 3 Гиперболическая спираль R=a/ φ

11


Пример 4 Кривые Хабеннихта Математическим исследованием формулы цветов и листьев занимался также немецкий геометр Л. Хабеннихт Лист кислицы Лист плюща

12


Лист стрелолиста Лист кувшинкиЛист клёна r = a (1 + cosφ)

13


r = 1 + 7cos(k φ ) + 4sin 2 (k φ ) + 3sin 4 (k φ ) Цветы

14


Цветы При к=5При к=6 При к=6,3При к=7,5

15


Цветы

16


Над презентацией работали учащиеся 11Б класса МОУ «Ломоносовская СОШ 3» Наталья Ващенко Самсон Приёмышев Учитель – Торопова Елена Владимировна

«Районная научно-практическая конференция

«От исследования — к научному поиску»

Учреждение: МБОУ «Многопрофильная гимназия г. Лагани»

Секция: Естественно-научная

Тема работы:

«Построение и исследование графиков

 функций при помощи электронных

Таблиц Excel.»

Автор работы: Белкин Алексей Васильевич,

ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»

Научный руководитель: Никифоров Евгений Алексеевич,

учитель математики МБОУ «Многопрофильная гимназия г. Лагани»

г. Лагань — 2013

ОГЛАВЛЕНИЕ

Введение	2
Инструкция по построению кривых с помощью программы Microsoft  Excel.	3-5
1.2. Полярная система координат	5-6
1.3. Инструкция по построению кривых  в полярных координатах с помощью программы Microsoft  Excel	6-10
1.4.  Построение кусочно-заданной  функции на примере построения эскиза национального орнамента	11-12
Заключение	13 — 14
Список литературы	15

ВВЕДЕНИЕ

Актуальность работы. При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые  в школьных учебниках по информатике  не оговариваются.

Вопрос (мотивация): Как построить график с изменяющимся параметром, для дальнейшего его изучения?

Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и  уравнений степеней выше второй с двумя переменными.

Гипотеза: для решения поставленной проблемы, возможно использовать инструменты  прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.

Поэтому, объект нашего исследования — прикладная программа Microsoft Excel, ее возможности для построений графиков функций и исследования их.

Исходя из этого, предметом нашего исследования стали уравнения элементарных функций  и кривых высших порядков.

Цель  работы – показать алгоритм  построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:

• Научился строить графики  функций, с дальнейшей возможностью изучения их свойств
• изучил переход от декартовой системы координат к полярной и обратно;
• исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
• познакомились с некоторыми замечательными кривыми известных математиков.

Планы и перспективы: продолжить изучение плоских кривых.

1. Инструкция по построению кривых с помощью программы

Microsoft  Excel.

Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.

Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.

Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение  функции.

По построенным   данным строим график функции.

Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования

. Рассмотрим в качестве примера тригонометрическую функцию 

Построим компьютерную модель исследования.

Для дальнейших исследований будем одновременно строить график исходной элементарной функции y= sinx и преобразованной функции и сравнивать полученные результаты.

Формулы будут записаны в терминах электронных таблиц следующим образом:

А3= -7 А4 =А3+0,1 (шаг можно уменьшить например до 0,001) B3 =sin(a3) у меня независимая переменна изменяется  на интервале (-7;7), что примерно соответствует  интервалу ()

d3= -7 d4 =d3+0,1 E3 =sin($f$1*d3) В ячейке F1 будем задавать значение параметра k, и рассматривать полученные изменения графика функции

Фрагмент произведенных расчетов из электронной таблицы приведен ниже

В приложенном к  работе файле  Microsoft Excel работа графики можно увидеть полные вычисления и полученные результаты

Для детального изучения преобразований графики построил в одной системе координат, что дает возможность сравнить полученные результаты.

Для дальнейших исследований достаточно теперь изменить значение в ячейке f1, и получим иную картину. Например f1=-4

Как видно значения функции автоматически пересчитаны, и построен уже другой график. Данные возможности мною были продемонстрированы одноклассникам на уроке математики. В дальнейшем мои товарищи на уроки изучили свойства полученных графиков функций и наглядно изучили преобразования графиков следующих функций

( и др.)

1.2.  Полярная система координат.

Мои исследования, на этом не закончились, возник вопрос в построении более сложных графиков. В качестве примера мною рассмотрено уравнение

В полярной системе координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел . Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).

Если в декартовой системе координат предельно простое выражение  определяет прямую линию, то это же выражение, переписанное в форме , уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата  берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида, которым соответствует одна и та же точка при любых натуральных . Для полюса , угол  произвольный.

Связь между полярной и декартовой системами координат.

Точка О — полярный полюс,  луч ОЕ будем называть полярной осью, отрезок ОМ — называют длиной полярного радиуса R, положительный угол от луча ОЕ до луча F — полярный угол.

Если известны полярные координаты R и , точки М, то можно уставить связь с её декартовыми координатами.

Построим прямоугольный ОМЕ. В этом треугольнике гипотенуза ОМ=R, ЕОМ = , катет ЕМ = у, катет ОЕ = х координаты точки М.

Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: , , . Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: , затем , .

Некоторые замечательные кривые. На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея, Фибоначчи,  кардиоида, овалы Кассини,  лемниската Бернулли, фигуры Лиссажу, розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези)  и т.д.

1.3. Инструкция по построению кривых

в полярных координатахс помощью программы Microsoft  Excel.

Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.

Задача. Построить кривую, заданную уравнением .

Решение. Найдем уравнение данной линии в полярных координатах.

Для программы Microsoft  Excel:  R=4*COS(3*F)

Предположим, что угол F изменяется в интервалах от 0 до 2. Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.

Построим компьютерную модель исследования.

Формулы будут записаны в терминах электронных таблиц следующим образом:

А2 0,1                      А3 =А2+0,1                             B2 =4*COS(3*F)
C2 =SIN(А2)           D2 =COS(А2)                         E2 =B2*D2             F2 =В2*C2

Тогда получаем следующее распределение по столбцам электронной таблицы:

f	r	sin(f)	cos(f)	x	y
0,1	3,821346	0,099833	0,995004	3,802255	0,381498
0,2	3,301342	0,198669	0,980067	3,235535	0,655875
0,3	2,48644	0,29552	0,955336	2,375387	0,734793
0,4	1,449431	0,389418	0,921061	1,335014	0,564435
0,5	0,282949	0,479426	0,877583	0,248311	0,135653
0,6	-0,90881	0,564642	0,825336	-0,75007	-0,51315
0,7	-2,01938	0,644218	0,764842	-1,54451	-1,30092
0,8	-2,94957	0,717356	0,696707	-2,05499	-2,1159
0,9	-3,61629	0,783327	0,62161	-2,24792	-2,83274
1	-3,95997	0,841471	0,540302	-2,13958	-3,3322
1,1	-3,94992	0,891207	0,453596	-1,79167	-3,5202

и т. д.

Для построения графика выделим информационный блок E2..F64, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.  Получим следующий график.

Исследование формы кривой, в зависимости от изменения значений входящих в её уравнение. Внося изменения в ячейку H27 , не меняя более ничего, мы можем получать различные виды уравнения

Еще примеры …

Обратимся к исследованию формы роз. Поскольку правая часть уравнения не может превышать величины a, то и вся роза, очевидно, уменьшается внутри круга радиусом a. Количество же лепестков розы зависит от величины модуля k:

1. Если модуль k – целое число, то роза состоит из k лепестков, при нечетном k, и из 2k лепестков при k четном.

2.Если модуль k – рациональное число, равное   то роза состоит из m лепестков в случае, когда оба числа  m и n  нечетные, и из 2m лепестков, если одно из этих чисел является четным.

При этом, в отличие от первого случая каждый следующий лепесток будет частично перекрывать предыдущий.

3.Если модуль k – иррациональное число, то роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга.

Математическим исследованием формы цветов и листьев занимался также Хабеннихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т. д. Вот некоторые из этих кривых:

В полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений: 

• кувшинки:   (рис. а);
• кислицы:  (рис. б);
• настурции:  (рис. в);

• стрелолиста:  (рис. г).

Рис. А                                    Рис. Б                        Рис. В                          Рис. Г

1.4.  Построение кусочно-заданной функции на примере построения эскиза национального орнамента

Свои исследования я продолжил, возник вопрос в построении графиков функций состоящих из нескольких кривых на заданном интервале. В качестве примера мною рассмотрено построение эскиза калмыцкого орнамента (геометрического) в Excel.

Если рассмотреть любой геометрический орнамент, то с математической точки он представляет собой набор прямых или кривых на заданном интервале, иногда на одном интервале может быть задано несколько различных линий. Совокупность этих линий и кривых образует рисунок который и будем считать орнаментом.

Также можно заметить, что орнамент представляет собой периодическую функцию (рисунок повторяется, через заданный интервал). Для того, чтобы построить заданный орнамент мы его построим на определенном интервале, а затем перенесем все вычисления на заданный шаг и т. д.

Приведенный ниже орнамент представляет собой семейство прямых заданных на отрезках, причем прямые параллельны одной из осей координат т.е. их уравнения принимают вид у =a или х =а.

Построим эти прямые.

Примеры таблиц вычислений:

x y 0 0 0,1 0 0,2 0 0,3 0 0,4 0 0,5 0 0,6 0 0,7 0 0,8 0 0,9 0 1 0

1,1 0 1,2 0 1,3 0 1,4 0 1,5 0 1,6 0 1,7 0 1,8 0 1,9 0 2 0

2 0 2 0,1 2 0,2 2 0,3 2 0,4 2 0,5 2 0,6 2 0,7 2 0,8 2 0,9 2 1

(Полные вычисления можно увидеть в файле приложении1)

График функции приведен ниже:

Заключение

Проделав данную исследовательскую работу я пришел к следующим выводам: Microsoft  Excel предоставляет большие возможности для построения и исследования графиков функций.

Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров  с минимальными усилиями. Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.

В классе котором я обучаюсь, мною была дана обзорная лекция с практическим ознакомлением, на которой  одноклассников я ознакомил учащихся с принципами построения графиков функций на примере тригонометрических функций, был предложен вариант построения графика функции с параметром. Построение графиков с параметром позволяет рассмотреть особенности графика в зависимости от параметра, изучить свойства функции, научиться строить графики функций путем преобразований исходной. В какой то мере благодаря этой работе мои одноклассники разобрались на отлично с темой построение графиков тригонометрических функций и их преобразований.

Мне удалось добиться поставленных целей работы. Был проработан алгоритм построения графиков элементарных функций, для построения кривых высших порядков мною был изучен дополнительный материал: построение кривых высших порядков в полярных координатах, где основополагающим является угол преобразования и радиус вектор. Был проработан алгоритм решения данной задачи: при помощи формул перехода от полярных координат к декартовым и обратно.

Изучая кривые линии высших порядков, ведь используя Microsoft excel, это не составляет труда, мне представился удивительный мир графиков различных функций. Оказывается таким образом можно построить, меняя параметры в данных уравнениях графики, которые напоминают листья растений и деревьев (например: кувшинки или лотоса). Оказывается математика  — живая наука.

Опыт, приобретенный мною в процессе выполнения работы, несомненно, пригодится мне в дальнейшей жизни. Так, например, умея строить графики уравнений с параметрами можно найти корни уравнений и их  зависимость от введенного параметра, что даст наглядную картину решения данного уравнения. Это позволяет решать задания ЕГЭ по математике части С5.

Также данные навыки будут необходимы при построении графиков и диаграмм в дальнейшей профессиональной деятельности, так excel прикладная программа применимая во многих сферах деятельности человека, например бухгалтерии, дизайн, аналитика, инженерия и другие.

Строя график функции на примере орнамента у меня возник вопрос, который остался не разрешенным. Как вы видели, я строил график по интервалам, что конечно занимает некоторое время. Возникает вопрос, как упростить данные построения. У меня есть три способа решения данной проблемы: 1) попытаться найти оптимальное уравнение функции, которое позволить заменить одновременно несколько этапов построения. Для решения этого вопроса нужно провести поиск в математических источниках.

2) найти возможности программы Excel для решения этой задачи. Как я говорил, в данной программе, много возможностей, многие из них, я еще не изучил.

3) найти другие программы построения графиков, которые позволят построить график данных функций. Такие программы существуют, например Adgrapher или DPlot и др. Данные программы, я планирую изучить в дальнейшем. Оптимальным решением, конечно же, будет создание своей программы, используя языки программирования.

Список используемой литературы

1. Б.П. Демидович. Сборник задач и упражнений по математическому анализу, Москва, Наука, 1969 г.
2. Дороднов А.М. Краткие сведения о построении графиков в полярной системе координат. Москва, 1972 г.
3. И.М. Гельфанд и др. Метод координат. Москва, Наука, 1973 г.
4. И.И. Привалов. Аналитическая геометрия, Москва, Высшая школа, 1966 г.
5. Н.В. Ефимов. Краткий курс аналитической геометрии. Москва, Высшая школа, 1972
6. Г.И. Запорожец. Руководство к решению задач по математическому анализу. Москва, Высшая школа, 1974 г.
7. Егерев В.К. Радунский Б.А., Тальский Д.А. Методика построения графиков функций. Москва, 1970 г.
8. Линии: определение, исследование и построение: Метод. рекомендации / Краснояр. гос. ун-т; Сост. А.П. Ляпин. Красноярск, 2001

Сайты и ссылки

1. http://ru.wikipedia.org

2. http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Cassini.html 

подробная биография Кассини

   3. http://www.2dcurves.com/higher/highercc.html прекрасная страничка для любителей красивых кривых, из нее мы узнали об овалах с тремя и более фокусами.

   4. http://arbuz.uz/x_stati.html

   5. http://otherreferats.allbest.ru/mathematics/00125991_0.html — Построение кривых высшего порядка