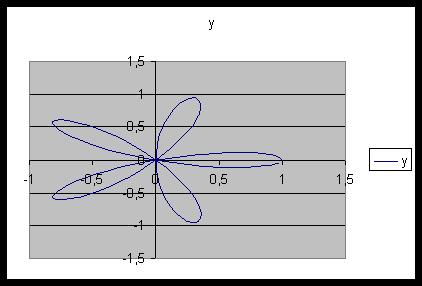
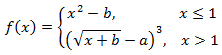Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.
Пусть дана система уравнений
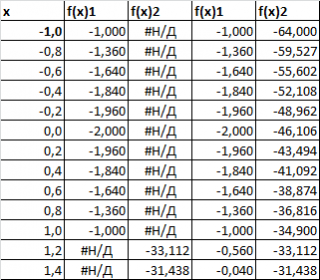
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ
: О построении диаграмм см. статью
Основы построения диаграмм в MS EXCEL
. О различии диаграмм Точечная и График см. статью
График vs Точечная диаграмма в MS EXCEL
.
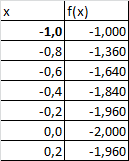
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см.
файл примера, лист Ряд1
):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
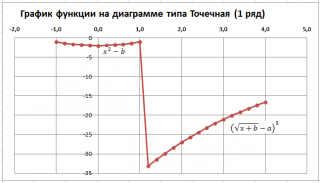
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
-
во вкладке
Вставка
в группе
Диаграммы
выберите диаграмму
Точечная с прямыми отрезками и маркерами
.
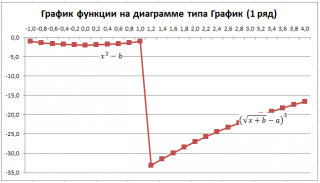
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
-
во вкладке
Вставка
в группе
Диаграммы
выберите диаграмму
График маркерами
.
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график
используя 2 ряда данных
.
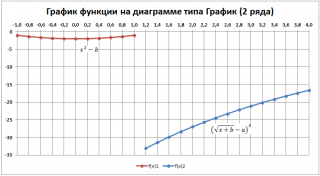
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в
файле примера, лист График
:
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
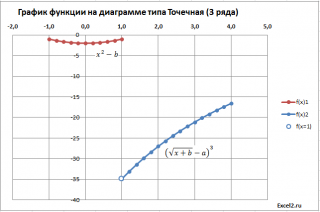
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см.
файл примера, лист График
.
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
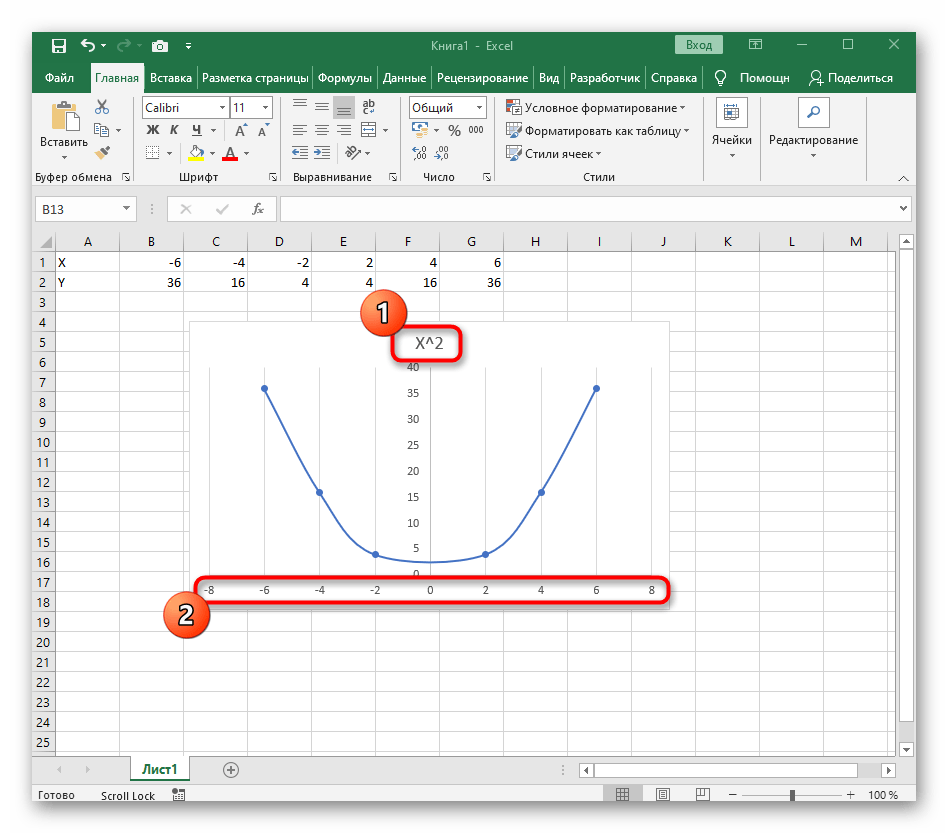
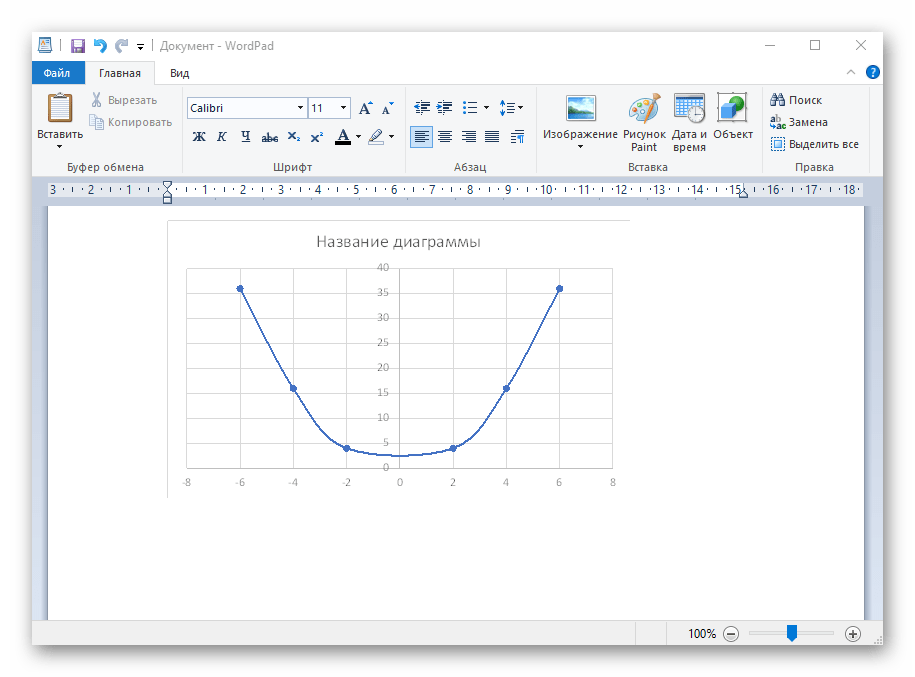
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
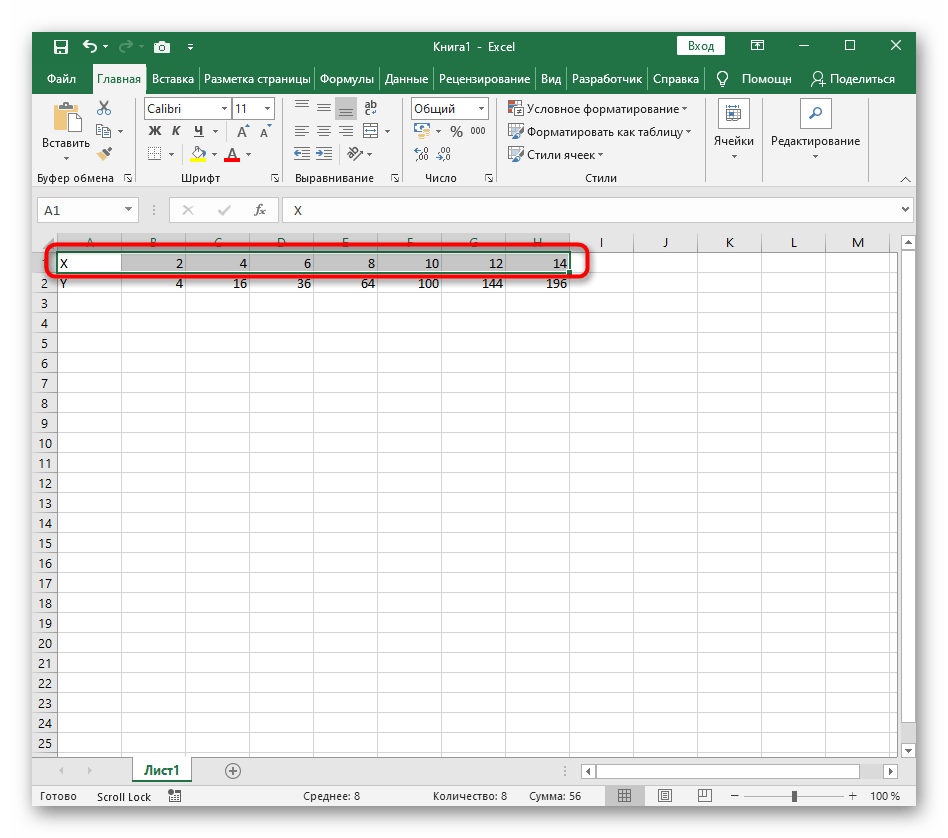
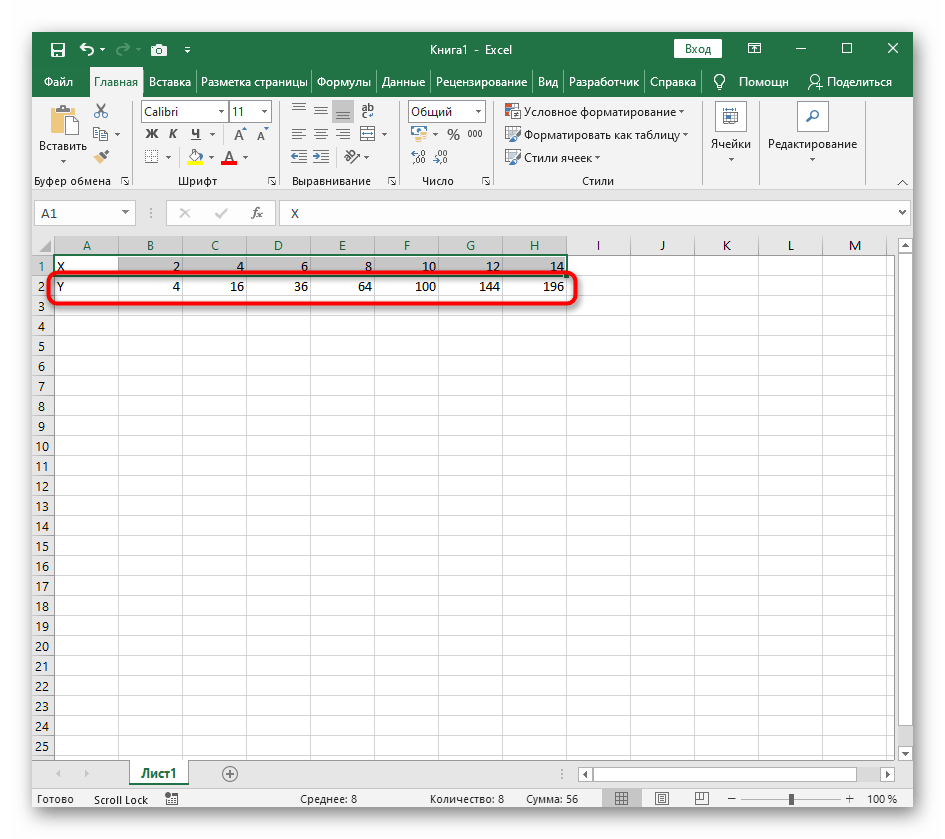
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
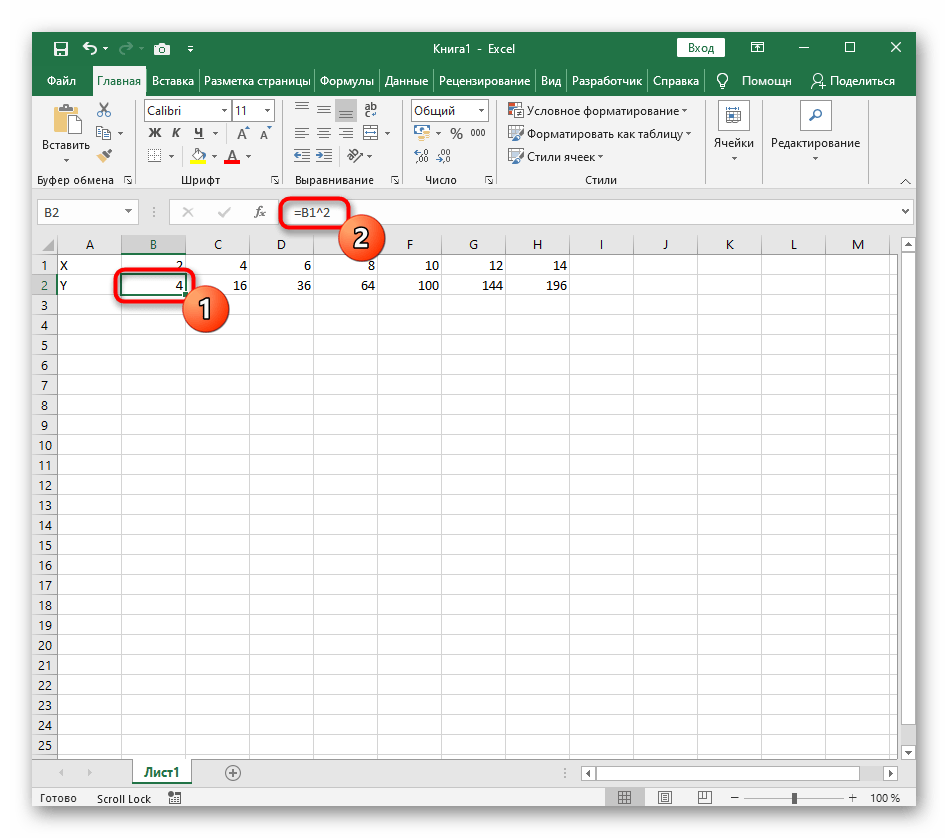
- Нажмите по первой ячейке и впишите
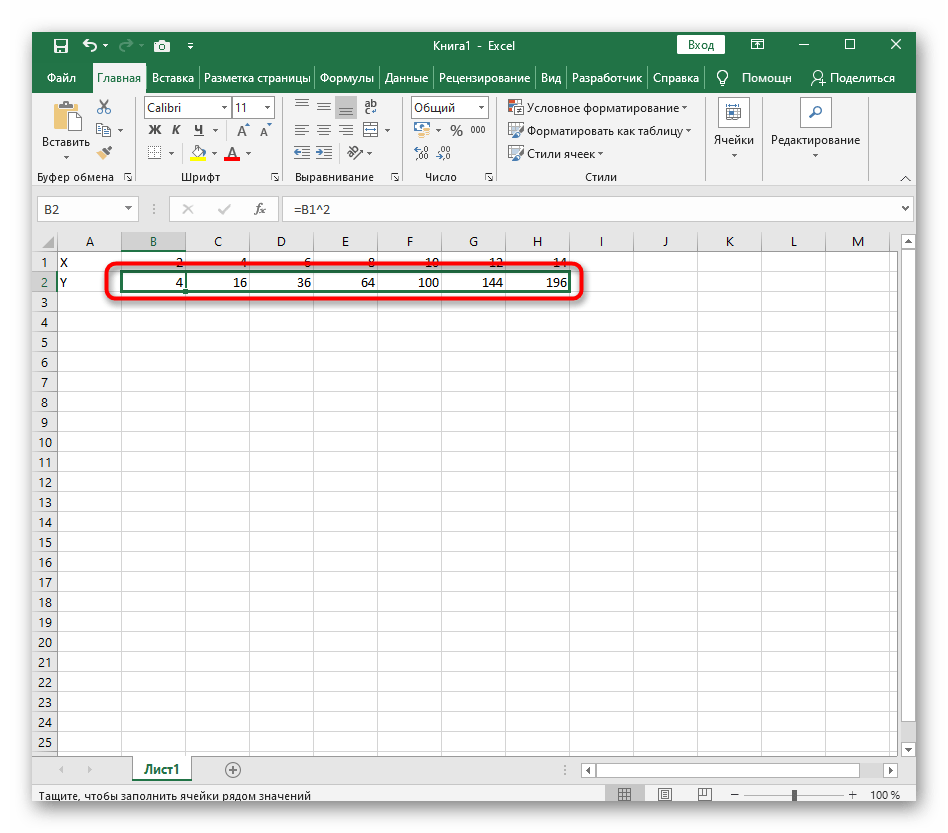
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
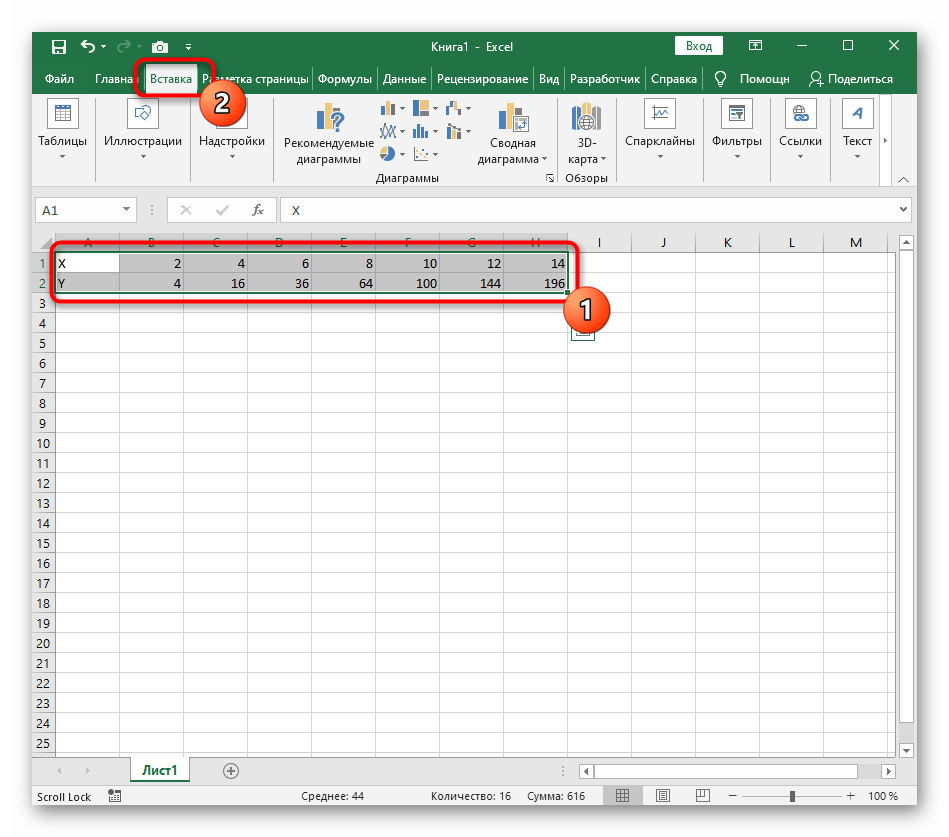
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
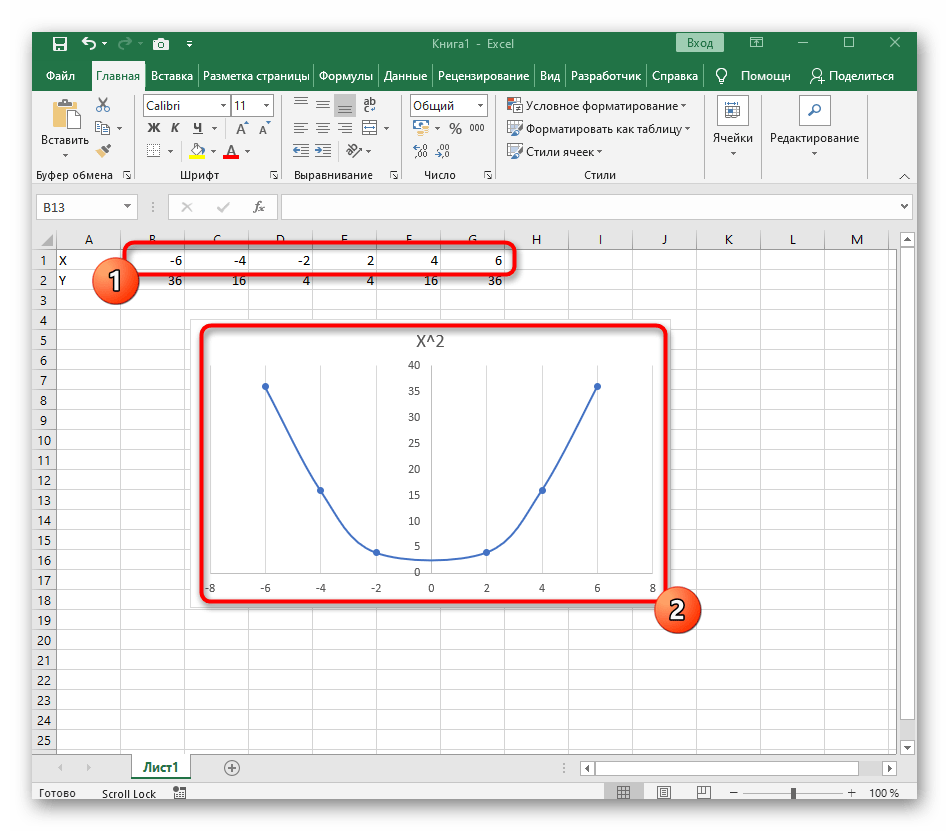
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
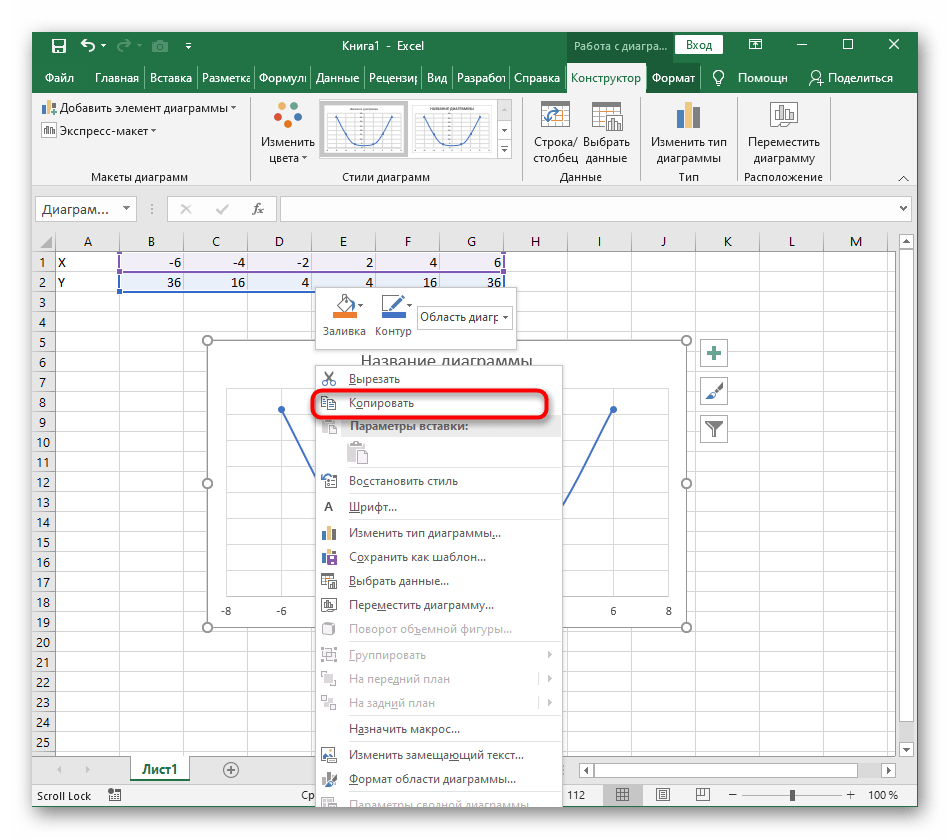
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Используемое оборудование и ПО: Программы Microsoft Office Excel 2003, Microsoft Office Power Point 2003, проектор, компьютеры.
Учебно-методические материалы: инструкции (Приложение 1, Приложение 2), презентация (Power Point 2003) (Приложение 3).
План урока:
- Актуализация.
- Повторение.
- Инструктаж по выполнению работы. Рассмотрение примера построения графика функции.
- Практическая работа.
- Подведение итогов.
Ход урока
I. Актуализация.
Раскрыть значимость данного урока в теме, межпредметные связи (с математикой).
II. Повторение.
Перед практической работой необходимо повторить знаки основных арифметических операций, а так же правила записи функций SIN, COS, КОРЕНЬ и аргументов функций (Приложение3 , Слайд 2). Правила записи формул по математическим выражениям.
| Знак математической операции | Правила записи в электронных таблицах | Пример |
| Деление | / | а/в |
| Умножение | * | а*в |
| Сложение | + | а+в |
| Вычитание | — | а-в |
| Квадратный корень | КОРЕНЬ() | КОРЕНЬ (а) |
| Синус | Sin() | Sin(a) |
| Косинус | Cos() | Cos(a) |
Напомнить учащимся основные ошибки, которые могут возникнуть при заполнении таблиц и способы их устранения .
При использовании формул возможны ошибки, вследствие которых формула вместо нужного результата возвращает соответствующее сообщение (Приложение 3, Слайд 3-4).
Сведения об ошибках
| Сообщение об ошибке | Пояснение |
| #### | Числовое значение полностью не помещается в ячейке. Для устранения ошибки выполните двойной щелчок на правой границе соответствующего столбца для установки оптимальной ширины, либо установите формат с меньшим количеством знаков после запятой. |
| #ИМЯ? | Microsoft Excel не может распознать имя, использованное в формуле. Это может произойти, если используемое в формуле имя было удалено, в формулу включен текст без двойных кавычек или отсутствует двоеточие в ссылке на диапазон ячеек. |
| #ДЕЛ/0 | В формуле возникла ситуация деления на нуль. При создании формулы следует позаботиться о том, чтобы в знаменателе не была задана ссылка, на пустую ячейку, содержащую нуль. Возможно, что при копировании данной формулы из другой ячейки в ней неправильно использована относительная ссылка вместо абсолютной. Для устранения ошибки необходимо выполнить двойной щелчок на ячейке с формулой, при этом программа выделит цветом все ячейки, используемые в формуле, найти пустую ячейку, исправить формулу. |
| #ЧИСЛО! | Нарушены правила операторов, принятые в математике. |
| #Н/Д | Такое сообщение может появиться, если в качестве аргумента задана ссылка, на пустую ячейку, в которой нет данных (см. исправление ошибки в строке #ДЕЛ/0). |
| #ПУСТО! | Неверно указано пересечение двух областей: они не имеют общих ячеек. |
| #ССЫЛКА! | Указана недопустимая ссылка на ячейку (например, ячейка, на которую ссылается формула, была удалена), (см. исправление ошибки в строке #ДЕЛ/0). |
| #ЗНАЧ! | Указан неправильный тип аргумента, например, при использовании текста вместо числового значения. |
III. Инструктаж по выполнению работы.
Для распечатки (Приложение 1)
IV. Практическая работа «Графики сложных функций»
(Для распечатки Приложение 2)
V. Подведение итогов, выставление оценок.
Используемая литература:
- Библиотека журнала «Информатика и образование». Е.Н. Новоселова «Практикум по MS Excel 2000». — Москва: «Образование и Информатика», 2004. -128с.
- Методическое пособие по MS Excel (для студентов заочного отделения).
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Плоский график подразумевает две оси – вертикальную и горизонтальную. Они могут быть подписаны совершенно произвольно, но всегда смысл один – каждой точке на горизонтальной оси соответствует значение по вертикали. Или как привыкли из школы: каждому иксу – свой игрек. А вот это соответствие может сразу задаваться некой уже имеющейся таблицей или даётся формулой.
Простой график
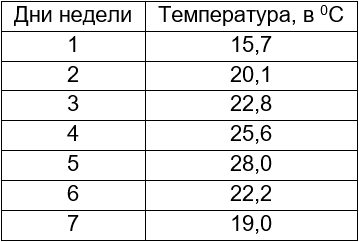
Самая простая таблица – из двух столбцов.
Уже с ней могут возникнуть проблемы. Например, выделяем эту таблицу в excel, нажимаем на Вставка в верней строке и попадаем в:
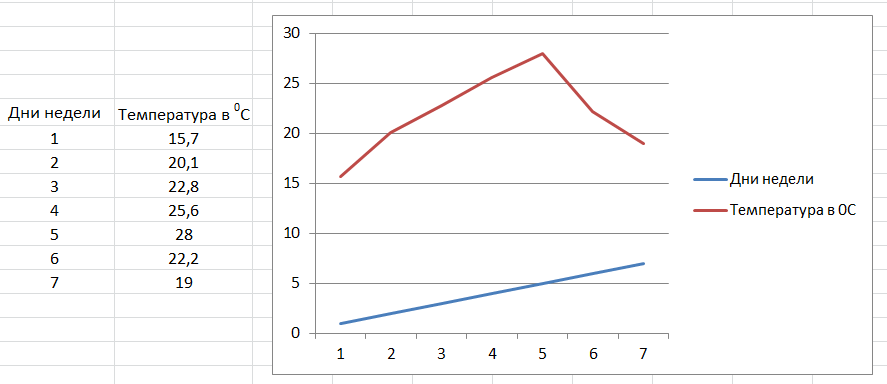
Нажимаем на График (что под Данные), открывается оконце:
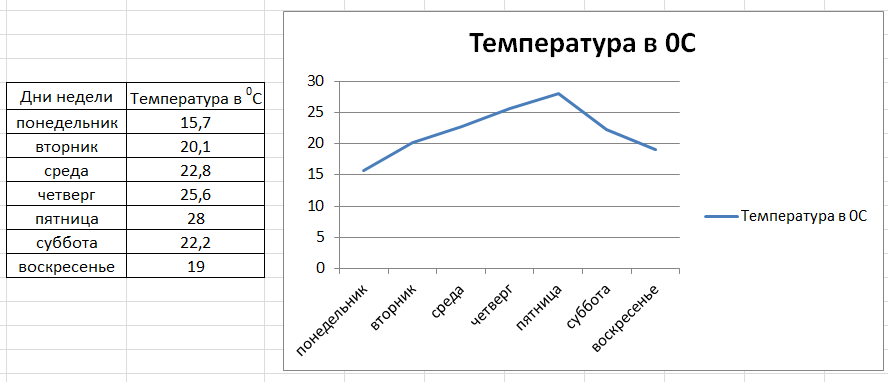
Нажимаем на первый (верхний слева) и получаем график:
Разве это мы хотели? Думали, что дни недели образуют нижнюю ось, а они выстроились второй линией на графике. Как быть?
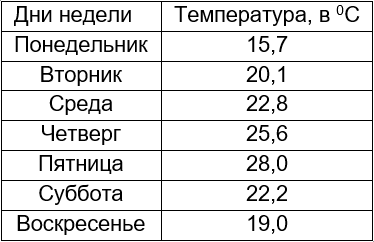
Вариант 1 – поменять цифры на названия:
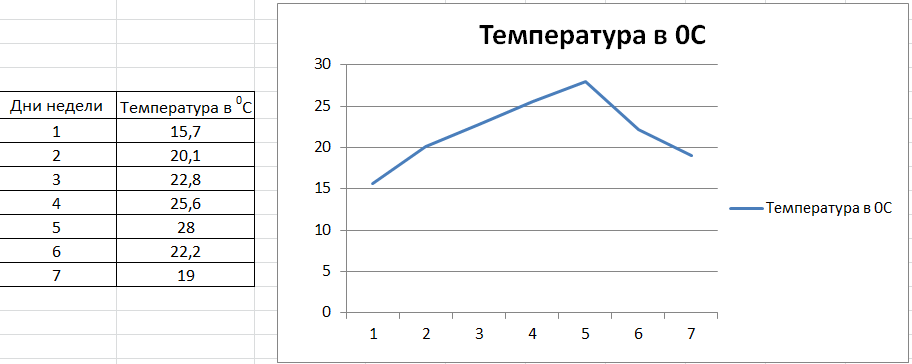
Выделяем эту табличку в excel и повторяем действия по рисованию графика, получаем:
Дни недели расположились на горизонтальной оси, как и хотелось. Как же вернуть на горизонталь дни недели в цифрах? Очень просто – выделять в excel только столбец с Температурой, тогда получится:
Это важно: если первый столбец цифровой и есть желание расположить его на горизонтальной оси, не надо выделять его при рисовании графика.
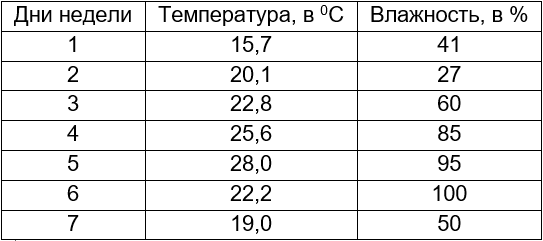
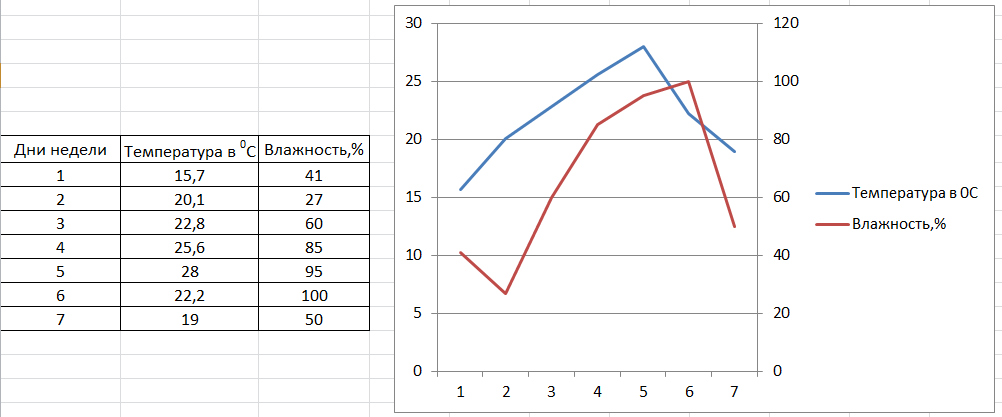
Из приведённого примера уже понятно, что если в таблице будет больше двух столбцов, то это приведёт просто к дополнительным линиям на графике. Например:
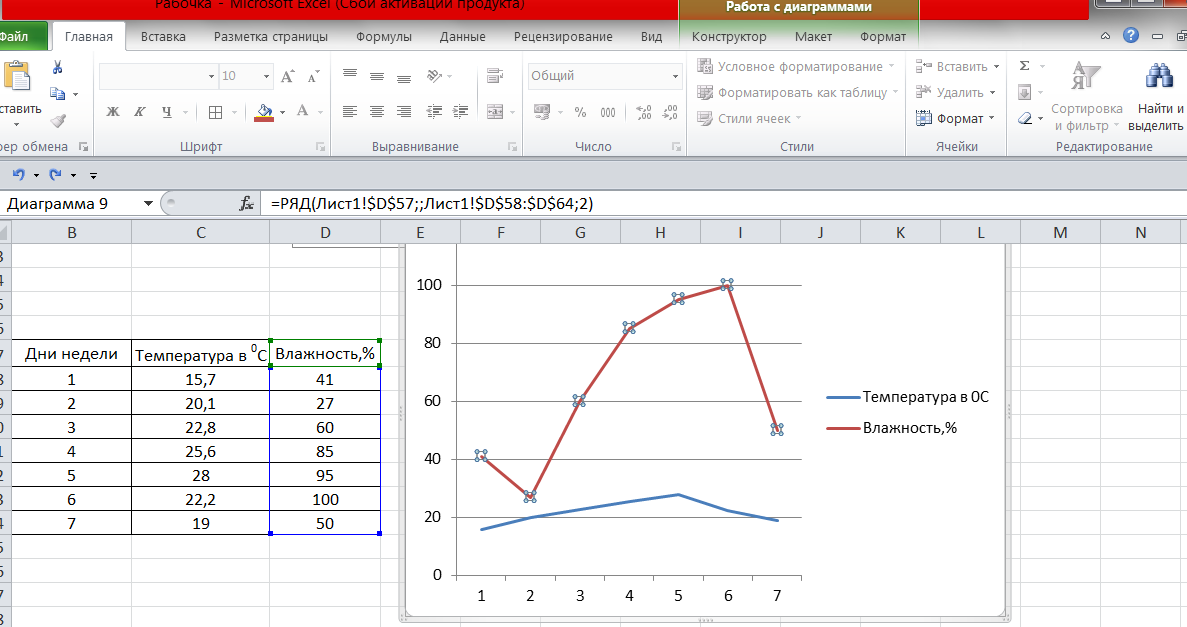
Видно неудобство: на одной вертикальной оси отражены и шкала температуры, и шкала влажности. Проблема решается вводом дополнительной вертикальной оси справа. Пусть справа будет шкала по влажности. Тогда наводим курсор на красную кривую влажности и кликаем по ней. Наверху страницы активировалось окно Работа с диаграммами:
В окне активированы Конструктор, Макет и Формат. Нажимаем на Формат:
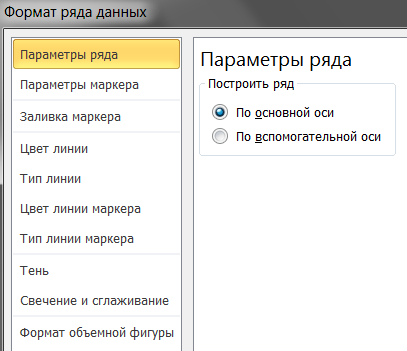
И в левом столбце нажимаем на фрагмент выделенного. Открывается окно Формат ряда данных:
В правом столбце осталось поставить крыжик в строке По вспомогательной оси. И нажать на Закрыть. Появляется ось справа:
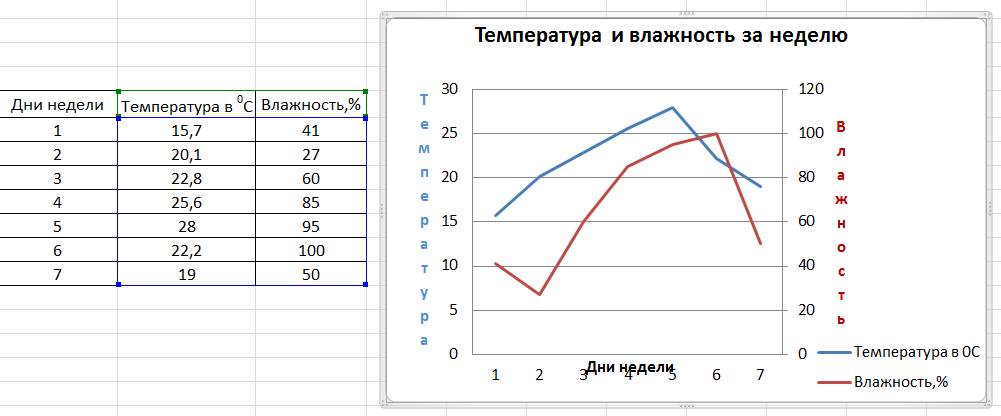
Осталось улучшить оформление: подписать оси, сделать заголовок.
Оформление простого графика
Кликая левой кнопкой по графику (в excel), активируем сверху блок Работа с диаграммами. В нём – Макет, открывается:
Входя в Названия осей, по очереди даём названия горизонтальной оси и двум вертикальным. При этом правой кнопкой можно менять размер шрифта, цвет. Также выбираем написание вертикальных осей – горизонтальное или вертикальное.
Входя в Название диаграммы, пишем название графика, также правой мышкой выбирая размер, цвет, выравнивание.
Можно также задать сеть (нажимая Сетка) и заливку (правой мышкой):
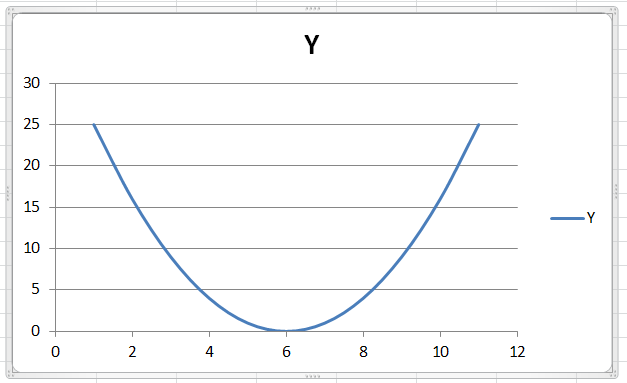
Построение графика функции
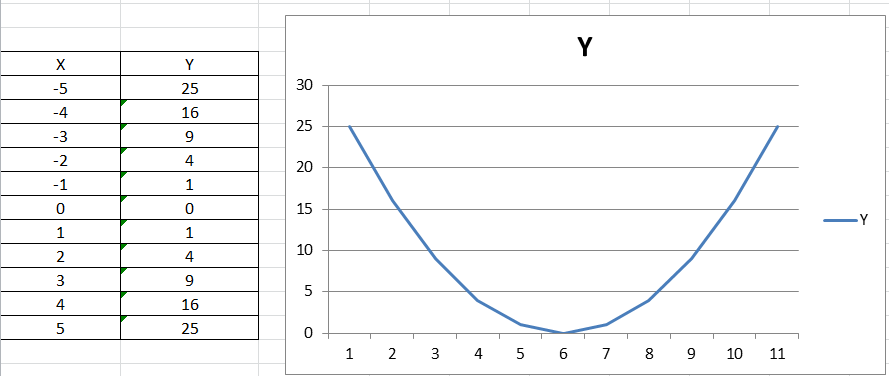
Для начала – график простой функции, например, квадратной y=x2. Поскольку построение графика по таблице не вызывает уже проблем, то и надо этим воспользоваться, создать таблицу. В excel это очень просто:
В столбце Y напротив -5 ставится = и нажимается значок функции fx. В появившемся окне Мастер функций выбирается категория Математические и находится (по алфавиту) СТЕПЕНЬ. Курсор на неё и нажать ОК. В появившемся окне Аргументы функции вставить курсор в строку Число, а потом в таблице выделить значения Х. В строке Число введётся диапазон. В строке окошка Степень поставить 2, раз функция квадратичная. В столбце Y таблицы напротив -5 появится цифра 25. Курсор в нижний правый угол ячейки с 25 и протащить вниз до конца таблицы. В каждой ячейке появится цифра.
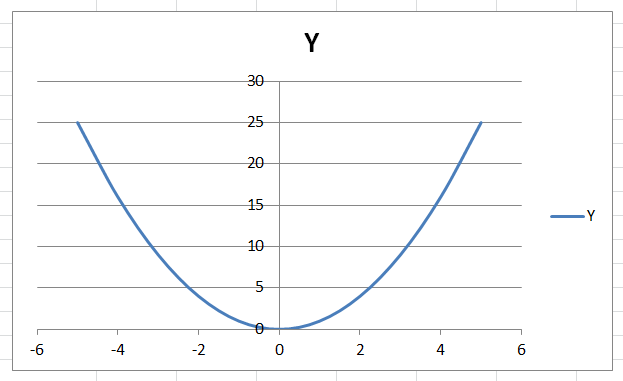
Далее – по отработанной схеме: выделяем столбец Y, потом – Вставка-График-первый из появившегося окна. Получаем:
Кривая построена по точкам, её надо сгладить. Для этого наводим курсор на график, правой кнопкой выбираем Изменить тип диаграммы, переходим на Точечную диаграмму, а в ней на ту, что без точек и жмём ОК. Получается:
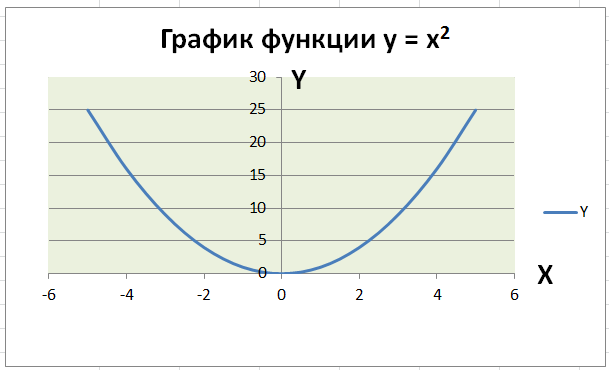
Но это ещё не график функции y=x2, (при х=0, у=6). Для корректировки горизонтальной оси наводим курсор на эту ось, правой кнопкой нажимаем на Выбрать данные и в левом столбце появившегося окошка жмём Изменить. Появляется окошко Изменение ряда. В нём в строку Х вносим столбец Х из нашей таблицы (только значения), два раза – ОК и получаем:
После нескольких завершающих штрихов:
Несколько общих советов:
• когда график нарисован, то с помощью правой кнопки можно выбрать нужный шрифт, его размеры – для всех названий;
• все названия можно перетаскивать по графику в нужное место;
• можно также в разных стилях размещать подписи, используя Метки данных из окошка Элементы диаграммы;
• можно поиграть с видами графиков из вкладки Конструктор, выбирая шаблоны в Стилях диаграмм.
График сложной функции
Как в excel построить график любой сложной функции?
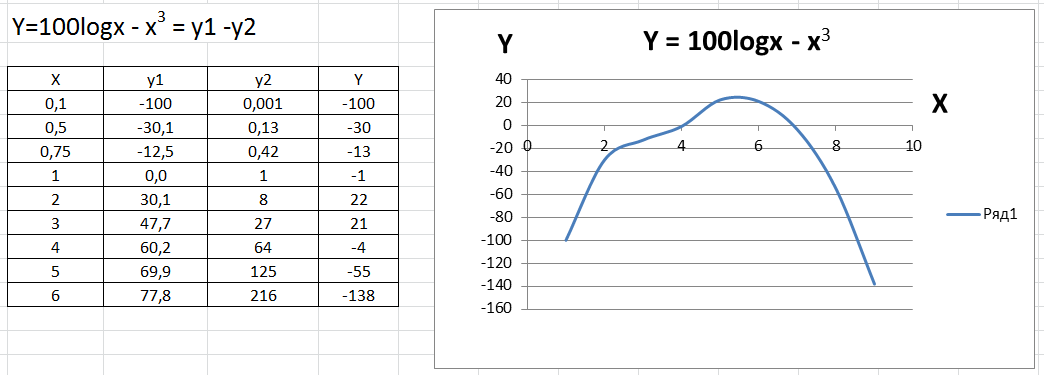
Зная, как построить график простой функции, то есть функции из Математических функций Мастера функций, можно легко построить любую сложную функцию – из произвольного сочетания тригонометрических, степенных, показательных, логарифмических функций, просто надо искомую функцию представить как сумму (алгебраическую) функций: Y = y1 + y2 +y3 +… И таблицу делать из аргументов и этих функций. Далее – всё, как было описано для графика простой функции.
Например, Y=100logx — х3 = y1 -y2
Возможности Excel гораздо шире описанных в статье, и знакомство с ними расцветит красками оформление графиков, их подачу. Но основной подход построения – через составление (или изначальное наличие) предварительной таблицы – описан и позволит любому пользователю построить график любой зависимости.