Построение графика платежей в excel - Word и Excel - помощь в работе с программами

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

А – сумма платежа по кредиту;
К – коэффициент аннуитетного платежа;
S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

где i – процентная ставка за месяц, результат деления годовой ставки на 12;
n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

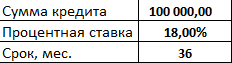
Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.

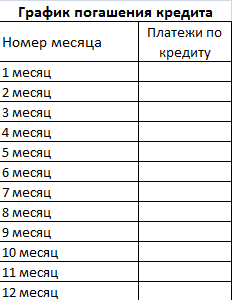
Составим график погашения кредита. Пока пустой.

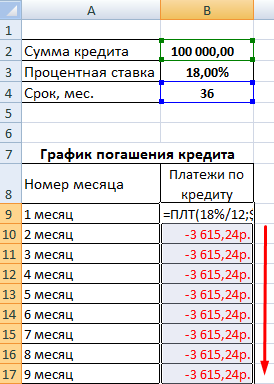
В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

ПЛТ.

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

сумма основного долга распределена по периодам выплат равными долями;
проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

ДП – ежемесячный платеж по кредиту;
ОСЗ – остаток займа;
ПП – число оставшихся до конца срока погашения периодов;
ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

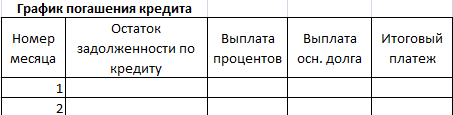
Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

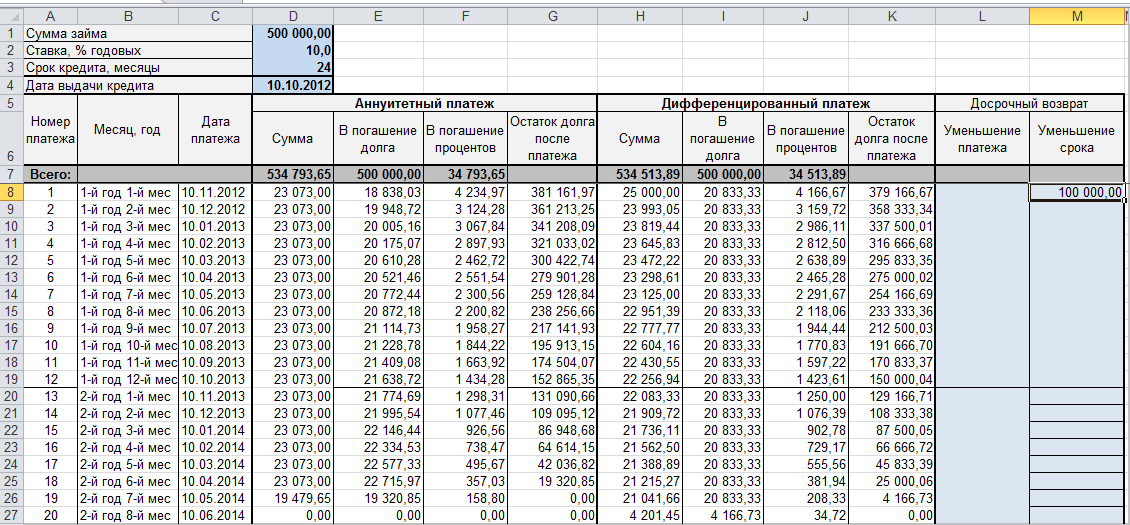
Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

взяли кредит 500 000 руб.;
вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
переплата составила 184 881, 67 руб.;
процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

ПСК = i * ЧБП * 100;
где i – процентная ставка базового периода;
ЧБП – число базовых периодов в календарном году.

Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Источник

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

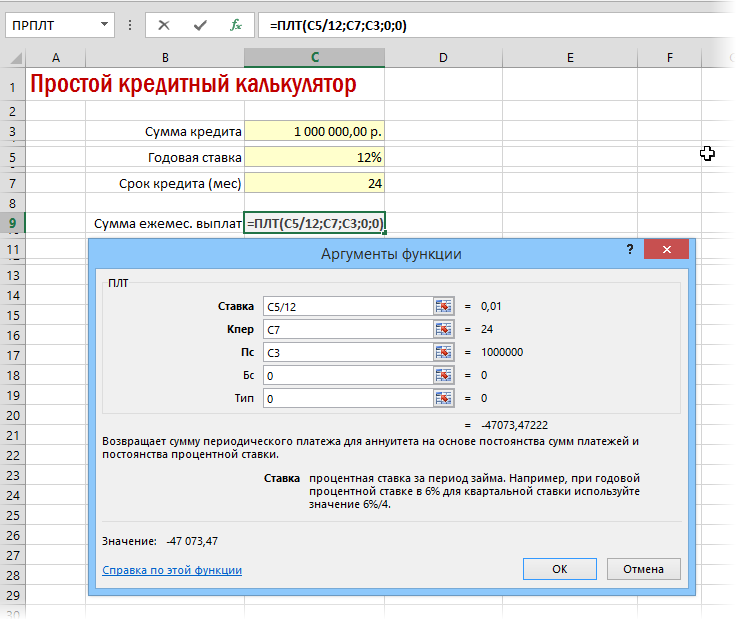
Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
Кпер — количество периодов, т.е. срок кредита в месяцах.
Пс — начальный баланс, т.е. сумма кредита.
Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.

Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

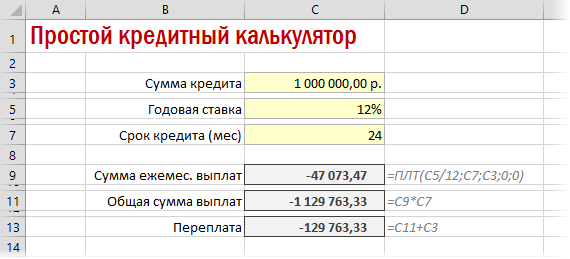
Вариант 2. Добавляем детализацию

Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

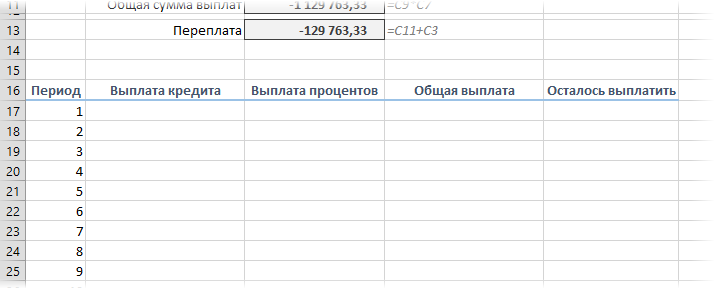
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

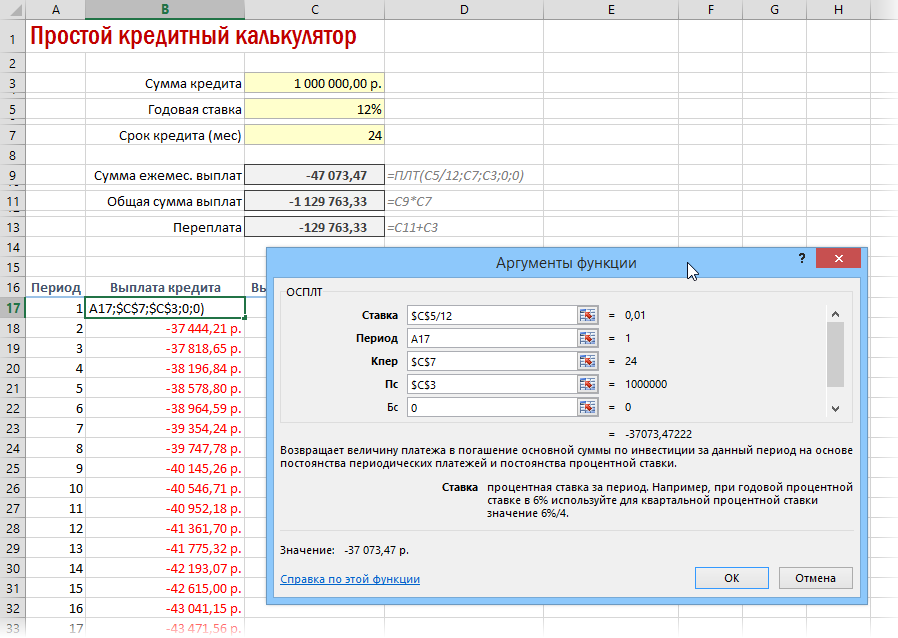
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

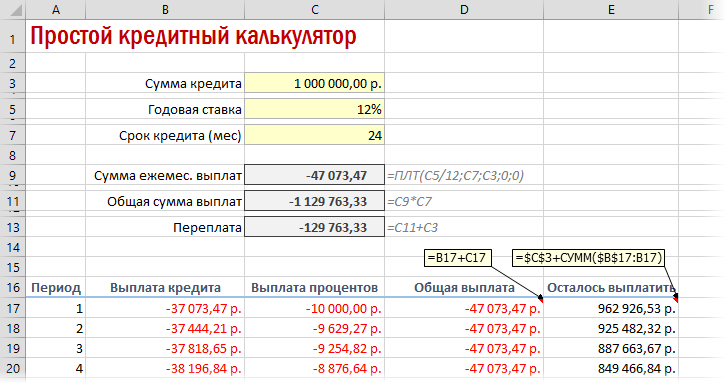
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

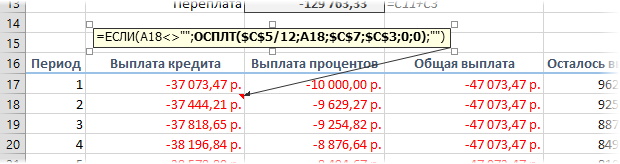
Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

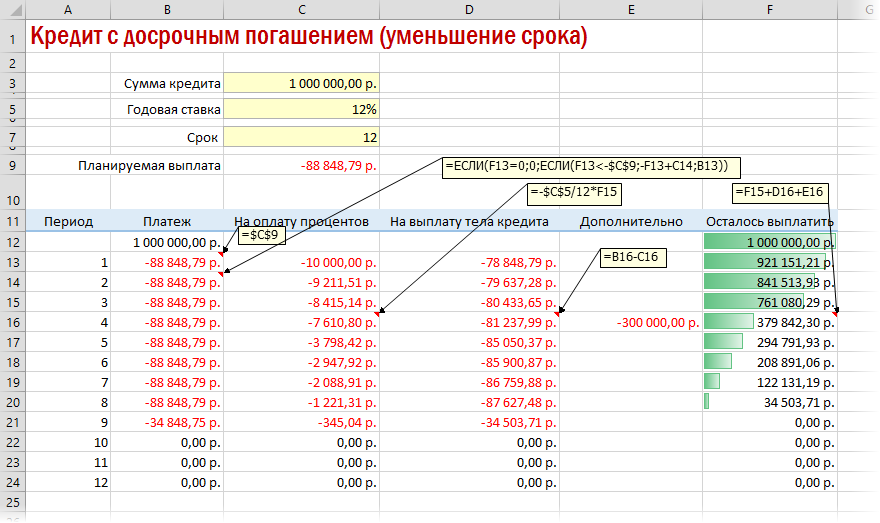
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

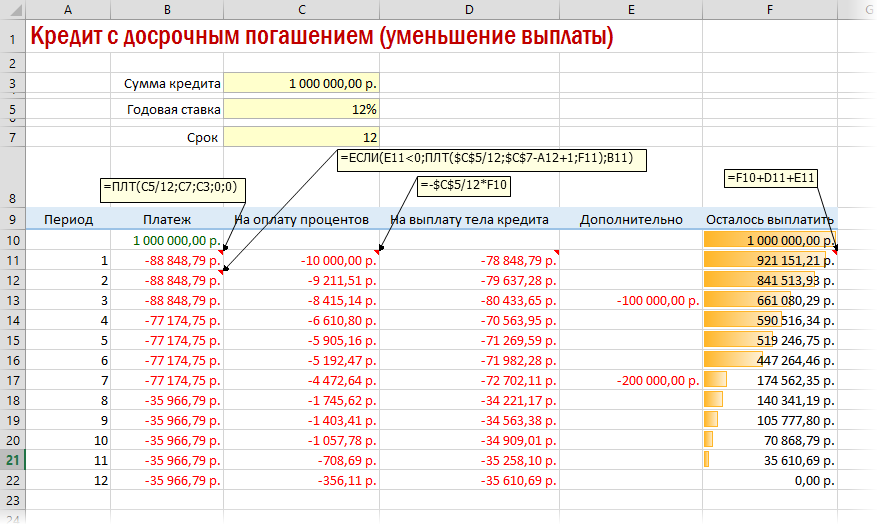
Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

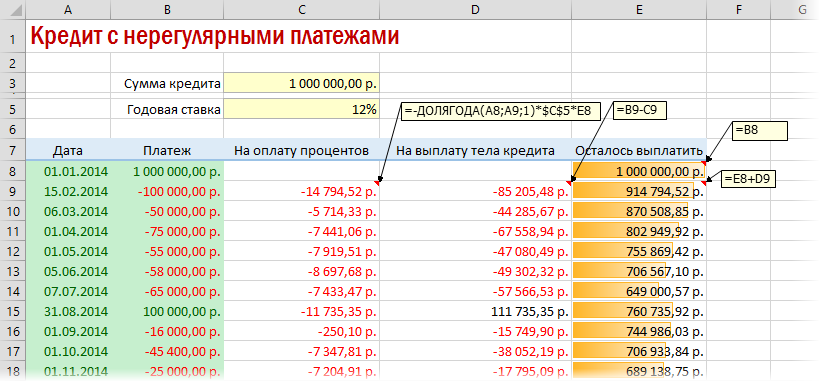
Предполагается что:

в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

Источник

Рассчитаем в

MS

EXCEL

сумму регулярного аннуитетного платежа при погашении ссуды. Сделаем это как с использованием функции

ПЛТ()

, так и впрямую по формуле аннуитетов. Также составим таблицу ежемесячных платежей с расшифровкой оставшейся части долга и начисленных процентов.

При кредитовании банки наряду с

дифференцированными платежами

часто используют

аннуитетную схему погашения

. Аннуитетная схема предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат.

Задача1

Определить величину ежемесячных равновеликих выплат по ссуде, размер которой составляет 100 000 руб., а процентная ставка составляет 10% годовых. Ссуда взята на срок 5 лет.

Разбираемся, какая информация содержится в задаче:

Заемщик ежемесячно должен делать платеж банку. Этот платеж включает:

сумму в счет погашения части ссуды

и

сумму для оплаты начисленных за прошедший период процентов на остаток ссуды

;
Сумма ежемесячного платежа (аннуитета)

постоянна

и не меняется на протяжении всего срока, так же как и процентная ставка. Также не изменяется порядок платежей – 1 раз в месяц;
Сумма для оплаты начисленных за прошедший период процентов

уменьшается

каждый период, т.к. проценты начисляются только на непогашенную часть ссуды;
Как следствие п.3 и п.1, сумма, уплачиваемая в счет погашения основной суммы ссуды,

увеличивается

от месяца к месяцу.
Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
Проценты начисляются

в конце

каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0. Платеж должен производиться также в конце каждого периода;
Процент за пользование заемными средствами в месяц (за период) составляет 10%/12 (ставка);
В конце срока задолженность должна быть равна 0 (БС=0).

Расчет суммы выплаты по ссуде за один период, произведем сначала с помощью финансовой функции MS EXCEL

ПЛТ()

.

Примечание

. Обзор всех функций аннуитета в статье

найдете здесь

Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.

Примечание

: Функция

ПЛТ()

входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).

Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за месяц. Ставка =10%/12 (в году 12 месяцев). Кпер – общее число периодов платежей по аннуитету, т.е. 60 (12 мес. в году*5 лет) Пс —

Приведенная стоимость

всех денежных потоков аннуитета. В нашем случае, это сумма ссуды, т.е. 100 000. Бс —

Будущая стоимость

всех денежных потоков аннуитета в конце срока (по истечении числа периодов Кпер). В нашем случае Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Если этот параметр опущен, то он считается =0. Тип — число 0 или 1, обозначающее, когда должна производиться выплата. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).

Примечание

: В нашем случае проценты начисляются в конце периода. Например, по истечении первого месяца начисляется процент за пользование ссудой в размере (100 000*10%/12), до этого момента должен быть внесен первый ежемесячный платеж. В случае начисления процентов в начале периода, в первом месяце % не начисляется, т.к. реального пользования средствами ссуды не было (грубо говоря % должен быть начислен за 0 дней пользования ссудой), а весь первый ежемесячный платеж идет в погашение ссуды (основной суммы долга).

Решение1

Итак, ежемесячный платеж может быть вычислен по формуле

=ПЛТ(10%/12; 5*12; 100 000; 0; 0)

, результат -2 107,14р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые

банк

дал

нам, -2107,14 – это деньги, которые мы

возвращаем банку

.

Альтернативная формула для расчета платежа (общий случай):

=-(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+

ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)

Если процентная ставка = 0, то формула упростится до

=(Пс + Бс)/Кпер

Если Тип=0 (выплата в конце периода) и БС =0, то Формула 2 также упрощается:

Вышеуказанную формулу часто называют формулой аннуитета (аннуитетного платежа) и записывают в виде А=К*S, где А — это аннуитетный платеж (т.е. ПЛТ), К — это коэффициент аннуитета, а S — это сумма кредита (т.е. ПС). K=-i/(1-(1+i)^(-n)) или K=(-i*(1+i)^n)/(((1+i)^n)-1), где i=ставка за период (т.е. Ставка), n — количество периодов (т.е. Кпер). Напоминаем, что выражение для K справедливо только при БС=0 (полное погашение кредита за число периодов Кпер) и Тип=0 (начисление процентов в конце периода).

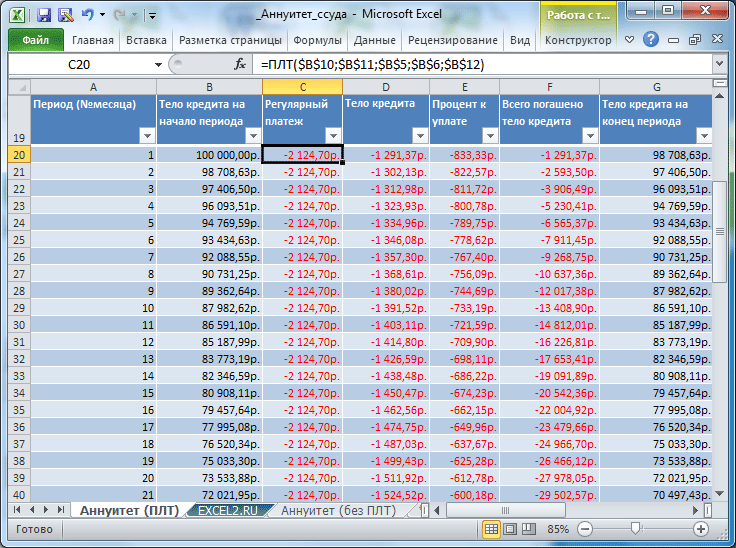
Таблица ежемесячных платежей

Составим таблицу ежемесячных платежей для вышерассмотренной задачи.

Для вычисления ежемесячных сумм идущих на погашение основной суммы долга используется функция ОСПЛТ(ставка; период; кпер; пс; [бс]; [тип]) практически с теми же аргументами, что и

ПЛТ()

(подробнее см. статью

Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга

). Т.к. сумма идущая на погашение основной суммы долга изменяется от периода к периоду, то необходим еще один аргумент

период

, который определяет к какому периоду относится сумма.

Для вычисления ежемесячных сумм идущих на погашение процентов за ссуду используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип]) с теми же аргументами, что и

ОСПЛТ()

(подробнее см. статью

Аннуитет. Расчет в MS EXCEL выплаченных процентов за период

Примечание

. Для определения суммы переплаты по кредиту (общей суммы выплаченных процентов) используйте функцию

ОБЩПЛАТ()

, см.

здесь

Конечно, для составления таблицы ежемесячных платежей можно воспользоваться либо

ПРПЛТ()

или

ОСПЛТ()

, т.к. эти функции связаны и в любой период: ПЛТ= ОСПЛТ + ПРПЛТ

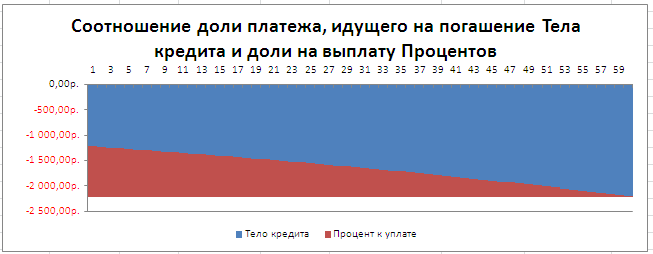
Соотношение выплат основной суммы долга и начисленных процентов хорошо демонстрирует график, приведенный в

файле примера

.

Примечание

. В статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад

показано как рассчитать величину регулярной суммы пополнения вклада, чтобы накопить желаемую сумму.

График платежей можно рассчитать без использования формул аннуитета. График приведен в столбцах K:P

файла примера лист Аннуитет (ПЛТ)

, а также на

листе Аннуитет (без ПЛТ)

. Также тело кредита на начало и конец периода можно рассчитать с помощью функции ПС и БС (см.

файл примера лист Аннуитет (ПЛТ), столбцы H:I

).

Задача2

Ссуда 100 000 руб. взята на срок 5 лет. Определить величину ежеквартальных равновеликих выплат по ссуде, чтобы через 5 лет невыплаченный остаток составил 10% от ссуды. Процентная ставка составляет 15% годовых.

Решение2

Ежеквартальный платеж может быть вычислен по формуле

=ПЛТ(15%/12; 5*4; 100 000; -100 000*10%; 0)

, результат -6 851,59р. Все параметры функции

ПЛТ()

выбираются аналогично предыдущей задаче, кроме значения БС, которое = -100000*10%=-10000р., и требует пояснения. Для этого вернемся к предыдущей задаче, где ПС = 100000, а БС=0. Найденное значение регулярного платежа обладает тем свойством, что сумма величин идущих на погашение тела кредита за все периоды выплат равна величине займа с противоположным знаком. Т.е. справедливо равенство: ПС+СУММ(долей ПЛТ, идущих на погашение тела кредита)+БС=0: 100000р.+(-100000р.)+0=0. То же самое и для второй задачи: 100000р.+(-90000р.)+БС=0, т.е. БС=-10000р.

Источник

Loan repayment is the act of paying back money previously borrowed from a lender, typically through a series of periodic payments that include principal plus interest. Did you know you can use the software program Excel to calculate your loan repayments?

This article is a step-by-step guide to setting up loan calculations.

Key Takeaways:

Use Excel to get a handle on your mortgage by determining your monthly payment, your interest rate, and your loan schedule.
You can take a more in-depth look at the breakdown of a loan with excel and create a repayment schedule that works for you.
There are calculations available for each step that you can tweak to meet your specific needs.
Breaking down and examining your loan step-by-step can make the repayment process feel less overwhelming and more manageable.

Understanding Your Mortgage

Using Excel, you can get a better understanding of your mortgage in three simple steps. The first step determines the monthly payment. The second step calculates the interest rate, and the third step determines the loan schedule.

You can build a table in Excel that will tell you the interest rate, the loan calculation for the duration of the loan, the decomposition of the loan, the amortization, and the monthly payment.

Calculate the Monthly Payment

First, here’s how to calculate the monthly payment for a mortgage. Using the annual interest rate, the principal, and the duration, we can determine the amount to be repaid monthly.

The formula, as shown in the screenshot above, is written as follows:

=-PMT(rate;length;present_value;[future_value];[type])

The minus sign in front of PMT is necessary as the formula returns a negative number. The first three arguments are the rate of the loan, the length of the loan (number of periods), and the principal borrowed. The last two arguments are optional, the residual value defaults to zero; payable in advance (for one) or at the end (for zero) is also optional.

The Excel formula used to calculate the monthly payment of the loan is:

= PMT((1+B2)^(1/12)-1;B4*12;B3)=PMT((1+3,10%)^(1/12)-1;10*12;120000)

Explanation: For the rate, we use the monthly rate (period of rate), then we calculate the number of periods (120 for 10 years multiplied by 12 months) and, finally, we indicate the principal borrowed. Our monthly payment will be $1,161.88 over 10 years.

Calculate the Annual Interest Rate

We have seen how to set up the calculation of a monthly payment for a mortgage. But we may want to set a maximum monthly payment that we can afford that also displays the number of years over which we would have to repay the loan. For that reason, we would like to know the corresponding annual interest rate.

As shown in the screenshot above, we first calculate the period rate (monthly, in our case), and then the annual rate. The formula used will be RATE, as shown in the screenshot above. It is written as follows:

=RATE(Nper;pmt;present_value;[future_value];[type])

The first three arguments are the length of the loan (number of periods), the monthly payment to repay the loan, and the principal borrowed. The last three arguments are optional, and the residual value defaults to zero; the term argument for managing the maturity in advance (for one) or at the end (for zero) is also optional. Finally, the estimate argument is optional but can give an initial estimate of the rate.

The Excel formula used to calculate the lending rate is:

=RATE(12*B4;-B2;B3) = RATE(12*13;-960;120000)

Note: the corresponding data in the monthly payment must be given a negative sign. This is why there’s a minus sign before the formula. The rate period is 0.294%.

We use the formula = (1 + B5) is 12-1 ^ = (1 + 0.294 %) ^ 12-1 to obtain the annual rate of our loan, which is 3.58%. In other words, to borrow $120,000 over 13 years to pay $960 monthly, we should negotiate a loan at an annual 3.58% maximum rate.

Using Excel is a great way of keeping track of what you owe and coming up with a schedule for repayment that minimizes any fees that you might end up owing.

Determining the Length of a Loan

We will now see how to determine the length of a loan when you know the annual rate, the principal borrowed, and the monthly payment that is to be repaid. In other words, how long will we need to repay a $120,000 mortgage with a rate of 3.10% and a monthly payment of $1,100?

The formula we will use is NPER, as shown in the screenshot above, and it is written as follows:

=NPER(rate;pmt;present_value;[future_value];[type])

The first three arguments are the annual rate of the loan, the monthly payment needed to repay the loan, and the principal borrowed. The last two arguments are optional, the residual value defaults to zero. The term argument payable in advance (for one) or at the end (for zero) is also optional.

=NPER((1+B2)^(1/12)-1;-B4;B3) = NPER((1+3,10%)^(1/12)-1;-1100;120000)

Minus Sign Before the Formula

The corresponding data in the monthly payment must be given a negative sign. This is why we have a minus sign before the formula. The reimbursement length is 127.97 periods (months in our case).

We will use the formula = B5 / 12 = 127.97 / 12 for the number of years to complete the loan repayment. In other words, to borrow $120,000, with an annual rate of 3.10% and to pay $1,100 monthly, we should repay maturities for 128 months or 10 years and eight months.

Decomposing the Loan

A loan payment is composed of principal and interest. The interest is calculated for each period—for example, the monthly repayments over 10 years will give us 120 periods.

The table above shows the breakdown of a loan (a total period equal to 120) using the PPMT and IPMT formulas.The arguments of the two formulas are the same and are broken down as follows:

=-PPMT(rate;num_period;length;principal;[residual];[term])

The arguments are the same as for the PMT formula already seen, except for «num_period,» which is added to show the period over which to break down the loan given the principal and interest. Here’s an example:

=-PPMT((1+B2)^(1/12)-1;1;B4*12;B3) = PPMT((1+3,10%)^(1/12)-1;1;10*12;120000)

The result is shown in the screenshot above «Loan Decomposition» over the period analyzed, which is «one;» that is, the first period or the first month. We pay $1,161.88 broken down into $856.20 principal and $305.68 interest.

Loan Computation in Excel

It is also possible to calculate the principal and interest repayment for several periods, such as the first 12 months or the first 15 months.

=-CUMPRINC(rate;length;principal;start_date;end_date;type)

We find the arguments, rate, length, principal, and term (which are mandatory) that we already saw in the first part with the formula PMT. But here, we need the «start_date» and «end_date» arguments also. The «start_date» indicates the beginning of the period to be analyzed, and the «end_date» indicates the end of the period to be analyzed.

Here’s an example:

=-CUMPRINC((1+B2)^(1/12)-1;B4*12;B3;1;12;0)

The result is shown in the screenshot «Cumul 1st year,» so the analyzed periods range from one to 12 of the first period (first month) to the twelfth (12th month). Over a year, we would pay $10,419.55 in principal and $ 3,522.99 in interest.

Amortization of the Loan

The prior formulas allow us to create our schedule period by period, to know how much we will pay monthly in principal and interest, and to know how much is left to pay.

Creating a Loan Schedule

To create a loan schedule, we will use the different formulas discussed above and expand them over the number of periods.

In the first period column, enter «1» as the first period and then drag the cell down. In our case, we need 120 periods since a 10-year loan payment multiplied by 12 months equals 120.

The second column is the monthly amount we need to pay each month—which is constant over the entire loan schedule. To calculate the amount, insert the following formula in the cell of our first period:

=-PMT(TP;B4*12;B3) =-PMT((1+3,10%)^(1/12)-1;10*12;120000)

The third column is the principal that will be repaid monthly. For example, for the 40th period, we will repay $945.51 in principal on our monthly total amount of $1,161.88.

To calculate the principal amount redeemed, we use the following formula:

=-PPMT(TP;A18;$B$4*12;$B$3) =-PPMT((1+3,10%)^(1/12);1;10*12;120000)

The fourth column is the interest, for which we use the formula to calculate the principal repaid on our monthly amount to discover how much interest is to be paid:

=-INTPER(TP;A18;$B$4*12;$B$3) =-INTPER((1+3,10%)^(1/12);1;10*12;120000)

The fifth column contains the amount left to pay. For example, after the 40th payment, we will have to pay $83,994.69 on $120,000.

The formula is as follows:

=$B$3+CUMPRINC(TP;$B$4*12;$B$3;1;A18;0)

The formula uses a combination of principal under a period ahead of the cell containing the principal borrowed. This period begins to change when we copy and drag the cell down. The table below shows that at the end of 120 periods, our loan is repaid.

Источник

Расчет кредита в Excel

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю 🙂 Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial) . Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
Кпер — количество периодов, т.е. срок кредита в месяцах.
Пс — начальный баланс, т.е. сумма кредита.
Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.

Вариант 2. Добавляем детализацию

Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT) . Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

=ЕСЛИ(A18<>«»; текущая формула; «»)

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)

Ипотечный кредитный калькулятор в Excel. Как правильно рассчитать кредит в Excel?

Когда вы взяли кредит, вы так или иначе думаете о досрочном погашении.
Есть люди которые платят кредит и все. А есть те, которые каждый раз смотрят, сколько осталось платить, какая сумма основного долга. Я отношу себя ко второму типу людей, я смотрю сколько сейчас сумма основного долга, пытаюсь рассчитать, сколько будет платеж, если я сделаю досрочное погашение.
На данный момент у меня есть два калькулятора кредита для своих расчетов. Оба калькулятора сделаны в Excel. Калькуляторы позволяют достаточно быстро и просто рассчитать ипотеку.
Читайте также: Как рассчитать кредит в Excel самому?

Скачать кредитный калькулятор в Excel

Первый кредитный калькулятор в Excel можно скачать по ссылке.
Но Excel есть не на всех компьютерах. Пользователи MAC и Linux не пользуются Excel обычно, т.к. это продукт Microsoft.
Для расчета досрочного погашения можно также воспользоваться онлайн версией калькулятора с досрочным погашением. В нем предусмотрена возможность экспорта результатов расчета в Excel.

На основе этого калькулятора был разработан ипотечный калькулятор для Android и iPhone. Найти и скачать мобильные версии калькуляторов можно с главной страницы сайта.

Достоинства данного калькулятора:

Кредитный калькулятор в Excel практически точно считает аннуитетный график платежей и дифференцированный график платежей
Изменения в графике платежей — учет досрочных погашений в уменьшение суммы основного долга
Построение и расчет графика платежей в виде таблицы в Excel. Таблица графика платежей может также редактироваться
При расчете учитывается високосный и невисокосный год. За счет этого сумма начисленных процентов практически совпадает с значениями, рассчитываемыми ВТБ24 и Сбербанком
Точность расчетов — рассчеты совпадают с расчетами кредитного калькулятора ВТБ24 и Сбербанка
Калькулятор можно редактировать под себя, задавая разные варианты расчета.

Недостатки калькулятора

Нет учета возможное изменение процентной ставки во время выплат кредита
Если сделать расчет, делая досрочные платежи в изменение срока и суммы, то расчет будет неверным
Если сумма процентов, начисленных за период больше суммы аннуитетного платежа, то расчет будет не верным
Не рассчитывается вариант — первый платеж только проценты. В случае когда дата выдачи не совпадает с датой первого платежа, вам нужно будет заплатить проценты банку за период между датой выдачи и датой первого платежа.
Расчет производится для процентой ставки с 2мя знаками после запятой.

Всех выше названных недостатков лишен кредитный калькулятор для iPad/iPhone. В целом недостатки не сильно критичны и они присущи любому кредитному калькулятору онлайн.
Другой кредитный калькулятор в Excel можно скачать по данной ссылке. Данный кредитный калькулятор не позволяет рассчитать досрочное погашение. Однако его плюс в том, что он рассчитывает кредит с несколькими процентными периодами. Если сумма процентов по кредиту за данный месяц больше суммы аннуитетного платежа, то график для первого кредитного калькулятора в excel строится некорректно. В графике получаются отрицательные суммы.

Попробуйте посчитать к примеру кредит 1 млн. руб под 90 процентов на срок 30 лет.
У второго калькулятора нет данного недостатка. Однако он делит кредит на 2 периода, т.е. возможно что после деления в графике снова будут отрицательные значения. Тогда график платежей нужно делить на 3 и более периода.
Естественно сам файл также можно отредактировать под свои нужды.

Калькулятор расчета кредита в Excel и формулы ежемесячных платежей

Как рассчитать платежи по кредиту в Excel

Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А – сумма платежа по кредиту;
К – коэффициент аннуитетного платежа;
S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

где i – процентная ставка за месяц, результат деления годовой ставки на 12;
n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
Составим график погашения кредита. Пока пустой.
В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

сумма основного долга распределена по периодам выплат равными долями;
проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

ДП – ежемесячный платеж по кредиту;
ОСЗ – остаток займа;
ПП – число оставшихся до конца срока погашения периодов;
ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

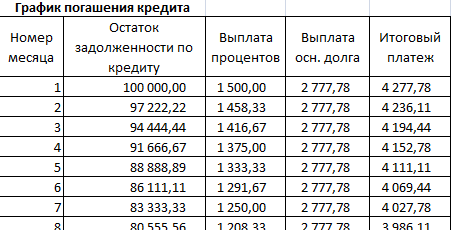
Составим график погашения займа:

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

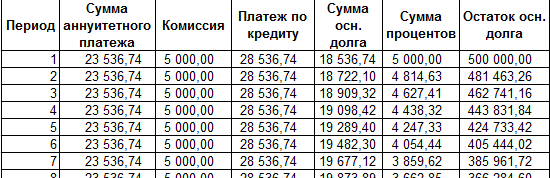
Заполним таблицу вида:

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

взяли кредит 500 000 руб.;
вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
переплата составила 184 881, 67 руб.;
процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

ПСК = i * ЧБП * 100;
где i – процентная ставка базового периода;
ЧБП – число базовых периодов в календарном году.

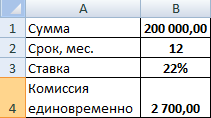
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Далее находим ЧБП: 365 / 28 = 13.

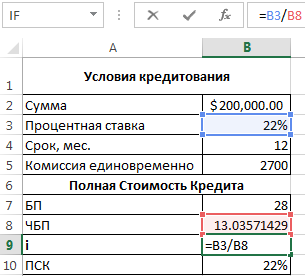
Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Расчет кредита в excel: скачайте готовые формулы и калькуляторы

Если вы хотите расчитать платежи по кредиту (аннуитетные или дифференцированные), переплату и график платежей по месяцам в excel, то скачайте следующие xls-файлы:

Альтернатива использованию MS Excel — кредитный калькулятор on-line (функционал практически такой же, ничего качать на компьютер не нужно: все операции выполняются на нашем сайте).

Расскажем о файлах подробнее: дадим мини-инструкции.

Кредитный калькулятор в Excel

Считать оба вида платежей.
Показывать полный график платежей.
Разбивать сумму выплаты на «погашение долга» и «погашение процентов».
Учитывать досрочные возвраты (отдельно для уменьшения срока и уменьшения размера выплат).

Пользоваться файлом довольно удобно: вбиваете значения в верхние четыре поля (сумма, процентная ставка, срок в месяцах, дата получения — последнее нужно для определения точного графика) и умное детище Билла Гейтса тут же заполняет все графы таблицы актуальной информацией.

Простая функция для платежей

Вы и сами может сконстурировать подобный расчет — подробно это описано в статье про расчет по формуле аннуитета. Ничего сложного нет, но для удобства мы подготовили специальный файл.

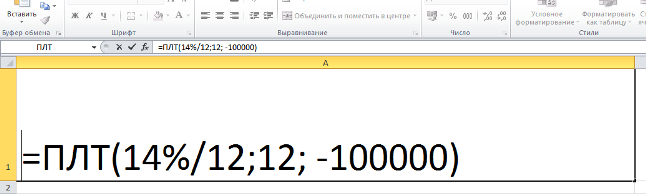
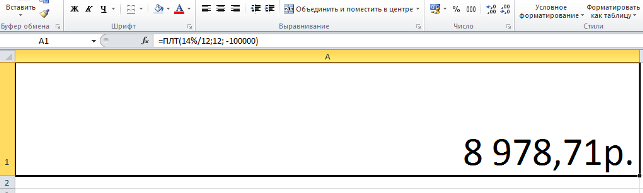
Содержит всего одну функциональную ячейку:

Поменяйте значения на свои (вместо 14 — свою ставку, вместо 12 во втором случае — свой срок кредита в месяцах, вместо 100000 — свою сумму займа).

После смены данных достаточно нажать на «Энтер», чтобы получить результат:

Напоминаем, ссылки на оба xls-файла представлены в начале страницы.

Что такое кредитный калькулятор в Excel

Кредитный калькулятор в Excel – это программа, которая позволяет осуществлять расчеты выплат по кредиту без выхода в интернет. Для этого достаточно просто скачать файл программы и использовать его в любое удобное время. Программа в Excel позволяет осуществлять любые математические расчеты. Неспроста она широко используется в бухгалтерии.

Конечно, можно использовать обычный кредитный калькулятор, который расположен на сайтах различных банков, но лучше иметь дома свой собственный кредитный калькулятор в Excel.

Для всех подсчетов потребуются следующие данные:

— размер кредита;
— цель кредита;
— размер процентов по кредиту.

Пользование программой Excel может доставить некоторые сложности тем, кто видит ее впервые, но небольшая таблица все упростит. Все строки таблицы заполняются конкретными данными, при этом используются специальные функции:

— функция КПЕР – сумма кредита;
— функция СТАВКА – ставка процентов по кредиту;
— функция ПС – цель кредита;
— функция ПЛТ – ежемесячный платеж по кредиту.

Если программа знает первые три показателя, то последний она рассчитает самостоятельно.

В программе можно составить собственный график гашения кредита, но потребуется дата его начала, которая обычно указывается в кредитном договоре.

При желании, можно погасить кредит досрочно, при этом никаких комиссий или штрафов банк не должен требовать.

Достоверная информация о кредите, ежемесячных платежах, фактической переплате доступна у кредитора. Стоит помнить и о том, что некоторые кредитные программы включают в себя скрытые комиссии, а значит, ежемесячный платеж и прочие показатели по кредиту могут отличаться от заранее рассчитанных. Так же может изменяться и размер процентной ставки.

Источник