Построение графика функции заданной параметрически excel

Параметрический график функции в Excel

Отдельного типа диаграмм для вывода параметрического представления функции в Excel нет, но это легко сделать следующим образом:

  • определить ряд данных для величины t, меняющейся от 0 до 2*π c заданным шагом;
  • определить зависимые ряды данных x(t), y(t);
  • построить диаграмму типа «Точечная диаграмма» по выделенным рядам x(t), y(t).

Скрин и документ Excel 2007 или выше прилагаются. Функция взята из этой заметки.

Параметрический график в Excel, как построить, скриншот

Параметрический график в Excel, как построить, скриншот

 Скачать этот пример в архиве .zip с документом Excel .xlsx (73 Кб)

30.10.2022, 04:44 [232 просмотра]

К этой статье пока нет комментариев, Ваш будет первым

Источник

Построение
графиков 3-х видов в электронной таблице
Excel

1.
Построить несколько графиков параметрически
заданной функции при разных значениях
конcтант
а, b,
.
Оси графика – х и y,
которые зависят от аргумента t
или .

№

Название

кривой

Вид
графика

Параметри­ческие
уравнения

Диапазон

аргумента

Кол-во

граф.

Значения
констант

1

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

5

a = 1;
1.25;
1.5; 1.75; 2

2

Циклоида

x = a(t — sin
t)

y = a(1 — cos
t)

t  0  6

шаг
0,5

6

a = 2

 = 0.4;
0.7; 1.0;
1.3; 1.6; 2.0

3

Трохоида

x = at — bsin
t

y = a — bcos
t

t  0  10

шаг
0,1

5

a = -1

b
= 0.1; 1; 2; 3; 4

4

Эпитрохоида

x = acos
(t)
— bcos
(t + t)

y = asin
(t)
— bsin
(t + t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

5

Гипотрохоида

x = acos
(t)
— bcos
(t — t)

y = asin
(t)
— bsin
(t — t)

t  0  10

шаг
0,5

6

a = 0;
1; 2; 3; 10; 15

b = 2
 = 0.25

6

Декартов

лист

x = at   / (1 + t3)

y = a
t2 / (1 + t3)

t  -6  6

шаг
0,3

6

a = 1;
2; 3; 4; 5; 6

7

Циссоида
Диоклеса

x = a
t2 / (1 + t2)

y = a
t3 / (1 + t2)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

8

Строфоида

x = a
 (t2 — 1) / (t2 + 1)

y = at(t2 — 1) / (t2 + 1)

t  -6  6

шаг
0,2

6

a = 1;
2; 3; 4; 5; 6

9

Конхоида

Никомеда

x = a + bcos
t

y = atg
t + bsin
t

t  0

10

шаг
0,2

5

a = 2

b
= 1; 10; 30; 50; 90

10

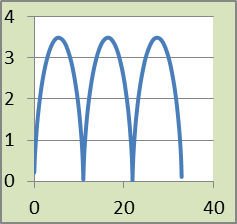
Улитка

Паскаля

x = acos2
t + bcos
t

y = a
cos
t sin
t + bsin
t

t  0  2

шаг
0,1

6

a = 1;
2; 3; 4; 5; 6

b
= 3

11

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a sin[(a + b)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1;
2; 3; 4; 5; 6

12

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  10

Шаг
0,2

6

a = 3;
b = 4

 = 0.5;
0.7; 1;
1.5; 2; 3

13

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 4; 6

14

Эпици­клоида

x = (a + b)cos

— acos[(a + b)/a]

y = (a + b)
sin 
— a
sin[(a + b)/a]

  0  2

Шаг
0,1

6

a = 7;
b = 4

 = 0.5;
1; 2; 4; 6; 8

15

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  2

Шаг
0,1

6

a
= 1

b = 1.5;
2.5; 3;
3.5; 4; 5

16

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a sin[(b — a)/a]

  0  6

Шаг
0,5

6

a
= 1.5; 2; 2.5;
3; 3,5; 4

b = 1

17

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  2

Шаг
0,1

6

a = 1;
b = 4

 = 0.5;
1; 1.5; 2; 3; 4

18

Гипоци­клоида

x = (b — a)cos

— acos[(b — a)/a]

y = (b — a)
sin 
— a
sin[(b — a)/a]

  0  10

Шаг
0,2

6

a = 5;
b = 2

 = 0.2;
0.5; 0.7;
1; 1.5; 2

19

Спираль

x = atcos
t

y = btsin
t

t  0  10

Шаг
0,5

6

a
= 2

b = -2;
-1; 1; 2; 3; 4

20

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  -6  6

Шаг
0,3

5

a = 2

b = 1;
2; 3; 4; 5

21

Гиперболич.

спираль

x = (acos
t) / t

y = (b
sin
t) / t

t  0.5  20

Шаг
0,5

5

a = 3

b = 1;
2; 3; 4; 5

22

Астроида

x = acos3
(t / 4)

y = b
sin3
(t / 4)

t  0  8

Шаг
0,1

5

a
= 2

b = 1;
2;
3;
4;
5

23

Астроида

x = acos3
(t – b)

y = a
sin3
t

t  0  8

Шаг
0,2

5

a
= 2

b = 0;
1; 2; 3; 4

24

Астроида

x = acos3
(bt
)

y = a
sin3
t

t  0  8

Шаг
0,1

5

a
= 2

b = 0.5;
1; 1.5; 3; 3.5

25

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  -10 10

Шаг
0,5

4

a
= -2;
-1; 1; 2

26

Эволь­вента

x = acos
t + at
sin
t

y = a
sin
t + atcos
t

t  0 20

Шаг
0,5

4

a
= -2;
-1; 1; 2

27

Эллипс

x = acos
t

y = b
sin
t

t  0  2

Шаг
0,5

5

a
= 7

b = 1;
4; 7; 10; 13

28

Эллипс

x = acos(c
+ t)

y = b
sin(c
— t)

t  0  2

Шаг
0,11

5

a
= 3 b = 2

b = 1;
2; 3; 4; 5

29

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Построение графика параметрически заданной функции

arinarezanova

 Дата: Воскресенье, 02.07.2017, 02:29 |
Сообщение № 1

Группа: Пользователи

Ранг: Прохожий

Сообщений: 1


Репутация:
0
±

Замечаний:
0% ±


Excel 2010

Помогите пожалуйста построить графики
на интервале [-5,5]
не могу построить интервал,где функция не определена

Сообщение отредактировал arinarezanova — Воскресенье, 02.07.2017, 02:30
 

Ответить

Pelena

 Дата: Воскресенье, 02.07.2017, 07:43 |
Сообщение № 2

Группа: Админы

Ранг: Местный житель

Сообщений: 18797


Репутация:
4284
±

Замечаний:
±


Excel 2016 & Mac Excel

У меня получилось только с ручным удалением значений ошибки

К сообщению приложен файл:

0542054.xlsx
(14.0 Kb)

«Черт возьми, Холмс! Но как??!!»
Ю-money 41001765434816

 

Ответить
Источник

Содержание

  1. Построение графиков в Excel
  2. Тема 4: Построение графиков в Excel
  3. График функции в Excel: как построить?
  4. Создание таблицы
  5. Вычисление значений функции
  6. Построение графика
  7. Создание таблицы и вычисление значений функций
  8. Построение графиков
  9. Отзывы
  10. Анализ электронных таблиц. Параметрические таблицы, подбор параметра и принятие решений. — презентация
  11. Похожие презентации
  12. Презентация на тему: » Анализ электронных таблиц. Параметрические таблицы, подбор параметра и принятие решений.» — Транскрипт:

Построение графиков в Excel

Работа в Microsoft Excel

Дано: Построить в электронной таблице Excel графики параметрически заданной функции при разных значениях конcтант а, b, l. Оси графика – х и y, которые зависят от аргумента t или j Форматировать элементы диаграммы:

· Оси подписать, цифры на осях 14 пунктов, полужирный курсив

· толщина осей 2 пт

· линии сетки по оси x и y 1пт, тип линии пунктир

· заливка области диаграммы

· заливка области построения

· ряд данных – красная линия, красные маркеры точек, размер маркера=6

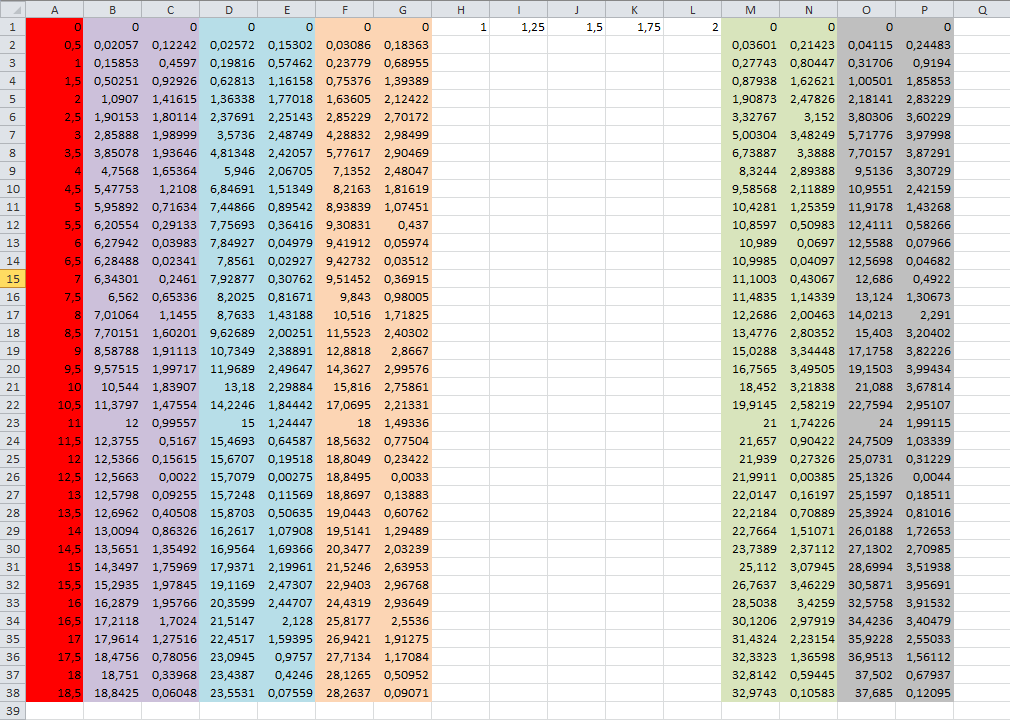
Вариант 1: x=a×(t — sin t); y=a×(1- cos t); a=1;1.25;1.5;1.75;2;tÎ0¸6p Шаг 0,5

=$H$1*(A1-SIN(A1)) для x=a×(t — sin t)

=$H$1*(1-COS(A1)) для y=a×(1- cos t)

Для построения графика в Microsoft Excel в первую строку и в первый столбец таблицы вводим данные. С помощью команды Выполнить — Прогрессия заполняю все остальные ячейки в таблицы, с заданным интервалом. Затем следуя математическим правилам записываем данную нам формулу в том виде, в котором это требуется в программе Microsoft Excel. Далее выделяем 2 столбца с координатами нашего будущего графика, и через команду вставка – диаграмма – график – график с маркерами. После всех правильно выполненных операций в таблице Microsoft Excel мы увидим готовые графики.

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)

Источник

Тема 4: Построение графиков в Excel

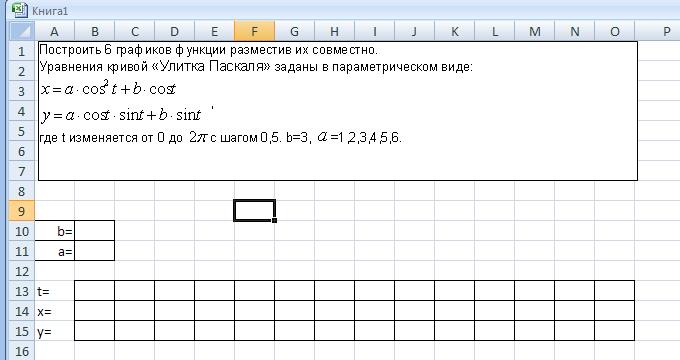
Задание. Построить график функции заданной в параметрическом виде.

Перенесём задание на лист Excel и создадим таблицу для расчета данных необходимых для построения графика заданной функции.

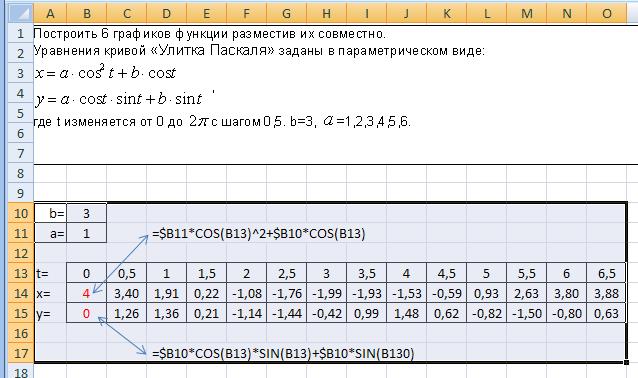
Внесем в таблицу значения коэффициентов a=1 и b=3, последовательность значений параметра t в заданных пределах и заданным шагом и формулы для расчета координат X и Y.

Значения коэффициентов b и a введены соответственно в ячейки В10 и В11, значения параметра t введены как последовательность методом протяжки маркера заполнения по строке.

Формулы для вычисления Х и У вводятся изначально в ячейки В14 и В15 и копируются на всю строку методом протяжки.

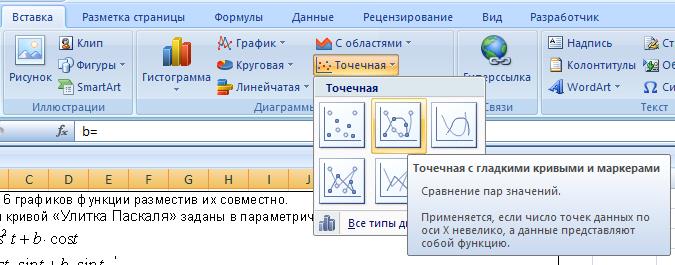
Построение графика функции начнем с выбора типа будущей диаграммы (графика) для этого необходимо перейти на вкладку Вставка и выбрать необходимый тип. В нашем случае это будет Точечная , поскольку функция задана в параметрическом виде и мы рассчитываем координаты Х и У (т.е. точки ) по которым строится кривая.

Выбираем Точечная с гладкими кривыми и маркерами щелкнув левой клавишей по нужной кнопке (вторая в верхнем ряду).

На листе Excel появляется пустое окно диаграммы, которое при помощи мыши можно перетащить в любое место листа и изменить размеры. используя маркеры расположенные на границах окна.

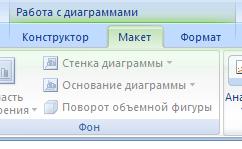
После того как созданная диаграмма отобразится в рабочем листе, станет доступна контекстная вкладка Работа с диаграммами с тремя наборами инструментов (вкладками) для изменения диаграмм:

· Конструктор – содержит параметры, определяющие тип диаграммы, источник данных и их упорядочивание, макеты диаграмм, а также команду Переместить диаграмму;

· Макет – позволяет указывать свойства диаграмм, добавлять или редактировать элементы диаграммы (подписи данных и осей, добавление легенды и элементов рисования), а также выбирать параметры, связанные с трехмерными графиками:

· Формат – содержит опциивыбора различных элементов диаграммы, присвоения стилей ее графическим элементам, включая трехмерные края, тени, фаски и пр.

При активном окне диаграммы, для этого необходимо щелкнуть по нему указателем мыши если оно находится в неактивном состоянии, выбрать вкладку

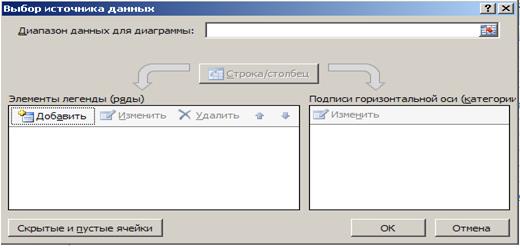
Конструктор и на панели Данные выбрать опцию Выбрать данные.

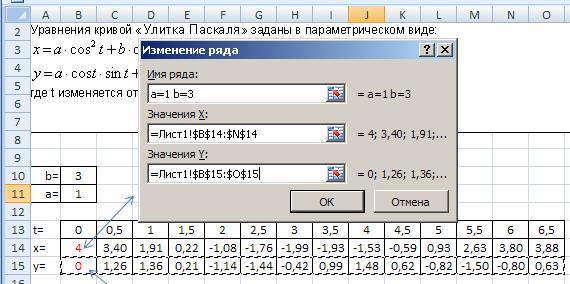
В результате открывается диалоговое окно, в котором необходимо выбрать опцию Добавить данные,

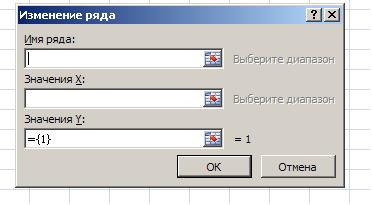
после чего открывается следующее окно для указания диапазона ячеек, где расположены данные для переменной Х и У и указания имени ряда (имени данной кривой).

В нашем случае в качестве имени ряда внесем значения коэффициентов a и b, при которых были рассчитаны значения Х и У, в наборных полях для значений самих этих переменных укажем диапазоны ячеек, в которых они находятся:

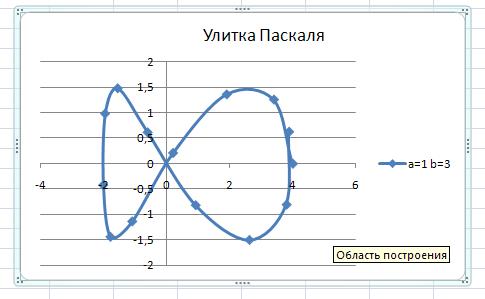
Щелкнув по кнопке ОК, получаем график нашей кривой:

Изменим имя графика, поскольку по умолчанию оно приняло имя ряда, и получим окончательный вариант:

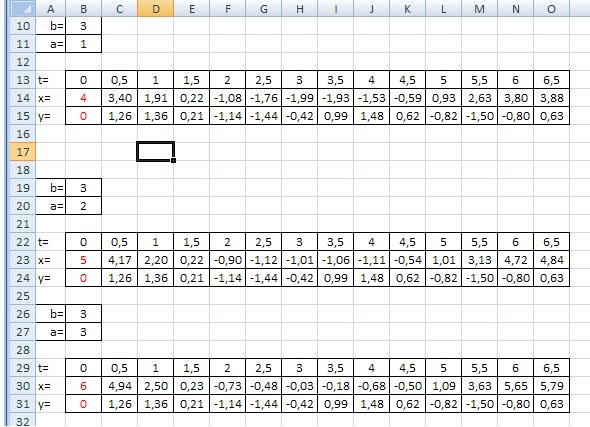
Для построения следующих вариантов графиков скопируем созданную таблицу на другие свободные строки ниже:

Меняя значение коэффициента a, получаем пересчитанные значения Х и У. Повторив для каждой таблицы все ранее описанные шаги по построению диаграмм, начиная с выбора типа диаграммы, получим шесть отдельных графиков. Для совмещения всех вариантов на одной диаграмме необходимо, пропустив первый этап выбора типа диаграммы, активизировать уже созданную и перейти к этапу выбора данных из другой таблицы.

При совместном расположении графиков проще анализировать влияние отдельных параметров на изменение характера получаемой зависимости.

Источник

График функции в Excel: как построить?

В MS Office Excel можно построить график математической функции. Рассмотрим построение графиков на примерах.

Пример 1

Дана функция:

Нужно построить ее график на промежутке [-5;5] с шагом равным 1.

Создание таблицы

Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

Построение графика

Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).

Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.

Пример 2

Даны функции:

и y=50x+2. Нужно построить графики этих функций в одной системе координат.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Построение графиков

Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.

Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.

Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями

Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.

Кстати, такая возможность есть
на всех страницах нашего сайта

Отзывы

2007-2023 «Педагогическое сообщество Екатерины Пашковой — PEDSOVET.SU».
12+ Свидетельство о регистрации СМИ: Эл №ФС77-41726 от 20.08.2010 г. Выдано Федеральной службой по надзору в сфере связи, информационных технологий и массовых коммуникаций.
Адрес редакции: 603111, г. Нижний Новгород, ул. Раевского 15-45
Адрес учредителя: 603111, г. Нижний Новгород, ул. Раевского 15-45
Учредитель, главный редактор: Пашкова Екатерина Ивановна
Контакты: +7-920-0-777-397, info@pedsovet.su
Домен: https://pedsovet.su/
Копирование материалов сайта строго запрещено, регулярно отслеживается и преследуется по закону.

Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.

Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.

О работе с сайтом

Мы используем cookie.

Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.

При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.

Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены.

Источник

Анализ электронных таблиц. Параметрические таблицы, подбор параметра и принятие решений. — презентация

Презентация была опубликована 7 лет назад пользователемСтанислав Бердяев

Похожие презентации

Презентация на тему: » Анализ электронных таблиц. Параметрические таблицы, подбор параметра и принятие решений.» — Транскрипт:

1 Анализ электронных таблиц. Параметрические таблицы, подбор параметра и принятие решений

2 Введение Электронная таблица — это набор ячеек, составляющих таблицу. Внутри каждой ячейки может находиться либо текстовая информация, либо числовые или какие-нибудь другие данные (например, дата или время), либо формула. Электронная таблица — это набор ячеек, составляющих таблицу. Внутри каждой ячейки может находиться либо текстовая информация, либо числовые или какие-нибудь другие данные (например, дата или время), либо формула. В вычислениях формулы внутри ячейки могут участвовать данные или результаты вычисления формул из других ячеек электронной таблицы. В вычислениях формулы внутри ячейки могут участвовать данные или результаты вычисления формул из других ячеек электронной таблицы. Ячейка с формулой должна хранить два значения: саму формулу и результат её вычисления. Ячейка с формулой должна хранить два значения: саму формулу и результат её вычисления. Электронные таблицы применяются везде, где встречаются данные в виде таблиц и вычисления над данными, представленными в табличном виде. Электронные таблицы применяются везде, где встречаются данные в виде таблиц и вычисления над данными, представленными в табличном виде.

3 Анализ данных Для исследования экономической информации широко используются статистические методы обработки. Электронная таблица EXCEL содержит набор встроенных функций категории Статистические, а также специальные модули, выполняемые в среде Пакета анализа. Команда меню Сервис – Надстройки позволяет выбрать Пакет анализа. После установки Пакета анализа изменяется состав команд меню режима Сервис – появляется новая команда Анализ данных. Для исследования экономической информации широко используются статистические методы обработки. Электронная таблица EXCEL содержит набор встроенных функций категории Статистические, а также специальные модули, выполняемые в среде Пакета анализа. Команда меню Сервис – Надстройки позволяет выбрать Пакет анализа. После установки Пакета анализа изменяется состав команд меню режима Сервис – появляется новая команда Анализ данных.

4 Исходные данные для анализа могут быть представлены на рабочем листе в виде списка значений. Как правило, для идентификации массива значений используются названия столбцов – метки, а также создаются именованные блоки. При выполнении команды Сервис, Анализ данных вызывается диалоговое окно Анализ данных, в котором выбирается режим Описательная статистика; в одноименном диалоговом окне задаются соответствующие установки. Исходные данные для анализа могут быть представлены на рабочем листе в виде списка значений. Как правило, для идентификации массива значений используются названия столбцов – метки, а также создаются именованные блоки. При выполнении команды Сервис, Анализ данных вызывается диалоговое окно Анализ данных, в котором выбирается режим Описательная статистика; в одноименном диалоговом окне задаются соответствующие установки.

5 Встроенные функции для расчета показателей описательной статистики СРЗНАЧ СРЗНАЧ МИН МИН МАКС МАКС СРГЕОМ СРГЕОМ ДИСПР ДИСПР СРОТКЛ СРОТКЛ СТАНДОТКЛОН СТАНДОТКЛОН МЕДИАНА МЕДИАНА МОДА МОДА СКОС СКОС

6 При выполнении команды Сервис – Анализ данных выбирается режим Регрессия, появляется одноименное диалоговое окно. При выполнении команды Сервис – Анализ данных выбирается режим Регрессия, появляется одноименное диалоговое окно.

7 СЕРВИС-АНАЛИЗ ДАННЫХ-РЕГРЕССИЯ В окне задаются: Входной интервал Y, Входной интервал Х, Уровень надежности, Выходной интервал. В окне задаются: Входной интервал Y, Входной интервал Х, Уровень надежности, Выходной интервал. Результаты регрессионного анализа размещаются в трех таблицах. Результаты регрессионного анализа размещаются в трех таблицах.

8 Дополнительные функции для анализа временных рядов и числовых последовательностей. Дополнительные функции для анализа временных рядов и числовых последовательностей. ЛИНЕЙН ЛИНЕЙН ТЕНДЕНЦИЯ ТЕНДЕНЦИЯ ПРЕДСКАЗ ПРЕДСКАЗ НАКЛОН НАКЛОН ОТРЕЗОК ОТРЕЗОК

9 Уравнения с одной переменной Решать уравнения с одной переменной можно с помощью команды Сервис, Подбор параметра. Относительная точность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры. Далее в ячейки таблицы вводится цепочка вычислений. Значение, которое нужно найти (переменная), находится в определённой ячейке, а результат вычислений – в другой. В диалоговом окне Подбор параметра в поле Установить в ячейке вводится ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (или результат вычислений). В поле Значение вводим ноль (для решения уравнений) или требуемое число. В поле Изменяя значение ячейки вводится ссылка на ячейку, отведённую под переменную. После нажатия ОК находится приближённое решение. Решать уравнения с одной переменной можно с помощью команды Сервис, Подбор параметра. Относительная точность вычислений и предельное число итераций задаются на вкладке Вычисления диалогового окна Параметры. Далее в ячейки таблицы вводится цепочка вычислений. Значение, которое нужно найти (переменная), находится в определённой ячейке, а результат вычислений – в другой. В диалоговом окне Подбор параметра в поле Установить в ячейке вводится ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (или результат вычислений). В поле Значение вводим ноль (для решения уравнений) или требуемое число. В поле Изменяя значение ячейки вводится ссылка на ячейку, отведённую под переменную. После нажатия ОК находится приближённое решение.

10 Технология использования средства Поиск решения определённые ячейки резервируем под значения переменных определённые ячейки резервируем под значения переменных в одну из ячеек вводим значение целевой функции в одну из ячеек вводим значение целевой функции в соседние ячейки вводим граничные значения в соседние ячейки вводим граничные значения выбираем Сервис – Поиск решения и заполняем открывшееся диалоговое окно выбираем Сервис – Поиск решения и заполняем открывшееся диалоговое окно

11 Подбор параметра Подбор параметра – средство Excel,позволяющее решать так называемую обратную задачу, когда требуется, меняя значение одного из исходных данных (параметров), получить заданное значение результата. Подбор параметра – средство Excel,позволяющее решать так называемую обратную задачу, когда требуется, меняя значение одного из исходных данных (параметров), получить заданное значение результата.

12 Поиск решения Средство Excel Поиск решения используется в тех случаях, когда необходимо найти оптимальное (минимальное или максимальное) или заданное значение для отдельной ячейки (целевой ячейки) путем подбора значений других ячеек (изменяемых ячеек) с учетом требуемых ограничений. Средство Excel Поиск решения используется в тех случаях, когда необходимо найти оптимальное (минимальное или максимальное) или заданное значение для отдельной ячейки (целевой ячейки) путем подбора значений других ячеек (изменяемых ячеек) с учетом требуемых ограничений.

Источник

Adblock
detector

Источник

Понравилась статья? Поделить с друзьями:
  • Построение графика функции двух переменных excel
  • Построение графика функции в excel с помощью функции если
  • Построение графика функции в excel пример
  • Построение графика функции в excel по точкам
  • Построение графика функции в excel на примере