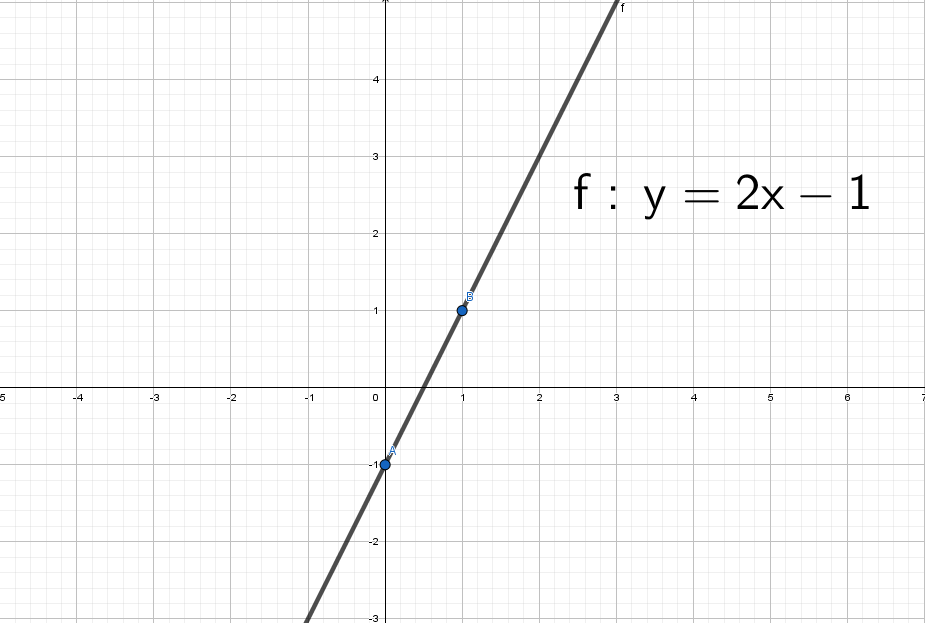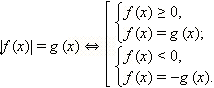Построение графика функции с модулем excel

Тема урока:Построение графиков функций, содержащих модули. Знакомство с функциями ЕСЛИ и ABS.

Учитель математики и информатики МОБУ СОШ №2 села Новобелокатай, Белокатайского района Галиуллина Юлия Рафаиловна.

Учебник «Алгебра и начала математического анализа. 10-11 класс» под ред. Колмогорова, Угринович Н.Д. «Информатика и ИКТ 10 класс».

Тип урока: обучающий урок с применением информационных технологий.

Цель урока: проверить знания, умения, навыки по данной теме.

Задачи урока:

Обучающая

1. систематизация и обобщение знаний по данной теме;

2. научить определять наиболее удобный метод решения;

3. научить строить графики функции с использованием электронной таблицы.

Развивающая

1. развитие способности самоконтроля;

2. активизация мыслительной деятельности учащихся;

Воспитательная

воспитание мотивов учения, добросовестного отношения к труду.

Методы обучения: частично-поисковый, исследовательский, индивидуальный.

Форма организации учебной деятельности: индивидуальная, фронтальная, карточки.

Средства обучения: мультимедийный проектор, экран, карточки

Ход урока

I. Организационный момент

Приветствие, проверка присутствующих. Объяснение хода урока

II. Повторение

1. Закрепление знаний по построению графиков в табличном процессоре.

Фронтальный опрос.

-Как вставить график в Еxcel?

— Какие виды графиков существуют в Еxcel?

1. Закрепление знаний по теме график с модулями.

— В чем смысл функции с модулем?

Разбор примера: y = | x | – 2.

Нужно рассмотреть два случая, когда х=0. Если х=0, то функция будет выглядеть y = x – 2. Построить в тетрадях график данной функции.

А теперь построим график функции с помощью табличного процессора MS Excel. График данной функции можно построить двумя способами:

1 способ: Использование функции ЕСЛИ

1. Для того чтобы построить график для начала нам нужно заполнить таблицу значений Х и У.

2. Называем ячейку А2-Х, ячейку В2-У. Следовательно в столбце А будет значение переменной, в столбце В значение функции.

3. В столбец А вводим переменной в интервале от -5 до 5 с шагом 0,5. Для этого в ячейку А3 вводим -5, а в ячейку А4 формулу =A4+0,5, копируем формулу в последующие ячейки, так как здесь относительная адресация то формула будет меняться при копировании.

4. После заполнения значений Х, переходим ко второму столбцу, для заполнения которого нужно ввести формулу. В ячейку В4 вводим формулу, в которой используем функцию ЕСЛИ.

5. Функция «Если» в электронных таблицах MS Excel (Категория — Логические) анализирует результат выражения или содержимое указанной ячейки и помещает в заданную ячейку одно из двух возможных значений или выражений.

6. Синтаксис функции «ЕСЛИ».

=ЕСЛИ (Логическое выражение; Значение_если_истина; Значение_если_ложь). Логическое выражение или условие, которое может принимать значение ИСТИНА или ЛОЖЬ. Значение_если_истина – значение, которое принимает логическое выражение в случае его выполнения. Значение_если_ложь – значение, которое принимает логическое выражение в случае его невыполнения».

Логические выражения или условия строятся с помощью операторов сравнения (, =, , =) и логических операций (И, ИЛИ, НЕ).

Рис.22 Функция ЕСЛИ

Функция ЕСЛИ относится к логическим.

1. Вспоминаем смысл функции с модулем: если х=0, то функция будет выглядеть y = x – 2.

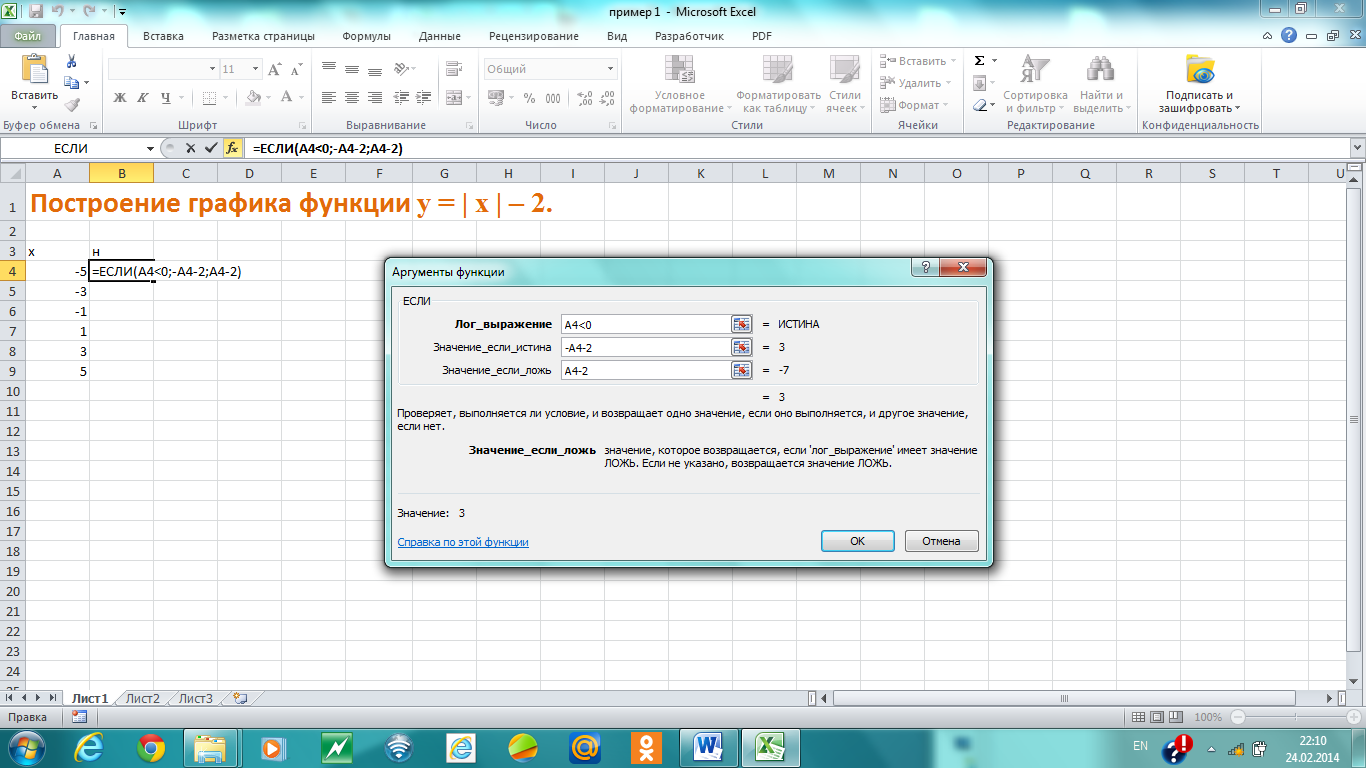
Данную формулировку нужно ввести в ячейку В4 в понятном таблице виде. Значение Х находится в столбце А, следовательно если А4

=-А4-2, иначе =А4-2.

Рис.23 Аргументы функции ЕСЛИ

Формула имеет вид: =ЕСЛИ(A5A5-2;A5-2)

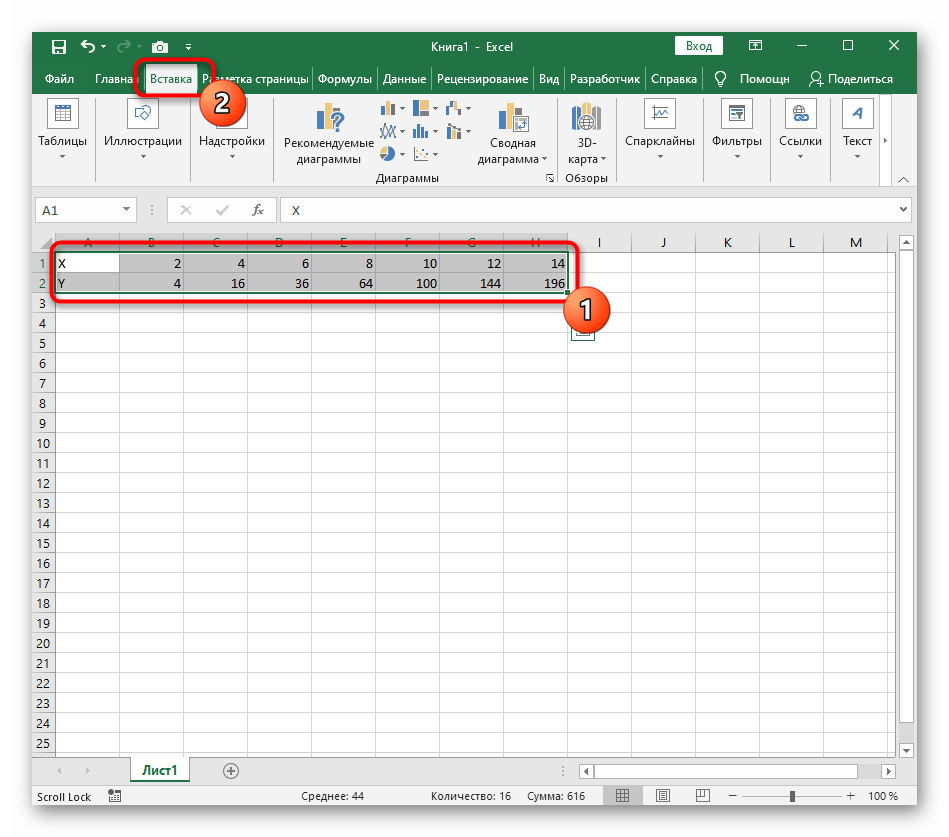
1. После заполнения таблицы значений. Строим график функции

2. Пункт меню Вставка-Диаграммы-Точечная. Выбираем один из макетов. На листе появляется пустое поле диаграммы. В контекстном меню данного поля выбираем пункт Выбрать данные. Появляется диалоговое окно Выбрать данные .

3. В данном диалоговом окне выбираем имя ряда в ячейке А1 или же также можно ввести название с клавиатуры.

4. В поле значение Х выбираем столбец, в который мы вводили значение переменной.

5. В поле значение У выбираем столбец, в котором мы с помощью условного оператора ЕСЛИ находили значение функции.

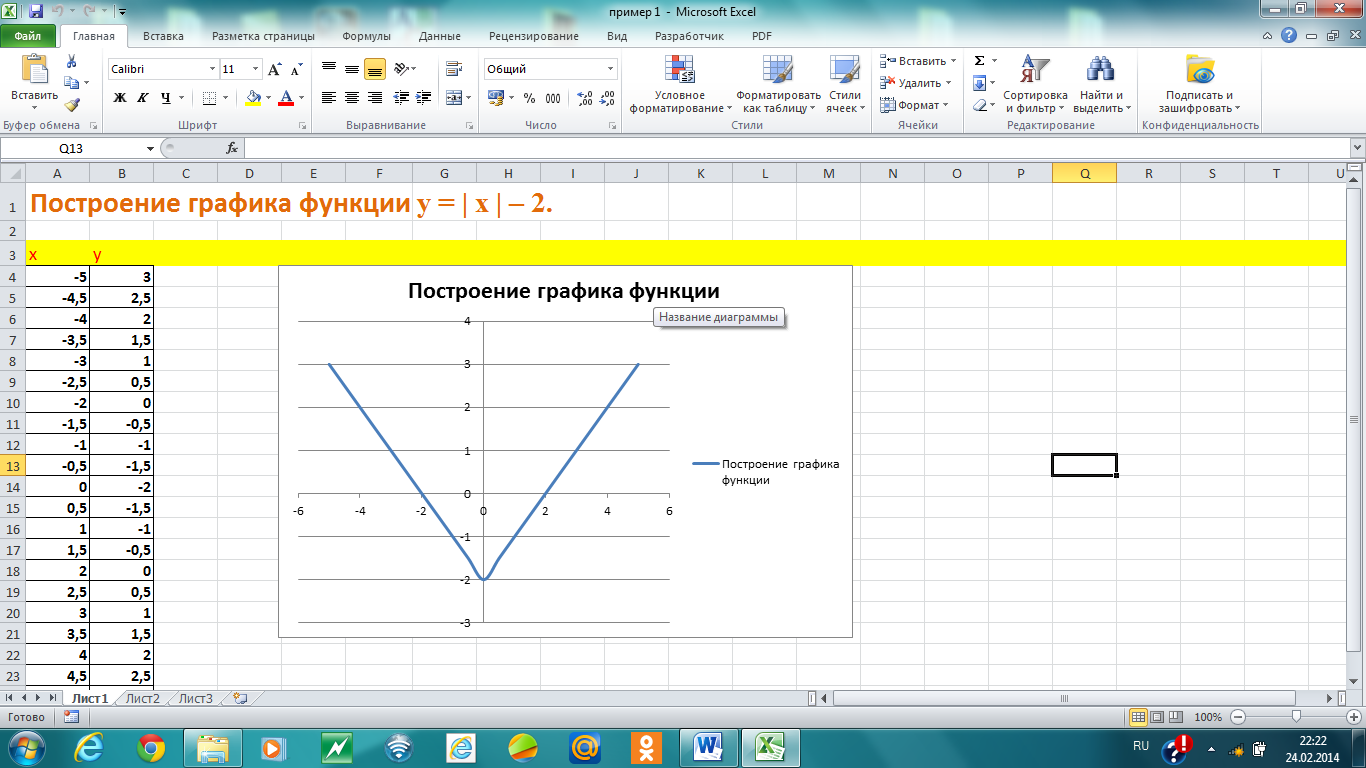
Рис. 24. График функции y = | x | – 2.

2 способ: Использование функции ABS

— Также для построения графика с модулем, можно использовать функцию ABS.

Построим график функции y = | x | – 2 с помощью функции ABS.

1. В примере 2 даны значения переменной Х.

2. В ячейку В4 вводим формулу с использованием функции АВS

Рис.25. Ввод функции ABS с помощью мастера функций

1. Формула будет иметь вид: =ABS(A4)-2.

2. Далее строим точечную диаграмму.

IV. Выполнение практической работы

После разбора двух примеров ученикам раздается практическое задание.

-В этих заданиях вам приведены несколько функций с модулями. Вы должны выбрать какую из функции целесообразнее применять в каждом из примеров.

Практическая работа

Ученики рассматривают линейную функцию y = x – 2 и строят её график.

Задача 1. Построить график функции y = | x – 2 |

Задача 2. Построить график функции y = | x | – 2

Задача 3. Построить график уравнения | y | = x – 2

Ученики рассматривают квадратичную функцию y = x²– 2х – 3 и строят график.

Задача 1. Построить график функции y = | x² – 2х – 3 |

Задача 2. Построить график функции y = | x² | – 2 | х | — 3

Задача 3. Построить график уравнения | y | = x² – 2х — 3

V. Информация о домашнем задании.

VI.Подведение итогов урока, рефлексия. Ученики и учитель подводят итоги урока, анализируют выполнение поставленных задач.

Построение графиков с модулем
путём преобразований

Модуль аргумента и модуль функции

Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.

В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.

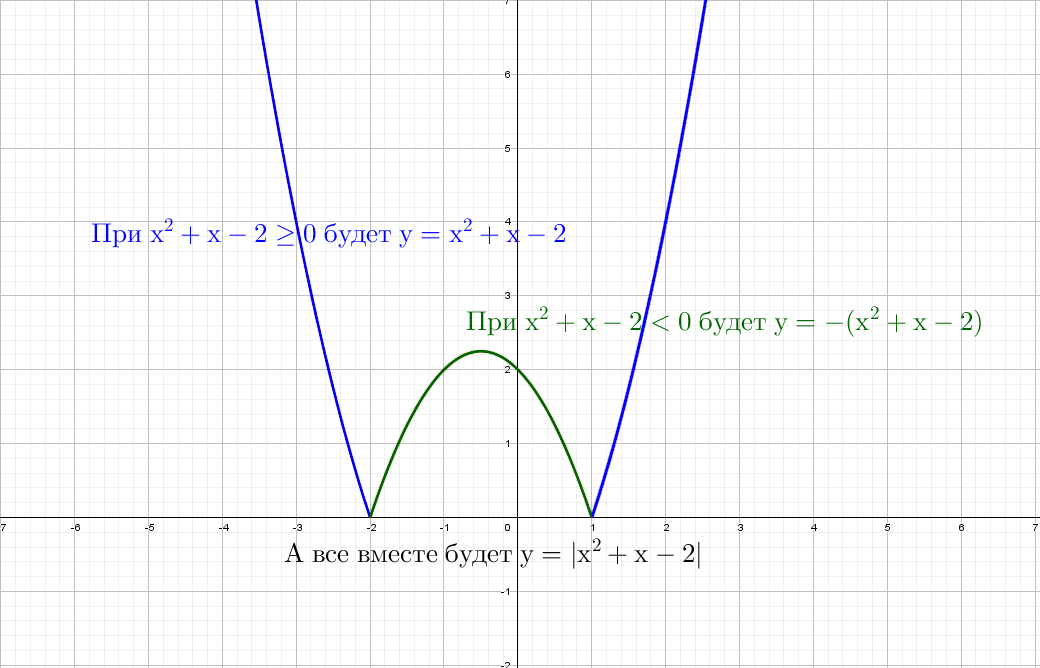
Пример 1.

В этом примере оба графика получены из графика функции y = x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .

Пример 2.

В этом примере оба графика получены из графика функции y = x 2 − 2x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .

Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.

III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.

Ниже показаны примеры графиков различных функций, содержащих модуль, которые получены из графика функции (y=sqrt.) y = √|x| __ .

1. (y=sqrt) √x _ —>

2. (y=sqrt<|x|>) √|x| __ —>

3. (y=sqrt<|x-1|>) y = √|x − 1| _____

4. (y=sqrt<|x|-1>) y = √|x| − 1 _____

5. (y=|sqrt-1|.) y = | √x − 1 _ |

IV Равенство вида |y| = f (x) по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции y = f(x) .
Для этого нужно:

1. Построить график функции y = f(x) .
2. Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
3. Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.

Эти кривые также получены из графика функции (y=sqrt). y = √x _ .

6. (|y|=sqrt)

7. (|y|=|sqrt-1|)

8. (|y|=sqrt<|x|>.)

Пример 3.

Задан график функции y = x 2 .
Построить кривые, удовлетворяющие уравнению, |y| = x 2 − 2|x| − 5 .

Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.

Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.

1.y = x 2	2.y = (x − 1) 2	3.y = (x − 1) 2 − 6	4.y = (|x| − 1) 2 − 6
5.y = (|x| − 1) 2 − 6, y ≥ 0	6.|y| = (|x| − 1) 2 − 6

Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.

Пример 4.

Задан график функции y = x 2 .
Построить график функции y = |x 2 − 2x − 5| .

Сумма модулей

Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.

Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.

Пример 5.

Построить график функции y = |x + 2| + |x − 1| .

Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.

На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1| , используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участках, например, при x = −3 и x = 3 . На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).

Теперь проверьте себя.

Пример 6.

Построить график функции y = |x + 2| + |x − 1| − |x| .

Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.

Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.

Графики прямой, параболы, гиперболы, с модулем

Пошаговое построение графиков.

«Навешивание» модулей на прямые, параболы, гиперболы.

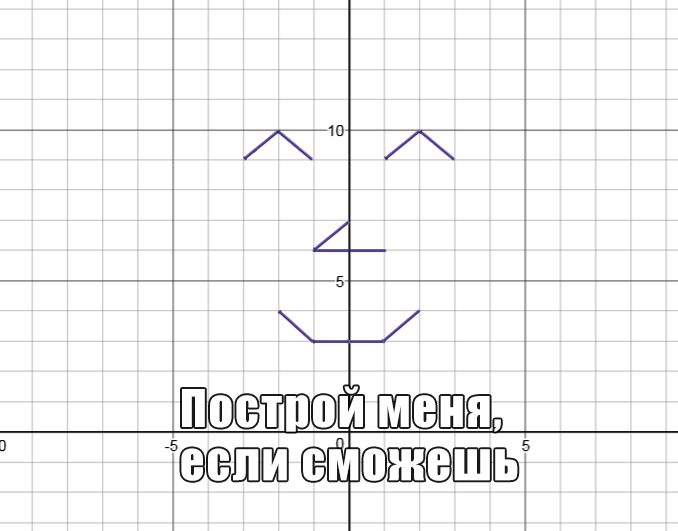
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.

Для понимания друг друга введу немного «обзываний» системы координат:

Для начала построим график прямой y = 2x − 1.

Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.

Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1

Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:

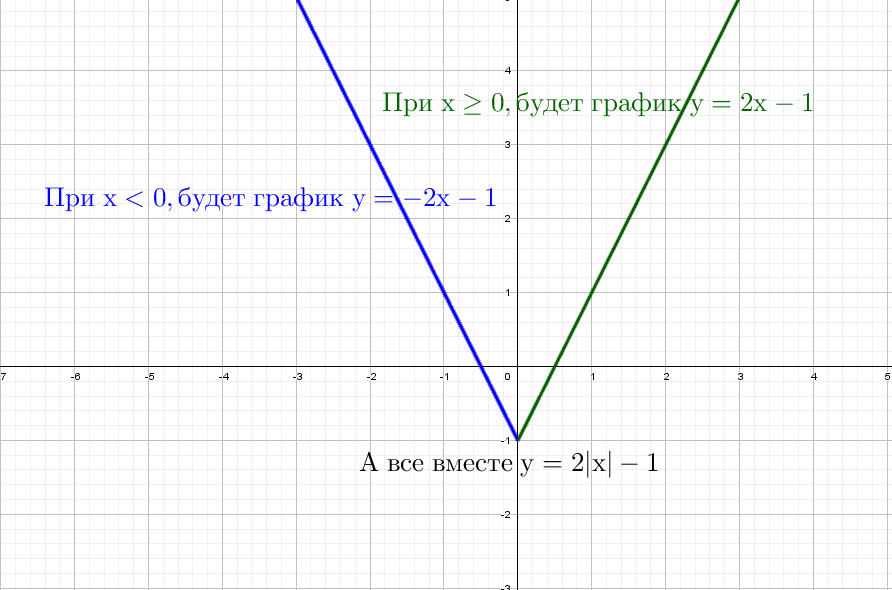
А если теперь добавить модуль y = |2x − 1|.

Модуль — это всегда положительное значение , получается, что «y» должен быть всегда положительным.

Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

Получается такая зеленая «галочка».

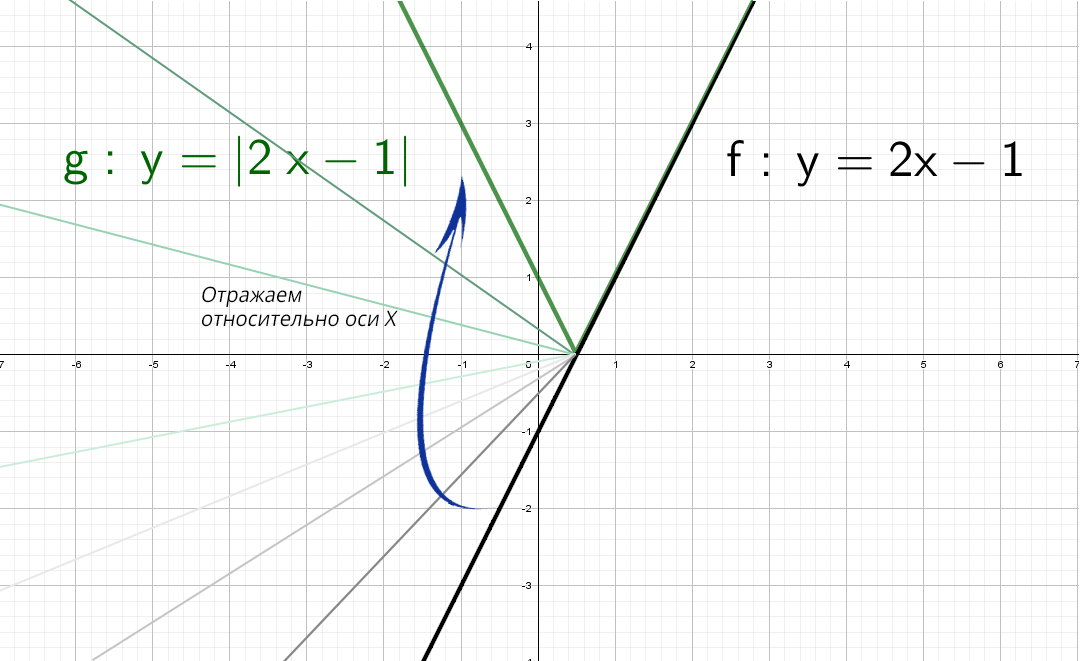
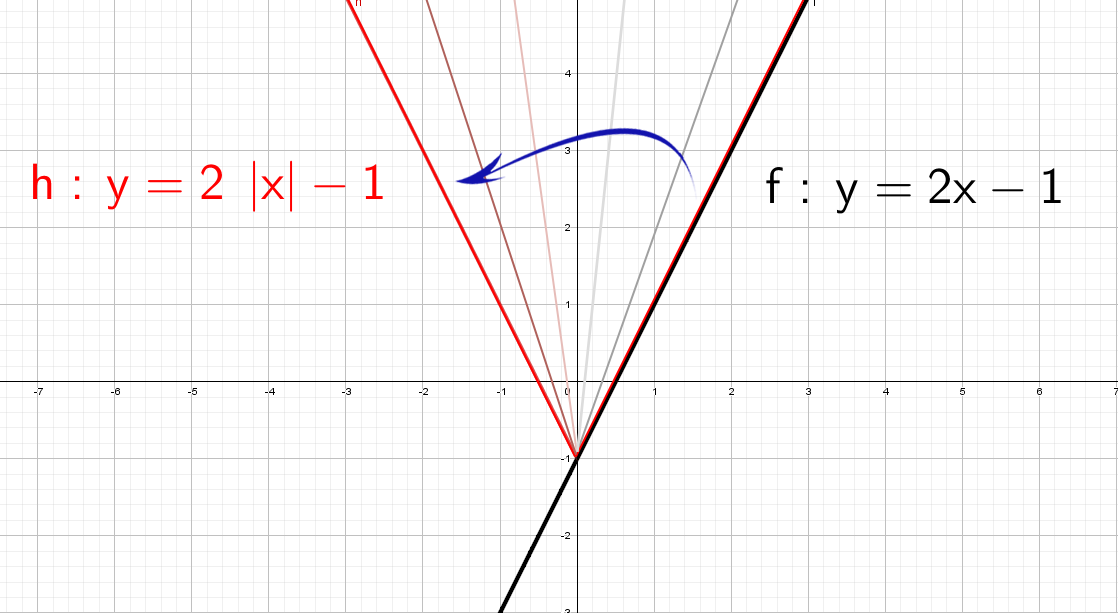
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?

Одна строчка рассуждений и рисуем:

Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.

Здесь отражаем относительно оси «y» . Такая же галочка, только теперь через другую ось.

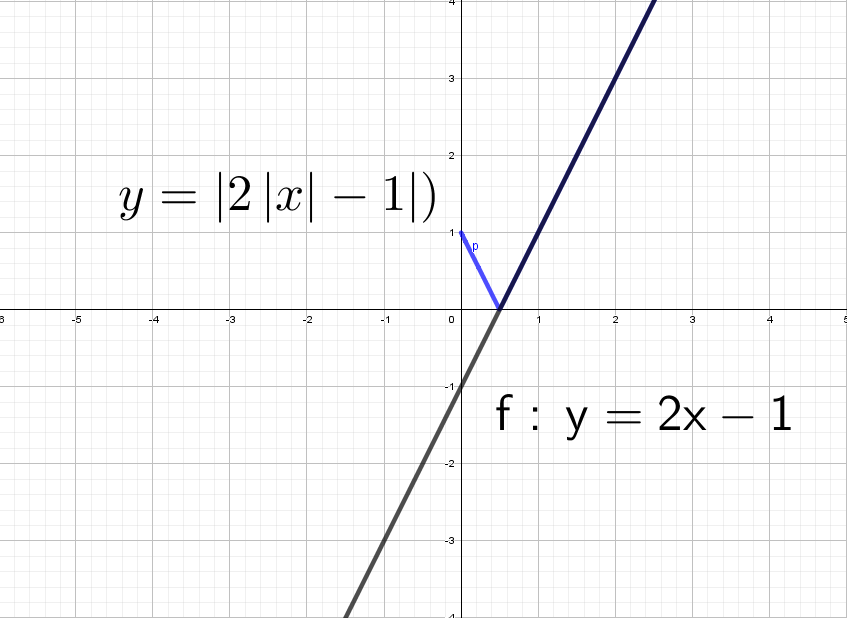
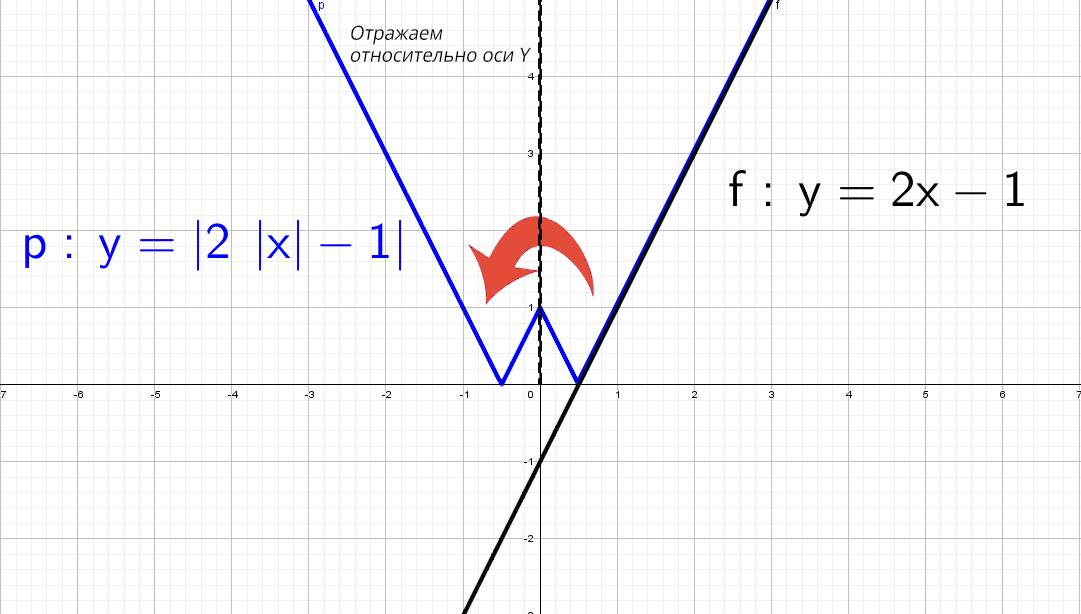
Смертельный номер: y = |2|x| − 1|.

Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.

В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!

А после этого отражаем относительно оси «y» то, что мы получили справа налево:

Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.

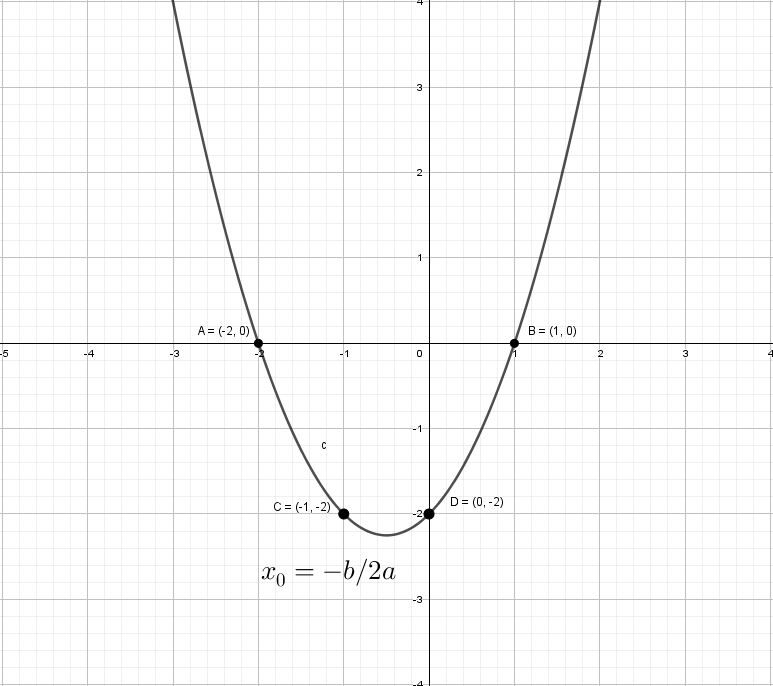
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x ₁ = 1 и x ₂ = -2.

Можно найти вершину у параболы и взять пару точек для точного построения.

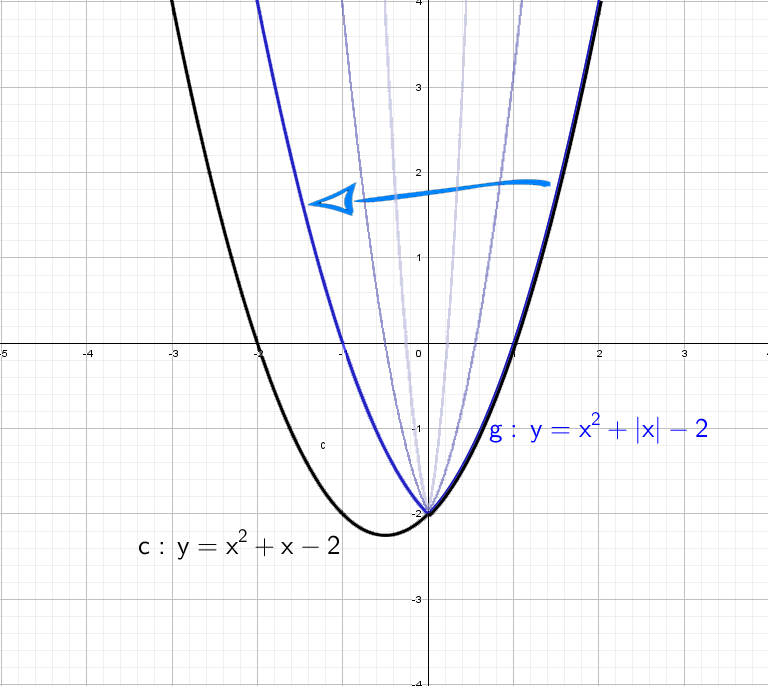
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.

При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:

А дальше что мелочиться: рассмотри сразу остальные графики с модулем!

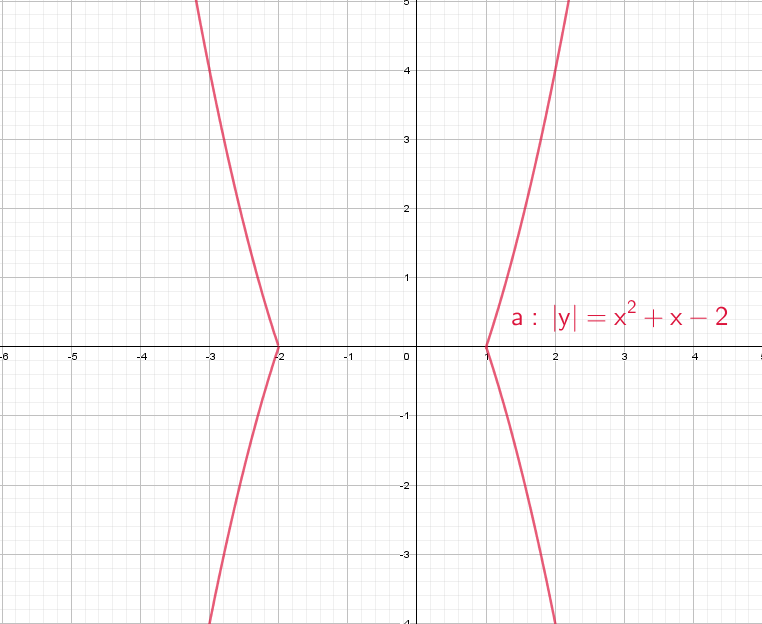
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.

При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!

Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.

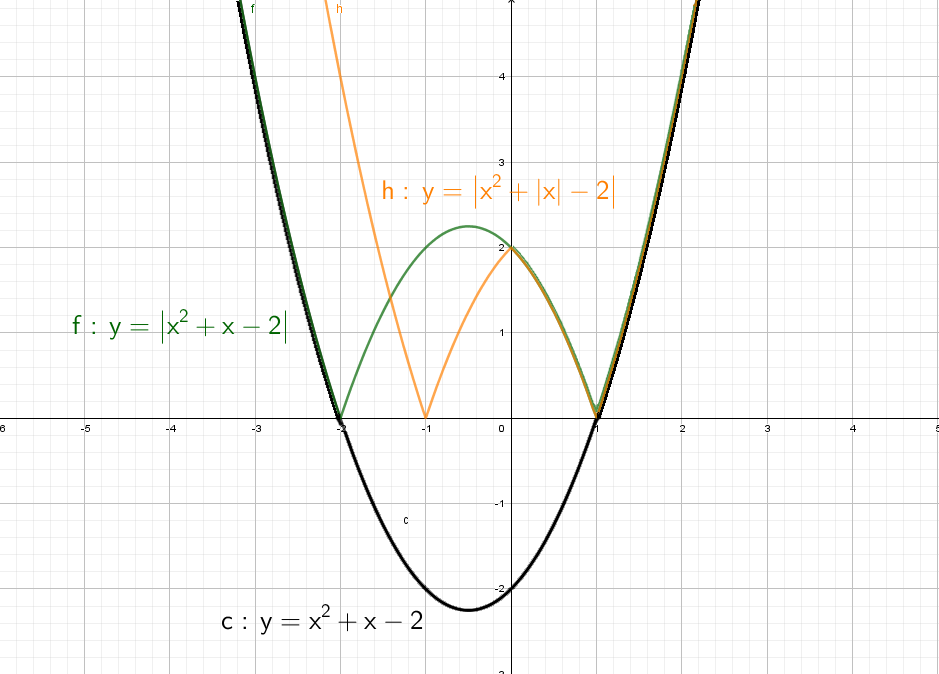
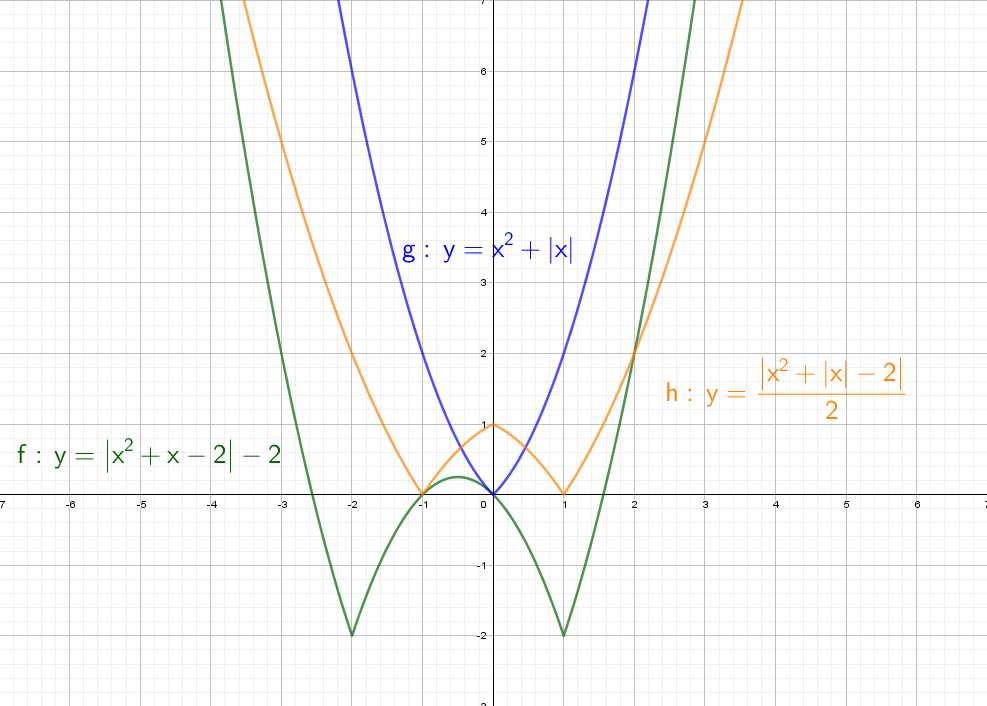
А теперь сразу комбо:

Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.

Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.

Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.

Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум , потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.

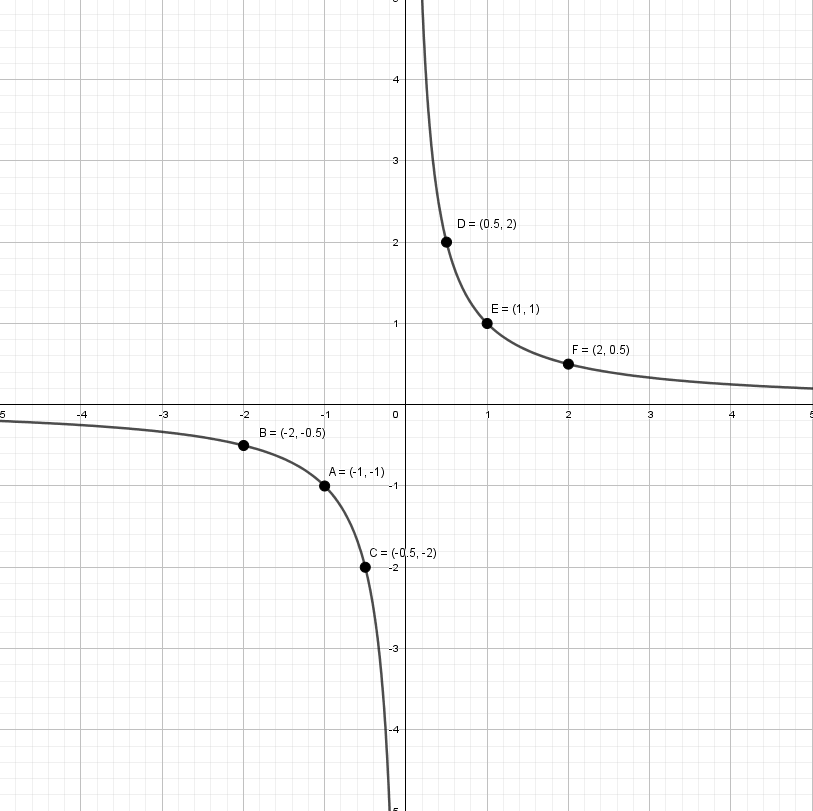
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:

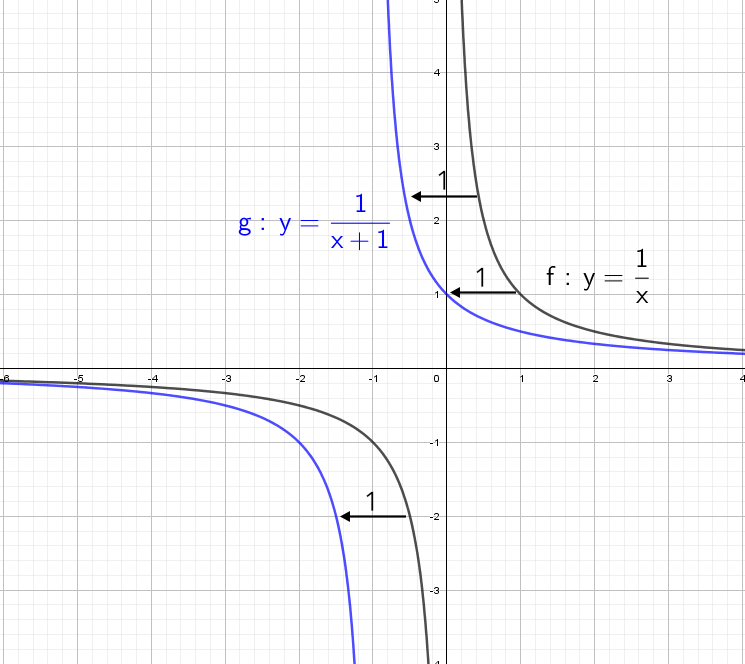
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:

А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.

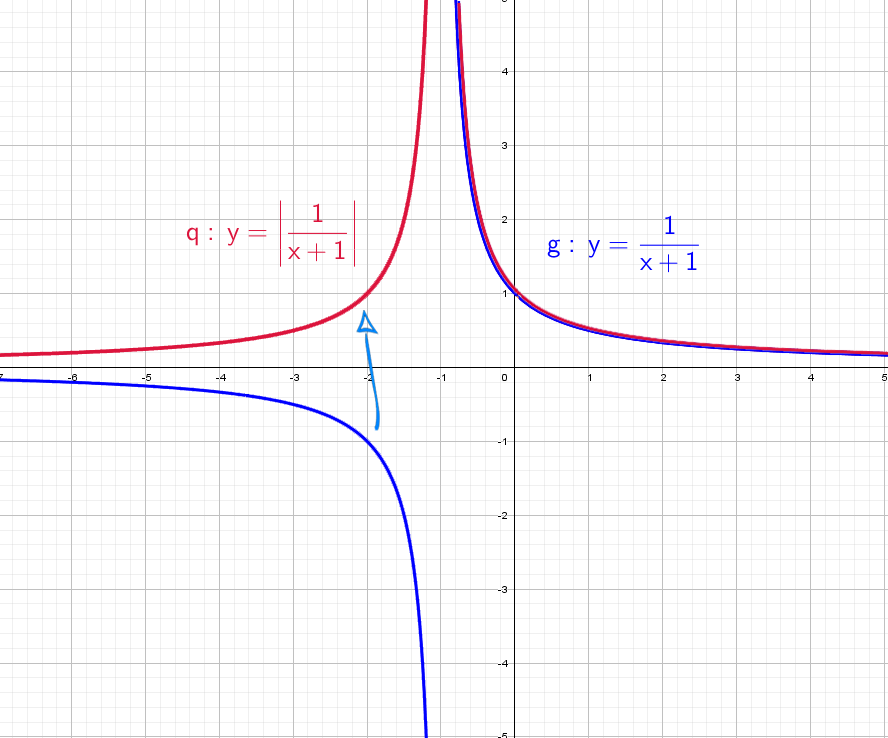
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!

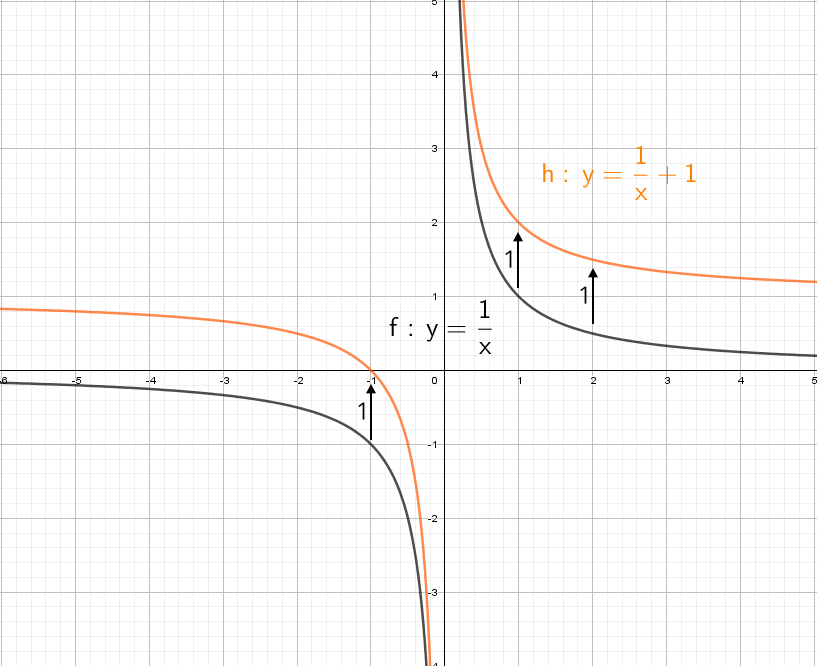
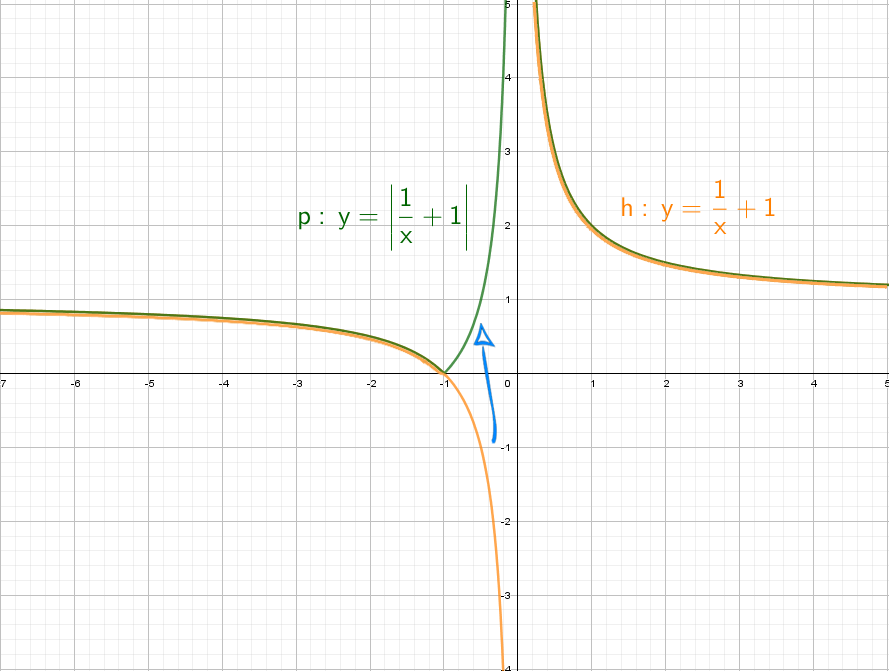
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.

Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.

Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.

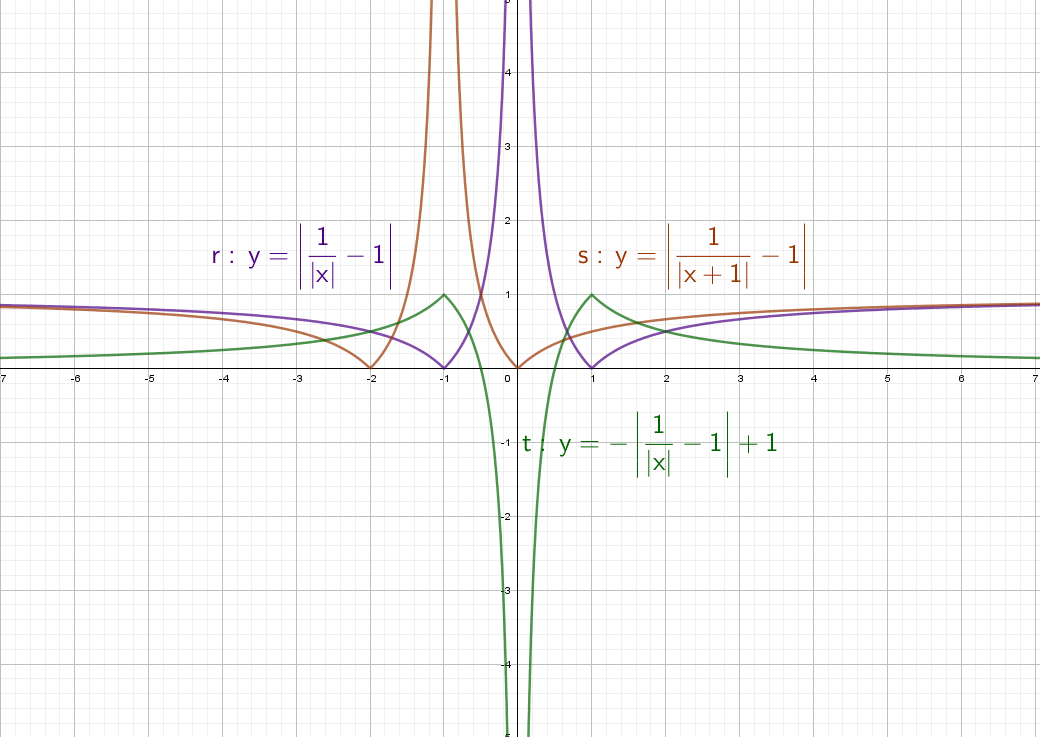
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.

Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.

Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.

Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:

И построить график, разбив его на кусочно-заданные функции.

Например для прямой:

Для параболы с одним модулем будет два кусочно-заданных графика:

C двумя модулями кусочно-заданных графиков будет четыре:

Таким способом, медленно и кропотливо можно построить любой график!

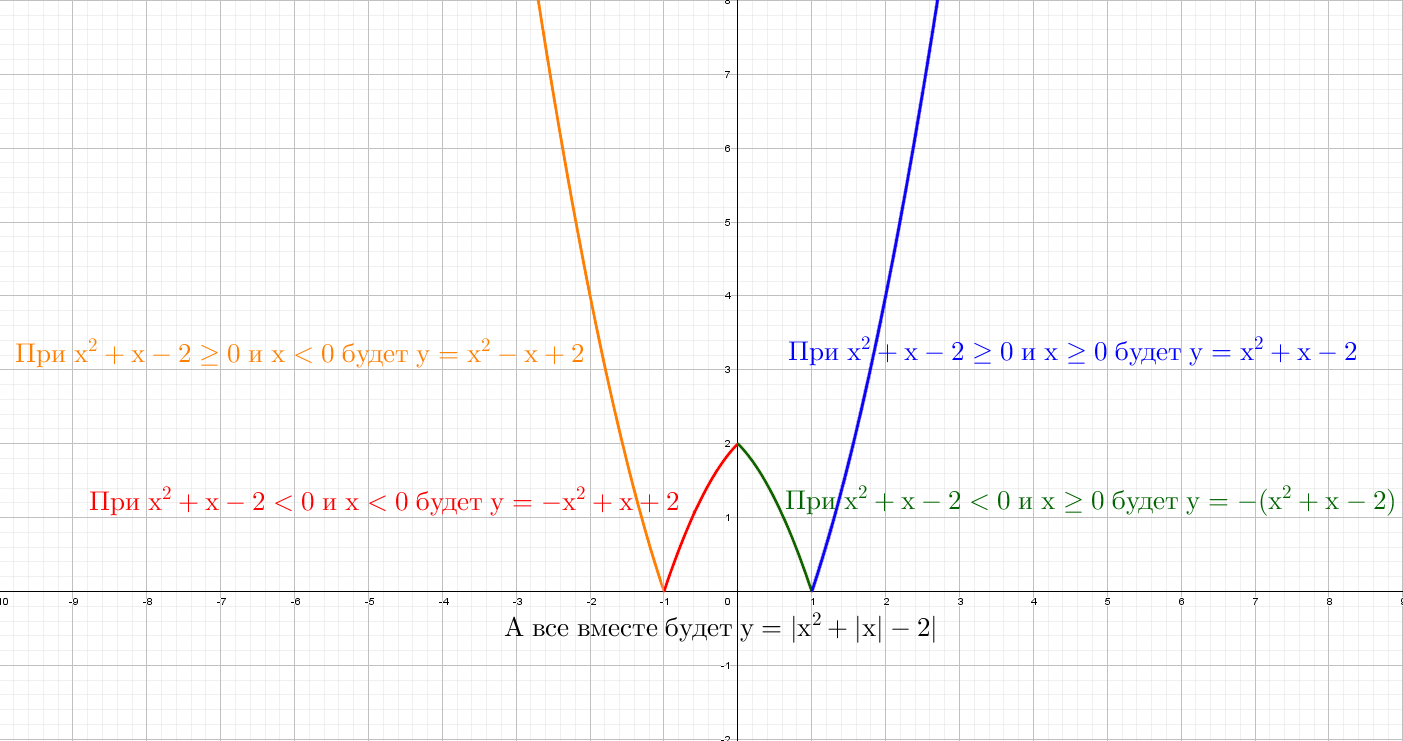
1. Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
2. Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
3. Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль .
4. Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:

• Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
• Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
• Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
• Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.

Уравнения графиков функций с модулями

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Цели:

• Найти способ раскрытия модуля, при построении
  графиков функции;
• Развить умения и навыки построения графиков
  квадратичной функции;
• Вызвать интерес у учащихся к самостоятельному и
  научному поиску.

Для достижения данной цели учащимся
предлагается решить следующие задачи:

1. Изучить литературу по теме “модуль” и
   “построения графиков квадратичной функции”;
2. Построить данные графики математическим
   способом;
3. Построить графики с помощью компьютера,
   используя программу EXCEL;
4. Сравнить результаты построения и сделать к
   каждому типу задач выводы.
5. Оформить результаты, как научно
   исследовательскую работу.

Учитель предлагает рассмотреть решение задач
типа:

Задача 1. Построить график функции у =? f(х)c , где
f(х)- квадратичная функция.

Задача 2. Построить график функции у =f(c хc ), где
f(х)- квадратичная функция.

Задача 3. Построить график функции у =f( -c хc ), где
f(х)- квадратичная функция.

Задача 4. Построить график функции у =c f(c хc )c ,
где f(х)- квадратичная функция.

Для решения данных задач необходимо

• Знать определение модуля и умение его
  раскрывать;
• Знать общие методы построение графика
  квадратичной функции;
• Рассмотреть 2-3 примера каждой задачи.
• Сравнить их с графиком функции у =f(х) , где f(х) —
  квадратичная функция.
• Сделать соответствующие выводы.

По решению данных задач рассмотреть следующие
примеры:

f(х) = c х2 -2х – 3c f(х) = х2 -2c хc – 3 f(х) = х2 +2c хc – 3 f(х) = c х2 -2c хc – 3 c f(х) = х2 -2х – 3

f(х) = c -х2 + 6х – 5c f(х) = — х2 +6c хc – 5 f(х) = -х2 -6c хc – 5 f(х) = c -х2 +6c хc – 5 c f(х) = -х2 +6х – 5

Занятие 1

Построить графики функций
математическим способом.

Цель занятия:

• Повторить теорию необходимую для построения
  графиков функций, содержащих знак модуля.
• Построить заданные графики функций.

Чтобы построить график функции необходимо
знать

1. что модуль числа не может быть отрицательным.

• Для положительного числа и нуля он равен самому
  числу, а для отрицательного — противоположному.

2. общую схему построение графика квадратичной
функции:

• нахождение координат вершины параболы;
• составление таблицы значений;
• построение графика функции.

Учащиеся дают понятие модуль и как построить
график квадратичной функции (общую схему).

• Модулем числа называют расстояние от точки,
  изображающей это число на координатной прямой,
  до начала отсчета. Возьмем два противоположных
  числа а и –а, точки изображающие их на
  координатной прямой, расположены на одинаковом
  расстоянии от начала отсчета. Для такого
  расстояния придумано специальное название –
  модуль числа а. Обозначают так:| а| . В самом деле
  расстояние от точки А(5) до нуля равно 5, а
  расстояние от точки В(-3) до нуля равно 3. Модули
  противоположных чисел равны. Раз модуль – это
  расстояние, он никогда не бывает отрицательным.
  Поэтому для положительного числа и нуля он равен
  самому числу, а для отрицательного —
  противоположному.
• Для построения графика квадратичной функции
  вершина параболы находится по формулам:

Х= -В¤ 2а; у =ах²+вх +с, затем составляется
таблица и строится график.

I. Рассмотрим построение графиков функции вида
у = c f(х)c на примерах:

а)f(х) = c х² -2х – 3c , б) f(х) = c -х² + 6х – 5c .

А) Построим график функции f(х) = c х² -2х – 3c .

1. Раскроем модуль:

c х² -2х – 3c = х² -2х – 3, если х² -2х
– 3? 0 ,

c х² -2х – 3c = — (х² -2х – 3), если х²
-2х – 3< 0

Построим график квадратичной функции у = х²
-2х – 3.

Координатами вершины параболы у=х² -2х – 3
будет точка с координатами (1;4).

Составим таблицу (*)значений для графика
функции у=х² -2х – 3

Х	-4	-3	-2	-1	0	1	2	3	4
у	21	12	5	0	-3	-4	-3	0	5

С учетом того, что при х² -2х – 3< 0 функция
задана иным графиком у = — (х² -2х – 3), таблица
будет следующей:

Х	-4	-3	-2	-1	0	1	2	3	4
у	21	12	5	0	3	4	3	0	5

По данной таблице построю график функции.

Б) Построение графика функции f(х) = c -х² + 6х
– 5c . При аналогичном рассуждении, получу график
функции .

Занятие 2

Построение графиков функции с помощью
компьютера.

Цель занятия:

• Изучить теорию построения графиков с помощью
  компьютера.
• Построить графики заданных функций с помощью
  компьютера.

Используя компьютерную программу MS Excel. Эта
программа позволила мне еще изучить изменения
графиков в зависимости от значения тех или иных
параметров. Процесс разработки моделей и их
исследование на компьютере можно разделить на
несколько основных этапов.

• Описательная информационная модель (выделяем с
  точки зрения целей проводимого исследования,
  параметры объекта, а несущественными
  параметрами пренебрегаем);
• Формализованная модель (описание
  информационной модели в программе MS Excel с помощью
  формул);
• Компьютерная модель (построение компьютерной
  модели с использованием электронных таблиц MS
  Excel);
• Компьютерный эксперимент (построение графиков
  функций);
• Анализ полученных результатов и корректировка
  исследуемой модели (в случае несоответствия
  результатов, полученных при исследовании
  информационной модели, измеряемым параметрам
  реальных объектов можно сделать вывод, что на
  предыдущих этапах построения модели были
  допущены ошибки).

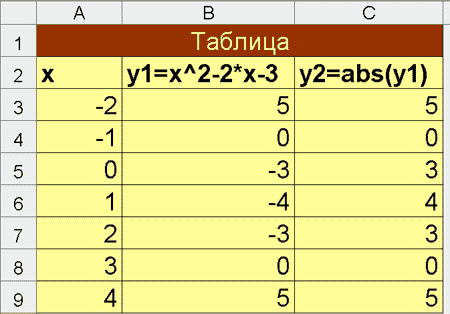
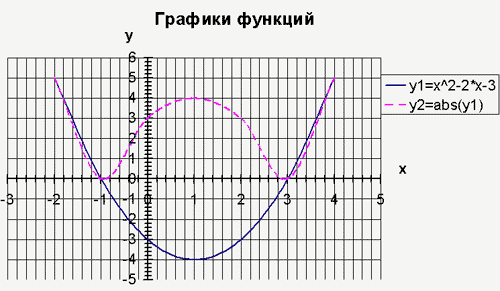
Исследуем графики функций y = f(x) и y=¦f(x) ¦, где f(x) =
x ²-2x-3 на промежутке [-2; 4]. Представим данные
функции в табличной форме

а) данные в представлены виде чисел

б) данные представлены в виде чисел и
формул

Используя мастер диаграмм, по полученным
данным строим точечную диаграмму со значениями,
соединенными сглаживающими линиями без
маркеров. Полученный результат не удовлетворяет
результатам нашего предварительного
исследования. Это хорошо видно на диаграмме.

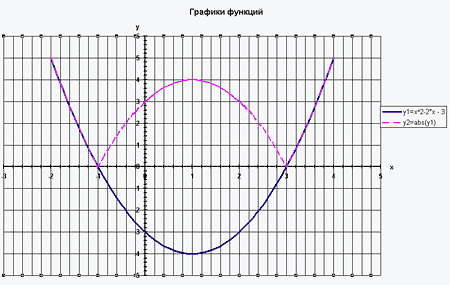
 Для уменьшения погрешности исследований
при построении графиков функций, значения
аргумента изменяю на 0,1 (шаг), в формулах для
автоматизации расчетов использую относительную,
абсолютную и смешенные адресации ячеек. (Приложение 1).
Скорректированные параметры позволяют более
точно выполнить построения графиков функций в
программе MS Excel и подтвердить правильность моих
исследований математическим путем — “на
бумаге”.

(Приложение 2)

График функции f(х) = c -х² + 6х – 5c исследую
аналогичным образом. (Приложение
3).

Занятие 3

Построение графиков

(практическое занятие)

Цель занятия:

• Отработка навыков построения графиков
  квадратичной функции двумя способами.

Решить задачи типа 2,3,4. на предложенных
примерах (аналогично занятиям 1и 2)

Приведу некоторые решения:

а)f(х) =х² -2c хc – 3,

б)f(х) =-х² + 6c х c – 5.

1. Если х? 0, то c хc =х, тогда получим f(х) =х² -2х
– 3,

если х< 0, то c хc = — х, тогда получим

2. Построю графики функций f(х) =х² -2х – 3, f(х)
=х² +2х – 3 в одной системе координат. Точки с
координатами (1;-4) и (-1;-4) координаты вершин
парабол соответственно.

Составлю таблицу значений (**) для построение
графика функции

f(х) =х² +2х– 3.

Х	-4	-3	-2	-1	0	1	2	3	4
у	5	0	-3	-4	-3	0	5	12	21

Воспользовавшись таблицей (*) и (**) Искомый
график функции будет часть параболы f(х) =х²
-2х – 3 при х> 0 и часть параболы f(х) =х²
+2х – 3 при х< 0.

(Приложение 4)

б) Построение графика функции f(х) =-х² + 6c хc
– 5. При аналогичном рассуждении, построю график
функции и проверю правильность построения
используя компьютер. (Приложение
5).

Решение третий тип задач , на примерах функций:

а) f(х) = х² +2c хc – 3;

б) f(х) = -х² -6c хc – 5.

Чтобы построить график функции f(х) = х² +2c
хc – 3 опять использую:

1. Раскрытие знака модуль.

Если х>0,то получим f(х) =х² +2х – 3,

Если х< 0,то получим f(х) =х² -2х – 3.

2. Построю график функции, воспользовавщися
таблицами (*) и (**) и с учетом, что

f(х) =х² +2х – 3, при х>0, а f (х) =х² -2х
– 3. при х< 0. Получим график функции. Исследую
построение графика в компьютерной программе.
(приложение 4).

Рассмотрю построение графика функции f(х) = -х²
-6c хc – 5 аналогично. (Приложение
5).

Для решение последней задачи я использовала
также два примера.

А)f(х) =? х² -2c хc – 3? , б) (х) = -? х² + 6c х c –
5? .

Чтобы построить данные графики функции уже
использую известные мне преобразования, построю
графики функций f(х) =х² -2c хc – 3 и f(х) =? х²
-2c хc – 3? . В результате получаю следующий график
функции. (Приложение 6).

При построении графика f(х) =-? х² + 6c х c – 5?
также использую преобразования и построю
графики функций f(х) = — х² +6c хc – 5 и f(х) =-? х²
+6c хc – 5? . (Приложение 7).

Занятия 4.

Итоговое занятие.

Цель занятия:

• Рассмотреть полученные графики функций каждого
  типа задач на рассмотренных примерах и сделать
  соответствующие выводы.

1. Результаты построенных графиков функций
первого типа позволили сделать следующий вывод:

График функции у = c f(х)c совпадает с графиком
функции у = f(х) на тех промежутках, где f(х)>0, а
на промежутках где f(х)< 0, график функции

у = c f(х)c получается из графика функции у = f(х) с
помощью симметрии относительно оси Ох.

2. Глядя, на построенные графики второго типа
замечаем:

Для построения графика функции у =f(c хc ), где f(х)-
квадратичная функция надо построить функцию у =
f(х), затем оставить только его часть, лежащую
справа от оси Оу, и отобразить эту часть
симметрично той же оси.

3. Рассматривая графики функций третьего вида
получаем следующий вывод:

Для построения графика функции у =f (- c хc ), где
f(х)- квадратичная функция надо построить функцию
у = f(х), затем оставить только его часть, лежащую
справа (слева) от оси Оу, и отобразить эту часть
симметрично той же оси.

4. Для построения графика функции у =c f(c хc )c , где
f(х)- квадратичная функция надо построить график
функции у = f(х). Тогда, используя известные
преобразования, построим у =f(c хc ) и у = c f(х)c .

Выводы:

При решении данных задач мне удалось оказать
помощь в построении графиков функций, содержащих
знак модуля, а главное убедить, что математика –
это содержательное, увлекательное и доступное
поле деятельности, дающее ученику богатую пищу
ума, связывающее его с общечеловеческой
культурой, формирующее важнейшие черты его
личности. РАССМАТРИВАЕМЫЕ ПРИЕМЫ ПОСТРОЕНИЯ
ГРАФИКОВ ФУНКЦИЙ МОЖНО ПРИМЕНИТЬ НЕ ТОЛЬКО К
КВАДРАТИЧНЫМ ФУНКЦИЯМ, НО И К ЛИНЕЙНЫМ,
ТРИГОНОМЕТРИЧЕСКИМ, ПОКАЗАТЕЛЬНЫМ И
ЛОГАРИФМИЧЕСКИМ.

Список литературы

1. “Математика”. Учебник 6 класс Н.Я. Виленкин, В.И.
   Жохов. – Изд.4 –е.- М. Издательство “Русское
   слово”, 1997г.
2. “Алгебра”. Учебник 9 класс. Ю.Н. Макарычев, Н.Г.
   Миндюк . М. Просвещение, 2004г.
3. “Математика” Еженедельная
   учебно-методическая газета. Издательский дом
   “Первое сентября”. №48, 2003г.
4. “Математика” Еженедельная
   учебно-методическая газета. Издательский дом
   “Первое сентября”. №7, 1998г.
5. Тесты и экзаменационные задания по математике.
   Учебное пособие. Е.С.Баранова, Н.В. Васильева. –
   Издательский дом “Питер”, 2005 г.
6. “Абсолютная величина”. Гайдуков И.И.. – М.:
   Просвещение, 1968.
7. “Функции и построение графиков”. Гурский И.П..-
   М.: Просвещение, 1968.
8. “Задачи повышенной трудности в курсе алгебры
   для 7-9 классов”. Кострикина Н.П.. М.: Просвещение,
   1991.

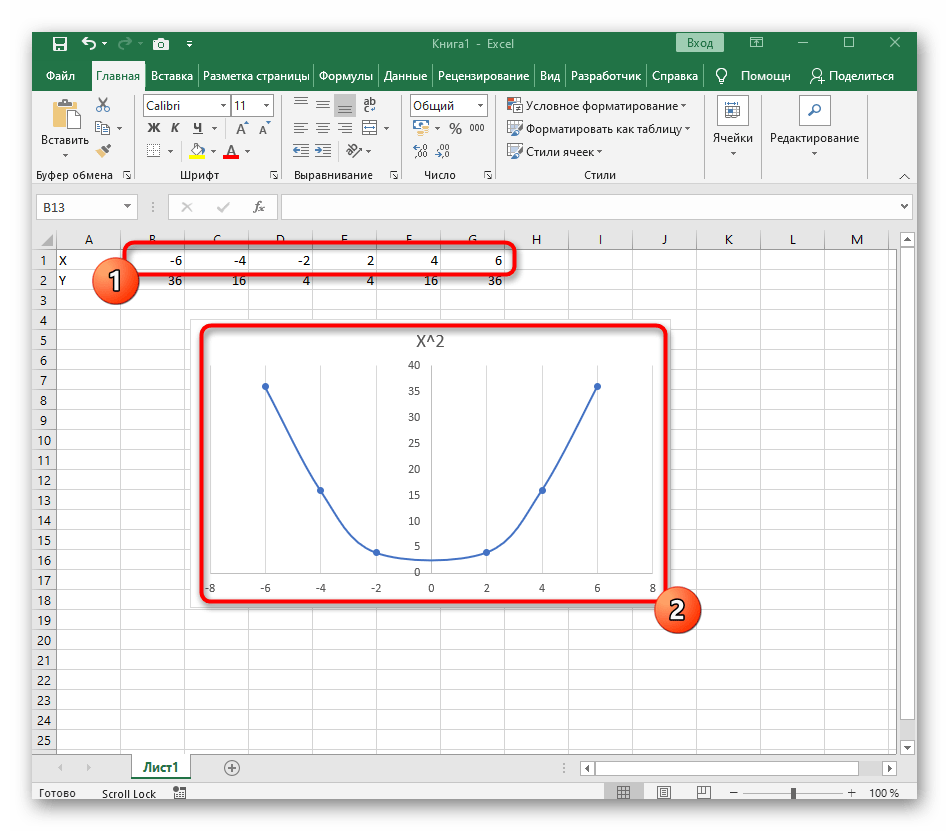
Вариант 1: График функции X^2

В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

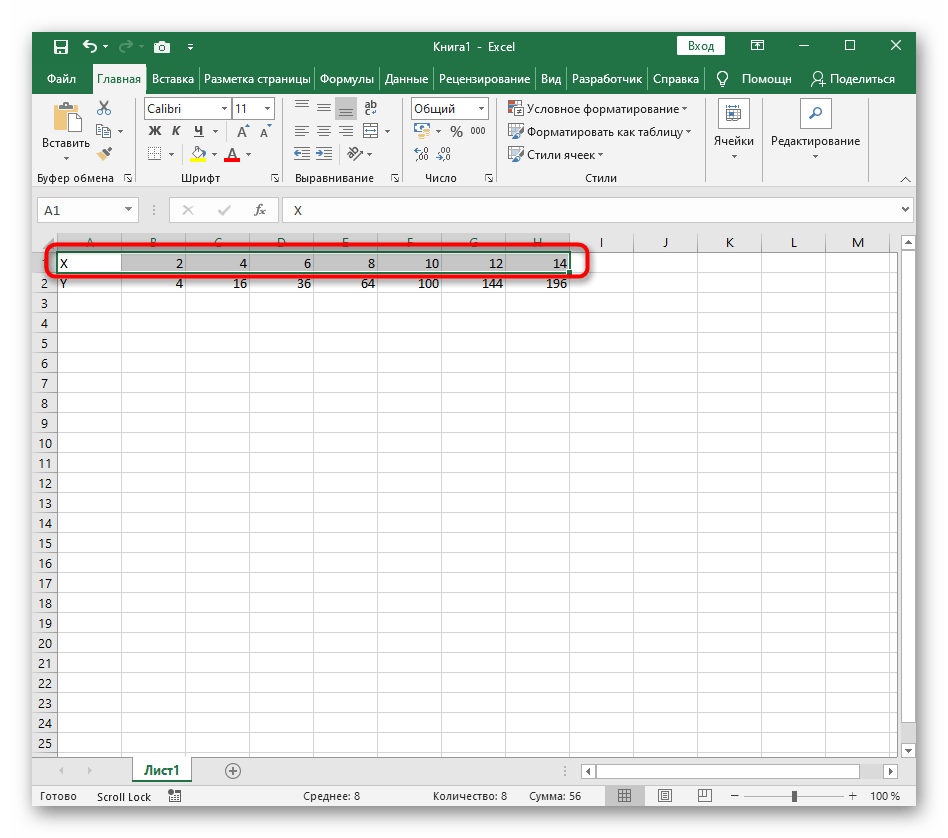
1. Создайте строку X, где укажите необходимый диапазон чисел для графика функции.



2. Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.



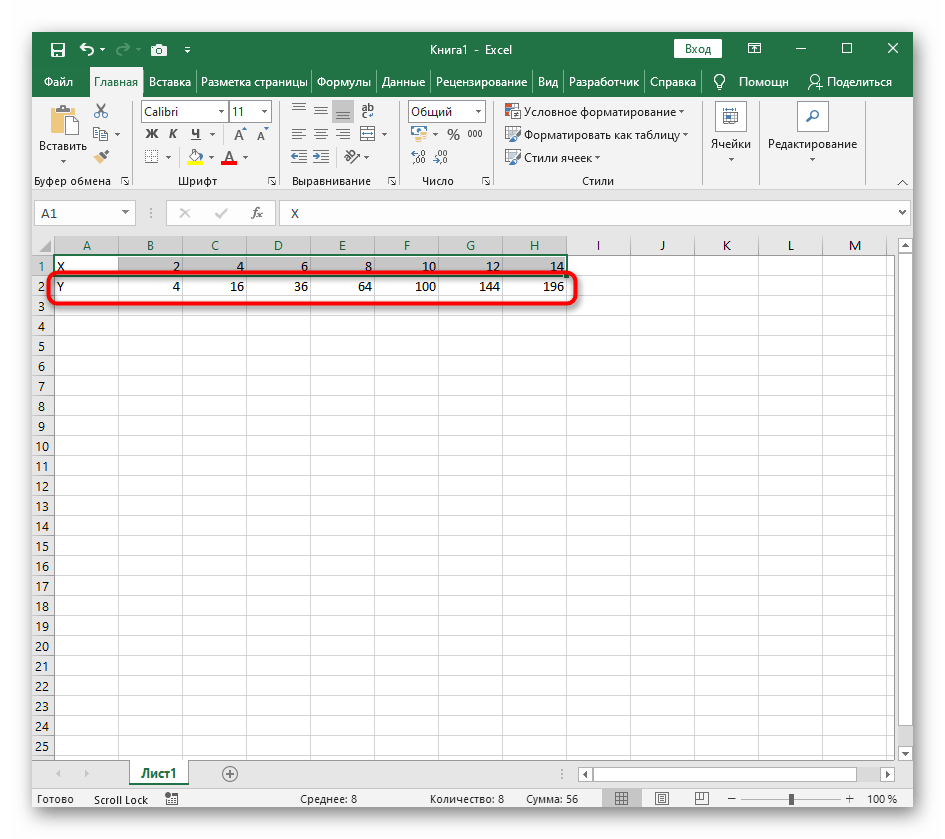
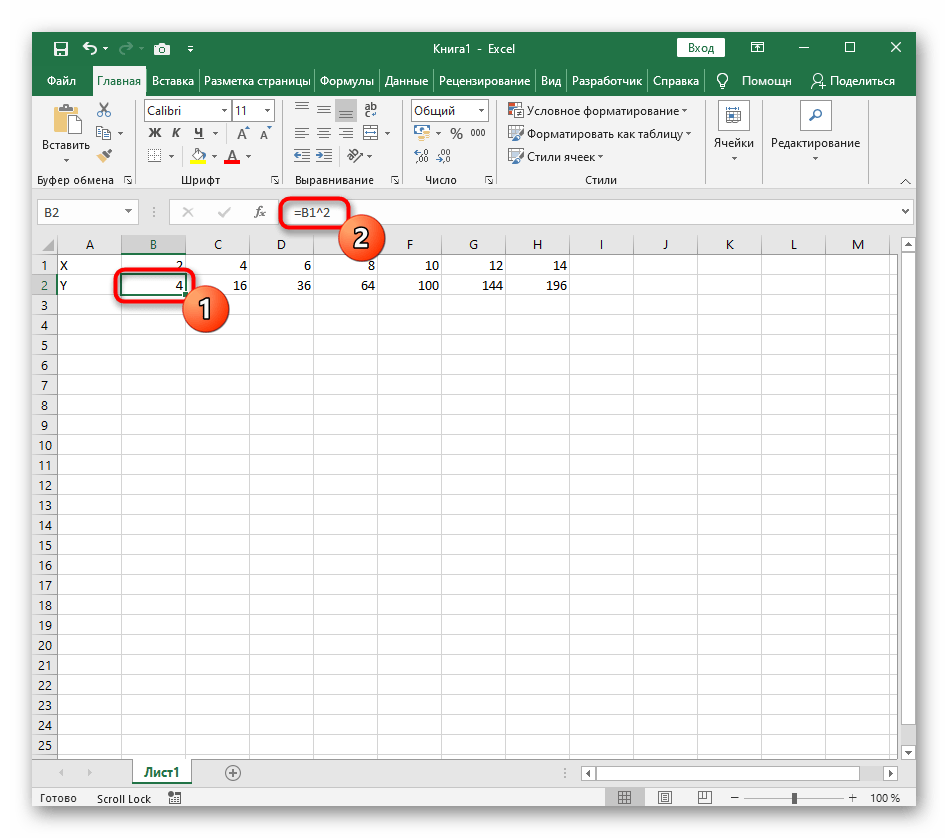
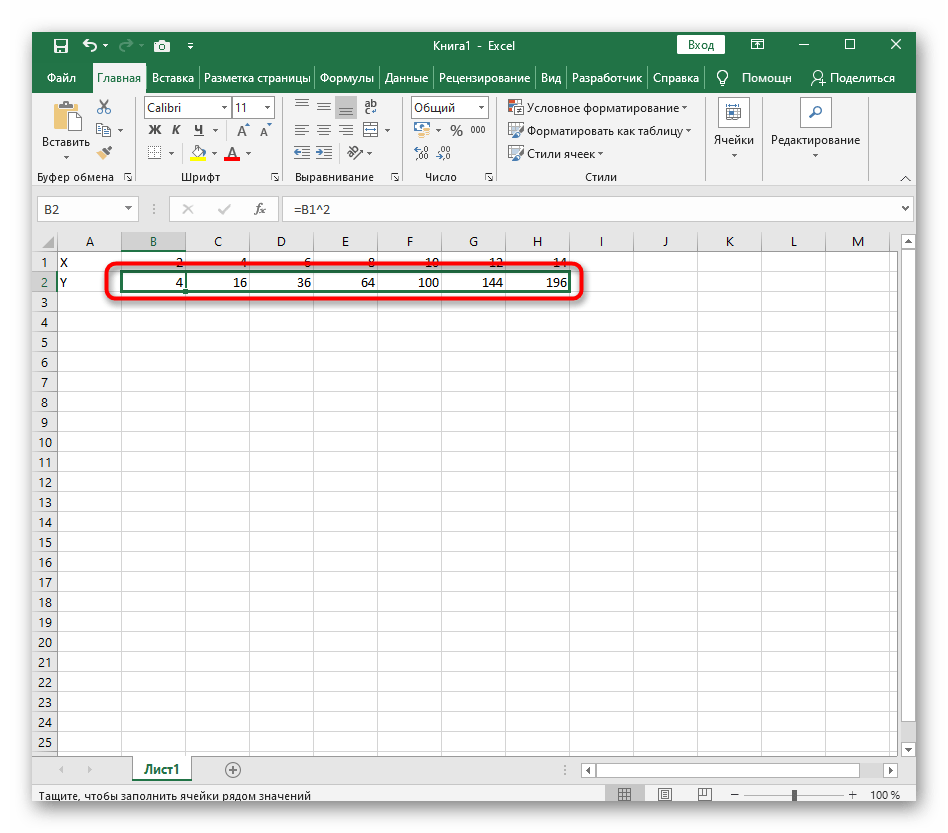
3. Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.



4. Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.



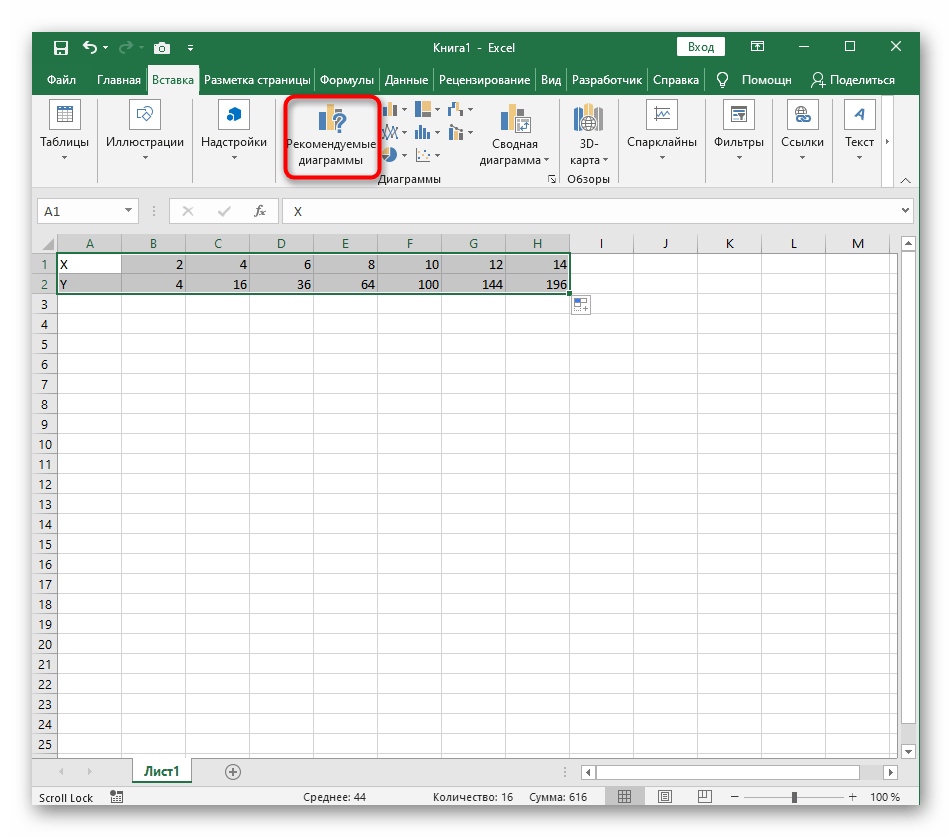
5. Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».



6. На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».



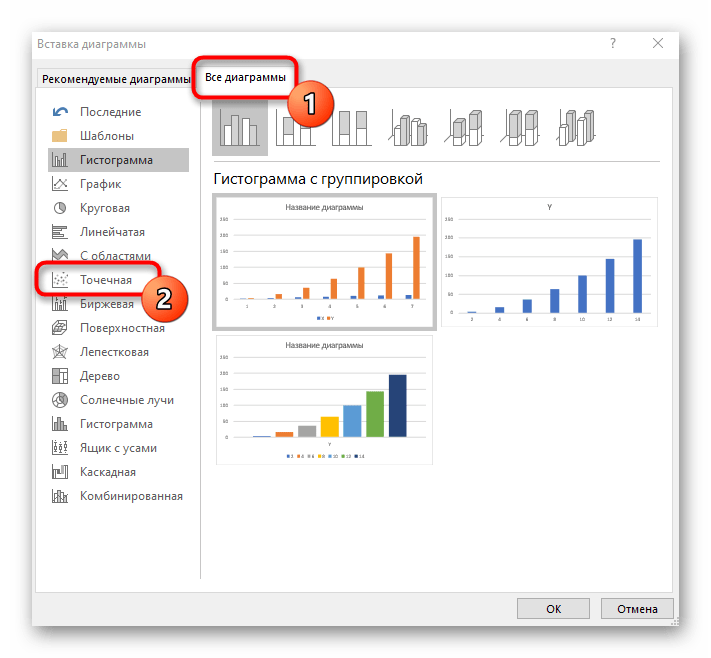
7. В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».



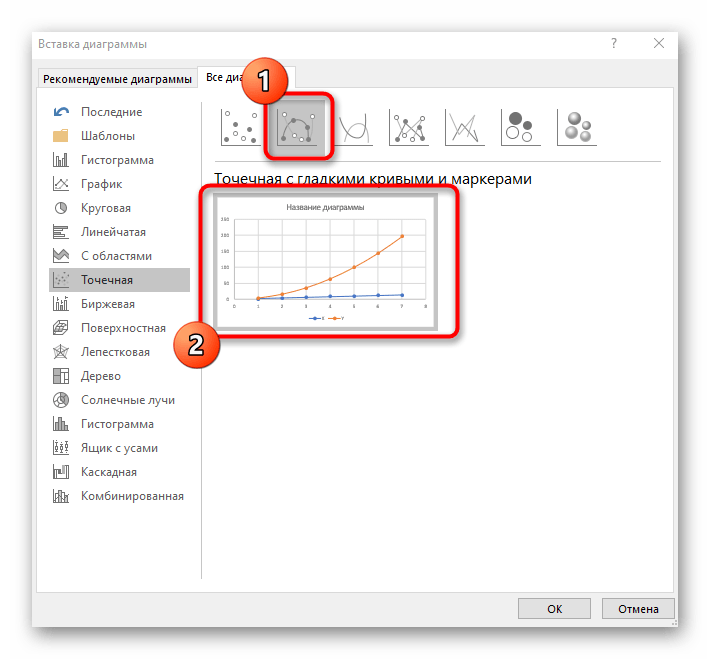
8. Подойдет вариант «Точечная с гладкими кривыми и маркерами».



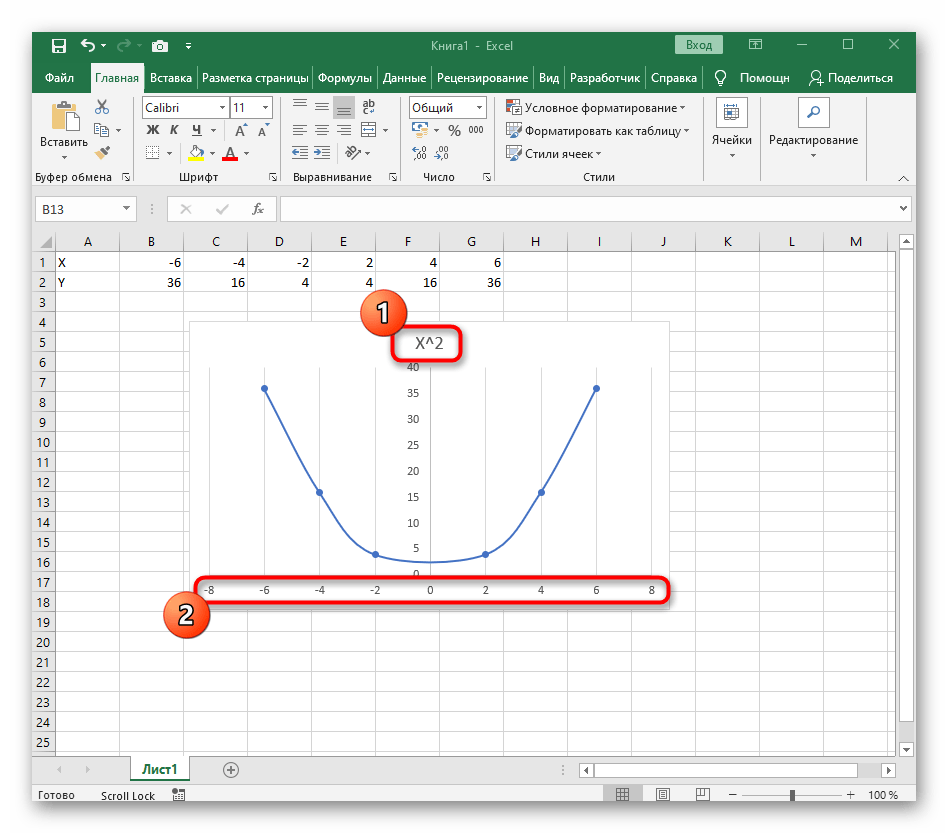
9. После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.



10. Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.



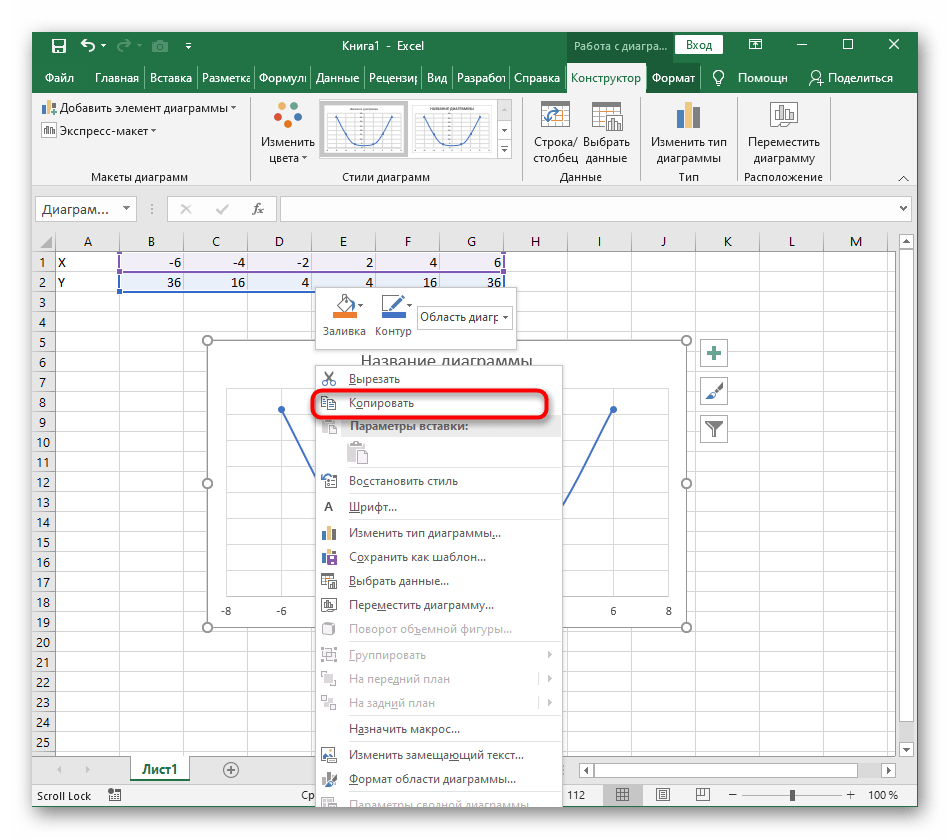
11. Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».



12. Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

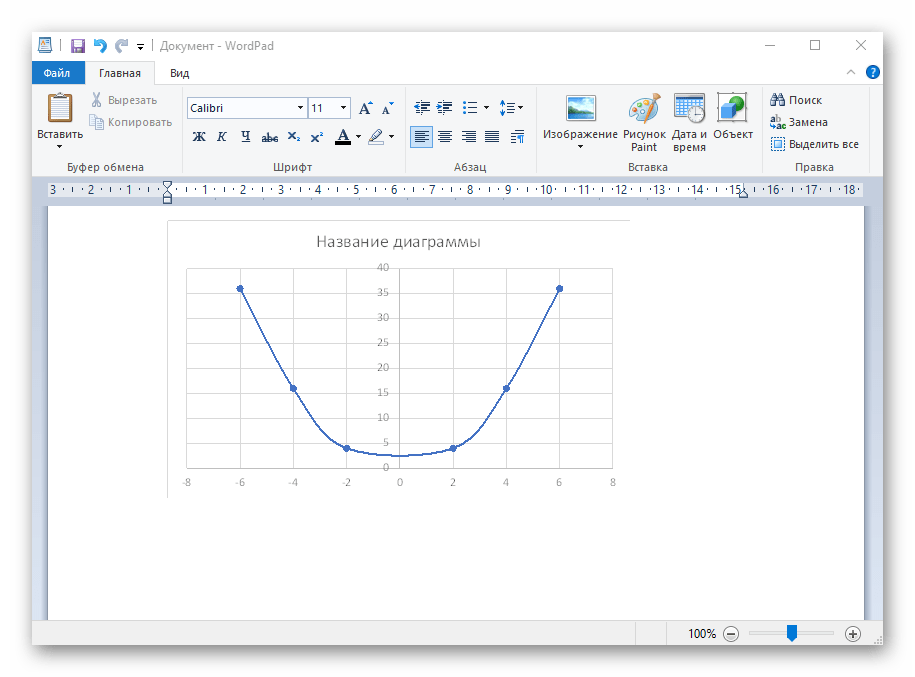
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

1. Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.



2. Создайте сразу два столбца — X и Y, куда будете записывать данные.



3. Запишите самостоятельно первые два или три значения с указанным шагом.



4. Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.



5. Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.



6. Сама функция автоматически высчитает синус заданного числа.



7. Растяните столбец точно так же, как это было показано ранее.



8. Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.



9. Выделите столбец с Y и перейдите на вкладку «Вставка».



10. Создайте стандартный график, развернув выпадающее меню.



11. График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Еще статьи по данной теме:

Помогла ли Вам статья?

ИНТЕГРИРОВАННЫЙ УРОК АЛГЕБРЫ И ИНФОРМАТИКИ В 9 КЛАССЕ

по элективному  курсу «Модули».

Тема урока: «ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ С МОДУЛЯМИ»

«libera mann ducta»

(пер. с лат. «начерчена просто от руки»)

Л. Эйлер

Цели УРОКА АЛГЕБРЫ: выработать умение построения
графиков функций с модулями.

Цели УРОКА ИНФОРМАТИКИ: повторить построение
графиков функций в электронном процессоре EXCEL.

Тип урока: интегрированный урок-закрепление
изученного материала по теме элективного курса  «Модули» «Построение графиков
функций» и теме предмета информатика «Построение графиков функций в табличном
процессоре EXCEL».

Оборудование: компьютерный класс,
интерактивная доска в комплекте с управляющим компьютером, презентация по теме
урока, раздаточный материал в виде карточек с заданиями.

Ход урока

I.                  
ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

Объявление темы урока «Построение
графиков функции с модулями» и целей урока учителями математики и информатики.
(Слайды №1 и №2).

II.               
ОСНОВНАЯ ЧАСТЬ УРОКА. Учитель математики
приводит исторические сведения о понятии «функция»: «Понятие функции – одно из
сложных в математике. Термин «функция» впервые появился в 1692 году у Готфрида
Лейбница. Наиболее близко к современному этот термин употребил в письме к
Готфриду Лейбницу через 6 лет швейцарский ученый Иоганн Бернулли. А общие
формулировки впервые встречаются у Леонарда Эйлера в 1750 году в трактате «Introduction». Он дает два различных определения функции. Вот одно из них очень
соответствует духу нашего сегодняшнего урока. «Функция, — по определению
Леонарда Эйлера, — определяется тем, что в плоскости XOY начерчена просто от руки некоторая кривая («libera mann ducta»).
(Слайд №3).

III.            
АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ.

Учитель информатики: Функцию можно
представить графически  и на компьютере с помощью электронного процессора EXCEL. Давайте повторим алгоритм построения графика функции. (Слайд №4,
используется интерактивная доска, на которой вручную  чертится график по «подсказкам»
детей). Ученики вспоминают функцию ABS, позволяющую
определить модуль числа или математического выражения.

А теперь каждый из вас построит свой график функции по
предложенным заданиям на карточках (задание 1). Один ученик (по желанию)
строит график функции на компьютере с выводом на интерактивную доску.

После выполнения задания учитель математики в ходе
коллективного обсуждения с ребятами делает выводы и выводит алгоритм построения
графиков с несколькими модулями:

1)     
график представляет ломаную линию,
количество звеньев в которой на 1 больше, чем количество модулей;

2)     
вершины ломаной  — это нули подмодульных
выражений;

3)     
для построения крайних звеньев в ломаной
требуется взять дополнительные точки.

IV. ЗАКРЕПЛЕНИЕ
МАТЕРИАЛА.

Учитель математики: А теперь давайте построим графики
функции с модулями без использования компьютера, аналитически.  Каждый из вас
выполняет задание 2 в карточках, а желающий  выходит к интерактивной доске и
строит график по своему варианту. (Слайд №5).

 V. ИГРОВОЙ МОМЕНТ. Учитель информатики: а
теперь небольшая пауза. Давайте еще раз вспомним основные математические
понятия, зашифрованные в виде ребусов. (Слайды №6, 7, 8). Первый отгадавший
зашифрованное слово выходит к доске и записывает его.

VI. ИТОГ УРОКА. Учитель математики: подводя итог нашему уроку, хочется
отметить ваше активное участие в нем, ваши неплохие навыки в построении
графиков функций с модулями как на компьютере, так и аналитическим способом,
ваше умение делать выводы, исследуя по графику функцию с модулями.