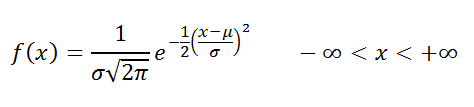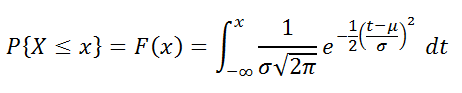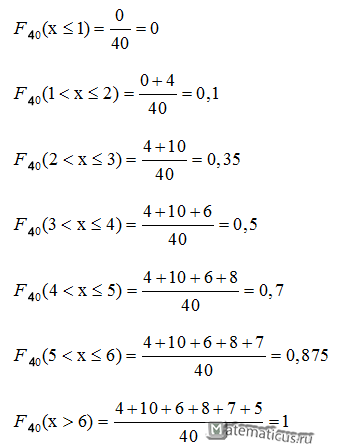Построение графика функции распределения в excel

Рассмотрим Нормальное распределение. С помощью функции

MS EXCEL

НОРМ.РАСП()

построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения

.

Нормальное распределение

(также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения

Нормального распределения

(англ.

Normal

distribution

)

во многих областях науки вытекает из

Центральной предельной теоремы

теории вероятностей.

Определение

: Случайная величина

x

распределена по

нормальному закону

, если она имеет

плотность распределения

:

СОВЕТ

: Подробнее о

Функции распределения

и

Плотности вероятности

см. статью

Функция распределения и плотность вероятности в MS EXCEL

.

Нормальное распределение

зависит от двух параметров: μ

(мю)

— является

математическим ожиданием (средним значением случайной величины)

, и σ (

сигма)

— является

стандартным отклонением

(среднеквадратичным отклонением). Параметр μ определяет положение центра

плотности вероятности

нормального распределения

, а σ — разброс относительно центра (среднего).

Примечание

: О влиянии параметров μ и σ на форму распределения изложено в статье про

Гауссову кривую

, а в

файле примера на листе Влияние параметров

можно с помощью

элементов управления Счетчик

понаблюдать за изменением формы кривой.

Нормальное распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для

Нормального распределения

имеется функция

НОРМ.РАСП()

, английское название — NORM.DIST(), которая позволяет вычислить

плотность вероятности

(см. формулу выше) и

интегральную функцию распределения

(вероятность, что случайная величина X, распределенная по

нормальному закону

, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

Вышеуказанное распределение имеет обозначение

N

(μ; σ).

Так же часто используют обозначение через

дисперсию

N

(μ; σ

²

).

Примечание

: До MS EXCEL 2010 в EXCEL была только функция

НОРМРАСП()

, которая также позволяет вычислить функцию распределения и плотность вероятности.

НОРМРАСП()

оставлена в MS EXCEL 2010 для совместимости.

Стандартное нормальное распределение

Стандартным нормальным распределением

называется

нормальное распределение

с

математическим ожиданием

μ=0 и

дисперсией

σ=1. Вышеуказанное распределение имеет обозначение

N

(0;1).

Примечание

: В литературе для случайной величины, распределенной по

стандартному

нормальному закону,

закреплено специальное обозначение z.

Любое

нормальное распределение

можно преобразовать в стандартное через замену переменной

z

=(

x

-μ)/σ

. Этот процесс преобразования называется

стандартизацией

.

Примечание

: В MS EXCEL имеется функция

НОРМАЛИЗАЦИЯ()

, которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то

нормализацией

. Формулы

=(x-μ)/σ

и

=НОРМАЛИЗАЦИЯ(х;μ;σ)

вернут одинаковый результат.

В MS EXCEL 2010 для

стандартного нормального распределения

имеется специальная функция

НОРМ.СТ.РАСП()

и ее устаревший вариант

НОРМСТРАСП()

, выполняющий аналогичные вычисления.

Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации

нормального распределения

N

(1,5; 2).

Для этого вычислим вероятность, что случайная величина, распределенная по

нормальному закону

N(1,5; 2)

, меньше или равна 2,5. Формула выглядит так:

=НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА)

=0,691462. Сделав замену переменной

z

=(2,5-1,5)/2=0,5

, запишем формулу для вычисления

Стандартного нормального распределения:

=НОРМ.СТ.РАСП(0,5; ИСТИНА)

=0,691462.

Естественно, обе формулы дают одинаковые результаты (см.

файл примера лист Пример

).

Обратите внимание, что

стандартизация

относится только к

интегральной функции распределения

(аргумент

интегральная

равен ИСТИНА), а не к

плотности вероятности

.

Примечание

: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по

стандартному

нормальному закону,

закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле

=НОРМ.СТ.РАСП(z;ИСТИНА)

. Вычисления производятся по формуле

В силу четности функции

плотности стандартного нормального

распределения f(x), а именно f(x)=f(-х), функция

стандартного нормального распределения

обладает свойством Ф(-x)=1-Ф(x).

Обратные функции

Функция

НОРМ.СТ.РАСП(x;ИСТИНА)

вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется

квантилем

стандартного

нормального распределения

.

В MS EXCEL для вычисления

квантилей

используют функцию

НОРМ.СТ.ОБР()

и

НОРМ.ОБР()

.

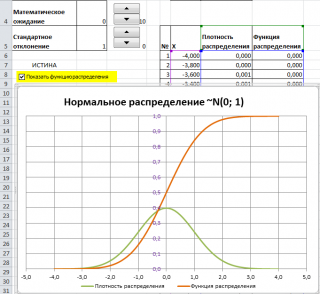
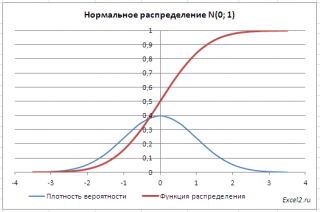
Графики функций

В

файле примера

приведены

графики плотности распределения

вероятности и

интегральной функции распределения

.

Как известно, около 68% значений, выбранных из совокупности, имеющей

нормальное распределение

, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для

стандартного нормального распределения

можно записав формулу:

=

НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)

которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от

среднего

(см.

лист График в файле примера

).

В силу четности функции

плотности стандартного нормального

распределения:

f

(

x

)=

f

(-х)

, функция

стандартного нормального распределения

обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:

=

2*НОРМ.СТ.РАСП(1;ИСТИНА)-1

Для произвольной

функции нормального распределения

N(μ; σ) аналогичные вычисления нужно производить по формуле:

=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1

Вышеуказанные расчеты вероятности требуются для

построения доверительных интервалов

.

Примечание

: Для построения

функции распределения

и

плотности вероятности

можно использовать диаграмму типа

График

или

Точечная

(со сглаженными линиями и без точек). Подробнее о построении

диаграмм

читайте статью

Основные типы диаграмм

.

Примечание

: Для удобства написания формул в

файле примера

созданы

Имена

для параметров распределения: μ и σ.

Генерация случайных чисел

С помощью надстройки

Пакет анализа

можно сгенерировать случайные числа, распределенные по

нормальному закону

.

СОВЕТ

: О надстройке

Пакет анализа

можно прочитать в статье

Надстройка Пакет анализа MS EXCEL

.

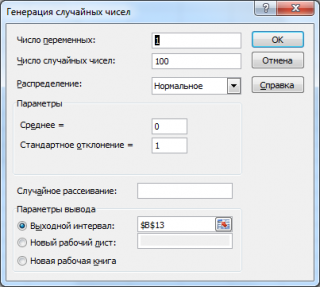
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне

Генерация

случайных чисел

установим следующие значения для каждой пары параметров:

Примечание

: Если установить опцию

Случайное рассеивание

(

Random Seed

), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции

Случайное рассеивание

может запутать. Лучше было бы ее перевести как

Номер набора со случайными числами

.

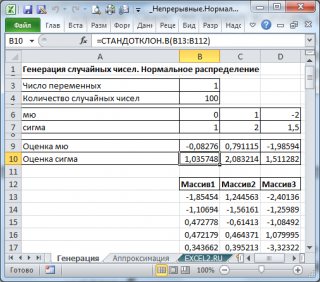
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ

.

Оценку для μ можно сделать с использованием функции

СРЗНАЧ()

, а для σ – с использованием функции

СТАНДОТКЛОН.В()

, см.

файл примера лист Генерация

.

Примечание

: Для генерирования массива чисел, распределенных по

нормальному закону

, можно использовать формулу

=НОРМ.ОБР(СЛЧИС();μ;σ)

. Функция

СЛЧИС()

генерирует

непрерывное равномерное распределение

от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.

файл примера лист Генерация

).

Задачи

Задача1

. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.

Решение1

: =

1-НОРМ.РАСП(36;41;2;ИСТИНА)

Задача2

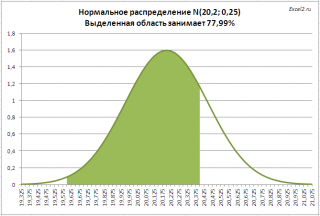
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?

Решение2

: =

НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)

На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.

Решение приведено в

файле примера лист Задачи

.

Задача3

. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?

Решение3

: =

НОРМ.ОБР(0,975; 20,20; 0,25)

=20,6899 или =

НОРМ.СТ.ОБР(0,975)*0,25+20,2

(произведена «дестандартизация», см. выше)

Задача 4

. Нахождение параметров

нормального распределения

по значениям 2-х

квантилей

(или

процентилей

). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я

процентиля

(например, 0,5-

процентиль

, т.е. медиана и 0,95-я

процентиль

). Т.к. известна

медиана

, то мы знаем

среднее

, т.е. μ. Чтобы найти

стандартное отклонение

нужно использовать

Поиск решения

. Решение приведено в

файле примера лист Задачи

.

Примечание

: До MS EXCEL 2010 в EXCEL были функции

НОРМОБР()

и

НОРМСТОБР()

, которые эквивалентны

НОРМ.ОБР()

и

НОРМ.СТ.ОБР()

.

НОРМОБР()

и

НОРМСТОБР()

оставлены в MS EXCEL 2010 и выше только для совместимости.

Линейные комбинации нормально распределенных случайных величин

Известно, что линейная комбинация нормально распределённых случайных величин

x

(

i

)

с параметрами μ

(

i

)

и σ

(

i

)

также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ

(1)+ μ(2)

и

КОРЕНЬ(σ(1)^2+ σ(2)^2).

Убедимся в этом с помощью MS EXCEL.

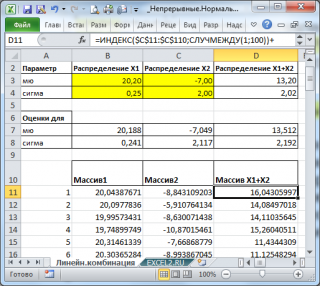
С помощью надстройки

Пакет анализа

сгенерируем 2 массива по 100 чисел с различными μ и σ.

Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.

С помощью функций

СРЗНАЧ()

и

СТАНДОТКЛОН.В()

вычислим

среднее

и

дисперсию

получившейся

выборки

и сравним их с расчетными.

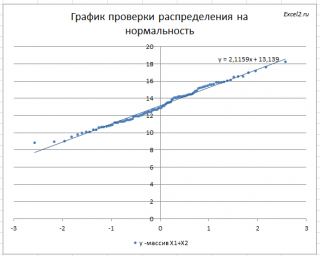
Кроме того, построим

График проверки распределения на нормальность

(

Normal

Probability

Plot

), чтобы убедиться, что наш массив соответствует выборке из

нормального распределения

.

Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой

стандартного отклонения

, а пересечение с осью y (параметр b) –

среднего

значения.

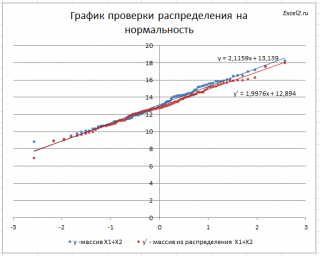
Для сравнения сгенерируем массив напрямую из распределения

N

(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)

).

Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.

В качестве примера можно провести следующую задачу.

Задача

. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.

Решение

. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и

стандартным отклонением

=КОРЕНЬ(СУММКВ(1,5;1,2))

, запишем решение =

1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)

Ответ

: 15% (см.

файл примера лист Линейн.комбинация

)

Аппроксимация Биномиального распределения Нормальным распределением

Если параметры

Биномиального распределения

B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то

Биномиальное распределение

можно аппроксимировать

Нормальным распределением

.

При значениях

λ

>15

,

Распределение Пуассона

хорошо аппроксимируется

Нормальным распределением

с параметрами: μ

=λ

, σ

²

=

λ

.

Подробнее о связи этих распределений, можно прочитать в статье

Взаимосвязь некоторых распределений друг с другом в MS EXCEL

. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ

: О других распределениях MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

2.1.2. Эмпирическая функция распределения

Это статистический аналог функции распределения из теорвера. Данная функция определяется, как отношение:
, где – количество вариант СТРОГО МЕНЬШИХ, чем ,
при этом «икс» «пробегает» все значения от «минус» до «плюс» бесконечности.

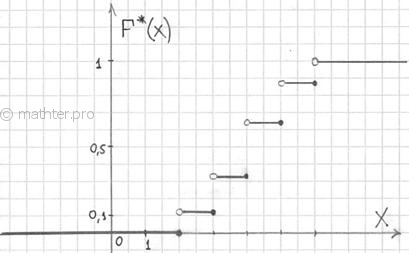
Построим эмпирическую функцию распределения для нашей задачи. Чтобы было нагляднее, отложу варианты и их количество на числовой оси:

На интервале – по той причине, что левее ЛЮБОЙ точки этого интервала вариант нет. Кроме того, функция равна нулю ещё и в точке . Почему? Потому, что значение определяет количество вариант (см. определение), которые СТРОГО меньше двух, а это количество равно нулю.

На промежутке – и опять обратите внимание, что значение не учитывает рабочих 3-го разряда, т.к. речь идёт о вариантах, которые СТРОГО меньше трёх (по определению).

На промежутке – и далее процесс продолжается по принципу накопления частот:
– если , то ;
– если , то ;
– и, наконец, если , то – и в самом деле, для ЛЮБОГО «икс» из интервала ВСЕ частоты расположены СТРОГО левее этого значения «икс» (см. чертёж выше).

Накопленные относительные частоты удобно заносить в отдельный столбец таблицы, при этом алгоритм вычислений очень прост: сначала сносим слева частоту (красная стрелка), и каждое следующее значение получаем как сумму предыдущего и относительной частоты из текущего левого столбца (зелёные обозначения):

Вот ещё, кстати, один довод за вертикальную ориентацию данных – справа по надобности можно приписывать дополнительные столбцы.

Построенную функцию принято записывать в кусочном виде:

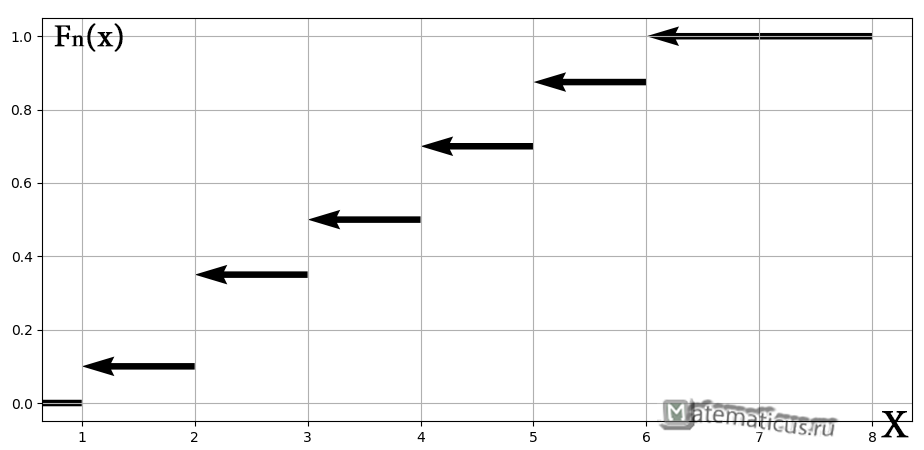
а её график представляет собой ступенчатую фигуру:

Эмпирическая функция распределения не убывает и принимает значения лишь из промежутка , и если у вас вдруг получится что-то не так, то ищите ошибку.

Теперь смотрим видео, о том, как построить эту функцию в Экселе (Ютуб).

И, конечно, вспомним основной метод математической статистики. Эмпирическая функция распределения строится по выборке и приближает теоретическую функцию распределения . Легко догадаться, что последняя появляется в результате исследования всей генеральной совокупности, но если рабочих в цехе ещё пересчитать можно, то звёзды на небе – уже вряд ли. Вот поэтому и важнА функция эмпирическая, и ещё важнее, чтобы выборка была репрезентативна, дабы приближение было хорошим.

Миниатюрное задание для закрепления материала:

Пример 5

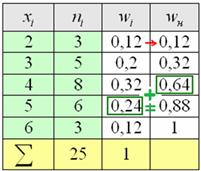
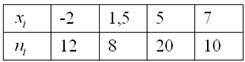
Дано статистическое распределение совокупности:

Составить эмпирическую функцию распределения, выполнить чертёж

Решаем самостоятельно – все числа уже в Экселе! Свериться с образцом можно в конце книги. По поводу красоты чертежа сильно не запаривайтесь, главное, чтобы было правильно – этого обычно достаточно для зачёта.

Из таблицы n=40, т.е.
n=4+10+6+8+7+5=40
Вычислим функцию распределения выборки

Эмпирическая функция распределения имеет вид

Построим график кусочно-постоянной эмпирической функции распределения

таким образом, по данным выборки можно приближенно построить функцию для неизвестной функции выборки.

2 комментария

У вас опечатка, где вы написали n=30, n=4+10+6+8+7+5=30 и F_30, так как n=40.

Построить эмпирическое распределение результатов тестирования в баллах для следующей выборки: 69, 85, 78, 85, 83, 81, 95, 88, 97, 92, 74, 83, 89, 77, 93.

В ячейку А1 введите слова Результаты, в диапазон А2:А16 – результаты тестирования.

Выберите ширину интервала 5 баллов. Тогда при крайних результатах 69 и 97 баллов, получится 7 интервалов. В ячейку С1 введите название интервалов Границы. В диапазон С2:С8 введите граничные значения интервалов: 70, 75, 80, 85, 90, 95, 100.

Введите заголовки создаваемой таблицы: в ячейку D1 – Абсолютные частоты, в ячейку Е1 – Относительные частоты, в F1 – Накопленные частоты.

Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек D2:D8, вызовите Мастер функций, категория – Статистические, функция – Частота, в поле Массив данных введите диапазон данных тестирования А2:А16, в поле Массив интервалов введите диапазон интервалов С2:С8, нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце D2:D8 появится массив абсолютных частот.

В ячейке D9 найдите общее количество результатов тестирования, с помощью Автосумма.

Заполните столбец относительных частот. В ячейку Е2 введите формулу =$D2/$D$9 .

Протягиванием скопируйте полученное значение в диапазон Е3:Е8. Получим массив относительных частот.

Заполните столбец накопленных частот. В ячейку F2 скопируйте значение относительной частоты из ячейки Е2. В ячейку F3 введите формулу =F2+E3. Протягиванием скопируйте полученное значение в диапазон F4:F8. Получим массив накопленных частот.

В результате получим таблицу, представленную на рисунке 1.

Пусть Nх — число наблюдений, при которых значение при­знака Х меньше Х. При объеме выборки, равном П, относитель­ная частота события Х XK.

Сама же функция F*(X) служит для оценки теоретической функции распределения F(X) генеральной совокупности.

Пример 3. Построить эмпирическую функцию по заданному распределению выборки:

Решение. Находим объем выборки: П = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F*(X) = 0 при Х ≤ 2. Значение Х 6. Напишем формулу искомой эмпирической функции:

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала, например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку такого измерения, необходимо увеличить число возможных ответов на конкретный критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим этот параметр через х. Тогда в процессе ответа на вопрос величина х примет дискретное значение х, принадлежащее определенному интервалу значений. Поставим в соответствие каждому из ответов определенное числовое значение параметра х (см. табл. 1).

Рассмотренные в лабораторной работе 2 распределения вероятностей СВ
опираются на знание закона распределения СВ. Для практических задач такое
знание – редкость. Здесь закон распределения обычно неизвестен, или известен с
точностью до некоторых неиз­вестных параметров. В частности, невозможно
рассчитать точное значение соот­ветствующих вероятностей, так как нельзя
определить количество общих и благо­приятных исходов. Поэтому вводится статистическое
определение вероятности. По этому определению вероятность равна отношению
числа испытаний, в ко­торых событие произошло, к общему числу произведенных
испытаний. Такая вероятность называется статистической частотой.

Связь
между эмпирической функцией распределения и функцией распределения
(теоретической функцией распределения) такая же, как связь между частотой со­бытия
и его вероятностью.

Для
построения выборочной функции распределения весь диапазон изменения случайной
величины X (выборки)
разбивают на ряд интервалов (карманов) одинаковой ширины. Число интервалов
обычно выбирают не менее 3 и не более 15. Затем определяют число значений
случайной величины X, попавших
в каждый интервал (абсолютная частота, частота интервалов). 

Частота интервалов – число, показывающее сколько раз значения,
относящиеся к каждому интервалу группировки, встречаются в выборке. Поделив эти
чис­ла на общее количество наблюдений (n), находят относительную частоту (частость) попадания
случайной величины X в заданные
интервалы.

По
найденным относительным час­тотам строят гистограммы выборочных функций
распределения. Гистограмма распределения частот – это графическое
представление выборки, где по оси абсцисс (ОХ) отложены величины интервалов, а
по оси ординат (ОУ) – величины частот, попадающих в данный классовый интервал.
При увеличении до бесконечности размера выборки выборочные функции
распределения превращаются в теоретические: гистограмма превращается в график
плотности распределения.

Накопленная частота интервалов – это число, полученное
последовательным суммированием частот в направлении от первого интервала к
последнему, до того  интервала
включительно, для которого определяется накопленная частота.

В Excel для построения выборочных функций распределения
используются спе­циальная функция ЧАСТОТА
и процедура Гистограмма из пакета анализа.

Функция ЧАСТОТА (массив_данных,
двоичный_массив) вычисляет частоты появления случайной величины в интер­валах
значений и выводит их как массив цифр, где

•     
массив_данных
— это массив или ссылка на
множество данных, для которых
вычисляются частоты;

•     
двоичный_массив
— это массив интервалов, по
ко­торым группируются значения выборки.

Процедура
Гистограмма из Пакета анализа выводит
результаты выборочного распределения в виде таблицы и графика. Параметры диалогового окна Гистограмма:

•     
Входной диапазон — диапазон исследуемых данных
(выборка);

•     
Интервал карманов — диа­пазон ячеек или набор граничных
значений, определяющих выбранные интервалы (карманы). Эти значения должны быть
введены в воз­растающем порядке. Если
диапазон карманов не был введен, то набор интерва­лов, равномерно распределенных между минимальным и
максимальным зна­чениями данных, будет создан
автоматически.

•     
выходной диапазон предназначен для ввода ссылки на левую верхнюю ячейку выходного диапазона.

•     
переключатель
Интегральный процент позволяет установить режим включения в
гистограмму гра­фика интегральных
процентов.

•     
переключатель
Вывод графика позволяет установить режим автоматическо­го создания встроенной диаграммы на листе, содержащем
выходной диапа­зон.

Пример 1. Построить эмпирическое распределение веса
студентов в килограм­мах для следующей
выборки: 64, 57, 63, 62, 58, 61, 63, 70, 60, 61, 65, 62, 62, 40, 64, 61, 59, 59, 63, 61.

Решение

1.  В ячейку А1 введите слово Наблюдения,
а в диапазон А2:А21 — значения веса
студентов (см. рис. 1).

2.        
В
ячейку В1 введите названия интервалов Вес, кг. В диапазон В2:В8 введите
граничные значения ин­тервалов (40, 45,
50, 55, 60, 65, 70).

3.        
Введите
заголовки создаваемой таблицы: в ячейки С1 — Абсолютные час­тоты, в ячейки D1 — Относительные
частоты, в ячейки E1 — Накоплен­ные частоты.(см. рис. 1).

4.        
С
помощью функции Частота заполните столбец абсолютных частот, для этого
выделите блок ячеек С2:С8. С
па­нели инструментов Стандартная
вызовите Мастер функций (кнопка fx). В появив­шемся диалоговом окне
выберите категорию Статистические и функцию
ЧАСТОТА, после чего нажмите кнопку ОК. Указателем мыши в рабочее поле Массив_данных
введите диапазон данных наблюдений (А2:А8). В рабочее поле Двоичный_массив
мышью введите диапазон интервалов (В2:В8). Слева на клавиатуре последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце C должен появиться мас­сив абсолютных частот (см. рис.1).

5.        
В
ячейке C9 найдите общее количество
наблюдений. Активизируйте ячейку С9, на
панели инструментов Стандартная нажмите кнопку Ав­тосумма.
Убедитесь, что диапазон суммирования указан правильно и нажмите клавишу Enter.

6.        
Заполните столбец относительных частот. В ячейку введите формулу
для вычисления относительной частоты: =C2/$C$9.
Нажмите клавишу Enter. Протягиванием (за правый
нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон и получите массив относительных частот.

7.        
Заполните
столбец накопленных частот. В ячейку D2 скопируйте значение от­носительной
частоты из ячейки E2. В ячейку D3 введите формулу: =E2+D3. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу
в диапазон D3:D8. Получим массив накопленных
частот.

                     Рис. 1. Результат вычислений из
примера 1

8.   
Постройте диаграмму относительных и накопленных частот. Щелчком ука­зателя
мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите закладку Нестандартные
и тип диаг­раммы График/гистограмма. После 
редактирования диаграмма будет иметь такой вид, как на рис. 2.

Рис. 2
Диаграмма относительных и накопленных частот из примера 1

Задания для самостоятельной работы

1. Для данных из примера 1 построить выборочные функции распределения, воспользовавшись процедурой Гистограмма из пакета Анализа.

2.  Построить выборочные функции распределения
(относительные и накопленные частоты) для роста
в см. 20 студентов: 181, 169, 178, 178, 171, 179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181,
183, 172, 176.

3. Найдите распределение по абсолютным частотам для
следующих результатов тестирования в
баллах: 79, 85, 78, 85, 83, 81, 95, 88, 97, 85 (используйте границы интервалов 70, 80, 90).

4. Рассмотрим любой из критериев оценки качеств педагога-профессионала,
например, «успешное решение задач обучения и воспитания». Ответ на этот вопрос
анкеты типа «да», «нет» достаточно груб. Чтобы уменьшить относительную ошибку
такого измерения, необходимо увеличить число возможных ответов на конкретный
критериальный вопрос. В табл. 1 представлены возможные варианты ответов.

Обозначим 
этот параметр через х. Тогда в процессе ответа на вопрос величина х
примет дискретное значение х, принадлежащее определенному интервалу значений.
Поставим в соответствие каждому из ответов определенное числовое значение
параметра х (см. табл. 1).

Табл. 1 Критериальный вопрос: успешное решение задач обучения и воспитания

При проведении анкетирования в каждой отдельной
анкете параметр х принимает случайное значение, но только в пределах числового
интервала от 0,1 до 1.

Тогда в результате измерений мы получаем
неранжированный ряд случайных значений (см. табл. 2).

Таблица 2.
Результаты опроса ста учителей

Сгруппируйте полученную выборку, рассчитайте среднее
значение выборки, стандартное отклонение, абсолютную и относительную частоту
появления параметра, а также постройте график плотности вероятности f(x)=

где

W(x) – относительная частота наступления события;

          — стандартное
отклонение;

          =3,14.

Постройте график функции f(x) и сравните его с
нормальным распределением Гаусса.

Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (п. 3), затем в следующей ячейке ниже — к полученной сумме и т.д. Так постепенно доходим до максимального значения. Вот мы и построили интервалы карманов в виде столбца значений. Интервалом считается следующий диапазон : (i-1; i] или iСкачать бесплатно видеокурc по Excel

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Поделиться ссылкой:

Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.

Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.

Характеристики нормального распределения

Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.

Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.

Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.

Создание массива с нормальным распределением

Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:

=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)

Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.

Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.

Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.

Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:

=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)

Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.

Построение графика нормального распределения

Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:

=ЕСЛИ(A12;B11+$B$6; «»)

В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.

Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.

Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.

Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.

График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.

Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.

Имеются следующие данные о количестве выпавших осадков:

Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):

Выбираем «Гистограмма»:

Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:

После нажатия ОК получаем такой график с таблицей:

В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.

Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.

Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:

Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.

Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».

Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.

Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:

Вычислим относительные частоты (как в предыдущем способе).

Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».

Частота распределения заданных значений:

Круговые диаграммы для иллюстрации распределения

С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.

С помощью любой круговой диаграммы можно показать распределение в том случае, если

• имеется только один ряд данных;
• все значения положительные;
• практически все значения выше нуля;
• не более семи категорий;
• каждая категория соответствует сегменту круга.

На основании имеющихся данных о количестве осадков построим круговую диаграмму.

Доля «каждого месяца» в общем количестве осадков за год:

Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:

Получили количество выпавших осадков в процентном выражении по сезонам.

В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.

Уровень сложности: продвинутый.

На следующем рисунке показано, как выглядит готовая динамическая гистограмма:

Что такое гистограмма или график распределения частот?

Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.

В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.

На какие вопросы отвечает гистограмма распределения?

Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.

В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.

«Неужели наше мероприятие не интересно гражданам в возрасте от 20 до 29 лет?»

Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:

Динамическая гистограмма

После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.

Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!

Как это работает?

Краткий ответ: Формулы, динамические именованные диапазоны, элемент управления «Полоса прокрутки» в сочетании с гистограммой.

Формулы

Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.

Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.

Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.

=ЧАСТОТА(tblData;C13:C22)
=FREQUENCY(tblData,C13:C22)

Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.

Динамический именованный диапазон

В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.

Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).

Элемент управления «Полоса прокрутки»

Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).

На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.

Гистограмма

График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.

Есть вопросы?

Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.

Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.

Более простой вариант гистограммы можно создать, используя сводные таблицы.

Пишите в комментариях любые вопросы и предложения. Спасибо!

Урок подготовлен для Вас командой сайта office-guru.ru
Источник: /> Перевел: Антон Андронов

Правила перепечаткиЕще больше уроков по Microsoft Excel

Оцените качество статьи. Нам важно ваше мнение:

•