Построение градуировочного графика в excel для спектрофотометра - Word и Excel

Сразу скажу могу ошибаться. Корень из r2= корреляция

Справка из Excel функции ЛИНЕЙН

Пример 4. Использование F-статистики и r2-статистики

В предыдущем примере коэффициент детерминированности r2 равен 0,99675 (см. ячейку A17 в результатах функции ЛИНЕЙН), что указывает на сильную зависимость между независимыми переменными и продажной ценой. Можно использовать F-статистику, чтобы определить, является ли этот результат (с таким высоким значением r2) случайным.

Предположим, что на самом деле взаимосвязи между переменными не существует, просто статистический анализ вывел сильную взаимозависимость по взятой равномерной выборке 11 зданий. Величина «Альфа» используется для обозначения вероятности ошибочного вывода о существовании сильная взаимозависимости.

В выходных данных функции ЛИНЕЙН величины F и df используются для оценки вероятности случайного получения наибольшего значения F. Величину F можно сравнить с критическими значениями в публикуемых таблицах F-распределения, либо для вычисления возможности случайного получения наибольшего значения F можно использовать функцию Microsoft Excel FРАСП. Соответствующее F-распределение имеет степени свободы v1 и v2. Если величина n представляет количество точек данных и аргумент конст имеет значение ИСТИНА или опущен, то v1 = n – df – 1 и v2 = df. (При конст = ЛОЖЬ v1 = n – df и v2 = df). Функция FРАСП — с синтаксисом FРАСП(F,v1,v2) — возвращает вероятность случайного получения наибольшего значения F. В примере 4 df = 6 (ячейка B18), а F = 459,753674 (ячейка A18).

Предположим, что значение «Альфа» равно 0,05, v1 = 11 – 6 – 1 = 4 и v2 = 6, а критический уровень F равен 4,53. Поскольку значение F = 459,753674 намного больше 4,53, вероятность случайного получения такого большого значения F исключительно мала (при Альфа = 0,05 гипотеза об отсутствии связи между аргументами известные_значения_y и известные_значения_x отвергается, если значение F превышает критический уровень 4,53). Использование функции Microsoft Excel FРАСП дает возможность вычислять вероятность случайного получения больших значений F. Значение вероятности FРАСП(459,753674; 4; 6) = 1,37E-7 чрезвычайно мало. Из этого можно заключить через нахождение критического уровня F в таблице или использование функции Microsoft Excel FРАСП, что уравнением регрессии можно воспользоваться для предсказания оценочной стоимости зданий под офис в данном районе. Следует учесть, что использование правильных значений v1 и v2, вычисление которых показано в предыдущем абзаце, является критически важным.

По мне так пять точек и 0,95 достаточно. Я так понимаю такие расчёты в нашей стране вряд ли кто производит.

Источник

Как построить график в Excel по данным таблицы

При работе в Excel табличных данных часто не достаточно для наглядности информации. Для повышения информативности ваших данных советуем использовать графики и диаграммы в Эксель. В этой статье рассмотрим пример того, как построить график в Excel по данным таблицы.

Кликните по кнопке ниже и мы пришлем Вам Excel файл с примером графика, построенного по данным таблицы на E-mail:

Видеоурок

Как построить простой график в Excel

Представим, что у нас есть таблица с ежемесячными данными среднего курса Доллара в течении года:

На основе этих данных нам нужно нарисовать график. Для этого нам потребуется:

Выделить данные таблицы, включая даты и курсы валют левой клавишей мыши:

На панели инструментов перейти во вкладку “Вставка” и в разделе “Диаграммы” выбрать “График”:

Во всплывающем окне выбрать подходящий стиль графика. В нашем случае, мы выбираем график с маркерами:

Система построила нам график:

Как построить график в Excel на основе данных таблицы с двумя осями

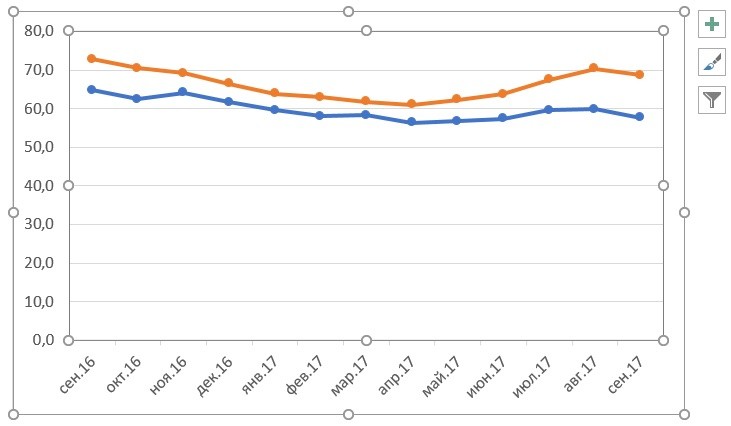
Представим, что у нас есть данные не только курса Доллара, но и Евро, которые мы хотим уместить на одном графике:

Для добавления данных курса Евро на наш график необходимо сделать следующее:

Выделить созданный нами график в Excel левой клавишей мыши и перейти на вкладку “Конструктор” на панели инструментов и нажать “Выбрать данные”:

Изменить диапазон данных для созданного графика. Вы можете поменять значения в ручную или выделить область ячеек зажав левую клавишу мыши:

Готово. График для курсов валют Евро и Доллара построен:

Если вы хотите отразить данные графика в разных форматах по двум осям X и Y, то для этого нужно:

Перейти в раздел “Конструктор” на панели инструментов и выбрать пункт “Изменить тип диаграммы”:

Перейти в раздел “Комбинированная” и для каждой оси в разделе “Тип диаграммы” выбрать подходящий тип отображения данных:

Нажать “ОК”

Ниже мы рассмотрим как улучшить информативность полученных графиков.

Как добавить название в график Эксель

На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:

Нажать на графике левой клавишей мыши;
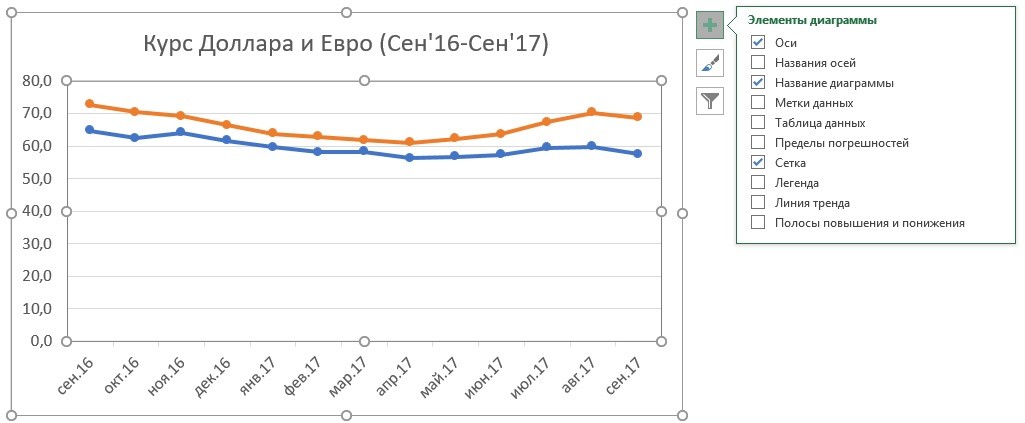
Нажать на “зеленый крестик” в правом верхнем углу графика;
Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:

Над графиком появится поле с названием графика. Кликните по нему левой клавишей мыши и внесите свое название:

Как подписать оси в графике Excel

Для лучше информативности нашего графика в Excel есть возможность подписать оси. Для этого:

Щелкните левой клавишей мыши по графику. В правом верхнем углу графика появится “зеленый крестик”, нажав на который раскроются настройки элементов диаграммы:

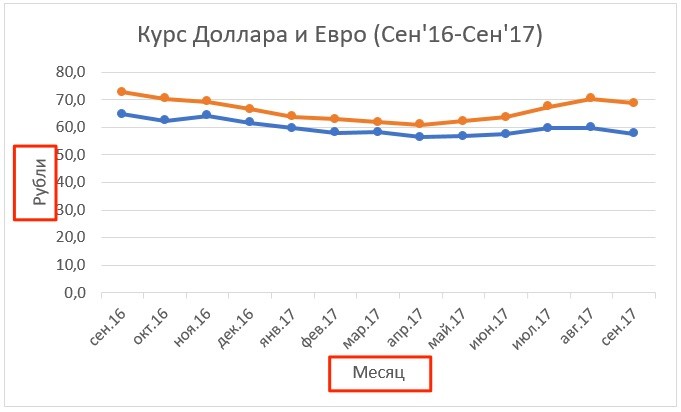
Щелкните левой клавишей мыши на пункте “Названия осей”. На графике под каждой осью появятся заголовки, в которые вы можете внести свой текст:

Как добавить подписи данных на графике Excel

Ваш график может стать еще более информативным с помощью подписи отображаемых данных.

На примере курсов валют мы хотим отобразить на графике стоимость курса Доллара и Евро помесячно. Для этого нам потребуется:

Щелкнуть правой кнопкой мыши по линии графика, на которую хотим добавить данные. В раскрывающемся меню выбрать пункт “Добавить подписи данных”:

Система отобразила курс Доллара на линии графика, но наглядность данных это не улучшило, так как значения сливаются с графиком. Для настройки отображения подписи данных потребуется сделать следующие шаги:

Кликните правой кнопкой мыши на любом значении линии графика. В всплывающем окне выберите пункт “Формат подписей данных”:

В этом меню вы сможете настроить положение подписи, а также из чего будет состоять подпись данных: из имени ряда, категории, значения и.т.д.

Помимо настроек расположения, в том же меню вы сможете настроить размер подписей, эффекты, заливку и.т.д:

Настроив все параметры у нас получился такой график курса валют:

Техническая гальванопластика

Гальванопластика — направление прикладной электрохимии, направленное на создание изделий путем электрохимического осаждения металлов и сплавов на различные носители формы (формообразующие элементы) в жидких средах.

Принцип формирования металлического осадка на поверхности модели, такой же как и при гальваническом нанесении покрытий, но в отличии от классической гальваники (гальваностегии) – толщина формируемых металлических осадков может достигать нескольких сантиметров.

В первой половине 20 века применение гальванопластики с целью получения технических изделий превратилось в полноценную промышленную технологию получения сложных и точных изделий.

Правила построения градуировочного графика при фотометрическом анализе

Фотометрический анализ при контроле гальванических электролитов применяется для определения малых концентраций добавок и примесей, титриметрический анализ которых затруднён или нецелесообразен.

Распространёнными фотометрическими измерениями являются определения:
• солей хрома III в электролите хромирования и растворе хромитирования,

• общего кобальта и никеля в электролитах твёрдого золочения, серебрения и нанесения сплава «Никель-Кобальт»,

• висмута в электролите нанесения сплава «Олово-Висмут»,

• определение палладия в активаторе для металлизации диэлектриков,

• определение примесей меди, железа и никеля в различных электролитах,

• а также турбидиметрическое определение сульфатов в электролите хромирования и в сульфаматных электролитах для определения степени гидролиза сульфаматов и пр.
Физико-химические методы анализа основаны на взаимосвязи между составом системы и ее физическими и физико-химическими свойствами. Функциональная зависимость между численным значением данного физического или физико-химического свойства и содержанием анализируемого вещества может быть выражена графиком или формулой.

Основой для построения градуировочного графика является приготовление стандартных растворов.

Стандартные растворы необходимо готовить из аттестованных государственных образцов (ГСО). Если таковых не имеется, необходимо четко придерживаться основных требований к точности приготовления стандартных растворов:

• следует применять соединения квалификации не ниже ч.д.а;

• использование реактивов с просроченным сроком годности недопустимо;

• для приготовления стандартных растворов использовать только гостированную мерную посуду.

Особое внимание обратить на условия и сроки хранения растворов с содержанием вещества 1 мг/см3 хранят 1 год, 0,1 мг/см3 – 3 месяца (если нет других указаний, а также если нет помутнения, хлопьев, осадка), растворы с меньшим содержанием применяются свежеприготовленными. Стандартные растворы фильтровать не допускается.

Для определения содержания вещества методом градуировочного графика готовят 3 серии шкал стандартов. Указания по приготовлению шкалы стандартов конкретно оговорены в каждой методике.

При приготовлении параллельных шкал рабочие растворы готовят соответствующим разбавлением основного стандартного раствора, который готовится из одной взятой навески или ГСО.

Градуировочный график строят на миллиметровой бумаге или в электронной форме при помощи Excel, откладывая на оси абсцисс, указанную в методике определения концентрацию, а по оси ординат – измеренные значения оптической плотности.

Количественное значение оптической плотности для каждой точки градуировочного графика определяется как среднее арифметическое результатов параллельных измерений 3-х шкал.

С целью уменьшения погрешности графического измерения, необходимо подобрать такой масштаб графика, чтобы угол его наклона приблизительно равнялся 45º.

Градуировочный график должен нести следующую информацию:

• НД на метод проведения исследования;

• марка КФК, его заводской номер;

• длина рабочей грани кюветы;

• раствор сравнения (растворитель, нулевой раствор и т.д.), т.е. относительно чего снимались показания испытуемого раствора;

• на графике должны присутствовать данные 3-х параллельных измерений и среднее арифметическое значение (в виде таблицы).

Градуировочный график строится один раз в год и после ремонта прибора. Поверка графика должна проводиться 1 раз в квартал (если нет других указаний в методике определения), а также после приготовления реактивов из новой партии, поверки прибора. Поверка проводится по 3-м точкам графика наиболее часто встречающихся в работе концентраций. Данные поверки заносятся в журнал поверок градуировочных графиков или наносятся на обратную сторону графика в виде таблицы.

При построении градуировочного графика должна соблюдаться прямая зависимость между оптической плотностью и концентрацией. Прямолинейность графика сохраняется только в интервале концентраций, указанных в методике. Поэтому продлевать градуировочную прямую выше последней указанной в методике точки не допустимо. Находить значение концентраций испытуемого раствора по градуировочному графику ниже первой точки графика не рекомендуется, т.к. это определение несет большую погрешность. В таком случае результат исследования следует записывать в виде «менее . мг/дм3».

Несмотря на простоту и удобство, практическое использование градуировочных графиков в ряде случаев вносит дополнительную погрешность при определении концентрации растворов как за счет субъективного построения графической зависимости, так и за счет несоответствия графичеких (масштабных) погрешностей и погрешностей измерения оптических плотностей. Поэтому для получения более объективных результатов в фотометрическом анализе целесообразно построение градуировочного графика методом регрессивного анализа (уравнение регрессии).

Описание метода наименьших квадратов и пример построение уточнённого градуировочного графика на примере фотометрического определения железа – здесь.

Дополнение для приборов, имеющих стрелочное регистрирующее устройство:

На многих предприятиях до сих пор в эксплуатации находятся приборы, при работе на которых значение измеренного пропускания отсчитывают по стрелочному прибору. Эти устройства являются обычным источником погрешности именно при отсчитывании показаний. Для правильно сконструированного стрелочного прибора погрешность при отсчёте будет постоянной и, возможно, равной толщине стрелки, которая соответствует определённому отсчёту по шкале прибора. При допущении, что отсчёты пропускания, полученные каждым таким устройством, имеют постоянную недостоверность (обусловленную изменением мощности источника света, характеристиками детектора, электрическими шумами, положением кюветы, и обычно приводящую к суммарной погрешности от 0,2 до 1%), можно рассчитать погрешность, которую вызовет ненадёжность при регистрации концентрации определяемых частиц.
Для расчёта концентрационной погрешности необходимо изучить влияние недостоверности измерения пропускания на вычисленное значение концентрации. Для этого запишем закон Бера в форме, которая показывает, что зависимость от концентрации является экспоненциальной:

T = P/P0 = 10-abC, где (1)

b– толщина поглощающего слоя раствора в кювете,

С – концентрация оптически активного вещества,

а – удельная поглощательная способность, зависящая от природы вещества.

Из графика этой зависимости на рисунке можно определить, какое влияние на рассчитанное значение С окажет постоянная погрешность в пропускании.

Сначала рассмотрим спектрофотометрическое измерение раствора с низкой концентрацией (С1) определяемых частиц. Согласно рисунку этот раствор будет иметь высокое значение пропускание (Т1). Допуская, что недостоверность при отсчёте стрелочного прибора соответствует постоянной абсолютной погрешности в Т, можно определить из рисунка результирующую погрешность в определение С. Из экстраполирования линии видно, что абсолютная погрешность в концентрации (ΔС1) мала, когда раствор имеет высокое пропускание. Однако поскольку сама концентрация (С1) мала, относительная погрешность в концентрации (ΔС1/С1) довольно велика.

Теперь рассмотрим случай, когда имеется высокая концентрация (С2) определяемого вещества. Этот раствор будет иметь относительно низкое значение пропускания (Т2). Если снова допустить наличие постоянной погрешности в Т, то получим большую абсолютную погрешность (ΔС2) в концентрации, и хотя концентрация велика, относительная погрешность (ΔС2/С2) также будет велика.

Эти результаты свидетельствуют, что где-то между экстремальными значениями концентрации в пробах, имеющих высокие и низкие пропускания, должно существовать значение пропускания, для которого относительная погрешность в концентрации (ΔС/С) минимальна. В действительности относительная погрешность минимальна при 36,8%-ном пропускании. К этому выводу можно прийти и расчётным путём, вспомнив определение понятия поглощения:

А = lg (1/T) = 1/2,303 ln(1/T) = 0,434 ln (1/T) (2)

Если это уравнение продифференцировать относительно Т, то получим

dA/dT = -0,434/T или dA = (-0,434/T) dT (3)

Для того чтобы оценить относительную погрешность в значении поглощения и тем самым в концентрации, необходимо разделить каждую часть уравнения (3) на поглощение (А). Тогда

dA/А = (-0,434/TА) dT= (0,434/TlgT) dT (4)

Чтобы найти относительную погрешность в концентрации, заменим в этом уравнении А соответствующей величиной согласно закону Ламберта-Бера (1):

d(abC)/abC = (ab)dC/abC = dC/C = (0,434/T lgT) dT (5)

Уравнение (5) показывает, что относительная погрешность в концентрации (dC/C) непосредственно зависит от абсолютной недостоверности в пропускании (dT), а также от обратной величины произведения (TlgT), включающего значение самого пропускания. Графическая зависимость этого уравнения, показывающая относительную погрешность в концентрации (dC/C) как функцию пропускания (в %) при постоянной погрешности в отсчёте (dT), равной 1%, показана на рисунке:

Из рисунка видно, что относительная погрешность в концентрации достаточно низка при пропусканиях между 20 и 70%, но при переходе к очень низким или высоким значениям пропускания погрешность резко возрастает. Можно найти минимальную относительную погрешность в концентрации путём дифференцирования уравнения (5) и приравнивая выражения к нулю. Как указано ранее, минимальная погрешность имеет месть при 36,8%-ном пропускании или при поглощении, равном 0,434. Поэтому для спектрофотометров, имеющих стрелочное регистрирующее устройство, можно проводить измерение с наименьшей погрешностью, если отсчёты по шкале ограничены пределом от 20% до 70% пропускания (или от 0,7 до 0,2 единиц поглощения), а в оптимальном случае эти расчёты приближаются к значениям 36,8% пропускания или к 0,434 единиц поглощения. Обычно можно соблюдать эти ограничения путём соответствующего выбора толщины поглощающего слоя пробы (b) или путём разбавления раствора пробы, взятого для анализа.

Приведённые выше рассуждения применимы только к измерениям на спектрофотометрах, имеющих постоянную погрешность, связанную с отсчётом пропускания. Современные приборы обладают цифровой регистрацией, погрешность отсчёта не является для них фактором, лимитирующим правильность.

1) Переярченко П.В., Афанасьева О.Л., Замковая Л.А., Махоня Т.В., Гольнева Л.Н. Информационное письмо о правилах построения градуировочных графиков при фотоколориметрических методах исследования.

2) Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение. Теория и практика аналитической химии. – М.: «Химия», 1978. – 816 с.

3) Булатов М.И., Малинкин И.П. Практическое руководство по фотометрическим методам анализа, Ленинград, Химия, 1986;

4) Справочник по физико-химическим методам исследования объектов окружающей среды под редакцией Арановича Г.И., Ленинград, Судостроение, 1979;

5) Новиков Ю.В., Ласточкина К.О., Болдина З.Н. Методы исследования качества воды водоемов, Москва, Медицина, 1990;

6) ГОСТ 4212–76 «Реактивы. Методика приготовления растворов для колориметрического, нефелометрического и других видов анализа».

Как построить график в Excel

Предыдущей статье мы уже рассмотрели, как сделать диаграмму в Excel. Теперь настало время узнать, как построить график в Excel.

В первую очередь перед тем как построить график по таблице, нам нужно определиться какой тип графика мы будем использовать – график или точечную диаграмму. В случае если необходимо построить график по данным таблицы, используя значения как х, так и у, т.е. построить график x y в Excel, то в таком случае используется точечная диаграмма. Диаграмма График равномерно распределяет значения по оси х, т.е. при построении графика используются только значения у.

Тип график используется, когда необходимо построить график по данным для отображения тенденции по времени (по годам, месяцам и дням) или по категориям, в которых важен порядок. Данный тип применяется, если есть много данных и важен порядок их следования.

Тип точечная диаграмма применяется когда, необходимо построить график по данным для сравнения не менее двух наборов значений или пар данных. Данный тип диаграммы применяется для построения графика зависимости, когда точек данных немного, а данные представляют отдельные измерения.

Разберем примеры данных типов.

Построить график в Excel по данным таблицы

Для примера рассмотрим, как построить график в Excel по данным изменения курса доллара за 2016 год.

Как построить график в Excel – Данные для построения графика

Выделяем всю таблицу. Заголовки столбцов будут использоваться для подписи данных. Переходим во вкладка « Вставка », в группе «Диаграммы» выбираем пункт «График».

Как построить график в Excel – График

В результате получаем график по данным таблицы:

Как построить график в Excel – График курса доллара за 2016 год

По построенному графику по таблице мы наглядно можем проследить тренд изменения курса валют по месяцам за 2016 год. Перейдем к построению графика по точкам в Excel.

Построить график по точкам в Excel

Точечная диаграмма используется для того, чтобы построить график зависимости в Excel. Очень часто точечный график используется для того, чтобы построить график функции в Excel. Поэтому мы рассмотрим несколько примеров построения графиков функций.

Начнем с примера, в котором рассмотрим, как построить график квадратичной функции.

Создадим следующую таблицу:

Как построить график в Excel – Построение графика функции, исходные данные

В первом столбце (столбец А) у нас значения х с единичным шагов, во втором (столбец В) значения формулы квадратичной функции.

Исходные данные готовы. Переходим к построению графика функции. Выделяем всю таблицу, переходим во вкладку « Вставка », в группе «Диаграммы» выбираем пункт « Точечная с гладкими кривыми и маркерами ».

Как построить график в Excel – Точечная диаграмма

Получаем следующий график функции:

Как построить график в Excel – Точечный график квадратичной функции

Вы также можете поработать с оформлением получившегося графика, применив к нему понравившийся стиль.

Как построить два графика в Excel

Перейдем к вопросу, как построить два графика в Excel. Добавим еще один график кубической параболы. Создадим в таблице еще один столбец (столбец С), в котором введем формулу кубической параболы. Теперь наша таблица выглядит следующим образом:

Как построить график в Excel – Расширение таблицы исходных данных

Теперь во вкладке « Конструктор » выбираем пункт « Выбрать данные ».

Как построить график в Excel – Выбрать данные

В появившемся окне, Excel предлагает выбрать источник данных.

Как построить график в Excel – Выбор источника данных

Мы можем либо изменить « Диапазон данных для диаграммы », выбрав нашу обновленную таблицу; либо добавить еще один ряд с помощью кнопки « Добавить ». Мы воспользуемся вторым способом, и просто добавим еще один ряд.

В открывшемся окне в поле « Имя ряда » выбираем ячейку с заголовком столбца, в поле « Значения Х » – выбираем первый столбец таблицы, « Значения У » – третий. Нажимаем кнопку « ОК ».

Как построить график в Excel – Изменение ряда

Теперь в окне « Выбор источника данных » содержится два ряда:

Как построить график в Excel – Построить два графика

Нажимаем « ОК ». И на нашей диаграмме уже отображаются два графика.

Как построить график в Excel – Два графика на одной точечной диаграмме

Для удобства добавим легенду и название диаграммы, и выберем желаемый стиль. Ну вот, график функции в Excel построен:

Как построить график в Excel – Графики функций

Теперь вы знаете, как построить график функции в Excel. Давайте рассмотрим, как быстро оформить график, и как переместить график.

Редактирование графика

Если вы хотите изменить размещение графика, то дважды кликаем по графику, и в « КОНСТРУКТОРЕ » выбираем « Переместить диаграмму ».

Как построить график в Excel – Переместить диаграмму

В открывшемся диалоговом окне выбираем, где хотим разместить наш график.

Как построить график в Excel – Перемещение диаграммы

Мы можем разместить наш график на отдельном листе с указанным в поле названием, для этого выбираем пункт « на отдельном листе ».

В случае если необходимо перенести график на другой лист, то выбираем пункт « на имеющемся листе », и указываем лист, на который нужно переместить наш график.

Разместим график по данным таблицы на отдельном листе с названием « Курс доллара, 2016 год ».

Как построить график в Excel – Перемещение графика на отдельный лист

Теперь книга Excel содержит лист с графиком, который выглядит следующим образом:

Как построить график в Excel – График курса доллара на отдельном листе

Поработаем с оформлением графика. С помощью Excel можно мгновенно, практически в один клик изменить внешний вид диаграммы, и добиться эффектного профессионального оформления.

Во вкладке « Конструктор » в группе « Стили диаграмм » находится коллекция стилей, которые можно применить к текущему графику.

Как построить график в Excel – Стили диаграмм

Для того чтобы применить понравившийся вам стиль достаточно просто щелкнуть по нему мышкой.

Как построить график в Excel – Коллекция стилей диаграмм

Теперь наш график полностью видоизменился.

Как построить график в Excel – График с оформлением

При необходимости можно дополнительно настроить желаемый стиль, изменив формат отдельных элементов диаграммы.

Ну вот и все. Теперь вы знаете, как построить график в Excel, как построить график функции, а также как поработать с внешним видом получившихся графиков. Если вам необходимо сделать диаграмму в Excel, то в этом вам поможет эта статья.

Программы для компьютера

Общие сведения о проекте

На сегодняшний день наш сайт является уникальным проектом на просторах российского интернета. На страницах сайта infowall.ru всегда можно найти самую свежую и исчерпывающую информацию о новинках компьютерных программ, а также практические советы по работе в сети Интернет, настройке и использованию компьютера, установке программного обеспечения и другую полезную информацию. Информационное наполнение сайта, а также программы для компьютера рассчитаны как на простых пользователей, так и на людей, имеющих практический опыт в области информационных технологий, программного обеспечения и администрирования сетевых ресурсов (операторов компьютерных систем, программистов, а также системных администраторов). Целью проекта является создание оптимизированного ресурса для размещения актуальной и полезной информации, а также практическая поддержка пользователей сайта.

Практические руководства и инструкции

Многие бесплатные программы, которые размещены на нашем сайте, зачастую требуют от пользователей определенных базовых навыков работы с ними. Для облегчения процесса знакомства с новыми популярными программами в разделе База знаний мы ежедневно размещаем подробные инструкции по использованию тех или иных наиболее востребованных на наш взгляд программ, с которыми приходится сталкиваться в повседневной работе. Все инструкции написаны живым языком и будут интересны как начинающим, так и более опытным пользователям. Кроме того, на сайте пополняется база практических руководств по работе в интернете, обслуживанию компьютера, установке и использованию пакетов популярных и профессиональных программ и многое другое. Отныне сайт infowall.ru станет для вас надежным проводником в мире интернета и персональных компьютеров. И если вы еще новичок в этой области, то с нашим проектом вы незаметно для себя получите практический опыт и обширные знания, посещая наш сайт, хотя бы раз в день!

Наш сайт также содержит регулярно обновляемый каталог программ, которые станут вашими незаменимыми помощниками в процессе практической работы на компьютере, как дома, так и на работе. Наши специалисты тестируют и размещают бесплатные программы для компьютера, различные утилиты, антивирусы и прочий софт. У нас можно скачать офисные программы и приложения, мультимедиа софт, кодеки, утилиты для восстановления данных, файловые менеджеры, архиваторы, программы для интернета, для работы с электронной почтой и многое другое.

Мы стремимся обеспечить максимальный комфорт для наших пользователей, именно поэтому все программы для компьютера, размещенные на нашем сайте, доступны для простого и бесплатного скачивания, а также имеют в своей структуре подробное описание, что позволяет пользователям предварительно ознакомиться с той или иной программой.

Кроме того, если в процессе работы с компьютером у вас возникли какие-либо сложности, то вы всегда можете оставить у нас заявку в специальном разделе Помогите найти или задать вопрос в разделе Вопросы. Мы ежедневно прилагаем все усилия, чтобы в максимально сжатые сроки предоставить вам исчерпывающую и подробную информацию по всем интересующим вопросам.

Мы также приветствуем всякую посильную помощь от наших пользователей в развитии проекта. Если у вас есть чем поделиться с другими, вы всегда можете разместить на сайте любую программу, которая, по вашему мнению, будет полезна пользователям и посетителям нашего сайта.

Источник

Я с эксель вообще не дружу и понять не могу,как простейший график закончить делать.
Помогите пожалуйста(
Нужно поставить точку 0,5 на самом графике (на линии), а потом определить значение икса.
как это сделать?
Икс в данном случае будет массой металла в растворе.Нужно найти затем массовую долю металла.

Задача такая:

Для определения металла навеску образца 0,1г растворили, перевели в мерную колбу на 100 мл, провели фотометрическую реакцию, довели до метки дистиллированной водой и измерили оптическую плотность: А_х=0,5. Для построения градуировочного графика в 5 мерных колб на 100 мл поместили стандартный раствор, содержащий: 2,00; 4,00; 6,00; 8,00; 10 мг металла, провели фотометрическую реакцию, довели до метки дистиллированной водой и измерили оптическую плотность: А₁= 0,24; А₂= 0,46; А₃ = 0,72; А₄ = 0,95, А₅ = 1,15.

Постройте градуировочный график в координатах А — масса металла m(Me),мг в растворе, по нему найдите массу металла в растворе, затем рассчитайте массовую долю металла в образце массой m г.

Изменено 18 Июня, 2020 в 14:04 пользователем colddawm

Источник

Что такое калибровочная кривая и как Excel полезен при ее создании?

Чтобы выполнить калибровку, вы сравниваете показания устройства (например, температуру, отображаемую термометром) с известными значениями, называемыми стандартами (например, точки замерзания и кипения воды). Это позволяет вам создать серию пар данных, которые вы затем будете использовать для построения калибровочной кривой.

Двухточечная калибровка термометра с использованием точек замерзания и кипения воды будет иметь две пары данных: одну с момента, когда термометр помещают в ледяную воду (32 ° F или 0 ° C), и одну в кипящую воду (212 ° F). или 100 ° С). Когда вы построите эти две пары данных в виде точек и проведете линию между ними (калибровочную кривую), а затем, предполагая, что реакция термометра является линейной, вы можете выбрать любую точку на линии, которая соответствует значению, которое отображает термометр, и вы мог найти соответствующую «истинную» температуру.

Таким образом, линия, по сути, заполняет информацию между двумя известными для вас точками, так что вы можете быть достаточно уверенными при оценке фактической температуры, когда термометр показывает 57,2 градуса, но когда вы никогда не измеряли «стандарт», который соответствует это чтение.

В Excel есть функции, которые позволяют графически отображать пары данных на графике, добавлять линию тренда (калибровочную кривую) и отображать уравнение калибровочной кривой на графике. Это полезно для визуального отображения, но вы также можете рассчитать формулу линии, используя функции Excel SLOPE и INTERCEPT. Когда вы введете эти значения в простые формулы, вы сможете автоматически рассчитать «истинное» значение на основе любого измерения.

Давайте посмотрим на пример

Для этого примера мы разработаем калибровочную кривую из серии из десяти пар данных, каждая из которых состоит из значения X и значения Y. Значения Х будут нашими «стандартами», и они могут представлять что угодно, от концентрации химического раствора, который мы измеряем с помощью научного прибора, до входной переменной программы, которая управляет пусковой машиной для мрамора.

Значения Y будут «откликами», и они будут представлять собой показания прибора, полученные при измерении каждого химического раствора, или измеренное расстояние, на котором расстояние от пусковой установки, на которую упал мрамор, используя каждое входное значение.

После того, как мы графически изобразим калибровочную кривую, мы будем использовать функции SLOPE и INTERCEPT, чтобы вычислить формулу калибровочной линии и определить концентрацию «неизвестного» химического раствора на основании показаний прибора или решить, какой ввод мы должны дать программе, чтобы мрамор приземляется на определенном расстоянии от пусковой установки.

Шаг первый: создайте свою диаграмму

Наш простой пример электронной таблицы состоит из двух столбцов: X-Value и Y-Value.

Начнем с выбора данных для построения графика.

Сначала выберите ячейки столбца «X-значение».

Теперь нажмите клавишу Ctrl и затем щелкните ячейки столбца Y-значения.

Перейдите на вкладку «Вставить».

Перейдите в меню «Графики» и выберите первый вариант в раскрывающемся меню «Разброс».

Появится диаграмма, содержащая точки данных из двух столбцов.

Выберите серию, нажав на одну из синих точек. После выбора Excel обрисовывает в общих чертах точки.

Щелкните правой кнопкой мыши одну из точек и выберите опцию «Добавить линию тренда».

На графике появится прямая линия.

В правой части экрана появится меню «Format Trendline». Установите флажки рядом с «Показать уравнение на графике» и «Показать значение R-квадрат на графике». Значение R-квадрат является статистикой, которая говорит вам, насколько точно линия соответствует данным. Наилучшее значение R-квадрата равно 1.000, что означает, что каждая точка данных касается линии. По мере роста различий между точками данных и линией значение r-квадрата уменьшается, причем 0,000 является наименьшим возможным значением.

Уравнение и R-квадрат статистики трендовой линии появятся на графике. Обратите внимание, что в нашем примере корреляция данных очень хорошая, значение R-квадрата равно 0,988.

Уравнение имеет вид «Y = Mx + B», где M — наклон, а B — пересечение оси y прямой.

Теперь, когда калибровка завершена, давайте поработаем над настройкой диаграммы, отредактировав заголовок и добавив заголовки осей.

Чтобы изменить заголовок диаграммы, щелкните по нему, чтобы выделить текст.

Теперь введите новый заголовок, который описывает диаграмму.

Чтобы добавить заголовки к осям X и Y, сначала перейдите к «Инструменты диаграммы»> «Дизайн».

Нажмите «Добавить элемент диаграммы».

Теперь перейдите к Названия осей> Первичная горизонтальная.

Появится название оси.

Чтобы переименовать заголовок оси, сначала выделите текст, а затем введите новый заголовок.

Теперь перейдите к Названию осей> Первичная вертикаль.

Появится название оси.

Переименуйте этот заголовок, выделив текст и введя новый заголовок.

Ваша диаграмма теперь завершена.

Шаг второй: Рассчитать линейное уравнение и R-квадрат

Теперь давайте вычислим линейное уравнение и R-квадрат, используя встроенные в Excel функции SLOPE, INTERCEPT и CORREL.

К нашему листу (в строке 14) мы добавили заголовки для этих трех функций. Мы выполним фактические вычисления в ячейках под этими заголовками.

Сначала рассчитаем НАКЛОН. Выберите ячейку A15.

Перейдите к формулам> Дополнительные функции> Статистические> НАКЛОН.

Откроется окно «Аргументы функции». В поле «Known_ys» выберите или введите ячейки столбца Y-значения.

В поле «Known_xs» выберите или введите ячейки столбца X-Value. Порядок полей ‘Known_ys’ и ‘Known_xs’ имеет значение в функции SLOPE.

Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:

=SLOPE(C3:C12,B3:B12)

Обратите внимание, что значение, возвращаемое функцией SLOPE в ячейке A15, соответствует значению, отображенному на графике.

Затем выберите ячейку B15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «ПЕРЕКРЫТЬ».

Откроется окно «Аргументы функции». Выберите или введите в ячейки столбца Y-значение для поля «Known_ys».

Выберите или введите в ячейки столбца X-Value поле «Known_xs». Порядок полей «Known_ys» и «Known_xs» также имеет значение в функции INTERCEPT.

Нажмите «ОК». Окончательная формула в строке формул должна выглядеть следующим образом:

=INTERCEPT(C3:C12,B3:B12)

Обратите внимание, что значение, возвращаемое функцией INTERCEPT, соответствует точке пересечения y, отображаемой на диаграмме.

Затем выберите ячейку C15 и перейдите к «Формулы»> «Дополнительные функции»> «Статистические данные»> «CORREL».

Откроется окно «Аргументы функции». Выберите или введите любой из двух диапазонов ячеек для поля «Массив1». В отличие от SLOPE и INTERCEPT, порядок не влияет на результат функции CORREL.

Выберите или введите другой из двух диапазонов ячеек для поля «Array2».

Нажмите «ОК». Формула должна выглядеть следующим образом на панели формул:

=CORREL(B3:B12,C3:C12)

Обратите внимание, что значение, возвращаемое функцией CORREL, не соответствует значению «r-квадрат» на графике. Функция CORREL возвращает «R», поэтому мы должны возвести ее в квадрат, чтобы вычислить «R-квадрат».

Щелкните внутри панели функций и добавьте «^ 2» в конец формулы, чтобы возвести в квадрат значение, возвращаемое функцией CORREL. Заполненная формула теперь должна выглядеть так:

=CORREL(B3:B12,C3:C12)^2

Нажмите Ввод.

После изменения формулы значение «R-квадрат» теперь соответствует значению, отображенному на графике.

Шаг третий: настройка формул для быстрого расчета значений

Теперь мы можем использовать эти значения в простых формулах, чтобы определить концентрацию этого «неизвестного» раствора или то, что мы должны ввести в код, чтобы шарик пролетел определенное расстояние.

Эти шаги настроят формулы, необходимые для того, чтобы вы могли ввести значение X или значение Y и получить соответствующее значение на основе калибровочной кривой.

Уравнение линии наилучшего соответствия имеет вид «Y-значение = НАКЛОН * X-значение + INTERCEPT», поэтому решение для «Y-значения» выполняется путем умножения значения X и SLOPE, а затем добавив ИНТЕРЦЕПТ.

В качестве примера мы вводим ноль в качестве значения X. Возвращаемое значение Y должно быть равно ПЕРЕКЛЮЧЕНИЮ линии наилучшего соответствия. Это соответствует, поэтому мы знаем, что формула работает правильно.

Решение для значения X на основе значения Y выполняется путем вычитания INTERCEPT из значения Y и деления результата на НАКЛОН:

  Х-значение = (Y-значение-ОТРЕЗОК) / СКЛОН

В качестве примера мы использовали INTERCEPT в качестве значения Y. Возвращаемое значение Х должно быть равно нулю, но возвращаемое значение равно 3.14934E-06. Возвращаемое значение не равно нулю, потому что мы непреднамеренно обрезали результат INTERCEPT при вводе значения. Однако формула работает правильно, потому что результат формулы равен 0,00000314934, что по существу равно нулю.

Вы можете ввести любое значение X в первую ячейку с толстыми границами, и Excel автоматически вычислит соответствующее значение Y.

Ввод любого значения Y во вторую ячейку с толстой рамкой даст соответствующее значение X. Эта формула используется для расчета концентрации этого раствора или того, что необходимо для запуска мрамора на определенном расстоянии.

В этом случае прибор показывает «5», поэтому при калибровке будет предложена концентрация 4,94, или мы хотим, чтобы шарик прошел пять единиц расстояния, поэтому при калибровке предлагается ввести 4,94 в качестве входной переменной для программы, управляющей пусковой установкой мрамора. Мы можем быть достаточно уверены в этих результатах из-за высокого значения R-квадрата в этом примере.

Источник

Распространёнными фотометрическими измерениями являются определения: • солей хрома III в электролите хромирования и растворе хромитирования,

• висмута в электролите нанесения сплава «Олово-Висмут»,

• определение палладия в активаторе для металлизации диэлектриков,

• определение примесей меди, железа и никеля в различных электролитах,

• а также турбидиметрическое определение сульфатов в электролите хромирования и в сульфаматных электролитах для определения степени гидролиза сульфаматов и пр. Физико-химические методы анализа основаны на взаимосвязи между составом системы и ее физическими и физико-химическими свойствами. Функциональная зависимость между численным значением данного физического или физико-химического свойства и содержанием анализируемого вещества может быть выражена графиком или формулой.

Основой для построения градуировочного графика является приготовление стандартных растворов.

• следует применять соединения квалификации не ниже ч.д.а;

• использование реактивов с просроченным сроком годности недопустимо;

• для приготовления стандартных растворов использовать только гостированную мерную посуду.

Особое внимание обратить на условия и сроки хранения растворов с содержанием вещества 1 мг/см3 хранят 1 год, 0,1 мг/см3 — 3 месяца (если нет других указаний, а также если нет помутнения, хлопьев, осадка), растворы с меньшим содержанием применяются свежеприготовленными. Стандартные растворы фильтровать не допускается.

Градуировочный график строят на миллиметровой бумаге или в электронной форме при помощи Excel, откладывая на оси абсцисс, указанную в методике определения концентрацию, а по оси ординат — измеренные значения оптической плотности.

Градуировочный график должен нести следующую информацию:

• название определения;

• НД на метод проведения исследования;

• метод определения;

• марка КФК, его заводской номер;

• длина волны;

• длина рабочей грани кюветы;

• дата построения;

• даты поверки;

Описание метода наименьших квадратов и пример построение уточнённого градуировочного графика на примере фотометрического определения железа — здесь.

Дополнение для приборов, имеющих стрелочное регистрирующее устройство:

На многих предприятиях до сих пор в эксплуатации находятся приборы, при работе на которых значение измеренного пропускания отсчитывают по стрелочному прибору. Эти устройства являются обычным источником погрешности именно при отсчитывании показаний. Для правильно сконструированного стрелочного прибора погрешность при отсчёте будет постоянной и, возможно, равной толщине стрелки, которая соответствует определённому отсчёту по шкале прибора. При допущении, что отсчёты пропускания, полученные каждым таким устройством, имеют постоянную недостоверность (обусловленную изменением мощности источника света, характеристиками детектора, электрическими шумами, положением кюветы, и обычно приводящую к суммарной погрешности от 0,2 до 1%), можно рассчитать погрешность, которую вызовет ненадёжность при регистрации концентрации определяемых частиц. Для расчёта концентрационной погрешности необходимо изучить влияние недостоверности измерения пропускания на вычисленное значение концентрации. Для этого запишем закон Бера в форме, которая показывает, что зависимость от концентрации является экспоненциальной: T = P/P0 = 10-abC, где (1)

b— толщина поглощающего слоя раствора в кювете,

С — концентрация оптически активного вещества,

а — удельная поглощательная способность, зависящая от природы вещества.

А = lg (1/T) = 1/2,303 ln(1/T) = 0,434 ln (1/T) (2)

Если это уравнение продифференцировать относительно Т, то получим

dA/dT = −0,434/T или dA = (-0,434/T) dT (3)

dA/А = (-0,434/TА) dT= (0,434/TlgT) dT (4)

d(abC)/abC = (ab)dC/abC = dC/C = (0,434/T lgT) dT (5)

Литература:

2) Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение. Теория и практика аналитической химии. — М.: «Химия», 1978. — 816 с.

5) Новиков Ю.В., Ласточкина К.О., Болдина З.Н. Методы исследования качества воды водоемов, Москва, Медицина, 1990;

Источник