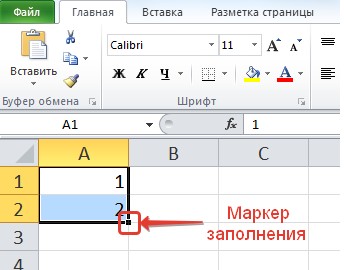
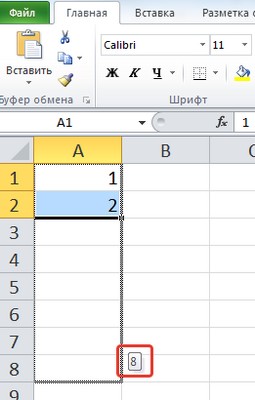
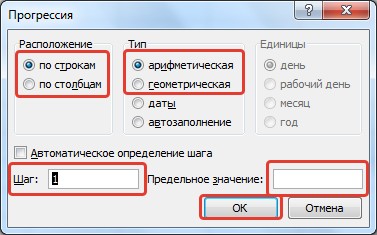
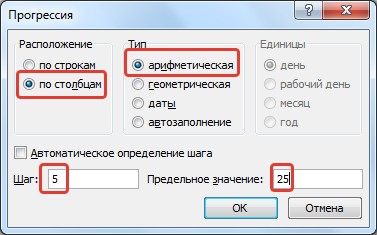
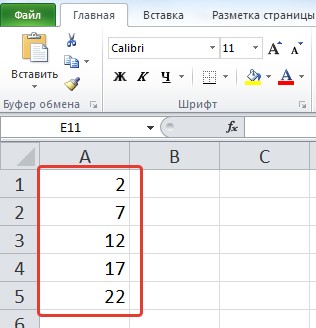
Создадим числовые последовательности различных видов: 1, 2, 3, … 1, 3, 5, 7, … I, II, III, IV, …. 100, 200, 300,…00-01
,
00-02, … 1, 1, 1, 2, 2, 2,… и пр.
Используем формулы
Сформируем последовательность 1, 2, 3, … Пусть в ячейке
A2
введен первый элемент последовательности — значение
1
. В ячейку
А3
, вводим формулу
=А2+1
и копируем ее в ячейки ниже (см.
файл примера
).
Так как в формуле мы сослались на ячейку выше с помощью
относительной ссылки
, то EXCEL при копировании вниз модифицирует вышеуказанную формулу в
=А3+1
, затем в
=А4+1
и т.д., тем самым формируя числовую последовательность 2, 3, 4, …
Если последовательность нужно сформировать в строке, то формулу нужно вводить в ячейку
B2
и копировать ее нужно не вниз, а вправо.
Чтобы сформировать последовательность нечетных чисел вида 1, 3, 7, … необходимо изменить формулу в ячейке
А3
на
=А2+2
. Чтобы сформировать последовательность 100, 200, 300, … необходимо изменить формулу на
=А2+100
, а в ячейку
А2
ввести 100.
Другим вариантом создания последовательности 1, 2, 3, … является использование формулы
=СТРОКА()-СТРОКА($A$1)
(если первый элемент последовательности располагается в строке
2
). Формула
=СТРОКА(A2)-СТРОКА($A$1)
позволяет создать вертикальную последовательность, в случае если ее первый элемент последовательности располагается в любой строке. Тот же результат дают формулы
=ЧСТРОК($A$1:A1)
,
=СТРОКА(A1)
и
=СТРОКА(H1)
. Формула
=СТОЛБЕЦ(B1)-СТОЛБЕЦ($A$1)
создает последовательность, размещенную горизонтально. Тот же результат дают формулы
=ЧИСЛСТОЛБ($A$1:A1)
,
=СТОЛБЕЦ(A1)
.
Чтобы сформировать последовательность
I, II, III, IV
, … начиная с ячейки
А2
, введем в
А2
формулу
=РИМСКОЕ(СТРОКА()-СТРОКА($A$1))
Сформированная последовательность, строго говоря, не является числовой, т.к. функция
РИМСКОЕ()
возвращает текст. Таким образом, сложить, например, числа
I+IV
в прямую не получится.
Другим видом числовой последовательности в текстовом формате является, например, последовательность вида
00-01
,
00-02, …
Чтобы начать нумерованный список с кода
00-01
, введите формулу
=ТЕКСТ(СТРОКА(A1);»00-00″)
в первую ячейку диапазона и перетащите
маркер заполнения
в конец диапазона.
Выше были приведены примеры арифметических последовательностей. Некоторые другие виды последовательностей можно также сформировать формулами. Например, последовательность
n2+1
((n в степени 2) +1) создадим формулой
=(СТРОКА()-СТРОКА($A$1))^2+1
начиная с ячейки
А2
.
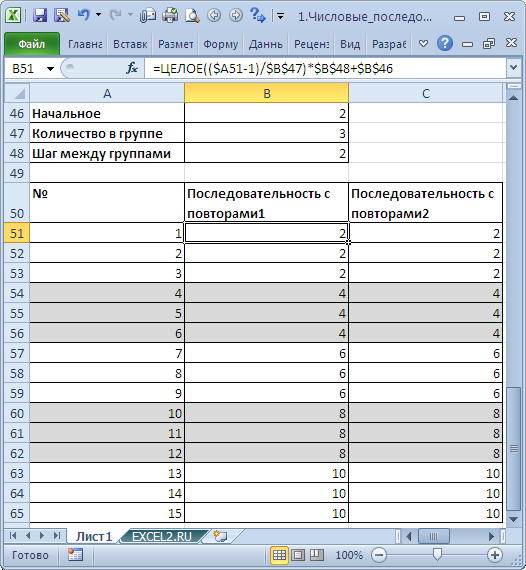
Создадим последовательность с повторами вида
1, 1, 1, 2, 2, 2,…
Это можно сделать формулой
=ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/3+1)
. С помощью формулы
=ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2
получим последовательность
2, 2, 2, 2, 4, 4, 4, 4,…
, т.е. последовательность из четных чисел. Формула
=ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2-1
даст последовательность
1, 1, 1, 1, 3, 3, 3, 3, …
Примечание
. Для выделения повторов использовано
Условное форматирование
.
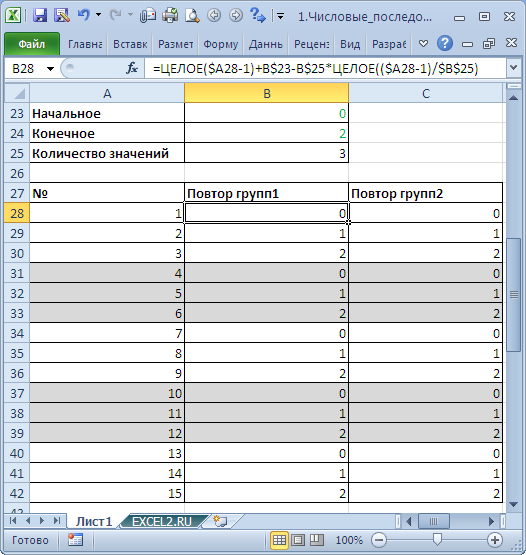
Формула
=ОСТАТ(ЧСТРОК(A$2:A2)-1;4)+1
даст последовательность
1, 2, 3, 4, 1, 2, 3, 4, …
Это пример последовательности с периодически повторяющимися элементами.
Примечание
. Последовательности с повторами использованы, например, в статьях
Перебор всех возможных Сочетаний с повторениями в MS EXCEL
и
Перебор всех возможных целочисленных комбинаций в MS EXCEL
.
Используем клавишу CTRL
Пусть, как и в предыдущем примере, в ячейку
A2
введено значение
1
. Выделим ячейку
A2
. Удерживая клавишу
CTRL
, скопируем
Маркером заполнения
(при этом над курсором появится маленький плюсик), значение из
A
2
в ячейки ниже. Получим последовательность чисел 1, 2, 3, 4 …
ВНИМАНИЕ!
Если на листе часть строк скрыта с помощью
фильтра
, то этот подход и остальные, приведенные ниже, работать не будут. Чтобы разрешить нумерацию строк с использованием клавиши
CTRL
, выделите любую ячейку с заголовком
фильтра
и дважды нажмите
CTRL
+
SHIFT
+
L
(сбросьте фильтр).
Используем правую клавишу мыши
Пусть в ячейку
A2
введено значение
1
. Выделим ячейку
A2
. Удерживая правую клавишу мыши, скопируем
Маркером заполнения
, значение из
A2
в ячейки ниже. После того, как отпустим правую клавишу мыши появится контекстное меню, в котором нужно выбрать пункт
Заполнить
. Получим последовательность чисел 1, 2, 3, 4 …
Используем начало последовательности
Если начало последовательности уже задано (т.е. задан первый элемент и шаг последовательности), то создать последовательность 1, 2, 3, … можно следующим образом:
-
пусть в ячейке
А2
введено значение
1
, а в ячейке
А3
значение
2
; -
выделяем ячейки
A
2
и
A
3
; -
беремся за правый нижний угол и
Маркером заполнения
протягиваем вниз.
Получаем результат как в предыдущем случае. Если в ячейке
А3
введено значение
3
, т.е. задан шаг последовательности равный 2, то мы получим последовательность нечетных чисел.
Создадим последовательность вида
1, 2, 3, 1, 2, 3,…
для этого введем в первые три ячейки значения 1, 2, 3, затем
маркером заполнения
, удерживая клавишу
CTRL
, скопируем значения вниз.
Использование инструмента Прогрессия
Воспользуемся стандартным средством EXCEL для создания прогрессий, в то числе и арифметических.
-
вводим в ячейку
А2
значение
1
; -
выделяем диапазон
A
2:А6
, в котором будут содержаться элементы последовательности; -
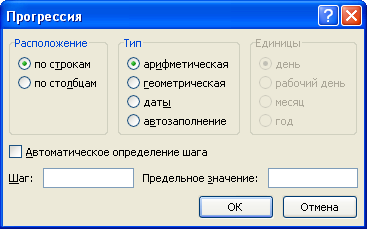
вызываем инструмент
Прогрессия
(
), в появившемся окне нажимаем ОК.
Использование в работе
:
Подходы для создания числовых последовательностей можно использовать для
нумерации строк
,
сортировки списка с числами
,
разнесения значений по столбцам и строкам
.
СОВЕТ:
О текстовых последовательностях вида
первый, второй, …, 1), 2), 3), …
можно прочитать в статье
Текстовые последовательности
. О последовательностях значений в формате дат (и времени) вида
01.01.09, 01.02.09, 01.03.09, …, янв, апр, июл, …, пн, вт, ср, …
можно прочитать в статье
Последовательности дат и времен
. О массивах значений, содержащих последовательности конечной длины, используемых в
формулах массива
, читайте в статье
Массив значений (или константа массива или массив констант)
.
Числовые последовательности
Чтобы, к примеру, сделать нумерацию строк, можно вводить номера 1, 2, 3 и т.д. вручную. А можно использовать автозаполнение.
Для автоматического ввода номеров напишем в ячейке А1 число 1, в ячейке А2 число 2. Выделим обе ячейки. Обратим внимание, что при наведении курсора в правый нижний угол ячейки А2 появился черный квадратик — это маркер заполнения.
Если навести на него курсор мыши, то курсор примет вид черного крестика. Теперь нужно нажать левую кнопку мыши и, удерживая, потянуть вниз. Рядом с курсором появляется значение, которое будет введено в последнюю ячейку, если отпустить кнопку мыши.
- Если в ячейку А1 ввести значение 1, а потом нажать на клавиатуре клавишу Ctrl и потянуть вниз за маркер заполнения этой ячейки, то значения следующих ячеек будут увеличиваться на 1.
- Чтобы ввести последовательность нечетных чисел (шаг увеличения чисел равен 2), введем в ячейку А1 число 1, а в ячейку А2 число 3. Далее выделим обе ячейки и за маркер заполнения потянем вниз. Мы получим последовательность чисел 1, 3, 5, 7 и т.д.
- Аналогично можно получить последовательность четных чисел, для этого нужно ввести числа 2 и 4 (шаг равен 2).
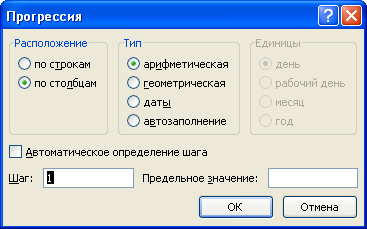
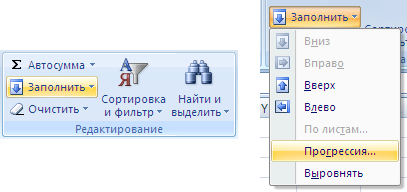
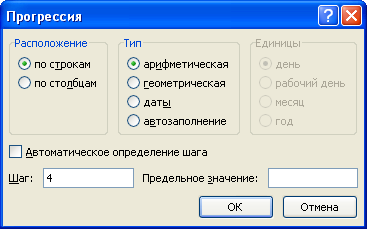
- Ввод арифметической (геометрической) прогрессии. Для создания арифметической прогрессии введем в ячейку А1 значение первого члена прогрессии. На вкладке Главная в группе Редактирование выберем команду Заполнить — Прогрессия.
В диалоговом окне Прогрессия можно установить параметры: Расположение, Тип прогрессии, Шаг, Предельное значение.
Если выбрать расположение по столбцам арифметической прогрессии с шагом 5 и предельным значением 25 (при этом в ячейке А1 введено значение 2, а сама ячейка выделена), то получим следующее заполнение:
Примечание
- Автозаполнение можно использовать не только по столбцам, но и по строкам. Для этого нужно вводить начальные значения в сроке и перетаскивать маркер заполнения не вниз, а вправо.
- Если нужно заполнять последовательность чисел в порядке возрастания, то маркер нужно перетаскивать вниз или вправо. Если в порядке убывания — вверх или влево.
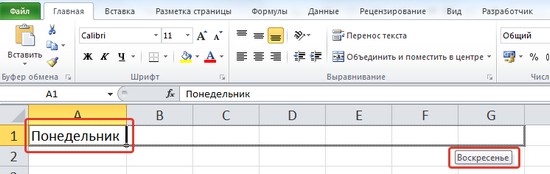
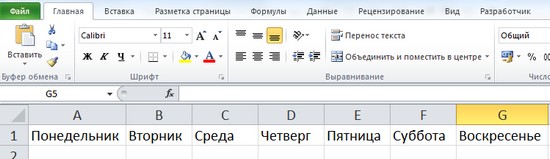
Последовательность дней недели
Чтобы ввести последовательность дней недели, достаточно в первую ячейку ввести Понедельник (или другой день) и потянуть за маркер заполнения этой ячейки в нужном направлении.
Последовательность Месяцы
Точно так же, как и в примере последовательности дней недели, в Excel можно получить последовательность месяцев, введя в первую ячейку нужный месяц (например, январь).
Последовательность дат
Введя в ячейку дату (например, 20.06.2015), можно получить последовательность дат.
Повторение последовательности
Если в ячейки А1, А2, А3 введены числа 1, 2, 3 соответственно и мы хотим, чтобы эта последовательность повторялась, выделим эти ячейки и при нажатой клавише Ctrl за маркер заполнения протянем вниз (или вправо), то мы получим последовательность 1, 2, 3, 1, 2, 3, 1, 2, 3…
Примечание
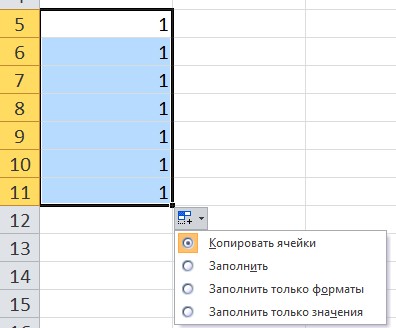
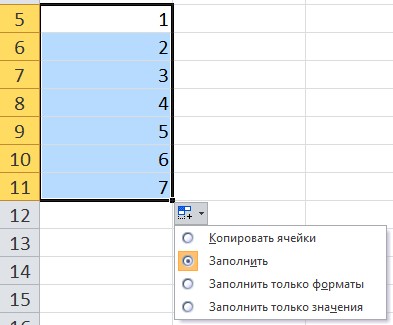
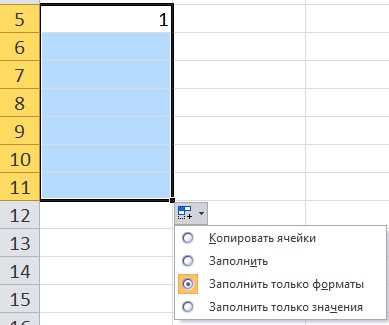
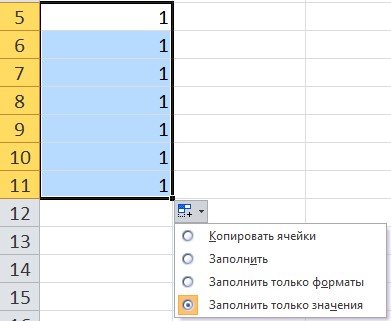
При использовании функции автозаполнения рядом с диапазоном появляется кнопка Параметры автозаполнения. При нажатии на нее можно выбрать нужный вариант.
В качестве примера введем в ячейку значение 1, за маркер заполнения протянем вниз. Обратим внимание, какой результат будет, если выбрать каждый из вариантов автозаполнения:
- Копирование ячейки — все значения равны 1.
- Заполнить — получим прогрессию с шагом 1.
- Заполнить только форматы — не будет значений, копируется форматирование ячеек.
Заполнить только значения — все значения равны 1, при этом форматирование ячейки не копируется.
Кстати, Excel позволяет делать свои списки последовательностей, которые потом можно использовать для автозаполнения таблиц. Читайте инструкцию >>>
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Автозаполнение ячеек Excel в прогрессии
Прогрессией называется последовательность чисел, каждое из которых может быть получено из предыдущего путем выполнения некоторой операции. Например, последовательность 1, 2, 3, 4 и т.д. является арифметической прогрессией с шагом 1 (каждое следующее число на 1 больше предыдущего). Даты тоже могут образовывать прогрессию. Например: 15.02.2014, 16.02.2014, 17.02.2014 (шаг — один день).
На фото приведены примеры таблиц, в которых есть ячейки, содержащие прогрессию.
- В стартовую ячейку диапазона ввести первое число ряда.
- Сделать щелчок в стартовой ячейке (ячейка будет выбрана, выделена рамкой).
- Установить указатель мыши на маркер в правом нижнем углу активной ячейки (указатель примет форму крестика), нажать и удерживать клавишу (рядом с указателем мыши появится знак «плюс»).
- Нажать левую кнопку мыши и, удерживая кнопку нажатой, переместить указатель мыши в последнюю ячейку диапазона.
- Отпустить кнопку мыши. Ячейки выделенного диапазона будут заполнены числами, образующими прогрессию.
Прогрессия дат вводится в ячейки таблицы аналогичным образом (за исключением того, что клавишу нажимать не надо). В процессе выделения диапазона рядом с курсором отображается дата, которая будет записана в последнюю ячейку диапазона. После записи в ячейки диапазона прогрессии дат, рядом с последней ячейкой диапазона отображается кнопка настройки параметров автозаполнения. Сделав щелчок на этой кнопке, можно выбрать правило формирования прогрессии дат, например, задать, что прогрессия должна состоять из дат рабочих дней.
Другие настройки Прогрессии можно посмотреть на вкладке Главная -> Редактирование выбрать команду Заполнить и из раскрывшегося списка — команду Прогрессия…
Опубликовано: 26.11.2015
Смотрите видео />
Программа предлагает уникальную возможность ввода данных. Давайте рассмотрим конкретный пример. При заполнении документа вам необходимо ввести порядковые номера с 1-го по 14-й. Можно вводить их вручную. Мы же воспользуемся возможностями программы.
Введите в ячейки значения как показано на рисунке.
Выделите ячейки В3 и В4, в которых расположены порядковые номера и , и поместите указатель мыши в правый нижний угол ячейки В4. Указатель примет вид черного крестика, который называется маркером автозаполнения.
Нажмите левую кнопку мыши и, удерживая её нажатой, перемещайте указатель вниз. Рядом с крестиком на жёлтом фоне появляется подсказка, показывающая какое сейчас значение порядкового номера. Когда значение будет равно , отпустите левую кнопку мыши.
Представьте, если бы вам понадобилось вводить вручную несколько сотен порядковых номеров. Данный приём автозаполнения позволяет вам значительно ускорить эту работу и избежать ошибок ввода.
В вышеприведённом примере мы вводили порядковые номера. Часто нам приходится вводить значения не по порядку, а в виде прогрессии с определённым шагом. Программа предоставляет нам эту возможность, которая значительно облегчит нам работу и предотвратит ошибки.
Автоматический ввод прогрессии
Прогрессия – ряд увеличивающихся или уменьшающихся чисел, в котором разность или отношение между соседними числами сохраняют постоянную величину.
Арифметическая прогрессия – последовательность чисел, каждое из которых получается из предыдущего путём прибавления или вычитания некоего постоянного числа.
Геометрическая прогрессия – последовательность чисел, каждое из которых получается из предыдущего путём умножения или деления на некое постоянное число.
Давайте рассмотрим пример заполнения арифметической прогрессии с шагом 4, т.е. каждый следующий член прогрессии образуется прибавлением к предыдущему числа 4 (1,5,9,13…).
Есть 2 варианта заполнения прогрессии. В первом примере мы будем использовать приём перетаскивания маркера автозаполнения. Во втором воспользуемся командами меню.
1. Введите в ячейку В2 значение «», а в ячейку В3 значение «». Выделите ячейки как показано на рисунке.
2. Поместите указатель мыши в правый нижний угол ячейки В3, при этом он примет вид чёрного крестика.
3. Нажмите левую кнопку мыши и, удерживая её нажатой, перемещайте указатель вниз. Рядом с указателем появляется подсказка, указывающая числовое значение. Когда дойдёте до нужного значения, отпустите левую кнопку мыши.
В данном примере программа автоматически определяет шаг последовательности. Достаточно только ввести два первых члена прогрессии.
Использование меню предоставляет нам больше возможностей для ввода прогрессий.
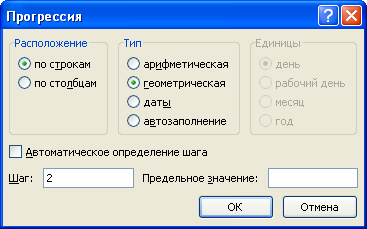
Давайте рассмотрим пример ввода геометрической прогрессии. В ходе рассмотрения примера вы легко разберётесь, как с помощью меню вводить любую прогрессию (и арифметическую, и геометрическую).
1. Введите в ячейку В2 значение «». Выделите необходимый диапазон ячеек, как показано на рисунке.
2. Установите указатель на надпись «Меню» на Ленте и один раз щёлкните левой кнопкой мыши.
3. Установите указатель на надпись «Правка» и один раз щёлкните левой кнопкой мыши. Справа автоматически появится ещё один список.
4. Установите указатель мыши на пункт «Прогрессия…» и один раз щёлкните левой кнопкой мыши.
На экране появится окно «Прогрессия». В этом окне необходимо сделать следующие установки:
1. Установите указатель на надпись «геометрическая» и один раз щёлкните левой кнопкой мыши.
2. Введите шаг прогрессии, например, 2.
3. Если необходимо, установите предельное значение. В этом случае будут заполнены только те ячейки, значение в которых не превысит предельное значение. Давайте зададим предельное значение «».
4. Установите указатель мыши на кнопку «ОК» и один раз щёлкните левой кнопкой мыши.
Если вы всё сделали правильно, выделенный диапазон будет заполнен, как показано на рисунке. Обратите внимание, что не все ячейки выделенного диапазона были заполнены. Это связано с тем, что мы ввели максимальные ограничения для прогрессии. Следующий после 640 член прогрессии больше 1000. На этом заполнение прогрессии было остановлено.
Ещё раз внимательно изучите окно Прогрессия. Теперь вы без труда сможете ввести в ячейки любую прогрессию по вашему желанию. Помимо числовых значений в качестве членов прогрессии могут выступать и даты.
Автозаполнение можно производить не только вертикально, но и по горизонтали. Давайте рассмотрим часто встречающийся пример, когда необходимо в качестве наименований столбцов указать месяца года.
1. Введите в ячейку В2 значение «Январь».
2. Установите указатель мыши в правый нижний угол ячейки.
После того как указатель примет вид чёрного крестика, нажмите левую кнопку мыши и перемещайте указатель вправо. Рядом с крестиком появляется подсказка, указывающая значение месяца. После достижения нужного месяца отпустите левую кнопку мыши. Ячейки будут заполнены месяцами.
Часто приходится вводить одинаковые значения в соседние ячейки. Можно, конечно, каждый раз копировать содержимое в ячейки. Гораздо удобнее и быстрее это можно сделать, используя маркер автозаполнения.
Заполнение ячеек одинаковым содержимым
1. Введите значение в первую ячейку диапазона.
2. Установите указатель в правый нижний угол ячейки.
3. После того, как указатель примет вид чёрного крестика, нажмите левую кнопку мыши и, удерживая её нажатой, переместите указатель в нужном направлении. После заполнения нужного диапазона отпустите левую кнопку мыши.
Мы использовали стандартный приём автоматического заполнения.
Удобно для заполнения ячеек одинаковым содержимым использовать следующий приём. Например, вам необходимо заполнить несколько ячеек столбца одинаковыми значениями.
1. Введите содержимое первой ячейки диапазона.
2. Выделите те ячейки, в которые необходимо скопировать данное значение.
3. Войдите в меню «Правка» и выберите пункт «Заполнить».
4. Слева от пункта «Заполнить» появится список с указанием направления, в котором будут заполнены ячейки. Установите указатель мыши на пункт «Вниз» и один раз щёлкните левой кнопкой мыши.
Программа подсказывает, что для заполнения диапазона ячеек вниз можно воспользоваться комбинацией клавиш:
Ctrl + D
Пункты 3 и 4 вы можете заменить простым нажатием вышеуказанной комбинации клавиш.
Нажмите на клавиатуре клавишу и, удерживая её нажатой, нажмите клавишу с английской буквой «D» (русская буква «В»).
До этого мы вводили в ячейки числовые и текстовые значения.
Теперь мы приступаем к изучению самого важного раздела, который позволит вам научиться вводить в ячейки нужные формулы.
Изучим как сделать арифметическую и геометрическую прогрессии в Excel, а также в общем случае рассмотрим способы создания числовых последовательностей.
Перед построением последовательностей и различных прогрессий, как обычно, вспомним их детальные определения.
Числовая последовательность — это упорядоченный набор произвольных чисел a1, a2, a3, …, an, … .
Арифметической прогрессией называется такая числовая последовательность, в которой каждый член, начиная со второго, получается из предыдущего добавлением постоянной величины d (также называют шагом или разностью):
Геометрическая прогрессия — это последовательность чисел, в котором каждый член, начиная со второго, получается умножением предыдущего члена на ненулевое число q (также называют знаменателем):
С определениями закончили, теперь самое время перейти от теории к практике.
Рассмотрим 2 способа задания прогрессии в Excel — с помощью стандартного инструмента Прогрессия и через формулы.
В первом случае на панели вкладок выбираем Главная -> Редактирование -> Заполнить -> Прогрессия:
Далее мы увидим диалоговое окно с настройками параметров:
В данных настройках мы можем выбрать дополнительные параметры, которые позволят нам более детально настроить и заполнить прогрессию в Excel:
- Расположение — расположение заполнения (по столбцам или строкам);
- Тип — тип (арифметическая, геометрическая, даты и автозаполнение);
- Единицы — вид данных (при выборе даты в качестве типа);
- Шаг — шаг (для арифметической) или знаменатель (для геометрической);
- Автоматическое определение шага — автоматическое определение шага, если заданы несколько значений последовательности;
- Предельное значение — ограничение по значению последнего элемента последовательности.
Разберем как сделать арифметическую прогрессию в Excel на конкретном примере.
Создадим набор чисел 3, 7, 11, … , то есть первый элемент равняется 3, а шаг равен 4.
Выделяем диапазон (к примеру, A1:J1) в котором мы хотим разместить набор чисел (диапазон можно и не выделять, однако в этом случае в настройках будет необходимо указать предельное значение), где в первой ячейке будет указан первый элемент (в нашем примере это 3 в ячейке A1), и указываем параметры (расположение, тип, шаг и т.д.):
В результате мы получим заполненный диапазон с заданным набором чисел:
Аналогичный результат можно получить и при задании элементов с помощью формул.
Для этого также задаем начальный элемент в первой ячейке, а в последующих ячейках указываем рекуррентную формулу члена арифметической прогрессии (то есть текущий член получается как сумма предыдущего и шага):
Геометрическая прогрессия в Excel
Принцип построения геометрической прогрессии в Excel аналогичен разобранному выше построению арифметической.
Единственное отличие — в настройках характеристик указываем в качестве типа геометрическую прогрессию.
Например, создадим набор чисел 4, 8, 16, … , то есть первое число равно 4, а каждое последующее в 2 раза больше предыдущего.
Также задаем начальный элемент (4 в ячейке A1), выделяем диапазон данных (например, A1:J1) и указываем параметры:
В итоге получаем:
Идентичного результата также можно добиться и через использование формул:
Числовая последовательность в Excel
Арифметическая и геометрическая прогрессии являются частными случаями числовой последовательности, в общем же случае ее можно создать, как минимум, тремя способами:
- Непосредственное (прямое) перечисление элементов;
- Через общую формулу n-го члена;
- С помощью рекуррентного соотношения, которое выражает произвольный член через предыдущие.
Первый способ подразумевает под собой ручной ввод значений в ячейки. Удобный вариант при вводе небольшого количества значений, в обратном же случае данный способ достаточно трудозатратный.
Второй и третий способы более универсальны, так как позволяют автоматически посчитать значения членов с помощью формул, что удобно при большом количестве элементов.
Поэтому поподробнее остановимся на построении последовательностей данными способами.
Рассмотрим создание числовой последовательности на примере построения обратных чисел к натуральным, то есть набора чисел 1, 1/2, 1/3, … , в котором общая формула n-го члена принимает вид Fn=1/n.
Создадим дополнительный ряд в отдельной строчке, куда для удобства расчета поместим порядковые номера (1, 2, 3 и т.д.), на которые будут ссылаться формулы:
В варианте с рекуррентной формулой рассмотрим пример с набором чисел Фибоначчи, в котором первые два числа равны 1 и 1, а каждый последующее число равно сумме двух предыдущих.
В итоге произвольный член можно представить в виде рекуррентного соотношения Fn = Fn-1 + Fn-2 при n > 2.
Определяем начальные элементы (две единицы) в двух ячейках, а остальные задаем с помощью формулы:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!
Кроме простого автозаполнения ячеек данными при необходимости можно создать и арифметическую прогрессию. Excel 2007 может автоматически продолжать заполнение прогрессии числами, комбинациями чисел и текста, датами и временем, основываясь на установленном образце.
1 способ:
- В окне открытого листа введите начальные значения создаваемого ряда прогрессии в первую ячейку и вторую ячейку диапазона.
Например: 1, 2; 07:00, 08:00; пн, вт; янв, фев. - Выделите эти ячейки и наведите курсор на правый нижний угол выделенной зоны.
- Курсором в виде тонкого черного креста при нажатой левой кнопке мыши протащите маркер заполнения по столбцу (вверх или вниз) либо по строке (вправо или влево).
Получится результат – 4,5; 09:00, 10:00; ср, чт; мар, апр.
Примечание
Чтобы использовать принцип автозаполнения ячеек, а не создание арифметической прогрессии, при использовании маркера заполнения нажмите и держите клавишу Ctrl.
2 способ:
- В окне открытого листа в первую ячейку диапазона введите начальное значение создаваемого ряда прогрессии.
- Наведите курсор мыши на правый нижний угол ячейки и, когда курсор станет тонким черным крестом, при нажатой ПРАВОЙ кнопке мыши протащите маркер заполнения вверх или вниз по столбцу либо вправо, либо влево по строке.
- В конце нужного диапазона отпустите правую кнопку мыши.
- В контекстном меню выберите пункт «Заполнить».
3 способ:
- В окне открытого листа введите начальные значения создаваемого ряда прогрессии в первую ячейку и вторую ячейку диапазона.
- Выделите эти ячейки и наведите курсор на правый нижний угол выделенной зоны.
- Курсором в виде тонкого черного креста при нажатой ПРАВОЙ кнопке мыши протащите маркер заполнения по столбцу (вверх или вниз) или по строке (вправо или влево) и отпустите кнопку мыши.
- В контекстном меню выберите в списке пункт «Линейное приближение» (рис. 2.108).
Рис. 2.108. Контекстное меню прогрессии
4 способ:
- В окне открытого листа введите начальное значение создаваемого ряда прогрессии в первую ячейку диапазона.
- Выделите диапазон ячеек и перейдите к вкладке «Главная».
- В группе «Редактирование» раскройте меню кнопки «Заполнить» и в списке команд выберите пункт «Прогрессия» (рис. 2.109).
- В окне «Прогрессия» (рис. 2.110) в группе «Тип» активируйте пункт «Арифметическая».
- В графе «Шаг» введите число развития прогрессии, то есть значение, на которое будут увеличиваться все числа, а в графе «Предельное значение» при необходимости задайте максимально возможное число прогрессии.
- Закройте окно кнопкой «ОК»
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel для iPad Excel для iPhone Excel для планшетов с Android Excel для телефонов с Android Еще…Меньше
Функция ПОСЛЕДОВ позволяет создать список последовательных чисел в массиве, например 1, 2, 3, 4.
В приведенном ниже примере создан массив из 4 строк и 5 столбцов с помощью формулы =ПОСЛЕДОВ(4;5).
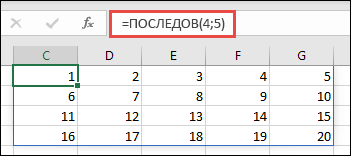
=ПОСЛЕДОВ(строки;[столбцы];[начало];[шаг])
|
Аргумент |
Описание |
|---|---|
|
строки Обязательный |
Количество возвращаемых строк |
|
[столбцы] Необязательный |
Количество возвращаемых столбцов |
|
[начало] Необязательный |
Первое число в последовательности |
|
[шаг] Необязательный |
Величина приращения каждого последующего значения в массиве |
Примечания:
-
Любому отсутствующему необязательному аргументу по умолчанию присваивается значение 1. Если опустить аргумент rows, необходимо указать хотя бы один другой аргумент.
-
Массив может рассматриваться как строка со значениями, столбец со значениями или комбинация строк и столбцов со значениями. В приведенном выше примере массивом для формулы ПОСЛЕДОВ является диапазон C1:G4.
-
Функция ПОСЛЕДОВ возвращает массив, который будет рассеиваться, если это будет конечным результатом формулы. Это означает, что Excel будет динамически создавать соответствующий по размеру диапазон массива при нажатии клавиши ВВОД. Если ваши вспомогательные данные хранятся в таблице Excel, тогда массив будет автоматически изменять размер при добавлении и удалении данных из диапазона массива, если вы используете структурированные ссылки. Дополнительные сведения см. в статье Поведение рассеянного массива.
-
Приложение Excel ограничило поддержку динамических массивов в операциях между книгами, и этот сценарий поддерживается, только если открыты обе книги. Если закрыть исходную книгу, все связанные формулы динамического массива вернут ошибку #ССЫЛКА! после обновления.
Пример
Ниже приведен пример быстрого создания набора данных с использованием функции ПОСЛЕДОВ совместно с функциями ТЕКСТ, ДАТА, ГОД и СЕГОДНЯ, позволяющий получить динамический список месяцев для строки заголовка, в котором исходной датой всегда будет текущий год. Наша формула: =ТЕКСТ(ДАТА(ГОД(СЕГОДНЯ()),ПОСЛЕДОВ(1,6),1),»mmm»).
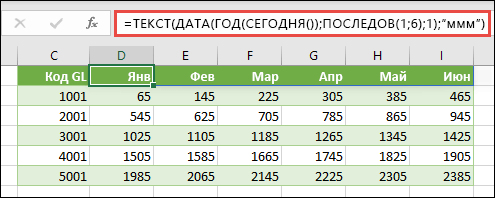
Ниже приведен пример использования в функции ПОСЛЕДОВ вложенных функций ЦЕЛОЕ и СЛЧИС для создания массива из 5 строк и 6 столбцов со случайным набором возрастающих целых чисел. Наша формула: =ПОСЛЕДОВ(5,6,ЦЕЛОЕ(СЛЧИС()*100),ЦЕЛОЕ(СЛЧИС()*100)).
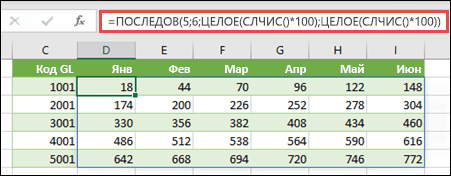
Кроме того, можно использовать формулу =ПОСЛЕДОВ(5;1;1001;1000), чтобы создать последовательный список кодов Главной книги (GL) в примерах.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Функция ФИЛЬТР
Функция СЛУЧМАССИВ
Функция СОРТ
Функция СОРТПО
Функция УНИК
Ошибки #ПЕРЕНОС! в Excel
Динамические массивы и поведение массива с переносом
Оператор неявного пересечения: @
Нужна дополнительная помощь?
Изучим как сделать арифметическую и геометрическую прогрессии в Excel, а также в общем случае рассмотрим способы создания числовых последовательностей.
Перед построением последовательностей и различных прогрессий, как обычно, вспомним их детальные определения.
Числовая последовательность — это упорядоченный набор произвольных чисел a1, a2, a3, …, an, … .
Арифметической прогрессией называется такая числовая последовательность, в которой каждый член, начиная со второго, получается из предыдущего добавлением постоянной величины d (также называют шагом или разностью):
Геометрическая прогрессия — это последовательность чисел, в котором каждый член, начиная со второго, получается умножением предыдущего члена на ненулевое число q (также называют знаменателем):
С определениями закончили, теперь самое время перейти от теории к практике.
Рассмотрим 2 способа задания прогрессии в Excel — с помощью стандартного инструмента Прогрессия и через формулы.
В первом случае на панели вкладок выбираем Главная -> Редактирование -> Заполнить -> Прогрессия:
Далее мы увидим диалоговое окно с настройками параметров:
В данных настройках мы можем выбрать дополнительные параметры, которые позволят нам более детально настроить и заполнить прогрессию в Excel:
- Расположение — расположение заполнения (по столбцам или строкам);
- Тип — тип (арифметическая, геометрическая, даты и автозаполнение);
- Единицы — вид данных (при выборе даты в качестве типа);
- Шаг — шаг (для арифметической) или знаменатель (для геометрической);
- Автоматическое определение шага — автоматическое определение шага, если заданы несколько значений последовательности;
- Предельное значение — ограничение по значению последнего элемента последовательности.
Разберем как сделать арифметическую прогрессию в Excel на конкретном примере.
Создадим набор чисел 3, 7, 11, … , то есть первый элемент равняется 3, а шаг равен 4.
Выделяем диапазон (к примеру, A1:J1) в котором мы хотим разместить набор чисел (диапазон можно и не выделять, однако в этом случае в настройках будет необходимо указать предельное значение), где в первой ячейке будет указан первый элемент (в нашем примере это 3 в ячейке A1), и указываем параметры (расположение, тип, шаг и т.д.):
В результате мы получим заполненный диапазон с заданным набором чисел:
Аналогичный результат можно получить и при задании элементов с помощью формул.
Для этого также задаем начальный элемент в первой ячейке, а в последующих ячейках указываем рекуррентную формулу члена арифметической прогрессии (то есть текущий член получается как сумма предыдущего и шага):
Геометрическая прогрессия в Excel
Принцип построения геометрической прогрессии в Excel аналогичен разобранному выше построению арифметической.
Единственное отличие — в настройках характеристик указываем в качестве типа геометрическую прогрессию.
Например, создадим набор чисел 4, 8, 16, … , то есть первое число равно 4, а каждое последующее в 2 раза больше предыдущего.
Также задаем начальный элемент (4 в ячейке A1), выделяем диапазон данных (например, A1:J1) и указываем параметры:
В итоге получаем:
Идентичного результата также можно добиться и через использование формул:
Числовая последовательность в Excel
Арифметическая и геометрическая прогрессии являются частными случаями числовой последовательности, в общем же случае ее можно создать, как минимум, тремя способами:
- Непосредственное (прямое) перечисление элементов;
- Через общую формулу n-го члена;
- С помощью рекуррентного соотношения, которое выражает произвольный член через предыдущие.
Первый способ подразумевает под собой ручной ввод значений в ячейки. Удобный вариант при вводе небольшого количества значений, в обратном же случае данный способ достаточно трудозатратный.
Второй и третий способы более универсальны, так как позволяют автоматически посчитать значения членов с помощью формул, что удобно при большом количестве элементов.
Поэтому поподробнее остановимся на построении последовательностей данными способами.
Рассмотрим создание числовой последовательности на примере построения обратных чисел к натуральным, то есть набора чисел 1, 1/2, 1/3, … , в котором общая формула n-го члена принимает вид Fn=1/n.
Создадим дополнительный ряд в отдельной строчке, куда для удобства расчета поместим порядковые номера (1, 2, 3 и т.д.), на которые будут ссылаться формулы:
В варианте с рекуррентной формулой рассмотрим пример с набором чисел Фибоначчи, в котором первые два числа равны 1 и 1, а каждый последующее число равно сумме двух предыдущих.
В итоге произвольный член можно представить в виде рекуррентного соотношения Fn = Fn-1 + Fn-2 при n > 2.
Определяем начальные элементы (две единицы) в двух ячейках, а остальные задаем с помощью формулы:
Удачи вам и до скорых встреч на страницах блога Tutorexcel.ru!