Показательное уравнение регрессии
В случае b = e (примерное значение экспоненты e ≈ 2.718281828 ), показательное уравнение регрессии называется экспоненциальным и записывается как y=a·e x .
Здесь b — темп изменения в разах или константа тренда, которая показывает тенденцию ускоренного и все более ускоряющегося возрастания уровней.
Пример . Необходимо изучить зависимость потребительским расходами на моторное масло (у) и располагаемым личным доходом (х).
Составляем систему нормальных уравнений с помощью онлайн-калькулятора Нелинейная регрессия .
Для наших данных система уравнений имеет вид
21a + 20439.4 b = 32.32
20439.4 a + 20761197.38 b = 31007.03
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = -0.000515, a = 2.04
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e 2.04 *e -0.000515x = 7.69529*0.99948 x
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
a•n + b∑x = ∑y a∑x + b∑x 2 = ∑y•x
| log(y) 2 | x·log(y) | |||
| 622.9 | 1.59 | 388004.41 | 2.53 | 989.93 |
| 658 | 1.65 | 432964 | 2.72 | 1084.82 |
| 700.4 | 1.7 | 490560.16 | 2.91 | 1194.01 |
| 740.6 | 1.72 | 548488.36 | 2.97 | 1275.88 |
| 774.4 | 1.72 | 599695.36 | 2.97 | 1334.11 |
| 816.2 | 1.67 | 666182.44 | 2.78 | 1361.18 |
| 853.5 | 1.61 | 728462.25 | 2.59 | 1373.66 |
| 876.8 | 1.55 | 768778.24 | 2.39 | 1356.9 |
| 900 | 1.53 | 810000 | 2.33 | 1373.45 |
| 951.4 | 1.61 | 905161.96 | 2.59 | 1531.22 |
| 1007.9 | 1.69 | 1015862.41 | 2.84 | 1699.72 |
| 1004.8 | 1.44 | 1009623.04 | 2.06 | 1441.97 |
| 1010.8 | 1.44 | 1021716.64 | 2.06 | 1450.58 |
| 1056.2 | 1.53 | 1115558.44 | 2.33 | 1611.82 |
| 1105.4 | 1.48 | 1221909.16 | 2.2 | 1637.77 |
| 1162.3 | 1.55 | 1350941.29 | 2.39 | 1798.73 |
| 1200.7 | 1.55 | 1441680.49 | 2.39 | 1858.16 |
| 1209.5 | 1.36 | 1462890.25 | 1.85 | 1646.1 |
| 1248.6 | 1.28 | 1559001.96 | 1.64 | 1599.37 |
| 1254.4 | 1.28 | 1573519.36 | 1.64 | 1606.8 |
| 1284.6 | 1.39 | 1650197.16 | 1.92 | 1780.83 |
| 20439.4 | 32.32 | 20761197.38 | 50.1 | 31007.03 |
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Показательная парная регрессия.
1.4 Гиперболическая парная регрессия рассчитывается по формуле:
Для определения параметров a и b необходимо линеаризировать предыдущую формулу. Для этого сделаем замену:
Тогда
Для определения параметров a и b используем следующие формулы:
В таблице рассчитываем средние значения величин x, x*, y, x*y, x* 2 .
| n | у | х | x*=1/x | x*x* | x*y |
| 11,92 | 18,26 | 0,0548 | 0,002999 | 0,652793 | |
| 8,34 | 21,90 | 0,0457 | 0,002085 | 0,380822 | |
| 7,08 | 12,12 | 0,0825 | 0,006808 | 0,584158 | |
| 10,52 | 17,52 | 0,0571 | 0,003258 | 0,600457 | |
| 18,68 | 26,28 | 0,0381 | 0,001448 | 0,710807 | |
| 8,24 | 11,86 | 0,0843 | 0,007109 | 0,694772 | |
| 10,50 | 15,08 | 0,0663 | 0,004397 | 0,696286 | |
| 7,34 | 10,56 | 0,0947 | 0,008968 | 0,695076 | |
| 7,28 | 10,40 | 0,0962 | 0,009246 | 0,7 | |
| 6,72 | 10,78 | 0,0928 | 0,008605 | 0,623377 | |
| 8,18 | 10,80 | 0,0926 | 0,008573 | 0,757407 | |
| 9,04 | 13,64 | 0,0733 | 0,005375 | 0,662757 | |
| 7,34 | 10,74 | 0,0931 | 0,008669 | 0,683426 | |
| 6,56 | 11,78 | 0,0849 | 0,007206 | 0,556876 | |
| 9,20 | 12,52 | 0,0799 | 0,00638 | 0,734824 | |
| 7,60 | 10,42 | 0,0960 | 0,00921 | 0,729367 | |
| 8,78 | 12,52 | 0,0799 | 0,00638 | 0,701278 | |
| 6,88 | 10,42 | 0,0960 | 0,00921 | 0,660269 | |
| 8,02 | 13,16 | 0,0760 | 0,005774 | 0,609422 | |
| 10,28 | 14,92 | 0,0670 | 0,004492 | 0,689008 | |
| среднее | 8,9250 | 13,7840 | 0,0775 | 0,0063 | 0,6562 |
Вычислим значение коэффициента регрессии b:
Вычислим значение коэффициента регрессии a:
Тогда показательное уравнение регрессии будет выглядеть следующим образом:
Гиперболическая парная регрессия.
- Оцените тесноту связи с помощью показателей корреляции и детерминации.
Оценка тесноты связи с помощью показателей корреляции.
2.1.1 Показатель корреляции для линейной регрессии:



| n | у | х | xx | xy | yy |
| 11,92 | 18,26 | 333,4276 | 217,6592 | 142,0864 | |
| 8,34 | 21,9 | 479,6100 | 182,6460 | 69,5556 | |
| 7,08 | 12,12 | 146,8944 | 85,8096 | 50,1264 | |
| 10,52 | 17,52 | 306,9504 | 184,3104 | 110,6704 | |
| 18,68 | 26,28 | 690,6384 | 490,9104 | 348,9424 | |
| 8,24 | 11,86 | 140,6596 | 97,7264 | 67,8976 | |
| 10,5 | 15,08 | 227,4064 | 158,3400 | 110,2500 | |
| 7,34 | 10,56 | 111,5136 | 77,5104 | 53,8756 | |
| 7,28 | 10,4 | 108,1600 | 75,7120 | 52,9984 | |
| 6,72 | 10,78 | 116,2084 | 72,4416 | 45,1584 | |
| 8,18 | 10,8 | 116,6400 | 88,3440 | 66,9124 | |
| 9,04 | 13,64 | 186,0496 | 123,3056 | 81,7216 | |
| 7,34 | 10,74 | 115,3476 | 78,8316 | 53,8756 | |
| 6,56 | 11,78 | 138,7684 | 77,2768 | 43,0336 | |
| 9,2 | 12,52 | 156,7504 | 115,1840 | 84,6400 | |
| 7,6 | 10,42 | 108,5764 | 79,1920 | 57,7600 | |
| 8,78 | 12,52 | 156,7504 | 109,9256 | 77,0884 | |
| 6,88 | 10,42 | 108,5764 | 71,6896 | 47,3344 | |
| 8,02 | 13,16 | 173,1856 | 105,5432 | 64,3204 | |
| 10,28 | 14,92 | 222,6064 | 153,3776 | 105,6784 | |
| среднее | 8,925 | 13,784 | 207,236 | 132,2868 | 86,6963 |
Определим среднеквадратические отклонения:
Определим показатель корреляции: 
2.1.2 Показатель корреляции для степенной регрессии:



| n | у | х | x*=lg(x) | y*=lg(y) | y*y* | ŷ* | e=y*-ŷ* | ee |
| 11,92 | 18,26 | 1,2615 | 1,0763 | 1,1584 | 1,0435 | 0,0328 | 0,0011 | |
| 8,34 | 21,90 | 1,3404 | 0,9212 | 0,8485 | 1,1048 | -0,1836 | 0,0337 | |
| 7,08 | 12,12 | 1,0835 | 0,8500 | 0,7226 | 0,9053 | -0,0553 | 0,0031 | |
| 10,52 | 17,52 | 1,2435 | 1,0220 | 1,0445 | 1,0296 | -0,0075 | 0,0001 | |
| 18,68 | 26,28 | 1,4196 | 1,2714 | 1,6164 | 1,1663 | 0,1051 | 0,0111 | |
| 8,24 | 11,86 | 1,0741 | 0,9159 | 0,8389 | 0,8980 | 0,0179 | 0,0003 | |
| 10,50 | 15,08 | 1,1784 | 1,0212 | 1,0428 | 0,9790 | 0,0422 | 0,0018 | |
| 7,34 | 10,56 | 1,0237 | 0,8657 | 0,7494 | 0,8589 | 0,0068 | 0,0000 | |
| 7,28 | 10,40 | 1,0170 | 0,8621 | 0,7433 | 0,8537 | 0,0084 | 0,0001 | |
| 6,72 | 10,78 | 1,0326 | 0,8274 | 0,6845 | 0,8658 | -0,0385 | 0,0015 | |
| 8,18 | 10,80 | 1,0334 | 0,9128 | 0,8331 | 0,8664 | 0,0463 | 0,0021 | |
| 9,04 | 13,64 | 1,1348 | 0,9562 | 0,9143 | 0,9452 | 0,0110 | 0,0001 | |
| 7,34 | 10,74 | 1,0310 | 0,8657 | 0,7494 | 0,8646 | 0,0011 | 0,0000 | |
| 6,56 | 11,78 | 1,0711 | 0,8169 | 0,6673 | 0,8957 | -0,0788 | 0,0062 | |
| 9,20 | 12,52 | 1,0976 | 0,9638 | 0,9289 | 0,9163 | 0,0475 | 0,0023 | |
| 7,60 | 10,42 | 1,0179 | 0,8808 | 0,7758 | 0,8544 | 0,0264 | 0,0007 | |
| 8,78 | 12,52 | 1,0976 | 0,9435 | 0,8902 | 0,9163 | 0,0272 | 0,0007 | |
| 6,88 | 10,42 | 1,0179 | 0,8376 | 0,7016 | 0,8544 | -0,0168 | 0,0003 | |
| 8,02 | 13,16 | 1,1193 | 0,9042 | 0,8175 | 0,9331 | -0,0289 | 0,0008 | |
| 10,28 | 14,92 | 1,1738 | 1,0120 | 1,0241 | 0,9754 | 0,0366 | 0,0013 | |
| среднее | 8,9250 | 13,7840 | 1,1234 | 0,9363 | 0,8876 | 0,936325 | 0,000003 | 0,003364 |
Определим индекс корреляции:



2.1.3 Показатель корреляции для показательной регрессии:

| n | у | х | y*=lg(y) | y*y* | ŷ* | e=y*-ŷ* | ee |
| 11,92 | 18,26 | 1,0763 | 1,1584 | 1,0303 | 0,0460 | 0,0021 | |
| 8,34 | 21,90 | 0,9212 | 0,8485 | 1,1067 | -0,1855 | 0,0344 | |
| 7,08 | 12,12 | 0,8500 | 0,7226 | 0,9013 | -0,0513 | 0,0026 | |
| 10,52 | 17,52 | 1,0220 | 1,0445 | 1,0147 | 0,0073 | 0,0001 | |
| 18,68 | 26,28 | 1,2714 | 1,6164 | 1,1987 | 0,0727 | 0,0053 | |
| 8,24 | 11,86 | 0,9159 | 0,8389 | 0,8959 | 0,0201 | 0,0004 | |
| 10,50 | 15,08 | 1,0212 | 1,0428 | 0,9635 | 0,0577 | 0,0033 | |
| 7,34 | 10,56 | 0,8657 | 0,7494 | 0,8686 | -0,0029 | 0,0000 | |
| 7,28 | 10,40 | 0,8621 | 0,7433 | 0,8652 | -0,0031 | 0,0000 | |
| 6,72 | 10,78 | 0,8274 | 0,6845 | 0,8732 | -0,0458 | 0,0021 | |
| 8,18 | 10,80 | 0,9128 | 0,8331 | 0,8736 | 0,0392 | 0,0015 | |
| 9,04 | 13,64 | 0,9562 | 0,9143 | 0,9332 | 0,0229 | 0,0005 | |
| 7,34 | 10,74 | 0,8657 | 0,7494 | 0,8723 | -0,0066 | 0,0000 | |
| 6,56 | 11,78 | 0,8169 | 0,6673 | 0,8942 | -0,0773 | 0,0060 | |
| 9,20 | 12,52 | 0,9638 | 0,9289 | 0,9097 | 0,0541 | 0,0029 | |
| 7,60 | 10,42 | 0,8808 | 0,7758 | 0,8656 | 0,0152 | 0,0002 | |
| 8,78 | 12,52 | 0,9435 | 0,8902 | 0,9097 | 0,0338 | 0,0011 | |
| 6,88 | 10,42 | 0,8376 | 0,7016 | 0,8656 | -0,0280 | 0,0008 | |
| 8,02 | 13,16 | 0,9042 | 0,8175 | 0,9232 | -0,0190 | 0,0004 | |
| 10,28 | 14,92 | 1,0120 | 1,0241 | 0,9601 | 0,0519 | 0,0027 | |
| среднее | 8,9250 | 13,7840 | 0,9363 | 0,8876 | 0,9363 | 0,0001 | 0,0033 |
Определим индекс корреляции:



2.1.4 Показатель корреляции для гиперболической регрессии:

| n | у | х | x*=1/x | y*y | ŷ | e=y-ŷ | ee |
| 11,92 | 18,26 | 0,0548 | 142,0864 | 11,6717 | 0,2483 | 0,0617 | |
| 8,34 | 21,90 | 0,0457 | 69,5556 | 12,7713 | -4,4313 | 19,6367 | |
| 7,08 | 12,12 | 0,0825 | 50,1264 | 8,3200 | -1,2400 | 1,5376 | |
| 10,52 | 17,52 | 0,0571 | 110,6704 | 11,3922 | -0,8722 | 0,7608 | |
| 18,68 | 26,28 | 0,0381 | 348,9424 | 13,6907 | 4,9893 | 24,8929 | |
| 8,24 | 11,86 | 0,0843 | 67,8976 | 8,1015 | 0,1385 | 0,0192 | |
| 10,50 | 15,08 | 0,0663 | 110,2500 | 10,2765 | 0,2235 | 0,0499 | |
| 7,34 | 10,56 | 0,0947 | 53,8756 | 6,8475 | 0,4925 | 0,2426 | |
| 7,28 | 10,40 | 0,0962 | 52,9984 | 6,6715 | 0,6085 | 0,3703 | |
| 6,72 | 10,78 | 0,0928 | 45,1584 | 7,0810 | -0,3610 | 0,1303 | |
| 8,18 | 10,80 | 0,0926 | 66,9124 | 7,1017 | 1,0783 | 1,1627 | |
| 9,04 | 13,64 | 0,0733 | 81,7216 | 9,4308 | -0,3908 | 0,1527 | |
| 7,34 | 10,74 | 0,0931 | 53,8756 | 7,0392 | 0,3008 | 0,0905 | |
| 6,56 | 11,78 | 0,0849 | 43,0336 | 8,0323 | -1,4723 | 2,1677 | |
| 9,20 | 12,52 | 0,0799 | 84,6400 | 8,6385 | 0,5615 | 0,3153 | |
| 7,60 | 10,42 | 0,0960 | 57,7600 | 6,6938 | 0,9062 | 0,8212 | |
| 8,78 | 12,52 | 0,0799 | 77,0884 | 8,6385 | 0,1415 | 0,0200 | |
| 6,88 | 10,42 | 0,0960 | 47,3344 | 6,6938 | 0,1862 | 0,0347 | |
| 8,02 | 13,16 | 0,0760 | 64,3204 | 9,1077 | -1,0877 | 1,1831 | |
| 10,28 | 14,92 | 0,0670 | 105,6784 | 10,1906 | 0,0894 | 0,0080 | |
| среднее | 8,9250 | 13,7840 | 0,0775 | 86,6963 | 8,9195 | 0,0055 | 2,6829 |
Определим индекс корреляции:



Вывод:
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1
источники:
http://lumpics.ru/regression-analysis-in-excel/
http://zdamsam.ru/b52151.html
17 авг. 2022 г.
читать 2 мин
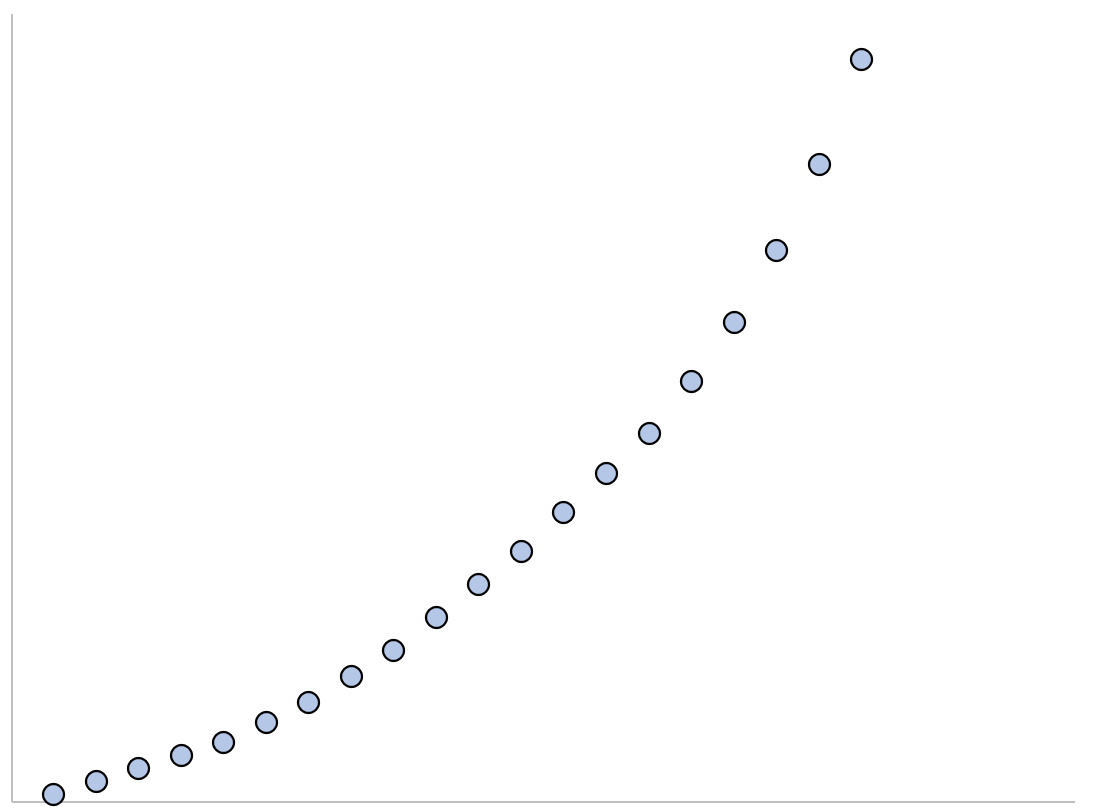
Экспоненциальная регрессия — это тип модели регрессии, который можно использовать для моделирования следующих ситуаций:
1. Экспоненциальный рост: рост начинается медленно, а затем стремительно ускоряется без ограничений.
2. Экспоненциальное затухание: затухание начинается быстро, а затем замедляется, приближаясь к нулю.
Уравнение модели экспоненциальной регрессии принимает следующий вид:
у = аб х
куда:
- y: переменная ответа
- x: предикторная переменная
- a, b: коэффициенты регрессии, описывающие взаимосвязь между x и y .
В следующем пошаговом примере показано, как выполнить экспоненциальную регрессию в Excel.
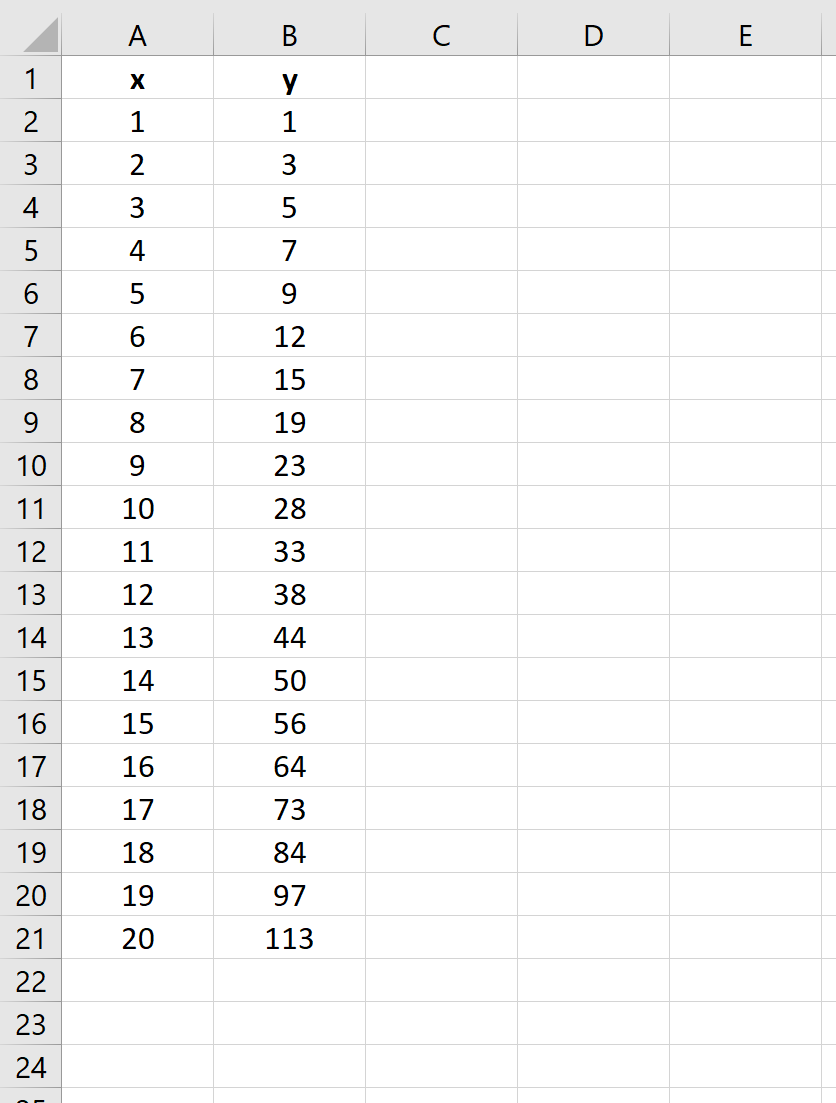
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных, содержащий 20 наблюдений :
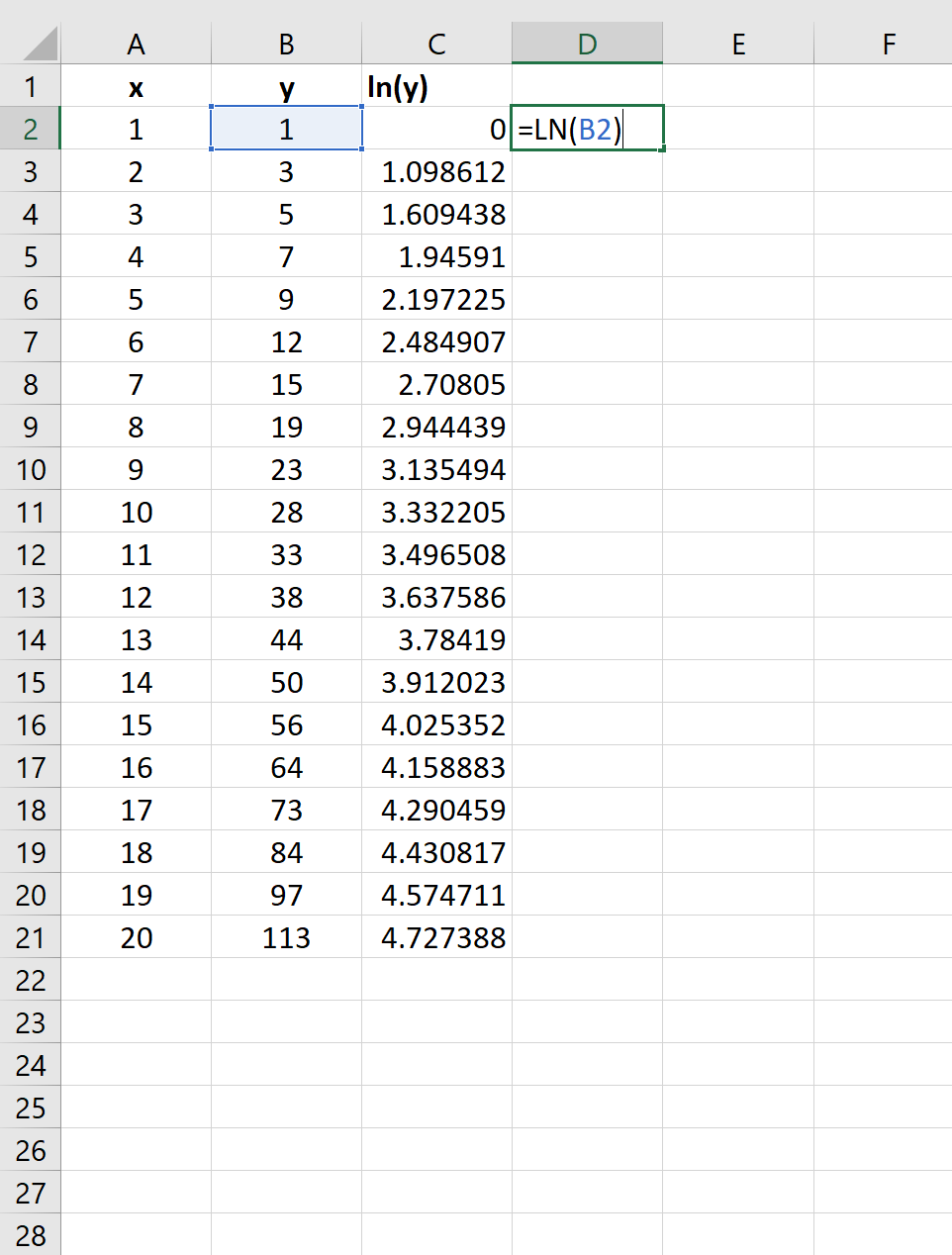
Шаг 2: возьмите натуральный логарифм переменной отклика
Далее нам нужно создать новый столбец, представляющий естественный журнал переменной ответа y :
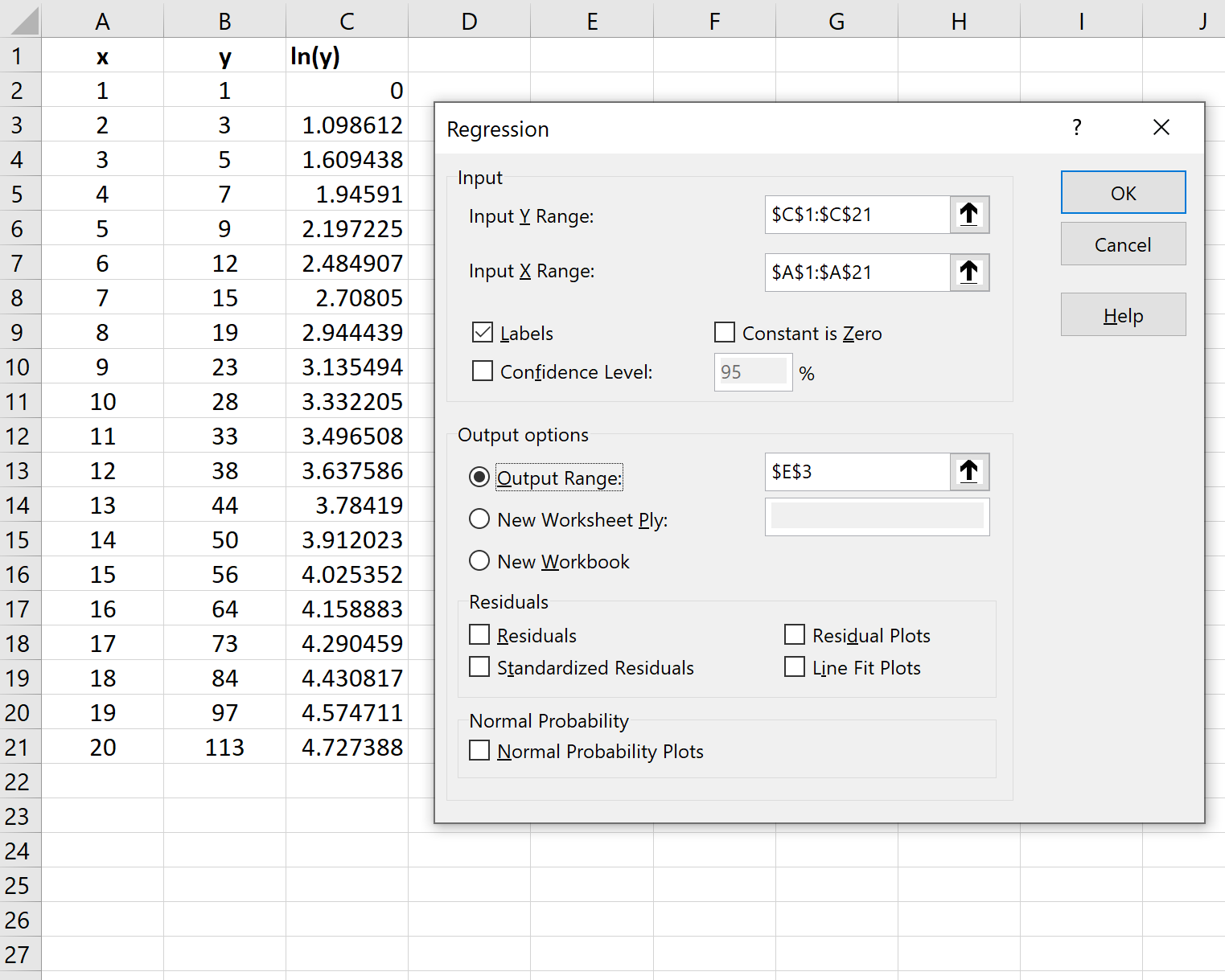
Шаг 3: Подберите модель экспоненциальной регрессии
Далее мы подгоним модель экспоненциальной регрессии. Для этого щелкните вкладку « Данные » на верхней ленте, затем щелкните « Анализ данных» в группе « Анализ ».
Если вы не видите Data Analysis в качестве опции, вам нужно сначала загрузить Analysis ToolPak .
В появившемся окне нажмите Регрессия.В появившемся новом окне введите следующую информацию:
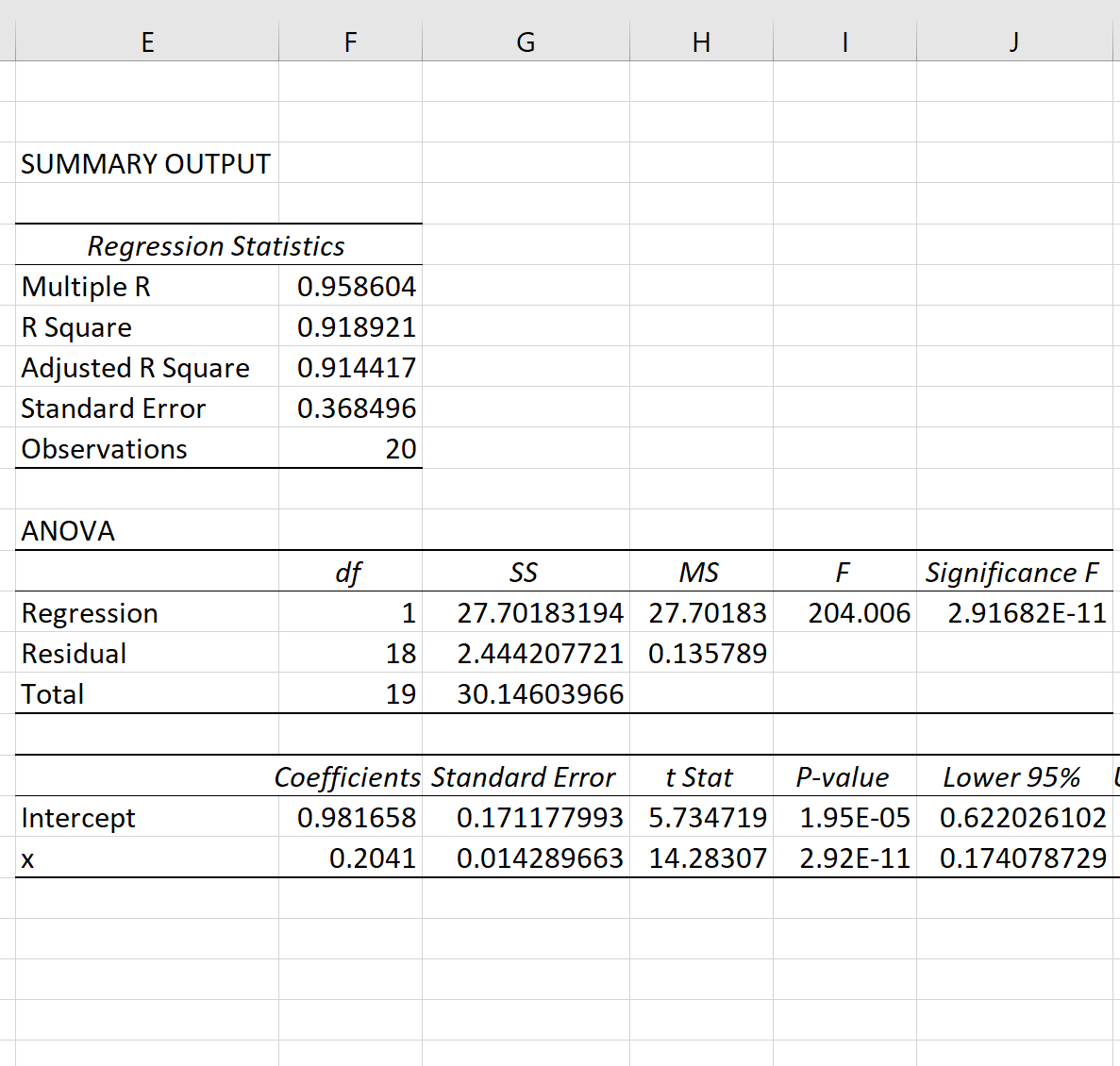
Как только вы нажмете OK , будут показаны результаты модели экспоненциальной регрессии:
Общее значение F модели составляет 204,006, а соответствующее значение p чрезвычайно мало, что указывает на то, что модель в целом полезна.
Используя коэффициенты из выходной таблицы, мы видим, что подобранное уравнение экспоненциальной регрессии:
ln(у) = 0,9817 + 0,2041(х)
Применив e к обеим частям, мы можем переписать уравнение как:
у = 2,6689 * 1,2264 х
Мы можем использовать это уравнение для прогнозирования переменной отклика y на основе значения переменной-предиктора x.Например, если x = 14, то мы можем предсказать, что y будет равно 46,47 :
у = 2,6689 * 1,2264 14 = 46,47
Бонус: не стесняйтесь использовать этот онлайн- калькулятор экспоненциальной регрессии для автоматического вычисления уравнения экспоненциальной регрессии для заданного предиктора и переменной отклика.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
Теперь, когда мы перейдем во вкладку «Данные»
, на ленте в блоке инструментов «Анализ»
мы увидим новую кнопку – «Анализ данных»
.
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y
означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x
– это различные факторы, влияющие на переменную. Параметры a
являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k
обозначает общее количество этих самых факторов.
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат
. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение»
и столбца «Коэффициенты»
. Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1»
и «Коэффициенты»
показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
ŷ — ожидаемое значение у при заданном значении х,
x — независимая переменная,
a — отрезок на оси y для прямой линии,
b — наклон прямой линии.
На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением
На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по .
Использование Excel для определения линейной регрессии
Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа
. Найти ее можно, перейдя по вкладке Файл –> Параметры
(2007+), в появившемся диалоговом окне Параметры
Excel
переходим во вкладку Надстройки.
В поле Управление
выбираем Надстройки
Excel
и щелкаем Перейти.
В появившемся окне ставим галочку напротив Пакет анализа,
жмем ОК.
Во вкладке Данные
в группе Анализ
появится новая кнопка Анализ данных.
Чтобы продемонстрировать работу надстройки, воспользуемся данными , где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.
Перейдите во вкладку Данные,
в группе Анализ
щелкните Анализ данных.
В появившемся окне Анализ данных
выберите Регрессия
, как показано на рисунке, и щелкните ОК.
Установите необходимыe параметры регрессии в окне Регрессия
, как показано на рисунке:
Щелкните ОК.
На рисунке ниже показаны полученные результаты:
Эти результаты соответствуют тем, которые мы получили путем самостоятельных вычислений в .
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами
как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН
.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
4) В окне Категория
выберете Статистические
, в окне функция — ЛИНЕЙН
. Щёлкните по кнопке ОК
как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у
Известные значения х
Константа
— логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика
— логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК
;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу
, а затем на комбинацию клавиш ++
.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Стандартная ошибка y | |
| F-статистика | |
| Регрессионная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее
, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия
можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа
. В главном меню последовательно выберите: Файл/Параметры/Надстройки
.
2) В раскрывающемся списке Управление
выберите пункт Надстройки Excel
и нажмите кнопку Перейти.
3) В окне Надстройки
установите флажок Пакет анализа
, а затем нажмите кнопку ОК
.
Если Пакет анализа
отсутствует в списке поля Доступные надстройки
, нажмите кнопку Обзор
, чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да
, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия
, а затем нажмите кнопку ОК
.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y
— диапазон, содержащий данные результативного признака;
Входной интервал X
— диапазон, содержащий данные факторного признака;
Метки
— флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль
— флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал
— достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК
.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций
: в главном меню выберете Формулы / Вставить функцию
.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК
.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k
объясняющих переменных) по данным примера 3.6.
В таблице регрессионной статистики
приводятся значения:
Множественный R
– коэффициент множественной корреляции ;
R
—
квадрат
– коэффициент детерминации R
2 ;
Нормированный R
—
квадрат
– скорректированный R
2 с поправкой на число степеней свободы;
Стандартная ошибка
– стандартная ошибка регрессии S
;
Наблюдения –
число наблюдений n
.
В таблице Дисперсионный анализ
приведены:
1. Столбец df
— число степеней свободы, равное
для строки Регрессия
df
= k
;
для строкиОстаток
df
= n
– k
– 1;
для строкиИтого
df
= n
– 1.
2. Столбец SS –
сумма квадратов отклонений, равная
для строки Регрессия
;
для строкиОстаток
;
для строкиИтого
.
3. Столбец MS
дисперсии, определяемые по формуле MS
= SS
/df
:
для строки Регрессия
– факторная дисперсия;
для строкиОстаток
– остаточная дисперсия.
4. Столбец F
– расчетное значение F
-критерия, вычисляемое по формуле
F
= MS
(регрессия)/MS
(остаток).
5. Столбец Значимость F
–значение уровня значимости, соответствующее вычисленной F
-статистике.
Значимость F
= FРАСП(F-
статистика, df
(регрессия), df
(остаток)).
Если значимость F
< стандартного уровня значимости, то R
2 статистически значим.
| Коэффи-циенты |
Стандартная ошибка |
t-cта-тистика |
P-значение |
Нижние 95% |
Верхние 95% |
|
| Y |
65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X |
0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты
– значения коэффициентов a
, b
.
2. Стандартная ошибка
–стандартные ошибки коэффициентов регрессии S a
, S b
.
3. t-
статистика
– расчетные значения t
-критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р
-значение (значимость t
)
– это значение уровня значимости, соответствующее вычисленной t-
статистике.
Р
-значение = СТЬЮДРАСП
(t
-статистика, df
(остаток)).
Если Р
-значение < стандартного уровня значимости, то соответствующий коэффициент статистически значим.
5. Нижние 95% и Верхние 95%
– нижние и верхние границы 95 %-ных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии.
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное y | Остатки e |
| 72,70 | -29,70 | |
| 82,91 | -20,91 | |
| 94,53 | -4,53 | |
| 105,72 | 5,27 | |
| 117,56 | 12,44 | |
| 129,70 | 19,29 | |
| 144,22 | 20,77 | |
| 166,49 | 24,50 | |
| 268,13 | -27,13 |
В таблице ВЫВОД ОСТАТКА
указаны:
в столбце Наблюдение
– номер наблюдения;
в столбце Предсказанное y
– расчетные значения зависимой переменной;
в столбце Остатки e
– разница между наблюдаемыми и расчетными значениями зависимой переменной.
Пример 3.6.
Имеются данные (усл. ед.) о расходах на питание y
и душевого дохода x
для девяти групп семей:
| x | |||||||||
| y |
Используя результаты работы пакета анализа Excel (Регрессия), проанализируем зависимость расходов на питание от величины душевого дохода.
Результаты регрессионного анализа принято записывать в виде:
где в скобках указаны стандартные ошибки коэффициентов регрессии.
Коэффициенты регрессии а
= 65,92 и b
= 0,107. Направление связи между y
и x
определяет знак коэффициентарегрессии b
= 0,107, т.е. связь является прямой и положительной. Коэффициент b
= 0,107 показывает, что при увеличении душевого дохода на 1 усл. ед. расходы на питание увеличиваются на 0,107 усл. ед.
Оценим значимость коэффициентов полученной модели. Значимость коэффициентов (a, b
) проверяется по t
-тесту:
Р-значение (a
) = 0,00080 < 0,01 < 0,05
Р-значение (b
) = 0,00016 < 0,01 < 0,05,
следовательно, коэффициенты (a, b
) значимы при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости. Таким образом, коэффициенты регрессии значимы и модель адекватна исходным данным.
Результаты оценивания регрессии совместимы не только с полученными значениями коэффициентов регрессии, но и с некоторым их множеством (доверительным интервалом). С вероятностью 95 % доверительные интервалы для коэффициентов есть (38,16 – 93,68) для a
и (0,0728 – 0,142) для b.
Качество модели оценивается коэффициентом детерминации R
2 .
Величина R
2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R
2 проверяется по F-
тесту: значимость F
= 0,00016 < 0,01 < 0,05, следовательно, R
2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как . Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача:
Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
Теперь стали видны и данные регрессионного анализа.
Exponential regression is a type of regression model that can be used to model the following situations:
1. Exponential growth: Growth begins slowly and then accelerates rapidly without bound.
2. Exponential decay: Decay begins rapidly and then slows down to get closer and closer to zero.
The equation of an exponential regression model takes the following form:
y = abx
where:
- y: The response variable
- x: The predictor variable
- a, b: The regression coefficients that describe the relationship between x and y
The following step-by-step example shows how to perform exponential regression in Excel.
Step 1: Create the Data
First, let’s create a fake dataset that contains 20 observations:
Step 2: Take the Natural Log of the Response Variable
Next, we need to create a new column that represents the natural log of the response variable y:
Step 3: Fit the Exponential Regression Model
Next, we’ll fit the exponential regression model. To do so, click the Data tab along the top ribbon, then click Data Analysis within the Analysis group.
If you don’t see Data Analysis as an option, you need to first load the Analysis ToolPak.
In the window that pops up, click Regression. In the new window that pops up, fill in the following information:
Once you click OK, the output of the exponential regression model will be shown:
The overall F-value of the model is 204.006 and the corresponding p-value is extremely small, which indicates that the model as a whole is useful.
Using the coefficients from the output table, we can see that the fitted exponential regression equation is:
ln(y) = 0.9817 + 0.2041(x)
Applying e to both sides, we can rewrite the equation as:
y = 2.6689 * 1.2264x
We can use this equation to predict the response variable, y, based on the value of the predictor variable, x. For example, if x = 14, then we would predict that y would be 46.47:
y = 2.6689 * 1.226414 = 46.47
Bonus: Feel free to use this online Exponential Regression Calculator to automatically compute the exponential regression equation for a given predictor and response variable.
Additional Resources
How to Perform Simple Linear Regression in Excel
How to Perform Multiple Linear Regression in Excel
How to Perform Quadratic Regression in Excel
How to Perform Polynomial Regression in Excel
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.