Поиск решения excel практическая работа - Word и Excel - помощь в работе с программами

Применение команды «Поиск решений»

в работе с профессионально-ориентированными задачами

Постановка задачи

В ресторане установлены 7 графиков работы официантов:

График	Выходные
1	Суббота. Воскресение
2	Воскресение, Понедельник
3	Понедельник, Вторник
4	Вторник, Среда
5	Среда, Четверг
6	Четверг, Пятница
7	Пятница, Суббота

Количество работающих по ним соответственно – №1, №2, №3, №4, №5, №6, №7. Опытным путём было определено требуемое количество официантов на каждый день недели:

День недели	Пн	Вт	Ср	ЧТ	Пт	Сб	Вс
Требуется, чел.	11	10	9	10	12	12	13

Необходимо распределить работающих официантов по каждому графику таким образом, чтобы затраты на еженедельную зарплату всем официантам были минимальными (найти N1, N2, N3, N4, N5, N6, N7). При этом нужно учитывать следующие факторы:

Ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности.
Число работников, работающих по каждому графику, не может быть отрицательным.
Число работников, работающих по каждому графику, должно быть целочисленным.

Рассмотреть ситуацию, когда по графику 1 обязательно должно работать 3 человека.

Создание таблицы для анализа данных

Исходя из условий постановки задачи, создадим в табличном процессоре Excel таблицу, где будем потом рассматривать и анализировать ситуации.

Открываем программу Excel, например, щёлкнув два раза её ярлык на рабочем столе или через Пуск – Программы – Microsoft Excel.
Устанавливаем поля документа через Файл — Параметры страницы:
Сохраняем книгу (файл в Excel) через Файл – Сохранить как под именем Анализ графиков работы.xls.
Начиная с ячейки A1, оформляем таблицу (см. следующий лист). В те дни недели, где предусмотрен по графику рабочий день, ставим 1, а где выходной – 0. при этом формат данных в этих ячейках оставляем по умолчанию – Общий.
После заполнения таблицы данными, отформатируем ячейки так, чтобы текст и числа в них располагались по горизонтали и вертикали По центру. Для этого выделим мышкой всю таблицу и используем меню Формат – Ячейки – вкладка Выравнивание (или по правой клавише мыши).
Оформим внешние и внутренние границы ячеек.
Получим таблицу следующего вида:

Здесь A2…G2 – количество официантов, работающих в соответствующий день недели, A1..G1 – требуемое (определённое опытным путём, меньше нельзя).

Всего работников – N.

K – дневная заработная плата одного официанта, она составляет, к примеру, 200 рублей.

Поскольку файл в программе Excel называется книга, а каждая книга состоит из листов, переименуем ярлычок первого листа книги, где создана таблица, и назовём его Заготовка. Переименовать можно щелчком правой клавишей по ярлычку листа, выбрать пункт Переименовать или просто два раза щёлкнуть по ярлычку листа, название Лист1 выделиться, можно вводить новое название.
Мышкой выделим всю таблицу и скопируем её в Буфер обмена.
Перейдём на Лист2 книги, щёлкнув ярлычок этого листа.
Вставим из буфера скопированную таблицу: щёлкнем значок на панели Стандартная.
В ячейках C2:C8 удалим набранный текст. В этих ячейках будут вычисляться значения при применении команды Поиск решения.
В ячейки D10:J10 введём определённое опытном путём минимальное количество официантов по дням недели.

Требуется (определено опыт. путём)

Цвет шрифта этих ячеек для лучшей наглядности сделаем синим.

В ячейках D9:J9 также удалим текст. Сюда необходимо вписать формулы.
В ячейку C12 запишем 200, изменим формат данных в ячейке на Денежный в рублях, получим 200р.
Переименуем Лист2 в Ситуация 1.

Таблица для проведения анализа готова.

Ввод формул для получения решения

Чтобы в дальнейшем проанализировать ситуации, необходимо в ячейки D9:J9 ввести формулы. рассчитывающие фактическое количество официантов по дням недели и по графикам работы.

Формулы для вычислений могут быть простыми, такими как сложение содержимого двух ячеек, а могут быть сложными, такими как определение отклонения какой-либо величины от других значений последовательности.

Ввод формулы в Excel начинается со знака =. За ним записывается функция, потом в скобках () аргументы. Некоторые функции, например, многие статистические, финансовые используют несколько аргументов. Тогда аргументы отделяются друг от друга запятыми.

Простейшие формулы, такие как сложение, вычитание, умножение, деление состоят из двух частей: арифметического оператора и хотя бы одного адреса ячейки.

При составлении формул для вычислений или преобразований данных необходимо указать содержимое каких именно ячеек используется в формулах.

Введём в ячейку D9 формулу =D2*C2+D5*C5+D6*C6+D7*C7+C8.

Она рассчитывает сколько официантов должно работать в понедельник с учётом графиков их работы. Там, где в таблице 0, т.е. выходной, ячейки не обсчитываем.

Для подсчёта работников во вторник в ячейку E9 запишем формулу

=C2*E2+E3*C3+E6*C6+E7*C7+E8*C8.

Для ячейки F9 – =F2*C2+F3*C3+F4*C4+F7*C7+F8*C8. Среда.

Для ячейки G9 – =G2*C2+G3*C3+G4*C4+G5*C5+G8*C8. Четверг.

Для ячейки H9 – =H2*C2+H3*C3+H4*C4+H5*C5+H6*C6. Пятница.

Для ячейки I9 – =I3*C3+I4*C4+I5*C5+I6*C6+I7*C7. Суббота.

Для ячейки J9 – =J4*C4+J5*C5+J6*C6+J7*C7+J8*C8. Воскресенье.

В ячейку C11 нужно записать формулу подсчёта общего количества официантов с учётом всех семи графиков работы: =СУММ(C2:C8), т.е. просуммировать всех официантов, работающих по графикам 1…7.

В ячейку C13 введём формулу подсчёта недельной зарплаты всех официантов:

=(C11*C12).

Все необходимые формулы и данные введены в таблицу. Теперь можно приступать к поиску решения поставленной задачи.

Поиск решения

Команда Поиск решения из меню Сервис анализирует ситуацию с учётом ограничений, накладываемых на отдельные ячейки, рассчитывает значение целевой ячейки, изменяя значения указанных нами ячеек.

При поиски решения целевая ячейка должна содержать формулу, но ячейки, которые будут изменяться, должны содержать значения, а не формулу.

Для решения нашей задачи выполним следующие действия:

Выделим ячейку C13. (Еженедельная зарплата, она должна быть минимальной.)
Сервис — Поиск решения.
Установим целевую ячейку $C$13 равной минимальному значению.

Укажем, что будут меняться значения ячеек $C$2:$C$8. Это можно сделать, щёлкнув по красной стрелке в правом углу окошечка, перейдя в таблицу и выделив нужные ячейки.
Введём ограничения на значения отдельных ячеек: в ячейках C2…C8 должно быть целое число; ячейка D9>=11, E9>=10, F9>=9, G9>=10, H9>=12, I9>=12, J9>=13. Ввод ограничений проводим через кнопку.
Через кнопку Параметры установим, что значения в изменяемых ячейках должны быть неотрицательными. Другие параметры в открывшемся окне Параметры поиска решения оставляем внесёнными по умолчанию.

Нажимаем кнопку Выполнить. Получаем решение задачи для первой ситуации, когда определяем минимальное количество официантов с учётом всех графиков их работы при условии, что ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности. Решение представлено в Приложении.
В ситуации 2 официантов, работающих по графику №1, должно быть обязательно 3. Для учёта этого обстоятельства при новом поиске решения введём ещё одно ограничение: $C$2 =3. Тогда после нажатия кнопки Выполнить получим решение для этой ситуации. Это решение представлено также в Приложении.
Проанализировав обе ситуации видим, что общее количество официантов одинаково (16). Это минимальное количество при заданных условиях. Соответственно подсчитана и еженедельная зарплата всех официантов. Но в ситуации 2 распределение официантов по графикам работы другое. Фактическое количество работающих по дням недели также изменилось.

Заключение

Табличный процессор Excel обладает удобными возможностями для анализа и обработки данных. Такие команды или средства программы как Подбор параметров и Поиск решения можно использовать для решения задач прогнозирования различных ситуаций в работе менеджера, финансиста и других специалистов, гибкого подбора новых параметров при изменении ситуации, поиска более гибкого и многовариантного решения задачи с учётом различных обстоятельств и ограничений.

Приложение

Решение задачи, найденное с помощью программы MS Excel

Ситуация 1

Ситуация 2

Источник

Практическая работа №11

Тема: Задачи оптимизации (поиск решения) в MS Excel.

Цель: — изучение технологии поиска решения для задач
оптимизации (минимизации, максимизации).

Вид
работы: фронтальный

Время
выполнения: 2 часа

Задания к практической работе

Задание
1. Минимизация фонда заработной платы
фирмы.

Пусть известно, что для нормальной работы фирмы
требуется 5…7 курьеров, 8…10 младших менеджеров, 10 менеджеров, 3 заведующих
отделами, главный бухгалтер, программист, системный аналитик, генеральный
директор фирмы.

Общий месячный фонд зарплаты должен быть минимален.
Необходимо определить, какими должны быть оклады сотрудников фирмы, при
условии, что оклад курьера не должен быть меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную
модель. Тогда условие задачи имеет вид N₁*A₁*x+N₂*(A₂*x+B₂)+…+N₈*(A₈*x+B₈)
= Минимум, где N_i – количество работников данной специальности; x
– зарплата курьера; A_i и B_i– коэффициенты заработной
платы сотрудников фирмы.

Ход работы

1.
Запустите редактор электронных
таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл
«Штатное расписание».

Скопируйте содержимое листа «Штатное расписание 1» на
новый лист и присвойте копии листа имя «Штатное расписание 2».

2.
В меню Данные – Анализ «что –
если» активизируйте команду Поиск решения (рис. 1).

3.
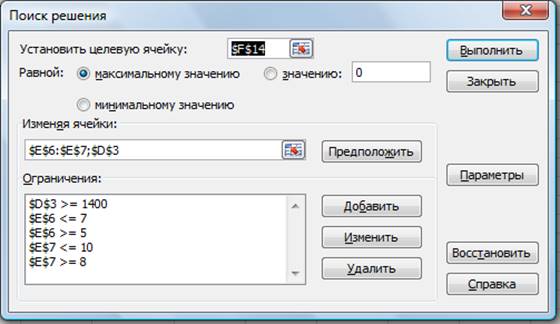
В окне Установить целевую
ячейку укажите ячейку F14, содержащую модель – суммарный фонд заработной
платы.

Рисунок 1 — Задание условий для минимизации фонда заработной
платы

Поскольку необходимо минимизировать общий месячный
фонд зарплаты, активизируйте кнопку равный – Минимальному значению.

В окне Изменяя ячейки укажите адреса ячеек, в
которых будет отражено количество курьеров и младших менеджеров, а также
зарплата курьера — $E$6:$E$7:$D$3 (при задании ячеек E6, E7 и D3 держите
нажатой клавишу [Ctrl]).

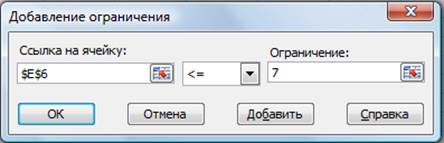
Используя кнопку Добавить в окнах Поиск
решения и Добавление ограничений, опишите все ограничения задачи:
количество курьеров изменяется от 5 до 7, младших менеджеров од 8 до 10, а
зарплата курьера >1400 (рис.2).

Рисунок
2 — Добавление ограничений для минимизации фонда заработной платы

Ограничения наберите в виде

$D$3>=1400

$E$6>5

$E$6<7

$E$7>=8

$E$7 <=10.

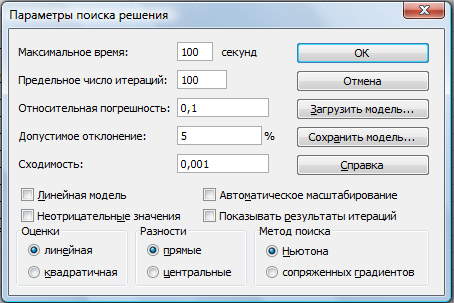
Активизируйте кнопку Параметры, введите
параметры поиска, как показано на рис. 3.

Рисунок
3 — Задание параметров поиска решения по минимизации фонда заработной платы.

Окончательный вид окна Поиск решения приведен
на рис. 1.

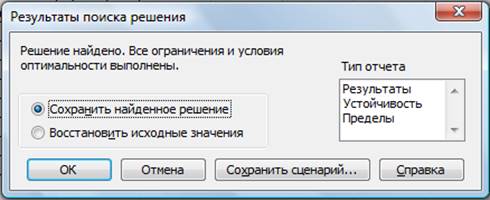
Запустите процесс поиска решения нажатием кнопки Выполнить.
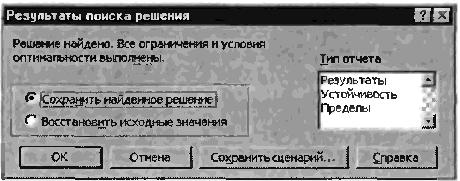
В открывшемся диалоговом окне Результаты поиска решения задайте
опцию Сохранить найденное решение (рис. 4).

Рисунок
4 — Сохранение найденного при поиске решения

Решение задачи приведено на рис. 5. Оно тривиально:
чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд
заработной платы.

Рисунок
5 — Минимизация фонда заработной платы

Задание
2. Составление плана выгодного
производства.

Фирма производит несколько видов продукции из одного и
того же сырья – А, В и С. Реализация продукции А дает прибыль 10 р., В – 15 р.
и С – 20 р. на единицу изделия.

Продукцию можно производить в любых количествах,
поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо
определить, какой продукции и сколько надо произвести, чтобы общая прибыль от
реализации была максимальной.

Нормы расхода сырья на производство продукции каждого
вида приведены в табл. 1.

Таблица 1

Сырье	Нормы расхода сырья	Запас сырья
А	В	С
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20

Ход работы

1.
Запустите редактор электронных таблиц
Microsoft Excel и создайте новую электронную книгу.

2.
Создайте расчетную таблицу как на
рис. 6. Введите исходные данные и формулы в электронную таблицу. Расчетные
формулы имеют такой вид:

Расход сырья 1=(количество сырья 1) * (норма расхода
сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья
1) * (норма расхода сырья С).

Значит, в ячейку F5 нужно ввести формулу =
B5*$B$9+C5*$C$9+D5*$D$9.

Обратите внимание, что значения количества сырья
каждого вида пока не известны и будут подобраны в процессе решения задания
(ячейки В9:D9 пока пустые).

(Общая прибыль по А) = (прибыль на ед.
изделий А) * (количество А),

Следовательно в ячейку В10 следует
ввести формулу = В8 * В9.

Итоговая общая прибыль = (Общая прибыль
по А) + (Общая прибыль по В) + (Общая прибыль по С),

значит в ячейку Е10 следует ввести
формулу = СУММ(В10:D10).

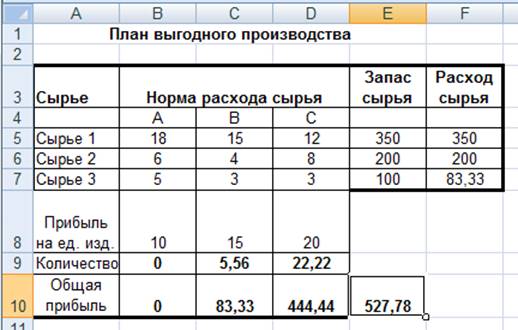
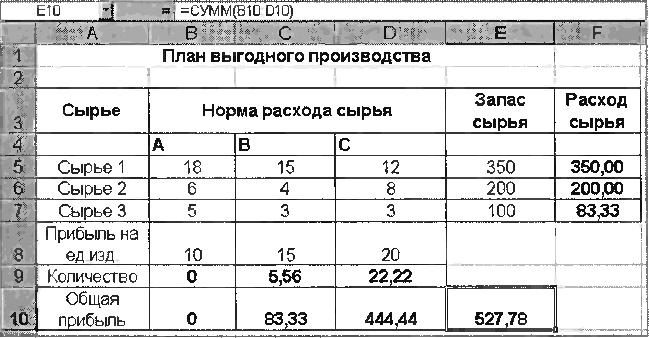
Рисунок 6 — Исходные
данные для Задания 2

3.
В меню Данные активизируйте
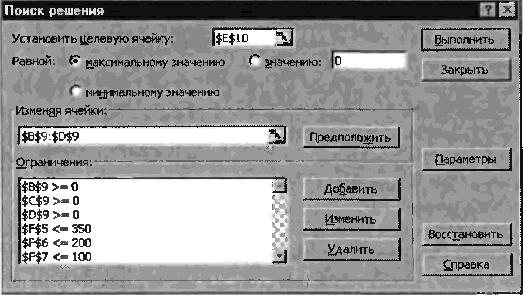
команду Поиск решения и введите параметры поиска, как указано на рис 7.

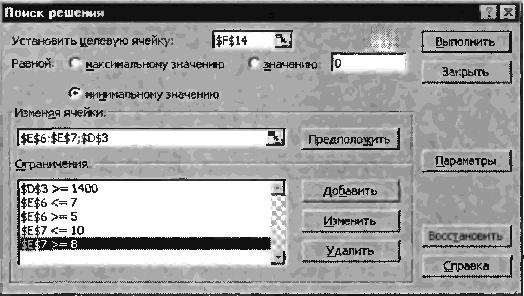
Рисунок 7 — Задание
условий и ограничений для поиска решений

В качестве целевой ячейки укажите ячейку «Итоговая
общая прибыль» (Е10), в качестве изменяемых ячеек – ячейки количества сырья –
(В9:D9).

Не забудьте задать максимальное значение суммарной
прибыли и указать ограничения на запас сырья:

расход сырья 1<=350; расход сырья 2<=200; расход
сырья 3<=100, а также положительные значения количества сырья А, В, С
>=0.

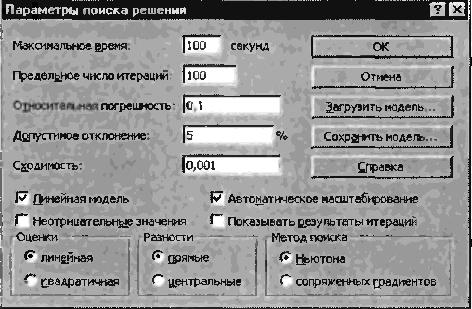
Установите параметры поиска решения (рис. 8). Для
этого кнопкой Параметры откройте диалоговое окно Параметры поиска
решения, установите параметры по образцу, задайте линейную модель расчета (Линейность
модели).

Рисунок 8 — Задание
параметров поиска решения

4.
Кнопкой Выполнить запустите
Поиск решения. Если вы сделали все верно, то решение будет как на рис.
9.

Рисунок 9 — Найденное
решение максимизации прибыли при заданных ограничениях

5.
Сохраните созданный документ под
именем «План производства».

Вывод. Из решения видно, что оптимальный план выпуска предусматривает
изготовление 5,56 кг продукции В и 22,22
кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом
состоит 527,78 р.

Задание
3. Используя файл «План производства»
(см.задание 2), определить план выгодного производства, т. е. какой продукции и
сколько необходимо произвести, чтобы общая прибыль от реализации была
максимальной.

Выберите нормы расхода сырья на производство продукции
каждого вида и ограничения по запасам сырья из таблицы соответствующего
варианта (5 вариантов):

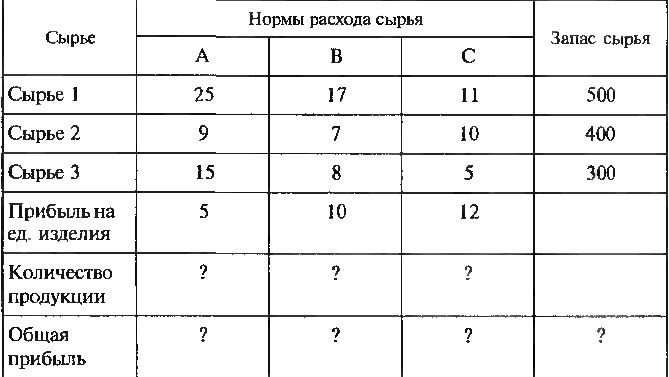
Вариант 1

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	25	17	11	500
Сырье 2	9	7	10	400
Сырье 3	15	8	5	300
Прибыль на ед. изделия	5	10	12
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

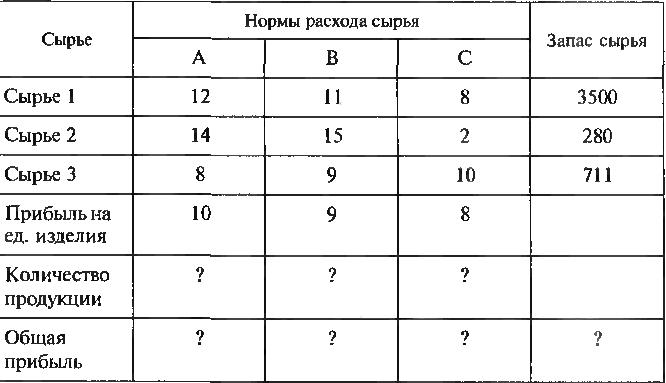
Вариант 2

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	11	8	3500
Сырье 2	14	15	2	280
Сырье 3	8	9	10	711
Прибыль на ед. изделия	10	9	8
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

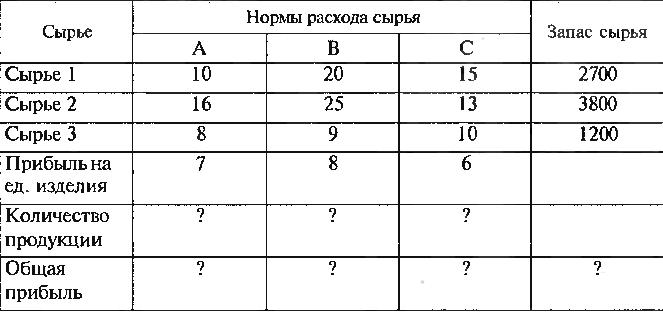
Вариант 3

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	10	20	15	2700
Сырье 2	16	25	13	3800
Сырье 3	8	9	10	1200
Прибыль на ед. изделия	7	8	6
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

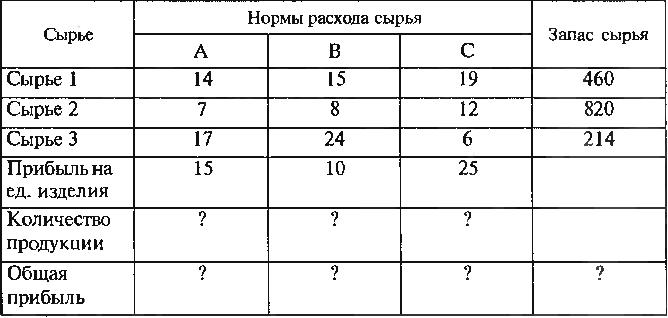
Вариант 4

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	14	15	19	460
Сырье 2	7	8	12	820
Сырье 3	17	24	6	214
Прибыль на ед. изделия	15	10	25
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

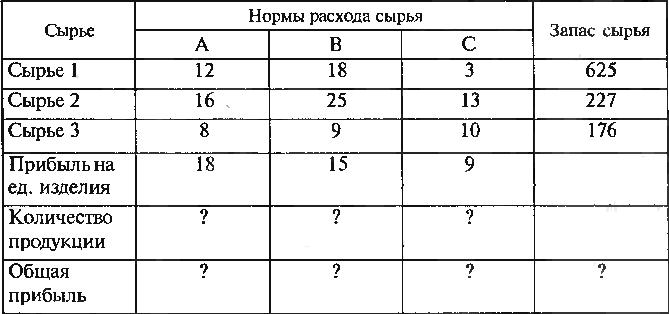
Вариант 5

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	18	3	625
Сырье 2	16	25	13	227
Сырье 3	8	9	10	176
Прибыль на ед. изделия	18	15	9
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Рекомендуемая
литература: 1, 2, 3, 4

Источник

Практическая
работа: Поиск решения.

Большинство задач, решаемых с помощью электронной таблицы,
предполагают нахождение искомого результата по известным исходным данным. Но в
Excel есть инструменты, позволяющие решить и обратную задачу: подобрать
исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения,
который особенно удобен для решения так называемых «задач
оптимизации».

Если Вы раньше не использовали Поиск решения, то Вам
потребуется установить соответствующую надстройку.

Сделать это можно через диалоговое
окно Параметры Excel

Начиная с версии Excel 2007 кнопка для запуска Поиска
решения появится на вкладке Данные.

Задание
1. Распределение премии

Предположим, что Вы начальник
производственного отдела и Вам предстоит по-честному распределить премию в
сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным
окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности
для вычисления размера премии по окладу.

Первым делом создаём таблицу с
исходными данными и формулами, с помощью которых должен быть получен результат.
В нашем случае результат — это суммарная величина премии. Очень важно, чтобы
целевая ячейка (С8) посредством формул была связана с искомой изменяемой
ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие
размер премии для каждого сотрудника (С2:С7).

Теперь запускаем Поиск решения и в открывшемся
диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых
окон в разных версиях несколько различается:

Начиная с Excel 2010

1. Целевая
ячейка, в которой должен получиться желаемый результат. Целевая ячейка может
быть только одна

2. Варианты
оптимизации: максимальное возможное значение, минимальное возможное
значение или конкретное значение. Если требуется получить
конкретное значение, то его следует указать в поле ввода

3. Изменяемых
ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно
в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное
значение

Ограничения задаются с помощью кнопки Добавить.
Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение
формул. Именно ограничения обеспечивают получение правильного результата.
Ограничения можно задавать как для отдельных ячеек, так и для диапазонов.
Помимо всем понятных знаков =, >=, <=, при задании ограничений можно
использовать варианты цел (целое), бин (бинарное
или двоичное, т.е. 0 или 1), раз (все разные — только начиная
с версии Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть
положительным. Это ограничение можно задать по-разному: либо установить явно,
воспользовавшись кнопкой Добавить, либо поставить флажок Сделать
переменные без ограничений неотрицательными.

5.
Кнопка, включающая итеративные вычисления с заданными параметрами.

После нажатия кнопки Найти решение (Выполнить) Вы
уже можете видеть в таблице полученный результат. При этом на экране появляется
диалоговое окно Результаты поиска решения.

Начиная с Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в
диалоговом окне Результаты поиска решения нажимаете ОК и
фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и
возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

Важно: при любых изменениях исходных данных
для получения нового результата Поиск решения придется
запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной
прибыли)

Задание
2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных
книжных полок.

Их производство ограничено наличием сырья
(высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3
м² досок, а для изделия модели В — 4 м². Фирма может получить от своих
поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12
мин машинного времени, а для изделия модели В — 30 мин. в неделю можно
использовать 160 ч машинного времени.

Сколько изделий каждой модели следует
выпускать фирме в неделю для достижения максимальной прибыли, если
каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В —
120 руб. прибыли?

Порядок действий:

1.
Сначала создаем таблицы с исходными данными и формулами.
Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно
автору. Например, как на рисунке

2.
Запускаем Поиск решения и в диалоговом окне
устанавливаем необходимые параметры

1.
Целевая ячейка B12 содержит формулу для расчёта прибыли

2.
Параметр оптимизации — максимум

3.
Изменяемые ячейки B9:C9

4.
Ограничения: найденные значения должны быть целыми,
неотрицательными; общее количество машинного времени не должно превышать 160 ч
(ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м²
(ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было
указать числа, но при использовании ссылок какие-либо изменения ограничений
можно производить прямо в таблице

5.
Нажимаем кнопку Найти решение (Выполнить) и после
подтверждения получаем результат

Но даже если Вы правильно создали формулы
и задали ограничения, результат может оказаться неожиданным. Например, при
решении данной задачи Вы можете увидеть такой результат:

И это несмотря на то, что было задано ограничение целое.
В таких случаях можно попробовать настроить параметры Поиска решения.
Для этого в окне Поиск решения нажимаем кнопку Параметры и
попадаем в одноимённое диалоговое окно

Первый из выделенных параметров отвечает
за точность вычислений. Уменьшая его, можно добиться более точного результата,
в нашем случае — целых значений. Второй из выделенных параметров (доступен,
начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться
дробные результаты при ограничении целое? Оказывается Поиск
решения это ограничение просто проигнорировал в соответствии с
установленным флажком.

Задание 3. Транспортная задача
(минимизация затрат)

На заказ строительной компании песок
перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным
площадкам). Стоимость на доставку включается в себестоимость объекта,
поэтому строительная компания заинтересована обеспечить потребности своих
стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах;
потребности в песке стройплощадок; затраты на транспортировку между каждой
парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок
для удовлетворения нужд (откуда и куда), при которой общие затраты на
транспортировку были бы минимальными.

Пример расположения ячеек с исходными
данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и
столбцам, а в целевой ячейке формула для подсчёта общих затрат на
транспортировку.

Запускаем Поиск решения и устанавливаем необходимые параметры (см.
рисунок)

Нажимаем Найти решение (Выполнить) и
получаем результат, изображенный ниже

Иногда транспортные задачи усложняются с
помощью дополнительных ограничений. Например, по каким-то причинам невозможно
возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно
ограничение $D$13=0. И после запуска Поиска решения получаем другой
результат

И последнее, на что следует обратить внимание, это выбор метода
решения. Если задача достаточно сложная, то для достижения результата может
потребоваться подобрать метод решения

Начиная с Excel 2010

Задача для самостоятельного решения.

Крестьянин на базаре за 100 рублей купил
100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек.
Сколько быков, коров и телят купил крестьянин?

Источник

Цель
работы: Научиться решать задачи
оптимизации различных типов

средствами
MS Excel.

Требования к содержанию, оформлению и порядку выполнения

Для выполнения
лабораторной работы необходимо создать
новую рабочую книгу Excel
под именем «Ваша фамилия, Лабораторная
работа №2, (например: «Иванов И.П.
Лабораторная работа №2»).

Перед выполнением
лабораторной работы изучите теоретическую
часть.

Рабочие листы
рабочей книги должны быть именованы
Задание1, Задание2, Задание3. Результаты
решения задач поместите в файл отчета.

После выполнения
лабораторной работы ответьте на
контрольные вопросы. Ответы на контрольные
вопросы поместите в файл отчета. Свою
рабочую книгу вместе с ответами на
контрольные вопросы необходимо
предоставить преподавателю на дискете,
подписав ее вышеуказанным образом.

Теоретическая часть

Оптимизации
занимают очень важное место в экономике
организаций и предприятий. Задачи по
поиску наилучшего
(оптимального)
решения из множества допустимых решений
называются оптимизационными
задачами (экстремальными
задачами, задачами линейного
программирования). Решение любой
оптимизационной задачи сводится к
нахождению некоторого набора условий,
при которых интересуемая величина будет
минимальной или максимальной. Целями
решения оптимизационных задач в экономике
могут быть увеличение прибыли, снижение
затрат, повышение производительности
труда, рациональное использование
оборудования, повышение эффективности
инвестиций и многие другие.

Все оптимизационные
задачи имеют три свойства:

имеется единственная
максимизируемая или минимизируемая
цель (прибыль, производительность,
ресурсы и т.д.);
имеются ограничения,
выражающиеся, как правило, в виде
неравенств (например, объем
используемого сырья не может превышать
объем имеющегося сырья на складе,
или время работы станка за сутки не
должно быть больше 24 часов минус время
на обслуживание);
имеется набор
входных значений-переменных, прямо или
косвенно влияющих на ограничения и на
оптимизируемые величины.

Для решения
оптимизационной задачи необходимо
описать заданную цель (например, получение
максимальной прибыли), а также запас
имеющихся ресурсов и условия их
использования для достижения цели. При
таком описании выделяют следующие два
понятия:

Математическую
модель;
Целевую функцию.

Математическая
модель задачи оптимизации задает
множество допустимых решений X
. Множество X
определяется имеющимися запасами
ресурсов и условиями их использования
для достижения цели. Множество допустимых
решений называют также ограничениями
задачи. Т.о. формулировка таких задач
представляет собой систему уравнений
с несколькими неизвестными и набор
ограничений на решения.

Целевая функция
f(x) представляет собой числовую
характеристику, максимальному или
минимальному значению которой
соответствует оптимальное решение.

Примерами задач
оптимизации в экономике могут служить
задачи максимизации прибыли предприятия
в условиях ограниченных ресурсов;
транспортные задачи (минимизация
расходов на перевозку); планирование
штатного расписания; оптимальный
раскрой материалов, получение заданного
качества смеси при наименьших расходах
и т.д.

Рассмотрим подробнее
на примере задачи максимизации
прибыли предприятия в условиях
ограниченных ресурсов
процесс описания математической модели
и целевой функции.

Предприятие может
выпускать n
видов продукции, используя для этого m
видов ресурсов. Пусть для производства
одной единицы продукции

-го
вида используется

единиц ресурса

-го
вида. Прибыль от реализации одной единицы
продукции

-го
вида обозначим через

,

рублей. Требуется определить такой
объем выпуска продукции, который
обеспечивает предприятию наибольшую
прибыль.

Обозначим через

,

объем продукции j
— го вида, выпускаемой в соответствии с
некоторым планом. Тогда математическую
модель задачи можно записать в следующем
виде

(1)

Эта модель
определяется ограничениями на выпуск
продукции, обусловленными имеющимися
запасами ресурсов. Целевую функцию
задачи можно записать следующим образом

(2)

После построения
математической модели и записи целевой
функции задача определения объема
выпуска продукции, обеспечивающего
предприятию наибольшую прибыль, может
быть сформулирована как задача

Найти
(3)

при условии (1) и

(4)

Условие (4), указывает
на неотрицательность выпуска продукции.

В (3), (1), (4) отсутствуют
ограничения по спросу на продукцию,
которым в рыночной экономике принадлежит
важная роль. Введем эти ограничения в
задачу следующим образом. Обозначим
через

,

верхнее ограничение по спросу на
продукцию

-го
вида, а через

нижнее ограничение по спросу на продукцию

-го
вида, тогда задача примет следующий
вид

Найти
(5)

при условии

(6)

(7)

(8)

В общем случае
прибыль с ростом объема производства
может начать уменьшаться из-за
дополнительных затрат, связанных,
например, с реализацией продукции.

Обозначим через

степень влияния на прибыль объема
выпуска j-го
изделия. Тогда целевая функция задачи
может быть записана в следующем виде:

(9)

а сама задача
примет вид

(10)

при условиях (6),
(7), (8).

Заметим, что если

,
то прибыль не зависит от объема выпуска
j-го
изделия.

Для решения задач
оптимизации в Excel имеется специальная
надстройка «Поиск
решения» (Solver).
Поскольку пакет Поиск
решения
является надстройкой, то перед началом
работы необходимо установить ее. Для
этого выберите в меню пункт Сервис/Надстройки.
В диалоговом окне найдите в списке
надстроек Поиск
решения,
установите слева от него флажок и
щелкните на кнопке ОК (если будет выдано
сообщение, что данный компонент не
установлен, Вам придется сначала его
установить). В дальнейшем при запуске
Excel Solver
будет загружаться автоматически,
пока Вы не снимите флажок в окне Надстройки
и запустить этот пакет можно выбрав в
меню Сервис
пункт Поиск
решения.

В целом решение
задач оптимизации с помощью пакета
Поиск решения состоит из следующих
этапов:

Оформление рабочего
листа (ввод на рабочий лист исходных
данных и формул);
Вызов диалогового
окна Поиск решения.
Указание целевой
ячейки (ячейки в которой хранится
целевая функция);
Указание изменяемых
значений;
Указание условий
(ограничений);
Изменение настроек
поиска решения (при необходимости);

На этапе
оформления
необходимо:

1.Ввести исходные
данные в ячейки рабочего листа Excel;

2.Разметить блоки
ячеек, необходимые для формирования
элементов математической модели и
целевой функции;

3.Сформировать на
рабочем листе EXCEL элементы математической
модели и целевую функцию.

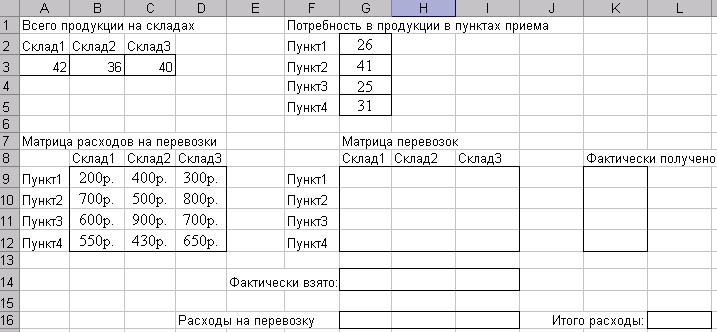
Рис.1. Пример
оформления рабочего листа для решения
задачи оптимизации связанной с
минимизацией расходов на перевозки
(транспортная задача).

Когда рабочий лист
будет оформлен, нужно активизировать
компонент Поиск
решения. В
результате откроется диалоговое окно
Поиск решения
(рис.2).

Рис.2. Вид диалогового
окна Поиск решения.

Для указания
целевой ячейки, необходимо ввести ее
адрес в поле
Установить целевую ячейку
или выбрать адрес ячейки щелкнув на ней
мышкой (предварительно установив курсор
в вышеописанное поле).

Затем в зависимости
от того хотим ли мы максимизировать и
минимизировать целевую функцию выбрать
с помощью переключателя необходимый
параметр максимальному
значению или
минимальному значению.

В поле Изменяя
ячейки
вводится адрес интервала ячеек, значения
которых будут изменяться в ходе поиска
оптимального решения.

С помощью кнопки
Добавить
можно
добавлять
ограничения, а с помощью двух других
можно изменять имеющиеся ограничения
или удалять. После нажатия на кнопку
Добавить
открывается диалоговое окно Добавление
ограничения
(рис.3).

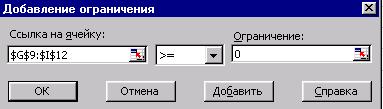
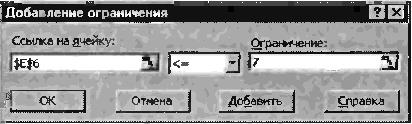
Рис.3. Вид диалогового
окна Добавление ограничения.

В этом окне в поле
Ссылка на
ячейку выбирается
адрес ячейки или интервала ячеек, на
значение которых накладывается
ограничение, далее в следующем поле
выбирается отношение (равно, больше или
равно, меньше или равно и т.д.) и в поле
ограничение вводится некое число или
адрес ячеек. С помощью кнопки Добавить
можно добавить описанное ограничение
и прейти к следующему. После закрытия
этого окна осуществляется возврат к
предыдущему окну Поиск
решения.

После того как
будут определены основные поля можно
приступать к поиску оптимального решения
для этого предназначена кнопка Выполнить.
Через некоторое время после нажатия на
эту кнопку откроется диалоговое окно
Результаты
поиска решения (рис.4.),
в котором можно выбрать сохранять
найденное решение (по месту изменяемых
ячеек) или восстановить их исходные
значения и далее ОК.

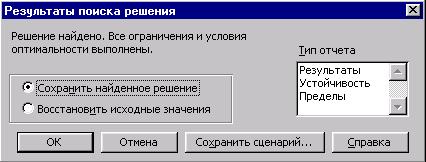
Рис.4. Вид диалогового
окна Результаты поиска решения.

После решения
задачи можно выбрать одну из следующих
возможностей:

Сохранить найденное
решение на место изменяемых ячеек;
Восстановить
исходные значения в изменяемых ячейках;
Создать несколько
отчетов по процедуре поиска. Причем
можно выбрать три типа отчетов (используя
клавишу Ctrl
или Shift):
- Результаты.
  Используется для создания отчета,
  состоящего из целевой ячейки и списка
  влияющих ячеек модели, их исходных и
  конечных значений, а также формул
  ограничений и дополнительных сведений
  о наложенных ограничениях.
- Устойчивость.
  Используется для создания отчета,
  содержащего сведения о чувствительности
  решения к малым изменениям в формуле
  (поле Установить целевую ячейку,
  диалоговое окно Поиск решения) или в
  формулах ограничений.
- Ограничения.
  Используется для создания отчета,
  состоящего из целевой ячейки и списка
  влияющих ячеек модели, их значений, а
  также нижних и верхних границ. Такой
  отчет не создается для моделей, значения
  в которых ограничены множеством целых
  чисел.
Сохранить сценарий.
Для сохранения решения в виде сценария,
который можно будет использовать в с
помощью диспетчера сценариев Microsoft
Excel.

С помощью кнопки
Параметры
диалогового окна Поиск
решения
(рис.2) можно вызвать диалоговое окно
Параметры
поиска решения
(рис.5) и с помощью его элементов изменить
параметры работы инструмента Поиск
решения.

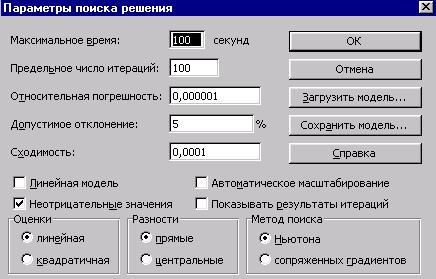
Рис.5. Вид диалогового
окна Параметры поиска решения.

Если решение в
ходе выполнения процедуры Поиска решения
не было найдено, зачастую его можно
найти, изменив параметры и повторно
запустив Поиск решения.

С помощью элементов
диалогового окна Параметры поиска
решения можно изменить следующее:

Максимальное
время. Если
появится сообщение о том, что время на
поиск решение истекло, то нужно добавить
время на поиск решения;
Предельное число
итераций.
Ограничивает число промежуточных
решений, допускаемых при поиске решения;
Относительная
погрешность.
Служит для задания точности, с которой
определяется соответствие ячейки
целевому значению или приближение к
указанным границам;
Допустимое
отклонение.
Позволяет установить максимальное
отклонение в % для целочисленных
итераций.
Сходимость.
Когда относительное изменение значения
в целевой ячейке за последние пять
итераций становится меньше числа,
указанного в поле Сходимость,
поиск прекращается. Сходимость
применяется только к нелинейным задачам.
Линейная модель.
Служит для ускорения поиска решения
линейной задачи оптимизации. Можно
использовать, если все зависимости в
модели линейные. Нельзя использовать
эту опцию, если изменяемые ячейки
умножаются или делятся или в задаче
используется возведение в степень.
Неотрицательные
значения.
Позволяет установить нулевую нижнюю
границу для тех влияющих ячеек, для
которых не были установлены ограничения.
Автоматическое
масштабирование.
Служит для включения автоматической
нормализации входных и выходных
значений, качественно различающихся
по величине — например, максимизация
прибыли в процентах по отношению к
вложениям, исчисляемым в миллионах
рублей.
Показывать
результаты итераций.
Позволяет просматривать результаты
отдельных итераций.
Разделы
Оценка, Разности и Методы поиска.
Позволяют контролировать некоторые
технические аспекты решения задач. В
большинстве случаем нет необходимости
изменять их установки.
Сохранить модель.
Служит для отображения на экране
диалогового окна, в котором можно задать
ссылку на область ячеек, предназначенную
для хранения модели оптимизации. Данный
вариант предусмотрен для хранения на
листе более одной модели оптимизации –
первая модель сохраняется автоматически.
Загрузить модель.
Служит для отображения на экране
диалогового окна, в котором можно задать
ссылку на область ячеек, содержащих
загружаемую модель.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Практическая работа №2

Тема: Подготовка и применение электронных таблиц при решении задач оптимизации (на примере функции «Поиск решения» MS Excel

Цель занятия Изучение технологии поиска решения для задач оптимизации (минимизация, максимизации).

Задание12.1.Используя режим подбора параметра (Сервис /Подбор параметра), определить штатное расписание фирмы. Известно, что в штате фирмы состоят: 6 курьеров, 8 младших менеджеров, 10 менеджеров, 3 заведующих отделом, 1 главный бухгалтер, 1 программист, 1 системный аналитик, 1 генеральный директор. Общий месячный фонд зарплаты составляет 100 000р. Определить, какими должны быть оклады сотрудников.

Каждый оклад является линейной функцией от оклада курьера, а именно:

зарплата = Ai*x + Bi,

где х — оклад курьера; Ai и Вi — коэффициенты, показывающие:

Ai — во сколько раз превышается значение х; Bi — на сколько превышается значение х. Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel.

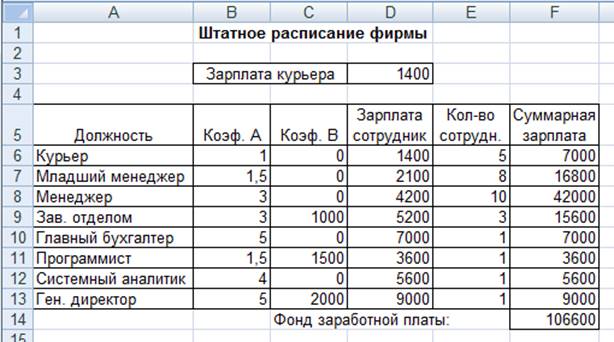
2. Создайте таблицу штатного расписания фирмы Введите исходные данные в рабочий лист электронной книги.

Штатное расписание фирмы
	Зарплата курьера

Должность	Коэф А	Коэф В	Зарплата сотрудника	Количество сотрудников	Суммарная зарплата
Курьер	1	0		6
Младший менеджер	1,5	0		8
Менеджер	3	0		10
Зав. отделом	3	1000		3
Главный бухгалтер	5	0		1
Программист	1,5	1500		1
Системный аналитик	4	0		1
Ген. директор	5	2000		1
Фонд заработной платы

3. Выделите отдельную ячейку D3 для зарплаты курьера (переменная «х») и все расчеты задайте с учетом этого. В ячейку D3 временно введите произвольное число.

4. В столбце D введите формулу для расчета заработной платы по каждой должности.

= B6*$D$3 + С6

Далее скопируйте формулу из ячейки D6 вниз по столбцу автокопированием.

В столбце F задайте формулу расчета заработной платы всех работающих в данной должности. =D6*E6.

Далее скопируйте формулу из ячейки F6 вниз по столбцу автокопированием.

В ячейке F14 автосуммированием вычислите суммарный фонд заработной платы фирмы.

5. Произведите подбор зарплат сотрудников фирмы для суммарной заработной платы, 100 000 р. Для этого в меню Сервис активизируйте команду Подбор параметра.

В поле Установить в ячейке появившегося окна введите ссылку на ячейку F14,

содержащую формулу расчета фонда заработной платы; в поле Значение наберите искомый результат 100 000; в поле Изменяя значение ячейки введите ссылку на изменяемую ячейку D3,в которой находится значение зарплаты курьера, и щелкните по кнопке ОК. Произойдет обратный расчет зарплаты сотрудников по заданному условию при фонде зарплаты, равном 100000 р.

Присвойте рабочему листу имя «Штатное расписание 1». Сохраните созданную книгу под именем «Штатное расписание» в своей папке.

Задание 2. Используя режим подбора параметра и таблицу расчета штатного расписания , определить заработные платы сотрудников фирмы для ряда заданных значений фонда заработной платы.

Порядок работы

Запустите редактор электронных таблиц Microsoft Excel и откройте ранее созданный файл «Штатное расписание».

Методом подбора параметров последовательно определите зарплаты сотрудников фирмы для различных значений фонда заработной платы: 100 000, 150 000, 200 000, 250000, Результаты подбора значений зарплат скопируйте в таблицу в виде специальной вставки. Выделить копируемые данные Правка/Копировать, установить курсор в ячейку таблицы ответов Правка/Специальная вставка/ вставить значения.

Штатное расписание фирмы

	100000	150000	200000	250000
Должность	Зарплата	Зарплата	Зарплата	Зарплата
Курьер
Младший курьер
Менеджер
Зав. отделом
Главный бухгалтер
Программист
Системный аналитик
Ген. директор

Задание 3. Задачи оптимизации (поиск решения)

Минимизация фонда заработной платы фирмы.

Пусть известно, что для нормальной работы фирмы требуется 5…7 курьеров, 8… 10 младших менеджеров, 10 менеджеров, 3 заведующих отделами, главный бухгалтер, Программист, системный аналитик, генеральный директор фирмы.

Общий месячный фонд зарплаты должен быть минимален. Необходимо определить, какими должны быть оклады сотрудников фирмы, при условии, что оклад курьера не должен меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную модель. Тогда условие задачи имеет вид

N₁ * А₁* х + N₂ * (А₂ * х + В₂) + ... + N₈ * (A_g * х + B_g) = Минимум,

Где N — количество работников данной специальности; х — зарплата курьера; A_i и Bi —

коэффициенты заработной платы сотрудников фирмы.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и откройте ранее созданный файл «Штатное расписание». Скопируйте содержимое листа «Штатное расписание 1» на новый лист и присвойте копии листа имя «Штатное расписание 2».

2. В меню Сервис/надстройка активизируйте команду Поиск решения

3. В окне Установить целевую ячейку укажите ячейку F14, содержащую модель суммарный фонд заработной платы.

Поскольку необходимо минимизировать общий месячный фонд зарплаты, активизируйте кнопку равный — Минимальному значению. В окне Изменяя ячейки укажите адреса ячеек, в которых будет отражено количество курьеров и младших менеджеров, а также зарплата курьера — $E$6:$E$7:$D$3 (при задании ячеек Е6, Е7 и D3 держите нажатой клавишу [Ctrl]).

Используя кнопку Добавить в окнах Поиск решения и Добавление ограничений, опишите все ограничения задачи: количество курьеров изменяется от 5 до 7, младших менеджеров от 8 до 10, а зарплата курьера 1400 Ограничения наберите в виде

$D$3 = 1400 $Е$6 = 5 $Е$6 = 8 $Е$7

Активизировав кнопку Параметры, введите параметры поиска

Рис.12.1 Задание условий для минимизации фонда заработной платы

Рис.12.2 Добавление ограничений для минимизации фонда заработной платы

Используя кнопку Добавить в окнах Поиск решения и Добавление ограничений ,опишите все ограничения задачи: Количество курьеров изменяется от 5 до 7 ,младших менеджеров от 8 до 10, а зарплата курьера 1400 (рис.12.2).Ограничения наберите в виде

$D$3=1400

$Е$6=5

$Е$6

$Е$7=8

$Е$7

Активизировав кнопку Параметры , введите параметры поиска, как показано на рис.12.3.

Окончательный вид окна Поиск решения приведен на рис. 12.1

Запустите процесс поиска решения нажатием кнопки Выполнить. В открывшемся диалоговом окне Результаты поиска решения задайте опцию Сохранить найдено решение (рис.12.4).

Решение задачи приведено на рис. 12.5. Оно тривиально: чем меньше сотрудников и чем меньше их оклад ,тем меньше месячный фонд заработной платы.

Рис.12.3. Задание параметров поиска решения по минимизации фонда заработной платы

Рис.12.4. Сохранение найденного при поиске решения

Штатное расписание фирмы

Зарплата курьера

Должность

Коэф А

Коэф В

Зарплата сотрудника

Количество сотрудников

Суммарная зарплата

Курьер

1

0

1400,00

5

7000,00

Младший менеджер

1,5

0

2100,00

8

16800,00

Менеджер

3

0

4200,00

10

42000,00

Зав. отделом

3

1000

5200,00

3

15600,00

Главный бухгалтер

5

0

7000,00

1

7000,00

Программист

1,5

1500

3600,00

1

3600,00

Системный аналитик

4

0

5600,00

1

5600,00

Ген. директор

5

2000

9000,00

1

9000,00

Фонд заработной платы

106600,00

Рис.12.5. Минимизация фонда заработной платы

Таблица 12.1

Сырьё

Нормы расхода сырья

Запас сырья

А

В

C

Сырье 1

18

15

12

350

Сырье 2

6

4

8

200

Сырье 3

5

3

3

100

Прибыль

10

15

20

Задание 12.2. Составление плана выгодного производства.

Фирма производит несколько видов продукции из одного и того же сырья – А,В, С.

Реализация продукции А дает прибыть 10 р.., В- 15 р. и С- 20 р. на единицу изделия.

Продукцию можно производить в любых количествах , поскольку известно, что сбыт обеспечен ,но ограничены запасы сырья .Необходимо определить ,какой продукции и сколько надо произвести, чтобы общая прибыть от реализации была максимальной.

Нормы расхода сырья на производство продукции каждого вида приведены в табл. 12.1.

Порядок работы

1.Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу .

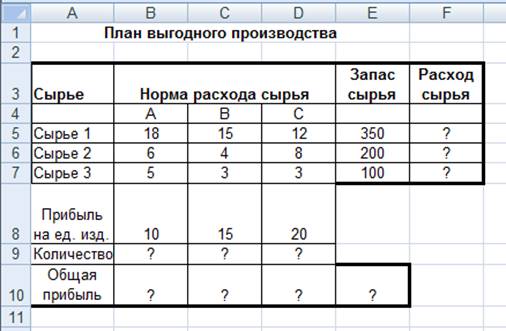
2.Создайте расчетную таблицу как на рис. 12.6 введите исходные данный

И формулу в электронную таблицу. Расчетные формулы имеют такой вид:

Расходы сырья 1= (количество сырья 1) *(норма расхода сырья А)+(количество сырья 1)*(норма расхода сырья В)+(количество сырья 1)*(норма расхода сырья С)

Значит , в ячейку F5 нужно ввести формулу = В5*$B$9+ C5* $C$9 + D5 *$D$9.

Обратите внимание ,что значения количества сырья каждого вида пока не известны и будут подобраны в процессе решения задания(ячейки В9:D9 пока пустые)

(Общая прибыль по А)=(прибыль на ед.изделий А)*(количество А),

Следовательно в ячейку В10 следует ввести формулу =В8*В9

Итоговая общая прибыль =(общая прибыль по А) * (общая прибыль по В) + (Общая прибыль по С),

Значит в ячейку Е10 следует ввести формулу =СУММ(В10:В10).

Рис.12.6. Исходные данные для задания 12.2

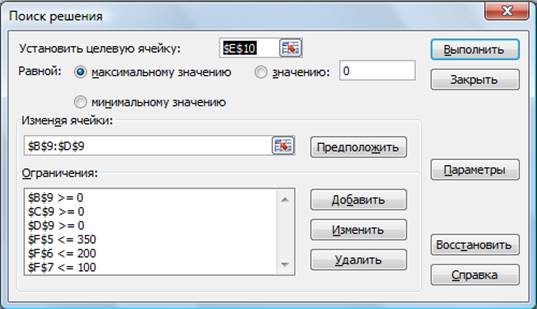
3.В меня сервис активизируйте команду Поиск решения и введите параметры писка, как указано на рис.12.7.

В качестве целевой ячейки укажите ячейку «Итоговая общая прибыть» (Е10) , в качестве изменяемых ячеек – ячейки количества сырья – (В9:D9).

Не забудьте задать максимальное значение суммарной прибыли и указать ограничения на запас сырья:

Расход сырья 1 ; расход сырья 2 также положительные значения количества сырья А, В, С = 0.

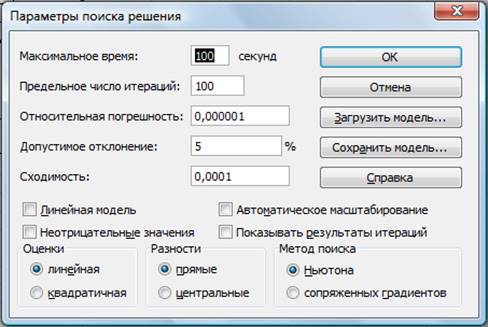
Установите параметры поиска решения (рис.12.8).Для этого кнопкой Параметры откройте диалоговое окно Параметры поиска

Рис.12.7. Задание условий и ограничений для поиска решений

Рис.12.8. Задание параметров поиска решения

Рис.12.9.Найденное решение максимизации прибыли при заданных ограничениях

решение , установите параметры по образцу ,задайте линейную модель расчета (Линейность модели).

4. Кнопкой Выполнить запустите Поиск решения .Если вы сделали все верно ,то решение будет как на рис.12.9.

5.Сохраните созданный документ под именем «План производства»

Вывод: Из решения видно ,что оптимальный план выпуска предусматривает изготовление 5,56 кг продукции В и 22,22кг продукции А производитель не стоит .Полученная прибыль при этом состоит 527,78р.

Дополнительное задания

Используя файл «План производства» (см. задание 12.2),определить план выгодного производства , т.е. какой продукции и сколько не обходимо произвести , чтобы общая прибыть от реализации была максимальной.

Выберите нормы расхода сырья на производство продукции каждого вида и ограничения по запасам сырья из таблицы соответствующего варианта( 5 вариантов ):

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Источник

Сырьё	Нормы расхода сырья	Запас сырья
А	В	C
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20