«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
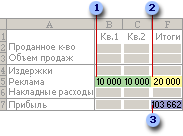
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
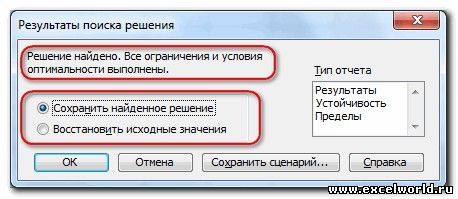
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
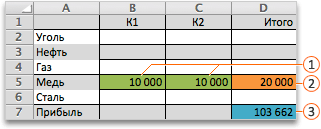
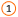
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование «Решения» для бюджетов с использованием средств на счете вех
Использование «Решение» для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.
Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».
Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.
Сделать это можно так:
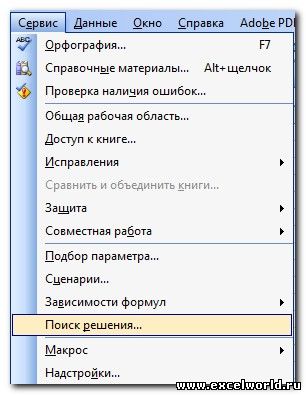
для версий старше Excel 2007 через команду меню Сервис —> Надстройки;
начиная с Excel 2007 через диалоговое окно Параметры Excel
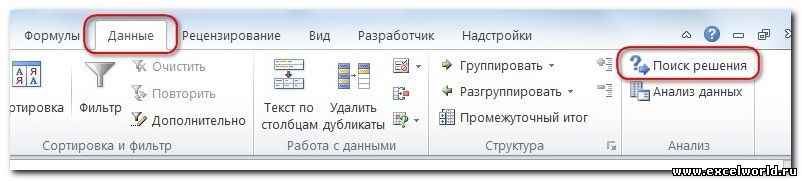
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.
В версиях до Excel 2007 аналогичная команда появится в меню Сервис
Разберём порядок работы Поиска решения на простом примере.
Пример 1. Распределение премии
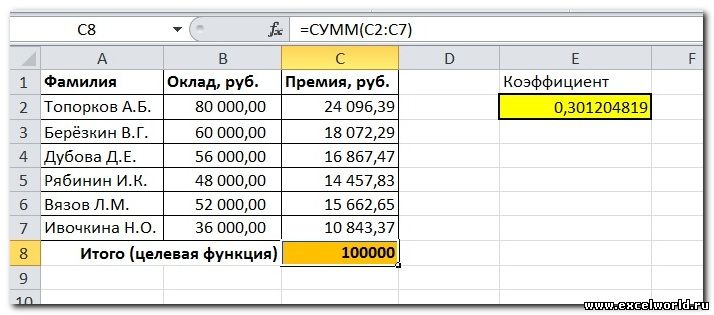
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
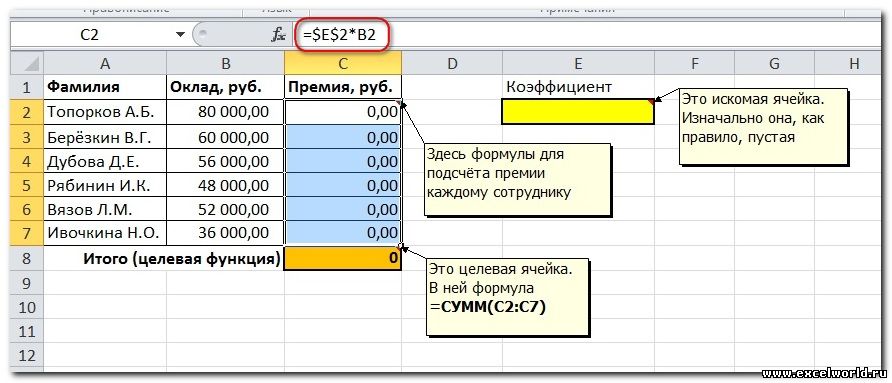
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
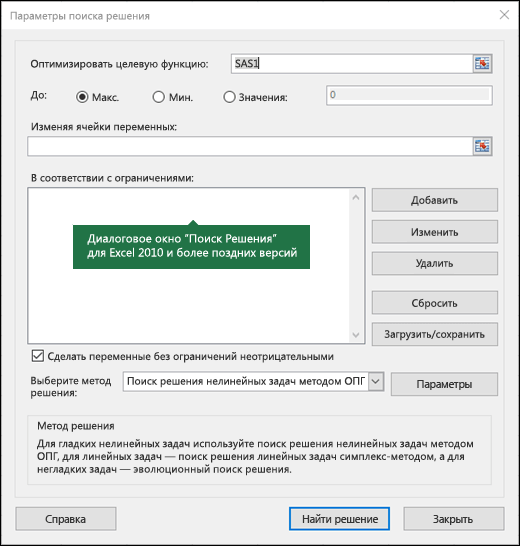
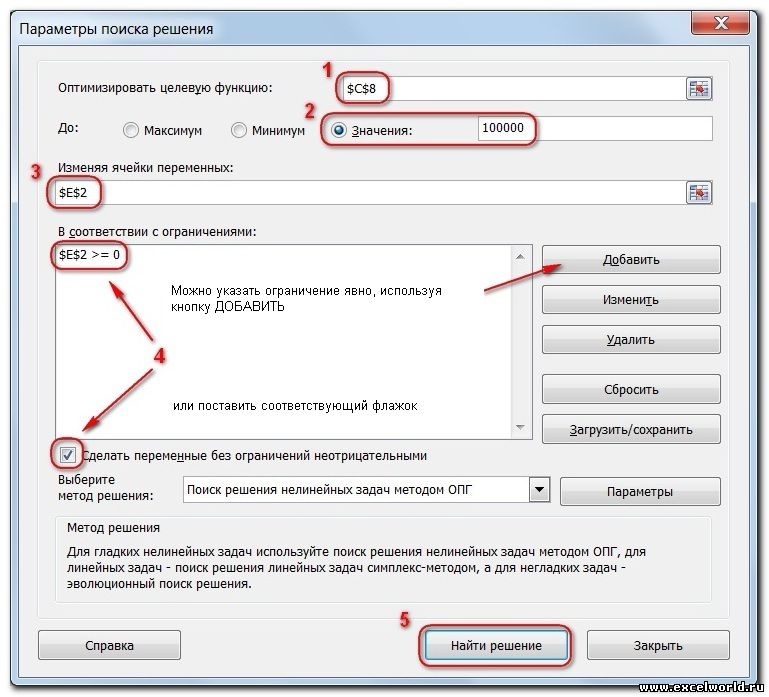
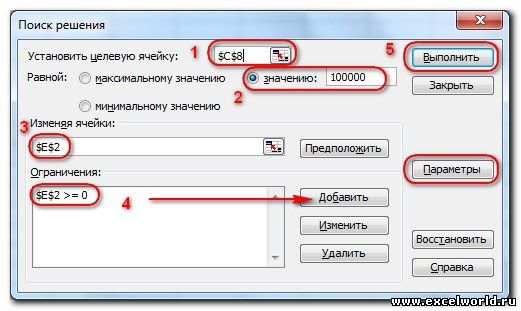
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
До Excel 2010
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
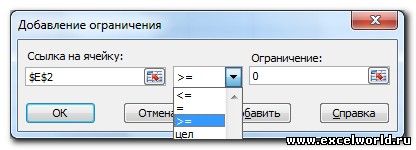
- Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).
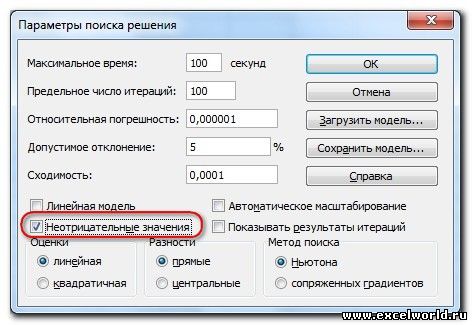
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
- Кнопка, включающая итеративные вычисления с заданными параметрами.
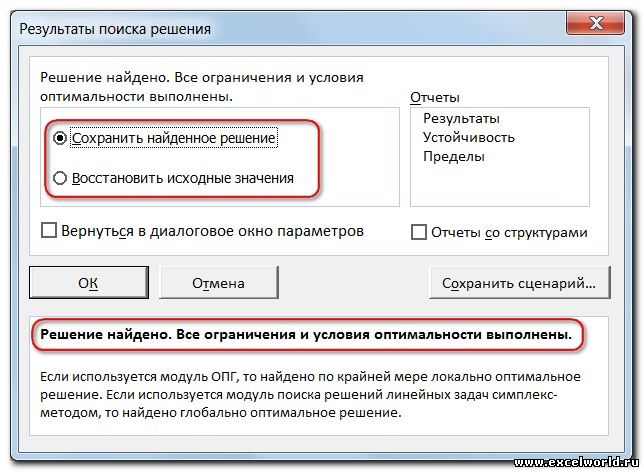
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
До Excel 2010
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
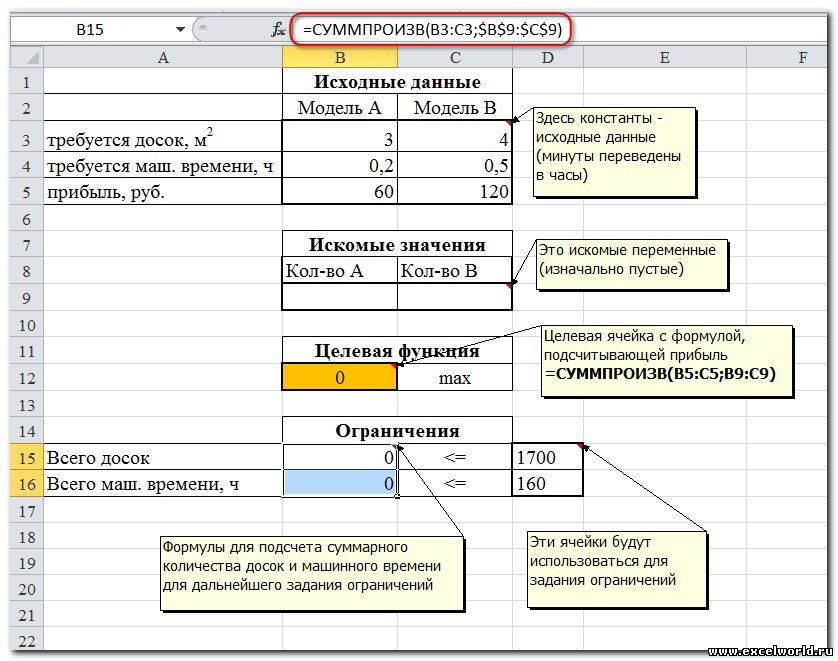
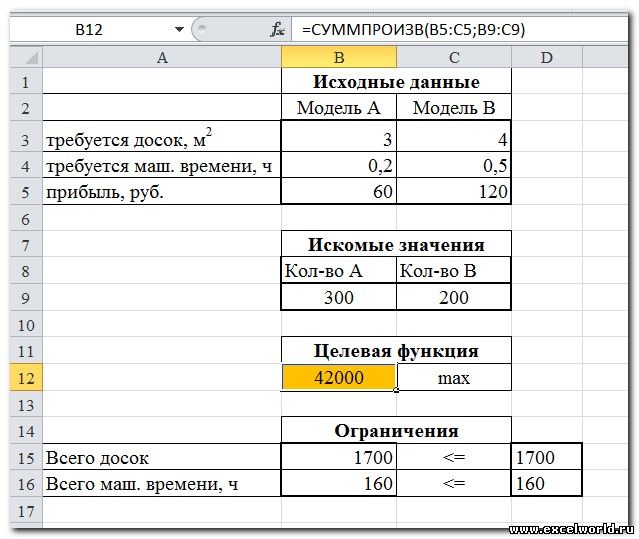
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
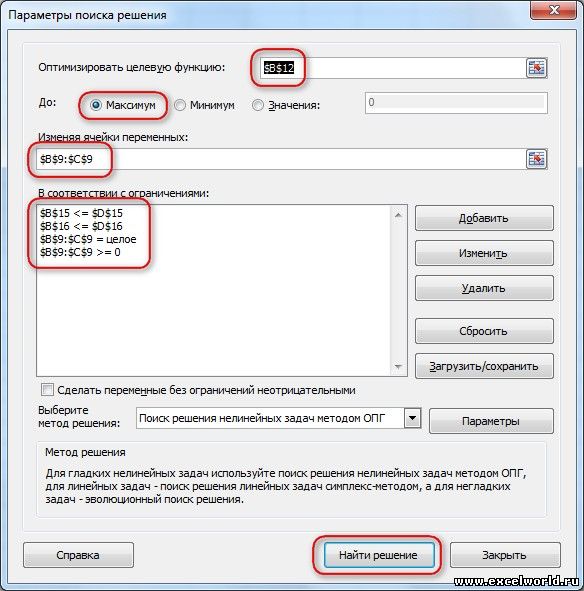
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
- Целевая ячейка B12 содержит формулу для расчёта прибыли
- Параметр оптимизации — максимум
- Изменяемые ячейки B9:C9
- Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
- Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
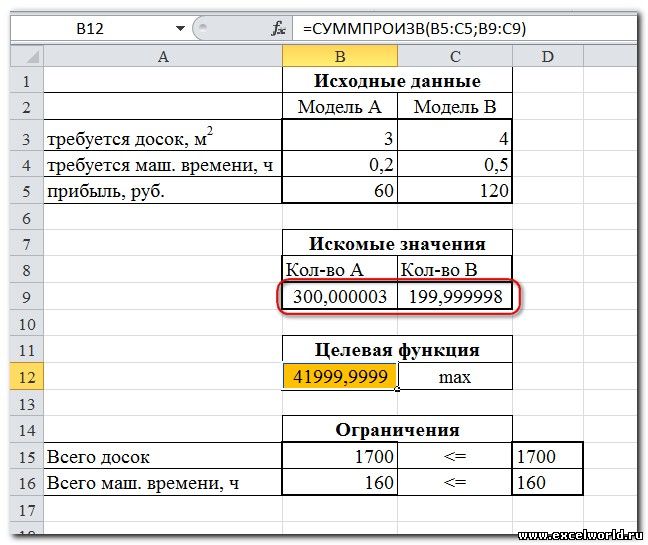
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
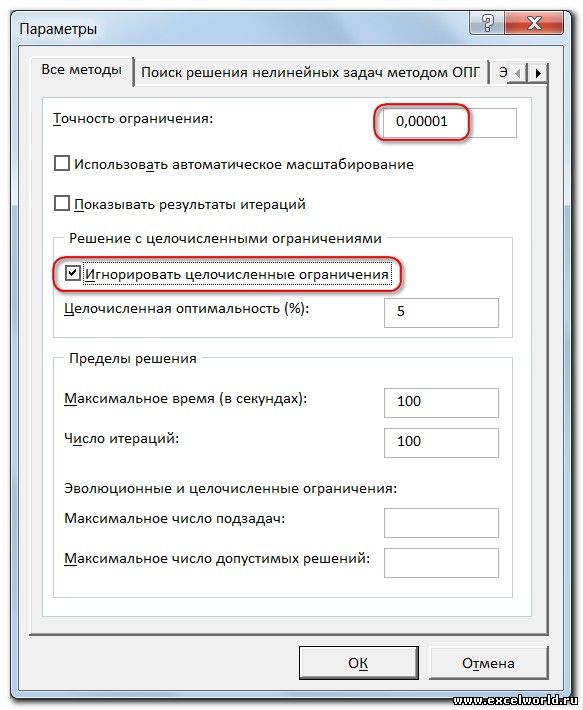
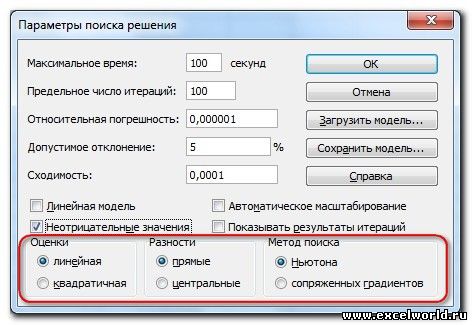
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
Пример 3. Транспортная задача (минимизация затрат)
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
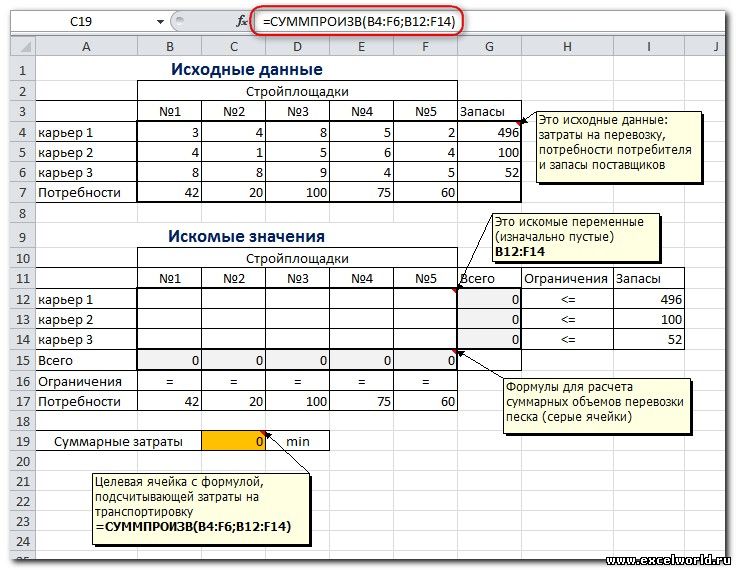
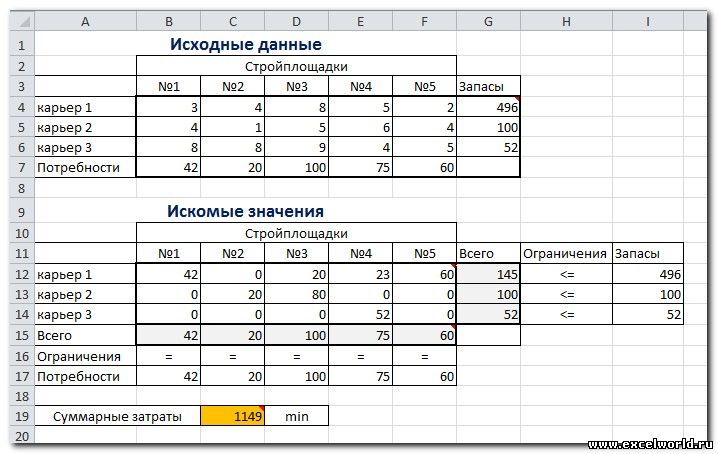
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
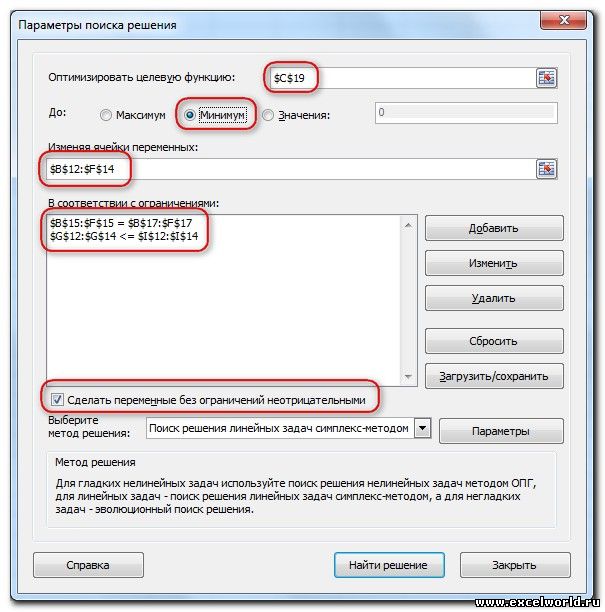
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
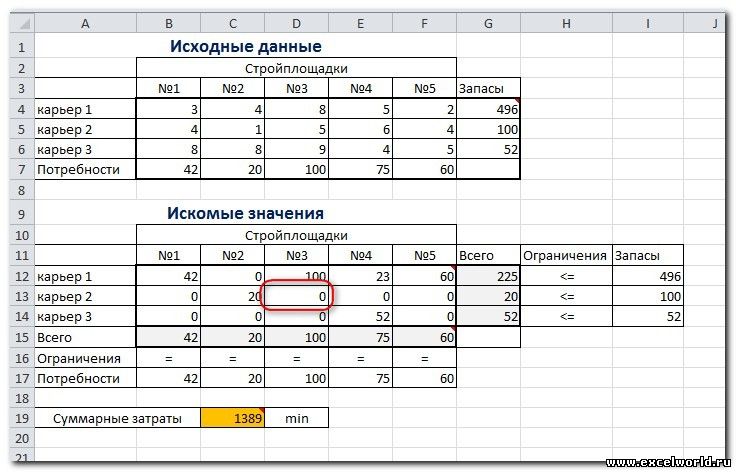
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
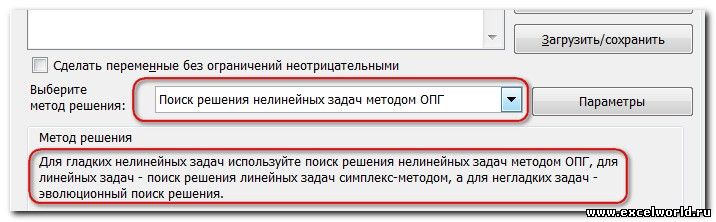
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Начиная с Excel 2010
До Excel 2010
В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:
Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?
dremastar
Пользователь
Сообщений: 25
Регистрация: 07.11.2013
Добрый день, уважаемые знатоки.
Столкнулся с трудностью которую самостоятельно не могу решить.
Во вложении задача по поиску минимальной стоимости Гигакалории в зависимости от включённого оборудования.
Поиск решения минимизирует стоимость, однако работает только в том случае, если я в ручном режиме указываю какое оборудование включено, а какое выключено.
Как изменить постановку задачи, чтобы инструмент Поиск решения сам находил оптимальные сочетания оборудования при необходимой производительности??
Заранее благодарен…
history 23 марта 2015 г.
- Группы статей
- Надстройка «Поиск решения»
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в MS EXCEL 2010 (эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в MS EXCEL 2007) . В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
- настройку Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда Поиск решения находится в группе Анализ на вкладке Данные .
Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:
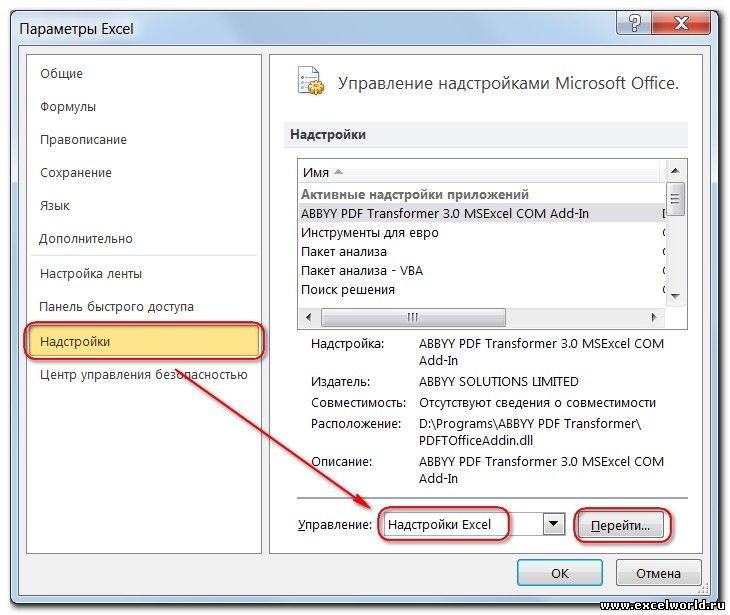
- На вкладке Файл выберите команду Параметры , а затем — категорию Надстройки ;
- В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
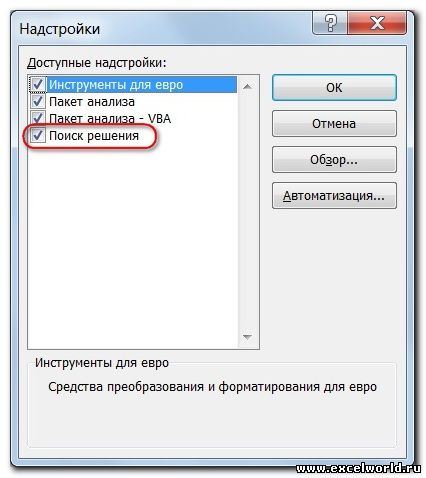
- В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.
Примечание . Окно Надстройки также доступно на вкладке Разработчик . Как включить эту вкладку читайте здесь .
После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно .
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа .
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет . Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка Поиск решения помогает определить лучший способ сделать что-то :
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
- Определить план производства , при котором доход от реализации произведенной продукции максимальный;
- Определить схему перевозок , при которой общие затраты на перевозку были бы минимальными;
- Найти распределение нескольких станков по разным видам работ , чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией ). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание . В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра . Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра . Основные отличия Подбора параметра от Поиска решения :
- Подбор параметра работает только с моделями с одной переменной;
- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет . Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).
Приведем алгоритм работы с Поиском решения , который советуют сами разработчики ( ]]> www.solver.com ]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
- С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
- Запустите Поиск решения для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см. файл примера ).
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) . Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет : в статье » Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями » показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью Поиска решения является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью Поиска решения . Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью Поиска решения рассмотрено в этом разделе .
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете Симплекс метод решения линейных задач , то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).
Примечание . О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства .
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.
При ограничении 17 м3 Поиск решения найдет решение.
Некоторые настройки Поиска решения
Метод решения Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Бинарные ограничения excel solver (Simplex LP)
Я решаю проблему оптимизации. проблема имеет двоичные ограничения. решатель (во время итерации) устанавливает эти двоичные ограничения на десятичные значения от 0 до 1 (приближение к расслабленному поиску градиента). Я хочу указать решателю, что он должен просто искать по разрытым значениям для 0..1.
Есть ли способ сделать это?
Альтернативно, есть ли в OpenSolver алгоритм, который делает это, который имитирует симплекс-lp и обеспечивает глобальный оптимум?
дешевый способ сделать это, — это право на цикл и повторение значений. Мне было интересно, есть ли способ выразить это так, чтобы нелинейная проблема стала линейной проблемой.
Методы GRG Nonlinear и Simplex LP используют метод Branch & Bound, когда сталкиваются с целыми ограничениями. Этот метод сначала «расслабляет» целочисленное требование, находит решение, затем фиксирует одно из ограничений на целое и находит новое решение. См. Интерактивную документацию Solver.
Это метод поиска грубой силы и может занять значительное количество времени.
Эволюционный метод использует собственный алгоритм для решения целочисленных ограничений и, как правило, намного быстрее, чем два других метода.
Вы спрашиваете о линеаризации нелинейной проблемы — вам нужно будет предоставить более конкретную информацию, чтобы ответить на это (например, каково ваше уравнение? Как вы решили проблему решателя?) И т.д.
Чтобы
получить целочисленное решение задачи
линейного программирования с помощью
программы Excel,
к
обычным ограничениям задачи добавляются
условия целочнсленности. Это можно
сделать в окне Добавление
ограничения, вид
которого для нашего примера (см. раздел
1.1) показан на рис. 2.2.
В
поле
Ссылка
на ячейки (Ссылка на ячейку) задается
диапазон ячеек содержащих значения
переменных, а в раскрывающемся списке
вместо знака выбирается один из следующих
пунктов:
-
цел
—
целое число;
в
бин в
Excel
2010
(или двоич
в
предыдущих версиях)—
бинарное
(двоичное) число 0 или 1;
-
раз
(только
в Excel
2010)
— разные целые числа от 1 до N
(где
N
—
число переменных).
При
этом в поле Ограничение
автоматически
появляется слова: целое,
бинарное
(двоичное) или
Все
разные.
Если
переменные в модели — разных типов
(целые, бинарные, разные целые,
вещественные), можно задать несколько
условий целочнсленности, для каждого
типа переменных в отдельности.
Поскольку
нахождение целочисленного решения
зачастую является довольно длительной
процедурой, предусмотрена возможность
ее ускорения. Для этого используются
следующие параметры, задаваемые в Excel
2010
в окне Параметры
(см.
рис. 1.26), а в предыдущих версиях — в окне
Параметры
поиска решения (см.
рис. 1.27) (названия параметров, используемые
в предыдущих версиях, даны в скобках):
-
Игнорировать
целочисленные ограничения (только
в Excel
2010)
—
Добавление
ограничения
Ссылка
на ячеикм:
ГШ
Ограничение:
ок
Отмена
Добавить
Рис.
2.2. Добавление требования целочнсленности
переменных
флажок,
установка которого приводит к решению
задачи без учета условий целочисленное™.
-
Целочисленная
оптимальность (Допустимое отклонение)—
указывает, на сколько процентов
полученное значение целевой функции
может отличаться от оптимального
(по умолчанию в Excel
2010
— 1%, а в предыдущих версиях — 5% ). Для
ускорения можно увеличить это значение.
Если же необходимо получить точное
решение, то следует установить этот
параметр равным 0%, но это может значительно
увеличить время оптимизации, -
Максимальное
время —
позволяет задать в секундах максимальное
время, которое отводится на поиск
решения (значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях— 100
секунд). -
Число
итераций (Предельное число итераций)
—
позволяет определить максимальное
количество итераций при поиске решения
(значение по умолчанию в Excel
2010
не задано, а в предыдущих версиях—
100). Для целочисленных моделей данный
параметр указывает максимальное
количество итераций для каждой
подзадачи. -
Максимальное
число подзадач (только
в Excel
2010)—
позволяет задать максимальное количество
подзадач при целочисленном решении. -
Максимальное
число допустимых решений (только
в Excel
2010)
— позволяет определить максимальное
количество рассматриваемых допустимых
целочисленных решений.
Если
вы задали некоторые из перечисленных
предельных значений, то поиск решения
будет продолжаться до тех пор, пока
какое-нибудь нз них не будет достигнуто.
Тогда появится окно с предложением
остановить вычисления или продолжить.
Если вы решили продолжить вычисления,
достигнутое предельное значение
отменяется н расчеты продолжаются до
достижения следующего нз заданных
предельных значений. Если вы выбрали
вариант остановки вычислений, появится
окно с сообщением о том, что решение
остановлено по запросу пользователя и
на листе окажутся результаты, достигнутые
на этот момент. Прервать вычисления
можно также нажатием клавиши Esc.
При
этом также появляется окно с предложением
остановить пли продолжить вычисления.
Остальные
ограничения и параметры поиска решения
— те же, что и для обычной задачи линейного
программирования (см. раздел 1.3). Выполнив
вычисления с условием целочнсленности,
показанным на рис. 2.2, вы получите
целочисленное решение нашей задачи (5;
1; 3, 4).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
21.03.201614.11 Mб13МЕТОДИЧКА ЭТМ №2.rtf
- #
- #
- #
- #
- #
- #
- #
- #