1. Занятие 14
Надстройка Поиск решения
2. Надстройка «Поиск решения» в Microsoft Excel
Надстройка «Поиск решения» позволяет найти оптимальное значение для
результата, содержащегося в одной ячейке, называемой целевой, с учетом
ограничений на переменные.
«Поиск решения» работает с группой ячеек, прямо или косвенно связанных с
формулой в целевой ячейке. Чтобы получить заданный результат по формуле
из целевой ячейки, «Поиск решения» изменяет значения в назначенных
ячейках, называемых изменяемыми ячейками.
Для уменьшения количества значений, используемых в модели, применяются
ограничения, которые могут ссылаться на другие ячейки, влияющие на
формулу для целевой ячейки.
3. Решение задачи линейного программирования
Для того чтобы решить задачу линейного программирования (ЛП) в табличном
редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. Ввести условие задачи:
• a) создать экранную форму для ввода условия задачи:
– -переменных,
– -целевой функции (ЦФ),
– -ограничений,
– -граничных условий;
• b) ввести исходные данные в экранную форму:
– -коэффициенты ЦФ,
– -коэффициенты при переменных в ограничениях,
– -правые части ограничений;
• c) ввести зависимости из математической модели в экранную форму:
– -формулу для расчета ЦФ,
– -формулы для расчета значений левых частей ограничений;
4. Решение задачи линейного программирования
• d) задать ЦФ (в окне «Поиск решения»):
– -целевую ячейку,
– -направление оптимизации ЦФ (максимум или минимум);
• e) ввести ограничения и граничные условия (в окне «Поиск
• решения»):
– -ячейки со значениями переменных,
– -граничные условия для допустимых значений переменных,
– -соотношения между правыми и левыми частями ограничений.
2. Решить задачу:
• a) установить параметры решения задачи (в окне «Поиск решения»);
• b) запустить задачу на решение (в окне «Поиск решения»);
• c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
5. Установка надстройки «Поиск решения»
Метод поиска решения не всегда
присутствует на вкладке «Данные». Прежде
чем использовать этот метод, его надо
добавить из дополнительных надстроек.
Для этого необходимо выбрать пункт меню
Файл. В появившемся окне нажать на
кнопку «Параметры Excel»
6. Установка надстройки «Поиск решения»
Затем выбрать строку «Надстройки» и в нижней части
появившегося окна нажать на кнопку «Перейти»:
В появившемся окне поставить галочку в строке «Поиск
решения» и нажать на кнопку ОК. В результате на
ленте Данные появится возможность вызвать метод
«Поиск решения».
7. Решение задачи линейного программирования
Формулировка задачи. Доход от продажи краски 1 равен 2 рублям, а от продажи краски 2одному рублю. Для производства красок используются два ресурса А и В. На производство
единицы краски 1 расходуется одна единица ресурса А и 3 единицы ресурса В. Для
производства единицы краски 2 расходуется 2 единицы ресурса А и единица ресурса В.
Запасы каждого ресурса равны 3 единицам. При каком производстве каждой краски будет
достигнут максимальный доход?
Для удобства запишем исходные данные задачи в следующую таблицу.
Обозначим неизвестное нам количество краски каждого вида через х1 и х2
соответственно. Тогда можно записать условие задачи в виде следующих формул:
Необходимо найти максимум выражения 2 * х1 + х2 (это суммарный доход от продажи)
при ограничениях х1 + 2 * х2 <= 3, 3 * x1 + x2 <= 3 (ограничения на запасы сырья).
Для неизвестным нам значениям переменных отводим
ячейки В3 и С3. В этих ячейках будет формироваться
решение задачи. Первоначально их необходимо
оставить пустыми, что интерпретируется в расчетах как
нулевое значение данных ячеек.
8. Решение задачи линейного программирования
В ячейку D4 вводится формула для вычисления
целевой функции задачи (суммарного дохода)
Z=2 * x1 + x2. Для задач линейного
программирования удобно использовать
математическую функцию «СУММПРОИЗВ».
Установим курсор в ячейку D4, перейдем на
вкладку «Формулы» и в группе математических
функций выберем функцию «СУММПРОИЗВ».
В окне мастера функций нажать ОК и в
появившемся окне в поле «Массив1»
ввести адреса изменяемых ячеек В3:С3.
В поле Массив2 вводятся адреса ячеек
содержащих цены на краски В4:С4.
После нажатия на кнопку ОК в ячейке
D4 появится результат вычисления
равный 0.
Использование функции
«СУММПРОИЗВ» обусловлено
удобством проведения расчетов во всех
задачах линейного программирования.
9. Решение задачи линейного программирования
Используя ту же функцию в ячейку
D7вводим формулу для вычисления
израсходованного количества
продукта А: х1 + 2 * х2, а в ячейку D8
вводим формулу для вычисления
израсходованного количества
продукта В: 3 * х1 + х2.
После ввода
формул таблица
будет выглядеть
так
2
1
10. Применение метода «Поиск решения»
Следующий шаг — применение метода поиска решения для нахождения
максимума целевой функции. Вызовем этот метод с вкладки «Данные» и начнем
заполнять поля появившегося окна.
Целевая ячейка- это ячейка со
значением целевой функции D4. Для
ввода этого значения необходимо
щелкнуть мышкой на этой ячейке. В
поле «Изменяя ячейки» вводятся
адреса ячеек, которые мы
зарезервировали под значения
неизвестных х1 и х2 (В3 и С3).Так как
наша задача- максимизировать доход,
мы устанавливаем флажок на кнопке
«максимальному значению».
Для ввода ограничений необходимо нажать
кнопку «Добавить» и ввести очередное
ограничение в появившееся окно.
Ограничения добавляются последовательно.
Для задачи ЛП необходимо ввести
дополнительное ограничение х1, х2 >= 0, так
как объем производства не может быть
отрицательным.
11. Применение метода «Поиск решения»
12. Параметры метода «Поиск решения»
Точность ограничения – точность
приближенных вычислений
Использовать автоматическое
масштабирование – для одновременного
использования очень маленьких и очень
больших величин
Показывать результаты итераций – если
вычисления занимают много времени
Игнорировать целочисленные ограничения
– используется при решении целочисленных
задач
Максимальное время – ограничение на
время счета
Число итераций – ограничение на число
итераций
Другие вкладки используются для настройки
нелинейных методов решения задач ЛП
13. Вычисление оптимального значения
После задания всех параметров необходимо нажать кнопку «Выполнить» и получить в
ячейках В3 и С3 искомое значение неизвестных, при котором достигается максимум
целевой функции при выдвинутых ограничениях.
Таким образом, максимальный доход
размером 2,4 рубля достигается при
производстве 0,6 объема краски 1 и 1,2
объема краски 2. При этом будут
полностью израсходованы запасы
ресурсов 1 и 2.
Результат вычисления можно сохранить
или вернуться к исходным данным.
14. Отчет по результатам поиска решения
15. Отчеты об устойчивости и пределах
16. Представление модели в виде таблицы
На первом занятии была рассмотрена модель производства стульев. Эта модель
была представлена в виде следующей таблицы.
Самостоятельно разобрать следующий пример построив все таблицы, применить
метод поиска решения и получить отчет о результатах
17. Формулы в таблице
После того как надстройка Поиск решения загрузится в память, на экране появится
диалоговое окно, поля которого необходимо заполнить.
18. Заполнение полей диалогового окна
В поле Установить целевую ячейку диалогового окна Поиск решения вводится адрес
ячейки, содержащей значение целевой функции. Для модели Oak Product в это поле
следует ввести D4.
Опции области Равной диалогового окна Поиск решения позволяют задать тип
оптимизации. В данном случае необходимо максимизировать значение показателя
эффективности, т.е. прибыль компании Oak Product. Для этого нужно щелкнуть на
переключателе максимальному значению.
Щелчок на кнопке минимальному значению укажет, что надо минимизировать целевую
функцию.
Можно также сделать значение целевой функции равным заданному числу, установив
переключатель значению и введя это число.
19. Заполнение полей диалогового окна
Следующее поле Изменяя ячейки позволяет указать переменные решения модели, в
данном случае это диапазон В4:С4.
Теперь необходимо задать для средства Поиск решения ограничения Щелчок на кнопке
Добавить открывает диалоговое окно Добавление ограничения, которое позволяет
вводить ограничения.
20. Ввод частей ограничений типа «меньше или равно»
Внимание! Интервал
ограничений можно
задавать только в том
случае, когда эти
ограничения расположены
компактно
21. Ввод частей ограничений типа «больше или равно»
Далее надо не забывать об условиях не отрицательности для содержимого ячеек В4 и С4
Чтобы ввести эти ограничения, сначала следует вернуться в диалоговое окно Поиск
решения из диалогового окна Добавление ограничения, щелкнув на кнопке ОК в этом
окне.
На данном этапе диалоговое окно Поиск решения для модели Oak Production должно
выглядеть так, как показано на следующем слайде.
Описание презентации по отдельным слайдам:
-
1 слайд
Модели оптимального планирования
-
2 слайд
Объекты планирования:
деятельность отдельного предприятияотрасли промышленности или сельского хозяйства, региона, государства
-
3 слайд
Постановка задачи
имеются некоторые плановые показатели: x,y и др.
имеются некоторые ресурсы: r1,r2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены
имеется определенная стратегическая цель, зависящая от значений x,y и др. плановых показателей, на которую следует ориентировать планирование. -
4 слайд
Оптимальный план
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. -
5 слайд
Задача.
Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 шт изделий. Рабочий день – 8 часов. Если выпускать только пирожные, то за день можно произвести не более 250 штук, пирожков — 1000 шт.Стоимость пирожного в 2 раза выше стоимости пирожков. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха. -
6 слайд
Плановые показатели:
X – дневной план выпуска пирожков
Y — дневной план выпуска пирожных
Ресурсы производства:Длительность рабочего дня – 8 часов
Вместимость складского помещения – 700 мест -
7 слайд
Ограничения:
x+4y <=1000
x+y<=700
X>=0
Y>+0
Пусть цена 1 пирожка – r руб.
Цена пирожного в 2 раза больше = 2r руб.
Стоимость всей продукции за день:
rx+2ry= r(x+2y)
Целевая функция: F(x,y)= r(x+2y)
r – константа -
8 слайд
Организация ставит перед собой задачу, согласно выбранной рекламной стратегии, довести число публикаций рекламных объявлений, по крайней мере, до 800 тысяч экземпляров и разместить эти рекламные объявления в шести изданиях. Каждое издание имеет свое количество читателей и разумную стоимость печатной страницы. Для этих целей организация составила общий бюджет на печать и распространение рекламы в размере 12 000 000 рублей. Задача состоит в том, чтобы достичь заданного числа читателей, по возможности с наименьшими затратами при следующих дополнительных ограничениях:
в каждом издании должно появиться как минимум шесть объявлений;
на одно издание должно быть истрачено не более одной трети средств;
общая стоимость размещения рекламы в 3 и 4 издательствах не должна превышать 7 500 000 рублей.
Задача. Рекламная стратегия -
-
-
11 слайд
Надстройка «Поиск решения»
Задача. Производство автомобилей.
Для изготовления двух видов автомобилей (легкового и грузового) используются 4 вида ресурсов: сталь, пластмасса, резина и кожа.
Запасы ресурсов, число единиц ресурсов, затраченных на изготовление одного автомобиля каждого вида, приведены в таблице ниже.
Стоимость одного легкового автомобиля 10000 у.е., грузового 15000 у.е. Необходимо рассчитать, сколько автомобилей каждого вида надо произвести, чтобы получить максимальную прибыль. -
1
Лабораторная работа Тема занятия: Средства условного анализа в EXCEL. Основная цель: Научиться пользоваться программами Подбор параметра и Поиск решения.
2
Excel – ваши уверенные шаги в анализе и прогнозировании На этом занятии мы продолжим знакомиться с некоторыми возможностями анализа данных в Excel. Научимся: использовать средство «Подбор параметра»; использовать средство «Подбор параметра»; работать со средством «Поиск решения». работать со средством «Поиск решения».
3
Подбор параметра – это средство Excel для так называемого анализа «что, если » Программа «Подбор параметра» позволяет получить требуемое значение в определенной ячейке, которую называют целевой, путем изменения значения (параметра) другой ячейки, которую называют влияющей.
4
Найти решение уравнения X^3 — 3*X^2 + X = -1 средствами программы Excel Найти решение уравнения X^3 — 3*X^2 + X = -1 средствами программы Excel Занесем в ячейку A1 значение 0. Занесем в ячейку A1 значение 0. Занесем в ячейку B1 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку A1. Соответствующая формула будет иметь вид: =A1^3-3*A1^2+A1 Занесем в ячейку B1 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку A1. Соответствующая формула будет иметь вид: =A1^3-3*A1^2+A1 Даём команду Сервис — Подбор параметра. Даём команду Сервис — Подбор параметра.
5
Использование надстройки « Поиск решения». Программа «Поиск решения» позволяет получить результат на основе изменения значений нескольких ячеек. При выполнении поиска решения можно задать условия – ввести ограничения.
6
Поиск решения применим при вычислении площади треугольника Площадь треугольника вычисляется по формуле: S = ½*a*h (где a – основание треугольника, h – высота). Площадь треугольника вычисляется по формуле: S = ½*a*h (где a – основание треугольника, h – высота).
7
Подбор параметра выполняется с помощью команды меню Сервис – Подбор параметра. Задача 1. Известен размер вклада, который будет помещен в банк на неопределенный срок под определенный процент. Требуется рассчитать сумму возврата вклада в конце периода и определить условия помещения вклада, наиболее подходящие для его владельца. Известен размер вклада, который будет помещен в банк на неопределенный срок под определенный процент. Требуется рассчитать сумму возврата вклада в конце периода и определить условия помещения вклада, наиболее подходящие для его владельца.
8
Присвойте листу в книге имя Подбор. Создайте таблицу Введите формулы в ячейки B4 и B5 для вычисления коэффициента увеличения вклада и суммы возврата. С чего начинается формула ?
9
Скопируйте созданную таблицу на этот же лист, а так же на листы 2 и 3.
10
Выполнив команду Сервис – Подбор параметра, получаем диалоговое окно «Подбор параметра», в котором правильно устанавливаем нужные параметры.
11
В результате выполнения команды Сервис – Подбор параметра получили процентную ставку и срок вклада при которых сумма возврата вклада составляет 8000 рублей.
12
В первой копии таблицы, изменяя одновременно два параметра, подберите значения срока вклада и процентной ставки, при которых сумма возврата будет составлять 8000 рублей. Для этого выполните следующие действия: 1. Введите команду СЕРВИС – Поиск решения и в диалоговом окне «Поиск решения» установите следующие параметры: адрес целевой ячейки — $B$5 – сумма возврата вклада; адрес целевой ячейки — $B$5 – сумма возврата вклада; Подбираемое для целевой ячейки значение – 8000р; Подбираемое для целевой ячейки значение – 8000р; В поле Изменяя ячейки введите абсолютные адреса ячеек со сроком вклада и величиной процентной ставки. В поле Изменяя ячейки введите абсолютные адреса ячеек со сроком вклада и величиной процентной ставки. 2. Введите ограничения для ячейки со сроком вклада – цел – целое число лет. 3. Щелкните по кнопке Выполнить.
13
Обратите внимание на то, что оба изменяемых параметра косвенно связаны со значением целевой ячейки В5=В4*В1, так как входят в формулу расчета коэффициента увеличения вклада В4=(1+В3)^В2.
14
В диалоговом окне «Результаты поиска решения» установите: Сохранить найденное решение; Тип отчета – Результаты.
15
Во второй копии таблицы на листе Поиск выполнить еще раз операцию Поиск решения, установив следующие параметры: адрес и значение целевой ячейки – сумма возврата вклада 8000р.; адрес и значение целевой ячейки – сумма возврата вклада 8000р.; В поле Изменяя ячейки введите абсолютные адреса ячеек с размером вклада, сроком вклада и величиной процентной ставки; В поле Изменяя ячейки введите абсолютные адреса ячеек с размером вклада, сроком вклада и величиной процентной ставки; Добавьте ограничения для ячейки с величиной процентной ставки:
16
Диалоговое окно «Поиск решения» будет выглядеть следующим образом
17
Задача 2. Используя режим подбора параметра, определить штатное расписание фирмы. Исходные данные приведены в таблице 1(первый вариант).
18
Задача 3. Используя программу, Поиск решения, решите задачу оптимизации выпуска изделий на предприятии «Протон». (второй вариант). Предприятие выпускает приборы трех типов – прибор 1, 2 и 3. Количество комплектующих элементов, используемых для производства одного прибора каждого типа, и ежедневный запас комплектующих элементов приведены в таблице Предприятие выпускает приборы трех типов – прибор 1, 2 и 3. Количество комплектующих элементов, используемых для производства одного прибора каждого типа, и ежедневный запас комплектующих элементов приведены в таблице Расход элементов каждого типа вычисляется по формуле =B3*$B$6+C3*$C$6+D3*$D$6. Определите, каким образом следует изменить соотношение типов выпускаемых приборов, чтобы обеспечить максимальный суммарный выпуск приборов при оптимальном расходе имеющегося запаса комплектующих элементов?
19
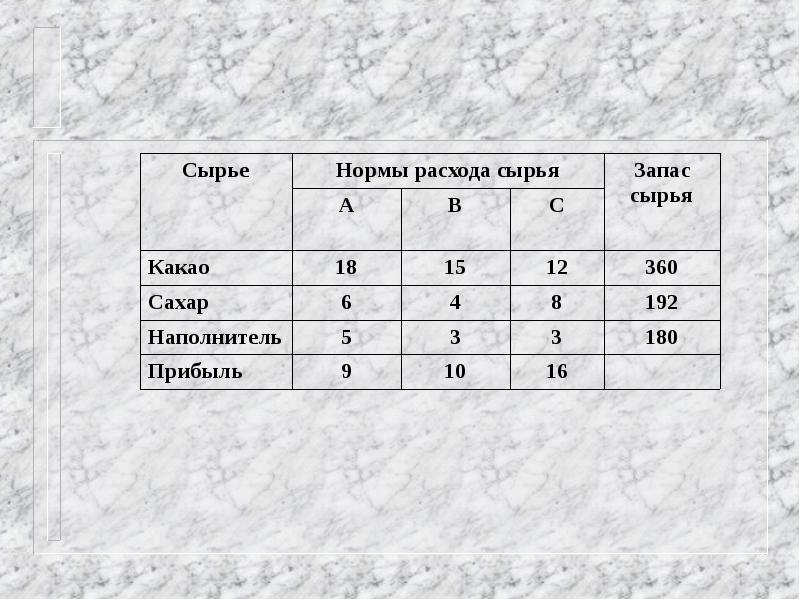
Домашнее задание. Домашнее задание. Задание 1. Составление плана выгодного производства Задание 1. Составление плана выгодного производства Фирма производит несколько видов продукции из одного и того же сырья – A, B и C. Реализация продукции A дает прибыль 10 р., B – 15 р. И C – 20 р. На единицу изделия. Фирма производит несколько видов продукции из одного и того же сырья – A, B и C. Реализация продукции A дает прибыль 10 р., B – 15 р. И C – 20 р. На единицу изделия. Продукцию можно производить в любых количествах, поскольку известно, что сбыт, обеспечен, но ограничены запасы сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы общая прибыль от реализации была максимальной. Продукцию можно производить в любых количествах, поскольку известно, что сбыт, обеспечен, но ограничены запасы сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы общая прибыль от реализации была максимальной. Нормы расхода сырья на производство продукции каждого вида приведены в таблице Нормы расхода сырья на производство продукции каждого вида приведены в таблице
20
Таблица для д/з План выгодного производства СырьеНорма расхода сырья Запас сырьяРасход сырья ABC Сырье ? Сырье ? Сырье ? Прибыль на ед. изделия Количество??? Общая прибыль????
Слайд 1
Описание слайда:
Поиск решений уравнений средствами EXCEL
Решение системы линейных алгебраических уравнений
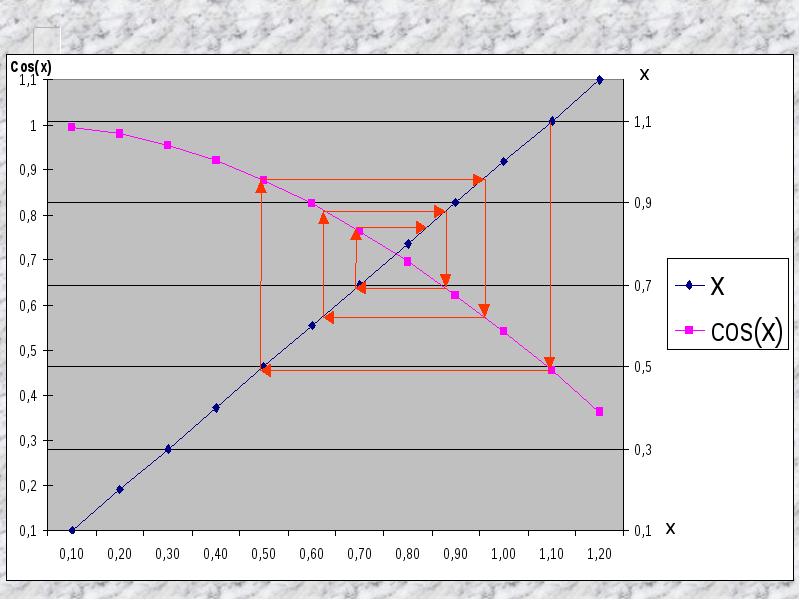
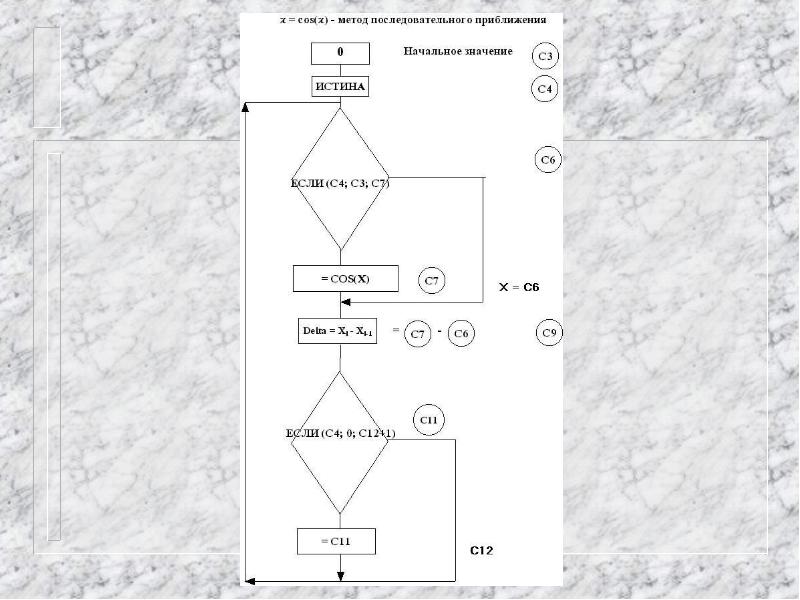
Метод последовательного приближения для решения нелинейных уравнений.
Использование средств Подбор параметров в Excel.
Использование средств Поиск Решений в Excel.
Слайд 2
Описание слайда:
Решение нелинейных алгебраических уравнений
Слайд 3
Описание слайда:
Метод последовательного приближения
Слайд 4
Слайд 5
Слайд 6
Слайд 7
Описание слайда:
Использование модуля подбор параметров
Слайд 8
Описание слайда:
Использование модуля подбор параметров
Слайд 9
Описание слайда:
Использование средств Поиск Решений в Excel
Слайд 10
Описание слайда:
Использование средств Поиск Решений в Excel
Слайд 11
Описание слайда:
Пример минимизации целевой функции с ограничениями
Слайд 12
Слайд 13
Слайд 14
Слайд 15
Слайд 1
Решение уравнений в Microsoft Excel Выполнила Соколова М.А.
Слайд 2
Вариант № 13 индивидуального расчетного задания Найдите приближенное значение уравнения с точностью 0,001 Представьте графически поставленную задачу;
Слайд 3
Состав задания: Ознакомиться с теоретической частью задания; Провести расчет для своего варианта индивидуального задания в Microsoft Excel Оформить презентацию в Ms Power Point , включающую: § постановку задачи; § алгоритм расчета; § таблицу с расчетом из Ms Excel , график исходной функции; результат расчета и его анализ.
Слайд 4
Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью. Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.
Слайд 5
Общая постановка задачи. Найти действительные корни уравнения f ( x ) =0 , где f ( x ) –алгебраическая или трансцендентная функция. Точные методы решения уравнений подходят только к узкому классу уравнений ( квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические) Задача численного нахождения корней уравнения состоит из двух этапов: 1.Отделение(локализация) корня; 2.Приближенное вычисление корня до заданной точности (уточнение корней)
Слайд 6
6 Уточнение корня . Если искомый корень уравнения f(x)=0 , отделен, т.е. определен отрезок [ a , b ], на котором существует только один действительный корень уравнения, то далее необходимо найти приближенное значение коня с заданной точностью. Такая задача называется уточнения корня. Уточнения корня можно производить различными методами: 1)Метод половинного деления(бисекции); 2)Метод итераций; 3)Метод хорд(секущих); 4)Метод касательных(Ньютона); 5)Комбинированные методы.
Слайд 7
индивидуальное расчетное задание Дано: Найти: Отделить корень заданного уравнения, пользуясь графическим методом, и вычислите один корень с точностью 0,001 при помощи программы Microsoft Excel
Слайд 8
Графический метод: Для отделения корней уравнения естественно применять графический метод. График функции у = f ( х ) с учетом свойств функции дает много информации для определения числа корней уравнения f ( х ) = 0. До настоящего времени графический метод предлагалось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появлением математических пакетов и электронных таблиц стало возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью. Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма: 1) если функция f ( x ) на концах отрезка [ а , b ] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз); 2) повторим действия предыдущего пункта для полученного отрезка. Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.
Слайд 9
Графический метод:
Слайд 10
Метод половинного деления: Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью. Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов. Метод половинного деления или дихотомии ): Метод основан на той идее, что корень лежит либо на середине интервала (a, b) , либо справа от середины, либо — слева, что следует из существования единственного корня на интервале (a, b) . Алгоритм для программной реализации: а:=левая граница b:= правая граница m:= ( a+b )/2 середина определяем f(a) и f(m) если f(a)*f(m)<0 то b:=m иначе a:=m если (a-b)/2>e повторяем , начиная с пункта2 m- искомый корень.
Слайд 11
Расчет уравнения по методу половинного деления:
Слайд 12
Метод простой итерации: Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде и по формуле будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найт и . Подготовка: Ищем числа m и M такие, что на (a, b) ; Представляем , где ; Алгоритм: 1. Выбираем х 0 из (a, b) ; 2.Вычисляем ; 3.Проверяем условие , где q=(M-m)/( M+m ) ; 4.Если оно ложно, то переходим к пункту 7; 5. х 0 =х 1 ; 6.Переходим к пункту 2 ; 7. х 1 –искомый корень.
Слайд 13
Расчет уравнения по методу простой итерации:
Слайд 14
Метод хорд Метод хорд заключается в замене кривой у = f ( x ) отрезком прямой, проходящей через точки ( а , f ( a )) и ( b , f ( b )) . Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение. Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки ( a , f ( a )) и ( b , f ( b )) и, приравнивая у к нулю, найдем х : Алгоритм метода хорд : 1) П усть k = 0; 2) В ычислим следующий номер итерации: k = k + 1. Найдем очередное k -e приближение по формуле: x k = a — f ( a )( b — a )/( f ( b ) — f ( a )). Вычислим f ( x k ); 3) Е сли f ( x k )= 0 (корень найден), то переходим к п. 5. Если f ( x k ) × f ( b )>0, то b = x k , иначе a = x k ; 4) Е сли |x k – x k -1 | > ε , то переходим к п. 2; 5) В ыводим значение корня x k ; 6) К онец.
Слайд 15
Расчет уравнения по методу хорд:
Слайд 16
Метод касательных В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных: Теорема. Пусть на отрезке [а, b]выполняются условия: 1) функция f(x)и ее производные f ‘(х)и f »(x)непрерывны; 2) производные f ‘(x)и f »(x)отличны от нуля и сохраняют определенные постоянные знаки; 3) f(a)× f(b) < 0 (функция f(x)меняет знак на отрезке). Тогда существует отрезок [α, β], содержащий искомый корень уравнения f(x) = 0, на котором итерационная последовательность сходится. Если в качестве нулевого приближения х0 выбрать ту граничную точку [α, β], в которой знак функции совпадает со знаком второй производной, т.е. f(x0)× f»(x0)>0, то итерационная последовательность сходится монотонно
Слайд 17
Расчет уравнения по методу касательных:
Слайд 18
Вывод о проделанной работе: Вывод: Решение уравнения в Microsoft Excel Было выполнено: графическим методом, методом половинного деления , хорд, касательных, простой итерации. Графический метод самый неточный, чем остальные методы. метод половинного деления быстрее графического метода, а метод простой итерации намного точнее предыдущих. Метод хорд более точный, чем все остальных методы. Метод касательный относительно быстрее и точнее всех методов.
Слайд 19
Список использованной литературы и интернет-источников Зенков , А.В. ЧИСЛЕННЫЕ МЕТОДЫ /А.В. Зенков . — Екатеринбург: Издательство Уральского университета, 2016. — 127с. Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019); Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019);