Содержание
- 1 Включение функции
- 2 Подготовка таблицы
- 3 Запуск инструмента Поиск решения
- 3.1 Помогла ли вам эта статья?
- 4 Что такое Поиск решений?
- 5 Зачем нужен Решатель?
- 6 Как работает Решатель?
- 7 Настройка параметров Поиска решений
- 8 Параметры задачи в функции Поиска решений
- 9 Формула в Excel
- 10 Создание формулы
- 11 Заключение
- 12 Краткое описание надстройки
- 13 Как установить надстройку?
- 14 Как подключить надстройку?
- 15 Где найти надстройку «Поиск решения» в Excel 2003/2007/2010?
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
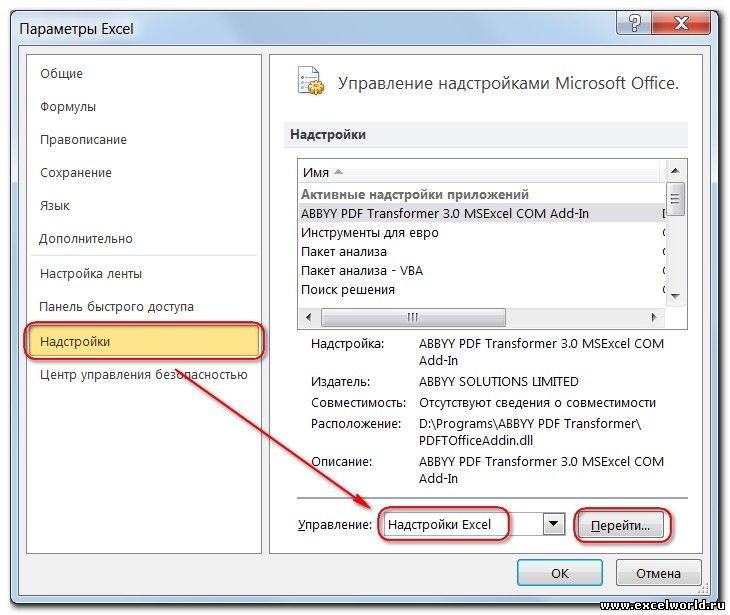
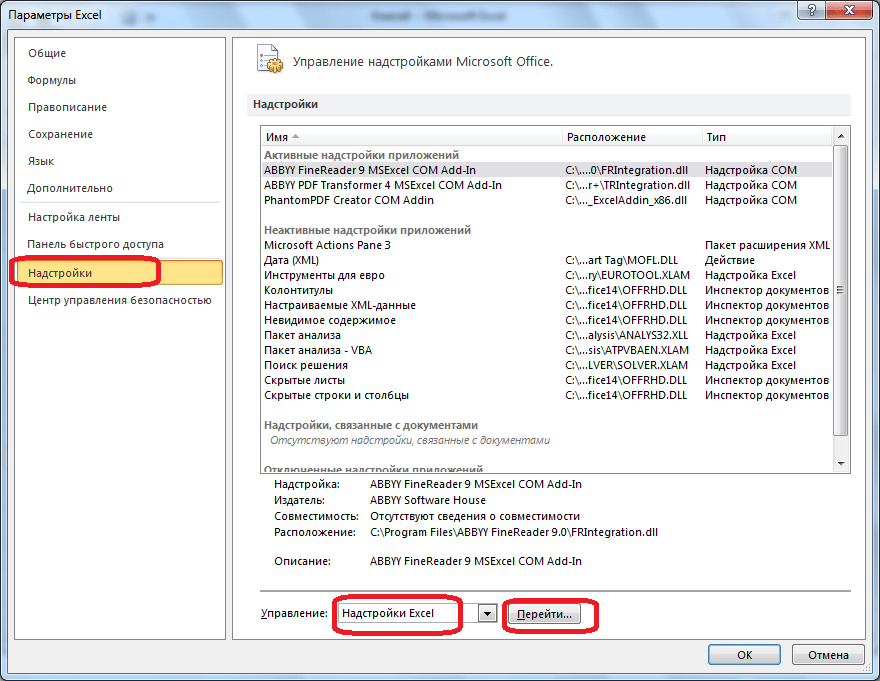
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
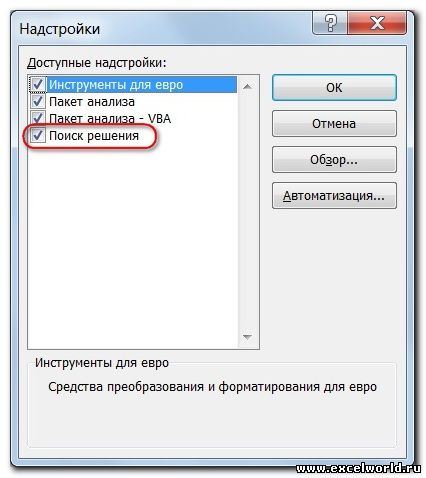
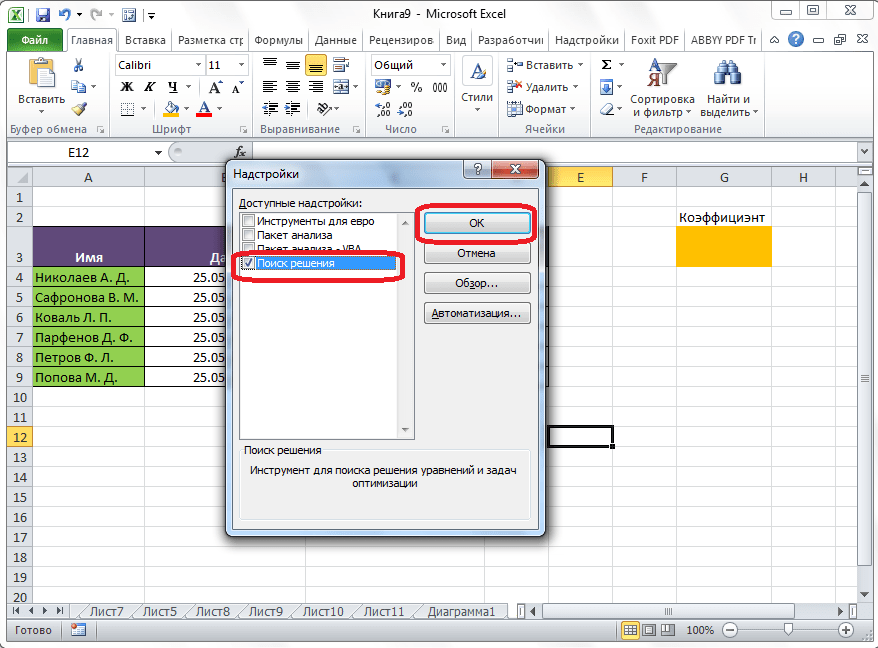
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
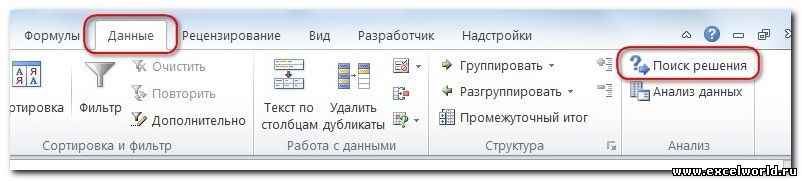
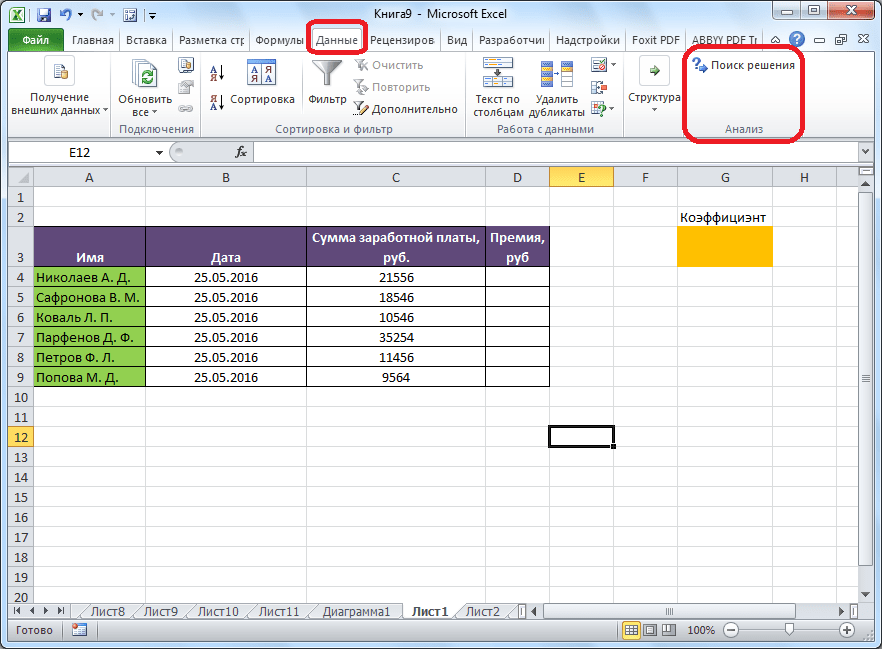
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
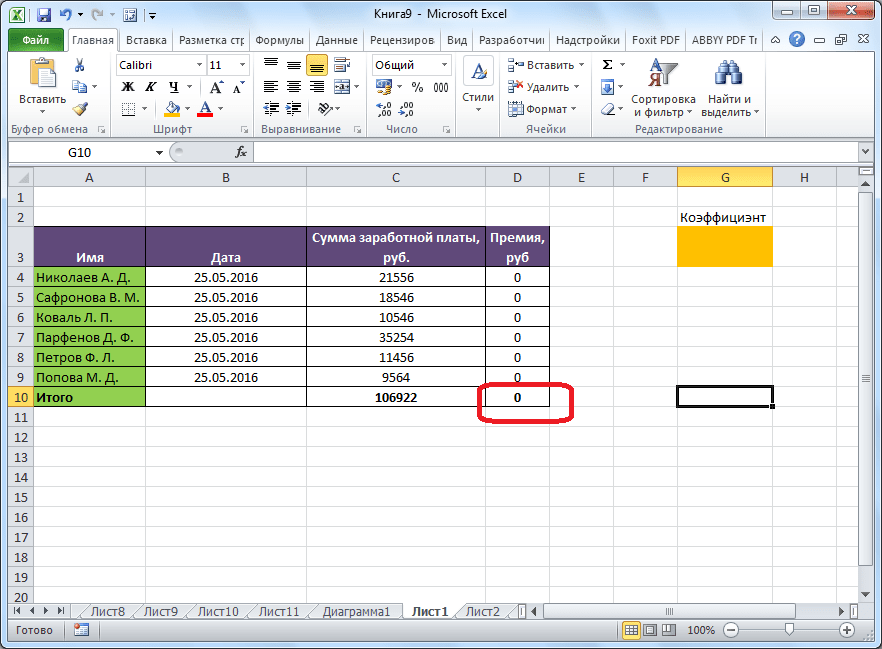
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
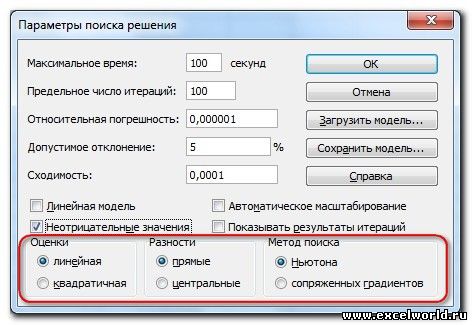
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
После того, как все настройки установлены, жмем на кнопку «Найти решение».
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
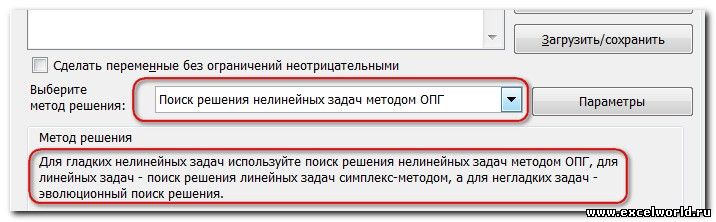
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Надстройка Поиск решений в Excel 2007 не является стандартной. Она предназначается для сложных вычислений, когда имеется больше одной неизвестной. Поэтому она не включается в обычный набор параметров программы. Но если в ней есть необходимость, то она способна предложить пользователю эффективную работу и высокую продуктивность.
Что такое Поиск решений?
Поиск решений в Excel 2007 является надстройкой программы. Это означает, что в обычной конфигурации, выпускаемой производителем, этот пакет не устанавливается. Его нужно загружать и настраивать отдельно. Дело в том, что чаще всего пользователи обходятся без него. Также надстройку нередко называют «Решатель», поскольку она способна вести точные и быстрые вычисления, зачастую независимо от того, насколько сложная задача ей представлена.
Если версия Microsoft Office является оригинальной, тогда проблем с установкой не возникнет. Пользователю нужно сделать несколько переходов:
Параметры→Сервис→Надстройки→Управление→Надстройки Excel.
Откроется окно, в котором есть кнопка перехода. После клика на нее на экране появится список всех предлагаемых надстроек, как установленных, так и неиспользуемых. Теперь нужно найти Поиск решений, затем поставить галочку. Инструмент активизирован, можно пользоваться им в любое время.
Зачем нужен Решатель?
Для чего можно использовать Поиск решений в Excel 2007, и стоит ли вообще его устанавливать? Когда у пользователя присутствует целевая функция, зависящая от нескольких параметров, надстройка будет подбирать решения задачи в соответствии с исходными данными. Таковыми может оказаться переменная, неизвестная или, например, итоговое значение. То есть, пользователь может иметь начальные характеристики и ответ, а программа подберет ход решения, предоставит формулу.
Таким образом, посредством надстройки можно найти:
- Удачное распределение рабочих ресурсов, чтобы достичь максимальной прибыли в ходе деятельности компании или отдельного отдела, филиала.
- Распределение вложений при минимизированных рисках.
- Решение задач, где есть больше одной неизвестной (будет предложено несколько вариантов ответов, из которых пользователь сам подберет наиболее подходящий).
- Сохранение и загрузка модели решения. Оптимальный вариант для сотрудников, которые вынуждены постоянно менять компьютер или ноутбук.
- Решение сразу нескольких задач с разными переменными, неизвестными, формулами и интегралами.
Программа открывает большие возможности, но ею нужно научиться правильно пользоваться.
Как работает Решатель?
Помимо решателя, в Excel есть такая функция, как подбор параметра. Она рекомендована к использованию в случаях, когда имеется только одно неизвестное значение. Эта возможность программы требует намного меньше ресурсных компьютерных затрат, поэтому быстрее выдаст результат.
Поиск решений в Excel 2007 применяется для самых сложных задач, где имеется несколько неизвестных, часто встречаются переменные. В общей постановке их можно сформулировать следующим образом:
- Найти неизвестные→несколько «x».
- При условии, что→формула или функция.
- При ограничениях→здесь обычно указывается неравенство, либо минимальные/максимальные значения.
Также нужно указать на ячейки, с которыми следует проводить вычисления. Есть возможность решать несколько разных задач, если задать программе соответствующие параметры.
Настройка параметров Поиска решений
Чтобы функция Поиска решений в Excel 2007 работала так, как необходимо пользователю, нужно ввести правильные параметры. Обычно они ограничиваются 1-3 характеристиками, но с более сложными задачами потребуется глобальная настройка.
Параметры в Поиске решений программы Office Excel 2007 могут быть следующими:
- Максимальное время – количество секунд, которые пользователь выделяет программе на решение. Оно зависит от сложности задачи.
- Максимальное число интеграций. Это количество ходов, которые делает программа на пути к решению задачи. Если оно увеличивается, то ответ не будет получен.
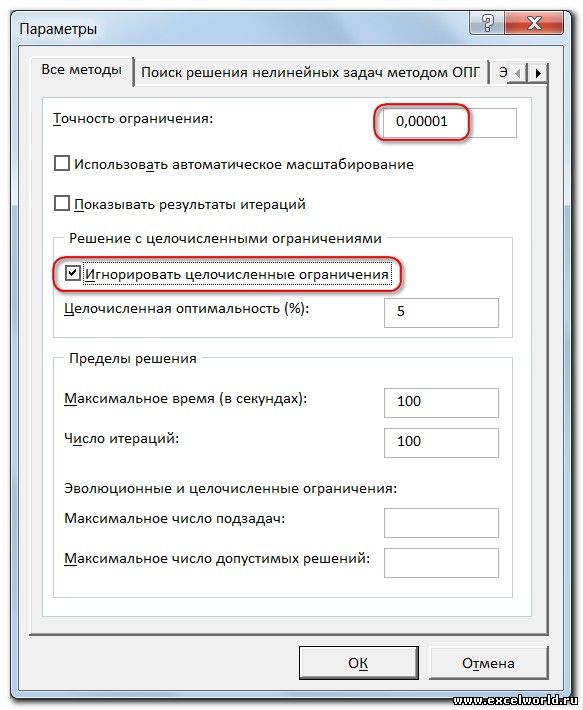
- Погрешность или точность, чаще всего применяется при решении десятичных дробей (к примеру, до 0,0001).
- Допустимое отклонение. Используется при работе с процентами.
- Неотрицательные значения. Применяется тогда, когда решается функция с двумя правильными ответами (например, +/-X).
- Показ результатов интеграций. Такая настройка указывается в случае, если важен не только результат решений, но и их ход.
- Способ поиска – выбор оптимизационного алгоритма. Обычно применяется «метод Ньютона».
После того как все настройки выбраны, обязательно нужно нажать кнопку сохранения.
Параметры задачи в функции Поиска решений
Работа такой надстройки, как Поиск решения в Excel, осуществляется в соответствии с заданными характеристиками вычисления. Наиболее важной из них является метод. Есть два их варианта. «Метод Ньютона» является настройкой по умолчанию. Он способен работать с большей памятью, но меньшими интеграциями. Поэтому для стандартных и не особо сложных уравнений он вполне подойдет.
Также есть «метод сопряженных градиентов». Здесь запрашивается меньше памяти, но требуется больше интеграций. Следовательно, при его использовании можно решать самые сложные уравнения, использовать масштабные формулы и функции.
Есть обязательный элемент, без которого не сможет функционировать надстройка Поиска решений в программе Excel 2007 – формулы. Они представляют собой такое выражение, которое выполняет то или иное вычисление. Без равенства формул не существует. Поэтому программа не начнет распознавать таковую, когда отсутствует соответствующий знак.
Формула может включать в себя следующее:
- Функция. Это стандартная формула, где присутствует определенный и конкретный порядок действий, поменять который не удастся.
- Ссылка. Она указывает на количество клеток, которые нужно решить. При этом ячейки могут располагаться хаотично или в определенном порядке.
- Оператор. Это символ, который задает тип вычисления (+ – сложение, * – умножение и т.д.).
- Константа. Постоянное значение, которое никогда не меняется. Также для его получения не нужно производить вычисления.
Решение формул осуществляется слева направо при соблюдении всех математических правил.
Создание формулы
Формулы являются уравнениями, которые способствуют выполнению вычислений программы. Если таковые не вводить, то не будет работать Поиск решения в Excel. Задачи, соответственно, тоже не станут решаться. Поэтому для удачного выполнения поставленного задания необходимо правильно ввести формулу.
Вычисление начинается со знака равенства. К примеру, если в ячейке указывается «=КОРЕНЬ(номер клетки)», то будет использована соответствующая функция.
После того как была напечатана основная формула со знаком «=», нужно указать на данные, с которыми она будет взаимодействовать. Это может быть одна или несколько ячеек. Если формула подходит для 2-3 клеток, то объединить их можно, используя знак «+».
Чтобы найти нужную информацию, можно воспользоваться функцией поиска. Например, если нужна формула с буквой «A», то ее и надо указывать. Тогда пользователю будут предложены все данные, ее в себя включающие.
Заключение
В заключении в программе Excel 2007 нужно сохранить заданные параметры решения задач. Сделать это можно несколькими способами. Стандартный вариант с кликом на соответствующую кнопку подойдет в том случае, если для всех данных используется один метод вычислений.
Когда нужно решить сразу несколько уравнений, к примеру, найти минимум и максимум функций, то нужно сохранять не все вычисление, а его модели. Затем пользователь сможет применить их к тому или иному решению.
Надстройка Microsoft Excel «Поиск решения» является мощным средством поиска решений и применяется при решении задач оптимизации. Процедура поиска решения позволяет находить оптимальное значение формулы содержащейся в ячейке, которую называют целевой. Процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке.
Краткое описание надстройки
Для получения заданного результата по формуле, процедура изменяет значения во влияющих ячейках. Для уменьшения интервала значений, используемых в модели, используются ограничения значений. Надстройка поиск решений является стандартной надстройкой Microsoft Office Excel и доступна сразу при установке Microsoft Office в целом или Microsoft Excel в частности.
Как установить надстройку?
Надстройку «Поиск решения» можно установить двумя способами. Стандартные надстройки, такие как «Поиск решения» и «Пакет анализа» устанавливаются вместе с MS Office или MS Excel. Если при первоначальной установке стандартная надстройка не была установлена, то следует запустить процесс установки повторно. Рассмотрим установку надстройки «Поиск решения» на примере Microsoft Office 2010. В версиях 2003 и 2007 все делается аналогично.
Итак, запускаем установочный диск с пакетом приложений MS Office 2010 и выбираем опцию «Добавить или удалить компоненты».
Далее, нажимаем кнопку «Продолжить», в параметрах установки находим приложение Microsoft Excel, в компонентах этого приложения находим раздел «Надстройки», выбираем надстройку «Поиск решения» и устанавливаем параметр «Запускать с моего компьютера».
Опять жмем кнопку «Продолжить» и ожидаем пока надстройка установится.
Как подключить надстройку?
Перед использованием необходимо предварительно включить надстройку, поставив галочку перед ее названием в списке доступных надстроек диалогового окна «Надстройки».
Вызов этого окна несколько различается в зависимости от версии приложения. Подробно об этом написано в отдельной статье «Как установить надстройку для Excel 2003/2007/2010?» со скриншотами для каждой из трех версий приложения Excel, поэтому не буду повторяться. Да, добавлю лишь несколько слов о втором способе установки этой надстройки. Можно отыскать на просторах Интернета файл с названием Solver.xla (это и есть надстройка «Поиск решения») и произвести установку в соответствии с описанием по ссылке выше.
Где найти надстройку «Поиск решения» в Excel 2003/2007/2010?
После установки и подключения надстройки в Excel 2007/2010 на вкладке «Данные» появляется группа «Анализ» с новой командой «Поиск Решения». В Excel 2003 — появляется новый пункт меню «Сервис» с одноименным названием. Поиск решения — стандартная надстройка, существуют также и другие надстройки для Excel, служащие для добавления в MS Excel различных специальных возможностей.
Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.
Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.
При решении данной задачи должны быть учтены следующие ограничения:
- общий объем производства – всего 300 изделий;
- должно быть произведено не менее 50 изделий А;
- должно быть произведено не менее 40 изделий В;
- должно быть произведено не более 40 изделий С.
Технология:
1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)
и в окне “Поиск решений” ввести данные:
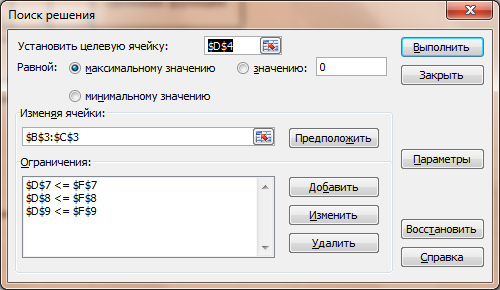
- в поле «Установить целевую ячейку» указать адрес D6;
- установить флажок «Равной максимальному значению»;
- в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
- в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5
Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.
Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых «задач оптимизации».
Если Вы раньше не использовали Поиск решения, то Вам потребуется установить соответствующую надстройку.
Сделать это можно так:
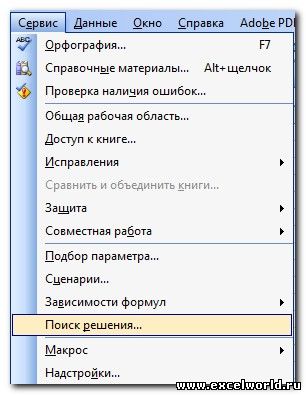
для версий старше Excel 2007 через команду меню Сервис —> Надстройки;
начиная с Excel 2007 через диалоговое окно Параметры Excel
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные.
В версиях до Excel 2007 аналогичная команда появится в меню Сервис
Разберём порядок работы Поиска решения на простом примере.
Пример 1. Распределение премии
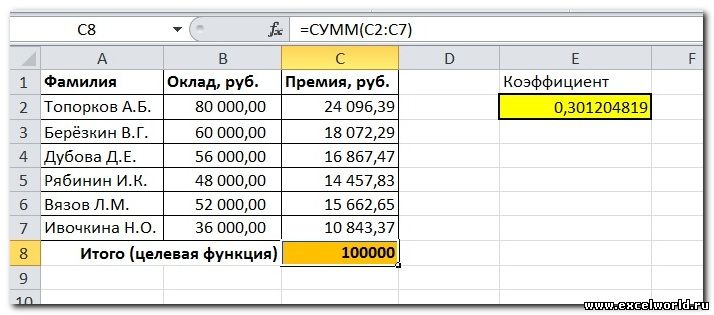
Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.
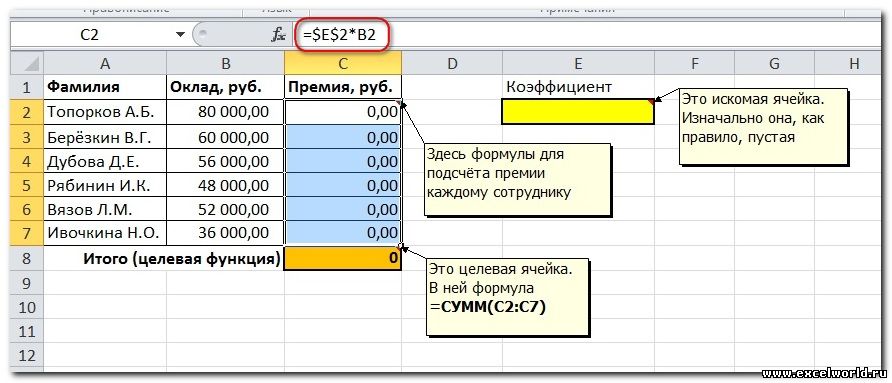
Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат — это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).
Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:
Начиная с Excel 2010
До Excel 2010
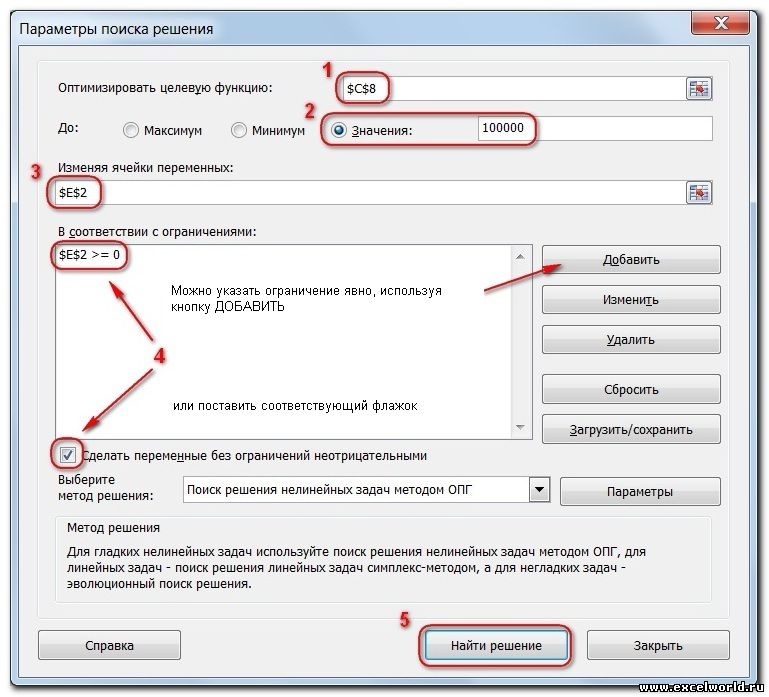
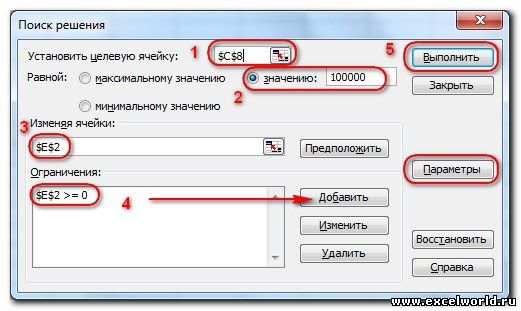
- Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна
- Варианты оптимизации: максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода
- Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение
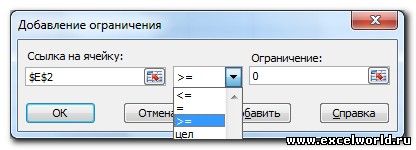
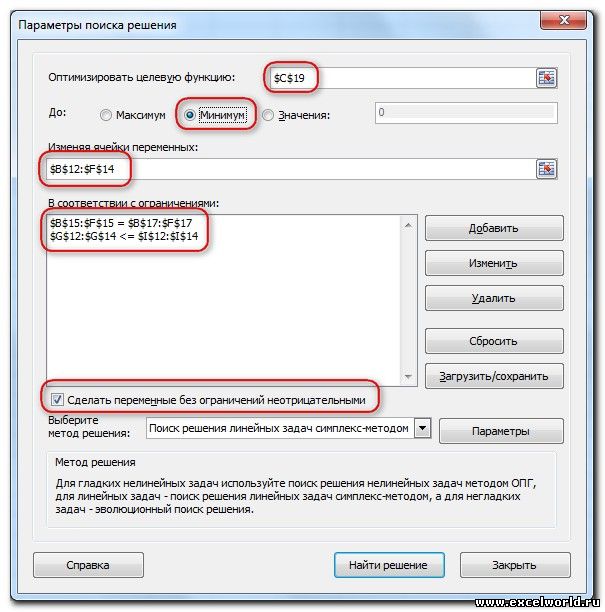
- Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимо всем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные — только начиная с версии Excel 2010).
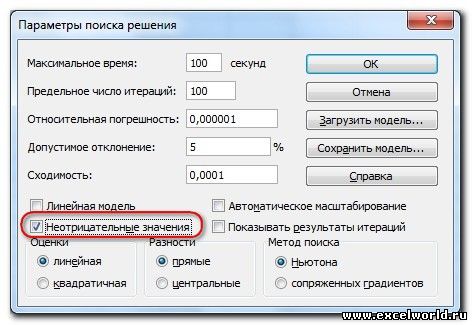
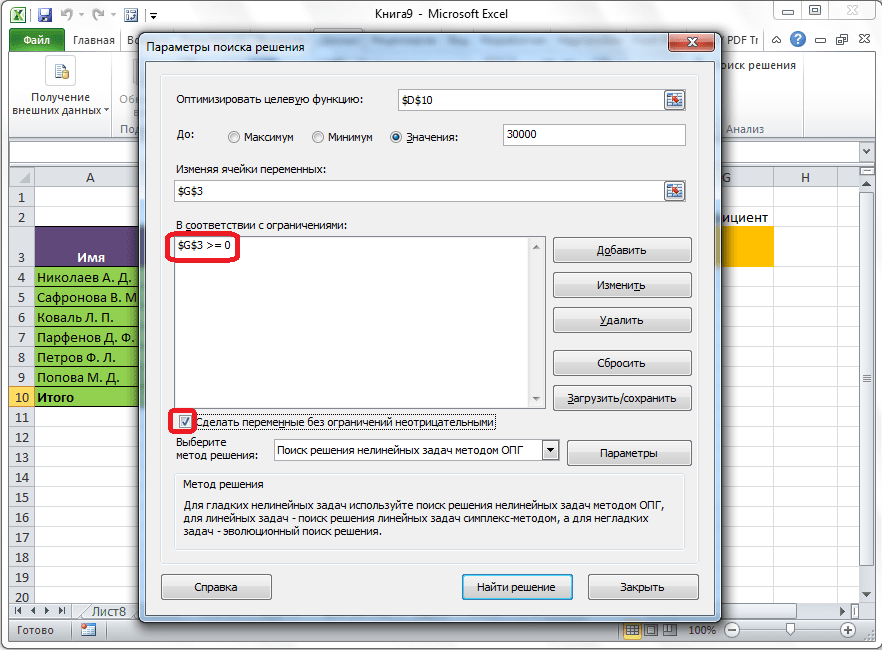
В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкой Добавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.
Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры
- Кнопка, включающая итеративные вычисления с заданными параметрами.
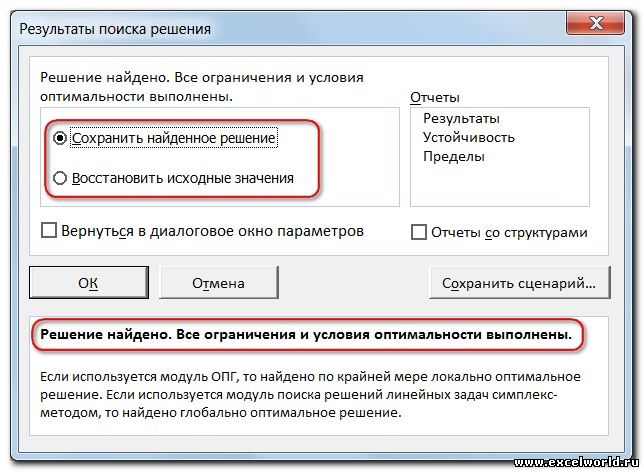
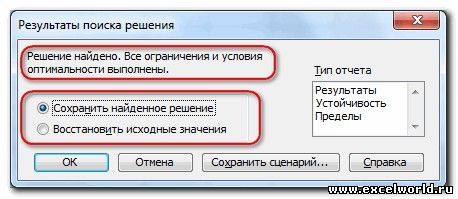
После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.
Начиная с Excel 2010
До Excel 2010
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.
Решение данной задачи выглядит так
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.
Разберём еще одну задачу оптимизации (получение максимальной прибыли)
Пример 2. Мебельное производство (максимизация прибыли)
Фирма производит две модели А и В сборных книжных полок.
Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.
Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.
Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. в неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В — 120 руб. прибыли?
Порядок действий нам уже известен.
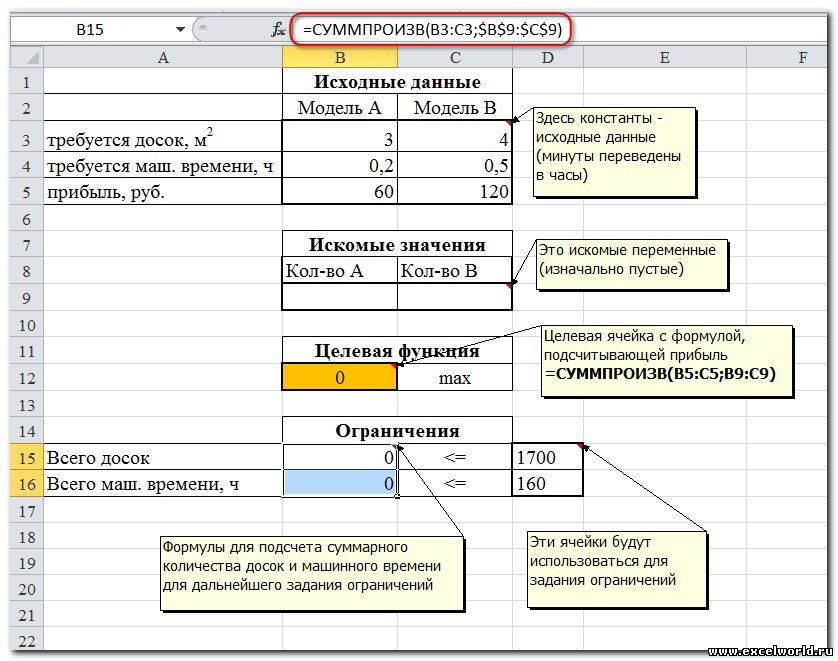
Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке
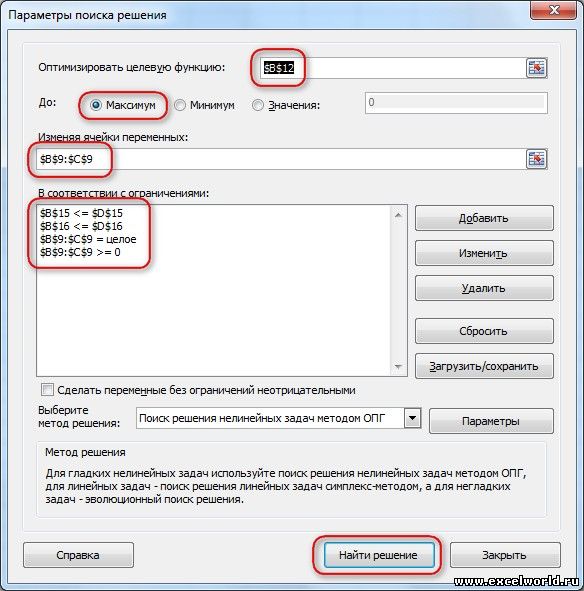
Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры
- Целевая ячейка B12 содержит формулу для расчёта прибыли
- Параметр оптимизации — максимум
- Изменяемые ячейки B9:C9
- Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
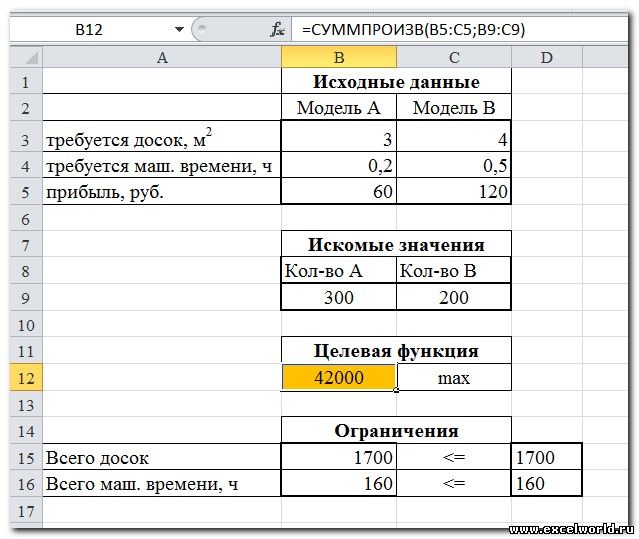
- Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат
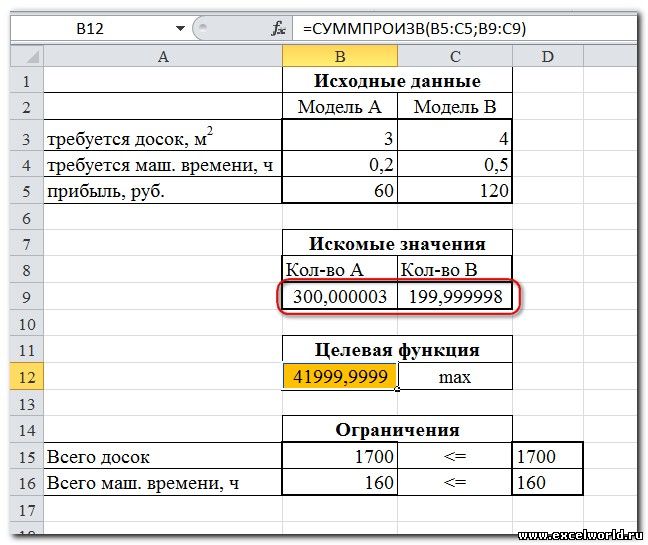
Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:
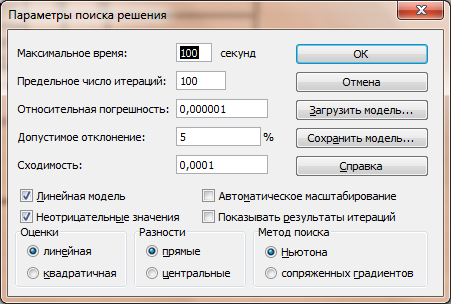
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае — целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.
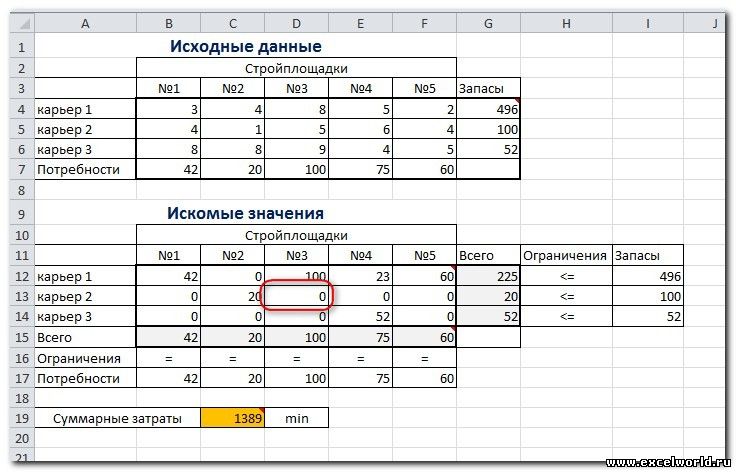
Пример 3. Транспортная задача (минимизация затрат)
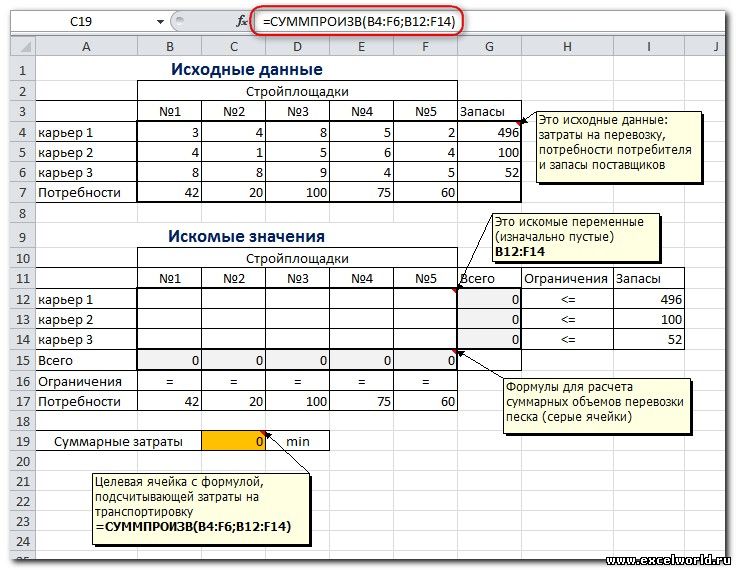
На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.
Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».
Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.
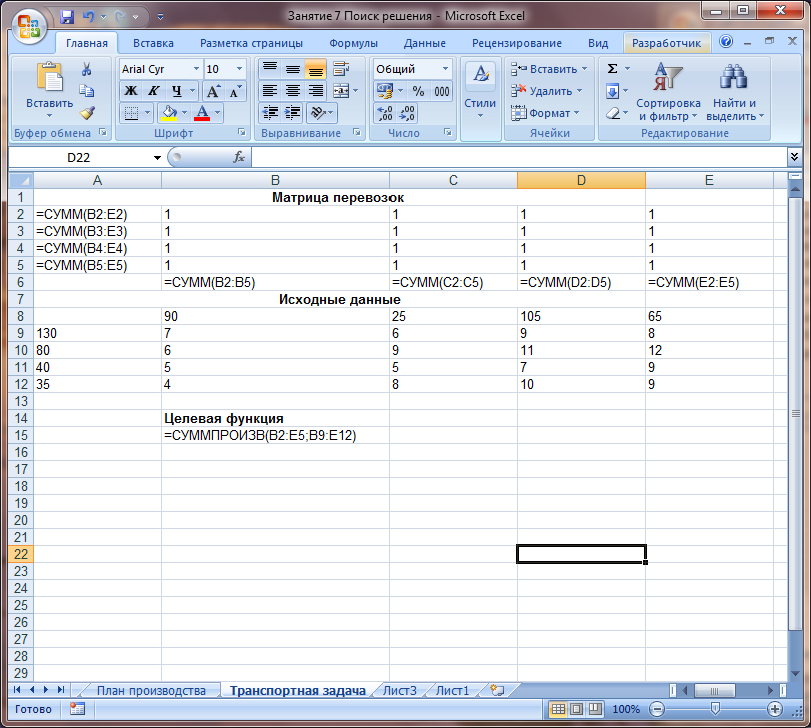
Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку.
Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)
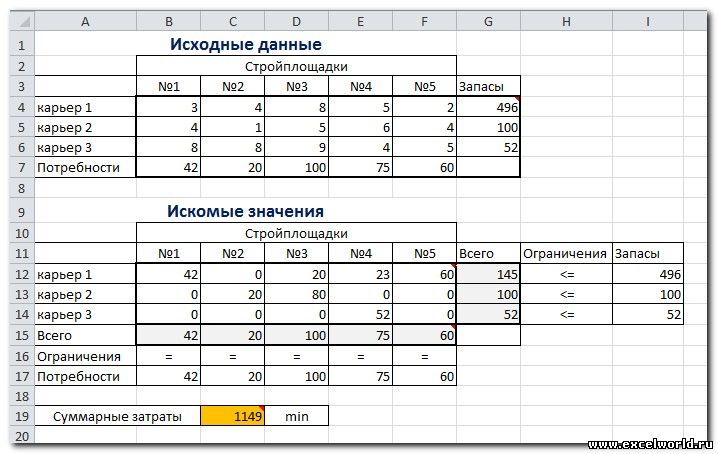
Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже
Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещё одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат
И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения
Начиная с Excel 2010
До Excel 2010
В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:
Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?
«Подбор параметра» является удобной надстройкой «Поиска решения» в Excel, однако имеет некоторые функциональные ограничения. Он используется, как правило, в частных случаях и подходит для быстрого поиска нужных параметров.
Что за функция, зачем нужна?
Метод предназначен для случаев, когда нужно найти неизвестное значение в одиночной формуле, исходя из уже известного результата. То есть все составные части формулы (результат и входные данные) известны, при этом решение не может быть сформулировано полностью из-за отсутствия одного из входных параметров.
Функционал по поиску решений подобного рода задач встроен в программу Excel в качестве стандартного расширения, поэтому пользователю не нужно использовать сторонние библиотеки. Достаточно будет сделать несколько кликов по кнопкам расположенным на главной панели и программа сама определит недостающий элемент.
Использование функции
В Microsoft Excel подобные задачи решаются с помощью стандартного меню. Подбор параметра в Excel 2007, 2010, 2013 и новее находится во вкладке «Данные», в группе «Работы с данными».
Следующий шаг – заполнение полей в появившемся окне. Первое поле предназначено для заданной формулы, второе для целевого значения, в третье для адреса элемента вывода (более подробно это будет разобрано далее на конкретных примерах).
Третий шаг это подтверждение операции и вывод результата.
Пример использования функции
Для большей наглядности функцию подбора параметров в Экселе лучше сразу рассматривать на примере.
Определить — какая будет процентная ставка (по займу). Входными данными являются срок (36) и сумма (150000). Для начала их нужно отобразить в табличном представлении.
Не определена только процентная ставка. Чтобы посчитать ежемесячный, платеж следует воспользоваться функцией подбора параметров. После внесения всех данных задачи в таблицу, нужно переключиться во вкладку, отвечающую за работу с данными. Затем найти группу инструментов по работе с данными и в выпадающем списке «Анализ “что если”» выбрать опцию соответствующую подбору параметра.
Во всплывающем окошке в поле «Установить в ячейке» должна быть указана ссылка ячейки, в которой содержится основная формула (B4). В текстовое поле «Значение» необходимо ввести предположительную сумму ежемесячного платежа. К примеру, -5 000 (знак «минус» обозначает, что денежная сумма будет отдана). В третьем поле «Изменяя значение ячейки» – следует списать ссылку табличного элемента, в которой будет выведен искомый параметр ($B$3).
После клика по кнопке «ОК» в новом окне отобразится результат подсчета.
Для подтверждения операции следует кликнуть по соответствующей кнопке.
Функция подбора неизвестного параметра будет перебирать значение искомого элемента до момента получения результата формулы. Команда выдаст только одно решение.
Решение уравнений
Подбор параметра также используют, если нужно найти какое-либо из значений в заданном уравнении. В качестве примера воспользуемся следующим выражением: 2*а+3*b=x, где x=21, а=3, неизвестная переменная — b.
Для начала нужно заполнить таблицу.
Параметры а и b следует вводить в ячейки B2 и B3 соответственно. Табличный элемент B4 отведен для формулы =2*B2+3*B3. Переменная x в ячейке B5 указана в качестве примечания.
Необходимо выделить ячейку, в которой вписана формула (B4) и вызвать целевую функцию по определению параметра (инструкция вызова подробно изложена в предыдущем примере).
Затем вписать во второе поле (значение) результат (21), а в третье адрес ячейки B3, поскольку именно она будет изменяться.
Подтвердить действие кликом по соответствующей кнопке.
В результате выполнения команды переменной b подобралось значение 5.
Конечно, искомый параметр можно определить в ручном режиме, путем последовательного ввода в ячейку B3 значений до момента пока оно не совпадет с целевым. Однако зачастую формулы имеют более сложную структуру, поэтому решить уравнение не используя автоматический подбор, будет сложно.
Для закрепления материала решим еще одно уравнение – 15*x+18*x=46. Для начала нужно записать формулу в ячейку B2. Вместо x необходимо указать ссылку на табличный элемент, где будет отображен результат, в данном случае A2.
Затем нужно запустить команду по высчитыванию параметра тем методом, который уже был описан ранее.
Во всплывающем окне, в первом верхнем текстовом поле нужно вписать ссылку ячейки, содержащей формулу (B2). Во втором поле — число из уравнения после знака равно, то есть 46. В третьем поле должна быть ссылка на ячейку со значением x, в данном случае это A2.
После того как все поля заполнены, нужно подтвердить операцию. На экране в новом всплывающем окне отобразиться правильное решение уравнения. Значение x будет равно 1,39393939393939.
После изучения функциональных преимуществ и способов применения функции подбора параметра, пользователю программы Excel будет очень просто определять недостающие элементы. С помощью этой функции можно производить как табличные вычисления, так и решать уравнения с одним неизвестным.
Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.
Включение функции
Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».
Подготовка таблицы
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.
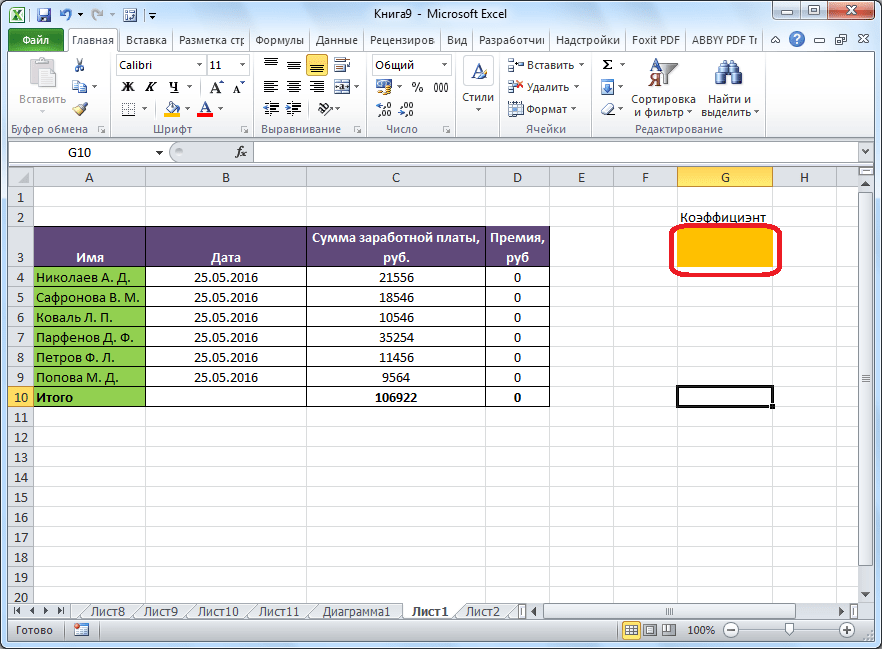
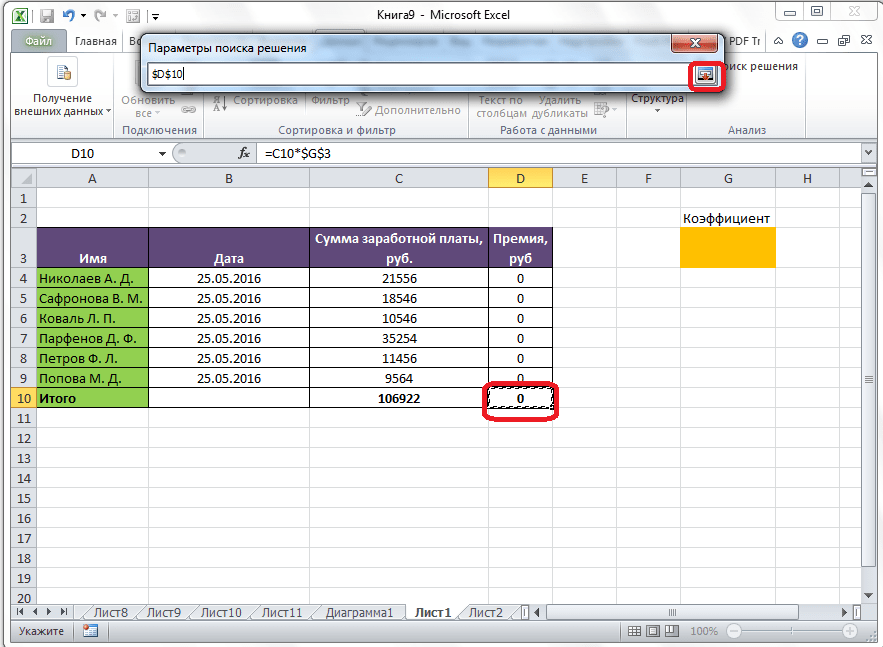
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.
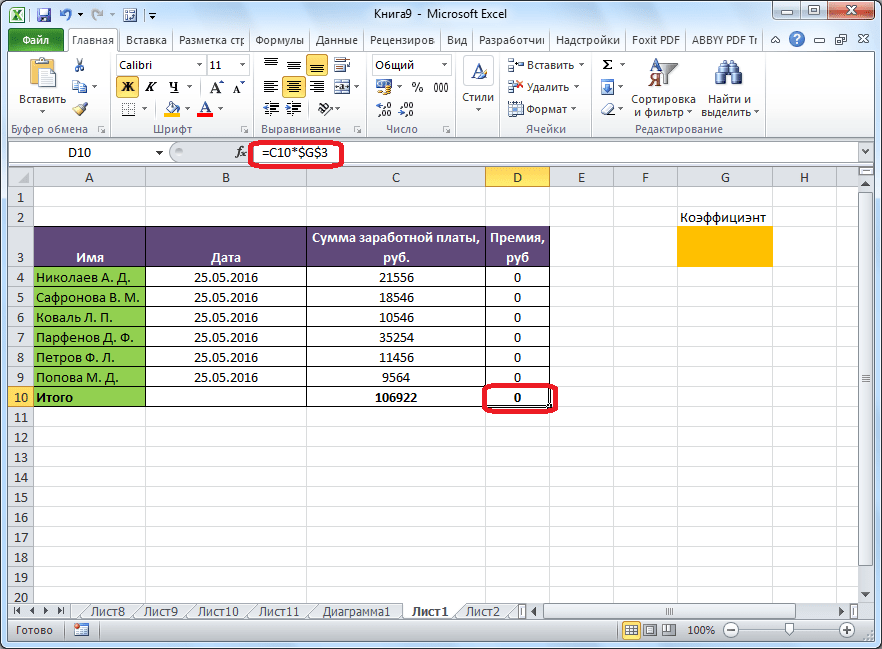
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.
Запуск инструмента Поиск решения
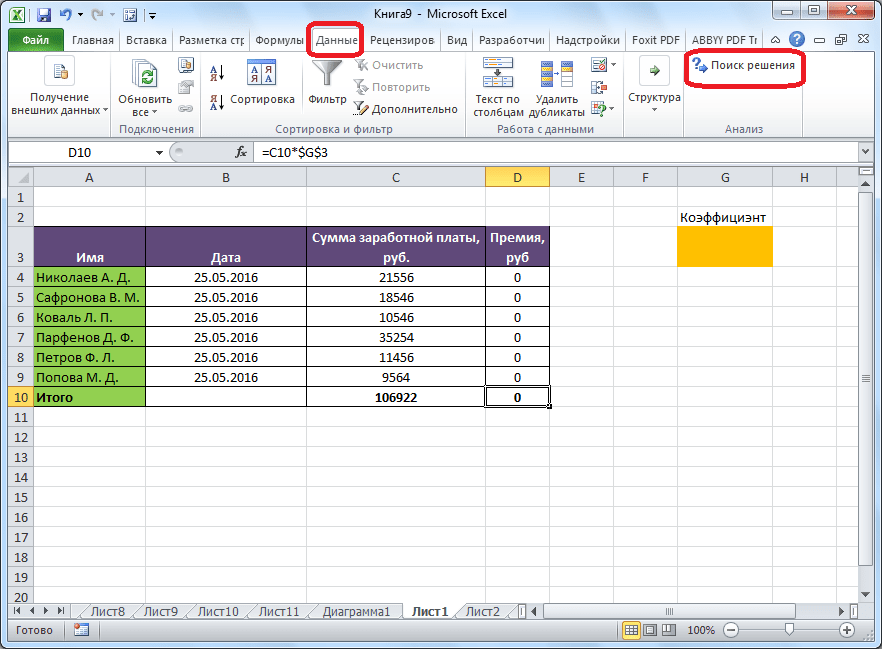
После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».
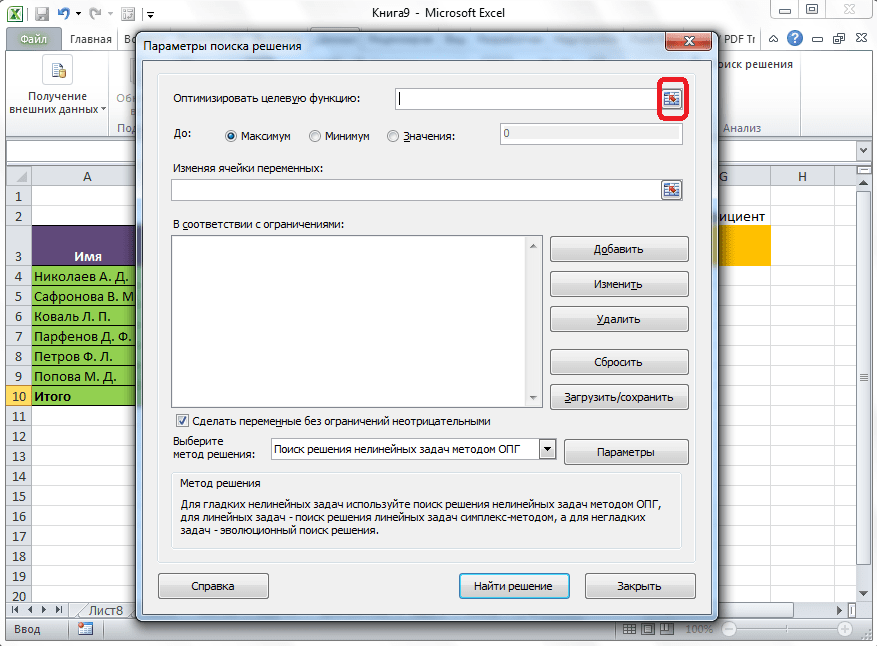
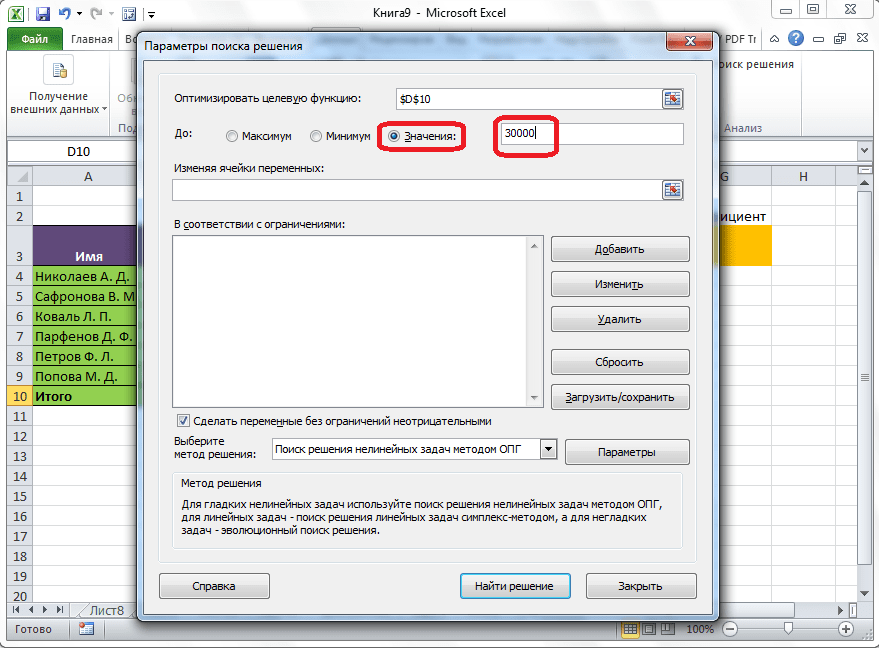
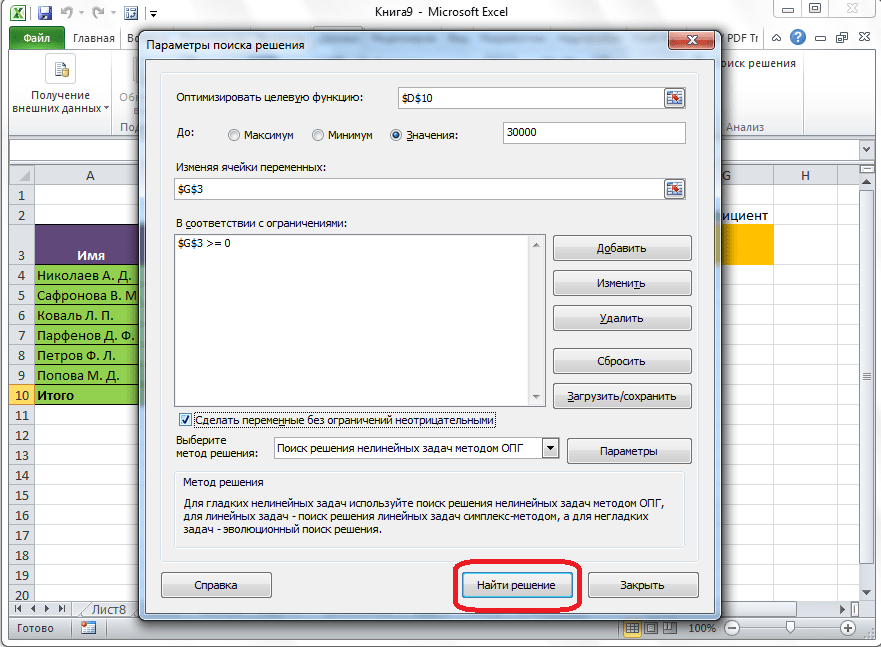
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.
После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.
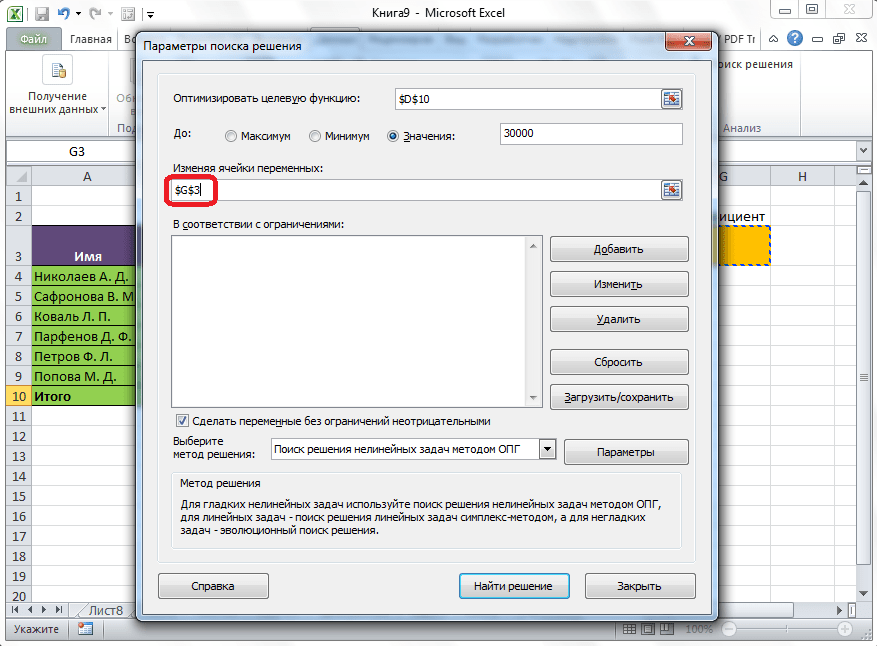
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.
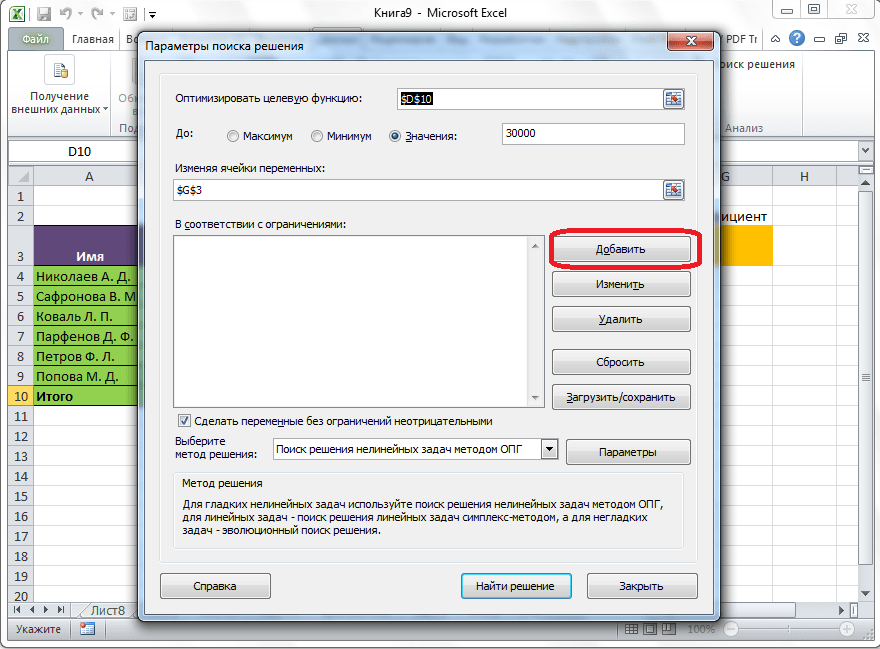
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».
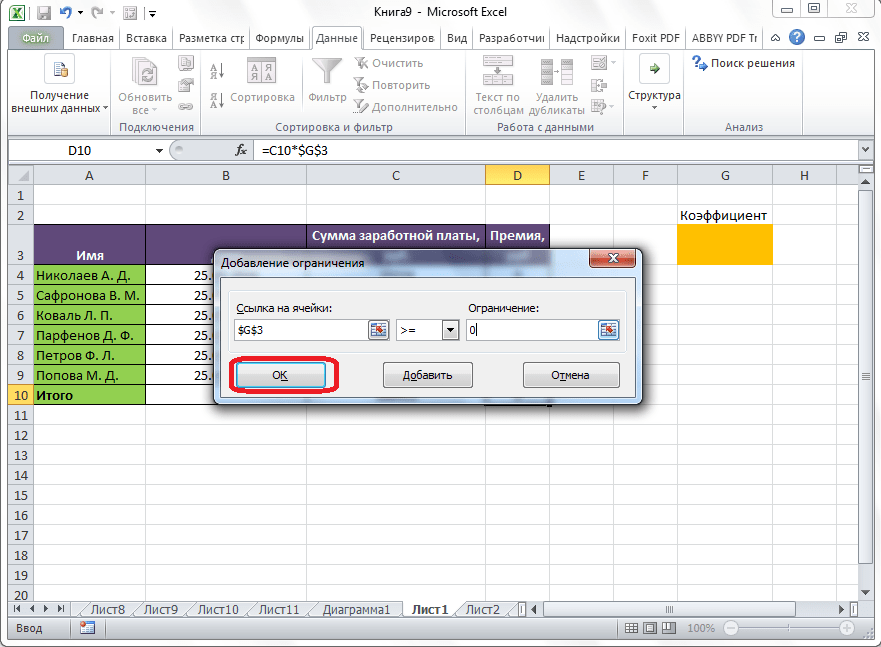
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.
Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.
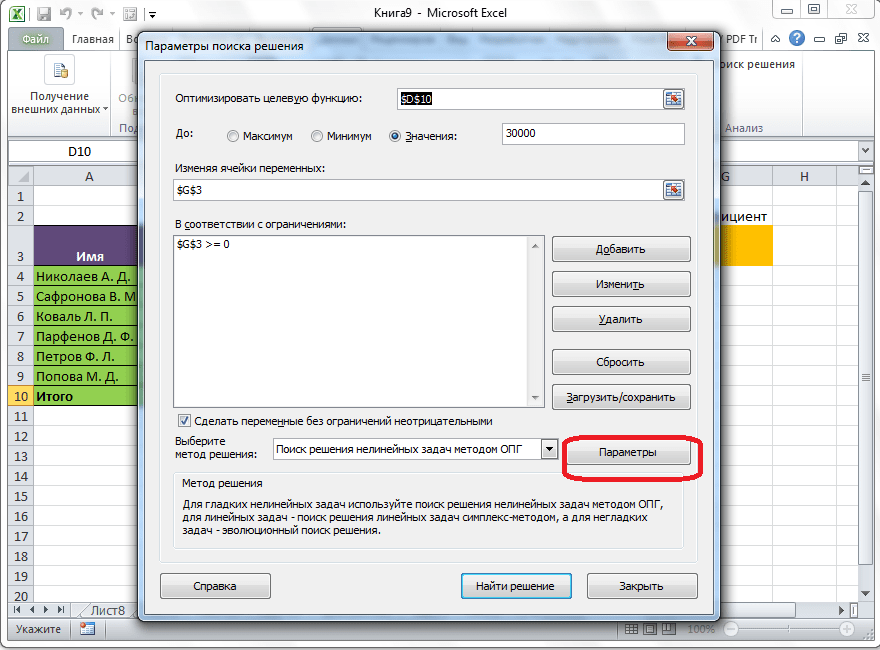
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».
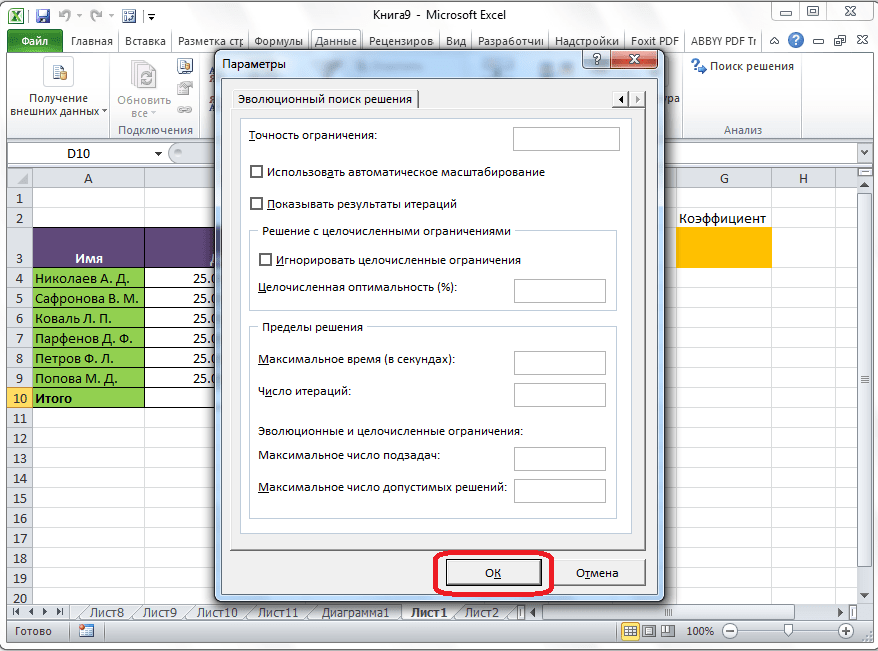
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.
После того, как все настройки установлены, жмем на кнопку «Найти решение».
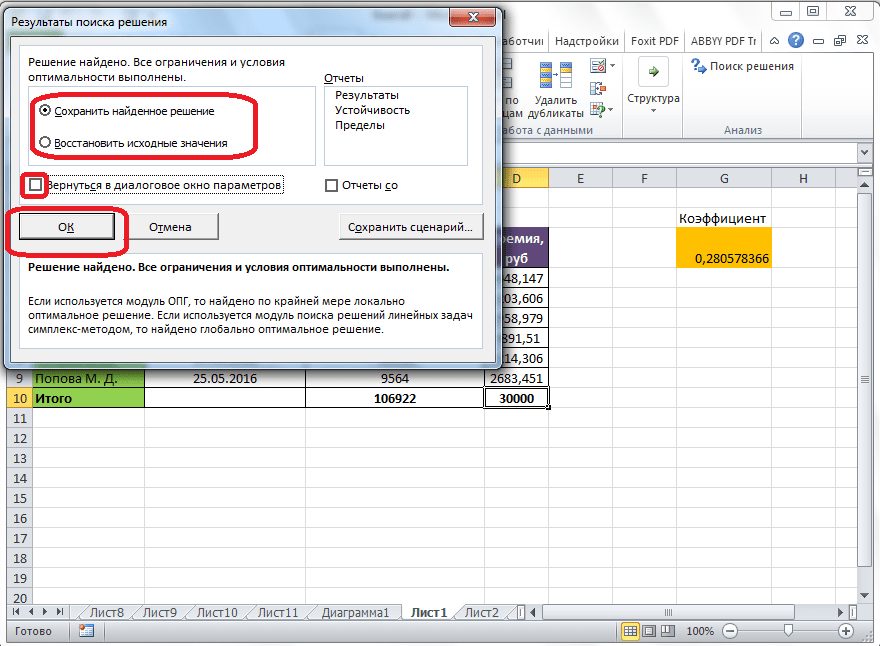
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».
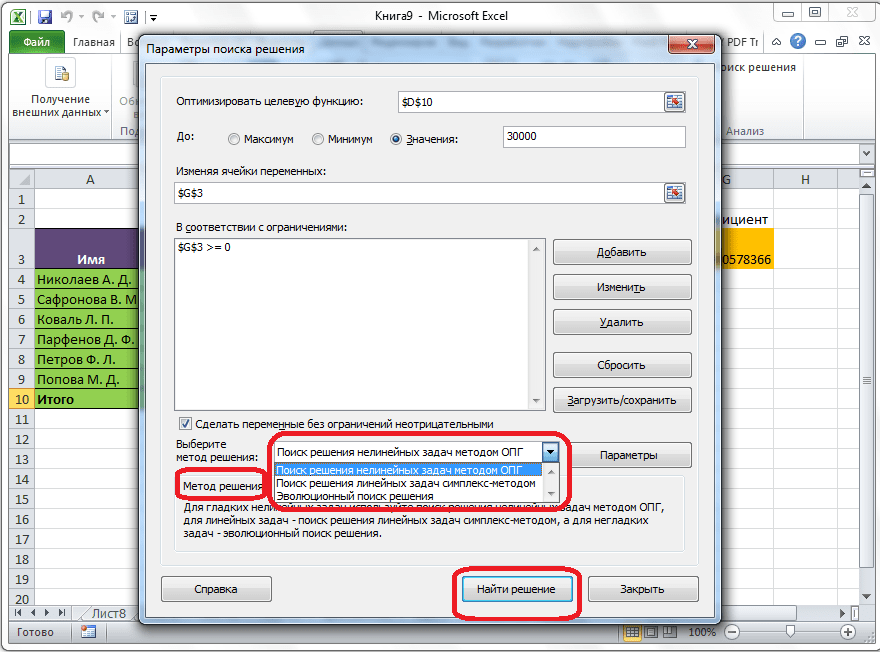
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.
Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.
-
Поиск решения и подбор параметров
Для анализа данных в
состав Microsoft
Excel
встроены такие средства как Подбор
параметров и Поиск решения. Подбор
параметров предназначен для нахождения
по известному значению функции y=f(x)
неизвестного значения величины х. Поиск
решения позволяет среди всех возможных
допустимых решений найти оптимальное
решение при заданных ограничениях.
Рассмотрим использование данных средств
на примерах.
-
Поиск решения
Поиск управленческого
решения зачастую бывает связан с решением
оптимизационных задач, которые имеют
следующие основные особенности:
-
задана целевая функция,
которую требуется максимизировать или
минимизировать, или приравнять результат
к конкретному значению; -
на неизвестные наложены
ограничения в форме неравенств или
уравнений; -
ряд неизвестных должен
быть неотрицателен.
Большой класс оптимизационных
задач составляют задачи, математической
моделью которых является модель линейного
программирования.
В таких моделях целевая функция является
линейной функцией и ограничения заданы
в виде линейных неравенств и уравнений.
В Excel
есть мощное средство решения оптимизационных
задач, в частности задач линейного
программирования — Поиск
решения. Рассмотрим
две типичные задачи такого рода.
Задача 1:
В таблице приведены
данные о предприятии, производящем
продукцию двух видов Р1
и Р2
из сырья трех видов S1,
S2,
S3.
Запасы сырья равны соответственно b1,
b2,
b3.
Расход i-го
вида сырья S1
на единицу j-го
вида продукции Рj
равен aij.
Доход, получаемый предприятием от
реализации единицы j-го
вида продукции Рj
равен сj.
|
Sj |
bi |
P1 |
P2 |
|
S1 |
b1= |
a11=1 |
a12=7 |
|
S2 |
b2=54 |
a21=3 |
a22=2 |
|
S3 |
b3=41 |
a31=2 |
a32=3 |
|
cj |
3 |
7 |
Найти план производства,
обеспечивающий предприятию максимум
дохода с помощью средства Поиск
решения.
Решение данной задачи
целесообразно выполнить в три этапа.
Первый
этап:
Сформулируйте экономико-математическую
модель задачи
(определите неизвестные, целевую функцию,
ограничения на неизвестные). Для этого
выполните следующие действия:
-
В предлагаемом примере
неизвестные величины х1
и х2.обозначают
соответственно планируемое количество
продукции первого вида Р1
и планируемое количество продукции
второго вида Р2,
которые должны обеспечить предприятию
максимальный доход. Эти величины должны
быть неотрицательны. -
Целевая функция (линейная
форма) представляет суммарный доход
предприятия от реализации продукции
и равна
z=3x1+7x2 (1).
-
Расход сырья вида S1,
S2,
и S3
на производство
продукции ограничен его запасами b1,
b2,
b3.
Таким образом, возникают ограничения:
1x1+7x2≤70;
3x1+2x2≤54; (2)
2x1+3x2≤41.
В результате приходим
к математической формулировке задачи:
среди неотрицательных решений системы
линейных неравенств (2) найти решение,
дающее максимум целевой функции z
(1).
Второй
этап:
Введите исходные
данные сформулированной модели на
рабочий лист
следующим образом
(рис.7.1):
Рисунок
7.45.. Информационная среда для решения
задачи линейного программирования
Сначала введите заголовки
для всех исходных данных, участвующих
в задании модели.
-
В ячейку B1
введите заголовок Искомые
переменные. -
В ячейки В2
и С2
введите соответственно обозначения
для количества производимой продукции
первого и второго вида х1
и х2
(мы помним, что это неизвестные величины,
значения которых при заданных условиях
хотим найти). -
В ячейку А3
введите текст Значения
искомых переменных. -
В ячейку А4
введите текст Коэффициенты
в целевой функции. -
В ячейке D3
введите текст Целевая
функция. -
В ячейку А5
введите текст Ограничения. -
В ячейку А6 введите текст
Виды ресурсов. -
В ячейки А7,
А8,
А9
соответственно введите названия вида
сырья S1,
S2,
и S3.
Отформатируйте таблицу
так, как показано на рис.1.
Таким образом, в этой
модели диапазон ячеек B3:C3
будет содержать оптимальное количество
продукции вида Р1
и вида Р2.
В качестве начальных значений принимаются
нули. После применения Поиска
решения в них будет
помещен результат решения задачи. Ячейки
B3
и C3
называются изменяемыми ячейками, т.к.
значения в них будут изменяться в ходе
решения для того, чтобы максимизировать
результат в оптимизируемой (целевой)
ячейке D4.
Поиск решения
позволяет задавать до 200 изменяемых
ячеек. Изменяемые ячейки не должны
содержать формул и их изменение влияет
на результат в оптимизируемой ячейке.
Диапазон ячеек B4:C4
должен содержать стоимость единицы
продукции первого и второго вида, в
терминах математической модели – это
коэффициенты в целевой функции.
D4
– оптимизируемая ячейка должна содержать
формулу, определяющую суммарный доход
предприятия от продажи произведенной
продукции.
Диапазон ячеек B7:C9
должен содержать количество сырья вида
S1,
S2,
и S3
используемого на единицу выпускаемой
продукции вида Р1
и вида Р2.
В диапазоне ячеек D7:D9
вычисляется объем используемого сырья.
Очевидно, что количество использованного
сырья не может превышать количество
имеющегося на складе. Количество сырья
на складе содержится в диапазоне ячеек
F7:F9.
Введите в созданную
форму остальной текст и исходные данные
(см. рис.7. 1), а затем добавьте формулы:
-
В ячейку D4
введите формулу =B4*B3+C4*C3,
определяющую суммарный доход предприятия
от реализации продукции. Поскольку
доход нужно максимизировать, то ячейку
D4
назовем оптимизируемой или целевой
ячейкой. -
В ячейку D7
введем формулу, вычисляющую количество
сырья вида S1
, необходимого для производства продуктов
вида Р1
и вида Р2.
Эта формула представляет собой сумму
произведений значений ячеек диапазона
B3:C3
на соответствующие значения ячеек из
диапазона B7:В9.
Формулу можно записать самим, а можно
воспользоваться функцией СУММПРОИЗВ.
В случае использования функции выполните
следующие действия:-
Активизируйте ячейку
D7. -
Вызовите Мастер
функций, нажав
в строке формул кнопку
fx. -
В появившемся диалоговом
окне Мастер функций
шаг 1 из 2 в окне
Категория
выделите Математические,
а в окне Выберите
Функцию щелкните
мышью по СУММПРОИЗВ
и нажмите на кнопку ОК. -
Во втором диалоговом
окне установите курсор ввода символов
в поле ввода Массив
1. Затем протащите
мышь при нажатой левой кнопке мыши по
ячейкам B3:C3,
предварительно отодвинув активное
диалоговое окно с этих ячеек. -
Установите курсор ввода
символов в поле ввода Массив
2. Затем протащите
мышь при нажатой левой кнопке мыши по
ячейкам B7:C7,
предварительно отодвинув активное
диалоговое окно с этих ячеек, и нажмите
на кнопку ОК
или клавишу Enter.
Таким образом, функция введена в ячейку
D7
и имеет вид =СУММПРОИЗВ(B3:C3;
B7:C7). -
Аналогичные функции
должны быть введены в ячейки D8
и D9.
Они отличаются от введенной в D7
функции диапазоном ячеек второго
массива, а первый массив во всех трех
случаях одинаков. Поэтому выполним
копирование введенной функции с помощью
маркера автозаполнения в ячейки D8,
D9,
но предварительно в параметрах функции
сделайте абсолютными имена ячеек B3
и C3.
Для этого выделите ячейку D7
и установите курсор ввода символов в
строку формул сначала перед буквой В
и нажмите на клавиатуре функциональную
клавишу F4,
а затем установите курсор ввода символов
перед буквой С
и снова нажмите на клавиатуре
функциональную клавишу F4,
а затем Enter.
Формула должна иметь вид, как на
рис. 7.1.
-
На этом ввод ограничений
и формул закончен. Обратите внимание
на то, что в таблице на рис.7.1 выбран
режим отображения формул, то есть нажата
кнопка Показать
формулы, и введенные
формулы видны в ячейках. В обычном режиме
в ячейках отображаются результаты,
полученные после расчета формул, а сами
формулы можно увидеть только в строке
формул.
Третий
этап: Этот шаг
связан с поиском
наилучшего решения
и требует выполнения следующих действий:
-
Сохраните построенную
модель на жестком диске при помощи
команды Office,
Сохранить как в
своей папке под именем Планирование
производства. -
Выделите оптимизируемую
ячейку D4. -
Выполните команду
Данные, Анализ,
Поиск решения1.
После этого появится диалоговое окно
Поиск решения
(рис. 2). -
В поле Установить
целевую ячейку уже
находится ссылка на оптимизируемую
ячейку, так как она была выделена перед
вызовом Поиска
решения. При
необходимости эту ссылку можно изменить
обычным образом. Программа Поиск
решения может
оптимизировать результат только в
одной ячейке. Напомним, что в целевой
ячейке должна находиться формула,
которая содержит ссылки на изменяемые
ячейки рабочего листа. -
Выберите тип взаимосвязи
между целевой ячейкой и решением путем
выбора переключателя в группе Равной
– Максимальному значению.
В этом случае отыскивается максимальный
результат для целевой ячейки.
Рисунок
7.46. Диалоговое окно Поиска решения
-
Перейдите в поле Изменяя
ячейки и укажите
смежные ячейки B3:C3,
которые должны изменяться в процессе
поиска наилучшего решения. Для этого
протащите мышь при нажатой левой кнопке
мыши по ячейкам B3:C3. -
Введите ограничения,
нажав на кнопку Добавить.
Откроется диалоговое окно Добавление
ограничения. -
Введите первое ограничение.
Для этого установите курсор ввода
символов в поле Ссылка
на ячейку и щелкните
левой кнопкой мыши по ячейке D7.
Справа от поля Ссылка
на ячейку в
раскрывающемся списке, выберите знак
отношения между левой и правой частью
введенного ограничения. В нашем случае
– это знак ≤. Установите курсор ввода
в поле Ограничение
и щелкните левой кнопкой мыши по ячейке
F7. -
Нажмите кнопку Добавить,
чтобы ввести следующее ограничение. -
Ввести остальные
ограничения. -
После ввода последнего
ограничения в диалоговом окне Добавление
ограничения нажмите
на кнопку Ок.
Появится заполненное диалоговое окно
Поиск решения. -
Введите дополнительные
параметры для решения задачи линейного
программирования (рис. 3):
-
Откройте окно Параметры
поиска решения,
нажав кнопку
Параметры в
окне Поиск решения. -
Установите флажок
Линейная модель. -
Установите флажок
Неотрицательные
значения. -
Нажмите кнопку Ок.
Вновь появится заполненное окно Поиск
решения.
Нажмите кнопку Выполнить.
По окончании поиска решения появится
диалоговое окно Результаты
поиска решения.
С его помощью можно сформировать отчет.
Рисунок
7.47. Диалоговое окно Параметры поиска
решения
-
Выберите переключатель
Сохранить найденное
решение и нажмите
кнопку ОК. -
Таблица с окончательным
решением представлена на рис. 7.4.
Самостоятельно проанализируйте
полученные результаты и сделайте
выводы. -
Рисунок
7.48. Решение задачи планирования
производства.
Задача 2.
Рассмотрим решение еще
одной задачи линейного программирования,
которую также можно решать с помощью
механизма Поиск
решения, –
транспортной задачи. Исходные данные
транспортной задачи заданы таблицей,
в которой:
-
В первом столбце указано,
сколько единиц груза может доставить
поставщик; -
В первой строке указано,
сколько единиц груза хочет получить
потребитель; -
В остальных ячейках
таблицы указаны удельные транспортные
затраты на перевозку единицы груза.
|
bj ai |
90 |
25 |
105 |
65 |
|
130 |
7 |
6 |
9 |
8 |
|
80 |
6 |
9 |
11 |
12 |
|
40 |
5 |
5 |
7 |
9 |
|
35 |
4 |
8 |
10 |
9 |
Используя средство Поиск
решения, найти
оптимальный план перевозок, минимизирующий
стоимость перевозок при условии, что
все поставщики вывезут груз, а все
потребители его получат в полном объеме.
Этапы
решения задачи:
Первый
этап:
Сформулируйте экономико-математическую
модель задачи
(определите неизвестные, целевую функцию,
ограничения на неизвестные).
-
В предлагаемом примере
16 неизвестных величин х11,
х12,
х13,
х14,
х21,
х22,
х23,
х24,
х31,
х32,
х33,
х34,
х41,
х42,
х43,
х44,обозначают
количество единиц груза, перевезенных
от i-го
поставщика j-му
потребителю, где i,
j
изменяются от 1 до 4. Эти величины должны
быть неотрицательны. -
Целевая функция (линейная
форма) представляет суммарную стоимость
перевозок, которую следует минимизировать:
z=7х11+6х12+9х13+8х14+6х21+9х22+11х23+12х24+
5х31+5х32+7х33+9х34+4х41+8х42+10х43+9х44
(1).
-
Все грузы должны быть
перевезены, все потребности должны
быть удовлетворены. Таким образом,
возникают ограничения (2):
х11+
х12+
х13+
х14=130;
х21+
х22
+х23
+х24=80;
(2)
х31+
х32
+х33
+х34=40;
х41
+х42
+х43
+х44=35;
х11+х21+х31+х41=90;
х12+
х22
+х32
+х42=25;
х13+
х23
+х33
+х43
=105;
х14+х24
+х34
+х44=65.
В результате приходим
к математической формулировке задачи:
среди неотрицательных решений системы
линейных уравнений (2) найти решение,
дающее минимум целевой функции z
(1).
Второй этап:
Введите исходные данные сформулированной
модели на рабочий лист
следующим образом:
-
Сначала введите заголовки
для всех исходных данных, участвующих
в определении модели (рис.7.5.). -
Введите исходные данные
– коэффициенты при неизвестных в
целевой функции в диапазон ячеек B9:E12,
количество груза у поставщиков в ячейки
A9:A12
и потребности в грузе у потребителей
в ячейки B8:E8. -
Для формирования левых
частей уравнений (2), являющихся
ограничениями, введите формулы в ячейки
А2:А5
и в ячейки В6:Е6,
как показано на рис.7.5. -
В ячейку В15
введите целевую функцию.
Таким образом, в этой
модели диапазон ячеек B2:Е5
будет содержать оптимальный план
перевозок xij.
В качестве начальных значений, для того
чтобы изменяемые ячейки были видны,
возьмем единицы. После применения Поиска
решения в них будет
помещен результат решения задачи. Ячейки
B2:Е5
называются изменяемыми ячейками, т.к.
значения в них будут изменяться в ходе
решения для того, чтобы минимизировать
результат в оптимизируемой (целевой)
ячейке В15.
Рисунок
7.49. Электронная таблица для решения
транспортной задачи
Диапазон ячеек B9:Е12
содержит стоимости перевозок единицы
груза от отправителя i
к потребителю j,
в терминах математической модели – это
коэффициенты в линейной форме.
В15
– оптимизируемая ячейка содержит
формулу, определяющую суммарную стоимость
перевозок.
Диапазон ячеек А9:А12
содержит количество груза, отправляемого
поставщиками.
Диапазон ячеек В8:Е8
содержит количество груза, которое
хотят принять потребители.
В диапазоне ячеек А2:А5
вычисляются суммы поставок отправителей.
Очевидно, что суммарное количество
отправленного груза для каждого
поставщика из условий задачи в точности
должно быть равно имеющемуся количеству
груза каждого поставщика. Количество
груза содержится в диапазоне ячеек
А9:А12.
В диапазоне ячеек В6:Е6
вычисляется суммарное количество груза,
поставляемое каждому потребителю.
Очевидно, что суммарное количество
полученного груза для каждого потребителя
из условий задачи в точности равно
заказу потребителя. Количество груза,
требующееся каждому потребителю,
содержится в диапазоне ячеек В8:Е8.
Третий этап:
Этот шаг связан с поиском
наилучшего решения
и требует выполнения следующих действий:
-
Сохраните построенную
модель на жестком диске при помощи
команды Office,
Сохранить как в
своей папке под именем Транспортная
задача. -
Выделите оптимизируемую
ячейку В15. -
Выполните команду
Данные, Анализ,
Поиск решения.
После этого появится диалоговое окно
Поиск решения. -
В поле Установить
целевую ячейку
уже находится ссылка на оптимизируемую
ячейку, так как она была выделена перед
вызовом Поиска
решения. -
Выберите тип взаимосвязи
между целевой ячейкой и решением путем
выбора переключателя в группе Равной
– Минимальному значению. -
Перейдите в поле Изменяя
ячейки и укажите
смежные ячейки В2:Е5,
которые должны изменяться в процессе
поиска наилучшего решения. Для этого
протащите мышь при нажатой левой кнопке
мыши по этим ячейкам. -
Введите ограничения,
нажав на кнопку Добавить.
Откроется диалоговое окно Добавление
ограничения. -
Введите первое ограничение.
Для этого установите курсор ввода
символов в поле Ссылка
на ячейку и
протащите мышь по ячейкам А2:А5. -
Справа от поля Ссылка
на ячейку в
раскрывающемся списке, выберите знак
отношения между левой и правой частью
введенного ограничения. В нашем случае
– это операция =. -
Установите курсор ввода
символов в поле Ограничение
и протащите мышь по ячейкам А9:А12. -
Нажмите кнопку Добавить,
чтобы ввести следующее ограничение. -
После ввода второго
ограничения (В6:Е6
= В8:Е8) в диалоговом
окне Добавление
ограничения
нажмите на кнопку Ок.
Появится заполненное диалоговое окно
Поиск решения. -
Введите дополнительные
параметры для решения задачи линейного
программирования:-
Откройте окно Параметры
поиска решения. -
Установите флажок
Линейная модель. -
Установите флажок
Неотрицательные
значения. -
Нажмите кнопку Ок.
Вновь появится заполненное окно Поиск
решения.
-
-
Нажмите кнопку Выполнить.
По окончании поиска решения появится
диалоговое окно Результаты
поиска решения.
С его помощью можно сформировать отчет.
-
Выберите переключатель
Сохранить найденное
решение и нажмите
кнопку ОК.
Проанализируйте полученные результаты
и сделайте выводы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #