Поиск не может найти подходящего решения excel

Решение оптимизационных задач с помощью электронных таблиц

Поиск решения

Подготовка к работе

Для выполнения упражнений и заданий необходимо наличие надстройки Поиск решения.

• · Выполните команду Сервис/Поиск решения…

• · Для загрузки надстройки выполните команду Сервис/Надстройки…

• · OK.

Рис. 11.1

Упражнение № 11. 1

Частная фирма занимается переработкой молока на нескольких заводах, расположенных в разных районах Москвы. Молоко поставляется объединениями фермеров, расположенными в городах Московской области. Стоимость молока одинакова, однако перевозка от объединения фермеров на завод зависит от расстояния и отличается для каждого объединения и завода. Потребность заводов в молоке различна. Объем молока в каждом объединении ограничен.

Потребителей (молокоперерабатывающие заводы) назовем по наименованию районов Москвы, в которых они расположены, а поставщиков (объединения фермеров) – по названиям городов Подмосковья.

Потребность перерабатывающих заводов в молоке.

Возможности объединений в доставке молока.

Для минимизации общих затрат на перевозку требуется определить, сколько поставлять молока, от какого объединения и на какой завод.

Затраты на перевозку тонны молока от объединения X к заводу, расположенному в районе Y, указаны в таблице.

Решение

• · Удалите все листы, кроме первого.

• · Сохраните файл под именем Транспортная задача.

• · Составьте модель задачи.

• §

• §

• §

• § =СУММ(C5:F5)

• § В диапазон ячеек С12:F16 занесите стоимость перевозки тонны молока, используя данные из таблицы. Для ячеек указанного диапазона установите формат Денежный с двумя знаками после запятой.

Решение задачи (объем молока для перевозки) будет расположено в диапазоне ячеек C5:F9.

Рис. 11.11

• § Полная стоимость перевозки молока по маршруту Наро-Фоминск – Лужники вычисляется по формуле =C5*C12.

• § Общая стоимость перевозок на завод в Лужники составит =C5*C12+C6*C13+C7*C14+C8*C15+C9*C16

• § Для подсчета общей стоимости перевозок на другие перерабатывающие заводы скопируйте формулу из ячейки С17 в диапазон ячеек D17:F

• § Для подсчета итоговой стоимости всех перевозок введите в ячейку B17 формулу =СУММ(C17:F17).

• § Выделите диапазон ячеек B17:F17 и установите для этих ячеек формат Денежный с двумя знаками после запятой.

• · Выполните команду Сервис/ Поиск решения…

• ·

— Поле Установить целевую ячейку: служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу. По условию задачи необходимо минимизировать расходы на перевозку, поэтому в поле Установить целевую ячейку: введите ячейку $B$17.

— Поле Равной: служит для выбора варианта оптимизации значения целевой ячейки. Установите переключатель в режим минимальному значению.

— Поле Изменяя ячейки: служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку. Установите диапазон ячеек $C$5:$F$9, так как необходимо определить, от какого производителя, на какой склад и сколько продукции следует перевезти.

Рис. 11.12

— Кнопка Предположить используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.

— Список Ограничения: служит для отображения списка граничных условий поставленной задачи. Добавьте ограничения.

Ограничение	Причина
B5:B9<=B12:B16	объем поставок не может превышать имеющиеся запасы
C4:F4>=C2:F2	запросы потребителей должны быть выполнены полностью
C5:F9=целое	количество перевозок не может быть дробным числом

— Кнопка Параметры служит для отображения диалогового окна Параметры поиска решения (рис. 11.13), в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения. Значения и состояния элементов управления окна, используемые по умолчанию, подходят для решения большинства задач.

 Поле Максимальное время: служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах), не превышающее число 32767.

 Поле Предельное число итераций: служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах), не превышающее число 32767.

 Поле Относительная погрешность служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать десятичную дробь от 0 (нуля) до 1. Чем больше десятичных знаков в задаваемом числе, тем выше точность. Например, число 0,0001 представлено с более высокой точностью, чем 0,01.

Рис. 11.13

 Поле Допустимое отклонение служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.

 Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков. Например, 0,0001 соответствует меньшему относительному изменению по сравнению с 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.

 Элемент управления Линейная модель служит для ускорения поиска решения линейной задачи оптимизации.

 Элемент управления Показывать результаты итераций служит для приостановки поиска решения для просмотра результатов отдельных итераций. Установите флажок Показывать результаты итераций.

 Элемент управления Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине. Например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.

 Элемент управления Неотрицательные значения позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение. Установите флажок Неотрицательные значения.

— Кнопка Закрыть служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки, сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить или Удалить.

— Кнопка Восстановить служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.

— Кнопка Выполнить служит для запуска поиска решения поставленной задачи. Щелкните по кнопке Выполнить.

• Появится диалоговое окно Текущее состояние поиска решения (рис. 11.14). Щелкните по кнопке Продолжить.

Рис. 11.14

• После каждой итерации на экране будет отображаться окно Текущее состояние поиска решения.

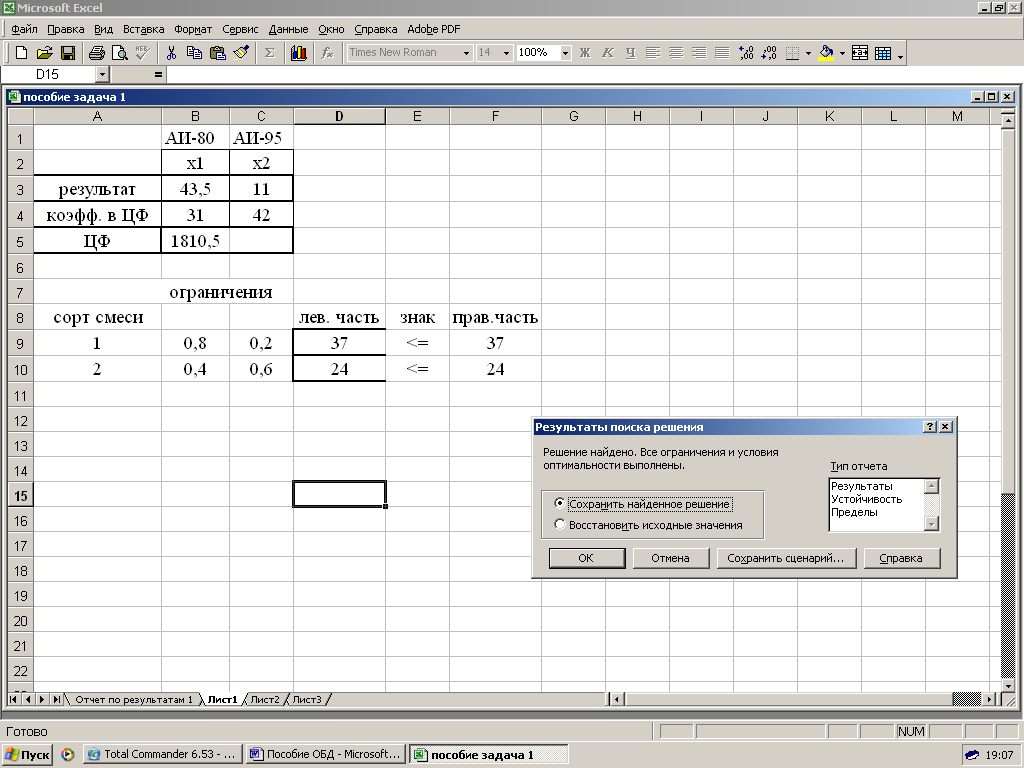
• После окончания поиска решения на экране появится окно Результаты поиска решения (рис. 11.15), сообщающее о том, что решение найдено.

Рис. 11.15

 Установите переключатель в значение Сохранить найденное решение.

 Раздел Тип отчета служит для указания типов отчета, которые могут быть добавлены в книгу.

 Результаты. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.

 Устойчивость. Используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле Установить целевую ячейку, диалоговое окно Поиск решения) или в формулах ограничений. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа. В отчет по нелинейным моделям включаются ограниченные затраты, фиктивные цены, объективный коэффициент (с некоторым допуском), а также диапазоны ограничений справа.

 Ограничения. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.

• Щелкните по кнопке OK.

Ответ

Минимальная сумма затрат на перевозки при соблюдении всех условий составит 2.795.450 рублей. Предлагается выполнять перевозки по следующим маршрутам:

Примечание

При записи ограничения С5:F9=целое в окне Ссылка на ячейку: укажите диапазон ячеек С5:F9, в следующем окне – цел. В окне Ограничение: будет выведено – целое. OK.

Упражнение № 11.2

Предположим, что фабрика производит зимние сапоги двух разных фасонов. Продукция обоих типов поступает в оптовую продажу. Для производства сапог используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 60 и 80 единиц соответственно. Расходы продуктов А и В на одну пару сапог приведены в таблице.

Изучение рынка сбыта показало, что суточный спрос на сапоги второго фасона никогда не превышает спроса на сапоги первого фасона более чем на одну пару. Кроме того установлено, что спрос на сапоги второго фасона никогда не превышает двух пар в сутки. Оптовые цены одной пары сапог равны 1500 руб. для сапог первого фасона и 1000 руб. для сапог второго фасона. Какое количество сапог каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Решение

• · Составим математическую модель задачи.

Обозначим переменной X суточный объём производства сапог первого фасона, переменной Y – второго фасона. Тогда суммарная суточная прибыль от производства сапог обоих типов составит 1500*X+1000*Y (функция цели).

Задача состоит в определении всех допустимых значений X и Y таким образом, чтобы суммарная суточная прибыль была максимальна и выполнялись следующие условия:

Перенесем построенную модель на лист Microsoft Excel (рис. 11.16).

 

Рис. 11.16

— Задайте ячейке B1 имя X, а ячейке B2 – Y.

— Стоимость сапог первого фасона составляет 1500 руб., а стоимость сапог второго фасона – 1000 руб., поэтому суммарная суточная прибыль от сапог обоих фасонов вычисляется по формуле =1500*X+1000*Y. Введите эту формулу в ячейку B4 (рис. 11.16).

— В диапазон ячеек B7:C10 введите ограничения, наложенные условием задачи (рис. 11.16).

• · Для поиска оптимального решения выполните команду Сервис/Поиск решения…

• · Найдите максимальную прибыль от производства сапог.

— Установите целевую ячейку B4.

— Равной: максимальному значению. 

— Изменяя ячейки: B1:B2 (количество сапог первого и второго фасонов).

— Ограничения: B7:B10<=C7:C10 (данные ячеек B7:B10 должны быть меньше либо равны данным, находящимся в ячейках C7:C10).

— Щелкните по кнопке Параметры. Установите флажок Неотрицательные значения (так как количество сапог не может быть отрицательным числом). OK.

Щелкните по кнопке Выполнить (рис. 11.17).

 

Рис. 11.17

Ответ

Максимальная суточная прибыль будет получена при производстве 39 пар сапог первого фасона и двух пар сапог второго фасона и составит 60500 руб.

Итоговые сообщения процедуры поиска решения

Если поиск решения успешно завершен, в диалоговом окне Результаты поиска решения выводится одно из следующих сообщений.

• · Решение найдено. Все ограничения и условия оптимальности выполнены.

Все ограничения соблюдены с точностью, установленной в диалоговом окне Параметры поиска решения и найдено заданное значение целевой ячейки.

• · Поиск свелся к текущему решению. Все ограничения выполнены.

Относительное изменение значения в целевой ячейке за последние пять итераций стало меньше установленного значения параметра Сходимость в диалоговом окне Параметры поиска решения. Чтобы найти более точное решение, установите меньшее значение параметра Сходимость, но это займет больше времени.

Если поиск не может найти оптимальное решение, в диалоговом окне Результаты поиска решения выводится одно из следующих сообщений.

• · Поиск не может улучшить текущее решение. Все ограничения выполнены.

В процессе поиска решения нельзя найти такой набор значений влияющих ячеек, который был бы лучше текущего решения. Приблизительное решение найдено, но либо дальнейшее уточнение невозможно, либо погрешность, заданная в диалоговом окне Параметры поиска решения, слишком высока. Измените погрешность на меньшее число и запустите процедуру поиска решения снова.

• · Поиск остановлен (истекло заданное на поиск время).

Время, отпущенное на решение задачи, исчерпано, но достичь удовлетворительного решения не удалось. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или Сохранить сценарий.

• · Поиск остановлен (достигнуто максимальное число итераций).

Произведено разрешенное число итераций, но достичь удовлетворительного решения не удалось. Увеличение числа итераций может помочь, однако следует рассмотреть результаты, чтобы понять причины остановки. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или нажмите кнопку Сохранить сценарий.

• · Значения целевой ячейки не сходятся.

Значение целевой ячейки неограниченно увеличивается (или уменьшается), даже если все ограничения соблюдены. Возможно, следует в задаче снять одно ограничение или сразу несколько. Изучите процесс расхождения решения, проверьте ограничения и запустите задачу снова.

• · Поиск не может найти подходящего решения.

В процессе поиска решения нельзя сделать итерацию, которая удовлетворяла бы всем ограничениям при заданной точности. Вероятно, ограничения противоречивы. Исследуйте лист на предмет возможных ошибок в формулах ограничений или в выборе ограничений.

• · Поиск остановлен по требованию пользователя.

Нажата кнопка Стоп в диалоговом окне Текущее состояние поиска решения после прерывания поиска решения в процессе выполнения итераций.

• · Условия для линейной модели не удовлетворяются.

Установлен флажок Линейная модель, однако итоговый пересчет порождает такие значения, которые не согласуются с линейной моделью. Это означает, что решение недействительно для данных формул листа. Чтобы проверить линейность задачи, установите флажок Автоматическое масштабирование и повторно запустите задачу. Если это сообщение опять появится на экране, снимите флажок Линейная модель и снова запустите задачу.

• · При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.

При пересчете значений ячеек обнаружена ошибка в одной формуле или в нескольких сразу. Найдите целевую ячейку или ячейку ограничения, порождающие ошибку, и измените их формулы так, чтобы они возвращали подходящее числовое значение.

Набрано неверное имя или формула в окне Добавить ограничение или в окне Изменить ограничение, либо в поле Ограничение было задано целое или двоичное ограничение. Чтобы ограничить значения ячейки множеством целых чисел, выберите оператор целого ограничения в списке условных операторов. Чтобы установить двоичное ограничение, выберите оператор для двоичного ограничения.

• · Мало памяти для решения задачи.

Система не смогла выделить память, необходимую для поиска решения. Закройте некоторые файлы или приложения и попытайтесь снова выполнить процедуру поиска решения.

Задание к лабораторной работе

Для каждой задачи составьте математическую модель задачи. Найдите ответ поиском решения.

Подготовьте и сдайте отчет (распечатанный электронный документ, не рукописный, с указанием № группы, Ф.И.О.)

Задача 1

Рацион для питания животных на ферме состоит из двух видов кормов I и II. Содержание веществ в килограмме корма представлено в таблице:

	Корм I	Корм II
Жиры	1	3
Белки	3	1
Углеводы	1	8
Нитраты	2	4
Цена 1 кг	20 руб	10 руб

Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 единиц, белков не менее 9 единиц, углеводов не менее 8 единиц, нитратов не более 16 единиц.

Задача 2

Для производства телевизоров необходимо 4 вида деталей. Количество деталей, необходимых для производства одного телевизора, представлено в таблице.

	I деталь	II деталь	III деталь	IV деталь
Витязь	4	0	2	2
Рекорд	3	2	0	3

Прибыль от реализации одного телевизора марки Витязь – 3 у.е., Рекорд – 2 у.е.Со склада этих деталей привозят: I вида не менее 120, II вида – не более 100, III вида не более 133, IV вида не более 222. Сколько телевизоров и какого вида нужно производить, чтобы прибыль была наибольшей?

Задача 3

Задача об экономии химического сырья. На химическом предприятии оказалось возможным отходы производства возвращать в установки и использовать как добавку к исходному сырью. Установка давала за смену 50 т продукции, потребляя 84 т сырья. Выделенные отходы в количестве 34 т состояли из трех видов: первый вид –12 т, второй вид – 8 т, третий вид – 14 т. При меньшем потреблении сырья отходы выделяются в тех же пропорциях. Отходы до использования должны пройти соответствующую обработку. При этом для обработки первого и третьего видов отходов может быть использован старый, но находящийся в хорошем состоянии двухсекционный агрегат, устроенный таким образом, что в нем могут обрабатываться (в разных секциях) сразу два вида отходов. При обработке этих отходов в агрегате вырабатывается тепло в следующих количествах: для первого вида – 187 ккал/т, для третьего вида – 95 ккал/т.

Обе секции агрегата имеют систему охлаждения, устойчивая работа которых возможна только в том случае, если разность между выделяемым теплом в обеих секциях по абсолютной величине не превышает 500 ккал.

При обработке отходов в агрегате имеют место некоторые потери, сос­тавляющие для первого вида 20% отходов, для третьего вида 40% отходов. Для обработки отходов второго вида требуется простой агрегата и тепло в количестве 120 ккал/т. Это тепло может быть получено от первого агрегата, если охлаждающую воду после ее нагрева в этом агрегате направить во второй. В результате предварительного расчета установлено, что использование одной тонны отходов каждого вида дает следующую экономию: первый вид – 4000 руб., второй вид – 2000 руб., третий вид – 5000 руб.

В каких количествах использовать отходы, чтобы обеспечить максимально возможную экономию?

Задача 4

В течение каждого квартала на четырех строительствах требуется соответственно 5, 10, 20 и 15 вагонов материалов. Возможности различных заводов по производству строительных материалов соответственно равны 10, 15 и 25 вагонам в квартал.

Стоимость перевозки одного вагона приведена в таблице. Определите такой план перевозок, при котором стоимость последних была бы минимальна.

Строительство № Завод №	1	2	3	4
1	8	3	5	2
2	4	1	6	7
3	1	9	4	3

Дмитрий Пользователь Сообщений: 7 Регистрация: 24.09.2020

Добрый день. Задача: распределить выпуск по времени с приоритетом «чем раньше, тем лучше». Не могу понять, почему Поиск решения не справляется с такой задачей. В прикрепленном файле, для примера, 3 продукта требуется распределить по времени выпуска с 07 до 15 часов с часовым интервалом. Известна общая потребность и дополнительное условие — часть продукции должна быть выпущена ровно в определенное время. Для выполнения условия «чем раньше, тем лучше» я строю дополнительную таблицу, совпадающую по размеру с таблицей переменных и для каждого столбца даю порядковый номер (от 1 до 9 в примере), после этого подставляю в эту таблицу значения на основе значений из таблицы переменных: если значение в таблице переменных присутствует, то ставлю 1, если отсутствует — 0 и далее перемножаю полученное значение на порядковый номер столбца. Получается, что для соблюдения условия «чем раньше, тем лучше» сумма получаемых значений должна быть минимальной. Поиск решения при использовании метода ОПГ распределяет равномерно по каждому дню; при эволюционном методе просит верхние ограничения переменных и всё равно неоптимально распределяет выпуск. Подскажите, в чем ошибка? Возможно, для такой задачи требуется использовать другие инструменты Excel или другие параметры в Поиске решения? Спасибо.

Андрей VG Пользователь Сообщений: 11878 Регистрация: 22.12.2012 Excel 2016, 365	#2 24.09.2020 13:45:33 Доброе время суток Цитата Дмитрий написал: или другие критерии оптимальности. Так как по текущим — всё выполнено.

Дмитрий Пользователь Сообщений: 7 Регистрация: 24.09.2020

#3 24.09.2020 13:56:05 День добрый. Не очень понял Цитата Андрей VG написал: Так как по текущим — всё выполнено. Целевая функция — не минимизируется. Минимальное значение целевой функции при текущих параметрах должно быть 10. У меня не получилось добиться от Поиска решения такого значения. Я напрямую забил 10 в значение целевой функции — «В ходе поиска не удалось найти подходящего решения». Какое значение целевой функции система выдает у вас? Если при текущих критериях принципиально невозможно получить требуемое значение целевой функции — какого рода критерии посоветуете применить?

Дмитрий Пользователь Сообщений: 7 Регистрация: 24.09.2020	Поднимаю вопрос. Самому разобраться до сих пор не удалось. Надеюсь на помощь сообщества.

	а что мешает в 7:00 выпустить 1271 шт. продукта1 и 1583 шт. продукта3 итого: процесс завершен в 7:00 все что нужно было к 10:00, готово уже в 7:00 что еще? Программисты — это люди, решающие проблемы, о существовании которых Вы не подозревали, методами, которых Вы не понимаете!

Дмитрий Пользователь Сообщений: 7 Регистрация: 24.09.2020

Игорь, добрый день. В принципе-то ничего не мешает. Вопрос в том, что Поиск решения не дает такого варианта, хотя он был бы оптимальным. В данном примере можно предположить, что выпуск в 10-00 обозначенного объема — это требование свежести продукции — выпустить в определенный момент по предзаказу определенный ассортимент для передачи конечному потребителю. Далее я в эти ограничения забью максимальную часовую производительность. Но пока я не добился от Поиска решения стабильной работы на маленьком количестве данных — не хочу переходить к следующему шагу.

Gata Пользователь Сообщений: 14 Регистрация: 18.04.2015

Дмитрий, по заданным Вами ограничениям поиск не понимает, каким образом ему нужно рассчитать и распределить суммы выпуска во времени, поэтому он либо размазывает его равномерно, либо выполняет условие на 10 часов, а прочие игнорирует и завершает итерационный процесс. В первом варианте для него минимум целевой функции  =34, в последнем =8. Т.е. он сначала выполняет ограничение по выпуску на 10 часов, а далее сам «догадаться», что вы хотите остаток бросить одной суммой на ранее время — не может. Не заданы ему такие параметры, в качестве изменяемых ячеек — целый массив и он его заполняет, как умеет. Нигде не указан метод как дробить потребность и он выдает локальное решение в виде равномерного распределения, либо просто не дает глобального решения. Ваша задача поиском решаема, если в качестве изменяемых ячеек задавать структуру распределения, а не саму сумму. Пример прилагаю, но пришлось еще дополнительную таблицу сделать для сумм по продуктам, которые нужно раскидать по часам. Вот так поиск находит целевое, равное 10. Рекомендую копать в этом направлении при постановке задачи.

Дмитрий Пользователь Сообщений: 7 Регистрация: 24.09.2020	#8 01.10.2020 11:54:49 Gata,спасибо большое! Стало гораздо понятнее. Я не дошел в рассуждениях до вспомогательной таблицы с коэффициентами и поиском значений этих коэффициентов вместо поиска итоговых значений выпуска. Проверил — теперь можно регулировать шаг расчета путем задания верхнего ограничения на коэффициенты и получить распределение с дополнительным ограничением по производительности так, чтобы фактический выпуск на каждый час не был кратен максимальной часовой производительности (это я заменил таблицу ограничений по максимальной сумме выпуска). К тому же, это соотносится с задачей по «вертикальному» ограничению — на столбец (максимально возможное количество выпущенных изделий зависит от места на складе) — я не стал о нем упоминать, чтобы не перегружать задачу. Теперь и по нему работает. Ещё раз благодарю.

Продолжение таблицы 28

Поиск не может найти подходящего решения.	В процессе поиска решения нельзя сделать итерацию, которая удовлетворяла бы всем ограничениям (ОДП задачи пуста)*.	Если необходимо поставить задачу так, чтобы она была разрешима, следует исключить противоречия в ограничениях. Возможно, следует в задаче снять одно ограничение или сразу несколько.
Условия для линейной модели не удовлетворяются.	Установлен флажок “Линейная модель”, однако итоговый пересчет порождает такие значения, которые не согласуются с линейной моделью (попытка решить нелинейную задачу, как линейную).	Следует исправить ошибки в исходных данных, чтобы задача стала линейной.
При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.	При пересчете значений ячеек обнаружена ошибка в одной формуле или в нескольких сразу.	Следует найти целевую ячейку или ячейку ограничения, порождающие ошибку, и изменить формулы в них так, чтобы они возвращали подходящее числовое значение.
Мало памяти для решения задачи.	Система не смогла выделить память, необходимую для поиска решения.	Закройте некоторые файлы или приложения, и попытайтесь снова выполнить процедуру поиска решения.
Другой экземпляр Excel использует SOLVER.DLL. Попробуйте повторить через какое-то время.	Запущено несколько копий Microsoft Excel, в одном из которых используется файл Solver.dll, который необходим для «Поиска решения».

6.6 Типы отчетов

Заголовок каждого отчета состоит из названия версии
электронной таблицы, названия типа отчета, указания на рабочий лист (с
указанием в квадратных скобках названия книги), а также даты и времени создания
отчета, например:

Microsoft Excel 10.0 Отчет по результатам
Рабочий лист: [Пример.xls]Лист7
Отчет создан: 04.12.2005 19:49:24

Отчеты состоят из таблиц,
соответствующих целевой функции, ограничениям и переменным. Первые две графы в
каждой из них называются «Ячейка» и «Имя». В первой графе указываются
адреса соответствующих ячеек. Для ограничений в графе «Ячейка» дается адрес
ячейки, на которую имеется ссылка в левой части соответствующего ограничения. Имя
ячейки составляется из содержания ближайших текстовых  ячеек (см. раздел 6.2).

6.6.1 Отчет по результатам

Данный тип отчета состоит из трех таблиц,
озаглавленных «Целевая ячейка», «Изменяемые ячейки» и
«Ограничения». Первые две таблицы для примера из раздела 6.2 примут вид
таблицы 29. После заголовка «Целевая ячейка» в
скобках стоит указание направления экстремизации. В примере заголовок последней
таблицы примет вид «Целевая
ячейка (Максимум)», так как целевая функция максимизируется.

В первых двух таблицах третья и четвертая графы
называются «Исходно» и «Результат». В них указываются соответственно исходное и
конечное значения в ячейках. Каждой изменяемой ячейке соответствует одна строка
таблицы, таблица «Целевая ячейка» состоит из
одной строки.

Таблица 29 – Отчет по
результатам для целевой функции и переменных

Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$B$11	Прибыль от производства карамели, руб.	0	193066,67
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$6	Производство карамели «Снежинка», т	0	266,66667
$C$6	Производство карамели «Яблочная», т	0	1173,3333

Из таблицы 29 видно, что фабрике следует выпускать
266,7 т карамели «Снежинка»
и 1173,3 т карамели «Яблочная», при этом она получит
прибыль 193066,7 руб.

Это
совпадает с ответом, полученным в разделах 2.1 и 3.3.

Поиск решения– это надстройкаEXCEL, позволяющая
реализовывать модели линейной, нелинейной
и дискретной оптимизации. Если в менюДанныеотсутствует командаПоиск решения, значит необходимо
загрузить эту надстройку.

Решение оптимизационной задачи состоит
из нескольких этапов:

Этап
1.

Построить
математическую модель задачи: выбрать
управляющие переменные
,
определить функцию цели и записать
систему ограничений.

Этап
2.

Подготовить
таблицу данных в EXCEL
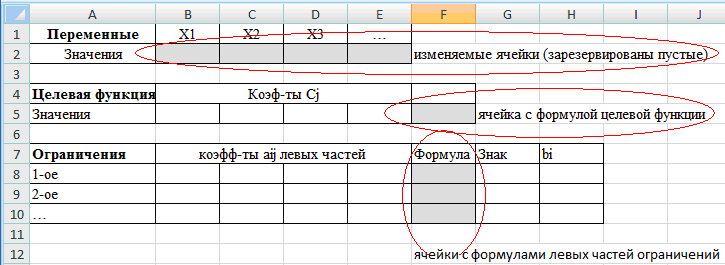
(рис 1).

• На
  листе Excelобозначить
  имеющиеся переменные:
  В1:Е1;

• Зарезервировать
  ячейки для их значений – изменяемые
  ячейки В2:Е2: эти ячейки пока оставим
  пустыми, по окончании решения в этих
  ячейках будут находится оптимальные
  значения управляющих переменных;

• Ввести в
  отдельные ячейки В5:Е5 коэффициенты
  целевой функции
  ;

• Обозначить
  целевую функцию
  :
  в ячейкуF5 (целевая ячейка)
  ввести формулу для вычисления значения
  этой функциисо ссылкой на ячейки значений коэффициентов
  В5:Е5 и переменных В2:Е2.

• Для
  каждого из ограничений задачи заполнить
  ячейки с исходными данными: в ячейки
  В8:Е10 ввести коэффициентылевых
  частей неравенств;
  в ячейки Н8:Н10 ввести правые части
  ограничений;
  в ячейкахG8:G10
  указать знак неравенства (<=, >= или
  =);

• В
  ячейки F8:F10
  ввести формулы для вычисления значений
  левых частей ограничений.

Рис. 1.

Для ввода формул
,удобно
использовать мастер функций:/ математические / СУММПРОИЗВ.

Этап
3.

Для запуска Поиск решениявыбрать
команды ДанныеПоиск решения.После выбора командыПоиск решенияпоявиться диалоговое
окноПоиск решения (рис 2.).
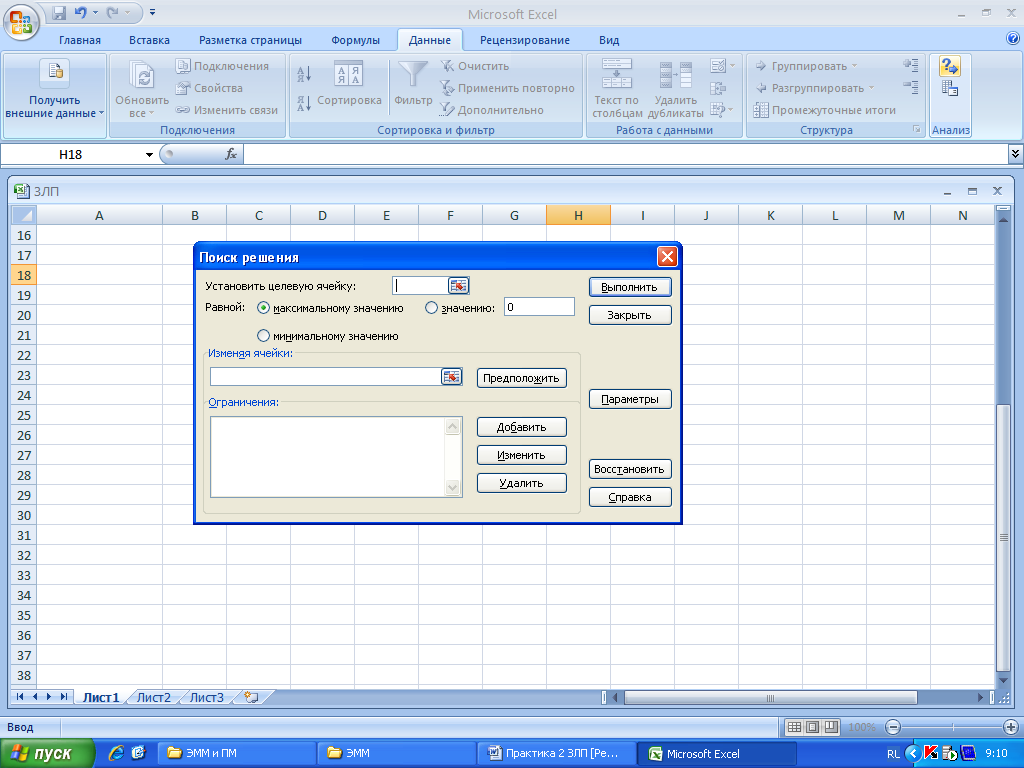
В нем есть три основных поля:

• Установить
  целевую ячейку;

• Изменяя
  ячейки;

• Ограничения;

Установить
целевую ячейку– указывается
ячейка, в которой находится формула для
вычисления значения функции цели-F5. Эта ячейка связана с
другими ячейками с помощью формул. Здесь
же выбирается направление оптимизации:
наибольшее или наименьшее значение
функции цели ищется в задаче.

Рис. 2.

Изменяя ячейки— указываются
зарезервированные изменяемые ячейки
В2:Е2, соответствующие управляющим
переменным в модели, значения в которых
будут изменяться для достижения
экстремума целевой функции. В этих
ячейках в результате расчета будут
находиться значения переменных
оптимального плана.
Для поиска решения можно указать до
200 изменяемых ячеек.

К этим ячейкам предъявляются два основных
требования: они не должны содержать
формул и должны влиять на значение
целевой ячейки, т.е. их адреса должны
использоваться в формуле, введенной в
целевую ячейку.

Ограничения модели определяются
с помощью значений соответствующих
ячеек (рис 3). Структура ограничения,
введенного вПоиске решения, полностью
соответствует ограничению, построенному
в модели: левая часть, знак, правая часть:

ссылка
на ячейку– указываются ячейки, в
которых введеныформулыдля вычисления
левых частей неравенств системы
ограниченийF8:F10
(не путать с ячейками, содержащимикоэффициентылевых частей ограничений
В8:Е10). Ограничения могут налагаться как
на целевую ячейку, так и на переменные
(до 100 дополнительных ограничений);

типкаждого из ограничений модели ()
задается (вводится) в специальном окне
диалога при выполнении команды;

ограничение
— указываются ячейки, в которых
введены правые части выражений в системе
ограничений Н8:Н10.

Рис3.

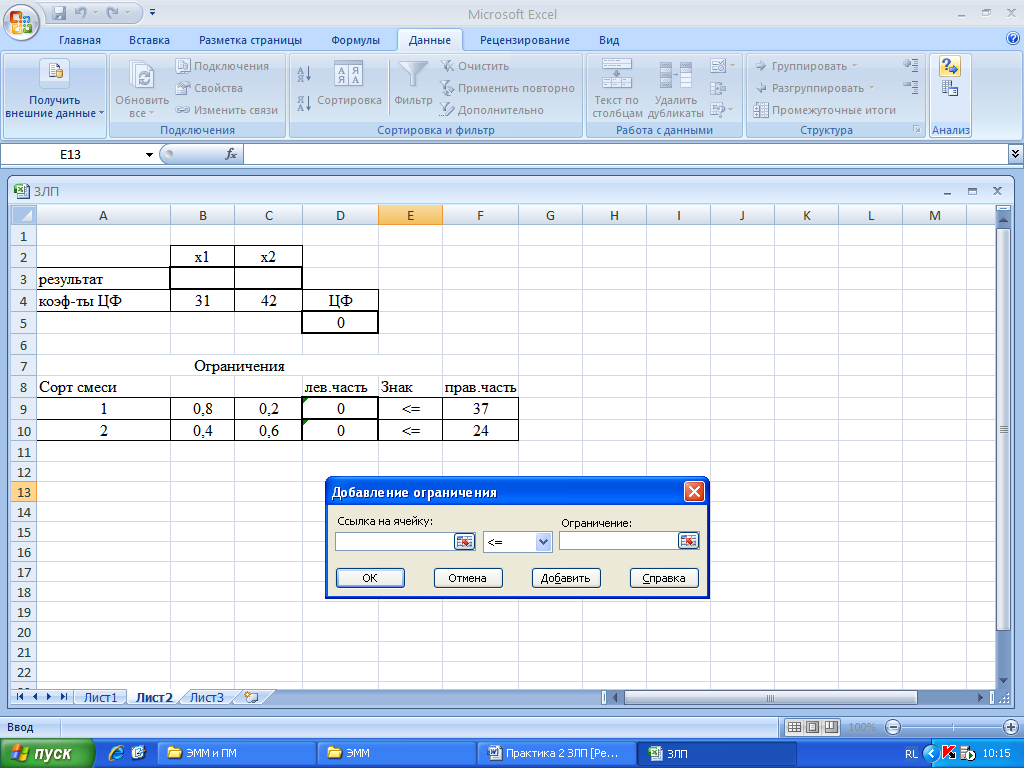
В
режиме Параметры(Рис. 4) окна
диалогаПоиск решениязадается
тип модели (линейная или нелинейная) и
прямые ограничения ( отмечаются галочками
поля «Линейная модель» и «Неотрицательные
значения»).

Рис. 4

Этап
4.

После
команды Выполнитьосуществляется
поиск оптимального решения и в итоге
появляется диалоговое окноРезультат
поиска решения(Рис. 5).

Рис. 5

В этом диалоговом окне содержатся
сведения об итоговых сообщениях процедуры
поиска решения. Например, в случае
несовместности системы ограничений
EXCEL будет выдавать
сообщение Поиск не может найти
подходящего решения.Если решение
задачи отсутствует вследствие
неограниченности целевой функции на
множестве допустимых решений, тоEXCELбудет выдавать сообщениеЗначения
целевой ячейки не сходятся.

Необходимо проконтролировать успешное
завершение решения задачи: появляется
сообщение Решение найдено. Все
ограничения и условия оптимальности
выполнены.

Задача
1.

Найти
оптимальный план
выпуска
двух видов смеси, обеспечивающий максимум
прибыли, если прибыль от реализации 1
ед. каждого вида смеси составляет 31 и
42 ден.ед. На производство 1 ед. 1-й смеси
расходуется 0,8 ед. ресурса Р1 и 0,4 ед.
ресурса Р2; для второго вида смеси эти
расходы составляют – 0,2 и 0,6, соответственно.
Запасы ресурсов Р1 и Р2 составляют 37 и
24 ед., соответственно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #