Поиск минимума функции excel

Skip to content

Как найти при помощи функции МИН минимальное значение в Excel — 6 примеров

В этой статье вы узнаете, как использовать функцию МИН в Excel 2007-2019, найти минимальное значение, наименьшее значение по условию и выделить самое маленькое число в вашем диапазоне.

Сегодня мы расскажем вам, как использовать базовую, но очень важную функцию МИН в Excel. Вы увидите способы найти минимальное значение, в том числе исключая нули, абсолютный минимум и наименьшее значение с учётом условий. Кроме того, я покажу вам пошагово, как выделить цветом наименьшее число, а также подскажу, что делать, если ваша функция МИН возвращает ошибку вместо нужного результата.

  1. Функция Excel МИН — синтаксис
  2. 1. Нахождение наименьшего значения
  3. 2. Как найти самую раннюю дату
  4. 3. Поиск абсолютного минимума в Excel
  5. Как найти самое маленькое значение в Excel, исключая нули
  6. Нахождение минимума на основе условия
  7.  Как подсветить наименьшее число в Excel
  8. Почему не работает функция МИН?

Итак, начнем :)

Функция Excel МИН — синтаксис

Функция МИН проверяет ваш диапазон данных и возвращает минимальное значение в этом наборе.

Синтаксис для Excel МИН следующий:

    МИН (число 1; [число 2]; …)

число1, [число2],… — это серия чисел, откуда вы хотите получить минимум. Число1 — обязательный аргумент, в то время как [число 2] и следующие являются необязательными. В одной формуле МИН допускается до 255 аргументов. Аргументы могут быть числами, ссылками на ячейки и диапазонами.

Функция МИН является одной из самых простых в применении. Вот пару примеров, доказывающих это:

1. Нахождение наименьшего значения

Допустим, у вас есть фрукты на складе. Ваша задача — проверить, какие из них заканчиваются. Есть несколько способов это сделать:

1: Ввести каждое значение из столбца «Количество на складе» в формулу:

= МИН(366;476;398;982;354;534;408)

2: Сделать ссылки на каждую ячейку столбца Количество:

= МИН(В2; В3; В4; В5; В6; В7; В8)

3: Или просто сослаться на весь диапазон ячеек:

= МИН(В2:В8)

Получить минимальное значение с помощью функции МИН

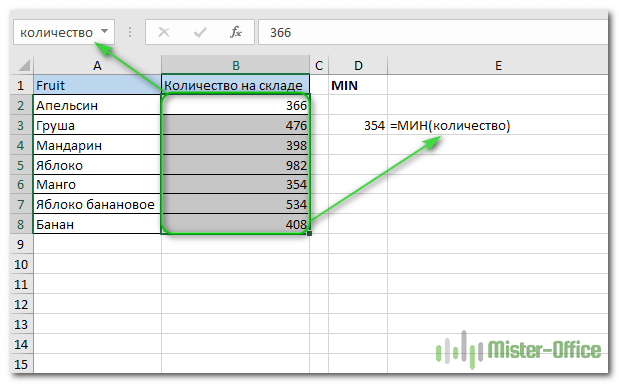
4: в качестве альтернативы вы можете создать именованный диапазон и использовать его вместо этого, чтобы избежать любых прямых ссылок:

найти наименьшее из именованного диапазона

2. Как найти самую раннюю дату

Представьте, что вы ждете несколько доставок и хотели бы быть готовыми к самой ближайшей. Как узнать самую раннюю дату в Excel? Легко! Используйте функцию МИН, следуя логике из примера 1:

Примените МИН и выберите даты, ссылаясь непосредственно на ячейки:

= МИН(В2:В8)

или на именованный диапазон:

= МИН(дата_поставки)

Найти самую раннюю дату

3. Поиск абсолютного минимума в Excel

Предположим, что у вас есть диапазон чисел, и вам нужно определить не просто самое маленькое из них, но найти абсолютный минимум или минимум по абсолютному значению (по модулю). Одна только МИН функция не сможет справиться с этим, поскольку она просто будет искать минимальное число. Здесь вам нужна вспомогательная функция, которая может конвертировать все отрицательные числа в положительные.

Есть ли готовое решение для этого случая? Вопрос был риторическим, в Excel есть решение любой задачи. Если у вас есть какие-либо сомнения, просто просмотрите наш блог. :)

Но вернемся к нашей задаче. Готовое решение для этого конкретного случая называется функцией ABS, которая возвращает абсолютное значение заданных вами чисел. Таким образом, комбинация функций МИН и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:

{= МИН(ABS(А1:Е12))}

Абсолютный минимум, найденный МИН и ABS

Важно! Вы заметили фигурные скобки вокруг формулы? Это признак того, что это формула массива, и ее нужно вводить с помощью комбинации клавиш Ctrl + Shift + Enter, а не просто Enter.

Как найти самое маленькое значение в Excel, исключая нули

Вам кажется, что вы уже знаете все о поиске минимальных значений в Excel? Не спешите с выводами, всегда есть чему поучиться. Например, как бы вы определили наименьшее ненулевое значение? Есть идеи? Не обманывай и не гугли, просто продолжай читать;)

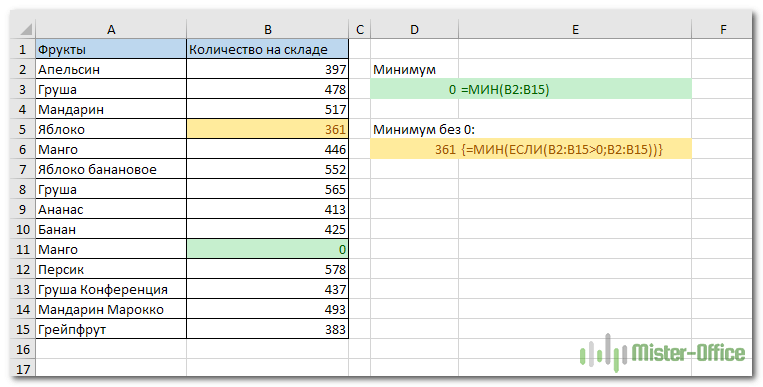
Дело в том, что Excel МИН работает не только с положительными и отрицательными числами, но и с нулями. Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:

{= МИН(ЕСЛИ(В2:В15>0;В2:В15))}

минимальное значение, исключая ноль

Вы, наверное, заметили фигурные скобки вокруг формулы массива. Просто помните, что вы не вводите их вручную. Они появляются в тот момент, когда вы нажимаете Ctrl + Shift + Enter на клавиатуре.

Нахождение минимума на основе условия

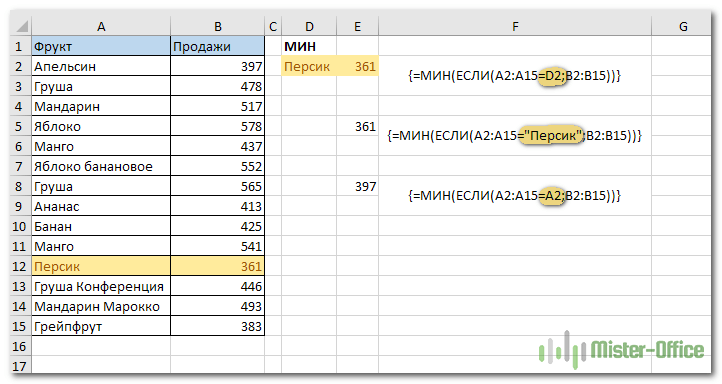
Предположим, вам нужно найти наименьшее количество продаж определенного фрукта в списке. Другими словами, ваша задача — определить минимальное значение на основе некоторого критерия. В Excel условия обычно требуют использования функции ЕСЛИ. Все, что вам нужно сделать, это создать идеальную комбинацию МИН и ЕСЛИ для решения этой задачи:

Определить минимум по критериям, используя МИН и ЕСЛИ

Нажмите Ctrl + Shift + Enter, чтобы эта функция массива работала, и наслаждайтесь результатом.

 Выглядит довольно легко, правда? И как вы определите минимум на основе 2 или более условий? Может быть, есть более простая формула для этой задачи, доступная в Excel? Читайте дальше, чтобы узнать ответ. ;)

 Как подсветить наименьшее число в Excel

А что, если вам не нужно возвращать минимальное значение, а вы просто хотите найти его в своей таблице? Самый простой способ найти ячейку — выделить ее. И самый простой способ сделать это — применить условное форматирование. Это даже проще, чем создать формулу:

1 Создайте новое правило условного форматирования, щелкнув Условное форматирование -> Создать правило

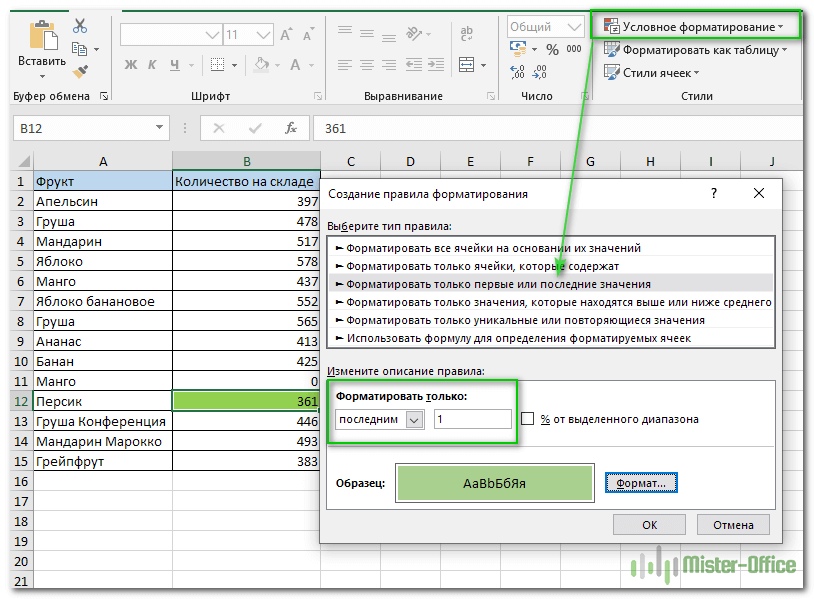
2 Когда откроется диалоговое окно «Создание правила форматирования», выберите тип правила «Форматировать только первые или последние значения».

3 Поскольку задача состоит в том, чтобы найти одно-единственное наименьшее значение, выберите опцию «последним» в раскрывающемся списке и укажите 1 в качестве количества ячеек, которые нужно выделить.

выделить наименьшее число с условным форматированием

Но что делать, если в вашей таблице снова есть ноль? Как игнорировать нули при выделении минимального значения? Не беспокойтесь, для этого случая тоже есть маленькая хитрость:

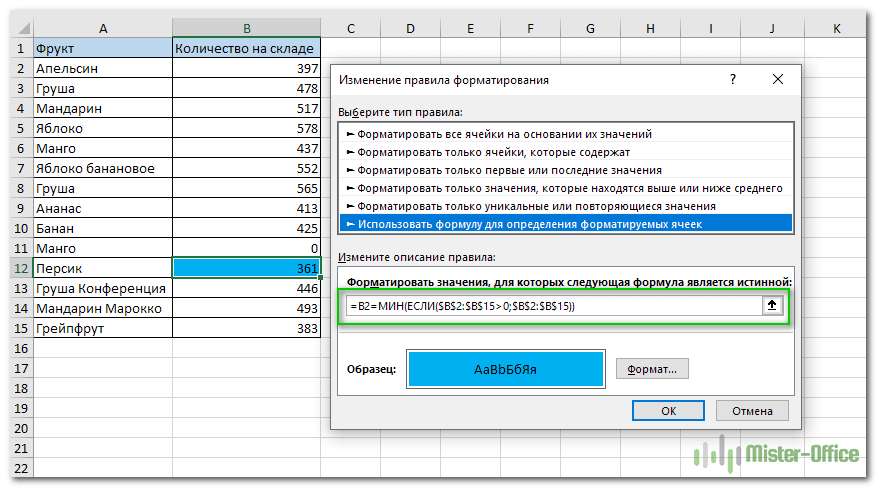
1. Создайте новое правило условного форматирования, выбрав опцию «Использовать формулу для определения форматируемых ячеек».

2. Введите это выражение в поле «Значения формата» для проверки условия:

=B2=МИН(ЕСЛИ($B$2:$B$15>0;$B$2:$B$15))

Где B2 — первая ячейка диапазона, в которой будет найдено самое маленькое значение

выделить самое маленькое без нуля

3. Выберите цвет ( Формат… -> Заливка) и нажмите ОК.

4. Наслаждайтесь :)

Почему не работает функция МИН?

В идеальном мире все формулы будут работать как часы и возвращать правильные результаты, когда вы нажмете Enter. Но в мире, в котором мы живем, формулы иногда возвращают ошибку, а не результат, который нам нужен. Не беспокойтесь, сама ошибка всегда намекает на ее возможную причину. Вам просто нужно всмотреться в вашу формулу.

Исправление ошибки #ЗНАЧ! в формуле МИН

Как правило, вы получаете #ЗНАЧ! сообщение об ошибке, когда хотя бы одно из значений, использованных в формуле, неверно. Что касается МИН, это может произойти, когда один из аргументов поврежден, например, что-то не так с ячейками, которые использует формула.

Например, #ЗНАЧ! может появиться, если один из аргументов является ячейкой с ошибкой или в ссылке на ячейку есть опечатка.

ошибка #ЗНАЧ! в МИН

Что может вызвать ошибку #ЧИСЛО! ?

Excel показывает ошибку #ЧИСЛО!, когда невозможно рассчитать вашу формулу. Обычно это происходит, когда числовое значение слишком велико или мало для отображения в Excel. В Excel допустимы номера от -2,2251E-308 до 2,2251E-308. Если один из ваших аргументов находится вне этого диапазона, функция вернет #ЧИСЛО!

ошибка #ЧИСЛО!

Я получаю сообщение #ДЕЛ/0!, что делать?

Исправление #ДЕЛ/0! —  это легко. Не делите на ноль! :) Не шучу, это единственное решение этой проблемы. Проверьте диапазон ваших данных, исправьте ошибку #ДЕЛ/0!, и формула незамедлительно вернет правильный результат.

#ДЕЛ/0!

Ищете минимум, но получаете #ИМЯ?

Сообщение #ИМЯ? означает, что Excel не может распознать формулу или ее аргументы. Наиболее вероятная причина этого результата — опечатка. Вы можете либо неправильно написать формулу, либо указать неверные аргументы для получения такого результата.

сообщение #ИМЯ?

Другая возможная причина этой проблемы лежит в именованном диапазоне. Итак, если вы ссылаетесь на несуществующий диапазон или в нем есть опечатка, вы увидите #ИМЯ? в ячейке с результатом.

#ИМЯ? ошибка в именованном диапазоне в МИН

Это были некоторые из способов найти минимум в Microsoft Excel с помощью функции МИН. Для вас я рассмотрел различные подходы, чтобы найти самое маленькое значение в Excel и найти абсолютный минимум. Вы можете считать эту статью своей шпаргалкой и использовать всякий раз, когда вам нужно найти минимальное число в зависимости от условия, чтобы предотвратить и исправить возможные ошибки.

Вот и все на сегодня. Пожалуйста, не стесняйтесь делиться своими мыслями и вопросами в разделе комментариев, я буду рад получить от вас обратную связь! :)

Еще полезная дополнительная информация:

Функция МАКС в Excel: как найти максимальное значение — В этой статье объясняется функция МАКС с множеством примеров формул, которые показывают, как найти наибольшее значение в Excel и выделить наибольшее число на листе. МАКС — одна из самых простых и простых в использовании функций Excel. Тем не менее, у нее…
Как сделать зависимый выпадающий список в Excel? — Одной из наиболее полезных функций проверки данных является возможность создания выпадающего списка, который позволяет выбирать значение из предварительно определенного перечня. Но как только вы начнете применять это в своих таблицах, то неизбежно столкнетесь с проблемой: нужно сделать один выпадающий список…
использование формул для выпадающего списка Создаем выпадающий список в Excel при помощи формул — Задача: Создать выпадающий список в Excel таким образом, чтобы в него автоматически попадали все новые значения. Сделаем это при помощи формул, чтобы этот способ можно было использовать не только в Excel 2007 и старше, но и в Excel 2003. Как…
автоматическое добавление значений в выпадающий список 5 способов создать выпадающий список в ячейке Excel — Одной из наиболее полезных функций при вводе данных является возможность использовать выпадающий список в Excel. Он позволяет выбирать значение из предварительно определенного перечня и разрешает вводить только те данные, которые соответствуют вашим требованиям. Мы предложим вам несколько простых способов, как…

Источник

Если функция F(x) непрерывна на отрезке [a, b] и имеет внутри этого отрезка локаль-ный экстремум, то его можно найти, используя надстройку Excel Поиск решения. Рассмотрим последовательность нахождения экстремума функции на примере.

Пример 12. Задана неразрывная функция Y= X 2 +X +2. Требуется найти ее экстремум (минимальное значение) на отрезке [-2, 2].

Решение:

1. В ячейку А3 рабочего листа введите любое число, принадлежащее заданному отрезку, в этой ячейке будет находиться значение Х.

2. В ячейку В3 введите формулу, определяющую заданную функциональную зависимость (рис. 18). Вместо переменной Х в этой формуле должна быть ссылка на ячейку А3: = A2^2 + A2 +2.

3. Выполните команду меню Сервис — Поиск решения.

4. В открывшемся окне диалога Поиск решения в поле Установить целевую ячейку укажите адрес ячейки, содержащей формулу (В3), установите пере-ключатель Минимальному значению, в поле Изменяя значение ячейки укажите адрес ячейки, в которой содержится переменная х.

5. Добавьте два ограничения в соответствующее поле: A3>= -2 и A3<= 2.

6. Щелкните на кнопке Параметры и в от крывшемся диалоговом окне Пара-метры поиска решения установите относительную погрешность вычислений и предельное число итераций.

7. Щелкните на кнопке Выполнить.

В ячейке А3 будет помещено значение аргумента Х функции, при котором она принимает минимальное значение, а в ячейке В3 – минимальное значение функции. В результате выполнения вычислений в ячейке А3 будет получено значение независимой переменной, при котором функция принимает наименьшее значение, а в ячейке В3 – минимальное значение функции, равное 1,75. Постройте график заданной функции и убедитесь, что решение найдено верно.

Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями

history 14 января 2021 г.
    Группы статей

  • Надстройка «Поиск решения»

Пусть дана функция с несколькими переменными F(x1, x2, . )=a1*x1+a2*x2+. Также даны граничные условия в виде b1*x1+b2*x2+. файл примера ).

Переменные (выделено зеленым) . В качестве переменных модели, очевидно, выступают x1, x2, x3, x4. Эта задача хороша тем, что переменные задаются однозначно, не требуется осмысливать житейскую задачу, например как с оптимизацией затрат . Хотя математически — это эквивалентные задачи, только количество переменных разное.

После запуска Поиск решения будет методично (последовательно) по своему алгоритму подставлять в зеленые ячейки числовые значения и вычислять функцию F (красная ячейка).

Ограничения (выделено серым) . Ограничения модели — это ограничения на область изменения переменных. Они могут задаваться как простыми выражениями для одной переменной, например х1>=0, так и для некой комбинации переменных 5*x1+4*x2-x3-2*x4 =0 ограничения можно ввести прямо в окне Поиска решения (будет показано ниже), для более сложных зависимостей удобно подготовить вспомогательную таблицу (С26:Е29).

Составить модель, особенно первую, непросто. Может помочь такой подход: считать, что переменные (зеленые ячейки) уже содержат некие значения, пусть даже не оптимальные. Так легче составлять огграничения. В нашем случае ограниечение 5*x1+4*x2-x3-2*x4 можно записать с помощью формулы = СУММПРОИЗВ($D$19:$D$22;C26:C29) . В диапазоне D19:D22 содержатся коэффициенты 5; 4; -1; -2. Кроме того, если значения переменных заданы, то и значение целевой функции также автоматически рассчитано (тоже не оптимальное пока, до запуска Поиска решения).

Целевая функция (выделено красным) . Целевая функция — это то, что требуется оптимизировать, т.е. F. Формула для ее вычисления задана в явном виде — не нужно догадываться из условий обычной задачи как ее подсчитать. Это не всегда очевидно (см., например, статью про пропускную способность трубопровода ).

Ниже приведено окно Поиска решения с заполненными полями: целевая функция, переменные и ограничения.

После запуска Поиска решения ответ будет вычислен за доли секунды: F=3.

Источник

Section 6.3 Critical Points and Extrema

Subsection 6.3.1 Critical Points

With functions of one variable we were interested in places where the derivative is zero, since they made candidate points for the maximum or minimum of a function. If the derivative is not zero, we have a direction that is downhill and moving a little in that direction gives a lower value of the function. Similarly, with functions of two variables we can only find a minimum or maximum for a function if both partial derivatives are 0 at the same time. Such points are called critical points.

The point ((a,b)) is a critical point for the multivariable function (f(x,y)text{,}) if both partial derivatives are 0 at the same time.

In other words,

begin{equation*}
frac{partial }{partial x} f(x,y)|_{x=a,y=b}=0
end{equation*}

and

begin{equation*}
frac{partial }{partial y} f(x,y)|_{x=a,y=b}=0text{.}
end{equation*}

Example 6.3.1. Finding a Local Minimum of a Function.

Figure 6.3.2. Video presentation of this example

Use the partial derivatives of (f(x,y)=x^2+ 2xy+3y^2-4x-3y) to find the minimum of the graph.

Solution.

Critical Point by Algebra

In the previous section, we already computed

begin{align*}
frac{partial }{partial x} f(x,y) amp = 2x+2y-4\
frac{partial }{partial y} f(x,y) amp = 2x+6y-3text{.}
end{align*}

We need to find the places where both partial derivatives are 0. With this simple system, I can solve this system algebraically and find the only critical point is ((9/4, -1/4)text{.})

begin{align*}
0 amp = 2x+2y-4\
0 amp = 2x+6y-3text{.}
end{align*}

Subtract the equations to eliminate (xtext{:})

begin{equation*}
0=0-4y-1text{.}
end{equation*}

Solve for (ytext{:})

begin{align*}
4y amp = -1\
y amp = -1/4text{.}
end{align*}

Substitute back and solve for (xtext{:})

begin{align*}
0 amp = 2x+2(-1/4)-4\
2x amp = 9/2\
x amp =9/4text{.}
end{align*}

Critical Point by Solver

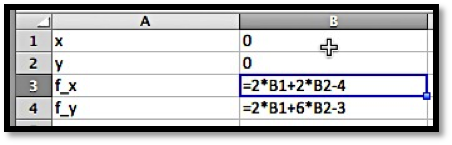
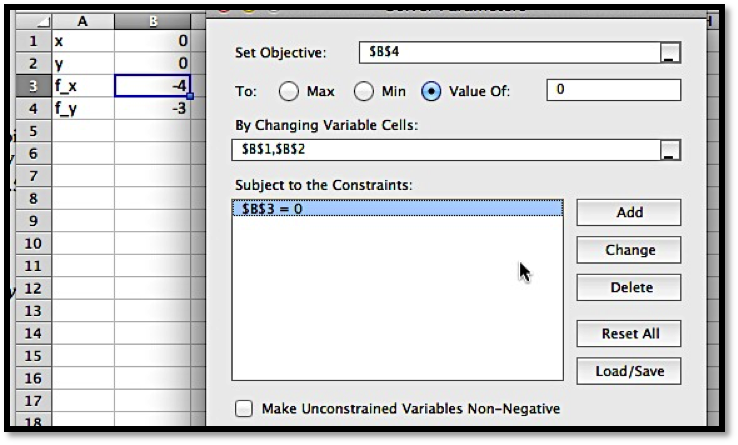
If the partials are more complicated, I will want to find the critical points another way. I can find the point with Solver.

To get solver to set both partials to 0 at the same time, I ask it to solve for (f_y=0text{,}) while setting (f_x=0) as a constraint. Make sure to uncheck the box that makes unconstrained variables non-negative.

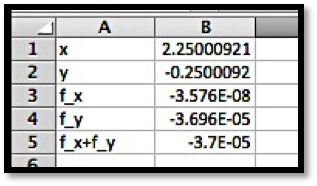
This finds our critical point within our error tolerance.

Critical Point by CAS

We can also use Wolfram|Alpha to find the solution to our system of equations.

Determining the Critical Point is a Minimum

We thus get a critical point at ((9/4,-1/4)) with any of the three methods of solving for both partial derivatives being zero at the same time. Once we have a critical point we want to determine if it is a maximum, minimum, or something else. The easiest way is to look at the graph near the critical point.

It is clear from the graph that this critical point is a local minimum.

It is easy to see that (f(x,y)=x^2+y^2) has a critical point at ((0,0)) and that that point is a minimum for the function. Similarly, (f(x,y)=-x^2-y^2) has a critical point at ((0,0)) and that that point is a maximum for the function. For some functions, like (f(x,y)=x^2-y^2text{,}) which has a critical point at ((0,0)text{,}) we can have a maximum in one direction and a minimum in another direction. Such a point is called a saddle point. We note that we can have a saddle point even if the (x) and (y) slice curves both indicate a minimum.

Example 6.3.3. A Saddle Point at a Minimum on Both Axes.

Figure 6.3.4. Video presentation of this example

Show that (f(x,y)=x^2-3xy+y^2) has a critical point at ((0,0)text{,}) which is a minimum of both slice curves, but is not a local minimum.

Solution.

We look at the two partial derivatives, and notice they are both zero at the origin.

begin{align*}
frac{partial }{partial x} f(x,y) amp = 2x-3y\
frac{partial }{partial x} f(x,y) amp = -3x+2ytext{.}
end{align*}

We then see that both slice curves are parabolas that bend up, with a minimum at 0.

begin{align*}
f(x,0) amp = x^2\
f(0,y) amp = y^2text{.}
end{align*}

However if we take the slice with (x=ytext{,}) we get a parabola bending down, so we don’t have a minimum.

begin{equation*}
f(x,-x)=x^2-3x x+x^2=-x^2text{.}
end{equation*}

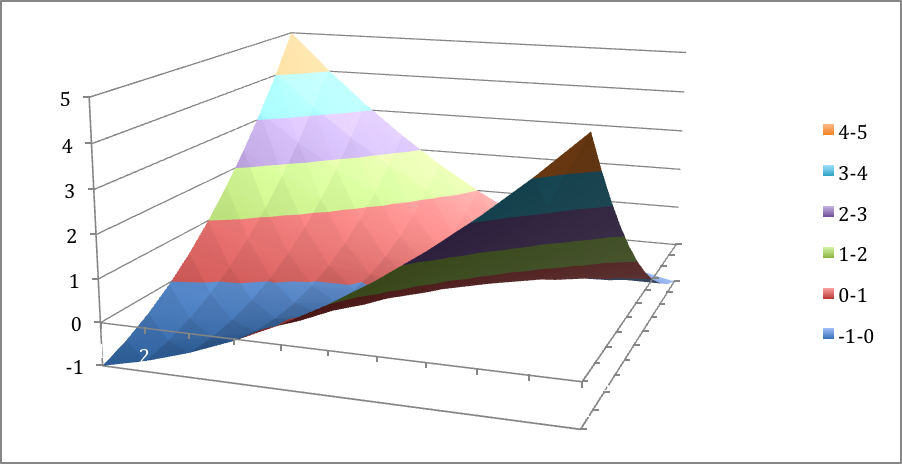
Looking at the graph, we see that this graph does not have a minimum.

Subsection 6.3.2 Second Partial Derivatives

With only first derivatives, we can just find the critical points. To check if a critical point is maximum, a minimum, or a saddle point, using only the first derivative, the best method is to look at a graph to determine the kind of critical point. For some applications we want to categorize the critical points symbolically.

With functions of one variable we used the second derivative to test if a critical point was a maximum or minimum. In the two variable case we need to define the second derivatives and use them to define the discriminant of a function to test if a critical point is a minimum, maximum, or saddle point. We first need to define second partial derivatives.

Second partials.

begin{equation*}
f_{ab}=(f_a )_b=frac{partial}{partial b}(frac{partial}{partial a} f)text{.}
end{equation*}

Note that (f_{xx}) is simply the old second derivative of the curve (f(x,y_0)) and (f_{yy}) is simply the old second derivative of the curve (f(x_0,y)text{.}) For functions with continuous second partial derivatives, the mixed partials, (f_{yx}) and (f_{xy}) are the same.

Example 6.3.5. Finding Second Partial Derivatives.

Find the second partial derivatives of

begin{equation*}
f(x,y)=x^2+ 3xy+5y^3-7x-11ytext{.}
end{equation*}

Solution.

We start by computing the first partial derivatives.

begin{align*}
f_x amp = frac{partial}{partial x} f(x,y)=2x+3y-7\
f_y amp = frac{partial}{partial y} f(x,y)=3x+15y^2-11text{.}
end{align*}

Then we compute the second partial derivatives.

begin{align*}
f_{xx} amp = frac{partial}{partial x} f_x=2\
f_{xy} amp = frac{partial}{partial y} f_x=3\
f_{yx} amp = frac{partial}{partial x} f_y=3\
f_{yy} amp = frac{partial}{partial y} f_y=30ytext{.}
end{align*}

As expected, the mixed partials are the same.

Subsection 6.3.3 Using the Discriminant to Test Critical Points

To test if a critical point is a maximum, minimum, or saddle point we compute the discriminant of the function.

Discriminant.

begin{equation*}
D(f(x,y))=f_{xx} f_{yy}-f_{xy}^2text{.}
end{equation*}

Example 6.3.6. Finding the Discriminant of a Function.

Find the discriminant of

begin{equation*}
f(x,y)=x^2+ 3xy+5y^3-7x-11ytext{.}
end{equation*}

Solution.

We have already computed the second partial derivatives.

begin{equation*}
f_xx=2,quad f_xy=3,quad f_yy=30ytext{.}
end{equation*}

Substituting into the formula,

begin{equation*}
D=(2)(30y)-3^2=60y-9text{.}
end{equation*}

Discriminant test.

Let ((a,b)) be a critical point of (f(x,y)text{.})

If (D(a,b)>0) and (f_{xx} (a,b)>0) then ((a,b)) is a local minimum of (f(x,y)text{.})

If (D(a,b)>0 ) and (f_{xx} (a,b)lt 0) then ((a,b)) is a local maximum of (f(x,y)text{.})

If (D(a,b)lt 0) then ((a,b)) is a saddle point of (f(x,y)text{.})

If (D(a,b)=0) we do not have enough information to classify the point.

Example 6.3.7. Using the Discriminant to Classify Critical Points.

Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.

p ({f_x}) ({f_y}) (f_{xx}) (f_{xy}) (f_{yy})
A 0 0 0 0 1
B 0 1 3 2 4
C 1 0 0 2 3
D 0 0 1 2 0
E 0 0 -1 2 3
F 0 0 -3 1 -2
G 0 0 3 3 3

Solution.

We need to compute the discriminant and apply the test.

p (f_x) (f_y) (f_{xx}) (f_{xy}) (f_{yy}) Discriminant Classification
A 0 0 0 0 1 0 Not enough information
B 0 1 3 2 4 8 Not a critical point
C 1 0 0 2 3 -4 Not a critical point
D 0 0 1 2 0 -4 Saddle point
E 0 0 -1 2 3 -7 Saddle point
F 0 0 -3 1 -2 5 Maximum
G 0 0 3 3 3 0 Not enough information

Example 6.3.8. Finding and Classifying Critical Points.

Let (f(x,y)=x^3-3x+y^3-3y^2text{.}) Find the critical points and classify them using the discriminant.

Solution.

We start by computing the first partial derivatives.

begin{align*}
f_x amp = 3x^2-3=3(x-1)(x+1)\
f_y amp = 3y^2-6y=3(y-2)(y)text{.}
end{align*}

Then we compute the second partial derivatives and the discriminant.

begin{equation*}
f_{xx}=6x,quad f_{xy}=0,quad f_{yy}=6y-6,quad D=(6x)(6y-6)-0^2=36xy-36xtext{.}
end{equation*}

We have critical points when both first partials are 0, so at ((1,2)text{,}) ((-1,2)text{,}) ((1,0)text{,}) and ((-1,0)text{.})

At ((1,2)text{,}) both (D) and (f_{xx}) are positive, so we have a local minimum.

At ((-1,2)) and ((1,0)text{,}) (D) is negative, so we have a saddle point.

At (((-1,0)text{,}) (D) is positive and (f_{xx}) is negative, so we have a local maximum.

Exercises 6.3.4 Exercises: Critical Points and Extrema Problems

Exercise Group.

For the given functions and region:

  • Find the partial derivatives of the original function.

  • Find any critical points in the region.

  • Produce a small graph around any critical point.

  • Determine if the critical points are maxima, minima, or saddle points.

1.

The function is (f(x,y)=x^2+2xy+4y^2+5x-6ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})

Solution.

  • begin{align*}
    f_x (x,y) amp = 2x+2y+5\
    f_y (x,y) amp = 2x+8y-6text{.}
    end{align*}

  • Set the partial derivatives equal to 0 and solve for (x) and (ytext{.})

    begin{align*}
    f_x (x,y) amp = 2x+2y+5=0\
    f_y (x,y) amp = 2x+8y-6=0text{.}
    end{align*}

    We can use either the method of substitution (solve for (x) or (y) in one equation and substitute into the other and solve), or method by elimination (multiply both equations by carefully chosen numbers and ass/subtract the equations from each other.)

    We will demonstrate method of elimination:

    begin{align*}
    -1×(2x+2y+5 amp = 0) amp text{gives }-2x-2y-5amp=0\
    1×(2x+8y-6 amp = 0) amp text{gives } 2x+8y-6amp =0text{.}
    end{align*}

    Adding the two equations gives (6y-11=0text{;}) hence, (y= 11/6text{.})

    Pick one of the equations to solve for x (it does not matter which one):

    begin{equation*}
    2x+2y+5=0 quad text{and }y= 11/6
    end{equation*}

    implies that (2x+2(11/6)+5=0) so (x= (2(11/6)+5)/(-2)=-13/3text{.})

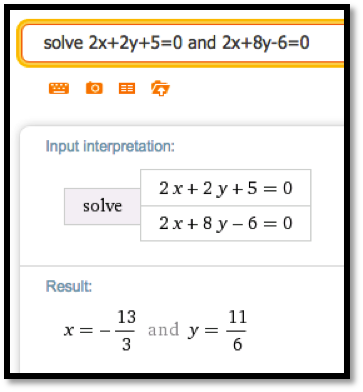
    We can also solve this system of equations using Wolfram Alpha:

  • The command in Wolfram Alpha is:

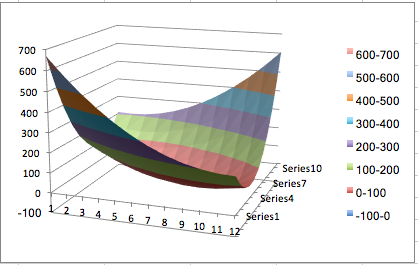
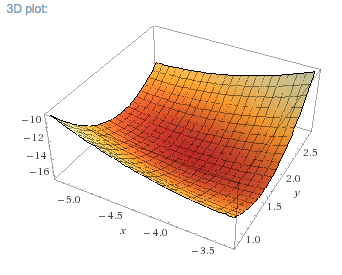
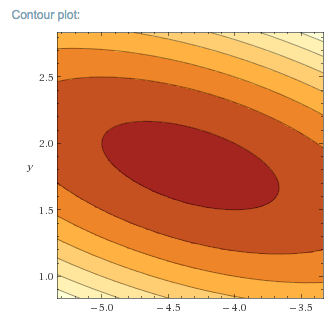
    It is worth looking at both the 3D Plot and the Contour Plot.

  • The 3D plot suggests a minimum, and this is confirmed by the contour plot which shows they typical view of a local minimum.

    As an alternative we can find the discriminant.

    begin{align*}
    f_{xx} (x,y) amp = 2\
    f_{xy} (x,y) amp = 2\
    f_{yy} (x,y) amp = 8\
    D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2=2*8-2^2=12>0text{.}
    end{align*}

    Since (Dgt 0) and (f_{xx} (x,y)gt 0) we have a local minimum.

2.

The function is (f(x,y)=x^2+7xy+2y^2+4x-3ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})

3.

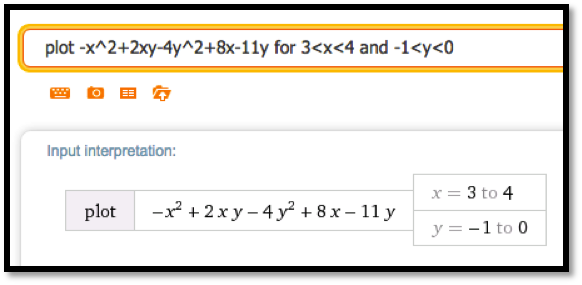
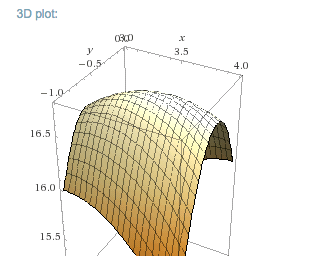
The function is (f(x,y)=-x^2+2xy-4y^2+8x-11ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})

Solution.

  • begin{align*}
    f_x (x,y) amp = -2x+2y+8\
    f_y (x,y) amp = 2x-8y-11text{.}
    end{align*}

  • Set the partial derivatives equal to 0 and solve for (x) and (ytext{.})

    begin{align*}
    f_x (x,y) amp = -2x+2y+8=0\
    f_y (x,y) amp = 2x-8y-11=0text{.}
    end{align*}

    Adding the equations (-6y-3=0text{,}) and so (y=-1/2text{.})

    Substituting in the first equation give (-2x+7=0text{,}) and so (x=7/2text{.})

    Hence we have a critical points at ((7/2,-1/2)text{.})

  • For ((x,y)= (2,1)text{:})

  • From the picture we conclude that the critical point is a maximum. As an alternative we can find the discriminant.

    begin{align*}
    f_{xx} (x,y) amp = -2\
    f_{xy} (x,y) amp = 2\
    f_{yy} (x,y) amp = -8\
    D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2=2*8-2^2=12gt 0text{.}
    end{align*}

    Since (Dgt 0) and (f_{xx} (x,y)lt 0) we have a local maximum.

4.

The function is (f(x,y)=x^3-12x+y^3-3ytext{,}) for the region (-10le xle 10text{,}) and (-10le yle 10text{.})

5.

The function is the revenue function for selling widgets and gizmos with demand price functions

begin{align*}
PriceGizmo amp = 25-frac{QuantityGizmo}{50}-frac{QuantityWidget}{200}\
PriceWidget amp = 30-frac{QuantityWidget}{45}-frac{QuantityGizmo}{300}
end{align*}

for the region (0le QuantityWidgetle 1500text{,}) and (0le QuantityGizmole 1500text{.})

Solution.

To solve this problem we will rename Gizmos (x) and Widgets (ytext{.}) This will make using Wolfram Alpha slightly easier, and symbol manipulation a tad more straight forward.

begin{align*}
PriceX amp = 25-frac{x}{50}-frac{y}{200}\
PriceY amp = 30-frac{y}{45}-frac{x}{300}\
revenue (x,y) amp =x*PriceX+y *PriceY\
amp =x left[25-frac{x}{50}-frac{y}{200}right]+yleft[30-frac{y}{45}-frac{x}{300}right]\
amp = frac{-36x^2-15xy+45000x-40y^2+54000y}{1800} text{.}
end{align*}

  • begin{align*}
    revenue_x (x,y)amp = frac{-24x-5y+1000}{600} \
    revenue_y (x,y)amp = frac{-3x-16y+10800}{360}
    end{align*}

  • Using WolframALpha, the critical point is at ((62000/123, 23800/41) approx (504, 580.5)text{.})

  • Using WolframAlpha we get:

  • From the picture we conclude that the critical point is a maximum.

    As an alternative we can find the discriminant.

    begin{align*}
    f_{xx} (x,y) amp = -frac{1}{25}\
    f_{xy} (x,y) amp = -frac{1}{120}\
    f_{yy} (x,y) amp = -frac{4}{25}\
    D amp = f_{xx} (x,y)f_{yy} (x,y)-f_{xy} (x,y)^2 gt 0text{.}
    end{align*}

    Since (Dgt 0) and (f_{xx} (x,y)lt 0) we have a local maximum.

6.

The function is the revenue function for selling widgets and gizmos with demand price functions

begin{align*}
PriceGizmo amp = 30(0.9)^{(QuantityGizmo/150) }-frac{QuantityWidget}{250}\
PriceWidget amp = 20(0.97)^{(QuantityWidget/50) }-frac{QuantityGizmo}{350}
end{align*}

for the region (0le QuantityWidgetle 1500text{,}) and (0le QuantityGizmole 1500text{.}) (Warning: There are several critical points.)

7.

Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.

p (f_x) (f_y) (f_{xx}) (f_{xy}) (f_{yy})
A 1 2 3 4 5
B 0 0 0 0 0
C 0 1 2 5 3
D 0 0 2 2 2
E 0 0 1 2 3
F 0 0 0 1 0
G 0 0 0 -1 0

Solution.

Add a column for D and classify.

p (f_x) (f_y) (f_{xx}) (f_{xy}) (f_{yy}) (D) Classification
A 1 2 3 4 5 -1 Not Critical
B 0 0 0 0 0 0 Not Enough Info
C 0 1 2 5 3 -19 Not Critical
D 0 0 2 2 2 0 Not Enough Info
E 0 0 1 2 3 -1 Saddle Point
F 0 0 0 1 0 0 Not Enough Info
G 0 0 0 -1 0 0 Not Enough Info

8.

Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify.

p (f_x) (f_y) (f_{xx}) (f_{xy}) (f_{yy})
A 1 2 3 4 5
B 0 0 0 0 0
C 0 1 2 5 3
D 0 0 2 2 2
E 0 0 1 2 3
F 0 0 0 1 0
G 0 0 0 -1 0

9.

Using polynomials of the form (f(x,y)=ax^3+bx^4+cy^3+dy^4text{,}) produce a function that has a critical point at ((0, 0)text{,}) of each type.

  1. A local maximum.

  2. A local minimum.

  3. A saddle point where the function f(x,0) has a local maximum and f(0,y) has a local minimum.

  4. A saddle point where the function f(x,0) and f(0,y) both have inflection points.

Solution.

It helps to consider the question with only one variable.

(f(x)=ax^3) has an inflection point at (x=0) and neither a max nor a minimum.

(f(x)=ax^4) has minimum at (x=0) if (agt 0) and a maximum if (alt 0text{.})

Since all terms are of degree at least three, all second partial derivatives are zero at the origin, so the discriminant test fails.

  1. A local maximum: ((x,y) = -x^4-y^4text{.}) Both (x^4) and (y^4) are nonnegative, so the function is negative everywhere except at the origin where it is 0.

  2. A local minimum: (f(x,y)= x^4+y^4text{.}) Both (x^4) and (y^4) are nonnegative, so the function is positive everywhere except at the origin where it is 0.

  3. A saddle point where the function (f(x,0)) has a local maximum and (f(0,y)) has a local minimum: ((x,y)= -x^4+y^4text{.})

  4. A saddle point where the function (f(x,0)) and (f(0,y)) both have inflection points: (f(x,y)= x^3+y^3)

You have attempted of activities on this page.

external/Examples/Section-6-3-Examples.xlsx

Источник

Понравилась статья? Поделить с друзьями:
  • Поиск минимальной даты excel
  • Поиск минимального значения при условии в excel
  • Поиск массива в массиве vba excel
  • Поиск максимума в таблице excel
  • Поиск максимальных значений excel vba