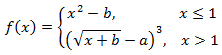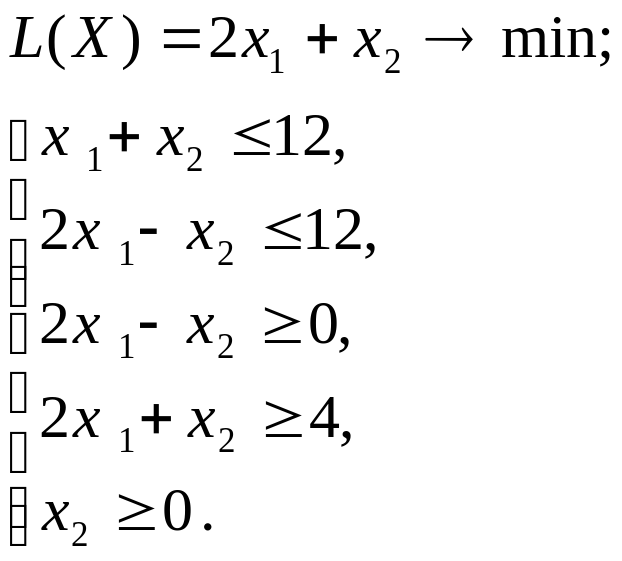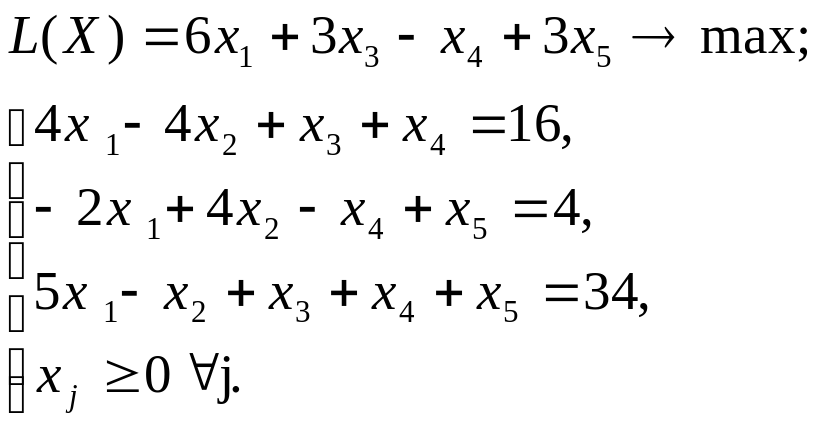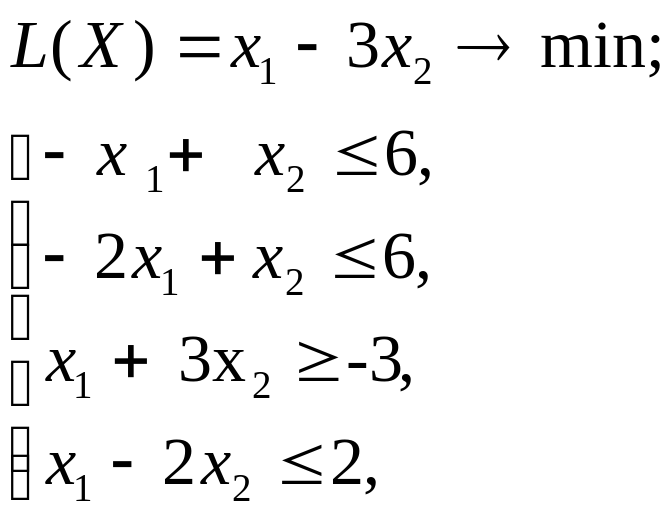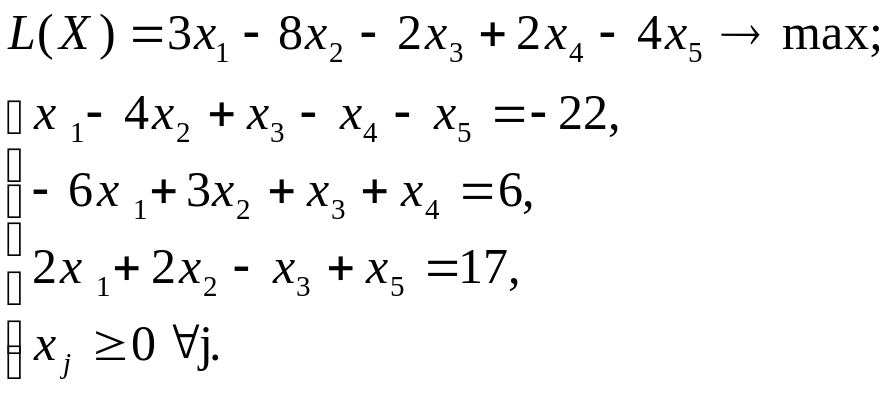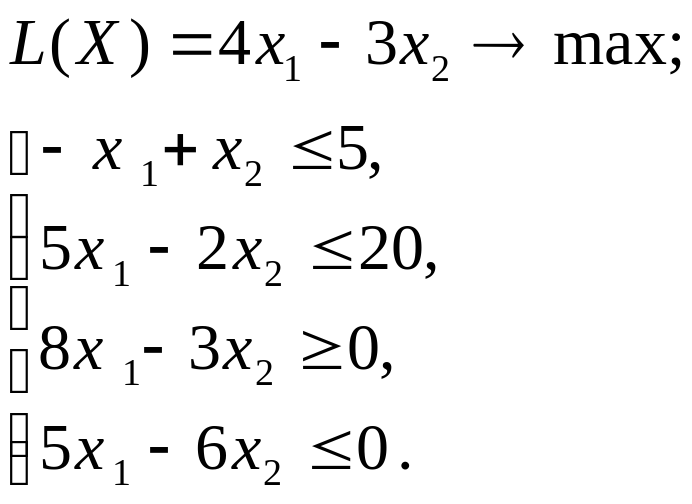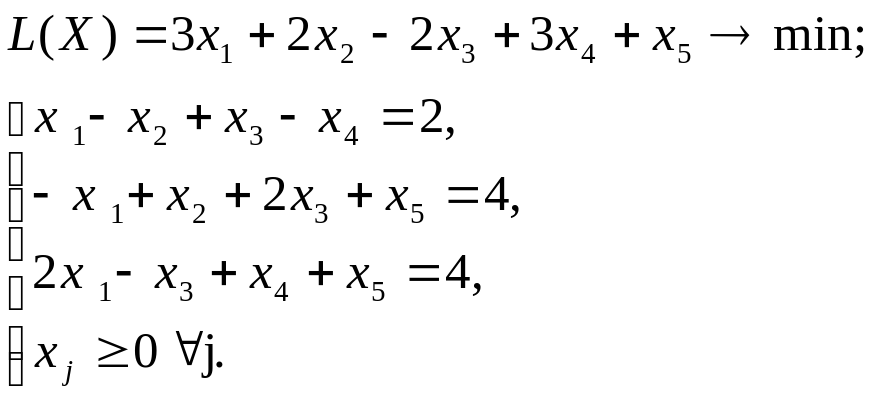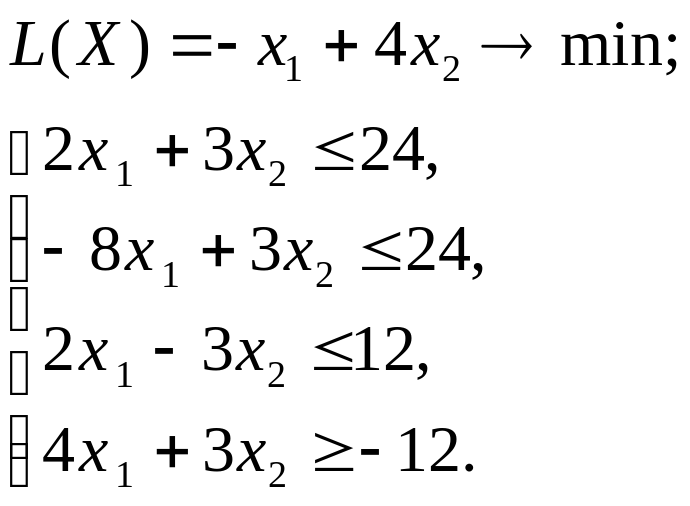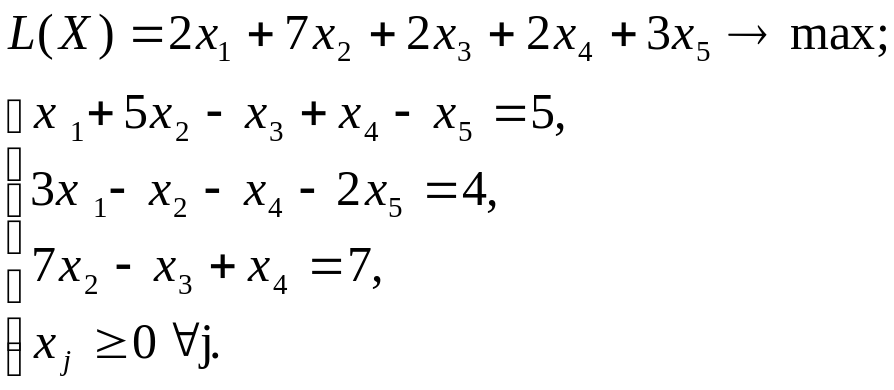Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/
Применение табличного процессора Microsoft Excel для
графического решения уравнений n-ой степени
·
Москалёва
Елена Александровна
·
Разделы: Математика, Информатика
Из курса математики
известно, что корнями уравнения являются значения точек пересечения графика
функции с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями
будут координаты точек пересечения графиков функций. Этот метод нахождения
корней уравнения называется графическим. Мы уже знаем, что с помощью EXCEL
можно строить практически любые графики. Воспользуемся этими знаниями для
нахождения корней системы уравнений:
Преобразуем данную систему в приведенную:
Для оценки решений воспользуемся диаграммой, на которой
отобразим графики обеих функций. Сначала построим таблицу:
Первая строка – строка заголовков.
При заполнении столбца А: в ячейку А2 заносится начальное
значение аргумента Х = – 10, для автоматического заполнения всего столбца в
ячейку А3 занести формулу “= А2 + 1” и скопировать ее до ячейки А22.
При заполнении столбца В: в ячейку В2 заносится формула “= А2 *
А2”, которая затем копируется до ячейки В22.
При заполнении столбца С: в ячейку С2 заносится формула “ = 2 *
А2 + 9”, и также копируется до С22
Рисунок 1
С помощью Мастера диаграмм построим в одной координатной
плоскости графики заданных функций для первоначальной оценки решений/
Рисунок 2
На диаграмме видно, что оба графика имеют точки пересечения –
координаты этих точек и есть решения системы. Так как шаг изменения аргумента
достаточно велик, то мы получим приближенные значения решений.
Рисунок 3
Уточним их, построив два графика в интервалах от – 3 до 0, где
находится первое решение, и от 3 до 5, где находится второе решение. Составим
новые таблицы. Для первого решения – рисунок 4, для второго – рисунок 5.
Рисунок 4
Рисунок 5
Для более точного построения мы уменьшили шаг изменения
аргумента. Решением нашей системы будут координаты точек пересечения графиков:
Х1 = – 2,2; Y1 =
4,6; Х2 = 4,2; Y2 =
17,4. Как вы уже поняли, графическое решение системы дает приблизительные результаты.
Это можно сделать, построив график и определив координаты точек его пересечения
с осью OX, либо построив два графика: Y = X3;
Y = 2X2 + 4X – 12 и определив точки их пересечения.
Рисунок 6
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.
Решение (1 ряд данных)
Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .
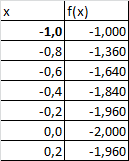
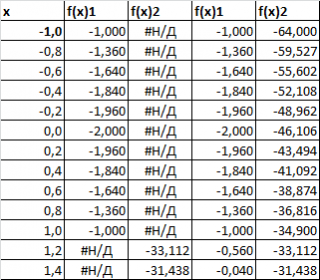
Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.
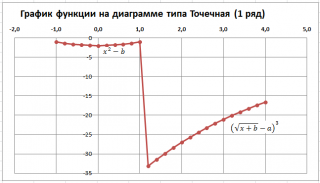
Чтобы построить диаграмму типа Точечная:
- выделите любую ячейку таблицы;
- во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .
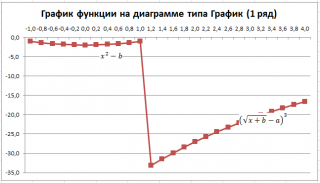
Чтобы построить диаграмму типа График:
- выделите любую столбец f(x) вместе с заголовком;
- во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .
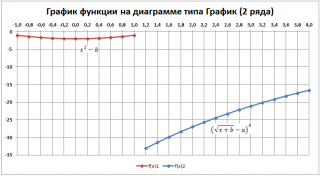
У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .
Решение (2 ряда данных)
Создадим другую таблицу с исходными данными в файле примера, лист График :
Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.
У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Практическая работа «Графический метод решения уравнений в Excel»
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Просмотр содержимого документа
«Практическая работа «Графический метод решения уравнений в Excel»»
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с 2 и движение по оси OY можно считать равноускоренным;
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:


3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Использование графических возможностей Excel для решения математических задач
методическая разработка по алгебре на тему
Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Скачать:
| Вложение | Размер |
|---|---|
| ispolzovanie_graficheskih_vozmozhnostey_excel.doc | 292 КБ |
Предварительный просмотр:
Использование графических возможностей Excel для решения математических задач
Возможности ЭТ Microsoft Excel весьма многогранны. Всем известно, что Excel является мощным вычислительным инструментом, позволяющим производить простые и сложные расчеты в различных областях человеческой деятельности: математике, физике, инженерных науках, экономике, технологии. Но помимо осуществления расчетов возможно применение ЭТ Excel и в других областях. Данная статья посвящена использованию Excel для построения графиков элементарных и сложных функций, изучение графических способов решения уравнений и систем уравнений, а также построения трехмерных поверхностей.
Построение графиков элементарных функций в Excel
Для построения графика функции в Excel прежде всего надо построить таблицу, в одну колонку которой занести значение аргумента функции, а в другую — значение функции при заданном значении аргумента.
Для этого в рабочем поле Excel в ячейках 1-й строки напечатаем наименование работы, во 2-ой строке – заголовок «Расчетная таблица», в 3-й – наименование колонок (столбцов) расчетной таблицы.
Начиная с ячейки А5 произведем формирование значение таблицы. Для этого необходимо в ячейку А5 ввести первое значение аргумента вычисляемой функции из заданного диапазона значений аргументов. В ячейку А6 введем второе значение аргумента, отличающееся от первого на заданный шаг изменения аргумента. Далее пометим эти ячейки и, ухватив указателем мыши квадратную точку в правом нижнем углу помеченной области ячеек, движением вниз по столбцу с нажатой левой кнопкой мыши рассчитаем значения аргумента с шагом, который вычислил Excel по указанным первым двум ячейкам (рис.1).
Пометив ячейку В5, вычисляем первое значении функции, используя Мастер формул, и если функция проста, то записываем формулу вручную. Запись формулы в ячейку вручную следует начать со знака «=» и закончить нажатием клавиши Enter. Затем, используя квадратную точку помеченной ячейки, копируем формулу в остальные ячейки.
Для построения графика заданной функции по построенной таким образом таблице необходимо воспользоваться Мастером диаграмм. Следуя указаниям Мастера, выбираем форму диаграммы Точечная.
Построение графика функции y=ax 2 +bx+c.
Построим график указанной функции при а-2, b=5, c=-10. Для построения графика функции будем изменять аргумент в диапазоне -5≤x≤2,5 с шагом 0,5.
Выполним последовательно все действия, описанные выше, сравнивая получаемый результат с рис.1.
Лабораторная работа №2
ЛАБОРАТОРНАЯ РАБОТА №2
“ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ” 2.1. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения задач линейного программирования графическим методом.
2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи и найдите оптимальное решение графическим методом.
2. Найдите оптимальное решение задачи в Excel.
3. Оформите отчет по лабораторной работе, который должен содержать:
-
титульный лист;
-
исходные данные варианта;
-
решение задачи;
-
результаты решения задачи.
2.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП ГРАФИЧЕСКИМ МЕТОДОМ
Рассмотрим пример нахождения оптимального решения графическим методом для следующей задачи линейного программирования:
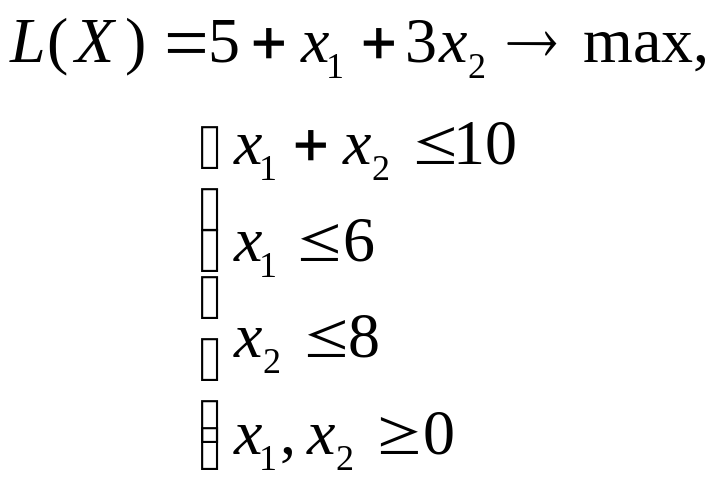
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. В столбце А, начиная с ячейки А2, задаем последовательность значений переменной x1 как арифметическую прогрессию с первым членом, равным нулю, разностью 0,2, предельным значением 6.
2. В ячейке В2 вводим формулу =10-А2 и копируем ее в столбце В. Прямые х1=6, х2=8 зададим позже, как границы рисунка.
3. Вводим в ячейку С2 формулу линии уровня =($D$2-5-A2)/3 и копируем ее в столбце С.
4. В ячейке D2 вводим значение 0.
5. Выделяем диапазон А2:С32 и «Мастером диаграмм» строим точечную диаграмму:
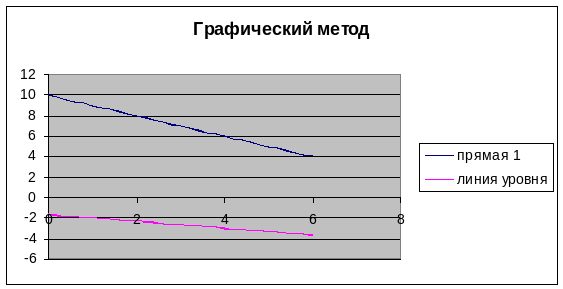
6. Убираем лишнее через контекстное меню:
Командами Формат оси Шкала открываем диалоговое окно:
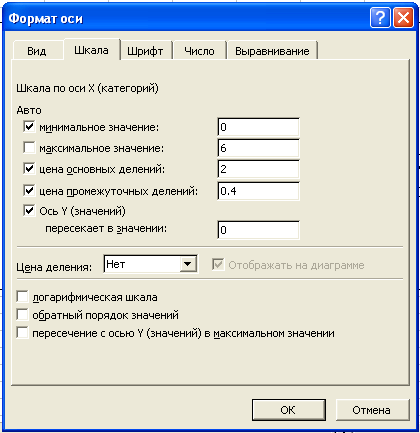
Устанавливаем в нем максимальное значение: 6, нажимаем ОК. Аналогично по оси Y задаем минимальное значение 0, максимальное значение 8.
Приводим диаграмму к виду, показанному на рисунке:
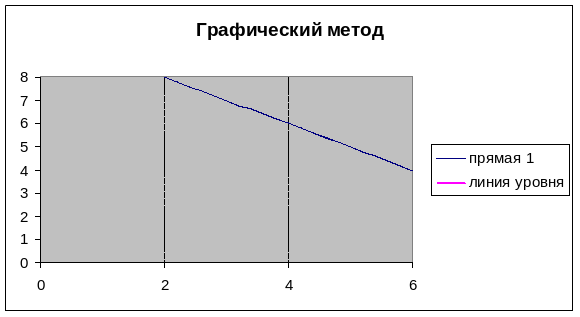
7. Изменяя значения ячейки D2, передвигаем линию уровня в сторону выхода из области допустимых решений:
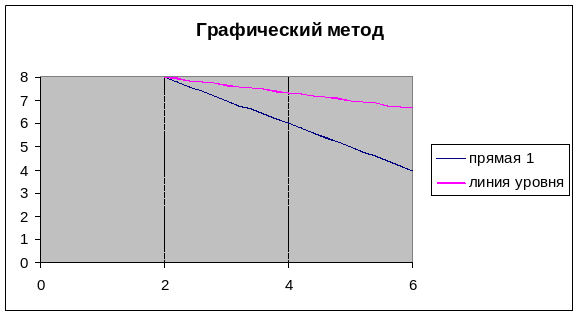
Из диаграммы видно, что точкой выхода линии уровня из многоугольника допустимых решений является точка (2; 
Графическим методом можно решить задачи ЛП, записанные в каноническом виде и удовлетворяющие условию , где n – число неизвестных системы ограничений; r – ранг системы векторов условий.
Рассмотрим пример решения задачи ЛП:
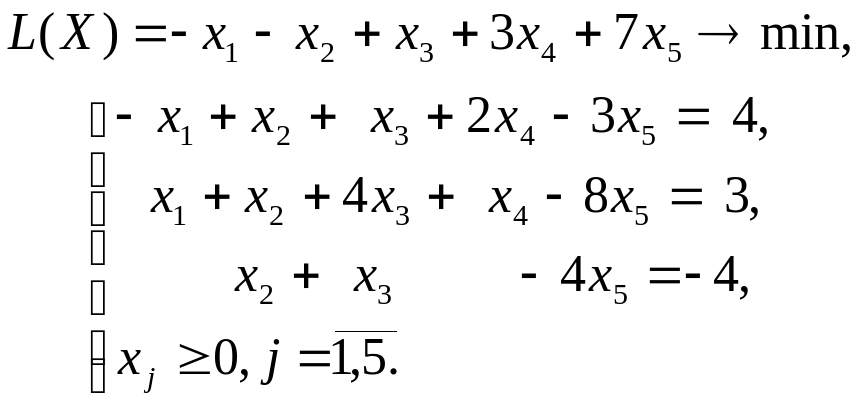
Графический метод применим, так как . Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной.
Введем расширенную матрицу системы ограничений и коэффициенты целевой функции в диапазон B2:G5:

В ячейке В7 зададим формулу =B2/$B$2 и методом «протаскивания» маркера заполнения скопируем ее в ячейки С7:G7:
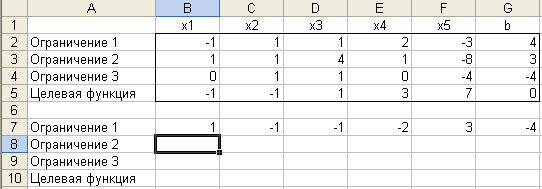
Тем самым первая строка расширенной матрицы системы ограничений разделена на -1 и выделен разрешающий элемент 1.
Замечание. Если в диапазоне В7:G7 окажутся результаты в форме десятичных дробей, то откройте контекстное меню и в диалоговом окне «Формат ячеек» установите формат числа «Дробный», со знаменателем до двух (или трех) цифр.
Далее в ячейку В8 вводим формулу =B3-B$7*$B3. Копируем ее, методом «протаскивания» маркера заполнения, в остальные ячейки диапазона С8:G8, делаем такие же элементарные преобразования диапазонов (строк) В4:G4 и В5:G5, получаем нули ниже разрешающего элемента:
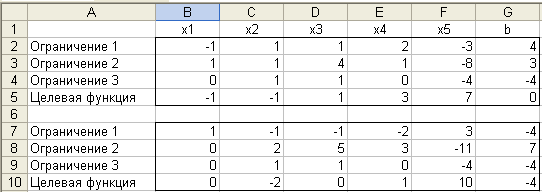
В ячейку С13 вводим формулу =C8/$C$8 и методом «протаскивания» маркера заполнения копируем ее в остальные ячейки диапазона В13:G13, что дает:
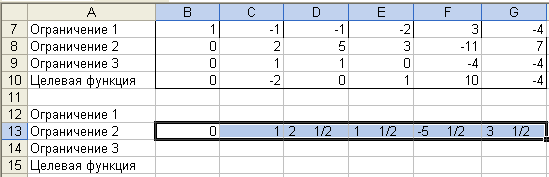
В ячейке С14 задаем формулу =C9-C$13*$C9 и копируем ее в остальные ячейки диапазона В14:G14. Далее проводим аналогичные элементарные преобразования диапазонов В12:G12 и В15:G15:
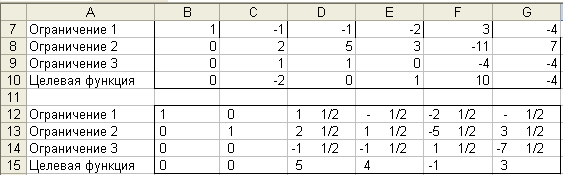
Повторяя алгоритм, приходим к окончательному результату:
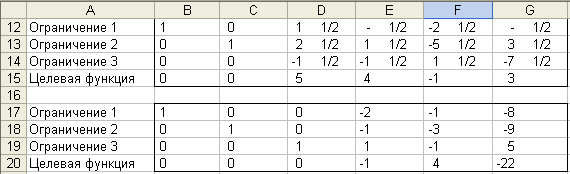
Задача ЛП после преобразований имеет вид:
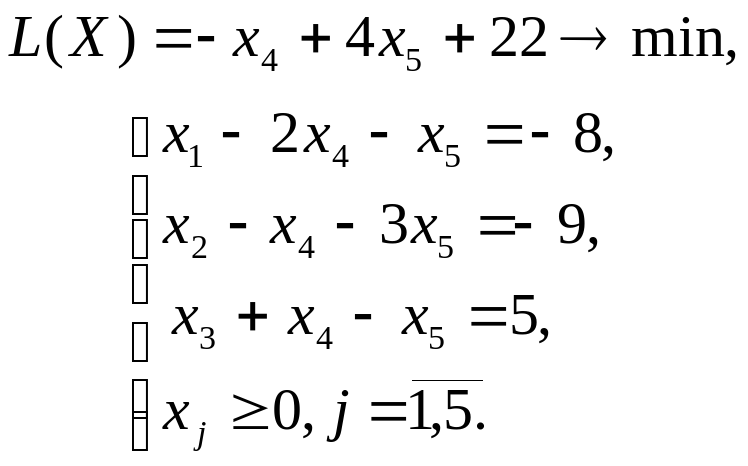
Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные х1, х2, х3 и заменим знак равенства знаками неравенства «», получим вспомогательную задачу ЛП с двумя переменными
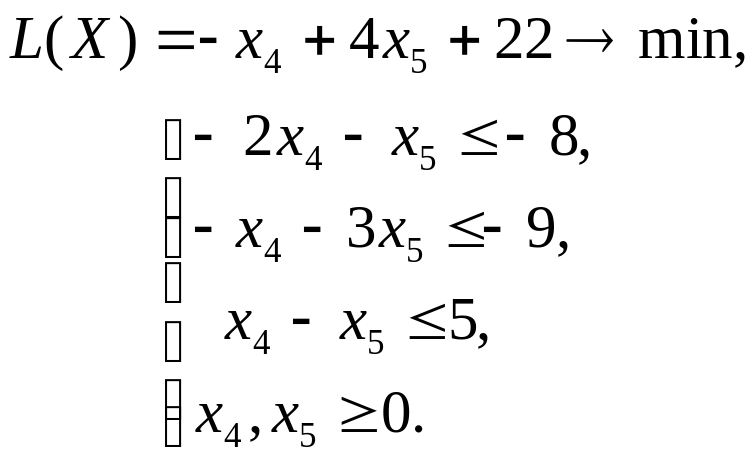
Далее она решается аналогично, как в первом примере, графическим методом.
2.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Каковы основные этапы решения задач ЛП графическим методом?
2. Как определить, какая полуплоскость отвечает линейному неравенству?
3. Что называется областью допустимых решений?
4. Какая линия называется линией уровня?
5. Как определить максимальное и минимальное значения линейной целевой функции в области допустимых решений?
6. Какие случаи возможны при решении задачи ЛП графическим методом?
7. В каких случаях задачу линейного программирования можно решить графическим методом?
2.5. ВАРИАНТЫ
Используя MS Excel, найти решение графическим методом для задачи ЛП, соответствующей заданному варианту (табл.3.1).
Таблица 3.1
Варианты задач к лабораторной работе №3
|
№ варианта |
Математическая модель |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
9
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений
















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):