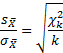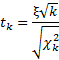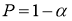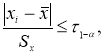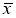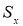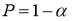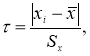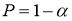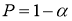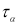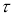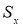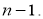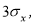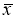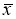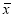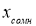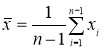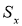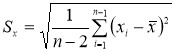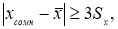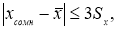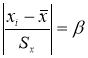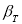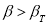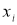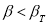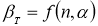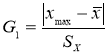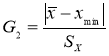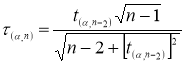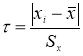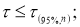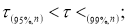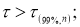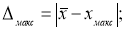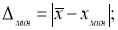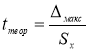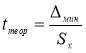Погрешность по стьюденту в excel - Word и Excel - помощь в работе с программами

Содержание

Определение термина
Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
Вопросы и ответы

Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.

Определение термина

Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.

Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.

Способ 1: Мастер функций

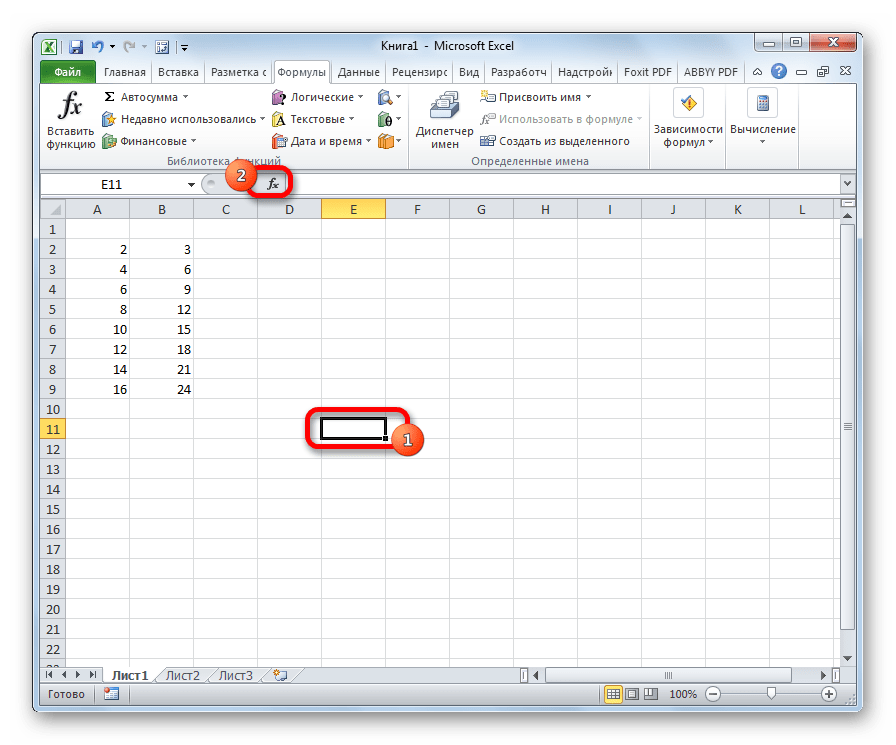
Проще всего производить вычисления данного показателя через Мастер функций.

Строим таблицу с двумя рядами переменных.

Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.

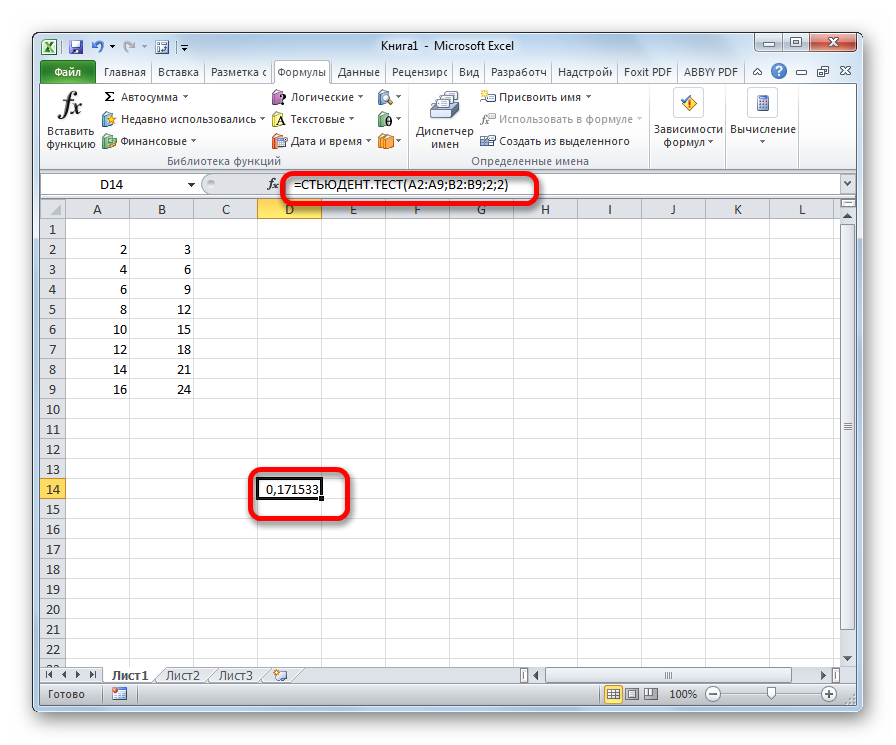
После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».

Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.

В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.

Способ 2: работа со вкладкой «Формулы»

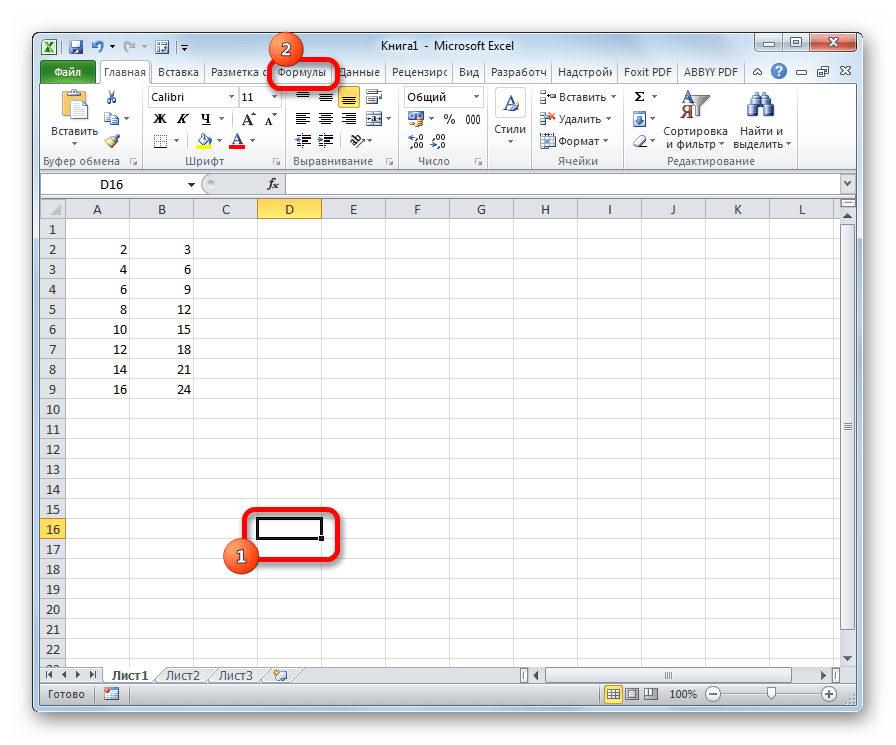
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.

Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».

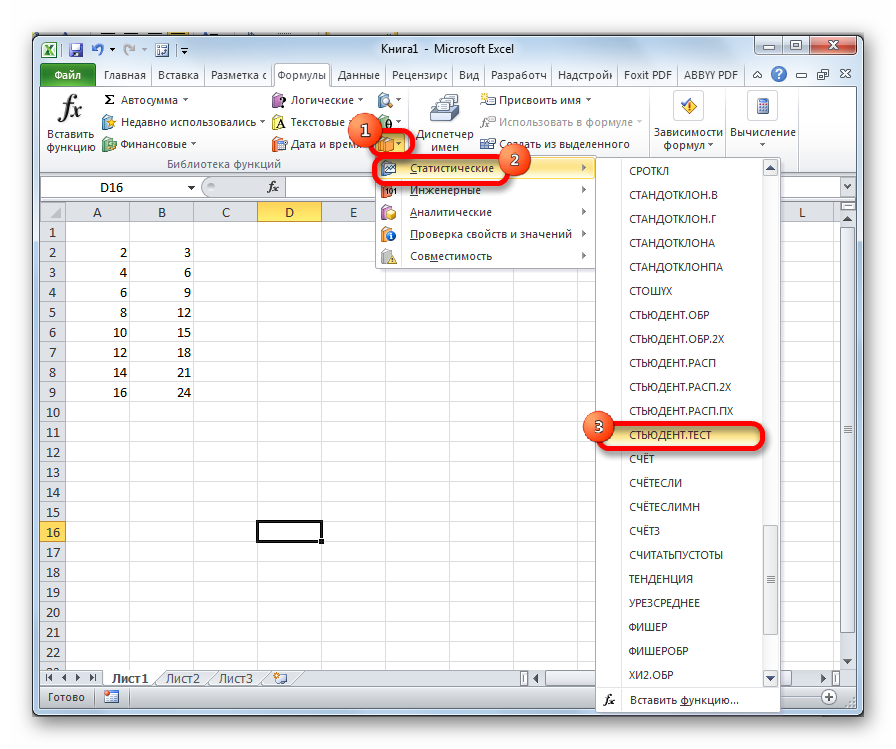
Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».

Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.

Способ 3: ручной ввод

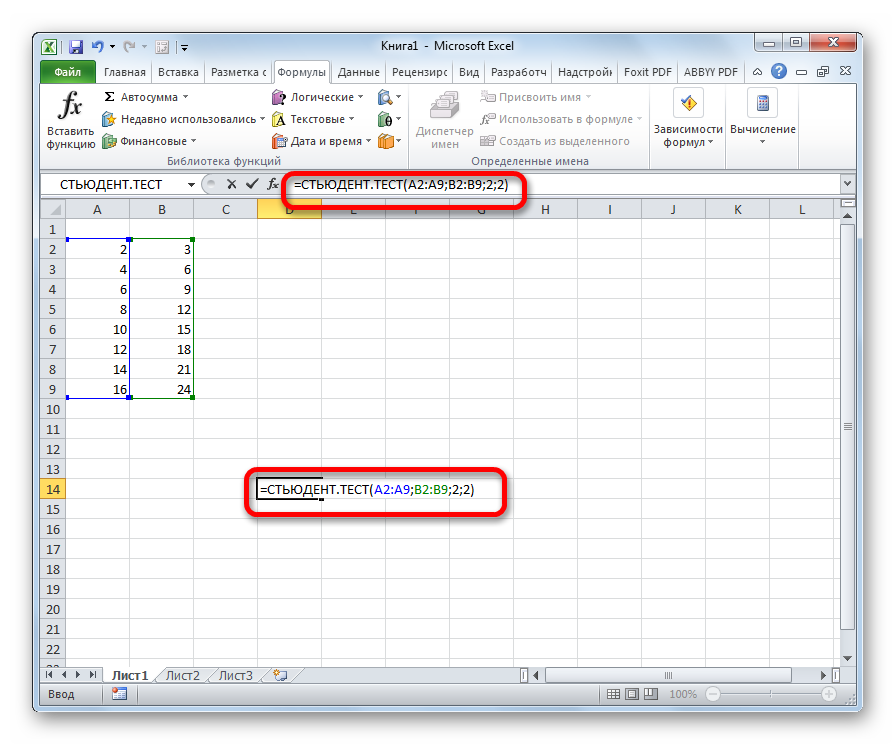
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:

= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)

Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.

После того, как данные введены, жмем кнопку Enter для вывода результата на экран.

Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).

Распределение Стьюдента

Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ². Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией

Тогда случайная величина

имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.

Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:

где

Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96s_x̅. Другими словами, являются ли распределения случайных величин

эквивалентными.

Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.

Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.

Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.

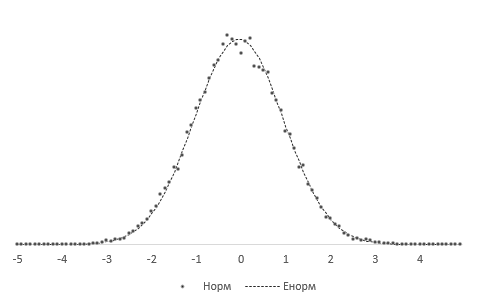
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:

Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.

Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.

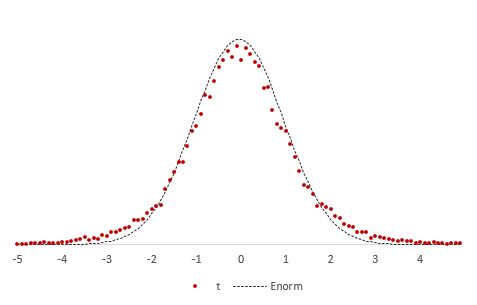
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.

Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.

Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».

У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина

зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.

Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:

1. средняя X̅ и выборочная дисперсия s² являются независимыми величинами;

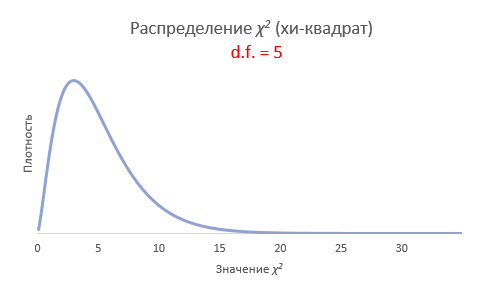
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ²(хи-квадрат) с таким же количеством степеней свободы, т.е.

где k – количество степеней свободы (на английском degrees of freedom (d.f.))

Вернемся к распределению средней. Разделим числитель и знаменатель выражения

на σ_X̅. Получим

Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.

Тогда исходное выражение примет вид

Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.

Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.

Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин

где ξ распределена по стандартному нормальному закону, а χ²_k подчиняется распределению χ² c k степенями свободы.

Таким образом, формула критерия Стьюдента для средней арифметической

есть частный случай стьюдентова отношения

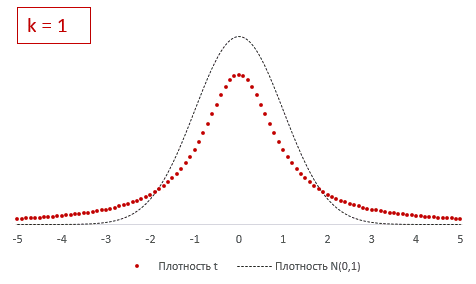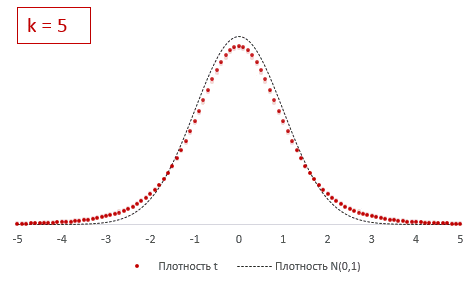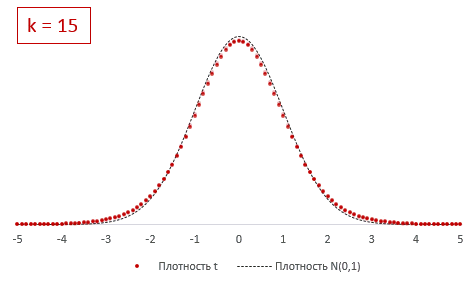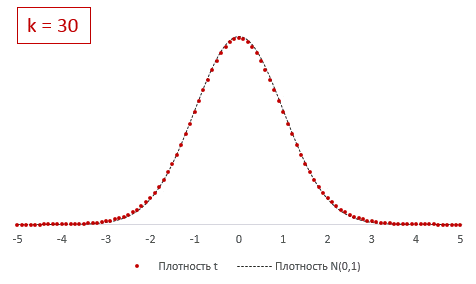
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.

При k > 30 t-критерий практически не отличается от стандартного нормального распределения.

В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.

Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.

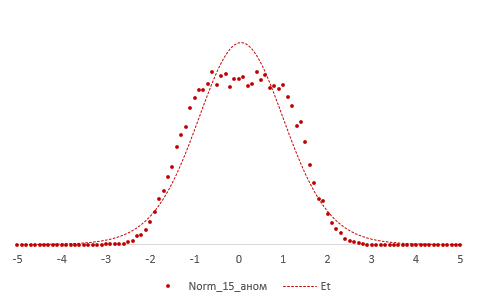
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

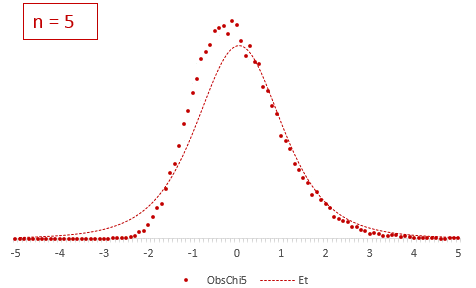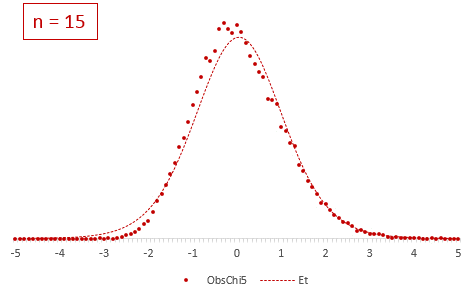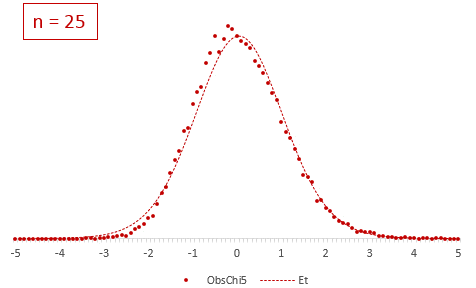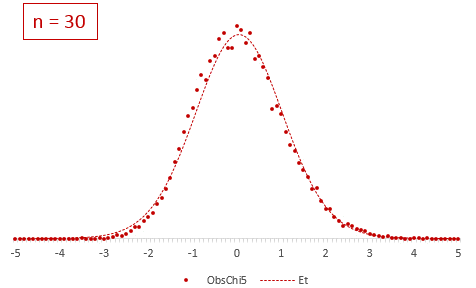
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.

Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.

Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel

В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.

СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.

СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).

СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.

СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.

СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058

СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.

ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.

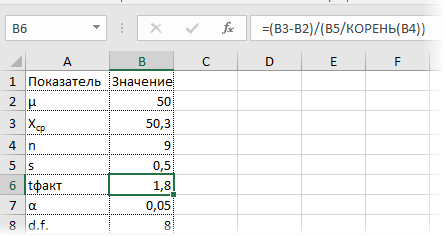
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.

Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.

Краткое условие в обще принятых обозначениях выглядит так.

H₀: μ = 50 кг

H_a: μ ≠ 50 кг

Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.

Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:

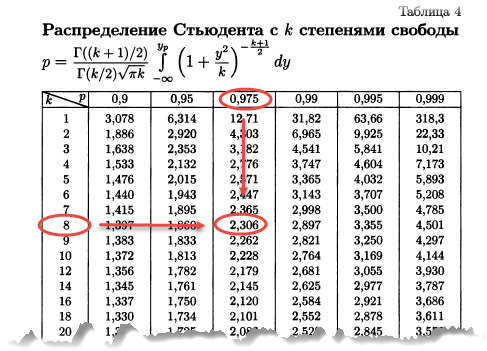
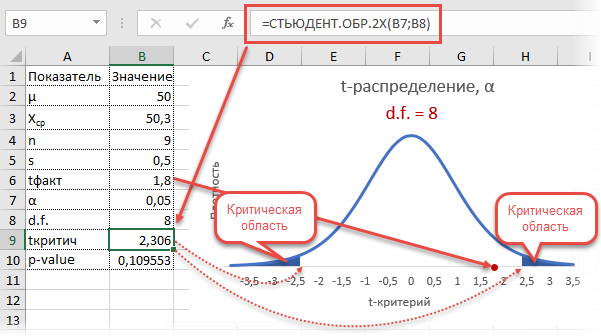
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.

Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H₀ о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.

Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.

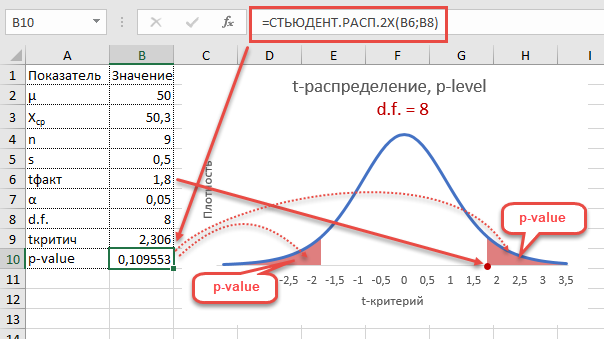
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.

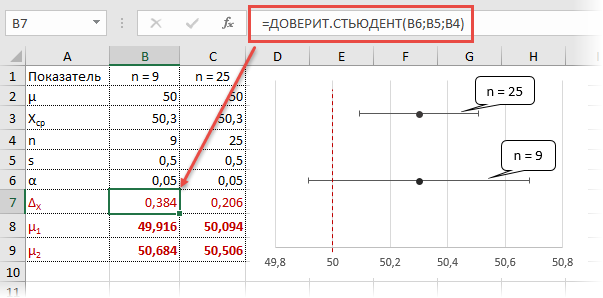
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.

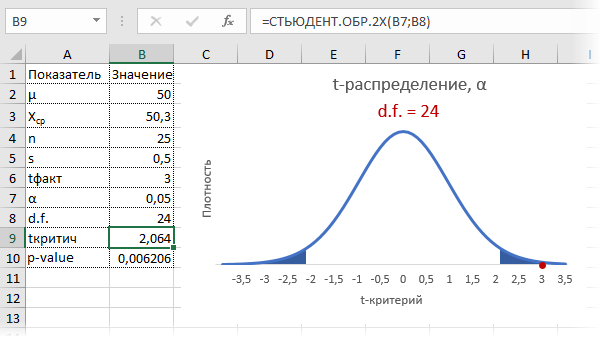
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.

Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Скачать файл с примером.

Всего доброго, будьте здоровы.

Поделиться в социальных сетях:

Источник

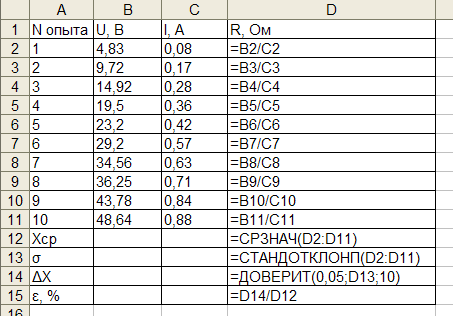
С использованием встроенных функций
Excel расчет доверительного
интервала проводится следующим образом.

1) Рассчитывается среднее значение

=СРЗНАЧ(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
среднее.

2) Рассчитывается стандартное отклонение

=СТАНДОТКЛОНП(число1; число2;
…)
число1, число2,
… — аргументы, для которых вычисляется
стандартное отклонение.

3) Рассчитывается абсолютная погрешность

=ДОВЕРИТ(альфа ;станд_откл;размер)

альфа —
уровень значимости используемый для
вычисления уровня надежности.

(,
т.е.

означает надежности);
станд_откл
— стандартное отклонение, предполагается
известным;
размер — размер выборки.

Лабораторная работа
1

Тема: Обработка прямых
измерений в Excel (2 часа ).

Задание:
Обработать заданный набор экспериментальных
данных методом Стьюдента, построить
экспериментальные кривые методом
наименьших квадратов.

Пример расчета	Используемуе формулы

Для построения графика используем
мастер диаграмм.

Расчет
погрешности при косвенных измерениях

При измерении
величины косвенным методом предполагается,
что известна математическая модель

связывающая искомую
величину

с величинами
,
измеряемыми непосредственно. Далее
предполагается, выполнена обработка
всех прямых измерений, т. е. определены
доверительные интервалы для величин
:

Погрешность величины у
определяется по формуле:

где
.

Расчет косвенной
погрешности в Maple

Рассмотрим расчет погрешности на примере
функции одной переменной

,
где

Таким образом, найден доверительный
интервал величины
.

В случае, если определяемая в косвенном
измерении величина, является функцией
нескольких переменных, рекомендуем:

вычисление погрешности оформить в виде
процедуры

>dy:=proc(y, dx) ……код
процедуры
…… end proc

Код процедуры учащийся должен составить
самостоятельно на основе примера,
рассмотренного выше.

параметр dx считать массивом из N
переменных
для определения списка аргументов и
их количества величины y
можно использовать операторы op() и
nops():

Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).

Задание:
Написать программу нахождения погрешности
косвенного измерения в среде Maple.

Выполнение задания

1. Ввести выборку значений измеряемых
величин в матричном виде

2. Определить размерность выборки

3. Задать уровень значимости и определить
степень доверия:

4. Вычислить среднее значение выборки
измеряемой величины:

a) с помощью операций
суммирования

б) с помощью встроенных функций

5. Вычислить значения среднеквадратичного
отклонения.

а) с помощью операций суммирования

в) с помощью встроенных функций

6. Вычислить доверительный интервал:

а) Задать коэффициент Стьюдента для
данных размерности выборки и степени
доверия:

б) Вычислить абсолютную случайную
погрешность

в) Вычислить верхнюю и нижнюю границы
доверительного интервала.

7. Учесть приборные погрешности:

а) Задать приборные погрешности

б) Вычислить абсолютную случайную
погрешность с учетом приборных
погрешностей

8. Представить результат:

а) Абсолютная погрешность:

б) Относительная погрешность:

в) Верхняя и нижняя границы доверительного
интервала.

Примечание. Вычисления провести:

а) в обычном виде,

(См. Дов_инт_01)

б) с помощью операций суммирования,

(См. Дов_инт_02)

в) с помощью встроенных функций.

(См. Дов_инт_03)

2. Вычисление косвенных погрешностей

Выполнение задания

1. Провести аналитические вычисления:

а) Ввести выражение для исследуемой
функции:

б) Получить выражение для среднего
значения величины исследуемой функции:

в) Получить выражение косвенной
погрешности исследуемой функции в общем
виде и для значения :

1. Провести численные вычисления:

а) Ввести численные значения постоянных,

б) Ввести средние значения и доверительные
интервалы переменных,

в) Вычислить относительные погрешности
переменных,

г) Вычислить среднее значение исследуемой
функции:

г) Вычислить косвенную погрешность
(абсолютную погрешность) исследуемой
функции

г) Вычислить относительную погрешность
исследуемой функции

в) Вычислить верхнюю и нижнюю границы
доверительного интервала исследуемой
функции:

(См. Косв_погр).

3. Построение графиков. Полиномиальная
регрессия

Выполнение задания

1. Ввод выборок значений величин :

2. Вычислить верхнюю и нижнюю границы
доверительного величины Y:

3. Полиномиальная регрессия:

а) Задать степень полинома k:

б) Задать число точек данных:

в) Задать регрессионную зависимость:

г) Определить коэффициенты уравнения
регрессии

4. Построить графики:

а) точечных график данных,

б) кривую регрессии,

в) доверительные интервалы величины Y.

(См. Постр_граф).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.

Ключевые слова:

грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.

Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.

Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.

На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.

Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят

,

однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.

Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:

Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).

В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.

В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].

Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.

Задаются вероятностью

Р

или уровнем значимости

α

(

) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».

Проверяемая гипотеза состоит в утверждении, что результат наблюдения

x
_i

не содержит грубой погрешности, т. е. является одним из значений случайной величины

x

с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
_max
или наименьший xmin из результатов наблюдений.

Предложим для практического использования наиболее простые методы отсева грубых погрешностей.

Если в распоряжении экспериментатора имеется выборка небольшого объема

n

≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:

(1)

где

x

_i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения

и среднеквадратичного отклонения

;

τ

_1-
_p
— табличное значение статистики

τ

, вычисленной при доверительной вероятности

Таким образом, для выделения аномального значения вычисляют значение статистики,

(2)

которое затем сравнивают с табличным значением

τ
_1-α

:

τ

≤

τ
_1-α

. Если неравенство

τ

≤

τ

_1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.

Квантили распределения статистики

τ

при уровнях значимости

α

= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности

=

0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости

α

= 0,05 (результат получается с 95 %-й доверительной вероятностью).

Функции распределения статистики

τ

определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности

или уровне значимости

α

можно для чисел измерения п = 3–25 найти те наибольшие значения

которые случайная величина

может еще принять по чисто случайным причинам.

Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения

и среднеквадратичного отклонения

для выборки нового объема

Таблица 1

Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]

n	Уровень значимости α	n	Уровень значимости α
0,10	0,05	0,025	0,01	0,10	0,05	0,025	0,01
3	1,41	1,41	1,41	1,41	15	2,33	2,49	2,64	2,80
4	1,65	1,69	1,71	1,72	16	2,35	2,52	2,67	2,84
5	1,79	1,87	1,92	1,96	17	2,38	2,55	2,70	2,87
6	1,89	2,00	2,07	2,13	18	2,40	2,58	2,73	2,90
7	1,97	2,09	2,18	2,27	19	2,43	2,60	2,75	2,93
8	2,04	2,17	2,27	2,37	20	2,45	2,62	2,78	2,96
9	2,10	2,24	2,35	2,46	21	2,47	2,64	2,80	2,98
10	2,15	2,29	2,41	2,54	22	2,49	2,66	2,82	3,01
11	2,19	2,34	2,47	2,61	23	2,50	2,68	2,84	3,03
12	2,23	2,39	2,52	2,66	24	2,52	2,70	2,86	3,05
13	2,26	2,43	2,56	2,71	25	2,54	2,72	2,88	3,07
14	2,30	2,46	2,60	2,76

В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.

Критерий «трех сигм» применяется для случая, когда измеряемая величина

x

распределена по нормальному закону. По этому критерию считается, что с вероятностью

Р

= 0,9973 и значимостью

α

= 0,0027 появление даже одной случайной погрешности, большей, чем

маловероятное событие и ее можно считать промахом, если

−

x
_i

> 3

S
_x

, где

S
_x

_—

оценка среднеквадратического отклонения (СКО) измерений. Величины

и

S
_x

вычисляют без учета экстремальных значений

x
_i

. Данный критерий надежен при числе измерений

n

≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при

6 <

n

≤100 она равна 4

S
_x

; при 100 <

n

≤1000 − 4,5

S
_x

; при 1000 <

n

≤10000–5

Sx

. Данное правило также используется только при нормальном распределении.

Практические вычисления проводят следующим образом [5, с. 65]:

Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
Вычисляют среднее арифметическое значение выборки

без учета сомнительного значения

измеряемой величины.

(3)

Вычисляют оценку СКО выборки

без учета сомнительного значения

измеряемой величины.

(4)

Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.

Если

то сомнительное значение отбрасывают, как промах.

Если

то сомнительное значение оставляют как равноправное в ряду наблюдений.

Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.

Критерий В. И. Романовского применяется, если число измерений невелико,

n

≤ 20. При этом вычисляется соотношение

(5)

где

— результат, вызывающий сомнение,

— коэффициент, предельное значение которого

определяют по таблице 2. Если

, сомнительное значение

исключают («отбрасывают») как промах. Если

,

сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].

Таблица 2

Значение критерия Романовского

Уровень значимости, α	Число измерений, n
n = 4	n = 6	n = 8	n = 10	n = 12	n = 15	n = 20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.

Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.

(6)

Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев

t

-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.

Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.

Если G1

GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2

GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.

Отсев грубых погрешностей можно производить и для больших выборок (

n

= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].

Известно, что критическое значение

τ

_p
(

p

— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента

t
_{α, n-2}

[6, с. 26]:

(7)

Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (

n

= 100):

1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;

2)

по формуле

вычисляют значение статистики

τ

;

3)

по таблице (или в программе Excel) находят процентные точки

t

-распределения Стьюдента

t

₍

_α,
_n
_-2

₎
:

t

₍₉₅

_{%, 98)}
= 1,6602, и

t
₍

₉₉

_{%, 98)}
= 3,1737;

По предыдущей формуле в программе Excel вычисляют соответствующие точки

t

₍₉₅

_{%, 100)}
= 1,66023и

t

₍₉₉

_{%, 100)}
=3,17374.

Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.

Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)

Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.

Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.

Пример 1.

Имеется выборка из 100 шт. резисторов с номинальным сопротивлением

R

_н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.

Заносим данные измерений в таблицу Excel в ячейки В2:В101
Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)

Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда

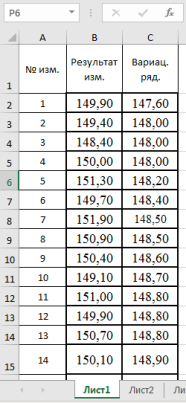
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).

Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки

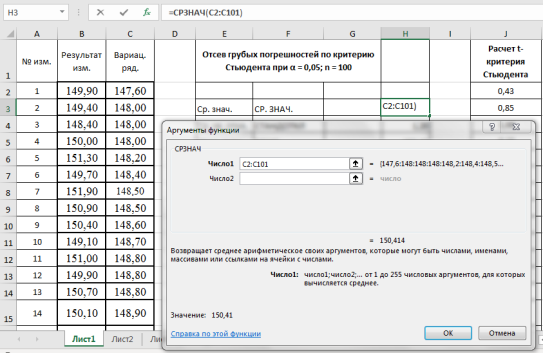
Находим среднеквадратическое отклонение —

S

_x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).

Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения

Находим максимальное значение в выборке —

x

_макс
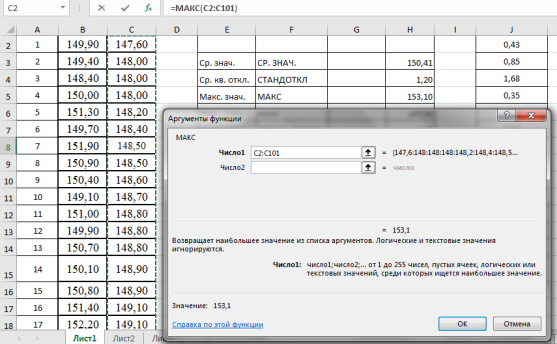
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).

Рис. 4. Фрагмент диалогового окна при нахождении максимального значения

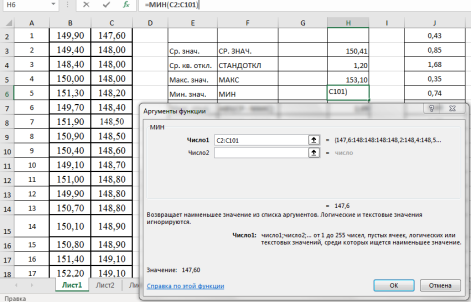
Находим минимальное значение в выборке —

x

_мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).

Рис. 5. Фрагмент диалогового окна при нахождении минимального значения

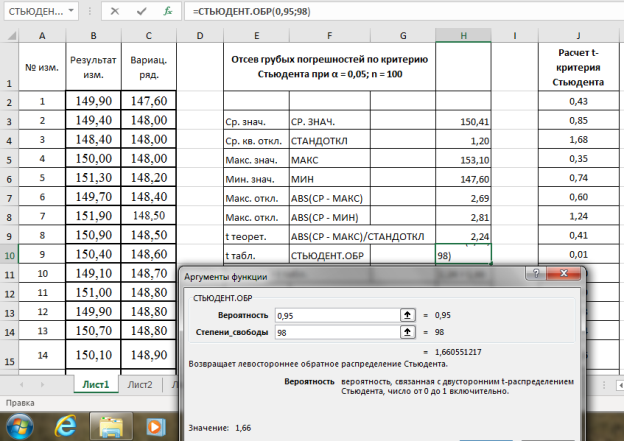
Находим максимальное и минимальное отклонения — Δ
_макс
и Δ
_мин
. Вводим в ячейки Н7 и Н8 формулы:

Находим теоретическое значение —

t

_теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу

. и

Находим табличное значение

t

_табл.
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (

n

-2) — 98, результат в ячейке Н10–1,66 (рис. 6).

Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента

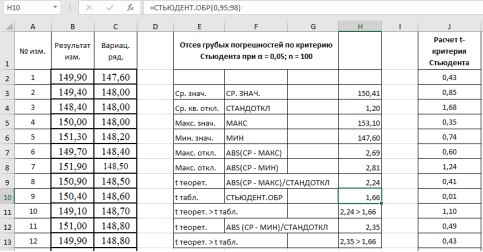
Сравниваем теоретическое значение

t

_теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:

t

_табл
.= 1,6605.
Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).

Рис. 7. Фрагмент диалогового окна при окончательном анализе данных

Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.

Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений

n

= 20, β
_табл
= 2,78 (из таблицы 2).

Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского

Выводы

Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.

Литература:

1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.

2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.

3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.

4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.

5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.

6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.

Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.

Источник

Автор: Цыбенко Валерия Александровна

Место работы/учебы (аффилиация): Государственный университет управления, г. Москва, студент

В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов. Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.

Ключевые слова: грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.

Источник

Определение термина

Способ 1: Мастер функций

Способ 2: работа со вкладкой «Формулы»

Способ 3: ручной ввод

Еще статьи по данной теме:

Помогла ли Вам статья?

Распределение Стьюдента

Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

Лабораторная работа 2 Тема: Обработка косвенных измерений в Maple (4 часа).