Функция ПИРСОН (вводить следует PEARSON на английском) предназначена для вычисления коэффициента корреляции Пирсона r. Данную функцию используют в работе в том случае, когда необходимо отразить степень линейной зависимости между двумя массивами данных. В Excel имеется несколько функций с помощью которых можно получить такой же результат, однако универсальность и простота функции Пирсон делают выбор в ее пользу.
Как работает функция ПИРСОН в Excel?
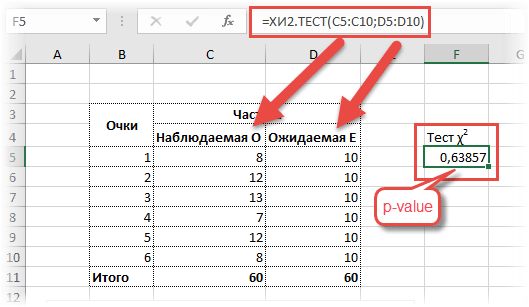
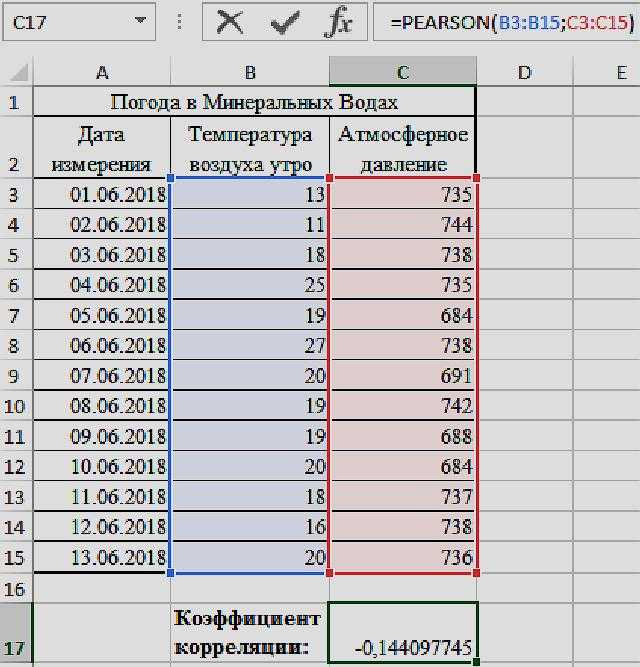
Рассмотрим пример расчета корреляции Пирсона между двумя массивами данных при помощи функции PEARSON в MS EXCEL. Первый массив представляет собой значения температур, второй давление в определенный летний период. Пример заполненной таблицы изображен на рисунке:
Задача следующая: необходимо определить взаимосвязь между температурой и давлением за июнь месяц.
Пример решения с функцией ПИРСОН при анализе в Excel
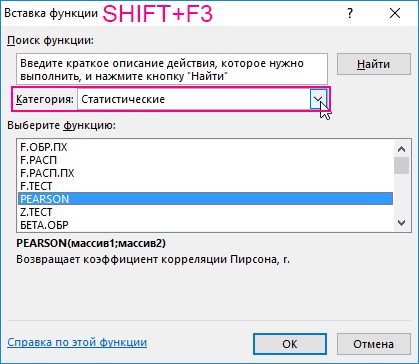
- Выберем ячейку С17 в которой должен будет посчитаться критерий Пирсона как результат и нажмем кнопку мастер функций «fx» или комбинацию горячих клавиш (SHIFT+F3). Откроется мастер функций, в поле Категория необходимо выбрать «Статистические». В списке статистических функций выбрать PEARSON и нажать Ok:
- В меню аргументов выбрать Массив 1, в примере это утренняя температура воздуха, а затем массив 2 – атмосферное давление.
- В результате в ячейке С17 получим коэффициент корреляции Пирсона. В нашем случае он отрицательный и приблизительно равен -0,14.
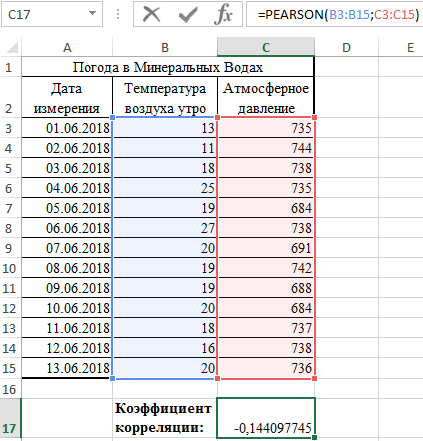
Данный показатель -0,14 по Пирсону, который вернула функция, говорит об неблагоприятной зависимости температуры и давления в раннее время суток.
Функция ПИРСОН пошаговая инструкция
Коэффициент корреляции является самым удобным показателем сопряженности количественных признаков.
Задача: Определить линейный коэффициент корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курящих людей. Первый массив х — представляет собой возраст курящего, второй массив y представляет собой количество сигарет, выкуренных в день.
- Выберем ячейку В4 в которой должен будет посчитаться результат и нажмем кнопку мастер функций fx (SHIFT+F3).
- В группе Статистические выберем функцию PEARSON.
- Выделим Массив 1 – возраст курящего, затем Массив 2 – число сигарет, выкуренных в день.
- Нажмем кнопку ОК и увидим критерий нормального распределения Пирсона в ячейке В4.

Таким образом, по результату вычисления статистическим выводом эксперимента выявлена отрицательная зависимость между возрастом и количеством выкуренных сигарет в день.
Корреляционный анализ по Пирсону в Excel
Задача: школьникам были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Пример решения: представим исходные данные в виде таблицы:
- Переходим курсором в ячейку F2. Откроем мастер функций fx (SHIFT+F3) или вводим вручную.
- Выберем функцию PEARSON.
- Выделим мышкой Массив1, затем Массив 2.
- Нажмем ОК и в ячейке F2 получим критерий согласия Пирсона.
Интерпретация результата вычисления по Пирсону
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 – являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 – следовательно, произошла ошибка в вычислениях.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.
Скачать примеры функции ПИРСОН для корреляции в Excel
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. Эти положения очень важно четко усвоить для правильной интерпретации полученной корреляционной зависимости.
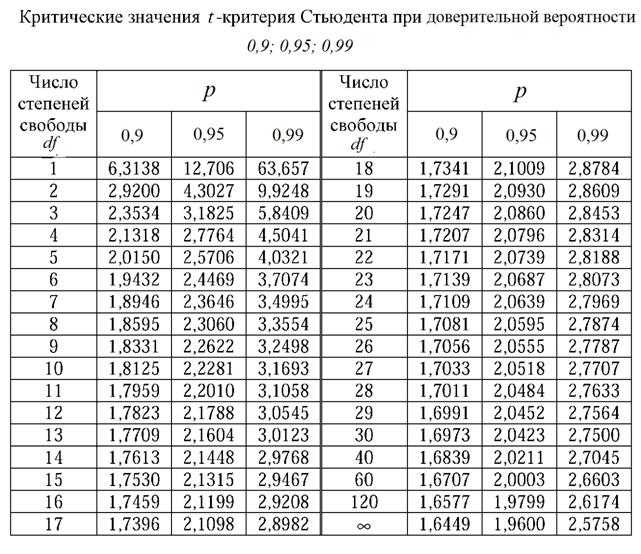
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции Пирсона (r) — безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
Синтаксис
PEARSON(массив1;массив2)
Аргументы функции PEARSON описаны ниже.
-
Массив1 Обязательный. Множество независимых значений.
-
Массив2 Обязательный. Множество зависимых значений.
Замечания
-
Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если массив1 или массив2 пуст, либо число точек данных в этих массивах не совпадает, функция PEARSON возвращает значение ошибки #Н/Д.
-
Коэффициента корреляции Пирсона (r) вычисляется по следующей формуле:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (результат) |
Результат |
|
=PEARSON(A3:A7;B3:B7) |
Коэффициент корреляции Пирсона для приведенных выше данных (0,699379) |
0,699379 |
Нужна дополнительная помощь?
Correlations are important in many areas of science. Although correlation doesn’t equal causation, it’s often the first step to understanding the true relationship between two variables and can give a valuable hint that there is a causal relationship somewhere.
Learning to calculate a correlation is crucial, and you can easily find the “r value” in Excel using either built-in functions or by working through the calculation in pieces using the more basic functions of the program. The simplest way is using the built-in function, but understanding the calculation is helpful if you ever need to use a different program to find it.
What Is Pearson’s Correlation Coefficient?
Pearson’s correlation coefficient is a simple way of calculating the degree of correlation between two variables, returning a value (called r) ranging from −1 to 1. A perfect correlation (r = 1) between two variables would be where an increase in one variable by a certain amount leads to a correspondingly-sized increase in the other, or vice-versa.
A perfect negative correlation (r = −1) is basically the same, except an increase in one variable leads to a correspondingly-sized decrease in the other. Finally, no correlation whatsoever means there is no relationship at all between two things.
In practice, you’ll almost never see a perfect correlation, and most values will be some decimal value between −1 and 1. So when you find the Pearson r in Excel, the result will usually be some decimal value, where the magnitude of the number tells you the strength of the correlation between your variables.
Pearson Correlation in Excel
The easiest method for finding the Pearson correlation in Excel is using the built-in “Pearson” function or (equivalently) the “Correl” function. The function has a simple syntax: PEARSON(array 1, array 2).
In short, you just need two arrays of values (i.e. columns of results, for example, age and blood pressure arranged so there is a row for each individual patient) that are equal in length, then type “=PEARSON(” into an empty cell, followed by the range of values for the first array, a comma, then the range of values for the second. Then you close out the brackets, hit “Enter” and it will return the r value.
As always, you can highlight the values you want to search for correlations with your mouse or by navigating to the relevant cells with the arrow keys on your keyboard.
You can also use the “Correl” function, which performs the same calculation as “Pearson” and on versions of Excel from 2003 onward, leads to the exact same result. However, if you have an older version of Excel, you should use the “Correl” function because there can be rounding errors with “Pearson.”
Finding Pearson’s r “By Hand”
You can also calculate the r value in Excel in the more traditional method but with the help of the automatic calculations from the program. First, put the values for your variables (which can be referred to as x and y for clarity) in two columns, then create three more columns: xy, x2 and y2. Now multiply each value in the x column by the y column in the xy column (using the cell numbers in the calculation so you can drag it down for the rest of the column), square the x values for the next column, and square the y values for the final one.
Create a “sum” row underneath your data, and take the sum of all the values for each column. You can then use the formula to calculate your r value:
Here, n is the number of pairs of values you have. You can follow this through in pieces: Take the number of pairs of values, multiply it by the sum of your xy column, and then subtract the product of the sums of the x and y values.
Then, multiply the sum of your x2 column by n, subtract the sum of your x column squared, do the same thing for y and multiply these together, then take the square root of the whole thing. Finally, divide the first result by the second to get your r value.
Функция PEARSON возвращает коэффициент корреляции Пирсона
Описание функции PEARSON
Возвращает коэффициент корреляции Пирсона (r) — безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
Синтаксис
=PEARSON(массив1; массив2)Аргументы
искомое_значениеискомое_значение
Обязательный. Множество независимых значений.
Обязательный. Множество зависимых значений.
Замечания
- Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
- Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
- Если массив1 или массив2 пуст, либо число точек данных в этих массивах не совпадает, функция PEARSON возвращает значение ошибки #Н/Д.
- Коэффициента корреляции Пирсона (r) вычисляется по следующей формуле:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Home » Misc » Критерий пирсона в excel
Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel
Функция ПИРСОН (вводить следует PEARSON на английском) предназначена для вычисления коэффициента корреляции Пирсона r. Данную функцию используют в работе в том случае, когда необходимо отразить степень линейной зависимости между двумя массивами данных. В Excel имеется несколько функций с помощью которых можно получить такой же результат, однако универсальность и простота функции Пирсон делают выбор в ее пользу.
Как работает функция ПИРСОН в Excel?
Рассмотрим пример расчета корреляции Пирсона между двумя массивами данных при помощи функции PEARSON в MS EXCEL. Первый массив представляет собой значения температур, второй давление в определенный летний период. Пример заполненной таблицы изображен на рисунке:
Задача следующая: необходимо определить взаимосвязь между температурой и давлением за июнь месяц.
Пример решения с функцией ПИРСОН при анализе в Excel
- Выберем ячейку С17 в которой должен будет посчитаться критерий Пирсона как результат и нажмем кнопку мастер функций «fx» или комбинацию горячих клавиш (SHIFT+F3).
Откроется мастер функций, в поле Категория необходимо выбрать «Статистические». В списке статистических функций выбрать PEARSON и нажать Ok:
- В меню аргументов выбрать Массив 1, в примере это утренняя температура воздуха, а затем массив 2 – атмосферное давление.
- В результате в ячейке С17 получим коэффициент корреляции Пирсона. В нашем случае он отрицательный и приблизительно равен -0,14.
Данный показатель -0,14 по Пирсону, который вернула функция, говорит об неблагоприятной зависимости температуры и давления в раннее время суток.
Функция ПИРСОН пошаговая инструкция
Коэффициент корреляции является самым удобным показателем сопряженности количественных признаков.
Задача: Определить линейный коэффициент корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курящих людей. Первый массив х — представляет собой возраст курящего, второй массив y представляет собой количество сигарет, выкуренных в день.
- Выберем ячейку В4 в которой должен будет посчитаться результат и нажмем кнопку мастер функций fx (SHIFT+F3).
- В группе Статистические выберем функцию PEARSON.
- Выделим Массив 1 – возраст курящего, затем Массив 2 – число сигарет, выкуренных в день.
- Нажмем кнопку ОК и увидим критерий нормального распределения Пирсона в ячейке В4.
Таким образом, по результату вычисления статистическим выводом эксперимента выявлена отрицательная зависимость между возрастом и количеством выкуренных сигарет в день.
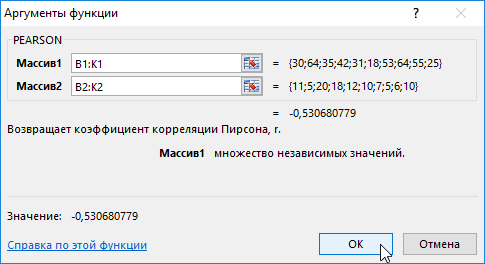
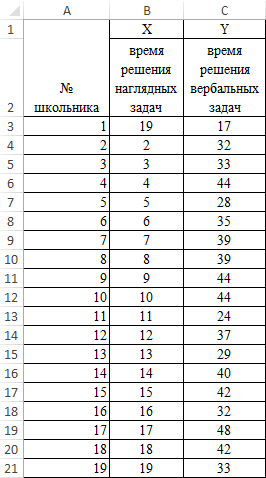
Корреляционный анализ по Пирсону в Excel
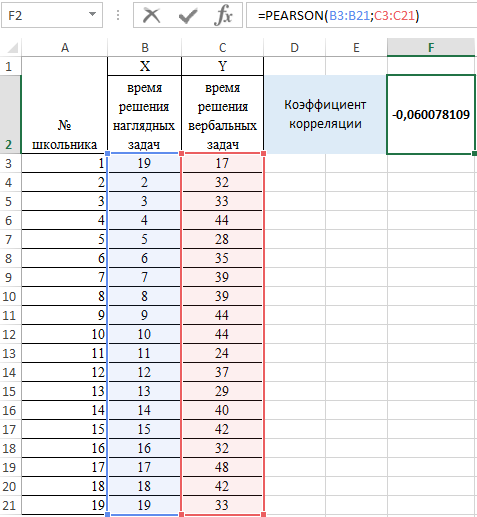
Задача: школьникам были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли взаимосвязь между временем решения этих задач?
Пример решения: представим исходные данные в виде таблицы:
- Переходим курсором в ячейку F2. Откроем мастер функций fx (SHIFT+F3) или вводим вручную.
- Выберем функцию PEARSON.
- Выделим мышкой Массив1, затем Массив 2.
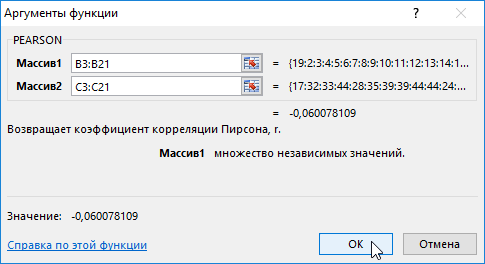
- Нажмем ОК и в ячейке F2 получим критерий согласия Пирсона.
Интерпретация результата вычисления по Пирсону
Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 – являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 – следовательно, произошла ошибка в вычислениях.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными.
Скачать примеры функции ПИРСОН для корреляции в Excel
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. Эти положения очень важно четко усвоить для правильной интерпретации полученной корреляционной зависимости.
Функция ПИРСОН — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции Пирсона (r) — безразмерный индекс в интервале от -1,0 до 1,0 включительно, который отражает степень линейной зависимости между двумя множествами данных.
Синтаксис
PEARSON(массив1;массив2)
Аргументы функции PEARSON описаны ниже.
Замечания
-
Аргументы должны быть либо числами, либо содержащими числа именами, массивами или ссылками.
-
Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Если массив1 или массив2 пуст, либо число точек данных в этих массивах не совпадает, функция PEARSON возвращает значение ошибки #Н/Д.
-
Коэффициента корреляции Пирсона (r) вычисляется по следующей формуле:
где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (результат) |
Результат |
|
=PEARSON(A3:A7;B3:B7) |
Коэффициент корреляции Пирсона для приведенных выше данных (0,699379) |
0,699379 |
функция PEARSON — служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Дополнительно.
В этой статье описаны синтаксис формулы и использование функции PEARSON в Microsoft Excel.
Описание
Возвращает коэффициент корреляции момента продукта Пирсона, r, безразмерный индекс, который находится в диапазоне от -1,0 до 1,0 включительно и отражает степень линейной зависимости между двумя наборами данных.
Синтаксис
ПИРСОН (массив1, массив2)
Синтаксис функции ПИРСОН имеет следующие аргументы:
Замечания
-
Аргументы должны быть либо числами, либо именами, константами массива или ссылками, содержащими числа.
-
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако включаются ячейки с нулевым значением.
-
Если массивы1 и массив2 пусты или содержат разное количество точек данных, PEARSON возвращает значение ошибки #Н/Д.
-
Формула для коэффициента корреляции момента продукта Пирсона, r, выглядит следующим образом:
, где x и y — выборочные значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
|
Данные |
||
|
Независимые значения |
Зависимые значения |
|
|
9 |
10 |
|
|
7 |
6 |
|
|
5 |
1 |
|
|
3 |
5 |
|
|
1 |
3 |
|
|
Формула |
Описание (Результат) |
Р результат |
|
=ПИРСОН(A3:A7;B3:B7) |
Коэффициент корреляции момента продукта Пирсона для наборов данных выше (0,699379) |
0,699379 |
Функция ПИРСОН для расчета коэффициента корреляции Пирсона в Excel
Функция ПИРСОН используется для расчета коэффициента корреляции Пирсона r.
Как PEARSON работает в Excel?
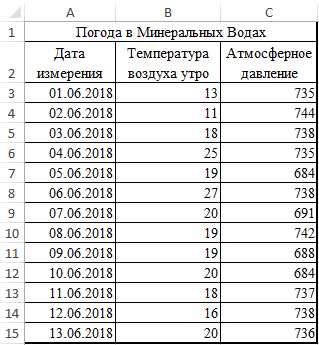
Рассмотрим пример вычисления корреляции Пирсона между двумя массивами данных с помощью функции ПИРСОН в MS EXCEL. Первый массив представляет собой значения температуры, второй – давления в определенный летний период. Пример заполненной таблицы показан на рисунке:
Задача следующая: необходимо определить зависимость между температурой и давлением для месяца июнь.
Пример решения с функцией ПИРСОН при анализе в Excel
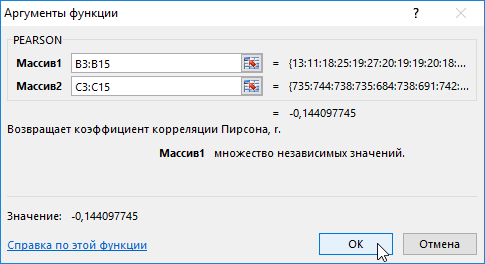
- Выберите ячейку C17, в которой должен быть рассчитан критерий Пирсона как результат, и нажмите мастер-кнопку функции «fx» или комбинацию горячих клавиш (SHIFT+F3). Откроется мастер функций, в поле «Категория» выберите «Статистические».
В списке статистических функций выберите и нажмите Ok:
- В меню аргументов выберите Массив 1; в примере это утренняя температура воздуха, а затем Массив 2 — атмосферное давление.
- В результате в ячейке С17 получаем коэффициент корреляции Пирсона. В нашем случае он отрицательный и примерно равен -0,14.
Этот показатель -0,14 по Пирсону, вернувшему функцию, свидетельствует о неблагоприятной зависимости температуры и давления в раннее время суток.
Пошаговая инструкция функции ПИРСОНА
Коэффициент корреляции является наиболее удобным показателем сопряженности количественных признаков.
Задача: Определить коэффициент линейной корреляции Пирсона.
Пример решения:
- В таблице приведены данные для группы курильщиков. Первый массив x — представляет возраст курильщика, второй массив y — количество выкуриваемых сигарет в день.
- Выберите ячейку B4, в которой будет вычисляться результат, и нажмите главную кнопку функции fx (SHIFT + F3).
- В группе Статистические выберите функцию ПИРСОН.
- Выберите Массив 1 — возраст курения, затем Массив 2 — количество выкуриваемых сигарет в день.
- Нажмите кнопку ОК и посмотрите критерий нормального распределения Пирсона в ячейке B4.
Таким образом, по результату расчета статистический вывод эксперимента выявил отрицательную связь между возрастом и количеством выкуриваемых сигарет в день.
Корреляционный анализ по Пирсону в Excel
Задание: учащимся были даны тесты на наглядное и вербальное мышление. Измерялось среднее время решения тестовых задач в секундах. Психолога интересует вопрос: есть ли связь между временем решения этих задач?
Пример решения: исходные данные представляем в виде таблицы:
- Подводим курсор к ячейке F2. Откройте мастер функций fx (SHIFT+F3) или введите его вручную.
- Выберите функцию.
- Выберите массив 1 B3:B21 с помощью мыши, затем массив 2 C3:C21.
- Нажимаем ОК и в ячейке F2 получаем критерий совместимости Пирсона.
Learn more


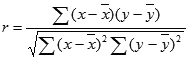

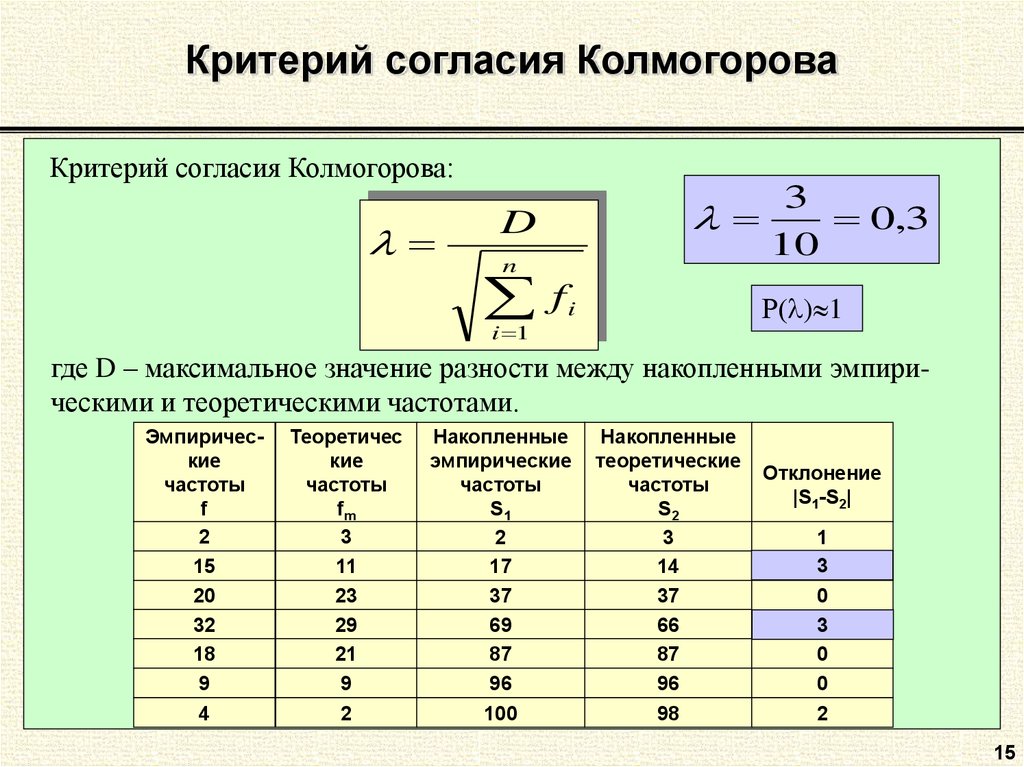



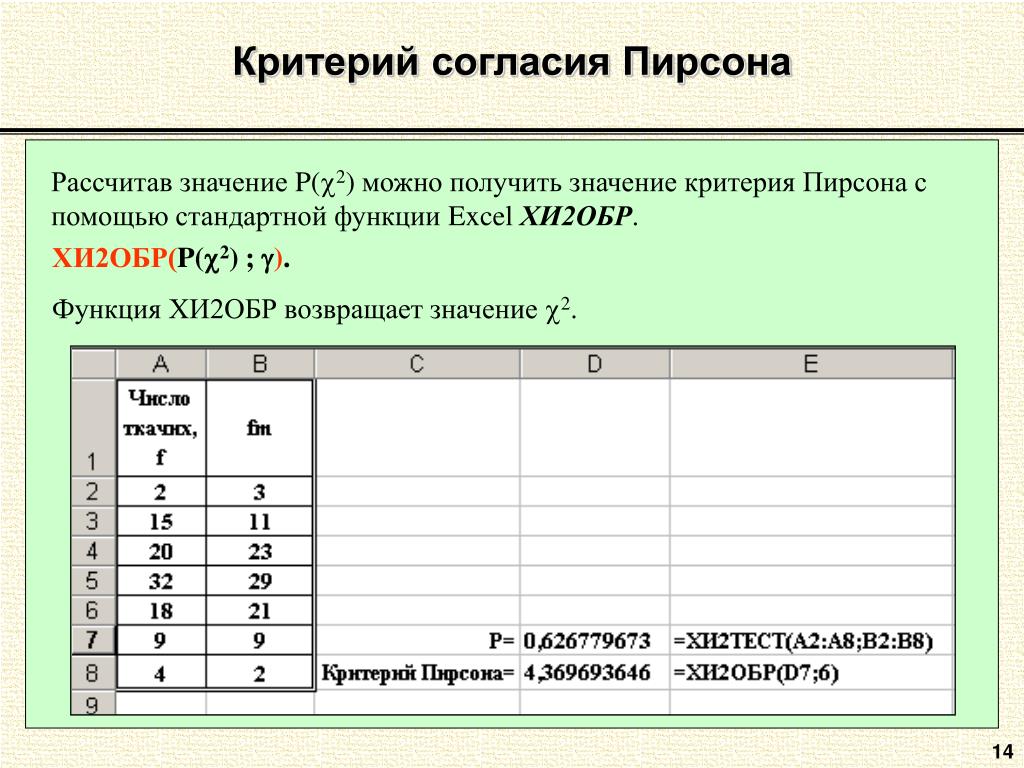 В списке статистических функций выберите и нажмите Ok:
В списке статистических функций выберите и нажмите Ok: