17 авг. 2022 г.
читать 3 мин
Фиктивная переменная — это тип переменной, которую мы создаем в регрессионном анализе, чтобы мы могли представить категориальную переменную как числовую переменную, которая принимает одно из двух значений: ноль или единицу.
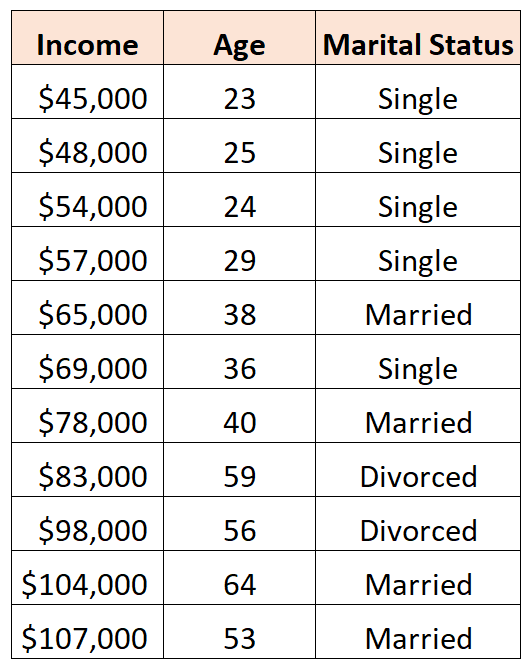
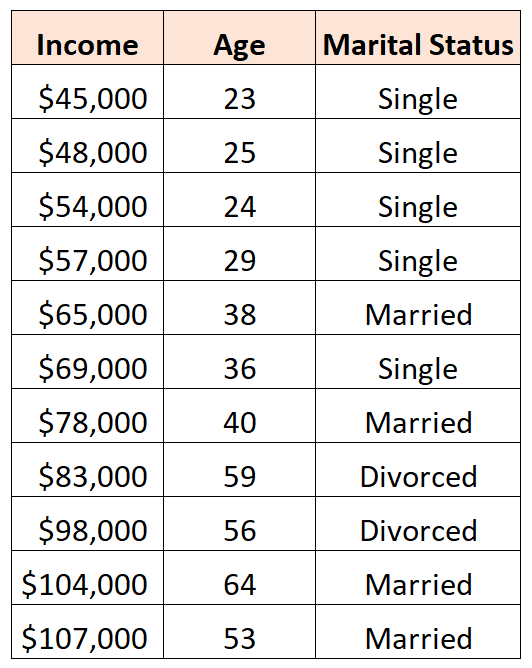
Например, предположим, что у нас есть следующий набор данных, и мы хотели бы использовать возраст и семейное положение для прогнозирования дохода :
Чтобы использовать семейное положение в качестве предиктора в регрессионной модели, мы должны преобразовать его в фиктивную переменную.
Поскольку в настоящее время это категориальная переменная, которая может принимать три разных значения («Холост», «Женат» или «Разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
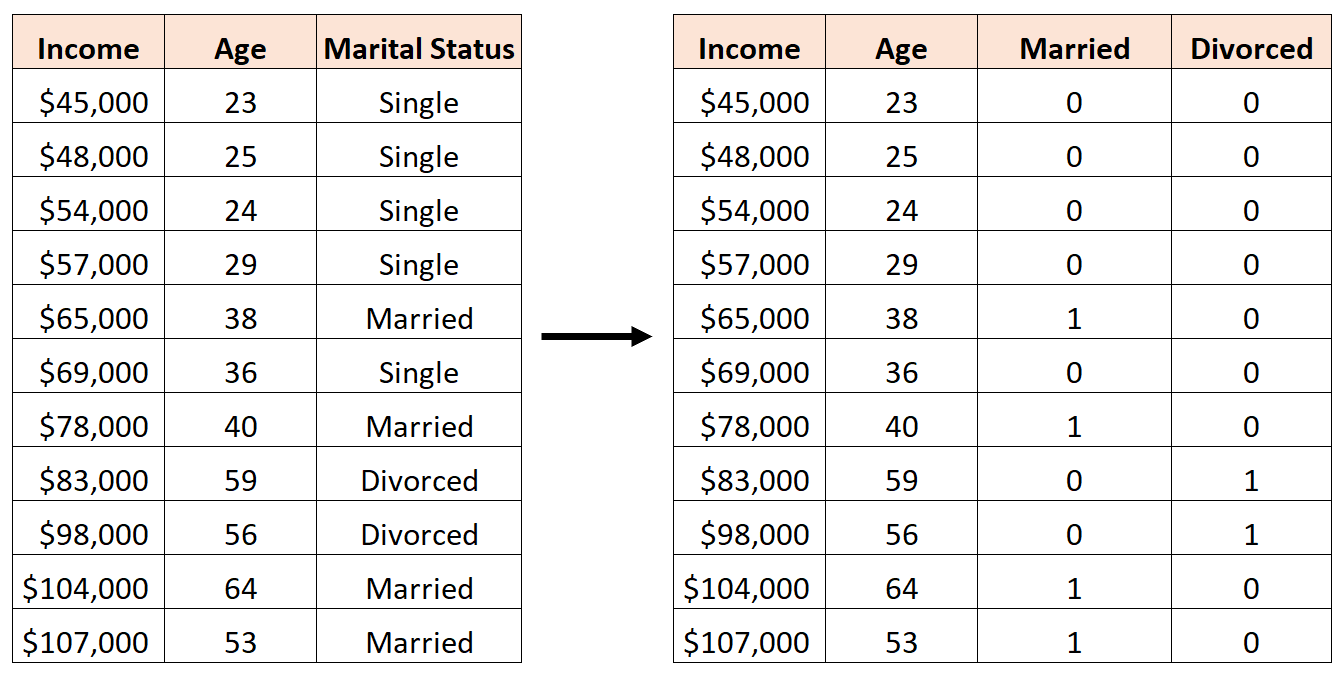
Чтобы создать эту фиктивную переменную, мы можем позволить «Single» быть нашим базовым значением, поскольку оно встречается чаще всего. Вот как мы можем преобразовать семейное положение в фиктивные переменные:
В этом руководстве представлен пошаговый пример того, как создать фиктивные переменные для этого точного набора данных в Excel, а затем выполнить регрессионный анализ, используя эти фиктивные переменные в качестве предикторов.
Шаг 1: Создайте данные
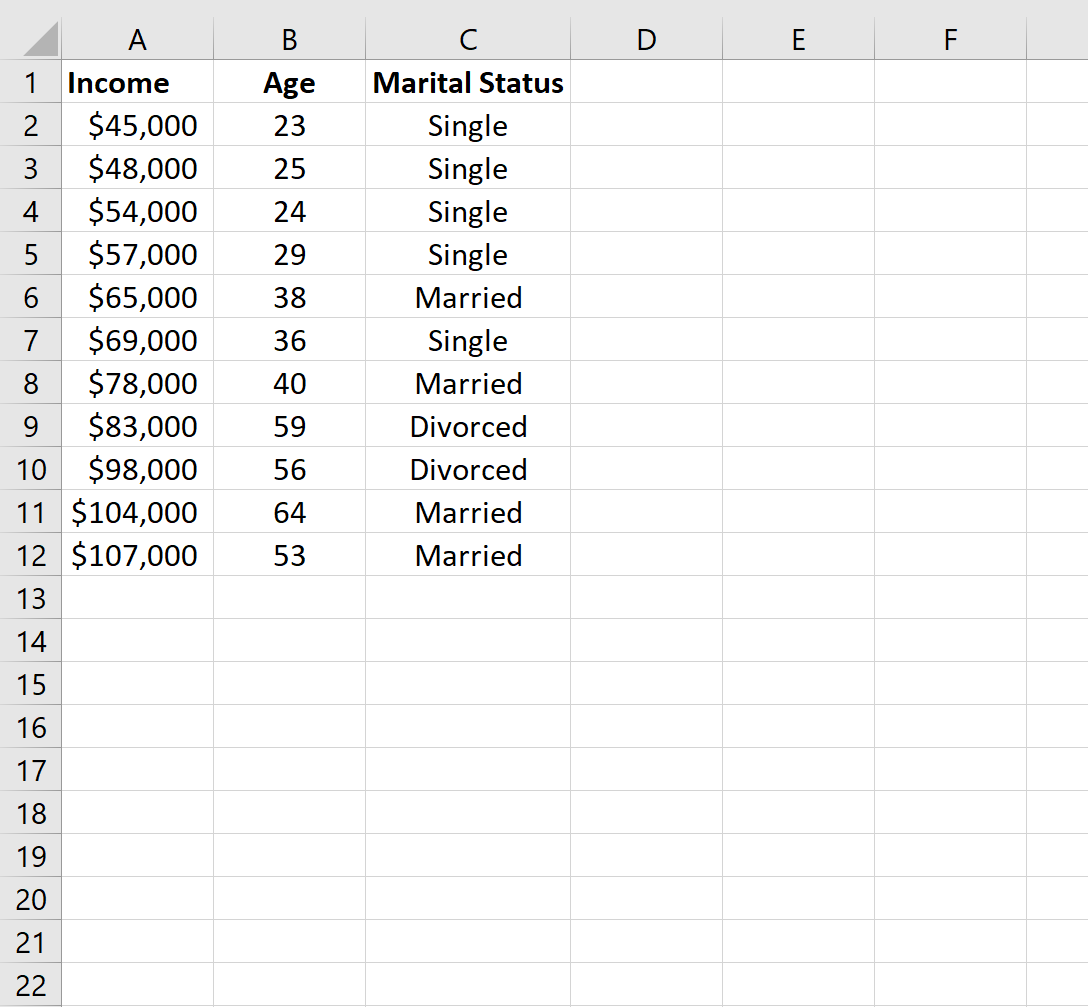
Сначала создадим набор данных в Excel:
Шаг 2: Создайте фиктивные переменные
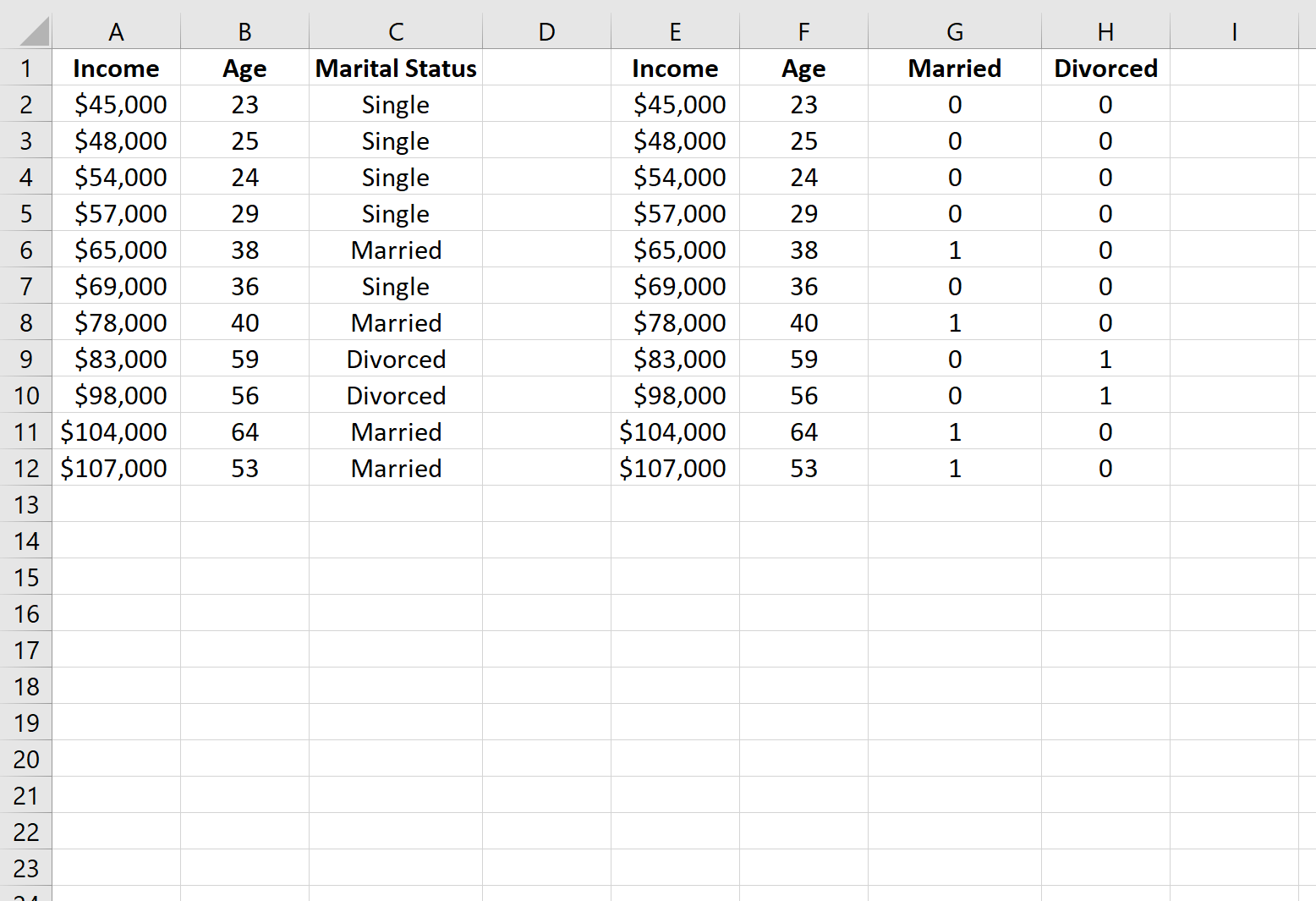
Затем мы можем скопировать значения из столбцов A и B в столбцы E и F, а затем использовать функцию IF() в Excel, чтобы определить две новые фиктивные переменные: Married и Divorced.
Вот формула, которую мы использовали в ячейке G2 , которую мы скопировали в остальные ячейки в столбце G:
= IF (C2 = "Married", 1, 0)
А вот формула, которую мы использовали в ячейке H2 , которую мы скопировали в остальные ячейки в столбце H:
= IF (C2 = "Divorced", 1, 0)
Затем мы можем использовать эти фиктивные переменные в регрессионной модели для прогнозирования дохода.
Шаг 3: выполните линейную регрессию
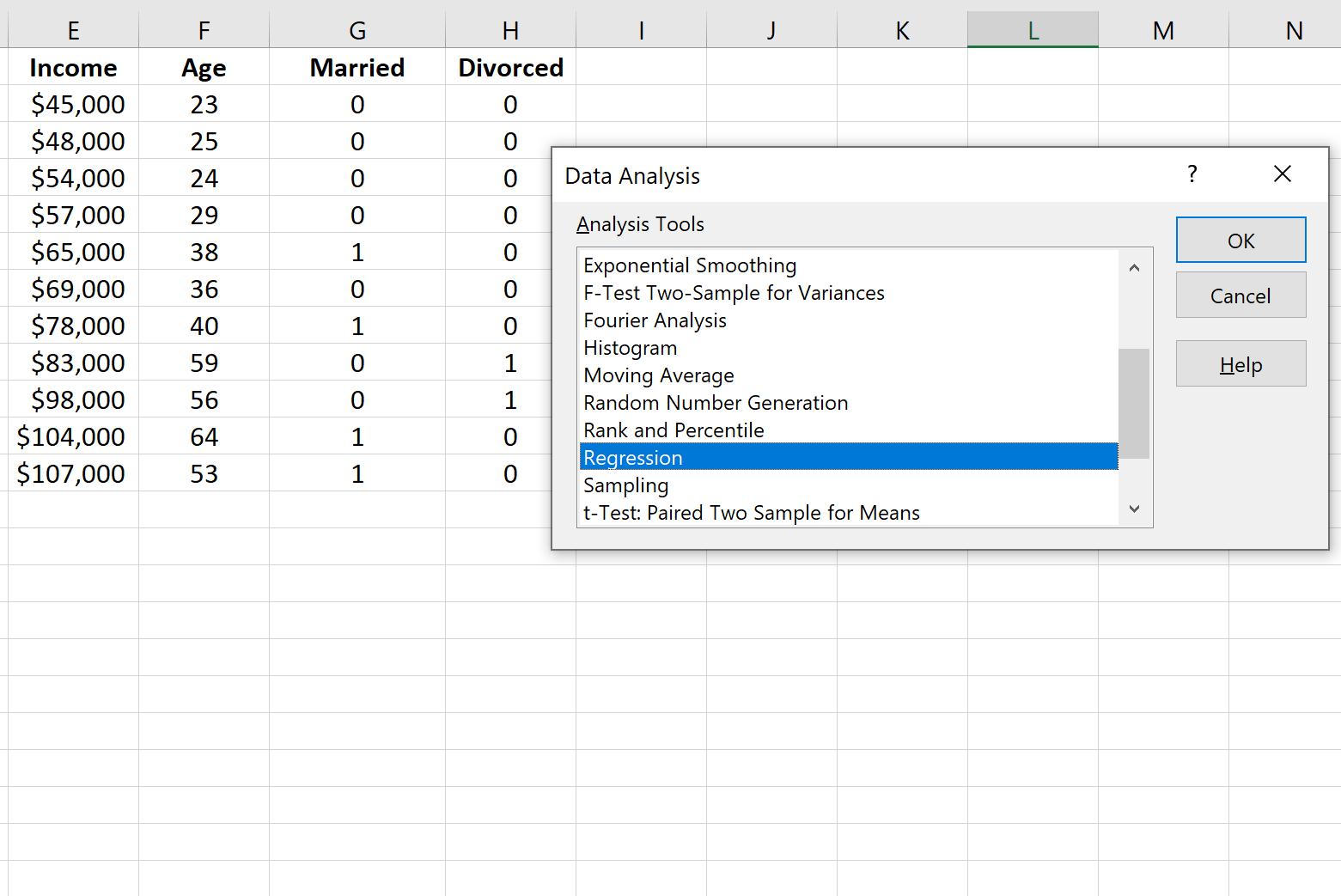
Чтобы выполнить множественную линейную регрессию, нам нужно щелкнуть вкладку « Данные » на верхней ленте, а затем « Анализ данных» в разделе « Анализ »:
Если вы не видите эту опцию доступной, вам нужно сначала загрузить пакет инструментов анализа .
В появившемся окне нажмите « Регрессия », а затем нажмите « ОК ».
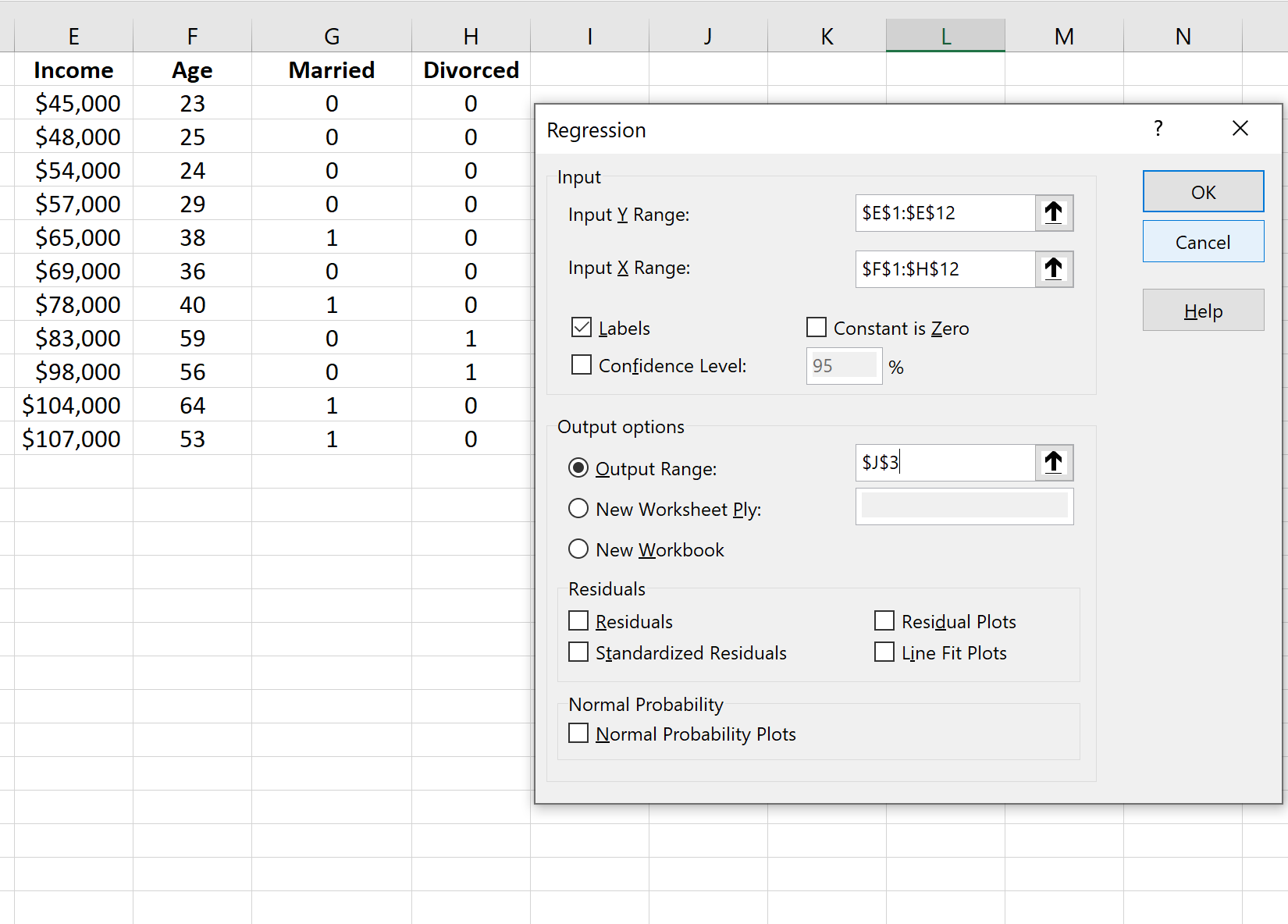
Затем заполните следующую информацию и нажмите OK .
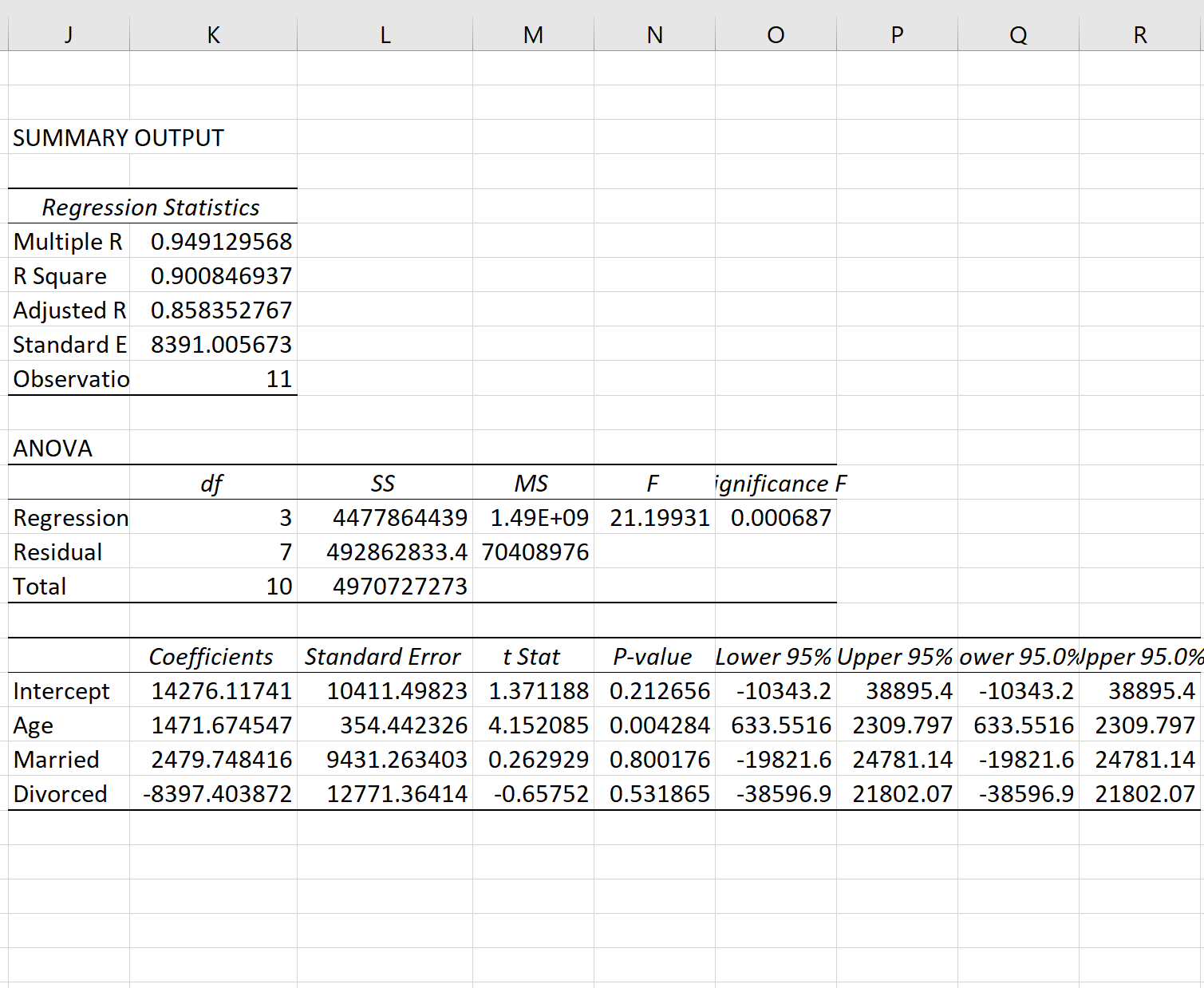
Это дает следующий результат:
Из вывода мы видим, что подобранная линия регрессии:
Доход = 14 276,12 + 1 471,67*(возраст) + 2 479,75*(замужем) – 8 397,40*(разведен)
Мы можем использовать это уравнение, чтобы найти предполагаемый доход для человека в зависимости от его возраста и семейного положения. Например, доход 35-летнего человека, состоящего в браке, оценивается в 68 264 доллара США :
Доход = 14 276,12 + 1 471,67 * (35) + 2 479,75 * (1) — 8 397,40 * (0) = 68 264 доллара США.
Вот как интерпретировать коэффициенты регрессии из таблицы:
- Пересечение: Пересечение представляет собой средний доход одного человека в возрасте 0 лет. Поскольку человеку не может быть ноль лет, в этой конкретной регрессионной модели нет смысла интерпретировать саму точку пересечения.
- Возраст: каждый год увеличения возраста связан со средним увеличением дохода на 1471,67 доллара. Поскольку p-значение (0,004) меньше 0,05, возраст является статистически значимым предиктором дохода.
- Женат: женатый человек в среднем зарабатывает на 2479,75 долларов больше, чем одинокий человек. Поскольку p-значение (0,800) не менее 0,05, эта разница не является статистически значимой.
- Разведен: разведенный человек в среднем зарабатывает на 8 397,40 долларов меньше, чем одинокий человек. Поскольку p-значение (0,532) не менее 0,05, эта разница не является статистически значимой.
Поскольку обе фиктивные переменные не были статистически значимыми, мы могли исключить из модели семейное положение в качестве предиктора, поскольку оно, по-видимому, не добавляет никакой прогностической ценности для дохода.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как рассчитать остаточную сумму квадратов в Excel
Как выполнить полиномиальную регрессию в Excel
Как создать остаточный график в Excel
Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.
Поиск решения будем рассматривать в
MS EXCEL 2010
(эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в
MS EXCEL 2007)
. В этой статье рассмотрим:
- создание оптимизационной модели на листе MS EXCEL
-
настройку
Поиска решения;
- простой пример (линейная модель).
Установка Поиска решения
Команда
Поиск решения
находится в группе
Анализ
на вкладке
Данные
.
Если команда
Поиск решения
в группе
Анализ
недоступна, то необходимо включить одноименную надстройку. Для этого:
-
На вкладке
Файл
выберите команду
Параметры
, а затем — категорию
Надстройки
; -
В поле
Управление
выберите значение
Надстройки Excel
и нажмите кнопку
Перейти;
-
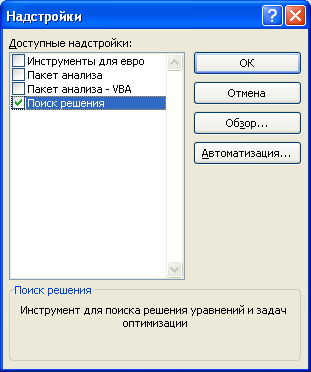
В поле
Доступные надстройки
установите флажок рядом с пунктом
Поиск решения
и нажмите кнопку ОК.
Примечание
. Окно
Надстройки
также доступно на вкладке
Разработчик
. Как включить эту вкладку
читайте здесь
.
После нажатия кнопки
Поиск решения
в группе
Анализ,
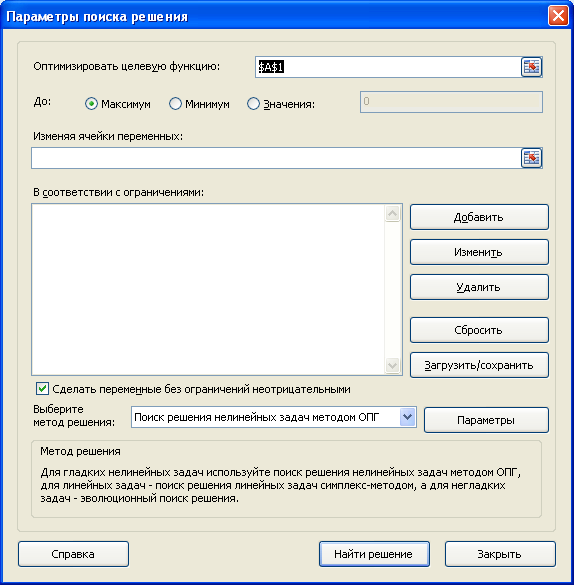
откроется его диалоговое окно
.
При частом использовании
Поиска решения
его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт
Добавить на панель быстрого доступа
.
О моделях
Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.
Совет
. Перед использованием
Поиска решения
настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.
Ниже приведен небольшой ликбез по этой теме.
Надстройка
Поиск решения
помогает определить
лучший способ
сделать
что-то
:
- «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
- «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.
Вот некоторые типичные примеры оптимизационных задач:
-
Определить
план производства
, при котором доход от реализации произведенной продукции максимальный;
-
Определить
схему перевозок
, при которой общие затраты на перевозку были бы минимальными;
-
Найти
распределение нескольких станков по разным видам работ
, чтобы общие затраты на производство продукции были бы минимальными;
- Определить минимальный срок исполнения всех работ проекта (критический путь).
Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется
Поиском решения
только по одному показателю
(этот оптимизируемый показатель называется
целевой функцией
). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения
подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.
Примечание
. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента
Подбор параметра
. Перед первым знакомством с
Поиском решения
имеет смысл сначала детально разобраться с родственным ему инструментом
Подбор параметра
. Основные отличия
Подбора параметра
от
Поиска решения
:
Подбор параметра
работает только с моделями с одной переменной;- в нем невозможно задать ограничения для переменных;
- определяется не максимум или минимум целевой функции, а ее равенство некому значению;
- эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).
Подготовка оптимизационной модели в MS EXCEL
Поиск решения
оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул). Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных. Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне
Поиска решения
возможен только с этого листа. Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.
Совет
. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки
Поиска решения
(см. ниже).
Приведем алгоритм работы с
Поиском решения
, который советуют сами разработчики (
]]>
www.solver.com
]]> ):
- Определите ячейки с переменными модели (decision variables);
- Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
- Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
-
С помощью диалогового окна
Поиск решения
введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений; -
Запустите
Поиск решения
для нахождения оптимального решения.
Проделаем все эти шаги на простом примере.
Простой пример использования
Поиска решения
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.
Данные модели организуем следующим образом (см.
файл примера
).
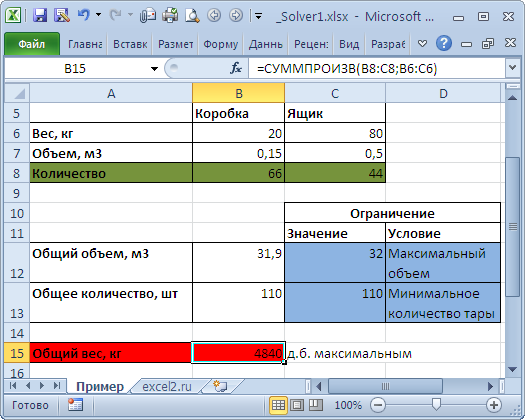
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему (<=32) – синим. Целевая функция рассчитывается по формуле
=СУММПРОИЗВ(B8:C8;B6:C6)
– это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем —
=СУММПРОИЗВ(B7:C7;B8:C8)
. Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков (<=32). Также для задания ограничения модели рассчитаем общее количество тары
=СУММ(B8:C8)
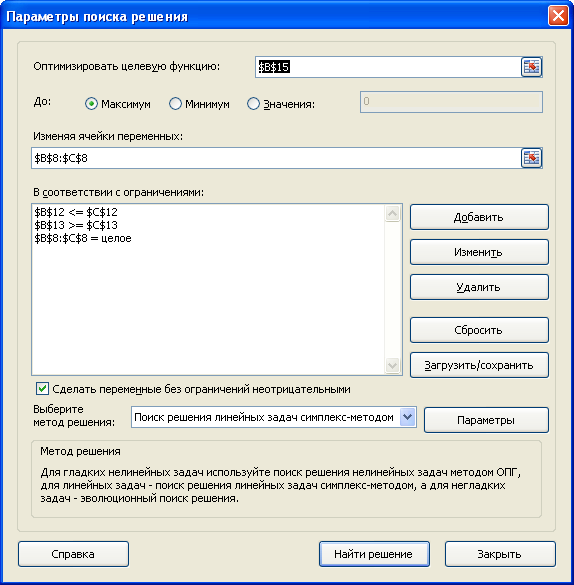
. Теперь с помощью диалогового окна
Поиск решения
введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.
После нажатия кнопки
Найти решение
будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.
Совет
: в статье »
Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями
» показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.
Резюме
На самом деле, основной проблемой при решении оптимизационных задач с помощью
Поиска решения
является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью
Поиска решения
. Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу. Решение классических оптимизационных задач с помощью
Поиска решения
рассмотрено
в этом разделе
.
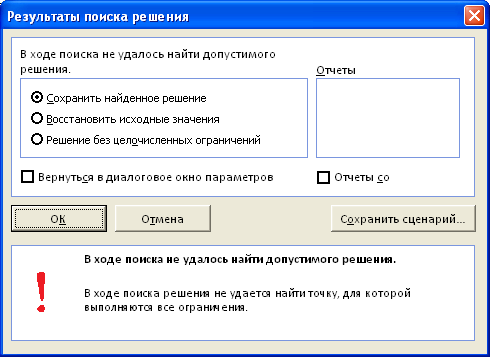
Поиску решения не удалось найти решения (Solver could not find a feasible solution)
Это сообщение появляется, когда
Поиск решения
не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям. Если вы используете
Симплекс метод решения линейных задач
, то можно быть уверенным, что решения действительно не существует. Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите
Поиск решения
с другими начальными значениями переменных, то, возможно, решение будет найдено. Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и
Поиск решения
не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае,
Поиск решения
может найти решение (если оно действительно существует).
Примечание
. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи
Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства
.
В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, <= вместо >=) или граничного значения. Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3,
Поиск решения
не найдет решения.
При ограничении 17 м3
Поиск решения
найдет решение.
Некоторые настройки
Поиска решения
Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2
Поиска решения
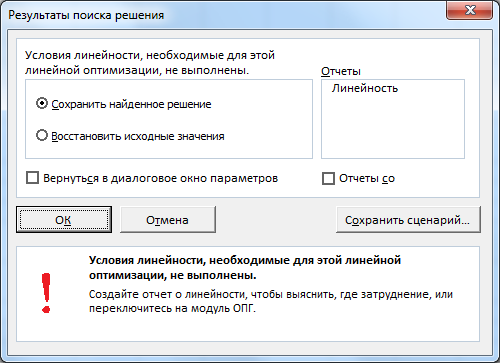
можно также проверить на линейность саму модель. В случае нелинейной модели Вы получите следующее сообщение:
В этом случае необходимо выбрать метод для решения нелинейной задачи. Примеры нелинейных зависимостей: V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2, где x – переменная, а V – целевая функция.
Кнопки Добавить, Изменить, Удалить
Эти кнопки позволяют добавлять, изменять и удалять ограничения модели.
Кнопка Сбросить
Чтобы удалить все настройки
Поиска решения
нажмите кнопку
Сбросить
– диалоговое окно очистится.
Сохранение и загрузка модели
Эта опция удобна при использовании разных вариантов ограничений. При сохранении параметров модели (кнопка
Загрузить/ Сохранить,
далее нажмите кнопку
Сохранить
) предлагается выбрать верхнюю ячейку диапазона (столбца), в который будут помещены: ссылка на целевую функцию, ссылки на ячейки с переменными, ограничения и параметры методов решения (доступные через кнопку
Параметры
). Перед сохранением убедитесь в том, что этот диапазон не содержит данных модели. Для загрузки сохраненных параметров нажмите сначала кнопку
Загрузить/ Сохранить
, затем, в появившемся диалоговом окне кнопку
Загрузить
, после чего задайте диапазон ячеек, содержащих сохраненные ранее настройки (нельзя указывать только одну верхнюю ячейку). Нажмите кнопку OK. Подтвердите сброс текущих значений параметров задачи и их замену на новые.
Точность
При создании модели исследователь изначально имеет некую оценку диапазонов варьирования целевой функции и переменных. Принимая во внимание
ограниченную точность
вычислений в MS EXCEL, рекомендуется, чтобы эти диапазоны варьирования были значительно выше точности вычисления (она обычно устанавливается от 0,001 до 0,000001). Как правило, данные в модели нормируют так, чтобы диапазоны варьирования целевой функции и переменных были в пределах 0,1 – 100 000. Конечно, все зависит от конкретной модели, но если ваши переменные изменяются более чем на 5-6 порядков, то возможно следует «загрубить» модель, например, с помощью операции логарифмирования.
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Финансовая модель — это функциональный инструмент, который поможет оперативно просчитать влияние различных факторов и изменений на результаты работы и финансовое состояние организации. За счёт формул и уравнений расчётов после изменения исходных данных все зависимые характеристики, будут пересчитаны программой автоматически.
Для финансового моделирования наиболее удобен и доступен формат Excel. Использовать его могут как бухгалтеры, так и руководители различных уровней.
Набор показателей для финансовой модели зависит от специфики деятельности организации. Основных групп, как правило, четыре:
- активы — имущество, принадлежащее организации;
- пассивы — обязательства;
- финансовые потоки — различные денежные поступления и платежи;
- доходы и расходы.
Результаты расчётов можно представить в виде баланса, отчётов о доходах и расходах и о движении денежных средств (по состоянию на определённую дату).
Алгоритм построения финансовой модели
Начните финансовое моделирование в Excel с создания простой модели. Из внешних параметров можно, например, взять стоимость продукции и спрос на неё. Например, в качестве внутренних показателей можно взять размер выручки и затрат. На первом этапе количество элементов может быть минимальным, а особой точностью можно пренебречь. Основная цель — установить рабочие взаимосвязи для автоматического пересчёта. Далее модель можно развивать, детализировать и усложнять.
Рассмотрим пример простого моделирования в Excel с небольшим количеством ключевых переменных. Для каждой таблицы необходимо отвести отдельную страницу.
1. Задаём исходные параметры
Попробуем спрогнозировать выручку. За основу можно взять план реализации товаров или услуг за год. Размер выручки на первом этапе можно округлить или указать приблизительные данные (рисунок 1).
Рисунок 1 — План реализации услуг (тыс.руб.)

Выручка рассчитывается как сумма услуг.
2. Определяем переменные затраты
В качестве переменных введём затраты на заработную плату сотрудникам. Допустим, она зависит от объёма реализованных услуг и составляет 25% от выручки. Зарплата рассчитывается помесячно как произведение коэффициента 0,25 (25/100) и плана продаж на конкретный месяц.
Расходы на аренду и управление внесём как фиксированные значения.
Например, чтобы посчитать зарплату за январь, берём план реализации на январь и умножаем на коэффициент
151 * 0,25 = 38 тыс. руб.
В Excel прописываем формулу: fx = 0,25*название страницы с таблицей по плану реализации!B8
Общий размер планируемых затрат будет равен сумме зарплаты, аренды и управленческих расходов (рисунок 2).
Рисунок 2 — План затрат

3. Составляем план доходов и расходов
Обратите внимание на строки «операционные доходы» и «операционные расходы» (рисунок 3). Чтобы их заполнить, потребуется прописать ссылки на соответствующие ячейки функциональных планов.
Рисунок 3 — План доходов и расходов, тыс. руб.

Так, операционные доходы будут равны суммам от услуг 1-4. Например, чтобы рассчитать операционный доход за январь, складываем 15+30+46+60. Получаем 151 тыс. руб.
В формулу прописываем: fх =СУММ(B5:B8)
Числовые значения по услугам прописываем ссылками на ячейки таблицы «План реализации услуг».
Графа «Итого» считается как сумма ячеек с B4 по M4
fх =СУММ(B4:M4)
Аналогично рассчитываются операционные расходы. Данные синхронизируем с таблицей «План затрат».
Операционная прибыль рассчитывается как разность операционные доходы — операционные расходы.
Например, операционная прибыль за январь равна: 151 — 96 = 55 тыс. руб.
Рентабельность рассчитывается как отношение операционной прибыли к операционному доходу помноженное на 100.
За январь получаем: 55/151*100 = 36,69%
fх = B13/B4*100
Обратите внимание, что итоговая рентабельность рассчитывается не как сумма за предыдущие месяцы, а как отношение итоговой операционной прибыли к итоговому операционному доходу.
Прибыль нарастающим итогом — это прибыли (убытки) за прошлый и текущий отчётные периоды. В январе мы берём данные операционной прибыли, равные 55 тысячам рублей. В феврале прибавляем 58 тысяч. Получаем 113 тысяч рублей. В марте прибавляем ещё 64 тысячи. Получаем 176 тысяч. И так суммируем по каждому месяцу.
В нашем финансовом плане прибыль нарастающим итогом за февраль будет прописываться формулой: fх=B15+C13
4. Составляем план движения денежных средств
Допустим, что в организации осуществляется только операционная деятельность, без капитальных вложений и заёмных средств. Также для упрощения исключим дебиторскую задолженность, допустив что время оплаты и время оказания услуг совпадают.
Платежи по заработной плате и аренде происходят в месяце, следующем за месяцем их начисления, а управленческие расходы — в месяц их осуществления (рисунок 4).
Рисунок 4 — План движения денежных средств, тыс. руб.

Платежи по операционной деятельности рассчитываются, как сумма зарплата + аренда + управленческие расходы.
Сальдо по операционной деятельности — это разность поступлений по операционной деятельности и платежей по операционной деятельности.
Сальдо операционной деятельности за январь будет равно: 151 — 38 = 113 тысяч рублей.
Сальдо на конец периода рассчитывается как сумма сальдо на начало периода и сальдо по операционной деятельности. Если принять сальдо на начало января равное 10 тысячам рублей, сальдо на конец периода будет равно 123 тысячам рублей.
5. Делаем прогнозный баланс
На основании плана доходов и расходов и плана движения денежных средств можно построить прогнозный баланс. Начальные остатки нужно взять из баланса предыдущего периода. Допустим, что все они равны 10 тысячам рублей (рисунок 5).
Рисунок 5 — Прогнозный баланс, тыс. руб.

В графу «денежные средства» подставляем значение сальдо на конец периода предыдущего месяца. Так, денежные средства за февраль = 123 тысячам рублей.
Активы будут равны сумме: денежные средства + основные средства + дебиторская задолженность.
Кредиторская задолженность рассчитывается: кредиторская задолженность предыдущего периода + планируемые затраты на заработную плату и аренду предыдущего месяца — планируемы движения денежных средств по зарплате и аренде предыдущего месяца.
Так, кредиторская задолженность на 1 февраля составит 58 тысяч рублей
0+38+20-0-0.
Капитал = капитал за предыдущий период + операционная прибыль предыдущего периода.
Капитал на 1 февраля составляет 65 тысяч рублей. 10+55.
Пассив — это сумма капитала и кредиторской задолженности
Обратите внимание, что дебиторская задолженность будет рассчитываться как дебиторская задолженность за предыдущую дату + отгрузка периода — поступление денежных средств.
Далее финансовую модель можно детализировать. Например, разбить по видам управленческие расходы, расписать зарплаты по сотрудникам, детализировать план продаж.
Финансовую модель можно корректировать, заменять плановые данные фактическими, отслеживать риски и контролировать финансовые результаты.
Узнайте больше о финансовом моделировании в Excel и прогнозировании финансового состояния бизнеса на семинаре в Учебном центре «Финконт».
Содержание
- Как создать фиктивные переменные в Excel (шаг за шагом)
- Шаг 1: Создайте данные
- Шаг 2: Создайте фиктивные переменные
- Шаг 3: выполните линейную регрессию
- Понятие переменных и констант в макросах Excel
- Типы данных
- Объявление констант и переменных
- Оператор Option Explicit
- Область действия констант и переменных
- Зачем нужны константы и переменные
- Выводы
Как создать фиктивные переменные в Excel (шаг за шагом)
Фиктивная переменная — это тип переменной, которую мы создаем в регрессионном анализе, чтобы мы могли представить категориальную переменную как числовую переменную, которая принимает одно из двух значений: ноль или единицу.
Например, предположим, что у нас есть следующий набор данных, и мы хотели бы использовать возраст и семейное положение для прогнозирования дохода :
Чтобы использовать семейное положение в качестве предиктора в регрессионной модели, мы должны преобразовать его в фиктивную переменную.
Поскольку в настоящее время это категориальная переменная, которая может принимать три разных значения («Холост», «Женат» или «Разведен»), нам нужно создать k -1 = 3-1 = 2 фиктивных переменных.
Чтобы создать эту фиктивную переменную, мы можем позволить «Single» быть нашим базовым значением, поскольку оно встречается чаще всего. Вот как мы можем преобразовать семейное положение в фиктивные переменные:
В этом руководстве представлен пошаговый пример того, как создать фиктивные переменные для этого точного набора данных в Excel, а затем выполнить регрессионный анализ, используя эти фиктивные переменные в качестве предикторов.
Шаг 1: Создайте данные
Сначала создадим набор данных в Excel:
Шаг 2: Создайте фиктивные переменные
Затем мы можем скопировать значения из столбцов A и B в столбцы E и F, а затем использовать функцию IF() в Excel, чтобы определить две новые фиктивные переменные: Married и Divorced.
Вот формула, которую мы использовали в ячейке G2 , которую мы скопировали в остальные ячейки в столбце G:
А вот формула, которую мы использовали в ячейке H2 , которую мы скопировали в остальные ячейки в столбце H:
Затем мы можем использовать эти фиктивные переменные в регрессионной модели для прогнозирования дохода.
Шаг 3: выполните линейную регрессию
Чтобы выполнить множественную линейную регрессию, нам нужно щелкнуть вкладку « Данные » на верхней ленте, а затем « Анализ данных» в разделе « Анализ »:
Если вы не видите эту опцию доступной, вам нужно сначала загрузить пакет инструментов анализа .
В появившемся окне нажмите « Регрессия », а затем нажмите « ОК ».
Затем заполните следующую информацию и нажмите OK .
Это дает следующий результат:
Из вывода мы видим, что подобранная линия регрессии:
Доход = 14 276,12 + 1 471,67*(возраст) + 2 479,75*(замужем) – 8 397,40*(разведен)
Мы можем использовать это уравнение, чтобы найти предполагаемый доход для человека в зависимости от его возраста и семейного положения. Например, доход 35-летнего человека, состоящего в браке, оценивается в 68 264 доллара США :
Доход = 14 276,12 + 1 471,67 * (35) + 2 479,75 * (1) — 8 397,40 * (0) = 68 264 доллара США.
Вот как интерпретировать коэффициенты регрессии из таблицы:
- Пересечение: Пересечение представляет собой средний доход одного человека в возрасте 0 лет. Поскольку человеку не может быть ноль лет, в этой конкретной регрессионной модели нет смысла интерпретировать саму точку пересечения.
- Возраст: каждый год увеличения возраста связан со средним увеличением дохода на 1471,67 доллара. Поскольку p-значение (0,004) меньше 0,05, возраст является статистически значимым предиктором дохода.
- Женат: женатый человек в среднем зарабатывает на 2479,75 долларов больше, чем одинокий человек. Поскольку p-значение (0,800) не менее 0,05, эта разница не является статистически значимой.
- Разведен: разведенный человек в среднем зарабатывает на 8 397,40 долларов меньше, чем одинокий человек. Поскольку p-значение (0,532) не менее 0,05, эта разница не является статистически значимой.
Поскольку обе фиктивные переменные не были статистически значимыми, мы могли исключить из модели семейное положение в качестве предиктора, поскольку оно, по-видимому, не добавляет никакой прогностической ценности для дохода.
Источник
Понятие переменных и констант в макросах Excel
В этой статье вы узнаете, что такое константы и переменные в макросах, где они могут использоваться, и в чем заключается основное отличие между разными типами данных. Также будет раскрыто, зачем нужны константы, если можно просто прописать переменную и никогда ее не изменять.
Аналогично иным языкам программирования, хранение данных может осуществляться в переменных или константах (и те, и другие также нередко называются контейнерами данных). В этом и заключается основное отличие между этими понятиями. Первые могут изменяться в зависимости от того, что происходит в программе. В свою очередь, константы задаются один раз и не меняют своего значения.
Константы могут быть полезными, если необходимо одно и то же большое значение использовать несколько раз. Вместо копирования числа можно просто написать название константы. Например, вы можете использовать константу «Pi» для хранения числа Пи, которое является постоянным значением. Оно очень большое, и каждый раз писать его или искать и копировать довольно затруднительно. А так, достаточно написать два символа, и среда автоматически использует нужное число.
Пользователю Excel необходимо объявлять переменные, если ему надо время от времени менять значение, хранящееся в них. Например, можно задать переменную с названием sVAT_Rate, в которой будет храниться текущая ставка НДС на товар. Если она изменяется, можно быстро скорректировать ее. Особенно это полезно тем, кто ведет бизнес в Соединенных Штатах, где некоторые товары могут вообще не облагаться НДС (а также этот налог отличается в разных штатах).
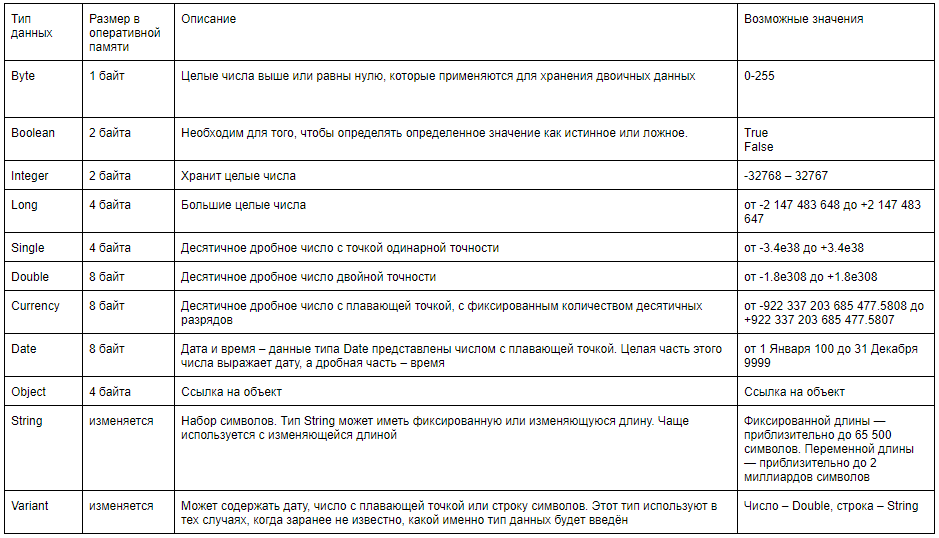
Типы данных
Каждый контейнер данных может относиться к одному из нескольких типов. Приводим таблицу, описывающую стандартные типы обрабатываемой информации. Их много, и новичку может показаться изначально, что они повторяют друг друга. Но это иллюзорное ощущение. Дальше вы узнаете, почему указание правильного типа данных так важно.
Не рекомендуется использовать тип данных, занимающий больше места в памяти, для небольших чисел. Например, для цифры 1 достаточно использовать тип Byte. Это положительно скажется на быстродействии исполняемого модуля, особенно на слабых компьютерах. Но важно не перегнуть палку и здесь. Если использовать слишком компактный тип данных, чрезмерно большое значение может в нем не поместиться.
Объявление констант и переменных
Использование контейнера данных без его предварительного объявления настоятельно не рекомендуется. Тогда может возникнуть ряд проблем, для избежания которых необходимо написать несколько небольших строчек кода с перечислением переменных или констант.
Чтобы объявить переменную, используется оператор Dim. Например, так:
Dim Variable_Name As Integer
Variable_Name – это название переменной. Далее пишется оператор As, указывающий на тип данных. Вместо строк «Variable_Name» и «Integer» можно вставить свое название и тип данных.
Константы тоже можно объявлять, но предварительно нужно указать их значение. Как один из вариантов, так:
Const iMaxCount = 5000
Справедливости ради, в некоторых случаях можно обойтись и без объявления переменной, но в таком случае им автоматически будет назначен тип Variant. Тем не менее, делать этого не рекомендуется по следующим причинам:
- Variant обрабатывается значительно медленнее, и если таких переменных много, обработка информации может существенно замедлиться на слабых компьютерах. Казалось бы, что те секунды решат? Но если приходится писать большое количество строк кода, а потом еще и запускать его на слабых компьютерах (которые до сих пор продаются, учитывая то, что современные офисные пакеты требуют много оперативной памяти), можно полностью остановить работу. Известны случаи, как непродуманное написание макросов приводило к зависанию смартбуков, которые имеют небольшое количество оперативной памяти и не рассчитаны на выполнение сложных задач.
- Допускается наличие опечаток в названиях, предотвращение которых возможно с помощью оператора Option Explicit, позволяющего найти необъявленную переменную, если такая обнаруживается. Это простой способ определения ошибок, поскольку малейшая опечатка приводит к тому, что интерпретатор не может идентифицировать переменную. А если включить режим объявления переменных, интерпретатор просто не даст запустить макрос, если обнаруживаются контейнеры данных, которые не были объявлены в самом начале модуля.
- Избежание ошибок, вызванных тем, что значения переменной не соответствуют типу данных. В норме, если присвоить текстовое значение целочисленной переменной, будет выдана ошибка. Да, с одной стороны, без объявления присваивается универсальный тип, но если заранее их объявить, то можно избежать случайных ошибок.
Поэтому, несмотря на все, настоятельно рекомендуется объявлять все переменные в макросах Excel.
При объявлении переменных нужно учитывать еще один момент. Можно при объявлении переменной не присваивать ей никаких значений, но в этом случае она обретает значение по умолчанию. Например:
- Строки делаются пустыми.
- Числа обретают значение 0.
- Переменные с типом Boolean изначально считаются ложными.
- По умолчанию выставляется дата 30 декабря 1899 года.
Например, не нужно присваивать целочисленной переменной значение 0, если ранее не было указано никакого значения. Она и так содержит это число.
Оператор Option Explicit
Этот оператор позволяет декларировать все переменные, которые используются в коде VBA и определять наличие каких-то незадекларированных контейнеров до того, как код будет запущен. Чтобы использовать эту возможность, достаточно просто написать строку кода Option Explicit в самом верху кода макроса.
Если вам нужно включать этот оператор в код в каждом случае, это можно сделать с помощью специальной настройки VBA редактора. Чтобы включить эту опцию, необходимо:
- Перейти в среде разработки по пути – Tools > Options.
- В открывшемся после этого окне следует открыть вкладку Editor.
- И наконец, поставить флажок возле пункта Require Variable Declaration.
По завершению этих действий нажать на кнопку «ОК».
Все, теперь при написании каждого нового макроса эта строчка будет вставляться в верхнюю часть кода автоматически.
Область действия констант и переменных
Каждая переменная или константа имеет лишь ограниченную область действия. Это зависит от того, где ее декларировать.
Предположим, у нас есть функция Total_Cost() , и в ней используется переменная sVAT_Rate . В зависимости от позиции в модуле, она будет иметь разную область действия:
| Option Explicit
Dim sVAT_Rate As Single Function Total_Cost() As Double End Function |
Если переменная объявляется вверху самого модуля, она распространяется на весь этот модуль. То есть, она может читаться каждой процедурой.
Причем, если одна из процедур изменила значение переменной, то следующая будет также читать это скорректированное значение. Но в других модулях эта переменная все равно не будет читаться. |
| Option Explicit
Function Total_Cost() As Double Dim sVAT_Rate As Single End Function |
В этом случае переменная объявляется внутри процедуры, и интерпретатор будет выдавать ошибку, если она будет использоваться в другой процедуре. |
Если необходимо, чтобы переменная читалась другими модулями, необходимо использовать вместо ключевого слова Dim ключевое слово Public. Точно так же, можно ограничить область распространения переменной только на текущий модуль с помощью оператора Public, который прописывается вместо слова Dim.
Задавать область действия констант можно аналогичным образом, но ключевое слово здесь прописывается вместе с оператором Const.
Вот таблица с наглядным примером, как это работает с константами и переменными.
| Option Explicit
Public sVAT_Rate As Single Public Const iMax_Count = 5000 |
В этом примере вы можете увидеть, как ключевое слово Public применяется для объявления переменной, и что нужно прописывать в редакторе Visual Basic для объявления публичной константы. Область распространения этих контейнеров для значений касается всех модулей. |
| Option Explicit
Private sVAT_Rate As Single Private Const iMax_Count = 5000 |
Здесь переменные и константы объявляются с помощью ключевого слова Private. Это означает, что их можно увидеть только в рамках текущего модуля, а процедуры в других модулях не смогут их использовать. |
Зачем нужны константы и переменные
Использование констант и переменных позволяет увеличить степень понятности кода. И если у новичков в целом не возникает вопросов, зачем нужны переменные, то касаемо необходимости констант существует множество неясностей. И этот вопрос кажется, на первый взгляд, вполне логичным. Ведь можно один раз объявить переменную и больше ее никогда не менять.
Ответ оказывается где-то в той же плоскости, что и касаемо использования типов данных, занимающих большое пространство в памяти. Если мы имеем дело с огромным количеством переменных, можно случайно уже существующий контейнер изменить. Если же пользователь прописывает, что определенное значение никогда не будет изменяться, то среда автоматически проконтролирует это.
Особенно это важно, когда макрос пишется несколькими программистами. Один может знать о том, что какая-то переменная не должна меняться. А другой – нет. Если же указывать оператор Const, иной разработчик будет знать, что данное значение не меняется.
Или же, если есть константа с одним именем, а переменная имеет другое, но похожее название. Разработчик может попросту перепутать их. Например, одна переменная, которую не нужно менять, называется Variable11, а другая, которую можно редактировать – Variable1. Человек может на автомате, когда пишет код, случайно пропустить лишнюю единицу и не заметить этого. В результате, будет изменен контейнер для значений, который не следовало бы трогать.
Или же сам разработчик может забыть, какие переменные ему можно трогать, а какие – нет. Это часто случается, когда код пишется несколько недель, и его размер становится большим. За это время очень легко забыть даже то, что означает та или иная переменная.
Да, можно в этой ситуации обойтись комментариями, но не проще ли указать слово Const?
Выводы
Переменные являются важнейшей составляющей программирования макросов, которые позволяют выполнять сложные операции, начиная вычислениями и заканчивая информированием пользователя об определенных событиях или указанием конкретных значений в ячейках электронной таблицы.
Константы нужно использовать, если разработчик точно знает, что содержимое этих контейнеров не будет меняться в дальнейшем. Рекомендуется не использовать переменные вместо них, поскольку можно случайно ошибиться.
Источник