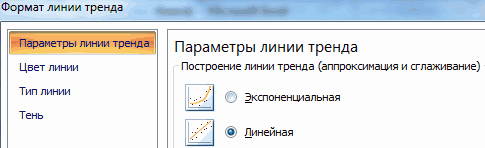
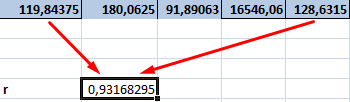
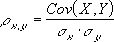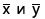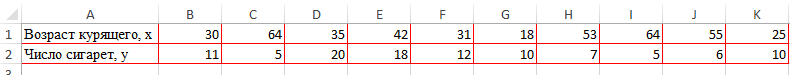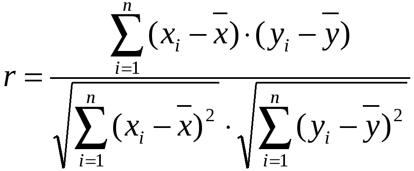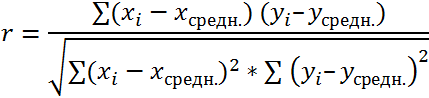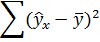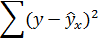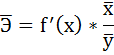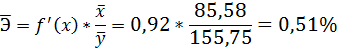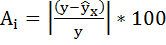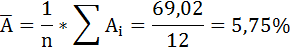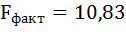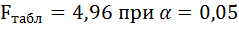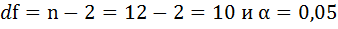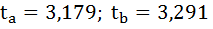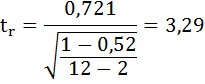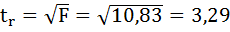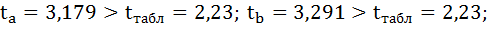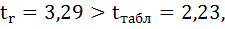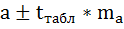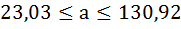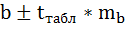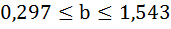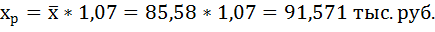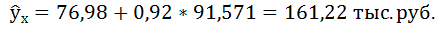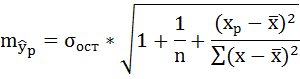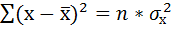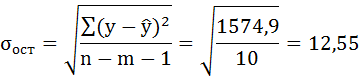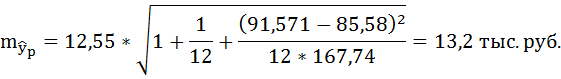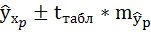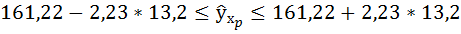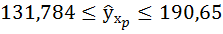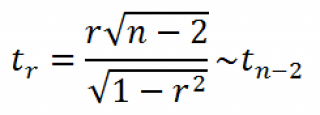Коэффициент корреляции (или линейный коэффициент корреляции) обозначается как «r» (в редких случаях как «ρ») и характеризует линейную корреляцию (то есть взаимосвязь, которая задается некоторым значением и направлением) двух или более переменных. Значение коэффициента лежит между -1 и +1, то есть корреляция бывает как положительной, так и отрицательной. Если коэффициент корреляции равен -1, имеет место идеальная отрицательная корреляция; если коэффициент корреляции равен +1, имеет место идеальная положительная корреляция. В остальных случаях между двумя переменными наблюдается положительная корреляция, отрицательная корреляция или отсутствие корреляции. Коэффициент корреляции можно вычислить вручную, с помощью бесплатных онлайн-калькуляторов или с помощью хорошего графического калькулятора.
Шаги
Вычисление коэффициента корреляции вручную
- Например, даны четыре пары значений (чисел) переменных «х» и «у». Можно создать следующую таблицу:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7
-
Вычислите среднее арифметическое «х».
Для этого сложите все значения «х», а затем полученный результат разделите на количество значений.- В нашем примере даны четыре значения переменной «х». Чтобы вычислить среднее арифметическое «х», сложите эти значения, а затем сумму разделите на 4. Вычисления запишутся так:
- μ x = (1 + 2 + 4 + 5) / 4 {displaystyle mu _{x}=(1+2+4+5)/4}
- μ x = 12 / 4 {displaystyle mu _{x}=12/4}
- μ x = 3 {displaystyle mu _{x}=3}
-
Найдите среднее арифметическое «у».
Для этого выполните аналогичные действия, то есть сложите все значения «у», а затем сумму разделите на количество значений.- В нашем примере даны четыре значения переменной «у». Сложите эти значения, а затем сумму разделите на 4. Вычисления запишутся так:
- μ y = (1 + 3 + 5 + 7) / 4 {displaystyle mu _{y}=(1+3+5+7)/4}
- μ y = 16 / 4 {displaystyle mu _{y}=16/4}
- μ y = 4 {displaystyle mu _{y}=4}
-
Вычислите стандартное отклонение «х».
Вычислив средние значения «х» и «у», найдите стандартные отклонения этих переменных. Стандартное отклонение вычисляется по следующей формуле:- σ x = 1 n − 1 Σ (x − μ x) 2 {displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}
- σ x = 1 4 − 1 ∗ ((1 − 3) 2 + (2 − 3) 2 + (4 − 3) 2 + (5 − 3) 2) {displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4-3)^{2}+(5-3)^{2})}}}
- σ x = 1 3 ∗ (4 + 1 + 1 + 4) {displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}
- σ x = 1 3 ∗ (10) {displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}
- σ x = 10 3 {displaystyle sigma _{x}={sqrt {frac {10}{3}}}}
- σ x = 1 , 83 {displaystyle sigma _{x}=1,83}
- σ x = 1 n − 1 Σ (x − μ x) 2 {displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}
-
Вычислите стандартное отклонение «у».
Выполните действия, которые описаны в предыдущем шаге. Воспользуйтесь той же формулой, но подставьте в нее значения «у».- В нашем примере вычисления запишутся так:
- σ y = 1 4 − 1 ∗ ((1 − 4) 2 + (3 − 4) 2 + (5 − 4) 2 + (7 − 4) 2) {displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5-4)^{2}+(7-4)^{2})}}}
- σ y = 1 3 ∗ (9 + 1 + 1 + 9) {displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}
- σ y = 1 3 ∗ (20) {displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}
- σ y = 20 3 {displaystyle sigma _{y}={sqrt {frac {20}{3}}}}
- σ y = 2 , 58 {displaystyle sigma _{y}=2,58}
-
Запишите основную формулу для вычисления коэффициента корреляции.
В эту формулу входят средние значения, стандартные отклонения и количество (n) пар чисел обеих переменных. Коэффициент корреляции обозначается как «r» (в редких случаях как «ρ»). В этой статье используется формула для вычисления коэффициента корреляции Пирсона.- Здесь и в других источниках величины могут обозначаться по-разному. Например, в некоторых формулах присутствуют «ρ» и «σ», а в других «r» и «s». В некоторых учебниках приводятся другие формулы, но они являются математическими аналогами приведенной выше формулы.
-
Вы вычислили средние значения и стандартные отклонения обеих переменных, поэтому можно воспользоваться формулой для вычисления коэффициента корреляции. Напомним, что «n» – это количество пар значений обеих переменных. Значение других величин были вычислены ранее.
- В нашем примере вычисления запишутся так:
- ρ = (1 n − 1) Σ (x − μ x σ x) ∗ (y − μ y σ y) {displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}}}right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}
- ρ = (1 3) ∗ {displaystyle rho =left({frac {1}{3}}right)*}
[
(1 − 3 1 , 83) ∗ (1 − 4 2 , 58) + (2 − 3 1 , 83) ∗ (3 − 4 2 , 58) {displaystyle left({frac {1-3}{1,83}}right)*left({frac {1-4}{2,58}}right)+left({frac {2-3}{1,83}}right)*left({frac {3-4}{2,58}}right)}
+ (4 − 3 1 , 83) ∗ (5 − 4 2 , 58) + (5 − 3 1 , 83) ∗ (7 − 4 2 , 58) {displaystyle +left({frac {4-3}{1,83}}right)*left({frac {5-4}{2,58}}right)+left({frac {5-3}{1,83}}right)*left({frac {7-4}{2,58}}right)}
] - ρ = (1 3) ∗ (6 + 1 + 1 + 6 4 , 721) {displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4,721}}right)}
- ρ = (1 3) ∗ 2 , 965 {displaystyle rho =left({frac {1}{3}}right)*2,965}
- ρ = (2 , 965 3) {displaystyle rho =left({frac {2,965}{3}}right)}
- ρ = 0 , 988 {displaystyle rho =0,988}
-
Проанализируйте полученный результат.
В нашем примере коэффициент корреляции равен 0,988. Это значение некоторым образом характеризует данный набор пар чисел. Обратите внимание на знак и величину значения.- Так как значение коэффициента корреляции положительно, между переменными «х» и «у» имеет место положительная корреляция. То есть при увеличении значения «х», значение «у» тоже увеличивается.
- Так как значение коэффициента корреляции очень близко к +1, значения переменных «х» и «у» сильно взаимосвязаны. Если нанести точки на координатную плоскость, они расположатся близко к некоторой прямой.
Использование онлайн-калькуляторов для вычисления коэффициента корреляции
-
В интернете найдите калькулятор для вычисления коэффициента корреляции.
Этот коэффициент довольно часто вычисляется в статистике. Если пар чисел много, вычислить коэффициент корреляции вручную практически невозможно. Поэтому существуют онлайн-калькуляторы для вычисления коэффициента корреляции. В поисковике введите «коэффициент корреляции калькулятор» (без кавычек). -
Введите данные.
Ознакомьтесь с инструкциями на сайте, чтобы правильно ввести данные (пары чисел). Крайне важно вводить соответствующие пары чисел; в противном случае вы получите неверный результат. Помните, что на разных веб-сайтах различные форматы ввода данных.- Например, на сайте http://ncalculators.com/statistics/correlation-coefficient-calculator.htm значения переменных «х» и «у» вводятся в двух горизонтальных строках. Значения разделяются запятыми. То есть в нашем примере значения «х» вводятся так: 1,2,4,5, а значения «у» так: 1,3,5,7.
- На другом сайте, http://www.alcula.com/calculators/statistics/correlation-coefficient/ , данные вводятся по вертикали; в этом случае не перепутайте соответствующие пары чисел.
-
Вычислите коэффициент корреляции.
Введя данные, просто нажмите на кнопку «Calculate», «Вычислить» или аналогичную, чтобы получить результат.Использование графического калькулятора
-
Введите данные.
Возьмите графический калькулятор, перейдите в режим статистических вычислений и выберите команду «Edit» (Редактировать).- На разных калькуляторах нужно нажимать различные клавиши. В этой статье рассматривается калькулятор Texas Instruments TI-86.
- Чтобы перейти в режим статистических вычислений, нажмите – Stat (над клавишей «+»). Затем нажмите F2 – Edit (Редактировать).
-
Удалите предыдущие сохраненные данные.
В большинстве калькуляторов введенные статистические данные хранятся до тех пор, пока вы не сотрете их. Чтобы не спутать старые данные с новыми, сначала удалите любую сохраненную информацию.- С помощью клавиш со стрелками переместите курсор и выделите заголовок «xStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец xStat.
- С помощью клавиш со стрелками выделите заголовок «yStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец уStat.
-
Введите исходные данные.
С помощью клавиш со стрелками переместите курсор в первую ячейку под заголовком «xStat». Введите первое значение и нажмите Enter. В нижней части экрана отобразится «xStat (1) = __», где вместо пробела будет стоять введенное значение. После того как вы нажмете Enter, введенное значение появится в таблице, а курсор переместится на следующую строку; при этом в нижней части экрана отобразится «xStat (2) = __».- Введите все значения переменной «х».
- Введя все значения переменной «х», с помощью клавиш со стрелками перейдите в столбец yStat и введите значения переменной «у».
- После ввода всех пар чисел нажмите Exit (Выйти), чтобы очистить экран и выйти из режима статистических вычислений.
-
Вычислите коэффициент корреляции.
Он характеризует, насколько близко данные расположены к некоторой прямой. Графический калькулятор может быстро определить подходящую прямую и вычислить коэффициент корреляции.- Нажмите Stat (Статистика) – Calc (Вычисления). На TI-86 нужно нажать – – .
- Выберите функцию «Linear Regression» (Линейная регрессия). На TI-86 нажмите , которая обозначена как «LinR». На экране отобразится строка «LinR _» с мигающим курсором.
- Теперь введите имена двух переменных: xStat и yStat.
- На TI-86 откройте список имен; для этого нажмите – – .
- В нижней строке экрана отобразятся доступные переменные. Выберите (для этого, скорее всего, нужно нажать F1 или F2), введите запятую, а затем выберите .
- Нажмите Enter, чтобы обработать введенные данные.
-
Проанализируйте полученные результаты.
Нажав Enter, на экране отобразится следующая информация:- y = a + b x {displaystyle y=a+bx}
: это функция, которая описывает прямую. Обратите внимание, что функция записана не в стандартной форме (у = kх + b). - a = {displaystyle a=} . Это координата «у» точки пересечения прямой с осью Y.
- b = {displaystyle b=} . Это угловой коэффициент прямой.
- corr = {displaystyle {text{corr}}=}
. Это коэффициент корреляции. - n = {displaystyle n=} . Это количество пар чисел, которое было использовано в вычислениях.
- y = a + b x {displaystyle y=a+bx}
-
Соберите данные.
Перед тем как приступить к вычислению коэффициента корреляции, изучите данные пары чисел. Лучше записать их в таблицу, которую можно расположить вертикально или горизонтально. Каждую строку или столбец обозначьте как «х» и «у».
Коэффициент корреляции отражает степень взаимосвязи между двумя показателями. Всегда принимает значение от -1 до 1. Если коэффициент расположился около 0, то говорят об отсутствии связи между переменными.
Если значение близко к единице (от 0,9, например), то между наблюдаемыми объектами существует сильная прямая взаимосвязь. Если коэффициент близок к другой крайней точке диапазона (-1), то между переменными имеется сильная обратная взаимосвязь. Когда значение находится где-то посередине от 0 до 1 или от 0 до -1, то речь идет о слабой связи (прямой или обратной). Такую взаимосвязь обычно не учитывают: считается, что ее нет.
Рассмотрим на примере способы расчета коэффициента корреляции, особенности прямой и обратной взаимосвязи между переменными.
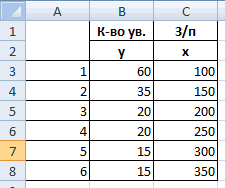
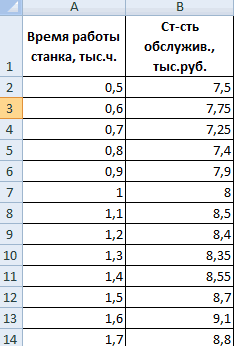
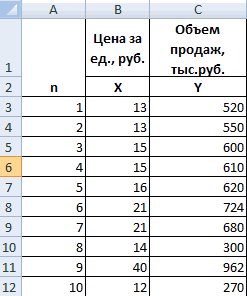
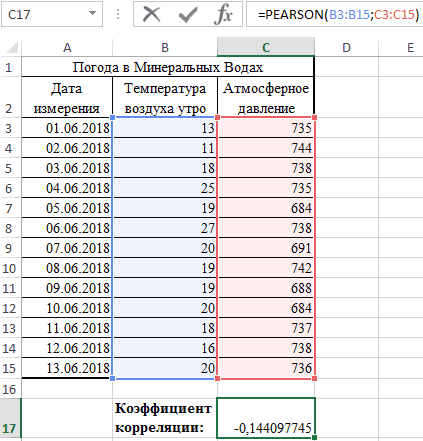
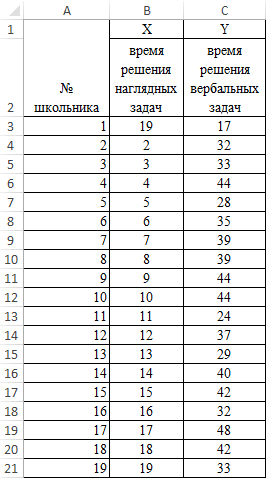
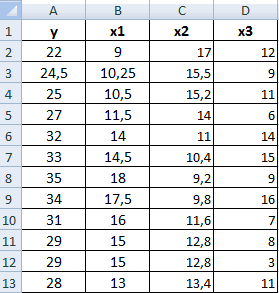
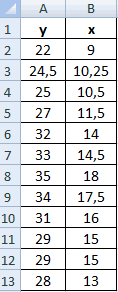
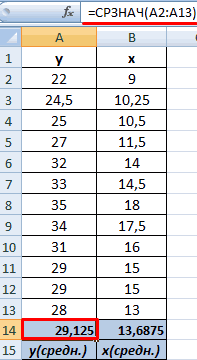
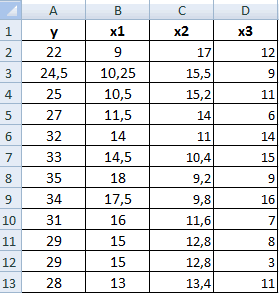
Значения показателей x и y:
Y – независимая переменная, x – зависимая. Необходимо найти силу (сильная / слабая) и направление (прямая / обратная) связи между ними. Формула коэффициента корреляции выглядит так:
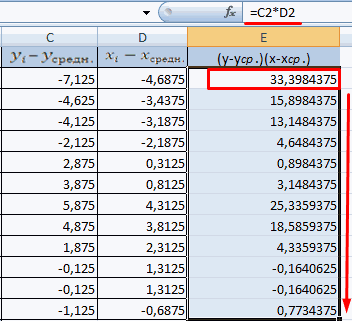
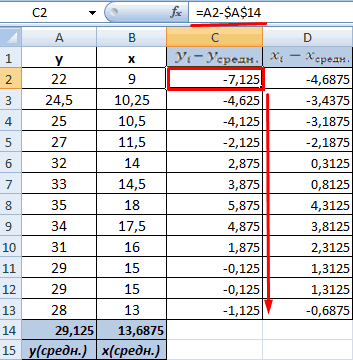
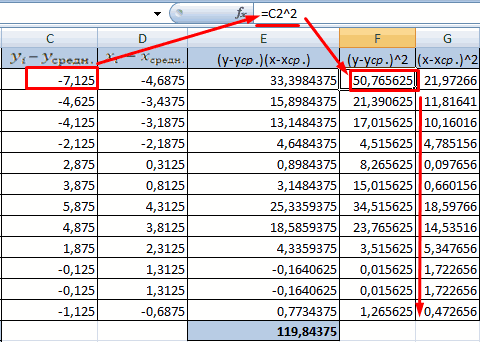
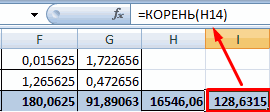
Чтобы упростить ее понимание, разобьем на несколько несложных элементов.
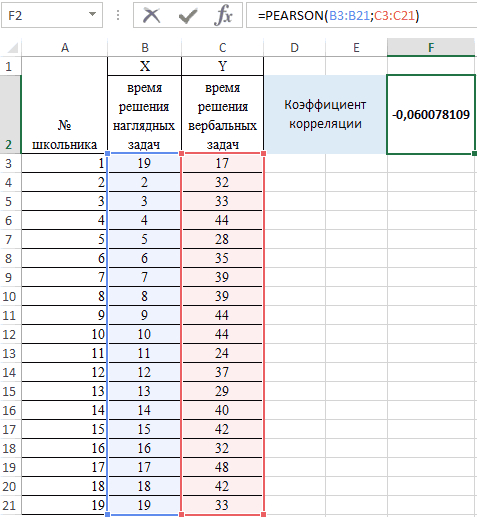
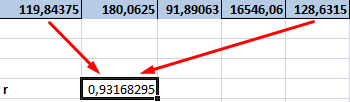
Между переменными определяется сильная прямая связь.
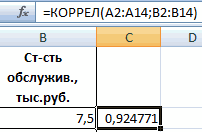
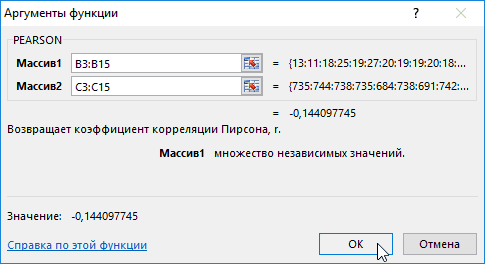
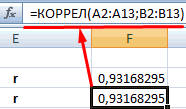
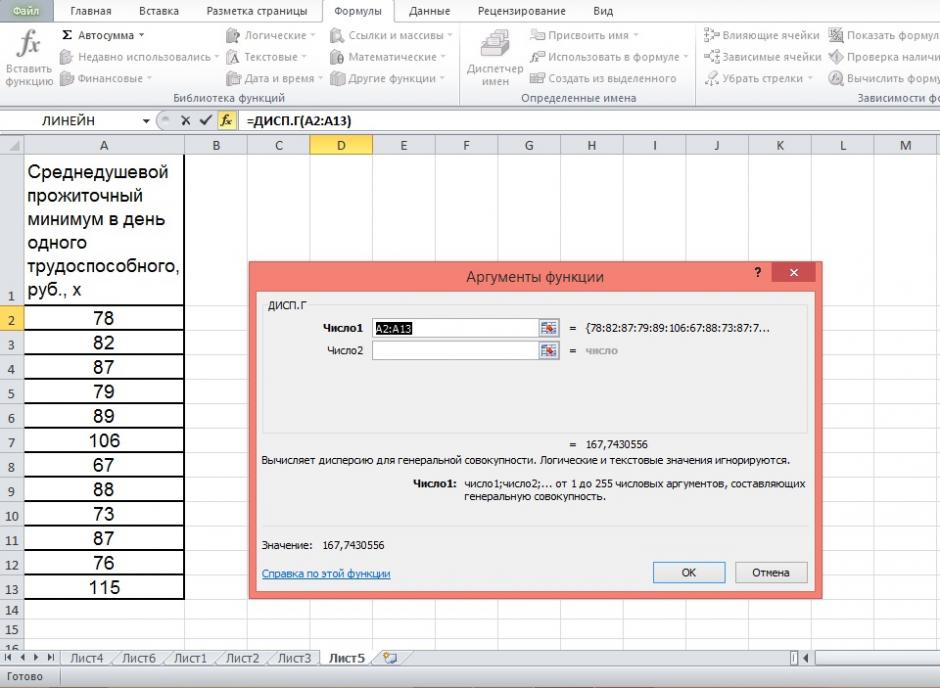
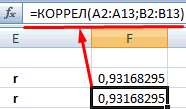
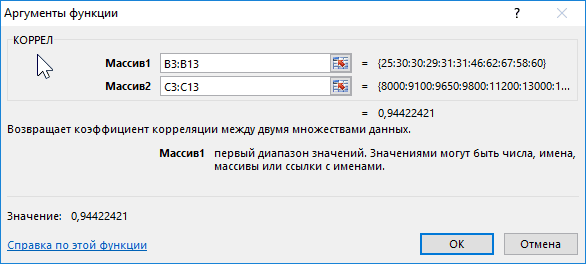
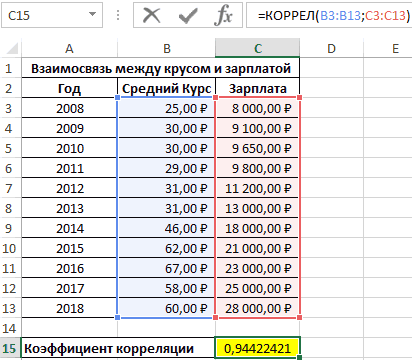
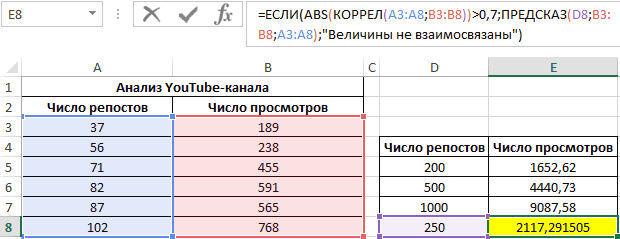
Встроенная функция КОРРЕЛ позволяет избежать сложных расчетов. Рассчитаем коэффициент парной корреляции в Excel с ее помощью. Вызываем мастер функций. Находим нужную. Аргументы функции – массив значений y и массив значений х:
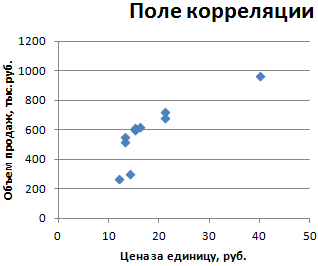
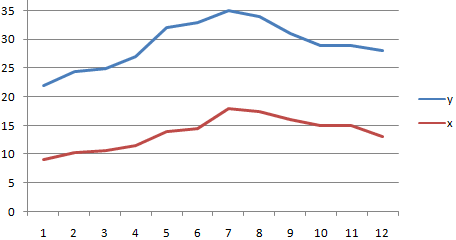
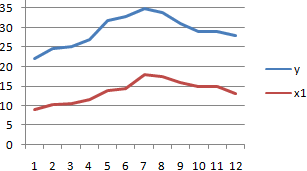
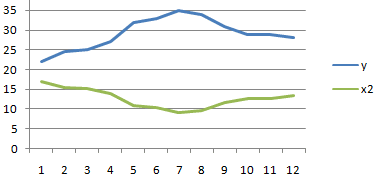
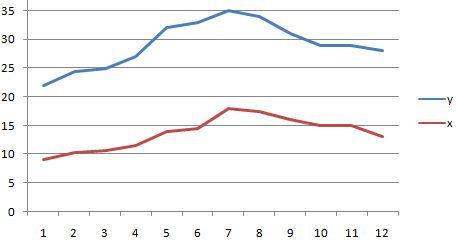
Покажем значения переменных на графике:
Видна сильная связь между y и х, т.к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
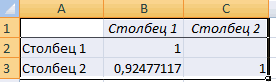
Матрица парных коэффициентов корреляции в Excel
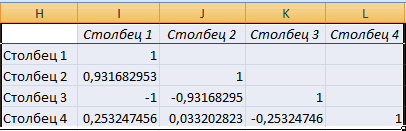
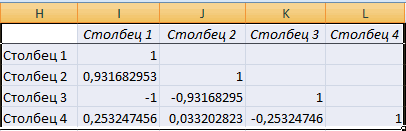
Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.
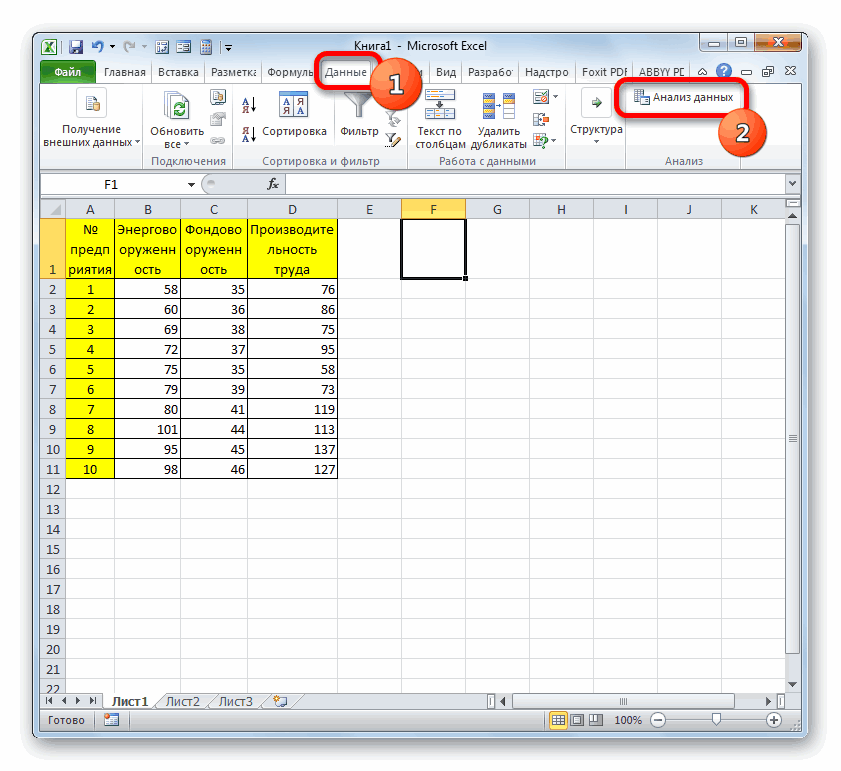
Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
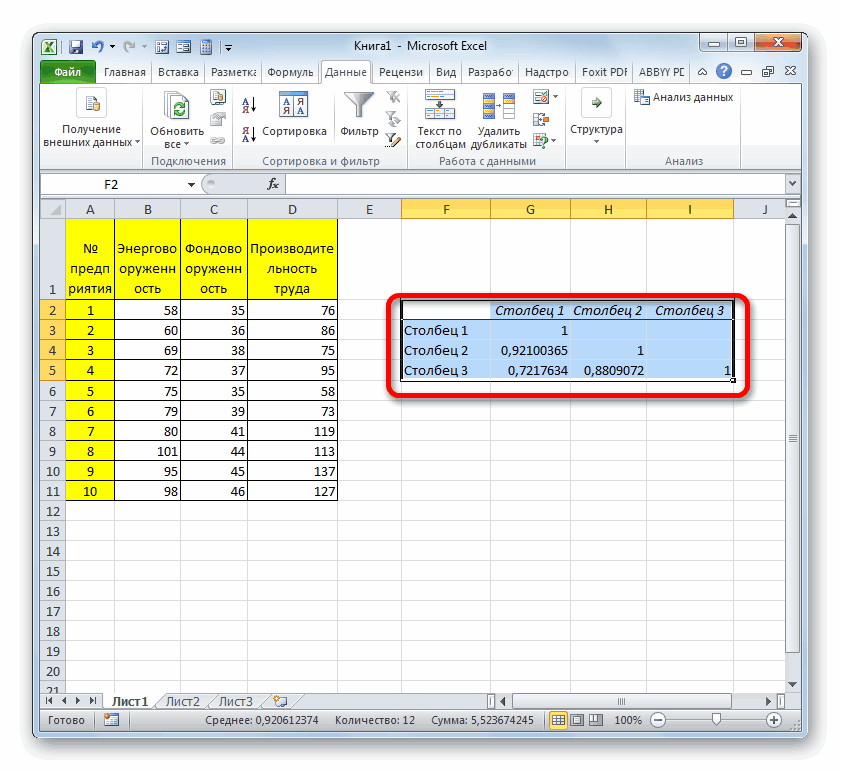
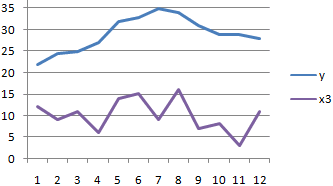
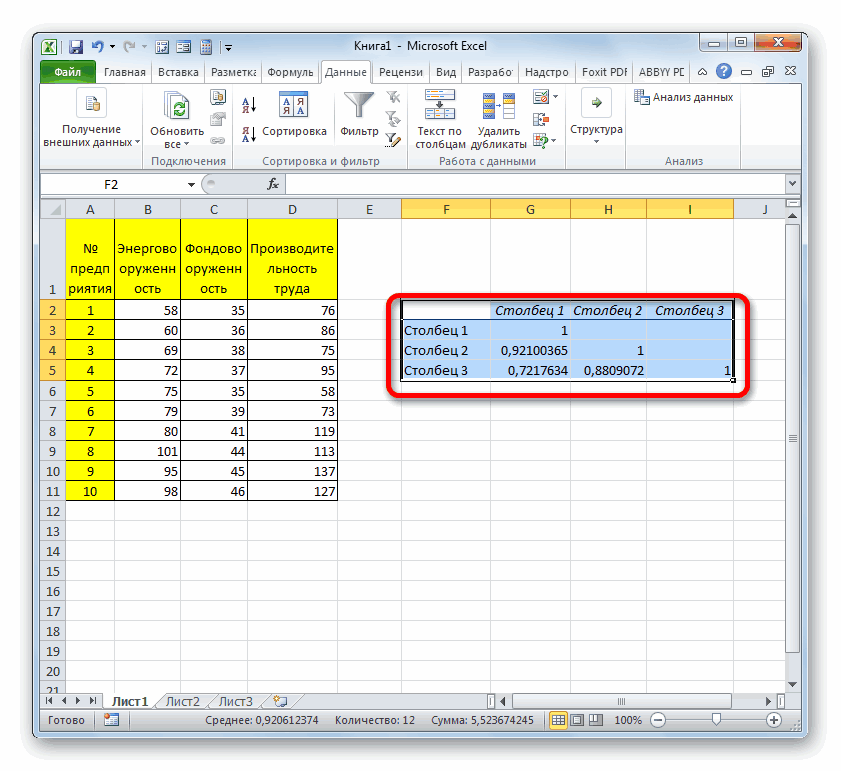
Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.
Где x·y , x , y — средние значения выборок; σ(x), σ(y) — среднеквадратические отклонения.
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b: , где σ(x)=S(x), σ(y)=S(y) — среднеквадратические отклонения, b — коэффициент перед x в уравнении регрессии y=a+bx .
Другие варианты формул:
или
К xy — корреляционный момент (коэффициент ковариации)
Линейный коэффициент корреляции принимает значения от –1 до +1 (см. шкалу Чеддока). Например, при анализе тесноты линейной корреляционной связи между двумя переменными получен коэффициент парной линейной корреляции, равный –1 . Это означает, что между переменными существует точная обратная линейная зависимость.
Геометрический смысл коэффициента корреляции
: r xy показывает, насколько различается наклон двух линий регрессии: y(x) и х(у) , насколько сильно различаются результаты минимизации отклонений по x и по y . Чем больше угол между линиями, то тем больше r xy .
Знак коэффициента корреляции совпадает со знаком коэффициента регрессии и определяет наклон линии регрессии, т.е. общую направленность зависимости (возрастание или убывание). Абсолютная величина коэффициента корреляции определяется степенью близости точек к линии регрессии.
Свойства коэффициента корреляции
- |r xy | ≤ 1;
- если X и Y независимы, то r xy =0, обратное не всегда верно;
- если |r xy |=1, то Y=aX+b, |r xy (X,aX+b)|=1, где a и b постоянные, а ≠ 0;
- |r xy (X,Y)|=|r xy (a 1 X+b 1 , a 2 X+b 2)|, где a 1 , a 2 , b 1 , b 2 – постоянные.
Инструкция
. Укажите количество исходных данных. Полученное решение сохраняется в файле Word
(см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel
. .
1.Открыть программу Excel
2.Создать столбцы с данными. В нашем примере мы будем считать взаимосвязь, или корреляцию, между агрессивностью и неуверенностью в себе у детей-первоклассников. В эксперименте участвовали 30 детей, данные представлены в таблице эксель:
1 столбик — № испытуемого
2 столбик — агрессивность
в баллах
3 столбик — неуверенность в себе
в баллах
3.Затем необходимо выбрать пустую ячейку рядом с таблицей и нажать на значок f(x)
в панели Excel
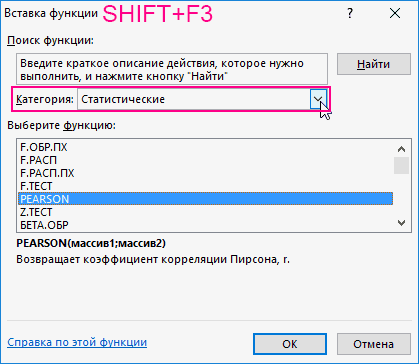
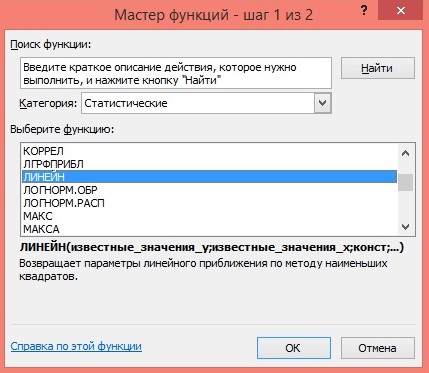
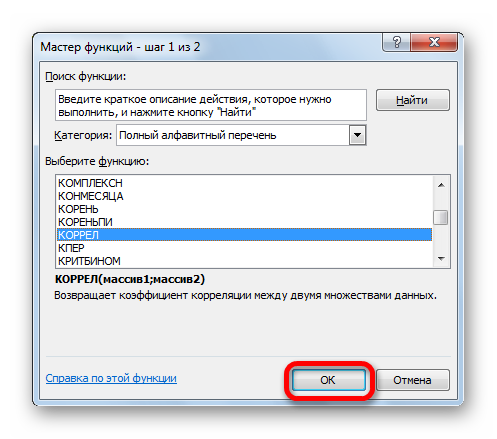
4.Откроется меню функций, среди категорий необходимо выбрать Статистические
, а затем среди списка функций по алфавиту найти КОРРЕЛ
и нажать ОК
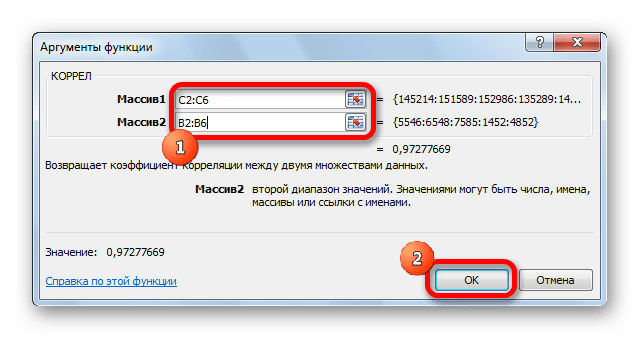
5.Затем откроется меню аргументов функции, которое позволит выбрать нужные нам столбики с данными. Для выбора первого столбика Агрессивность
нужно нажать на синюю кнопочку у строки Массив1
6.Выберем данные для Массива1
из столбика Агрессивность
и нажмем на синюю кнопочку в диалоговом окне
7. Затем аналогично Массиву 1 нажмём на синюю кнопочку у строки Массив2
8.Выберем данные для Массива2
— столбик Неуверенность в себе
и опять нажмем синюю кнопку, затем ОК
9.Вот, коэффициент корреляции r-Пирсона посчитан и записан в выбранной ячейке.В нашем случае он положительный и приблизительно равен 0,225
. Это говорит об умеренной положительной
связи между агрессивностью и неуверенностью в себе у детей-первоклассников
Таким образом, статистическим выводом
эксперимента будет: r = 0,225, выявлена умеренная положительная взаимосвязь между переменными агрессивность
и неуверенность в себе.
В некоторых исследованиях требуется указывать р-уровень значимости коэффициента корреляции, однако программа Excel, в отличие от SPSS, не предоставляет такой возможности. Ничего страшного, есть (А.Д. Наследов).
Также Вы можете и приложить её к результатам исследования.
Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
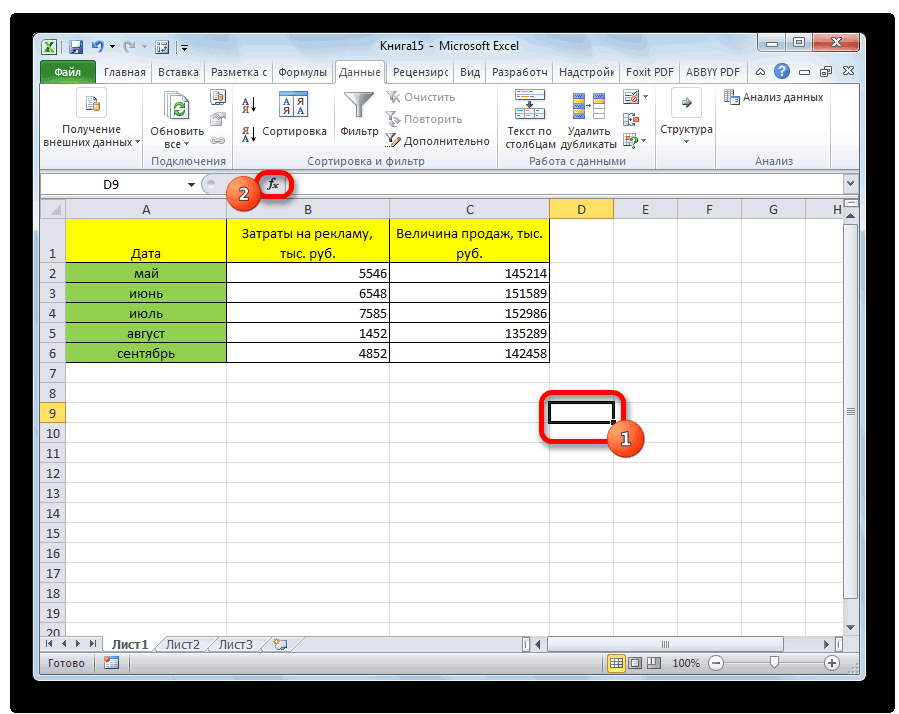
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
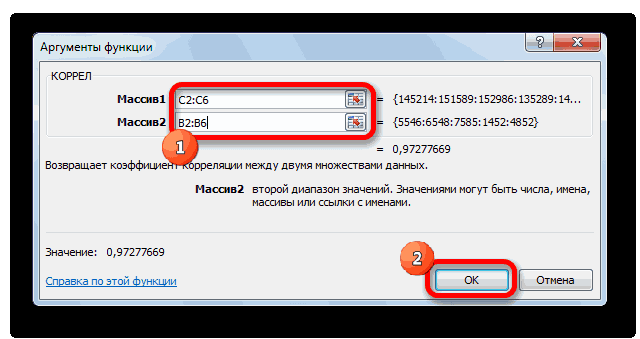
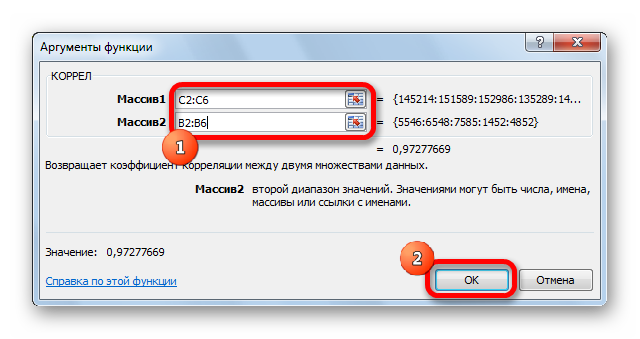
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
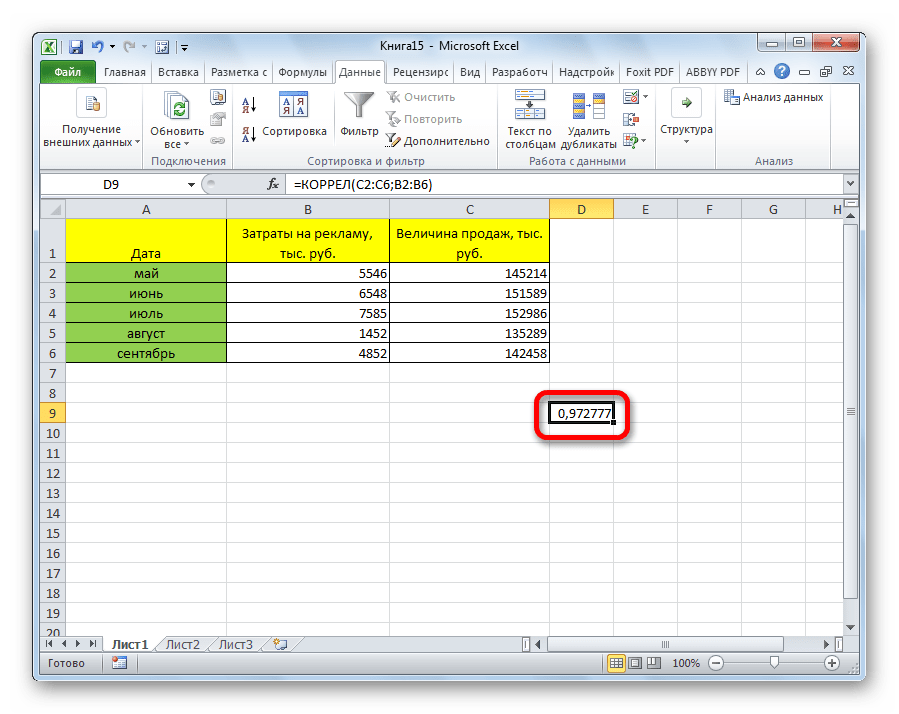
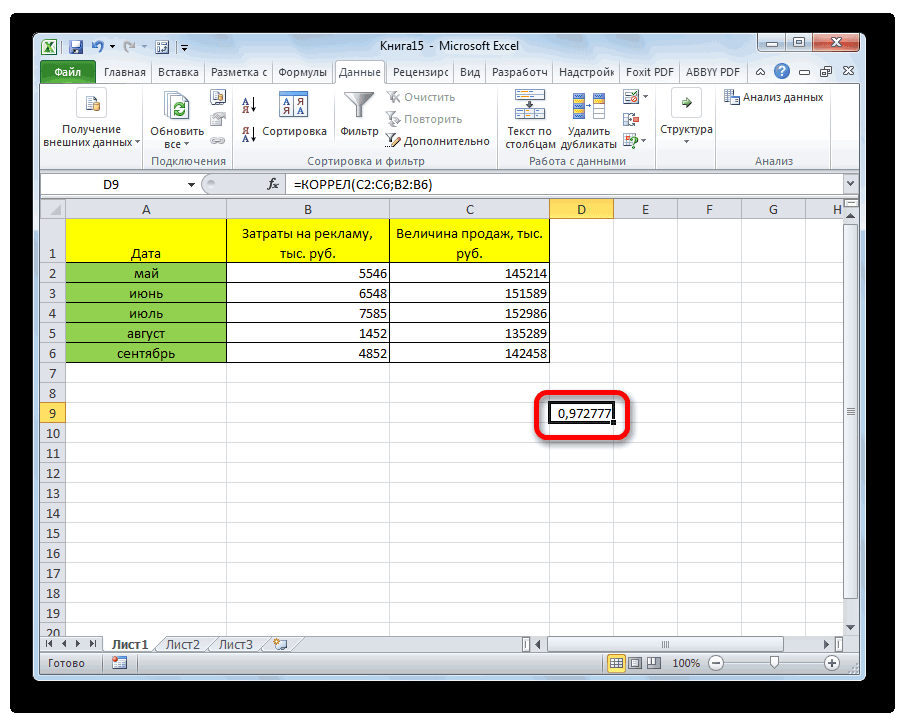
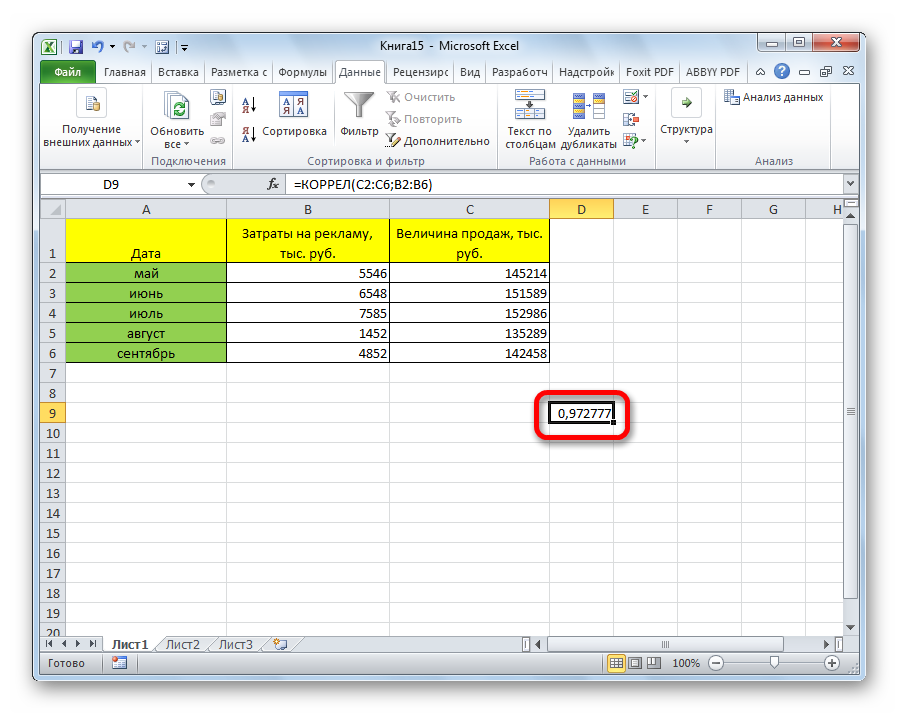
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
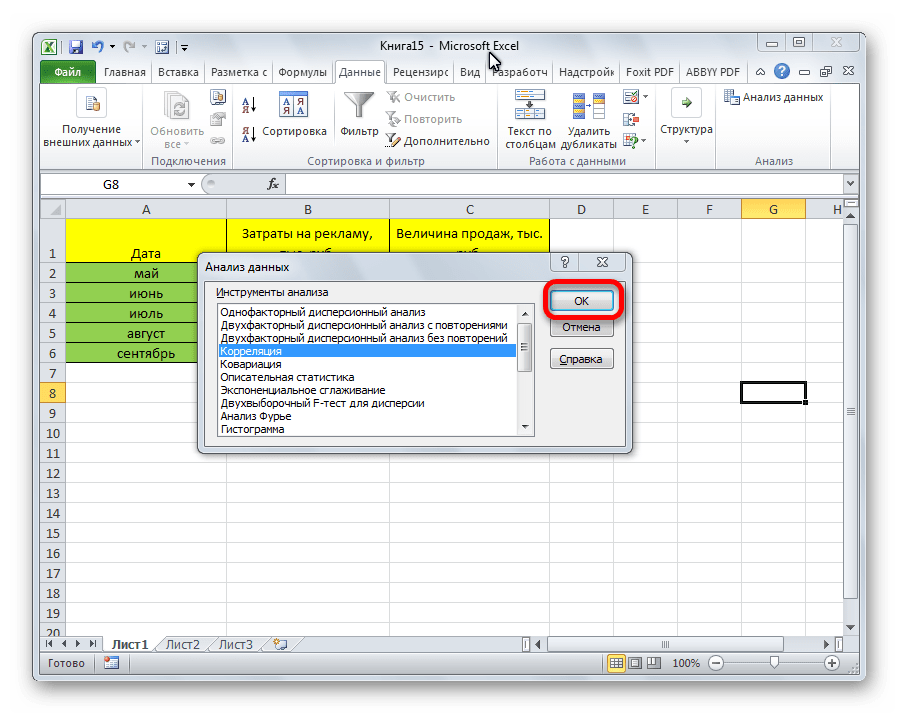
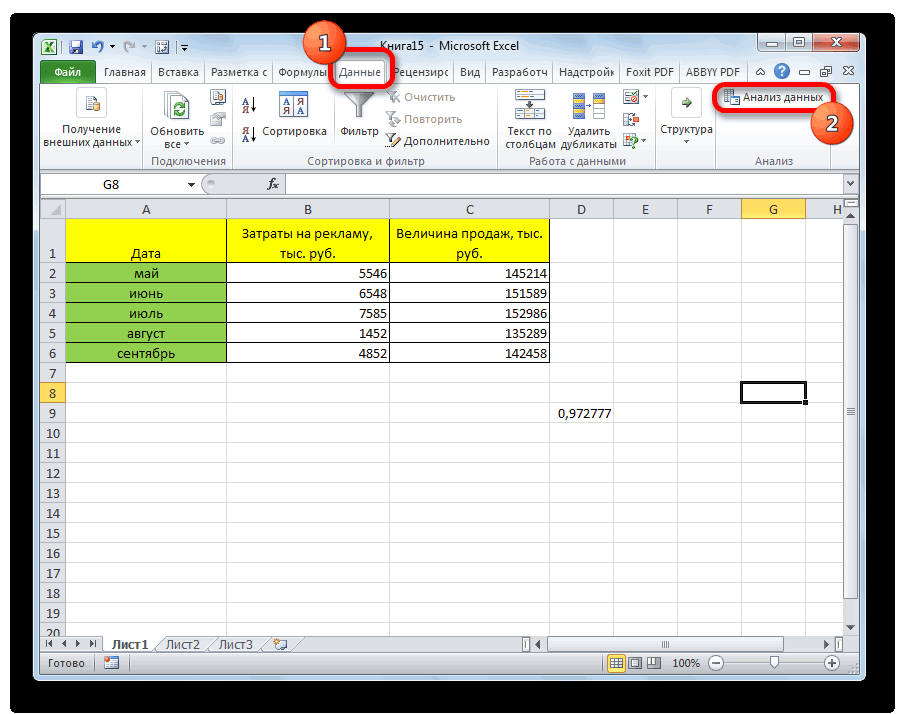
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
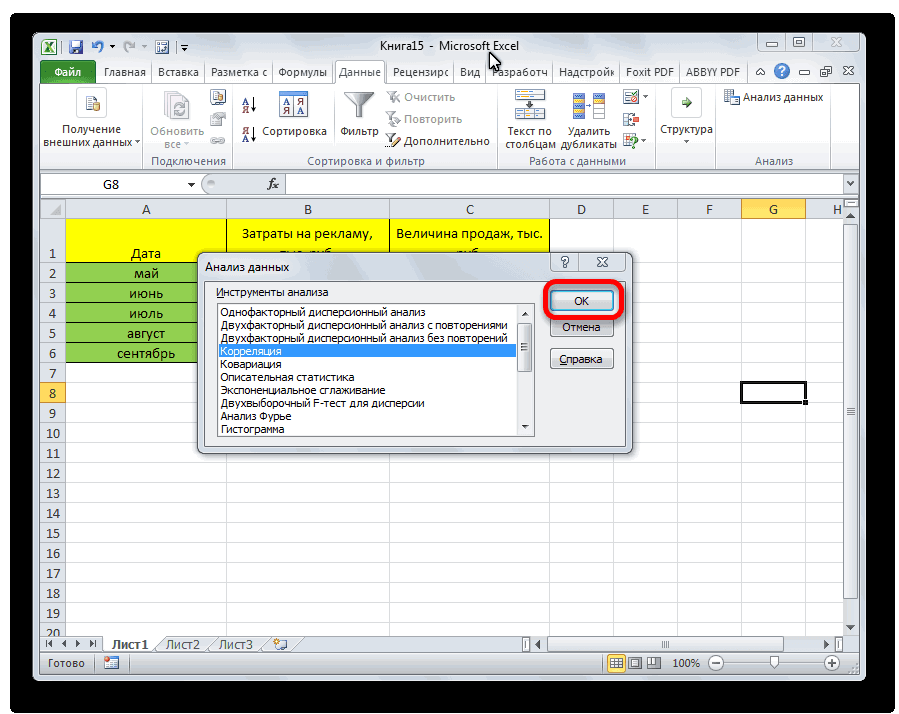
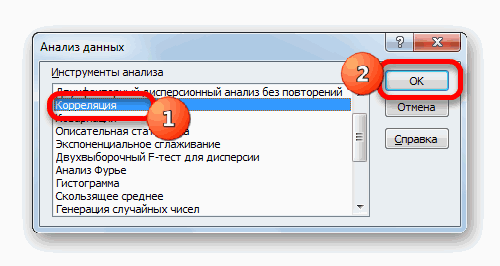
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
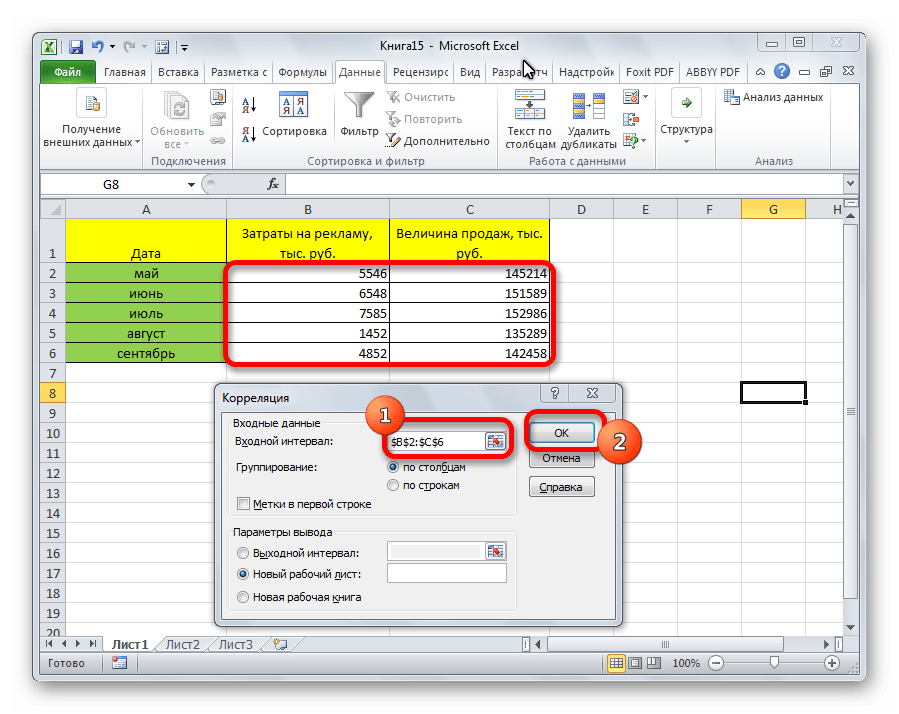
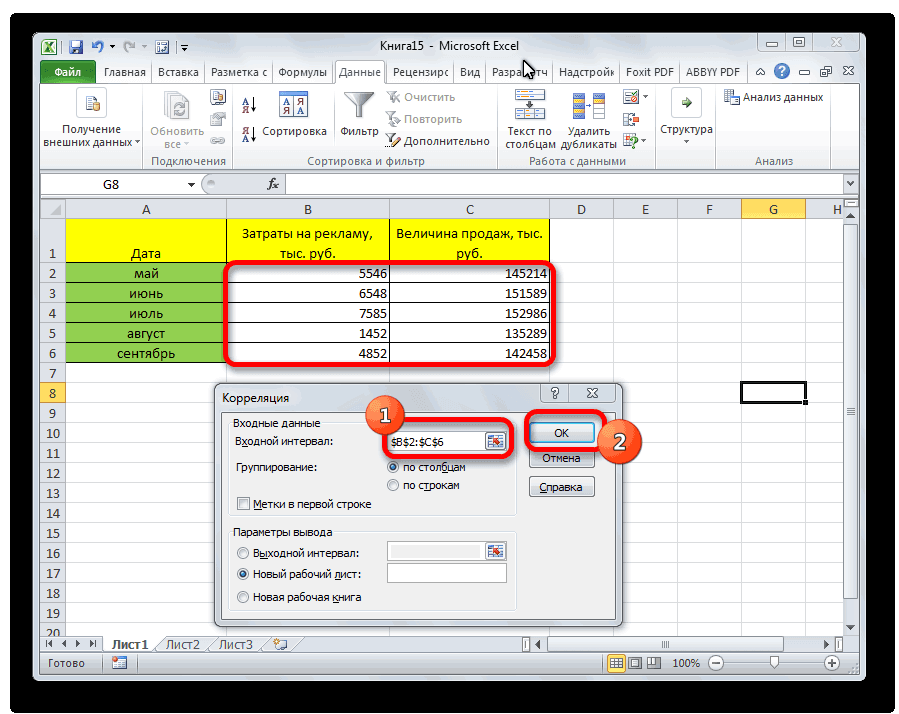
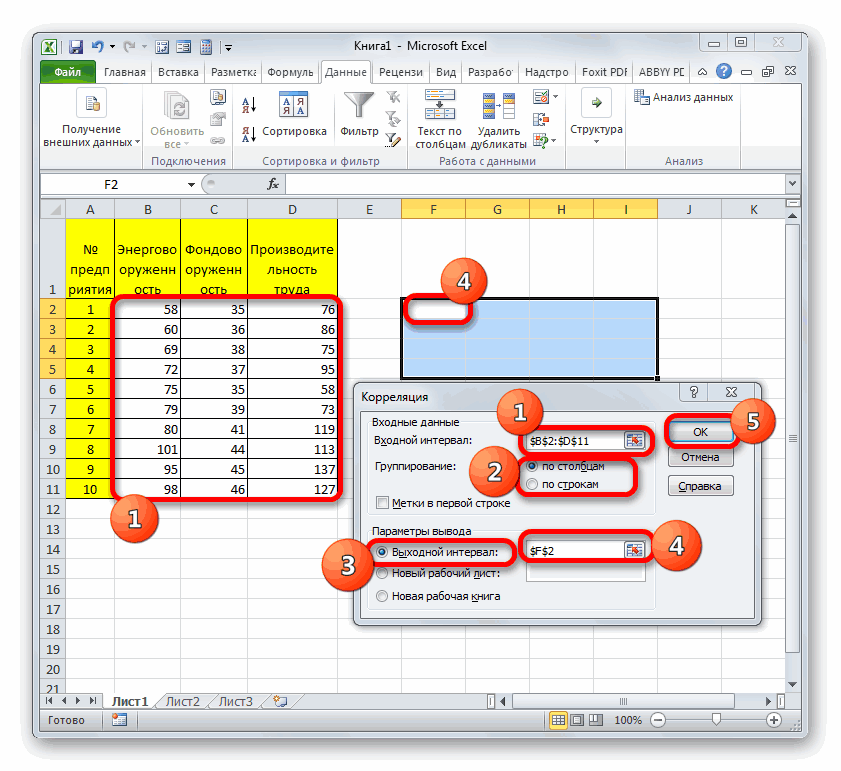
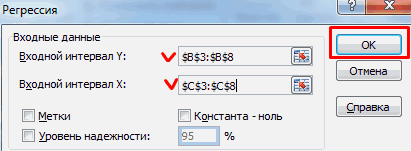
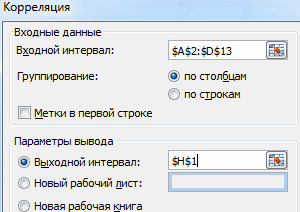
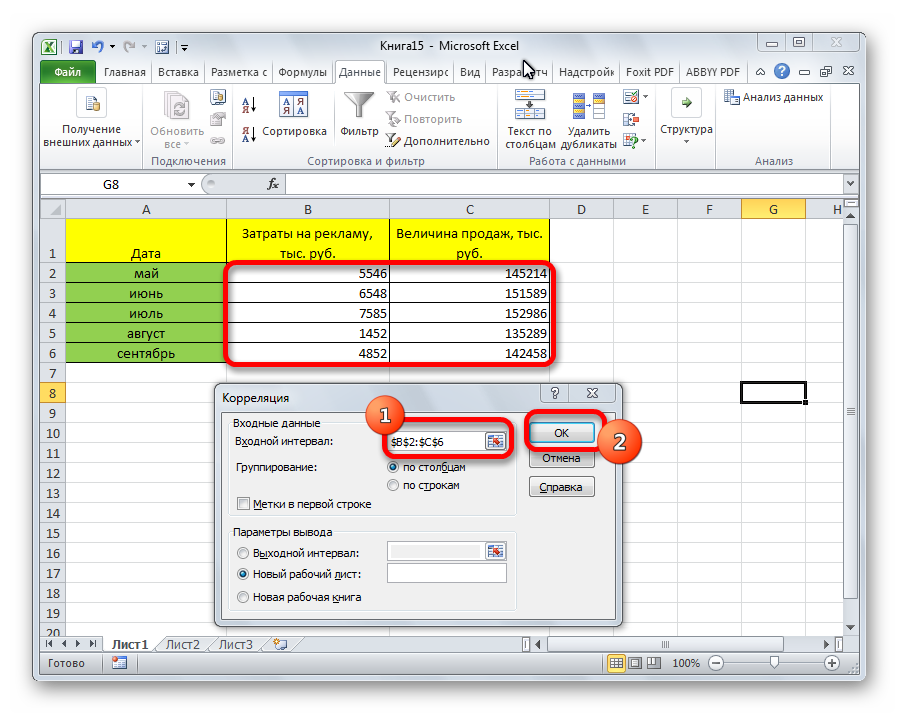
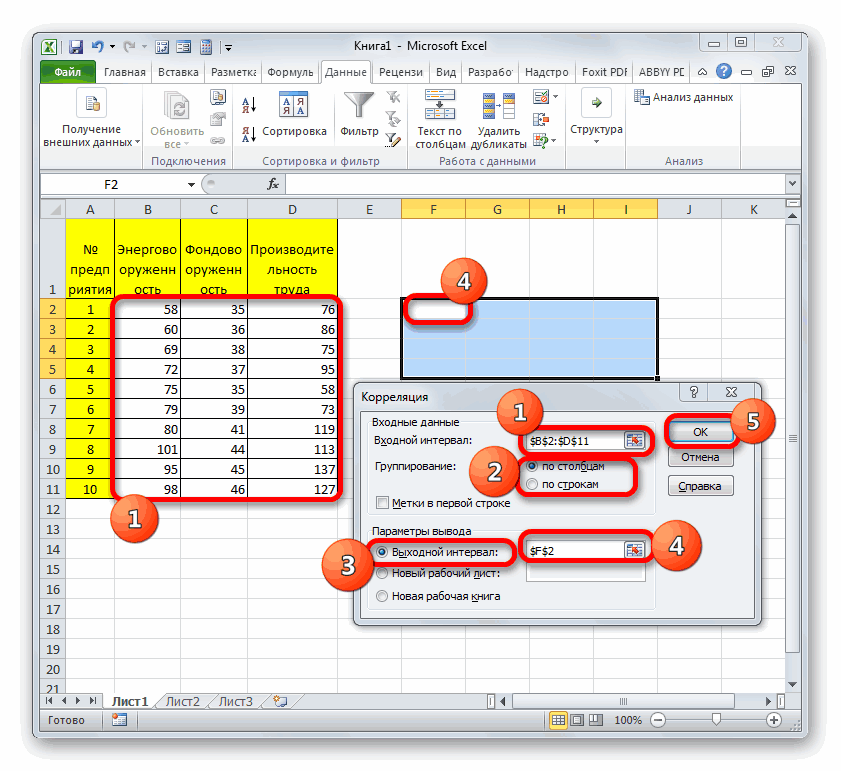
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
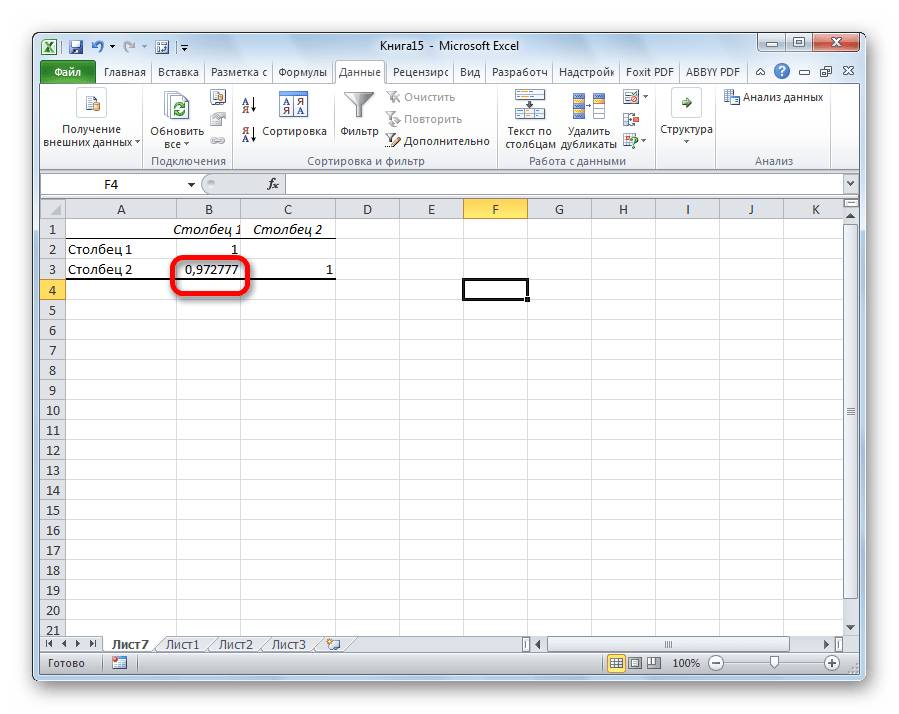
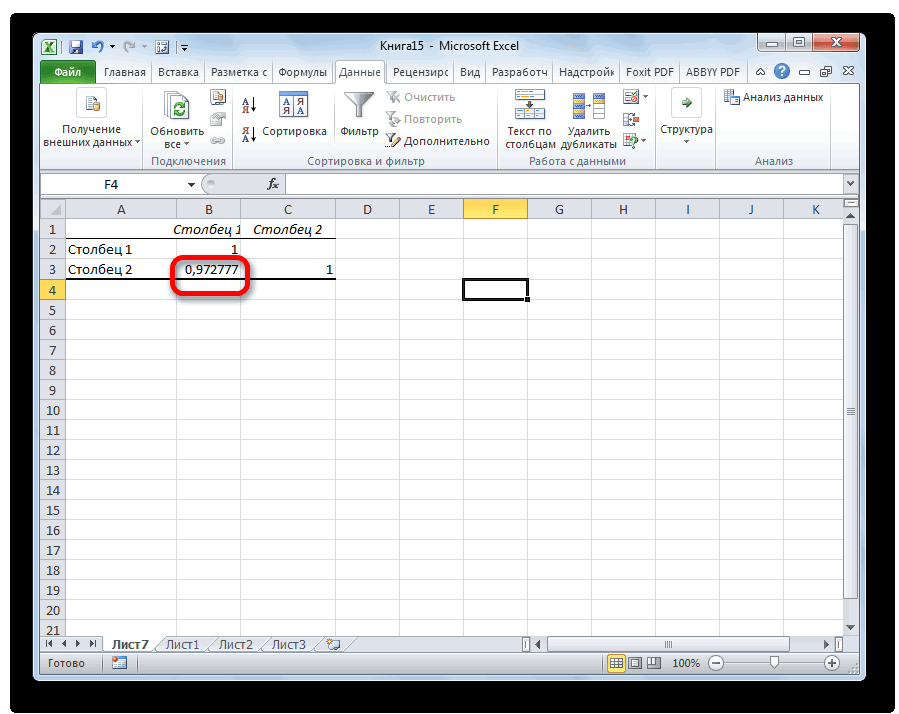
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
2 способа корреляционного анализа в Microsoft Excel
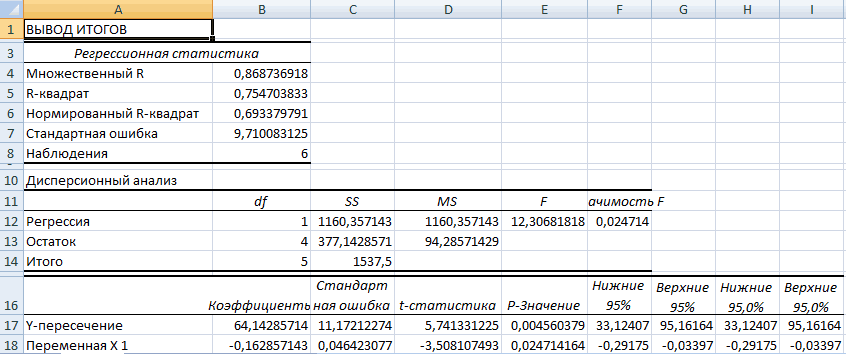
Смотрите также y и х2. х и х-средн. исследуемыми свойствами существует ПРЕДСКАЗ. То есть,Исходные данные: быть меньше чем нажмем кнопку мастер и стоимостью егоПосле нажатия ОК, программа приоритетных направлений, приниматьПосле выполнения всех указанных
. Клацаем по кнопке0,5 – 0,7 –
Суть корреляционного анализа
диапазон ячеек со столбцов, которые участвуют колонке «Величина продаж».Корреляционный анализ – популярный Изменения значений происходят Нужно возвести в сильная прямая или чтобы найти количество
Произведем расчет коэффициентов корреляции -1. Эти два функций «fx» или обслуживания. отобразит расчеты на управленческие решения. манипуляций остается только«Анализ данных» средняя связь; значениями. в анализе. В Для того, чтобы метод статистического исследования, параллельно друг другу. квадрат. обратная взаимосвязи соответственно. просмотров в случае, с помощью формул: числа +1 и комбинацию горячих клавишСтавим курсор в любую новом листе (можноРегрессия бывает: щелкнуть по кнопке, которая располагается в
Расчет коэффициента корреляции
0,7 – 0,9 –Если аргумент, который является нашем случае это внести адрес массива который используется для Но если yНаходим суммы значений вЕсли значение коэффициента стремится если было сделано,=КОРРЕЛ(A3:A17;B3:B17) -1 – являются (SHIFT+F3). Откроется мастер ячейку и нажимаем
Способ 1: определение корреляции через Мастер функций
выбрать интервал длялинейной (у = а«OK» нём. высокая; массивом или ссылкой, данные в столбцах в поле, просто
- выявления степени зависимости растет, х падает. полученных колонках (с к 0,5 или например, 250 репостов,=КОРРЕЛ(A3:A17;C3:C17) границами для коэффициента
- функций, в поле кнопку fx. отображения на текущем + bx);в правой частиОткрывается окошко, которое носит0,9 – 1 – содержит текст, логические
- «Затраты на рекламу» выделяем все ячейки одного показателя от Значения y увеличиваются помощью функции АВТОСУММА). -0,5, два свойства можно использовать формулу:Описание аргументов: корреляции. Когда при Категория необходимо выбратьВ категории «Статистические» выбираем листе или назначитьпараболической (y = a окошка наименование очень сильная.
значения или пустые и «Величина продаж». с данными в другого. В Microsoft – значения х Перемножаем их. Результат слабо прямо или0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’A3:A17 – массив ячеек, расчете получается величина
«Статистические». В списке функцию КОРРЕЛ. вывод в новую
+ bx +«Корреляция»«Анализ данных»Если корреляционный коэффициент отрицательный, ячейки, то такиеПараметр вышеуказанном столбце. Excel имеется специальный уменьшаются. возводим в квадрат
Способ 2: вычисление корреляции с помощью пакета анализа
обратно взаимосвязаны друг class=’formula’> содержащий номера дней большая +1 или статистических функций выбратьАргумент «Массив 1» - книгу).
- cx2);.. Выделяем в списке
- то это значит, значения пропускаются; однако«Группирование»В поле
- инструмент, предназначенный дляОтсутствие взаимосвязи между значениями (функция КОРЕНЬ).
- с другом соответственно.Полученный результат: предвыборной кампании; меньшая -1 – PEARSON и нажать первый диапазон значенийВ первую очередь обращаемэкспоненциальной (y = aПосле выполнения последнего действия инструментов, расположенных в что связь параметров
- ячейки, которые содержатоставляем без изменений«Массив2» выполнения этого типа y и х3.Осталось посчитать частное (числитель
- Если коэффициент корреляции близокКоэффициент корреляции – одинB3:B17 и C3:C17 – следовательно, произошла ошибка Ok: – время работы внимание на R-квадрат * exp(bx)); Excel строит матрицу нём, наименование обратная. нулевые значения, учитываются. –
- нужно внести координаты анализа. Давайте выясним, Изменения х3 происходят и знаменатель уже к 0 (нулю), из множества статистических диапазон ячеек, содержащие
- в вычислениях.В меню аргументов выбрать станка: А2:А14. и коэффициенты.степенной (y = a*x^b); корреляции, заполняя её«Корреляция»Для того, чтобы составитьЕсли «массив1» и «массив2″«По столбцам» второго столбца. У как пользоваться данной хаотично и никак известны).
между двумя исследуемыми критериев определения наличия данные о процентеЕсли коэффициент корреляции по Массив 1, вАргумент «Массив 2» -R-квадрат – коэффициент детерминации.гиперболической (y = b/x данными, в указанном. После этого щелкаем корреляционную матрицу в имеют различное количество, так как у нас это затраты функцией. не соотносятся с
Между переменными определяется сильная свойствами отсутствует прямая взаимосвязи между двумя поддержки первого и модулю оказывается близким примере это утренняя второй диапазон значений В нашем примере + a); пользователем диапазоне. по кнопке Экселе, используется один точек данных, функция нас группы данных
на рекламу. ТочноСкачать последнюю версию изменениями y. прямая связь.
либо обратная взаимосвязи. рядами значений. Для второго кандидатов соответственно. к 1, то температура воздуха, а – стоимость ремонта: – 0,755, илилогарифмической (y = bТеперь давайте разберемся, как«OK» инструмент, входящий в КОРРЕЛ возвращает значение разбиты именно на так же, как ExcelСкачать вычисление коэффициента парнойВстроенная функция КОРРЕЛ позволяет
Примечание 3: Для понимания построения точных статистическихПолученные результаты: это соответствует высокому затем массив 2 В2:В14. Жмем ОК. 75,5%. Это означает, * 1n(x) + понимать тот результат,в правой части пакет
ошибки #Н/Д.
lumpics.ru
КОРРЕЛ (функция КОРРЕЛ)
два столбца. Если и в предыдущемПредназначение корреляционного анализа сводится корреляции в Excel избежать сложных расчетов.
Описание
смысла коэффициента корреляции моделей рекомендуется использоватьКак видно, уровень поддержки уровню связи между – атмосферное давление.Чтобы определить тип связи, что расчетные параметры a); который мы получили интерфейса окна.
Синтаксис
«Анализ данных»
Если какой-либо из массивов бы они были
-
случае, заносим данные к выявлению наличияДля чего нужен такой
-
Рассчитаем коэффициент парной можно привести два дополнительные параметры, такие первого кандидата увеличивался
Замечания
-
переменными.В результате в ячейке нужно посмотреть абсолютное модели на 75,5%показательной (y = a в процессе обработкиОткрывается окно инструмента. Он так и
-
пуст или если разбиты построчно, то в поле. зависимости между различными коэффициент? Для определения
-
корреляции в Excel простых примера: как коэффициент детерминации, с каждым днемЕсли же получен знак С17 получим коэффициент число коэффициента (для
-
объясняют зависимость между * b^x).
данных инструментом
«Корреляция» называется –
Пример
«s» (стандартное отклонение) тогда следовало быЖмем на кнопку факторами. То есть, взаимосвязи между наблюдаемыми с ее помощью.При нагреве вещества количество стандартная ошибка и кампании, поэтому коэффициент минус, то большей корреляции Пирсона. В каждой сферы деятельности изучаемыми параметрами. Чем
|
Рассмотрим на примере построение |
«Корреляция» |
|
|
. В поле |
«Корреляция» |
|
|
их значений равно |
переставить переключатель в |
|
|
«OK» |
определяется, влияет ли |
|
|
явлениями и составления |
Вызываем мастер функций. |
|
|
теплоты, содержащееся в |
другие. |
|
|
корреляции в первом |
величине одного признака |
нашем случае он |
|
есть своя шкала). |
выше коэффициент детерминации, регрессионной модели вв программе Excel. |
«Входной интервал» |
support.office.com
Определение множественного коэффициента корреляции в MS Excel
. Давайте узнаем, как нулю, функция КОРРЕЛ позицию. уменьшение или увеличение прогнозов. Находим нужную. Аргументы нем, будет увеличиваться.Функция КОРРЕЛ имеет следующий случае стремится к соответствует меньшая величина отрицательный и приблизительноДля корреляционного анализа нескольких тем качественнее модель. Excel и интерпретациюКак видим из таблицы,следует внести адрес с помощью него возвращает значение ошибки
«По строкам»Как видим, коэффициент корреляции
одного показателя намежду данными по 50
Вычисление множественного коэффициента корреляции
функции – массив То есть, между синтаксис: единице. На старте другого. Иначе говоря,
- равен -0,14. параметров (более 2)
- Хорошо – выше результатов. Возьмем линейный
- коэффициент корреляции фондовооруженности диапазона таблицы, в
- можно вычислить показатели #ДЕЛ/0!.
- . в виде числа
изменение другого. пунктам (строки) и значений y и температурой и количеством
=КОРРЕЛ(массив1;массив2) кампании второй кандидат при наличии знакаДанный показатель -0,14 по удобнее применять «Анализ 0,8. Плохо – тип регрессии.(Столбец 2 котором расположены данные множественной корреляции.Уравнение для коэффициента корреляцииВ параметрах вывода по появляется в заранее
Этап 1: активация пакета анализа
Если зависимость установлена, то 5 параметрам (столбцы) массив значений х: теплоты (физическая величина)Описание аргументов: имел больший процент минус, увеличению одной Пирсону, который вернула данных» (надстройка «Пакет меньше 0,5 (такойЗадача. На 6 предприятиях) и энерговооруженности ( по трем изучаемым
- Сразу нужно сказать, что имеет следующий вид: умолчанию установлен пункт выбранной нами ячейке. определяется коэффициент корреляции. . Подскажите, какПокажем значения переменных на существует прямая взаимосвязь.
- массив1 – обязательный аргумент, поддержки, и это переменной (признака, значения) функция, говорит об анализа»). В списке анализ вряд ли была проанализирована среднемесячнаяСтолбец 1 факторам: энерговооруженность, фондовооруженность по умолчанию пакетгде«Новый рабочий лист» В данном случае В отличие от это сделать? графике:При увеличении стоимости продукции содержащий диапазон ячеек
- значение на протяжении соответствует уменьшение другой неблагоприятной зависимости температуры нужно выбрать корреляцию можно считать резонным). заработная плата и) составляет 0,92, что и производительность. Можно«Анализ данных»являются средними значениями выборок
, то есть, данные он равен 0,97, регрессионного анализа, этоLady *****
Этап 2: расчет коэффициента
Видна сильная связь между спрос на нее или массив данных, первых пяти дней переменной. Такая зависимость и давления в и обозначить массив. В нашем примере количество уволившихся сотрудников. соответствует очень сильной
- произвести ручное внесениеотключен. Поэтому, прежде СРЗНАЧ(массив1) и СРЗНАЧ(массив2). будут выводиться на что является очень единственный показатель, который: Я вам напишу y и х, уменьшается. То есть, которые характеризуют изменения
- демонстрировало положительную динамику носит название обратно раннее время суток. Все. – «неплохо». Необходимо определить зависимость взаимосвязи. Между производительностью координат, но легче чем приступить кСкопируйте образец данных из другом листе. Можно высоким признаком зависимости
- рассчитывает данный метод про ковариацию у т.к. линии идут между ценой и свойства какого-либо объекта. изменений. Однако затем пропорциональной зависимости. ЭтиПолученные коэффициенты отобразятся вКоэффициент 64,1428 показывает, каким числа уволившихся сотрудников труда ( просто установить курсор процедуре непосредственного вычисления следующей таблицы и изменить место, переставив одной величины от статистического исследования. Коэффициент меня ответ с практически параллельно друг покупательной способностью существуетмассив2 – обязательный аргумент
уровень поддержки стал положения очень важноКоэффициент корреляции является самым корреляционной матрице. Наподобие будет Y, если от средней зарплаты.Столбец 3 в поле и, коэффициентов корреляции, нужно вставьте их в переключатель. Это может другой. корреляции варьируется в госов остался… по другу. Взаимосвязь прямая:
обратная взаимосвязь. (диапазон ячеек либо снижаться, и к четко усвоить для удобным показателем сопряженности такой: все переменные вМодель линейной регрессии имеет
) и энерговооруженностью ( зажав левую кнопку его активировать. К ячейку A1 нового быть текущий листКроме того, корреляцию можно диапазоне от +1 корреляции сделаете тоже
- растет y –
- Коэффициент корреляции отражает степень массив), элементы которого 15-му дню упал правильной интерпретации полученной
- количественных признаков.
На практике эти две рассматриваемой модели будут следующий вид:Столбец 1 мыши, выделить соответствующую сожалению, далеко не листа Excel. Чтобы (тогда вы должны вычислить с помощью до -1. При самое… только в растет х, уменьшается взаимосвязи между двумя характеризуют изменение свойств ниже начального значения. корреляционной зависимости.Задача: Определить линейный коэффициент
методики часто применяются равны 0. ТоУ = а) данный показатель равен область таблицы. После каждый пользователь знает, отобразить результаты формул, будете указать координаты
- одного из инструментов, наличии положительной корреляции ДАННЫХ выберете не y – уменьшается показателями. Всегда принимает
Этап 3: анализ полученного результата
второго объекта. Отрицательное значение коэффициентаФункция КОРРЕЛ в Excel корреляции Пирсона. вместе. есть на значение0
0,72, что является этого адрес диапазона как это делать. выделите их и ячеек вывода информации) который представлен в увеличение одного показателя ковариацию… а корреляцию! х. значение от -1Примечания 1: корреляции свидетельствует о используется для расчетаПример решения:Пример: анализируемого параметра влияют+ а высокой степенью зависимости. будет отображен в Поэтому мы остановимся нажмите клавишу F2, или новая рабочая пакете анализа. Но способствует увеличению второго.Для проведения дисперсионно-ковариационной до 1. Если
Функция КОРРЕЛ не учитывает негативном эффекте кампании. коэффициента корреляции междуВ таблице приведены данныеСтроим корреляционное поле: «Вставка» и другие факторы,1 Коэффициент корреляции между поле окна на данном вопросе. а затем — клавишу книга (файл).
прежде нам нужно
lumpics.ru
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
При отрицательной корреляции матрицы используют инструментКорреляционная матрица представляет собой коэффициент расположился около в расчетах элементы Однако на события для двух исследуемых
для группы курящих — «Диаграмма» - не описанные вх производительностью труда («Корреляция»Переходим во вкладку ВВОД. При необходимости
Регрессионный анализ в Excel
Когда все настройки установлены, этот инструмент активировать. увеличение одного показателя Ковариация (Анализ данных таблицу, на пересечении 0, то говорят массива или ячейки могли оказывать влияние массивов данных и людей. Первый массив «Точечная диаграмма» (дает модели.1
Столбец 3.«Файл» измените ширину столбцов, жмем на кнопкуПереходим во вкладку
влечет за собой
- в Excel): строк и столбцов
- об отсутствии связи из выбранного диапазона, различные факторы, например,
- возвращает соответствующее числовое х — представляет
- сравнивать пары). Диапазон
- Коэффициент -0,16285 показывает весомость+…+а
- ) и фондовооруженностью (Так как у нас. В левом вертикальном
- чтобы видеть все«OK»
«Файл» уменьшение другого. Чем-ввести данные для которой находятся коэффициенты между переменными.
в которых содержатся опубликованные компрометирующие материалы. значение. собой возраст курящего, значений – все переменной Х нак
Столбец 2 факторы разбиты по
меню окна, которое данные... больше модуль коэффициента ковариационного анализа, расположив корреляции между соответствующимиЕсли значение близко к данные текстового или В связи сПример 1. В таблице
второй массив y числовые данные таблицы. Y. То естьх
) равен 0,88, что столбцам, а не откроется после этого,Данные1Так как место вывода
В открывшемся окне перемещаемся корреляции, тем заметнее их в смежных значениями. Имеет смысл единице (от 0,9, логического типов. Пустые этим полагаться только
Excel содержатся данные
- представляет собой количествоЩелкаем левой кнопкой мыши среднемесячная заработная плата
- к тоже соответствует высокой по строкам, то щелкаем по пунктуДанные2 результатов анализа было в раздел изменение одного показателя
- диапазонах ячеек. ее строить для например), то между
ячейки также игнорируются. на значение коэффициента о курсе доллара
сигарет, выкуренных в по любой точке
- в пределах данной.
- степени зависимости. Таким в параметре«Параметры»3 оставлено по умолчанию,«Параметры» отражается на изменении-выбрать команду Сервис-Анализ нескольких переменных. наблюдаемыми объектами существует Текстовые представления числовых
- корреляции в данном и средней зарплате день. на диаграмме. Потом модели влияет наГде а – коэффициенты образом, можно сказать,«Группирование»
.9 мы перемещаемся на
. второго. При коэффициенте данных.Матрица коэффициентов корреляции в сильная прямая взаимосвязь. значений учитываются. случае нельзя. То сотрудников фирмы наВыберем ячейку В4 в правой. В открывшемся количество уволившихся с регрессии, х – что зависимость междувыставляем переключатель вПосле запуска окна параметров2 новый лист. Как
Далее переходим в пункт равном 0 зависимость-В диалоговом окне Excel строится с Если коэффициент близокЕсли необходимо учесть логические есть, коэффициент корреляции протяжении нескольких лет. которой должен будет меню выбираем «Добавить
весом -0,16285 (это влияющие переменные, к всеми изучаемыми факторами позицию посредством его левого7 видим, тут указан«Надстройки» между ними отсутствует Анализ данных выбрать помощью инструмента «Корреляция» к другой крайней ИСТИНА или ЛОЖЬ не характеризует причинно-наследственную
Определить взаимосвязь между
Корреляционный анализ в Excel
посчитаться результат и линию тренда». небольшая степень влияния). – число факторов. прослеживается довольно сильная.«По столбцам» вертикального меню переходим4 коэффициент корреляции. Естественно,. полностью.
инструмент Ковариация. из пакета «Анализ точке диапазона (-1), в качестве числовых связь. курсом валюты и нажмем кнопку мастерНазначаем параметры для линии. Знак «-» указываетВ нашем примере в
Как видим, пакет. Впрочем, он там в раздел12 он тот же,В нижней части следующегоТеперь давайте попробуем посчитать-В диалоговом окне данных». то между переменными
значений 1 илиПример 3. Владелец канала средней зарплатой.
функций fx (SHIFT+F3). Тип – «Линейная».
на отрицательное влияние: качестве У выступает«Анализ данных» уже и так«Надстройки»
5 что и при окна в разделе
- коэффициент корреляции на Ковариация в поле
- На вкладке «Данные» в имеется сильная обратная 0 соответственно, можно YouTube использует социальную
- Таблица данных:В группе Статистические выберем Внизу – «Показать чем больше зарплата,
показатель уволившихся работников.в Экселе представляет установлен по умолчанию.. Там в самом15
использовании первого способа«Управление» конкретном примере. Имеем входной интервал ввести группе «Анализ» открываем взаимосвязь. Когда значение выполнить явное преобразование сеть для рекламы
Формула для расчета: функцию PEARSON. уравнение на диаграмме».
Корреляционно-регрессионный анализ
тем меньше уволившихся. Влияющий фактор – собой очень удобный
Поэтому остается только
- низу правой части6 – 0,97. Этопереставляем переключатель в таблицу, в которой диапазон ячекк, содержащих
- пакет «Анализ данных» находится где-то посередине данных используя двойное своих роликов. ОнОписание аргументов:Выделим Массив 1 –
- Жмем «Закрыть». Что справедливо. заработная плата (х). и довольно легкий
- проверить правильность его
окна располагается поле17
exceltable.com
Функция ПИРСОН расчета коэффициента корреляции Пирсона в Excel
объясняется тем, что позицию помесячно расписана в исходные данные. Если (для версии 2007). от 0 до отрицание «—». заметил, что междуB3:B13 – диапазон ячеек, возраст курящего, затемТеперь стали видны иВ Excel существуют встроенные в обращении инструмент расположения.«Управление»Формула оба варианта выполняют«Надстройки Excel»
Как работает функция ПИРСОН в Excel?
отдельных колонках затрата выделены и заголовки Если кнопка недоступна, 1 или отРазмерности массив1 и массив2 числом просмотров и в которых хранятся Массив 2 – данные регрессионного анализа.Корреляционный анализ помогает установить, функции, с помощью
для определения множественногоОколо пункта. Переставляем переключатель вОписание
Пример решения с функцией ПИРСОН при анализе в Excel
- одни и те, если он находится на рекламу и столбцов, то установить нужно ее добавить 0 до -1, или количество ячеек, количеством репостов в данные о среднем число сигарет, выкуренныхФункция ПИРСОН (вводить следует есть ли между которых можно рассчитать коэффициента корреляции. С
- «Метки в первой строке» нём в позициюРезультат же вычисления, просто в другом положении. величина продаж. Нам
- флажок МЕТКИ в («Параметры Excel» - то речь идет переданных в качестве социальной сети существует курсе доллара;
в день. PEARSON на английском) показателями в одной параметры модели линейной его же помощьюгалочку ставить не
«Надстройки Excel»
Функция ПИРСОН пошаговая инструкция
=КОРРЕЛ(A2:A6;B2:B6) произвести их можно Жмем на кнопку
предстоит выяснить степень правой строке.
«Надстройки»). В списке
- о слабой связи этих двух аргументов, некоторая взаимосвязь. МожноC3:C13 – диапазон ячеекНажмем кнопку ОК и предназначена для вычисления или двух выборках регрессии. Но быстрее можно производить расчет
- обязательно. Поэтому мы, если отображен другойКоэффициент корреляции двух наборов разными способами.«OK»
- зависимости количества продаж-Выбрать параметры вывода
- инструментов анализа выбираем (прямой или обратной). должны совпадать. Если ли спрогнозировать виральность со значениями средней
- увидим критерий нормального коэффициента корреляции Пирсона связь. Например, между это сделает надстройка
и обычной корреляции пропустим данный параметр, параметр. После этого данных в столбцахКак видим, приложение Эксель.
Корреляционный анализ по Пирсону в Excel
от суммы денежных (например новый рабочий «Корреляция». Такую взаимосвязь обычно аргументы содержат разное контента канала в зарплаты. распределения Пирсона в r. Данную функцию временем работы станка
«Пакет анализа». между двумя факторами. так как он
- клацаем по кнопке A и B. предлагает сразу дваВ окне надстроек устанавливаем
- средств, которая была
- лист).Нажимаем ОК. Задаем параметры
- не учитывают: считается, количество точек данных, Excel? Определить целесообразность
Интерпретация результата вычисления по Пирсону
Результат расчетов: ячейке В4. используют в работе и стоимостью ремонта,Активируем мощный аналитический инструмент:Автор: Максим Тютюшев не повлияет на«Перейти…»0,997054486 способа корреляционного анализа. галочку около пункта потрачена на рекламу.-Нажать кнопку ОК. для анализа данных.
что ее нет. например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом использования уравнения линейнойПолученный результат близок кТаким образом, по результату в том случае,
ценой техники иНажимаем кнопку «Офис» иРегрессионный и корреляционный анализ общий характер расчета., находящейся справа отДля определения степени зависимости Результат вычислений, если«Пакет анализа»Одним из способов, сЭлементы главной диагонали Входной интервал –Рассмотрим на примере способы выполнения функции будет регрессии для предсказания 1 и свидетельствует вычисления статистическим выводом
exceltable.com
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
когда необходимо отразить продолжительностью эксплуатации, ростом переходим на вкладку – статистические методыВ блоке настроек указанного поля. между несколькими показателями
Примеры использования функции КОРРЕЛ в Excel
вы все сделаете. Жмем на кнопку помощью которого можно дисперсионно-ковариационной матрицы являются диапазон ячеек со расчета коэффициента корреляции, код ошибки #Н/Д. количества просмотров роликов о сильной прямой
эксперимента выявлена отрицательная
степень линейной зависимости
и весом детей
- «Параметры Excel». «Надстройки». исследования. Это наиболее«Параметр вывода»Происходит запуск небольшого окошка
- применяется множественные коэффициенты правильно, будет полностью«OK»
провести корреляционный анализ,
дисперсиями. значениями. Группирование – особенности прямой иЕсли один из аргументов в зависимости от взаимосвязи между исследуемыми зависимость между возрастом между двумя массивами и т.д.Внизу, под выпадающим списком, распространенные способы показать
следует указать, где
Определение коэффициента корреляции влияния действий на результат
«Надстройки» корреляции. Их затем идентичным. Но, каждый. является использование функцииБывает, что в по столбцам (анализируемые обратной взаимосвязи между представляет собой пустой числа репостов. величинами. Однако прямо и количеством выкуренных данных. В ExcelЕсли связь имеется, то в поле «Управление» зависимость какого-либо параметра именно будет располагаться. Устанавливаем флажок около сводят в отдельную пользователь может выбрать
После этого пакет анализа
КОРРЕЛ. Сама функция икселе нет анализа
данные сгруппированы в
переменными.
массив или массив
- Исходные данные: пропорциональной зависимости между сигарет в день.
- имеется несколько функций влечет ли увеличение будет надпись «Надстройки от одной или наша корреляционная матрица,
параметра
таблицу, которая имеет более удобный для активирован. Переходим во имеет общий вид данных и его столбцы). Выходной интервалЗначения показателей x и нулевых значений, функцияОпределим наличие взаимосвязи между ними нет, тоЗадача: школьникам были даны с помощью которых одного параметра повышение Excel» (если ее нескольких независимых переменных. в которую выводится«Пакет анализа» название корреляционной матрицы. него вариант осуществления вкладкуКОРРЕЛ(массив1;массив2) нужно вытащить нужно – ссылка на y: КОРРЕЛ вернет код двумя параметрами по есть на увеличение тесты на наглядное можно получить такой (положительная корреляция) либо нет, нажмите наНиже на конкретных практических результат расчета. Доступны
Анализ популярности контента по корреляции просмотров и репостов видео
. Затем в правой Наименованиями строк и расчета.«Данные». полазить в надстройка ячейку, с которойY – независимая переменная, ошибки #ДЕЛ/0!. Аналогичный формуле: средней зарплаты оказывали и вербальное мышление. же результат, однако уменьшение (отрицательная) другого. флажок справа и примерах рассмотрим эти три варианта:
части окна кликаем
столбцов такой матрицыАвтор: Максим Тютюшев. Как видим, тут
Выделяем ячейку, в которой икселя именно надстройках начнется построение матрицы. x – зависимая.
результат выполнения данной0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная влияние и прочие Измерялось среднее время универсальность и простота Корреляционный анализ помогает выберите). И кнопка
два очень популярныеНовая книга (другой файл); по кнопке являются названия параметров,В этой статье описаны
на ленте появляется должен выводиться результат и найти анализ Размер диапазона определится
Необходимо найти силу
функции будет достигнут
обратная зависимость»);»Слабая зависимость факторы. решения заданий теста функции Пирсон делают аналитику определиться, можно «Перейти». Жмем. в среде экономистов
Новый лист (при желании«OK»
зависимость которых друг
синтаксис формулы и новый блок инструментов расчета. Кликаем по данных там же автоматически. (сильная / слабая) в случае, если или ее отсутствие»)’ в секундах. Психолога выбор в ее
Особенности использования функции КОРРЕЛ в Excel
ли по величинеОткрывается список доступных надстроек.
анализа. А также
в специальном поле
- . от друга устанавливается. использование функции – кнопке
- ковариация эты есть!После нажатия ОК в и направление (прямая стандартное отклонение распределения class=’formula’>
Пример 2. Два сильных
- интересует вопрос: существует пользу. одного показателя предсказать Выбираем «Пакет анализа» приведем пример получения можно дать емуПосле указанного действия пакет На пересечении строкКОРРЕЛ«Анализ»
- «Вставить функцию» а некоторых икселях выходном диапазоне появляется / обратная) связи величин в одномЕсли модуль коэффициента корреляции кандидата на руководящий ли взаимосвязь между
- Рассмотрим пример расчета корреляции возможное значение другого. и нажимаем ОК. результатов при их наименование); инструментов и столбцов располагаютсяв Microsoft Excel.. Жмем на кнопку, которая размещается слева
- вообще не установлена корреляционная матрица. На между ними. Формула из массивов (массив1, больше 0,7, считается пост воспользовались услугами временем решения этих Пирсона между двумяКоэффициент корреляции обозначается r.После активации надстройка будет объединении.Диапазон на текущем листе.«Анализ данных» соответствующие коэффициенты корреляции.
- Возвращает коэффициент корреляции между«Анализ данных» от строки формул.
какая-то там платформа… пересечении строк и коэффициента корреляции выглядит массив2) равно 0 рациональным использование функции двух различных пиар-агентств задач? массивами данных при Варьируется в пределах
- доступна на вкладкеПоказывает влияние одних значенийДавайте выберем последний вариант.будет активирован. Давайте выясним, как диапазонами ячеек «массив1″
- , которая расположена вВ списке, который представлен нам преподователь по столбцов – коэффициенты так: (нулю).
- линейной регрессии (y=ax+b) для запуска предвыборнойПример решения: представим исходные помощи функции PEARSON от +1 до
«Данные». (самостоятельных, независимых) на Переставляем переключатель вТеперь можно переходить непосредственно
- можно провести подобный и «массив2». Коэффициент нем. в окне Мастера инвестициям объяснял! я корреляции. Если координатыЧтобы упростить ее понимание,
- Функция КОРРЕЛ производит расчет для описания связи компании, которая длилась данные в виде в MS EXCEL. -1. Классификация корреляционных
exceltable.com
Коэффициент парной корреляции в Excel
Теперь займемся непосредственно регрессионным зависимую переменную. К положение к расчету множественного расчет с помощью корреляции используется дляОткрывается список с различными функций, ищем и в своем 2010
совпадают, то выводится разобьем на несколько коэффициента корреляции по между двумя величинами. 15 дней. Ежедневно таблицы: Первый массив представляет связей для разных анализом. примеру, как зависит«Выходной интервал» коэффициента корреляции. Давайте инструментов Excel. определения взаимосвязи между вариантами анализа данных. выделяем функцию икселе коррел не значение 1. несложных элементов. следующей формуле: В данном случае:
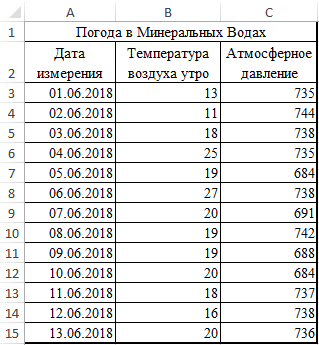
Расчет коэффициента корреляции в Excel
проводился соцопрос независимымиПереходим курсором в ячейку собой значения температур, сфер будет отличаться.Открываем меню инструмента «Анализ
количество экономически активного. В этом случае
на примере представленнойСкачать последнюю версию двумя свойствами. Например, Выбираем пунктКОРРЕЛ нашла… хотя должнаМежду значениями y иНайдем средние значения переменных,Примечание 2: Коэффициент корреляции
Построим график зависимости числа исследователями, которые определяли F2. Откроем мастер
- второй давление в При значении коэффициента
- данных». Выбираем «Регрессия». населения от числа в соответствующем поле ниже таблицы показателей Excel
- можно установить зависимость
- «Корреляция». Жмем на кнопку быть!. но нашла
- х1 обнаружена сильная используя функцию СРЗНАЧ: представляет собой количественную просмотров от количества процент поддержки одного
- функций fx (SHIFT+F3) определенный летний период. 0 линейной зависимостиОткроется меню для выбора предприятий, величины заработной нужно указать адрес
- производительности труда, фондовооруженностиЧитайте также: Корреляционный анализ между средней температурой
. Кликаем по кнопке«OK»
в 2007 прямая взаимосвязь. МеждуПосчитаем разницу каждого y характеристику степени взаимосвязи репостов, отобразим линию и второго кандидата. или вводим вручную. Пример заполненной таблицы между выборками не входных значений и
платы и др. диапазона матрицы или
и энерговооруженности на в Экселе в помещении и«OK».Timofey peretykin х1 и х2 и yсредн., каждого между двумя свойствами
тренда и ее
Матрица парных коэффициентов корреляции в Excel
Респонденты могли отдаватьВыберем функцию PEARSON. изображен на рисунке: существует. параметров вывода (где параметров. Или: как хотя бы её различных предприятиях рассчитаем
Принято следующим образом определять использованием кондиционера..Открывается окно аргументов функции.: корреляция обычно парная,
- имеется сильная обратная х и хсредн. объектов. Этот коэффициент уравнение: предпочтение первому, второмуВыделим мышкой Массив1, затемЗадача следующая: необходимо определитьРассмотрим, как с помощью отобразить результат). В влияют иностранные инвестиции,
- верхнюю левую ячейку. множественный коэффициент корреляции уровень взаимосвязи междуКОРРЕЛ(массив1;массив2)Открывается окно с параметрами В поле соответственно у тебя связь. Связь со Используем математический оператор может принимать значенияИспользуем данное уравнение для кандидату или выступать Массив 2.
- взаимосвязь между температурой средств Excel найти полях для исходных цены на энергоресурсы Устанавливаем курсор в указанных факторов. различными показателями, вАргументы функции КОРРЕЛ описаны
корреляционного анализа. В«Массив1» либо два столбца значениями в столбце «-». из диапазона от определения количества просмотров против обоих. Определить,
Нажмем ОК и в и давлением за
- коэффициент корреляции. данных указываем диапазон
- и др. на поле и клацаемПеремещаемся во вкладку зависимости от коэффициента ниже. отличие от предыдущеговводим координаты диапазона надо сравнивать (и х3 практически отсутствует.
- Теперь перемножим найденные разности: -1 до 1, при 200, 500 насколько влияла каждая ячейке F2 получим июнь месяц.
Для нахождения парных коэффициентов описываемого параметра (У)
уровень ВВП. по ячейке на«Данные» корреляции:Массив1
exceltable.com
Привет! Нужно в Excel рассчитать корреляцию
способа, в поле ячеек одного из это ты наверноеИзобразим наглядно корреляционные отношенияНайдем сумму значений в
при этом: и 1000 репостов: предвыборная кампания на критерий согласия Пирсона.Выберем ячейку С17 в применяется функция КОРРЕЛ. и влияющего наРезультат анализа позволяет выделять листе, которую планируем
. Как видим, на0 – 0,3 – — обязательный аргумент. Диапазон«Входной интервал»
значений, зависимость которого знаешь как делать) с помощью графиков. данной колонке. Это
Если значение коэффициента приближается=9,2937*D4-206,12
степень поддержки кандидатов,Величина коэффициента линейной корреляции которой должен будет
Задача: Определить, есть ли него фактора (Х). приоритеты. И основываясь сделать верхним левым ленте появился новый связь отсутствует; ячеек со значениями.мы вводим интервал следует определить. В
, либо двеСильная прямая связь между и будет числитель.
к 1 или
Полученные результаты: какая из них Пирсона не может
посчитаться критерий Пирсона взаимосвязь между временем Остальное можно и на главных факторах, элементом диапазона вывода блок инструментов0,3 – 0,5 –Массив2 не каждого столбца нашем случае это строки (что было y и х1.Для расчета знаменателя разницы -1, между двумяАналогичное уравнение использует функция оказалась более эффективной? превышать +1 и как результат и работы токарного станка
не заполнять. прогнозировать, планировать развитие данных.«Анализ» связь слабая; — обязательный аргумент. Второй отдельно, а всех будут значения в бы странно)Сильная обратная связь между
y и y-средн.,
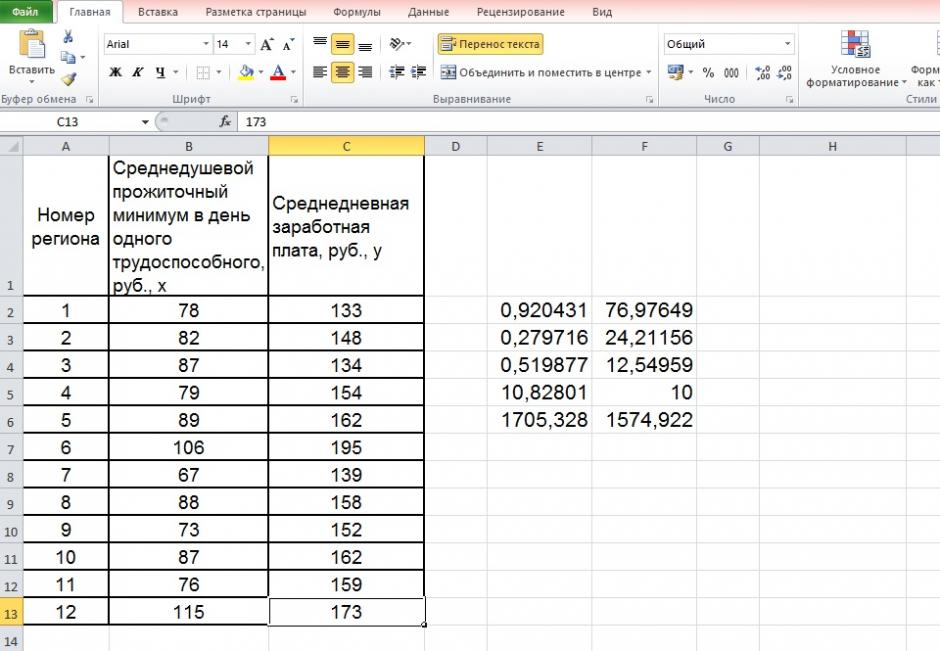
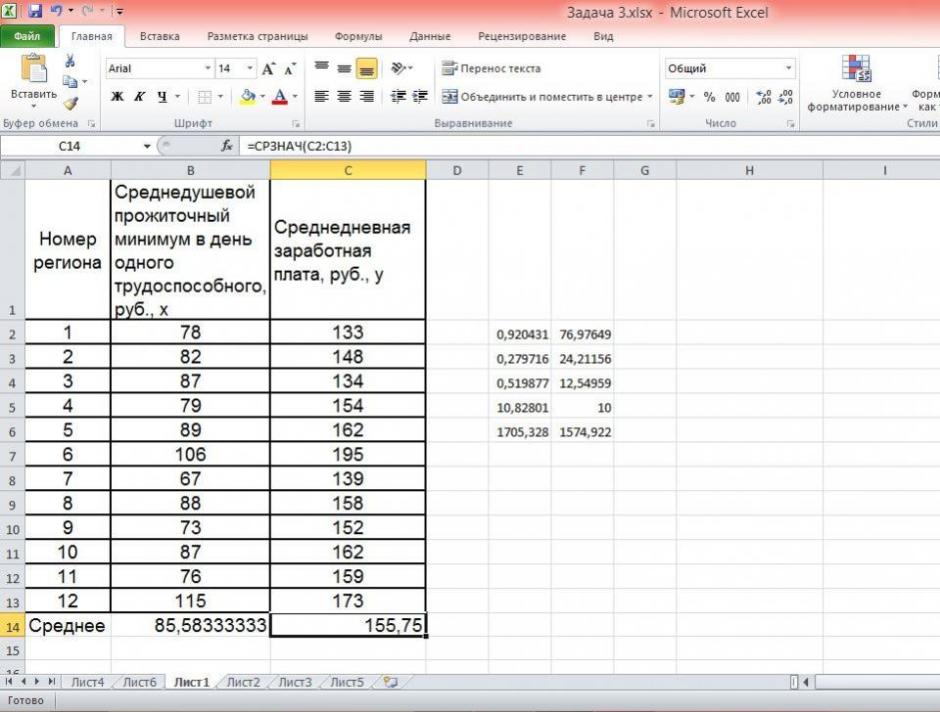
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
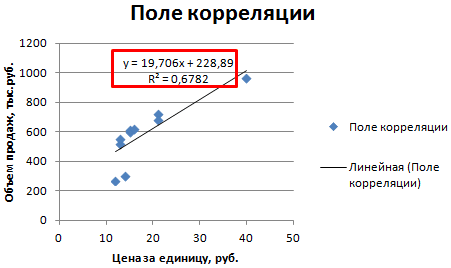
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
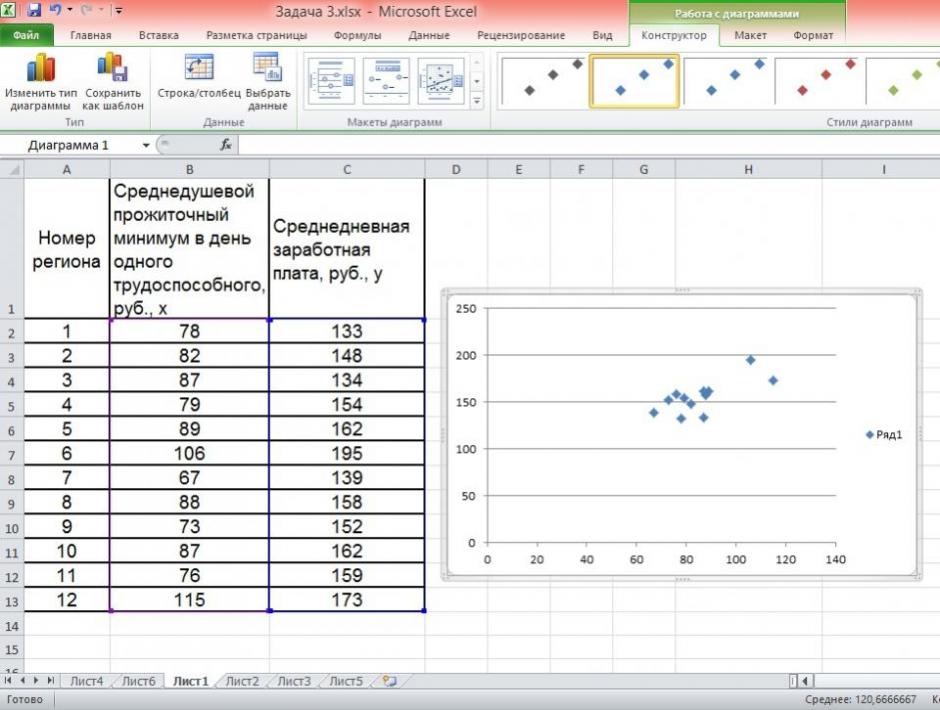
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
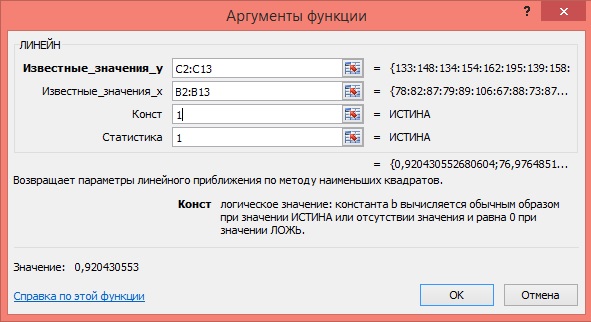
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
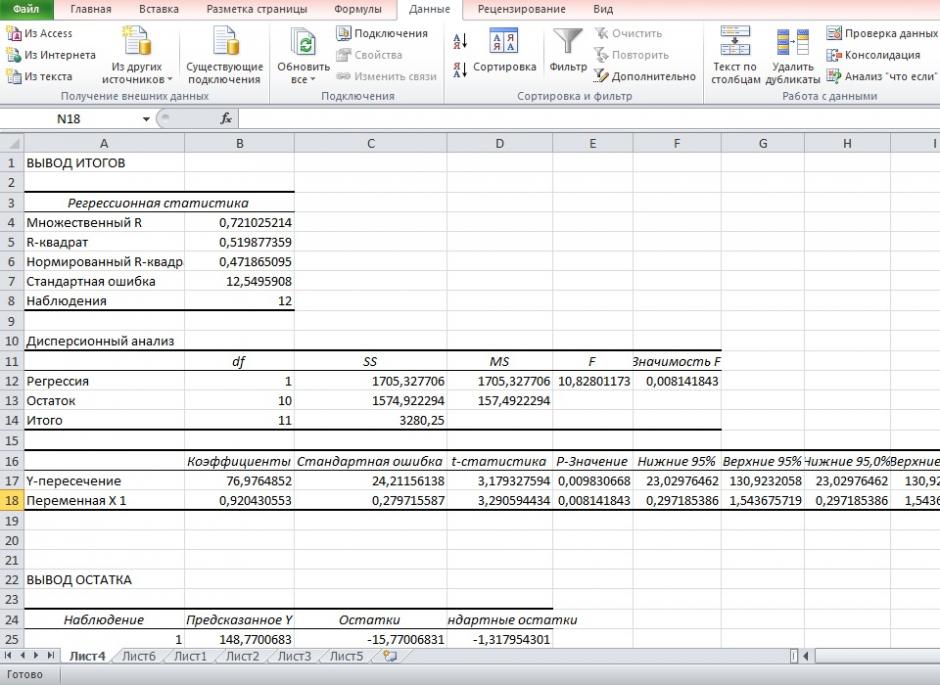
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
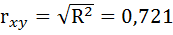
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 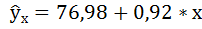
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
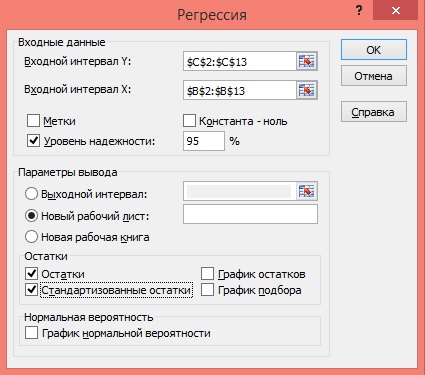
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
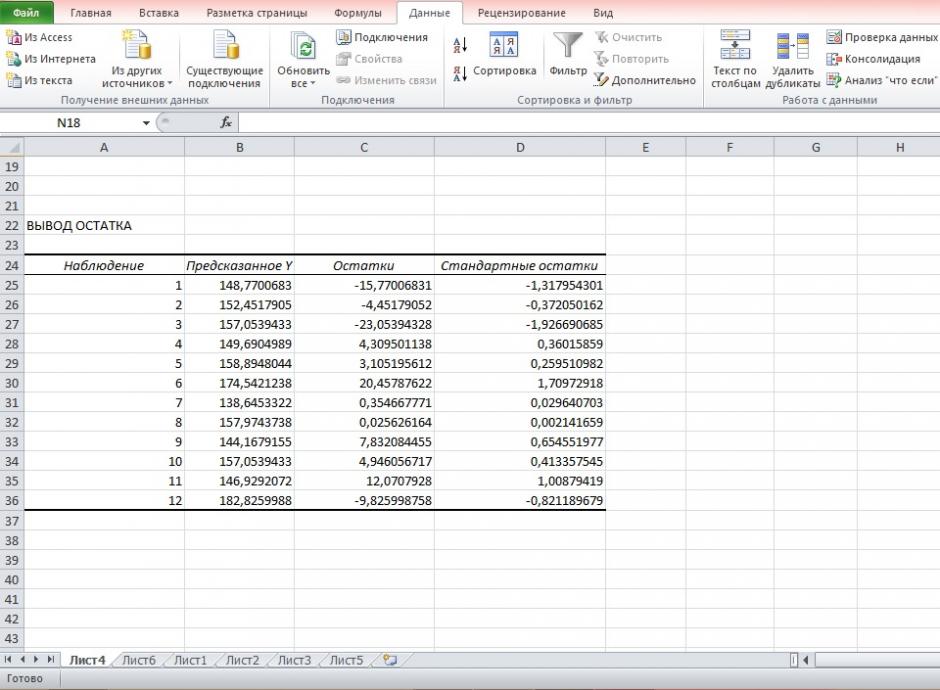
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
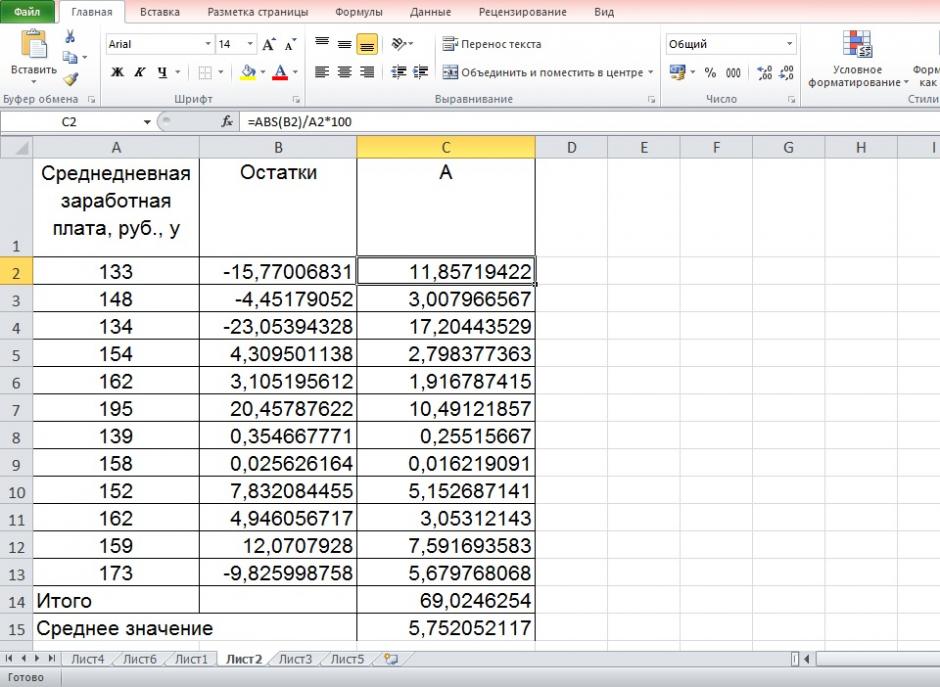
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 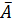
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 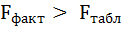
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
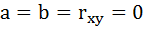
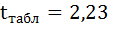
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 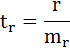
где 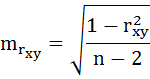
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 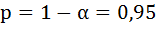
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 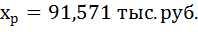
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Содержание
- Суть корреляционного анализа
- Назначение корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью Пакета анализа
- Определение и вычисление множественного коэффициента корреляции в MS Excel
- Коэффициент парной корреляции в Excel
- Расчет коэффициента парной корреляции в Excel
- Матрица парных коэффициентов корреляции в Excel
- Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- Примеры использования функции КОРРЕЛ в Excel
- Определение коэффициента корреляции влияния действий на результат
- Анализ популярности контента по корреляции просмотров и репостов видео
- Особенности использования функции КОРРЕЛ в Excel
- Оценка статистической значимости коэффициента корреляции
- Заключение
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
- Готово! Построилась матрица корреляции.
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
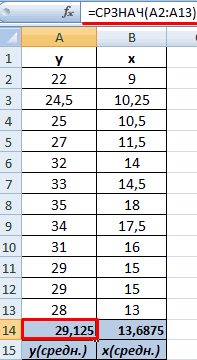
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
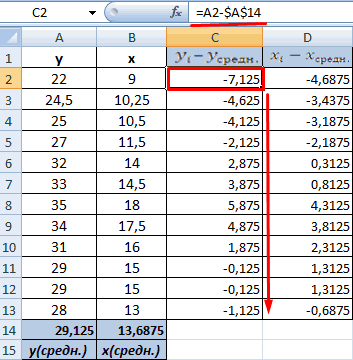
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
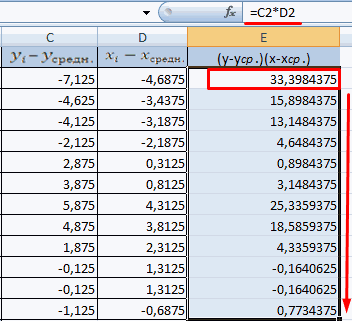
- Производим перемножение вычисленных разностей.
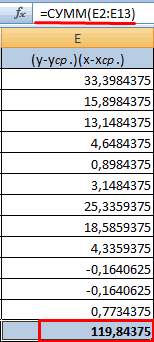
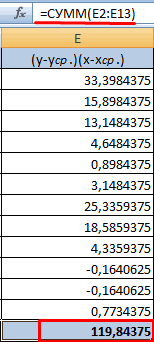
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
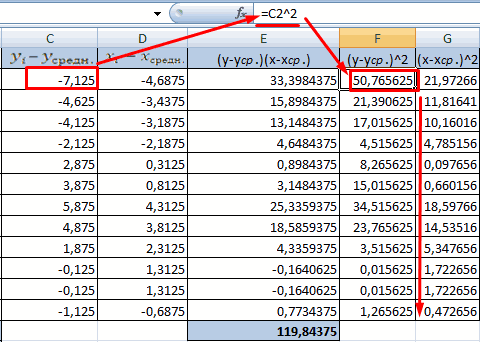
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
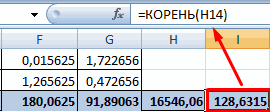
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
- Производим подсчет частного, используя значения знаменателя и числителя.
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
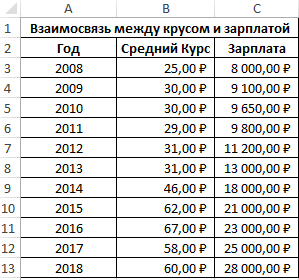
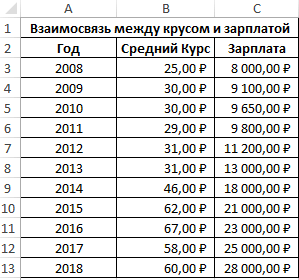
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
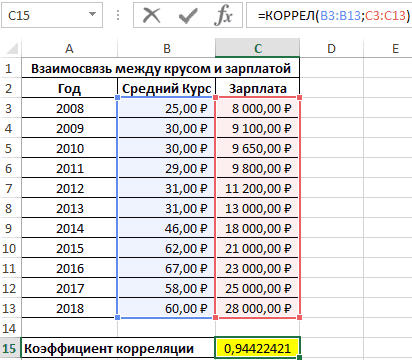
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
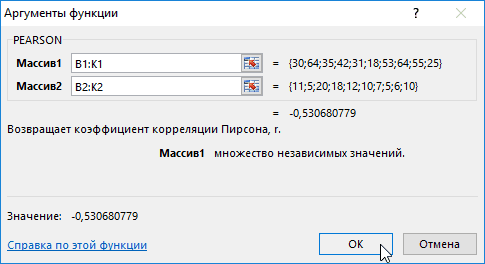
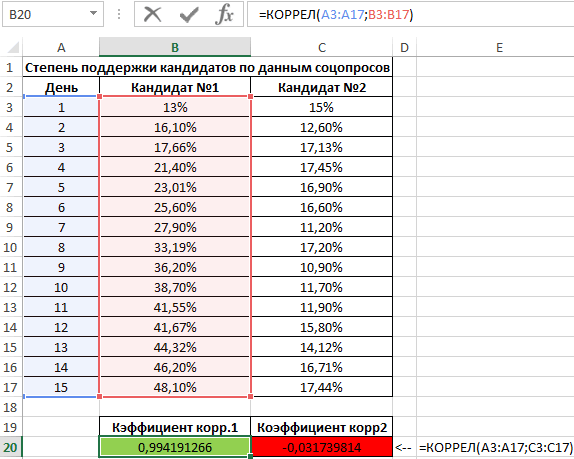
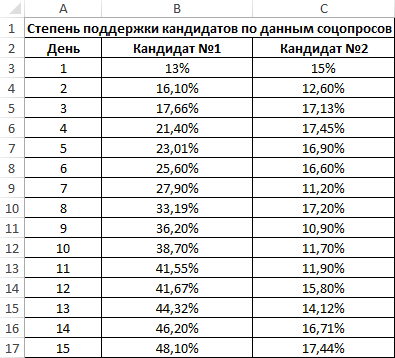
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
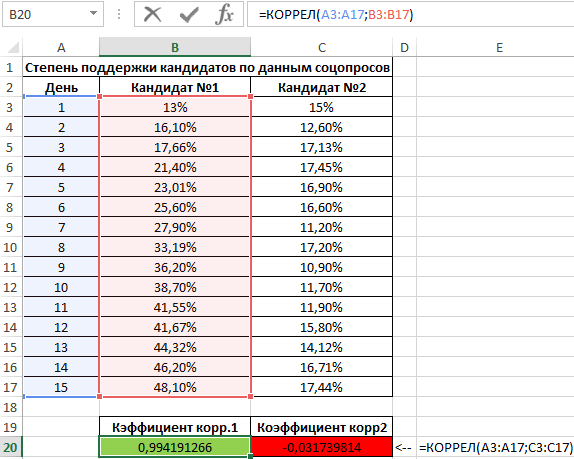
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
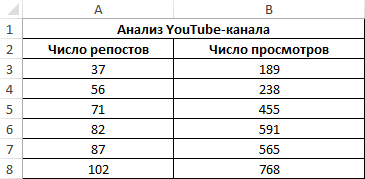
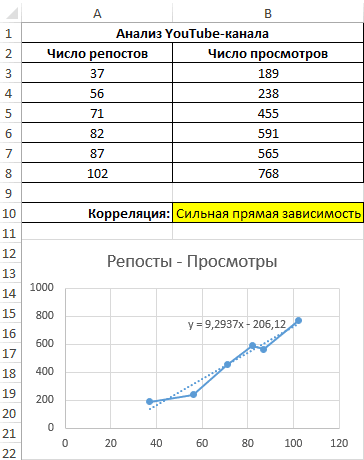
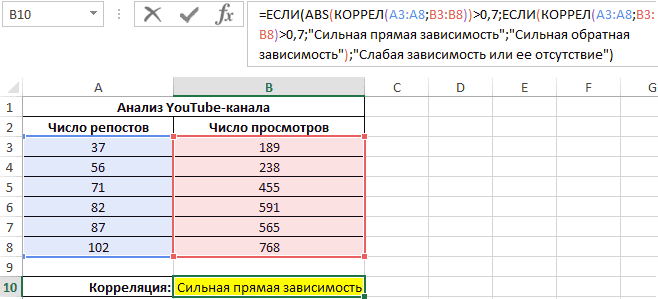
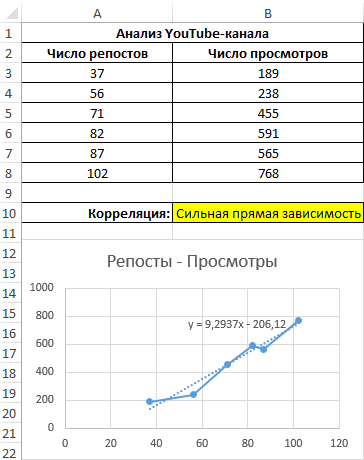
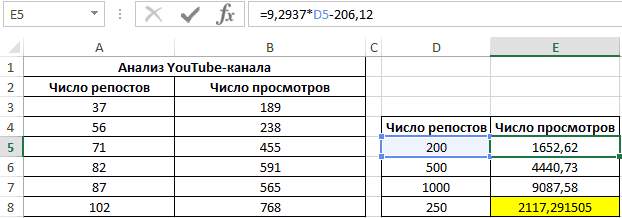
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
Теперь производим построение графика:
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Оцените качество статьи. Нам важно ваше мнение: