Оптимизация управленческих решений excel

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

• составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
• выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
• внести в ячейку формулу для целевой функции,
• запустить надстройку Поиск решения,
• установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):


Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Полезные ссылки

Методички

• Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
• Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

В данной статье рассматривается расчет инструмента Excel «Поиск решений». Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья и штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы.

Зачастую экономисты в своей практике встречаются с вопросами оптимизации расходов.

Рассмотрим пример оптимизации транспортных расходов с помощью инструмента Excel «Поиск решений».

Пример 1

На предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде .

Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными.

Для успешного решения этой задачи необходимо выбрать минимизируемую ячейку, определить ограничения, а также правильно сформировать таблицы с исходными и расчетными данными (рис. 1). 

 

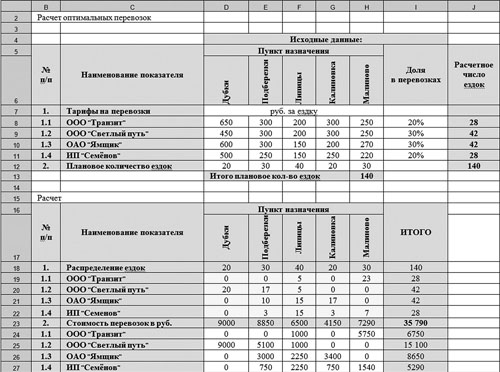
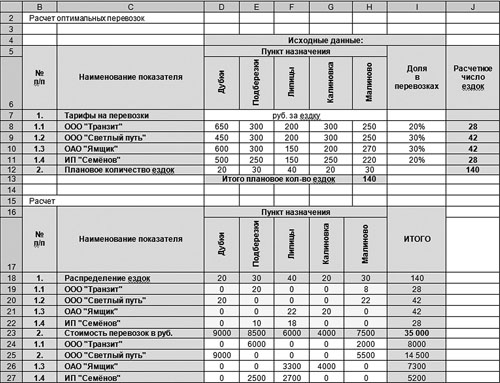
 Рис. 1. Расчет оптимальных перевозок

На рис. 1 расположены две таблицы: с исходными данными и расчетными данными. В ячейках D8:H11 расположены тарифы за 1 ездку в разрезе транспортных компаний до пунктов назначения, в ячейках D12:H12 — плановое количество ездок за период до пунктов назначения, в ячейках I8:I11 — удельный вес перевозок каждой транспортной компании в общем количестве планируемых перевозок за период. Эти ячейки для удобства не раскрашены. В ячейках J8:J12 и Н13 рассчитано число ездок по каждой транспортной компании и в целом за период. Формулы в этих ячейках выглядят следующим образом:

Ячейка Н13: =СУММ(D12:H12),

Ячейка J8: =I8*$H$13.

Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11.

Ячейка J12: =СУММ(J8:J11).

Следующая таблица на листе посвящена расчету и называется «Расчет». Ячейки D19:Н22 предназначены для распределения количества ездок до пунктов назначения между транспортными компаниями. На рис. 1 в ячейках дано такое распределение, заполненное вручную. В ячейках D23:I27 рассчитаны суммы расходов на транспортные перевозки в разрезе транспортных компаний, оказывающих транспортные услуги, и пунктов назначений, а также итоги.

Приведем формулы, представленные в этих ячейках.

Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу:

=D19*D8.

Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27.

В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу:

=СУММ(D24:D27).

Протащим (скопируем) эту формулу в ячейки Е23:I23.

В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу:

=СУММ(D24:H24).

Протащим (скопируем) ее в ячейки I25:I27.

Таким образом, стоимость транспортных расходов по компании в целом формируется в ячейке I23. В первоначальном расчете, представленном на рис. 1, данная сумма равна 35 790 руб.

Скопируем данный лист в эту же книгу. Далее необходимо приступить непосредственно к оптимизации. Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений».

Для начала надо выбрать оптимизируемую ячейку (I23). Затем вызовем диалоговое окно «Поиск решений», представленное на рис. 2.

Это важно. Надстройку «Поиск решений» не всегда можно обнаружить в меню рабочего стола компьютера, так как она может быть не подключена. Для ее подключения необходимо выполнить ряд действий, которые аналогичны во всех версиях MS Office: «Сервис — Надстройки — Поиск решений (установить флажок)». Теперь данный инструмент можно будет найти на панели инструментов рабочего стола.

 

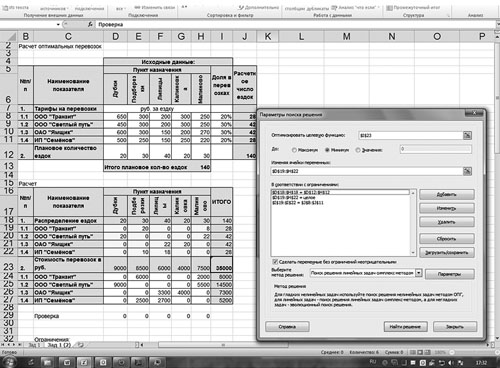
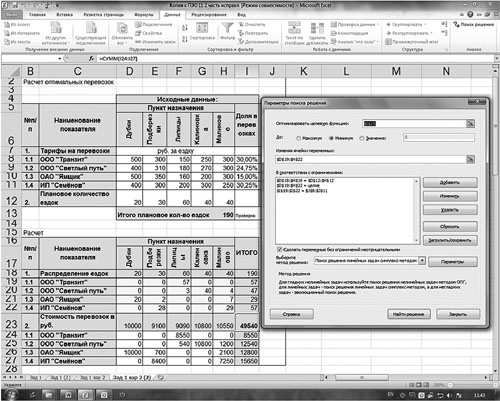
Рис. 2. Использование надстройки «Поиск решений»

В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22).

В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений:

$D$19:$H$22 = целое,

$D$12:$H$12 = $D$18:$H$18,

$J$8:$J$11 = $I$19:$I22.

Чтобы добавить следующее ограничение, в этом же окне нажмите на кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, а поля окна «Добавить ограничения» будут очищены для ввода следующего ограничения. После того как введено последнее из ограничений, необходимо нажать на кнопку «ОК».

Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.

В данном примере все ограничения представлены в виде равенств. Но существуют задачи, в которых требуются ввести ограничения в виде неравенств. Например, в транспортных компаниях объем перевозимого груза не может превышать грузоподъемности автомобиля (или время работы автотранспортного средства не может превышать количества часов в сутки за вычетом нормативных простоев).

Очень важно правильно сформулировать ограничения. Для того чтобы не забыть ни одно из ограничений, необходимо правильно поставить задачу и определить ее цели. Не бывает мелочей в постановке задачи. В задаче о поставке деталей необходимо учесть, что количество деталей на складе на начало периода плюс количество поступивших за планируемый период деталей должно равняться сумме их остатка на складе на конец периода плюс количество отгруженных деталей за планируемый период. Или, например, количество деталей на начало планируемого периода должно равняться количеству деталей на конец периода, предшествующему планируемому.

Необходимо также помнить о том, что некоторые показатели могут быть только положительными значениями (например, сумма поступления от покупателя на расчетный счет поставщик). В данном случае в ограничениях целесообразно указать, что эта величина не может быть отрицательной, иначе надстройка «Поиск решений», вполне возможно, предложит в качестве решения отрицательное число.

Далее следует выбрать метод решения. Для этого необходимо определить, является модель линейной или нелинейной. Напомним, что линейной моделью является такая модель, связи в которой между данными для расчета и результирующим показателем можно описать линейными функциями. Линейная функция имеет следующий вид:

F(x) = a1 × x1 + а2 × x2 + … + аn × xn,

где a1, а2, …, аn — константы;

x1, x2, …, xn — переменные.

Данная модель является линейной.

Примером нелинейной модели является оптимизация перевозок с целью минимизации расходов, когда тарифы на перевозки распределены по интервалам:

• от 0 до 10 км — стоимость перевозки 200 руб.;
• от 11 до 20 км — стоимость перевозки 250 руб.;
• от 21 до 50 км — стоимость перевозки 500 руб. и т. д.

Вернемся к диалоговому окну «Параметры поиска решений». Далее нажимаем кнопку «Найти решение», в результате чего появится окно с результатом поиска решения. Так как нам необходимо сохранить найденный результат, то ставим флажок «Сохранить найденное решение», в результате чего на нашем листе сохранится найденное решение. Нажмем кнопку «ОК».

В ячейках $D$19:$Н$22 появляются подобранные системой значения, при которых в ячейке I23 формируется минимальное значение стоимости транспортных услуг — 35 000 руб.

В данном случае отклонения от подобранного нами вручную результата составляют лишь 2,2 %, или 790 руб., но это означает лишь то, что мы вручную удачно подобрали решение.

На рис. 3 представлены полученные при оптимизации данные.

Рис. 3. Результаты оптимизации

Для того чтобы использовать ссылки на ячейки в составе сценария, необходимо сохранить этот сценарий, нажав на кнопку «Сохранить сценарий» в окне «Результат поиска решения», введя имя сценария и нажав кнопку «ОК». При этом исходные данные сохраняются.

Таким образом, предоставлена возможность сохранить все варианты решений при изменении исходных данных. Затем можно создавать отчеты, по которым можно сравнивать влияние изменений исходных данных и ограничений на результат решения.

Существует одна важная деталь: при расчетах количества ездок лучше всего в ячейках J8:J11 использовать функцию округления, чтобы значения были целыми числами.

По этому случаю рассмотрим пример с другими исходными данными.

Пример 2

В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид:

Ячейка J8: =ОКРУГЛ(I8*$H$13;0).

Протащим (скопируем) эту формулу в ячейки J9:J11.

Как видим (рис. 4) плановое количество ездок в ячейке Н13 отличается от суммы в ячейках J8:J11, записанной в ячейке J12: значение в ячейке J12, полученное в результате суммирования округленных результатов расчетов числа ездок в ячейках J8:J11, не равно значению в ячейке Н13, полученному суммированием планового числа ездок до пунктов назначения. Это издержки примененной функции округления. Для того чтобы избежать данной ошибки, проделаем следующую процедуру. Для контроля и удобства вычислений введем проверочную ячейку J13. Формула в этой ячейке будет представлять собой разницу полученных значений в ячейках J12 и H13. Ячейка понадобится нам для коррекции вычислений.

 

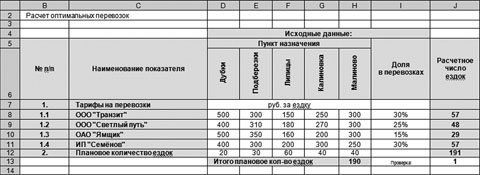
Рис. 4. Пример с функцией округления расчетного числа ездок до целого числа

Используем для коррекции инструмент «Подбор параметра». Процедура подбора иллюстрируется на рис. 5.

 

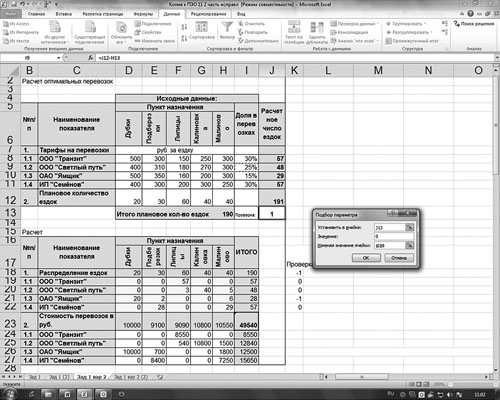
Рис. 5. Использование инструмента «Подбор параметра»

Здесь необходимо применить следующую схему: подобрать в ячейке J13 значение равное 0, изменяя значение в ячейке I9 (доля в перевозках). Предварительно в ячейку I11 целесообразно ввести следующую формулу:

=100 % – I8 – I9 – I10.

Тогда при изменении значения в ячейке I9 в результате применения инструмента «Подбор параметра» автоматически изменится и значение в ячейке I11.

Так как в ячейках I8:I11 применено округление до целого значения, изменения в ячейках I9 и I11 на 0,25 % не обнаруживаются. Эти изменения будут видны, если мы добавим знаки после запятой.

Результат применения инструмента «Подбор параметра» приведен на рис. 6 (на с. …).

Необходимо проделать процедуры, что и в предыдущем примере (см. рис. 1, 2, 3). В ячейках D19:H22 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения:

D19:H22 = целое,

D12:H12 = D18:H18,

J8:J11 = I19:I22.

Сумма транспортных расходов в ячейке I23 на рис. 6 рассчиталась равной 49 540 руб., а наша задача — минимизировать ее.

 

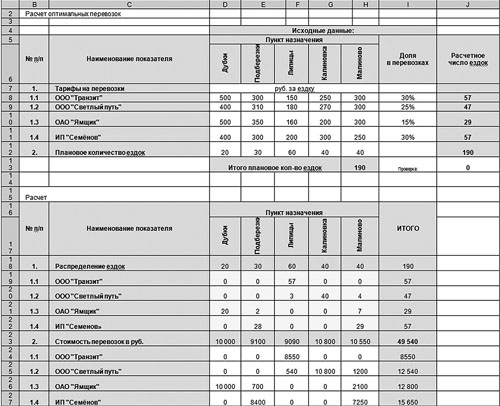
Рис. 6. Скорректированный вариант

На рис. 7 представлена демонстрация использования инструмента «Поиск решений» для оптимизации результата.

 

Рис. 7. Минимизация значения в ячейке I23 с помощью надстройки «Поиск решения»

На рис. 8 в ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. Отклонения от достигнутого при первоначальном распределении результата составило 9 %, или 4550 руб.

Возможно, имеет право на существование такой вопрос: «Для чего нужна табличная часть со стоимостями перевозок в разрезе транспортных компаний и пунктов назначений?». Ведь можно было бы просто в итоговую ячейку I23 ввести формулу:

=СУММПРОИЗВ(D8:D11;D19:D22)+СУММПРОИЗВ(E8:E11;E19:E22)+СУММПРОИЗВ(F8:F11;F19:F22)+СУММПРОИЗВ(G8:G11;G19:G22)+СУММПРОИЗВ(H8:H11;H19:H22).

Следует помнить следующее:

• строк и столбцов может быть достаточно большое количество. Это значит, что написание самой формулы в ячейках будет слишком трудоемкой задачей;
• потеряется возможность анализа данных по компаниям и пунктам назначения. Значит, целесообразнее использовать вспомогательную таблицу (в нашем примере это ячейки B23:I27), которая содержала бы множество простых формул. Эти формулы записываются всего в два мгновения: запись в одной из ячеек и копирование или протаскивание в остальные ячейки. Такая таблица несет в себе полезную для анализа информацию о стоимости транспортных услуг в разрезе перевозчиков и пунктов назначения.

 

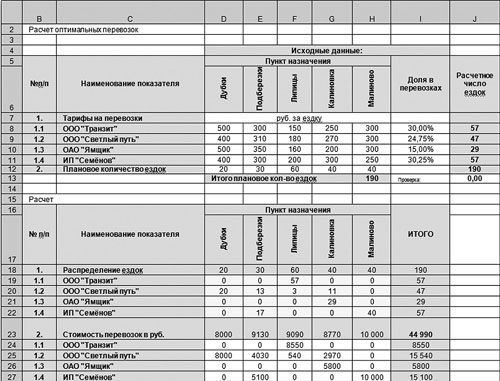
Рис. 8. Результат оптимизации примера с округлением

Заключение

В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.

Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.

Включение функции

Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.

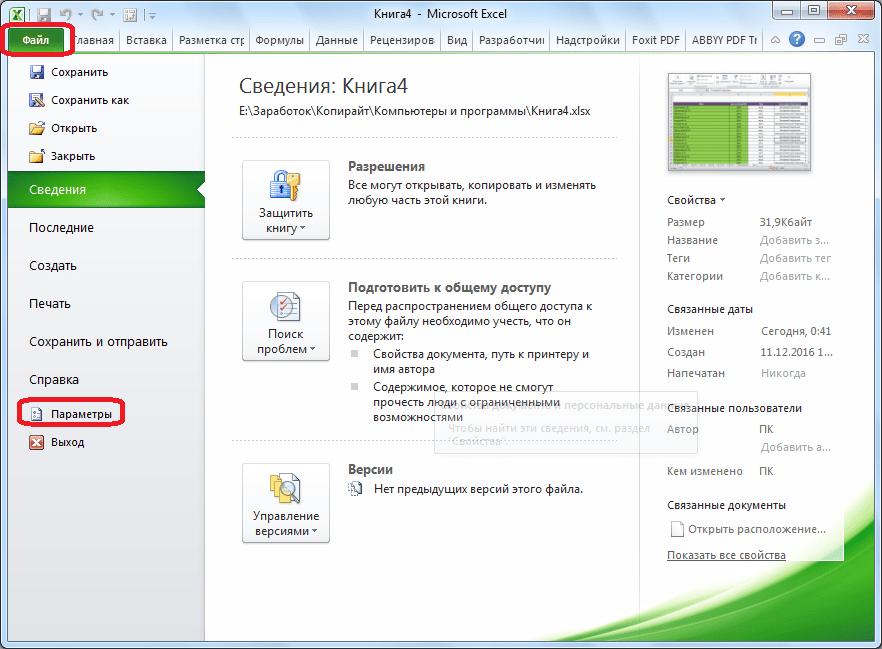
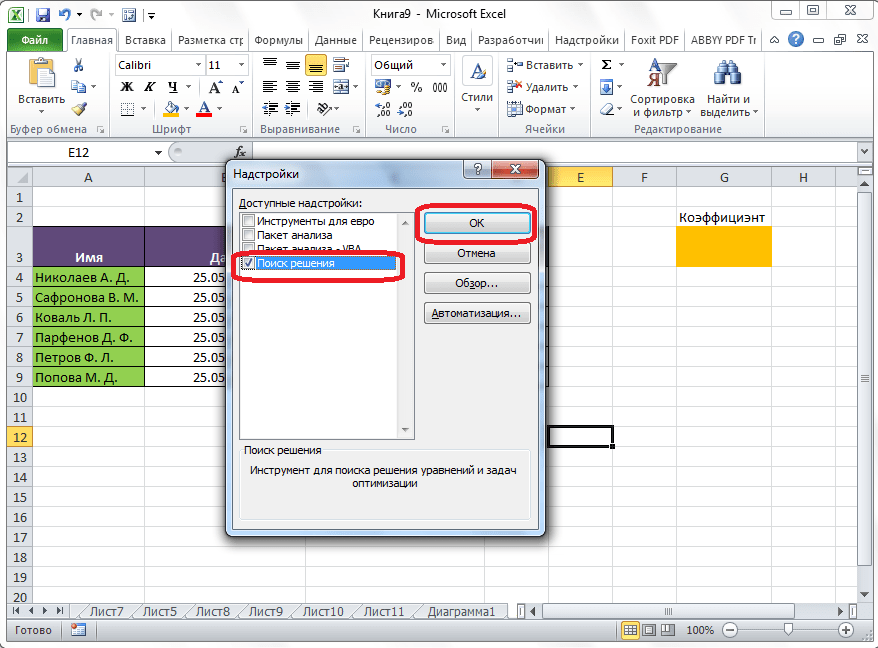
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».

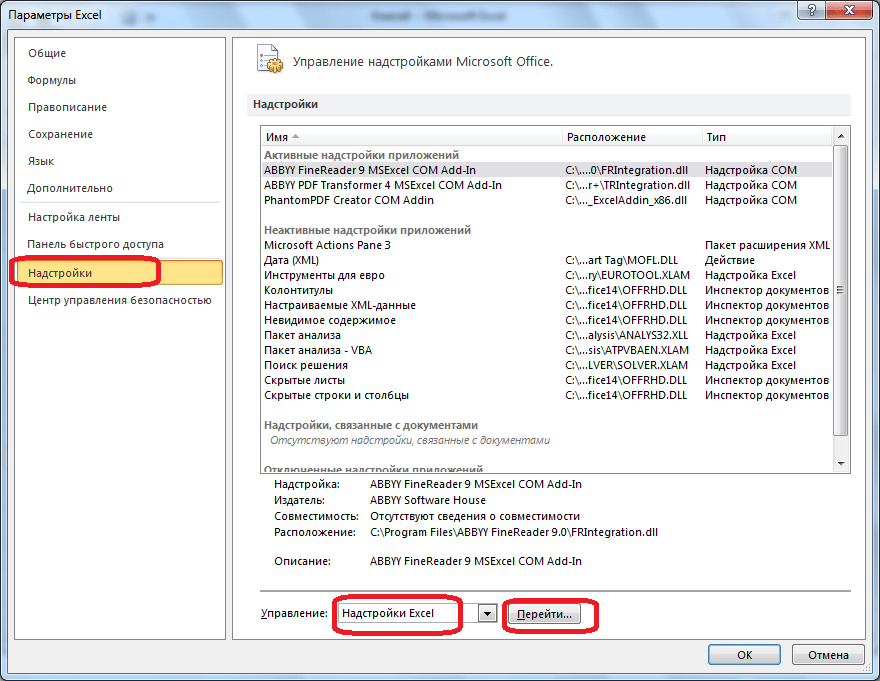
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».

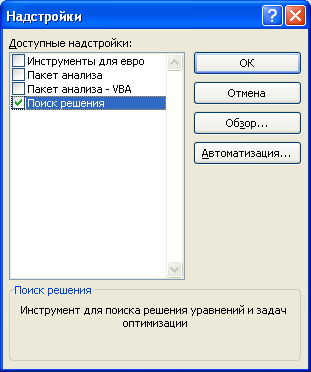
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».

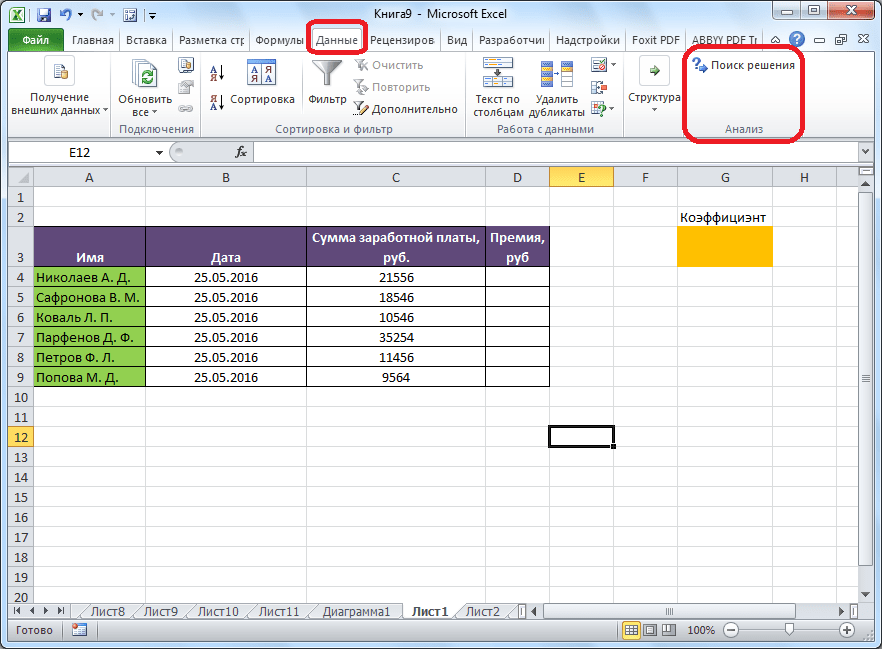
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».

Подготовка таблицы

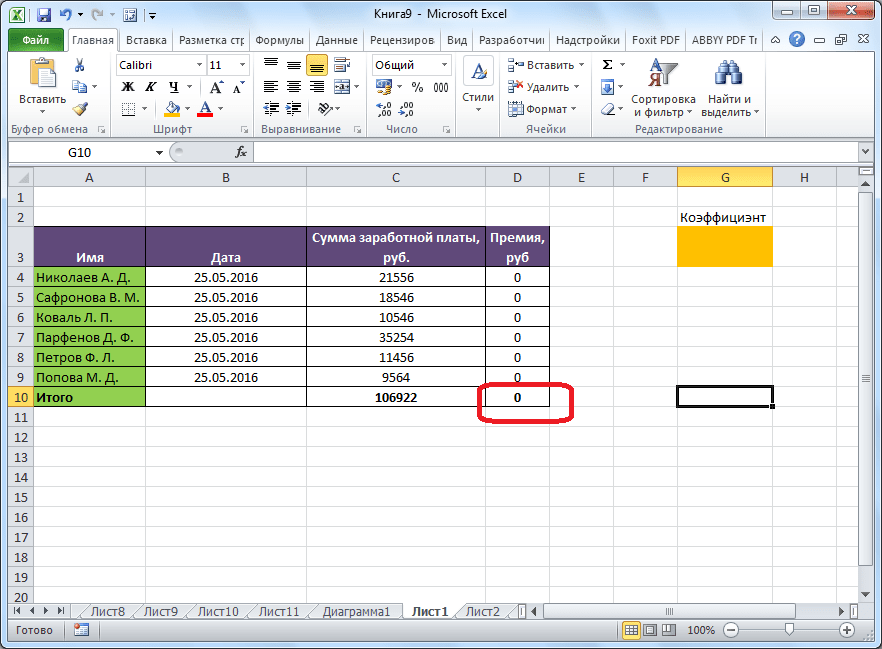
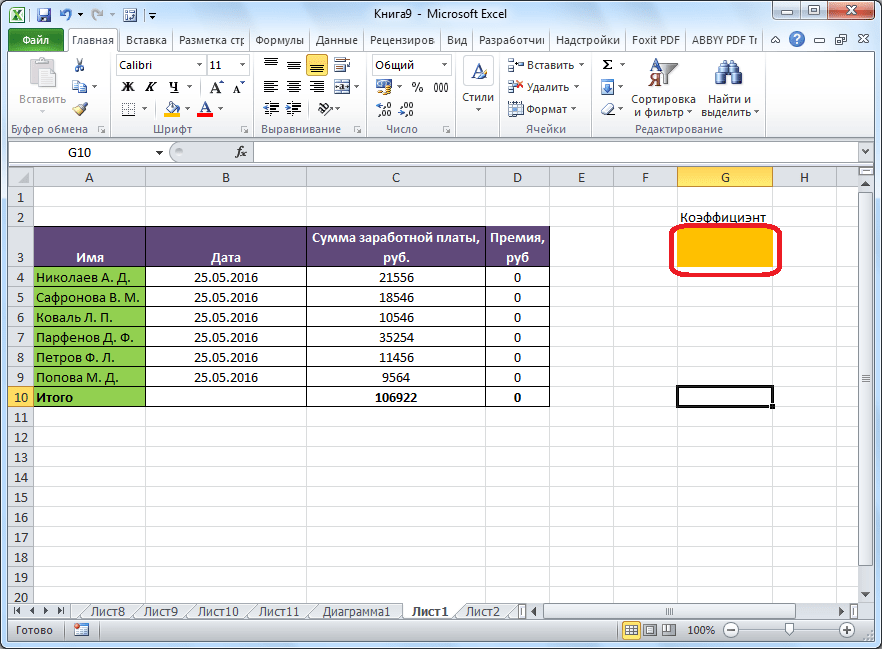
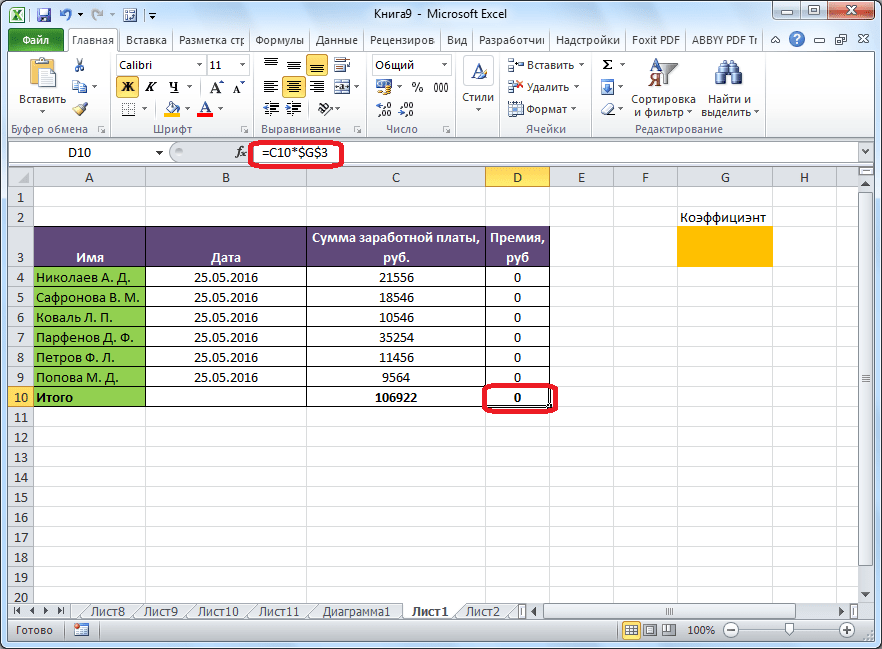
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

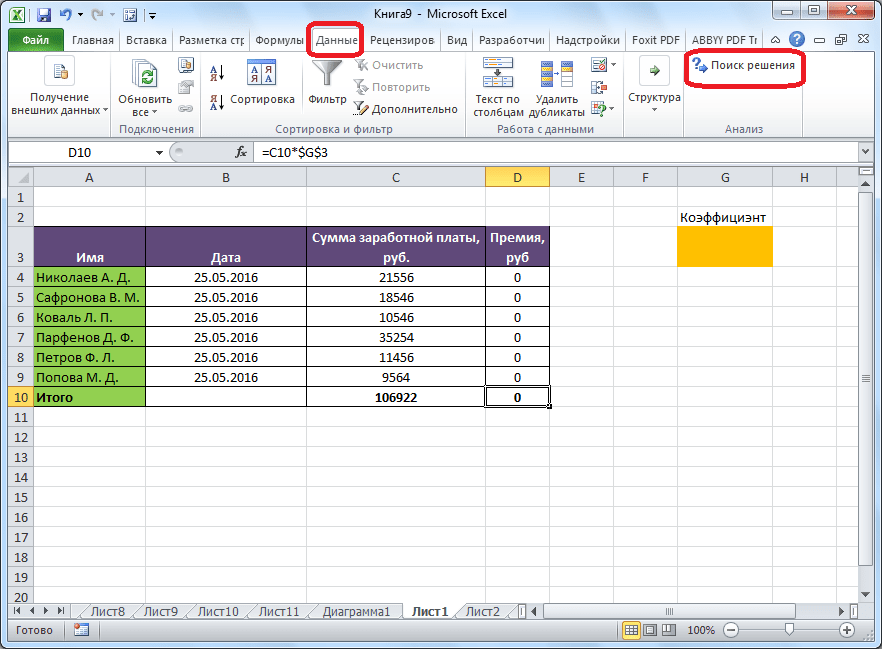
Запуск инструмента Поиск решения

После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».

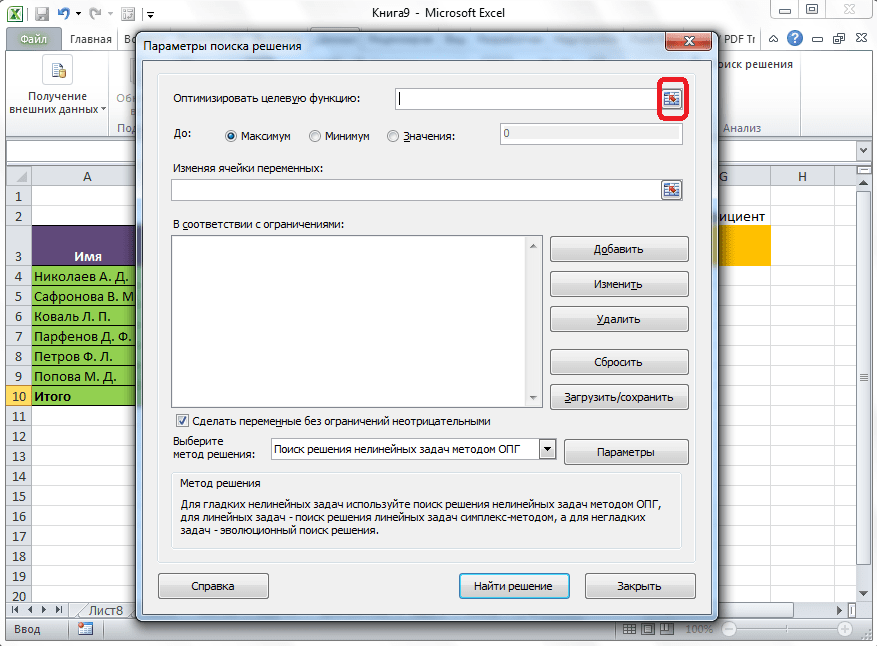
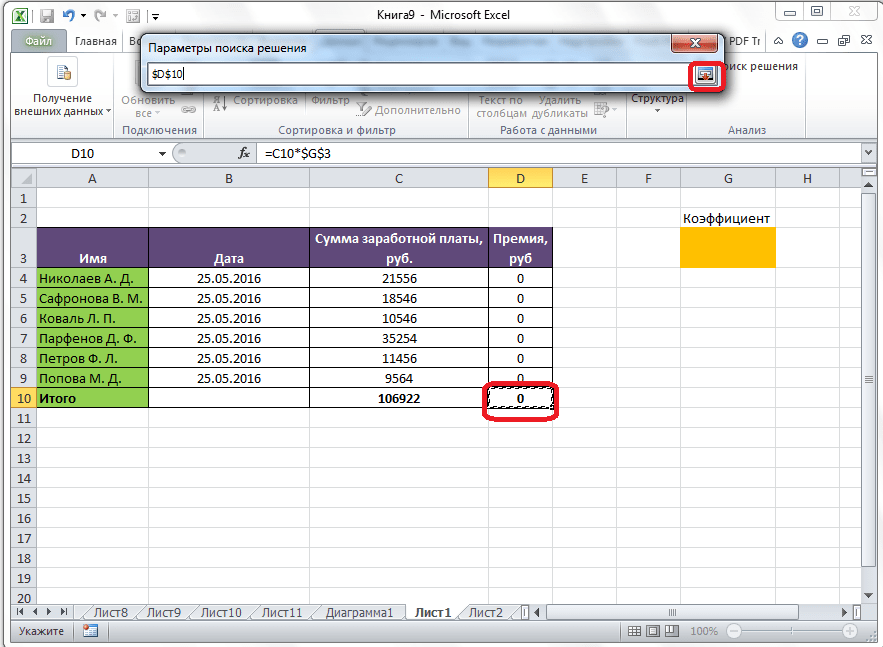
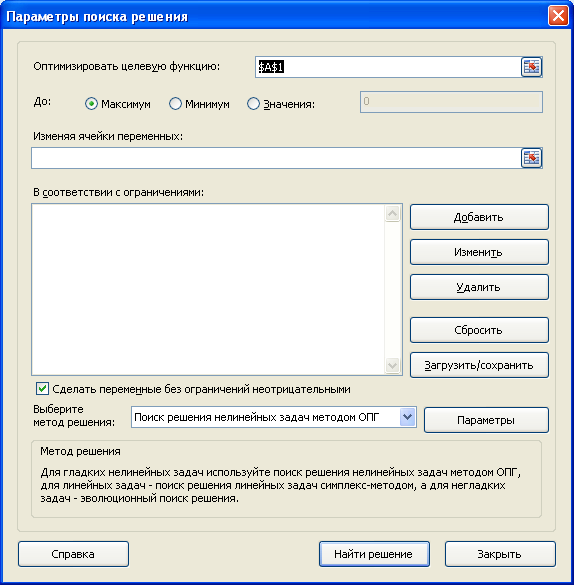
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.

После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.

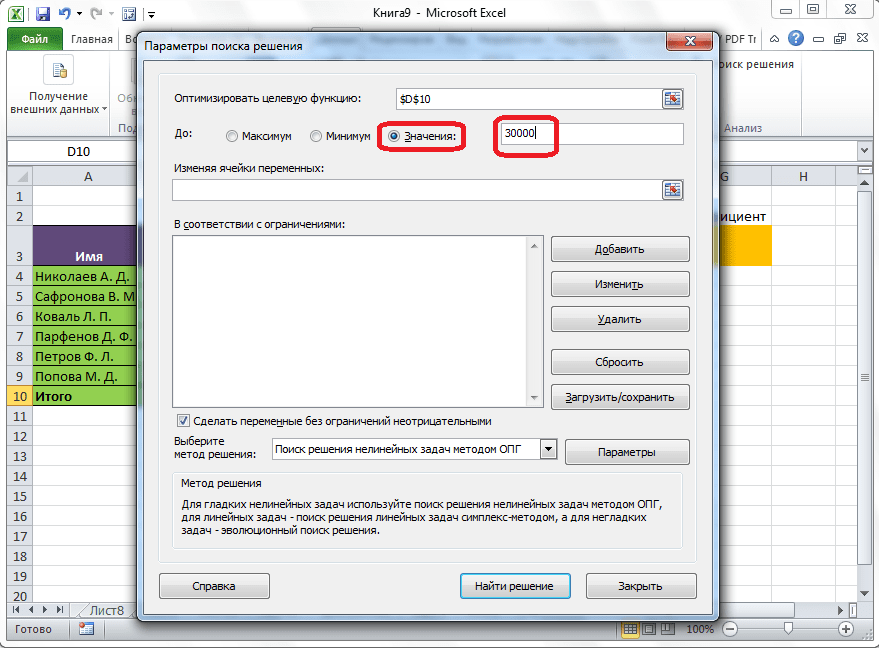
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.

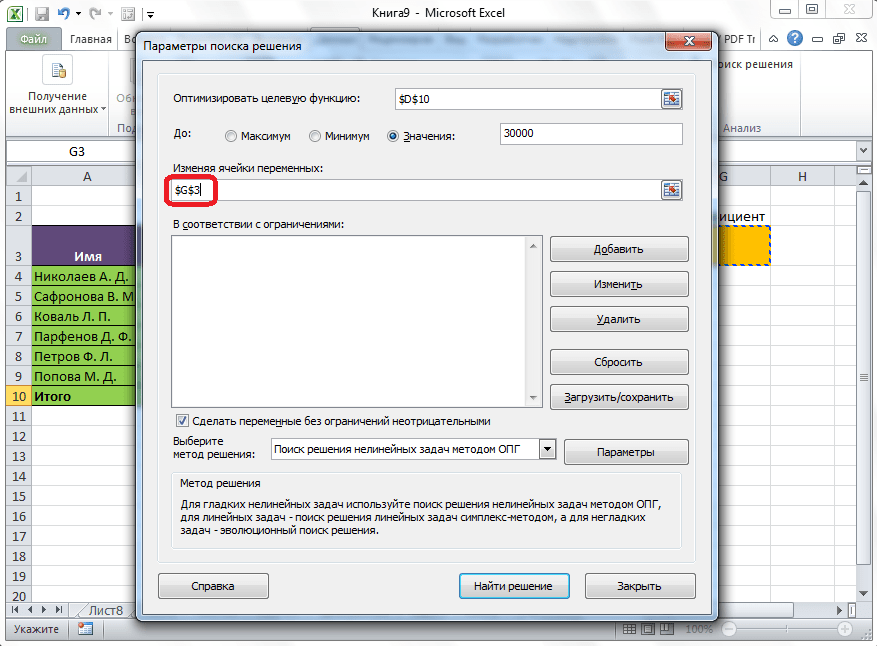
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.

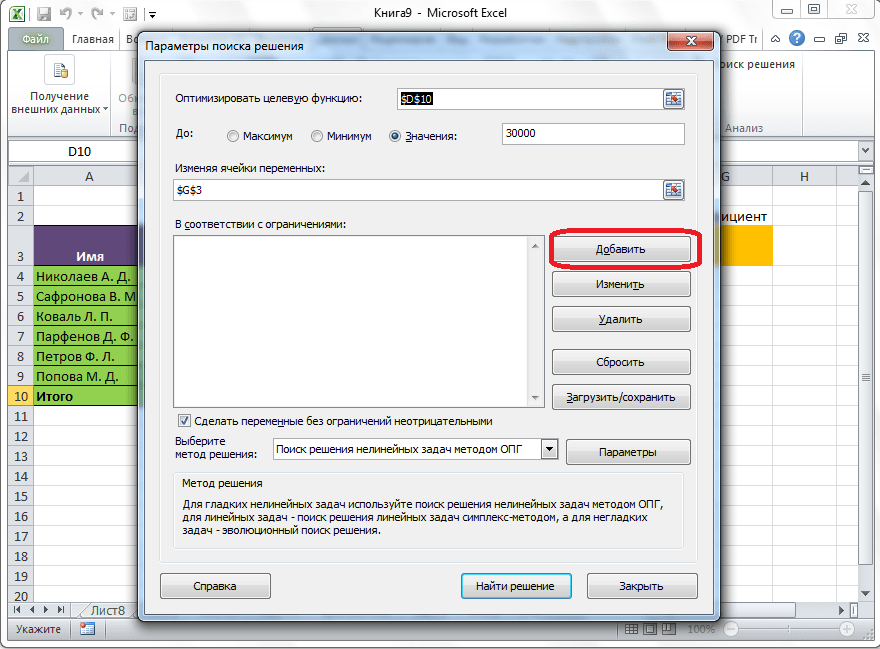
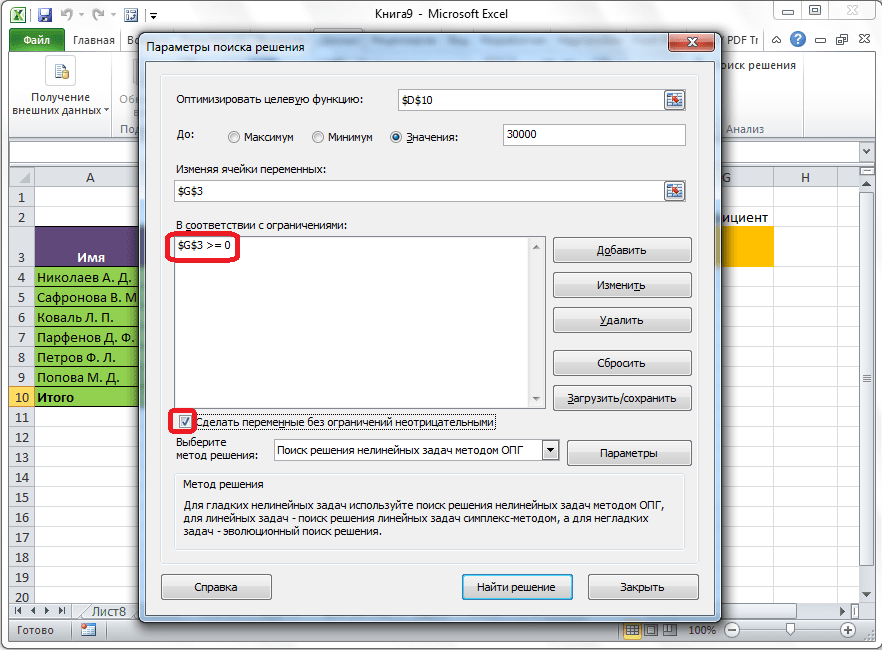
В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».

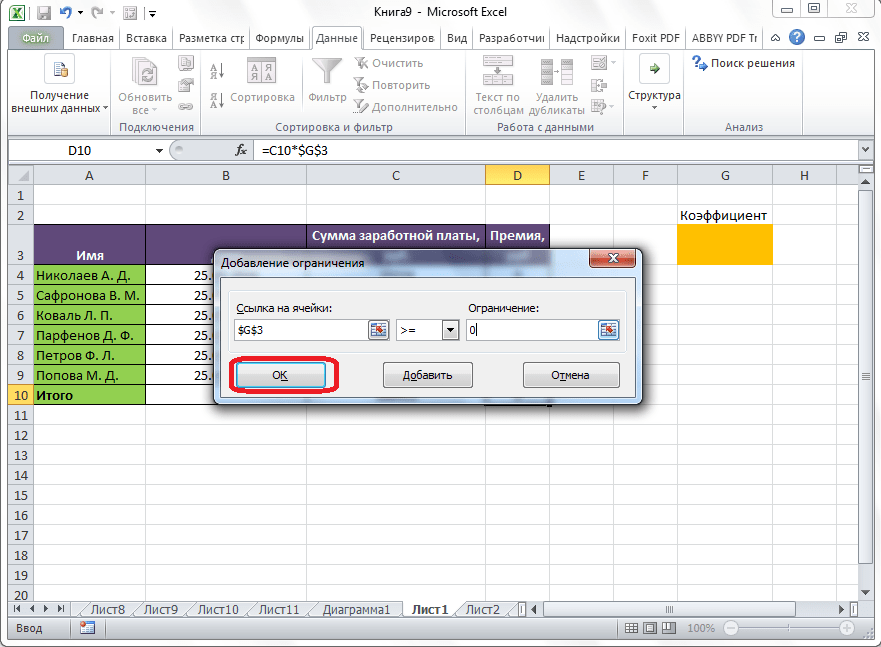
После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.

Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.

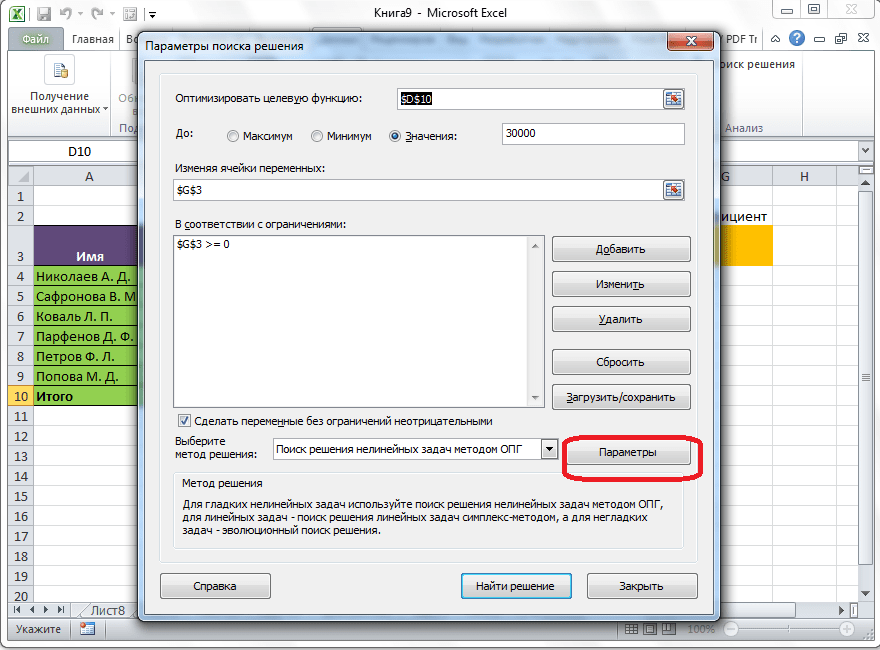
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».

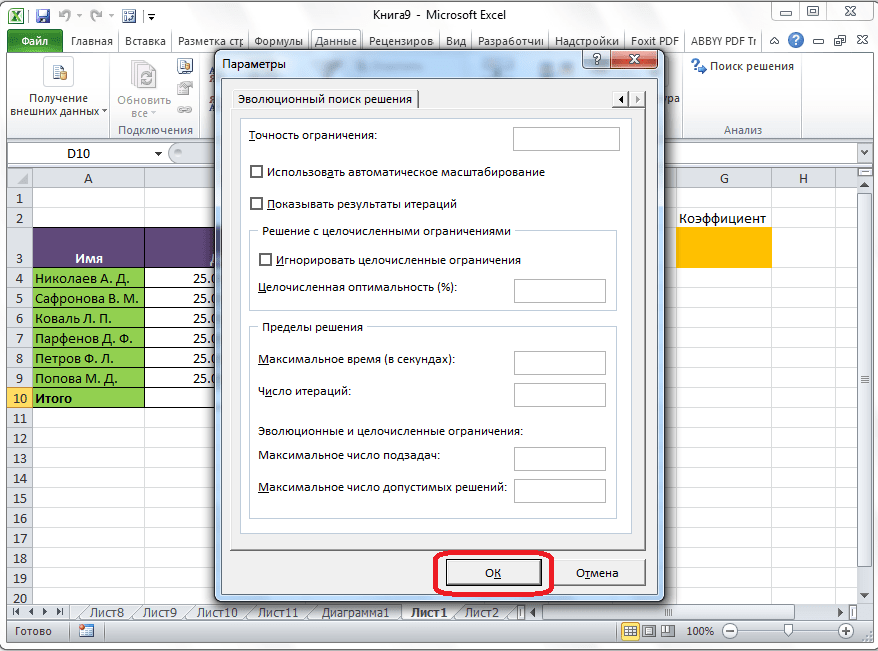
Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.

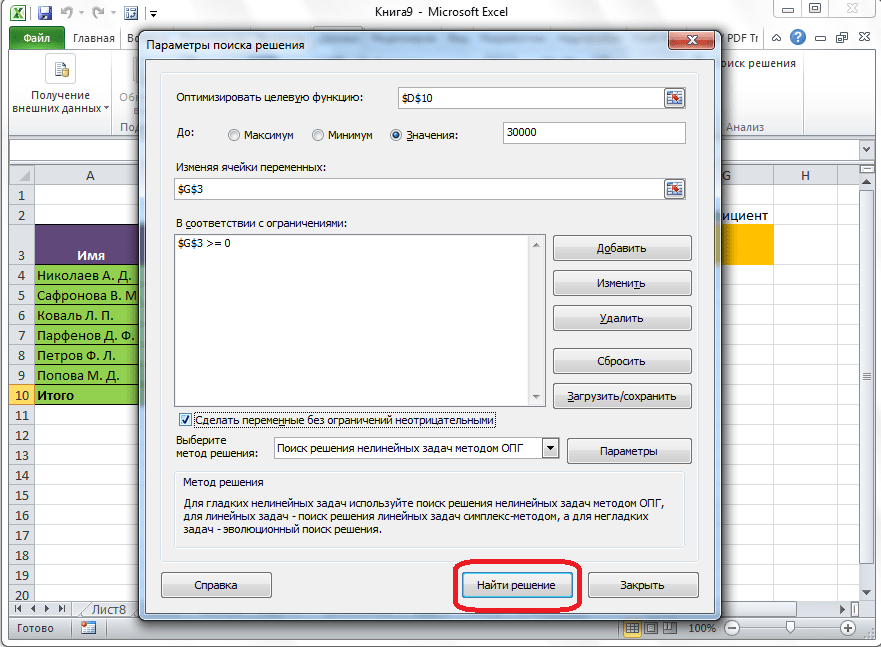
После того, как все настройки установлены, жмем на кнопку «Найти решение».

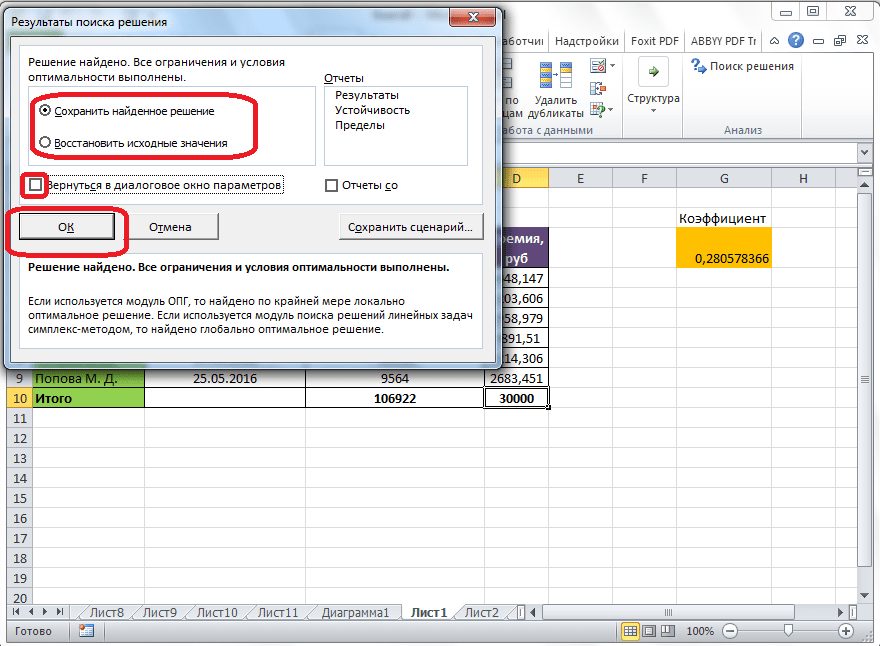
Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».

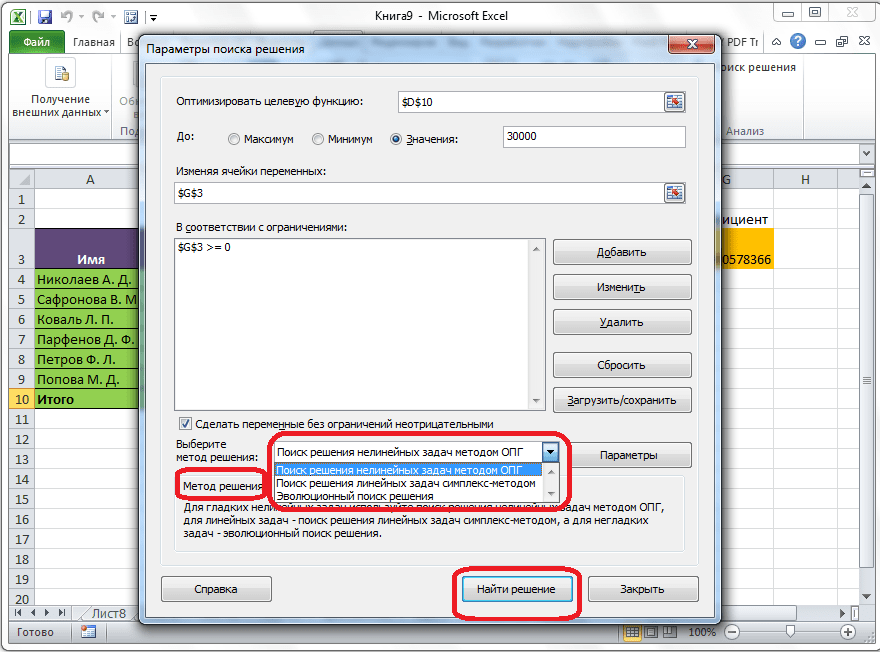
Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.

Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Поиск решения — это надстройка Microsoft Excel, с помощью которой можно найти оптимальное решение задачи с учетом заданных пользователем ограничений.

Поиск решения будем рассматривать в MS EXCEL 2010 (эта надстройка претерпела некоторые изменения по сравнению с предыдущей версией в MS EXCEL 2007).
В этой статье рассмотрим:

• создание оптимизационной модели на листе MS EXCEL
• настройку Поиска решения;
• простой пример (линейная модель).

Установка Поиска решения

Команда Поиск решения находится в группе Анализ на вкладке Данные.

Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку.
Для этого:

• На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки;
• В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
• В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

Примечание. Окно Надстройки также доступно на вкладке Разработчик. Как включить эту вкладку читайте здесь.

После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно.

При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа.

О моделях

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет. Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка Поиск решения помогает определить лучший способ сделать что-то:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить план производства, при котором доход от реализации произведенной продукции максимальный;
• Определить схему перевозок, при которой общие затраты на перевозку были бы минимальными;
• Найти распределение нескольких станков по разным видам работ, чтобы общие затраты на производство продукции были бы минимальными;
• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией).
В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений.
Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра. Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра.
Основные отличия Подбора параметра от Поиска решения:

• Подбор параметра работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Подготовка оптимизационной модели в MS EXCEL

Поиск решения оптимизирует значение целевой функции. Под целевой функцией подразумевается формула, возвращающая единственное значение в ячейку. Результат формулы должен зависеть от переменных модели (не обязательно напрямую, можно через результат вычисления других формул).
Ограничения модели могут быть наложены как на диапазон варьирования самих переменных, так и на результаты вычисления других формул модели, зависящих от этих переменных.
Все ячейки, содержащие переменные и ограничения модели должны быть расположены только на одном листе книги. Ввод параметров в диалоговом окне Поиска решения возможен только с этого листа.
Целевая функция (ячейка) также должна быть расположена на этом листе. Но, промежуточные вычисления (формулы) могут быть размещены на других листах.

Совет. Организуйте данные модели так, чтобы на одном листе MS EXCEL располагалась только одна модель. В противном случае, для выполнения расчетов придется постоянно сохранять и загружать настройки Поиска решения (см. ниже).

Приведем алгоритм работы с Поиском решения, который советуют сами разработчики ( ]]> www.solver.com ]]> ):

• Определите ячейки с переменными модели (decision variables);
• Создайте формулу в ячейке, которая будет рассчитывать целевую функцию вашей модели (objective function);
• Создайте формулы в ячейках, которые будут вычислять значения, сравниваемые с ограничениями (левая сторона выражения);
• С помощью диалогового окна Поиск решения введите ссылки на ячейки содержащие переменные, на целевую функцию, на формулы для ограничений и сами значения ограничений;
• Запустите Поиск решения для нахождения оптимального решения.

Проделаем все эти шаги на простом примере.

Простой пример использования Поиска решения

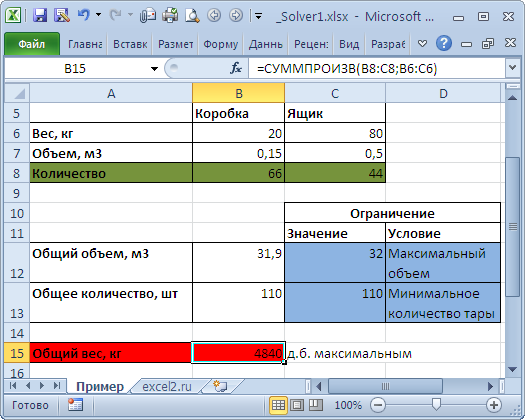
Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см. файл примера ).

Переменные модели (количество каждого вида тары) выделены зеленым.
Целевая функция (общий вес всех коробок и ящиков) – красным.
Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер.
Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) .
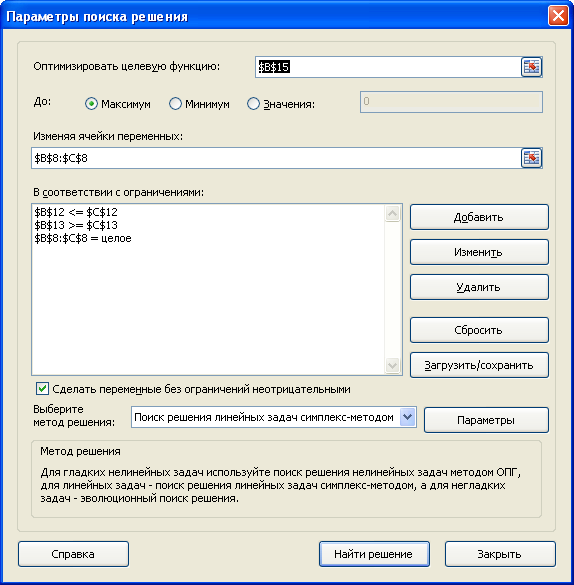
Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки).
Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.

После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.

Резюме

На самом деле, основной проблемой при решении оптимизационных задач с помощью Поиска решения является отнюдь не тонкости настройки этого инструмента анализа, а правильность построения модели, адекватной поставленной задаче. Поэтому в других статьях сконцентрируемся именно на построении моделей, ведь «кривая» модель часто является причиной невозможности найти решение с помощью Поиска решения.
Зачастую проще просмотреть несколько типовых задач, найти среди них похожую, а затем адаптировать эту модель под свою задачу.
Решение классических оптимизационных задач с помощью Поиска решения рассмотрено в этом разделе.

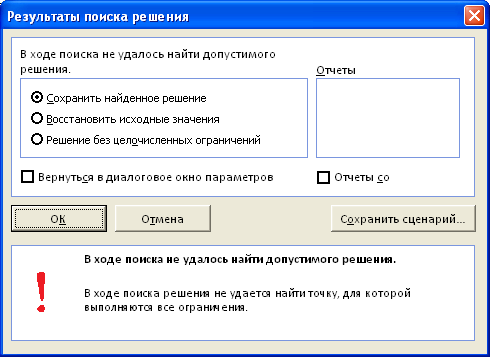
Поиску решения не удалось найти решения (Solver could not find a feasible solution)

Это сообщение появляется, когда Поиск решения не смог найти сочетаний значений переменных, которые одновременно удовлетворяют всем ограничениям.
Если вы используете Симплекс метод решения линейных задач, то можно быть уверенным, что решения действительно не существует.
Если вы используете метод решения нелинейных задач, который всегда начинается с начальных значений переменных, то это может также означать, что допустимое решение далеко от этих начальных значений. Если вы запустите Поиск решения с другими начальными значениями переменных, то, возможно, решение будет найдено.
Представим, что при решении задачи нелинейным методом, ячейки с переменными были оставлены не заполненными (т.е. начальные значения равны 0), и Поиск решения не нашел решения. Это не означает, что решения действительно не существует (хотя это может быть и так). Теперь, основываясь на результатах некой экспертной оценки, в ячейки с переменными введем другой набор значений, который, по Вашему мнению, близок к оптимальному (искомому). В этом случае, Поиск решения может найти решение (если оно действительно существует).

Примечание. О влиянии нелинейности модели на результаты расчетов можно прочитать в последнем разделе статьи Поиск решения MS EXCEL (4.3). Выбор места открытия нового представительства.

В любом случае (линейном или нелинейном), Вы должны сначала проанализировать модель на непротиворечивость ограничений, то есть условий, которые не могут быть удовлетворены одновременно. Чаще всего это связано с неправильным выбором соотношения (например, =) или граничного значения.
Если, например, в рассмотренном выше примере, значение максимального объема установить 16 м3 вместо 32 м3, то это ограничение станет противоречить ограничению по минимальному количеству мест (110), т.к. минимальному количеству мест соответствует объем равный 16,5 м3 (110*0,15, где 0,15 – объем коробки, т.е. самой маленькой тары). Установив в качестве ограничения максимального объема 16 м3, Поиск решения не найдет решения.

При ограничении 17 м3 Поиск решения найдет решение.

Некоторые настройки Поиска решения

Метод решения
Рассмотренная выше модель является линейной, т.е. целевая функция (M – общий вес, который может быть максимален) выражена следующим уравнением M=a1*x1+a2*x2, где x1 и x2 – это переменные модели (количество коробок и ящиков), а1 и а2 – их веса. В линейной модели ограничения также должны быть линейными функциями от переменных. В нашем случае ограничение по объему V=b1*x1+b2*x2 также выражается линейной зависимостью. Очевидно, что другое ограничение — Максимальное количество тары (n) – также линейно x1+x2 Похожие задачи

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.