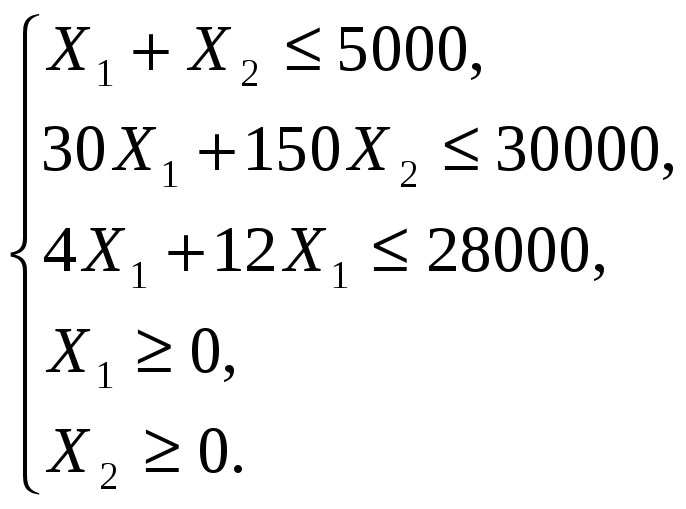Урок
№___
Тема: Практическая
работа №18
«Решение задач оптимального
планирования в Microsoft Excel»
Тип урока: практическая работа
Цели:
·
Получение представления о построении оптимального плана методом
линейного программирования;
·
Практическое освоение раздела Microsoft
Excel «Поиск
решения» для построения оптимального плана;
·
Формирование навыка по работе в MS Excel;
·
Развитие системного мышления, позволяющего выделять
в окружающей действительности системы, элементы систем, адекватные поставленной
задаче;
·
Формирование профессиональных навыков работы.
Оборудование:
·
ПК;
·
Интерактивная доска;
·
MS Excel
Ход
урока:
I. Организационный момент (5 мин.)
Приветствие.
Сообщение темы.
II. Актуализация
знаний (5 мин.)
Проверка
домашнего задания.
III. Практическая
работа (30 мин.)
Практическая работа
Справочная информация
Средство,
которое используется в данной работе, называется Поиск решения.
Соответствующая команда находится в меню Сервис. Поиск решения —
одно из самых мощных средств табличного процессора Excel.
Покажем на простейшем примере («пирожки и пирожные», см. учебник, § 39), как
воспользоваться указанным средством.
Задание 1
Реализовать
поиск оптимального решения для задачи планирования работы школьного
кондитерского цеха, описанной в § 39 учебника.
1. Подготовить таблицу к решению задачи
оптимального планирования.
В
режиме отображения формул таблица показана на рисунке. Ячейки В5 и С5
зарезервированы соответственно для значений х (план по
изготовлению пирожков) и у (план по изготовлению
пирожных). Ниже представлена система неравенств, определяющая ограничения на
искомые решения. Неравенства разделены на левую часть (столбец В) и правую
часть (столбец D).
Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая
функция занесена в ячейку В15.
|
А |
В |
С |
D |
|
|
1 |
Оптимальное |
|||
|
2 |
||||
|
3 |
Плановые |
|||
|
4 |
X (пирожки) |
У |
||
|
5 |
||||
|
6 |
||||
|
7 |
Ограничения |
|||
|
8 |
||||
|
9 |
Левая |
Знак |
Правая |
|
|
10 |
Время производства: |
1000 |
<= |
1000 |
|
11 |
Общее |
700 |
<= |
700 |
|
12 |
Положительность |
600 |
>= |
0 |
|
13 |
Положительность |
100 |
>= |
0 |
|
14 |
||||
|
15 |
Целевая |
=B5+2*C5 |
2.
Вызвать программу оптимизации и сообщить ей, где расположены данные. Для этого
выполнить следующие действия:
1.
Перейти на вкладку Данные
2.
В группе Анализ щелкнуть на
кнопку Поиск решений
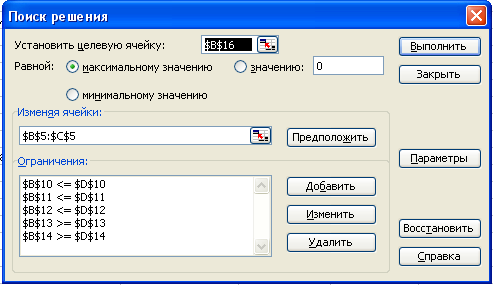
На
экране откроется соответствующая форма:
3.
Выполнить следующий алгоритм:
1. ввести
адрес ячейки с целевой функцией. В нашем случае это $В$15 (заметим, что если
перед этим установить указатель мыши на ячейку В15, то ввод произойдет
автоматически);
2. поставить
отметку максимальному значению, т. е. сообщить программе, что нас
интересует нахождение максимума целевой функции;
3. в
поле Изменяя ячейки ввести $В$5:$С$5, т. е. сообщить, какое место
отведено под значения переменных — плановых показателей;
4. в
поле Ограничения ввести неравенства-ограничения, которые имеют вид: B10<=D10;
B11<=D11;
B12>=D12;
B13>=D13.
Ограничения вводятся следующим образом:
a. щелкнуть
на кнопке Добавить;
b. в
появившемся диалоговом окне Добавление ограничения ввести ссылку на
ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10;
c. снова
щелкнуть на кнопке Добавить и аналогично ввести второе ограничение B11<=D11
и т. д.
d. в
конце щелкнуть на кнопке ОК.
5. закрыть
диалоговое окно Добавление ограничения. Перед нами снова форма Поиск
решения:
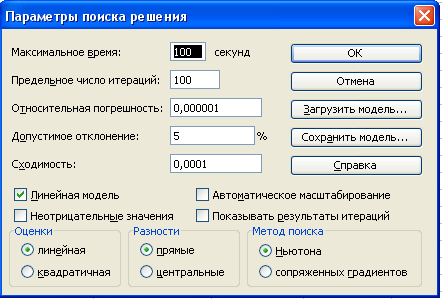
6. указать,
что задача является линейной (это многократно облегчит программе ее решение).
Для этого щелкнуть на кнопке Параметры, после чего открывается форма Параметры
поиска решения:
7.
установить флажок линейная
модель. Остальная информация на форме Параметры поиска решения чисто
служебная, автоматически устанавливаемые значения нас устраивают, и вникать в
их смысл не будем. Щелкнуть на кнопке ОК. Снова откроется форма Поиск
решения.
8. щелкнуть
на кнопке Выполнить — в ячейках В5 и С5 появляется оптимальное решение:
Справочная
информация
В
результате применения инструмента Поиск решения, получен следующий
оптимальный план дневного производства кондитерского цеха: нужно выпускать 600
пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис.
6.9 в учебнике. В этой точке значение целевой функции f(600,
100) = 800. Если один пирожок стоит 5 руб., то полученная выручка составит 4000
руб.
Задание
2
Требуется
решить задачу поиска оптимального плана производства школьного кондитерского
цеха с измененными условиями.
Представьте
себе, что в школе учатся неисправимые сладкоежки. И, кроме всех прочих
ограничений, перед кондитерским цехом ставится обязательное условие: число
пирожных должны быть не меньше числа пирожков. При такой постановке задачи
система неравенств (см. § 39) примет вид:
1.
Внести соответствующие изменения в
электронную таблицу, построенную при выполнении предыдущего задания.
2.
Получить оптимальный план с помощью
средства Поиск решения.
Проанализировать
полученные результаты. Сопоставить их с результатами задания 1.
Задание для самостоятельного выполнения по теме
«Оптимальное
планирование»
Задание
Составить
оптимальный план проведения экскурсионных поездок школьников во время каникул в
следующей ситуации. Областной департамент образования может профинансировать
поездки школьников из пяти районов области (районы будем обозначать номерами) в
три города (назовем эти города X, У и Z).
Количество
учащихся, которых следует отправить в поездки, таково:
|
Номер района |
1 |
2 |
3 |
4 |
5 |
|
Количество |
300 |
250 |
400 |
350 |
200 |
Экскурсионное
бюро может в данные каникулы обеспечить поездку следующего количества учащихся
в каждый из трех городов:
|
Город |
X |
Y |
Z |
|
Количество |
400 |
500 |
600 |
Стоимость
поездки (в рублях) приведена в следующей таблице.
|
Город |
Номер района |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
X |
500 |
700 |
750 |
1000 |
1100 |
|
Y |
700 |
600 |
400 |
500 |
800 |
|
Z |
1200 |
1000 |
800 |
600 |
500 |
Смысл
чисел в таблице таков: если в ячейке Y2
стоит 600, то это значит, что поездка одного учащегося из района 2 в город У
обходится в 600 рублей.
Необходимо составить такой план экскурсий,
который бы:
·
позволил каждому из намеченных к
поездке учащихся побывать на экскурсии;
·
удовлетворил условию об общем числе
экскурсантов в каждый из городов;
·
обеспечил максимально низкие
суммарные расходы финансирующей стороны.
Поскольку
эта задача непроста, поможем вам с ее математической формулировкой.
План
перевозок, который нам надлежит составить, будет отражен в следующей таблице:
|
1 |
2 |
3 |
4 |
5 |
|
|
X |
X1 |
X2 |
X3 |
X4 |
X5 |
|
Y |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
|
Z |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
Величины,
стоящие в этой таблице, и являются объектами поиска. Так, X3
есть число учащихся из района № 3, которые
по разрабатываемому плану поедут в город X.
Первое
условие (ограничение задачи) состоит в том, что все учащиеся из каждого района
поедут на экскурсию. Математически оно выражается следующими уравнениями:
(1)
Второе
условие — в каждый город поедут столько учащихся, сколько этот город в
состоянии принять:
(2)
Кроме
того, искомые величины, разумеется, неотрицательны:
(3)
Теперь
запишем общую стоимость расходов на экскурсии. Поскольку привести, например, на
экскурсию X1
учащихся в целом стоит X1*500
рублей (см. таблицу стоимости поездки), то общие
расходы составят:
|
|
(4) |
Теперь
имеется все для полной математической формулировки задачи: требуется найти
наименьшее значение функции (4) при
условии, что входящие в нее переменные удовлетворяют системам уравнений (1) и
(2)
и неравенств (3).
Это
весьма непростая задача. Однако ее решение (как и задач, существенно более
сложных) вполне «по плечу» программе Excel
с помощью средства Поиск решений, которым вам и надлежит воспользоваться.
Приведем результат решения задачи:
|
X1 |
X2 |
X3 |
X4 |
X5 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Z1 |
Z2 |
Z3 |
Z4 |
Z5 |
|
300 |
100 |
0 |
0 |
0 |
0 |
100 |
400 |
0 |
0 |
0 |
50 |
0 |
350 |
200 |
Итог:
в город X поедут
на экскурсию 300 учащихся из района №1 и 100 учащихся из района № 2, в город У —
100 учащихся из района № 2 и 400 из района № 3, в город Z
— 50 учащихся из района № 2, 350 — из
района № 4 и 200 — из района № 5.
Полученный
результат можно сформулировать следующим образом: все учащиеся из района №1
уедут в город X, учащиеся из района № 2 поделятся между городами X, У и
Z
(соответственно 100, 100 и 5), все
учащиеся из района № 3 уедут в город У, а все учащиеся из районов № 4 и № 5
поедут в город Z.
Такое неочевидное, на первый взгляд,
разделение обеспечивает в данном случае наибольшую экономию средств.
IV. Итог урока (2 мин.) Объявляются оценки.
V.
Домашнее задание (3 мин.) Подготовка к к/р. Подготовка
докладов по § 40-43
Решение задачи оптимального планирования в
Решение задачи оптимального планирования в MS Excel
R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты
имеются некоторые плановые показатели: х, у и другие;
имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.
Постановка задачи планирования
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс
Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами:
пашня — 5000 га,
труд — 300 тыс. чел.-ч,
возможный объем тракторных работ — 28 000 условных га.
Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).
Найдите оптимальное сочетание посевных площадей культур.
Рассмотрим пример
Этап I. Решение. культуры Затраты на 1 га посева
Этап I.
Решение.
|
культуры |
Затраты на 1 га посева |
Стоимость валовой продукции с 1 га, р. |
|
|
труда, чел.-ч |
тракторных работ, усл. га |
||
|
Зерновые |
30 |
4 |
400 |
|
Картофель |
150 |
12 |
1000 |
Для поиска оптимального решения задачи обозначим через х1 -га площадь, отводимую под зерновые, х2 га — площадь, отводимую под картофель
Для поиска оптимального решения задачи обозначим через
х1 -га площадь, отводимую под зерновые,
х2 га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х1 р.,
а стоимость картофеля — 1000 х2 р.
Отсюда стоимость всей валовой продукции составит ( 400 х1 + 1000 х2) р.
Обозначим это выражение через у и назовем его целевой функцией:
у = 400 х1 + 1000 х2
Нам надо найти максимум этой целевой функции при соблюдении следующих условий: а) общая площадь зерновых и картофеля не должна превышать 5000 га, т
Нам надо найти максимум этой целевой функции при соблюдении следующих условий:
а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х1 + х2≤5000;
б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х1 + 150 х2≤ 300 000;
в) общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х1 + 12 х2≤28 000;
г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х1≥0 и х2 ≥0.
Таким образом, условия задачи выражаются следующей системой неравенств
Таким образом, условия задачи выражаются следующей системой неравенств
Требуется найти такие значения х1 и х2, при которых целевая функция у = 400 х1 + 1000 х2 принимает наибольшее значение.
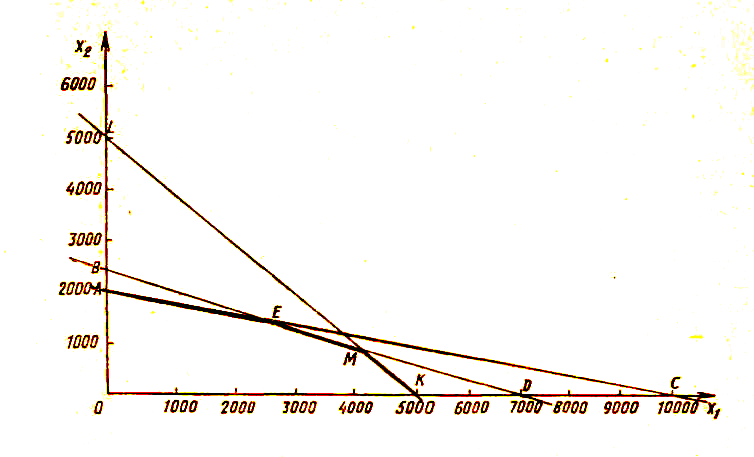
Этап II. Решим задачу графически
Этап II. Решим задачу графически.
Построим прямую х1 + х2=5000.
Построим прямую х1 + х2=5000.
Построим прямую 30 х1 + 150 х2=300 000.
Построим прямую 4 х1 + 12 х2=28 000.
А
Е
М
К
О
Таким образом, наибольшее значение целевой функции достигается в вершине
Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.
Решение задачи оптимального планирования в
Решение задачи оптимального планирования в MS Excel
Поиск решения». Для этого надо выполнить команду =>
программа оптимизации «Поиск решения». Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма
Далее надо выполнить следующий алгоритм:
Далее надо выполнить следующий алгоритм:
Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.
В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B1K=D11; B12>=D12; B13>=D13.
Закрыть диалоговое окно «Добавление ограничения»
Закрыть диалоговое окно «Добавление ограничения». Снова появится форма «Поиск решения»
Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение)
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения»
Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках
Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение
Практическая работа в парах (делятся на пары, каждая пара вытягивает задачу
Практическая работа в парах (делятся на пары, каждая пара вытягивает задачу. Приступают к решению)
Итоги (что получилось в решении, мнение о работе)
Спасибо за урок!
Спасибо за урок!
«Решение задачи оптимального планирования в MS Excel»
Цели работы:
• получение представления о построении оптимального плана методом
линейного программирования;
• практическое освоение раздела MS Excel «Поиск решения» для построения
оптимального плана.
Средство, о котором идет речь, называется «Поиск решения». Соответствующая
команда находится в меню Сервис. «Поиск решения» — одно из самых мощных
средств ТП Excel, и мы не будем даже пытаться освоить все его возможности.
Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как
воспользоваться указанным средством.
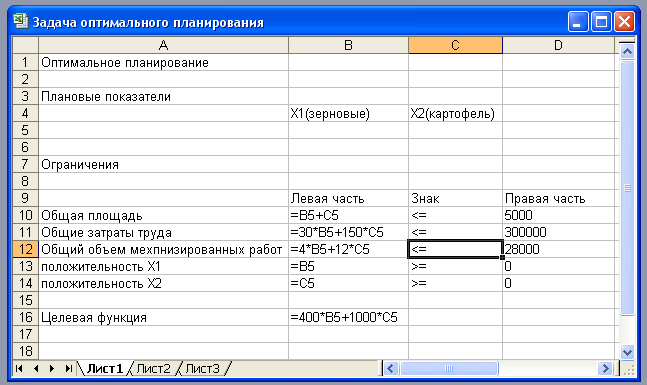
Вначале надо подготовить электронную таблицу к решению задачи оптимального
планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки
В5 и С5 зарезервированы соответственно для значений х
1
га (площадь отведенная для
посевов зерна ) и х
2
га (площадь отведенная под картофель). Ниже этих ячеек
представлена система неравенств (а), определяющая ограничения на искомые
решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец
D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая
функция (Р) занесена в ячейку В15.
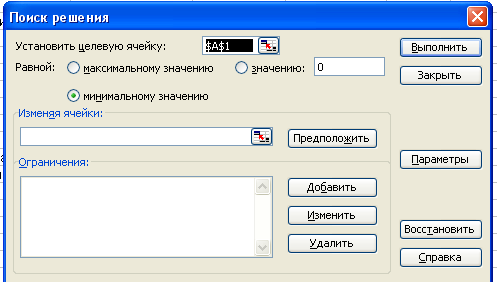
Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей,
где расположены данные. Для этого надо выполнить команду => Сервис => Поиск
решения. На экране откроется соответствующая форма (рис. 2)
МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия
Конспект урока по информатике в 11 классе
«Решение задачи оптимального планирования в MS Excel»
Урок подготовил и провел: учитель информатики и ИКТ Бахарев Юрий Владимирович
п. Преображенский -2013
Цель урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.
Задачи:
-
познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;
-
закрепить навыки работы с формулами в среде электронных таблиц;
-
развивать умение анализировать и обобщать материал, строить математическую модель задачи;
-
воспитывать самостоятельность и ответственность в принятии решения.
Оборудование:
-
Компьютер преподавателя
-
Компьютеры учащихся – 10 шт.
-
Локальная сеть
-
Программное обеспечение: MS PowerPoint, MS Excel
Продолжительность урока: 40 мин.
Ход урока
-
Организующее начало урока.
-
Выявление имеющихся знаний и умений.
1. а) Что такое корреляционная зависимость?
б) Что такое корреляционный анализ?
в) Какие типы задач можно решать с помощью корреляционного анализа?
г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?
-
С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?
-
а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.
б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.
3. Изучение нового материала.
Решение задачи оптимального планирования в MS Excel.
Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.
Постановка задачи планирования выглядит следующим образом:
-
имеются некоторые плановые показатели: х, у и другие;
имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены; имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Рассмотрим пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.
Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс. чел.-ч, возможный объем тракторных работ — 28 000 условных га.
Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).
Найдите оптимальное сочетание посевных площадей культур.
Решение.
Этап I. Для составления математической модели воспользуемся нормативами затрат и выхода продукции для данного совхоза.
Таблица 10
|
Культуры |
Затраты на 1 га посева |
Стоимость валовой продукции с 1 га, р. |
|
|
труда, чел.-ч |
тракторных работ, усл. га |
||
|
Зерновые Картофель |
30 150 |
4 12 |
400 1000 |
Критерием оптимальности является максимум стоимости валовой продукции. Этот максимум должен достигаться в условиях использования ограниченных ресурсов пашни, труда и механизированных работ.
Задача является многовариантной, так как имеется множество допустимых вариантов сочетания посевных площадей двух культур, но не все они равнозначны с точки зрения требования оптимальности.
Допустим, что примем решение всю площадь засеять картофелем, который обеспечивает наибольший выход валовой продукции с 1 га. Но для возделывания картофеля на площади 5000 та потребуется 150·5000 = 750 000 Чел.-ч., а мы такими ресурсами не располагаем. Ясно, что такое решение не является приемлемым. Если же засеем всю площадь зерновыми, объем валовой продукции не окажется наибольшим, да и значительная часть трудовых ресурсов не будет использована.
Для поиска оптимального решения задачи обозначим через х1 -га площадь, отводимую под зерновые, а через х2 га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х1 р., а стоимость картофеля — 1000 х2 р. Отсюда стоимость всей валовой продукции составит ( 400 х1 + 1000 х2) р. Обозначим это выражение через у и назовем его целевой функцией:
у = 400 х1 + 1000 х2
Нам надо найти максимум этой целевой функции при соблюдении следующих условий:
а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х1 + х2≤5000;
б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х1 + 150 х2≤ 300 000;
в) общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х1 + 12 х2≤28 000;
г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х1≥0 и х2 ≥0.
Таким образом, условия задачи выражаются следующей системой неравенств
Требуется найти такие значения х1 и х2, при которых целевая функция у = 400 х1 + 1000 х2 принимает наибольшее значение.
х1≥0 и х2 ≥0xi^O и х2^0.
Этап II. Решим задачу графически.
Построим прямую х1 + х2=5000. Координаты всех точек треугольника LOK удовлетворяют неравенству х1 + х2≤5000.
Построим прямую 30 х1 + 150 х2=300 000. Координаты всех точек треугольника АОС удовлетворяют неравенству 30 х1 + 150 х2≤ 300 000.
Построим прямую 4 х1 + 12 х2=28 000. Координаты всех точек треугольника BOD удовлетворяют неравенству 4 х1 + 12 х2≤28 000.
Неравенствам х1≥0 и х2 ≥0 удовлетворяют все точки I четверти координатной плоскости х10х2 .
Любая точка многоугольник» АЕМКО удовлетворяет системе неравенств. Для нахождения наибольшего значения целевой функции найдем ее значения в вершинах многоугольника АЕМКО.
Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.
В связи с тем что введение понятия о линейном программировании в массовой школе не предусмотрено, такая задачу мы можем выполнить используя средство «Поиск решения» которая реализована в MS Ехsel.
-
Практическая работа 19.
«Решение задачи оптимального планирования в MS Excel»
Цели работы:
• получение представления о построении оптимального плана методом линейного программирования;
• практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.
Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.
Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х1 га (площадь отведенная для посевов зерна ) и х2 га (площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.
Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду = Сервис = Поиск решения. На экране откроется соответствующая форма (рис. 2)
Далее надо выполнить следующий алгоритм:
-
Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
-
Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
-
В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.
-
В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10D10; B1K=D11; B12=D12; B13=D13. Ограничения вводятся следующим образом:
= щелкнуть по кнопке «Добавить»;
в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11D11 и так далее. В конце надо щелкнуть на кнопке ОК.
5. Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).
-
Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».
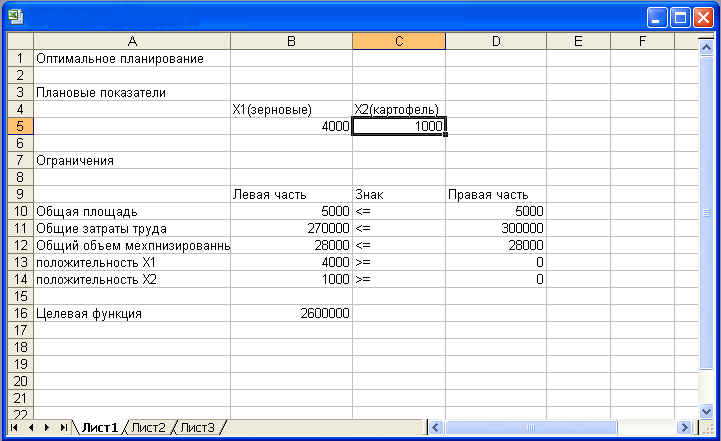
Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).
Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.
При х1=4000 и х2=1000 х1 + х2=5000, а это значит, что пашня используется полностью.
4 х1 + 12 х2≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.
30 х1 + 150 х2= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.
5. Закрепление новой темы по вопросам:
-
В чем состоит задача оптимального планирования?
-
Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.
-
Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.
-
Что такое математическое программирование, линейное программирование?
6. Д/З § 38, читать конспект, составить математическую модель для решения 1 задачи
Список используемой литературы:
1. Семакин И.Г Учебник Информатика и ИКТ. Базовый уровень 10-11 класс.. М. Бином.
2. И.М. Шапиро. Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.
В программу Excel встроены возможности
решения задач математического
программирования.
Средство «Поиск решения» реализовано
в форме надстройки. Соответствующая
команда находится в меню Сервис (MS
Excel 97-2003) или в группе
Анализ вкладки Данные.
Замечание. Средство поиска решения
является надстройкой — вспомогательной
программой, служащая для добавления в
Microsoft Office специальных команд или
возможностей. Чтобы использовать эту
надстройку в Excel, необходимо сначала
загрузить ее. Для этого в MS
Excel 7 нажмите кнопку MS
Office
,
а затем щелкните Параметры Excel.
Выберите команду Надстройки, а затем
в окне Управление выберите пункт
Надстройки Excel. Нажмите кнопку
Перейти. В окне Доступные надстройки
установите флажок Поиск решения и
нажмите кнопку ОК.
В случае появления сообщения о том, что
надстройка для поиска решения не
установлена на компьютере, нажмите
кнопку Да, чтобы установить ее.
Покажем на рассмотренном нами простейшем
примере («пирожки и пирожные»), как
воспользоваться средством Поиск Решения.
Вначале надо подготовить электронную
таблицу к решению задачи оптимального
планирования. В режиме отображения
формул таблица показана на рис. 2.20.
Ячейки В5 и С5 зарезервированы соответственно
для значений х (план по изготовлению
пирожков) и у (план по изготовлению
пирожных). Ниже этих ячеек представлена
система неравенств (а), определяющая
ограничения на искомые решения.
Неравенства разделены на левую часть
(столбец В) и правую часть (столбец D).
Знаки неравенств в столбце С имеют чисто
оформительское значение. Целевая функция
(p) занесена в ячейку В15.
|
А |
В |
С |
D |
|
|
1 |
Оптимальное |
|||
|
2 |
||||
|
3 |
Плановые показатели |
|||
|
4 |
X (пирожки) |
У (пирожные)^ |
||
|
5 |
||||
|
6 |
||||
|
7 |
Ограничения |
|||
|
8 |
||||
|
9 |
Левая часть |
Знак |
Правая часть |
|
|
10 |
Время производства: |
=В5+4*С5 |
<= |
1000 |
|
11 |
Общее количество: |
=В5+С5 |
<= |
700 |
|
12 |
Положительность |
=В5 |
>= |
0 |
|
13 |
Положительность |
=С5 |
>= |
0 |
|
14 |
||||
|
15 |
Целевая функция |
=В5+2*С5 |
||
|
16 |
Рис. 2.20. Таблица, подготовленная к
вычислению оптимального плана
Теперь следует вызвать программу
оптимизации «Поиск решения» и сообщить
ей, где расположены данные. Для этого
надо выполнить команду => Сервис =>
Поиск решения. На экране откроется
соответствующая форма (рис. 2.21).
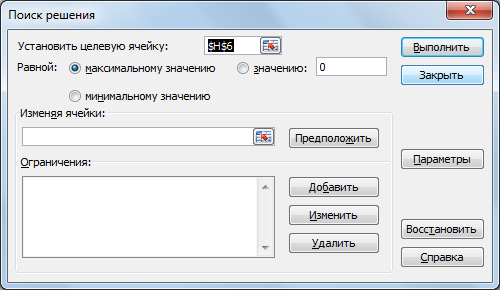
Рис. 2.21. Начальное состояние формы «Поиск
решения»
Далее надо выполнить следующий алгоритм:
Ввести координату ячейки с целевой
функцией. В нашем случае это В15. (Заметим,
что если перед этим установить курсор
на ячейку В15, то ввод произойдет
автоматически).
Поставить отметку «максимальному
значению», то есть сообщить программе,
что нас интересует нахождение максимума
целевой функции.
В поле «Изменяя ячейки» ввести В5:С5, то
есть сообщить, какое место отведено под
значения переменных — плановых показателей.
В поле «Ограничения» надо ввести
информацию о неравенствах-ограничениях,
которые имеют вид B10<=D10;
B1K=D11;
B12>=D12;
B13>=D13.
Ограничения вводятся следующим образом:
=> щелкнуть по кнопке «Добавить»;
в появившемся диалоговом окне «Добавление
ограничения» ввести ссылку на ячейку
В10, выбрать из меню знак неравенства <=
и ввести ссылку на ячейку D10; снова
щелкнуть по кнопке «добавить» и аналогично
ввести второе ограничение B11<=D11 и так
далее. В конце надо щелкнуть на кнопке
ОК.
Закрыть диалоговое окно «Добавление
ограничения».Снова появится форма
«Поиск решения» (рис. 2.22).
Теперь надо дать последние указания:
задача является линейной (это многократно
облегчит программе ее решение). Для
этого следует щелкнуть по кнопке
«Параметры» — появится форма «Параметры
поиска решения» (рис. 2.23).
Рис. 2.23. Форма «Параметры поиска решения»
Надо выставить флажок на переключателе
«Линейная модель» Остальная информация
в форме «Параметры поиска решения»
служебная, автоматически устанавливаемые
значения нас устраивают . Следует
щелкнуть по кнопке ОК, что возвратит
нас в форму «Поиск решения».
Вся информация введена. Далее надо
щелкнуть по кнопке «Выполнить» —
мгновенно в ячейках В5 и С5 появится
оптимальное решение (числа 600 и 100), а
также число 800 в ячейке В15 — максимальное
значение целевой функции (рис. 2.24).
|
А |
В |
С |
D |
|
|
1 |
Оптимальное планирование |
|||
|
2 |
||||
|
3 |
Плановые показатели |
|||
|
4 |
X (пирожки) |
Y (пирожные) |
||
|
5 |
600 |
100 |
||
|
в |
||||
|
7 |
Ограничения |
|||
|
8 |
||||
|
9 |
Левая часть |
Знак |
Правая часть |
|
|
10 |
Время производства: |
1000 |
<= |
1000 |
|
11 |
Общее количество: |
700 |
<= |
700 |
|
12 |
Положительность X: |
600 |
>= |
0 |
|
13 |
Положительность Y: |
100 |
>= |
0 |
|
14 |
||||
|
15 |
Целевая функция |
800 |
||
|
16 |
Рис. 2.24. Результаты решения задачи
Кроме того, на экране появилась еще одна
форма — «Результаты поиска решения».
На первом этапе освоения возможностей
программы на эту форму можно не обращать
внимания (хотя в принципе в ней может
оказаться очень полезная информация).
Итак, в результате применения инструмента
«Поиск решения», мы получим следующий
оптимальный план дневного производства
кондитерского цеха: нужно выпускать
600 пирожков и 100 пирожных. В этой точке
значение целевой функции f(600,100)
= 800. Если один пирожок стоит 2 рубля, то
полученная выручка составит 1600 рублей.
Решение, которое мы получили, вполне
разумно как с экономической точки
зрения, так и с медицинской. Много
сладкого — вредно для здоровья, а пирожки
и сытнее и полезнее.
Полученная электронная таблица и
настроенная на нее сервисная функция
«Поиск решения» являются средством, с
помощью которого можно решать задачу
оптимального планирования при меняющихся
условиях. Например, может измениться
длина рабочего дня. Тогда надо внести
новое значение в ячейку D10 и оптимальный
план автоматически пересчитается. Так
же может измениться допустимое суммарное
число изделий в ячейке D11.
Представьте себе, что в вашей школе
учатся неисправимые сладкоежки. И,
кроме всех прочих ограничений, перед
кондитерским цехом ставится обязательное
условие: число пирожных должно быть не
меньше числа пирожков. При такой
постановке задачи система неравенств
(а) примет вид:
х + 4у < 1000;
х + у < 700;
х >0; у>х.
Соответствующее изменение легко внести
в электронную таблицу. Для этого
достаточно в ячейке D13 вместо 0 записать
В5. Результаты поиска решения будут
следующими: х = 200, у = 200, f(x,y) = 600. Таким
планом вряд ли будет доволен директор
кондитерского цеха, поскольку потери
прибыли окажутся очень существенными.
Следует иметь в виду, что при решении
подобных задач могут возникнуть проблемы,
о которых мы здесь не говорили.
Например, искомого оптимального решения
может вовсе не существовать — тогда
программа об этом сообщит
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #