Рассмотрим возможности возведения экспоненты в степень и в частности использования числа Е в Excel, также известного как число Эйлера.
Число Е — основание натурального логарифма, математическая константа равная приблизительно 2,71828.
Также данное число называют как число Эйлера или число Непера.
Экспонента — показательная функция f(x) = exp (x) = e x , где е — число Эйлера.
Также в Excel есть возможность использовать другую известную математическую константу — число Пи.
Функция EXP в Excel
Чтобы возвести экспоненту в степень в Excel можно воспользоваться стандартной функцией:
EXP(число)
Возвращает экспоненту заданного числа.
- Число(обязательный аргумент) — степень, в которую возводится число Е (приблизительное значение 2,71828182845904).
Для получения числа Е в Excel достаточно в качестве аргумента функции EXP взять значение 1:
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
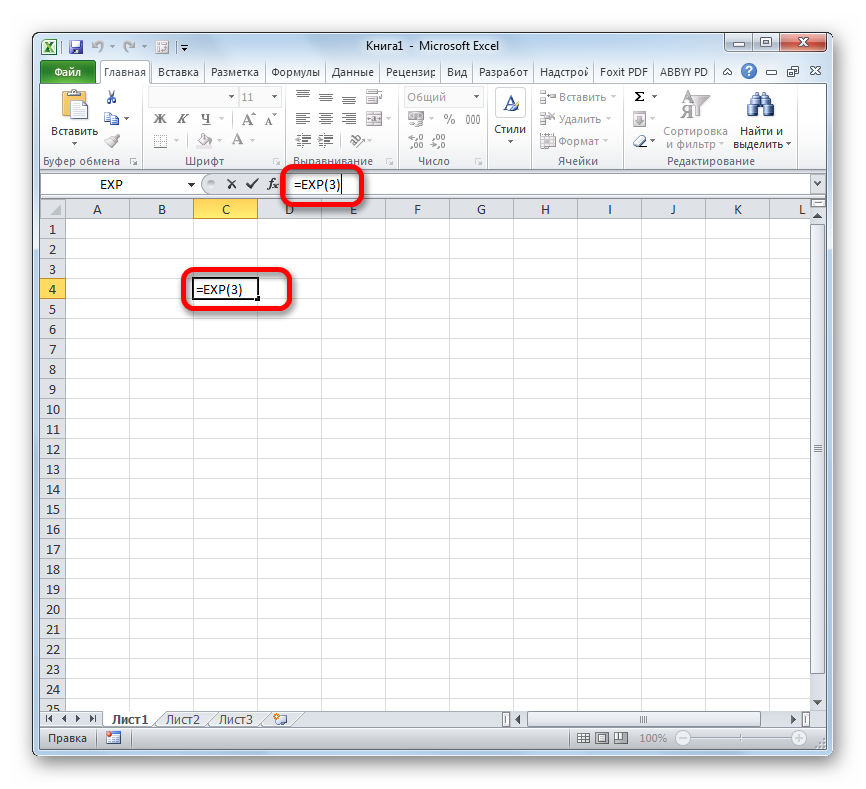
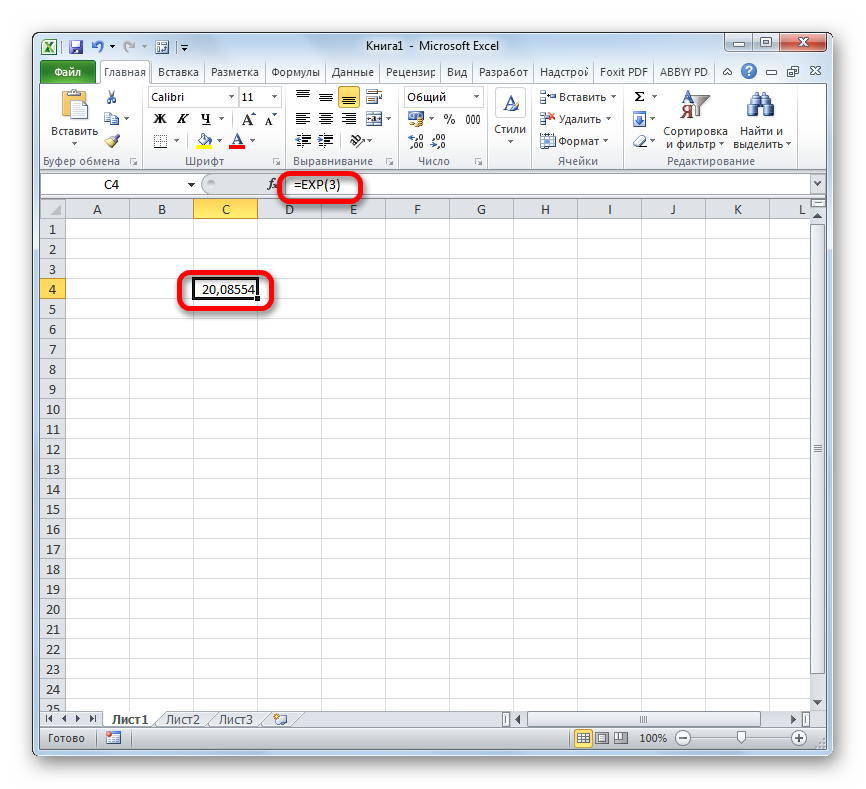
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
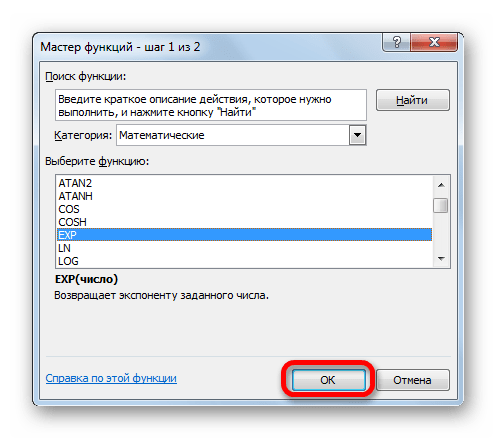
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
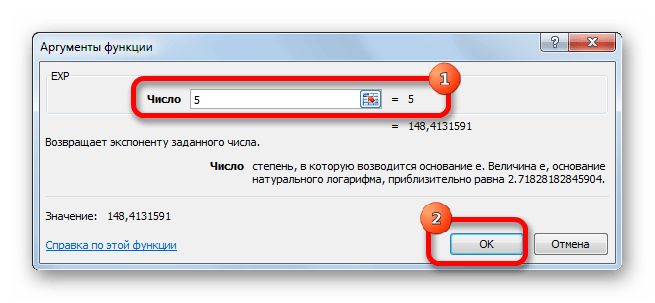
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».
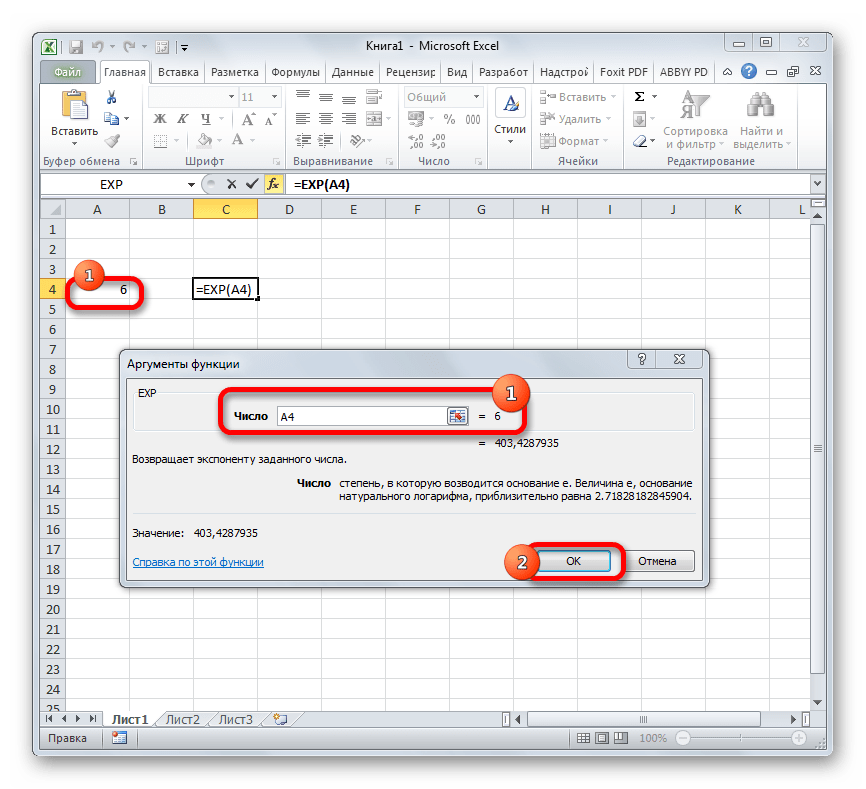
Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
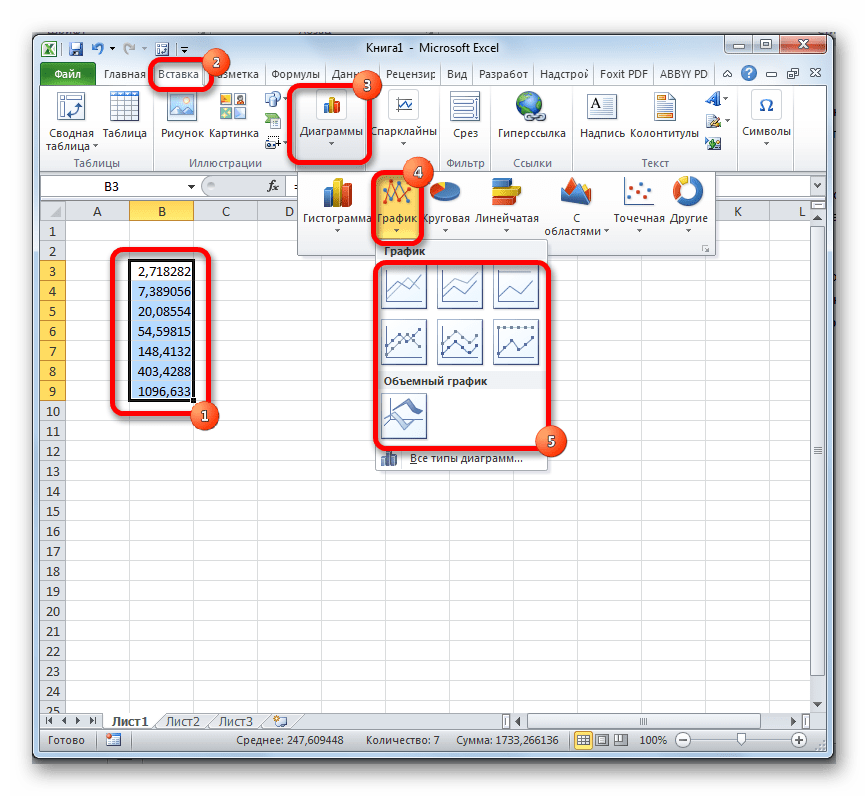
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.
Отблагодарите автора, поделитесь статьей в социальных сетях.
В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.
Описание
Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.
Синтаксис
Аргументы функции EXP описаны ниже.
Число — обязательный аргумент. Показатель степени, в которую возводится основание e.
Замечания
Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).
Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Определите что больше е пи или пи е в excel
Без калькулятора можете прикинуть что больше, число е в степени пи или число пи в степени е?)))) Полагаю, что вопрос не для всех) вопрос число степень калькулятор
Е в степени Пи больше, чем Пи в степени Е. Чтобы понять это, возьмем натуральный логарифм от обоих выражений. Е в степени Пи нам даст: Pi*ln(e) = Pi, а Пи в степени Е: e*ln(Pi). Т.е. задача сводится к тому, какой знак имеет функция f(x) = x — e*ln(x) в точке x = Pi. Производная этой функции имеет вид f'(x) = (x-e)/x. При x>e она положительна, значит, f(x) монотонно возрастает. Поскольку при х = е наша функция равна 0, то при x=Pi она будет больше нуля. Значит левая часть больше правой, т.е. e^Pi > Pi^e.
Это если без калькулятора.
Вот это я понимаю! Первый, полный ответ
Здравствуйте. Так как е и пи разные числа, да ещё и степень у них разная, надо возводить их в общую степень: пи умножить на е. Тогда чем больше число, тем больше оно в степени. Е меньше пи, поэтому оно и будет меньшим числом в степени. По моему так)
нет, не надо их возводить в общую степень
Сравним ln pi^e и ln e^pi, то есть сравним e * ln pi и pi.
f(x) = e * ln x — x
f'(x) = e/x — 1
f'(x) = 0 => e/x — 1 = 0 => x = e
При x (0;e) f'(x) > 0 => f(x) возрастает
При x (e;+00) f'(x) < 0 => f(x) убывает
Значит f(pi) < f(e) => e * ln pi — pi < e * ln e — e = e — e = 0
Значит e * ln pi — pi < 0 => e * ln pi < pi
ln pi^e < ln e^pi
pi^e < e^pi
Вот теперь правильно.
МОЖНО ПОДУМАТЬ БЫЛ И НЕПРАВИЛЬНЫЙ ОТВЕТ
АНТОН ПОДДУБНЫЙ GORLOVOE PENIE
сильняа исцляющая практика. посмотрите хотя бы пожалуйста. у него на канале обо всем. можете посмотреть про отношения, политику и т д. и сильные практики.
так с ходу и не сообразить. вопрос в том, что быстрее увеличивается. что бы сравнить степеные функции надо привести к одному основанию или к одиноковой степени. может быть через логариф, исследовать фнукцию.
Если не прибегать к помощи калькулятора, я исхожу из того, что «е»=2,71 меньше, чем «пи»=3,14. Подобно тому, что 2 в степни 9 больше, чем 9 в степени 2, я полагаю, что «е» в степени «пи» больше, чем «пи» в степени «е».
Если число е примерно 2,71,а пи 3,14. Ок давайте размышлять. Давайте считать 2 и 3. Допустим, 2 в степени 3 это 2×2×2= 8 А если 3 в степени 2, то это 3×3=9 вот и ответ. Конечно примитивно,но наглядно.
Практическая работа «Вычисление числа Пи» средствами электронных таблиц Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Практическая работа «Вычисление числа p »
средствами электронных таблиц E x cel


Формула для вычисления периметра многоугольника .
При увеличении количества сторон правильного многоугольника его периметр будет приближаться к длине окружности, в которую он вписан . Так как длина окружности и число p связаны формулой , при R=1 , откуда . Поэтому для вычисления числа p воспользуемся формулой .
Реализуем алгоритм подсчета числа p в электронной таблице E x cel следующим образом (таблица E xcel находится в режиме отображения формул):
Проанализируем полученный результат. Достоверно известно, что
p = 3,1415926535 8979323846 2643383279 5028841971 6939937510…..
Удваивая число сторон правильного многоугольника и используя формулу , мы приблизились к числу p = 3,1415926453212200 с 1 по 17 строки таблицы (с точностью до 7 знаков после запятой), с 17 по 20 строки результат оставался неизменным , а начиная с 21 строки начал отдаляться от истинного и перестал вычисляться совсем.
Excel храненит данные и осуществляет пересчет в формулах с точностью 15 разрядов. Так как Excel оперирует числами в двоичной системе счисления, и для хранения каждого двоичного числа использует 8 байт (64 бита). Поэтому любое десятичное число в Excel может содержать не более 15 значащих цифр. Если ввести десятичное число, содержащее более 15 значащих цифр, то «лишние» цифры просто отбрасываются или заменяются нулями, что мы и наблюдаем в нашей таблице.
воскресенье, 17 апреля 2011
Девушки, помогите, пожалуйста, срочно.
По информатике задали в Экселе сделать штуку — «что больше, пи в степени е или е в степени пи». Не через много формул с логарифмами, а какой-то экселевской функцией. Я обыскалась, везде пишут, что это просто, но я уже час сижу и не понимаю, куда, собственно, нажимать.
Очень прошу, помогите, пожалуйста. Заранее огромное спасибо!!!
@темы:
Помощь в учебе,
СРОЧНО!
Download PC Repair Tool to quickly find & fix Windows errors automatically
The PI function in Microsoft Excel is a Math and Trigonometry function, and it returns the value of PI. The formula for the PI formula is =PI (). The PI function syntax has no arguments.
Follow the steps below to use the PI function in Microsoft Excel:
- Launch Microsoft Excel
- Create a table or use an existing table from your files
- Place the formula into the cell you want to see the result
- Press the Enter Key
Launch Microsoft Excel.
Create a table or use an existing table from your files.
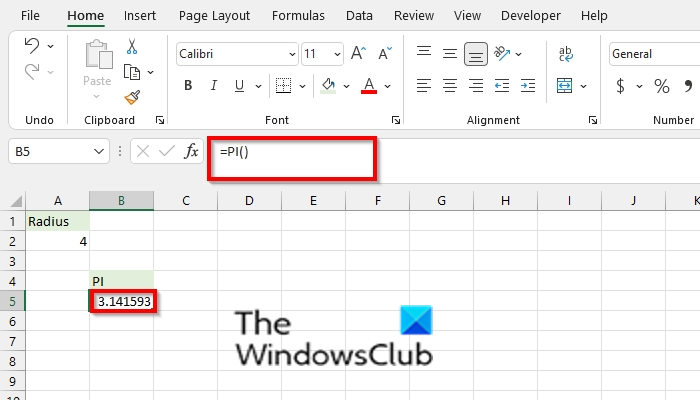
Place the formula =PI() into the cell you want to see the result.
Press the Enter key to see the result.
Excel will return the PI 3.141593.
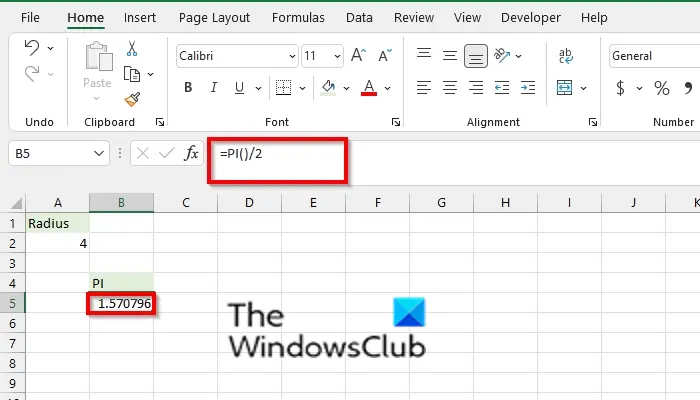
Type into the cell =PI()/2 and press enter. Excel will return the PI divided by 2, which gives the result of 1.570796.
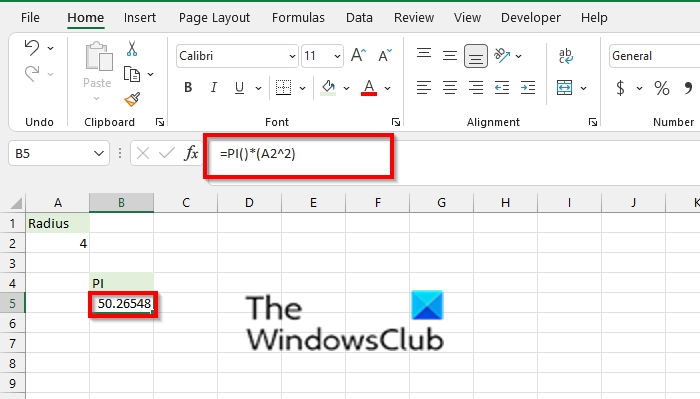
Type into the cell =PI()*(A2^2) and press enter. Excel will return the result 50.26548. The A2 cell contains the area of the circle with a radius.
There are two other methods to use the PI function.
Method one is to click the fx button on the top left of the Excel worksheet.
An Insert Function dialog box will appear.
Inside the dialog box in the section, Select a Category, select Math and Trigonometry from the list box.
In the section Select a Function, choose the PI function from the list.
Then click OK.
A Function Arguments dialog box will open.
Then click OK.
Method two is to click the Formulas tab, then click the Math and Trigonometry button in the Function Library group.
Then select PI from the drop-down menu.
A Function Arguments dialog box will open.
What does PI mean in math?
In Math, Pi is defined as the ratio of a circle’s circumference to its diameter. The value of PI is 3.14, and regardless of circle size, this ratio will always equal PI. PI is written as the Greek letter for p or π.
How to multiply by PI in Excel?
Excel is a program that can be used to calculate math. Normally, when users multiply PI in Excel, it is when they want to calculate the area of the circle from the diameter or radius; for example, calculating an area of the circle from the diameter, =PI()*3 or calculating an area of the circle from the radius =PI()/4*3^2.
We hope this tutorial helps you understand how to use the PI function in Microsoft Excel; if you have questions about the tutorial, let us know in the comments.
Shantel has studied Data Operations, Records Management, and Computer Information Systems. She is quite proficient in using Office software. Her goal is to become a Database Administrator or a System Administrator.
В этом учебном материале вы узнаете, как использовать Excel функцию ПИ с синтаксисом и примерами.
Описание
Microsoft Excel функция ПИ возвращает математическую константу, которая равна 3,14159265358979.
Функция ПИ — это встроенная в Excel функция, которая относится к категории математических / тригонометрических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
В качестве функции рабочего листа функцию ПИ можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции ПИ в Microsoft Excel:
ПИ()
Аргументы или параметры
Для функции ПИ нет параметров или аргументов.
Возвращаемое значение
Функция ПИ возвращает число π, равное 3,14159265358979.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции ПИ, чтобы понять, как использовать Excel функцию ПИ как функцию рабочего листа в Microsoft Excel:
Hа примере приведенной выше электронной таблицы Excel, будут возвращены следующие примеры функции ПИ:
|
=ПИ() Результат: 3.141592654 =ПИ() * A1 Результат: 47.1238898 =ПИ() / A2 Результат: 0.285599332 =ПИ() + A3 Результат: —5.858407346 |
Читайте также:
- как найти площадь круга.
- как найти длину окружности
Что больше e^п или п^e ? Как это доказать без калькулятора?
Е в степени Пи больше, чем Пи в степени Е. Чтобы понять это, возьмем натуральный логарифм от обоих выражений. Е в степени Пи нам даст: Pi*ln(e) = Pi, а Пи в степени Е: e*ln(Pi). Т.е. задача сводится к тому, какой знак имеет функция f(x) = x — e*ln(x) в точке x = Pi. Производная этой функции имеет вид f'(x) = (x-e)/x. При x>e она положительна, значит, f(x) монотонно возрастает. Поскольку при х = е наша функция равна 0, то при x=Pi она будет больше нуля. Значит левая часть больше правой, т.е. e^Pi > Pi^e.
Excel функция ПИ (PI)
Microsoft Excel функция ПИ возвращает математическую константу, которая равна 3,14159265358979.
Функция ПИ — это встроенная в Excel функция, которая относится к категории математических / тригонометрических функций.
Её можно использовать как функцию рабочего листа (WS) в Excel.
В качестве функции рабочего листа функцию ПИ можно ввести как часть формулы в ячейку рабочего листа.
Синтаксис
Синтаксис функции ПИ в Microsoft Excel:
Аргументы или параметры
Для функции ПИ нет параметров или аргументов.
Возвращаемое значение
Функция ПИ возвращает число π, равное 3,14159265358979.
Применение
- Excel для Office 365, Excel 2019, Excel 2016, Excel 2013, Excel 2011 для Mac, Excel 2010, Excel 2007, Excel 2003, Excel XP, Excel 2000
Тип функции
- Функция рабочего листа (WS)
Пример (как функция рабочего листа)
Рассмотрим несколько примеров функции ПИ, чтобы понять, как использовать Excel функцию ПИ как функцию рабочего листа в Microsoft Excel:
Hа примере приведенной выше электронной таблицы Excel, будут возвращены следующие примеры функции ПИ:



Группа: Участник
Сообщений: 489
Регистрация: 09.08.2004
Пользователь №: 3360
Вопрос задан в названии темы. Естественно, надо не просто ответить, но и доказать.
Для решения, по моим расчетам, достаточно полного школьного образования.
Если вы знаете решение задачи, или она вам кажется простой — лучше пришлите решение в ЛС, пусть другие тоже подумают.


Группа: Участник
Сообщений: 2846
Регистрация: 27.04.2004
Из: Москва
Пользователь №: 2211


Группа: Участник
Сообщений: 961
Регистрация: 01.01.2005
Из: Верхушка
Пользователь №: 6017


Группа: Участник
Сообщений: 489
Регистрация: 09.08.2004
Пользователь №: 3360
Duckbill — все верно. Интересно, какое доказательство вам давали в школе.
| QUOTE |
| А что это вообще такое? |


Группа: Участник
Сообщений: 961
Регистрация: 01.01.2005
Из: Верхушка
Пользователь №: 6017
| QUOTE (crystal @ Jan 2 2005, 04:39 PM) |
| Duckbill — все верно. Интересно, какое доказательство вам давали в школе. |
| QUOTE |
| А что это вообще такое? |


Группа: Участник
Сообщений: 2846
Регистрация: 27.04.2004
Из: Москва
Пользователь №: 2211
| QUOTE (crystal @ Jan 2 2005, 04:39 PM) |
| Duckbill — все верно. Интересно, какое доказательство вам давали в школе. |


Группа: Участник
Сообщений: 489
Регистрация: 09.08.2004
Пользователь №: 3360
Вообще, пока я сам до этого решения додумался, понял интересное свойство:
e^x >= x^e для любого x. То есть, в каком-то смысле e^x — самая «удельно быстрорастущая» показательная функция.
Этот факт, вообще говоря, практически полезен. Например, при решении NP-сложных задач методом последовательного деления пространства решения на части более выгодно использовать трисекцию, а не бисекцию, поскольку 3 ближе к е, чем два, и 3^x растет «удельно быстрее», чем 2^x.
Еще тогда одна простая задачка подобной тематики. Если первым решит Duckbill — жду от него ЛС, а не публичное сообщение
Рассматриваются отношения 2^n / 3^m для разных n и m. Вопрос — насколько близко это отношение может быть к единице, и если существует оптимум, то какой он?