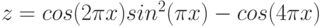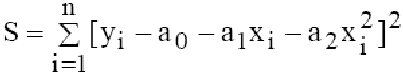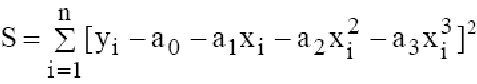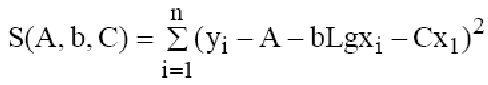Содержание
- Как по графику определить функцию в excel
- Часть 10. Подбор формул по графику. Линия тренда
- Найти функцию по ее графику (аппроксимация)
- Решение
- Как по графику в экселе определить значение точки
- Точки пересечения графиков в Excel
- Строим графики с точками пересечений
- Находим точку пересечения графиков в Excel
- Точки пересечения для трех показателей
- Особенности построения при неравномерном шаге по Х
- Построение графика функции на плоскости
- Построение плоских алгебраических кривых
- Построение диаграммы рассеяния
- Инструменты прогнозирования в Microsoft Excel
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
Как по графику определить функцию в excel
Часть 10. Подбор формул по графику. Линия тренда
Для рассмотренных выше задач удавалось построить уравнение или систему уравнений. Но во многих случаях при решении практических задач имеются лишь экспериментальные (результаты измерений, статистические, справочные, опытные) данные. По ним с определенной мерой близости пытаются восстановить эмпирическую формулу (уравнение), которая может быть использована для поиска решения, моделирования, оценки решений, прогнозов.
Процесс подбора эмпирической формулы P(x) для опытной зависимости F(x) называется аппроксимацией (сглаживанием). Для зависимостей с одним неизвестным в Excel используются графики, а для зависимостей со многими неизвестными – пары функций из группы Статистические ЛИНЕЙН и ТЕНДЕНЦИЯ, ЛГРФПРИБЛ и РОСТ .
В настоящем разделе рассматривается аппроксимация экспериментальных данных с помощью графиков Excel: на основе данных стоится график, к нему подбирается линия тренда, т.е. аппроксимирующая функция, которая с максимальной степенью близости приближается к опытной зависимости.
Степень близости подбираемой функции оценивается коэффициентом детерминации R 2 . Если нет других теоретических соображений, то выбирают функцию с коэффициентом R 2 , стремящимся к 1. Отметим, что подбор формул с использованием линии тренда позволяет установить как вид эмпирической формулы, так и определить численные значения неизвестных параметров.
Excel предоставляет 5 видов аппроксимирующих функций:
1. Линейная – y=cx+b. Это простейшая функция, отражающая рост и убывание данных с постоянной скоростью.
2. Полиномиальная – y=c0+c1x+c2x 2 +…+c6x 6 . Функция описывает попеременно возрастающие и убывающие данные. Полином 2-ой степени может иметь один экстремум (min или max), 3-ей степени – до 2-х экстремумов, 4-ой степени – до 3-х и т.д.
3. Логарифмическая – y=clnx+b. Эта функция описывает быстро возрастающие (убывающие) данные, которые затем стабилизируются.
4. Степенная – y=cx b , (х>0и y>0). Функция отражает данные с постоянно увеличивающейся (убывающей) скоростью роста.
5. Экспоненциальная – y=ce bx , (e – основание натурального логарифма). Функция описывает быстро растущие (убывающие) данные, которые затем стабилизируются.
Для всех 5-ти видов функций используется аппроксимация данных по методу наименьших квадратов (см. справку по F1 «линия тренда»).
В качестве примера рассмотрим зависимость продаж от рекламы, заданную следующими статистическими данными по некоторой фирме:
| Реклама (тыс. руб.) | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 |
| Продажи (тыс. руб.) |
Необходимо построить функцию, наилучшим образом отражающую эту зависимость. Кроме того, необходимо оценить продажи для рекламных вложений в 6 тыс. руб.
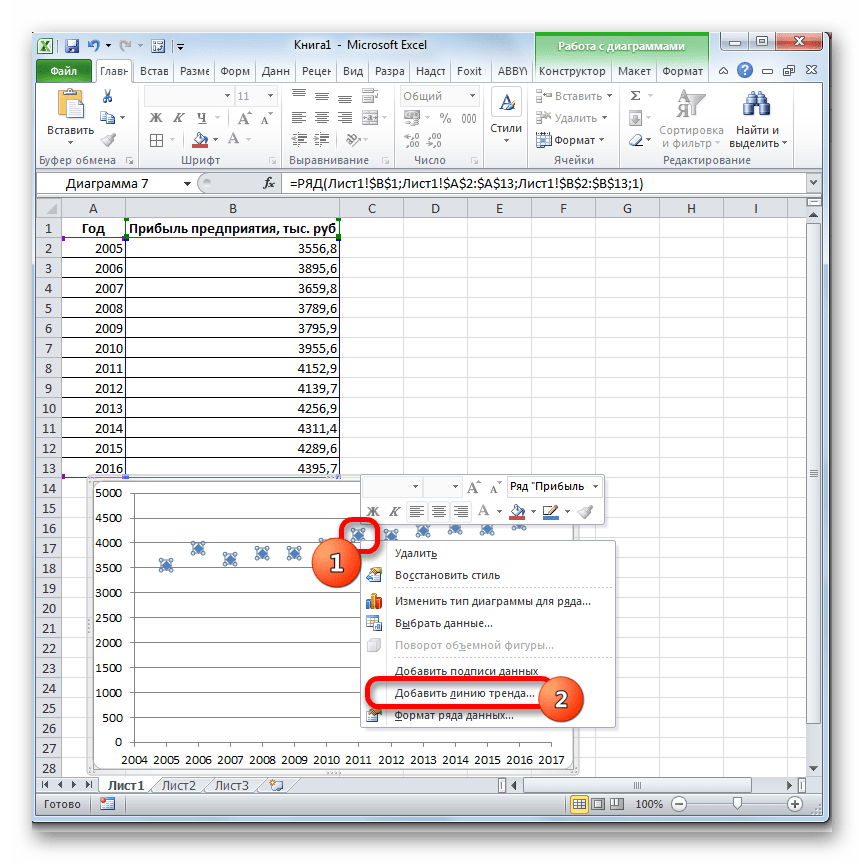
Приступим к решению. В первую очередь введите эти данные в Excel и постройте график, как на рис. 38. Как видно, график построен на основании диапазона B2:J2. Далее, щелкнув правой кнопкой мыши по графику, добавьте линию тренда, как показано на рис. 38.
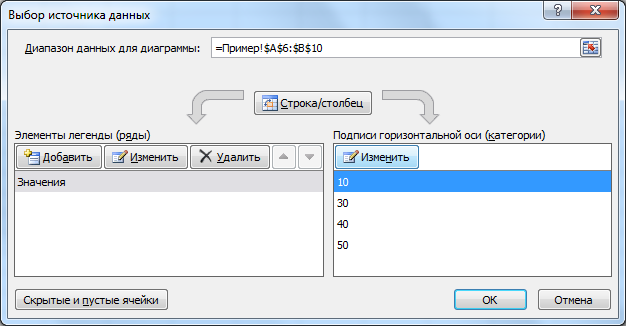
Чтобы подписать ось Х соответствующими значениями рекламы (как на рис. 38), следует в ниспадающем меню (рис. 38) выбрать пункт Исходные данные. В открывшемся одноименном окне, в закладке Ряд, в поле Подписи оси Х, укажите диапазон ячеек, где записаны значения Х (здесь $B$1:$K$1):
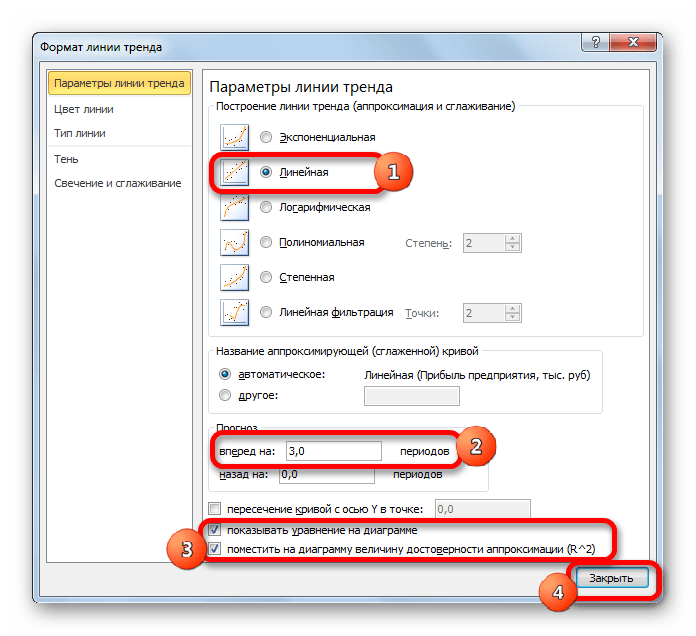
В открывшемся окне настройки (рис. 39), на закладке Тип выберите для аппроксимации логарифмическую линию тренда (по виду графика). На закладке Параметры установите флажки, отображающие на графике уравнение и коэффициент детерминации.
После нажатия ОК Вы получите результат, как на рис. 40. Коэффициент детерминации R 2 =0.9846, что является неплохой степенью близости. Для подтверждения правильности выбранной функции (поскольку других теоретических соображений нет) спрогнозируйте развитие продаж на 10 периодов вперед. Для этого щелкните правой кнопкой по линии тренда – измените формат – после этого в поле Прогноз: вперед на: установите 10 (рис. 41).
После установки прогноза Вы увидите изменение кривой графика на 10 периодов наблюдения вперед, как на рис. 42. Он с большой долей вероятности отражает дальнейшее увеличение продаж с увеличением рекламных вложений.
Вычисление по полученной формуле =237,96*LN(6)+5,9606 в Excel дает значение 432 тыс. руб.
В Excel имеется функция ПРЕДСКАЗ(), которая вычисляет будущее значение Y по существующим парам значений X и Y значениям с использованием линейной регрессии. Функция Y по возможности должна быть линейной, т.е. описываться уравнением типа c+bx. Функция предсказания для нашего примера запишется так: =ПРЕДСКАЗ(K1;B2:J2;B1:J1). Запишите – должно получится значение 643,6 тыс. руб.
Часть11. Контрольные задания
Найти функцию по ее графику (аппроксимация)
Дано:
Два параметра, зависящих друг от друга (X; Y). На их основании построен график.
Задача: найти функцию, отражающую (приблизительно) зависимость между параметрами.
Я эту задачу пытаюсь решить с помощью инструмента в экселе (построение тренда; полиноминальная линия тренда 6й степени).
Эксель подсказывает мне формулу функции, но по факту эта формула выдает не верные параметры (т.е. «Y» по данному формуле рассчитывается не правильно).
Помощь в написании контрольных, курсовых и дипломных работ здесь.
расчет.xlsx (15.9 Кб, 22 просмотров)
Аппроксимация к графику
Здравствуйте! Проблема такая, приходится работать с данными с осциллографа и с помощью программы.
Найти функцию по графику(парабола)
Нужно найти функцию по графику(только параболу), пробовал по формулам с википедии, но что то не.
Нужно найти функцию по графику
Вот собственно график и из него надо получить функцию для того чтобы написать программу на паскале.
найти функцию сигнала по графику
Доброго времени суток, как по графику сигнала найти его изображение (ну или сначала оригинал.
расчет (1).xlsx (16.1 Кб, 55 просмотров)
Сообщение было отмечено p1111 как решение
Решение
Как, оказывается, было просто.
Спасибо огромное, очень выручили.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Нужно найти функцию по графику
Здравствуйте, у меня есть данные для построения кусочка ВАХ-электрической дуги. Мне нужно найти.
Вывести функцию по графику
Процесс предполагается обратный от привычного, имея график, построить функцию. Как это сделать.
Написать функцию по графику
Помогите пожалуйста! По данному графику нужна функция (формула), чтобы я потом через if смог.
Составить функцию по графику.
Привет всем, помогите составить функцию, по графику, график приложен снизу функция в каком-то.
Источник
Как по графику в экселе определить значение точки
Точки пересечения графиков в Excel
Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.
Строим графики с точками пересечений
Имеются две функции, по которым нужно построить графики:
Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:
- Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
- Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.
Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.
Находим точку пересечения графиков в Excel
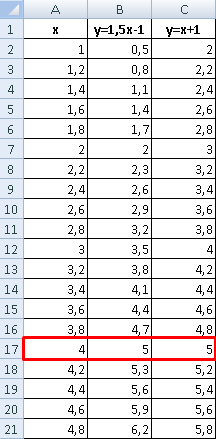
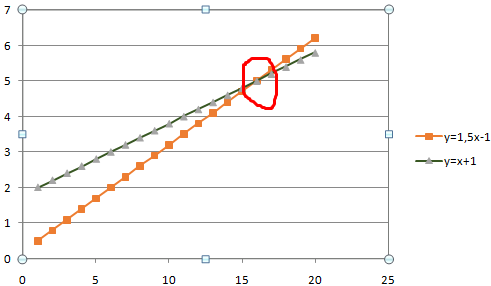
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.
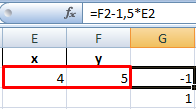
Первый способ. Найти общие значения в рядах данных для указанных функций.
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.
Изменим график, добавив новые данные. Получим две пересекающиеся линии.
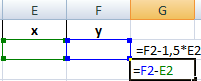
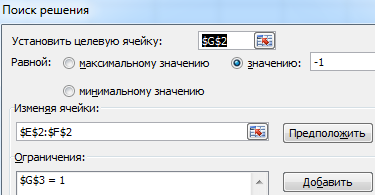
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.
Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.
Нажимаем «Выполнить» — инструмент предлагает решение уравнений.
Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.
Точки пересечения для трех показателей
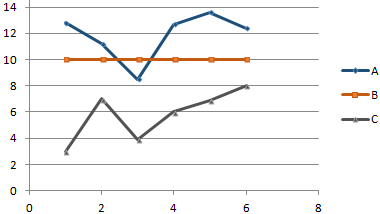
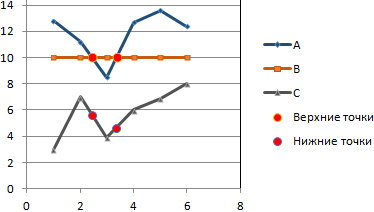
Существует три показателя, которые измерялись во времени.
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.
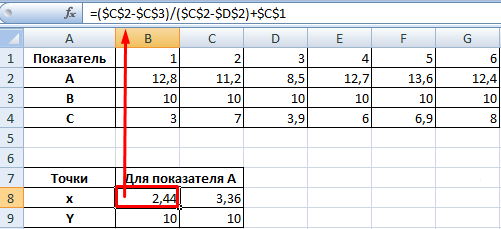
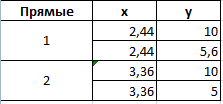
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:
На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.
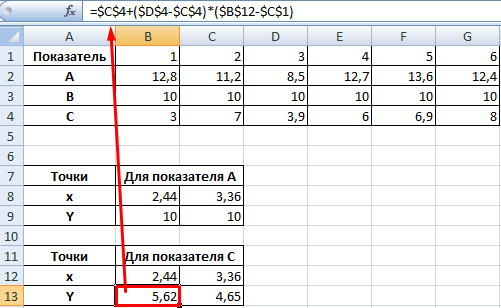
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:
На основе новых данных построим точечные диаграммы на том же поле (где наши графики).
Получается такой рисунок:
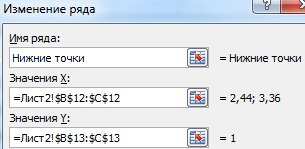
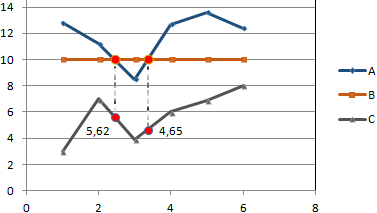
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:
Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.
Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.
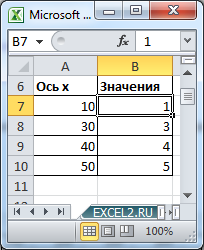
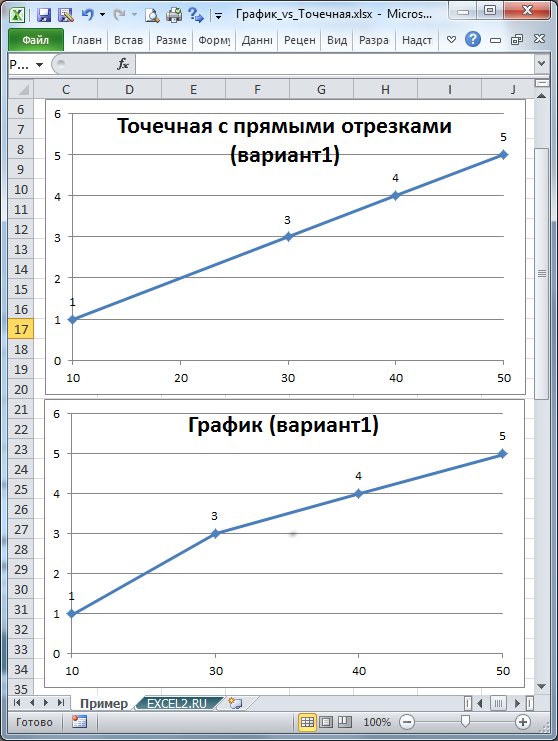
Особенности построения при неравномерном шаге по Х
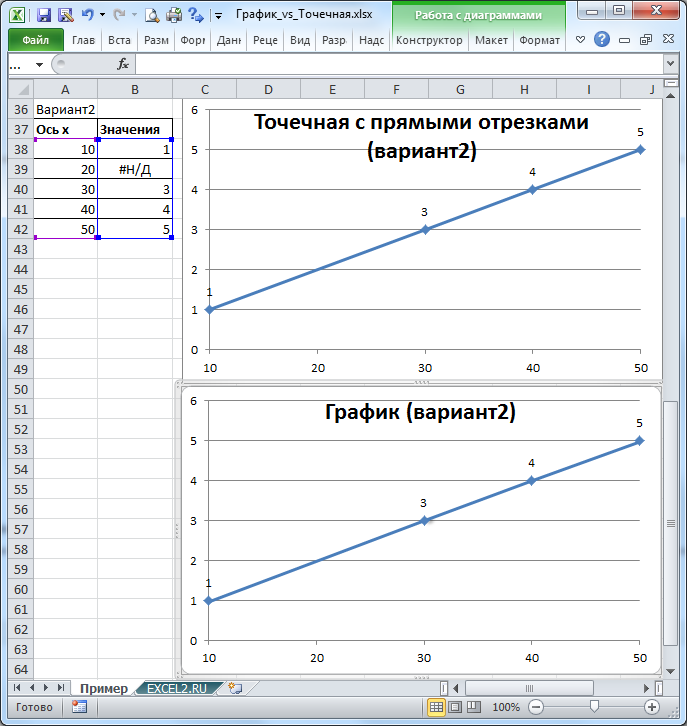
Пусть дана таблица с исходными данными (значения в исходной таблице расположены по оси Х равномерно с шагом 10, но точка с х=20 отсутствует).
Построим График и Точечную диаграмму с прямыми отрезками используя одну и туже таблицу.
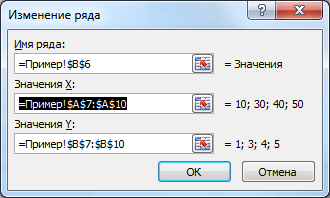
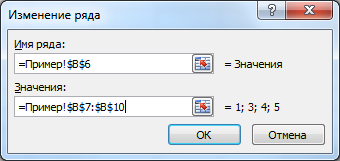
Точечная диаграмма использует все данные из исходной таблицы: как значения х, так и y.
Диаграмма График откладывает значения по оси х равномерно (значения из столбца Ось х не используются для построения).
Значения из столбца Ось х используются в Диаграмме График только для подписей данных по оси х (значения из столбца Ось х никак не влияют на расположение точек). Это часто используется для гибкой настройки подписей по оси х (можно в качестве подписей указать любые, в том числе и текстовые значения).
Вывод : если значения по оси х расположены неравномерно (в исходной таблице нет точки с х=20, поэтому кривая на Диаграмме График имеет излом), то использование Точечной диаграммы предпочтительней.
В случае, если данные расположены по оси х равномерно (с определенным шагом), то можно использовать оба типа диаграммы — линии на диаграмме будут выглядеть одинаково. Но если некоторые значения по оси Х пропущены, то для настройки диаграммы типа График нужно изменить таблицу с исходными данными. Можно использовать функцию НД() см. статью Функция НД() в MS EXCEL . Эта функция позволяет сделать кривую на диаграмме График аналогичной кривой на Точечной диаграмме (вариант2).
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Построение графика функции на плоскости
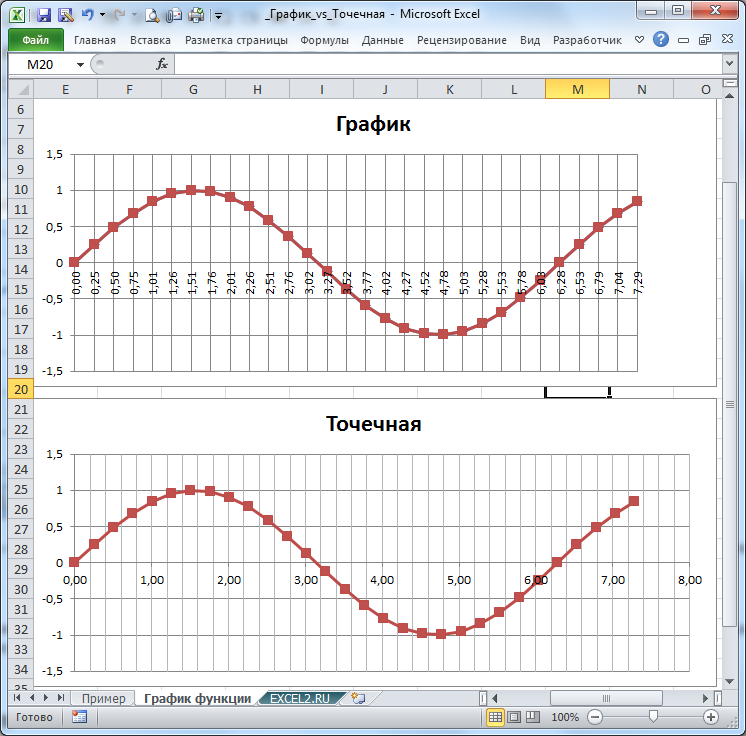
Элементарные функции (y=sin(x), y=x 2 ) удовлетворяют условию однозначности функции: одному значению Х соответствует единственное значение Y (горизонтальная линия, параллельная оси ординат, не может пересекать график функции более чем в одной точке). Поэтому, Диаграмма типа График, как и диаграмма типа Точечная, годятся для построения графика функции на плоскости.
Построим график функции y=sin(x) с использованием обоих типов диаграмм.
- подписи Оси Х: на диаграмме График на оси Х указаны фактические значения Х (могут также быть указаны любые подписи, даже текст), а на Точечной — цены основных и промежуточных делений вычислены автоматически. Т.е. подписи на этих типах диаграмм не обязательно совпадают (но можно добиться, чтобы совпадали).
- шаг вертикальной сетки: основные линии сетки на Графике проходят строго через точки значений, а на Точечной — шаг выбирается автоматически (точно предсказать не возможно, т.к. шаг зависит от размера самой диаграммы, диапазона изменения по Х и др.)
Эти графики построены в файле примера .
Построение плоских алгебраических кривых
Кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли можно построить только с помощью диаграммы типа Точечная, т.к. эти кривые НЕ удовлетворяют условию однозначности функции: одному значению Х могут соответствовать несколько значений Y. Эти графики построены в этой статье.
Построение диаграммы рассеяния
Диаграммы рассеяния используются для анализа временных рядов и в статистическом анализе. Про построение этой диаграммы (возможно использовать только Точечную) см. эту статью.
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
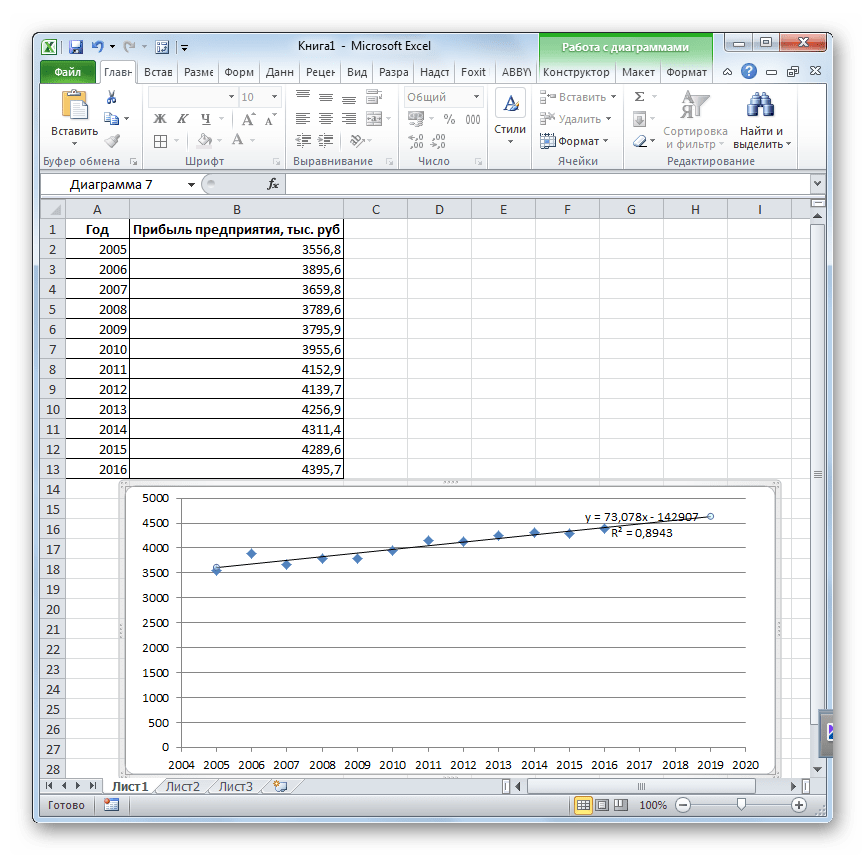
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
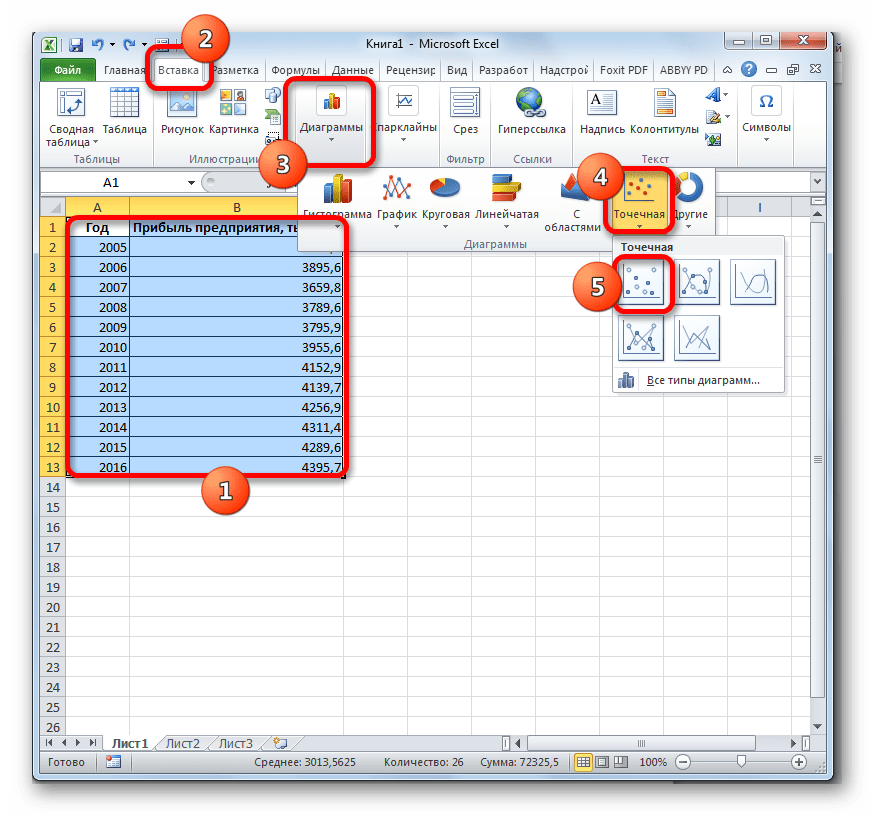
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
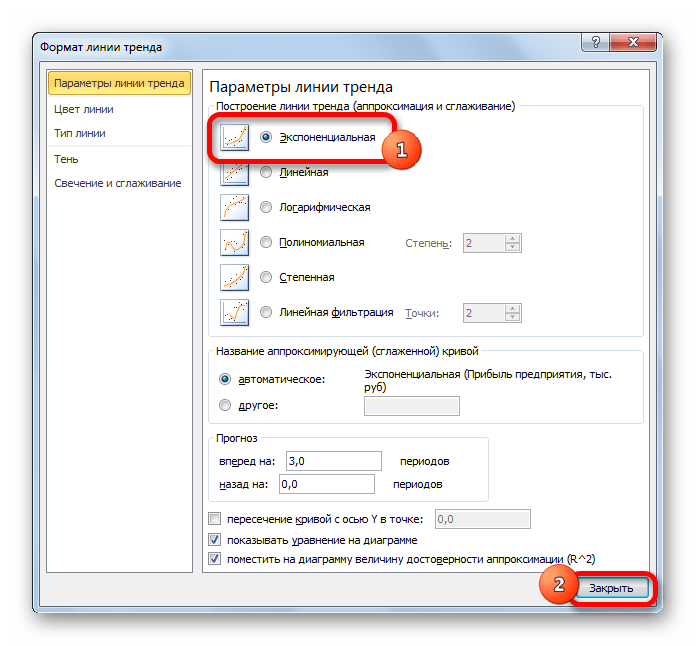
Давайте для начала выберем линейную аппроксимацию.
Способ 2: оператор ПРЕДСКАЗ
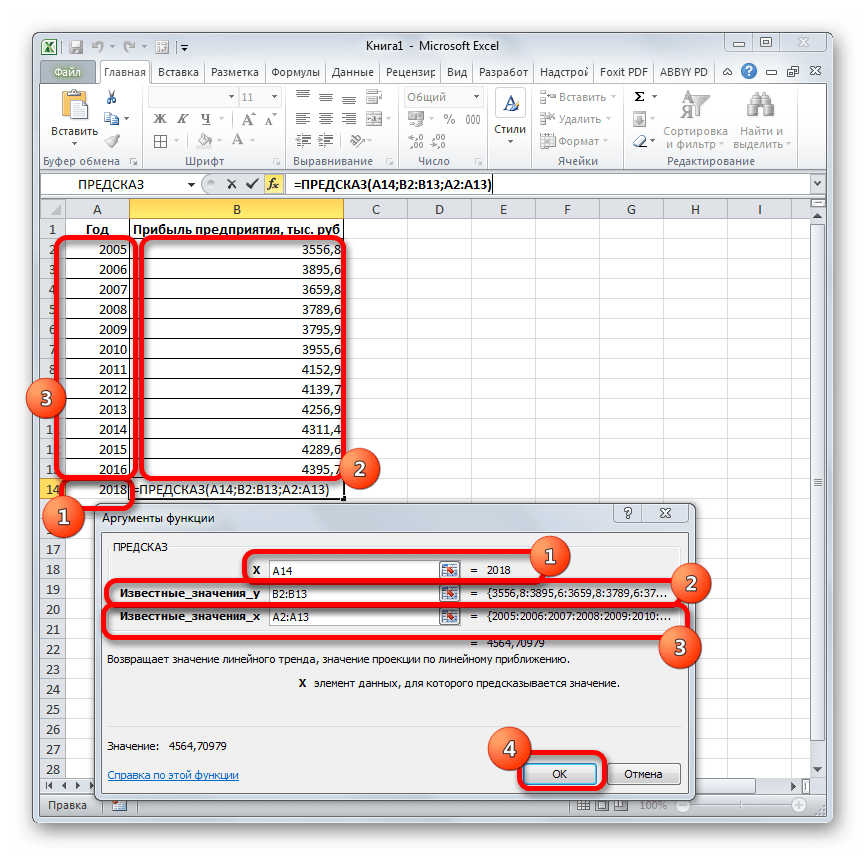
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
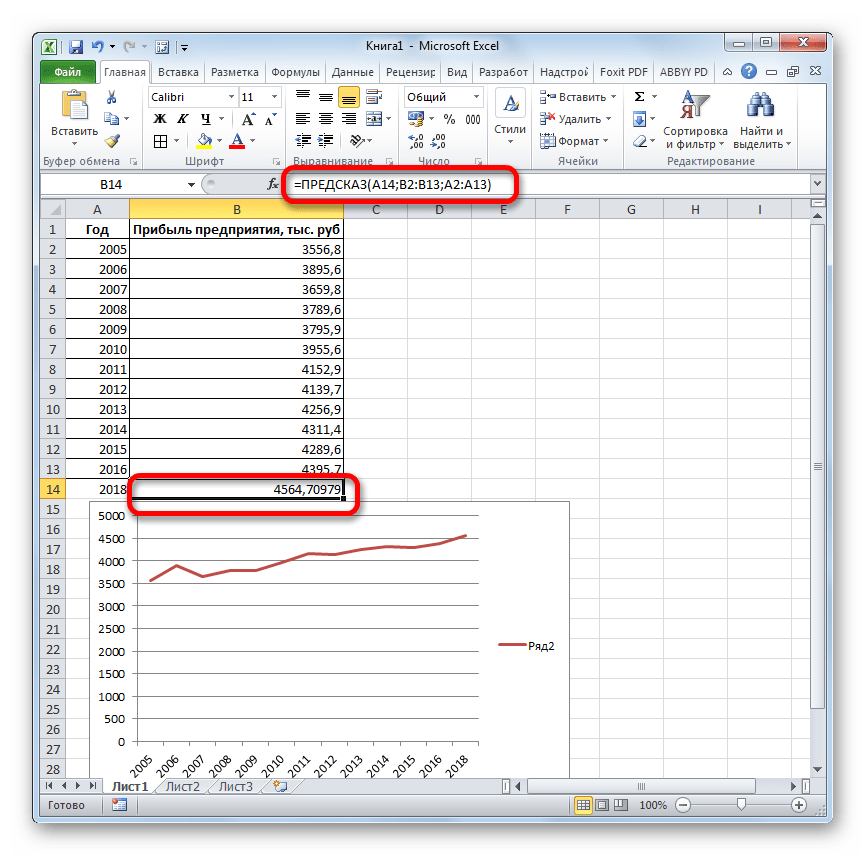
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
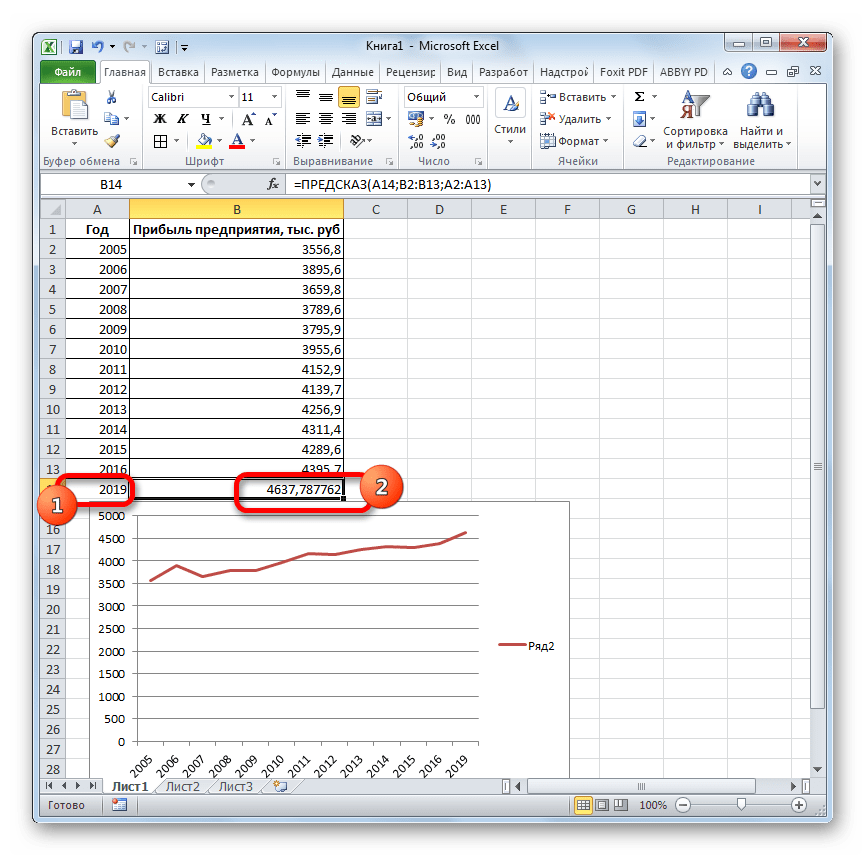
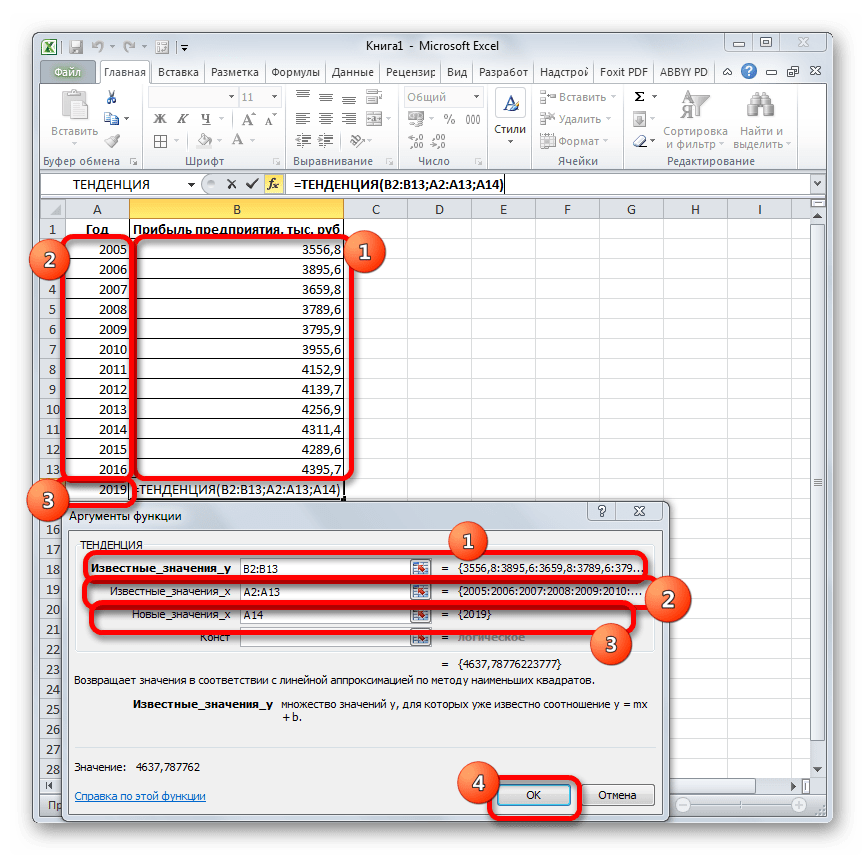
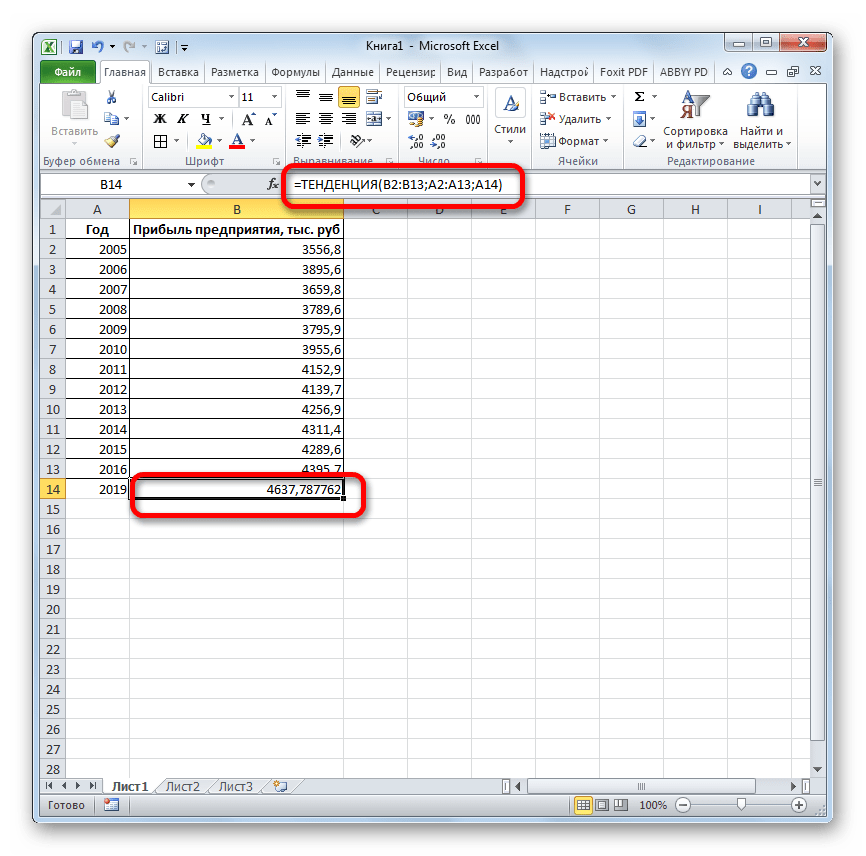
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
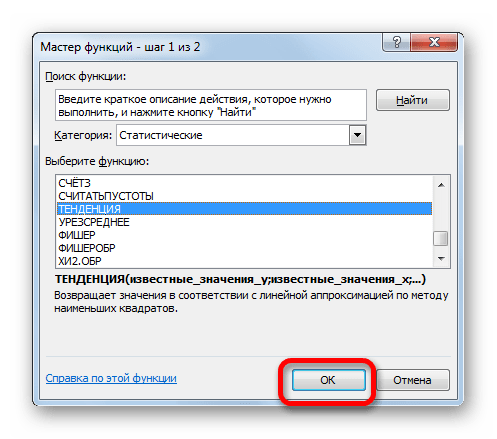
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
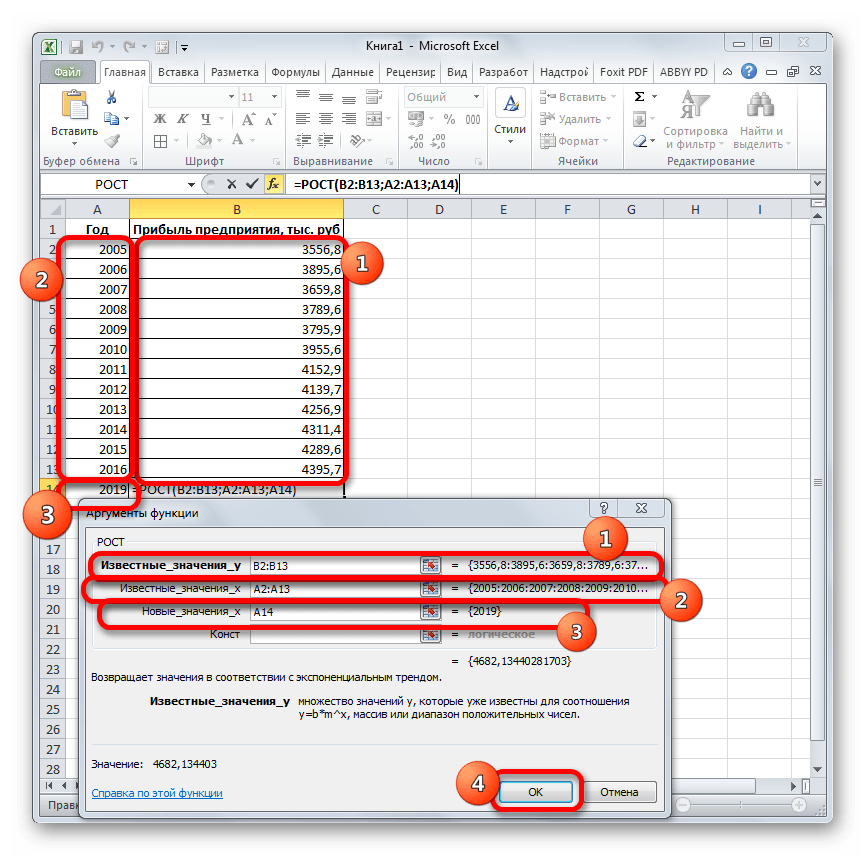
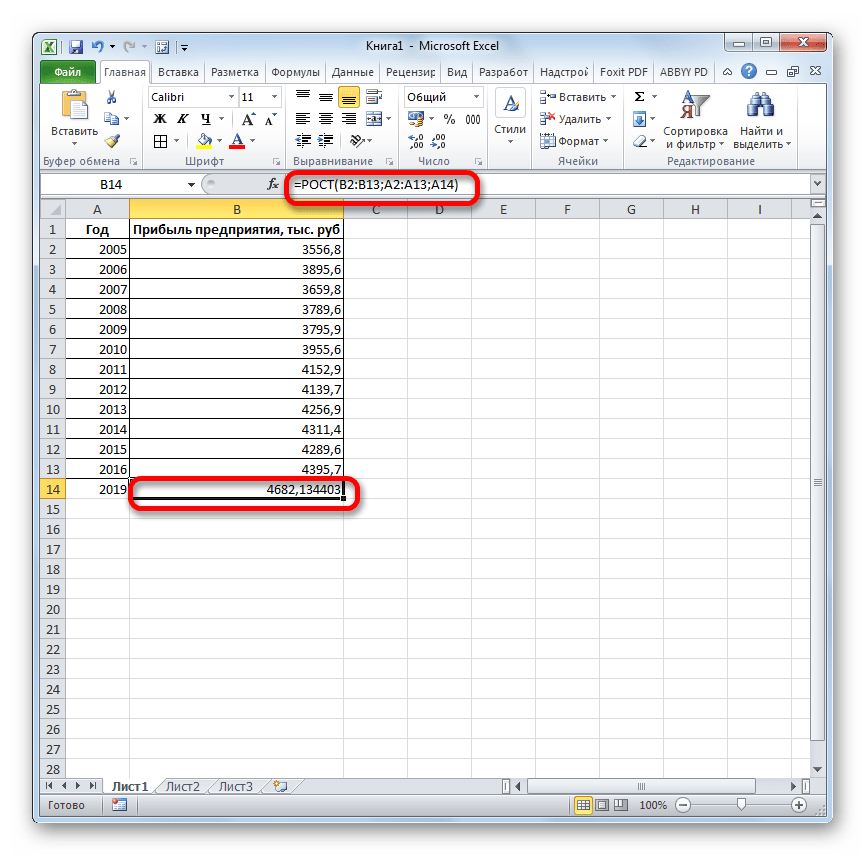
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
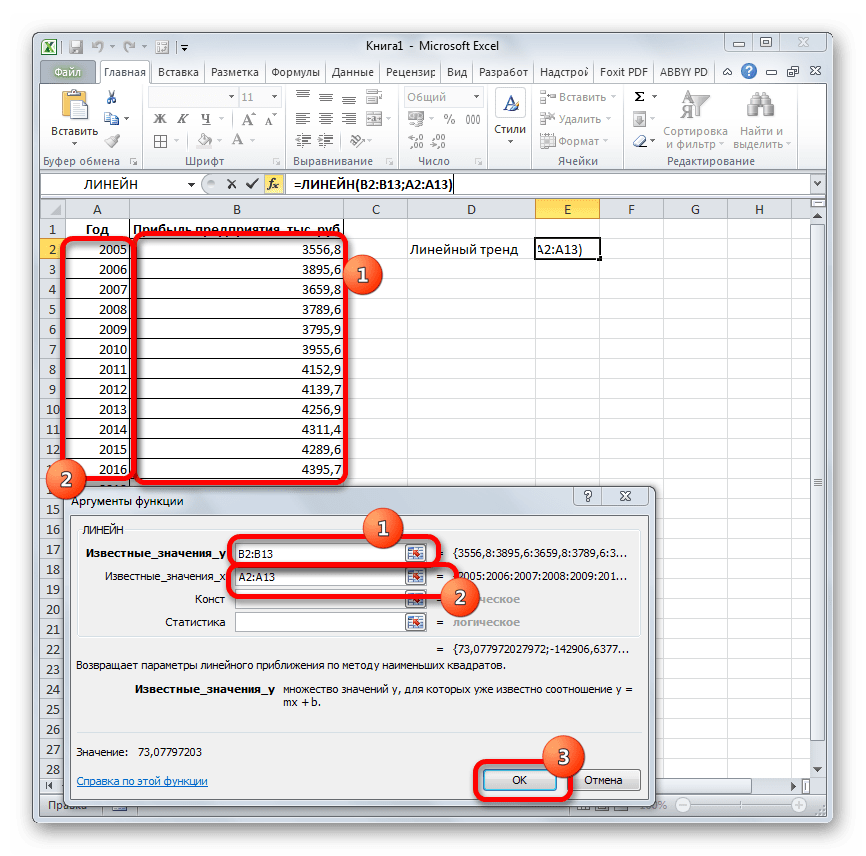
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
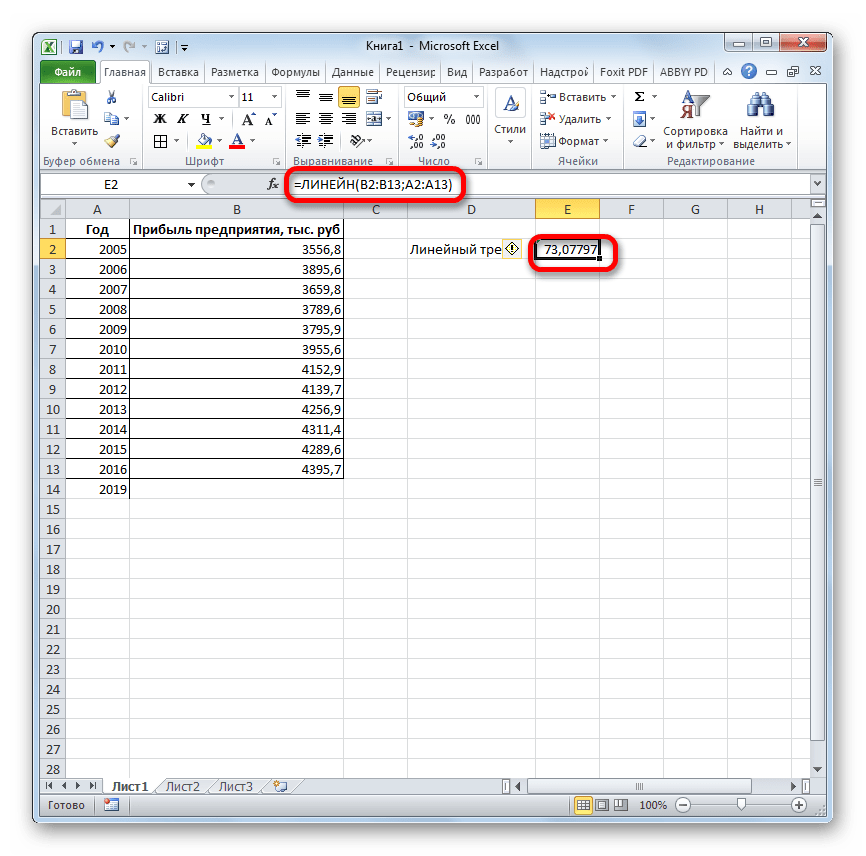
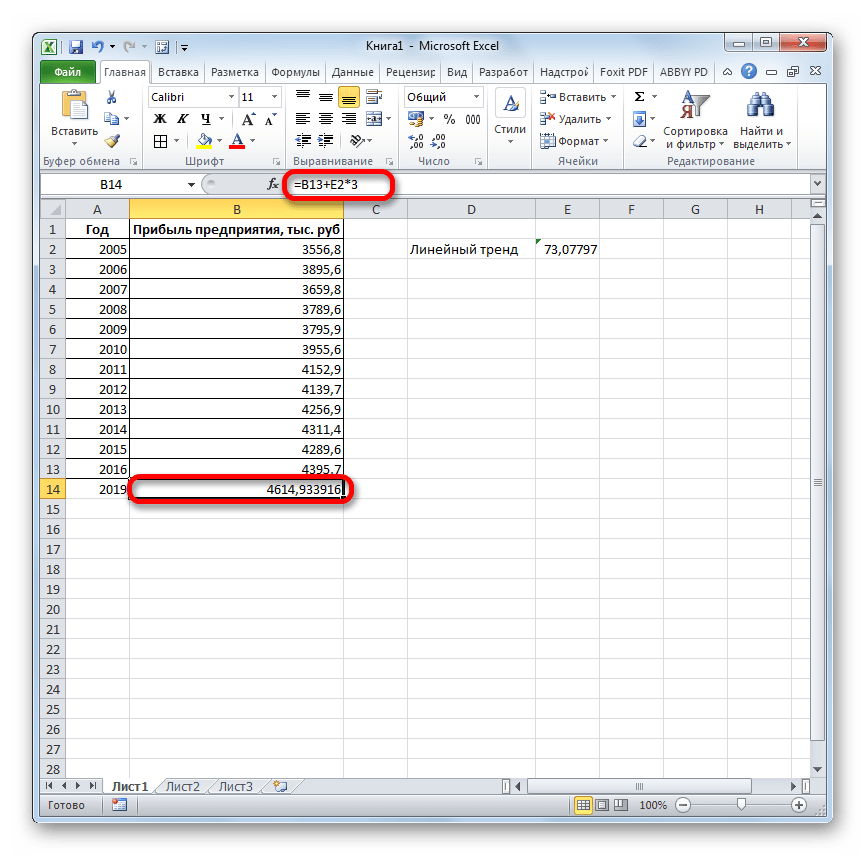
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
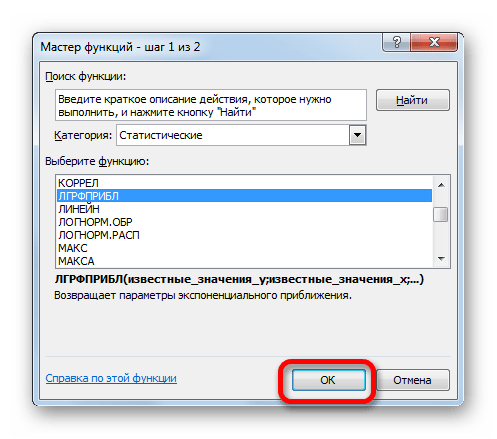
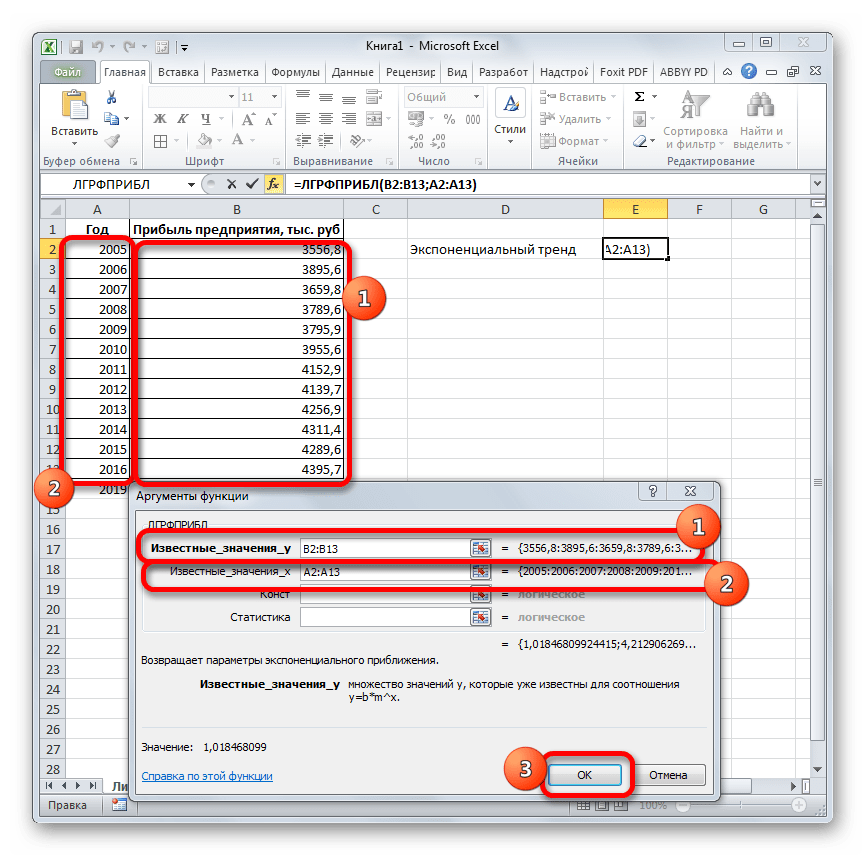
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
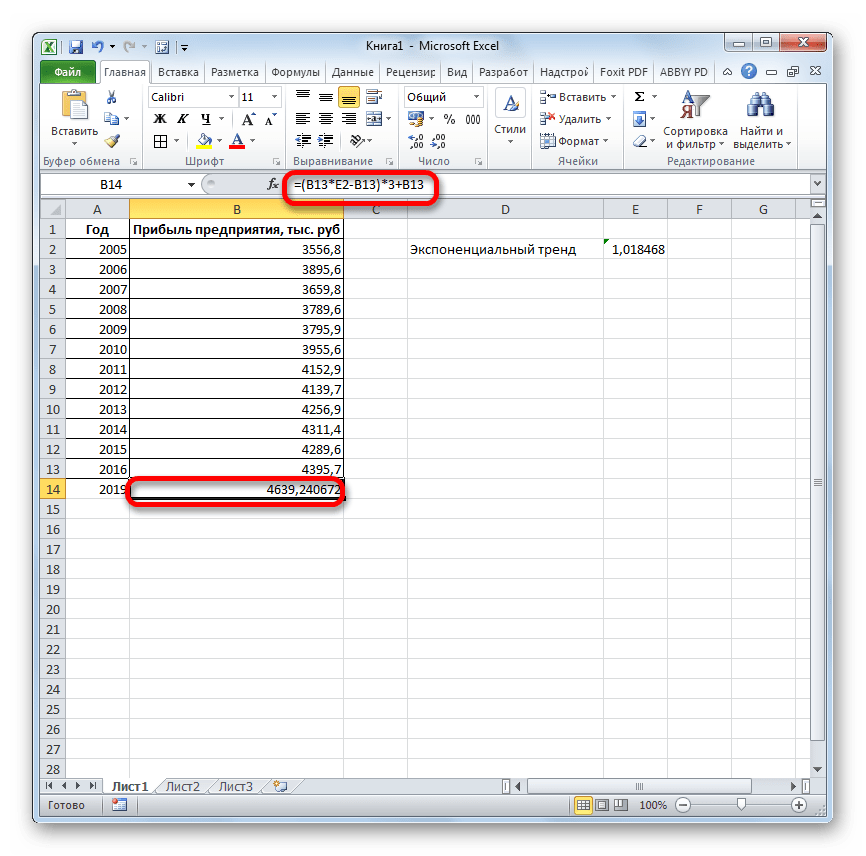
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
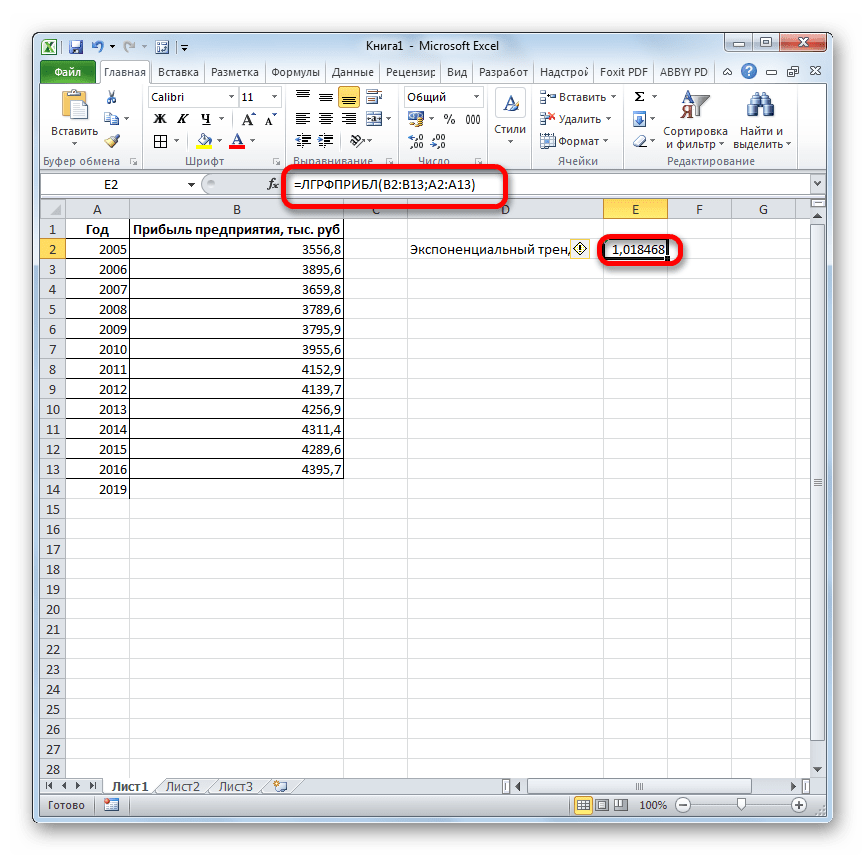
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Источник
Электронные таблицы EXCEL можно использовать при
изучении многих разделов физики, математики и
других предметов. Одной из данных тем является
математическая тема: “Анализ элементарных
функций”. Данная работа посвящена использованию
электронных таблиц EXCEL в анализе элементарных
функций.
Рис. 1 (см. Приложение 2)
На рис.1 представлена некоторая функция,
заданная с помощью таблицы, построение которой
приведено в Приложении 1.
Особенность анализа функций с помощью
электронных таблиц заключается в том, что анализ
проводится на дискретной информации.
Действительно, количество значений исследуемой
функции конечно и дано (как правило) с некоторым
постоянным шагом по аргументу.
При анализе исходной функции необходимо решить
следующие задачи:
- определение максимума (минимума) данной функции
на заданном интервале, - определение возрастания и/или убывания функции
на заданном интервале, - определение четности заданной функции,
- определение периодичности заданной функции,
- определение значения первой производной данной
функции и наличия экстремумов.
Для решения этих задач потребуется построить
таблицы ВводаИсходнойИнформации, таблицы
ВыводаРезультатов, Расчетной таблицы для
обработки информации и дополнительно построим
Вспомогательную таблицу. Таблицу
ВводаИсходнойИнформации и основу Расчетной
таблицу построены при введении значений
исследуемой функции в Приложении 1 и показанной
на рис.1. Построим решения задач анализа.
Приложение 1
Задача 1.
Для заданной функции на заданном интервале
аргумента определить ее минимальное и
максимальное значения.
Решение.
Для решения этой задачи построим таблицу
ВыводаРезультатов в виде
D E 1 комментарии Значения 2 Макс f(X) <формула> 3 Мин f(X) <формула>
В мастере функций Excel имеются функции МАКС(…) и
МИН(…), позволяющие решить нашу задачу. Для этого
необходимо в ячейки Е2 и Е3 ввести соответственно
формулы:
E2 => [=МАКС(с10:с50)]
и
E3 => [=МИН(с10:с50)]
Примечание. Если “протяжка” велась до
другой строки, то в интервале ссылок указать
соответствующий номер строки.
ЗАДАЧА РЕШЕНА.
Задача 2.
Определение возрастания и/или убывания функции
на заданном интервале.
Решение.
Для решения данной задачи в расчетной таблице
необходимо построить столбец D, в котором знак
будет указывать на возрастание или убывание
функции в данной точке. Для этого в ячейку D11
введем формулу
D11 => [=ЕСЛИ(a11<>””;ЗНАК(D11-D10);””)]
и “протянем” ее до строки №50.
И там, где знак положительный, функция
возрастает, а там, где знак отрицательный,
функция – убывает.
Далее построим вспомогательную таблицу, в
которой определим количество признаков
возрастания и убывания функции
F G 1 КОММЕНТАРИИ ЗНАЧЕНИЯ 2 Признак возрастания <формула> 3 Признак убывания <формула>
Для этого в ячейки g2 и g3 соответственно вводим
формулы:
G2 => [=СуммЕсли(d11:d50;”>0”)]
G3 => [=СуммЕсли(d11:d50;”<0”)]
Таблицу ВыводаРезультатов дополним строкой
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 Возрастание/Убывание <формула>
И для определения характера изменения заданной
функции остается ввести в ячейку Е4 формулу:
E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)
ЗАДАЧА РЕШЕНА.
Задача 3.
Определение четности данной.
Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком четности функции является
равенство f(X) = f(-X).
Для решения данной задачи в расчетной таблице
построим дополнительный столбец. В ячейку Е10
введем формулу
E10 => [=f(b10) – f(-b10)]
и “протянуть” ее до строки №50.
Таблицу ВыводаРезультатов дополним строкой
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 Возрастание/Убывание [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 четность <формула>
В ячейку Е4 таблицы ВыводаРезультатов вводим
формулу.
E4 => [ЕСЛИ(ABS(СУММ(E10:E50))<0,000001; “ЧЕТНАЯ”;
“НЕЧЕТНАЯ”)
ЗАДАЧА РЕШЕНА.
Задача 4.
Определить является ли введенный период
периодом заданной функции.
Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком периодичности функции
является равенство f(Х) = f(X+<период>).
Для данной задачи добавим в таблице
ВводаИсходнойИнформации строку №6, в которой
введем численное значение предполагаемого
периода.
А В 1 КОММЕНТАРИИ ЗНАЧЕНИЯ 2 Xn <значение> 3 Xk <значение> 4 Shag <значение> 5 N <формула> 6 период <значение>
В ячейку В6 вводится число – предполагаемый
период заданной функции.
Далее для решения данной задачи построим
дополнительный столбец в расчетной таблице, для
этого в ячейку F11 введем формулу
F10 => [=ЕСЛИ(a10<>””;f(b10)-f(b10+$b$6);””)]
и “потягиваем” эту формулу до строки №50.
В таблице ВыводаРезультатов добавим строчку.
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 период <формула>
В ячейке Е5 необходимо ввести формулу
Е5 => [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;”не
период”)]
Если данное значение предполагаемого периода
не подходит, то его можно изменить.
ЗАДАЧА РЕШЕНА.
Задача 5.
Для заданной функции определить:
- значения первой производной данной функции,
- наличия и количество экстремумов.
Решение.
Для решения первой части задачи, то есть
определения первой производной воспользуемся ее
разностным определение.
Построим столбец. Для этого в ячейку G11 вводим
формулу:
G11 => [= ЕСЛИ(a11<>””; ABS((c11-c10)/(b11-b10));””)]
и “протягиваем ее до строки с №50.
В результате получаем разностные приближенные
значения первой производной заданной функции в
заданных точках.
Для решения второй части задачи, то есть
определения наличия и количества экстремумов на
заданной функции в таблицу ВыводаРезультатов
дополнить строкой.
D E 1 комментарии значения 2 Макс f(X) =МАКС(с10:с50) 3 Мин f(X) =МИН(с10:с50) 4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)5 период [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;
”не период”)]6 Количество Экстремумов. <формула>
В ячейке Е6 необходимо ввести формулу
E6 => [=СчетЕсли(g11:g50;”<0,05”)]
ЗАДАЧА РЕШЕНА.
Рис 2, см. Приложение 3
На рис.2 приведена построенная таблица
решения задач.
Предложенные в данной работе задачи можно
использовать на интегрированных уроках
информатика-математика, на уроках информатики
при изучении электронных таблиц, в частности, в
теме: “Мастер функций”.
Аннотация:
Цель работы: научиться определять значения функций и строить графики, а также использовать логические функции в табличном процессоре Excel.
Содержание работы:
Построение графика функции с одной переменной.
Построение графика функции с двумя условиями.
Построение графика функции с тремя условиями.
Построение двух графиков в одной системе координат.
Построение поверхности.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Построение графика функции
Процесс построения графика функции состоит из двух этапов:
- создание таблицы значений функции
- непосредственного построения ее графика.
Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции.
Рассмотрим технологию построения графика на примере функции 
![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
Создание таблицы значений функции
В нашем случае возьмем в качестве шага изменения аргумента, например, 0.1. Нам надо найти у(0), у(0.1), у(0.2), …, у(1). С этой целью в ячейки диапазона A1:А11 последовательно введем 0, 0.1, …, 1, т. е. значения переменной х. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию.
Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.
Первый способ заключается в следующем:
- В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии, т.е. 0 и 0,1
- Выделите диапазон ячеек А1:А2.
- Расположите указатель мыши на маркере заполнения выделенного диапазона (рис. 4.1
рис.
4.1) и протяните его вниз (в данном случае на диапазон A3:А11) до тех пор, пока не получится числовой ряд нужной длины (рис. 4.2
рис.
4.2).
Второй способ позволяет пользоваться диалоговым окном Прогрессия. Для этого:
- В ячейку А1 введите первый член арифметической профессии.
- Выберите команду Главная > Редактирование > Заполнить > Прогрессия.
- В появившемся диалоговом окне Прогрессия (рис. 4.3
рис.
4.3) в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,1, а в поле Предельное значение – 1. - Нажмите кнопку ОК.
Рис.
4.1.
Вид указателя мыши на маркере заполнения
Рис.
4.2.
Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения
Рис.
4.3.
Диалоговое окно Прогрессия
Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.
Примечание. Диалоговое окно Прогрессия, отображаемое на экране выбором команды Главная > Редактировать > Заполнить > Прогрессия, также позволяет создавать геометрические прогрессии.
В ячейку В1 введите формулу: =СОS(ПИ( )*А1)^2.
Ввод формул в ячейку можно производить либо с клавиатуры, либо с помощью диалогового окна Мастер функций, которое отображается на экране либо выбором команды Формулы > Вставить Функцию, либо нажатием кнопки Вставка функции
Продемонстрируем работу с мастером функций на примере ввода упомянутой выше формулы.
- Выберите ячейку В1.
- Нажмите кнопку Вставка функции
панели инструментов Стандартная, либо выберите команду Формулы > Вставить Функцию. На экране отобразится диалоговое окно Мастер функций – шаг 1 из 2 (рис. 4.4
рис.
4.4). Оно состоит из двух частей: - Категория – со списком двенадцати категорий функций;
- Функция – со списком имен функций, входящих в выбранную категорию.
Категория Полный алфавитный перечень содержит все встроенные функции и их имена упорядочены в алфавитном порядке, категория 10 недавно использовавшихся содержит имена десяти последних примененных функций. Эта категория ускоряет вызов функций, постоянно используемых пользователем.
- Функция cos относится к категории Математические. Выберите эту функцию и нажмите кнопку ОК. На экране отобразится панель формул (рис. 4.5
рис.
4.5).
Рис.
4.4.
Диалоговое окно Мастер функций – шаг 1 из 2
Рис.
4.5.
Панель формул
В поле Число вводится аргумент функции – в рассматриваемом примере это ПИ ()*А1. С помощью клавиатуры в это поле введите только ПИ ( )*, а ссылку на ячейку А1 в формулу добавьте, щелкнув по ячейке А1 на рабочем листе. Конечно, ее можно было также ввести с клавиатуры, но предложенный способ дает дополнительную проверку правильности ввода. После нажатия кнопки ОК в ячейку В1 будет введена формула:
Примечание. При использовании мастера функции перед вводом формулы в ячейку не надо вводить знак =, он вставляется в формулу автоматически.
- С помощью клавиатуры добавьте в формуле =COS(ПИ ())*А1 операцию возведения в квадрат функции cos. После всех описанных действий в ячейке В1 должна появиться формула =COS(ПИ()*Al)^2
Таким образом, пока найдено значение функции cos2(x) для значения х из ячейки A1. Теперь нам осталось найти значения этой функции для диапазона ячеек А2:А11.
Для этого:
- Выберите ячейку В1.
- Расположите указатель мыши на маркере заполнения выделенной ячейки и протяните его вниз на диапазон В2:В11.
Процесс создания таблицы значений функции завершен (рис. 4.6
рис.
4.6).
На рис. 4.6
рис.
4.6 на правом рабочем листе приведены формулы, введенные в ячейки рабочего листа. Для того чтобы в ячейках рабочего листа отображались не значения, а формулы, надо выбрать команду Формулы > Зависимости формул и Показать формулы.
Рис.
4.6.
Результат табуляции функции до и после форматирования данных
На среднем рабочем листе (рис. 4.6
рис.
4.6) приведен результат табуляции функции. Выглядит он не очень презентабельно: после десятичной точки отображается различное количество десятичных знаков. Кроме того, происходит перемешивание числового и экспоненциального форматов.
А именно, в ячейке В6 вместо 0 отображается 3.75Е-33, что приблизительно и равно нулю. Поэтому форматы надо привести к какому-то общему виду, например, как показано на левом рабочем листе: значения аргумента выводятся в числовом формате с точностью до одного знака после десятичной точки, а значения функции – с точностью до трех знаков после десятичной точки. Отформатируем, например, значения аргумента.
Для этого надо выбрать диапазон A1:A11. Это можно сделать, например, следующим способом. Выберите ячейку А1, а затем при нажатой клавише <Shift> выделите ячейку А11. Диапазон А1:А11 выбран.
Переходим к форматированию данных. Выберите команду Главная > Число. В появившемся диалоговом окне Формат ячеек: Число в списке Числовые форматы выберите Числовой, а в поле Число десятичных знаков введите 1. Нажмите кнопку ОК. Данные в Al:A11 будут отформатированы, как показано на левом рабочем листе (рис. 4.6
рис.
4.6). Аналогичным образом разберитесь с диапазоном В1:В11.
Построение графика
Перейдем теперь к конструированию графика cos2(xх) функции по существующей таблице значений аргументов и соответствующих значений функции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм на выберите вариант График, а в списке Вид укажите стандартный график (рис. 4.7
рис.
4.7). Нажмите кнопку Далее. - Чтобы изменить (шаг 2 из 4): источник данных диаграммы (которое позднее переименовывается в окно Исходные данные) необходимо нажать на график, затем выбрать вкладку Конструктор, затем вкладку Данные, Выбрать данные. В поле Диапазон автоматически будет введена ссылка на необходимый диапазон в абсолютном формате. Проверьте его, удалите 1 ряд. В итоге у вас должно получится, что Диапазон, =Лист1!$В1$:$В$11.
Обратите внимание на полученный график функции, отображаемый на вкладке Диапазон данных. В нем по оси ординат откладываются значения функции, а вот по оси абсцисс порядковые номера точек, а не значения аргумента.
Для того чтобы по оси абсцисс откладывались значения аргумента, надо выделить диаграмму и воспользоваться командой Конструктор > Данные > Выбрать данные, далее Подписи горизонтальной оси (категории) > Изменить и указать диапазон ячеек в которых расположен аргумент х функции.
Рис.
4.7.
Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы
Рис.
4.8.
Вкладка Диапазон данных диалогового окна Исходные данные
Создав диаграмму, можно изменить любой из ее элементов. Например, можно изменить вид осей, добавить название диаграммы, переместить или скрыть легенду, а также добавить дополнительные элементы.
Чтобы изменить диаграмму, выполните одно или несколько из указанных ниже действий.
- Изменение вида осей диаграммы. Можно указать масштаб осей и изменить промежутки между значениями или категориями. Для удобства чтения диаграммы можно добавить на оси деления указать величину промежутков между ними.
- Добавление к диаграмме названий и меток данных. Для пояснения отображенных на диаграмме данных можно добавить название диаграммы, названия осей и метки данных.
- Добавление легенды и таблицы данных Можно отобразить или скрыть легенду, изменить ее расположение или элементы. Для некоторых диаграмм также можно отобразить таблицу данных, в которой содержатся ключи легенды и значения, представленные на диаграмме.
- Применение специальных параметров для диаграмм разных типов Для различных типов диаграмм можно применять различные специальные линии (например, коридор колебания и линии тренда), полосы (например, полосы повышения и понижения и планки погрешностей), маркеры данных и т.д.
Вместо того чтобы добавлять или изменять элементы диаграммы и форматировать их вручную, можно быстро применить к данным готовый макет или стиль диаграммы. В приложении Excel существует множество полезных готовых макетов и стилей, которые можно адаптировать, изменив вручную макет или формат отдельных элементов диаграммы, таких как область диаграммы, область построения, ряды данных и легенда.
При использовании готового макета диаграммы на ней в определенном порядке отображается заданный набор элементов (например, названия, легенда, таблица данных или метки данных). Можно подобрать подходящий макет из предоставленных для диаграмм конкретного типа.
При использовании готового стиля диаграммы ее форматирование основано на примененной теме документа, поэтому внешний вид диаграммы будет соответствовать цветам темы (набору цветов), шрифтам темы (набору шрифтов заголовков и основного текста) и эффектам темы (набору границ и заливок), принятым в организации или заданным пользователем.
Собственные стили или макеты диаграмм создавать нельзя, но можно создать шаблоны диаграмм, содержащие нужный макет и форматирование.
Помимо применения готового стиля диаграммы можно легко изменить форматирование ее отдельных элементов, например маркеров данных, области диаграммы, области построения, чисел и текста в названиях и подписях, что привлечет внимание и сделает диаграмму оригинальной. Можно также применять стили фигур и стили WordArt или форматировать фигуры и текст в элементах диаграммы вручную.
Чтобы изменить форматирование диаграммы, выполните одно или несколько из указанных ниже действий:
- Заливка элементов диаграммы. Для привлечения внимания к определенным элементам диаграммы можно залить их цветом, текстурой, рисунком или применить градиентную заливку.
- Изменение контуров элементов диаграммы. Для выделения элементов диаграммы можно изменить цвет, стиль или толщину линий.
- Добавление специальных эффектов к элементам диаграммы. Для придания диаграмме завершенности к ее элементам можно применить специальные эффекты, например тень, отражение, свечение, сглаживание краев, рельеф или объемное вращение.
- Форматирование текста и чисел Текст и числа в названиях, подписях и надписях на диаграмме можно форматировать так же, как текст и числа на листе. Чтобы выделить текст или число, можно даже применять стили WordArt.
Рис.
4.9.
Вкладка Конструктор: параметры диаграммы
Рис.
4.10.
Диалоговое окно Макет: параметры диаграммы
Рис.
4.11.
Результат построения графика функции
Математические функции рабочего листа
Наиболее часто употребляемые стандартные математические функции рабочего листа приведены в табл. 4.1
таблица
4.1.
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| ABS (число) | ABS (number) | Возвращает абсолютную величину аргумента |
| ACOS (число) | ACOS (number) | Возвращает арккосинус аргумента |
| ASIN (число) | ASIN (number) | Возвращает арксинус аргумента |
| ATAN (число) | ATAN (number) | Возвращает арктангенс аргумента |
| COS (число) | COS (number) | Возвращает косинус аргумента |
| EXP (число) | EXP (number) | Возвращает экспоненту аргумента, т.е результат возведения основания натурального логарифма в степень, равную значению аргумента |
| LN (число) | LN (number) | Возвращает натуральный логарифм аргумента |
| LOG (число) | LOG (number) | Возвращает логарифм аргумента по данному основанию, если основание опущено, то оно полагается равным 10 |
| LOG10 (число; основание) | LOG10 (number; base) | Возвращает десятичный логарифм аргумента |
| SIN (число) | SIN (number) | Возвращает синус аргумента |
| TAN (число) | TAN (number) | Возвращает тангенс аргумента |
| ЗНАК (число) | SGN (number) | Возвращает знак аргумента |
| ОСТАТ (число; делитель) | MOD (number1; number1) | Возвращает остаток от деления числа на делитель |
| ПИ ( ) | PI ( ) | Возвращает значение числа ? с точностью до 15 знаков (в данном случае 3.14159265358979). обратите внимание на то, что функция ПИ ( ) не имеет аргумента |
| СЛЧИС ( ) | RND ( ) | Возвращает случайное число между 0 и 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС ( )*(b-a)+a |
| ЦЕЛОЕ (число) | INT (number) | Округляет число до ближайшего меньшего целого |
График функции с двумя условиями
Рассмотрим пример построения графика функции при ![$хin[0;1]$$](https://intuit.ru/sites/default/files/tex_cache/5bbd057004769c8519124b98a54a24bf.png)
График строится по принципам, представленным в п. 4.1 «Построение графика функции»
«Построение графиков функций и использование логических формул»
, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.5;(1+ABS(0.2-А1))/(1+А1+А1^2);А1^ (1/3))
Примечание. Обратите внимание на то, что для возведения в степень в коде используется соответствующая операция, т.е. А1^(1/3), а не функция рабочего листа степень, т. е. степень (А1; 1/3). В обоих случаях получается один и тот же результат, но, применение операции возведения в степень здесь более разумно, т. к. делает код более очевидным.
В коде фигурирует функция логического ветвления Если (IF), которая имеет следующий синтаксис:
ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь)
Рассмотрим ее аргументы:
- лог выражение – это любое значение или выражение, принимающее значения истина или ложь. Например, А10=100 – это логическое выражение; если значение в ячейке А10 равно 100, то выражение принимает значение ИСТИНА. В противном случае – ЛОЖЬ. Данный аргумент может быть использован в любом операторе сравнения.
- значение_если_истина – это значение, которое возвращается, если лог выражение равно ИСТИНА. Например, если этот аргумент – строка «План реализации выполнен» и лог выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст План реализации выполнен. Если лог выражение равно, ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы отобразить слово ИСТИНА, необходимо использовать логическое значение ИСТИНА для этого аргумента. значение_если_истина может быть формулой.
- значение_если_ложь – это значение, которое возвращается, если лог выражение равно ЛОЖЬ. Например, если этот аргумент – строка «План реализации перевыполнен» и лог выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст План реализации перевыполнен. Если лог выражение равно ЛОЖЬ, а значение_если_ложь опущено (т. е. после значение_если_истина нет точки с запятой), то возвращается логическое значение ЛОЖЬ. Если лог выражение равно ЛОЖЬ, а значение_если_ложь пусто (т. е. после значение_если_истина стоит точка с запятой с последующей закрывающей скобкой), то возвращается значение 0. значение_если_ложь может быть формулой.
Логические функции
В MS Excel имеются функции логических условий, перечисленные в табл. 4.2.
таблица
4.2
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| И (лог знач1; лог знач2; …) | AND (arg1, arg2, …) | Логическое умножение. |
| Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=5) возвращает значение ИСТИНА. | ||
| Если ячейка В4содержит число из интервала от 1 до 100, то функция И (1<В4; В4<100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| ИЛИ (лог знач1; лог знач2; …) | OR (arg1, arg2, …) | Логическое сложение. |
| Возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=6) возвращает значение ИСТИНА. | ||
| Если ячейка В4 содержит число меньше 1 или больше 100, то ИЛИ (В4<1; В4>100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| НЕ (лог знач) | NOT (arg) | Логическое отрицание. Изменяет на противоположное значение логическое значение своего аргумента. Например, НЕ (2+5=5) возвращает значение ИСТИНА. |
| Если ячейка В4 содержит число меньше 1 или больше 100, то НЕ (ИЛИ(В4<1;В4>100)) возвращает ЛОЖЬ, а в противном случае – ЛОЖЬ. |
Примечание. Кроме функции ЕСЛИ в MS Excel имеются еще две функции, использующие логические условия. Это функции:
СЧЁТЕСЛИ (COUNTIF) – подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию;
СУММЕСЛИ (SUMIF) – суммирует значения тех ячеек диапазона, удовлетворяющих заданному критерию.
График функции с тремя условиями
Рассмотрим пример построения графика функции у при ![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
График строится так, как описано в разд. «Построение графика функции» ранее в этой работе, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8); (1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))
Тот же самый результат можно получить, введя в ячейку В1 более простую формулу:
=ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1); 2*ЕХР(-2*А1)))
Два графика в одной системе координат
Рассмотрим пример построения в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
- y = 2sin(x)
- z = 3 cos(2x) – sin(x)
Итак, начнем процесс построений.
- В ячейки А1, В1 и С1 введите соответственно х, у и z.
- Выделите диапазон А1:С1. Выберите команду Главная. На вкладке
Выравнивание появившегося диалогового окна Формат ячеек в группе Выравнивание в списке по горизонтали укажите значение по правому краю. Нажмите кнопку ОК. Заголовки столбцов окажутся выровненными по правому краю.
- В диапазон ячеек А2:А17 введите значения аргумента х от -3 до 0 с шагом 0.2.
- В ячейки В2 и С2 введите формулы: =2*SIN(A2), =3*COS(2*A2)-SIN(A2)
- Выделите диапазон В2:С2, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз так, чтобы заполнить диапазон В3:С17.
- Выделите диапазон В3:С17. Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выберите значение График. Нажмите кнопку Далее.
- На вкладке Данные > выбрать данные диалогового окна Исходные данные в поле ввода Подписи оси X укажите ссылку на диапазон А2:А17, значения из которого откладываются по оси абсцисс (рис. 4.12
рис.
4.12). В списке Ряд приводятся ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных). Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода Диапазон предыдущего шага алгоритма. В поле Значения автоматически выводится ссылка на диапазон, соответствующий выбранному ряду из списка Ряд. В поле ввода Имя отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда. Этот заголовок в дальнейшем используется мастером диаграмм для создания легенды.
Рис.
4.12.
Вкладка Ряд диалогового окна Исходные данные до задания имен рядов
- Выберите в списке Ряд элемент Ряд1. В поле ввода Имя укажите ссылку на ячейку В1, значение из которой будет использоваться в качестве идентификатора данного ряда. Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле Имя автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, =Лист1!$В$1. Теперь осталось только щелкнуть на элементе Ряд1 списка Ряд. Это приведет к тому, что элемент Ряд1 поменяется на у, т. е. на то значение, которое содержится в ячейке В1. Аналогично поступите с элементом Ряд2 списка Ряд. Сначала выберите его, затем в поле ввода Имя укажите ссылку на ячейку С1, а потом щелкните на элементе Ряд2. На рис. 4.13
рис.
4.13 показана вкладка Ряд диалогового окна Исходные данные после задания имен рядов. Теперь можно нажать кнопку Далее. - В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите График двух функций, в поле Ось X(категорий) введите х, в поле Ось Y(значений) введите у и z. На вкладке Легенда установите флажок Добавить легенду. Нажмите кнопку Далее.
- Нажмите кнопку Готово.
Результат проделанных шагов представлен на рисунке 4.14
рис.
4.14.
Рис.
4.13.
Вкладка Ряд диалогового окна Исходные данные после задания имен рядов
Для большей презентабельности построенной диаграммы в ней были произведены следующие изменения по сравнению с оригиналом:
- Изменена ориентация подписи оси ординат с вертикальной на горизонтальную. Для этого выберите подпись оси ординат. Нажмите правую кнопку мыши и в появившемся контекстном меню укажите команду Формат названия оси. На вкладке Выравнивание диалогового окна Формат названия оси в группе Ориентация установите горизонтальную ориентацию. Нажмите кнопку ОК.
- Для того чтобы пользователю было легче отличить, какая линия является графиком функции у, а какая – z, изменен вид графика функции z. С этой целью выделите график функции z. Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат рядов данных. На вкладке Вид диалогового окна Формат ряда данных, используя элементы управления групп Маркер и Линия, установите необходимый вид линии графика. Нажмите кнопку ОК.
- Изменен фон графика. С этой целью выделите диаграмму (но не область построения). Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат области диаграммы. На вкладке Вид диалогового окна Формат области диаграммы установите флажок скругленные углы, а используя элементы управления группы Заливка, установите цвет и вид заливки фона. Нажмите кнопку ОК.
Рис.
4.14.
Графики функций у(х) и z(x), построенные в одной системе координат
Построение поверхности
Продемонстрируем технологию построения поверхностей на примере следующей функции, зависящей от двух аргументов:
$z = x^{2}-y^{2}$ при ![$$хin [-2; 2], уin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/9ba0e461aae4f553cbb9279438619e6b.png)
Прежде чем воспользоваться мастером диаграмм, надо построить таблицу значений функции z по обоим ее аргументам, например, по аргументу х от -2 до 2 с шагом 0.2, а по у от -1 до 1 с шагом 0.2.
Для этого:
- Введите в ячейку А2 значение -2, а в ячейку А3 значение -1.8. Выберите диапазон ячеек А2:А3. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон А4:А22. Таким, образом, значения аргумента х протабулированы от -2 до 2 с шагом 0.2.
- Введите в ячейку В1 значение -1, а в ячейку С1 значение -0.8. Выберите диапазон ячеек В1:С1. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон D1:L1. Значения аргумента у протабулированы от -1 до 1 с шагом 0.2.
- В ячейку В2 введите формулу: =$А2^2 – В$1^2.
- Выберите ячейку В2, расположите указатель мыши на маркере ее заполнения и протяните его вниз на диапазон В2:L22.
На левом рабочем листе (рис. 4.15
рис.
4.15) показан результат табуляции функции, зависящей от двух аргументов, а на правом – часть формул, которые были введены в ячейке при копировании формулы, введенной в ячейку В2, перемещением маркера заполнения на диапазон В2:L22.
Рис.
4.15.
Таблица значений функции, зависящей от двух аргументов
Примечание. Использование в формуле абсолютной ссылки на строку и столбец существенно. Напомним, что знак $ в имени ячейки, стоящий перед номером строки, создает абсолютную ссылку на строку, а перед именем столбца – абсолютную ссылку на столбец. Поэтому при буксировке формулы из ячейки В2 на диапазоны B2:L22, в ячейках этого диапазона будут найдены значения функции z при соответствующих значениях аргументов х и у.
Перейдем к конструированию поверхности по результатам табуляции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в списке Тип выберите значение Поверхность, а в списке Вид укажите стандартную поверхность. Нажмите кнопку Далее.
- В следующем диалоговом окне мастера диаграмм на вкладке Диапазон данных выберите переключатель Ряды в столбцах, т. к. данные располагаются в столбцах. В поле ввода Диапазон приведите ссылку на диапазон данных A1:L22, т. е. диапазон, который содержит в себе как значения аргументов, так и значения функции. Нажмите кнопку Далее.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): в параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите поверхность, в поле Ось X (категорий) укажите х, в поле Ось Y (рядов данных) задайте у, в поле Ось Z (значений) введите z. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Готово.
- Поверхность построена, как показано на рисунке 4.16
рис.
4.16.
Рис.
4.16.
Построенная поверхность и диалоговое окно Формат трехмерной проекции
Примечание. MS Excel разрешает пользователю не только изменять размеры рабочей области диаграммы посредством маркеров изменения размеров, но и ориентацию поверхности в пространстве. Для этого достаточно выделить диаграмму, а затем выбрать команду Диаграмма > Объемный вид. На экране отобразится диалоговое окно Формат трехмерной проекции, элементы которого как раз и позволяют изменять ориентацию поверхности в пространстве.
ЗАДАНИЯ
Вариант 1.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 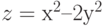
![$x,yin[-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/1dccee169ef8cd4747131b25d37db985.png)
Вариант 2.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 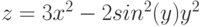
![$x, yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/53a8791dec1fce35a5f3ac0dd9605a3b.png)
Вариант 3.
1. Построить в разных системах координат при ![$xin[-2; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/075d390c8429b09a75c1effe8b21041a.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 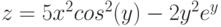
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 4.
1. Построить в разных системах координат при ![$хin [-1.5; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/f8ea986285591f482f6425385ca5802c.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность при мммх,yin [-1; 1]/ммм
Вариант 5.
1. Построить в разных системах координат при ![$хin [-1.8; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/78bc9ae987003e9c6801db7908c6bfbd.png)
2. Построить в одной системе координат при ![$хin [0; 3]$](https://intuit.ru/sites/default/files/tex_cache/153306b868b619790149dea95767b4f9.png)
3. Построить поверхность 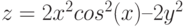
![$х,yin [-l; 1]$](https://intuit.ru/sites/default/files/tex_cache/f4f9de170788cb6bf2d9bec5dd801e0d.png)
Вариант 6.
1. Построить в разных системах координат при ![$хin [-2; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/0dbcf9e9bff0f78d00043ecdd4c74666.png)
2. Построить в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
3. Построить поверхность 
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 7.
1. Построить в разных системах координат при ![$хin [-1.7; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/68c9476760c3d9265176b82bcc296063.png)
2. Построить в одной системе координат при ![$хin [-3;0]$](https://intuit.ru/sites/default/files/tex_cache/625e1ce96d5bf506d83f626e5934b564.png)
3. Построить поверхность 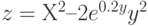
![$х,yin [-1;1]$](https://intuit.ru/sites/default/files/tex_cache/afd39bc8d16e67ea25b0fc35595fbb39.png)
Вариант 8.
1. Построить в разных системах координат при ![$хin [-1.5; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/2629a936172ba4ce71bd2c2e792ee4c2.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность при
Вариант 9.
1. Построить в разных системах координат при ![$хin [-1.4; 1.9]$](https://intuit.ru/sites/default/files/tex_cache/6c9405fb2d3d680c40a2b90ec8452bf2.png)
2. Построить в одной системе координат при ![$хin [0;2]$](https://intuit.ru/sites/default/files/tex_cache/adbba029f8747f8b59bce37c40dcc3a5.png)
3. Построить поверхность при
Вариант 10.
1. Построить в разных системах координат при ![$хin [-1.4; 1.4]$](https://intuit.ru/sites/default/files/tex_cache/077a3284889a9378e887806bcf4ea6f6.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность z = 3x2sin2(x) – 5e2yу при ![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Из каких этапов состоит процесс построения графика функции?
- Какими способами можно ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию?
- Как подписать ось X значениями аргумента?
Рассмотрим построение линии
регрессии с помощью MS Excel на примере
следующей задачи. Известна табличная
зависимость G(L). Построить линию регрессии
и вычислить ожидаемое значение в точках
0, 0.75, 1.75, 2.8,4.5.
Введем таблицу значений в лист MS Excel и
построим точечный график. Рабочий лист
примет вид (см. рис. 2).
Рисунок 2
Чтобы в ячейках K2,
L2
получить коэффициенты линейной
зависимости a и b
необходимо выделить эти две ячейки
мышью, выбрать функцию ЛИНЕЙН
в списке статистических
функций
Ввести в поле Известные_значения_y
значения из ячеек B2:J2,
а в поле Известные_значения_x
значения из ячеек B1:J1.
Нажать Ok.
Не забыть, что функция ЛИНЕЙН
работает со значениями x
и y в виде массивов.
Т. е. необходимо нажать F2,
а затем Ctrl+Shift+Enter.
В результате получим следующие
коэффициенты (см. рис 3)
Рисунок 3
В ячейке M2
будет рассчитываться
значение коэффициента корреляции, для
чего туда следует ввести формулу
=КОРРЕЛ(B1:J1;B2:J2).
В результате рабочий лист примет вид
(см. рис. 4).
Рисунок 4
Теперь с помощью функции
ТЕНДЕНЦИЯ вычислим
ожидаемое значение в точках 0,
0.75, 1.75, 2.8, 4.5. Для этого
в ячейки L9:L13
занесем эти значения, а в ячейки M9:M13
введем формулу =ТЕНДЕНЦИЯ(B2:J2;B1:J1;L9:L13)
для расчета ожидаемых
значений. Для этого выделим ячейки
M9:M13 выберем
в списке статистических функций функцию
ТЕНДЕНЦИЯ и
заполним ее как указано ниже
Нажимаем OK. Так
как функция ТЕНДЕНЦИЯ работает с данными
как с массивами то необходимо дополнительно
нажать F2,
а затем Ctrl+Shift+Enter.
В результате получим следующие
значения.
|
x |
y |
|
0 |
1,638667 |
|
0,75 |
2,351667 |
|
1,75 |
3,302333 |
|
2,8 |
4,300533 |
|
4,5 |
5,916667 |
Изобразим линию регрессии
на диаграмме. Для этого выделим
экспериментальные точки на графике,
щелкнем правой кнопкой мыши и выберем
команду Исходные данные.
В появившемся диалоговом окне (см. рис.
5), для добавления линии регрессии щелкнем
по кнопке Добавить.
Рисунок 5
В качестве имени введем Линия
регрессии, в качестве
Значения Х L9:L13,
в качестве Значения Y
M9:M13.
Далее выделяем линию регрессии, для
изменения ее типа щелкаем правой кнопкой
мыши и выбираем команду Тип
диаграммы (рис. 6).
Для форматирования линии регрессии
дважды щелкаем по ней (рис. 7), можно
изменить толщину линии, цвет, тип маркера
и т.д.
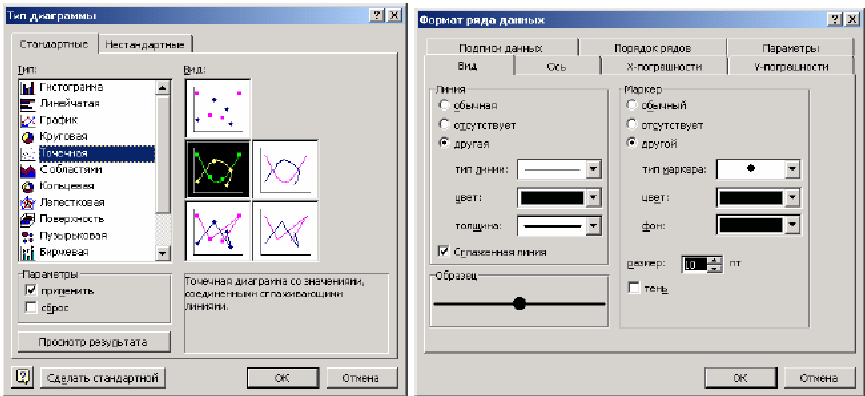
Рисунок 7
После форматирования графика рабочий
лист примет вид, изображенный на рис.
8.
Рисунок 8
Квадратичная функция
Необходимо определить
параметры функции y=a0+a1*x+a2*x2.
Составим функцию
Для этой функции запишем
систему уравнений:
Получим
Для нахождения параметров
a0,
a1,
a2
необходимо решить эту
систему линейных алгебраических
уравнений (например, методом Крамера
или методом обратной матрицы).
Кубическая функция
Необходимо определить
параметры многочлена третьей степени:
y=a0+a1*x+a2*x2+a3*x3.
СоставимфункциюS:
Система уравнений для
нахождения параметров a0,
a1,
a2,
a3
имеет вид:
Для нахождения параметров
a0, a1,
a2, a3
необходимо решить
систему четырёх линейных алгебраических
уравнений.
Если в качестве аналитической
зависимости выберем многочлен k-й степени
y=a0+a1x+…+ak
xk,
то система уравнений для определения
параметров ai
принимает вид:
Подбор параметров функции
y=a*xb.
Для нахождения параметров
функции y=a*xb
проведем логарифмирование
функции y.
Lg y = Lg a + b Lg x
Сделаем замену Y
= lg y; X
= lg x; A = lg
a. Получим линейную
зависимость Y = A+bX.
Найдем коэффициенты линии регрессии A
и b.
Затем определяем a=10A.
Мы получили значение параметров функции
y=a*xb.
Подбор параметров функции
y=a*ebx.
Прологарифмируем выражение
y = a*ebx;
Lg y = Lg a + b*x*Lg e;
Проведём замену Y=Lg
y. Вновь получаем линейную
зависимость Y=Bx+A,
где A= Lg a;
B=b*Lg e.
Найдем A и
B. Затем
определим значение параметров a
и b,
a=10A
и b=B/Lg(e).
Ниже проведены замены переменных,
которые преобразовывают функции вида
y=f(x, a, b) к
линейной зависимости Y=
Ax+B.
Подбор параметров функции
y=a*xb*ecx
Прологарифмируем выражение
y=a*xb*ecx,
после логарифмирования оно принимает
вид:
Lg y=Lg a+b*Lg x+c*Lg ex
Сделаем замену Y=Lgy,
A=Lga,
C=c*Lge.
После замены выражение принимает вид:
Y=A+b*Lg X+CX
Для функции этой составим
функцию S:
Параметры A,
b и С
следует выбрать таким
образом, чтобы функция S
была минимальной. После
элементарных преобразований получим
систему трёх линейных алгебраических
уравнений для определения коэффициентов
A, b
и C.
Решив систему, получим значения
A, b,
C. После
чего вычисляем
a=10A;
c=C/Lg(e).
Соседние файлы в папке Методички
- #
- #
- #
- #
- #
- #
- #
Задание . Табулирование функции с параметром. Рассчитайте
таблицу значений функции f(x) = ax2 + 7, где x меняется от -2 до 2 с шагом 0, 5. рассчитаем значения
аргумента и значения функции в таблице.
Заполнение диапазона x рис. 8. В ячейку B3
вводим – 2 в ячейку B4 – формулу B3+0,5. Этой формулой
заполняем значения аргументов. Используем автозаполнение.
Рис. 8. Заполнение диапазона x
Заполнение диапазона y рис. 9. В ячейку C3
вводим формулу =$D$3*B3*B3+7. Заполняем этой формулой значения функции.
Используем автозаполнение.
Рис. 9. Заполнение диапазона y
Построение графика, тип диаграммы точечная, рис. 10.
Рис. 10 График функции
Построение
графиков функций
1.
Запустите табличный
процессор OpenOffice.org Calc.
2.
Выделите ячейки А1:F1 и объедините их, используя кнопку 
объединить ячейки на панели инструментов Форматирование.
3.
Введите в объединенные
ячейки заголовок Построение графиков функций.
4.
В ячейку А3 введите
x, а в ячейку В3 – y=sin(x).
5.
В ячейку А4 введите
значение — 6, в А5 – значение —5,5. Выделите
эти две ячейки и наведите указатель мыши на правый нижний угол выделения –
черный квадратик (маркер заполнения). После того, как указатель примет
форму черного крестика, растяните область выделения до значения 6.
6.
В ячейку В4 введите
формулу =sin(A4) и
нажмите клавишу Enter.
7.
Используя маркер
заполнения, скопируйте формулу в остальные ячейки.
8.
Выделите значения двух
столбиков и запустите Мастер диаграмм (Вставка ► Диаграмма).
9.
Выберите тип диаграммы – Диаграмма
XY (только линии).
10.
Приведите диаграмму к
виду, представленному на рис. 2.
Рисунок 2. График функции у=sin(x)
11. Переименуйте Лист1 в Графики функций.
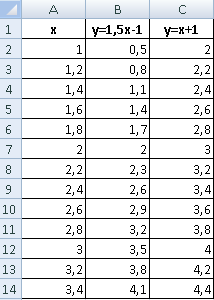
12. Постройте на этом же листе график функции:
на отрезке [-3;3] с шагом 0,2 (рис. 3).
Для того чтобы записать функцию y
воспользуемся логической функцией IF(Логическое выражение; значение_если
истина; значение_если ложь).
Функция IF проверяет
выполняется ли условие, и возвращает одно значение, если оно истинно и другое
значение, если нет.
В нашем случае если xÎ[-1;1], то y = 1–x2, в противном случае y = |x|–1.
Чтобы записать условие xÎ[-1;1] воспользуемся логической функцией
AND(логическое
выражение1; логическое выражение2; …).
В нашем случае получим AND(x >=
– 1;x <= 1).
Таким образом формула для нахождения значения функции
будет выглядеть следующим образом:
=IF(AND(А15 >= – 1;А15 <= 1); 1 – А15*А15; ABS(A15) –
1).
Для вычисления модуля используется функция ABS(число).
Рисунок 3. График функции
13.
На втором листе рабочей
книги самостоятельно постройте еще 2 графика:
y = |x2+5x-10|,
[-10;5], шаг 0,5
и

Задания на внеаудиторную
самостоятельную работу:
Постройте графики функций.
|
1 |
y = x5+x2–10, [-10;10], шаг 1 |
|
2 |
y |
|
3 |
y |
|
4 |
y |
|
10 |
y |




















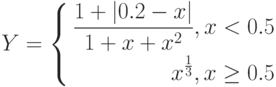
![$$
Y=left{
begin{aligned}
% nonumber to remove numbering (before each equation)
1+ln(1+x), x<0.2\
frac{1+x^{frac{1}{2}}}{1+x}, xin[0.2;0.8]\
2e^{-2x}, x>0.8
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/4205ce0704c58087ee2090c98d69defd.png)






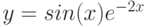
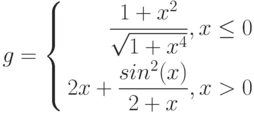
![$$
z=left{
begin{aligned}
frac{1+|x|}{sqrt[3]{1+x+x^{2}}},xleq-1\
2ln(1+x^{2}+frac{1+cos^{4}(x)}{2+x},xin [-1;0]\
(1+x)^{frac{3}{5}}, xgeq0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c4fbe6f0e5d1dfcbce7a704e471a929.png)
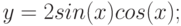
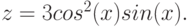
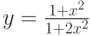
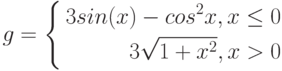
![$$
z=left{
begin{aligned}
frac{1+x}{sqrt[3]{1+x^{2}}},xleq0\
-x+2e^{-2x},xin(0,1)\
|2-x|^{frac{1}{3}},xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/b018b9edd908f216df636f345c6a0e0e.png)
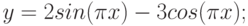
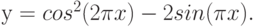
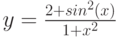
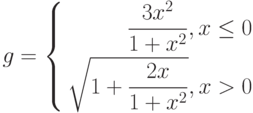
![$$
z=left{
begin{aligned}
3x+sqrt{1+x^{2}},x<0\
2cos(x)e^{-2x},xin[0,1]\
2sin(3x),x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/96eae18012c8cec7fa3195cb7cb16718.png)


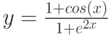
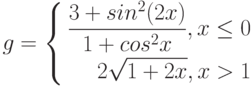
![$$
z=left{
begin{aligned}
sqrt{1+frac{x^{2}}{1+x^{2}}},x<0\
2cos^{2}(x),xin[0,1]\
sqrt{1+|2sin(3x)|^{frac{1}{3}}},x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0e0bd3f1b2b59b98e1d0aac6b9e4e060.png)

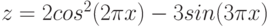
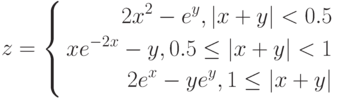
![$$y=sqrt[4]{1+e^{3x}}$$](https://intuit.ru/sites/default/files/tex_cache/38d26ef341d2e8b1539e5db30dd8d0fb.png)
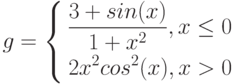
![$$
z=left{
begin{aligned}
|x|^{frac{1}{3}}, x<0\
-2x+frac{x}{1+x}, xin[0,1]\
frac{|3-x|}{1+x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/a336bbbfe739b8a27a42bc552dbba85d.png)
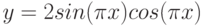

![$$
g=left{
begin{aligned}
sqrt{1+2x^{2}-sin(x)}, xleq0\
frac{2+x}{sqrt[3]{2+e^{-0.1x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/bf750a63e0bf1e99dcdc62a82b5ae8a1.png)
![$$
z=left{
begin{aligned}
frac{1+x}{1+x^{2}}, x<0\
sqrt{1+frac{x}{1+x}}, xin[0,1]\
2|sin(3x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0ba53b8c4d394ba14c7bea0640198a67.png)
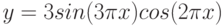
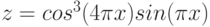
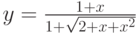
![$$
g=left{
begin{aligned}
sqrt{1+x^{2}}, x<0\
frac{1+x}{1+sqrt[3]{1+e^{-0.2x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c5f92dffe784f474d4780a60de478e2.png)
![$$
z=left{
begin{aligned}
frac{1+x+x^{2}}{1+x^{2}}, x<0\
sqrt{1+frac{2x}{1+x^{2}}}, xin[0,1]\
2|0.5+sin(x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/ea55ab481bac3e0b5e9e38e088173fa3.png)

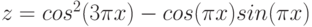
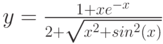
![$$
g=left{
begin{aligned}
sqrt{1+|x|}, xleq0\
frac{1+3x}{2+sqrt[3]{1+x}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5b2dfdc96ef1d57aec714b337234e6ad.png)
![$$
z=left{
begin{aligned}
1+frac{3+x}{1+x^{2}}, x<0\
sqrt{1+(1-x)^{2}},xin[0,1]\
frac{1+x}{1+cos^{2}(x)}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/d7447bf6d7e359d4eca3921d80e719a8.png)
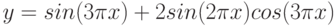

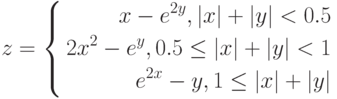
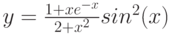
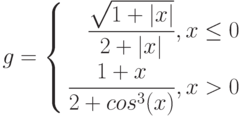
![$$
z=left{
begin{aligned}
frac{1+2x}{1+x^{2}}, x<0\
sin^{2}(x)sqrt{1+x},xin[0,1]\
sin^{2}(x)e^{0.2x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/12bdc437bdea736bdda75cef4a7e722c.png)
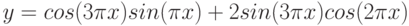
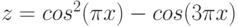
![$х,yin [-1; 1]$$](https://intuit.ru/sites/default/files/tex_cache/1398b5df6d8c02912de8ea030fafac71.png)
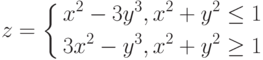
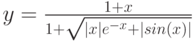
![$$
g=left{
begin{aligned}
sqrt[3]{1+x^{2}}, xleq0\
sin^{2}(x)+frac{1+x}{1+cos^{2}(x)}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5144de1617b0997002fd47d479761ecb.png)
![$$
z=left{
begin{aligned}
frac{|x|}{1+x^{2}}e^{-2x}, x<0\
sqrt{1+x^{2}},xin[0,1]\
frac{1+sin(x)}{1+x}+3x, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/fc2d46b4be846a82407b051315db3f0a.png)