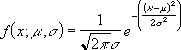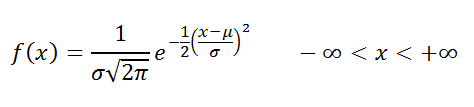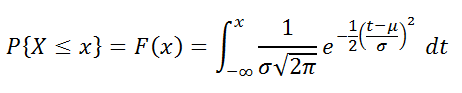Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.РАСП.
Синтаксис
НОРМРАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМРАСП описаны ниже.
-
X Обязательный. Значение, для которого строится распределение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Замечания
-
Если «standard_dev» не является числом, то возвращается #VALUE! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, то нормДАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
-
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМРАСП(A2;A3;A4;ИСТИНА) |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМРАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |
Нужна дополнительная помощь?
17 авг. 2022 г.
читать 3 мин
Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности .
В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:
- Сгенерируйте выборочное распределение.
- Визуализируйте распределение выборки.
- Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
- Рассчитайте вероятности относительно выборочного распределения.
Создание выборочного распределения в Excel
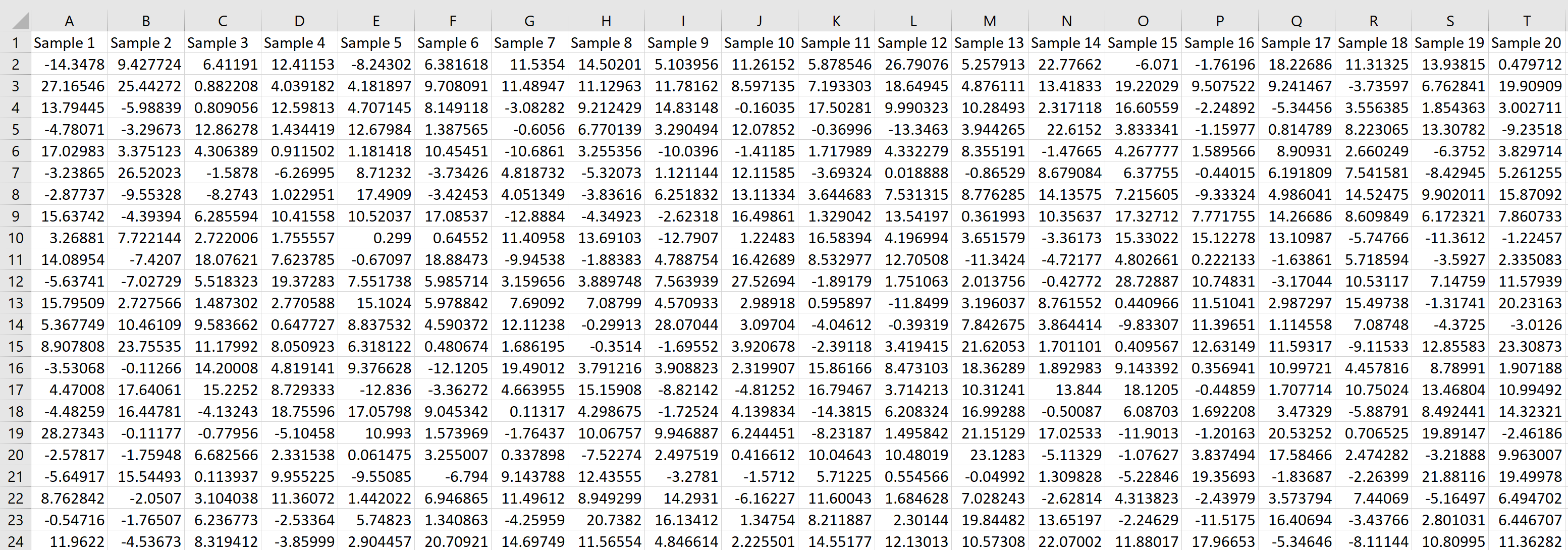
Предположим, мы хотим сгенерировать выборочное распределение, состоящее из 1000 выборок, в каждой из которых размер выборки равен 20 и происходит от нормального распределения со средним значением 5,3 и стандартным отклонением 9 .
Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашего рабочего листа:
= NORM.INV ( RAND (), 5.3, 9)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:
Каждая строка представляет выборку размера 20, в которой каждое значение получено из нормального распределения со средним значением 5,3 и стандартным отклонением 9.
Найдите среднее значение и стандартное отклонение
Чтобы найти среднее значение и стандартное отклонение этого выборочного распределения средних значений выборки, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:
= AVERAGE (A2:T2)
Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и дважды щелкнуть, чтобы скопировать эту формулу в каждую другую ячейку в столбце U:
Мы видим, что первая выборка имела среднее значение 7,563684, вторая выборка имела среднее значение 10,97299 и так далее.
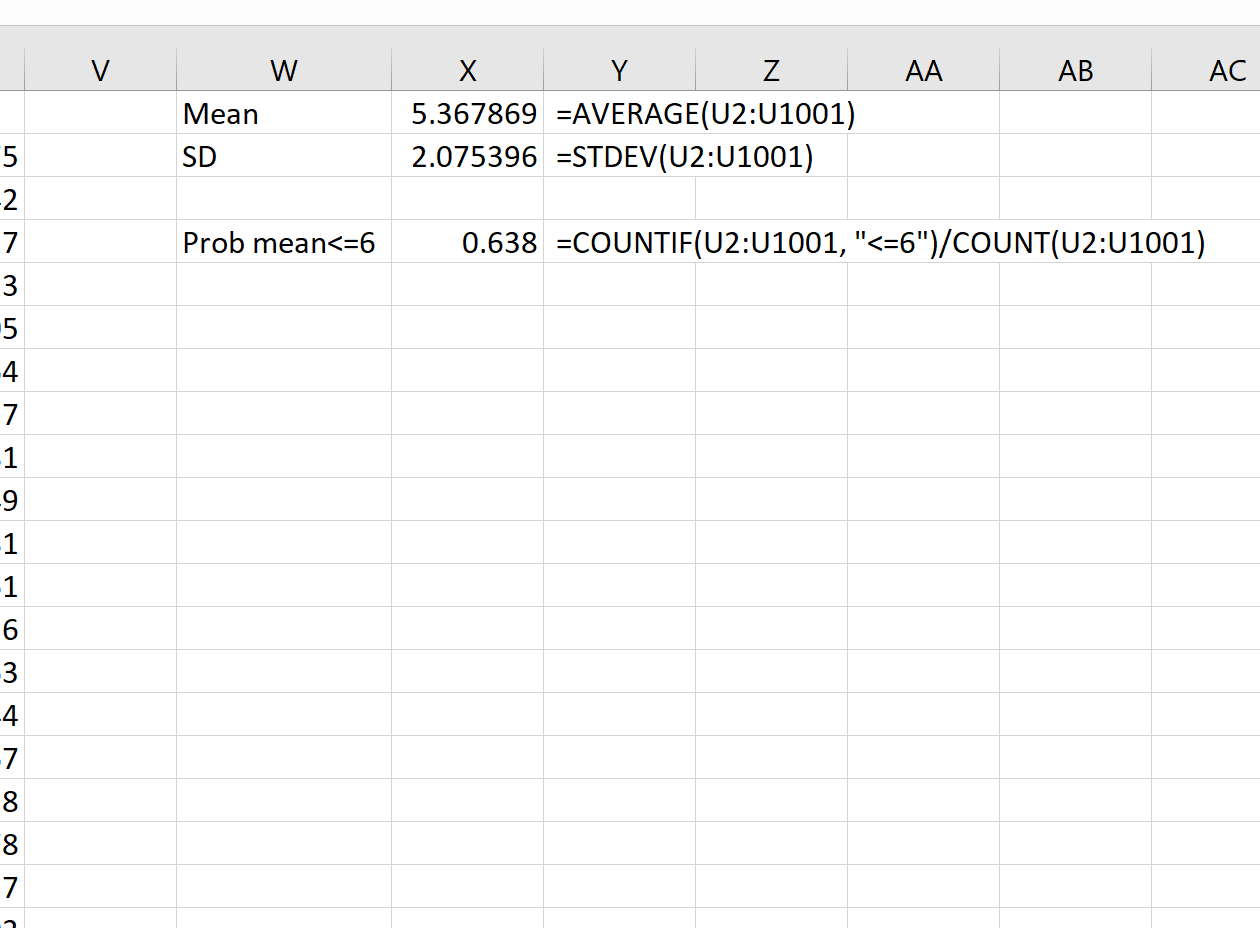
Затем мы можем использовать следующие формулы для расчета среднего значения и стандартного отклонения среднего значения выборки:
Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.
И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.
Визуализируйте распределение выборки
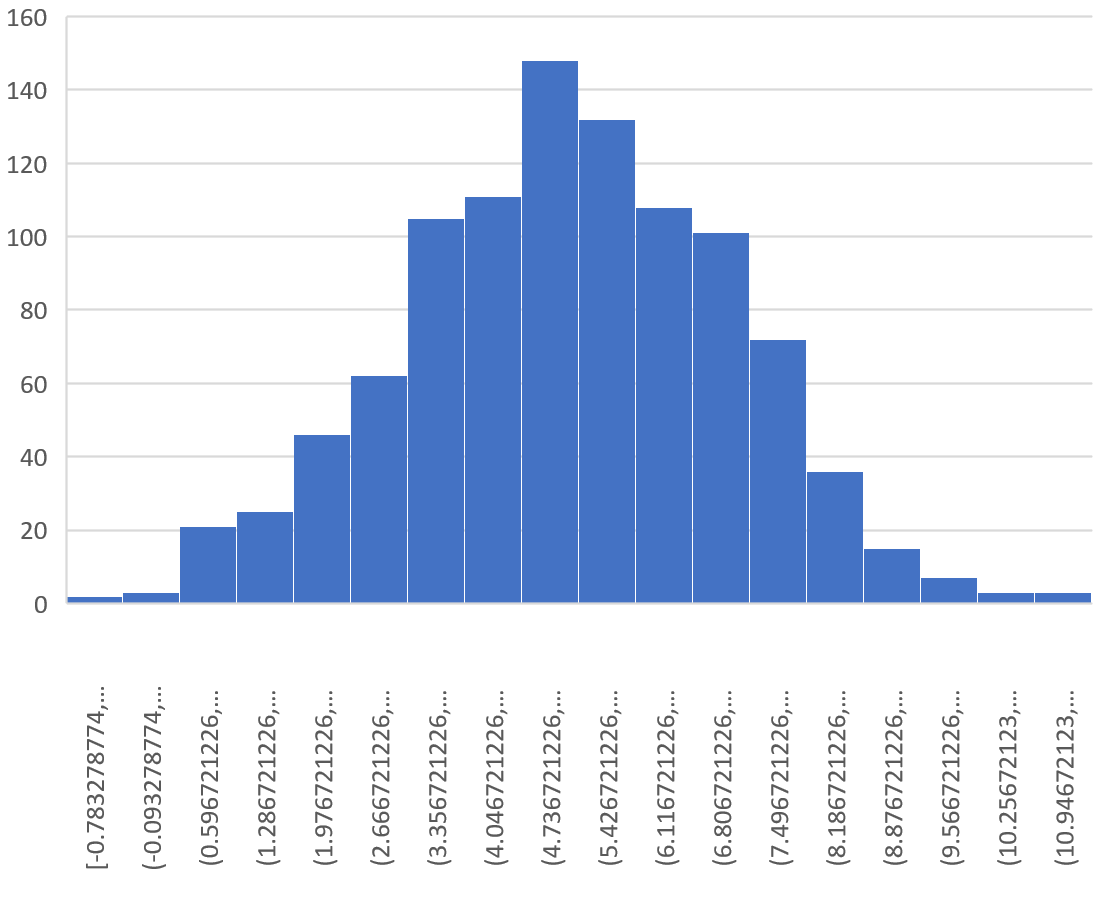
Мы также можем создать простую гистограмму для визуализации выборочного распределения выборочных средних.
Для этого просто выделите все средние значения выборки в столбце U, щелкните вкладку « Вставка », затем выберите параметр « Гистограмма » в разделе « Диаграммы ».
В результате получается следующая гистограмма:
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.
Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.
Рассчитать вероятности
Мы также можем рассчитать вероятность получения определенного значения среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.
Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9 и размер выборки равен:
= COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)
Мы видим, что вероятность того, что среднее значение выборки меньше или равно 6, составляет 0,638.
Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :
Дополнительные ресурсы
Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему
Рассмотрим Нормальное распределение. С помощью функции
MS EXCEL
НОРМ.РАСП()
построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения
.
Нормальное распределение
(также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения
Нормального распределения
(англ.
Normal
distribution
)
во многих областях науки вытекает из
Центральной предельной теоремы
теории вероятностей.
Определение
: Случайная величина
x
распределена по
нормальному закону
, если она имеет
плотность распределения
:
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Нормальное распределение
зависит от двух параметров: μ
(мю)
— является
математическим ожиданием (средним значением случайной величины)
, и σ (
сигма)
— является
стандартным отклонением
(среднеквадратичным отклонением). Параметр μ определяет положение центра
плотности вероятности
нормального распределения
, а σ — разброс относительно центра (среднего).
Примечание
: О влиянии параметров μ и σ на форму распределения изложено в статье про
Гауссову кривую
, а в
файле примера на листе Влияние параметров
можно с помощью
элементов управления Счетчик
понаблюдать за изменением формы кривой.
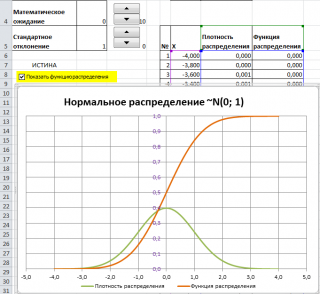
Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
Нормального распределения
имеется функция
НОРМ.РАСП()
, английское название — NORM.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина X, распределенная по
нормальному закону
, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Вышеуказанное распределение имеет обозначение
N
(μ; σ).
Так же часто используют обозначение через
дисперсию
N
(μ; σ
2
).
Примечание
: До MS EXCEL 2010 в EXCEL была только функция
НОРМРАСП()
, которая также позволяет вычислить функцию распределения и плотность вероятности.
НОРМРАСП()
оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением
называется
нормальное распределение
с
математическим ожиданием
μ=0 и
дисперсией
σ=1. Вышеуказанное распределение имеет обозначение
N
(0;1).
Примечание
: В литературе для случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение z.
Любое
нормальное распределение
можно преобразовать в стандартное через замену переменной
z
=(
x
-μ)/σ
. Этот процесс преобразования называется
стандартизацией
.
Примечание
: В MS EXCEL имеется функция
НОРМАЛИЗАЦИЯ()
, которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то
нормализацией
. Формулы
=(x-μ)/σ
и
=НОРМАЛИЗАЦИЯ(х;μ;σ)
вернут одинаковый результат.
В MS EXCEL 2010 для
стандартного нормального распределения
имеется специальная функция
НОРМ.СТ.РАСП()
и ее устаревший вариант
НОРМСТРАСП()
, выполняющий аналогичные вычисления.
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации
нормального распределения
N
(1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по
нормальному закону
N(1,5; 2)
, меньше или равна 2,5. Формула выглядит так:
=НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА)
=0,691462. Сделав замену переменной
z
=(2,5-1,5)/2=0,5
, запишем формулу для вычисления
Стандартного нормального распределения:
=НОРМ.СТ.РАСП(0,5; ИСТИНА)
=0,691462.
Естественно, обе формулы дают одинаковые результаты (см.
файл примера лист Пример
).
Обратите внимание, что
стандартизация
относится только к
интегральной функции распределения
(аргумент
интегральная
равен ИСТИНА), а не к
плотности вероятности
.
Примечание
: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по
стандартному
нормальному закону,
закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле
=НОРМ.СТ.РАСП(z;ИСТИНА)
. Вычисления производятся по формуле
В силу четности функции
плотности стандартного нормального
распределения f(x), а именно f(x)=f(-х), функция
стандартного нормального распределения
обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция
НОРМ.СТ.РАСП(x;ИСТИНА)
вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется
квантилем
стандартного
нормального распределения
.
В MS EXCEL для вычисления
квантилей
используют функцию
НОРМ.СТ.ОБР()
и
НОРМ.ОБР()
.
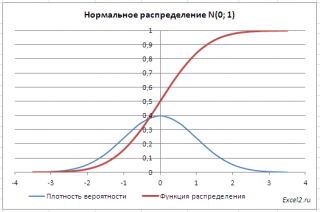
Графики функций
В
файле примера
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
Как известно, около 68% значений, выбранных из совокупности, имеющей
нормальное распределение
, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для
стандартного нормального распределения
можно записав формулу:
=
НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от
среднего
(см.
лист График в файле примера
).
В силу четности функции
плотности стандартного нормального
распределения:
f
(
x
)=
f
(-х)
, функция
стандартного нормального распределения
обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
=
2*НОРМ.СТ.РАСП(1;ИСТИНА)-1
Для произвольной
функции нормального распределения
N(μ; σ) аналогичные вычисления нужно производить по формуле:
=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1
Вышеуказанные расчеты вероятности требуются для
построения доверительных интервалов
.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении
диаграмм
читайте статью
Основные типы диаграмм
.
Примечание
: Для удобства написания формул в
файле примера
созданы
Имена
для параметров распределения: μ и σ.
Генерация случайных чисел
С помощью надстройки
Пакет анализа
можно сгенерировать случайные числа, распределенные по
нормальному закону
.
СОВЕТ
: О надстройке
Пакет анализа
можно прочитать в статье
Надстройка Пакет анализа MS EXCEL
.
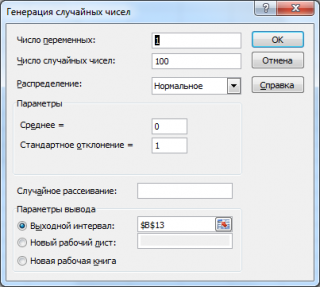
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне
Генерация
случайных чисел
установим следующие значения для каждой пары параметров:
Примечание
: Если установить опцию
Случайное рассеивание
(
Random Seed
), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции
Случайное рассеивание
может запутать. Лучше было бы ее перевести как
Номер набора со случайными числами
.
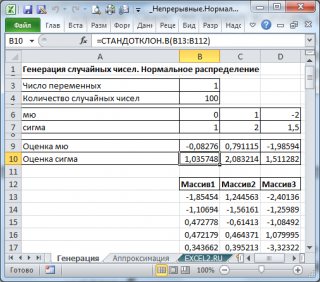
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ
.
Оценку для μ можно сделать с использованием функции
СРЗНАЧ()
, а для σ – с использованием функции
СТАНДОТКЛОН.В()
, см.
файл примера лист Генерация
.
Примечание
: Для генерирования массива чисел, распределенных по
нормальному закону
, можно использовать формулу
=НОРМ.ОБР(СЛЧИС();μ;σ)
. Функция
СЛЧИС()
генерирует
непрерывное равномерное распределение
от 0 до 1, что как раз соответствует диапазону изменения вероятности (см.
файл примера лист Генерация
).
Задачи
Задача1
. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.
Решение1
: =
1-НОРМ.РАСП(36;41;2;ИСТИНА)
Задача2
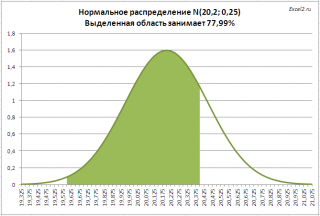
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?
Решение2
: =
НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)
На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.
Решение приведено в
файле примера лист Задачи
.
Задача3
. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?
Решение3
: =
НОРМ.ОБР(0,975; 20,20; 0,25)
=20,6899 или =
НОРМ.СТ.ОБР(0,975)*0,25+20,2
(произведена «дестандартизация», см. выше)
Задача 4
. Нахождение параметров
нормального распределения
по значениям 2-х
квантилей
(или
процентилей
). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я
процентиля
(например, 0,5-
процентиль
, т.е. медиана и 0,95-я
процентиль
). Т.к. известна
медиана
, то мы знаем
среднее
, т.е. μ. Чтобы найти
стандартное отклонение
нужно использовать
Поиск решения
. Решение приведено в
файле примера лист Задачи
.
Примечание
: До MS EXCEL 2010 в EXCEL были функции
НОРМОБР()
и
НОРМСТОБР()
, которые эквивалентны
НОРМ.ОБР()
и
НОРМ.СТ.ОБР()
.
НОРМОБР()
и
НОРМСТОБР()
оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин
x
(
i
)
с параметрами μ
(
i
)
и σ
(
i
)
также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ
(1)+ μ(2)
и
КОРЕНЬ(σ(1)^2+ σ(2)^2).
Убедимся в этом с помощью MS EXCEL.
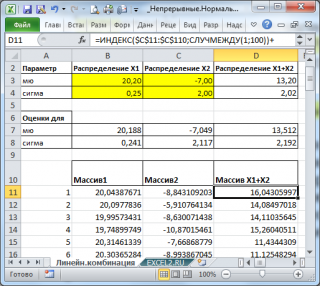
С помощью надстройки
Пакет анализа
сгенерируем 2 массива по 100 чисел с различными μ и σ.
Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
вычислим
среднее
и
дисперсию
получившейся
выборки
и сравним их с расчетными.
Кроме того, построим
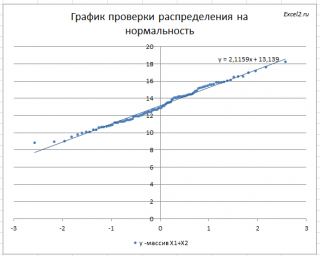
График проверки распределения на нормальность
(
Normal
Probability
Plot
), чтобы убедиться, что наш массив соответствует выборке из
нормального распределения
.
Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой
стандартного отклонения
, а пересечение с осью y (параметр b) –
среднего
значения.
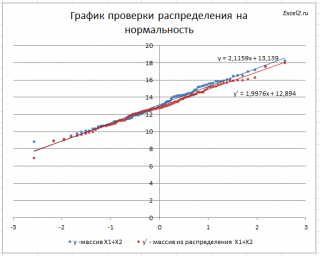
Для сравнения сгенерируем массив напрямую из распределения
N
(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)
).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.
В качестве примера можно провести следующую задачу.
Задача
. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.
Решение
. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и
стандартным отклонением
=КОРЕНЬ(СУММКВ(1,5;1,2))
, запишем решение =
1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)
Ответ
: 15% (см.
файл примера лист Линейн.комбинация
)
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры
Биномиального распределения
B(n;p) находятся в пределах 0,1<=p<=0,9 и n*p>10, то
Биномиальное распределение
можно аппроксимировать
Нормальным распределением
.
При значениях
λ
>15
,
Распределение Пуассона
хорошо аппроксимируется
Нормальным распределением
с параметрами: μ
=λ
, σ
2
=
λ
.
Подробнее о связи этих распределений, можно прочитать в статье
Взаимосвязь некоторых распределений друг с другом в MS EXCEL
. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в учебном процессе. Показываются преимущества данного метода перед ручным счетом по проверке рассмотренного критерия.
Ключевые слова: шаблон Excel, гистограмма, кривая распределения, критерий согласия Пирсона
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: металлургии, а также в экономике, биологии, политике, социологии и т. д. Рассмотрим использование некоторых средств статистического анализа, а именно — гистограмм для обработки больших массивов данных.
Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой мы наблюдали. Проверка того, насколько хорошо наблюдаемая выборка описывается теоретическим законом, осуществляется с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным, и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию или необоснованному отклонению проверяемой гипотезы [1].
Сходимость результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. Сама процедура проверки нормальности распределения относится к распространенной стандартной и довольно тривиальной задаче обработки данных и достаточно подробно и широко описана в различной литературе по метрологии и статистической обработке данных измерений [2- 4].
Данные, получаемые в результате измерений при контроле технологических процессов, оценке характеристик различных объектов и др. для дальнейшей обработки желательно представлять в виде теоретического распределения, максимально соответствующего экспериментальному распределению. Проверку гипотезы о виде функции распределения в настоящее время проводят по различным критериям согласия — Пирсона, Колмогорова, Смирнова и другим в соответствии с новыми разработанными нормативными документами — рекомендациями по стандартизации [5, 6].
Наиболее часто используется критерий Пирсона 2. Однако применение критериев согласия требует обычно довольно значительного объёма данных. Так, критерий Пирсона обычно рекомендуется использовать при объёме выборки не менее 50…100. Поэтому при небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами — графическим методом или по асимметрии и эксцессу. Применение критерия Пирсона для ручной обработки данных очень подробно было изложено в известной работе [2]. Как свидетельствует опыт проверок согласия экспериментальных данных с теоретическими по различным критериям, эта процедура является очень трудоемкой, требует некоторой усидчивости и особого внимания при обработке от исследователя, как правило, не исключает ошибок в работе и не вызывает особого энтузиазма у выполняющего эту работу.
Решение задач статистического анализа связано со значительными объемами вычислений. Проведение реальных многовариантных статистических расчетов в ручном режиме является очень громоздкой и трудоемкой задачей и без использования компьютера в настоящее время практически невозможно. В настоящее время разработано достаточное количество универсальных и специализированных программных средств для статистического анализа и обработки экспериментальных данных. Автор предлагает к рассмотрению достаточно простой и эффективный шаблон для быстрого построения гистограммы и кривой нормального распределения.
По виду гистограммы можно предположить (принять гипотезу) о том, что выборка случайных чисел подчиняется нормальному закону распределения. Далее, для того чтобы убедиться в правильности выбранной гипотезы надо, первое — построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонения) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы. И, второе — используя в данном случае, как пример, критерий согласия Пирсона, установить справедливость выбранной гипотезы.
Рассмотрим порядок действий при работе с критерием Пирсона в среде Excel.
1. Полученные в результате измерений значения 100 случайных результатов измерений внести в ячейки A1:A100 шаблона Excel и приступить к построению гистограммы на основе данных, назначая длину интервала (карман) и выбирая необходимое число интервалов.
2. Затем на этом же листе создается таблица, в которую посредством формул Excel вносятся основные расчетные величины, используемые для построения гистограммы и кривой Гаусса: среднее арифметическое, стандартное отклонение, минимальное и максимальное значения выборки, размах, величина кармана (рис. 1).
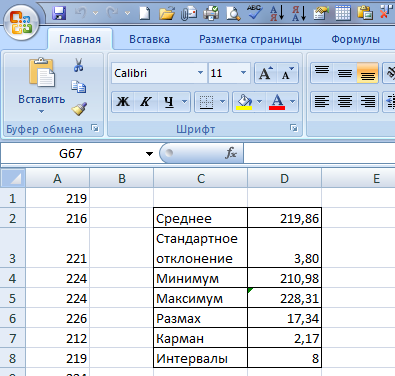
Рис. 1. Фрагмент таблицы с исходными данными
В ячейку D2 вносится формула =СРЗНАЧ(A1:A100), D3: =СТАНДОТКЛОН(A1:A100), D4: =МИН(A1:A100), D5: =МАКС(A1:A100), D6: =D5-D4, D7: =D6/D8. В ячейку D8 вводится число интервалов, которое для числа измерений, равным 100, может быть принято от 7 до 12.
Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: k~1+3,322lgN, где N— количество всех значений величины. Например, для N = 100, n = 7,6, которое должно быль округлено до целого числа, округляем до n = 8.
3. Интервал карманов вычисляют так: разность максимального и минимального значений массива, деленная на количество интервалов: .
4. Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (ячейка D4), затем в следующей ячейке ниже — к полученной сумме и т. д. Так постепенно доходим до максимального значения. Таким образом, мы и построили интервалы карманов в виде столбца значений.
Интервалом считается следующий диапазон: (i-1; i] или i<значения<=i (нестрогая верхняя граница интервала — это значение в ячейке, нижняя строгая граница — значение в предыдущей ячейке).
5. Выделяем столбец рядом с нашими карманами, нажимаем «F2» и вводим функцию: =ЧАСТОТА (массив данных; диапазон карманов) и нажимаем Ctr+Shift+Enter.
6. В выделенном нами столбце напротив границ интервалов (а мы знаем, что это нестрогие верхние границы) появилось количество значений исходного массива, которые попадают в интервал (рис. 2).
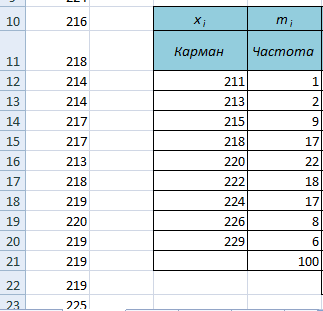
Рис. 2. Количество значений исходного массива, попавших в интервалы (частоты)
Построение теоретического закона распределения
Для построения теоретического закона распределения совместно с гистограммой и проверкой согласия по критерию хи-квадрат Пирсона автоматически заполняется таблица 1 после ввода экспериментальных данных в ячейки A1:A100.
Таблица 1
|
xi |
mi |
n∙pi |
|
|
карманы |
частота |
теоретическая частота |
статистика U |
Для построения этой таблицы надо воспользоваться таблицей карман — частота процедуры Гистограмма. В этой таблице обозначены:
xi — границы интервалов группировки (карманы — получены как результат выполнения процедуры Гистограмма);
mi — количество элементов выборки, попавших в i–ый интервал (частота — получена в результате процедуры Гистограмма).
Для построения этой таблицы в Excel к столбцам карман — частота процедуры Гистограмма надо добавить столбцы n∙pi (теоретическая частота) и (статистика U).
Проверка согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона.
В ячейку столбца, помеченного именем U, вводим формулу,
, (1)
Критическое значение статистики U, которая имеет распределениес r степенями свободы (число степеней свободы определяется как число частичных интервалов минус 1), определяется при помощи функции ХИ2ОБР.
Функция ХИ2ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию →в диалоговом окне Мастер функций— шаг 1 из 2 вкатегории Статистические →ХИ2ОБР (рис. 3).
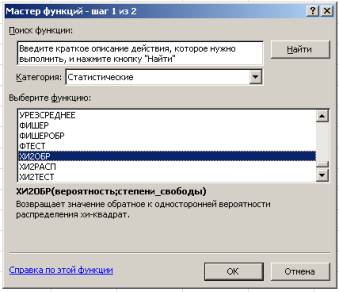
Рис. 3. Диалоговое окно выбора функции ХИ2ОБР
В диалоговом окне Аргументы функции ХИ2ОБР заполняются поля как показано на рис. 4, задаваясь уровнем значимости (например, 0,05, что соответствует доверительной вероятности Р = 0,95) и предварительно выбрав ячейку для результата вычисления функции.
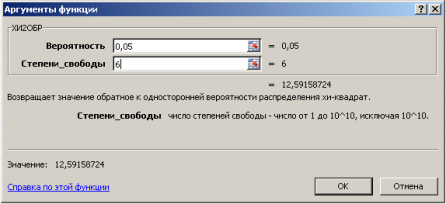
Рис. 4. Диалоговое окно функции ХИ2ОБР с заполненными полями ввода
Размножим формулу (1) в диапазонах ячеек [F12; F20] и [F51; F61]. В ячейке F21 получим сумму содержимого ячеек F12; F20 (рис. 5). В ячейке F62 получим сумму содержимого ячеек F51; F61 (рис. 6).
В ячейке F21 получено значение статистики: U = 2,09, а в ячейке F62 — U = 3,43 при доверительной вероятности Р = 0,95.
Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т. д.) на этом же листе Excel можно построить гистограммы распределения с кривой Гаусса для разных чисел интервалов (в данном случае n = 8 и n = 10) (рис. 5 и 6).
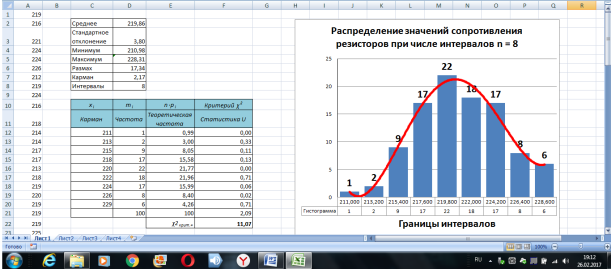
Рис. 5. Вид гистограммы и кривой распределения при числе интервалов n = 8 (пример)
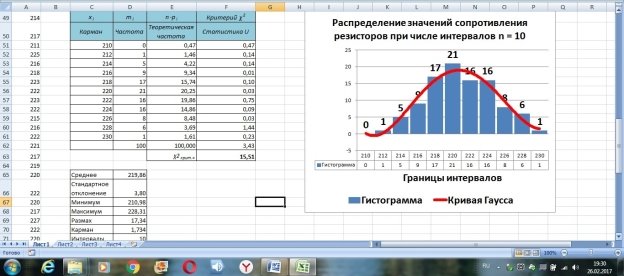
Рис. 6. Вид гистограммы и кривой распределения при числе интервалов n = 10 (пример)
Шаблон позволяет варьировать числом интервалов и величиной кармана, при этом автоматически изменяется внешний вид гистограммы и кривой нормального распределения. Исследователь может подобрать наиболее «красивый» вид гистограммы и аппроксимирующей кривой Гаусса, одновременно изменив значение доверительной вероятности и числа степеней свободы и добившись при этом выполнения критерия Пирсона.
Если значение статистики U оказалось меньше критического значения при заданной доверительной вероятности, то гипотеза, состоящая в том, что исследуемая выборка подчиняется нормальному закону распределения, принимается. Вданном примере значение обеих статистик U оказалось меньше критического значения
и
Следовательно, мы можем распространить данный закон распределения на всю генеральную совокупность исследуемых объектов (партию изделий, сменную выработку, месячный план и т. д.).
Более подробно указанная тема была рассмотрена в статье автора в сборнике «Законодательная и прикладная метрология» [7].
Выводы
- Существовавшая ранее традиционная «ручная» обработка данных при проверке нормального (и других) законов распределения и построении гистограмм являлась достаточно трудоемкой задачей, не исключавшей появление ошибок, обнаружение которых зачастую требовало значительных затрат времени и моральных сил исследователя.
- Появление пакетов офисных программ, в частности Excel 2010 и ее последующих версий, позволяет значительно сократить трудоемкость обработки данных и практически исключает появление ошибок в расчетах.
Литература:
1. Лемешко Б. Ю., Постовалов С. Н. О правилах проверки согласия опытного распределения с теоретическим. — Методы менеджмента качества. Надежность и контроль качества. — 1999, № 11. — С. 34–43.
2. Бурдун Г. Д., Марков Б. Н. Основы метрологии. Учебное пособие для вузов. — М.: Изд. стандартов, 1975. — 336 с.
3. Сулицкий В. Н. Методы статистического анализа в управлении: Учеб. пособие. — М.: Дело, 2002. — 520 с.
4. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
5. Рекомендации по стандартизации Р 50.1.033–2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. — М.: ФГУП «Стандартинформ», 2006. — 87 с.
6. Рекомендации по стандартизации Р 50.1.037–2002. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. — М.: ИПК Изд. стандартов, 2002. — 62 с.
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию согласия Пирсона средствами приложения Excel. — Законодательная и прикладная метрология, 2016, № 6. — С. 3–9.
Основные термины (генерируются автоматически): статистический анализ, критерий согласия, массив данных, вид функции распределения, интервал карманов, максимальное значение, минимальное значение, построение гистограммы, различный критерий согласия, стандартное отклонение.
To generate a normal distribution in Excel, you can use the following formula:
=NORMINV(RAND(), MEAN, STANDARD_DEVIATION)
You can then copy this formula down to as many cells in Excel as you’d like, depending on how large you’d like the dataset to be.
The following step-by-step example shows how to use this formula to generate a normal distribution in Excel.
Step 1: Choose a Mean & Standard Deviation
First, let’s choose a mean and a standard deviation that we’d like for our normal distribution.
For simplicity, we’ll choose 0 for the mean and 1 for the standard deviation:
Step 2: Generate a Normally Distributed Random Variable
Next, we’ll use the following formula to generate a single normally distributed random variable:
=NORMINV(RAND(), $B$1, $B$2)
The following screenshot shows how to do so:
Step 3: Choose a Sample Size for the Normal Distribution
Next, we can simply copy and paste this formula down to as many cells as we’d like.
For example, we may copy and paste this formula to a total of 20 cells:
The end result is a normally distributed dataset with a mean of 0, standard deviation of 1, and sample size of 20.
Note: You can quickly generate a brand new dataset that follows a normal distribution by simply double clicking on any cell and pressing Enter.
Additional Resources
Online Normal Distribution Dataset Generator
How to Perform a Normality Test in Excel
How to Make a Bell Curve in Excel