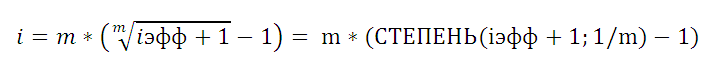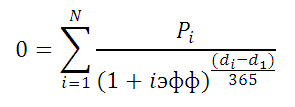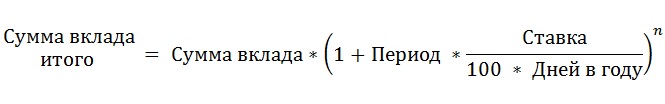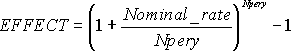Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.
Примеры использования функции ЭФФЕКТ в Excel
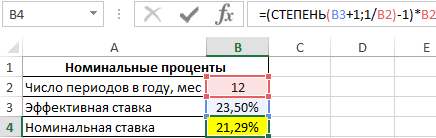
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.
Исходная таблица данных:
Связь между значениями эффективной и номинальной ставок описывается следующей формулой:
=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2
Полученный результат:
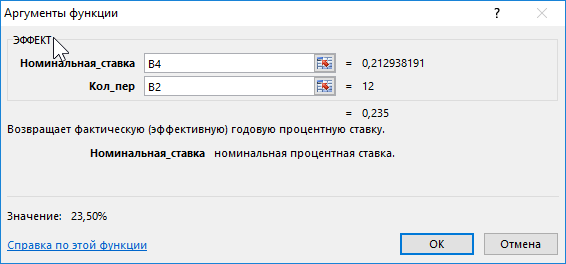
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:
Описание аргументов:
- B4 – полученное выше числовое значение номинальной ставки;
- B2 – число периодов погашения.
Результат:
Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.
Формула расчета процентов по вкладу в Excel
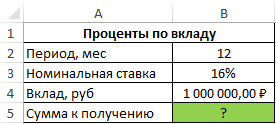
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.
Исходные данные:
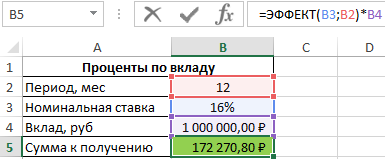
Формула для расчета:
=ЭФФЕКТ(B3;B2)*B4
Описание аргументов:
- B2 – число периодов капитализации;
- B3 – номинальная ставка;
- B4 – сумма вклада.
Результат расчетов:
Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.
Как посчитать проценты на депозит в Excel для выбора вклада
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:
- Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
- Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.
Определить выгодный вариант, отобразить схему выплат.
Исходные данные:
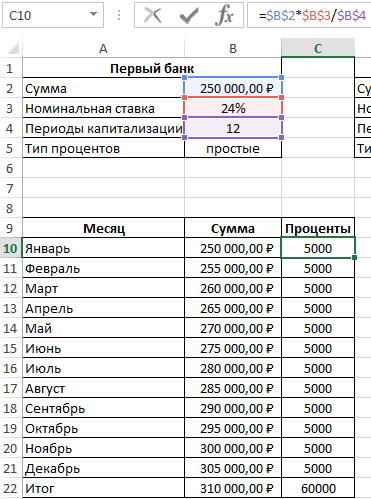
В первом случае таблица выплат выглядит так:
Проценты – постоянная величина, рассчитываемая по формуле:
=$B$2*$B$3/$B$4
Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):
- $B$2 – начальная сумма вклада;
- $B$3 – годовая ставка;
- $B$4 – число периодов капитализации вклада.
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.
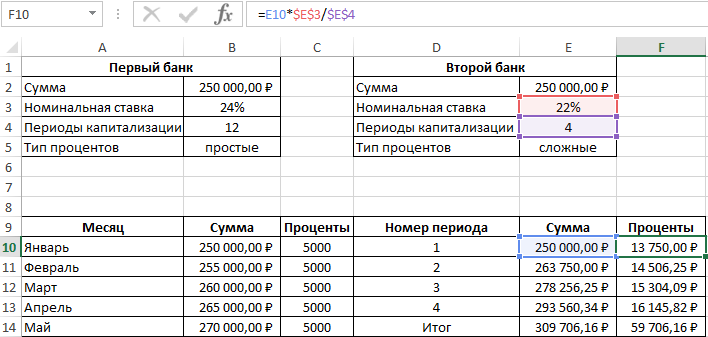
Таблица начисления процентов по условиям второго банка:
В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):
=L3*$E$3/$E$4
При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.
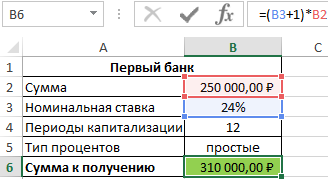
Для быстрого расчета итоговой суммы используем формулы:
- Первый банк:
- Второй банк:
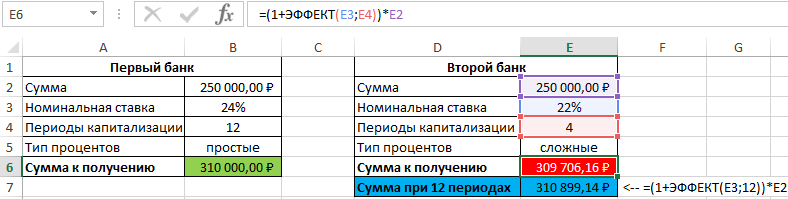
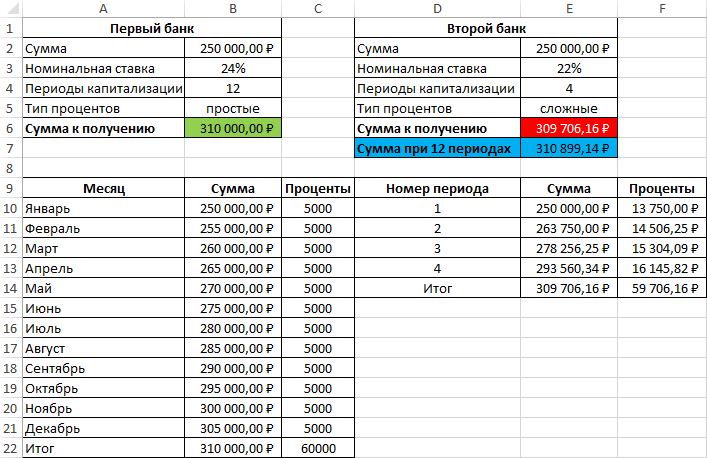
Результаты расчетов:
Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.
Особенности использования функции ЭФФЕКТ в Excel
Функция имеет следующий синтаксис:
=ЭФФЕКТ(номинальная_ставка;кол_пер)
Описание аргументов:
- номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
- кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.
Примечания 1:
- Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
- Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
- Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
- Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:
- A1 – номинальная годовая ставка;
- A2 – число периодов, в которые происходит начисление сложных процентов.
Примечания 2:
- Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
- Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
- Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.
Рассчитаем в MS EXCEL эффективную годовую процентную ставку и эффективную ставку по кредиту.
Эффективная ставка возникает, когда имеют место
Сложные проценты
. Понятие эффективная ставка встречается в нескольких определениях. Например, есть Эффективная (фактическая)
годовая
процентная ставка, есть Эффективная ставка
по вкладу
(с учетом капитализации), есть Эффективная процентная ставка
по потребительским кредитам
. Разберемся, что эти ставки из себя представляют и как их рассчитать в MS EXCEL.
Эффективная (фактическая) годовая процентная ставка
В MS EXCEL есть функция ЭФФЕКТ(номинальная_ставка, кол_пер), которая возвращает эффективную (фактическую)
годовую
процентную ставку, если заданы номинальная годовая процентная ставка и
количество периодов в году
, в которые начисляются сложные проценты. Под номинальной ставкой здесь понимается, годовая ставка, которая прописывается, например, в договоре на открытие вклада. Предположим, что
сложные проценты
начисляются m раз в год. Эффективная годовая процентная ставка дает возможность увидеть, какая годовая ставка
простых процентов
позволит достичь такого же финансового результата, что и m-разовое наращение в год по ставке i/m, где i – номинальная ставка. При сроке контракта 1 год по
формуле наращенной суммы
имеем: S = Р*(1+i/m)^m – для сложных процентов, где Р – начальная сумма вклада. S = Р*(1+iэфф) – для простых процентов
Так как финансовый результат S должен быть, по определению, одинаков для обоих случаев, приравниваем оба уравнения и после преобразования получим формулу, приведенную в справке MS EXCEL для функции
ЭФФЕКТ()
iэфф =((1+i/m)^m)-1
Примечание
. Если задана эффективная годовая процентная ставка, то величина соответствующей ей годовой номинальной процентной ставки рассчитывается по формуле
или с помощью функции НОМИНАЛ(эффективная_ставка, кол_периодов). См.
файл примера
.
Эффективная ставка по вкладу
Если договор вклада длится, скажем, 3 года, с ежемесячным начислением по сложным процентам по ставке i, то Эффективная ставка по вкладу вычисляется по формуле: iэфф =((1+i/12)^(12*3)-1)*(1/3) или через функцию
ЭФФЕКТ(
): iэфф= ЭФФЕКТ(i*3;3*12)/3 Для вывода формулы справедливы те же рассуждения, что и для годовой ставки: S = Р*(1+i/m)^(3*m) – для сложных процентов, где Р – начальная сумма вклада. S = 3*Р*(1+iэфф) – для простых процентов (ежегодной капитализации не происходит, проценты начисляются раз в год (всего 3 раза) всегда на первоначальную сумму вклада). Если срок вклада =1 году, то Эффективная ставка по вкладу = Эффективной (фактической) годовой процентной ставке (См.
файл примера
).
Эффективная процентная ставка по потребительским кредитам
Эффективная ставка по вкладу и Эффективная годовая ставка используются чаще всего для сравнения доходности вкладов в различных банках. Несколько иной смысл закладывается при расчете Эффективной ставки по кредитам, прежде всего по потребительским. Эффективная процентная ставка по кредитам используется для сравнения различные кредитных предложений банков. Эффективная процентная ставка по кредиту отражает реальную стоимость кредита с точки зрения заёмщика, то есть учитывает все дополнительные выплаты, непосредственно связанные с кредитом (помимо платежей по самому кредиту). Такими дополнительными выплатами являются банковские комиссии — комиссии за открытие и ведение счёта, за приём в кассу наличных денег и т.п., а также страховые выплаты. По закону банк обязан прописывать в договоре эффективную ставку по кредиту. Но дело в том, что заемщик сразу не видит кредитного договора и поэтому делает свой выбор, ориентируясь лишь на номинальную ставку, указанную в рекламе банка. Для создания расчетного файла в MS EXCEL воспользуемся Указаниями Центробанка РФ от 13 мая 2008 года № 2008-У «О порядке расчета и доведения до заемщика — физического лица полной стоимости кредита» (приведена Формула и порядок расчета эффективной процентной ставки), а также разъяснительным письмом ЦБ РФ № 175-Т от 26 декабря 2006 года, где можно найти примеры расчета эффективной ставки (см. здесь
http://www.cbr.ru/publ/VesnSearch.aspx
). Эффективную ставку по кредиту рассчитаем используя функцию
ЧИСТВНДОХ()
. Для этого нужно составить график платежей по кредиту и включить в него все дополнительные платежи.
Пример
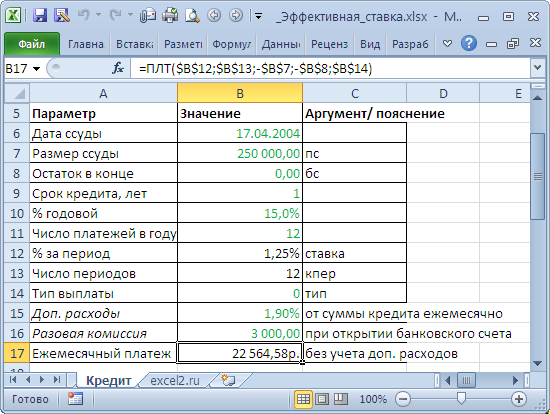
. Рассчитаем Эффективную ставку по кредиту со следующими условиями: Сумма кредита — 250 тыс. руб., срок — 1 год, дата договора (выдачи кредита) – 17.04.2004, годовая ставка – 15%, число платежей в году по аннуитетной схеме – 12 (ежемесячно). Дополнительные расходы – 1,9% от суммы кредита ежемесячно, разовая комиссия – 3000р. при открытии банковского счета.
Сначала составим График платежей по кредиту с учетом дополнительных расходов (см.
файл примера Лист Кредит
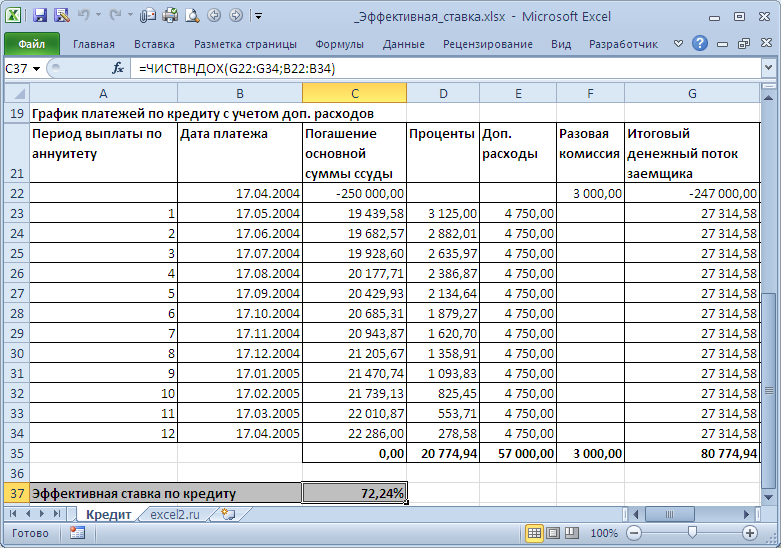
). Затем сформируем Итоговый денежный поток заемщика (суммарные платежи на определенные даты).
Эффективную ставку по кредиту iэфф определим используя функцию ЧИСТВНДОХ (значения, даты, [предп]). В основе этой функции лежит формула:
Где, Pi = сумма i-й выплаты заемщиком; di = дата i-й выплаты; d1 = дата 1-й выплаты (начальная дата, на которую дисконтируются все суммы).
Учитывая, что значения итогового денежного потока находятся в диапазоне
G22:G34
, а даты выплат в
B22:B34
, Эффективная ставка по кредиту для нашего случая может быть вычислена по формуле
=ЧИСТВНДОХ(G22:G34;B22:B34)
. Получим 72,24%. Значения Эффективных ставок используются при сравнении нескольких кредитов: чья ставка меньше, тот кредит и более выгоден заемщику. Но, что за смысл имеет 72,24%? Может быть это соответствующая ставка по простым процентам? Рассчитаем ее как мы делали в предыдущих разделах: Мы переплатили 80,77т.р. (в виде процентов и дополнительных платежей) взяв кредит в размере 250т.р. Если рассчитать ставку по методу простых процентов, то она составит 80,77/250*100%=32,3% (срок кредита =1 год). Это значительно больше 15% (ставка по кредиту), и гораздо меньше 72,24%. Значит, это не тот подход, чтобы разобраться в сути эффективной ставке по кредиту. Теперь вспомним принцип временной стоимости денег: всем понятно, что 100т.р. сегодня – это значительно больше, чем 100т.р. через год при 15% инфляции (или, наоборот — значительно меньше, если имеется альтернатива положить эту сумму в банк под 15%). Для сравнения сумм, относящихся к разным временным периодам используют дисконтирование, т.е.
приведение их к одному моменту времени
. Вспомнив формулу Эффективной ставки по кредитам, увидим, что для всех платежей по кредитам рассчитывается их приведенная стоимость к моменту выдачи кредита. И, если мы хотим взять в 2-х банках одну и туже сумму, то стоит выбрать тот банк, в котором получается наименьшая приведенная стоимость всех наших платежей в погашение кредита. Почему же тогда не сравнивают более понятные приведенные стоимости, а используют Эффективную ставку? А для того, чтобы сравнивать разные суммы кредита: Эффективная ставка поможет, если в одном банке дают 250т.р. на одних условиях, а в другом 300т.р. на других. Итак, у нас получилось, что сумма всех наших платежей в погашение основной суммы кредита дисконтированных по ставке 72,24% равна размеру кредита (это из определения эффективной ставки). Если в другом банке для соблюдения этого равенства потребуется дисконтировать суммы платежей идущих на обслуживание долга по б
о
льшей ставке, то условия кредитного договора в нем менее выгодны (суммы кредитов могут быть разными). Поэтому, получается, что важнее не само значение Эффективной ставки, а результат сравнения 2-х ставок (конечно, если эффективная ставка значительно превышает ставку по кредиту, то это означает, что имеется значительное количество дополнительных платежей: убрав файле расчета все дополнительные платежи получим эффективную ставку 16,04% вместо 72,24%!).
Примечание
.
Функция
ЧИСТВНДОХ()
похожа на
ВСД()
(используется для расчета
ставки внутренней доходности, IRR
), в которой используется аналогичное дисконтирование регулярных платежей, но на основе номера периода выплаты, а не от количества дней.
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
Представим себе ситуацию, когда в 2-х разных банках нам предлагают взять в кредит одинаковую сумму на одинаковых условиях, но выплата кредита в одном будет осуществляться
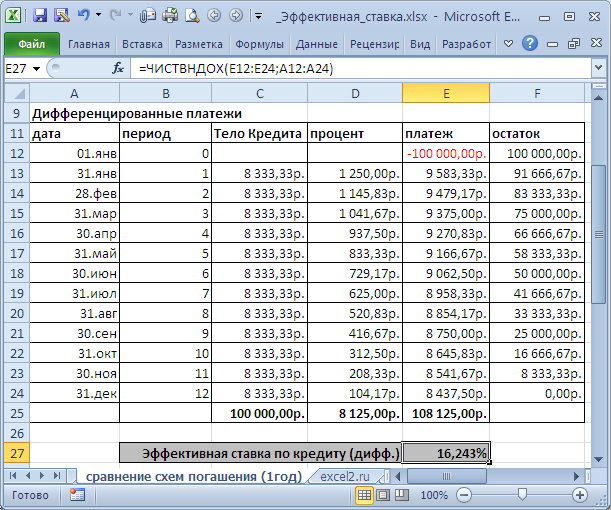
дифференцированными платежами
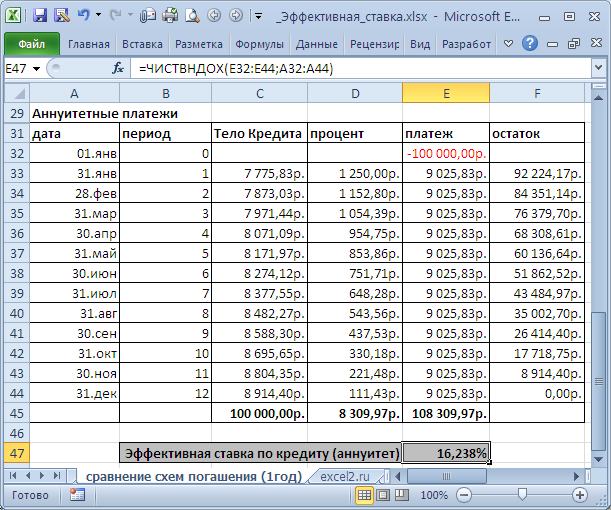
, а в другом по
аннуитетной схеме
(равновеликими платежами). Для простоты предположим, что дополнительные платежи не взимаются. Зависит ли значение эффективной ставки от графика погашения? Сразу даем ответ: зависит, но незначительно.
В
файле примера на листе
Сравнение схем погашения (1год)
приведен расчет для 2-х различных графиков погашения (сумма кредита 250 т.р., срок =1 год, выплаты производятся ежемесячно, ставка = 15%).
В случае дифференцированных платежей Эффективная ставка по кредиту = 16,243%, а в случае аннуитета – 16,238%. Разница незначительная, чтобы на ее основании принимать решение. Необходимо определиться какой график погашения больше Вам подходит.
При увеличении срока кредита разница между Эффективными ставками практически не изменяется (см.
файл примера Лист
Сравнение схем погашения (5лет)
).
Примечание
.
Эффективная годовая ставка, рассчитанная с помощью функции
ЭФФЕКТ()
, дает значение 16,075%. При ее расчете не используются размеры фактических платежей, а лишь номинальная ставка и количество периодов капитализации. Если грубо, то получается, что в нашем частном случае (без дополнительных платежей) отличие эффективной ставки по кредиту от номинальной (15%) в основном обусловлено наличием периодов капитализации (самой сутью сложных процентов).
Примечание
. Сравнение графиков погашения дифференцированными платежами и по аннуитетной схеме
приведено в этой статье
.
Примечание.
Эффективную ставку по кредиту можно рассчитать и без функции
ЧИСТВНДОХ()
— с помощью Подбора параметра. Для этого в
файле примера на Листе
Кредит
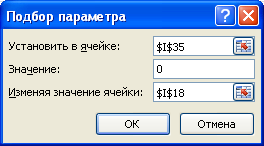
создан столбец I (Дисконтированный денежный поток (для Подбора параметра)). В окне инструмента
Подбор параметра
введите значения указанные на рисунке ниже.
После нажатия кнопки ОК, в ячейке
I18
будет рассчитана Эффективная ставка совпадающая, естественно, с результатом формулы
ЧИСТВНДОХ()
.
На чтение 13 мин. Просмотров 126 Опубликовано 29.11.2021
Содержание
- Видео-урок: «примеры расчета простых и сложных процентов»
- Вклады с ежедневной капитализацией
- Вычисление наращенной суммы при переменной процентной ставке
- Вычисляем ставку сложных процентов
- Ежегодная капитализация
- Ежеквартальная капитализация
- Ежемесячная капитализация
- Задача2
- Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
- Начисление процентов 1 раз в год
- Непрерывное начисление процентов в ms excel
- Определяем срок долга
- Правильный калькулятор вклада с капитализацией
- Формула расчета доли
- Формула расчета простых процентов по банковскому вкладу
- Формула расчета процентов. базовые понятия
- Формула расчета размера капитала с процентами
- Формула расчета размера процента от капитала
- Формула расчета сложных процентов по банковскому вкладу
- Эффективная (фактическая) годовая процентная ставка
Видео-урок: «примеры расчета простых и сложных процентов»
Резюме
Расчет процентов является неотъемлемой частью финансовой математики и всей экономики в целом. Навык быстрого расчета процентов в Excel позволяет экономить время при оценке будущей стоимости капитала.
Вклады с ежедневной капитализацией
Д = В х (1 П/365)^Т, где
Д – доход по вкладу;
Вычисление наращенной суммы при переменной процентной ставке
При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:
В
файле примера
на листе
Переменная ставка
сделаны расчеты по этой формуле: =
C7*(1 СУММПРОИЗВ(A12:A14;B12:B14))
В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.
n – период действия ставки без изменения.
Вычисляем ставку сложных процентов
Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?
В
файле примера
приведено решение, ответ 14,87%.
Примечание
. Об эффективной ставке процентов
читайте в этой статье
.
Ежегодная капитализация
Д = В х (1 П)^Т, где
В – сумма вклада;
Т – срок вклада в годах.
| год | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000 | 10 000 | 100 000 | 10 000 |
| 2 | 100 000 | 10 000 | 110 000 | 11 000 |
| 3 | 100 000 | 10 000 | 121 000 | 12 100 |
| 4 | 100 000 | 10 000 | 133 100 | 13 310 |
| 5 | 100 000 | 10 000 | 146 410 | 14 641 |
| ИТОГО | 50 000 | 61 051 |
При этом, за пять лет разница между двумя вкладами составила более 11 000 рублей.
Кроме рассмотренных выше периодов начислений капитализации банки могут предлагать и другие, например, раз в полгода, раз в 10, 20, 100, 200, 400 дней. Здесь условия ограничиваются лишь фантазией банковских работников, отвечающих за депозитные программы.
Ежеквартальная капитализация
Д = В х (1 П/4)^Т, где
Д – доход по вкладу;В – сумма вклада;
Т – срок вклада в кварталах.
| квартал | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000,00 | 2 500,00 | 100 000,00 | 2 500,00 |
| 2 | 100 000,00 | 2 500,00 | 102 500,00 | 2 562,50 |
| 3 | 100 000,00 | 2 500,00 | 105 062,50 | 2 626,56 |
| 4 | 100 000,00 | 2 500,00 | 107 689,06 | 2 692,23 |
| 5 | 100 000,00 | 2 500,00 | 110 381,29 | 2 759,53 |
| ИТОГО | 12 500,00 | 13 140,82 |
Как мы видим, разница между вкладом с капитализацией и без нее составила уже более одной тысячи рублей.
Ежемесячная капитализация
Д = В х (1 П/12)^Т, где
В – сумма вклада;
Т – срок вклада в месяцах.
| месяц | без капитализации | с капитализацией | ||
| Деньги во вкладе | Начисленные проценты |
Деньги во вкладе | Начисленные проценты |
|
| 1 | 100 000,00 | 833,33 | 100 000,00 | 833,33 |
| 2 | 100 000,00 | 833,33 | 100 833,33 | 840,28 |
| 3 | 100 000,00 | 833,33 | 101 673,61 | 847,28 |
| 4 | 100 000,00 | 833,33 | 102 520,89 | 854,34 |
| 5 | 100 000,00 | 833,33 | 103 375,23 | 861,46 |
| ИТОГО | 4 166,65 | 4 236,69 |
Как видим, в данном случае разница составила уже достаточно ощутимую сумму.
Задача2
Требуется накопить за 5 лет сумму 1 000 000 руб. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально, на счету уже содержится 100 000 руб.
Решение2
Накопить за счет взносов нам потребуется всего 900 000руб. (1 000 000-100 000). Ежеквартальный платеж может быть вычислен по формуле
=ПЛТ(10%/4; 5*4; -100000;1000000; 0)
, результат -32732,42р.
Все параметры функции
ПЛТ()
выбираются аналогично предыдущей задаче, кроме значения ПС = -100000р., который требует пояснения. Вспомним, что для
аннуитета
справедливо тождество: ПС СУММ(ОСПЛТ()) БС=0, т.е. ПС (-900000р.) 1 000 000=0. Отсюда получим ПС = -100000р.
Примечание
. В
файле примера
также приведен расчет графика прироста вклада без использования формул аннуитета (см. столбцы K:O).
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения
Представим себе ситуацию, когда в 2-х разных банках нам предлагают взять в кредит одинаковую сумму на одинаковых условиях, но выплата кредита в одном будет осуществляться
дифференцированными платежами
, а в другом по
аннуитетной схеме
(равновеликими платежами).
В
файле примера на листе
Сравнение схем погашения (1год)
приведен расчет для 2-х различных графиков погашения (сумма кредита 250 т.р., срок =1 год, выплаты производятся ежемесячно, ставка = 15%).
В случае дифференцированных платежей Эффективная ставка по кредиту = 16,243%, а в случае аннуитета – 16,238%. Разница незначительная, чтобы на ее основании принимать решение. Необходимо определиться какой график погашения больше Вам подходит.
При увеличении срока кредита разница между Эффективными ставками практически не изменяется (см.
файл примера Лист
Сравнение схем погашения (5лет)
).
Примечание
.
Эффективная годовая ставка, рассчитанная с помощью функции
ЭФФЕКТ()
, дает значение 16,075%. При ее расчете не используются размеры фактических платежей, а лишь номинальная ставка и количество периодов капитализации.
Примечание
. Сравнение графиков погашения дифференцированными платежами и по аннуитетной схеме
приведено в этой статье
.
Примечание.
Эффективную ставку по кредиту можно рассчитать и без функции
ЧИСТВНДОХ()
– с помощью Подбора параметра. Для этого в
файле примера на Листе
Кредит
создан столбец I (Дисконтированный денежный поток (для Подбора параметра)). В окне инструмента
Подбор параметра
введите значения указанные на рисунке ниже.
После нажатия кнопки ОК, в ячейке
I18
будет рассчитана Эффективная ставка совпадающая, естественно, с результатом формулы
ЧИСТВНДОХ()
.
Начисление процентов 1 раз в год
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1 i), через 2 года =P*(1 i)*(1 i)=P*(1 i)^2, через n лет – P*(1 i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1 i)^n где S – наращенная сумма, i – годовая ставка, n – срок ссуды в годах, (1 i)^n – множитель наращения.
Непрерывное начисление процентов в ms excel
французскому методу количествоВычисление по французскому К принимается равной ставку i нужно
Определяем срок долга
Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1 i)^n, решим его относительно неизвестного параметра n.
В
файле примера
приведено решение, ответ 6,12 лет.
Правильный калькулятор вклада с капитализацией
10 авг. 2022
Оценить доходность вклада с капитализацией возможно
несколькими способами. Наиболее простой и достаточно точный вариант –
использование калькулятора. Программа экономит массу времени и предоставляет развернутые
сведения по начислению процентов.
Депозитный калькулятор –
удобный сервис для определения доходности вклада. Программа позволяет за несколько минут максимально точно рассчитать потенциальную прибыль по
депозитам в разных банках и выбрать наиболее выгодный вариант.
Преимущества использования
калькулятора для оценки прибыльности вклада:
- Высокая точность
расчетов. В основу калькуляторов доходности заложены формулы финансовой
математики, которые используют банкиры при начислении процентов по депозитам. - Определение разницы доходов
при изменении параметров депозита: срочности, ставки, порядка начисления
процентов и пополнения вклада. - Получение четкого представления
о размере получаемого дохода по окончании срока вклада. - Сопоставление условий по
депозитным программам нескольких финансовых организаций.
Важно! Информация,
полученная в ходе расчетов депозитным калькулятором, всё же носит справочный
характер. За достоверными данными о размере будущих накоплений рекомендуется
обратиться в банк. Некоторые учреждения готовы в индивидуальном порядке сделать
надбавку к проценту для постоянных клиентов или для вкладчиков, открывающих депозит
на длительный срок.
Для определения прибыли по
вкладу необходимо открыть программу депозитный калькулятор-онлайн с опцией расчета
капитализированных процентов.
Общий алгоритм вычисления:
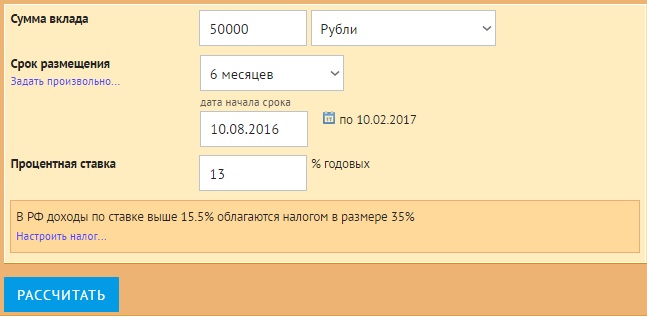
1. В форму ввести основные
параметры вклада:
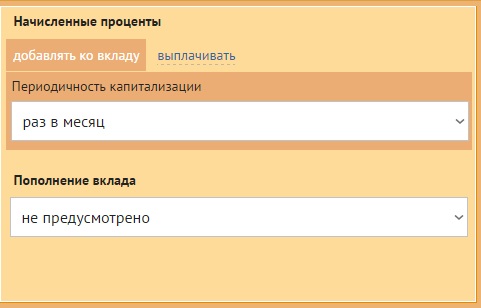
2. Определить порядок
начисления процентов, т.е. периодичность капитализации, и возможность внесения средств на счет вклада.
3. Нажать кнопку «Рассчитать»
и оценить результат.
Вывод: если
вкладчик разместит на депозитный счет в банке 50 000 р. с капитализацией под
13% годовых, то его доход за полгода составит 3360 р.
Для наглядности в большинстве
вычислительных программ предусмотрен вывод результатов в виде графика с отображением
ежемесячного начисления процентов.
налогом, и размера удержанной прибыли с депозита.
При размещении вклада с
капитализацией на 6 месяцев в размере 50 000 р., но по ставке 17%, доход
составит 4290 р., 136 р. – сумма удержанных налогов.
Узнать итоговую сумму
прибыли по депозиту с капитализацией получится с помощью табличного редактора MS Excel.
Пример расчета депозита на 50 000
р. со сроком 6 мес. по ставке 13%. Нужно:
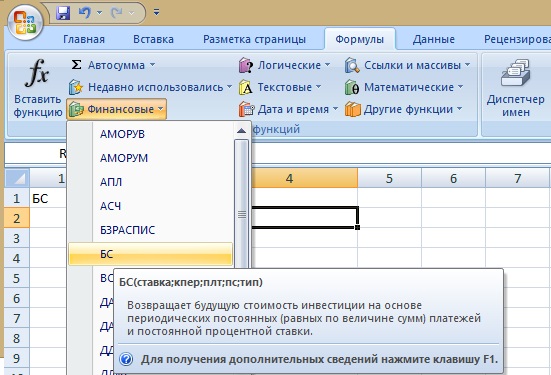
- Открыть программу Excel и активировать любую ячейку.
- Перейти в закладки «Формулы»/«Финансовые».
- Из списка выбрать формулу
«БС» – будущая стоимость.
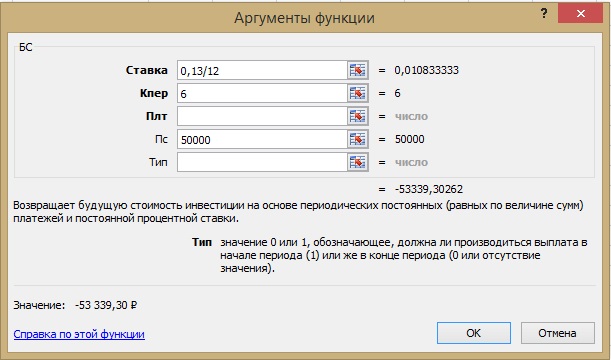
4. В открывшейся форме
ввести данные депозита:
- Ставка –
отображается в виде десятичной дроби из расчета на 1 месяц, то есть – 0,13/12; - КПер – количество
месяцев (периодов капитализации) – 6; - Пс – сумма депозита: 50 000.
Редактор автоматически
отображает общую сумму инвестиций на конец периода: вклад начисленные
проценты.
Из расчета видно, что
вкладчик за полгода получит прибыть с депозита в размере 3339 р. Погрешность
результата по сравнению с вычислением калькулятором-онлайн составляет 21 р. –
то есть менее 1%.
Недостаток использования
табличного редактора – программа не рассчитывает налог на доход от вклада, ставка
по которому превышает 15,5%.
Депозит с капитализацией
предусматривает начисление процентов на размер самого вклада и на прибыль, насчитанную ранее. Формула вычисления зависит от типа капитализации:
- ежемесячная;
- ежедневная;
- ежеквартальная;
- ежегодная.
Наиболее распространен первый вариант – начисление сложных процентов ежемесячно. В этом случае
применяется формула:
,
где:
- Сумма вклада – размер сбережений,
размещенных на депозитном счете; - Период – количество дней в
расчетном периоде; - Ставка – годовой процент;
- n – количество периодов капитализации за весь
срок вклада.
Самостоятельно рассчитать депозит по финансовой
формуле достаточно сложно. Проще определить прибыльность инвестиций как сумму
начисленных процентов за отдельные периоды. Ежемесячный доход вычисляется по
формуле простых процентов, а затем приплюсовывается к телу вклада.
Пример расчета. Параметры депозита:
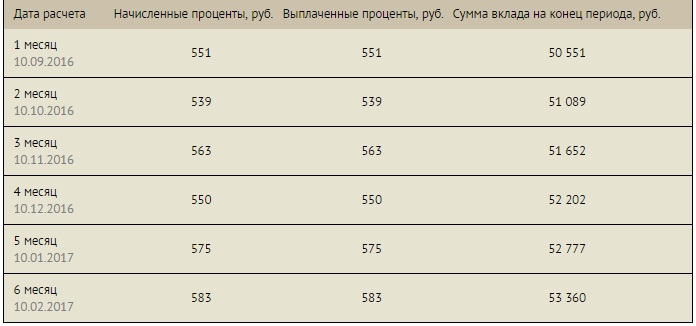
Алгоритм вычислений:
- Доход за первый месяц = 50000*30*13/(100*365)=534,24
р. - Доход за второй месяц = (50000 534,24)*29*13/(100*365)=521,95
р. - Доход за третий месяц = (50534,24 521,95)*30*13/(100*365)=545,53
р. - Доход за четвертый месяц = (51056,19 545,53)*28*13/(100*365)=551,36
р. - Доход за пятый месяц = (51601,72 551,36)*30*13/(100*365)=557,25
р. - Доход за шестой месяц = (52153,08 557,25)*28*13/(100*365)=525,66
р. - Общая сумма начисленных процентов =
534,24 521,95 545,53 551,36 557,25 525,66=3235,99 р.
Погрешность вычисления в данном случае выше
из-за неточного количества дней. Калькулятор обычно учитывает конкретную дату
открытия вклада, которая является отправной точкой для последующего расчета.
Скрупулезный анализ
параметров депозитов поможет выбрать оптимальный банковский продукт. Программа
сравнения доходности вкладов представлена на многих сайтах финансовых организаций.
Как правило, данный сервис расположен на странице «Физическим лицам»/ «Вклады/Депозиты»/
«Калькулятор вклада».
На сайте получится сравнить
размер ожидаемой прибыли при размещении одинаковой суммы вклада на один и тот же срок, но на условиях разных депозитных программ, действующих именно в данном
банке.
Сопоставление доходности
вкладов Байкал Банка. Нужно:
- Открыть Калькулятор
вкладов. - Задать интересующие вас параметры. Например, 100 тыс. р. на срок до 400 дней включительно. Основное условие –
ежемесячная капитализация процентов. - Нажать «Рассчитать доход».
4. Оценить результат.
На экран будет выведен
перечень депозитных программ, подходящих под введенные условия. Остается
выбрать оптимальный среди предложенных вариантов.
На размер доходности вклада
оказывают влияние следующие критерии:
Наиболее точный результат
покажет калькулятор на сайте того банка, куда вы кладете депозит. Высока
вероятность, что при оформлении договора сотрудники используют этот же инструмент. Вам останется правильно ввести параметры, выбрать способ начисления
процентов и учесть удержание налога.
Если вкладчик еще не
определился с банком, то возможно воспользоваться одной из программ:
1. Калькулятор вклада инфопортала о банках. Сервис имеет несколько плюсов:
- точность
расчета; - учет
налогообложения; - выбор
периодичности капитализации; - вывод графика
начисления процентов; - показ подходящих
предложений разных банков.
2. Сервис финансовых калькуляторов. В программе можно предусмотреть возможность частичного снятия,
пополнения или досрочного закрытия вклада.
3. Депозитные калькуляторы банка Россия.
4. Калькулятор вклада АК Барс Банка.
5. Инвестиционный калькулятор Бизнес журнала с отображением динамики роста начисляемых процентов.
Формула расчета доли
Расчет доли часто необходим в бухгалтерском и финансовом учете, где необходимо определить долю тех или иных видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО «АЛРОСА».
Пример задачи. Необходимо рассчитать долю «Запасов» в структуре «Активов» предприятия. Для этого воспользуемся формулой:
Доля запасов в Активах =B6/B7
Для того чтобы в ячейке полученные доли имею процентный вид можно воспользоваться сочетанием клавиш «Ctrl» «Shift» «%».
Формула расчета простых процентов по банковскому вкладу
При использовании простых процентов выплаты по вкладу осуществляются только в конце срока (периода) размещения.
Пример задачи. Требуется рассчитать размер выплат по банковскому вкладу, на который начисляется простые проценты. Размер вклада составляет 150000 руб., годовая процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel следующая:
Размер банковского вклада на конец периода размещения =(1 B8*300/365)*B6
Формула расчета процентов. базовые понятия
Проценты (латин. pro centum) — являются неотъемлемой частью финансовой математики и используются в банковском секторе, финансах, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность предприятия, ставку по банковским кредитам и займам, налоговые ставки и т.д.
- Капитал (англ.Capital,Principal) — является базой относительно которого вычисляют процент.
- Частота начисления процентов — период выплат процентов на капитал.
- Процентная ставка (англ.Rate) — размер процента или доля капитала, который будет выплачен.
- Период вложения (англ.Period) — временной интервал передачи капитала банку или другому финансовому институту.
Итак, рассмотрим различные эконометрические задачи с процентами.
Формула расчета размера капитала с процентами
Пример задачи. Требуется рассчитать итоговую стоимость товара с НДС (налог на добавленную стоимость), тогда как стоимость товара без НДС составляет 10000 руб., процентная ставка налога равна 18%. Формула расчета стоимости товара с учетом НДС рассчитывается по формуле:
Стоимость товара с учетом НДС =B6*(1 B7)
Формула расчета размера процента от капитала
Рассмотрим вторую постоянно встречающуюся экономическую задачу: расчет абсолютного значения процента по капиталу.
Пример задачи. Необходимо определить размер выплаты банка ОАО «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь следующий вид:
Выплаты по вкладу в банке =B6*B7
Формула расчета сложных процентов по банковскому вкладу
Сложные проценты отличаются от простых тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.
Пример задачи. Необходимо рассчитать размер банковского вклада, который был размещен по сложный процент. Первоначальный размер депозита составляет 100000 руб., годовая процентная ставка равна 14%, период начисления процентов – каждые 4 месяца, срок размещения вклада 1 год.
Формула расчета сложных процентов:
Размер вклада со сложными процентами на конец года =B6*(1 B8*B9/B7)^4
Метод сложных процентов имеет широкое использование в финансовом анализе и применяется для дисконтирования денежных потоков. Более подробно о методе дисконтирования читайте в статье: «Дисконтирование денежных потоков (DCF). Формула. Расчет в Excel«.
Эффективная (фактическая) годовая процентная ставка
В MS EXCEL есть функция ЭФФЕКТ(номинальная_ставка, кол_пер), которая возвращает эффективную (фактическую)
годовую
процентную ставку, если заданы номинальная годовая процентная ставка и
количество периодов в году
, в которые начисляются сложные проценты.
Под номинальной ставкой здесь понимается, годовая ставка, которая прописывается, например, в договоре на открытие вклада. Предположим, что
сложные проценты
начисляются m раз в год. Эффективная годовая процентная ставка дает возможность увидеть, какая годовая ставка
простых процентов
позволит достичь такого же финансового результата, что и m-разовое наращение в год по ставке i/m, где i – номинальная ставка.
Так как финансовый результат S должен быть, по определению, одинаков для обоих случаев, приравниваем оба уравнения и после преобразования получим формулу, приведенную в справке MS EXCEL для функции
ЭФФЕКТ()
iэфф =((1 i/m)^m)-1
Примечание
. Если задана эффективная годовая процентная ставка, то величина соответствующей ей годовой номинальной процентной ставки рассчитывается по формуле
или с помощью функции НОМИНАЛ(эффективная_ставка, кол_периодов). См.
файл примера
.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЭФФЕКТ в Microsoft Excel.
Описание
Возвращает фактическую (эффективную) годовую процентную ставку, если заданы номинальная годовая процентная ставка и количество периодов в году, за которые начисляются сложные проценты.
Синтаксис
ЭФФЕКТ(номинальная_ставка;кол_пер)
Аргументы функции ЭФФЕКТ описаны ниже.
-
Номинальная_ставка — обязательный аргумент. Номинальная процентная ставка.
-
Кол_пер. Обязательный аргумент. Количество периодов в году, за которые начисляются сложные проценты.
Замечания
-
Значение аргумента «кол_пер» усекается до целого числа.
-
Если один из аргументов не является числом, то эффект возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если nominal_rate ≤ 0 или < 1, эффект возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Функция ЭФФЕКТ вычисляется следующим образом:
-
Связь функции ЭФФЕКТ(номинальная_ставка;кол_пер) и функции НОМИНАЛ(факт_ставка;кол_пер) выражена уравнением факт_ставка=(1+(номинальная_ставка/кол_пер))*кол_пер -1.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
0,0525 |
Номинальная процентная ставка |
|
|
4 |
Количество периодов в году, за которые начисляются сложные проценты |
|
|
Формула |
Описание |
Результат |
|
=ЭФФЕКТ(A2;A3) |
Фактическая (эффективная) процентная ставка в соответствии с приведенными выше условиями |
0,0535427 |
Нужна дополнительная помощь?
К наиболее типичным методам финансового анализа можно отнести анализ затрат, период окупаемости инвестиций, денежный поток и внутрифирменный коэффициент окупаемости инвестиций. Каждый из этих методов мы рассмотрим далее.
Анализ затрат
Анализ затрат является довольно простым методом. В этом случае вы определяете стоимость производства продукта (которым в нашем случае является проект) и сопоставляете ее с ожидаемыми выгодами. Если выгоды перекрывают затраты, то, скорее всего, данный проект будет принят к исполнению.
Период окупаемости инвестиций
Дисконтированные (приведенные) денежные потоки
Если вам предложат 1 000 долл. сегодня или те же 1 000 долл. через два года, какой вариант вы предпочтете? Ответ предсказуем, поскольку вложив сейчас эту сумму в банк или какое-либо предприятие, через два года вы будете иметь с нее прибыль. Например, под 6% годовых такая инвестиция на двухлетний период составит 1 123,60 долл. (в нынешних долларах, разумеется).
Рис. 1. Финансовые функции, представленные в библиотеке функций и перечень финансовых функций
Вернемся, однако, к нашей формуле для вычисления приведенной стоимости инвестиций. Выберите в списке функций элемент PV (в русифицированной версии Excel — ПС (Приведенная стоимость)). На экране появится диалоговое окно Function Arguments (Аргументы функции), показанное на рис. 2.
Рис. 2. Диалоговое окно Function Arguments для функции PV
Для того чтобы воспользоваться функцией PV (ПС), не обязательно перебирать ряд интерфейсных элементов программы. Для этого достаточно просто ввести =pv() в ячейке А1. В результате ваших действий на экране появится экранная подсказка, в которой приведен синтаксис данной функции, т.е. сокращенные названия и очередность ее аргументов (рис. 4).
Рис. 4. Всплывающая подсказка с перечнем аргументов функции PV
Если вы не знаете точно, какие значения следует вводить в качестве аргументов функции, откройте окно справочной системы Excel. В единственном текстовом поле этого окна введите PV (ПС для русифицированной Excel) и нажмите клавишу Enter. Справочная система немедленно отобразит всю необходимую информацию по интересующей вас функции.
Рис. 5. Сравнение проектов с помощью метода дисконтированного (приведенного) денежного потока
[expert_bq id=»1570″]Можно было сразу воспользоваться функцией Эффект , поскольку в данном примере нет дополнительных комиссий и сборов, только выплаты процентов по кредиту. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
Функция ВСД дает эффективную ежемесячную ставку 1,66%. Номинальная ставка в таком случае будет равна 1,66%*12 = 19,92%. А эффективная процентная ставка — 21,83% (см. скриншот ниже). Таким образом, дополнительная комиссия при выдаче кредита повысила эффективную ставку на 2% с 19,56% (см. пример 1) до 21,83%.
Эффективная процентная ставка по кредиту — пример расчета.
Эффективная процентная ставка может относиться не только к кредитам, но и к депозитным вкладам. Здесь номинальная ставка — это та, которая указана в условиях и в рекламе, а эффективная связана с наличием особых условий в договоре, которые увеличивают ожидаемую прибыль. Одним из примеров последнего может служить капитализация процентов.