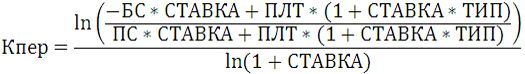Определение срока платежа в excel

Функция КПЕР в Excel предназначена для расчета количества периодов выплат погашения определенной суммы задолженности при известных значениях процентной ставки (простые проценты), суммы платежа для каждого периода (фиксированное значение), начальной суммы задолженности или общей суммы долга с учетом процентов, и возвращает соответствующее числовое значение.

Примеры как использовать функцию КПЕР в Excel

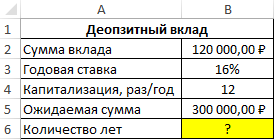
Пример 1. Вкладчик внес депозит под 16% годовых на сумму 120000 рублей с ежемесячной капитализацией вклада (простые проценты). Сколько лет потребуется для накопления 300000 рублей?

Исходные данные:

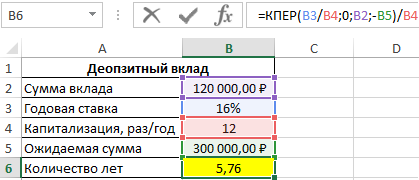
Формула для расчета:

=КПЕР(B3/B4;0;B2;-B5)/B4

Описание аргументов:

• B3/B4 – процентная ставка за период капитализации;
• 0 – числовое значение, характеризующее ежемесячный платеж (дополнительное пополнение депозитного счета не производится);
• B2 – начальная инвестиция;
• -B5 – конечная сумма по окончанию договора.

Возвращенный функцией КПЕР результат разделен на количество периодов капитализации в году для расчета числа лет, необходимых для накопления требуемой суммы. Результат расчетов:

Вкладчик должен оставлять деньги на депозитном счете на протяжении почти 6 лет.



Расчет реальной суммы долга с процентами и переплатой в Excel

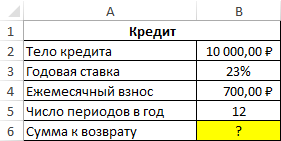
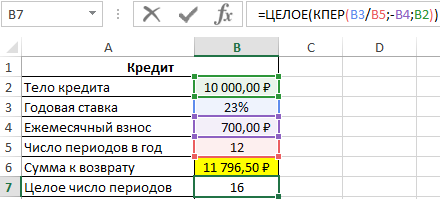
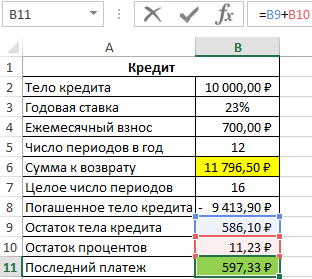
Пример 2. Клиенту банка был выдан кредит на сумму 10000 рублей под 23% годовых с ежемесячной оплатой 700 рублей. Сколько всего денег получит банк по окончанию срока кредитного договора?

Исходные данные:

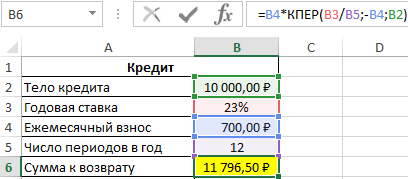
Формула для расчета:

=B4*КПЕР(B3/B5;-B4;B2)

Общая сумма кредита рассчитывается как произведение фиксированной суммы ежемесячного платежа и количества периодов выплат. В данном случае количество периодов равно 16,85 (нецелое число), значит, последняя выплата должна составить меньше 700 рублей. Найдем целое число периодов:

=ЦЕЛОЕ(КПЕР(B3/B5;-B4;B2))

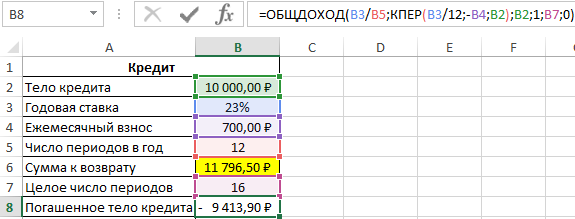
Чтобы определить, какую часть тела кредита было погашено за 16 целых периодов выплат, воспользуемся следующей функцией:

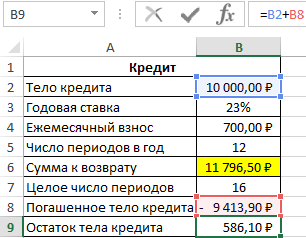
За последний неполный период необходимо вернуть следующую часть тела кредита:

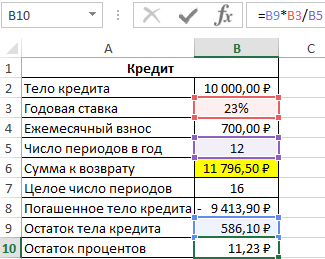
Рассчитаем оставшиеся проценты к уплате:

Так как платеж включает в себя оплату тела кредита и процентов, насчитанных за период, определим размер последнего платежа по формуле:

Общая сумма, которую получит банк, составит 11796 рублей, а размер последнего платежа – 597 рублей.

Расчет сроков погашения кредита с помощью функции КПЕР

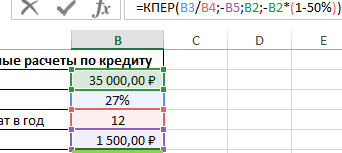
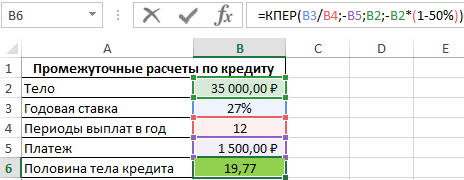
Пример 3. Банк выдал кредит на сумму 35000 рублей под 27% годовых. Размер ежемесячного платежа составляет 1500 рублей. Через сколько месяцев клиент выплатить 50% кредита?

Исходная таблица данных:

На основании тождества аннуитетных платежей (сумма величины платежа в погашение тела кредита за все периоды, тела кредита и будущей стоимости равна нулю, то есть ОБЩДОХОД+ПС+БС=0) используем следующую формулу:

=КПЕР(B3/B4;-B5;B2;-B2*(1-50%))

Выражение -B2*(1-50%)) характеризует будущую стоимость и было получено из уравнения:

-35000*50%+35000=-БС

Результат расчета:

Для выплаты 50% кредита потребуется вносить ежемесячный платеж на протяжении примерно 20 месяцев.

Особенности использования функции КПЕР в Excel

Функция КПЕР используется для решения финансовых задач совместно с функциями ПЛТ, БС, СТАВКА, ПС и имеет следующую синтаксическую запись:

=КПЕР(ставка;плт;пс;[бс];[тип])

Описание аргументов (первые три аргумента – обязательные для заполнения):

• ставка – числовое значение, характеризующее ставку за 1 период выплат (для ссуд) или капитализации (для депозитных вкладов). Аргумент может быть указан в виде дробного числа или в качестве значения в процентном формате (например, 14,5% или 0,145 – эквивалентные варианты записи). Если в условии задачи указана годовая ставка, необходимо выполнить пересчет по формуле Rп=Rг/12, где Rп – ставка за период, Rg – годовая ставка, 12 – число месяцев в году.
• плт – числовое значение, соответствующее сумме выплаты за период, которая является фиксированной величиной (простые проценты).
• пс – числовое значение, характеризующее текущую стоимость инвестиции (например, сумма, выданная кредитной организацией в долг клиенту, или сумма средств, положенных на депозитный счет в банк).
• [бс] – числовое значение, соответствующее будущей стоимости инвестиции. Например, данный аргумент может характеризовать сумму, которую получит вкладчик по окончанию действия договора по депозитному вкладу. Если аргумент явно не указан или принимает значение 0 (нуль), функция КПЕР вернет количество периодов выплат до полного погашения задолженности. Аргумент необязателен для заполнения, по умолчанию принимается значение 0.
• [тип] – необязательный аргумент, характеризующий способ выплат (0 – выплата на конец периода, 1 – выплата на начало периода).

Примечания 1:

1. Функция КПЕР возвращает код ошибки #ЧИСЛО! В случае, если сумма платежа за каждый период меньше, чем произведение начальной суммы инвестиции и ставки за период, при этом будущая стоимость инвестиции равна 0 (ситуация при расчете количества периодов для полного возврата задолженности), а выплата производится в конце периода (то есть, аргумент [тип] или явно указан как 0 (нуль).
2. Указанная выше особенность работы функции КПЕР вытекает из алгоритма, который она использует для расчета:



3. Все аргументы функции КПЕР должны указываться в виде числовых значений или конвертируемых в числа текстовых срок. Иначе рассматриваемая функция будет возвращать код ошибки #ЗНАЧ!.

Примечания 2:

1. Фактически, функция КПЕР позволяет определить количество периодов, по окончанию последнего из которых будущая стоимость инвестиции примет указанное значение.
2. В случае с кредитом, считается, что задолженность погашена полностью, если будущая стоимость инвестиции равна 0 (нулю).
3. Также функция КПЕР позволяет вычислить количество периодов капитализации депозитного вклада, необходимых для достижения требуемой суммы накоплений.
4. Для расчета количества периодов выплаты задолженности с нулевой процентной ставкой можно использовать формулу =A1/A2, где A1 – будущая стоимость, A2 – фиксированная сумма выплат за период.

В этой статье описаны синтаксис формулы и использование функции ЧИСЛКУПОН в Microsoft Excel.

Описание

Возвращает количество купонов, которые могут быть оплачены между датой соглашения и датой погашения, округленное до ближайшего целого купона.

Синтаксис

ЧИСЛКУПОН(дата_согл; дата_вступл_в_силу;частота;[базис])

Важно: Даты должны быть введены с использованием функции ДАТА или как результат вычисления других формул и функций. Например, для указания даты 23 мая 2008 г. воспользуйтесь выражением ДАТА(2008,5,23). Если ввести даты как текст, это может привести к возникновению проблем.

Аргументы функции ЧИСЛКУПОН описаны ниже.

• Дата_согл    — обязательный аргумент. Дата расчета за ценные бумаги (дата продажи ценных бумаг покупателю, более поздняя, чем дата выпуска).

• Дата_вступл_в_силу    — обязательный аргумент. Срок погашения ценных бумаг. Эта дата определяет момент, когда истекает срок действия ценных бумаг.

• Частота    — обязательный аргумент. Количество выплат по купонам за год. Для ежегодных выплат частота равна 1, для полугодовых — 2, для ежеквартальных — 4.

• Базис    — необязательный аргумент. Используемый способ вычисления дня.

Базис	Способ вычисления дня
0 или опущен	Американский (NASD) 30/360
1	Фактический/фактический
2	Фактический/360
3	Фактический/365
4	Европейский 30/360

Замечания

• В приложении Microsoft Excel даты хранятся в виде последовательных чисел, что позволяет использовать их в вычислениях. По умолчанию дате 1 января 1900 года соответствует номер 1, а 1 января 2008 года — 39448, так как интервал между этими датами составляет 39 448 дней.

• Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона. Предположим, например, что облигация со сроком действия 30 лет выпущена 1 января 2008 г. и приобретена покупателем через шесть месяцев после выпуска. Датой выпуска будет 1 января 2008 г., датой расчета — 1 июля 2008 г., а срок погашения такой облигации наступит 1 января 2038 г., то есть через 30 лет после даты выпуска.

• Все аргументы усекаются до целых.

• Если дата расчета или дата погашения не является допустимой датой, то датаКУПОН возвращает #VALUE! (значение ошибки).

• Если частота является любым числом, кроме 1, 2 или 4, то числоКУПОН возвращает #NUM! (значение ошибки).

• Если базис < 0 или базис > 4, то coupNUM возвращает #NUM! (значение ошибки).

• Если «≥», то «КУПОН» возвращает #NUM! значение ошибки.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
25-янв-2007	Дата соглашения
15-ноя-2008	Дата вступления в силу
2	Полугодовой купон (см. выше)
1	Базис фактический/фактический (см. выше)
Формула	Описание	Результат
=ЧИСЛКУПОН(A2;A3;A4;A5)	Количество выплат по купонам по облигации в соответствии с приведенными выше условиями	4

В
пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:

• определение
  наращенной суммы (будущей стоимости),

• определение
  начального значения (текущей стоимости),

• определение
  срока платежа и процентной ставки,

• расчет
  периодических платежей, связанных с
  погашением займов.

Общая
формула расчета, которуюExcel
использует при вычислении финансовых
аргументов, связанных с денежными
потоками, имеет вид:

где
pmt
– фиксированная
(неизменная) периодическая сумма платежа;

n
– общее
число периодов выплат,

r
– процентная
ставка за один период,

type
– число 0
или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 – в конце
периода),

—
текущая стоимость вклада (займа), по
которому начисляются проценты по ставке
r%
n—ное
число периодов или текущая стоимость
серии фиксированных платежей,

—будущая стоимость вклада (займа) или
будущая стоимость серии фиксированных
периодических платежей.

Если
процентная ставка за период начисления
r=0, то используется следующая формула:

Эти
формулы используют встроенные функцииБC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.

ПС
— текущий объём вклада

Позволяет
рассчитать текущий объем вклада.

Синтаксис

ПС
(норма;кпер;выплата;бс;тип)

норма
— процентная
ставка за период. Так, если Вы по­лучили
ссуду под станок под 15% годовых и делаете
ежемесяч­ные выплаты, то ставка
процента за месяц составит 15%/12, или
1,25%. Аргумент норма
в данном
случае может принимать значения 15%/12
или 1,25% или 0,0125.

кпер
— общее число
периодов выплат годовых процентов. Так,
если Вы получили ссуду на 3 года под
станок и делаете ежемесячные платежи,
то Ваша ссуда имеет 3*12 (или 36) периодов.
Аргумент кпер
в данном случае принимает значение 36.

выплата
—
размер выплаты, производимой в каждом
периоде и не меняющейся в течение всего
времени выплаты процентов. Обычно,
выплата включает основные платежи и
платежи по процентам без учета других
сборов или налогов. Напри­мер,
ежемесячная выплата по четырехгодичному
займу в 10 000 руб. под 12% годовых составит
308,3 руб. Аргумент выплата
в данном случае принимает значение
-308,3.

бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если бс
опущено, оно полагается равным 0 (будущая
стоимость займа, например, равна 0).
Например, если Вы хотите накопить 50000
руб. в течение18 лет, то 50 000 руб. это и
есть будущая стоимость. Вы можете сделать
предположение о сохранении заданной
процентной ставки и определить, сколько
нужно откладывать каждый месяц.

тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 означает — выплата в конце периода,
1 — выплата в начале периода.

• Выбранные
  единицы измерения для аргументов норма
  и кпер
  должны соответствовать друг другу.
  Если Вы делаете ежемесячные выплаты
  по четырехгодичному займу под 12% годовых,
  то используйте 12%/12 для задания аргумента
  норма,
  4*12 для задания аргумента кпер.
  Если Вы делаете ежегодные платежи по
  тому же займу, то используйте 12% для
  задания аргумента норма
  и 4 для задания аргумента кпер.

• В
  функциях, связанных с интервалами
  выплат, выплачи­ваемые деньги
  представляются отрицательным числом,
  а получаемые деньги представляются
  положительным числом. Например, депозит
  в банк на сумму 1 000 руб. представляется
  для вкладчика аргументом -1000, а для
  банка аргументом 1000.

Пример

Фирме
потребуется 5000 руб. через 12 лет. В
настоящее время фирма располагает
деньгами и готова положить их на депозит
единым вкладом, чтобы через 12 лет он
достиг 5000 руб. Определим необходимую
сумму текущего вклада, если ставка
процента по нему составляет 12% годовых.

Необходимая
сумма текущего вклада составит:

ПС
(12%;12;;5000)=-1283.38 руб.

БС
— стоимость постоянных платежей в
определенные периоды на основе постоянной
процентной ставки

Позволяет
рассчитать объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.

Синтаксис

БС(норма;кпер;выплата;пс;тип)

ставка
— процентная
ставка за период.

кпер
— количество
периодов, в которые производится вы­плата
годовых процентов.

выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.

пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.

тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.

Более
подробная информация об аргументах
функции БЗ и о других функциях выплат
по процентным вкладам приведена в
описании функции ПЗ.

• Единицы
  измерения для аргументов норма
  и кпер
  должны быть согласованы. Если производятся
  ежемесячные платежи по четырехгодичному
  займу из расчета 12% годовых, то норма
  должна быть 12%/12 , а кпер
  должно быть 4*12. Если про­изводятся
  ежегодные платежи по тому же займу, то
  норма
  должна быть
  12%, а кпер
  должно быть 4.

• Ваш
  вклад представляется отрицательным
  числом, а деньги, которые вы получите,
  представляются положительным числом.

Пример

Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.

Через
год на счете будет:

БС
(0,5%;12;-100;-1000;1)=2301,40 р.

ПРПЛТ
— платежи по процентам за период на
основе постоянных периодических выплат
и постоянной процентной ставки

С
помощью данной функции можно рассчитать
процентные платежи за текущий период
при периодических постоянных выплатах
и постоянной процентной ставке. Полное
описание аргументов функции ПРПЛТ
и более подробная информация о функциях,
связанных с ежегодными выплатами,
приведены в описании функции ПС.

Синтаксис

ПРПЛТ(норма;период;кпер;тс;бс;тип)

норма
—
процентная ставка за период.

период
— текущий
период, в котором требуется определить
прибыль (может принимать значения от 1
до кпер).

кпер
— общее число
периодов выплат.

тс
— сумма,
которую составят будущие платежи с
настоящего момента.

бс
— баланс
платежей, который нужно достичь после
последней выплаты.

тип
— число,
определяющее, когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплаты в конце периода, 1 — выплаты
в начале периода.

• Единицы
  измерения для аргументов норма
  и кпер
  должны быть согласованы. Если производятся
  ежемесячные платежи по трехгодичному
  займу из расчета 10% годовых, то норма
  должна быть 10%/12 , а кпер
  должно быть 3*12. Если производятся
  ежегодные платежи по тому же займу, то
  норма
  должна быть 10%, а кпер
  должно быть 3.

• Выплачиваемые
  денежные средства представляются
  отрицательным числом, а получаемые
  денежные средства представляются
  положительным числом.

Пример

Требуется
определить доход за первый месяц от
четырех­годичного займа в 1000000 рублей
из расчета 15% годовых:

ПРПЛТ(0,15/12;1;48;1000000)
равняется -12500 рублей.

ПЛТ
— расчет постоянных периодических
выплат

Функция
вычисляет величину выплаты за один
период на основе фиксированных
периодических выплат и постоянной
процентной ставки. Выплаты, рассчитанные
функцией ПЛТ, включают основные платежи
и платежи по процентам.

Синтаксис

ПЛТ(норма;кпер;нз;бс;тип)

норма
– норма
прибыли за период займа.

кпер
– общее
число периодов выплат годовой ренты

нз
– текущая стоимость: общая сумма всех
будущих платежей с настоящего момента.

бс
– будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты.

тип
— число,
определяющее, когда должна производиться
выплата.

Пример

Предположим,
что необходимо накопить 4000 руб. за 3
года, откладывая постоянную сумму в
конце каждого месяца. Какой должна быть
эта сумма, если норма процента по вкладу
составляет 12% годовых?

Величина
ежемесячных выплат составит:

ПЛТ(12%/12;12*3;;4000)=-92.86
руб.

ОСПЛТ
— расчет основных платежей по займу

Функция
вычисляет величину основного платежа
(выплаты задолженности) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
на указанный период.

Синтаксис

ОСПЛТ(норма;период;кпер;тс;бс;тип)

норма
– норма
прибыли за период.

период
– период,
который должен быть в интервале от 1 до
кпер.

кпер
– общее
число периодов выплат годовой ренты.

тс
– текущая
стоимость: общая сумма всех будущих
платежей с настоящего периода.

бс
– будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.

тип
—
число,
определяющее, когда должна производиться
выплата.

Пример

Банком
выдан кредит в 7000 руб. на 3 года под 17%
годовых, начисляемых один раз в конце
каждого периода.

Определите
размер ежегодных основных выплат по
займу.

Основная
часть платежа на каждый из трех периодов
составит соответственно:

ОСПЛТ(17%;1;3;-70000)=19780.16
руб.

ОСПЛТ(17%;2;3;-70000)=23142.78
руб.

ОСПЛТ(17%;3;3;-70000)=27077.06
руб.

ОБЩПЛТ
— расчет суммы платежей по процентам
по займу между двумя периодами выплат

Функция
вычисляет накопленный доход (сумму
платежей по процентам) по займу, который
погашается равными платежами в конце
или начале каждого расчетного периода,
между двумя периодами выплат.

Синтаксис

ОБЩПЛТ(ставка;кол_пер;нз;нач_период;кон_период;тип)

ставка
– процентная ставка.

кол_пер
– общее
количество периодов выплат.

нз
– текущее
значение.

нач_период
– первый
период.

кон_период
— последний период.

Пример

Пусть
заем под недвижимость сделан на следующих
условиях: процентная ставка –9% годовых;
срок-30 лет, размер ссуды – 125000 руб.,
проценты начисляются ежемесячно.

Найти
сумму выплат по процентам за 2-й год и
за 1-й месяц займа.

Общая
выплата по процентам за второй год
составит:

ОБЩПЛТ(9%/12;30*12;125000;13;24)=-11135.23
руб.

Одна
выплата за первый месяц составит:

ОБЩПЛТ(9%/12;30*12;125000;1;1)=-937.50
руб.

ОБЩДОХОД
— расчет суммы основных выплат по займу
между двумя периодами

Функция
вычисляет сумму основных выплат по
займу, который погашается равными
платежами в конце или начале каждого
расчетного периода, между двумя периодами.

Синтаксис

ОБЩДОХОД
(ставка;кол_пер;нз;нач_период; нач_период;)

ставка
– процентная ставка.

кол_пер
– общее
количество периодов выплат.

нз
– текущее
значение.

нач_период
– первый
период.

кон_период
— последний период.

Пример

Выдана
ссуда размером 1000$ сроком на 6 лет под
15% годовых; проценты начисляются
ежеквартально.

Определите
величину основных выплат за 5 год.

Если
ссуда погашается равными платежами в
конце каждого расчетного периода, то
размер выплаты задолженности за пятый
год составит:

ОБЩДОХОД(15%/4;6*4;1000;17;20)=-201.43$.

Комплексный
пример

Банком
выдан кредит в 10000$ на 5 лет под 12% годовых,
начисляемых один раз в конце каждого
периода. По условиям договора кредит
должен быть погашен равными долями в
течение указанного срока, выплачиваемыми
в конце каждого периода.

Разработать
план погашения кредита.

Периодический
платеж по данной операции составит:

ПЛТ(12%;5;-10000)=2774.10$.

Процентная
часть платежа на первый период составит:

ПРПЛТ(12%;1;5;-10000)=1200,00$.

Основная
часть платежа, направленная на погашение
долга за первый период, составит:

ОСПЛТ(12%;1;5;-10000)=1574.10$.

Как
видно выполняется тождество:

ПРПЛТ()+ОСПЛТ()=ПЛТ()=2774.10$.

Будущее
значение суммы, которую банк получит в
результате проведения операции:

ПЛТ(12%;5;-10000)*5=13870.50$.

Накопленная
сумма процентов за весь период составит:

ОБЩПЛТ(12%;5;10000;1;5;0)=-3870,49$.

Накопленная
сумма в счет погашения по займу за 5 лет
составит:

ОБЩДОХОД(12%;5;10;1;5;0)=-10000.00$.

Как
видно, сумма полученных величин равна
общей сумме, выплаченной по данному
займу:

ОБЩДОХОД()+ОБЩПЛАТ()=13870.49$.

(В
силу заложенного алгоритма расчета
функции ОБЩДОХОД() и ОБЩПЛАТ возвращают
отрицательные значения. Для получения
положительных значений можно задать
их со знаком минус).

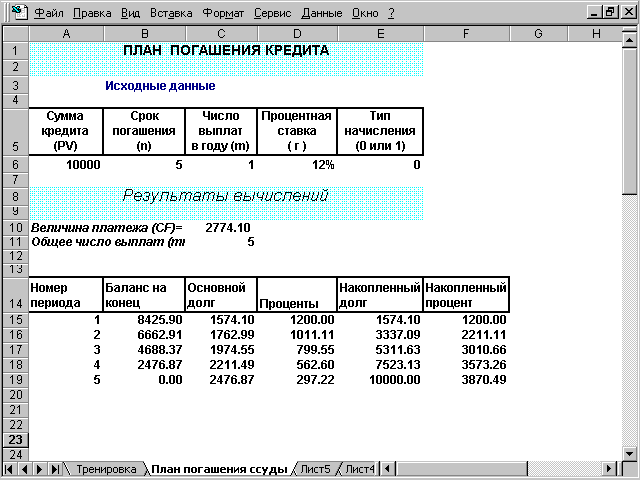
На
рис. 1 приведена таблица с планом погашения
кредита.

ЭФФЕКТ
— эффективная годовая процентная ставка

Позволяет
рассчитать фактическую годовую процентную
ставку, если известны годовая процентная
ставка и количество периодов в году.

Синтаксис

ЭФФЕКТ(нoмuнaльнaя_cmaвкa;кол_пep)

номинальная_ставка

—
номинальная годовая процентная ставка.

кол_пер
— количество
периодов в году.

Рис.
1. План погашения кредита

• Число
  периодов в году округляется до целого.

• Функция
  ЭФФЕКТ
  выдает значение ошибки #ЗНАЧ! в случае,
  если один из аргументов — не число либо,
  если номинальная_ставка
  меньше 0 или
  кол_пер
  меньше 1.

Пример

Рассчитаем
эффективную годовую процентную ставку
при став­ке 5,25% и четырех периодах в
году.

ЭФФЕКТ(5,25%;4)
равняется 0,053543 или 5,35%.

КПЕР
— определение срока платежа

Эта
функция вычисляет общее число периодов
выплат как для единой суммы вклада
(займа), так и для периодических постоянных
выплат на основе постоянной процентной
ставки. Если платежи производятся
несколько раз в год, найденное значение
необходимо разделить на число расчетных
периодов в году, чтобы найти число лет
выплат.

Синтаксис

КПЕР(норма;выплата;нз;бс;тип)

норма
– норма
прибыли за период.

выплата—
размер выплаты, производимой в каждом
периоде.

нз
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент нз опущен, то он
полагается равным 0.

бс
— будущая
стоимость или баланс наличности, который
нужно достичь после последней выплаты.

тип
— число,
определяющее, когда должна производиться
выплата.

Пример

Ожидается,
что ежегодные доходы от реализации
проекта составят 33 млн. руб. Необходимо
рассчитать срок окупаемости проекта,
если инвестиции к началу поступления
доходов составят 100 млн. руб., норма
дисконтирования 12.11%.

Срок
окупаемости проекта составит:

КПЕР(12.11%;33;-100)=4года.

Определение
скорости оборота инвестиций

ВНДОХ
— процентная ставка дохода для ряда
последо­вательных периодических
выплат или поступлений

Позволяет
рассчитать процентную ставку дохода
от инвестиций для ряда последовательных
операций с денежными средствами,
представленными числовыми значениями.
Объемы операций могут быть различны.
Однако они должны происходить через
равные промежутки времени, например,
ежемесячно или ежегодно. Процентная
ставка дохода, полученного от инвестиции,
состоит из выплат (отрицательные
значения) и поступлений (положительные
значения), которые происходят в регулярные
периоды времени.

Синтаксис

ВНДОХ
(значения;предположение)

значения
— массив или
ссылка на ячейки, содержащие числа, для
которых вычисляется процентная ставка
инвестиций.

предположение
—
прогнозируемая величина.

• Аргумент
  значения
  должен включать в себя по крайней мере
  одно положительное значение и одно
  отрицательное значение, для того, чтобы
  можно было вычислить процентную ставку.

• Начиная
  со значения прогноз, функция ВНДОХ
  выполняет
  циклические вычисления, пока не получит
  результат с точностью 0,00001 процента
  (такой метод вычисления на­зывается
  методом итераций).

• Функция
  ВНДОХ выдает значение ошибки #ЧИСЛО! в
  том случае, если не может получить
  результат после 20 попыток.

• Обычно
  нет необходимости задавать аргумент
  прогноз
  для вычислений с помощью функции ВНДОХ.
  Если прогноз
  опущен, то
  он полагается равным 0,1 (10 процентов).
  Если ВНДОХ
  выдает значение ошибки
  #ЧИСЛО!,
  можно попытаться вы­полнить вычисления
  еще раз с другим значением аргумента
  прогноз.

Пример

Предположим,
что затраты по проекту составят 500 тыс.
руб. Ожидаемые доходы составят 50 , 100 ,
300 и 200 тыс. руб. в течение последующих
4 лет. Оценим
экономическую целесообразность проекта
по скорости оборота инвестиций, если
рыночная норма дохода 12%.

Ячейки
А1:А5 содержат следующие значения: -500,
50, 100, 300 и 200 соответственно.

Внутренняя
скорость оборота инвестиций составит:

ВНДОХ(А1:А5)=9.25%.

Это
меньше, чем рыночная норма, поэтому
проект должен быть отвергнут.

В
том случае, если эта какая-либо из
финансовых функций недоступна из Excel,
следует установить надстройку Пакет
Анализа (Analysis
ToolPak),
а затем подключить его с помощью команды
Сервис
— Надстройки…

ЗАДАЧИ

Рассчитаем в MS EXCEL сколько времени потребуется для погашения кредита в случае равных ежемесячных платежей (по аннуитетной схеме). Процентная ставка и величина платежа — известны, начисление процентов за пользование кредитом – ежемесячное. Также в статье разберем случай накопления вклада.

Аннуитетная схема

предусматривает погашение кредита периодическими равновеликими платежами (как правило, ежемесячными), которые включают как выплату основного долга, так и процентный платеж за пользование кредитом. Такой равновеликий платеж называется аннуитет. В аннуитетной схеме погашения предполагается неизменность процентной ставки по кредиту в течение всего периода выплат. В статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

показано как рассчитать величину регулярной суммы для погашения кредита или ссуды. Расчет количества периодов, необходимых для погашения кредита произведем сначала с помощью финансовой функции MS EXCEL КПЕР(), затем приведем расчет с помощью эквивалентной формулы (см.

файл примера

).

Функция КПЕР(ставка; плт; пс; [бс]; [тип])

позволяет вычислить количество периодов, через которое

текущая сумма вклада

(пс) станет равной заданной сумме (бс) при известной процентной ставке за период (ставка) и известной величине пополнения вклада (плт). Бс (

будущая стоимость

) может быть =0 или опущена. Тип – это число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов): 0 – в конце периода, 1 – в начале. Также функцию

КПЕР()

можно использовать для определения количества периодов, необходимых для погашения долга по ссуде.

Примечание

. Обзор всех функций аннуитета

найдете здесь

.

Эквивалентная формула для расчета количества периодов:

Если ставка равна 0, то: Кпер = (Пс + Бс) /ПЛТ

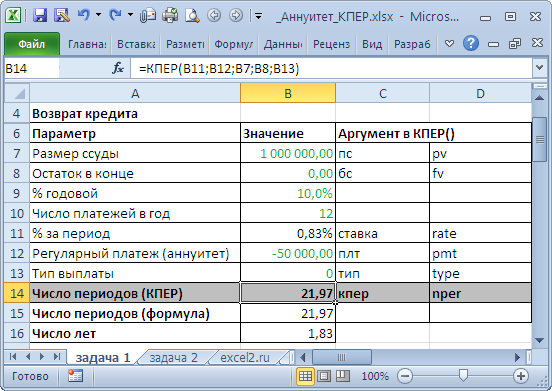
Задача1

Сколько времени потребуется для погашения кредита 1 млн. рублей в случае равных ежемесячных взносов. Начисление процентов за пользование кредитом – ежемесячное, годовая процентная ставка = 10%. Ежемесячный платеж 50 000р.

Решение

1

Так как погашение кредита производится ежемесячно (12 раз в году), то ставка за период составит 10%/12. Формула

=КПЕР(10%/12;-50000;1000000;0;0)

вернет количество периодов, после которых кредит будет возвращен в полном размере. Знак минус перед 2-м аргументом функции (величина ежемесячного платежа) показывает, что разнонаправленные денежные потоки должны иметь разные знаки (+1000000 – это деньги, которые

банк

дал

нам, -50000 – это деньги, которые мы

возвращаем банку

). Конечно, можно и наоборот: деньги, которые банк дал нам учитывать со знаком минус, а те деньги, которые мы отдаем банку учитывать со знаком +. Формула вернет 21,97, т.е. потребуется 22 месяца, чтобы полностью вернуть 1 млн. руб., возвращая ежемесячно по 50 тыс. руб. (последний платеж будет несколько меньше, о том, как его рассчитать – читайте ниже).

Расчет последнего платежа

При расчете количества периодов погашения ссуды может получиться нецелое количество периодов. В этом случае, последний платеж будет несколько меньше, чем предыдущие. Найдем величину этого платежа. Учтем, что в последнем периоде нам будет необходимо погасить оставшуюся задолженность и заплатить % банку (% от суммы оставшейся задолженности). Найдем сначала количество полных периодов

=ЦЕЛОЕ(КПЕР(10%/12;-50000;1000000;0;0))

и поместим результат в ячейку G21. Чтобы вычислить сколько было погашено основной суммы долга за все целые периоды можно использовать формулу

=СУММПРОИЗВ(ОСПЛТ(10%/12;СТРОКА(ДВССЫЛ(«1:»&G21)); КПЕР(10%/12;-50000;1000000;0;0);1000000;0;0))

(Альтернатива –

используйте функцию

ОБЩДОХОД()

)

Примечание

. Сумму платежа, идущую на оплату основной суммы долга в один определенный период, можно вычислить с помощью функции

ОСПЛТ()

. Складывая результат

ОСПЛТ()

для всех целых периодов с помощью функции

СУММПРОИЗВ()

получим сколько было погашено основной суммы долга.

Далее вычтем из суммы кредита выплаченную сумму за все целые периоды (с учетом знаков). Затем вычислим проценты за последний период = СУММПРОИЗВ(…)*10%/12 Сложим остаток основной суммы долга и проценты за последний (неполный) период (см.

файл примера

). В результате получим -48487,18р. (это несколько меньше регулярного платежа -50000р.)

Если функция КПЕР() возвращает ошибку

В некоторых случаях функция

КПЕР()

возвращает значение ошибки #ЧИСЛО! Разобраться, почему это происходит, можно, вспомнив альтернативную формулу (см. выше). Понятно, что логарифм числа может быть вычислен только для положительного числа, а это означает, что величина платежа ПЛТ должна быть больше величины ежемесячных процентов начисляемых на остаток тела кредита, т.е. больше ПС*СТАВКА (это справедливо только при БС=0 и ТИП=0). Оно и понятно, нам нужно ежемесячно не только оплачивать проценты, но и возвращать основную сумму долга.

Количество периодов, через которое будет погашено 80% кредита

Сколько времени потребуется, чтобы погасить кредит не полностью, а например, на 80%? Записав формулу

=КПЕР(10%/12;-50000;1000000;-1000000*(1-80%);0)

получим, что для этого потребуется 17,88 периодов (месяцев). Величину БС = -1000000*(1-80%) мы нашли пользуясь тождеством для аннуитета (справедливо, если Тип=0): СУММ(ОСПЛТ(за все периоды)) + ПС + БС = 0 Из условий задачи ПС = 1000000 (начальная сумма кредита), выплаченная сумма кредита, т.е.  СУММ(ОСПЛТ(за все периоды)) равна -1000000*80%. Решая уравнение, получим, что БС = -1000000*(1-80%). БС в данном случае – это непогашенная сумма кредита (конечно, чтобы найти, что БС=20% от суммы кредита, не требует использования тождества. Но важен знак БС).

Задача2

Рассчитать, через сколько времени вклад размером 200 000 руб. достигнет 1 000 000 руб., если годовая процентная ставка по вкладу 10% годовых, начисление процентов производится ежеквартально, также ежеквартально вклад пополняется на 10 000 руб.

Решение2

Так как взносы и начисление процентов происходит ежеквартально (4 раза в год), то ставка за период составит 10%/4. Формула

=КПЕР(10%/4;-10000;-200000;1000000;0)

вернет количество периодов, после которых вклад достигнет 1 млн. руб., т.е. 34,31 квартал (см.

файл примера, лист Задача2

).

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса — другое дело, а для обычных людей мышеловка»деньги за 15 минут, нужен только паспорт» срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это «потом» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами — таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

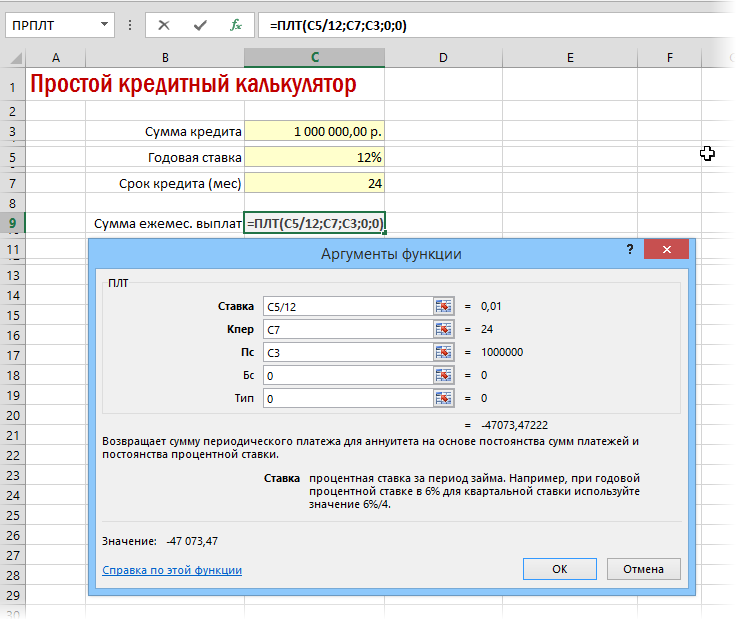
• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — начальный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип — способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

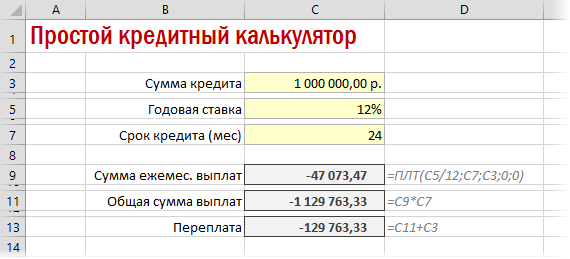
Вариант 2. Добавляем детализацию

Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

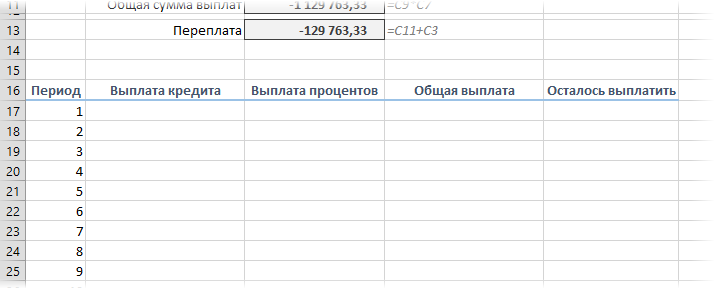
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

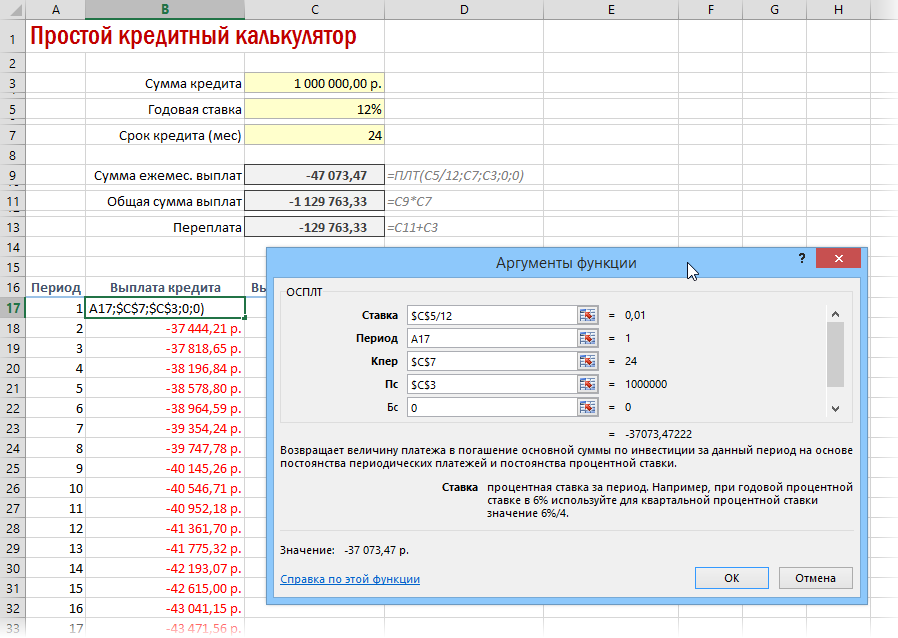
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

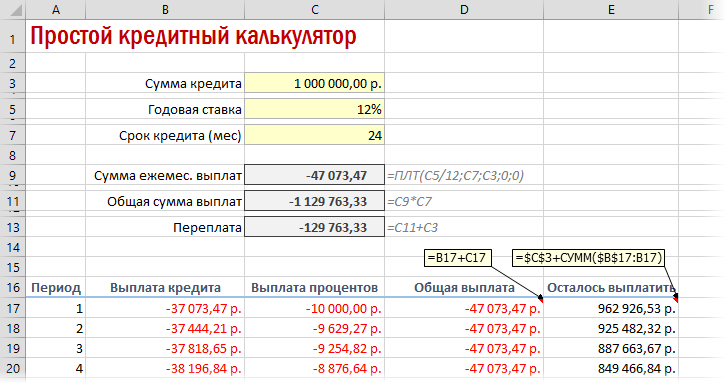
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;»»;A17+1)

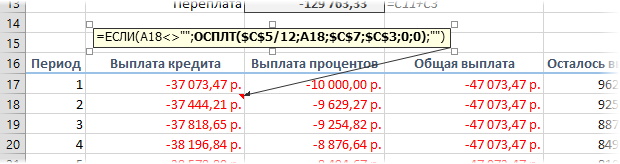
Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>»»; текущая формула; «»)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять — не достигли мы нулевого баланса раньше срока:

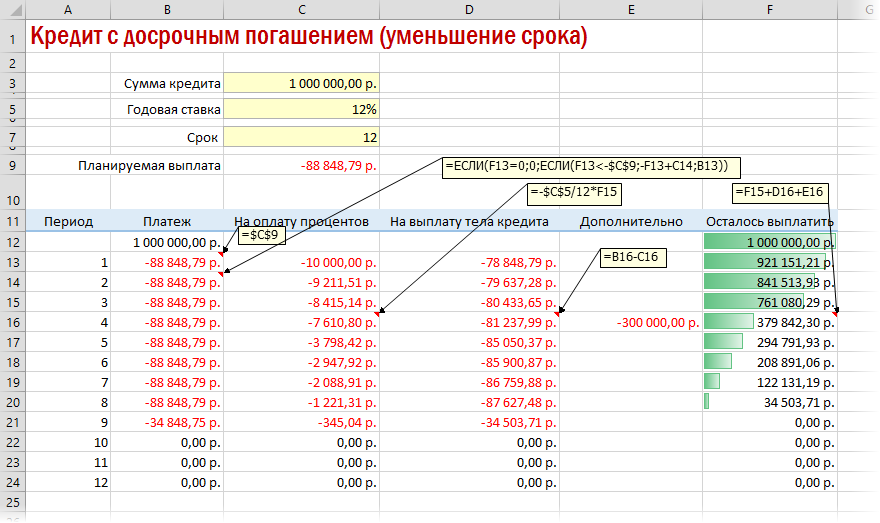
А в случае уменьшения выплаты — заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

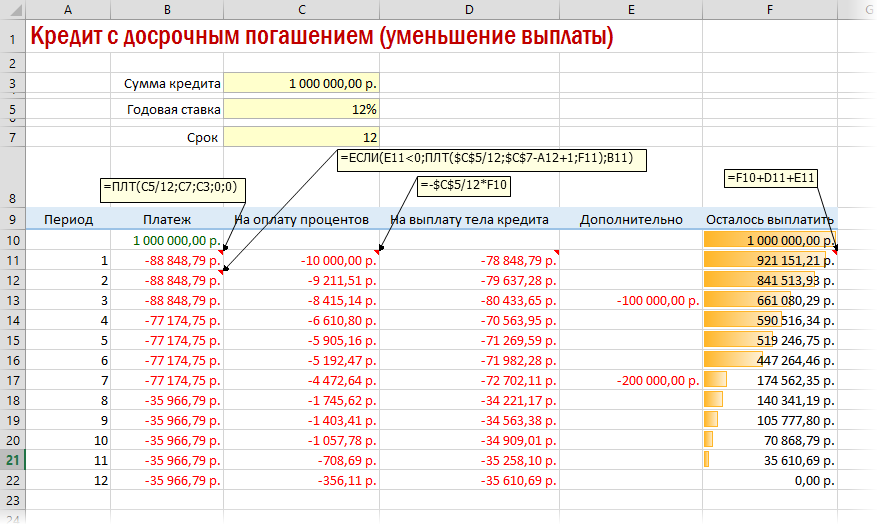
Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

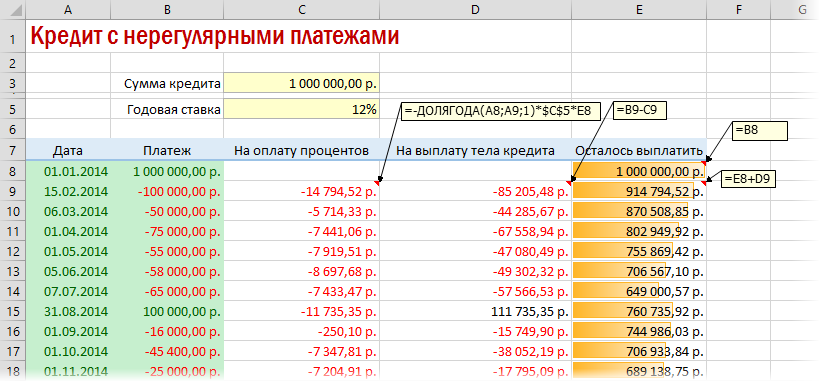
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы — наши выплаты банку, положительные — берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)