Определение области определения функции в excel

Автор: Пенский Владимир Константинович

Предмет: алгебра, информатика.

Тема урока: Построение и исследование графика функции в MS EXCEL.

Класс: 9.

Продолжительность: 45 минут.

Цель урока: применение электронных таблиц для построения графика и изучения основных свойств квадратичной функции.

Задачи урока:

Образовательные:

• систематизация знаний о свойствах квадратичной функции;

• закрепить умение строить графики квадратичной функции и по графику определять ее основные свойства;

• закрепление умения работать с электронными таблицами.

Развивающие:

• формирование умения сравнивать, обобщать изучаемые факты;

• повышение уровня учебной мотивации с использованием компьютерных технологий, развитие логического мышления;

• развитие умения грамотно излагать свои мысли, обосновывать свои действия.

Воспитательные:

• развитие коммуникативных умений, формирование адекватной оценки собственной деятельности;

• развитие чувства товарищества, взаимопомощи, деликатности, дисциплинированности.

Оборудование: компьютерный класс, мультимедийный проектор, экран.

Ход урока

1. Организационный момент.

2. Постановка цели урока.

Сегодня на уроке мы повторим свойства квадратичной функции и научимся строить соответствующие графики функций с помощью прикладного программного обеспечения компьютера и, используя полученный график, определим свойства этой функции.

3. Актуализация знаний. Фронтальный опрос.

Вспомним определение и основные свойства квадратичной функции. Для этого ответьте на вопросы.

1. Как называется функция вида у = aх² + bx + c (а ≠ 0), где а, b, c – действительные числа?

2. Что является графиком квадратичной функции?

3. При каких значениях х квадратичная функция у = х² возрастает? убывает?

4. Как называются значения переменной х, при которых значение функции равно нулю.

5. При а 0 ветви параболы у = ах² направлены … .

6. Если а х у = ах² принимает …(положительные, отрицательные) значения.

3. Повторение изученного материала.

1. Обоснуйте, что областью определения функции у = aх² + bx + c является множество всех действительных чисел.

2. Выясните, какие из следующих квадратичных функций являются: чётными; нечётными; не являются ни чётными, ни нечётными.

а) y = x²; б) y = 3 − 2x + x².

3. Найдите нули квадратичной функции:

а) y = 2x² + x − 3; б) y = x² − 8x + 15.

4. Найдите координаты вершины параболы у = х² – 4х + 4.

5. Укажите наибольшее (наименьшее) значение функции:

а) y = x²; б) y = 3x² + 1.

4. Изложение нового материала.

Можно ли, не проводя аналитических рассуждений определить свойства квадратичной функции? Действительно, по графику квадратичной функции можно определить все ее основные свойства.

Как построить график квадратичной функции? На помощь приходят современные компьютерные технологии. Сегодня существует множество программ, которые позволяют строить графики различных функций. Одним из простейших способов построения графика (в нашем случае графика квадратичной функции) является использование электронных таблиц Microsoft Excel.

Вспомним, каким образом можно построить график функции в данной программе.

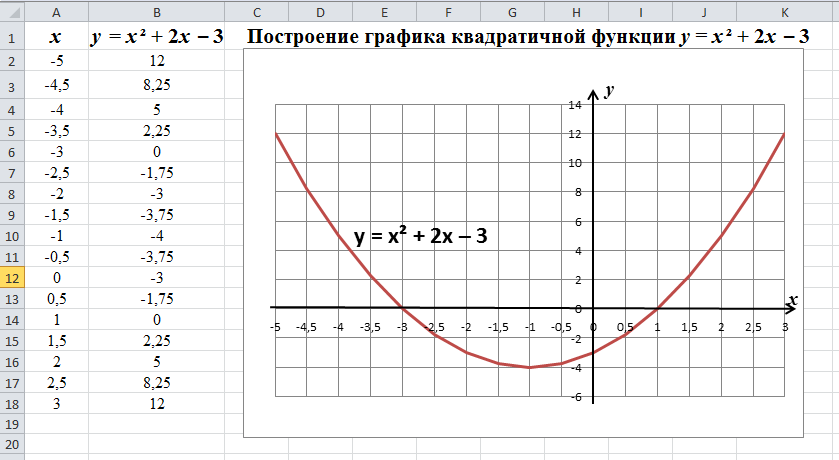
Построим, например, график квадратичной функции у = х² + 2х – 3 и исследуем ее свойства.

1) Составим таблицу значений зависимости переменной у от х:

– в ячейку А1 введите заголовок столбца «х»;

– в ячейку А2 введите значение –5, а в ячейку А3 – –4,5;

– выделите содержимое ячеек А2 и А3, далее с помощью функции автозаполнения скопируйте до ячейки А18 (получим соответствующие значения х от –5 до 3);

– в ячейку В1 введите заголовок столбца у = х² + 2х – 3;

– в ячейку В2 введите формулу = В1^2 + 2*B1 – 3;

– скопируйте формулу из ячейки В2 (используя функцию автозаполнения) до ячейки В19.

2) Построение графика с помощью мастера диаграмм:

– выделите подготовленные данные, начиная с заголовка В1:В18.

– вызовите мастер диаграмм (Вставка – график – график);

– при задании параметров название диаграммы оставить;

– нажмите «ОК» и график автоматически вставится.

3) Работа с графиком:

– вставьте названия осей (Макет – названия осей – название основной горизонтальной оси – название под осью; Макет – названия осей – название основной вертикальной оси – горизонтальное название) и перенесите (х справа от оси, у выше оси);

– щелчком мыши в готовой диаграмме по каждой из осей, вызовите контекстное меню и установите: «горизонтальная ось пересекает значение оси 0», «вертикальная ось пересекает в категории с номером 11»;

– добавьте сетку (Макет – сетка – вертикальные линии сетки по основной оси – основные линии сетки).

Задание. С помощью построенного графика квадратичной функции у = х² + 2х – 3 определите:

а) четность-нечетность функции;

б) нули функции;

в) промежутки монотонности;

г) наибольшее и наименьшее значение функции.

5. Проверка усвоения нового материала.

Класс делится на две группы. Каждой группе предлагается решить определенное задание. После того как все обучающиеся в группе решили это задание, происходит взаимопроверка полученных решений.

1 группа.

1. Найдите координаты точек пересечения параболы у = х² + х – 12 с осями координат.

2. Постройте график квадратичной функции y = −3x² в программе Microsoft Excel и определите по графику значения этой функции в точках x₁ = 5, x₂ = −3.

2 группа.

1. Найдите значения квадратичной функции y = −3x² в точках x₁ = 5, x₂ = −3.

2. Постройте график квадратичной функции у = х² + х – 12 в программе Microsoft Excel и по графику определите координаты точек пересечения параболы с осями координат.

6. Подведение итогов.

Итак, мы повторили материал, касающийся свойств квадратичной функции, решали задачи.

Что нового вы узнали сегодня?

Довольны ли вы своей работой?

7. Домашнее задание.

Задайте аналитически квадратичную функцию, которая:

а) имеет два нуля −3 и 0;

б) имеет только один нуль −3;

в) не имеет нулей.

Однозначно ли можно выполнить задание во всех случаях?

Список использованной литературы:

1. Алгебра: учебник для 9 класса / Гельфман Э.Г., Демидова Л.Н., Терре А.И. и др. – М: БИНОМ. Лаборатория знаний, 2013. – 272 с.

2. Семакин И.Г. Информатика и ИКТ: учебник для 9 класса / И.Г. Семакин, Л.А. Залогова, и др. – М: БИНОМ. Лаборатория знаний, 2012. – 341 с.

3. Социальная сеть работников образования «Наша сеть». – Режим доступа: http://nsportal.ru/shkola/informatika-i-ikt/library/2013/11/02/integrirovannyy-urok-po-algebre-i-informatike

Анализ области определения функции

Сущность анализа
состоит в том, чтобы выявить значения
аргумента функции, при которых функция
может быть не определена (не существует).

Известно, что не
существует логарифм нуля и отрицательного
числа (ln(0),ln(–x)),
квадратный корень отрицательного числа
().
Функцииarcsin(x) иarccos(x)
будут определены, еслиx<=1.
Недопустимо деление на ноль, а также
при вычислении значений функции могут
получаться неопределенности видаили,
которые должны быть раскрыты, например,
по правилу Лопиталя. Раскрытие
неопределенностей вида 0,–,
0⁰, ⁰,
1^после
алгебраических преобразований или
предварительного логарифмирования
также можно свести к использованию
правила Лопиталя. Именно такие ситуации
и нужно выявить при анализе функции, а
затем принять решение об исключении
вычислений значений функции в найденных
критических точках.

Пример оформления в отчёте текста анализа

Для рассматриваемой
функции при х0
получается неопределённость вида
,
так какln(1)=0
и e⁰=1.
При раскрытии этой неопределённости
по правилу Лопиталя получается единица.
Таким образом, значение функции в точке
x=0
можно положить равным sin(1)
(y(x=0)=sin(1)).
При х=<–1
функция будет не определена, так как
натуральный логарифм при таких значениях
аргумента (неположительных) не существует.
Итак, выражение в Excel
для табулирования рассматриваемой
функции будет иметь вид:

=ЕСЛИ(В12=0;SIN(1);

ЕСЛИ(В12>-1;SIN(LN(1+B12)/B12)*EXP(B12);

”Не сущ.”)).

Примечания:

1. Здесь предполагается,
   что значение аргумента функции введено
   в ячейку B12.

2. Вариант задания
   (таблица
   1)
   соответствует номеру студента в списке
   группы и при необходимости согласуется
   с преподавателем.

Оформление рабочего листа

Оформление рабочего
листа включает: ввод исходных данных,
конструирование таблицы, создание
диаграммы с графиком функции, форматирование
и защиту рабочего листа.

Ввод исходных данных

Для ввода исходных
данных необходимо выполнить следующие
действия:

1. В ячейку D1
   ввести текст Контрольная
   работа № 1.

2. В ячейку B2
   ввести текст Табулирование
   функции одной переменной.

3. На ячейке H2
   создать объект-формулу, задающий вид
   табулируемой функции. Объект-формула
   создаётся с помощью редактора (Мастера)
   формул Microsoft Equation 3.0.

Для создания
формулы надо выполнить следующие
операции:

• щёлкнуть
  мышкой по ячейке H2,
  сделав её активной;

• щёлкнуть
  мышкой по меню Вставкаи в раскрывшемся меню щёлкнуть по строкеОбъект;

• в
  диалоговом окне Вставка
  объектавыделить строку Microsoft
  Equation
  3.0и щёлкнуть по кнопкеОК;

• в
  окно объекта, используя нужные шаблоны,
  ввести аналитическое описание (формулу)
  функции. Увеличить окно (масштабировать)
  до нужных размеров символов созданного
  объекта и щёлкнуть мышкой по свободной
  ячейке. При необходимости переместить
  объект в продолжение строки текста
  ячейки B2.
  Примерный вид объекта-формулы:

.

1. В ячейку E4
   ввести текст Исходные
   данные.

2. В ячейку D5
   ввести текст Начальная
   граница отрезка a =.

3. В ячейку D6
   ввести текст Конечная
   граница отрезка b =;

4. В ячейку D7
   ввести текст Количество
   интервалов n =;

5. В ячейку D8
   ввести текст Шаг
   табулирования h =;

6. В ячейку I5
   ввести значение левой границы отрезка
   a;

7. В ячейку I6
   ввести значение правой границы отрезка
   b;

8. В ячейку I7
   ввести значение количества интервалов
   (n
   = 20);

9. В ячейку I8
   ввести формулу =(I6-I5)/I7.
   Ввод адресов ячеек в формулу (выражение)
   осуществляется щелчком мышки по
   соответствующей ячейке.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Здравствуйте!
Ребята, подскажите как сделать график тангенса с учетом ОДЗ? Я уже замучалась…
Вот что пишет преподаватель:
неделю назад:

задача 4. графики должны иметь разрывы, но и таблицы должны быть заполнены полностью, не должно быть в них пустых строк. для этого надо посчитать координаты выколотых точек. т.е. при аргументах функции tg(2x), кратных Пи/2, функция разрывается. требуется определить х. обозначения функций надо записать в формулы задания.

Я сделала как поняла. Она проверила, сделала замечания:
расчет выколотых точек должен быть представлен.
для третьей функции пустых строк не должно быть. см замечания к пред. версии задачи

Я снова переделала. И опять не то. Вот последнее ее замечание, которое никак не могу додумать:
если вся задача задана в Excel, почему расчет выколотых точек выполнен на калькуляторе или иным способом? он тоже должен быть выполнен средствами Excel. И дело не в отсутствии комментариев, как определены выколотые точки. Повторяю подробнее: «Расчет выколотых точек должен быть выполнен средствами Excel и представлен».

Я так полагаю, что ей нужно построить «кусочками» графики с условным оператором «Если» или «И». Но если я так строю, то у меня все равно «разрывов» нет. ПОЖАЛУЙСТА, помогите!!!!

Электронные таблицы EXCEL можно использовать при
изучении многих разделов физики, математики и
других предметов. Одной из данных тем является
математическая тема: “Анализ элементарных
функций”. Данная работа посвящена использованию
электронных таблиц EXCEL в анализе элементарных
функций.

Рис. 1 (см. Приложение 2)

На рис.1 представлена некоторая функция,
заданная с помощью таблицы, построение которой
приведено в Приложении 1.

Особенность анализа функций с помощью
электронных таблиц заключается в том, что анализ
проводится на дискретной информации.
Действительно, количество значений исследуемой
функции конечно и дано (как правило) с некоторым
постоянным шагом по аргументу.

При анализе исходной функции необходимо решить
следующие задачи:

1. определение максимума (минимума) данной функции
   на заданном интервале,
2. определение возрастания и/или убывания функции
   на заданном интервале,
3. определение четности заданной функции,
4. определение периодичности заданной функции,
5. определение значения первой производной данной
   функции и наличия экстремумов.

Для решения этих задач потребуется построить
таблицы ВводаИсходнойИнформации, таблицы
ВыводаРезультатов, Расчетной таблицы для
обработки информации и дополнительно построим
Вспомогательную таблицу. Таблицу
ВводаИсходнойИнформации и основу Расчетной
таблицу построены при введении значений
исследуемой функции в Приложении 1 и показанной
на рис.1. Построим решения задач анализа.

Приложение 1

Задача 1.
Для заданной функции на заданном интервале
аргумента определить ее минимальное и
максимальное значения.

Решение.
Для решения этой задачи построим таблицу
ВыводаРезультатов в виде

	D	E
1	комментарии	Значения
2	Макс f(X)	<формула>
3	Мин f(X)	<формула>

В мастере функций Excel имеются функции МАКС(…) и
МИН(…), позволяющие решить нашу задачу. Для этого
необходимо в ячейки Е2 и Е3 ввести соответственно
формулы:

E2 => [=МАКС(с10:с50)]
и
E3 => [=МИН(с10:с50)]

Примечание. Если “протяжка” велась до
другой строки, то в интервале ссылок указать
соответствующий номер строки.

ЗАДАЧА РЕШЕНА.

Задача 2.
Определение возрастания и/или убывания функции
на заданном интервале.

Решение.
Для решения данной задачи в расчетной таблице
необходимо построить столбец D, в котором знак
будет указывать на возрастание или убывание
функции в данной точке. Для этого в ячейку D11
введем формулу

D11 => [=ЕСЛИ(a11<>””;ЗНАК(D11-D10);””)]
и “протянем” ее до строки №50.

И там, где знак положительный, функция
возрастает, а там, где знак отрицательный,
функция – убывает.

Далее построим вспомогательную таблицу, в
которой определим количество признаков
возрастания и убывания функции

	F	G
1	КОММЕНТАРИИ	ЗНАЧЕНИЯ
2	Признак возрастания	<формула>
3	Признак убывания	<формула>

Для этого в ячейки g2 и g3 соответственно вводим
формулы:

G2 => [=СуммЕсли(d11:d50;”>0”)]
G3 => [=СуммЕсли(d11:d50;”<0”)]

Таблицу ВыводаРезультатов дополним строкой

	D	E
1	комментарии	значения
2	Макс f(X)	=МАКС(с10:с50)
3	Мин f(X)	=МИН(с10:с50)
4	Возрастание/Убывание	<формула>

И для определения характера изменения заданной
функции остается ввести в ячейку Е4 формулу:

E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)

ЗАДАЧА РЕШЕНА.

Задача 3.
Определение четности данной.

Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком четности функции является
равенство f(X) = f(-X).

Для решения данной задачи в расчетной таблице
построим дополнительный столбец. В ячейку Е10
введем формулу

E10 => [=f(b10) – f(-b10)]
и “протянуть” ее до строки №50.

Таблицу ВыводаРезультатов дополним строкой

	D	E
1	комментарии	значения
2	Макс f(X)	=МАКС(с10:с50)
3	Мин f(X)	=МИН(с10:с50)
4	Возрастание/Убывание	[=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и другое”;”возрастает”);”убывает”)
5	четность	<формула>

В ячейку Е4 таблицы ВыводаРезультатов вводим
формулу.

E4 => [ЕСЛИ(ABS(СУММ(E10:E50))<0,000001; “ЧЕТНАЯ”;
“НЕЧЕТНАЯ”)

ЗАДАЧА РЕШЕНА.

Задача 4.
Определить является ли введенный период
периодом заданной функции.

Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком периодичности функции
является равенство f(Х) = f(X+<период>).

Для данной задачи добавим в таблице
ВводаИсходнойИнформации строку №6, в которой
введем численное значение предполагаемого
периода.

	А	В
1	КОММЕНТАРИИ	ЗНАЧЕНИЯ
2	Xn	<значение>
3	Xk	<значение>
4	Shag	<значение>
5	N	<формула>
6	период	<значение>

В ячейку В6 вводится число – предполагаемый
период заданной функции.

Далее для решения данной задачи построим
дополнительный столбец в расчетной таблице, для
этого в ячейку F11 введем формулу

F10 => [=ЕСЛИ(a10<>””;f(b10)-f(b10+$b$6);””)]

и “потягиваем” эту формулу до строки №50.

В таблице ВыводаРезультатов добавим строчку.

	D	E
1	комментарии	значения
2	Макс f(X)	=МАКС(с10:с50)
3	Мин f(X)	=МИН(с10:с50)
4	четность	=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и другое”;”возрастает”);”убывает”)
5	период	<формула>

В ячейке Е5 необходимо ввести формулу

Е5 => [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;”не
период”)]

Если данное значение предполагаемого периода
не подходит, то его можно изменить.

ЗАДАЧА РЕШЕНА.

Задача 5.
Для заданной функции определить:

• значения первой производной данной функции,
• наличия и количество экстремумов.

Решение.
Для решения первой части задачи, то есть
определения первой производной воспользуемся ее
разностным определение.

Построим столбец. Для этого в ячейку G11 вводим
формулу:

G11 => [= ЕСЛИ(a11<>””; ABS((c11-c10)/(b11-b10));””)]

и “протягиваем ее до строки с №50.

В результате получаем разностные приближенные
значения первой производной заданной функции в
заданных точках.

Для решения второй части задачи, то есть
определения наличия и количества экстремумов на
заданной функции в таблицу ВыводаРезультатов
дополнить строкой.

	D	E
1	комментарии	значения
2	Макс f(X)	=МАКС(с10:с50)
3	Мин f(X)	=МИН(с10:с50)
4	четность	=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и другое”;”возрастает”);”убывает”)
5	период	[=ЕСЛИ(СУММ(f10:f50)<0,01;”период”; ”не период”)]
6	Количество Экстремумов.	<формула>

В ячейке Е6 необходимо ввести формулу

E6 => [=СчетЕсли(g11:g50;”<0,05”)]

ЗАДАЧА РЕШЕНА.

Рис 2, см. Приложение 3

На рис.2 приведена построенная таблица
решения задач.

Предложенные в данной работе задачи можно
использовать на интегрированных уроках
информатика-математика, на уроках информатики
при изучении электронных таблиц, в частности, в
теме: “Мастер функций”.

Функция ОБЛАСТИ в Excel используется для подсчета числа областей, содержащихся в переданной ссылке, и возвращает соответствующее значение. В Excel областью является одна ячейка либо интервал смежных ячеек.

Примеры работы функции ОБЛАСТИ в Excel для работы с диапазонами ячеек

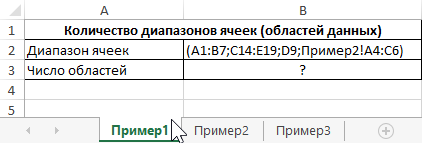
Пример 1. Вернуть число, соответствующее количеству областей в диапазонах A1:B7, C14:E19, D9, Пример2!A4:C6.

Исходные данные на листе «Пример1»:

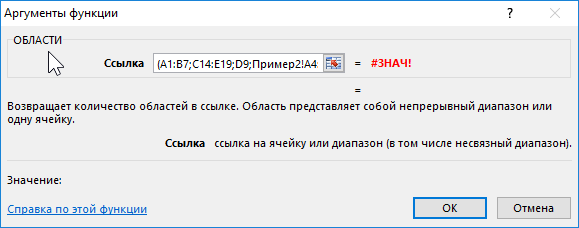
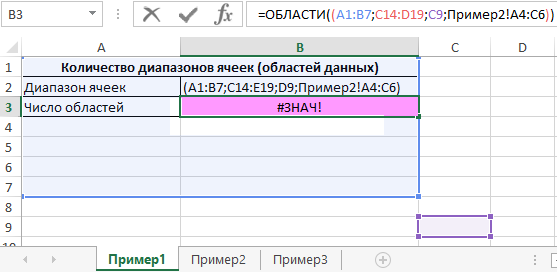
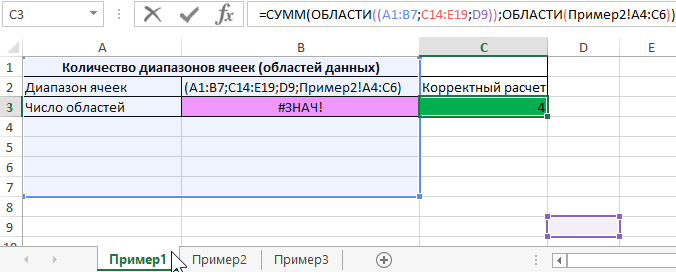
Для подсчета количества областей используем формулу:

Результат вычисления функции является ошибка #ЗНАЧ!, поскольку диапазон «Пример2!A4:C6» находится на другом листе.

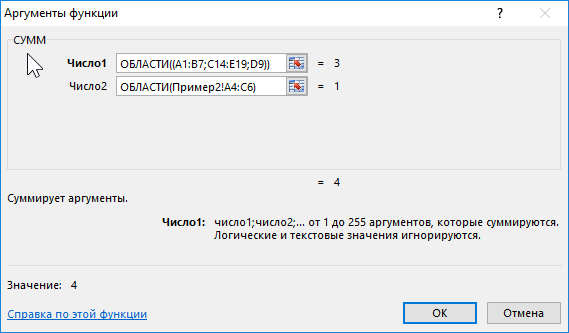
Для решения задачи используем формулу с помощью функции СУММ:

Данная функция вычисляет сумму полученных значений в результате выполнения функций ОБЛАСТИ для подсчета количества областей в диапазонах A1:B7;C14:E19;D9 и Пример2!A4:C6 соответственно. Результат:

С помощью такой не хитрой формулы мы получили правильный результат.



Как посчитать количество ссылок на столбцы таблицы Excel

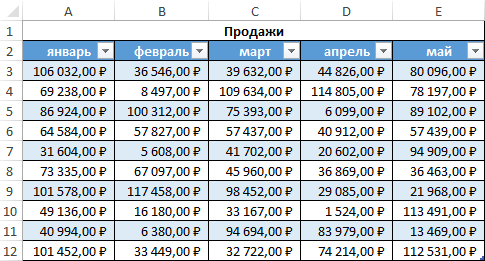
Пример 2. Определить количество столбцов в таблице и записать это значение в ячейку A16.

Таблица:

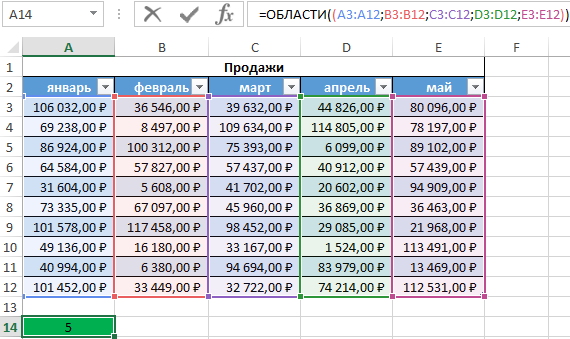
Используем формулу ОБЛАСТИ, поочередно выделяя каждый столбец ячейки в качестве параметра. Перед выбором последующего столбца нажимаем и удерживаем кнопку Ctrl. Если добавить символ «)» и нажать Enter, появится диалоговое окно с сообщением о том, что было введено слишком много аргументов. Добавим дополнительные открывающую и закрывающую скобки.

Результат вычислений:

Определение принадлежности ячейки к диапазону таблицы

Пример 3. Определить, принадлежит ли ячейка заданному диапазону ячеек.

Рассматриваемая функция также позволяет определить, принадлежит ли ячейка выделенной области. Выполним следующие действия:

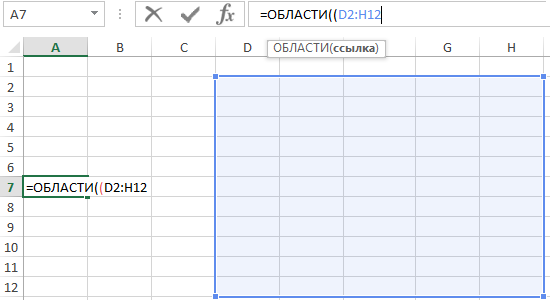
1. В какой-либо ячейке введем часть формулы «=ОБЛАСТИ((» и выделим произвольную область ячеек для заполнения аргументов:



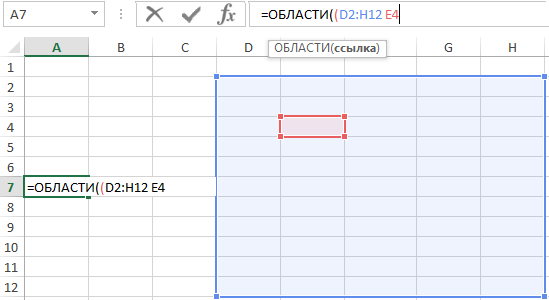
2. Поставим пробел и выберем любую ячейку из данного диапазона:



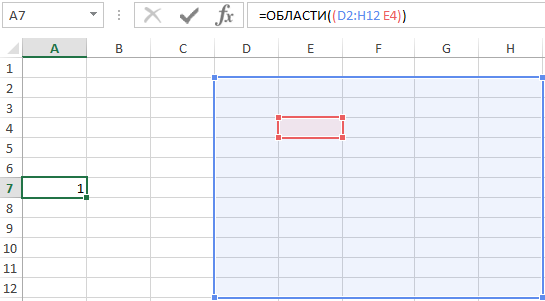
3. Закроем обе скобки и нажмем Enter. В результате получим:



4. Если выбрать ячейку не из указанного диапазона, получим ошибку #ПУСТО!.

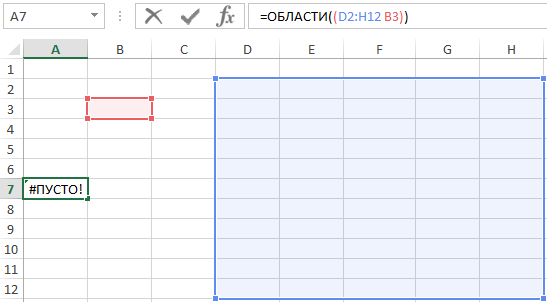
Данная ошибка означает, что ячейка не принадлежит выделенной области.

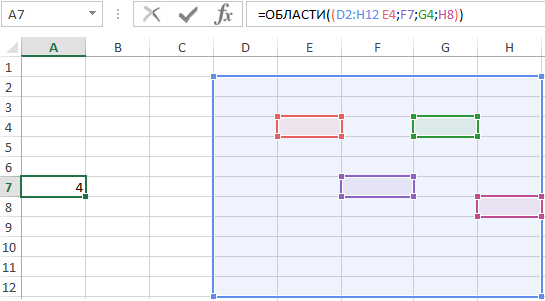
Если выделить несколько ячеек внутри диапазона, функция ОБЛАСТИ вернет количество выделенных ячеек:

Описанные особенности работы данной функции могут быть полезны при работе с большим количеством таблиц данных.

Особенности использования функции ОБЛАСТИ в Excel

Функция находиться в категории формул «Ссылки и Массивы». Она имеет следующую форму синтаксической записи:

=ОБЛАСТИ(ссылка)

Описание аргумента:

ссылка – обязательный для заполнения аргумент, который принимает ссылку на одну или несколько ячеек из указанного диапазона.

Примечания:

1. Аргументом рассматриваемой функции может являться только ссылка на диапазон ячеек. Если было передано текстовое или числовое значение, функция выполнена не будет, Excel отобразит диалоговое «В этой формуле обнаружена ошибка».
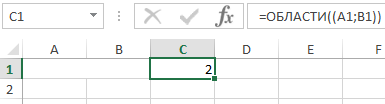
2. В качестве аргумента ссылка могут быть переданы несколько диапазонов ячеек. Для этого необходимо использовать еще по одной открывающей и закрывающей скобки (в этом случае Excel не будет распознавать символ «;» как разделитель аргументов в функции. Например, результатом выполнения функции с указанными аргументами: ((A1:C5;E1:H12)) будет значение 2, поскольку в качестве аргумента переданы два диапазона ячеек.
3. Если аргумент рассматриваемой функции ссылается на диапазон ячеек, находящихся на еще не созданном листе, Excel предложит создать лист с указанным именем и сохранить книгу.
4. Если некоторые ячейки, например, A1 и B1 были объединены, при выделении полученной ячейки в строке имен будет отображено имя «A1». Несмотря на объединение ячеек функция с аргументами ((A1;B1)) все равно вернет значение 2. Эта особенность показана на рисунке ниже:



5. Функция возвращает значения даже для заблокированных ячеек на листах со включенной функцией защиты.