Найдем векторное произведение 2-х векторов с помощью функций MS EXCEL. Также создадим таблицу для проверки
векторов
на коллинеарность.
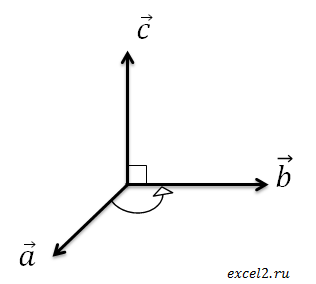
Сначала немного теории. Векторным произведением двух векторов
а
и
b
, заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор
c
, что:
-
он
перпендикулярен
обоим векторам
а
и
b
; -
длина вектора
с
равна произведению длин векторов
а
и
b
на синус угла между ними; -
вектор
с
направлен так, что тройка векторов
а
,
b
и
с
является правой (
с конца вектора
с
кратчайший поворот от вектора
a
к вектору
b
виден наблюдателю против часовой стрелки
).
Почему такое сложное определение? Дело в том, что результатом векторного произведения [
a
х
b
], в отличие от
скалярного
, является вектор. А для того, чтобы однозначно определить вектор нужно задать его длину (второй пункт определения) и направление (первый и третий пункты определения).
Векторное произведение
двух векторов
a
= {
a
x
;
a
y
;
a
z
} и
b
= {
b
x
;
b
y
;
b
z
} в декартовой системе координат можно вычислить, используя формулы:
[
a
х
b
] = {
a
y
b
z
—
a
z
b
y
;
a
z
b
x
—
a
x
b
z
;
a
x
b
y
—
a
y
b
x
}
или в матричной форме:
Теперь вычислим векторное произведение в MS EXCEL. Встроенная функция к сожалению отсутствует. Кроме того, формула должна возвращать три значения, т.е. 3 координаты вектора. Это может быть реализовано только
формулой массива
(вариант, когда 3 координаты рассчитываются независимо, с использованием 3-х различных формул, очевиден, но не интересен, хотя и приведен
файле примера
).
Пусть даны координаты векторов
а
и
b
, записанные в строках 8 и 9 (см.
файл примера
).
Обратим внимание, что запись в матричной форме напоминает
вычисление обратной матрицы методом алгебраических дополнений
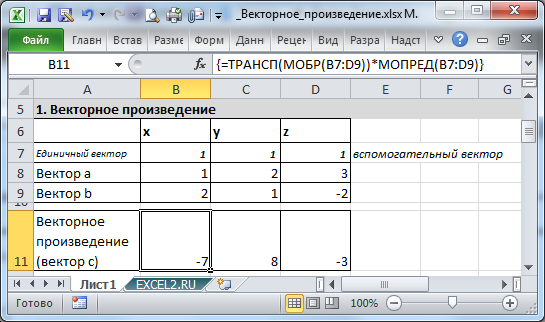
. Вместо единичных векторов i, j, k запишем вспомогательный вектор с координатами {1; 1; 1} и поместим его в строке 7 над векторами. Теперь у нас есть квадратная матрица А третьего порядка, для которой можно вычислить обратную матрицу.
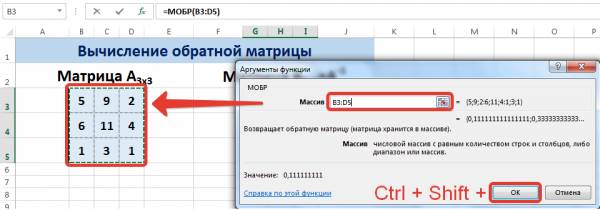
Попробуем использовать функцию
МОБР()
для вычисления векторного произведения. Заметим, что три слагаемых из определения векторного произведения в матричной форме совпадают со значениями верхней строки матрицы алгебраических дополнений.
Примечание
: Напомним, что алгебраическое дополнение A
ij
вычисляется по формуле A
ij
=(-1)
i+j
*М
ij
(где М — соответствующий минор, т.е. определитель, состоящий из элементов матрицы А за исключением всех элементов, расположенных на строке i и в столбце j).
Так как обратная матрица вычисляется по формуле:
то имея обратную матрицу, для вычисления верхней строки матрицы алгебраических дополнений и, соответственно, координат вектора
с
, необходимо ее
транспонировать
, а затем умножить ее на определитель матрицы А (той, что содержит координаты наших векторов
а
и
b
и единичный вектор).
Это реализовано с помощью
формулы массива
=ТРАНСП(МОБР(B7:D9))*МОПРЕД(B7:D9)
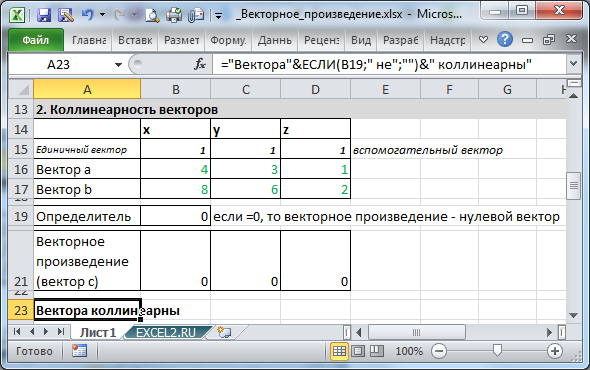
Коллинеарность векторов
Если два вектора коллинеарны, т.е. лежат на параллельных прямых, то их векторное произведение равно 0. В
файле примеров
приведена таблица для проверки векторов на коллинеарность.
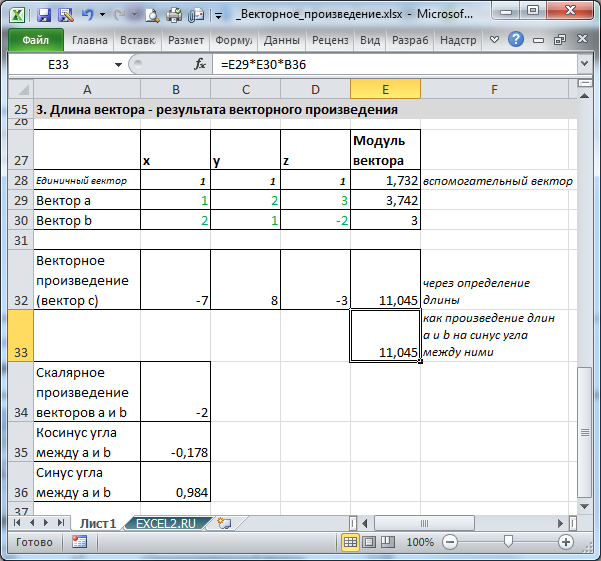
Нахождение длины вектора с — результата векторного произведения
Из определения векторного произведения
длина вектора
с
равна произведению длин векторов
а
и
b
на синус угла между ними.
Примечание
: Как вычислить длины векторов по их координатам показано в статье
Вычисление длины (модуля) вектора в MS EXCEL
.
Синус угла найдем через тригонометрическую формулe sin
2
x+cos
2
x=1
Конечно, можно также сначала найти векторное произведение, а затем длину полученного вектора. Естественно, оба метода расчета дают одинаковые результаты.
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
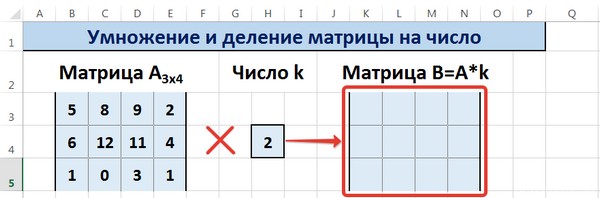
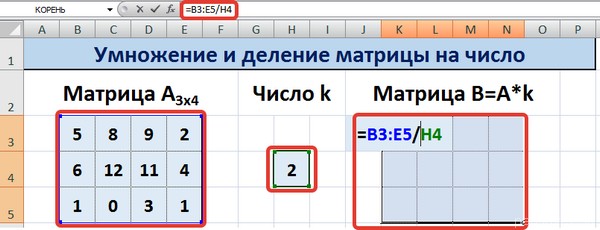
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
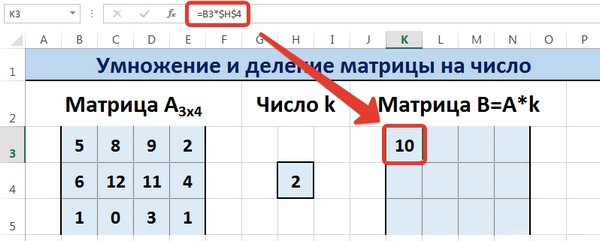
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
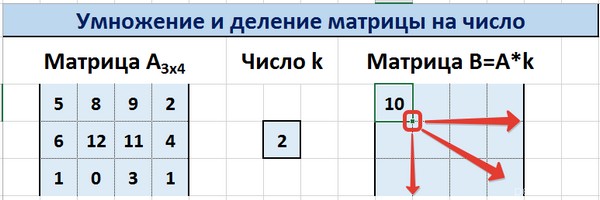
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
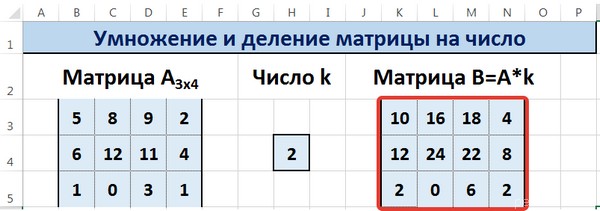
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
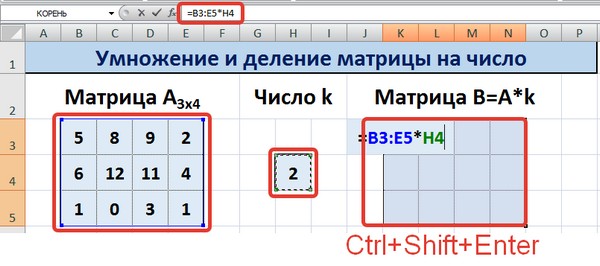
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
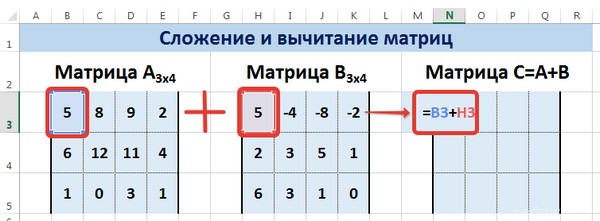
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
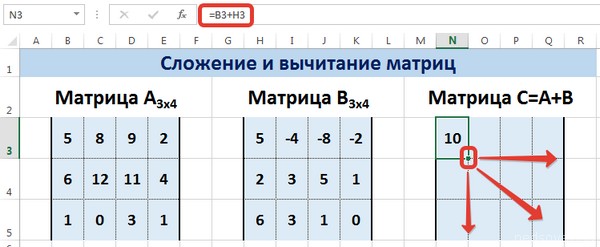
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
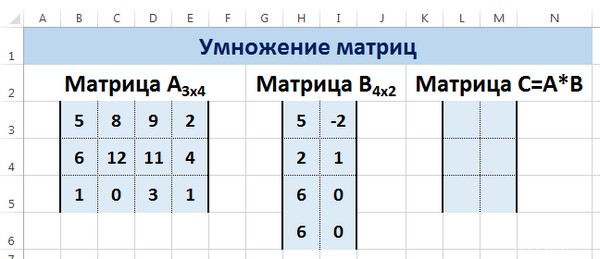
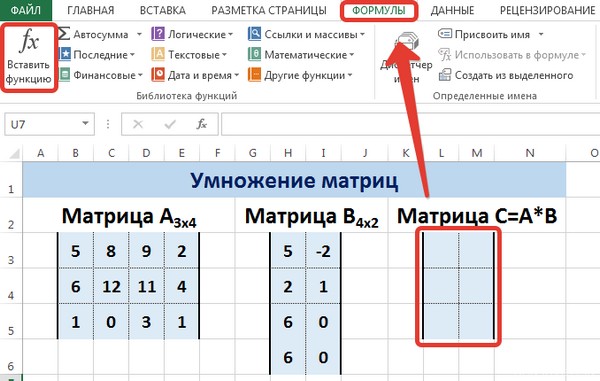
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
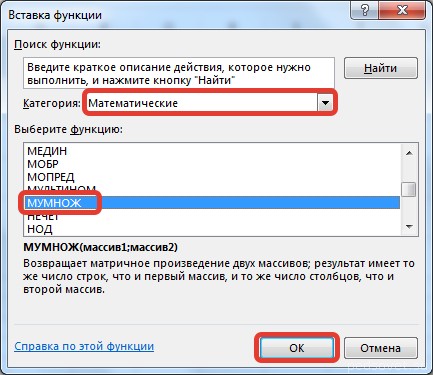
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
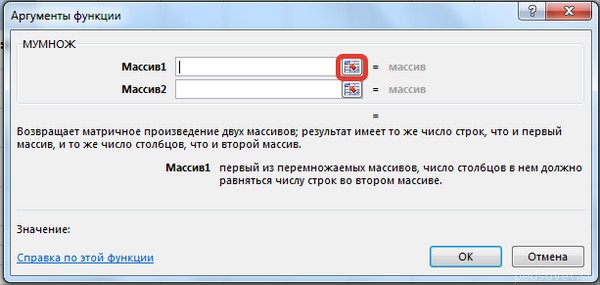
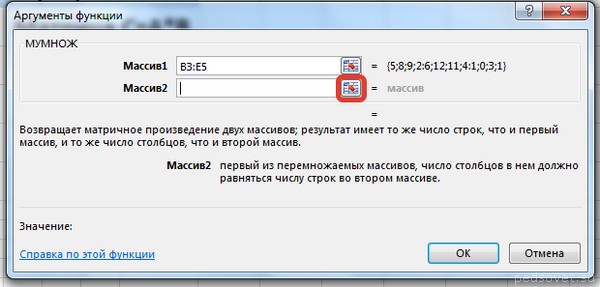
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
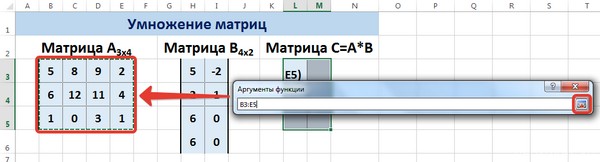
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
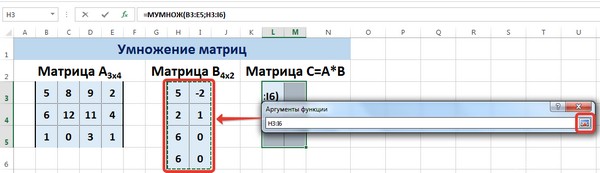
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
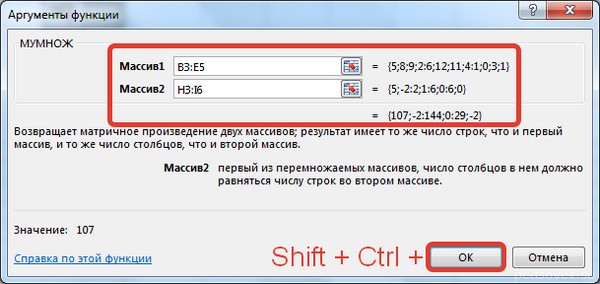
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
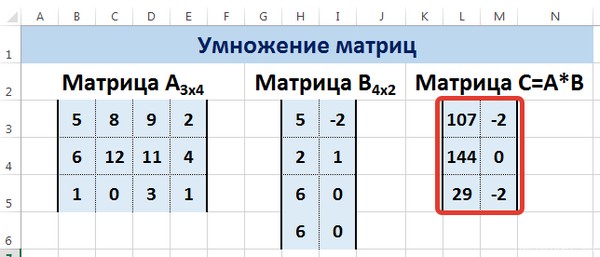
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
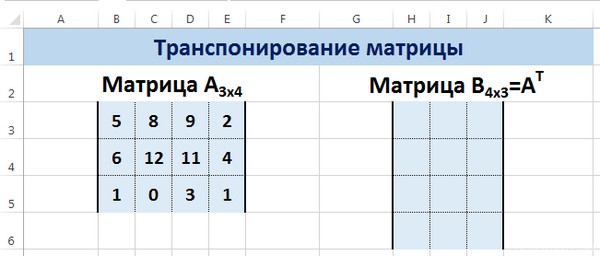
Транспонирование матрицы в Excel
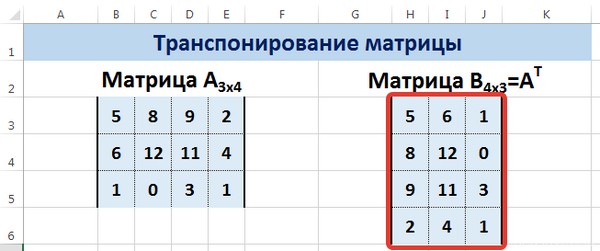
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
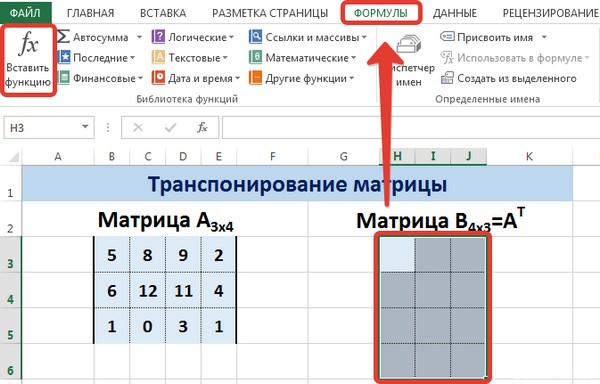
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
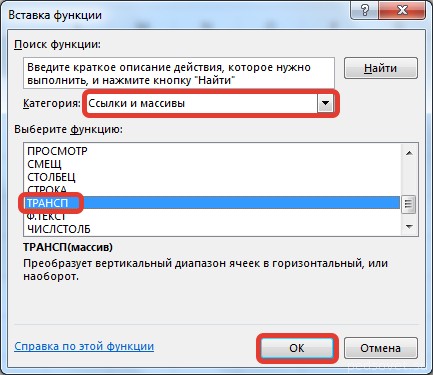
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
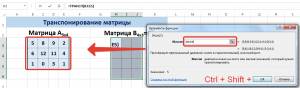
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
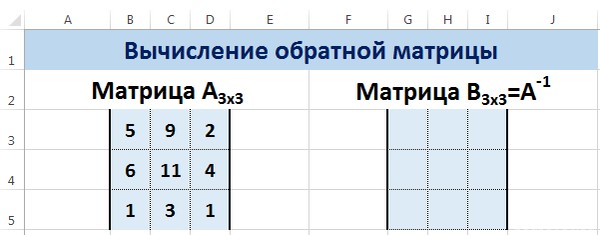
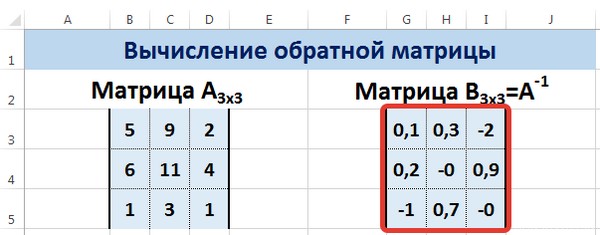
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
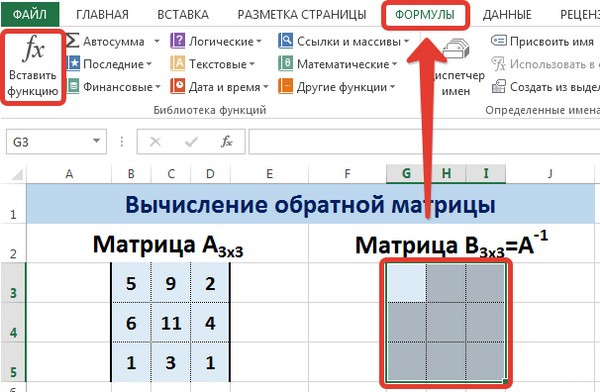
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
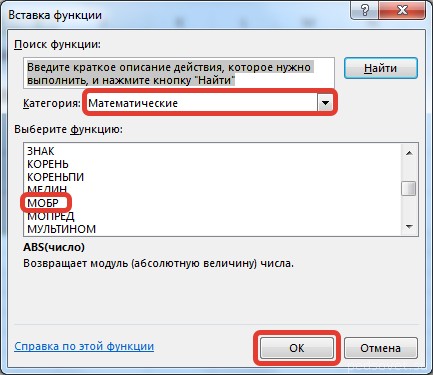
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
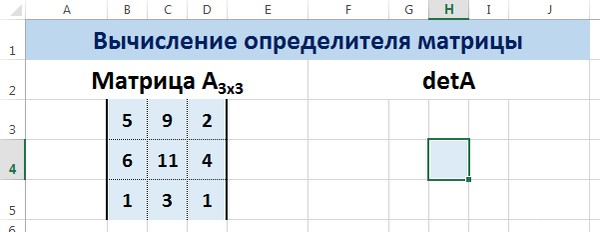
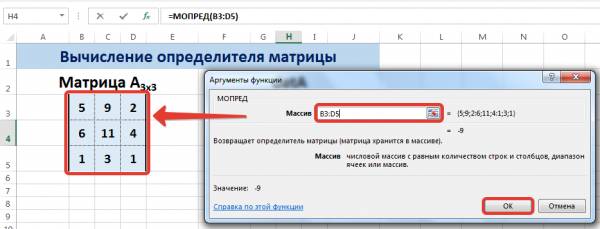
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
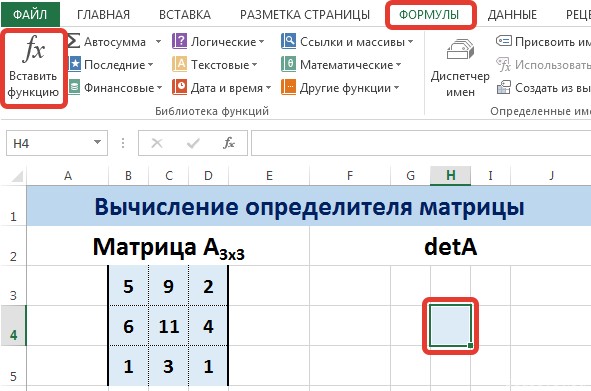
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
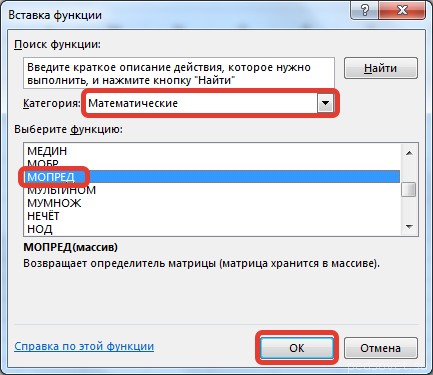
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
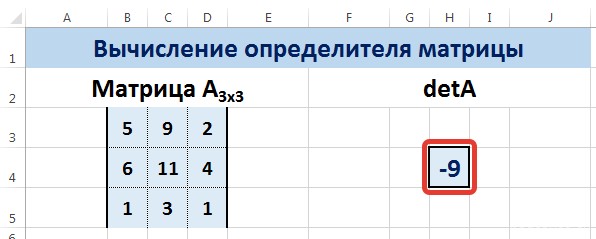
Нажмите для увеличения
Мы вычислили определитель матрицы А.
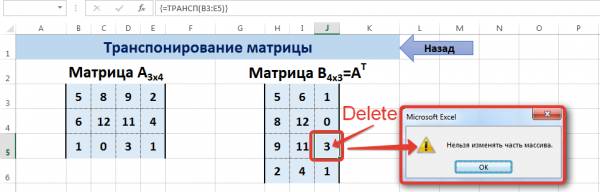
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Векторы и матрицы в Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Векторы и матрицы в Excel
C овокупность n чисел 
Два n -мерных вектора 


Суммой двух n -мерных векторов 

Операция сложения векторов обладает свойствами коммутативности 

Вектор 
Вектор 

Операция вычитания векторов определяется как сложение с противоположным вектором 
Под произведением вектора 

Умножение вектора на число обладает свойством ассоциативности 

Модуль (норма, длина) вектора 
Пример вычисления модуля вектора 
Р
исунок 1 – Вычисление длины вектора
Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.
В общем случае скалярное произведение двух векторов 




Операция скалярного умножения векторов обладает следующими свойствами:

В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).
Векторным произведением вектора 







Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.
Р
исунок 2 – Определение скалярного произведения двух векторов
Значение векторного произведения определяется следующим образом:
На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов 
Р
исунок 4 – Вычисление векторного произведения векторов
Перейдем к рассмотрению основных операций матричного исчисления.
Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :
Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:
Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.
Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается
При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы 
Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:
Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:
Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица
называемая транспонированной по отношению к матрице А.
Если А=А Т , то такая матрица называется симметричной.
В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.
Р
исунок 5 – Вызов функции ТРАНСП
Пример. Имеем исходную матрицу

Из определения ясно, что транспонированной будет матрица А Т :

Решение задачи в Excel представлено на рисунке 6
Рисунок 6 – Транспонирование матрицы
Порядок решения следующий:
— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);
— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);
— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;
— нажать Shit + Ctrl + Enter .
Суммой матриц А


Произведение матрицы на число — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:
Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы 





В Excel для вычисления произведения матриц используется функция
= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).
Р
исунок 7 – Умножение матриц
Формула для расчета произведения матриц должна быть введена как формула массива!
Пусть даны матрицы
Вычислим их произведение в Excel (рисунок 8).
— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);
— 
—
шаг 3 – выделить результирующий массив и нажать F2;
—
шаг 3 – нажать Shift+Ctrl+Enter.
Рисунок 8 – Вычисление произведения матриц
Действие умножения матрицы на матрицу обладает свойствами:
Отметим, что в общем случае
Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.
При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).
Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.
Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.
Для матрицы 2х2 определитель вычисляется как
Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:



Возможно разложение как по строкам, так и по столбцам.
В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).
Рисунок 9 – Расчет определителя матрицы
Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .
Детерминант треугольной матрицы равен произведению ее диагональных элементов
Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E
Обратную матрицу можно найти по следующей формуле:



Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).
Рисунок 10 – Расчет обратной матрицы
Заметим, что функция применяется к массиву как в ранее приведенных примерах.
Проверим выполнение условия А А -1 = E (рисунок 11)
Р
исунок 11- Произведение матрицы на обратную матрицу
Собственным числом квадратной матрицы
называется такое число 

Или, по-другому, собственными числами матрицы А являются корни уравнения 
Матрица 


Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:
Необходимо найти такие значения , при котором
Оформим лист Excel следующим образом (рисунок 12):
Рисунок 12 – Вычисление собственного числа матрицы
В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.
Из рисунка 12 видно, что при =0 определитель также равен 0, т.е. =0 есть первое собственное число матрицы.
Д
ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения , отображаемом в ячейке $F$2.
Рисунок 13 – Вычисление собственного числа матрицы
О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).
Рисунок 14 – Результат поиска решения
Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат =0.
П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):
Рисунок 15 – Ввод ограничения
В результате поиска получаем второе значение собственного числа: =3.
Повторим поиск при ограничении.
Если установить в ограничениях >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях
П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)
Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении
Рисунок 17 — Результат поиска третьего собственного числа
Собственным вектором соответствующим собственному числу λ называют такой вектор 
Найдем собственный вектор матрицы
Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.
1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).
2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.
3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.
4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор 
5. В ячейки (H2:H4) заносим умножение столбца 
6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).
7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.
Нажать кнопку « Выполнить ».
В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).
Рисунок 18 – Определение собственного вектора матрицы
Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.
Задания для самостоятельной работы
Повторить решение всех примеров, приведенных в Лекции №5.
Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15
Определить длину векторов.
Вычислить сумму и разность векторов.
Определить скалярное произведение этих векторов.
Определить угол между векторами.
Определить векторное произведение двух векторов.
Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.
Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.
Получить транспонированные матрицы исходных матриц.
Проверить правильность решения путем умножения исходной матрицы на транспонированную.
Определить произведение исходных матриц.
Найти матрицу 3-го порядка для исходной квадратной матрицы.
Определить детерминант исходной квадратной матрицы.
Перемножение одной матрицы на другую в Microsoft Excel
Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
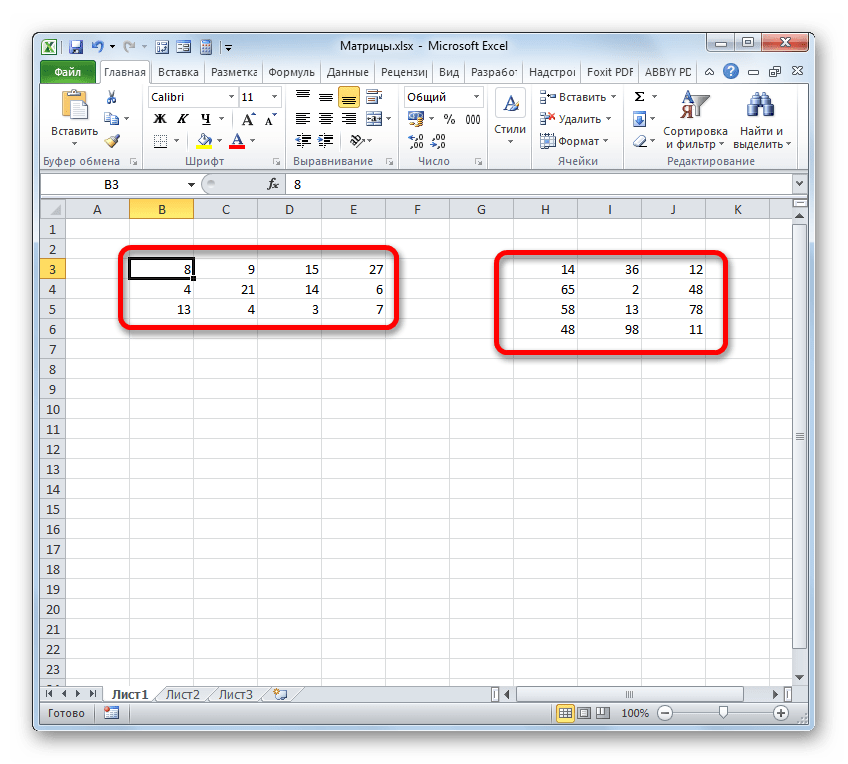
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
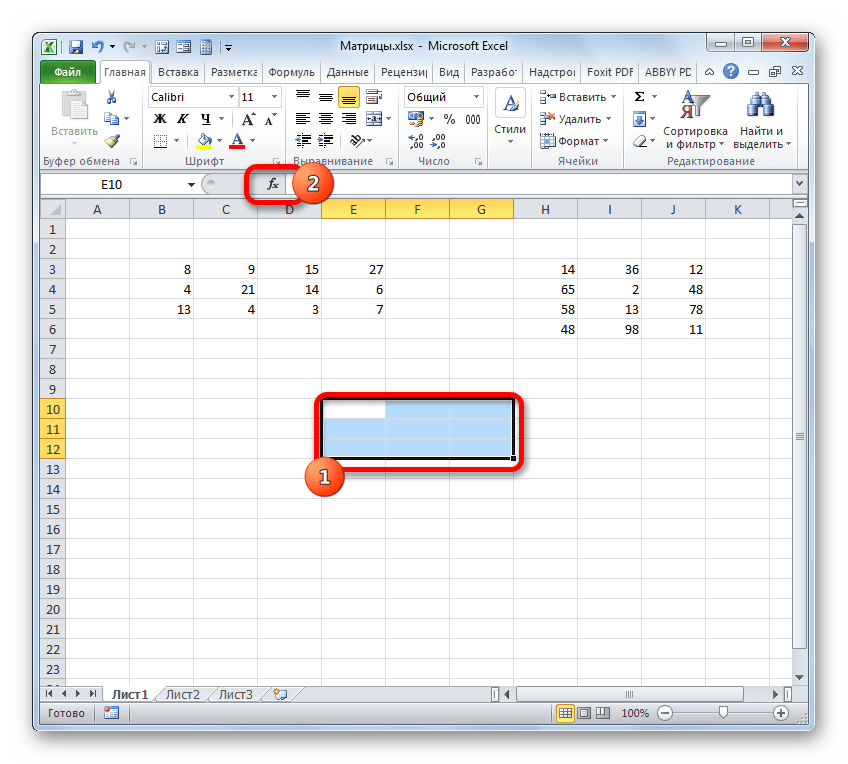
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
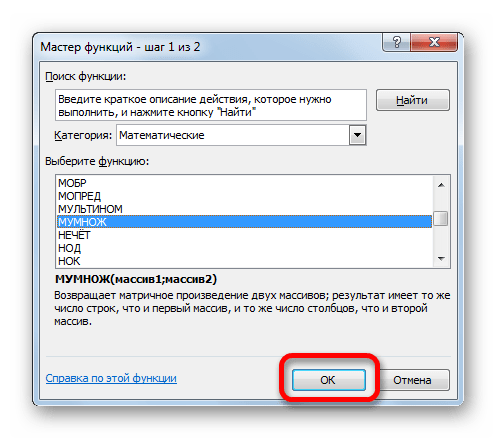
Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
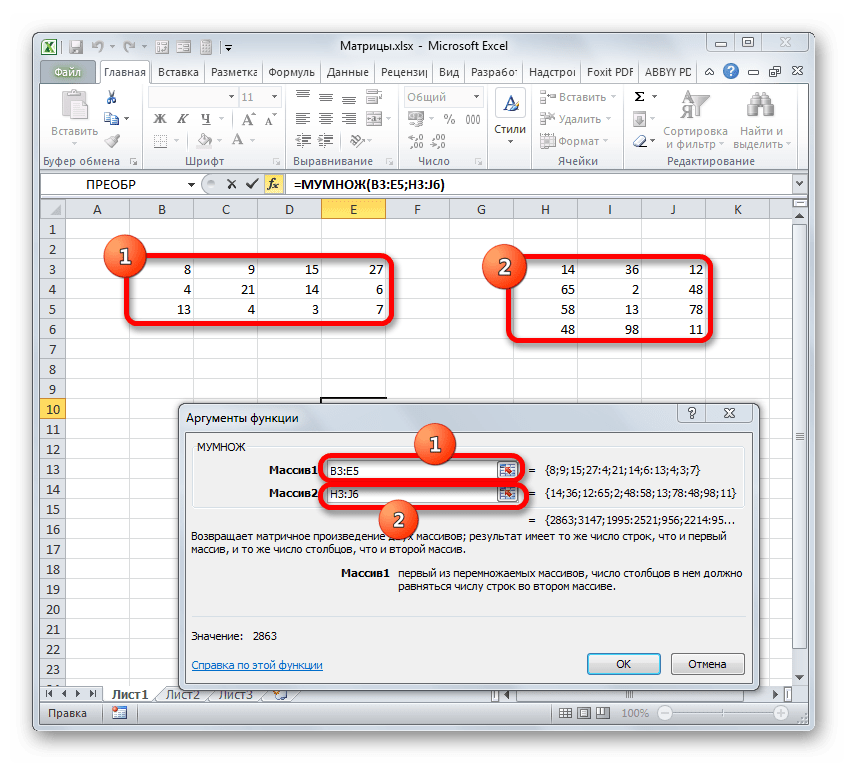
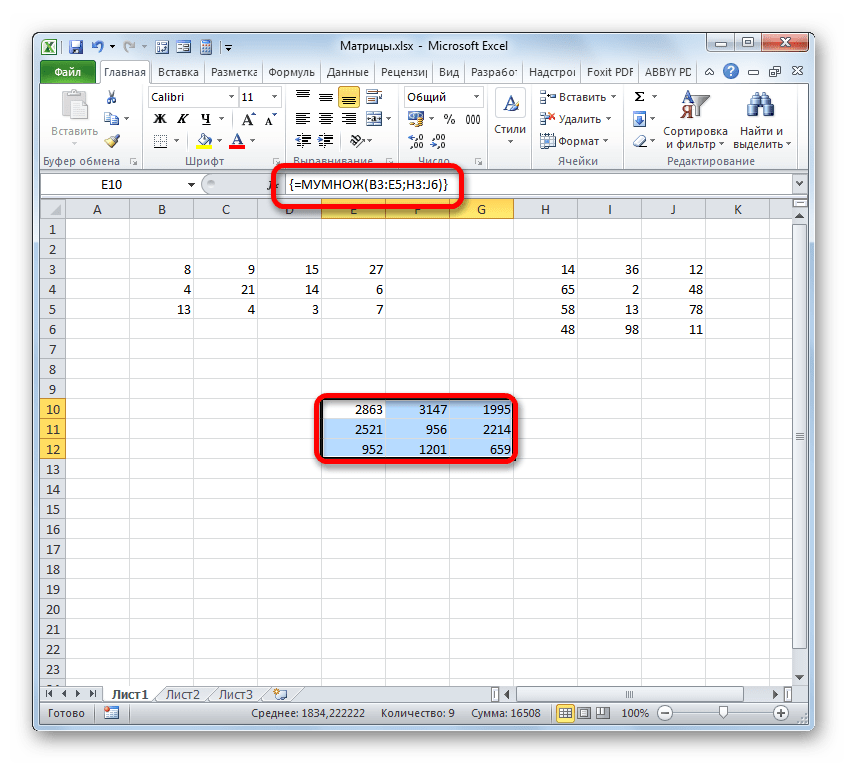
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки «OK» жмем комбинацию кнопок Ctrl+Shift+Enter.
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
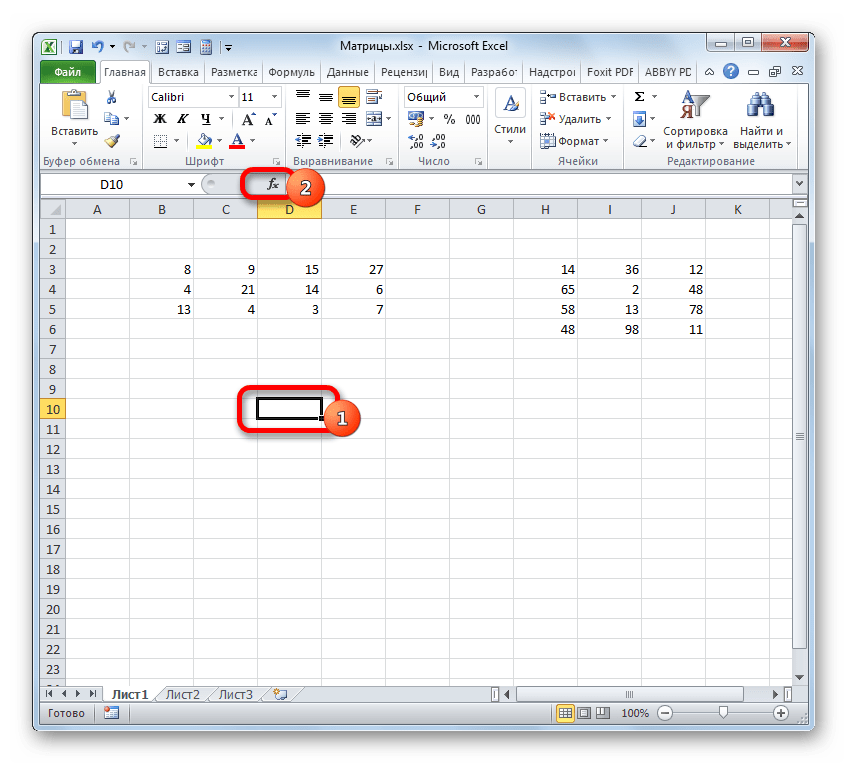
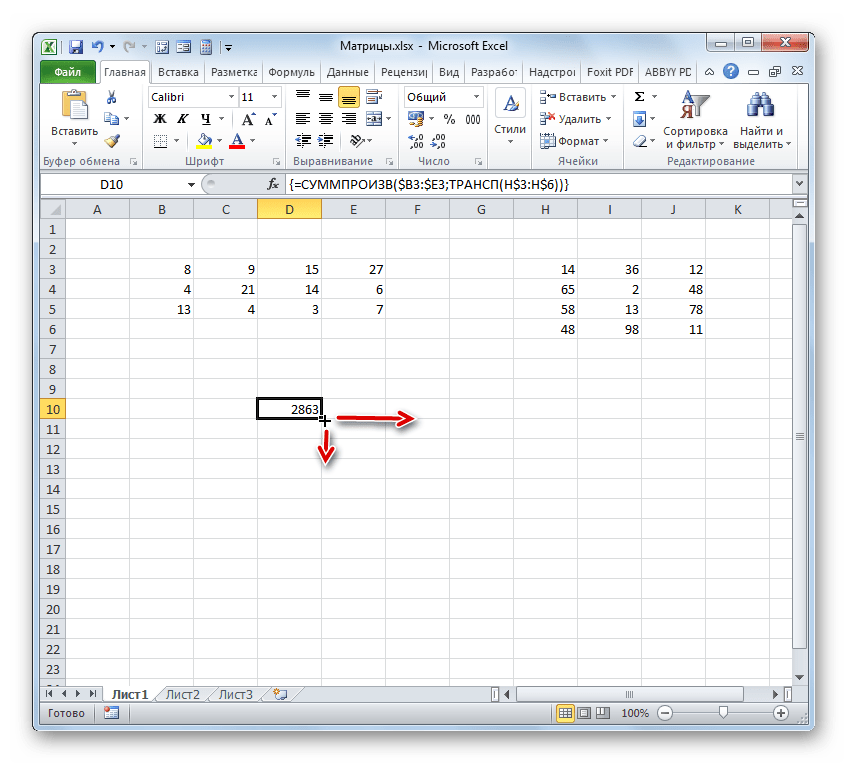
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
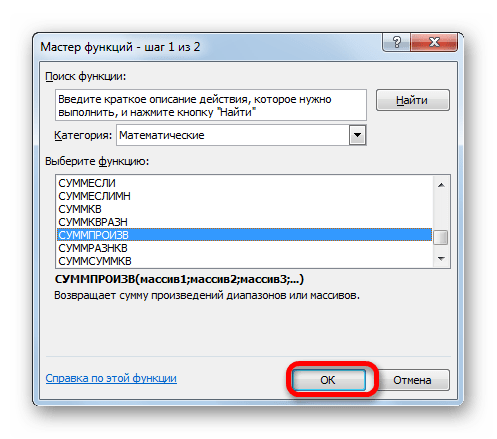
Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
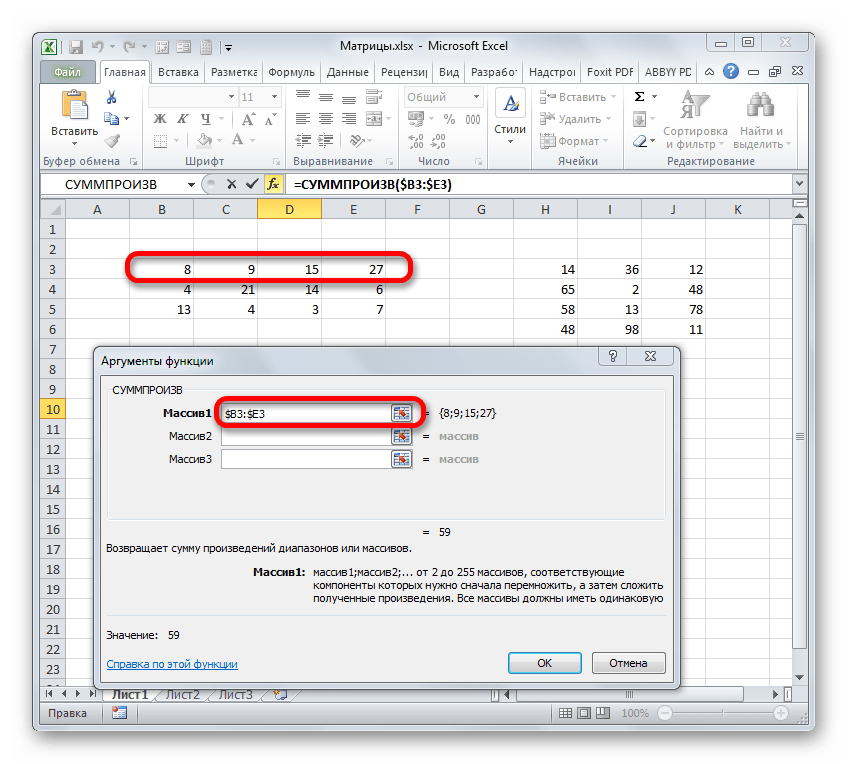
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
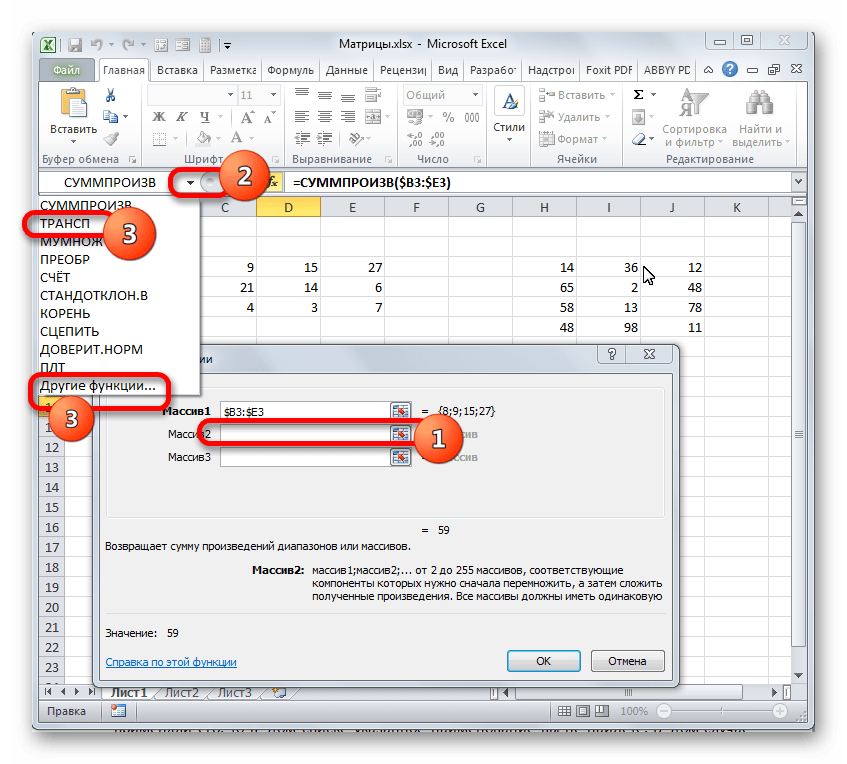
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
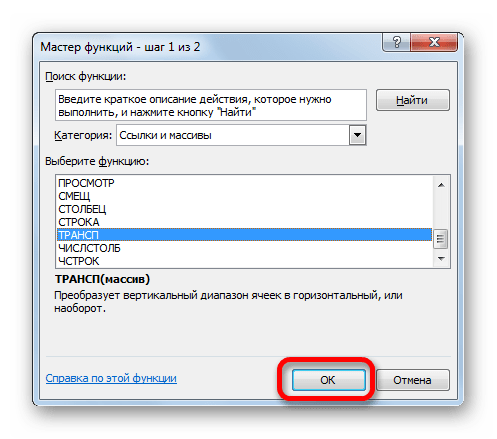
Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
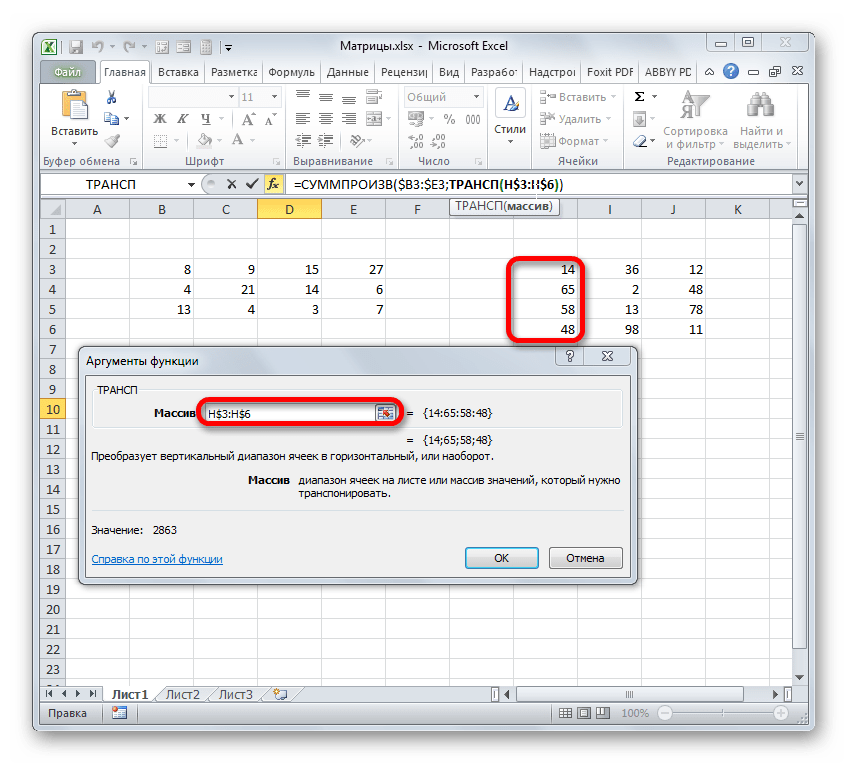
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
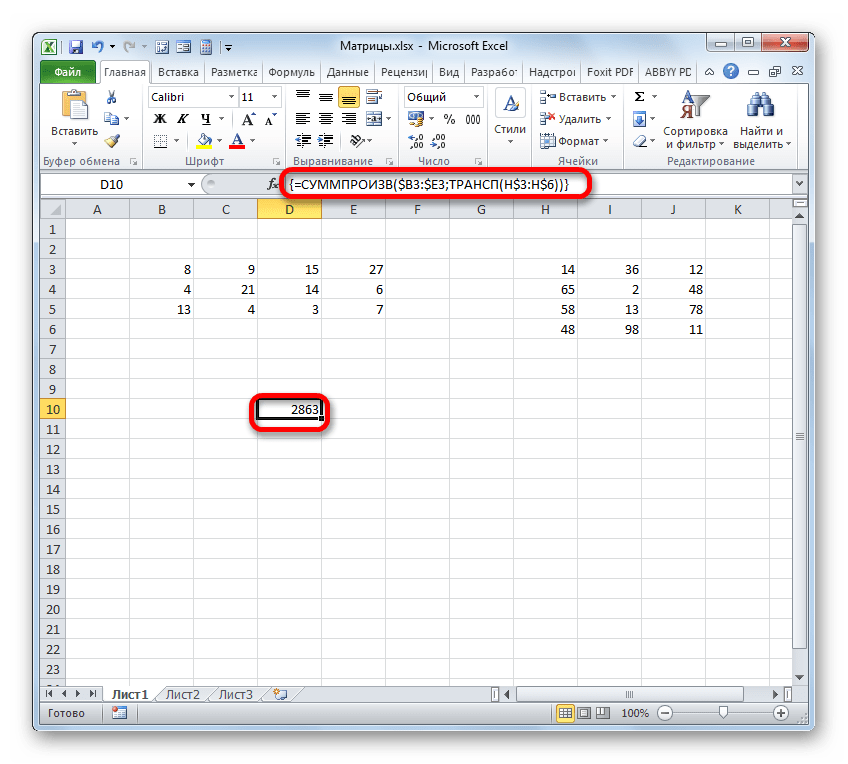
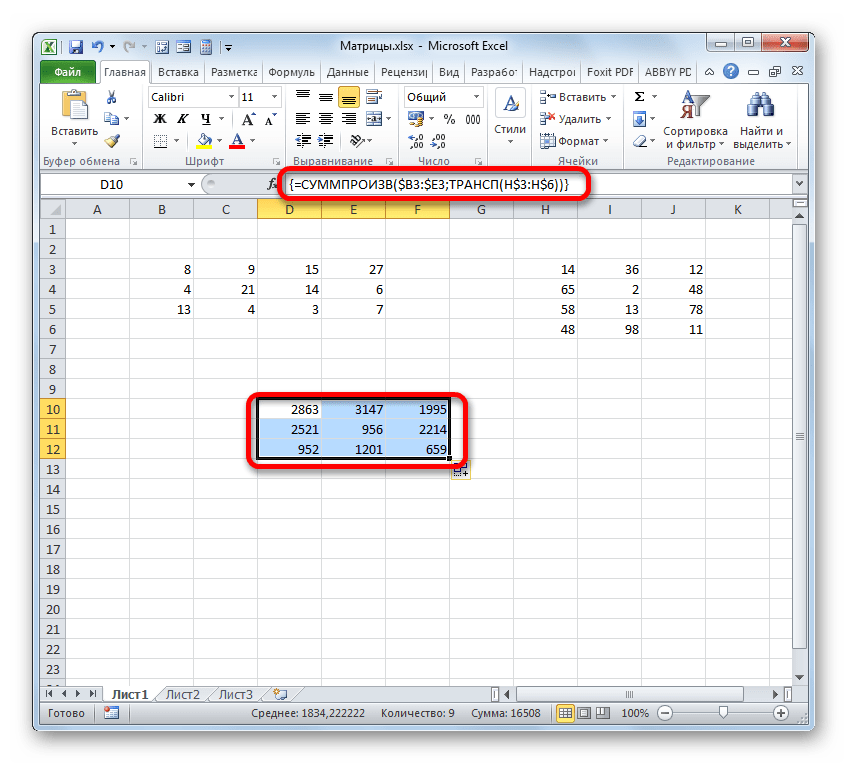
Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
Для копирования прибегнем к использованию маркера заполнения. Наводим курсор на нижний правый угол ячейки, в которой расположена формула. Курсор преобразуется в черный крестик. Это и есть маркер заполнения. Зажимаем левую кнопку мыши и протягиваем курсор по всему вышеуказанному диапазону. Сама начальная ячейка с формулой должна стать левым верхним элементом данного массива.
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Помимо этой статьи, на сайте еще 12604 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
источники:
http://infourok.ru/vektori-i-matrici-v-ecel-1119397.html
http://lumpics.ru/how-to-multiply-matrices-in-excel/
Министерство
образования и науки Российской Федерации
Саратовский
государственный технический университет
имени Гагарина Ю.А.
Методические
указания и задания для студентов
Саратов
2012
Введение
Методические
указания представлены в виде набора
практических и лабораторных работ для
развития навыков моделирования и
реализации решения инженерных задач.
Задачи сопровождаются инструкциями
выполнения. Предлагаемые упражнения и
задания помогут усвоить технику
использования MS Excel и найти эффективные
способы решения практических задач.
Основные понятия Массивы
Массив
данных – это совокупность однотипных
элементов. Тип элементов в MS Excel
определяется с помощью Формат Ячейки.
В MS Excel можно работать с одномерными
и двумерными массивами.
Одномерные
массивы (векторы), состоят из элементов
строк или столбцов, например, B2:B5, C9:G9
(рис. 1).
Рис. 1
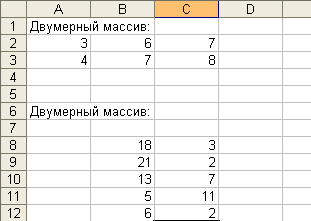
Двумерные
массивы (матрицы) состоят из элементов,
располагающихся в прямоугольном
диапазоне, например, A2:C3,
B8:C12 (рис.
2).
Рис. 2
Формулы массивов
Формулы
массивов используются для того, чтобы
производить вычисления над несколькими
значениями (массивом значений), не
производя копирования и заполнения.
П
ример.
Выполним сложение и вычитание двух
векторов А=(а1,а2,…аn)
и B=(b1,b2,…bn),
где n = 4, например, (рис.
3).
Рис. 3
Инструкция
для сложения элементов двух векторов
(рис. 3):
-
Выделить
диапазон (строка) D3:G3,
где будет результат сложения; -
Ввести
знак равенства в строку формул; -
Выделить
первый массив D1:G1; -
Вставить
знак «плюс»; -
Выделить
второй массив D2:G2; -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1+
D2:G2}.
Инструкция
для вычитания элементов двух векторов
(рис. 3):
-
Выделить диапазон (строка) D4:G4.
-
Ввести
знак равенства. -
Выделить
первый массив D1:G1. -
Вставить
знак «минус». -
Выделить
второй массив D2:G2. -
Нажать
комбинацию клавиш Ctrl+Shift+Enter. -
Просмотреть
содержимое ячеек полученного вектора.
В каждой ячейке будет отображена одна
и та же формула
{=D1:G1-
D2:G2}.
Изменить
содержимое ячеек полученных строк
(векторов) невозможно. Нельзя вставить
столбец в вектор. При таких попытках
будет выдано сообщение, что нельзя
изменить часть массива.
Если
при выполнении пункта 6 инструкций,
нажать на клавиатуре клавишу Enter вместо
клавиш Ctrl+Shift+Enter, то в этом случае формула
вычислит только одно, первое значение
вектора. Перейти в режим редактирования
нужно нажатием клавиши F2. Затем
одновременно нажать Ctrl+Shift+Enter.
Ошибки в формулах
При
наборе формул могут быть допущены
ошибки, например:
Набраны
две арифметические операции подряд,
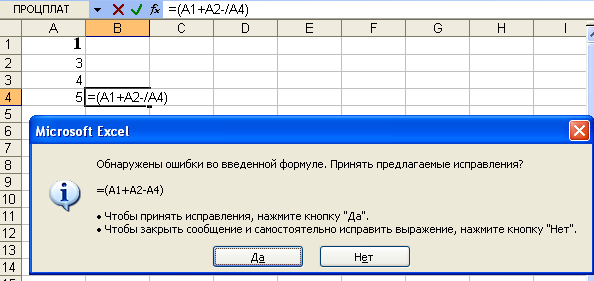
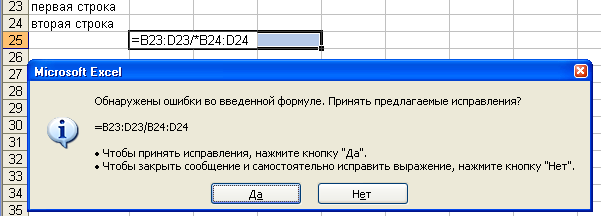
пропущен оператор, например, (рис. 4 а)
вод формулы =(A1+A2-/A4), при наборе допущена
элементарная ошибка или пропущен адрес
ячейки или ошибочно введены подряд две
арифметические операции вычитания и
деления (рис. 4 б–4 г).
Рис. 4 а
Рис. 4 б
Рис. 4 в
Рис. 4 г
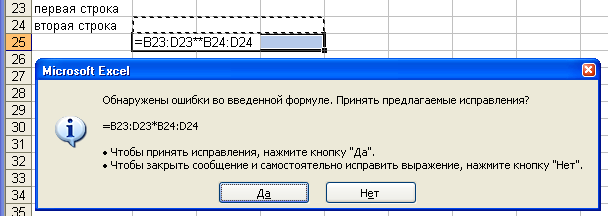
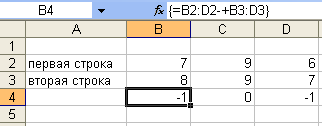
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «+», а затем «–», то не будет
ошибки, выполнится операция вычитания
(рис. 5).
Рис. 5
Рис. 6
Если
при выполнении сложения элементов двух
строк, ошибочно введены в формулу два
знака арифметических операций подряд,
сначала «–», а затем «+», то не будет
ошибки, опять выполнится операция
вычитания (рис. 6).
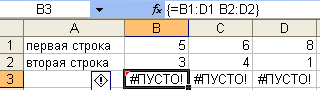
Пробел
между вектором А1:D1 и
В2:D2 означает пересечение
диапазонов (рис. 7). Пересечения ячеек
#ПУСТО!
Точка
с запятой – это объединение диапазонов
(рис. 8). В формуле ошибка.
Рис. 7
Рис. 8
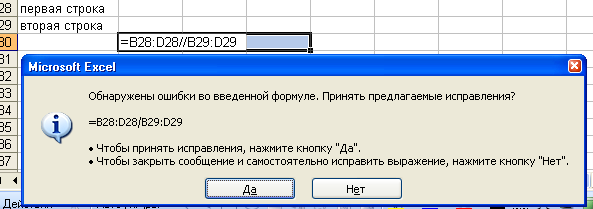
Могут
возникать ошибки в формулах при попытках
деления на 0
Рис. 9
Рис. 10
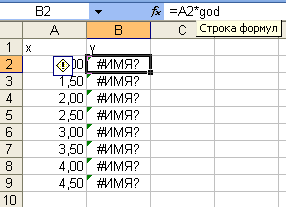
Ошибки
могут быть связаны с неопределенными
именами ячеек, использованных в формулах:
ошибка #ИМЯ? – не распознается имя,
используемое в формуле (рис. 11–12).
Имя адреса ячейки qod не
было присвоено;
Рис. 11
Рис. 12
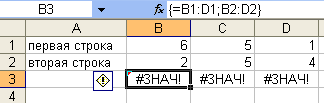
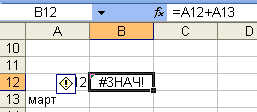
Ошибка
#ЗНАЧ! – используются операторы или
аргументы недопустимого типа (рис. 13).
В ячейке B12 возникла ошибка
#ЗНАЧ! В этом случае это значит, что
складываются содержимое ячеек А12 и А13
разного типа. A13 определено
как тип дата, а A12 — как
число.
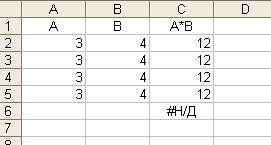
Ошибка
#Н/Д возникла в C6
неопределенных данных, т.е. не определены
значения ячеек A6 и B6
(рис. 14).
Рис.13
Рис. 14
В этом
примере ошибка #ПУСТО! возникает при
пересечении двух диапазонов, которые
в действительности не имеют общих ячеек
(рис. 15).
Рис. 15
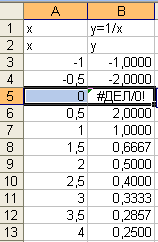
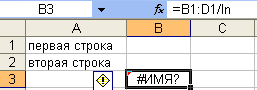
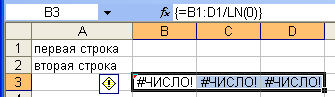
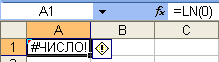
Ошибка
#ЧИСЛО! На рис. 16, 17 возникает при вычислении
натурального логарифма от нуля, что
невозможно.
Рис. 16
Рис. 17
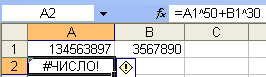
Такого
рода ошибка, как на рис. 18, происходит
при «переполнении», когда числовое
значение вычисляемой формулы слишком
велико или слишком мало для используемого
формата.
Рис. 18
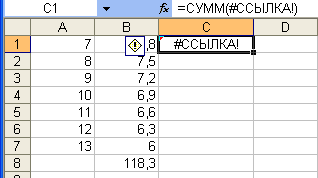
Ошибка
#ССЫЛКА! – неправильная ссылка на
ячейку. В ячейке В8 (рис. 19) вычислена
сумма элементов массива A1:B7.
При попытке скопировать содержимое
ячейки В8 в ячейку С1 и произошла ошибка.
При копировании часто возникает ошибка
#ССЫЛКА.
Рис.19
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 2 мин
Предполагая, что у нас есть вектор A с элементами (A 1 , A 2 , A 3 ) и вектор B с элементами (B 1 , B 2 , B 3 ), мы можем вычислить векторное произведение этих двух векторов как:
Перекрестное произведение = [(A 2 *B 3 ) — (A 3 *B 2 ), (A 3 *B 1 ) — (A 1 *B 3 ), (A 1 *B 2 ) — (A 2 *B 1 )]
Например, предположим, что у нас есть следующие векторы:
- Вектор А: (1, 2, 3)
- Вектор B: (4, 5, 6)
Мы могли бы вычислить векторное произведение этих векторов как:
- Перекрестное произведение = [(A 2 *B 3 ) — (A 3 *B 2 ), (A 3 *B 1 ) — (A 1 *B 3 ), (A 1 *B 2 ) — (A 2 *B 1 )]
- Кросс-произведение = [(2*6) – (3*5), (3*4) – (1*6), (1*5) – (2*4)]
- Перекрестное произведение = (-3, 6, -3)
В следующем примере показано, как вычислить это точное перекрестное произведение в Excel.
Пример: вычисление векторного произведения в Excel
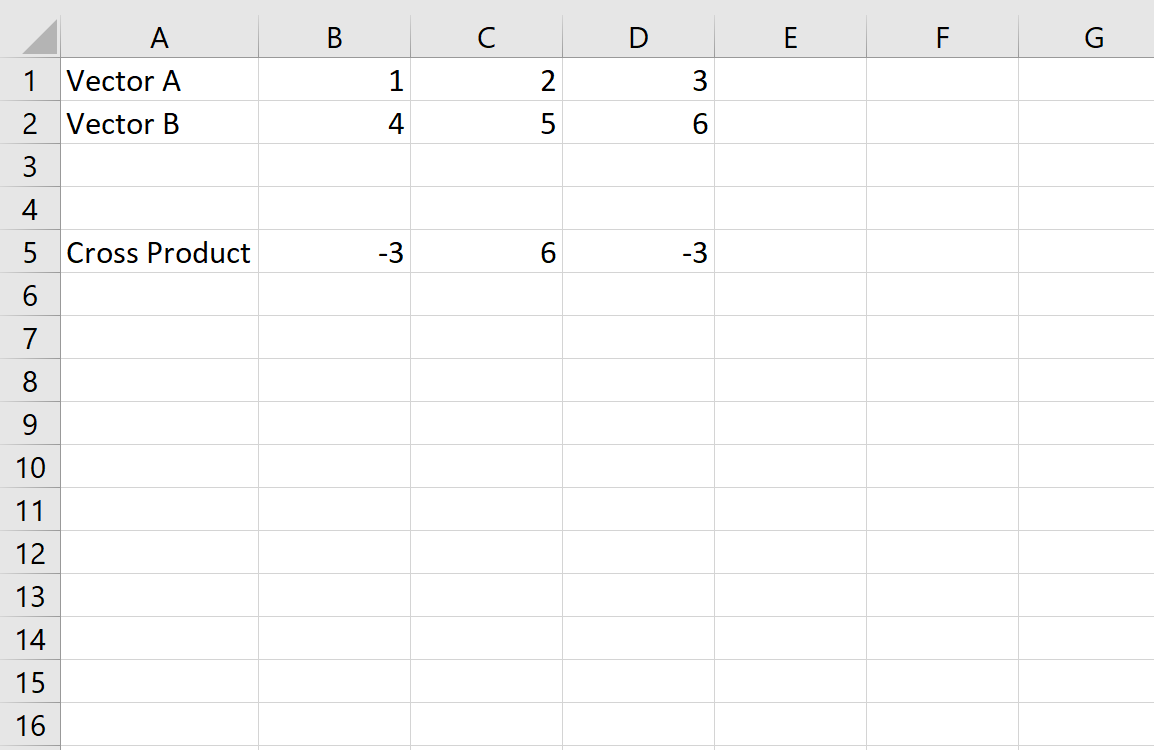
Чтобы вычислить векторное произведение между двумя векторами в Excel, мы сначала введем значения для каждого вектора:
Далее мы вычислим первое значение векторного произведения:
Затем вычислим второе значение:
Наконец, мы вычислим третье значение:
Перекрестное произведение оказывается (-3, 6, -3).
Это соответствует перекрестному произведению, которое мы вычислили ранее вручную.
Дополнительные ресурсы
Как рассчитать скалярный продукт в Excel
Как рассчитать скалярный продукт на калькуляторе TI-84
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Задача 7
Вычислить «сигнальную» матрицу B= sign(A).
Сигнальная матрица имеет ту же размерность, что и матрица, являющаяся аргументом. Ее возможные значения (1, 0, -1) определяются знаком соответствующего элемента матрицы A.
Bij =1; Если Aij > 0 Bij =0; Если Aij =0 Bij = -1; Если Aij <0
На этом примере я продемонстрирую действия, выполняемые над матрицей, а заодно покажу использование в рабочих формулах одной из любимых функций программиста — функции ЕСЛИ (IF). Для решения этой задачи я:
- Ввел матрицу A в ячейки B18:D20.
- Дал ей имя: » MatrA «.
- Выделил область ячеек F18:H20 для матрицы B.
- Дал ей имя: » MatrB «.
- Ввел в эту область формулу над массивами:
"{=ЕСЛИ(MatrA > 0; 1; ЕСЛИ(MatrA = 0; 0; -1))}" - Получил ожидаемый результат.
Заметьте, функция ЕСЛИ реализует полноценную If — Then — Else конструкцию, где в качестве Else может снова использоваться функция ЕСЛИ. Что же касается семантики нашей формулы над массивами, то понятно, что для ее реализации организуется двойной цикл по всем элементам исходной матрицы, на каждом шаге которого проверяется свое условие в If — операторе и в зависимости от его истинности вычисляется соответствующее значение элемента матрицы B.
В заключение взгляните, как выглядит рабочий лист, на котором показано решение задач 5, 6 и 7:
При локализации Excel введены русские имена для стандартных функций, вызываемых в формулах рабочего листа. Так вместо исходных имен IF и SUM следует использовать имена: ЕСЛИ и СУММ. Лично я предпочел бы, чтобы русские имена функций были бы синонимами, возможными, но не обязательными в использовании. Но правила нужно принимать. Вместе с тем хочу обратить внимание на то, что в функциях, написанных на VBA, при вызове стандартных функций следует использовать исходные имена функций. Более того, когда MacroRecorder создает макрос, он автоматически транслирует русские имена стандартных функций в исходные имена. Есть еще одна важное отличие в вызове стандартных функций в формулах рабочего листа и на VBA. Заметьте, разделителем параметров в формулах рабочего листа является символ » ; «, а для VBA — » ,».
Задача 8
Чтобы лучше понять семантику формул с массивами, давайте рассмотрим еще один пример. Вернемся к задаче о вычислении скалярного произведения двух векторов, успешное решение которой было только что продемонстрировано. Внесем некоторое, казалось бы, несущественное изменение в условия задачи. Предположим, что вектора A и B имеют разную ориентацию — один из них вытянут горизонтально, другой — вертикально. Если попытаться решить задачу аналогично тому, как решалась задача 5, то результат может показаться неожиданным, — скалярное произведение не будет вычислено правильно. Попробуем с этим разобраться.
Постановка задачи:
Вычислить скалярное произведение векторов разной ориентации: C = SUM(Aj*Bj).
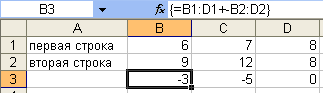
Вначале рассмотрим результаты следующего эксперимента. Вот мои действия:
- Создал вектор с горизонтальной ориентацией на рабочем листе, для чего в ячейки F5:H5 ввел значения: 6, 7, 8. Затем выделил этот диапазон и дал созданному вектору имя HorA3.
- Аналогично создал вектор с вертикальной ориентацией на рабочем листе, для чего в ячейки A6:A8 ввел значения: 3, 5, 7. Затем выделил этот диапазон и дал созданному вектору имя VerA3.
- После чего я попытался получить скалярное произведение этих векторов, используя ту же формулу, что и в похожей задаче 5. Для этого я записал в ячейку C11 формулу над массивами: » {=СУММ(VerA3*HorA3)} «
- Результатом вычислений по этой формуле является значение 240, которое и появилось в ячейке C11. Понятно, что в данном случае эта формула вычисляет не скалярное произведение векторов, значение которого равно 92, а нечто другое. Давайте разберемся, как работает машина вычислений Excel в подобных ситуациях.
Операции над векторами разной ориентации
То, что полученный результат в предыдущем примере, отличается от ожидаемого, очевидно не связано с функцией суммирования. Функция СУММ честно суммирует все компоненты своего аргумента. Все дело в том, как Excel выполняет основные операции — сложение, умножение, вычитание и деление над массивами. Результат выполнения элементарных операций над массивами есть массив, размерность и ориентация которого зависит от размерности и ориентации массивов, являющихся аргументами операции. Для простоты я ограничусь сейчас рассмотрением действий над векторами, отложив рассмотрение действий над матрицами до следующей главы. Поскольку структура массива результата не зависит от выполняемой операции, то я рассмотрю только операцию умножения, — для сложения, вычитания, деления все будет выполняться аналогично. Для того чтобы рассмотреть все возможные случаи я ввел 3 горизонтально расположенных вектора и 3 вектора с вертикальной ориентацией. Эти вектора получили соответственно имена: HorA3, HorB3, HorA2 и VerA3, VerB3, VerA2. Первые два вектора в каждой ориентации состоят из трех компонент, третий вектор имеет две компоненты, на что указывает имя вектора. Теперь все готово, чтобы рассмотреть семантику выполнения операций и продемонстрировать соответствующие примеры:
-
Операции над векторами одинаковой ориентации и одинаковой размерности. В этом случае результатом является вектор той же размерности и ориентации, что и вектора — аргументы. Каждая компонента результирующего вектора является результатом выполнения операции над соответствующими компонентами векторов — аргументов: cj = aj * bj. В качестве демонстрации я перемножил между собой два вектора горизонтальной ориентации и два вектора вертикальной ориентации. В первом случае я выделил для результата горизонтально расположенный диапазон ячеек B18:D18 и ввел формулу над массивами: » {=HorA3*HorB3} «. Во втором случае в ячейки A14:A16 ввел формулу: » {=VerA3*VerB3} «. В обоих случаях были получены ожидаемые результаты.
-
Операции над векторами одинаковой ориентации и разными размерностями N и M, где N>M. В этом случае результатом выполнения операции является вектор той же ориентации, размерность которого равна N. Вектор является частично определенным, у него будет вычислено лишь M компонент, остальные компоненты получат неопределенное значение — » Н/Д «. Заметьте, нельзя считать, что результатом является полностью определенный вектор размерности M, поскольку в дальнейших операциях участвуют все компоненты. Вот подтверждающий пример. В ячейку E11 я ввел формулу над массивами: » {=СУММ(VerA3*VerA2)} «. Результат вычислений по этой формуле не определен — » Н/Д «, поскольку в суммировании будет участвовать ячейка с неопределенным значением » Н/Д «.
-
Операции над векторами разной ориентации и одной и той же размерности N. Результатом операции над такими векторами будет квадратная матрица размерности N*N, элементы которой получены применением операции ко всем возможным парам элементов: ci,j = ai * bj. Для демонстрации я выделил область из 9 ячеек C14:E16 и ввел формулу над массивами: » {=VerA3*HorA3} «, в результате область заполнилась попарными произведениями элементов соответствующих векторов. Теперь можно объяснить, что произошло в примере, с которого я начал, пытаясь вычислить скалярное произведение векторов разной ориентации. Когда формула над массивами — » {СУММ(A*B)} » применяется к векторам одинаковой ориентации, то суммирование идет над элементами вектора и реализуется одинарным циклом —
Ak * Bk. Когда же эта формула применяется к векторам разной ориентации, то суммирование п
рименяется к
элементам матрицы и реализуется двойным циклом —(Aj * Bk), что, впрочем, эквивалентно произведению сумм:
.
-
Операции над вертикально ориентированным вектором размерности N и горизонтально ориентированным вектором размерности M. Как ни странно, несмотря на разную размерность векторов, результатом всегда будет полностью определенная матрица размерности N*M. Ее элементы получаются применением операции ко всем возможным парам элементов исходных векторов:
Заметьте, размерность матрицы — результата не зависит от порядка следования аргументов при записи формулы над массивами, так что операции сложения и умножения коммутативны. Вот два примера. В область ячеек G14:H16 я ввел формулу над массивами: » {=VerA3*HorA2} «, в результате вычислений была создана прямоугольная матрица размерности 3*2. Аналогичная матрица была создана, когда я выделил область ячеек J14:K16 и записал туда следующую формулу:
Результаты всех моих действий по работе с векторами разной ориентации показаны на следующем рисунке:
Вернемся теперь к задаче 8 и посмотрим, как же все-таки вычислить настоящее скалярное произведение в том случае, когда вектора имеют разную ориентацию. Ответ понятен, проще всего привести их к одной ориентации, для чего один из них следует транспонировать. Для транспонирования можно воспользоваться стандартной функцией ТРАНСП, что я и сделал, введя в одну из ячеек — J5 формулу над массивами: » {=СУММ(VerA3*ТРАНСП(HorA3))} «. Вычисление по этой формуле дает нужный результат.
В следующей главе я продолжу разговор о том, как работает машина вычислений Excel и рассмотрю еще ряд задач, которые обычно решают прикладные программисты на первых курсах обучения. Сейчас же, подводя итог, еще и еще раз хочу сказать, что мне нравится Excel и, по моему мнению, связка Excel + VBA является прекрасной платформой для обучения основам программирования.

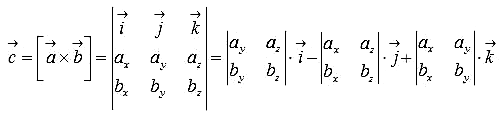
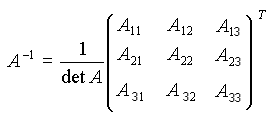



















































 .
.