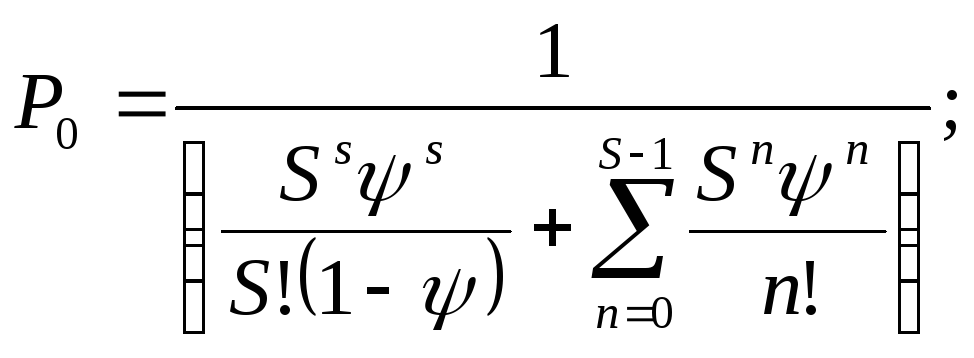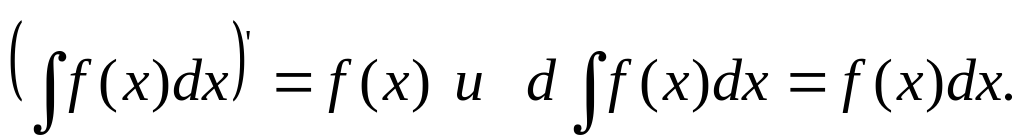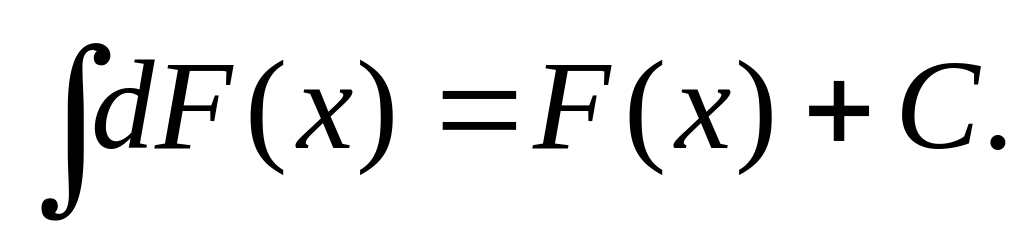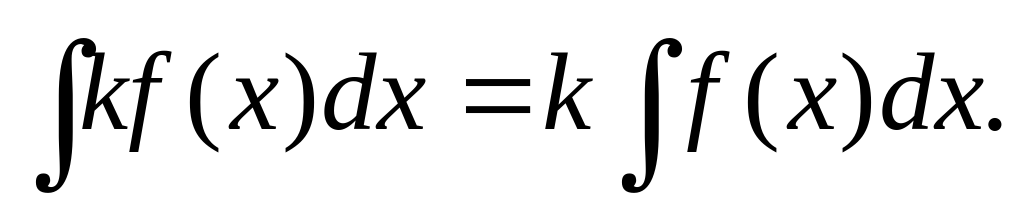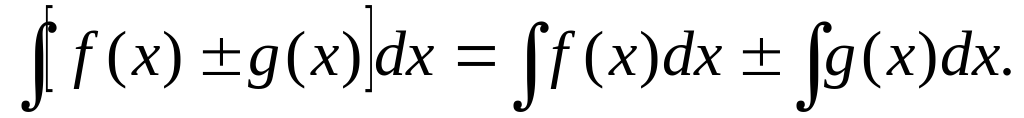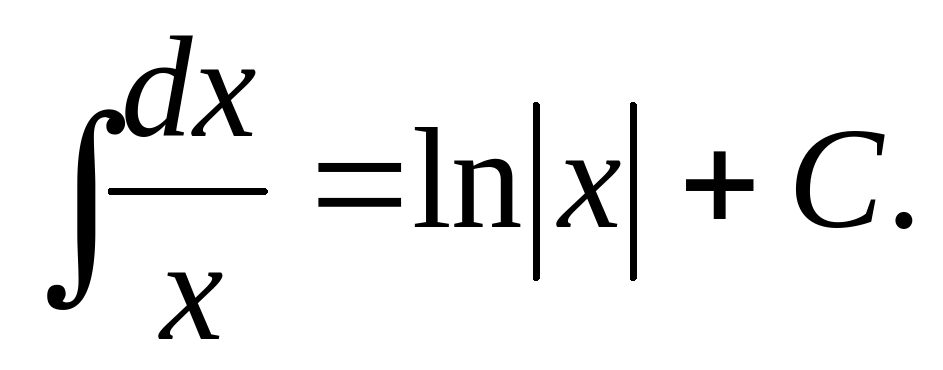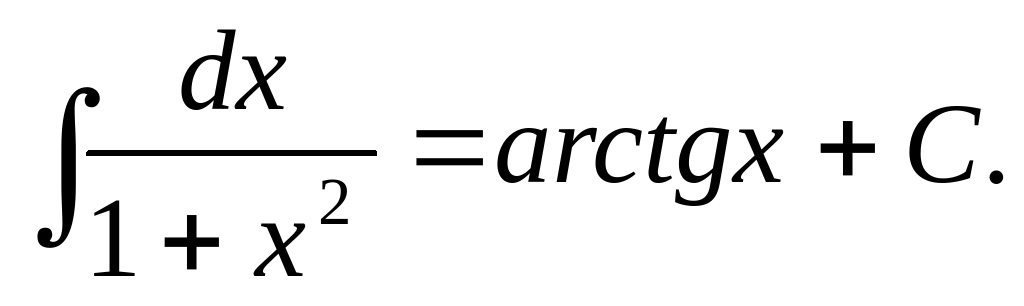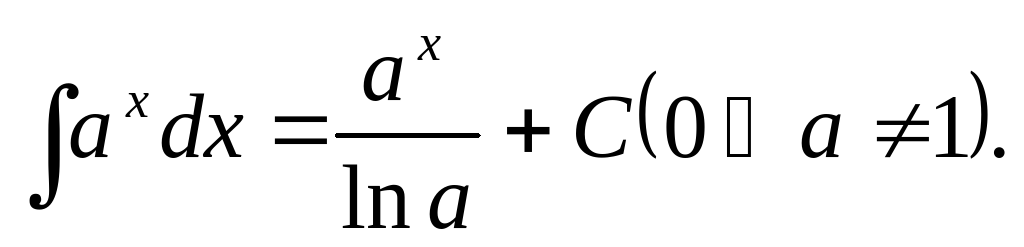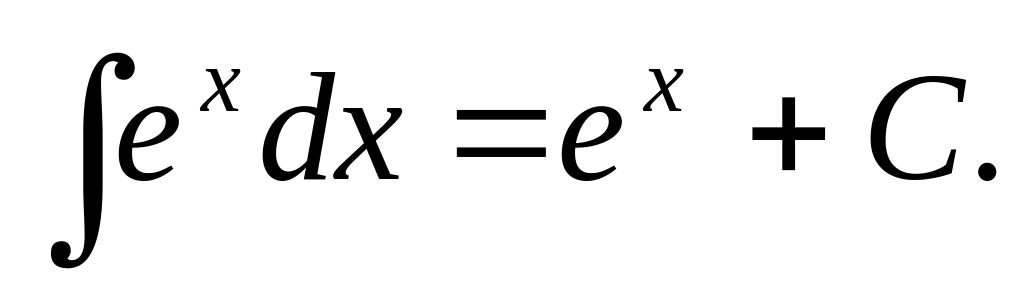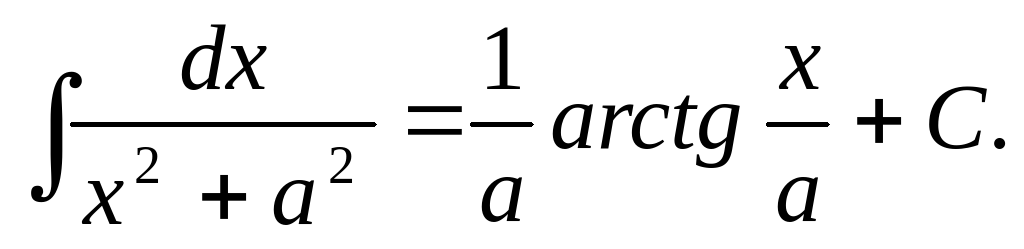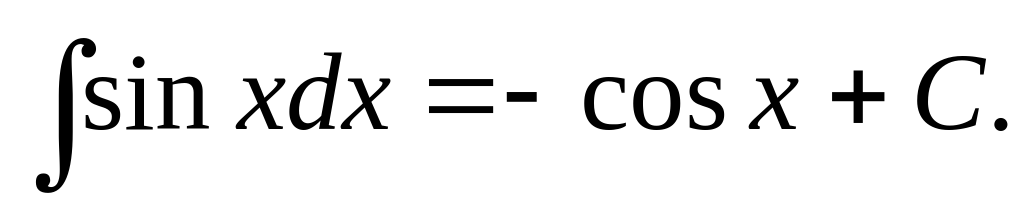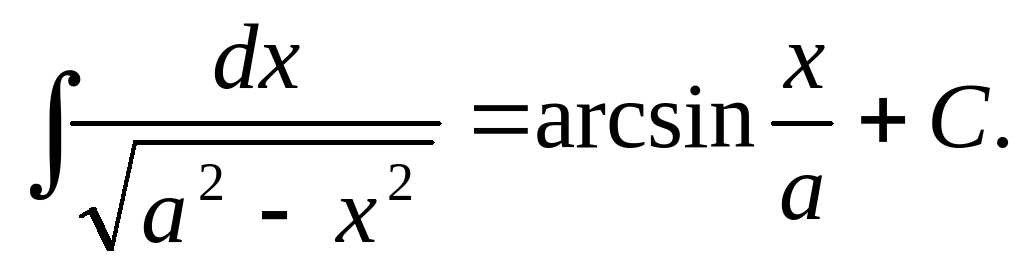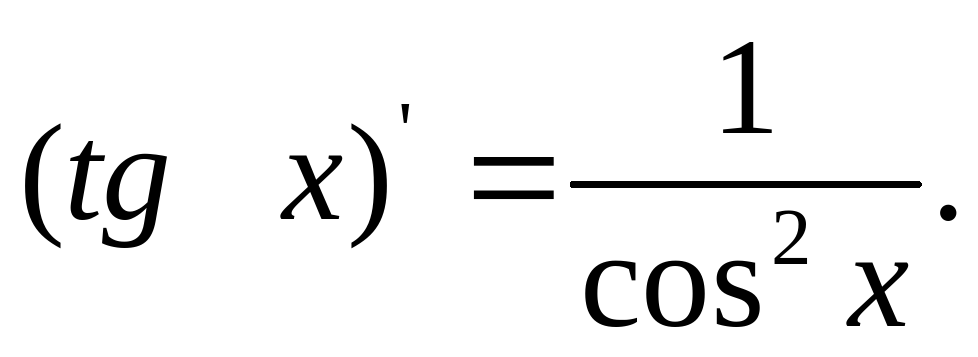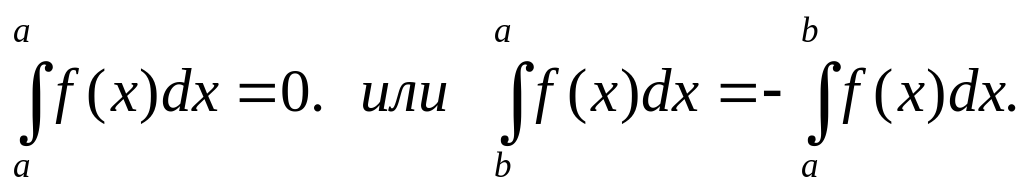Цель: изучить информационную технологию создания документов, содержащих формулы.
Программное обеспечение: MS Word.
Задания:
1. Запустите текстовый редактор Microsoft Word из меню ПУСК.
2. Загрузите редактор формул, выбрав команду вкладка Вставка – панель Текст – пункт Объект. В диалоговом окне выберите вид объекта Microsoft Equation 3.0. На экран выведется панель Редактор формул и окно для вставки формулы.
3. Изучите команды панели Редактор формул.
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Практическая работа «Работа с редактором формул»
Цель работы: научиться создавать и редактировать формулы с помощью встроенного редактора формул в программе MS Word.
Теоретический материал
|
Вставка формулы |
Команда Вставка — Формула |
|
Редактирование формулы |
Для редактирования созданной формулы достаточно щелкнуть на ней и загрузится редактор формул. Чтобы удалить формулу, необходимо нажать клавишу Delete на клавиатуре. |
Порядок работы:
Задание 1.
Набрать математические выражения вместе с текстом по образцу.
Квадратное уравнение – уравнение 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, где а, 𝑏 и с – заданные числа, причёма 0, х – неизвестное число.
Коэффициенты квадратного уравнения называют так: 𝑎 – первый или старший коэффициент, 𝑏 – второй коэффициент, с – свободный член.
Примеры квадратных уравнений:
2x2 x1 0,3x2 7x 0.
Неполное квадратное уравнение – квадратное уравнение 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, у которого хотя бы один из коэффициентов 𝑏 или 𝑐равен нулю.
Примеры неполных квадратных уравнений:
x2 0, 5x2 4 0, 8x2 x 0.
Формула корней квадратного уравнения:
x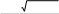
2a Например, уравнение 3x2 5x20 имеет два корня:
x
6 6 3
Приведённое квадратное уравнение – уравнение вида x2 pxq 0.
Формула корней приведённого квадратного уравнения:
x1,2 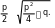
Н
Контрольные вопросы:
1.Для чего необходим редактор формул? 2.Как редактировать формулы в текстовом редакторе?
Вставка в документ формул с использованием редактора формул, встроенного в текстовой редактор Microsoft Word
1. В операционной системе Windows запустить текстовой редактор Microsoft Word командой [Программы — Microsoft Word]. Создать новый документ с помощью команды [Файл — Создать…].
Вызовем Редактор формул (Microsoft Equation).
2. Для вставки в документ формулы необходимо ввести команду [Вставка — Объект…], появится диалоговое окно Вставка объекта.
На вкладке Создание в списке Тип объекта: выбрать пункт Microsoft Equation 3.0 и щелкнуть по кнопе ОК.
3. В тексте документа появится рамка для ввода формулы, а в окне документа появится панель инструментов Редактор формул.
Вставим в документ формулу закона Ома.
4. Внутри рамки для ввода формул ввести на латинской клавиатуре левую часть формулы и знак равенства I=.
На панели инструментов Редактора формул щёлкнуть по кнопке Шаблоны дробей и радикалов.
На открывшейся панели выбрать кнопку с изображением дроби и щёлкнуть по ней мышью. В рамке для ввода формулы появится заготовка дроби, в которую ввести знаки U и R.
5. В результате в рамке для ввода формул появится формула закона Ома.
Используя данный урок введите следующие формулы.
Практическая
работа 7
Тема:
ОФОРМЛЕНИЕ ФОРМУЛ РЕДАКТОРОМ MS
EQUATION
Цель
занятия. Изучение
информационной технологии создания
документов,
содержащих формулы.
Порядок работы
-
Запустите
программу Microsoft
Word. -
С
помощью команд Вид/Колонтитулы
создайте
верхний колонтитул
следующего содержания: «Формулы для
финансово-экономических
расчетов» (шрифт 12, Times
New
Roman
Cyr,
полужирный, курсив).
3. Загрузите
редактор формул командами
Вставка/Объект/Microsoft
Equation.
На
экран выводится панель Equation
Editor
(Редактор
формул) (рис.
7.1).
Краткая
справка. На верхней панели (математических
символов)
расположены кнопки для вставки в формулу
более 150 математических
символов, большая часть которых недоступна
в стандартном шрифте Symbol.
Для вставки символов в формулу нажмите
кнопку в верхнем ряду панели инструментов,
а затем выберите
определенный символ из палитры,
появляющейся над кнопкой.
Н
а
нижней панели (шаблонов) расположены
кнопки, предназначенные
для вставки шаблонов или структур,
включающих символы
типа дробей, радикалов, сумм, интегралов,
произведений,
матриц и различных скобок или
соответствующих пар символов
типа круглых и квадратных скобок. Во
многих шаблонах содержатся
специальные места, в которые можно
вводить текст и вставлять
символы. В редакторе формул содержится
около 120 шаблонов,
сгруппированных в палитры. Шаблоны
можно вкладывать один в
другой для построения многоступенчатых
формул.
Рис.
7.1. Панель
Equation Editor
Назначение нижних
и верхних кнопок панели «Редактора
формул»
(согласно нумерации
кнопок панели на рис. 7.1)
-
— вставка символов
отношений; -
— вставка пробелов
и многоточий; -
—
надсимвольные
элементы, позволяющие добавлять к
математическим
переменным примы, крышки, черту или
точку; -
— вставка
операторов; -
— вставка стрелок;
-
— вставка логических
символов; -
— вставка символов
теории множеств; -
—
вставка разных
символов (символы дифференциального
исчисления,
символы градуса, угла, перпендикуляра
и др.); -
— вставка строчных
букв греческого алфавита;
-
— вставка прописных
букв греческого алфавита; -
—
вставка шаблонов
разделителей:
12 — вставка шаблонов
дробей и радикалов:
13 — создание
верхних и нижних индексов:
14 — создание сумм:
;
15 — вставка
интегралов
16 —
создание математических выражений с
чертой сверху и снизу:
17 —
создание стрелок с текстом:
;
-
вставка произведений
и шаблонов теории множеств; -
—
вставка шаблонов
матриц. Шаблоны этой палитры позволяют
создавать векторные столбцы, определители,
матрицы и другие
макеты типа таблиц:
-
Создайте
последовательно все формулы, приведенные
в п. 3 Практической
работы. -
С
оздайте
формулу следующего вида:
пользуясь кнопками:
-
кнопка 13, положение
12 (для ввода левой части формулы); -
«
знак «равно» и символ <х>
ввести с клавиатуры; -
кнопка 14, положение
5 (знак суммы); -
кнопка 13, положение
2 (ввод нижних индексов); -
ввести символ «*»
с клавиатуры (или кнопка 4, положение
5); -
кнопка 13, положение
2 (ввод нижних индексов).
6. Создайте
формулу для вычисления суммы платежей:
7.
Вставьте первую созданную формулу в
колонтитул путем копирования
формулы.
8. Сохраните
созданный файл в папке группы.
Задание
7.1. Используя
Мастер
формул, набрать
формулы по образцам:
Задание7.2.
Набрать формулы по образцу, используя
символы (Вставка/
Символ) (рис.
7.2) и преобразователи в верхний/нижний
индексы.
Рис. 7.2. Вставка
символа суммы ∑
Краткая
справка. Для настройки панели инструментов
ввода
верхних и нижних индексов (х2
и х2)
необходимо
вызвать команду Сервис/
Настройка/ Команды/ Формат. Преобразователи
в верхний/нижний индексы, представленные
иконками х2
и
х2,
перетащите
левой кнопкой мыши на панель инструментов
Word,
после чего
закройте меню Настройка.
Образец задания
∑(X02
+
Y02)
+
∑(Xn2
+ Yn2);
lgnx(n-1)
+ lgnx(n+1);
Cos(a0
+ a1
+ a2
+ … + an).
Задание
7.3.
Набрать и оформить формулу в соответствии
с методическими указаниями по оформлению
отчетов по практике, курсовых и дипломных
работ.
-
Пояснение значений
символов и числовых коэффициентов
следует приводить непосредственно под
формулой в той же числовой последовательности,
в которой они даны в формуле. Значение
каждого символа и числового коэффициента
следует давать с новой строки. Первую
строку пояснения начинают со слова
«где» без двоеточия. -
Уравнения и формулы
следует выделять из текста в отдельную
строку. -
Выше и ниже каждой
формулы или уравнения должно быть
оставлено не менее одной свободной
строки. Если уравнение не умещается в
одну строку, оно должно быть перенесено
после знака равенства «=», после знака
«+», или после других математических
знаков с их обязательным повторением
в новой строке. -
Формулы и уравнения
в работе следует нумеровать порядковой
нумерацией в пределах всей работы
арабскими цифрами в круглых скобках в
крайне правом положении напротив
формулы. Допускается нумерация формул
в пределах раздела. -
Если в работе
только одна формула или уравнение, то
их не нумеруют.
Пример
(3)
где
H(a)
–
энтропия системы,
N
– количество возможных состояний
системы.
Дополнительные
задания
Задание
7.4.
Набрать текст и формулы по образцу.
Образец задания
Коэффициент
корреляции Пирсона используется как
мера линейной
зависимости между множеством зависимых
переменных у
и
множеством независимых переменных х.
Значение коэффициента заключено в
пределах от -1 до +1 и определяется по
следующей формуле:
Задание
7.5.
Набрать
текст и формулы по образцу.
Образец задания
Пример
1. В
прямоугольном ∆
ABC
известны
длина гипотенузы АВ,
равная
числу 12,5, и косинус угла ABC,
равный
числу 44/125. Найти величины синуса угла
САB
и
площадь треугольника.
Дано:
с
=
12,5 и cos
β
= 44/125. Найти sin
α и S.
Решение:
имеем sin
α = а/с
= cos
β = 44/125 = 0,325;
a = c*sinα = 12,5*0,325 =
4,4;
S=
1/2
(a * с
* sinβ) = 1/2 * 4,4 * 12,5 * 0,936 = 25,74.
Ответ:
0,325; 25,74.
Пример
2.
В условиях предыдущей задачи найти
периметр треугольника
и радиус вписанной в него окружности.
Решение:
имеем b
=
с * sinβ
= 12,5 * 0,936 = 11,7;
2р
= а + b
+ с = 4,4 + 11,7
+ 12,5 = 28,6;
р=
14,3;
S
= p
*
r;
r
=S/p
= 22,74/14,3
=1,8.
Ответ: 28,6; 1,8.
Пример
3. В
треугольнике даны длины трех сторон,
равные 41, 84,
85. Вычислить радиус вписанной и удвоенный
радиус описанной
окружностей.
Дано:
а
=
41, b
= 84,
с
= 85.
Найти r
и
R.
Решение:
радиусы r
и
R
легко
выражаются через площадь S
треугольника.
Кроме того, площадь можно найти по
формуле Герона:
имеем
р(а
+b
+ с)/2 =
(41 + 84 + 85)/2 = 105; тогда
r=S/p=
1680/105
=
l6,2; R = a*b* c/2S=4l *
84 * 85/2 * 1680 = 87,125.
Ответ: 16; 87,125.
Задание
7.6.
Набрать текст и формулы по образцу.
Образец задания
Точки
X1
= -1, X2
= 5/4,
Х3=
1 делят
числовую ось на четыре промежутка.
Найдем
знаки произведения на каждом интервале
и отметим их на
схеме. Решением неравенства (4Х-
5)(Х-.2)(Х+ 1)
> 0 является объединение двух промежутков
[-1; 5/4] и [2;∞].
Решением
неравенства является объединение
промежутков [-1;
5/4] и [2; 3]. Серединами этих промежутков
являются числа 0,125
и 2,5.
Ответ: 0,125; 2,5.
Пример.
(2Х+
1):
(X2—
Y2+
1) > 2/(Х-2),
где
Y=(-X)l/2.
Решение: Область
допустимых значений (ОДЗ)
-Х≥
0
Х≤
0;
X-2≠0
X
2;
X≠
0
E
= [-∞;
0].
При
ХЕ
неравенство
примет вид
Квадратный
трехчлен Х2+
Х
+
1 положителен при всех X,
так
как
его дискриминант
отрицателен и коэффициент
при (Х2+
Х+ 1)
> 0, получим равносильное неравенство.
5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вставка в документ формул (учебное + практическое задание)
учебно-методическое пособие на тему
Цели урока:
- Приобрести навык работы в MS Word.
- Научиться оформлять математические формулы с помощью редактора формул.
- Совершенствовать культуру оформления документов.
Для учащихся:
Ученикам все чаще приходиться печатать разные текстовые документы с использованием формул, и они обращаются за помощью. Поэтому я считаю, что тема «Вставка формул в текстовой документ» обязательна для изучения.
Редактор Формул – это отдельная программа, которая может работать совместно с редактором Word и электронной таблицей Excel. В программе Microsoft Word средством ввода формул является редактор формул Equation 3.0. Он позволяет создавать формульные объекты и вставлять их в текстовой документ. При необходимости вставленный объект можно редактировать непосредственно в поле документа.
Желаю удачи в освоении нового метериала!
Скачать:
| Вложение | Размер |
|---|---|
| Вставка формул (теория) | 57 КБ |
| Вставка формул (практическая работа) | 39 КБ |
Предварительный просмотр:
Вставка в документ формул с использованием редактора формул, встроенного в текстовой редактор Microsoft Word
1. В операционной системе Windows запустить текстовой редактор Microsoft Word командой [ Программы — Microsoft Word ]. Создать новый документ с помощью команды [ Файл — Создать. ].
Вызовем Редактор формул (Microsoft Equation).
2. Для вставки в документ формулы необходимо ввести команду [ Вставка — Объект. ], появится диалоговое окно Вставка объекта .
На вкладке Создание в списке Тип объекта : выбрать пункт Microsoft Equation 3.0 и щелкнуть по кнопе ОК .
3. В тексте документа появится рамка для ввода формулы, а в окне документа появится панель инструментов Редактор формул .
Вставим в документ формулу закона Ома.
4. Внутри рамки для ввода формул ввести на латинской клавиатуре левую часть формулы и знак равенства I= .
На панели инструментов Редактора формул щёлкнуть по кнопке Шаблоны дробей и радикалов .
На открывшейся панели выбрать кнопку с изображением дроби и щёлкнуть по ней мышью. В рамке для ввода формулы появится заготовка дроби, в которую ввести знаки U и R .
5. В результате в рамке для ввода формул появится формула закона Ома.
Используя данный урок введите следующие формулы.
Практическая работа по теме «Редактор формул MicrosoftEquation3.0»

Данный урок позволяет освоить основные приемы по созданию формул в текстовом редакторе Microsoft Office Word. Закрепить знания и умения при работе в текстовом редакторе Microsoft Office Word.
Просмотр содержимого документа
«Практическая работа по теме «Редактор формул MicrosoftEquation3.0»»
Практическая работа «Редактор формул MicrosoftEquation3.0»
Цель работы: научится работать с редактором формул Microsoft Equation 3.0
Задание перепишите текст, с формулами используя редактора формул:
д 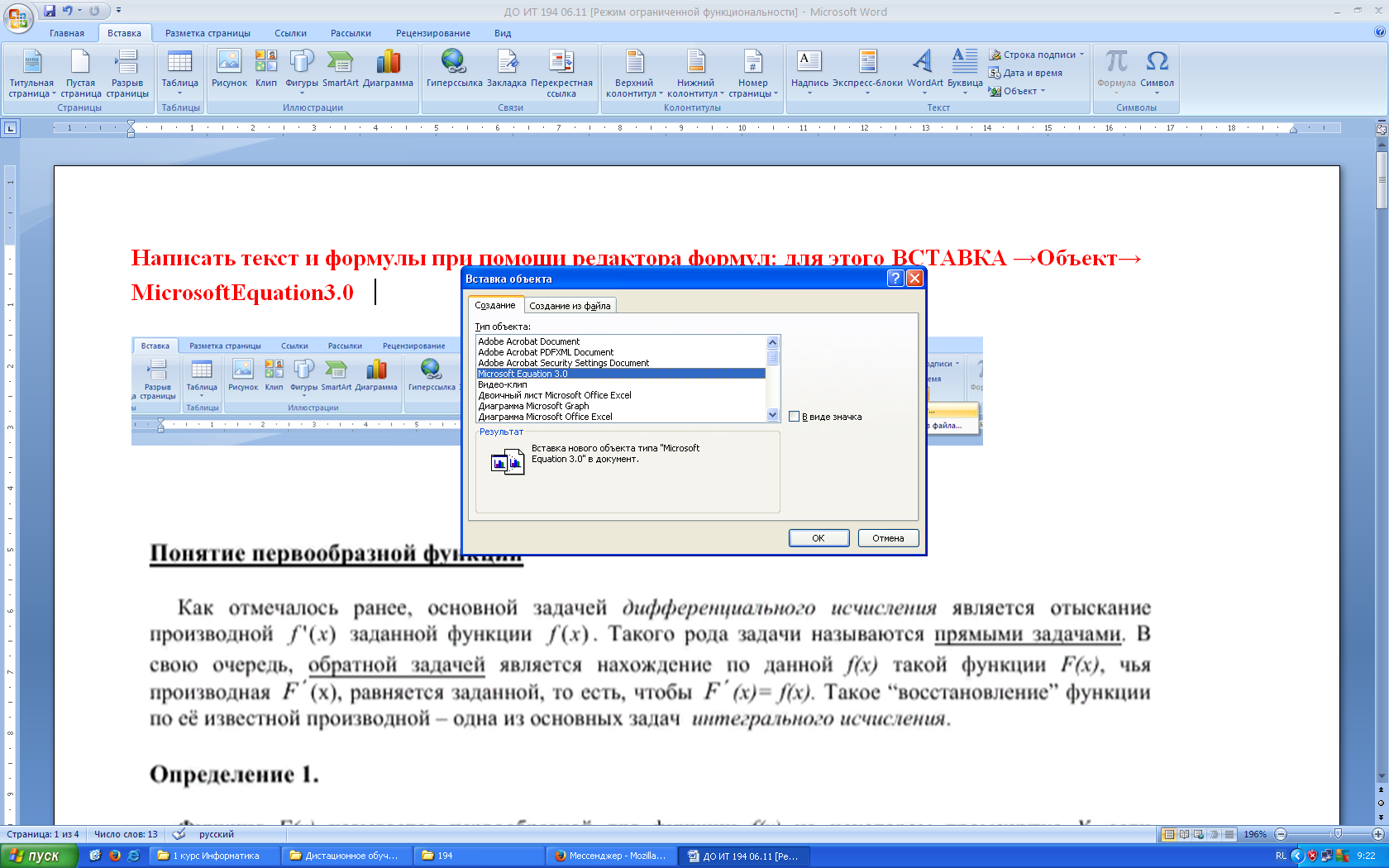
П 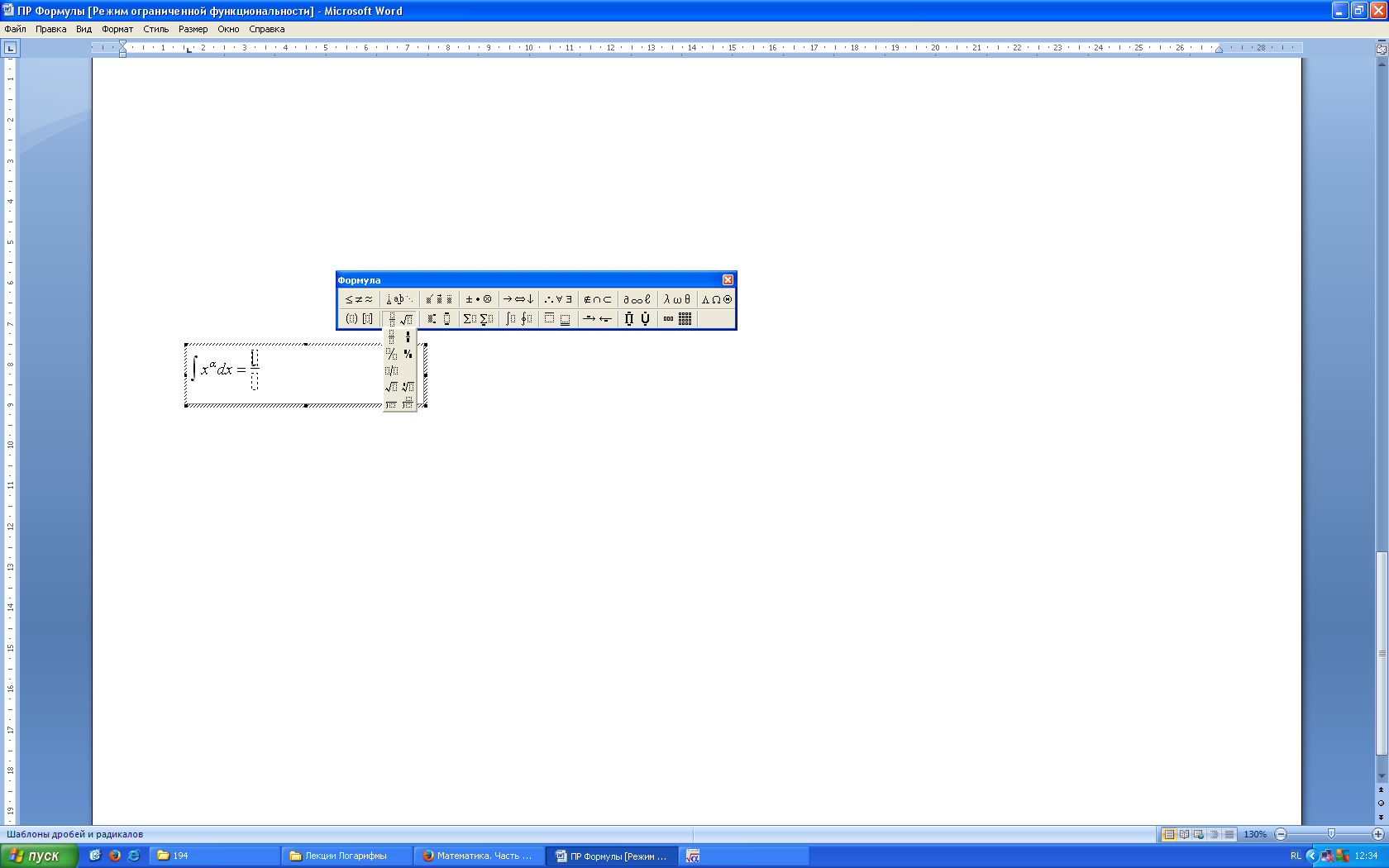
Ввод и редактирование формул завершается нажатием клавиши ESC или закрытием панели редактора формул.
Для редактирования формулы непосредственно в документе достаточно выполнить на ней двойной щелчок.
Таблица основных интегралов:
Основные свойства неопределённого интеграла:
Производная неопр. интеграла равна подинтегральной функции; дифференциал от неопр. интеграла равен подинтегр. выражению, т.е.
Неопр. интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const0, то
Неопр. интеграл от алгебраической суммы 2-х функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.
Основные свойства определённого интеграла:
Интеграл на отрезке нулевой длины, где ab:
Постоянный множитель можно вынести за знак определённого интеграла, т.е.
Определённый интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
Практическая работа по теме Создание формул
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Практическая работа « Создание формул в MS Word . »
Цель работы: освоить основные операции по созданию, редактированию и оформлению электронных таблиц.
Краткие теоретические сведения
Ввод формул в текстовом редакторе
Иногда в созданном документе необходимо вставить какое-либо математическое выражение, формулу. В программе Microsoft Word средством для вставки математических выражений в текстовый документ является редактор формул Microsoft Equation 3.0.
Для запуска редактора формул служит команда Вставка—>Объект .В открывшемся диалоговом окне Вставка объекта следует выбрать пункт Microsoft Equation 3.0 в списке Тип объекта на вкладке Создание. Откроется панель управления Формула, представленная на рисунке 3.
Задание 1.Вспомните и напишите любое:
Задание 2 Создайте формулы:
Сохраните свою работу и покажите учителю
Оцените свою работу в таблице
Выполнил всё 5 баллов
Затруднялся выполнять 4 балла
Помогал учитель 3 балла
Ни чего не выполнил 0 баллов
Выполнил всё 5 баллов
Затруднялся выполнять 4 балла
Помогал учитель 3 балла
Ни чего не выполнил 0 баллов
Менее 4 баллов –«2»
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 862 человека из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 48 человек из 20 регионов
Курс профессиональной переподготовки
Информатика: теория и методика преподавания в образовательной организации
- Сейчас обучается 223 человека из 62 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 843 433 материала в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 25.01.2016
- 1509
- 0
- 25.01.2016
- 11761
- 78
- 25.01.2016
- 1193
- 0
- 25.01.2016
- 2485
- 94
- 25.01.2016
- 536
- 0
- 25.01.2016
- 1204
- 0
- 25.01.2016
- 3263
- 21
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 25.01.2016 2733
- DOCX 126.9 кбайт
- 39 скачиваний
- Рейтинг: 2 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Савдинкина Мария Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 2
- Всего просмотров: 22240
- Всего материалов: 14
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
В Госдуме предложили унифицировать школьные программы
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Онлайн-конференция о профессиональном имидже педагога
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://multiurok.ru/index.php/files/prakticheskaia-rabota-po-teme-redaktor-formul-micr.html
http://infourok.ru/prakticheskaya-rabota-po-teme-sozdanie-formul-803849.html