Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Содержание
- Суть корреляционного анализа
- Назначение корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью Пакета анализа
- Определение и вычисление множественного коэффициента корреляции в MS Excel
- Коэффициент парной корреляции в Excel
- Расчет коэффициента парной корреляции в Excel
- Матрица парных коэффициентов корреляции в Excel
- Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- Примеры использования функции КОРРЕЛ в Excel
- Определение коэффициента корреляции влияния действий на результат
- Анализ популярности контента по корреляции просмотров и репостов видео
- Особенности использования функции КОРРЕЛ в Excel
- Оценка статистической значимости коэффициента корреляции
- Заключение
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
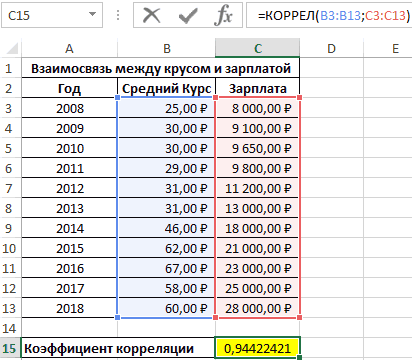
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
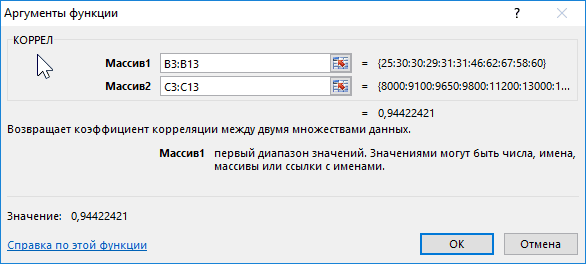
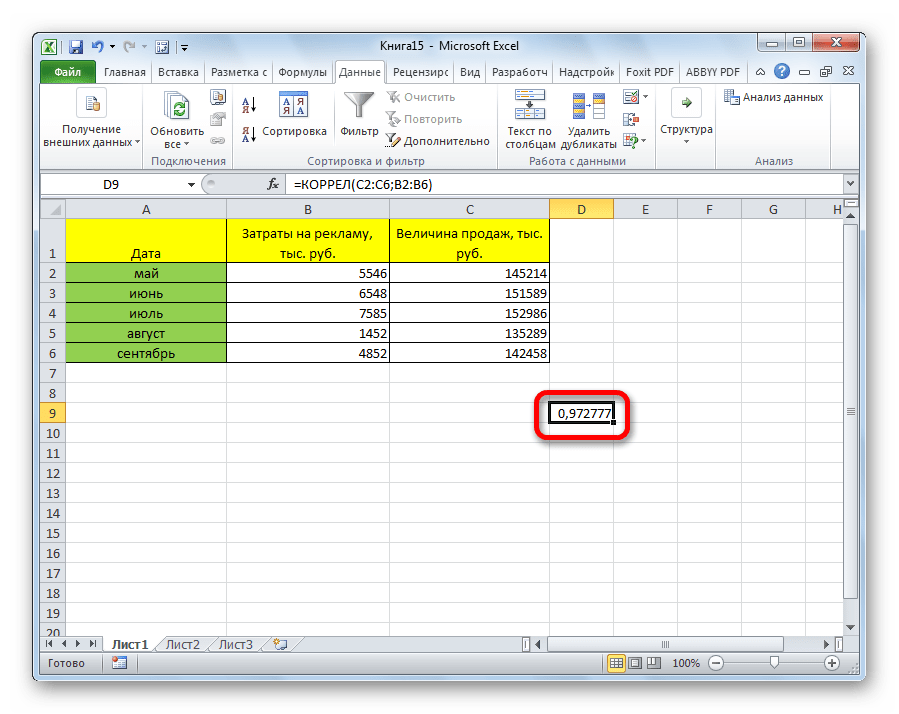
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
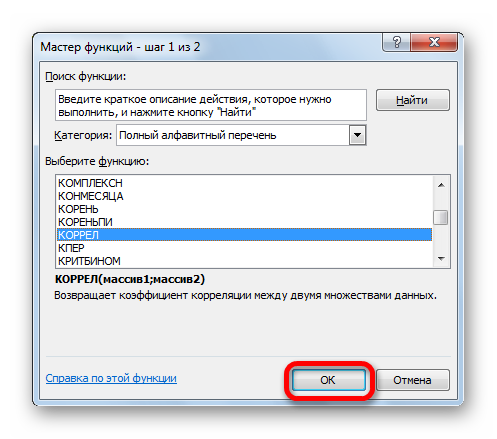
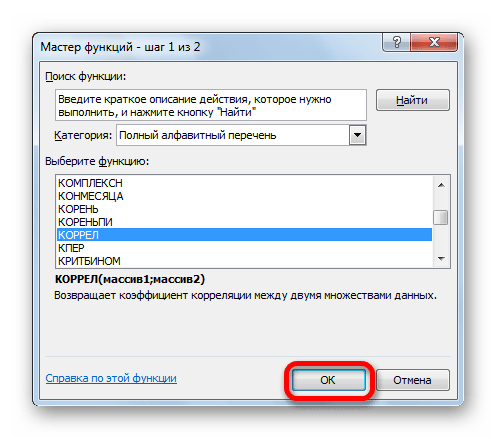
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
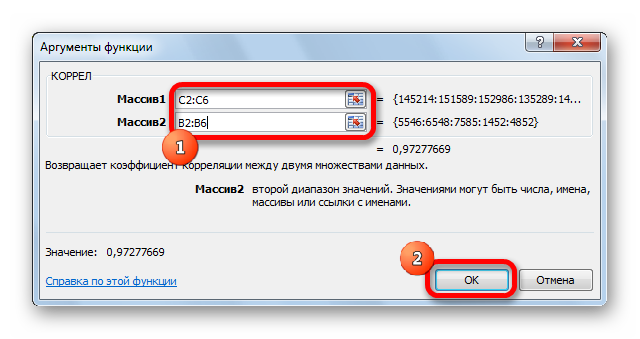
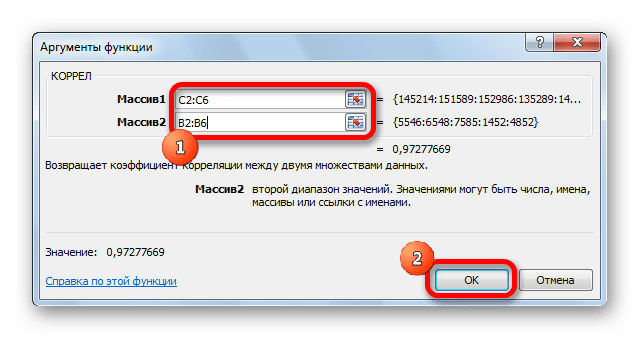
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
- После введения всех диапазонов кликаем на кнопку «ОК».
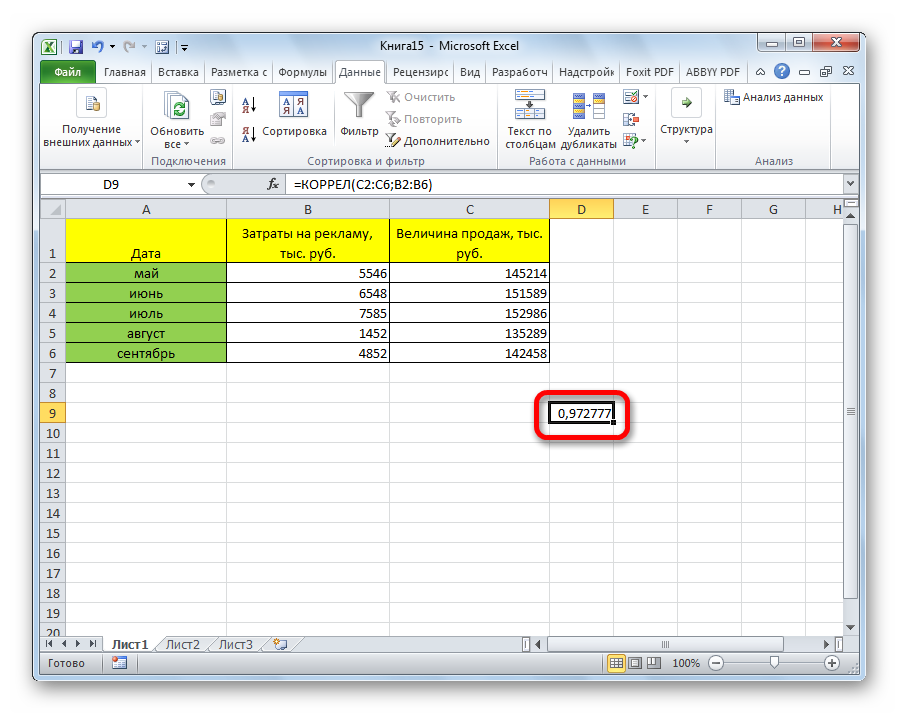
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
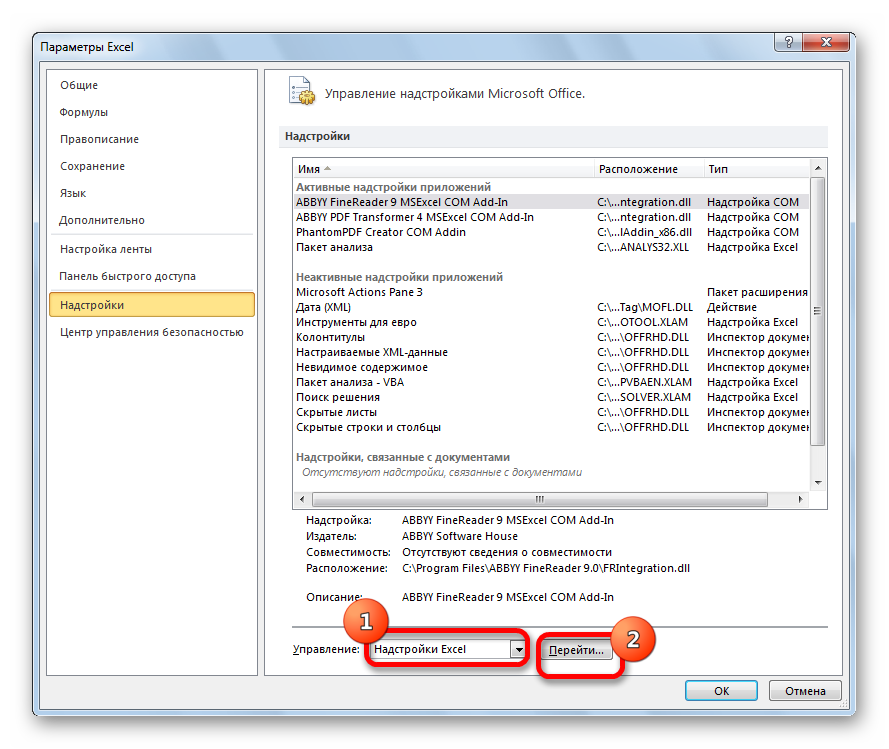
- Жмём на «Надстройки».
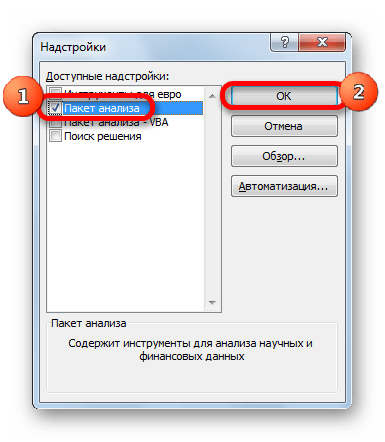
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
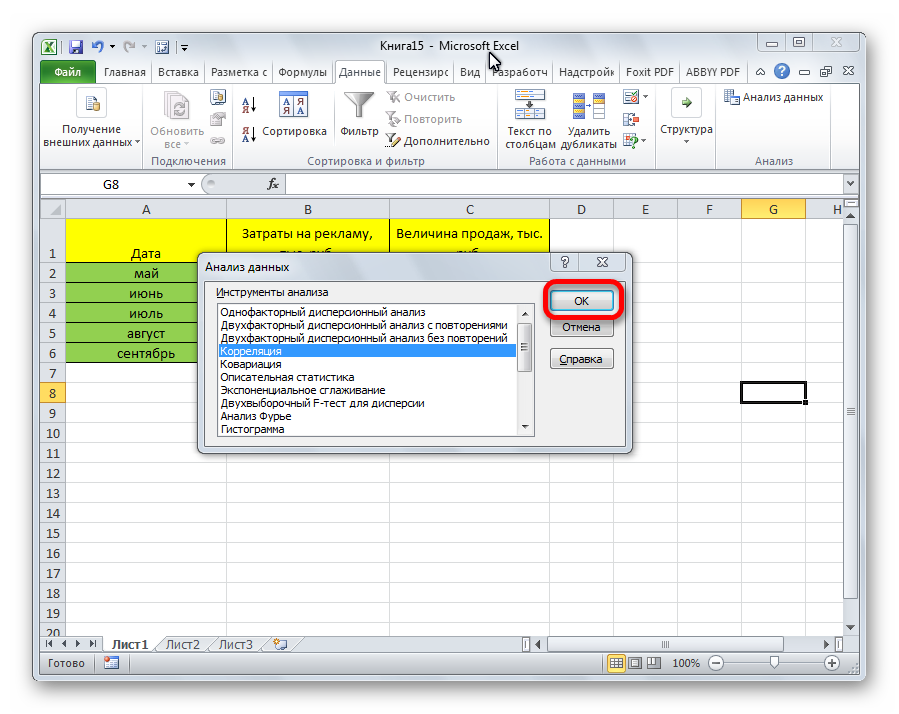
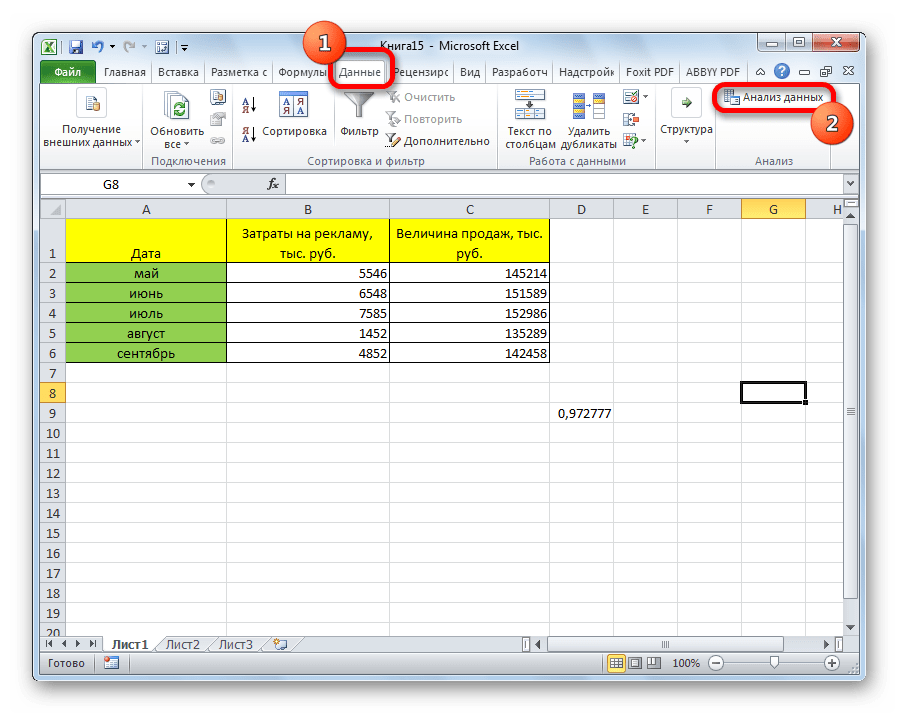
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
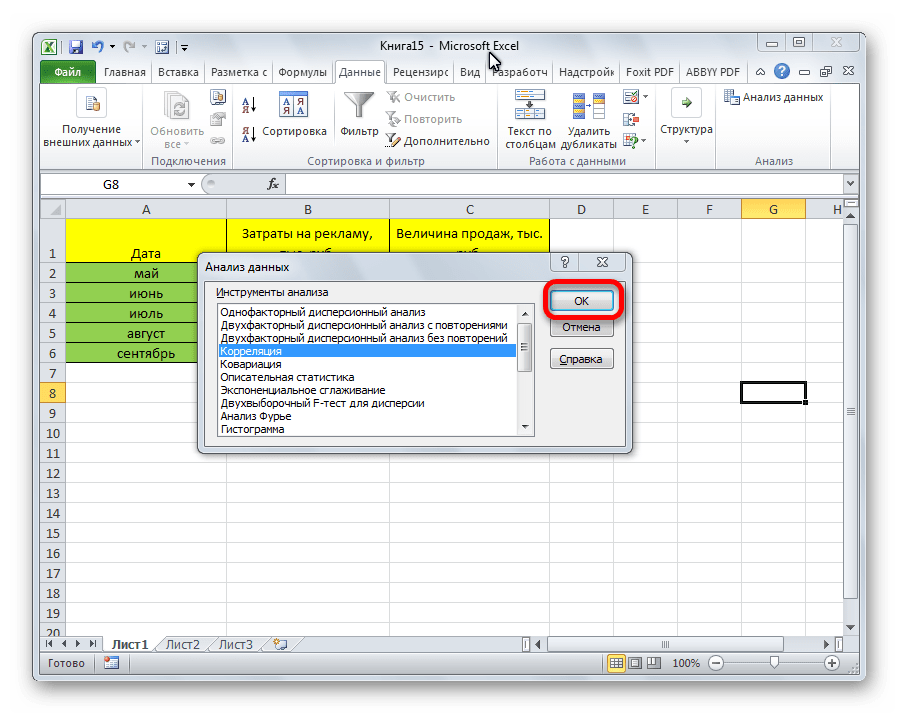
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
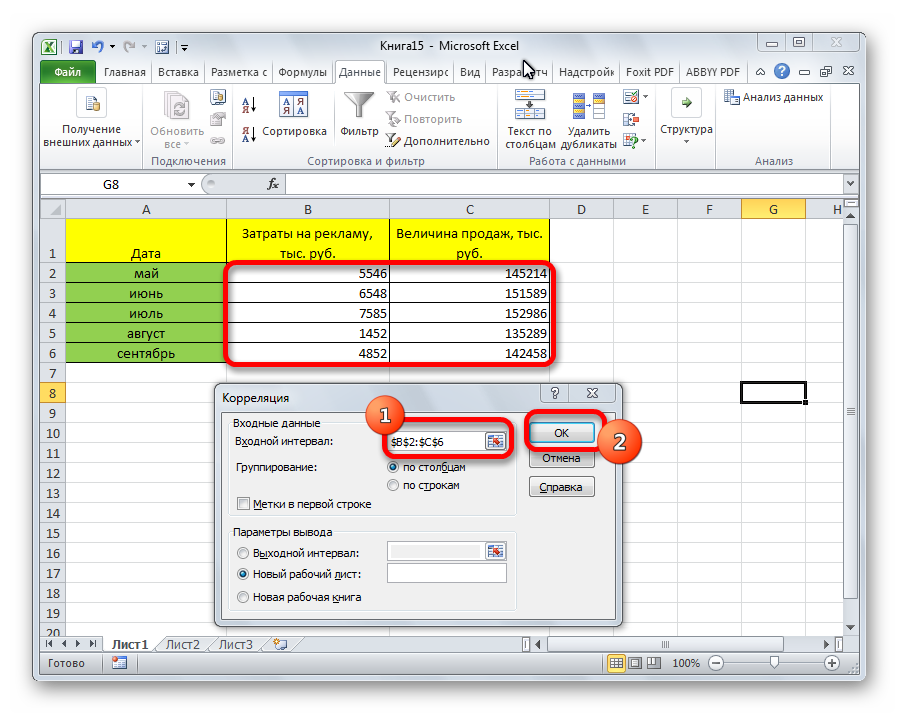
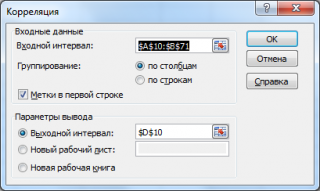
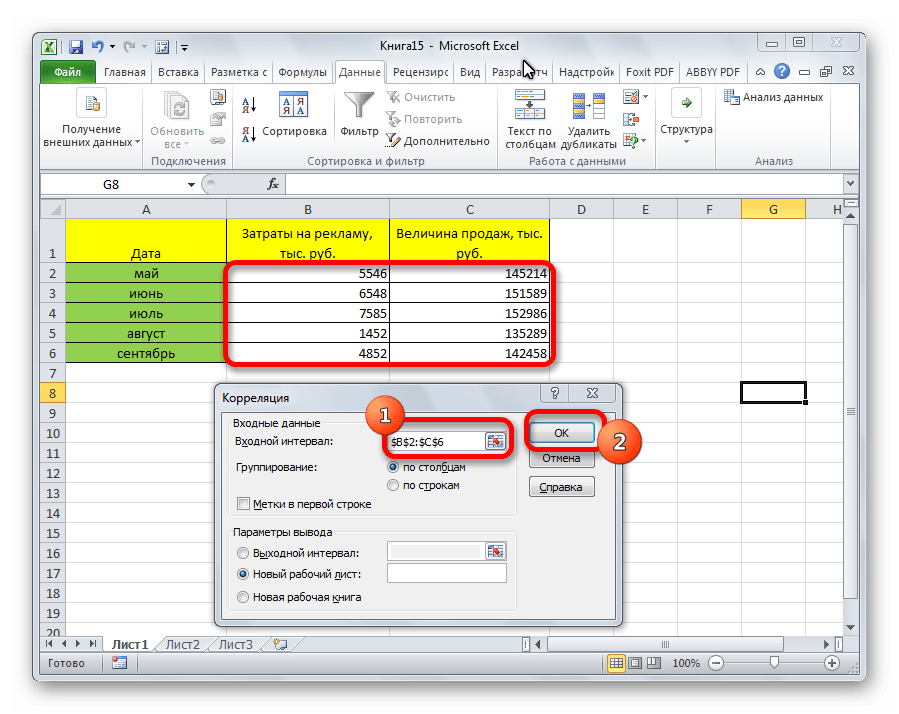
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
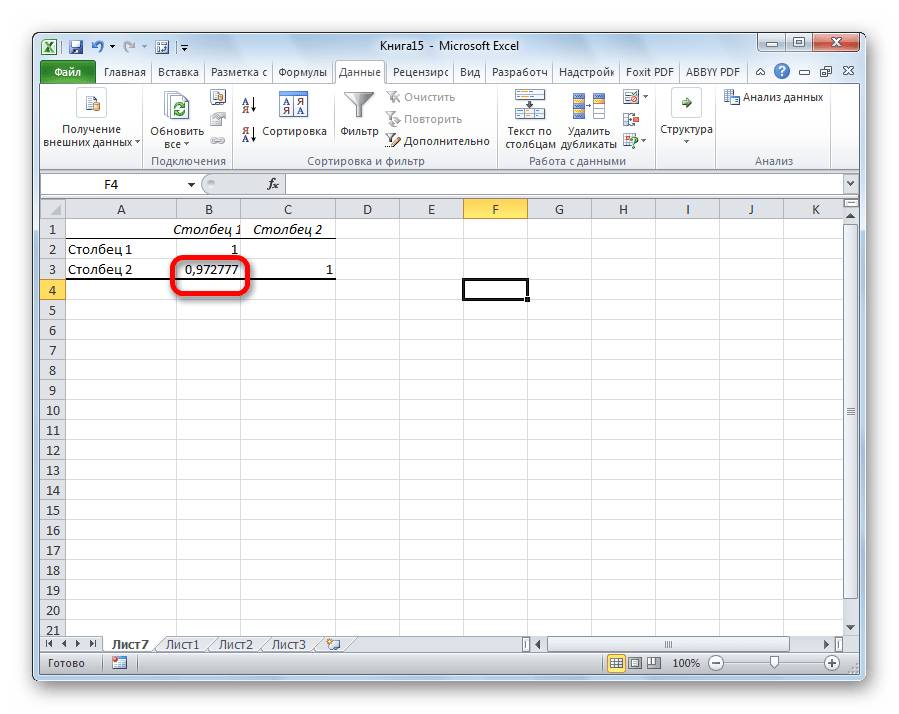
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Подробное руководство:
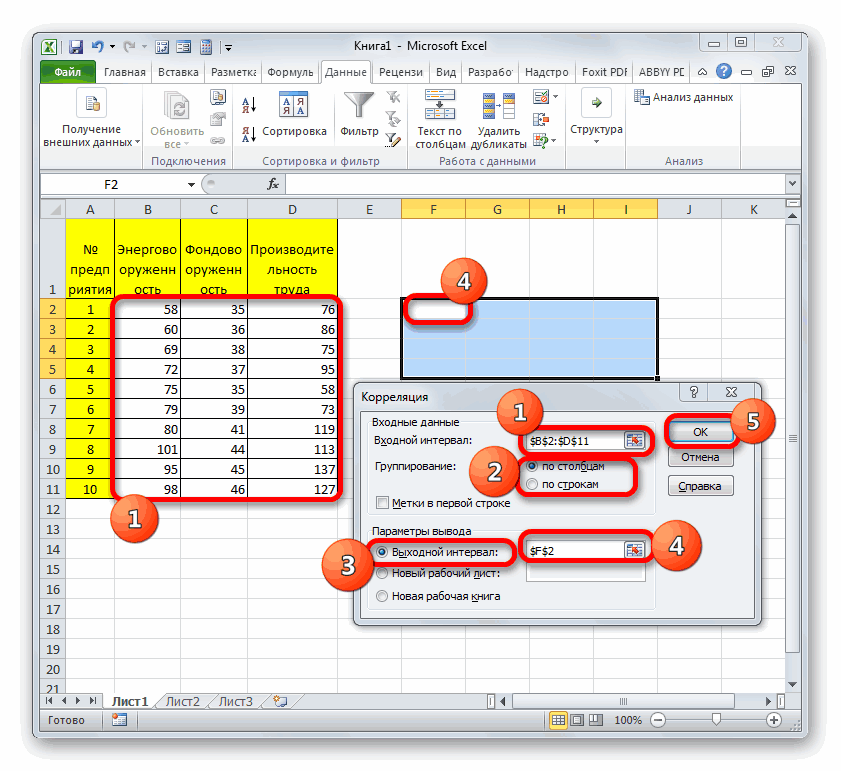
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
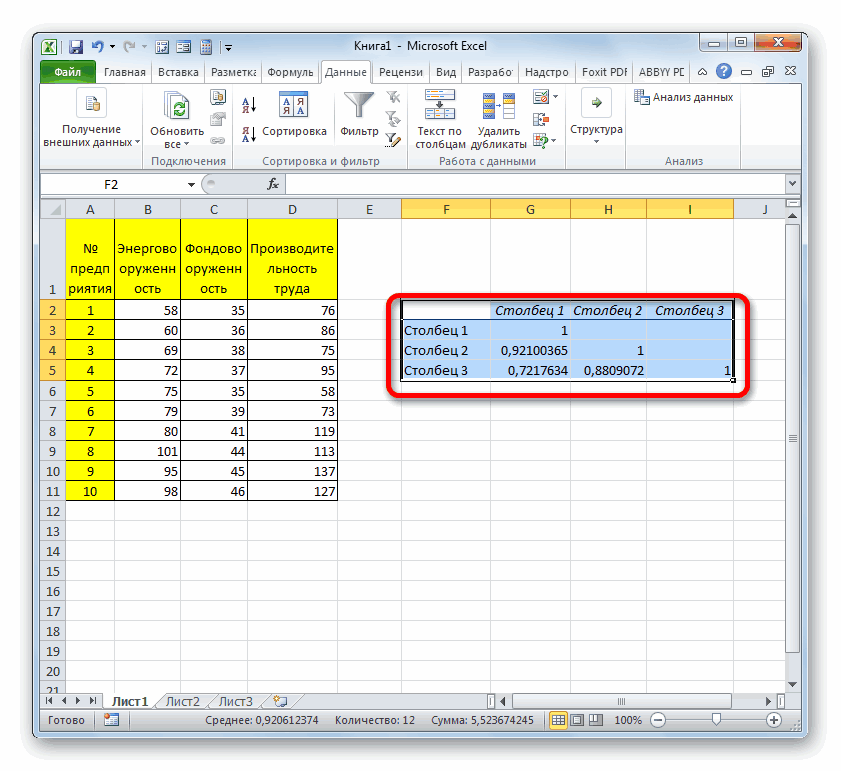
- Готово! Построилась матрица корреляции.
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
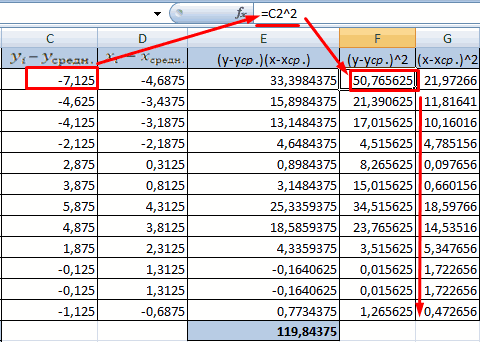
К примеру, у вас есть значения величин х и у.
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
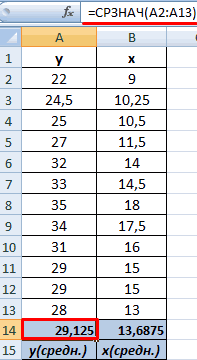
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
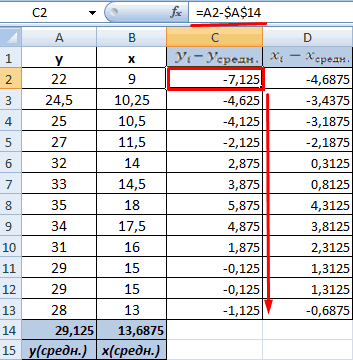
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
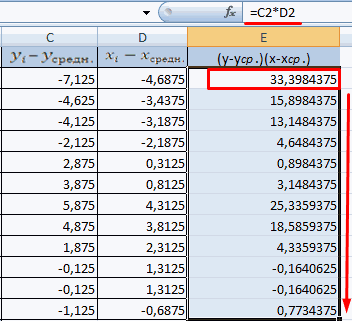
- Производим перемножение вычисленных разностей.
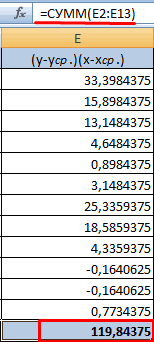
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
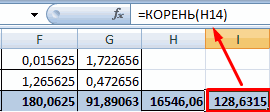
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
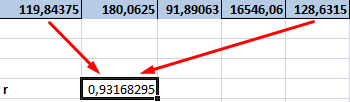
- Производим подсчет частного, используя значения знаменателя и числителя.
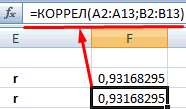
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
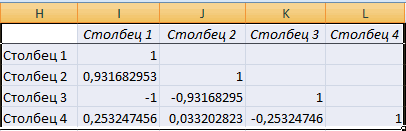
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
Пошаговая инструкция:
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
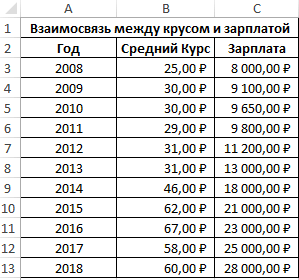
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
Определение коэффициента корреляции влияния действий на результат
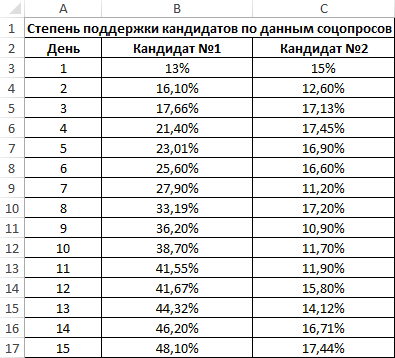
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
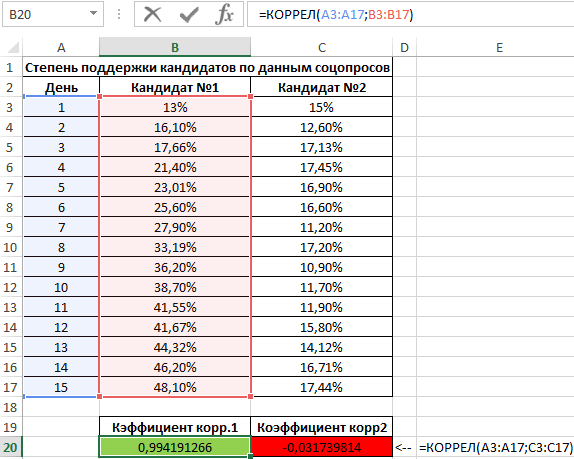
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
- =КОРРЕЛ(А3:А17;В3:В17).
- =КОРРЕЛ(А3:А17;С3:С17).
Результаты:
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
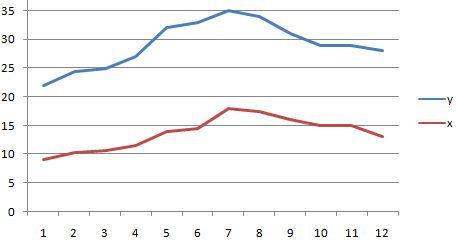
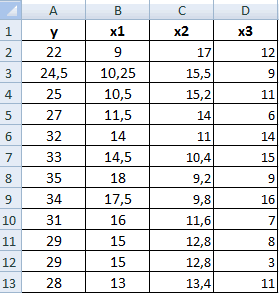
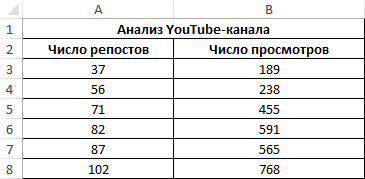
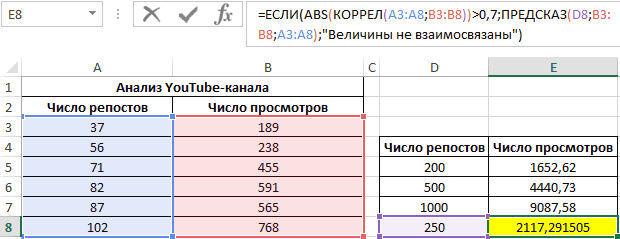
Анализ популярности контента по корреляции просмотров и репостов видео
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
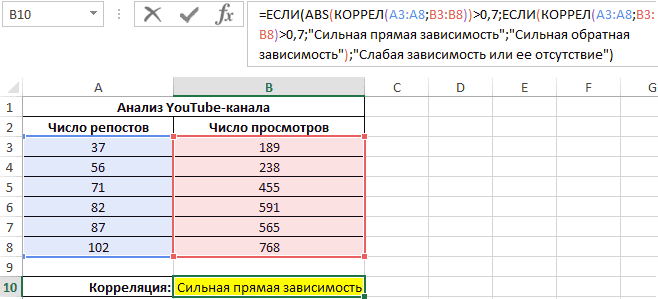
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ class=’formula’>
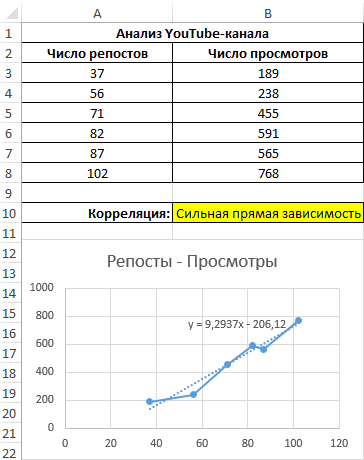
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
Теперь производим построение графика:
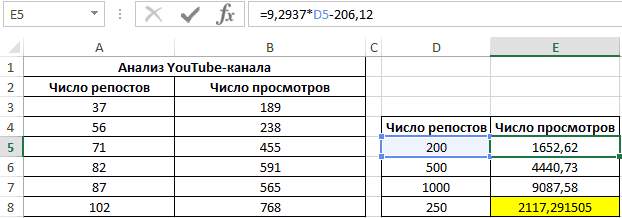
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ class=’formula’>. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Оцените качество статьи. Нам важно ваше мнение:
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции
(
критерий корреляции
Пирсона, англ. Pearson Product Moment correlation coefficient)
определяет степень
линейной
взаимосвязи между случайными величинами.
где Е[…] – оператор
математического ожидания
, μ и σ –
среднее
случайной величины и ее
стандартное отклонение
.
Как следует из определения, для вычисления
коэффициента корреляции
требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки
коэффициента корреляции
используется
выборочный коэффициент корреляции
r
(
еще он обозначается как
R
xy
или
r
xy
)
:
Как видно из формулы для расчета
корреляции
, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что
корреляция
оказывается безразмерным числом от -1 до 1.
Корреляция
и
ковариация
предоставляют одну и туже информацию, но
корреляцией
удобнее пользоваться, т.к. она является безразмерной величиной.
Рассчитать
коэффициент корреляции
и
ковариацию выборки
в MS EXCEL не представляет труда, так как для этого имеются специальные функции
КОРРЕЛ()
и
КОВАР()
. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.
Теоретическое отступление
Напомним, что
корреляционной связью
называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные
средние
значения другой (с изменением значения Х
среднее значение
Y изменяется закономерным образом). Предполагается, что
обе
переменные Х и Y являются
случайными
величинами и имеют некий случайный разброс относительно их
среднего значения
.
Примечание
. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о
корреляции
температуры и года наблюдения и, соответственно, применять показатели
корреляции
с соответствующей их интерпретацией.
Корреляционная связь
между переменными может возникнуть несколькими путями:
-
Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как
независимая переменная (фактор)
, вторая —
зависимая переменная (результат)
. Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот. - Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
- Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.
Таким образом,
показатель корреляции
показывает, насколько сильна
линейная взаимосвязь
между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Корреляция
, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если
диаграмма рассеяния
показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то
корреляция
замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение
коэффициента корреляции
может ввести в заблуждение (см.
файл примера
).
Корреляция
близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная
корреляция
означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
- количество переменных должно быть равно двум;
-
переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление
среднего значения
, которое требуется для нахождения
корреляции
, некорректно, а значит некорректно и вычисление самой
корреляции
; -
переменные должны быть случайными величинами и иметь
нормальное распределение
.
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
-
Для данных с нелинейной связью
корреляцию
нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования). -
С помощью
диаграммы рассеяния
у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования. - У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
- Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.
Использование MS EXCEL для расчета корреляции
В качестве примера возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х
i
; Y
i
). Для наглядности построим
диаграмму рассеяния
.
Примечание
: Подробнее о построении диаграмм см. статью
Основы построения диаграмм
. В
файле примера
для построения
диаграммы рассеяния
использована
диаграмма График
, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).
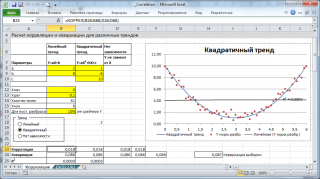
Расчеты
корреляции
проведем для различных случаев взаимосвязи между переменными:
линейной, квадратичной
и при
отсутствии связи
.
Примечание
: В
файле примера
можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
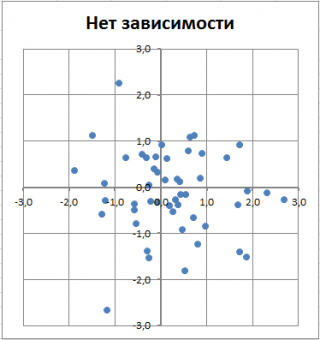
В
файле примера
для построения
диаграммы рассеяния
в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание
: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Как было сказано выше, для расчета
коэффициента корреляции
в MS EXCEL существует функций
КОРРЕЛ()
. Также можно воспользоваться аналогичной функцией
PEARSON()
, которая возвращает тот же результат.
Для того, чтобы удостовериться, что вычисления
корреляции
производятся функцией
КОРРЕЛ()
по вышеуказанным формулам, в
файле примера
приведено вычисление
корреляции
с помощью более подробных формул:
=
КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)
=
КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)
Примечание
: Квадрат
коэффициента корреляции
r равен
коэффициенту детерминации
R2, который вычисляется при построении линии регрессии с помощью функции
КВПИРСОН()
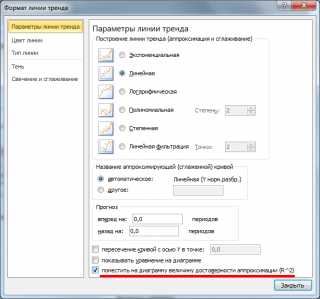
. Значение R2 также можно вывести на
диаграмме рассеяния
, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку
Макет
, затем в группе
Анализ
нажмите кнопку
Линия тренда
и выберите
Линейное приближение
). Подробнее о построении линии тренда см., например, в
статье о методе наименьших квадратов
.
Использование MS EXCEL для расчета ковариации
Ковариация
близка по смыслу с
дисперсией
(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а
дисперсия
— для одной. Поэтому, cov(x;x)=VAR(x).
Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
. В первом случае формула для вычисления аналогична вышеуказанной (окончание
.Г
обозначает
Генеральная совокупность
), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание
.В
обозначает
Выборка
.
Примечание
: Функция
КОВАР()
, которая присутствует в MS EXCEL более ранних версий, аналогична функции
КОВАРИАЦИЯ.Г()
.
Примечание
: Функции
КОРРЕЛ()
и
КОВАР()
в английской версии представлены как CORREL и COVAR. Функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета
ковариации
:
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)
Эти формулы используют свойство
ковариации
:
Если переменные
x
и
y
независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А
дисперсия
их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
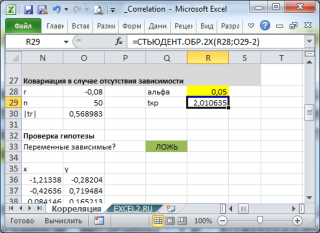
Оценка статистической значимости коэффициента корреляции
При проверке значимости
коэффициента корреляции
нулевая гипотеза состоит в том, что
коэффициент корреляции
равен нулю, альтернативная — не равен нулю (про
проверку гипотез
см. статью
Проверка гипотез
).
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.
коэффициента корреляции
r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t
r
:
которая имеет
распределение Стьюдента
с n-2 степенями свободы.
Если вычисленное значение случайной величины |t
r
| больше, чем критическое значение t
α,n-2
(α- заданный
уровень значимости
), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
Надстройка Пакет анализа
В
надстройке Пакет анализа
для вычисления ковариации и корреляции
имеются одноименные инструменты
анализа
.
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Входной интервал
: нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
Группирование
: как правило, исходные данные вводятся в 2 столбца
Метки в первой строке
: если установлена галочка, то
Входной интервал
должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
Выходной интервал
: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
17 авг. 2022 г.
читать 2 мин
Одним из способов количественной оценки взаимосвязи между двумя переменными является использование коэффициента корреляции Пирсона, который является мерой линейной связи между двумя переменными.
Он всегда принимает значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чтобы определить, является ли коэффициент корреляции статистически значимым, вы можете выполнить тест корреляции, который включает вычисление t-показателя и соответствующего p-значения.
Формула для расчета t-показателя:
т = г √ (п-2) / (1-г 2 )
куда:
- r: коэффициент корреляции
- n: размер выборки
Значение p рассчитывается как соответствующее двустороннее значение p для t-распределения с n-2 степенями свободы.
В следующем пошаговом примере показано, как выполнить тест корреляции в Excel.
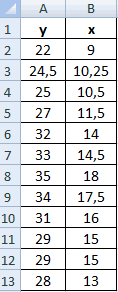
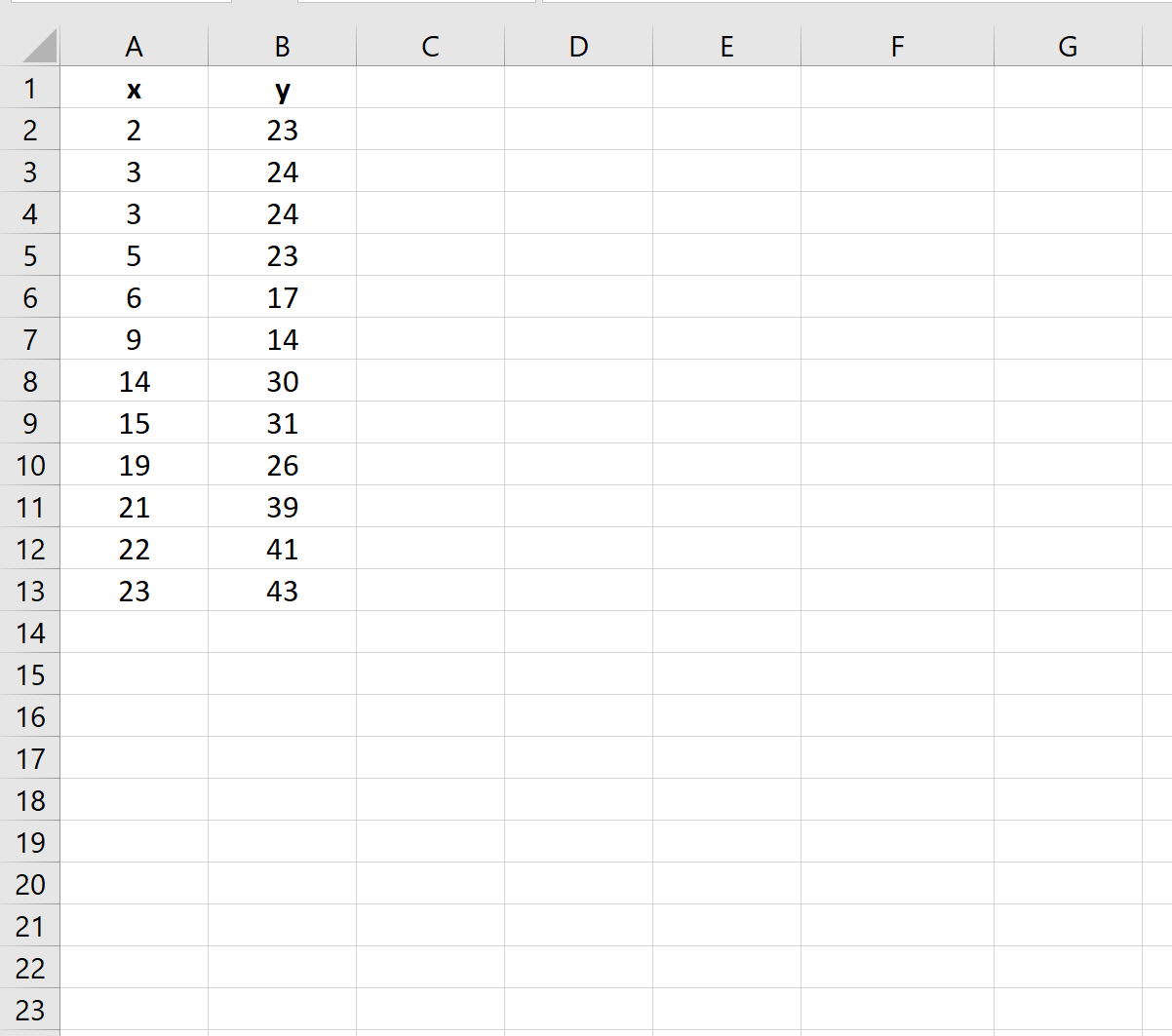
Шаг 1: введите данные
Во-первых, давайте введем некоторые значения данных для двух переменных в Excel:
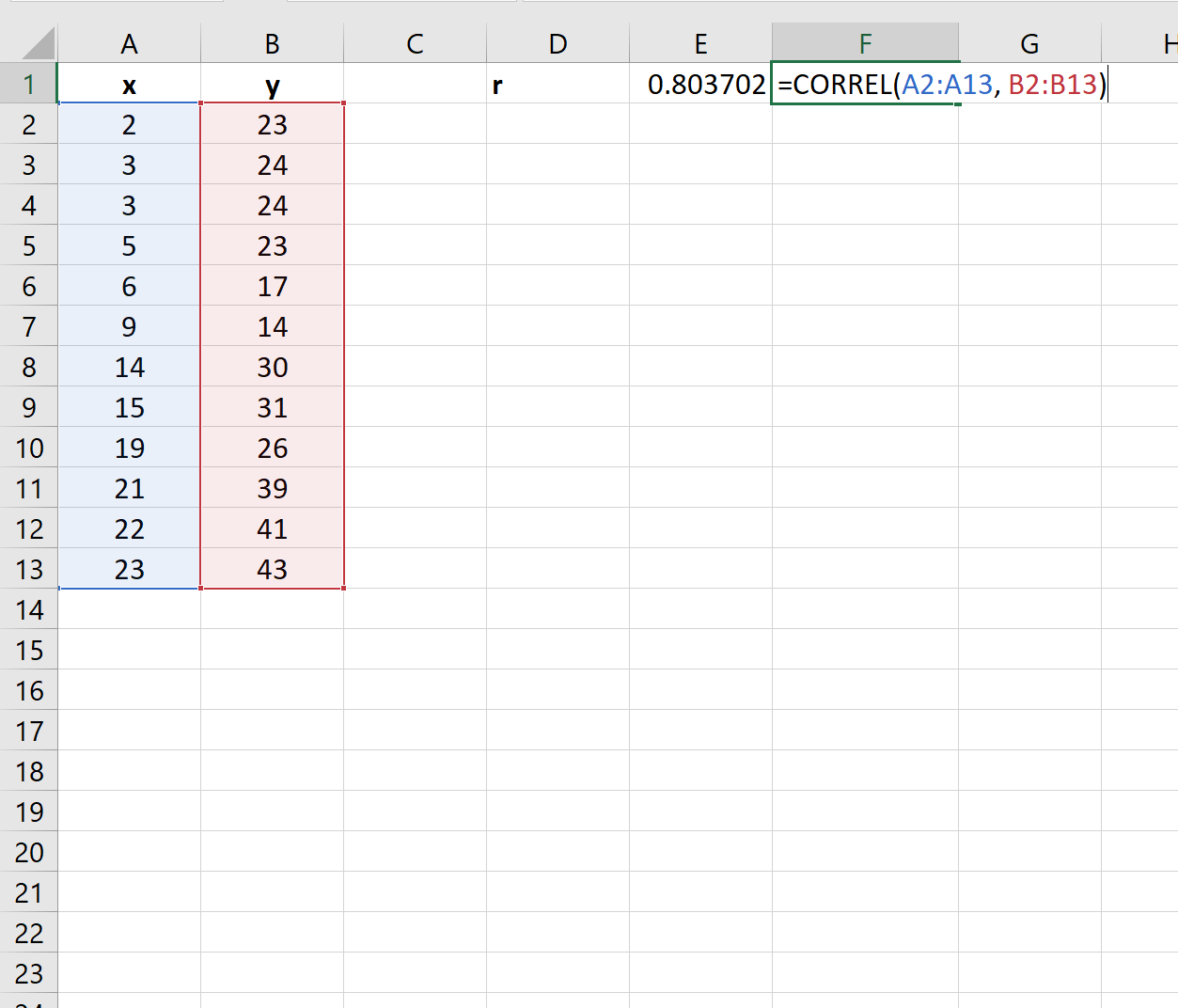
Шаг 2: Рассчитайте коэффициент корреляции
Затем мы можем использовать функцию CORREL() для вычисления коэффициента корреляции между двумя переменными:
Коэффициент корреляции между двумя переменными оказывается равным 0,803702 .
Это очень положительный коэффициент корреляции, но чтобы определить, является ли он статистически значимым, нам нужно рассчитать соответствующий t-показатель и p-значение.
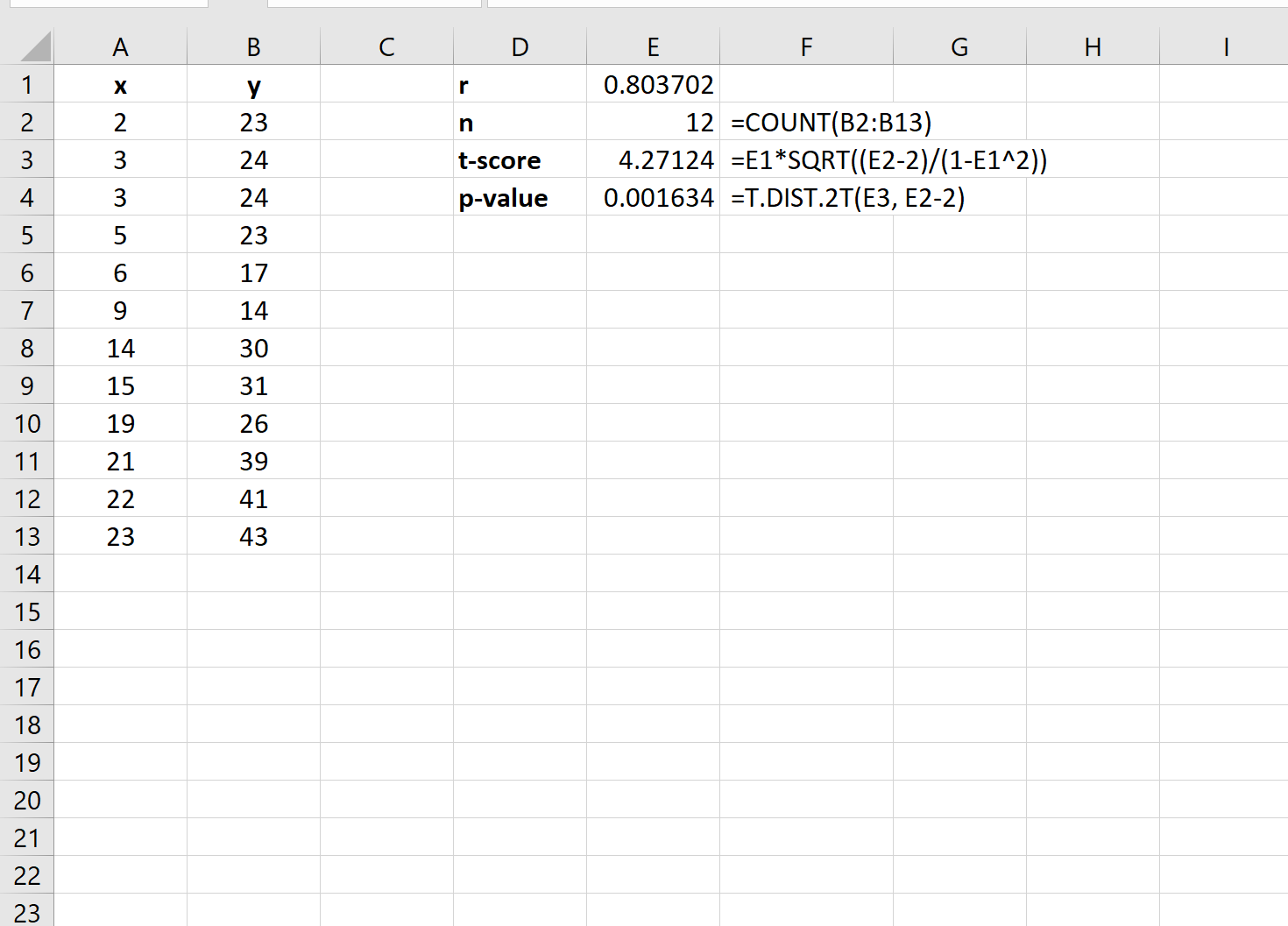
Шаг 3: Рассчитайте статистику теста и P-значение
Затем мы можем использовать следующие формулы для расчета тестовой статистики и соответствующего значения p:
Тестовая статистика оказывается равной 4,27124 , а соответствующее значение p равно 0,001634 .
Поскольку это p-значение меньше 0,05, у нас есть достаточно доказательств, чтобы сказать, что корреляция между двумя переменными является статистически значимой.
Дополнительные ресурсы
Как создать корреляционную матрицу в Excel
Как рассчитать ранговую корреляцию Спирмена в Excel
Как рассчитать скользящую корреляцию в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
|
Формула |
Функция |
Результат |
|
Коэффициент
|
КОРРЕЛ(массив1;массив2) Массив1 Массив2 |
Возвращает |
|
Оценка Вычисленное |
СТЬЮДРАСПОБР Вероятность — Степени_свободы — |
Возвращает |
|
Матрица
|
Обращение Для |
Инструмент |
Приложение
3
Регрессионный анализ в excel
|
Формула |
Функция |
Результат |
|||||||||||||||
|
Оценка
|
лнейн(изв_знач_у;изв_знач_х;константа;стат) Смысл изв_знач_у изв_знач_х константа стат |
Возвращает
|
|||||||||||||||
|
Оценка |
СервисАнализ
Для |
Возвращает Так |
|||||||||||||||
|
Оценка
Вычисленное |
СТЬЮДРАСПОБР(вероятность; Вероятность — Степени_свободы — |
Возвращает |
|||||||||||||||
|
Проверка F-критерий
|
FРАСПОБР(вероятность;степени_свободы1;степени_свободы2) Вероятность — Степени_свободы Степени_свободы
где |
Возвращает
FРАСПОБР
Чтобы |
Приложение
4
Значения
F-критерия Фишера при уровне значимости
=0,05
|
Число |
Число |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
8 |
12 |
24 |
|
|
|
1 |
161,45 |
199,50 |
215,72 |
224,57 |
230,17 |
233,97 |
238,89 |
243,91 |
249,04 |
254,32 |
|
2 |
18,5 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,37 |
19,41 |
19,45 |
19,50 |
|
3 |
10,13 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,84 |
8,74 |
8,64 |
8,53 |
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,04 |
5,91 |
5,77 |
5,63 |
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,82 |
4,68 |
4,53 |
4,36 |
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,15 |
4,00 |
3,84 |
3,67 |
|
7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,73 |
3,57 |
3,41 |
3,23 |
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,44 |
3,28 |
3,12 |
2,93 |
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,23 |
3,07 |
2,90 |
2,71 |
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,07 |
2,91 |
2,74 |
2,54 |
|
11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
2,95 |
2,79 |
2,61 |
2,40 |
|
12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,85 |
2,69 |
2,50 |
2,30 |
|
13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,77 |
2,60 |
2,42 |
2,21 |
|
14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,70 |
2,53 |
2,35 |
2,13 |
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,64 |
2,48 |
2,29 |
2,07 |
|
16 |
4,49 |
3.63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,59 |
2,42 |
2,24 |
2,01 |
|
17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,55 |
2,38 |
2,19 |
1,96 |
|
18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,51 |
2,34 |
2,15 |
1,92 |
|
19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,48 |
2,31 |
2,11 |
1,88 |
|
20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,45 |
2,28 |
2,08 |
1,84 |
|
21 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,42 |
2,25 |
2,05 |
1,81 |
|
22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,40 |
2,23 |
2,03 |
1,78 |
|
23 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,38 |
2,20 |
2,00 |
1,76 |
|
24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,36 |
2,18 |
1,98 |
1,73 |
|
25 |
4,24 |
3,38 |
2,99 |
2,76 |
2,60 |
2,49 |
2,34 |
2,16 |
1,96 |
1,71 |
|
26 |
4,22 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,32 |
2,15 |
1,95 |
1,69 |
|
27 |
4,21 |
3,35 |
2,96 |
2,73 |
2,57 |
2,46 |
2,30 |
2,13 |
1,93 |
1,67 |
|
28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,44 |
2,29 |
2,12 |
1,91 |
1,65 |
|
29 |
4,18 |
3,33 |
2,93 |
2,70 |
2,54 |
2,43 |
2,28 |
2,10 |
1,90 |
1,64 |
|
30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,27 |
2,09 |
1,89 |
1,62 |
|
35 |
4,12 |
3,26 |
2,87 |
2,64 |
2,48 |
2,37 |
2.22 |
2,04 |
1,83 |
1,57 |
|
40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,18 |
2,00 |
1,79 |
1,52 |
|
45 |
4,06 |
3,21 |
2,81 |
2,58 |
2,42 |
2,31 |
2,15 |
1,97 |
1,76 |
1,48 |
|
50 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,13 |
1,95 |
1.74 |
1,44 |
|
60 |
4,00 |
3,15 |
2,76 |
2,52 |
2,37 |
2,25 |
2,10 |
1,92 |
1,70 |
1,39 |
|
70 |
3,98 |
3,13 |
2,74 |
2,50 |
2,35 |
2,23 |
2,07 |
1,89 |
1,67 |
1,35 |
|
80 |
3,96 |
3,11 |
2,72 |
2,49 |
2,33 |
2,21 |
2,06 |
1,88 |
1,65 |
1,31 |
|
90 |
3,95 |
3,10 |
2,71 |
2,47 |
2,32 |
2,20 |
2,04 |
1,86 |
1,64 |
1,28 |
|
100 |
3,94 |
3,09 |
2,70 |
2,46 |
2,30 |
2,19 |
2,03 |
1,85 |
1,63 |
1,26 |
|
125 |
3,92 |
3,07 |
2,68 |
2,44 |
2,29 |
2,17 |
2,01 |
1,83 |
1,60 |
1,21 |
|
150 |
3,90 |
3,06 |
2,66 |
2,43 |
2,27 |
2,16 |
2,00 |
1,82 |
1,59 |
1,18 |
|
200 |
‘3,89 |
3,04 |
2,65 |
2,42 |
2,26 |
2,14 |
1,98 |
1,80 |
1,57 |
1,14 |
|
300 |
3,87 |
3,03 |
2,64 |
2,41 |
2,25 |
2,13 |
1,97 |
1,79. |
1,55 |
1,10 |
|
400 |
3,86 |
3,02 |
2,63 |
2,40 |
2,24 |
2,12 |
1,96 |
1,78 |
1,54 |
1,07 |
|
500 |
3,86 |
3,01 |
2,62 |
2,39 |
2,23 |
2,11 |
1,96 |
1,77 |
1,54 |
1,06 |
|
1000 |
3,85 |
3,00 |
2,61 |
2,38 |
2,22 |
2,10 |
1,95 |
1,76 |
1,53 |
1,03 |
|
|
3,84 |
2,99 |
2,60 |
2,37 |
2,21 |
2,09 |
1,94 |
1,75 |
1,52 |
Приложение
5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

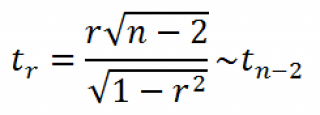
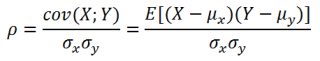
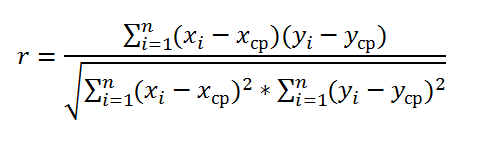
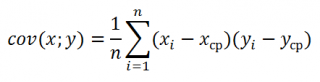
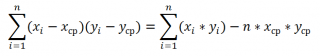
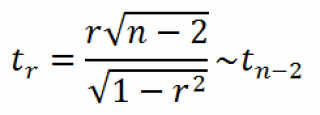





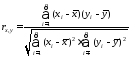
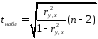
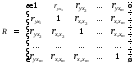
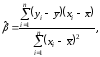
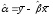
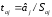 ,
,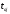
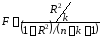
 как аргумент вероятность для FРАСПОБР.
как аргумент вероятность для FРАСПОБР.