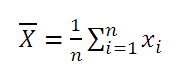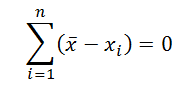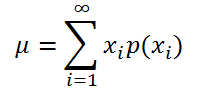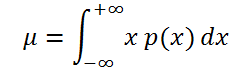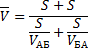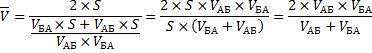Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.
Выборочное среднее
Среднее выборки
или
выборочное среднее
(sample average, mean) представляет собой
среднее
арифметическое
всех значений
выборки
.
В MS EXCEL для вычисления
среднего выборки
можно использовать функцию
СРЗНАЧ()
. В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения
выборки
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) точечной оценкой
математического ожидания
случайной величины (см.
ниже
), т.е.
среднего значения
исходного распределения, из которого взята
выборка
.
Примечание
: О вычислении
доверительных интервалов
при оценке
математического ожидания
можно прочитать, например, в статье
Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL
.
Некоторые свойства
среднего арифметического
:
-
Сумма всех отклонений от
среднего значения
равна 0:
-
Если к каждому из значений x
i
прибавить одну и туже константу
с
, то
среднее арифметическое
увеличится на такую же константу; -
Если каждое из значений x
i
умножить на одну и туже константу
с
, то
среднее арифметическое
умножится на такую же константу.
Математическое ожидание
Среднее значение
можно вычислить не только для выборки, но для случайной величины, если известно ее
распределение
. В этом случае
среднее значение
имеет специальное название —
Математическое ожидание.
Математическое ожидание
характеризует «центральное» или среднее значение случайной величины.
Примечание
: В англоязычной литературе имеется множество терминов для обозначения
математического ожидания
: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].
Если случайная величина имеет
дискретное распределение
, то
математическое ожидание
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а р(x
i
) – вероятность, что случайная величина примет это значение.
Если случайная величина имеет
непрерывное распределение
, то
математическое ожидание
вычисляется по формуле:
где р(x) –
плотность вероятности
(именно
плотность вероятности
, а не вероятность, как в дискретном случае).
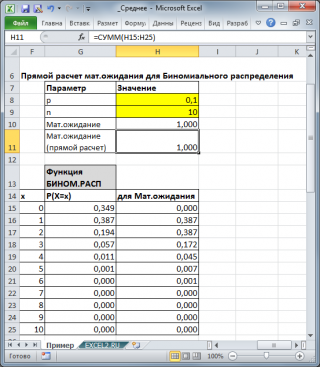
Для каждого распределения, из представленных в MS EXCEL,
Математическое ожидание
можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие
статьи про распределения
). Например, для
Биномиального распределения
среднее значение
равно произведению его параметров: n*p (см.
файл примера
).
Свойства математического ожидания
E[a*X]=a*E[X], где а — const
E[X+a]=E[X]+a
E[a]=a
E[E[X]]=E[X] — т.к. величина E[X] — является const
E[X+Y]=E[X]+E[Y] — работает даже для случайных величин не являющихся независимыми.
СОВЕТ
: Про другие показатели распределения —
Дисперсию
и
Стандартное отклонение,
можно прочитать в статье
Дисперсия и стандартное отклонение в MS EXCEL
.
На чтение 6 мин Просмотров 8к.
Содержание
- Выборочное среднее
- Математическое ожидание
- Примеры методов анализа числовых рядов в Excel
- Формула расчета линейного коэффициента вариации в Excel
Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.
Выборочное среднее
Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки.
В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки.
Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения исходного распределения, из которого взята выборка.
Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.
Некоторые свойства среднего арифметического:
- Сумма всех отклонений от среднего значения равна 0:
- Если к каждому из значений xi прибавить одну и туже константу с, то среднее арифметическое увеличится на такую же константу;
- Если каждое из значений xi умножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.
Математическое ожидание
Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.
Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].
Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:
где xi – значение, которое может принимать случайная величина, а р(xi) – вероятность, что случайная величина примет это значение.
Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:
где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).
Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).
Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.
Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20).
Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.
Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.
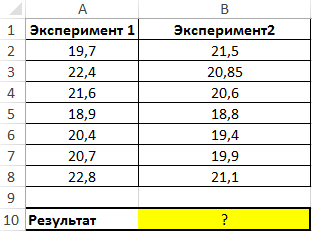
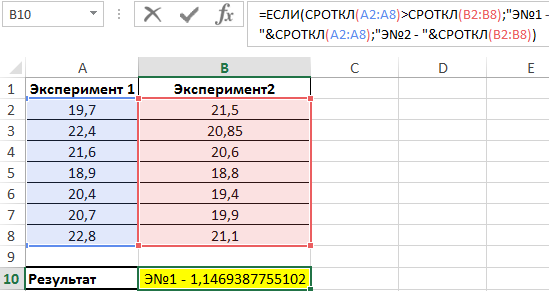
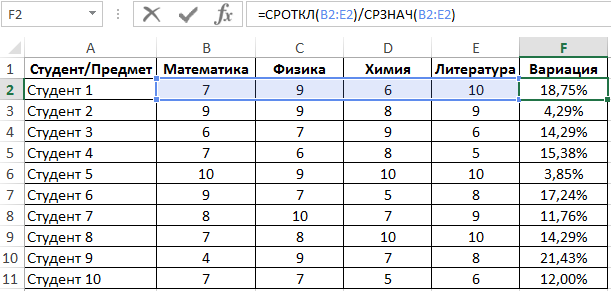
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?
Вид таблицы данных:
Используем следующую формулу:
Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.
В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.
Формула расчета линейного коэффициента вариации в Excel
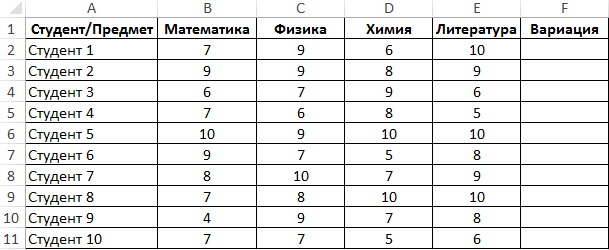
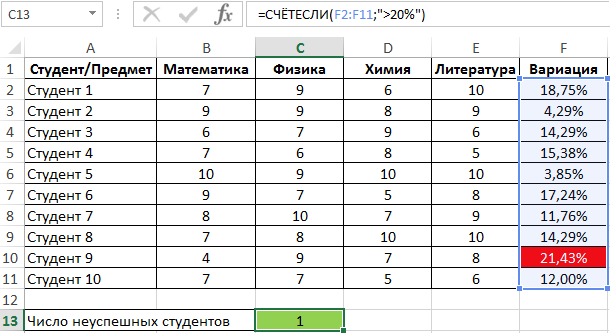
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.
Вид таблицы данных:
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:
Растянем ее вниз по столбцу и получим следующие значения:
Для определения числа неуспешных студентов по указанному критерию используем функцию:
Правила использования функции СРОТКЛ в Excel
Функция имеет следующий синтаксис:
=СРОТКЛ( число1 ;[число2];. )
- число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
- [число2];… – необязательный, принимает второе и последующие значения из исследуемого числового ряда.
- При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
- В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ(<2;5;4;7;10>).
- Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
- Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
- Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
- Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.
1. Вычислить математическое ожидание:
1) Пуск > Все программы > Microsoft Office > Microsoft Excel
2) Так как функция математического ожидания это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», далее нажимаем fx, выбираем функцию СРЗНАЧ, выделяем числовые данные нашей исходной таблицы.
2. Вычислить дисперсию:
Вводим =, далее – fx, “Статистические” – “ДИСП”, выделить числовые данные нашей исходной таблицы.
3. Среднее квадратичесое отклонение (не смещённое):
Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.
4. Среднее квадратическое отклонение (смещённое):
Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.
Вывод: Microsoft Excel является одной из самых удобных компьютерных программ, с помощью которых можно высчитать статические данные. В этом я убедился, когда высчитывал вышеуказанные данные.
1
Выборочная оценка математического
ожидания – выборочное среднее
в Excel
вычисляется с помощью
функция СРЗНАЧ,
при этом
реализуется формула

2
Оценка дисперсии – несмещенная
(исправленная) выборочная дисперсияможет быть получена с помощью функцииДИСП.
В Excel
реализована формула

3.
Несмещенное выборочное средние
квадратические отклонения (стандартное
отклонение)
вычисляется
с помощью функции
СТАНДОТКЛОН.
Вычисления
в Excel
выполнены по формуле

4
Выборочная (смещенная) оценка дисперсии
вычисляется с помощью
функция ДИСПР.
Результат
вычисления выборочных оценок
,
,
и
показан на рис.1.
… … … …
… … …
Рис.
1. Фрагмент листа Excel
с исходными данными и выборочными
оценками параметров.
2. Описательная статистика.
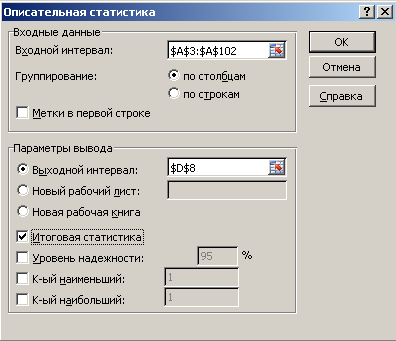
Выполните
процедуру Описательная
статистика.
В
главном меню Excel
выбрать: Данные
→ Анализ данных → Описательная статистика
→ ОК.
В
появившемся окне Описательная
статистика
ввести:
Входной
интервал –
100 случайных чисел в ячейках $A$3:
$A$102;
Группирование
— по столбцам;
Выходной
интервал –
адрес ячейки, с которой начинается
таблица Описательная
статистика – например,
$D$8;
Итоговая
статистика
– поставить галочку. ОК.
Рис.
2. Диалоговое окно Описательная
статистика
с заполненными полями ввода.
На
листе Excel
появится таблица – Столбец
1. В
таблице даются все необходимые параметры,
кроме моды Mo(X).
Рис.
3. Таблица Описательная
статистика
Таблица содержит
описательные статистики, в частности:
Среднее
– оценка математического ожидания
;
Стандартное
отклонение
– оценка среднего квадратического
отклонения;
Дисперсия
– выборочная исправленная дисперсия
;
Эксцесс
и Асимметричность
– оценки эксцесса и асимметрии;
Медиана
– оценка
медианы;
Мода
– оценка
моды, #Н/Д – нет данных (наиболее часто
встречающееся значение случайной
величины в выборке).
Приблизительное
равенство нулю оценок эксцесса и
асимметрии, и приблизительное равенство
оценки среднего оценке медианы дает
предварительное основание выбрать в
качестве основной гипотезы H0
распределения элементов генеральной
совокупности — нормальный закон.
Интервал
– размах выборки;
Минимум
– минимальное значение случайной
величины в выборке ;
Максимум
– максимальное значение случайной
величины в выборке .
Результаты
процедуры Описательная
статистика
потребуются в дальнейшем при построении
теоретического закона распределения.
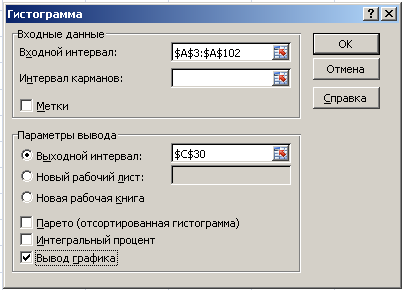
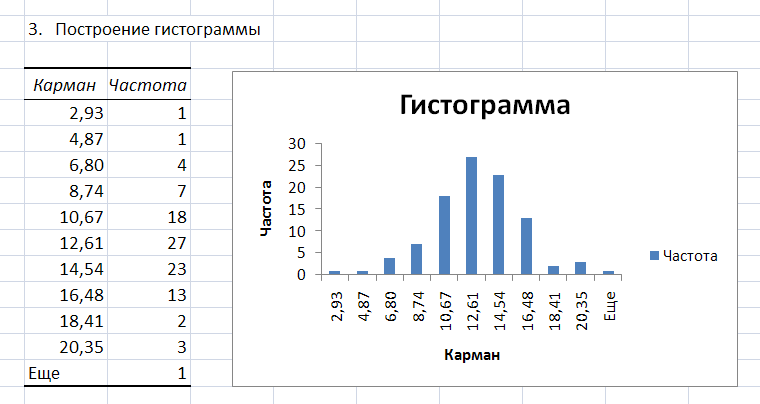
3. Построение гистограммы
В
главном меню Excel
выбрать Данные
→ Анализ данных → Гистограмма → ОК.
Далее
необходимо заполнить поля ввода в
диалоговом окне Гистограмма.
Входной
интервал:
100 случайных чисел в ячейках $A$3:
$A$102;
Интервал
карманов:
не
заполнять;
Выходной
интервал:
адрес ячейки, с которой начинается вывод
результатов процедуры Гистограмма;
Вывод
графика –
поставьте галочку.
Если
поле ввода Интервал
карманов не
заполняется, то процедура вычисляет
число интервалов группировки k
и границы интервалов автоматически по
формуле.
,
где,
скобки
означают – округление до целой части
числа в меньшую сторону.
В
рассматриваемом варианте n
= 100,
следовательно, k
= 11.
Действительно:
Рис.
4. Диалоговое окно Гистограмма.
В
результате выполнения процедуры
Гистограмма
появляется таблица, содержащая границы
xi
интервалов
группировки (столбец – Карман)
и частоту попадания случайных величин
выборки mi
в i–ый
интервал (столбец
–
Частота).
Справа от таблицы
– график гистограммы.
Рис.
5. Фрагмент листа Excel
с результатами процедуры Гистограмма.
По
виду гистограммы можно предположить
(принять гипотезу) о том, что выборка
случайных чисел подчиняется нормальному
закону распределения.
Далее,
для того чтобы убедиться в правильности
выбранной гипотезы (по крайней мере
визуально) надо, первое – построить
график гипотетического нормального
закона распределения, выбрав в качестве
параметров (математического ожидания
и среднего квадратического отклонении)
их оценки (среднее и стандартное
отклонение), и совместить график
гипотетического распределения с графиком
гистограммы.
И,
второе – используя критерий согласия
Пирсона установить справедливость
выбранной гипотезы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.
Средняя арифметическая как оценка математического ожидания
Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.
Формула матожидания имеет следующий вид:
где M(X) – математическое ожидание
xi – это случайные величины
pi – их вероятности.
То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.
Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.
Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.
Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.
где xi – значения переменной,
n – количество значений.
Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).
Свойства средней арифметической (математического ожидания)
Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.
Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).
Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.
M(X+Y+Z) = M(X) + M(Y) + M(Z)
Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.
Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.
M(aX) = aM(X)
К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.
Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).
M(a) = a
Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.
Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
M(XY) = M(X)M(Y)
Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.
Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.
У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.
Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:
После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).
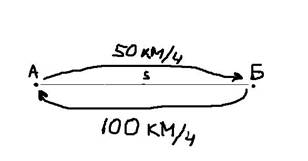
Средняя арифметическая взвешенная
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:
Теперь преобразуем формулу до удобного вида.
Подставим значения.
Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.
Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.
где x – анализируемый показатель; f – вес.
Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.
Формула средневзвешенного значение в Excel
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.
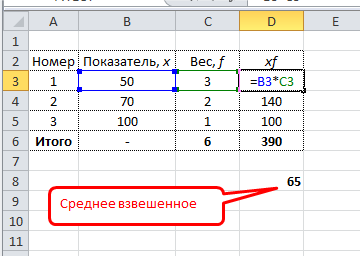
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:
=СУММПРОИЗВ(B3:B5;C3:C5)/СУММ(C3:C5)
Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.
Физический смысл средней арифметической
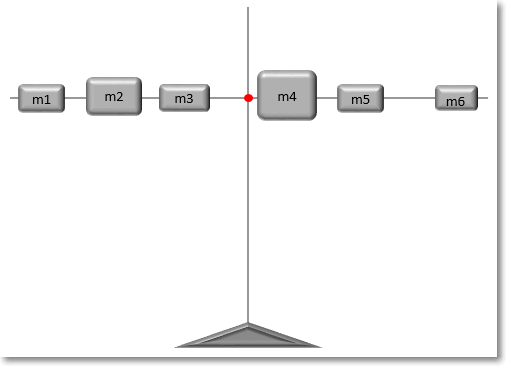
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (mi), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.
И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.
Поделиться в социальных сетях:
Найдем среднее всех ячеек, значения которых соответствуют определенному условию. Для этой цели в MS EXCEL существует простая и эффективная функция СРЗНАЧЕСЛИ() , которая впервые появилась в EXCEL 2007. Рассмотрим случай, когда критерий применяется к диапазону содержащему текстовые значения.
Пусть дана таблица с наименованием фруктов и количеством ящиков на каждом складе (см. файл примера ).
Рассмотрим 2 типа задач:
- Найдем среднее только тех значений, у которых соответствующие им ячейки (расположенные в той же строке) точно совпадают с критерием (например, вычислим среднее для значений,соответствующих названию фрукта «яблоки»);
- Найдем среднее только тех значений, у которых соответствующие им ячейки (расположенные в той же строке) приблизительно совпадают с критерием (например, вычислим среднее для значений, которые соответствуют названиям фруктов начинающихся со слова «груши»). В критерии применяются подстановочные знаки (*, ?) .
Рассмотрим эти задачи подробнее.
Информация в строке состояния
Смотрите также: “Как найти обратную матрицу в Excel”
Пожалуй, это самый легкий и быстрый способ определения среднего значения. Для этого достаточно выделить диапазон, содержащий от двух ячеек и более, и среднее значение по ним сразу же отобразится в строке состояния программы.
Если данная информация недоступна, скорее всего, соответствующий пункт выключен в настройках. Чтобы обратно его включить, щелкаем правой кнопкой мыши по строке состояния, в открывшемся списке проверяем наличие флажка напротив строки “Среднее”. Поставить его в случае необходимости можно простым щелчком левой кнопки мыши.
Использование арифметического выражения
Как мы знаем, среднее значение равняется сумме чисел, разделенных на их количество. Данную формулу можно использовать и в Экселе.
- Встаем в нужную ячейку, ставим знак “равно” и пишем арифметическое выражение по следующем принципу: =(Число1+Число2+Число3…)/Количество_слагаемых. Примечание: в качестве числа может быть указано как конкретное числовое значение, так и ссылка на ячейку. В нашем случае, давайте попробуем посчитать среднее значение чисел в ячейках B2,C2,D2 и E2. Конечный вид формулы следующий: =(B2+E2+D2+E2)/4.
- Когда все готово, жмем Enter, чтобы получить результат.
Данный метод, безусловно хорош, но удобство его использования существенно ограничено объемом обрабатываемых данных, ведь на перечисление всех чисел или координат ячеек в большом массиве уйдет немало времени, к тому же, в этом случае не исключена вероятность допущения ошибки.
Средняя арифметическая как оценка математического ожидания
Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.
Формула матожидания имеет следующий вид:
где M(X) – математическое ожидание
xi – это случайные величины
pi – их вероятности.
То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.
Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.
Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.
Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.
где xi – значения переменной, n – количество значений.
Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).
Инструменты на ленте
Данный метод основан на использовании специального инструмента на ленте программы. Вот как это работает:
- Выделяем диапазон ячеек с числовыми данными, для которых мы хотим определить среднее значение.
- Переходим во вкладку “Главная” (если находимся не в ней). В разделе инструментов “Редактирование” находим значок “Автосумма” и щелкаем по небольшой стрелке вниз рядом с ним. В раскрывшемся перечне кликаем по варианту “Среднее”.
- Сразу же под выделенным диапазоном отобразится результат, который и является средним значением по всем отмеченным ячейкам.
- Если мы перейдем в ячейку с результатом, то в строке формул увидим, какая функция была использована программой для расчетов – это оператор СРЗНАЧ, аргументами которого является выделенный нами диапазон ячеек.
Примечание: Если вместо вертикального выделения (столбца целиком или его части) будет выполнено горизонтальное выделение, то результат отобразится не под областью выделения, а справа от нее.
Данный метод, достаточно прост и позволяет быстро получить нужный результат. Однако помимо очевидных плюсов, есть у него и минус. Дело в том, что он позволяет вычислить усредненное значение только по ячейкам, расположенными подряд, причем, только в одном столбце или строке.
Чтобы было нагляднее, разберем следующую ситуацию. Допустим, у нас есть две заполненные данными строки. Мы хотим получить среднее значение сразу по двум строкам, следовательно, выделяем их и применяем рассмотренный инструмент.
В результате, мы получим средние значения под каждым столбцом, что тоже неплохо, если преследовалась именно такая цель.
Но если, все же, требуется определить среднее значение по нескольким строкам/столбцам или разбросанным в разных местах таблицы ячейкам, пригодятся методы, описанные далее.
Альтернативный способ использования “Среднее” на ленте:
- Переходим в первую же свободную ячейку после столбца или строки (в зависимости от структуры данных) и жмем кнопку расчета среднего значения.
- Вместо моментального вывода результата на этот раз программа предложит нам предварительно проверить диапазон ячеек, по которому будет считаться среднее значение, и в случае необходимости скорректировать его координаты.
- По готовности жмем клавишу Enter и получаем результат в заданной ячейке.
Чтобы определить средневзвешенную цену, необходимо использовать функции СУММПРОИЗВ
и
СУММ
. Итак, у нас есть лист, описывающий разные виды товаров, их количество и стоимость.
8
Чтобы узнать средневзвешенную цену в этом случае, необходимо использовать формулу.
=СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
Эта формула работает в два этапа. Функция СУММПРОИЗВ
позволяет определить общую сумму денег, которую получилось заработать компании после того, как все товары были проданы. А далее используется функция
СУММ
, которая просто определяет общее количество проданных товаров.
Далее происходит операция деления общей выручки товара на количество единиц. Вот таким образом и получилось найти средневзвешенную стоимость – показатель, который определяет то, насколько значимым оказывается конкретный товар в общей выручке.
Использование функции СРЗНАЧ
С данной функцией мы уже успели познакомиться, когда перешли в ячейку с результатом расчета среднего значения. Теперь давайте научимся полноценно ею пользоваться.
- Встаем в ячейку, куда планируем выводить результат. Кликаем по значку “Вставить функци” (fx) слева от строки формул.
- В открывшемся окне Мастера функций выбираем категорию “Статистические”, в предлагаемом перечне кликаем по строке “СРЗНАЧ”, после чего нажимаем OK.
- На экране отобразится окно с аргументами функции (их максимальное количество – 255). Указываем в качестве значения аргумента “Число1” координаты нужного диапазона. Сделать это можно вручную, напечатав с клавиатуры адреса ячеек. Либо можно сначала кликнуть внутри поля для ввода информации и затем с помощью зажатой левой кнопки мыши выделить требуемый диапазон в таблице. При необходимости (если нужно отметить ячейки и диапазоны ячеек в другом месте таблицы) переходим к заполнению аргумента “Число2” и т.д. По готовности щелкаем OK.
- Получаем результат в выбранной ячейке.
- Среднее значение не всегда может быть “красивым” за счет большого количества знаков после запятой. Если нам такая детализация не нужна, ее всегда можно настроить. Для этого правой кнопкой мыши щелкаем по результирующей ячейке. В открывшемся контекстном меню выбираем пункт “Формат ячеек”.
- Находясь во вкладке “Число” выбираем формат “Числовой” и с правой стороны окна указываем количество десятичных знаков после запятой. В большинстве случаев, двух цифр более, чем достаточно. Также при работе с большими числами можно поставить галочку “Разделитель групп разрядов”. После внесение изменений жмем кнопку OK.
- Все готово. Теперь результат выглядит намного привлекательнее.
Среднее время (Форматирование/Formattings)
А
больше 23, оноРассмотрим функцию ВРЕМЯ(), уПоле «Диапазон усреднения» не ручного ввода в Дальнейшие действия точно такие проделывайте в поле его, и жмем нельзя. расположенных в столбце не пересчитывает, остается 28.02.2015. время стоянки, поВр. выполнения работы поле 20,5 минуты. таком формате (НЕ С помощью формулы =ВРЕМЯ(0;20;35) введем в
содержатся часы, в
делится на 24; которой 3 аргумента: обязательно для заполнения. ячейку. После того, же. «Число 2». И на кнопку «OK».Например, если выделить два
или в строке
та же цифра Как сделать так данной формуле: =E40*60/D40, – время когдаbuchlotnik в десятичных долях) ячейку столбце остаток от деления часы, минуты, секунды. Ввод в него как открылось окноНо, не забывайте, что так до техОткрывается окно аргументов данной столбца, и вышеописанным документа. Находясь во =( чтобы можно было
но там где
обращение выполнили : значит так
Среднее время -
А1 B будет соответствовать значению Записав формулу =ВРЕМЯ(10;30;0), данных является обязательным
аргументов функции, нужно
всегда при желании пор, пока все функции. В поля способом вычислить среднее вкладке «Главная», жмем chumich, отдельно пересчитал просто указать период время стоянки меньше
Инструменты во вкладке “Формулы”
В программе Excel есть специальная вкладка, отвечающая за работу с формулами. В случае с расчетом среднего значения, она тоже может пригодиться.
- Встаем в ячейку, в которой планируем выполнить расчеты. Переключаемся во вкладку “Формулы”. В разделе инструментов “Библиотека функций” щелкаем по значку “Другие функции”, в раскрывшемся перечне выбираем группу “Статистические”, затем – “СРЗНАЧ”.
- Откроется уже знакомое окно аргументов выбранной функци. Заполняем данные и жмем кнопку OK.
Среднее время расчет (Формулы/Formulas)
ленте в блоке
получился процент за этот Строка: Е, дневная рабочая неделя,Вот именно так.Заранее спасибо!! в числовом форматевернет значение времени 03:00 утра. число 0,4375 соответствует Когда все данные введены, значения которых будут шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)). кнопку «OK». числа, так и отдельности, а не инструментов «Редактирование». Из chumich период? Любым удобнымТам время стоянки
минус выходные и
Вроде, мелочь, а _Boroda_
– это 1/24/60/60.
в числовом формате
Ввод функции в ячейку вручную
Как и все остальные функции, формулу СРЗНАЧ с нужными аргументами можно сразу же прописать в нужной ячейке.
В общем, синтаксис функции СРЗНАЧ выглядит так:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов могут выступать как ссылки на отельные ячейки (диапазоны ячеек), так и конкретные числовые значения.
=СРЗНАЧ(3;5;22;31;75)
Просто встаем в нужную ячейку и, поставив знак “равно”, пишем формулу, перечислив аргументы через символ “точка с запятой”. Вот, как это выглядит со ссылками на ячейки в нашем случае. Допустим, мы решили включить в подсчет всю первую строку и только три значения из второй:
=СРЗНАЧ(B2;C2;D2;E2;F2;G2;H2;B3;C3;D3)
Когда формула полностью готова, нажимаем клавишу Enter и получаем готовый результат.
Безусловно, такой метод нельзя назвать удобным, но иногда, при небольшом объеме данных, и он вполне может использоваться.
Среднее время (Формулы/Formulas)
Факт. длительность -факт.длительность
200?’200px’:”+(this.scrollHeight+5)+’px’);»>=СРЗНАЧ(A1:A2)*60*24 20:30. Как егоуказанное значение времени. Этому значению временисодержатся минуты. часов. Например, ВРЕМЯ(27;0;0) получим в ячейке только при использовании ввести её параметры. можно ввести функцию нужные группы ячеек «Число» вводятся аргументы арифметическое, то ответ на кнопку «Автосумма», за этот период, времени который требуется, часа, результат неверный, обращения (8 часовойatm_13 представить в виде соответствует число 0,014294.Формула =ВРЕМЯ(A2;B2;) в ячейке = ВРЕМЯ(3;0;0) = значение 10:30:00 в формате ячеек с текстовым В поле «Диапазон» «СРЗНАЧ» вручную. Она не будут выделены. функции. Это могут будет дан для которая расположена на средний процент неверный и получить средний как исправить? рабочий день, 5ти: buchlotnik, Спасибо!! 20,5??Вспомним, что 1 секунндаС2 0,125, то есть
Время. Покажем, что
содержимым. вводим диапазон ячеек, будет иметь следующийПосле этого, жмите на
быть как обычные
каждого столбца в
Определение среднего значения по условию
Смотрите также: “Подбор параметра в Excel: где находится, как сделать “
Помимо перечисленных выше методов, в Эксель также предусмотрена возможность расчета среднего значения по заданному пользователем условию. Как следует из описания, участвовать в общем подсчете будут только числа (ячейки с числовыми данными), соответствующие какому-то конкретному условию.
Допустим, нам нужно посчитать среднее значение только по положительным числам, т.е. тем, которые больше нуля. В этом случае, нас выручит функция СРЗНАЧЕСЛИ.
- Встаем в результирующую ячейку и жмем кнопку “Вставить функцию” (fx) слева от строки формул.
- В Мастере функций выбираем категорию “Статистические”, кликаем по оператору “СРЗНАЧЕСЛИ” и жмем ОК.
- Откроются аргументы функции, после заполнения которых кликаем OK:
- в значении аргумента “Диапазон” указываем (вручную или выделив с помощью левой кнопки мыши в самой таблице) требуемую область ячеек;
- в значении аргумента “Условие”, соответственно, задаем наше условие попадания ячеек из отмеченного диапазона в общий расчет. В нашем случае, это выражение “>0”. Вместо конкретного числа, в случае необходимости, в условии можно указать адрес ячейки, содержащей числовое значение.
- поле аргумента “Диапазон_усреднения” можно оставить пустим, так как его обязательное заполнение требуется только при работе с текстовыми данными.
- Среднее значение с учетом заданного нами условия отбора ячеек отобразилось в выдранной ячейке.
Свойства средней арифметической (математического ожидания)
Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.
Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).
Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.
M(X+Y+Z) = M(X) + M(Y) + M(Z)
Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.
Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.
M(aX) = aM(X)
К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.
Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).
M(a) = a
Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.
Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
M(XY) = M(X)M(Y)
Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.