Обработка статистических данных в excel лабораторные работы

Задание

Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:

1.Вывести
на лист Excel
исходные статистические данные.

2. Построить
вариационный ряд.

3. Вычислить
статистические характеристики.

4. Построить
интервальный статистический ряд.

5.Построить
гистограмму частот.

6. Составить
статистическую функцию распределения
статистического ряда.

7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.

В качестве примера
рассмотрим следующую выборку

Порядок выполнения работы

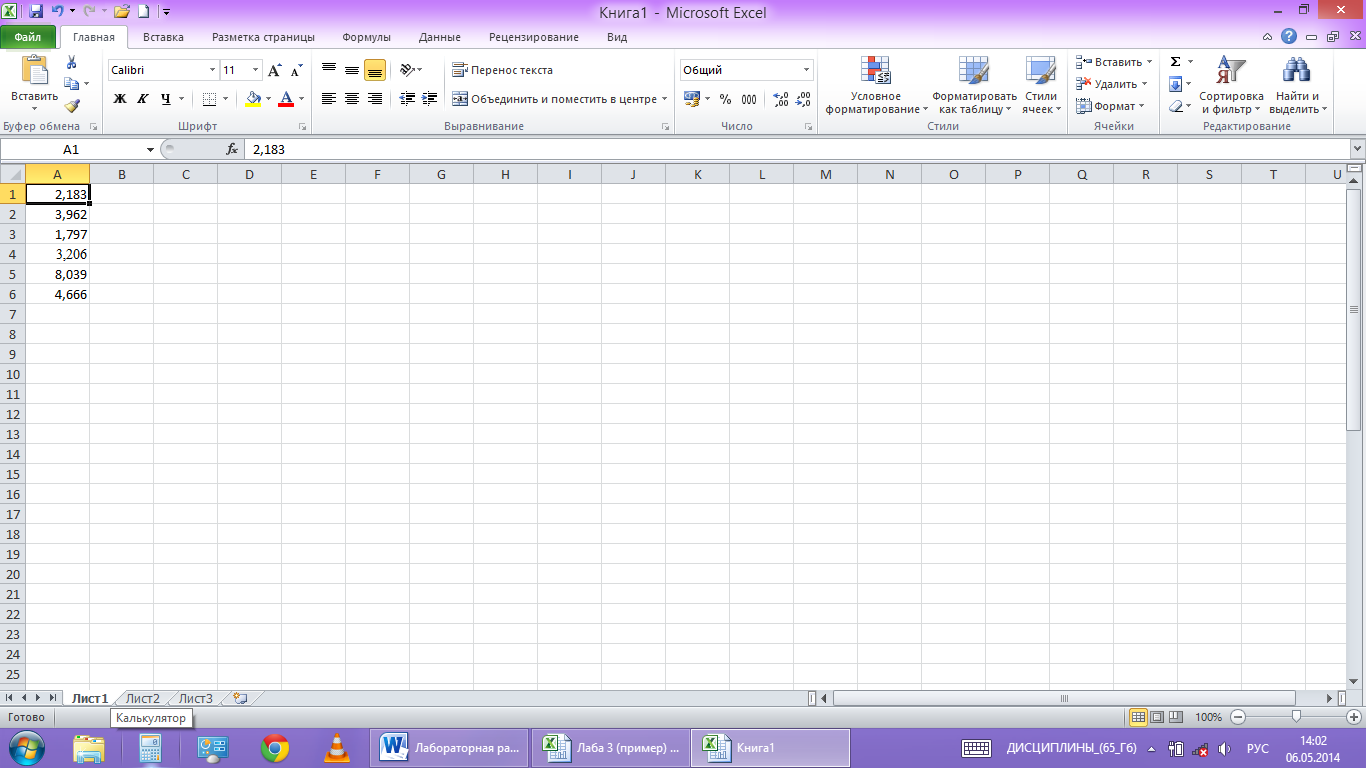
1.Ввод исходных статистических данных.

Вводим данные в
первый столбец таблицы (рис.1).

рис.1

2. Построение вариационного ряда.

Производим
сортировку данных в порядке возрастания.
Для этого:

а) выделяем первый
столбец;

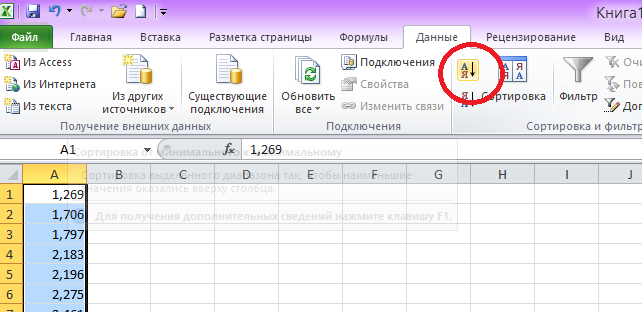
б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)

рис. 2

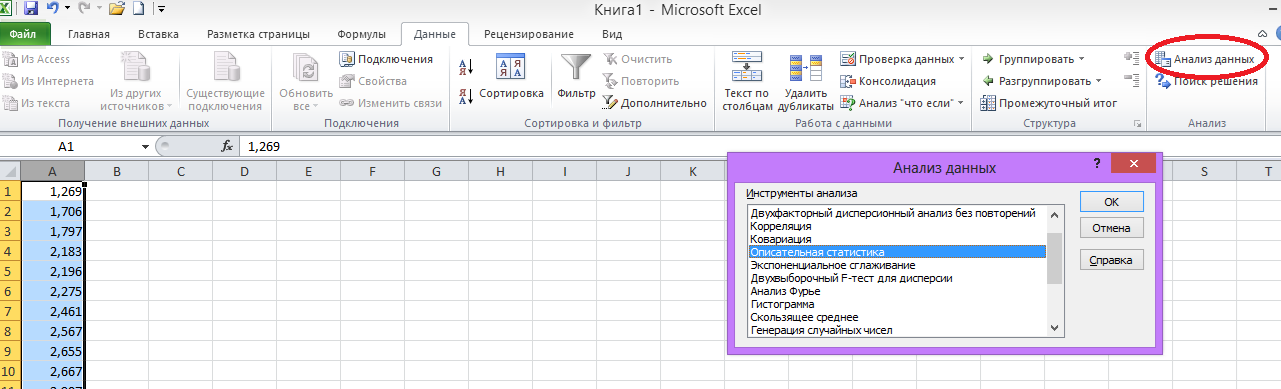
3. Вычисление статистических характеристик.

На ленте
во вкладке «Данные» выбираем «Анализ
данных» меню «Описательная статистика»
нажимаем ОК.

рис. 3

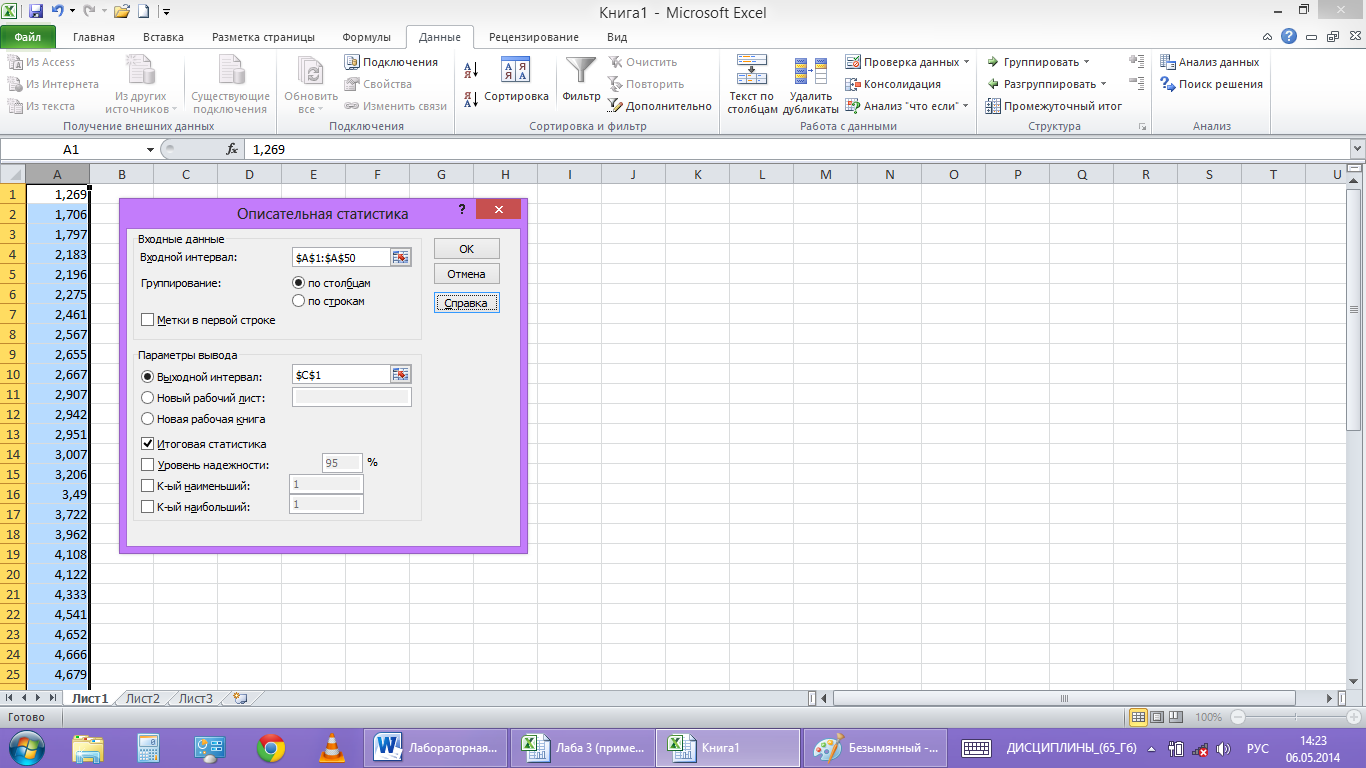
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)

рис. 4

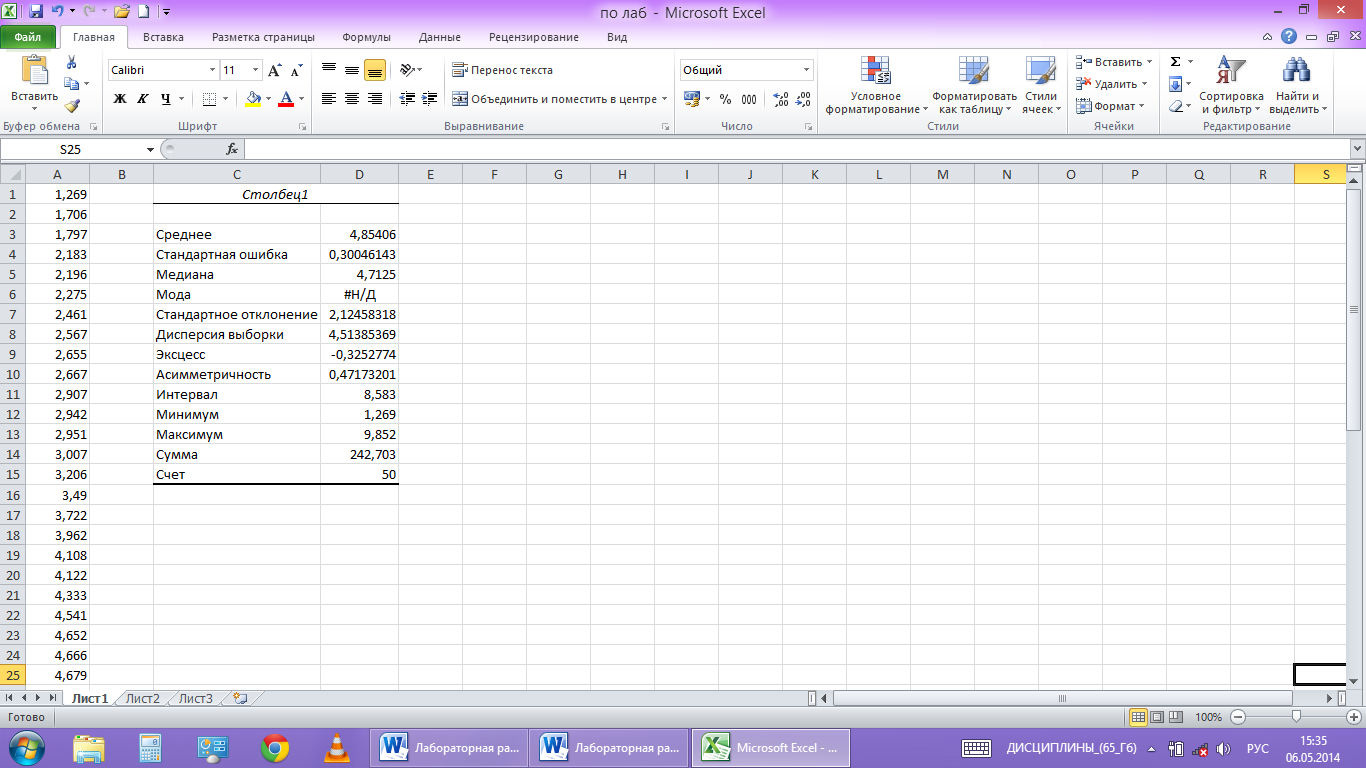
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)

рис. 5

Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.

4. Построение интервального статистического ряда.

Длину интервала
группировки определяем по формуле

Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.

В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу

в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу

В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.

Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.

В ячейку
F1
вводим формулу

В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу

В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).

Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.

Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)

рис. 6	рис. 7

В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
и введем в него адрес первой ячейки для
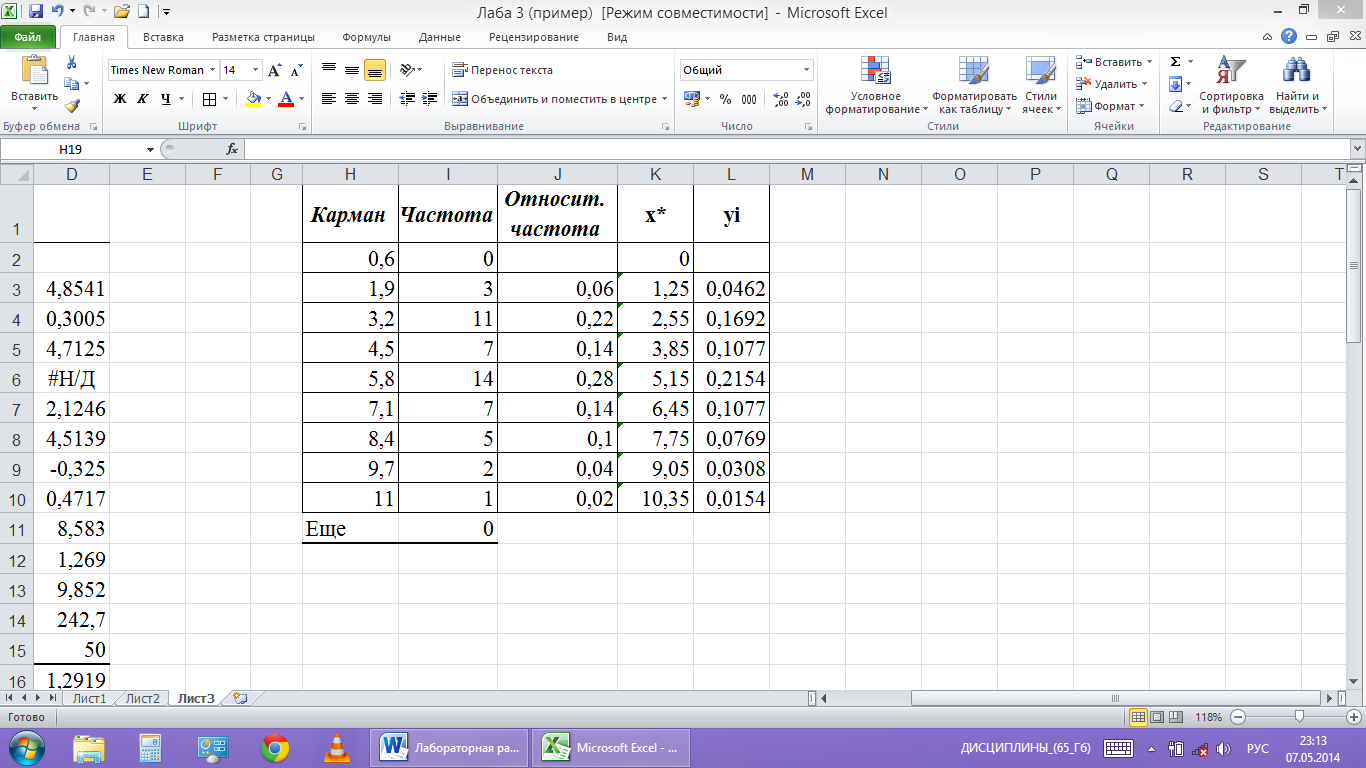
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).

Определим
относительные частоты р_i^*,
значения серединных точек интервалов

и высоты
прямоугольников

Для этого

1. в ячейку
   J1
   введем заголовок «Относительная
   частота»;

2. В ячейку
   J3
   введем формулу

и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;

1. в ячейку
   K1
   введем заголовок столбца Х*;

2. в ячейку
   К3 введем формулу

Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;

1. в ячейку
   L1
   введем заголовок столбца У_i;

2. в ячейку
   L3
   введем формулу

Протягиваем
её вниз до ячейки L10.

В
результате в пятом столбце таблицы
(рис.8) появятся значения У_i.

рис.8

Соседние файлы в папке Лаб.работы

• #
• #
• #
• #

Лабораторная работа
Статистические функции Excel

Цель работы: Освоение приемов работы с функциями массивов (табличными функциями). Изучение элементарных статистических функций Excel 

• Формулы массивов (табличные формулы)

Массивом называют блок ячеек электронной таблицы, который используется для создания формул, возвращающих некоторое множество результатов или оперирующих множеством значений, а не отдельными значениями. 

 Формулы массивов (иногда их называют табличными формулами), используют несколько множеств значений (массивов аргументов), и возвращают одно или несколько значений. Такие формулы позволяют обращаться с блоками, как с обычной ячейкой.

Рассмотрим работу с использованием массивов на следующем примере. Требуется определить прибыль для каждого года деятельности отеля, представленного в таблице 1.

Таблица 1.

Пример использования функций массива

	A	B	C	D
1	Год	Приход	Расход	Прибыль
2	2005	200	150	{B2:B5-C2:C5}
3	2006	360	230	{B2:B5-C2:C5}
4	2007	410	250	{B2:B5-C2:C5}
5	2008	200	180	{B2:B5-C2:C5}

Выделим блок D2:D5. Начнем ввод формулы – наберем знак =. Выделим блок B2:B5, наберем знак минус -, выделим блок С2:С5. Ввод формул массива заканчивается комбинацией клавиш Ctrl+Shift+Enter. После нажатия такой комбинации во всех ячейках блока D2:D5 появится формула {B2:B5-C2:C5}. 

• Основные правила работы с формулами массива:

• перед вводом формулы нужно выделить ячейку или диапазон для результатов, если формула возвращает несколько значений, то диапазон результатов должен быть того же размера, что и диапазон исходных данных;
• фигурные скобки, отмечающие формулу массива, вводятся при завершении ввода формулы клавишами Ctrl+Shift+Enter, если фигурные скобки ввести вручную, такой ввод будет воспринят Excel как текст.
• для редактирования формулы массива необходимо выделить блок, активировать строку формул, внести изменения и завершить редактированием клавишами Ctrl+Shift+Enter;
• блок ячеек может указываться присвоенным ему именем (клавиша F3 и выбор имени в диалоге «Вставка имени»;
• массив исходных данных и массив результатов могут быть многомерными, т.е. включать несколько строк и столбцов.

• Функции Excel, используемые для статистического анализа 

Статистический анализ данных необходим для оценки деятельности фирмы и прогноза ее работы на какой-то срок. Такой анализ основывается на сборе информации, определении по представленным массивам данных оценок, статистических показателей и тенденций развития фирмы.

В категорию статистических функций Excel входит около 80 функций, кроме того, значительное число функций статистического анализа входят в надстройку «Пакет анализа».

Для выполнения задания потребуются статистические функции, полное описание которых приведено ниже.

• МАКС(число1;число2; …) — возвращает наибольшее значение из набора значений.
• Число1, число2,…— от 1 до 30 чисел, среди которых требуется найти наибольшее.
• Можно задавать аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел. Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, вызывают значения ошибок. 
• Если аргумент является массивом или ссылкой, то в нем учитываются только числа. Пустые ячейки, логические значения или текст в массиве или ссылке игнорируются. Если логические значения или текст не должны игнорироваться, следует использовать функцию МАКСА. Если аргументы не содержат чисел, то функция МАКС возвращает 0 (ноль);
• МИН(число1;число2; …) — возвращает наименьшее значение из набора значений, в остальном полностью аналогична функции ^ МАКС;
• СРЗНАЧ(число1; число2; …) — возвращает среднее (арифметическое) своих аргументов.
• Число1, число2, … — это от 1 до 30 аргументов, для которых вычисляется среднее.
• Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
• Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются;

ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x; новые значения_x; конст) — возвращает значения в соответствии с линейным трендом, т.е. аппроксимирует прямой линией (по методу наименьших квадратов) массивы ”известные_значения_y” и “известные_значения_x”. Возвращает значения y, в соответствии с этой прямой для заданного массива новые_значения_x.

• Известные_значения_y — множество значений y, которые уже известны для соотношения y = mx + b.
• Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
  Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
• Известные_значения_x — необязательное множество значений x, которые уже известны для соотношения y = mx + b.
• Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y и известные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность. 
• Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).
  Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
• Новые_значения_x — новые значения x, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк.
• Если новые_значения_x опущены, то предполагается, что они совпадают с известные_значения_x.
• Если опущены оба массива известные_значения_x и новые_значения_x, то предполагается, что это массив {1;2;3;…} такого же размера, что и известные_значения_y.
• Конст — логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
• Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.
• Если конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.

РОСТ(известные_значения_y;известные_значения_x;новые_значения_x; конст) — возвращает значения y для последовательности новых значений x, задаваемых с помощью существующих x- и y-значений, т.е. функция рассчитывает прогнозируемый экспоненциальный рост на основании имеющихся данных.

• Известные_значения_y — это множество значений y, которые уже известны в соотношении y = b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
• Известные_значения_x — это необязательное множество значений x, которые уже известны для соотношения y=b*mx. Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_xинтерпретируется как отдельная переменная. Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные_значения_y иизвестные_значения_x могут иметь любую форму, при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец). Если известные_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y.
• Новые_значения_x — это новые значения x, для которых РОСТ возвращает соответствующие значения y. Новые_значения_x должны содержать столбец (или строку) для каждой независимой переменной, как иизвестные_значения_x. Таким образом, если известные_значения_y — это один столбец, то известные_значения_x и новые_значения_x должны иметь такое же количество столбцов. Если известные_значения_y — это одна строка, то известные_значения_x и новые_значения_x должны иметь такое же количество строк. Если аргумент новые_значения_x опущен, то предполагается, что он совпадает с аргументом известные_значения_x. Если оба аргумента известные_значения_x и новые_значения_x опущены, то предполагается, что это массив {1;2;3;…} такого же размера, как и известные_значения_y. 
• Конст — это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 1. Если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то b полагается равным 1, а значения m подбираются так, чтобы y = mx.

ПРЕДСКАЗ(x, известные_значения_y, известные_значения_x) – вычисляет или предсказывает будущее значение по существующим значениям. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эту функцию можно использовать для прогнозирования будущих продаж, потребностей в оборудовании или тенденций потребления.

• Функция ПРЕДСКАЗ имеет аргументы, указанные ниже.
• x — обязательный аргумент. Точка данных, для которой предсказывается значение.
• Известные_значения_y — обязательный аргумент. Зависимый массив или интервал данных.
• Известные_значения_x — обязательный аргумент. Независимый массив или интервал данных.
• Если x не является числом, функция ПРЕДСКАЗ возвращает значение ошибки #ЗНАЧ!.
• Если аргументы «известные_значения_y» и «известные_значения_x» пусты или количество точек данных в этих аргументах не совпадает, функция ПРЕДСКАЗ возвращает значение ошибки #Н/Д.
• Если дисперсия аргумента «известные_значения_x» равна 0, функция ПРЕДСКАЗ возвращает значение ошибки #ДЕЛ/0!.

• Замечания 
• 1) Формулы, которые возвращают массивы, должны быть введены как формулы массива.

2) При вводе константы массива для аргумента, такого как известные_значения_x, следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.

• Задание

Для приведенных в таблице 2 данных о реализации гостиничных услуг сетью отелей «Европа» вычислить:

• минимальные, максимальные и среднее показатели по каждому кварталу;
• средние показатели по каждому отелю;
• вычислить средний доход по всей сети отелей за отчетный период;
• дать оценку работы каждого отеля: «хорошо», если доход отеля превышает средний по сети, и «плохо», если доход меньше среднего по сети;
• построить линейную и экспоненциальную модель деятельности сети отелей и дать прогноз для двух следующих кварталов;
• оценить относительные отклонения для среднего значения и «Тенденции», для среднего значения и «Роста».

^ Таблица 2.

Исходные данные

	A	B	C	D	E	F	G
1	Отель	1 кв.	2 кв.	3 кв.	4 кв.	Среднее по	Оценка
						отелю
2	Швеция	1500	2000	6000	8000
3	Дания	1400	5000	4100	5000
4	Норвегия	3600	3600	3000	4500
5	Финляндия	1100	1045	9100	7800
6	Германия	3850	3650	7800	11000
7	Польша	6800	7250	8122	9450
8	Чехия	6590	7050	6400	6440
9	Словакия	930	3970	4512	4600
10	Венгрия	8912	7490	3570	8000
11	Болгария	3590	3800	5464	5954
12	Мин
13	Мах
14	Среднее
15		1	2	3	4
16	Тенденция по среднему
17	Рост по среднему
18	Погрешность
	тенденции
19	Погрешность
	роста
20	Лучший отель по сети
	Доход

• Технология выполнения

1. Минимальные, максимальные и средние значения по кварталам и средние значения по турам подсчитываются с помощью Мастера функций.
2. Для оценки работы отеля используется среднее значение дохода по сети и функция ЕСЛИ().
3. Функция Тенденция показывает динамику изменения данных и позволяет получить прогноз на будущее. При этом изменение данных описывается линейным уравнением. Для определения Тенденции:

• Выделить новый диапазон ячеек для размещения результатов (B16:E16);
• В строке формул вставить функцию Тенденция и в Мастере функций в поле аргумента известные_значения_y указать диапазон средних по кварталу значений.
• Известные_значения_x можно не устанавливать, т.к. это 1, 2, 3, 4 кварталы.
• Выйти из Мастера функций – Ok.
• Установить курсор в строке формул, нажать комбинацию клавиш Ctrl+Shift+Enter, в выделенном новом массиве появятся результаты.

1. Функция Тенденция показывает линейную модель изменения показателей, экспоненциальная модель строится функцией Рост.
2. Самостоятельно вычислите функцию Рост для средних по кварталам, подобно тому, как вычислялась функция Тенденция.
3. Вычислить прогноз развития событий на ближайшие два квартала, используя функцию Тенденция:

• Справа от ячейки со значением Тенденция для 4-го квартала выделить две свободные ячейки.
• Вставить функцию Тенденция и в Мастере функций указать:
• в поле известные_значения_y вычисленные ранее значения Тенденция за четыре квартала (диапазон B16:E16);
• в поле новые_значения_x – диапазон F15:G15 – кварталы 5 и 6, для которых выполняется прогноз.
• Завершить работу Мастера – Ok, завершить ввод функции массива Ctrl+Shift+Enter, в выделенных ячейках появятся предсказанные по линейной модели значения для 5 и 6 кварталов.

1. Таким же образом рассчитать прогноз по экспоненциальной модели с помощью функции Рост.
2. Оценить относительные отклонения в процентах для среднего значения и Тенденции, для среднего значения и Роста (для каждого из четырех кварталов) по формуле:

Относительное отклонение=(yфакт — yмодели)/yмодели,
где yфакт — среднее значение; 
      yмодели – значение, определенное с помощью Тенденции или Роста.

Пример расчета показателей работы отелей по первому кварталу приведен в таблице 3.

Таблица 3.

Пример расчета показателей работы отелей по первому кварталу

	A	B
13	Мин	=МИН(В3:В12)
14	Мах	=МАКС(В3:В12)
15	Среднее	=СРЗНАЧ(В3:В12)
17	Тенденция по среднему	=ТЕНДЕНЦИЯ(В15:Е15)
18	Рост по среднему	=РОСТ(В15:Е15)
19	Погрешность	=(В15-В17)/В17
	тенденции
20	Погрешность	=(В15-В18)/В18
	роста
21	Лучший отель по сети	=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);1)
22	Доход	=ИНДЕКС($А$3:В12;ПОИСКПОЗ(МАКС(В3:В12);В3:В12;0);2)

Результаты расчетов приведены в таблице 4.

Таблица 4.

Результаты расчетов

	A	B	C	D	E	F	G
1	Отель	1 кв.	2 кв.	3 кв.	4 кв.	Среднее по	Оценка
						отелю
2	Швеция	1500	2000	6000	8000	4375	Плохо
3	Дания	1400	5000	4100	5000	3875	Плохо
4	Норвегия	3600	3600	3000	4500	3675	Плохо
5	Финляндия	1100	1045	9100	7800	4761,25	Плохо
6	Германия	3850	3650	7800	11000	6575	Хорошо
7	Польша	6800	7250	8122	9450	7905,5	Хорошо
8	Чехия	6590	7050	6400	6440	6620	Хорошо
9	Словакия	930	3970	4512	4600	3503	Плохо
10	Венгрия	8912	7490	3570	8000	6993	Хорошо
11	Болгария	3590	3800	5464	5954	4702	Плохо
12	Мин	930	1045	3000	4500
13	Мах	8912	7490	9100	11000
14	Среднее	3827	4486	5807	7074	5298
15		1	2	3	4	5	6
16	Тенденция по среднему	3639	4745	5852	6958	8064	9170
17	Рост по среднему	3760	4639	5724	7063	8714	10752
18	Погрешность	5,17%	-5,48%	-0,77%	1,67%
	тенденции
19	Погрешность	1,79%	-3,32%	1,44%	0,17%
	роста
20	Лучший отель по сети	Венгрия	Венгрия	Финляндия	Германия
21	Доход	8912	7490	9100	11000

Дополнительные задания

1. Выполнить условное форматирование Столбца Оценка – выделить красным цветом отели, доход которых меньше среднего.
2. Определить лучший отель по сети за квартал и его доход.
3. Дополнить таблицу строкой Предсказание для 5 и 6 кварталов.
4. Построить диаграмму – график изменения доходов по кварталам и тенденцию изменения доходов по кварталам, включая прогноз на два следующие квартала, а также рост изменения доходов по кварталам.

Пример для отеля «Венгрия» представлен на диаграмме 1.

Диаграмма 1.

1. Добавить на график линию тренда.

• Проще всего построить график функции тренда непосредственно сразу после внесения имеющихся данных в массив. Для этого на листе с таблицей данных выделите не менее двух ячеек диапазона, для которого будет построен график, и сразу после этого вставьте диаграмму. Вы можете воспользоваться такими видами диаграмм, как график, точечная, гистограмма, пузырьковая, биржевая. Остальные виды диаграмм не поддерживают функцию построения тренда.
• В меню «Диаграмма» выберите пункт «Добавить линию тренда». В открывшемся окне на вкладке «Тип» выберите необходимый тип линии тренда, что в математическом эквиваленте также означает и способ аппроксимации данных. При использовании описываемого метода вам придется делать это «на глаз», т.к. никаких математических вычислений для построения графика вы не проводили.
• Поэтому просто прикиньте, какому типу функции более всего соответствует график имеющихся данных: линейной, логарифмической, экспоненциальной, степенной или иной. Если же вы сомневаетесь в выборе типа аппроксимации, можете построить несколько линий, а для большей точности прогноза на вкладке «Параметры» этого же окна отметить флажком пункт «поместить на диаграмму величину достоверности аппроксимации (R^2)».
• Сравнивая значения R^2 для разных линий, вы сможете выбрать тот тип графика, который характеризует ваши данные наиболее точно, а, следовательно, строит наиболее достоверный прогноз. Чем ближе значение R^2 к единице, тем точнее вы выбрали тип линии. Здесь же, на вкладке «Параметры», вам необходимо указать период, на который делается прогноз.
• Такой способ построения тренда является весьма приблизительным, поэтому лучше все-таки произвести хотя бы самую примитивную статистическую обработку имеющихся данных. Это позволит построить прогноз более точно.
• Если вы предполагаете, что имеющиеся данные описываются линейным уравнением, просто выделите их курсором и произведите автозаполнение на необходимое число периодов, или количество ячеек. В данном случае нет необходимости находить значение R^2, т.к. вы заранее подогнали прогноз к уравнению прямой.
• Если же вы считаете, что известные значения переменной лучше всего могут быть описаны с помощью экспоненциального уравнения, также выделите исходный диапазон и произведите автозаполнение необходимого количества ячеек, удерживая правую клавишу мыши. При помощи автозаполнения вы не сможете построить других типов линий, кроме двух указанных.

Рабочее окно для построения линии тренда представлено на рисунке 1.

Рисунок 1.

Введение

В современном обществе к статистическим методам проявляется повышенный интерес как к одному из важнейших аналитических инструментариев в сфере поддержки процессов принятия решений. Статистикой пользуются все- от политиков, желающих предсказать исход выборов, до предпринимателей, стремящихся оптимизировать прибыль при тех или иных вложениях капитала. Большим шагом вперёд к развитию статистической науки послужило применение экономико-математических методов и использование компьютерной техники в анализе социально-экономических явлений.

Программа обработки электронных таблиц MSExcel- мощная и достаточно простая в использовании программа, предназначенная для решения широкого круга планово-экономических, учетно-статистических, научно-технических и других задач, в которых числовая, текстовая или графическая информация с некоторой регулярной, повторяющейся структурой представлена в табличном виде.

Программа MSExcel предоставляет богатые возможности создания и изменения таблиц, которые могут содержать числа, тексты, даты, денежные единицы, графику, а также математические и иные формулы для выполнения вычислений.

Предусмотрены средства представления числовых данных в виде диаграммы, создания, сортировки и фильтрации списков, статического анализа данных и решения оптимизационных задач.

В данной работе я постараюсь показать, какие возможности для обработки статистических данных имеет программа MSExcel.

Объектом исследования данной работы являются возможности табличного процессора.

Предметом исследования является применение программы MSExcel для решения статистических задач.

Актуальность работы обусловлена недостаточной реализацией возможностей MSExcel для решения статистических задач.

Цель настоящего исследования заключается в формированииустойчивых знаний о возможностях MSExcel для решения статистических задач.

Для достижения поставленной цели потребовалось решить следующие задачи :

1. Раскрыть сущность возможностей MSExcel.

2. Определить способы применения этих возможностей при решении задач статистики.

В качестве гипотезы выдвигается следующее:

Использование возможностей программы MSExcel облегчает и ускоряет решения задач статистики.

Глава 1. Применение Microsoft Excel для решения

статистических задач.

1.1. Работа с данными

В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.

Графические изображения используются, прежде всего, для наглядного представления статистических данных, благодаря ним существенно облегчается их восприятие и понимание. Существенна их роль и тогда, когда речь идет о контроле полноты и достоверности исходного статистического материала, используемого для обработки и анализа.

Статистические данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает весьма трудно обнаружить в них имеющиеся неточности и ошибки.

В процессе анализа данных, как правило, присутствуют следующие основные этапы:

1. Ввод данных

Введенные данные обычно отражаются в форме электронной таблицы или матрицы данных, где столбцы представляют различные переменные (например, рост, вес), а строки — измерение значений этих переменных, произведенные в различных условиях, в различное время, у различных объектов и т.п.

2. Преобразование данных

Данные в электронной таблице можно просмотреть и скорректировать методами ручного редактирования или же полуавтоматического преобразования к виду, адекватному выбранному методу анализа. Здесь может быть использован широкий набор алгебраических, матричных, структурных преобразований, а также комбинирование этих операций в требуемой последовательности.

3. Визуализация данных

На данные обязательно следует просто посмотреть, чтобы составить общее (в том числе и интуитивное) представление о характере их изменения, специфических особенностях и закономерностях, что очень важно при выборе стратегии и тактики дальнейшего анализа. Для этого можно использовать как исходное числовое представление, так и различные формы графического изображения.

4. Статистический анализ

Собственно выбор метода, анализ данных и интерпретация результатов.

5. Представление результатов

Для наглядности производимых выводов полученные результаты желательно представлять в виде адекватных, убедительных и эффектных графиков.

Для успешного применения процедур анализа необходимы начальные знания в области статистических и инженерных расчетов, для которых эти инструменты были разработаны

В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного и дисперсионного анализа.

При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов, вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией.

Возможность использования формул и функций является одним из важнейших свойств программы обработки электронных таблиц. Это, в частности, позволяет проводить статистический анализ числовых значений в таблице.

Текст формулы, которая вводится в ячейку таблицы, должен начинаться со знака равенства (=), чтобы программа Excel могла отличить формулу от текста. После знака равенства в ячейку записывается математическое выражение, содержащее аргументы, арифметические операции и функции.

В качества аргументов в формуле обычно используются числа и адреса ячеек. Для обозначения арифметических операций могут использоваться следующие символы: + (сложение); — (вычитание); * (умножение); / (деление).

Формула может содержать ссылки на ячейки, которые расположены на другом рабочем листе или даже в таблице другого файла. Однажды введенная формула может быть в любое время модифицирована. Встроенный Менеджер формул помогает пользователю найти ошибку или неправильную ссылку в большой таблице.

Кроме этого, программа Excel позволяет работать со сложными формулами, содержащими несколько операций. Для наглядности можно включить текстовый режим, тогда программа Excel будет выводить в ячейку не результат вычисления формулы, а собственно формулу.

Программа Excel интерпретирует вводимые данные либо как текст (выравнивается по левому краю), либо как числовое значение (выравнивается по правому краю). Для ввода формулы необходимо ввести алгебраическое выражение, которому должен предшествовать знак равенства (=). [7]

Ввод формул можно существенно упростить, используя маленький трюк. После ввода знака равенства следует просто щелкнуть мышью по первой ячейке, затем ввести операцию деления и щелкнуть по второй ячейке.

1.2. Инструменты пакета анализа в MicrosoftExcel

Дисперсионный анализ

Пакет анализа включает в себя три средства дисперсионного анализа. Выбор конкретного инструмента определяется числом факторов и числом выборок в исследуемой совокупности данных. [6]

Однофакторный дисперсионный анализ

Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности. Этот метод распространяется также на тесты для двух средних (к которым относится, например, t-критерий).

Двухфакторный дисперсионный анализ с повторениями.

Представляет собой более сложный вариант однофакторного анализа, включающий более чем одну выборку для каждой группы данных. Рассмотрим пример применения данной функции MicrosoftExcel. Требуется при уровне α=0,05 выяснить, влияют ли на урожайность пшеницы вид удобрений и способ химической обработки почвы. Выборочные данные об урожайности пшеницы, выращенной на участках, на которые вносились различные виды удобрений и которые подвергались различной химической обработке, приведены в таблице ниже.

B	C	D	E	F	G
32	Номер участка	Вид удобрения	Способ химической обработки
33	Способ 1	Способ 2	Способ 3	Способ 4
34	Участок1	Удобрение1	21,4	20,9	19,6	17,6
35	Участок2	21,2	20,3	18,8	16,6
36	Участок3	20,1	19,8	16,4	17,5
37	Участок1	Удобрение2	12,0	13,6	13,0	13,3
38	Участок2	14,2	13,3	13,7	14,0
39	Участок3	12,1	11,6	12,0	13,9
40	Участок1	Удобрение3	13,5	14,0	12,9	12,4
41	Участок2	11,9	15,6	12,9	13,7
42	Участок3	13,4	13,8	12,1	13,0
43	Участок1	Удобрение4	12,8	14,1	14,2	12,0
44	Участок2	13,8	13,2	13,6	14,6
45	Участок3	13,7	15,3	13,3	14,0

Рассматриваемый в задаче эксперимент представляет собой факторный эксперимент типа 4×4, при котором четыре вида удобрений(фактор А) пересекаются с использованием четырёх способов химической обработки почвы(фактор В). Таким образом, в плане эксперимента имеется 16 условий. Но здесь каждому условию соответствует не одно, а три значения(3 участка земли, засеянных пшеницей).

Для решения задачи используем режим работы «Двухфакторный дисперсионный анализ с повторениями». Значения параметров, установленных в одноименном диалоговом окне, и рассчитанные в данном режиме показатели представлены в таблице, расположенной ниже .

B	C	D	E	F	G
48	Двухфакторный дисперсионный анализ с повторениями
49
50	ИТОГИ	Способ1	Способ2	Способ3	Способ4	Итого
51	Удобрение1
52	Счёт	3	3	3	3	12
53	Сумма	62,7	61	54,8	51,7	230,2
54	Среднее	20,90	20,33	18,27	17,23	19,18
55	Дисперсия	0,49	0,30	2,77	0,30	3,13
56
57	Удобрение2
58	Счёт	3	3	3	3	12
59	Сумма	38,3	38,5	38,7	41,2	156,7
60	Среднее	12,77	12,83	12,90	13,73	13,06
61	Дисперсия	1,54	1,16	0,73	0,14	0,82
62
63	Удобрение3
64	Счёт	3	3	3	3	12
65	Сумма	38,8	43,4	37,9	39,1	159,2
66	Среднее	12,93	14,47	12,63	13,03	13,27
67	Дисперсия	0,80	0,97	0,21	0,42	0,99
68
69	Удобрение4
70	Счёт	3	3	3	3	12
71	Сумма	40,3	42,6	41,1	40,6	164,6
72	Среднее	13,43	14,20	13,70	13,53	13,72
73	Дисперсия	0,30	1,11	0,21	1,85	0,73
74
75	Итого
76	Счёт	12	12	12	12
77	Сумма	180,1	185,5	172,5	172,6
78	Среднее	15,01	15,46	14,38	14,38
79	Дисперсия	13,26	9,71	6,39	3,52

B	C	D	E	F	G	H
82	Дисперсионный анализ
83	Источник вариации	SS	df	MS	F	P-значение	F критическое
84	Выборка	309,26	3	103,09	123,64	1,11Е-17	2,90
85	столбцы	9,97	3	3,32	3,99	0,016	2,90
86	Взаимодействие	25,68	9	2,85	3,42	0,005	2,19
87	Внутри	26,68	32	0,83
88
89	Итого	371,59	47

Так как попадает в критическую область, то гипотезу отвергаем, т.е. считаем, что вид удобрения влияет на урожайность пшеницы.

Выборочный коэффициент детерминации для фактора А

показывает, что 83 процента общей выборочной вариации урожайности пшеницы связано с влиянием вида удобрения.

Расчётное значение F — критерия фактора В (способ химической обработки) , а критическая область образуется правосторонним интервалом (2,90; +∞). Так как попадает вкритическую область, то гипотезу отвергаем, т.е. считаем, что способ химической обработки почвы также влияет на урожайность пшеницы.

Выборочный коэффициент детерминации для фактора В

показывает, что только около 3 процентов общей выборочной вариации урожайности пшеницы связано с влиянием способа химической обработки почвы.

Значимость фактора взаимодействия попадает в критический интервал (2,19;+∞) и указывает на то, что эффективность различных видов удобрения варьируется при различных способах химической обработки почвы. [6]

Двухфакторный дисперсионный анализ без повторения.

Представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности). Этот метод распространяется также на тесты для двух средних, такие как t-критерий.

Корреляционный и ковариационный анализ.

Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:

где:

X, Y — множества значений случайных величин размерности m ;

M(X) — математическое ожидание случайной величины Х ;

M(Y) — математическое ожидание случайной величины Y .

Как следует из формулы, положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабо выраженной зависимости значение показателя ковариации близко к 0.

Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель — коэффициент корреляции R, вычисляемый по формуле:

Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.

Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами:

· с помощью статистических функций КОВАР и КОРРЕЛ ;

· с помощью специальных инструментов статистического анализа.

Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.

Инструмент анализа данных «Корреляция»

1. Выберите в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.

2. Выберите из списка «Инструменты анализа» пункт «Корреляция» и нажмите кнопку «ОК» (рис.1). Результатом будет появление окна диалога инструмента «Корреляция».

3. Заполните поля диалогового окна, как показано на рис. 2 и нажмите кнопку «ОК».

Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рис. 3.

Рис. 1 Список инструментов анализа (выбор пункта «Корреляция»)

Рис.2. Заполнение окна диалога инструмента «Корреляция»

Рис. 3 Результаты корреляционного анализа

Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.

Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей. [12]

Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, . В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.

Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия и эксцесс. Для вычисления коэффициента асимметрии и эксцесса в EXCEL реализованы специальные статистические функции — СКОС () иЭКСЦЕСС(). [3]

1.3. Инструмент анализа данных «Описательная статистика»

Чем больше характеристик распределения случайной величины нам известно, тем точнее мы можем судить об описываемых ею процессов. Инструмент «Описательная статистика» автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом значения могут быть определены сразу для нескольких исследуемых переменных.

Определим параметры описательной статистики. Для этого необходимо выполнить следующие шаги.

1. Выберите в главном меню тему «Сервис» пункт «Анализ данных». Результатом выполнения этих действий будет появление диалогового окна «Анализ данных», содержащего список инструментов анализа.

2. Выберите из списка «Инструменты анализа» пункт «Описательная статистика» и нажмите кнопку «ОК». Результатом будет появление окна диалога инструмента «Описательная статистика».

3. Заполните поля диалогового окна, как показано на рис. 4 и нажмите кнопку «ОК».

Результатом выполнения указанных действий будет формирование отдельного листа, содержащего вычисленные характеристики описательной статистики для исследуемых переменных. Выполнив операции форматирования, можно привести полученную ЭТ к более наглядному виду (рис.5).

Рис.4. Заполнение полей диалогового окна «Описательная статистика»

Рис.5. Описательная статистика для исследуемых переменных

Вторая строка ЭТ содержит значения стандартных ошибок для средних величин распределений. Другими словами среднее или ожидаемое значение случайной величины М (Е) определено с погрешностью. [1]

Медиана — это значение случайной величины, которое делит площадь, ограниченную кривой распределения, пополам (т.е. середина численного ряда или интервала). Как и математическое ожидание, медиана является одной из характеристик центра распределения случайной величины. В симметричных распределениях значение медианы должно быть равным или достаточно близким к математическому ожиданию.

Мода — наиболее вероятное значение случайной величины (наиболее часто встречающееся значение в интервале данных). Для симметричных распределений мода равна математическому ожиданию. Иногда мода может отсутствовать. В данном случае ППП EXCEL вернул сообщение об ошибке. Таким образом, вычисление моды не представляется возможным.

Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь. [2]

Асимметричность (коэффициент асимметрии или скоса — s ) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь.

Для вычисления коэффициента асимметрии используется статистическая функция СКОС (). Формула для проверки значимости показателя эксцесса задается аналогичным образом. Числителем этой формулы будет функция ЭКСЦЕСС (), а знаменателем соотношение, реализованное средствами ППП EXCEL.

Оставшиеся показатели описательной статистики представляют меньший интерес. Величина «Интервал» определяется как разность между максимальным и минимальным значением случайной величины (численного ряда). Параметры «Счет» и «Сумма» представляют собой число значений в заданном интервале и их сумму соответственно. [3]

Последняя характеристика «Уровень надежности» показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия.По умолчанию уровень надежности принят равным 95%.

1.4. Анализ данных

Дополнение «Анализ данных» содержит целый ряд других полезных инструментов, позволяющих быстро и эффективно осуществить требуемый вид обработки данных. Вместе с тем, большинство из них требует осмысленного применения и соответствующей подготовки пользователя в области математической статистики.

Это средство анализа служит для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

Экспоненциальное сглаживание

Предназначается для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. Использует константу сглаживания a, по величине которой определяет, насколько сильно влияют на прогнозы погрешности в предыдущем прогнозе. [4]

Анализ Фурье

Предназначается для решения задач в линейных системах и анализа периодических данных, используя метод быстрого преобразования Фурье (БПФ). Эта процедура поддерживает также обратные преобразования, при этом, инвертирование преобразованных данных возвращает исходные данные.

Двухвыборочный F-тест для дисперсий

Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей. Например, F-тест можно использовать для выявления различия в дисперсиях временных характеристик, вычисленных по двум выборкам.

Гистограмма

Используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений, при этом, генерируются числа попаданий для заданного диапазона ячеек.

Скользящее среднее

Используется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Каждое прогнозируемое значение основано на формуле:

где

N число предшествующих периодов, входящих в скользящее среднее

Aj фактическое значение в момент времени j

Fj прогнозируемое значение в момент времени j

Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Процедура может использоваться для прогноза сбыта, инвентаризации и других процессов.

Проведение t-теста

Пакет анализа включает в себя три средства анализа среднего для совокупностей различных типов:

Двухвыборочный t-тест с одинаковыми дисперсиями

Двухвыборочный t-тест Стьюдента служит для проверки гипотезы о равенстве средних для двух выборок. Эта форма t-теста предполагает совпадение дисперсий генеральных совокупностей и обычно называется гомоскедастическим t-тестом.

Двухвыборочный t-тест с разными дисперсиями

Двухвыборочный t-тест Стьюдента используется для проверки гипотезы о равенстве средних для двух выборок данных из разных генеральных совокупностей. Эта форма t-теста предполагает несовпадение дисперсий генеральных совокупностей и обычно называется гетероскедастическим t-тестом.

Парный двухвыборочный t-тест для средних

Парный двухвыборочный t-тест Стьюдента используется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсийгенеральныхсовокупностей, из которых выбраны данные. Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды. [7]

Генерация случайных чисел

Используется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью данной процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей.

Ранг и персентиль

Используется для вывода таблицы, содержащей порядковый и процентный ранги для каждого значения в наборе данных. Данная процедура может быть применена для анализа относительного взаиморасположения данных в наборе. Рассмотрим пример применения данной функции.

Требуется с помощью коэффициента Спирмена определить зависимость между величиной уставного капитала предприятий Х и количеством выставленных акций Y. Данные о предприятиях города, выставивших акции на чековый аукцион, приведены ниже в таблице 1.

Таблица1

B	C	D
21	Номер предприятия	Уставный капитал, млн. руб. Х	Число выставленных акций Y

Продолжение таблицы 1

22	1	2954	856
23	2	1605	930
24	3	4102	1563
25	4	2350	682
26	5	2625	616
27	6	1795	495
28	7	2813	815
29	8	1751	858
30	9	1700	467
31	10	2264	661

Для решения задачи используем режим работы «Ранг и персентиль». Результаты выполнения данного режима приведены ниже в таблице.

B	C	D	E	F	G	H	I
35	Точка	Столбец1	Ранг	Процент	Точка	Столбец1	Ранг	Процент
36	3	4102	1	100,00	3	1563	1	100,00
37	1	2954	2	88,80	2	930	2	88,80
38	7	2813	3	77,70	8	858	3	77,70
39	5	2625	4	66,60	1	856	4	66,60
40	4	2350	5	55,50	7	815	5	55,50
41	10	2264	6	44,40	4	682	6	44,40
42	6	1795	7	33,30	10	661	7	33,30
43	8	1751	8	22,20	5	616	8	22,20
44	9	1700	9	11,10	6	495	9	11,10
45	2	1605	10	11,10	9	467	10	11,10

По данным этой сгенерированной таблицы заполняем в следующей таблице графы Ранг и Ранг , на основании которых производим вычисления квадратов разности рангов .

B	C	D	E	F	G
21	Номер предприятия	Уставный капитал, млн. руб. Х	Число выставленных акций Y	Ранг	Ранг	Квадрат разности рангов
22	1	2954	856	2	4	4
23	2	1605	930	10	2	64
24	3	4102	1563	1	1
25	4	2350	682	5	6	1
26	5	2625	616	4	8	16
27	6	1795	495	7	9	4
28	7	2813	815	3	5	4
29	8	1751	858	8	3	25
30	9	1700	467	9	10	1
31	10	2264	661	6	7	1
32		120

Заключительным этапом решения задачи является вычисление коэффициента Спирмена по формуле

,

подставляя в которую исходные данные и рассчитанные данные задачи получим

.

Значение коэффициента Спирмена свидетельствует о слабой связи между рассматриваемыми признаками. [9]

Регрессия

Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений. Электронные таблицы делают такой анализ легко доступным. Таким образом, регрессионные вычисления и подбор хороших уравнений — это ценный, универсальный исследовательский инструмент в самых разнообразных отраслях деловой и научной деятельности (маркетинг, торговля, медицина и т. д.). Усвоив технологию использования этого инструмента, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность.

Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. [8]

Выборка

Создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. [5]

Двухвыборочный z-тест для средних

Двухвыборочный z-тест для средних с известными дисперсиями используется для проверки гипотезы о различии между средними двух генеральных совокупностей.

1.5. Статистические функции

FРАСП Возвращает F-распределение вероятности. Эту функцию можно использовать, чтобы определить, имеют ли два множества данных различные степени плотности. Например, можно исследовать результаты тестирования мужчин и женщин, окончивших высшую школу, и определить отличается ли разброс результатов для мужчин и женщин.[10]

FРАСПОБР Возвращает обратное значение для F-распределения вероятности

БЕТАОБР Возвращает обратную функцию к интегральной функции плотности бета-вероятности

БЕТАРАСП Возвращает интегральную функцию плотности бета-вероятности

БИНОМРАСП Возвращает отдельное значение биномиального распределения

ВЕЙБУЛЛ Возвращает распределение Вейбулла

ВЕРОЯТНОСТЬ Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов

ГАММАНЛОГ Возвращает натуральный логарифм гамма функции

ГАММАОБР Возвращает обратное гамма-распределение

ГАММАРАСП Возвращает гамма-распределение

ГИПЕРГЕОМЕТ Возвращает гипергеометрическое распределение

ДОВЕРИТ Возвращает доверительный интервал для среднего значения по генеральной совокупности

КВАРТИЛЬ Возвращает квартиль множества данных

КВПИРСОН Возвращает квадрат коэффициента корреляции Пирсона

КРИТБИНОМ Возвращает наименьшее значение, для которого биномиальная функция распределения меньше или равна заданному значению

ЛГРФПРИБЛ Возвращает параметры экспоненциального тренда

ЛИНЕЙН Возвращает параметры линейного тренда

ЛОГНОРМОБР Возвращает обратное логарифмическое нормальное распределение

ЛОГНОРМРАСП Возвращает интегральное логарифмическое нормальное распределение

МАКСА Возвращает максимальное значение из списка аргументов, включая числа, текст и логические значения

МИНА Возвращает минимальное значение из списка аргументов, включая числа, текст и логические значения

НАИБОЛЬШИЙ Возвращает k-ое наибольшее значение из множества данных

НАИМЕНЬШИЙ Возвращает k-ое наименьшее значение в множестве данных

НАКЛОН Возвращает наклон линии линейной регрессии

НОРМАЛИЗАЦИЯ Возвращает нормализованное значение

НОРМОБР Возвращает обратное нормальное распределение

НОРМРАСП Возвращает нормальную функцию распределения

НОРМСТОБР Возвращает обратное значение стандартного нормального распределения

ОТРБИНОМРАСП Возвращает отрицательное биномиальное распределение

ОТРЕЗОК Возвращает отрезок, отсекаемый на оси линией линейной регрессии

ПЕРЕСТ Возвращает количество перестановок для заданного числа объектов

ПИРСОН Возвращает коэффициент корреляции Пирсона

ПРОЦЕНТРАНГ Возвращает процентную норму значения в множестве данных

ПУАССОН Возвращает распределение Пуассона

РОСТ Возвращает значения в соответствии с экспоненциальным трендом

СРГАРМ Возвращает среднее гармоническое

СРГЕОМ Возвращает среднее геометрическое

СРЗНАЧ Возвращает среднее арифметическое аргументов

СРЗНАЧА Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения.

СРОТКЛ Возвращает среднее абсолютных значений отклонений точек данных от среднего

СТАНДОТКЛОН Оценивает стандартное отклонение по выборке

СТАНДОТКЛОНА Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения

СТАНДОТКЛОНП Вычисляет стандартное отклонение по генеральной совокупности

СТАНДОТКЛОНПА Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения

СТЬЮДРАСП Возвращает t-распределение Стьюдента

СТЬЮДРАСПОБР Возвращает обратное t-распределение Стьюдента

СЧЁТЗ Подсчитывает количество значений в списке аргументов

ТЕНДЕНЦИЯ Возвращает значения в соответствии с линейным трендом

ТТЕСТ Возвращает вероятность, соответствующую критерию Стьюдента

УРЕЗСРЕДНЕЕ Возвращает среднее внутренности множества данных

ФИШЕР Возвращает преобразование Фишера

ФИШЕРОБР Возвращает обратное преобразование Фишера

ФТЕСТ Возвращает результат F-теста

ХИ2ОБР Возвращает обратное значение односторонней вероятности распределения хи-квадрат

ХИ2РАСП Возвращает одностороннюю вероятность распределения хи-квадрат

ХИ2ТЕСТ Возвращает тест на независимость

ЧАСТОТА Возвращает распределение частот в виде вертикального массива

ЭКСПРАСП Возвращает экспоненциальное распределение

1.6 Применение графических возможностей Excel

Графические изображения уже давно нашли широкое применение в самых разнообразных видах человеческой деятельности. Но, пожалуй, ни в одной области знаний и практической деятельности графические изображения не играют такой исключительной роли, как в статистике и экономике, имеющих дело с обработкой и анализом огромных массивов информации о социально- экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимают графические изображения статистических данных.

Графические изображения широко используются, прежде всего, для наглядного представления статистических данных, благодаря ним существенно облегчается их восприятие и понимание.

Огромные возможности для автоматического построения различных видов графических изображений статистических данных представляет программа обработки электронных таблиц MicrosoftExcel.

Статистическая диаграмма- это особый способ наглядного представления и изложения с помощью геометрических знаков и других графических средств статистической информации с целью её обобщения и анализа. Основным и наиболее важным свойством статистических диаграмм является их наглядность. Непосредственная наглядность статистических диаграмм делает их более выразительными и наглядными. [11]

При анализе статистических данных диаграммы могут использоваться для решения таких задач:

· Отображать распределение единиц статистической совокупности по значениям или разновидностям исследуемого признака;

· Характеризовать развитие изучаемых явлений во времени, их общую тенденцию развития, сезонность колебаний, абсолютную и относительную скорость их развития и изменения;

· Сравнивать размеры различных явлений, их разных частей, а также тенденцию их развития и изменения во времени и пространстве;

· Выявлять структуру изучаемых явлений и её изменения, т.е. структурные сдвиги;

· Устанавливать взаимозависимость между явлениями или их признаками, а также степень тесноты существующей между ними связи;

· Отображать степень распространения изучаемых явлений по той или иной территории и интенсивности этого распространения.

Статистические диаграммы являются очень ценным средством при проведении разного рода сравнений статистических данных.

Графические изображения статистических данных осуществляются в основном посредством геометрических плоскостных знаков- точек, линий, плоскостей, фигур, различного сочетания и их расположения. Графические изображения, как плоскостные, так и объёмные, бывают разнообразными, но почти каждое из них состоит из одних и тех, же основных элементов: поле диаграммы, графического образа, пространственных и масштабных ориентиров, экспликации диаграммы.

В Excel вместо понятия «поле диаграмм» применяются такие понятия, как область построения диаграммы и область диаграммы.

Область построения диаграмма — это область, в которой отображается только координатные оси и сама диаграмма, а область диаграммы — это область, в которой кроме координатных осей и самой диаграммы, заголовок диаграммы, обозначение единиц измерения координатных осей, легенда.

Каждый элемент диаграммы можно выделить, активизировать, а потом осуществлять с ним различные преобразования, как-то: изменять размеры, редактировать, форматировать (оформлять). [5]

С помощью перетаскивания можно перемещать область диаграммы и область построения диаграммы и область диаграммы, кроме того, можно изменять их размеры, а, следовательно, и размеры самой диаграммы и отдельных её элементов.

Кроме того, Excel позволяет изменять внешний вид области построения диаграммы и области диаграммы, т.е. изменять форму линий рамки обрамления, цвет и узор заполнения их внутренних частей.

Графический образ- это совокупность геометрических или графических знаков, с помощью которых отображаются статистические данные.

Графические средства Excel позволяют в качестве графического образа использовать различные знаки – символы, в том числе и рисунки. Точнее говоря, Excel автоматически заменяет геометрические знаки негеометрическими.

Изобразительные диаграммы, которые строятся с помощью негеометрических знаков, широко используется для пропаганды и популяризации статистических данных.

Excel имеет многочисленный арсенал средств для построения и оформления основных элементов диаграммы: линии могут быть разноцветными (существует 56 вариантов цветов) или иметь различную форму (тип) – сплошные, штриховые, точечные, штрих – пунктирные, а также разную толщину – тонкие, средние, полутолстые (полужирные) и толстые(жирные); точки данных могут быть изображены в виде маленьких кружков, квадратиков, треугольников, ромбов и других геометрических знаков с разными узорами. Excel предлагает 48 видов штриховки, а также позволяет изменять цвета, узоры, обрамления основных элементов диаграммы, в том числе, самых больших её частей – области построения диаграммы и области диаграммы. [5]

В Excel вместо понятия графического образа используется термин маркер данных. Вид символа маркера зависит от вида диаграммы: на гистограмме это (обычно) прямоугольники, на круговой диаграмме – сектора и т.п.

Пространственные ориентиры – это элементы диаграммы, определяющие порядок размещения графических знаков в поле диаграммы. Такой порядок задаётся определённой системой координат – совокупностью элементов, определяющих положение точки на прямой или кривой линии, на плоскости и в пространстве. При построении статистических диаграмм обычно применяются прямоугольная или декартова, полярная, треугольная или тригональная системы координат.

Прямоугольная система координат чаще всего применяется для статистических диаграмм по причине простоты её построения и наилучшей выразительности различных соотношений и зависимостей между изображаемыми статистическими величинами. Прямоугольная система координат образуется совокупностью двух пересекающихся перпендикулярных прямых, называемых осями координат. [11]

Для облегчения построения и чтения диаграммы её поля в пределах осей координат покрывают параллельными горизонтальными и вертикальными линиями, которые в совокупности образуют так называемую координатную сетку.

В Excel координатная сетка на плоскостных диаграммах наносится на область построения диаграммы, а на объёмных диаграммах, которые имеют две стенки и основания на них.

Графические средства Excel позволяют наносить линии координатной сетки либо на одну из осей, причём линии сетки могут проходить или через основные деления – основные линии, или через промежуточные деления – промежуточные линии.

Excel по умолчанию автоматически строит и размещает координатные оси в нужном месте диаграммы, используя встроенные установки для типа осевых линий, делений и размещений меток деления. Но все эти параметры можно изменять, а также управлять вводом, выводом и удалением координатных осей.

Можно задать нужный тип линий координатных осей и настроить её деления и метки делений.

Экспликация диаграммы – это пояснение содержания диаграммы и её основных элементов.

Экспликация включает общий заголовок диаграммы, подписи вдоль масштабных шкал и пояснительные надписи, раскрывающие смысл отдельных элементов графического образа. [5]

Excel располагает множеством инструментов, позволяющих выполнить экспликацию диаграммы, при этом каждый из элементов экспликации может быть отформатирован (оформлен) различными способами в зависимости от типа и вида диаграммы.

При построении диаграммы Excel по умолчанию, т.е. автоматически, размещает заголовок диаграммы в центре верхней области построения диаграммы, а надписи координатных осей возле каждой оси.

Отметим, что Excel имеет несколько инструментов, которые позволяют просто и быстро отформатировать любой текст т числа, имеющиеся на диаграмме. Они позволяют выбрать типы шрифтов и их размеры, способы выравнивания текста, оформления его жирным шрифтом, курсивом и подчеркиванием, а также добавить к нему рамки, узоры и цвет.

Excel позволяет выравнивать на диаграмме выделенный текст по горизонтали и вертикали, а также менять ориентацию текста, т.е. выравнивать его под определённым углом.

Кроме ввода, редактирования и форматирования заголовка диаграммы и надписей осей, Excel позволяет просто и быстро поместить на саму диаграмму дополнительные надписи, так называемые ярлыки, поясняющие её смысл и значение отдельных элементов. Этот дополнительный текст можно поместить в любое место диаграммы, изменить его размеры и отформатировать.

Excel позволяет форматировать имеющиеся на диаграмме объекты, в частности стрелки и надписи.

Специальное пояснение к маркерам или элементам, используемым в диаграмме, носит название легенды. Excel автоматически создаёт легенду из названий. Но также позволяет самостоятельно создавать легенду и перемещать её в нужное место.

1.7 Классификация статистических диаграмм

Диаграммы, применяемые для изображения статистических данных, очень разнообразны и имеют ряд особенностей, что обуславливает необходимость их классификации.

Классификация статистических диаграмм имеет чрезвычайное значение для их правильного построения и изучения. Она облегчает понимание отличительных особенностей различных типов и видов диаграмм, их возможностей в решении конкретных задач статистического исследования.

В Excel классификация диаграмм осуществлена по форме графического образа. По этому признаку выделено 14 основных, встроенных, или, как их принято называть, стандартных типов диаграмм, и 20 дополнительных, нестандартных, или специальных типов диаграмм. Каждый тип диаграмм представлен несколькими видами (форматами) как плоскостных, так и объёмных диаграмм, которые могут быть применены к данному типу диаграммы. Кроме того, Excel предоставляет пользователю возможность построения собственных типов диаграмм. [5]

Помимо основных, стандартных, типов диаграмм предлагает большое количество нестандартных, специальных, типов диаграмм. Основой нестандартных диаграмм являются стандартные типы диаграмм. Некоторые встроенные нестандартные типы диаграмм подобны стандартным типам. Вместе с тем они содержат дополнительные графические средства, которые расширяют не только наглядные, но и познавательные и аналитические возможности. В частности, они содержат такие встроенные графические элементы: легенду, координатную сетку, логарифмическую шкалу, объяснительные надписи; они имеют, скажем, более привлекательный вид, поскольку их форматирование выполнено с помощью специальных приёмов.

Кроме использования стандартных и нестандартных типов диаграмм, Excel предоставляет пользователю возможность создавать собственные типы диаграмм, сохранять и применять таким же образом, как и любые другие типы диаграмм. [5]

Чтобы создать собственный тип диаграммы, необходимо располагать диаграммой, которая будет служить основой для создания собственного типа диаграммы, при этом в качестве основы можно взять любой тип и вид уже построенной диаграммы, поскольку в любой момент графические средства Excel позволяют изменить его или создать диаграмму требуемого вида и типа.

Заключение

В развитых странах практически любое решение: политическое, финансовое, техническое, научно-исследовательское и даже бытовое решение принимается только после всестороннего анализа данных. Поэтому изучение прикладной статистики и методов анализа данных является неотъемлемым компонентом образования на всех уровнях, а компьютерные пакеты для аналитических исследований и прогнозирования являются настольным рабочим инструментом любого специалиста, так или иначе связанного с информационной сферой.

Таким образом, обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Вообще говоря, трудно назвать ту сферу, в которой она бы не использовалась. Но, пожалуй, ни в одной области знаний и практической деятельности обработка статистических данных не играет такой исключительно большой роли, как в экономике, имеющей дело с обработкой и анализом огромных массивов информации о социально-экономических явлениях и процессах. Всесторонний и глубокий анализ этой информации, так называемых статистических данных, предполагает использование различных специальных методов, важное место среди которых занимают возможности табличного процессора MSExcel.

Представление экономических и других данных в электронных таблицах в наши дни стало простым и естественным. Оснащение же электронных таблиц средствами анализа способствует тому, что из группы сложных, глубоко научных и потому редко используемых, почти экзотических методов, статистический анализ превращается для специалиста в повседневный, эффективный и оперативный аналитический инструмент. Электронные таблицы делают такой анализ легко доступным.

Усвоив технологию использования табличного процессора MSExcel, можно применять его по мере необходимости, получая знание о скрытых связях, улучшая аналитическую поддержку принятия решений и повышая их обоснованность.

В данной работе я показала, что табличный процессор MSExcel обладает огромными возможностями для решения задач статистики, облегчая работу специалистов, работающих в этой области.

Список литературы

1. Бернс Дж., Берроуз Э., Секреты Excel 97. – М.: Веста, 1999.

2. Фигурнов В. Э. ,IBMPC для пользователя. – М.: ИНФРА, 1998.

3. А. Гончаров «MicrosoftExcel 7.0 в примерах» — С.-П.: Питер, 1996

4. Пробитюк А., Excel 7.0 для Windows 95 в бюро. – К.:BHV, 1996

5. Лаврёнов С.М.,Excel: сборник примеров и задач-М: финансы и статистика,2000.-336с.

6. Макарова Н.В., Трофимец В.Я., Статистика в Excel: учеб. пособие.-М.: финансы и статистика,2003.-386с.

7. Сидоров М.Г., Обработка данных в Excel //информатика и образование.-2000.-№6.-с. 25-36.

8. Гутовская Г.В., Использование Excel для решения финансово-экономических задач//информатика и образование.-2003.-№3.-с. 15-21.

9. Ивинская Н.Л., решение прикладных задач в Excel//информатика и образование.-2003.-№6.-с.62-64.

10. Кирей Е.А., Базовый курс Excel для учащихся профильных экономических классов//информатика и образование.-2004.-№5.-с.39-41.

11. Андрусенко Н.Е., Использование стандартных функций Excel для поиска и связи данных в таблице//информатика и образование.-2003.-№11.-с.7-12.

12. [Электронный ресурс]. – Режим доступа:http://www.realcoding.net/article/view/3961