Обработка результатов тестирования excel - Word и Excel

В
процессе обучения постоянно ощущается потребность в хорошо разработанных
методах измерения уровня обученности в самых различных областях знаний. Известно,
что профессиональное тестирование было начато еще в 2200 году до нашей эры,
когда служащие Китайского императора тестировались, чтобы определить их
пригодность для императорской службы. По некоторым оценкам в 1986 году по
крайней мере 800 профессий лицензировались в Соединенных Штатах на основании
тестирования (А.А. Захаров, А.В. Колпаков Современные математические методы
объективных педагогических измерений)

Почти
каждый педагог разрабатывает тестовые задания по своей дисциплине, но не каждый
может грамотно обработать и интерпретировать результаты теста. Напротив,
грамотное конструирование теста на основе знания теории тестирования позволит
педагогу-исследователю создать инструмент, позволяющий провести объективное
измерение знаний, умений и навыков по данному курсу с необходимой точностью.

В
настоящее время существуют два теоретических подхода к созданию тестов:
классическая теория и современная теория IRT (Item Response Theory). Оба
подхода базируются на последующей статистической обработке так называемого
сырого балла (raw score), то есть балла, набранного в результате тестирования.
Только после проведения многократных статистических обработок можно говорить о
создании теста с устойчивыми параметрами качества (надежностью и валидностью).

Для
обработки данных, полученных на этапе тестирования, воспользуемся пакетом MS Office 2000 и электронными таблицами MS Excel.

После сбора эмпирических данных необходимо провести
статистическую обработку, которую будем проводить на ЭВМ. Этап
математико–статистической обработки разобьем на ряд шагов.

Шаг 1. Формирование матрицы тестовых результатов.

Результаты ответов учеников на задания тестов оцениваются в
дихотомической шкале: за каждый правильный ответ учащийся получает один балл, а
за неправильный ответ или за пропуск задания – нуль баллов (см. рис. 1).

Шаг 2. Преобразование
матрицы тестовых результатов.

На втором шаге из матрицы тестовых результатов устраняются строки и
столбцы, состоящие только из нулей или только из единиц. В приведенном выше
примере таких столбцов нет, а строк только две. Одна из них, нулевая строка
соответствует ответам одиннадцатого испытуемого, который не смог выполнить
правильно ни одного задания в тесте.

Рис. 1. Матрица результатов тестирования

В этом случае вывод довольно однозначен: тест непригоден для оценки
знаний такого ученика. Для выявления его уровня знаний тест необходимо
облегчить, добавив несколько более легких заданий, которые, скорее всего,
выполнит правильно большинство остальных испытуемых группы.

Столь же непригоден, но уже по другой причине, тест для оценки знаний
двенадцатого ученика, который выполнил правильно все без исключения задания
теста. Причина непригодности теста заключается в его излишней легкости, не
позволяющий выявить истинный уровень подготовки двенадцатого ученика. Возможно,
двенадцатый ученик знает много чего другого и в состоянии выполнить по
контролируемым разделам содержания гораздо более трудные задания, которые
просто не были включены в тест.

Таким образом, на данном шаге необходимо удалить из матрицы данных 11 и
12 строки.

Шаг 3. Подсчет индивидуальных баллов испытуемых и количество
правильных ответов на каждое задание теста.

Индивидуальный балл испытуемого получается суммированием всех единиц,
полученных им за правильное выполнение задания теста. В Excel для суммирования данных по строке
можно воспользоваться кнопкой Автосумма на панели
инструментов Стандартная. Для удобства полученные индивидуальные баллы
(Х_i)
приводятся в последнем столбце матрицы результатов (см. рис. 2).

Число правильных ответов на задания теста (Y_i) также получается
суммированием единиц, но уже расположенным по столбцам.(см. рис. 2)

Шаг 4. Упорядочение матрицы результатов.

Значения индивидуальных баллов необходимо
отсортировать по возрастанию, для этого в MS Excel:

1.
выделим блок ячеек, содержащих номера
испытуемых, матрицу результатов и индивидуальные баллы. Начинать выделение
необходимо со столбца X
(индивидуальные баллы).

2.
на панели инструментов Стандартная
нажимаем на кнопку Сортировка по возрастанию . Матрица результатов примет вид, изображенный на рис. 3.

Рис. 2. Матрица
с подсчетом итоговых сумм

Рис. 3 Упорядоченная матрица результатов

Шаг 5. Графическое представление данных.

Эмпирические результаты тестирования можно
представить в виде полигона частот, гистограммы, сглаженной кривой или графика.

Для
построения кривых упорядочим результаты эксперимента и подсчитаем частоту
получения баллов (см. рис. 4-6).

Рис. 4.
Несгруппированный ряд

Рис. 5.
Ранжированный ряд

Рис. 6. Частотное
распределение

Для расчета
рейтинга (ранга) каждого учащегося по индивидуальным балам необходимо применить
функцию РАНГ, которая возвращает ранг числа в списке чисел. Ранг числа –
это его величина относительно других значений в списке.

В MS Excel 2000 для вычисления
ранга используется функция

РАНГ (число;
ссылка; порядок), где

Число – адрес
на ячейку, для которой определяется ранг.

Ссылка — ссылка на массив индивидуальных баллов
(выборка).

Порядок – число, определяющее способ упорядочения. Если порядок
равен 0 (нулю), или опущен, то Excel
определяет ранг числа так, как если бы ссылка была списком, отсортированным в
порядке убывания. Если порядок – любое ненулевое число, то Excel определяет ранг числа так, как
если бы ссылка была списком, отсортированным в порядке возрастания.

Примечание. Функция РАНГ присваивает повторяющимся числам
одинаковый ранг. При этом наличие повторяющихся чисел влияет на ранг
последующих чисел. Например, если в списке целых чисел дважды встречается число
10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет
иметь ранг 6).

По частотному
распределению можно построить гистограмму (см. рис.7).

Гистограмму
можно построить и по индивидуальным баллам (см. рис. 8).

Рис. 7.
Столбиковая гистограмма

Рис. 8. Гистограмма распределения инд. баллов

При разработке тестов необходимо помнить о том, что кривая распределения
индивидуальных баллов, получаемых по репрезентативной выборке, является
следствием кривой распределения трудности заданий теста. Этот факт удачно
иллюстрируется на рис.9.

Рис. 9. Связь распределения
индивидуальных баллов и трудности заданий теста

Для первого распределения слева характерно явное смещение в тесте
в сторону легких заданий, что, несомненно, приведет к появлению большого числа
завышенных баллов у репрезентативной выборки учеников. Большая часть учеников
выполнит почти все задания теста.

Второй случай (слева) отражает существенное смещение в сторону
трудных заданий при разработке теста, что не может не сказаться на снижении
результатов учеников, поэтому распределение индивидуальных баллов имеет явно
выраженный всплеск вблизи начала горизонтальной оси. Основная часть учеников
выполнит незначительное число наиболее легких заданий теста.

B третьем случае
задания теста обладают оптимальной трудностью, поскольку распределение имеет
вид нормальной кривой. Отсюда автоматически возникает нормальность распределения
индивидуальных баллов репрезентативной выборки учеников, что в свою очередь
позволяет считать полученное распределение устойчивым по отношению к
генеральной совокупности.

В профессионально разработанных нормативно-ориентированных тестах
типичным является результат, когда приблизительно 70% учеников выполняют правильно от 30 до 70%
заданий теста. а наиболее часто встречается результат в 50%.

Шаг 6. Определение выборочных
характеристик результатов.

На данном этапе необходимо вычислить среднее
значение, моду, медиану, дисперсию, стандартное отклонение выборки, ассиметрию
и эксцесс (см. рис.10).

Степень отклонения распределения наблюдаемых частот выборки от
симметричного распределения, характерного для нормальной кривой, оценивается с
помощью асимметрии. Наличие асимметрии легко установить визуально, анализируя
полигон частот или гистограмму Более тщательный анализ можно провести с помощью
обобщенных статистических характеристик, предназначенных для оценки величины
асимметрии в распределении.

Функция СКОС MS Excel возвращает
ассиметрию распределения.

СКОС (число 1; число 2), где число1 – ссылка
на массив данных, содержащих индивидуальные баллы учеников.

При интерпретации полученного значения асимметриии 0,277
необходимо обратить внимание на то, что величина ассиметрии получилась
положительной и небольшой (см. рис. 10,
11).

Рис. 10.
Описательные характеристики выборки

Рис. 11. Кривые распределения с
отрицательной, нулевой и положительной ассиметрией (слева направо)
соответственно.

Асимметрия распределения положительна, если основная часть
значений индивидуальных баллов лежит справа от среднего значения, что обычно
характерно для излишне легких тестов.

Асимметрия распределения баллов отрицательна, если большинство
учеников получили оценки ниже среднего балла. Эффект отрицательной асимметрии
встречается в излишне трудных тестах, не сбалансированных правильно по
трудности при отборе заданий

В хорошо сбалансированном по трудности тесте, как уже отмечалось
ранее, распределение баллов имеет вид нормальной кривой. Для нормального
распределения характерна нулевая асимметрия, что вполне естественно, так как
при полной симметрии каждое значение балла, меньшее среднего значения,
уравновешивается другим симметричным, большим чем среднее.

С помощью эксцесса можно получить представление о том,
является ли функция распределения частот островершинной, средневершинной или
плоской.

Для расчета данного параметра применим функцию ЭКСЦЕСС
(число1; число2; …), где число1 – ссылка на массив данных,
содержащих индивидуальные баллы учеников.

В том случае, когда распределение данных бимодально
(имеет две моды), необходимо говорить об эксцессе в окрестности каждой моды.
Бимодальная конфигурация указывает на то, что по результатам выполнения теста
выборка учеников разделилась на две группы. Одна группа справилась с
большинством легких, а другая с большинством трудных заданий теста.

Источник

Тест Фллипса хорошо знаком школьным психологам. Он широко используется, потому что хорошо работает. Используя Excel можно облегчить процесс обработки данных диагностики и написания итоговыхпротоколов.

Если вы будете использовать для этого наши несложные разработки, то для получения протоколов достаточно из бумажных бланков, заполненных при тестировании перенести на лист «Список» фамилии и имена испытуемых, а н алист «Сырые» их ответы. Ответы «Да» надо обозначать «1», а ответы «Нет» — «0».

После внесения данных всех испытуемых на листе «Протокол 1» вы получите готовый к распчатке протокол группового обследования. Если при этом вам понадобятся протоколы индивидуального обследования, то надо перейти на страницу «Протокол 2». Для получения протокола для кого-либо из внесенных в список испытуемых достаточно на листе «Протокол 2» в первой строке в ячейке, расположенной после слова «ПРОТОКОЛ», надо поставить номер, под которым этот испытуемый записан на листе «Список» и нажать клавишу Enter. Протокол готов к распчатке.

Скачать:

Источник

В оличие от стандартной интерпретации данных показатели теста, меньшие 25% в нашей разработке в протоколе индивидуального обследования обозначаются как «низкий уровень тревожности».

И еще, на всякий случай, на странице «опросник» размещен текст вопросов теста Филлипса с ключами.

Файл Excel, предназначенный для обработки теста можно скачать здесь.

Успешной вам работы!

Источник

17 авг. 2022 г.
читать 3 мин

Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.

В этом руководстве представлено полное руководство по интерпретации результатов двухвыборочного t-теста в Excel.

Шаг 1: Создайте данные

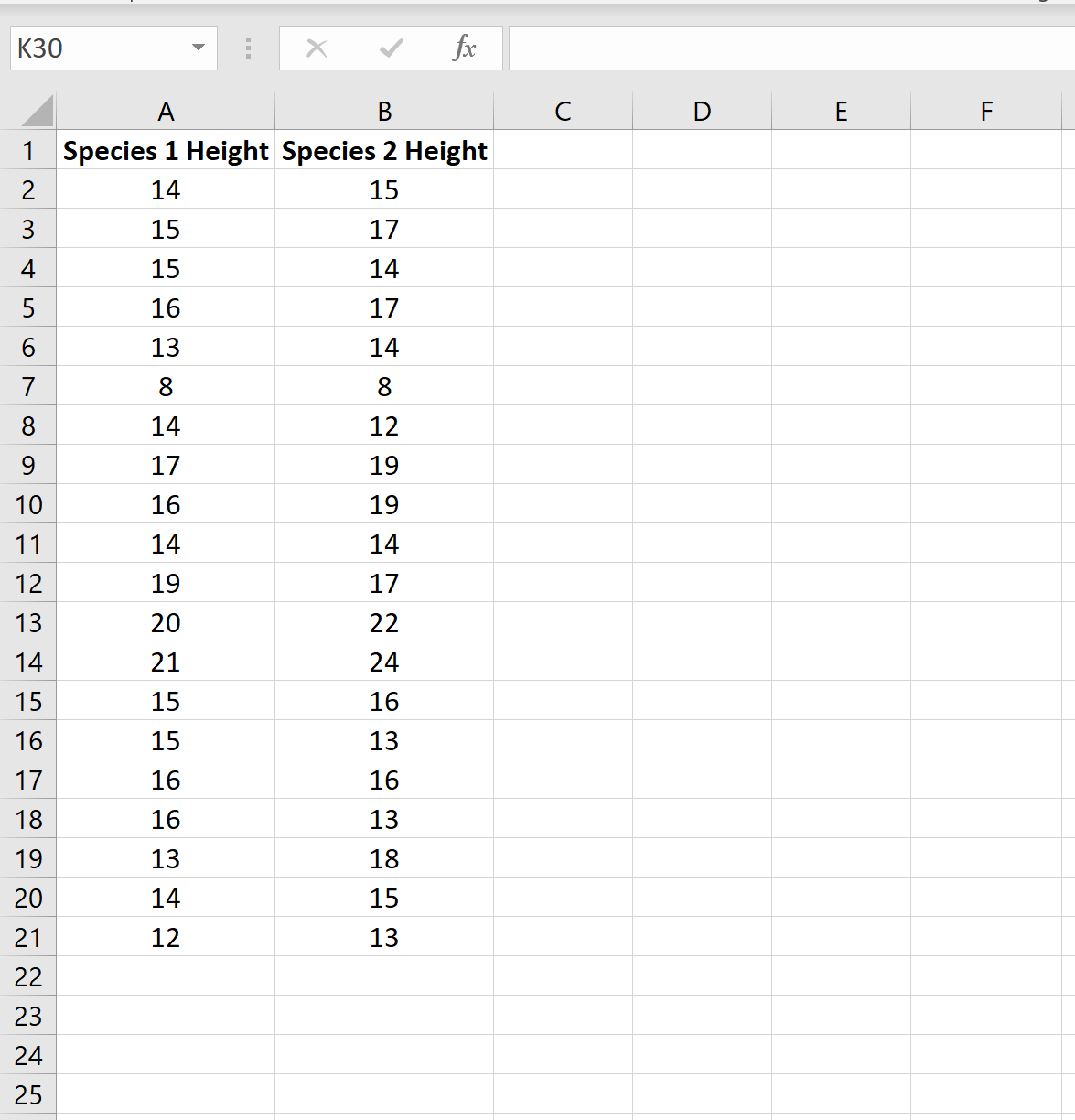
Предположим, биолог хочет знать, имеют ли два разных вида растений одинаковую среднюю высоту.

Чтобы проверить это, она собирает простую случайную выборку из 20 растений каждого вида:

Шаг 2. Выполните t-тест для двух выборок.

Чтобы выполнить двухвыборочный t-критерий в Excel, щелкните вкладку « Данные » на верхней ленте, а затем щелкните « Анализ данных» :

Если вы не видите эту опцию, вам необходимо сначала загрузить пакет инструментов анализа .

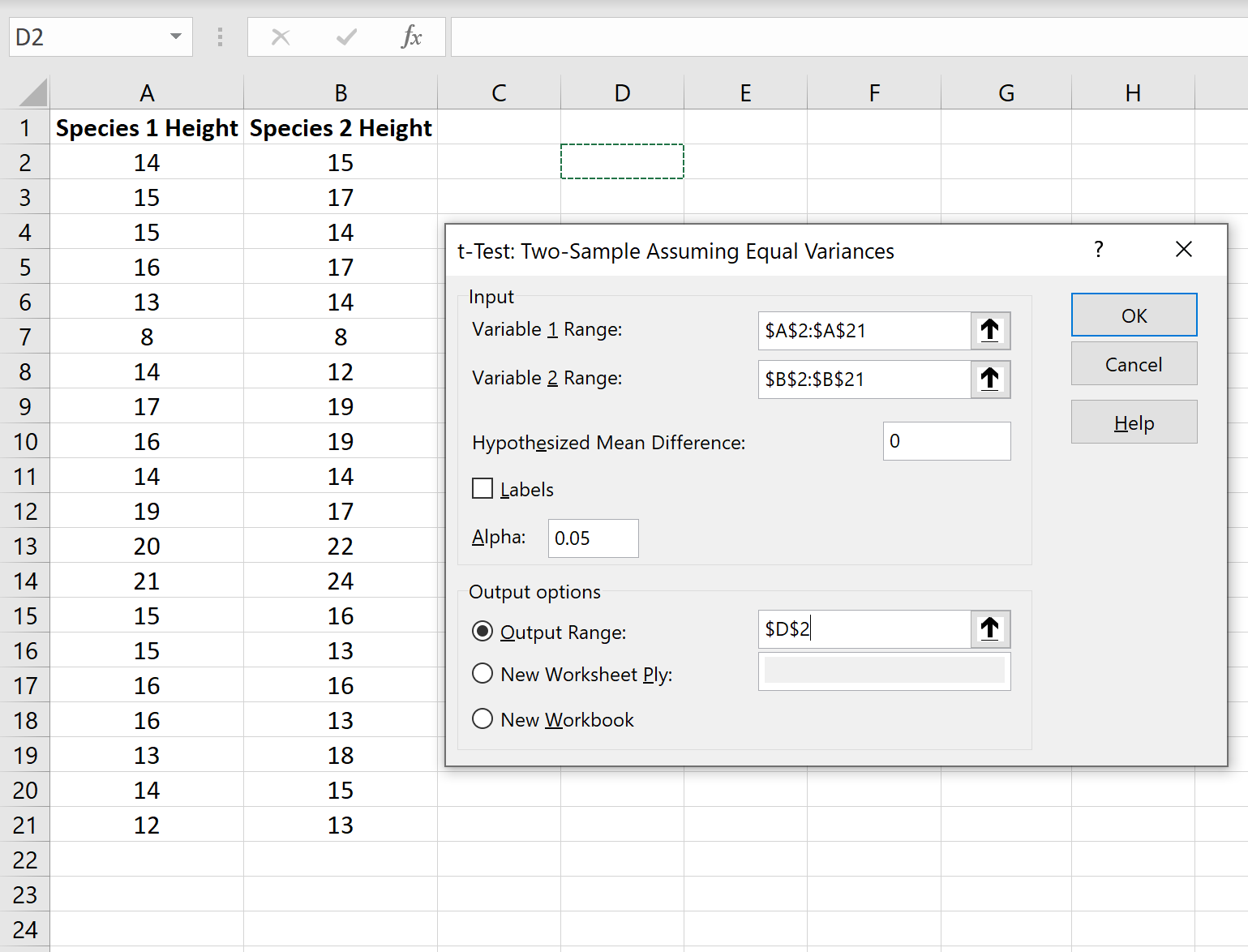
В появившемся окне выберите параметр под названием t-Test: Two-Sample, предполагающий равные отклонения , а затем нажмите OK.Затем введите следующую информацию:

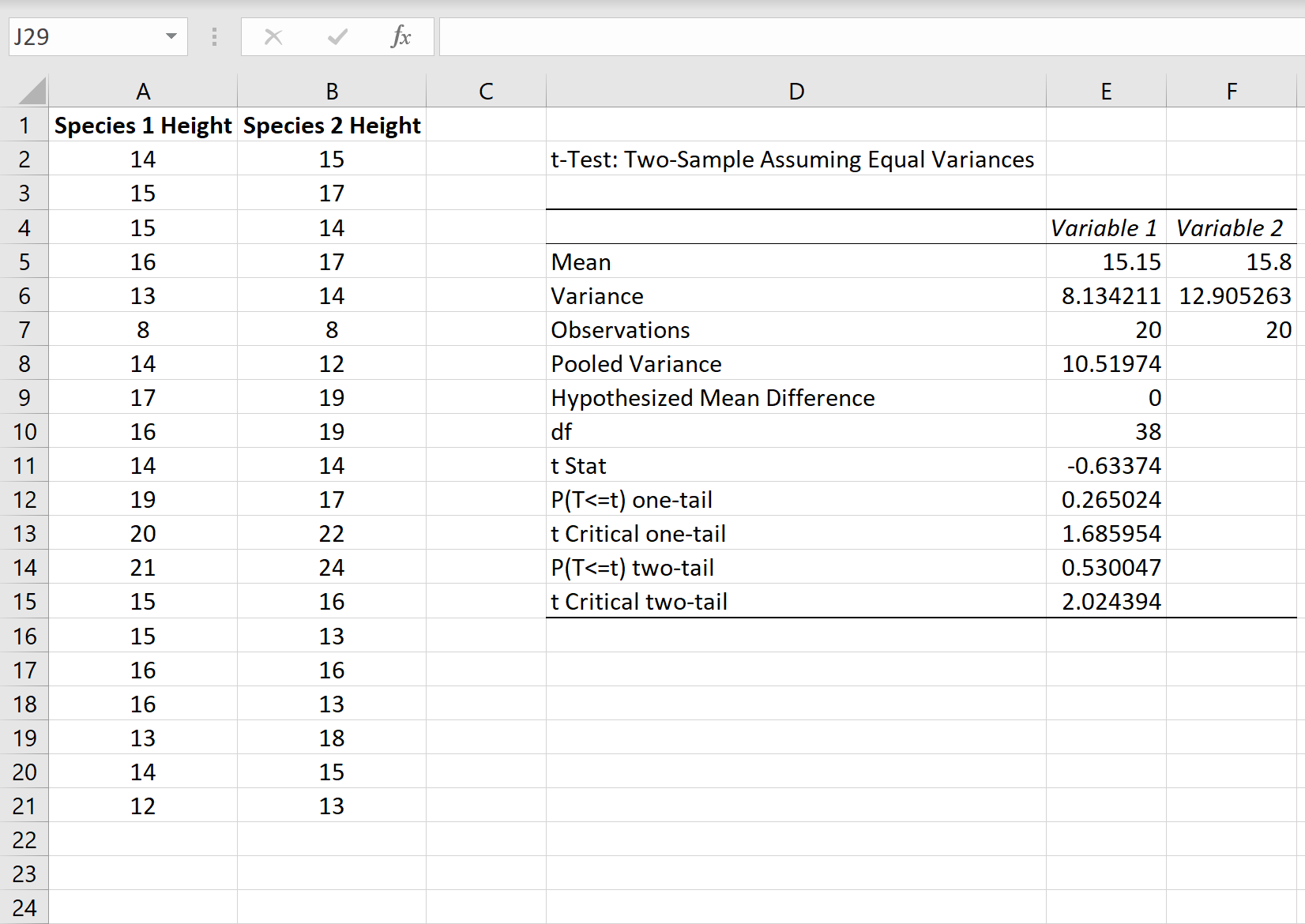
После того, как вы нажмете OK , отобразятся результаты t-теста:

Шаг 3: интерпретируйте результаты

Вот как интерпретировать каждую строку в результатах:

Среднее значение: среднее значение каждого образца.

Образец 1 Среднее значение: 15,15
Образец 2 Среднее значение: 15,8

Дисперсия: Дисперсия каждого образца.

Образец 1 Дисперсия: 8,13
Образец 2 Дисперсия: 12,9

Наблюдения: количество наблюдений в каждой выборке.

Образец 1 Наблюдения: 20
Образец 2 Наблюдения: 20

Объединенная дисперсия: средняя дисперсия выборок, рассчитанная путем «объединения» дисперсий каждой выборки вместе по следующей формуле:

s 2 p = ((n 1 -1)s 2 1 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
с 2 р = ((20-1)8,13 + (20-1)12,9) / (20+20-2)
с 2 р = 10,51974

Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В этом случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0.

df: Степени свободы для t-критерия, рассчитанные как:

df = n 1 + n 2 – 2
df = 20 + 20 – 2
дф = 38

t Stat: тестовая статистика t , рассчитанная как:

т знак равно ( Икс 1 — Икс 2 ) / √ с 2 п (1 / п 1 + 1 / п 2 )
t = (15,15–15,8) / √ 10,51974 (1/20+1/20)
т = -0,63374

P(T<=t) двухсторонний: значение p для двустороннего t-критерия. Это значение можно найти с помощью любого калькулятора T Score to P Value, используя t = -0,63374 с 38 степенями свободы.

В этом случае р = 0,530047.Это больше, чем 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы сказать, что средние значения двух популяций различны.

t Критический двухсторонний: это критическое значение теста. Это значение можно найти с помощью Калькулятора критического значения t с 38 степенями свободы и уровнем достоверности 95%.

В этом случае критическое значение оказывается равным 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. Еще раз, это означает, что у нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.

Примечание № 1. Вы придете к одному и тому же выводу независимо от того, используете ли вы метод p-значения или метод критического значения.

Примечание № 2. Если вы выполняете односторонний тест гипотезы , вместо этого вы будете использовать значения для одностороннего P(T<=t) и критического одностороннего t.

Дополнительные ресурсы

В следующих руководствах представлены пошаговые примеры выполнения различных t-тестов в Excel.

Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Как выполнить t-критерий Уэлча в Excel

Источник

Использование статистических методов для обработки результатов психолого-педагогических экспериментов

Рис. 4. Структура педагогического
исследования (Д.А. Новиков)

При обработке и анализе результатов
психолого-педагогического эксперимента
существенную роль играют статистические
методы, которые позволяют:

устанавливать степень достоверности
сходства и различия исследуемых объектов
на основании результатов измерений их
показателей^²;
доказывать правильность и обоснованность
используемых педагогических приемов
и методов;
анализировать результаты
психолого-педагогического эксперимента;
находить зависимости между
экспериментальными данными;
выявлять наличие существенных различий
между группами испытуемых (экспериментальной
и контрольной).

Алгоритм действий педагога-исследователя
при проведении статистического анализа
должен быть следующим:

1. На основании сравнения контрольной
и экспериментальной группы установить
совпадение начальных состояний
экспериментальной и контрольной группы.

2. Реализовать воздействие на
экспериментальную группу. При выполнении
данного шага необходимо быть уверенным,
что и экспериментальная, и контрольная
группы находятся в одинаковых условиях,
за исключением целенаправленно
изменяемых педагогом-исследователем.

3. На основании сравнения экспериментальной
и контрольной группы установить различие
конечных состояний.

Успешное решение вышеуказанных задач
предполагает наличие у педагога-исследователя
знаний о педагогическом измерении, об
измерительных шкалах, видах
психолого-педагогических данных, этапах
анализа данных, способах и методах
представления и обработки эмпирических
данных.

Практическая работа 3. Обработка результатов тестирования с использованием ms Excel

Главная цель применения традиционных
тестов — установить отношение порядка
устанавливаемых между испытуемыми по
уровню проявляемых при тестировании
знаний. И на этой основе определить
место (или рейтинг) каждого на заданном
множестве тестируемых испытуемых.

Исходные тестовые оценки – это
количество правильных и неправильных
ответов на вопросы теста, время его
выполнения и количество решенных заданий
теста. Эти данные называют первичными
или «сырыми» оценками. Итогом тестирования
являются тестовые нормы – таблицы
пересчета первичных тестовых оценок в
стандартные тестовые шкалы. На рис. 5
представлено множество стандартных
тестовых шкал. Общим для них является
соответствие нормальному распределению,
а различаются они только двумя
показателями: средним значением и
масштабом, определяющим дробность шкалы
[5, с. 55].

Задание:

Изучите статью о.А.Попова «Стандартизируем тест: процентили, стэны, станайны, t-баллы, iq-баллы» или какую-либо другую литературу и дайте определение понятиям: «стены», «сиенайны», «процентили».

Для обработки первичных данных,
полученных на этапе тестирования,
воспользуемся электронными таблицами
MS Excel. Этап
статистической обработки разобьем на
ряд шагов [7, с. 128].

Шаг 1. Формирование матрицы тестовых
результатов.

Результаты ответов учеников на задания
тестов оцениваются в дихотомической
шкале: за каждый правильный ответ
учащийся получает один балл, а за
неправильный ответ или за пропуск
задания – нуль баллов (см. рис. 6).

Рис. 6. Матрица результатов тестирования

Шаг 2. Преобразование матрицы тестовых
результатов.

На втором шаге из матрицы тестовых
результатов устраняются строки и
столбцы, состоящие только из нулей или
только из единиц. В приведенном выше
примере таких столбцов нет, а строк
только две. Одна из них, нулевая строка
соответствует ответам одиннадцатого
испытуемого, который не смог выполнить
правильно ни одного задания в тесте.

В этом случае вывод довольно однозначен:
тест непригоден для оценки знаний такого
ученика. Для выявления его уровня знаний
тест необходимо облегчить, добавив
несколько более легких заданий, которые,
скорее всего, выполнит правильно
большинство остальных испытуемых
группы.

Столь же непригоден, но уже по другой
причине, тест для оценки знаний
двенадцатого ученика, который выполнил
правильно все без исключения задания
теста.

Причина непригодности теста заключается
в его излишней легкости, не позволяющий
выявить истинный уровень подготовки
двенадцатого ученика. Возможно,
двенадцатый ученик знает много чего
другого и в состоянии выполнить по
контролируемым разделам содержания
гораздо более трудные задания, которые
просто не были включены в тест.

Таким образом, на данном шаге необходимо
удалить из матрицы данных 13 и 14 строки
(ответы 11 и 12 ученика).

Соседние файлы в папке Занятие 4

#
21.03.201532.77 Кб17~WRL0724.tmp
#
21.03.2015113.15 Кб16~WRL3140.tmp
#
#
21.03.201523.04 Кб49практика.xls
#

Источник