Удобство
использования данной программы
обусловлено тем фактом, что практически
на каждом компьютере сейчас установлен
популярный пакет Microsoft
Office
разных версий выпуска. С помощью Excel
можно
существенно облегчить рутинные
вычисления:
Пакет анализа
программы Microsoft
Excel
позволяет быстро и удобно, не прибегая
к помощи специализированных программ,
обработать данные психологических
исследований. С его помощью можно
осуществить:
-
Вычисление
статистических параметров -
Корреляционный
анализ (коэффициент корреляции Пирсона) -
Дисперсионный
анализ (различные виды) -
Ковариационный
анализ -
Т- тест (различные
виды) -
F-тест
для дисперсии -
Построить
гистограмму статистического распределения
Перед началом
работы необходимо установить Пакет
анализа. Для этого в диалоговом меню
«Надстройки» установите флажок напротив
пакета анализа.
После этого в меню
СЕРВИС (для версии Excel
2003) появится команда «АНАЛИЗ ДАННЫХ».
Такая же команда появится во вкладке
«ДАННЫЕ» (для версии Excel
2007).
Работа ведется
поэтапно:
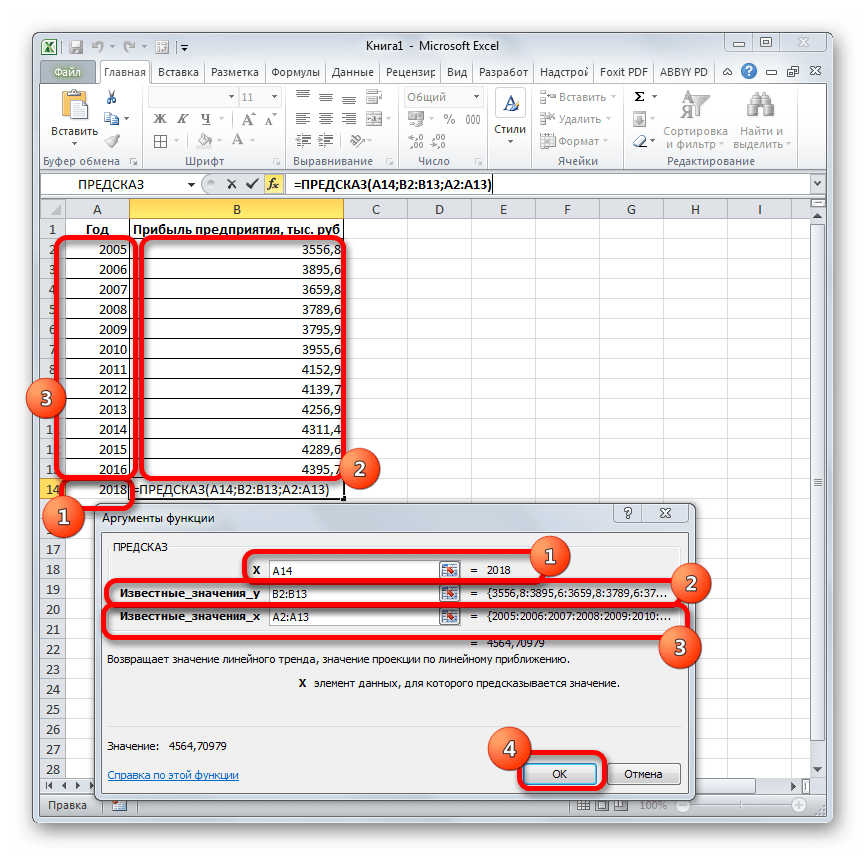
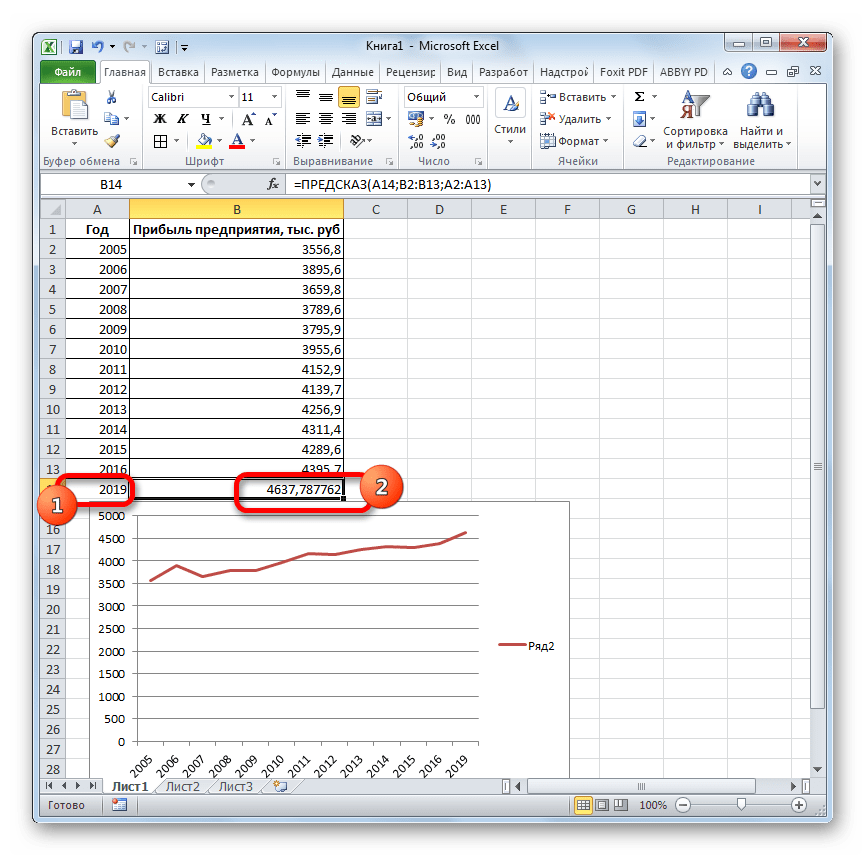
1 этап
– занесение данных исследования в
электронную таблицу Microsoft Excel
2 этап
– в меню «СЕРВИС» выберите режим «АНАЛИЗ
ДАННЫХ»
3 Этап – в диалоговом окне «анализ данных» выберите режим «описательная статистика»
4 этап
–
ввод данных в диалоговое окно «ОПИСАТЕЛЬНАЯ
СТАТИСТИКА»
Таким образом,
достаточно большой массив исследовательских
данных обработан очень быстро. Выполнены
трудоемкие вычисления значений
стандартного отклонения, асимметрии и
эксцесса.
Корреляционный анализ по пирсону
1 этап
– в диалоговом окне «АНАЛИЗ ДАННЫХ»
выберите режим «КОРРЕЛЯЦИЯ»
2
данных в диалоговое окно «КОРРЕЛЯЦИЯ»
Приложение
4
Области
библиографического описания и их
основные элементы
|
Порядок |
Название |
Знак перед |
Основные |
Пример |
|
1 |
Область |
Основное |
1. Я – Ты — Мы
Воспитание?
2. История 3. 4. 4.1. 4.2 |
|
|
/ |
Первые |
5. / / / |
||
|
2 |
Область |
. |
Сведения |
6. |
|
/ |
Первые |
7. |
||
|
, |
Дополнительные |
8. . |
||
|
/ |
Первые |
9. |
||
|
3 |
Область |
. |
Для |
|
|
4 |
Область |
. |
Первое |
10. . . . |
|
: |
Имя |
11. : БГТУ : СевКавГТУ : ПНЦ РАН : у И.Д. Сытина |
||
|
, |
Дата |
12. |
||
|
5 |
Область |
. |
Специфическое |
13. 14. |
|
6 |
Область |
. |
Основное |
15. . .– |
|
/ |
Первые |
16. . |
||
|
, |
Международный |
17. |
||
|
; |
Номер |
18. ; ; |
||
|
7 |
Область |
. |
Факультативна. |
19.
. . |
|
8 |
Область |
. |
Стандартный |
20. .– |
Область
заглавия и сведений об ответственности
содержит основное заглавие первоисточника,
а также иные заглавия (альтернативное,
параллельное, другое), прочие относящиеся
к заглавию сведения и сведения о лицах
и (или) организациях, ответственных за
создание документа, являющегося объектом
описания.
Основное заглавие.
1.
Основное заглавие приводят в том виде,
в каком оно дано в источнике информации
(на титульном листе, карточке каталога)
в той же последовательности и с теми же
знаками (пример
1).
2.
Если основное заглавие состоит из
нескольких предложений, между которыми
в источнике информации отсутствуют
знаки препинания, в описании эти
предложения отделяют друг от друга
точкой (пример
2)
3.
Если основное заглавие содержит
альтернативное заглавие, соединенное
с ним союзом «или», и записываемое с
прописной буквы, то перед союзом «или»
ставят запятую (пример
3).
4.
Указанные в источнике информации
хронологические и географические
данные, связанные по смыслу с основным
заглавием, приводят в описании после
основного заглавия и отделяют от него
запятой, если в источнике перед ними
нет других знаков (пример
4).
Сведения
от ответственности
содержат информацию о лицах и организациях,
участвовавших в создании первоисточника,
являющегося объектом описания.
Сведения
об ответственности записывают в той
форме, в какой они указаны в источнике
информации – титульном листе, карточке
каталога, библиографическом указателе
(пример
5).
Первым сведениям об ответственности
предшествует знак «косая черта».
Последующие группы сведений отделяют
друг от друга «точкой с запятой».
Обязательными являются первые сведения
об ответственности.
Область
издания
содержит информацию об изменениях и
особенностях данного издания по отношению
к предыдущему изданию того же произведения.
Сведения
об издании
обычно содержат слово «издание» или
«версия», «вариант», «выпуск», «редакция»,
«репринт». Их приводят в формулировках
и в последовательности, имеющихся в
источнике информации – титульном листе,
карточке каталога, библиографическом
указателе.
Порядковый
номер записывают арабскими цифрами,
добавляя окончание, согласно правилам
грамматики соответствующего языка
(пример
6).
Первые
сведения об ответственности, относящиеся
к изданию,
записывают в области издания, если они
относятся только к конкретному измененному
изданию произведения. Им предществует
«косая черта» (пример
7).
Дополнительные
сведение об издании
приводят в описании, если они есть в
источнике информации –
титульном листе, карточке каталога,
библиографическом указателе. Их
записывают после предыдущих сведений
области издания и отделяют запятой
(пример
8).
Первые
сведения об ответственности, относящиеся
к дополнительным сведениям об издании,
записывают после этих сведений по
правилам приведения сведения об
ответственности
(пример 9).
Область
выходных данных
содержит сведения о месте и времени
публикации, распространения и изготовления
первоисточника, а также сведения об его
издателе, распространителе и изготовителе.
Название
места издания,
распространения приводят в форме и
падеже, указаных в источнике информации
–
титульном листе, карточке каталога,
библиографическом указателе (пример
10).
Если указано несколько мест издания,
то приводят место, выделенное
полиграфическим способом или указанное
первым, а опущенные сведения отмечают
сокращением [и др.] (пример
11).
Имя
(наименование) издателя, распространителя
приводят после сведений о месте издания,
к которому оно относится, и отделяют
двоеточием. Сведения приводят в том
виде, как они указаны в источнике
информации, сохраняя слова или фразы,
указывающие функции (кроме издательской),
выполняемый лицом или организацией.
Сведения о форме собственности издателя,
распространителя (АО, ООО и др.), как
правило, опускают (пример
12).
|
В |
: |
|
Издательство |
: |
|
Издательский |
: |
|
ЗАО |
: |
|
Издательство |
: |
В
качестве даты издания
приводят год публикации документа,
являющегося объектом описания. Год
указывают арабскими цифрами, ему
предшествует запятая (пример
13).
Область
физической характеристики
содержит обозначение физической формы,
в которой представлен первоисточник,
в сочетании с указанием объема и, при
необходимости, размера документа, его
иллюстраций и сопроводительного
материала, являющегося частью объекта
описания (пример
14).
Область
серии
содержит сведения о многочастном
документе, отдельным выпуском которого
является объект описания.
Основное
заглавие серии
приводят по правилам для основного
заглавия первоисточника (пример
15).
Сведения
об ответственности
приводят в области серии, если они
необходимы для ее идентификации и
относятся к серии в целом (пример
16).
Международный
стандартный номер сериального издания
(ISSN)
приводят, если он указан в источнике
информации. Номер приводят в стандартной
форме. Ему предшествует запятая (пример
17).
Если указаны номера серии и подсерии,
то приводят номер ISSN
подсерии. Если издание многотомное, то
приводят номер ISSN
многотомного издания в целом.
Номер
выпуска серии
записывают арабскими цифрами и в той
форме, как он дан в объекте описания.
Ему предшествует точка с запятой (пример
18).
Область стандартного
номера (или его альтернативы) и условий
доступности.
Международные
стандартные номера,
присвоенные объекту описания: Международный
стандартный номер книги (ISBN)
или Международный стандартный номер
сериального издания (ISSN)
приводят с принятой аббревиатурой и
предписанными пробелами и дефисами.
Если номеров несколько, приводят тот,
который относится к объекту описания.
Если это трудно определить, приводят
все международные стандартные номера,
имеющиеся в источнике информации (пример
20).
Научное
издание
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Теоретическиеметоды исследования в науке дают возможность раскрыть качественные характеристики изучаемых явлений. Эти характеристики будут полнее и глубже, если накопленный эмпирический материал подвергнуть количественной обработке. Однако проблема количественных измерений, в частности, в рамках психолого-педагогических исследований очень сложна. Эта сложность заключается, прежде всего, в субъективно-причинном многообразии педагогической деятельности и ее результатов, в самом объекте измерения, находящемся в состоянии непрерывного движения и изменения. Вместе с тем введение в исследование количественных показателей стало сегодня необходимым и обязательным компонентом получения объективных данных о результатах труда. С этой целью при исследовании проблем психологии применяются методы математической статистики. С их помощью решаются различные задачи: обработка фактического материала, получение новых, дополнительных данных, обоснование научной организации исследования и др.
Правильное применение статистики позволяет экспериментатору:
-
строить статистические предсказания;
-
обобщать данные эксперимента;
-
находить зависимость между экспериментальными данными;
-
строго обосновывать экспериментальные планы;
-
доказывать правильность и обоснованность используемых методических приемов и методов.
Нельзя забывать, однако, что сами по себе методы статистики – это только инструментарий, помогающий экспериментатору эффективно разбираться в сложном исследуемом материале. Наиболее важным при проведении любого эксперимента является четкая постановка задачи, тщательное планирование эксперимента, построение непротиворечивых гипотез.
Методы математической статистики в руках исследователя могут и должны быть мощным инструментом, позволяющим не только успешно лавировать в море экспериментальных данных, но и, прежде всего, способствовать становлению его объективного мышления.
Актуальность данного исследования означена востребованностью статистической обработки экспериментальных данных в психолого-педагогических исследованиях.
Цель: проведение регрессионного анализа статистических данных психологического эксперимента для выявления уровня враждебности школьников в зависимости от уровней обиды и подозрительности (диагностика состояния враждебности Басса-Дарки).
Объект исследования: процесс статистической обработки данных психологического эксперимента.
Предмет исследования: зависимость уровня враждебности от таких психологических факторов личности как обида и подозрительность.
Задачи:
-
Проанализировать научную, учебную, специальную литературу по теме исследования;
-
Изучить теоретические аспекты разновидностей регрессионного анализа;
-
Выявить методы и средства статистического анализа данных психологического эксперимента;
-
Обработать статистические данные с помощью специальных функций, встроенных в табличный процессор Excel;
-
Провести аппроксимацию данных проведенного эксперимента.
Для решения поставленных задач используются следующие методы:
-
Теоретические:
-
анализ литературы;
-
систематизация изученного материала;
-
обобщение.
-
Эмпирические:
-
наблюдение;
-
анкетирование(опрос).
Глава 1. Регрессионный анализ экспериментальных данных 1.1. Первичная обработка экспериментальных данных
Современные задачи планирования, управления, прогнозирования невозможно решать, не располагая достоверными статистическими данными и не используя статистические методы обработки этих данных. Стремление объяснить настоящее и заглянуть в будущее всегда было свойственно человечеству, а для решения этих задач применялись различные методы. Статистика при описании случайных явлений использует язык науки – математику. Это значит, что реальные ситуации заменяются вероятностными схемами и анализируются методами теории вероятностей.
Любые статистические данные всегда неполны и неточны, и другими быть не могут. Задача статистики заключается в том, чтобы дать обоснованные выводы о свойствах изучаемого явления, анализируя неполные и неточные данные. Статистика доказала, что умеет справляться с подобными проблемами.
Методы первичной статистической обработки результатов эксперимента применяются при обработке материалов психологических исследований для того, чтобы извлечь из тех количественных данных, которые получены в экспериментах, при опросе и наблюдениях, как можно больше полезной информации. В частности, в обработке данных, получаемых при испытаниях по психологической диагностике, это будет информация об индивидуально-психологических особенностях испытуемых.
Методами статистической обработки результатов эксперимента называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами.
Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок.
Выборочное среднее (среднее арифметическое) как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, можно судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.
Выборочное среднее значение ряда из n числовых значений обозначается и подсчитывается так:
(1.1)
Здесь — это данные (набор чисел), полученные в результате регистрации значений некоторой случайной величины. Этот набор чисел называется выборкой. Величины 1,2…n являются так называемыми индексами. — принятый в математике знак суммирования тех переменных величин, которые находятся справа от этого знака. Числа, стоящие над и под знаком называются пределамисуммирования и указывают наименьшее и наибольшее значения индекса суммирования, между которыми расположены его промежуточные значения.
В том случае, если отдельные значения повторяются, то выборочное среднее вычисляют по формуле:
(1.2)
в таком случае называют взвешенной средней, где — частоты повторяющихся значений.
При вычислении величины средней по таблице чисел используется следующая формула:
(1.3)
где — значения всех переменных, полученных в эксперименте, или все элементы таблицы; при этом индекс jменяется от 1 до p, где p — число столбцов в таблице, а индекс iменяется от 1 до n, где n – число испытуемых или число строк в таблице. Тогда — общая средняя всех элементов в таблице (анализируемой совокупности экспериментальных данных) и в общем случае .
Символическое обозначение удобно для обозначения конкретного элемента таблицы. Символ (двойная сумма) означает, что вначале осуществляется суммирование всех элементов по индексу i– т.е. по строкам, затем полученные суммы по столбцам – по индексу j.
Дисперсия – это среднее арифметическое квадратов отклонений значений переменной от ее среднего значения. Иначе, дисперсия, как статистическая величина, характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных.
(1.4)
где n– объем выборки, i– индекс суммирования, — выборочное среднее.
Расчет дисперсии для таблицы чисел осуществляется по формуле:
(1.5)
где — значения всех переменных, полученных в эксперименте, или все элементы таблицы; — общее среднее арифметическое всех элементов таблицы; N – общее число всех элементов таблицы.
Иногда вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую выборочное отклонение (стандартное):
(1.6)
Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Можно дать второе определение, сказав, что медиана – это величина, по отношению к которой, по крайней мере 50% выборочных значений меньше нее и по крайней мере 50% — больше.
Мода – это количественное значение исследуемого признака, наиболее часто встречающееся в выборке.
Моду находят согласно следующим правилам:
1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет.
2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина, равная 3,5.
3) Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.
Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод).
4) Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой.
Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением.
Обычно полученные в результате наблюдений результаты представляют собой набор чисел (выборку). Просматривая этот набор, как правило, трудно выявить какую-либо закономерность. Поэтому данные подвергают некоторой первичной обработке, целью которой является упрощение дальнейшего анализа.
Дальнейшие действия зависят от того, насколько много в выборке различных чисел. Если величина дискретна и случайна, то различных чисел немного; если же величина непрерывна и случайна, то, скорее всего, все числа окажутся различными.
Дискретный случай
Первый этап обработки выборки – это составление вариационного ряда. Его получают так – среди всех чисел отбирают все различные и располагают в порядке возрастания: , где
Следующий этап обработки выборки – составление дискретной таблицы частот:
|
… |
|||
|
… |
|||
|
… |
Здесь n – число всех измерений, — число измерений, в которых наблюдалось значение . Величины называются частотами, а величины — относительными частотами.
Графической иллюстрацией дискретной таблицы частот является столбиковая диаграмма (рис.1).
Рис.1 Столбиковая диаграмма
Непрерывный случай
Если число различных значений в выборке велико, вычислить частоту каждого их них не имеет большого смысла. Поэтому поступают следующим образом. Весь промежуток изменения значений выборки, от минимального до максимального, разбивают на интервалы. После этого подсчитывают число значений из выборки, попадающих в каждый интервал (частоты), а затем – относительные частоты. В результате получается интервальная таблица частот:
|
… |
|||
|
… |
|||
|
… |
Здесь n – число всех измерений, m – число интервалов, — количество чисел, приходящихся на i-й интервал, — относительная частота попадания в i-й интервал. Интервалы обычно берут одинаковой длины, хотя это и не обязательно.
Графической иллюстрацией интервальной таблицы частот является гистограмма (рис.2). Гистограмма представляет собой ступенчатую линию; основанием i-й ступеньки является интервал , а площадь этой ступеньки равна .
Рис.2 Гистограмма
Таким образом, рассмотрены методы первичной обработки результатов эксперимента, в результате которых имеющиеся «серые» результаты наблюдений преобразовываются для достижения большей наглядности.
1.2. Однофакторный регрессионный анализ
С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики. Данную группу методов можно разделить на несколько подгрупп:
-
Регрессионный анализ;
-
Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам;
-
Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом;
-
Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ).
Регрессионный анализ – это метод математической статистики, позволяющий свести частные, разрозненные данные к их определенной внутренней взаимосвязи, которая по значению одной или нескольких переменных приблизительно оценивает вероятное значение другой переменной.
Регрессионный анализ устанавливает формы зависимости между случайной величиной y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость определяется обычно некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.
Регрессия может быть однофакторной (парной) и многофакторной (множественной). Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, можно использовать графическое изображение. При множественности причинных связей невозможно чётко разграничить одни причинные явления от других. В этом случае наиболее приемлемым способом определения зависимости (уравнения регрессии) является метод перебора различных уравнений, реализуемый с помощью компьютера.
После выбора вида регрессионной модели, используя результаты наблюдений зависимой переменной и факторов, нужно вычислить оценки (приближённые значения) параметров регрессии, а затем проверить значимость и адекватность модели результатам наблюдений.
Порядок проведения регрессионного анализа следующий:
-
выбор модели регрессии, что заключает в себе предположение о зависимости функций регрессии от факторов;
-
оценка параметров регрессии в выбранной модели методом наименьших квадратов;
-
проверка статистических гипотез о регрессии.
Графическое выражение регрессионного уравнения называют линиейрегрессии. Линия регрессии выражает наилучшие предсказания зависимой переменой (y) по независимым переменным (x,z). Эти независимые переменные, а их может быть много, носят название предикторов.
По характеру связи однофакторные уравнения регрессии подразделяются на:
а) линейные: , где x — экзогенная (независимая) переменная, y -эндогенная (зависимая, результативная) переменная, a, b параметры;
б) степенные: ;
в) показательные: и прочие.
Наиболее естественной с точки зрения единого метода оценки неизвестных параметров является модель регрессии, линейная относительно этих параметров:
(2.1)
(2.2)
где — свободные члены, — коэффициенты регрессии, или угловые коэффициенты, определяющие наклон линии регрессии по отношению к осям координат.
Линии регрессии пересекаются в точке , с координатами, соответствующими средним арифметическим значениям корреляционно связанных между собой переменных x и y.
Количественное представление связи (зависимости) между x и y (между yиx) и называется регрессионным анализом. Главная задача регрессионного анализа заключается в нахождении , и определения уровня значимости полученных аналитических выражений (2.1) и (2.2), связывающих между собой переменные x и y.
При этом коэффициенты регрессии показывают, насколько в среднем величина одной переменной изменяется при изменении на единицу меры другой. Коэффициент регрессии в уравнении (2.1) находится по формуле:
(2.3)
а коэффициент из уравнения (2.2) по формуле:
(2.4)
где — коэффициент корреляции между переменными X и Y;
— среднеквадратическое отклонение, подсчитанное для переменной x;
— среднеквадратическое отклонение, подсчитанное для переменной y.
Коэффициенты регрессии можно вычислить также без подсчета среднеквадратических отклонений по следующим формулам:
(2.5)
(2.6)
В том случае, если неизвестен коэффициент корреляции, коэффициенты регрессии можно вычислить по следующим формулам:
(2.7)
(2.8)
Сравнивая формулу для подсчета коэффициента корреляции Пирсона:
(2.9)
где — значения, принимаемые переменной x;
— значения, принимаемые переменной y;
— средняя по x;
— средняя по y.
С формулами (2.7), (2.8) видно, что в числе этих формул стоит одна и та же величина: . Последнее говорит о том, что величины и взаимосвязаны. Более того, зная две из них – всегда можно получить третью. Например, зная величины и , можно легко получить :
(2.10)
Эта формула очень важна, поскольку она позволяет по известным значениям коэффициентов регрессии и определить коэффициент корреляции, и, кроме того, сравнивая вычисления по формулам (2.9) и (2.10), можно поверить правильность расчета данного коэффициента. Как и коэффициент корреляции, коэффициенты регрессии характеризуют только линейную связь и при положительной связи имеют знак плюс, при отрицательной – знак минус.
В свою очередь свободные члены и в уравнениях регрессии вычисляются по формулам:
(2.11)
(2.12)
Вычисления по формулам (2.7), (2.8), (2.11) и (2.12) достаточно сложны, поэтому при расчетах коэффициентов регрессии используют, как правило, более простой метод. Он заключается в решении двух систем уравнений. При решении одной системы находятся величины и , и при решении другой — и .
Общий вид системы уравнений для нахождения величин и таков:
(2.13)
Общий вид системы уравнений для нахождения величин и таков:
(2.14)
В системах уравнений (2.13) и (2.14) используются следующие обозначения:
N – число элементов в переменной xили в переменной y,
— сумма всех элементов переменной x,
— сумма всех элементов переменной y,
— произведение всех элементов переменной yдруг на друга,
— произведение всех элементов переменной xдруг на друга,
— попарное произведение всех элементов переменной xна соответствующие элементы переменной y.
Для применения метода однофакторного регрессионного анализа необходимо соблюдать следующие условия:
-
Сравниваемые переменные x и yдолжны быть измерены в шкале интервалов или отношений.
-
Предполагается, что переменные x и yимеют нормальный закон распределения.
-
Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
Таким образом, можно сказать, что линейный регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений. В регрессионном анализе все признаки (переменные), входящие в уравнение, должны иметь непрерывную, а не дискретную природу.
1.3. Многофакторный регрессионный анализ
В общем случае, зависимость между несколькими переменными величинами выражают уравнением множественной регрессии (многофакторной), которая может быть как линейной, так и не линейной. В простейшем случае множественная линейная регрессия выражается уравнением с двумя независимыми переменными величинами x и z и имеет вид:
(3.1)
где y– зависимая переменная, a– свободный член, bи c– параметры уравнения (3.1).
Уравнение (3.1) может решаться относительно зависимой переменной z, тогда x и yявляются независимыми переменными, и уравнение множественной регрессии имеет следующий вид:
(3.2)
Можно решить уравнение (3.1) и относительно X, тогда Zи Yбудут независимыми переменными, и уравнение будет иметь следующий вид:
(3.3)
При проведении конкретных расчетов выбор зависимых и независимых переменных определяется планом эксперимента.
Решение уравнений (3.1), (3.2), (3.3) состоит в том, что находятся величины a, bи c на основе решения системы из трех уравнений.
Для решения уравнения (3.1) система имеет следующий вид:
(3.4)
Для решения уравнения (3.2) система будет выглядеть следующим образом:
(3.5)
Для решения уравнения (3.3) система будет иметь следующий вид:
(3.6)
В общем случае уравнение регрессии представляет собой сложный полином, описывающий зависимость сразу между несколькими переменными. Такое уравнение множественной регрессии имеет вид:
(3.7)
где и т.п. – интересующие психолога независимые переменные, а Y – зависимая переменная.
Для применения метода многофакторного регрессионного анализа необходимо соблюдать следующие условия:
-
Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.
-
Предполагается, что переменные имеют нормальный закон распределения.
-
Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.
Таким образом, качество полученного уравнения регрессии оценивают по степени близости между результатами наблюдений за показателем и предсказанными по уравнению регрессии значениями в заданных точках пространства параметров. Если результаты близки, то задачу регрессионного анализа можно считать решенной. В противном случае следует изменить уравнение регрессии (выбрать другую степень полинома или вообще другой тип уравнения) и повторить расчеты по оценке параметров.
Глава 2. Использование регрессионного анализа в интерпретации результатов методики изучения агрессии Басса-Дарки 2.1. Исследование уровня и рода враждебности школьников
Статистические методы раскрывают связи между изучаемыми явлениями. Однако необходимо твердо знать, что, как бы ни была высока вероятность таких связей, они не дают права исследователю признать их причинно-следственными отношениями.
Чтобы подтвердить или отвергнуть существование причинно-следственных отношений, исследователю зачастую приходится продумывать целые серии экспериментов. Если они будут правильно построены и проведены, то статистика поможет извлечь из результатов этих экспериментов информацию, которая необходима исследователю, чтобы либо обосновать и подтвердить свою гипотезу, либо признать ее недоказанной.
В работе с подростковой аудиторией педагогу и психологу всегда приходится учитывать особенности агрессии у подростков. А для выявления уровня и рода агрессии детей существуют различные методики. Одна из них – диагностика состояния агрессии (опросник Басса-Дарки). Данный опросник состоит из 75 утверждений, на которые испытуемый отвечает «да» или «нет» (Приложение 1).
Создавая свой опросник, дифференцирующий проявления агрессии и враждебности, А. Бассе и А. Дарки выделили следующие виды реакций:
-
Физическая агрессия – использование физической силы против другого лица.
-
Косвенная агрессия – агрессия, окольным путем направленная на другое лицо или ни на кого не направленная.
-
Раздражение – готовность к проявлению негативных чувств при малейшем возбуждении (вспыльчивость, грубость).
-
Негативизм – оппозиционная манера в поведении от пассивного сопротивления до активной борьбы против установившихся обычаев и законов.
-
Обида – зависть и ненависть к окружающим за действительные и вымышленные действия.
-
Подозрительность – в диапазоне от недоверия и осторожности по отношению к людям до убеждения в том, что другие люди планируют и приносят вред.
-
Вербальная агрессия – выражение негативных чувств как через форму (крик, визг), так и через содержание словесных ответов (проклятия, угрозы).
-
Чувство вины – выражает возможное убеждение субъекта в том, что он является плохим человеком, что поступает зло, а также ощущаемые им угрызения совести.
Обработка результатов: Обработка опросника Басса-Дарки производится при помощи индексов различных форм агрессивных и враждебных реакций, которые определяются суммированием полученных ответов. Физическая агрессия, косвенная агрессия, раздражение и вербальная агрессия вместе образуют суммарный индекс агрессивных реакций, а обида и подозрительность – индекс враждебности.
Данная методика была апробирована (в ходе государственной педагогической практики) 28.10.10 г. в 9а классе МАОУ СОШ № 5 г. Тобольска. В исследовании приняли участие 20 учащихся. Результаты опроса (значения параметров) представлены в сводной таблице (Приложение 2).
Для полной реализации сути опросника Басса-Дарки необходимо представить суммарный индекс агрессивных реакций и суммарный индекс враждебности (Приложение 3).
Перед началом регрессионного анализа осуществляется отбор факторов. Сначала отбираются факторы, связанные с изучаемым явлением, на основе данных теоретического исследования (психологическая теория, заключения экспериментатора и т.д.). При этом для построения множественной регрессии отбираются факторы, которые могут быть количественно измерены.
Проблему данного исследования составило рассмотрение и анализ уровня враждебности, вследствие этого регрессионный анализ экспериментальных данных методики Басса-Дарки будет проведен по индексу враждебности (зависимая переменная y), получающийся суммированием выявленных уровней обиды и подозрительности (независимые переменные xи z, соответственно).
2.2. Построение регрессионной модели
Регрессионный анализ экспериментальных данных методики Басса-Дарки будет проведен по индексу враждебности (зависимая переменная y), получающийся суммированием выявленных уровней обиды и подозрительности (независимые переменные xи z, соответственно).
Как будет варьировать индекс враждебности испытуемого, если будут изменяться уровни обиды и подозрительности? Ответ на этот вопрос психолог получит с помощью использования метода множественной регрессии. Данные для анализа представлены в таблице 3, в которой произведены предварительные вычисления.
Таблица 3. Исходные данные
|
№ |
Фамилия ученика |
||||||||
|
1 |
Бакиева |
5 |
8 |
13 |
25 |
40 |
65 |
64 |
104 |
|
2 |
Гатауллин |
1 |
4 |
5 |
1 |
4 |
5 |
16 |
20 |
|
3 |
Гатин |
2 |
2 |
4 |
4 |
4 |
8 |
4 |
8 |
|
4 |
Долженко |
5 |
4 |
9 |
25 |
20 |
45 |
16 |
36 |
|
5 |
Жарова |
4 |
7 |
11 |
16 |
28 |
44 |
49 |
77 |
|
6 |
Жуйкова |
6 |
3 |
9 |
36 |
18 |
54 |
9 |
27 |
|
7 |
Корикова |
5 |
7 |
12 |
25 |
35 |
60 |
49 |
84 |
|
8 |
Костерина |
7 |
7 |
14 |
49 |
49 |
98 |
49 |
98 |
|
9 |
Курманалиева |
4 |
7 |
11 |
16 |
28 |
44 |
49 |
77 |
|
10 |
Летунов |
3 |
2 |
5 |
9 |
6 |
15 |
4 |
10 |
|
11 |
Мороков |
4 |
5 |
9 |
16 |
20 |
36 |
25 |
45 |
|
12 |
Перовских В. |
4 |
9 |
13 |
16 |
36 |
52 |
81 |
117 |
|
13 |
Перовских М. |
4 |
7 |
11 |
16 |
28 |
44 |
49 |
77 |
|
14 |
Смирнова |
4 |
8 |
12 |
16 |
32 |
48 |
64 |
96 |
|
15 |
Солосина |
7 |
8 |
15 |
49 |
56 |
105 |
64 |
120 |
|
16 |
Тимирова |
1 |
2 |
3 |
1 |
2 |
3 |
4 |
6 |
|
17 |
Трухин |
2 |
4 |
6 |
4 |
8 |
12 |
16 |
24 |
|
18 |
Филиппов |
4 |
6 |
10 |
16 |
24 |
40 |
36 |
60 |
|
19 |
Хабисов |
6 |
3 |
9 |
36 |
18 |
54 |
9 |
27 |
|
20 |
Цыпанов |
0 |
2 |
2 |
0 |
0 |
0 |
4 |
4 |
|
Суммы: |
78 |
105 |
183 |
376 |
456 |
832 |
621 |
1117 |
С помощью решения системы уравнений (3.1) необходимо найти уравнение регрессии y на x, т.е. определить коэффициенты a, bи c, и таким образом ответить на поставленный вопрос.
Чтобы получить и решить уравнение множественной линейной регрессии (3.1), необходимо найти a, bи c. Для этого используется система уравнений (3.4). Благодаря вычислениям, приведенным в таблице 3, известны все необходимые величины сумм. Перепишем систему уравнений (3.4), учитывая N= 20, поскольку в эксперименте участвовало 20 человек, и учитывая данные таблицы 3:
(3.8)
Получили систему линейных уравнений (СЛУ) с тремя неизвестными. Решается данная система несколькими способами: по правилу Крамера, методом Гаусса и с помощью обратной матрицы.
В СЛУ (3.8) число уравнений равно числу неизвестных, поэтому целесообразно для нахождения неизвестных применить метод Крамера. Для начала составляется матрица третьего порядка:
(3.9)
Здесь последний столбец – это столбец свободных членов.
Теорема (правило Крамера). Пусть Δ – определитель матрицы СЛУ, а — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов. Тогда если , то система линейных уравнений имеет единственное решение, определяемое по формулам:
, где j = 1,2,…,n (3.10)
Формулы вычисления неизвестных (3.10) – решения системы линейных уравнений (3.8) – носят название формул Крамера.
Составляется и вычисляется главный определитель матрицы (3.9):
(3.11)
Так как вычисления данного определителя очень громоздкие, то целесообразно осуществлять все расчеты с помощью «Мастера функций» MS Excel. Для этого используется встроенная математическая функция МОПРЕД. Порядок вычисления следующий:
-
введите в упорядоченные ячейки электронной таблице исходные элементы определителя, сохраняя порядок следования элементов;
-
активируйте Мастер функций любым из способов:
а) в главном меню выберите команду Вставка/Функция;
б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;
-
в появившемся диалоговом окне «Мастер функций – шаг 1 из 2» в поле Категории выберите Математические, в окне Функция – МОПРЕД. Щелкните по кнопке ОК;
-
в появившемся окне Аргументы функции необходимо указать диапазон ячеек от первого элемента исходного определителя до последнего (например, А1:С3);
-
щелкните по кнопке ОК.
После выполнения данного алгоритма на экране компьютера появится результат – определитель.
Как видно, полученный определитель () отличен от нуля, стало быть, СЛУ (3.8) имеет единственное решение, которое вычисляется по формулам:
, , (3.12)
Чтобы применить формулы (3.12), необходимо составить определители по правилу Крамера (3.10) и произвести их расчеты с помощью «Мастера функций» MS Excel. Все расчеты представлены ниже.
.
Теперь, когда известны все определители, можно применить формулы (3.12):
; ; (3.13)
Решив систему уравнений (3.8), получилось a = — 3,34, b = 1,82, c = 1,02. следовательно, искомое уравнение регрессии y на x (3.1) примет вид:
(3.14)
гдеy– зависимая переменная, –3,34 — свободный член, 1,82 и1,02 – параметры уравнения.
Уравнение (3.14) дает ответ на поставленный ранее вопрос: Как будет варьировать индекс враждебности испытуемого, если будут изменяться уровни обиды и подозрительности? Так, при увеличении величины уровня обиды xна 1 балл, количественная величина индекса враждебности y увеличится на 1,82, при постоянной величине уровня подозрительности z. А при постоянной величине уровня обиды и при увеличении величины уровня подозрительности на 1 балл количественная величина индекса враждебности увеличится в среднем на 1,02 балла.
Полученное уравнение многофакторной регрессии (3.14) имеет еще одно приложение. Так, подставляя в него значения переменных xи z, можно определить ожидаемую величину переменной y (уровня враждебности).
2.3. Анализ регрессионной модели
В предыдущем параграфе была вычислена модель множественной регрессии (3.14): ,
гдеy– значение зависимой переменной,
xи z– значения зависимых переменных,
–3,34 – свободный член,
1,82 и 1,02 – параметры уравнения (коэффициенты при независимых переменных).
Для многофакторной регрессионной модели имеют место следующие предпосылки:
-
Зависимые переменные – величины неслучайные;
-
Математическое ожидание случайной составляющей в любом наблюдении равно нулю: ;
-
Дисперсия случайной составляющей постоянна для всех наблюдений: ;
-
Отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях: .
Факторы, включенные во множественную регрессию (3.14), количественно измерены и не сильно коррелируют друг с другом (корреляция– связь между собой двух и более переменных в одной или нескольких изучаемых группах). Кроме того, каждый фактор тесно связан с результатом.
Многофакторная регрессия представляет регрессию результативного признака с двумя и большим числом независимых переменных вида: .
В уравнении регрессии (3.14) случайная (зависимая) переменная yзависит не только от значений независимых переменных xи z, но и от ряда других факторов, влияющих на y, которые не могут быть проконтролированы. В связи с этим , где e – случайная величина, характеризующая отклонения результативного признака от теоретического, найденного по уравнению регрессии.
При исследовании зависимости результативного признака y в многофакторной модели необходимо решать такие же задачи, что и при однофакторной модели:
-
определение вида регрессии;
-
оценка параметров;
-
определение тесноты связи.
Однако наряду с этими задачами необходимо рассматривать и ряд задач, характерных лишь для многофакторной регрессии.
К таким задачам относится отбор факторов, существенно влияющих на фактор y, при наличии возможностей внутренней взаимосвязи между зависимыми переменными xи z. Такой отбор требует, прежде всего, глубокого теоретического и практического знания качественной стороны рассматриваемых психологических явлений.
Интерпретация результатов
До сих пор мы употребляли абстрактный математический язык. Перевод модели на язык экспериментатора называется интерпретацией модели. Задача интерпретации весьма сложна.
Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента регрессии – количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О характере влияния факторов говорят знаки коэффициентов. Знак плюс свидетельствует о том, что с увеличением значения фактора растет величина параметра оптимизации, а при знаке минус – убывает.
Анализируя сущность уравнения регрессии (3.14), следует отметить следующие положения. Рассмотренный подход не обеспечивает раздельной (независимой) оценки коэффициентов – изменение значения одного коэффициента влечет изменение значений других. Полученные коэффициенты не следует рассматривать как вклад соответствующего параметра в значение показателя. Уравнение регрессии является всего лишь хорошим аналитическим описанием имеющихся экспериментальных данных, а не законом, описывающим взаимосвязи параметров и показателя. Это уравнение применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.
В настоящее время регрессионный анализ широко используется в дифференциальной психологии и психодиагностике. С его помощью можно разрабатывать тесты, устанавливать структуру связей между отдельными психологическими характеристиками, измеряемыми набором тестов или заданиями теста.
Регрессионный анализ используется также для стандартизации тестовых методик, которая проводится на репрезентативной выборке испытуемых.
2.4. Аппроксимация экспериментальных данных
На практике часто приходится сталкиваться с задачей сглаживания экспериментальных зависимостей или задачей аппроксимации. Аппроксимацией называется процесс подбора эмпирической формулы для установленной из опыта функциональной зависимости . Эмпирические формулы служат для аналитического представления опытных данных.
Другими словами, аппроксимация, или приближение – это научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны).
Одна независимая переменная
Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости и, соответственно, вид эмпирической формулы, т.е. решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции. После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности, если функция задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности для точек .
Существуют различные меры близости и, соответственно, способы решения этой задачи. Некоторые из них очень просты, быстро приводят к результату, но результат этот является сильно приближенным, другие более точными, но более сложными. Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов. При этом функция считается наилучшим приближением к , если для нее сумма квадратов отклонений «теоретических» значений , найденных по эмпирической формуле, от соответствующих опытных значений ,
имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.
Используя методы дифференциального исчисления, метод наименьших квадратов формулирует аналитические условия достижения суммой квадратов отклонений своего наименьшего значения.
В простейшем случае задача аппроксимации экспериментальных данных выглядит следующим образом.
Пусть экспериментальные данные, полученные практическим путем, которые можно представить парами чисел , зависимость между которыми отражает таблица.
На основе данных требуется подобрать функцию , которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и, по возможности, точно отражала общую тенденцию зависимости междуx и y, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения в каком-то смысле были бы наименьшими.
Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек на координатной плоскости. Расположение экспериментальных точек может иметь самый различный вид, и каждому соответствует конкретный тип функции.
Построение эмпирической функции сводится к вычислению входящих в нее параметров, так чтобы их всех функций такого вида выбрать ту, которая лучше других описывает зависимость между изучаемыми величинами. То есть сумма квадратов разности между табличными значениями функции в некоторых точках и значениями, вычисленными по полученной формуле, должна быть минимальна.
Степень близости аппроксимации экспериментальных данных выбранной функцией оценивается коэффициентом детерминации (). Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных. Таким образом, если есть несколько подходящих вариантов типов аппроксимации функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1).
|
Количественная мератесноты связи |
Качественная характеристикасилы связи |
|
0,1-0,3 |
Слабая |
|
0,3-0,5 |
Умеренная |
|
0,5-0,7 |
Заметная |
|
0,7-0,9 |
Высокая |
|
0,9-0,99 |
Весьма высокая |
Таблица 4. Показатели тесноты связи
Таким образом, функциональная связь возникает при значении равном 1, а отсутствие связи – 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.
В MS Excel аппроксимация экспериментальных данных осуществляется путем построения графика – линии тренда (x, y – заданные величины).
Тренд – тенденция изменения показателей временного ряда. Тренды могут быть описаны различными функциями. Тип тренда устанавливают на основе данных временного ряда, путем осреднения показателей динамики ряда, на основе статистической проверки гипотезы о постоянстве параметров графика. Возможны следующие варианты функций:
-
Линейная – . Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.
-
Полиномиальная – , где до шестого порядка включительно (), — константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третей степени может дать один или два экстремума, четвертой степени – не более трех экстремумов и т.д.
-
Логарифмическая – , где a и b– константы, lnx– функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.
-
Степенная – , где a и b– константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.
-
Экспоненциальная – , где a и b– константы, e– основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений.
Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать всплывающее меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда на вкладке Тип выбирается вид аппроксимирующей функции, а на вкладке Параметры устанавливаются флажки в полях показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (). После чего нужно щелкнуть по кнопке ОК. В результате получим на диаграмме аппроксимирующую кривую.
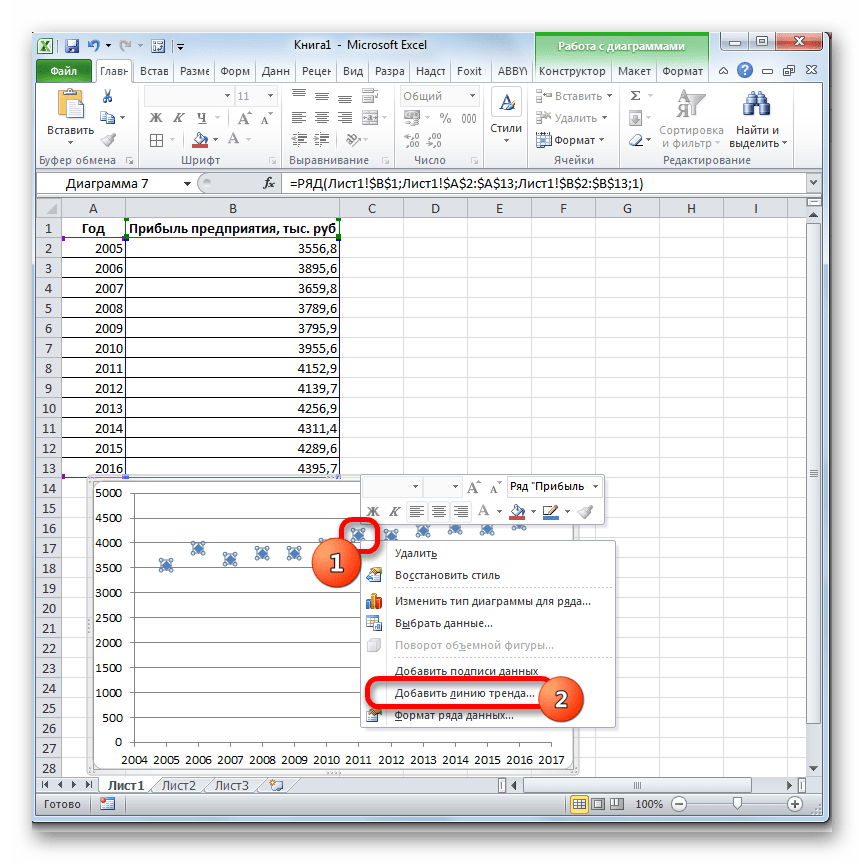
Проделав данную операцию несколько раз, можно представить линейную зависимость индексов с уравнениями линий тренда и коэффициентом детерминации – для анализа полной достоверности результатов исследуемых показателей (рис.3, рис.4).
Рис.3 Зависимость индекса враждебности от индекса обиды
Рис.4 Зависимость индекса враждебности от индекса подозрительности
Как видно, из рис.3,
Несколько независимых переменных
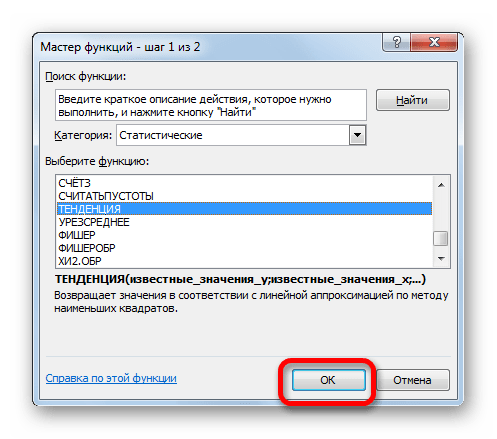
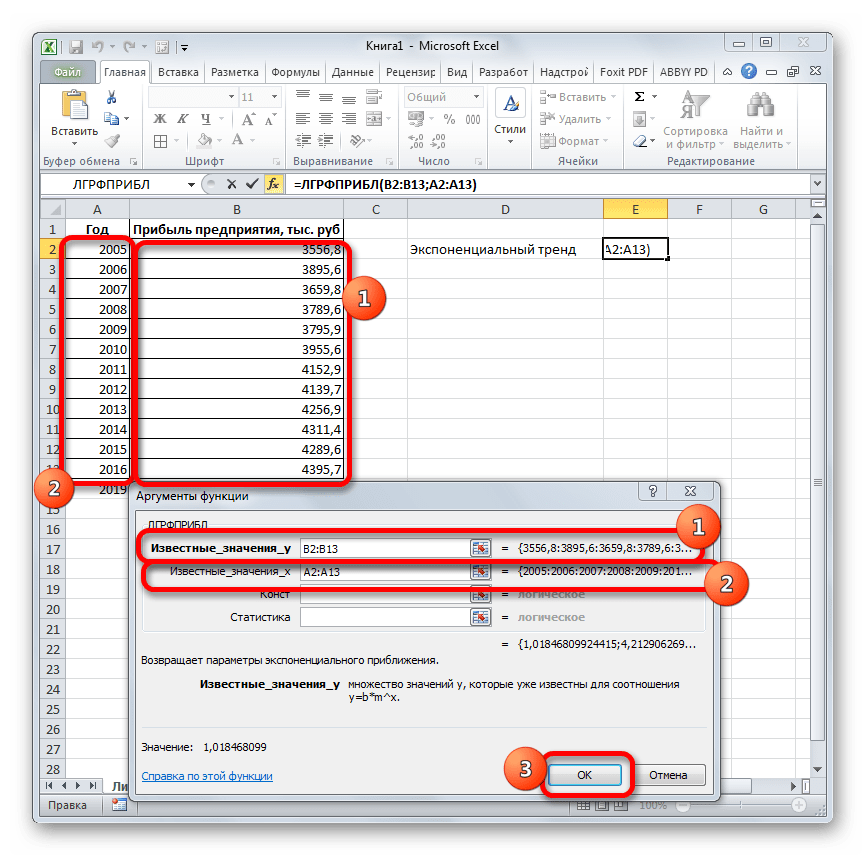
В тех случаях, когда аппроксимируемая переменная yзависит от нескольких независимых переменных , подход с построением линии тренда не дает решения. Здесь могут быть использованы следующие специальные функции MS Excel:
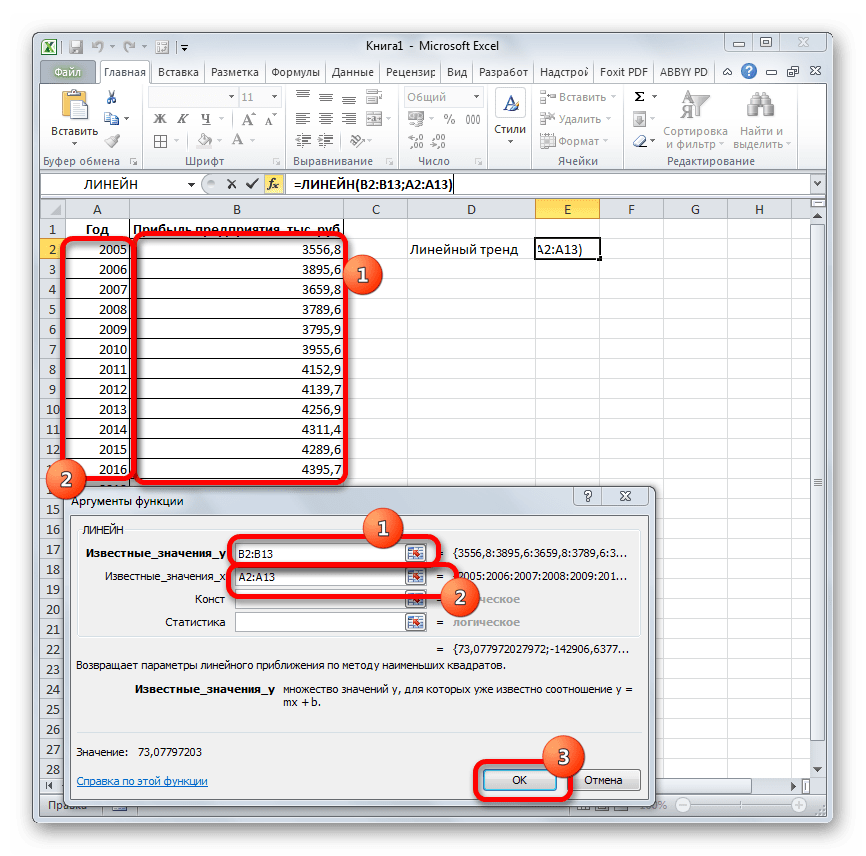
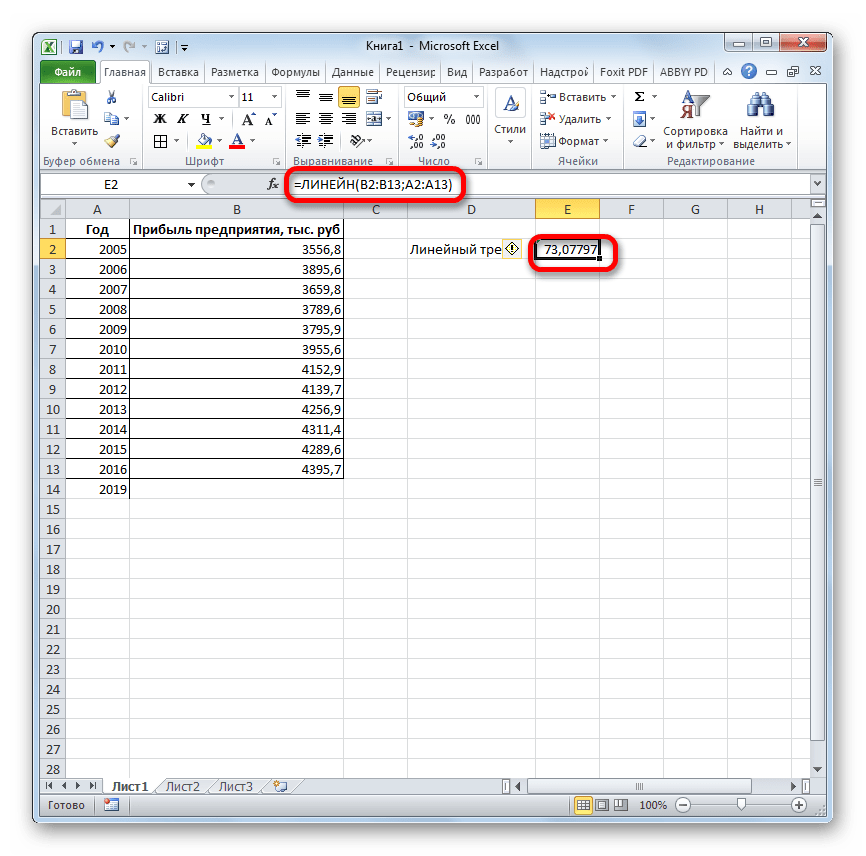
ЛИНЕЙН и ТЕНДЕНЦИЯ для аппроксимации линейных функций вида:
,
ЛГРФПРИБЛ и РОСТ для аппроксимации показательных функций вида:
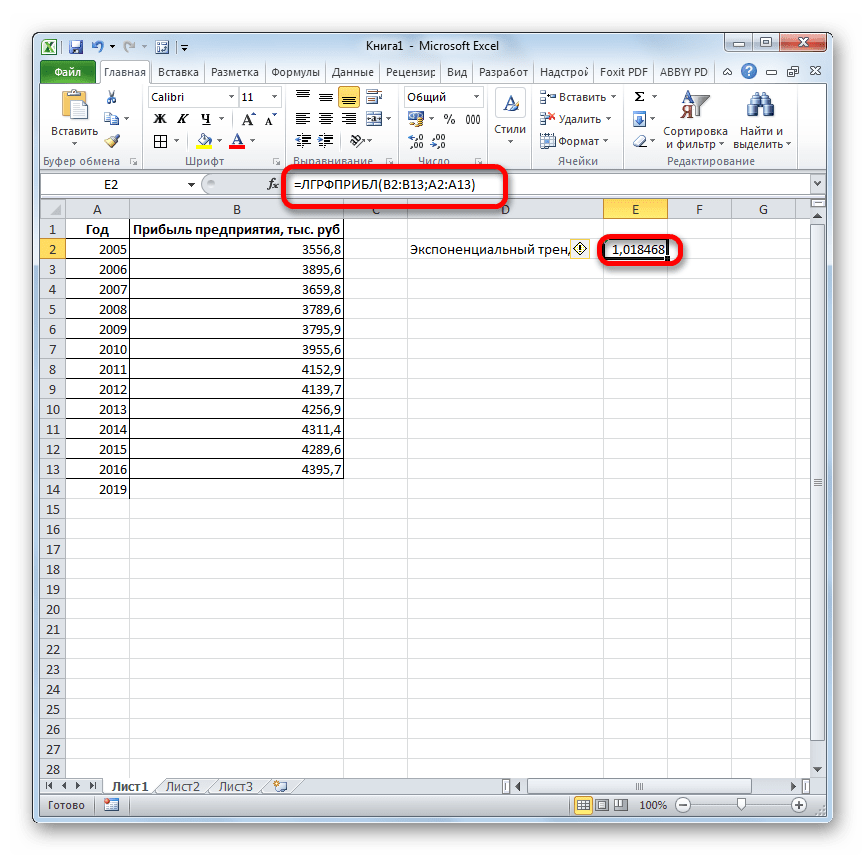
Функции ЛИНЕЙН и ЛГРФПРИБЛ служат для вычисления неизвестных коэффициентов , в указанных выражениях, а также коэффициентов детерминации (). Обе функции имеют одинаковые параметры:
ЛИНЕЙН (известные значения y; известные значения x; конст; статистика);
ЛГРФПРИБЛ (известные значения y; известные значения x; конст; статистика).
Здесь:
-
известные значения y – множество наблюдаемых значений y из казанных выражений;
-
известные значения x – множество наблюдаемых значений . Причем, если массив известные значения y имеет один столбец, то каждый столбец массива известные значения x интерпретируется как отдельная переменная, а если массив известные значения y имеет одну строку, то тогда каждая строка массива известные значения xинтерпретируется как отдельная переменная;
-
конст – логическое значение, которое указывает, требуется ли, чтобы константа была равна 0 (для функции ЛИНЕЙН) или 1 (для функции ЛГРФПРИБЛ). При этом, если конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то полагается равным 0 или 1;
-
статистика – логическое значение, которое указывает, требуется ли вычислять дополнительную статистику по регрессии, если введено значение ИСТИНА, то дополнительные параметры вычисляются, если ЛОЖЬ, то – нет.
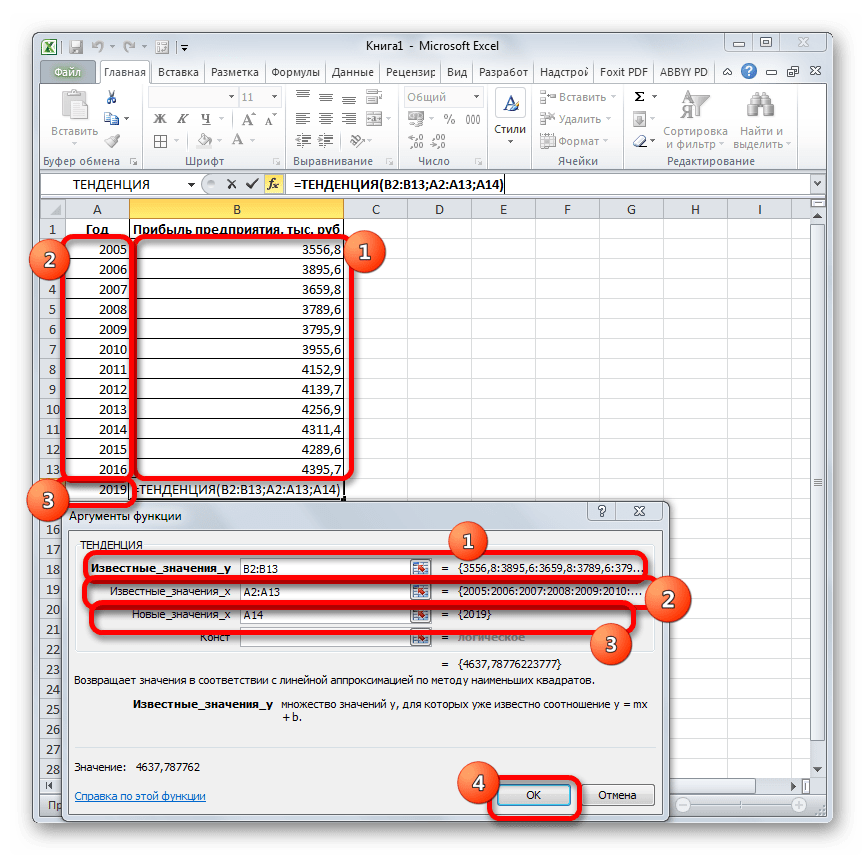
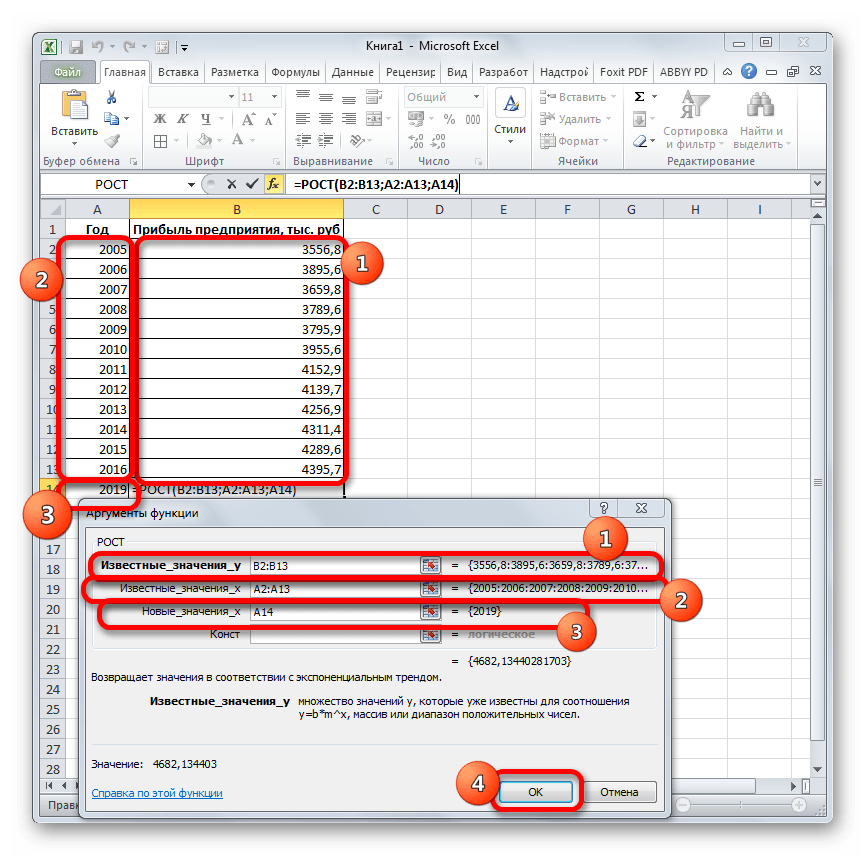
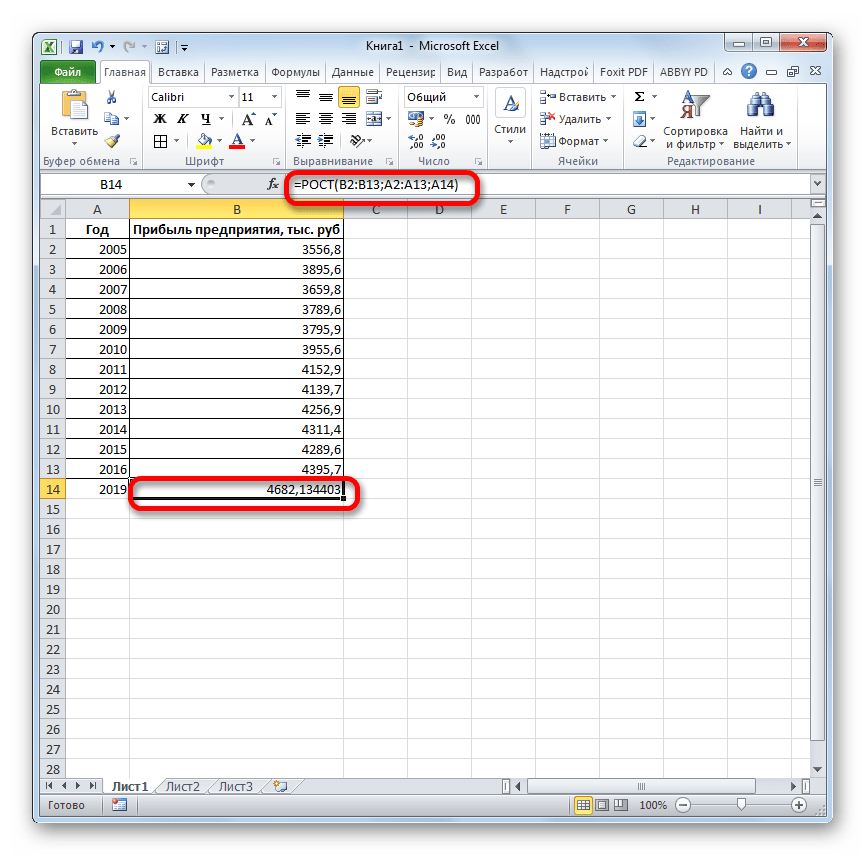
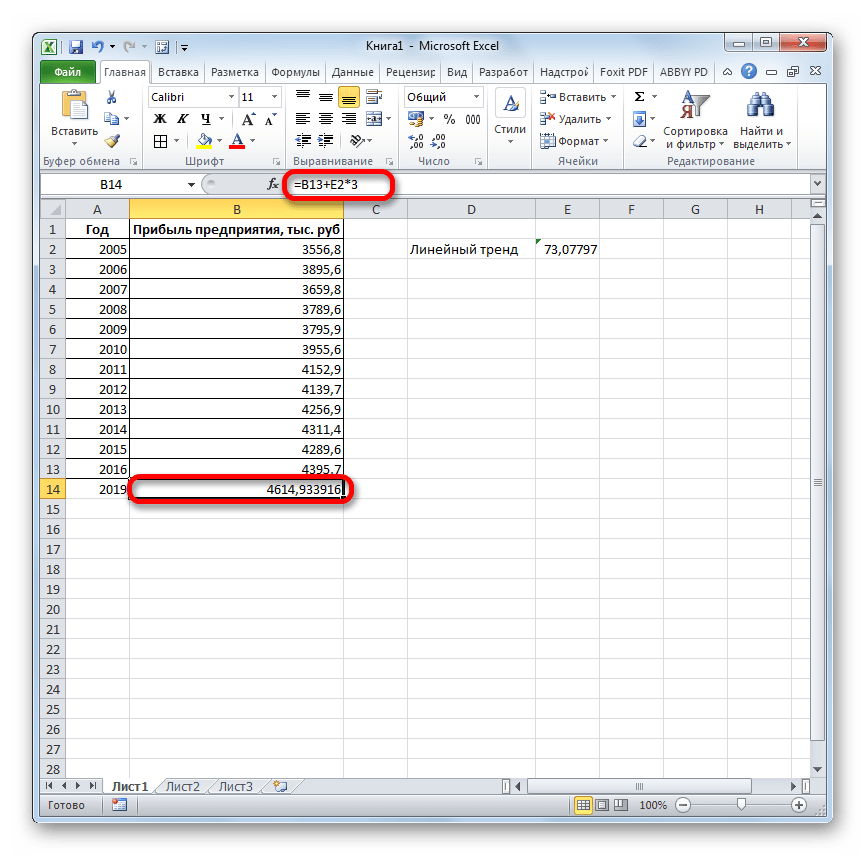
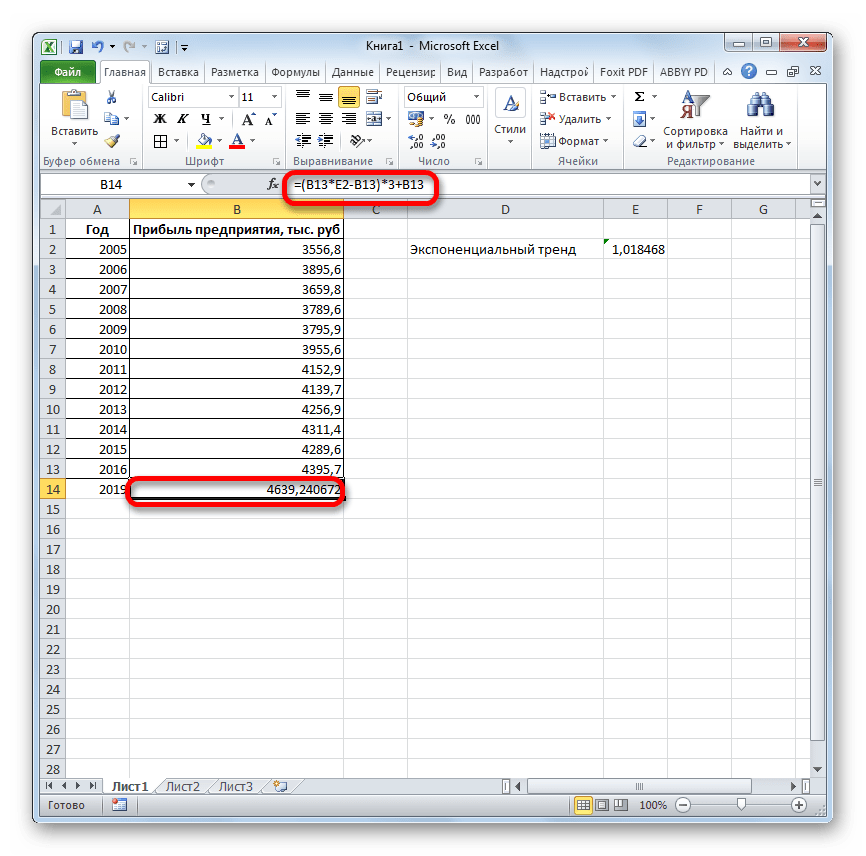
Функции ТЕНДЕНЦИЯ и РОСТ позволяют находить точки, лежащие на аппроксимирующих кривых, для значений коэффициентов , найденных функциями ЛИНЕЙН и ЛГРФПРИБЛ.
Обе функции имеют одинаковые аргументы:
ТЕНДЕНЦИЯ (известные значения y; известные значения x; новые значения x; конст);
РОСТ (известные значения y; известные значения x; новые значения x; конст).
Здесь:
-
известные значения y – множество значений y;
-
известные значения x – множество значений x;
-
новые значения x – те значений x, для которых необходимо определить соответствующие аппроксимирующие или предсказанные значения y.Новые значения x должны содержать столбец (или строку) для каждой независимой переменной, как и известные значения x. Если аргумент новые значения x опущен, то предполагается, что он совпадает с аргументом известные значения x;
-
конст – логическое значение, которое указывает, требуется ли, чтобы константа была равна 0 (для функции ТЕНДЕНЦИЯ) или 1 (для функции РОСТ). При этом, если конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то полагается равным 0 или 1.
Заключение
Тщательное, скурпулезное проведение эксперимента, несомненно, является главным условием успеха исследования. Это общее правило, и планирование эксперимента не относится к исключениям.
Однако экспериментатору не безразлично, как обработать полученные данные. Необходимо извлечь из них всю информацию и сделать соответствующие выводы. С одной стороны, не извлечь из эксперимента все, что из него следует, — значит пренебречь нелегким трудом экспериментатора. С другой стороны, сделать утверждения, не следующие из эксперимента, — значит создавать иллюзии, заниматься самообманом. Статистические методы обработки результатов эксперимента позволяют не перейти разумной меры риска.
Если данные, полученные в эксперименте, качественного характера, то правильность делаемых на основе их выводов полностью зависит от интуиции, эрудиции и профессионализма исследователя, а также от логики его рассуждений. Если же эти данные количественного типа, то сначала проводят их первичную, а затем вторичную статистическую обработку.
Вторичная статистическая обработка проводится в том случае, если для решения задач или доказательства предложенных гипотез необходимо определить статистические закономерности, скрытые в первичных экспериментальных данных. Приступая к вторичной статистической обработке, исследователь, прежде всего, должен решить, какие из различных вторичных статистик ему следует применить для обработки первичных экспериментальных данных.
Таким образом, реализована цель данной работы, т.е. разработана методика проведения регрессионного анализа статистических данных психологического эксперимента для прогнозирования исследуемых показателей. Это было достигнуто через реализацию всех поставленных задач с помощью теоретических и эмпирических методов. Таких как анализ различной литературы, систематизация полученной информации (знаний) и ее обобщение; наблюдение и анкетирование (опрос).
Математическая статистика – прикладная отрасль математики, основанная на теории вероятностей и предназначенная в самом общем плане для систематизации и анализа эмпирических (опытных) данных, получаемых при изучении повторяющихся и варьирующихся явлений.
Планирование и анализ экспериментов – это раздел математической статистики, включающий систему методов обнаружения и проверки причинных связей между переменными.
Таким образом, математическая статистика – это точная и полезная наука. Но лишь для думающего исследователя, не пренебрегающего необходимостью вникнуть в существо идей и методов теории вероятностей и математической статистики.
В целом же, статистические методы помогают исследователям описывать данные, делать выводы в отношении больших массивов данных и изучать причинные зависимости.
Список использованных источников
-
Дуброва, Т.А. Статистиские методы прогнозирования: Учебное пособие [Текст]/ Т.А. Дуброва. – М.: ЮНИТИ, 2003. – 204с.
-
Ермолаев О.Ю. Математическая статистика для психологов : Учебник [Текст]/ О.Ю. Ермолаев. – М.: Изд-во Флинта Московского психолого-социального института, 2004. – 335с.
-
Калинина, В.Н. Теория вероятностей и математическая статистика: Учебное пособие для вузов [Текст]/ В.Н. Калинина. – М.: Дрофа, 2008. – 471с.
-
Калинина, В.Н. Математическая статистика: Учебник для студентов [Текст]/ В.Н. Калинина, В.Ф. Панкин. – М.: Дрофа, 2002. – 335с.
-
Крамер, Д. Математическая обработка данных в социальных науках: современные методы: Учебное пособие для вузов [Текст]/ Дункан Крамер. – Академия, 2007. – 287с.
-
Красс, М.С. Математика для экономического бакалавриата: Учебник [Текст]/ М.С. Красс, Б.П. Чупрынов. – М.: Дело, 2005. – 574с.
-
Кричевец, А.Н. Математика для психологов: Учебник [Текст]/ А.Н. Кричевец, Е.В. Шикин, А.Г. Дьячков. – М.: Изд-во Флинта Московского психолого-социального института, 2005. – 371с.
-
Могилев, А.В, Информатика: Учебник [Текст]/ А.В. Могилев, Н.И. Пак, Е.К. Хеннер. – М.: Академия, 2003. – 809с.
-
Немов, Р.С. Психодиагностика. Введение в научное психологическое исследование с элементами математической статистики [Текст]/ Р.С. Немов. – М.: ВЛАДОС, 1998. – 632 с.
-
Палий, И.А. Прикладная статистика: Учебное пособие для вузов [Текст]/ И.А. Палий. – М.: Высшая школа, 2004. – 175с.
-
Рубинштейн, С.Л. Основы общей психологии [Текст]/ С.Л. Рубинштейн. – СПб.: Питер, 2008. – 705с.
-
Симонович, С.В. Специальная информатика: Учебное пособие [Текст]/ С.В. Симонович, Г.А. Евсеев, А.Г. Алексеев. – М., 2002. – 479с.
-
Созонова, М.С. Математические методы в психологии: Учебное пособие [Текст]/ М.С. Созонова. – Тобольск: ТГСПА им. Д.И. Менделеева, 2006. – 172с.
-
Фадеев, М.А. Элементарная обработка результатов эксперимента: Учебное пособие [Текст]/ М.А. Фадеев. – СПб, М., Краснодар: Лань, 2008. – 117с.
Приложение 1
Инструкция: опросник Басса-Дарки состоит из 75 утверждений, на которые испытуемый отвечает «да» или «нет».
-
Временами я не могу справиться с желанием причинить вред другим.
-
Иногда я сплетничаю о людях, которых не люблю.
-
Я легко раздражаюсь, но быстро успокаиваюсь.
-
Если меня не попросят по-хорошему, я не выполню просьбы.
-
Я не всегда получаю то, что мне положено.
-
Я знаю, что люди говорят обо мне за моей спиной.
-
Если я не одобряю поведения друзей, то даю им это почувствовать.
-
Если мне случалось обмануть кого-нибудь, я испытывал мучительные угрызения совести.
-
Мне кажется, что я не способен ударить человека.
-
Я никогда не раздражаюсь настолько, чтобы кидаться предметами.
-
Я всегда снисходителен к чужим недостаткам.
-
Если мне не нравится установленное правило, мне хочется нарушить его.
-
Другие умеют (лучше, чем я) почти всегда пользоваться благоприятными обстоятельствами.
-
Я держусь настороженно с людьми, которые относятся ко мне несколько более дружественно, чем я ожидал.
-
Я часто бываю не согласен с людьми.
-
Иногда мне на ум приходят мысли, которых я стыжусь.
-
Если кто-нибудь первым ударит меня, я не отвечу ему.
-
Когда я раздражаюсь, я хлопаю дверьми.
-
Я гораздо более раздражителен, чем кажется окружающим.
-
Если кто-нибудь корчит из себя начальника, я всегда поступаю ему наперекор.
-
Меня немного огорчает моя судьба.
-
Я думаю, что многие люди не любят меня.
-
Я не могу удержаться от спора, если люди не согласны со мной.
-
Люди, увиливающие от работы, должны испытывать чувство вины.
-
Тот, кто оскорбляет меня или мою семью, напрашивается на драку.
-
Я не способен на грубые шутки.
-
Меня охватывает ярость, когда надо мной насмехаются.
-
Когда люди строят из себя начальников, я делаю всё, чтобы они не зазнавались.
-
Почти каждую неделю я вижу кого-нибудь, кто мне не нравится.
-
Довольно многие люди завидуют мне.
-
Я требую, чтобы люди уважали мои права.
-
Меня угнетает то, что я мало делаю для своих родителей.
-
Люди, которые постоянно изводят Вас, стоят того, чтобы их щёлкнули по носу.
-
От злости я иногда бываю мрачен.
-
Если ко мне относятся хуже, чем я того заслуживаю, я не расстраиваюсь.
-
Если кто-то выводит меня из себя, я не обращаю на него внимания.
-
Хотя я и не показываю этого, иногда меня гложет зависть.
-
Иногда мне кажется, что надо мной смеются.
-
Даже если я злюсь, я не прибегаю к «сильным» выражениям.
-
Мне хочется, чтобы мои ошибки были прощены.
-
Я редко даю сдачи, даже если кто-нибудь ударит меня.
-
Когда получается не по-моему, я всегда обижаюсь.
-
Иногда люди раздражают меня просто своим присутствием.
-
Нет людей, которых бы я по-настоящему ненавидел.
-
Мой принцип: «Никогда не доверяй чужакам».
-
Если кто-нибудь раздражает меня, я готов сказать всё, что о нём думаю.
-
Я делаю много такого, о чём впоследствии сожалею.
-
Если я разозлюсь, я могу ударить кого-нибудь.
-
С десяти лет я никогда не проявлял вспышек гнева.
-
Я часто чувствую себя, как пороховая бочка, готовая взорваться.
-
Если бы все знали, что я чувствую, меня бы считали человеком, с которым нелегко ладить.
-
Я всегда думаю о том, какие тайные причины заставляют людей делать что-то приятное для меня.
-
Когда на меня кричат, я начинаю кричать в ответ.
-
Неудачи огорчают меня.
-
Я дерусь не реже и не чаще, чем другие.
-
Я могу вспомнить случай, когда я был настолько зол, что хватал попавшуюся мне под руку вещь и ломал её.
-
Иногда я чувствую, что готов первым начать драку.
-
Иногда я чувствую, что жизнь поступает со мной несправедливо.
-
Раньше я думал, что большинство людей говорит правду, но теперь я в это не верю.
-
Я ругаюсь только от злости.
-
Иногда я поступаю неправильно, меня мучает совесть.
-
Если для защиты своих прав мне надо применять физическую силу, я применяю её.
-
Иногда я выражаю свой гнев тем, что стучупо столу кулаком.
-
Я бываю грубоват по отношению к людям, которые мне не нравятся.
-
У меня нет врагов, которые хотели бы мне навредить.
-
Я не умею поставить человека на место, даже если он того заслуживает.
-
Я часто думаю, что жил неправильно.
-
Я знаю людей, которые способны довести меня до драки.
-
Я не раздражаюсь из-за мелочей.
-
Мне редко приходит в голову, что люди пытаются разозлить или оскорбить меня.
-
Я часто просто угрожаю людям, хотя и не собираюсь приводить угрозы в исполнение.
-
В последнее время я стал занудой.
-
В споре я часто повышаю голос.
-
Обычно я стараюсь скрывать плохое отношение к людям.
-
Я лучше соглашусь с чем-либо, чем стану спорить.
Обработка результатов: Обработка опросника производится при помощи индексов различных форм агрессивных и враждебных реакций, которые определяются суммированием полученных ответов.
1. Физическая агрессия:
Ответы «да» в вопросах №№ 1, 25, 33, 48, 55, 62, 68
Ответы «нет» в вопросах №№ 9, 17, 41 10
2. Косвенная агрессия:
Ответы «да» в вопросах №№ 2, 18, 34, 42, 56, 63
Ответы «нет» в вопросах №№ 10, 26, 49 9
3. Раздражение:
Ответы «да» в вопросах №№ 3, 19, 27, 43, 50, 57, 64, 72
Ответы «нет» в вопросах №№ 11, 35, 69 11
4. Негативизм:
Ответы «да» в вопросах №№ 4, 12, 20, 23, 36 5
5. Обида:
Ответы «да» в вопросах №№ 5, 13, 21, 29, 37, 51, 58
Ответы «нет» — № 44 8
6. Подозрительность:
Ответы «да» в вопросах №№ 6, 14, 22, 30, 38, 45, 52, 59
Ответы «нет» в вопросах — № 65, 70 10
7. Вербальная агрессия:
Ответы «да» в вопросах №№ 7, 15, 23, 31, 46, 53, 60, 71, 73
Ответы «нет» в вопросах №№ 39, 66, 74, 75 13
8. Угрызения совести, чувство вины:
Ответы «да» в вопросах №№ 8, 16, 24, 32, 40, 47, 54, 61, 67 9
Физическая агрессия, косвенная агрессия, раздражение и вербальная агрессия вместе образуют суммарный индекс агрессивных реакций, а обида и подозрительность – индекс враждебности.
Приложение 2
Таблица 1. Набранные индексы по видам реакций, их сумма.
|
№ |
Фамилия ученика |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Сумма |
|
1 |
Бакиева |
9 |
7 |
6 |
4 |
5 |
8 |
10 |
7 |
56 |
|
2 |
Гатауллин |
8 |
6 |
3 |
2 |
1 |
4 |
10 |
5 |
34 |
|
3 |
Гатин |
7 |
2 |
3 |
2 |
2 |
2 |
7 |
6 |
31 |
|
4 |
Долженко |
6 |
2 |
8 |
0 |
5 |
4 |
9 |
5 |
39 |
|
5 |
Жарова |
9 |
4 |
7 |
3 |
4 |
7 |
9 |
5 |
48 |
|
6 |
Жуйкова |
5 |
5 |
7 |
4 |
6 |
3 |
3 |
8 |
41 |
|
7 |
Корикова |
9 |
4 |
3 |
4 |
5 |
7 |
7 |
8 |
47 |
|
8 |
Костерина |
10 |
9 |
8 |
4 |
7 |
7 |
11 |
9 |
65 |
|
9 |
Курманалиева |
10 |
7 |
7 |
4 |
4 |
7 |
13 |
8 |
60 |
|
10 |
Летунов |
8 |
6 |
6 |
4 |
3 |
2 |
10 |
7 |
46 |
|
11 |
Мороков |
9 |
7 |
9 |
4 |
4 |
5 |
10 |
7 |
55 |
|
12 |
Перовских В. |
10 |
8 |
8 |
4 |
4 |
9 |
11 |
7 |
61 |
|
13 |
Перовских М. |
8 |
2 |
5 |
2 |
4 |
7 |
9 |
8 |
45 |
|
14 |
Смирнова |
5 |
5 |
9 |
5 |
4 |
8 |
10 |
7 |
53 |
|
15 |
Солосина |
4 |
7 |
7 |
1 |
7 |
8 |
9 |
7 |
50 |
|
16 |
Тимирова |
9 |
6 |
4 |
3 |
1 |
2 |
11 |
6 |
42 |
|
17 |
Трухин |
7 |
6 |
3 |
4 |
2 |
4 |
12 |
2 |
40 |
|
18 |
Филиппов |
8 |
3 |
5 |
4 |
4 |
6 |
10 |
8 |
48 |
|
19 |
Хабисов |
8 |
3 |
6 |
3 |
6 |
3 |
9 |
5 |
43 |
|
20 |
Цыпанов |
6 |
0 |
0 |
2 |
0 |
2 |
3 |
3 |
16 |
|
Максимальный набор индексов |
10 |
9 |
11 |
5 |
8 |
10 |
13 |
9 |
75 |
1 — физическая агрессия
2 — косвенная агрессия
3 — раздражение
4 — негативизм
5 — обида
6 — подозрительность
7 — вербальная агрессия
8 — угрызение совести, чувство вины
Приложение 3
Таблица 2. Индексы.
|
№ |
Фамилия ученика |
Индекс агрессии |
Индекс враждебности |
|
1 |
Бакиева |
32 |
13 |
|
2 |
Гатауллин |
27 |
5 |
|
3 |
Гатин |
19 |
4 |
|
4 |
Долженко |
25 |
9 |
|
5 |
Жарова |
29 |
11 |
|
6 |
Жуйкова |
20 |
9 |
|
7 |
Корикова |
23 |
12 |
|
8 |
Костерина |
38 |
14 |
|
9 |
Курманалиева |
37 |
11 |
|
10 |
Летунов |
30 |
5 |
|
11 |
Мороков |
35 |
9 |
|
12 |
Перовских В. |
37 |
13 |
|
13 |
Перовских М. |
24 |
11 |
|
14 |
Смирнова |
29 |
12 |
|
15 |
Солосина |
27 |
15 |
|
16 |
Тимирова |
30 |
3 |
|
17 |
Трухин |
28 |
6 |
|
18 |
Филиппов |
26 |
10 |
|
19 |
Хабисов |
26 |
9 |
|
20 |
Цыпанов |
9 |
2 |
|
Максимальный набор индексов |
43 |
18 |
Содержание
- Использование программы Excel для математико-статистической обработки психологических исследований
- 3 Этап – в диалоговом окне «анализ данных» выберите режим «описательная статистика»
- Корреляционный анализ по пирсону
- Инструменты прогнозирования в Microsoft Excel
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
Использование программы Excel для математико-статистической обработки психологических исследований
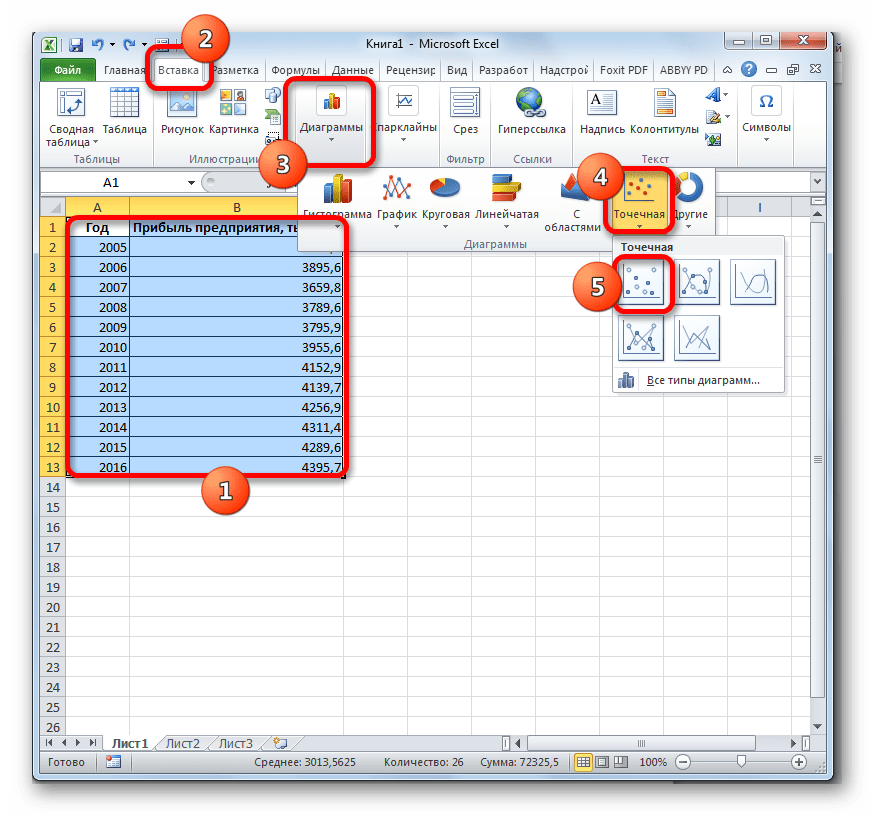
Удобство использования данной программы обусловлено тем фактом, что практически на каждом компьютере сейчас установлен популярный пакет Microsoft Office разных версий выпуска. С помощью Excel можно существенно облегчить рутинные вычисления:
Пакет анализа программы Microsoft Excel позволяет быстро и удобно, не прибегая к помощи специализированных программ, обработать данные психологических исследований. С его помощью можно осуществить:
Вычисление статистических параметров
Корреляционный анализ (коэффициент корреляции Пирсона)
Дисперсионный анализ (различные виды)
Т- тест (различные виды)
F-тест для дисперсии
Построить гистограмму статистического распределения
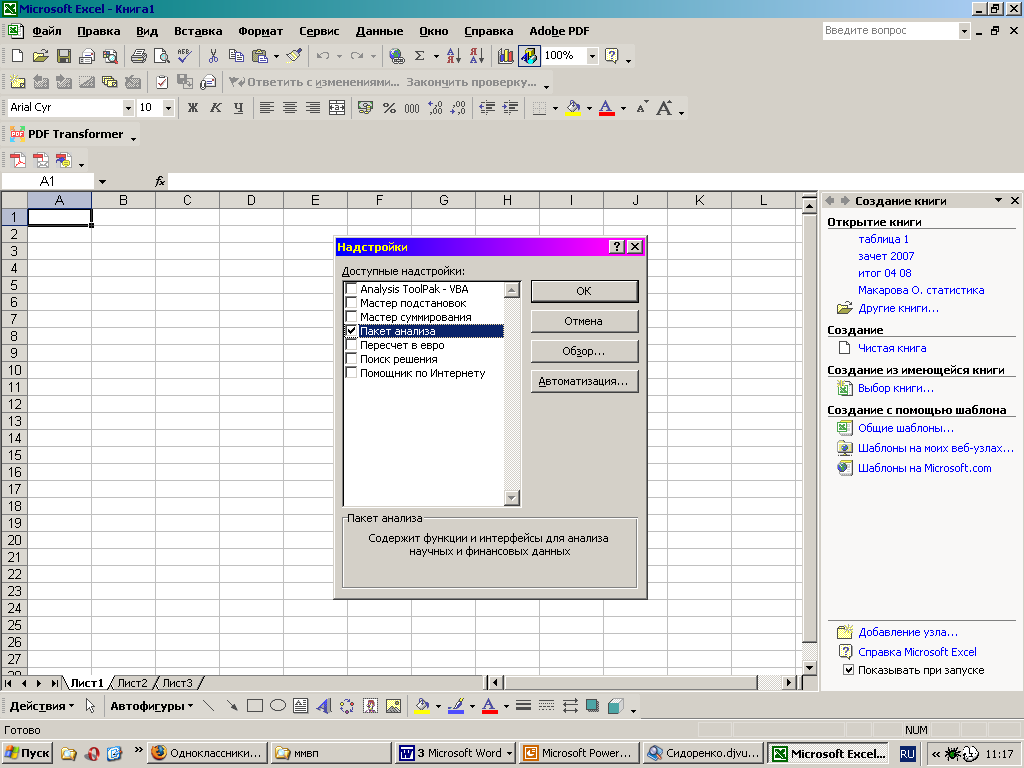
Перед началом работы необходимо установить Пакет анализа. Для этого в диалоговом меню «Надстройки» установите флажок напротив пакета анализа.
После этого в меню СЕРВИС (для версии Excel 2003) появится команда «АНАЛИЗ ДАННЫХ». Такая же команда появится во вкладке «ДАННЫЕ» (для версии Excel 2007).
Работа ведется поэтапно:
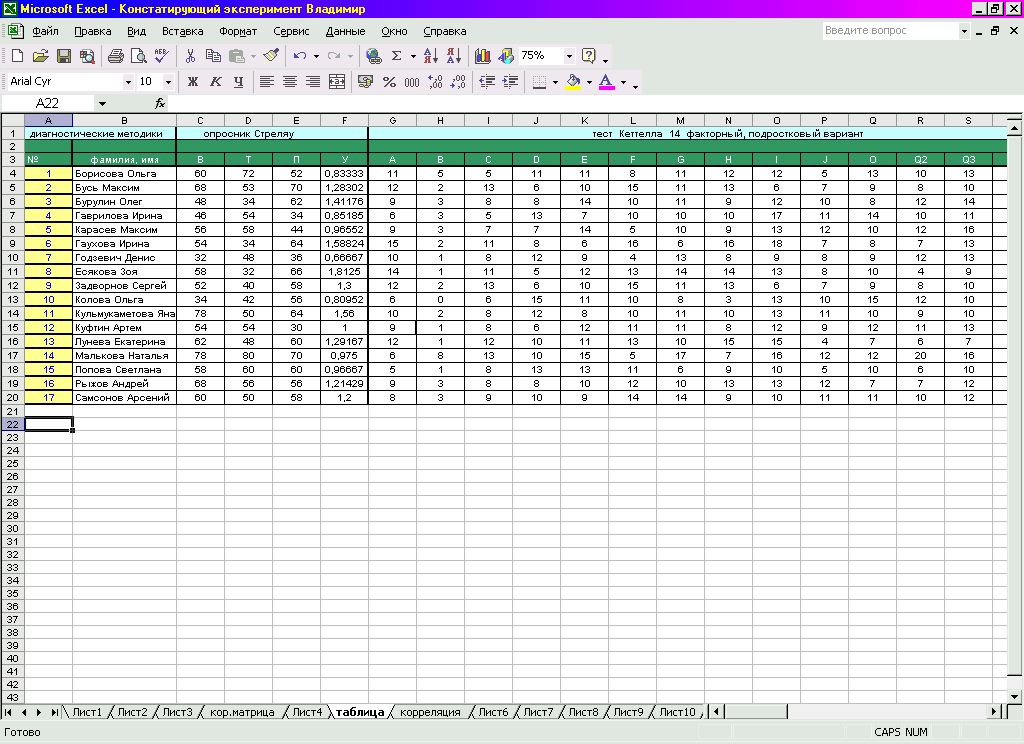
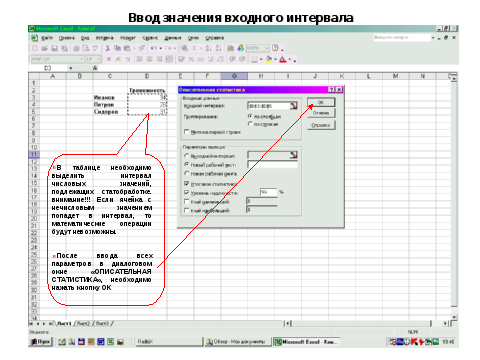
1 этап – занесение данных исследования в электронную таблицу Microsoft Excel
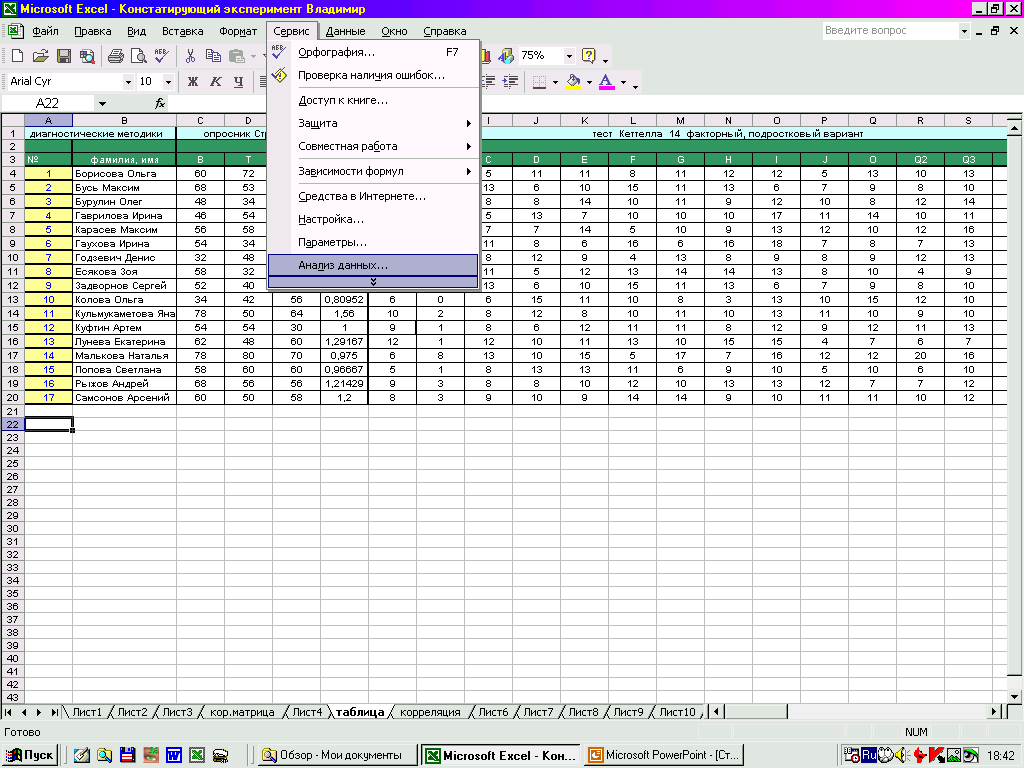
2 этап – в меню «СЕРВИС» выберите режим «АНАЛИЗ ДАННЫХ»
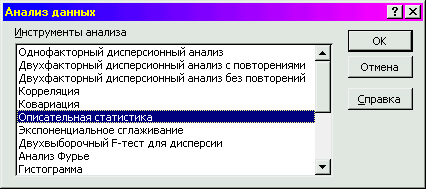
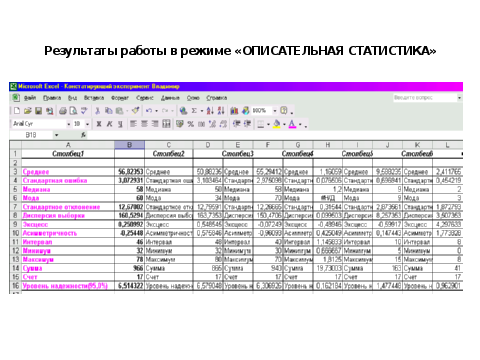
3 Этап – в диалоговом окне «анализ данных» выберите режим «описательная статистика»
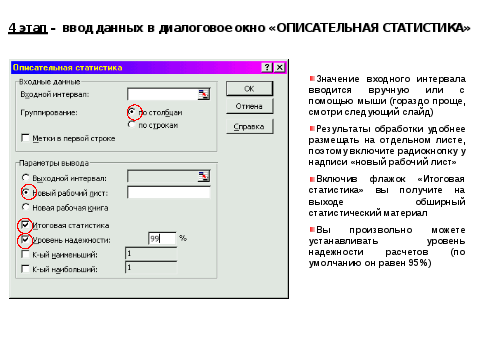
4 этап – ввод данных в диалоговое окно «ОПИСАТЕЛЬНАЯ СТАТИСТИКА»
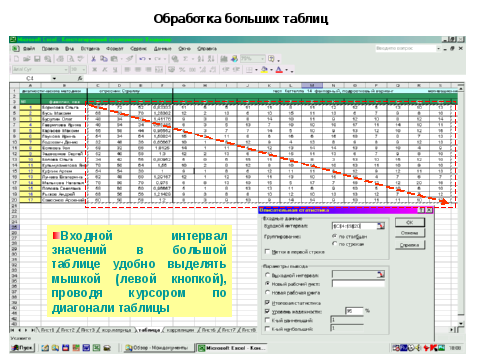
Таким образом, достаточно большой массив исследовательских данных обработан очень быстро. Выполнены трудоемкие вычисления значений стандартного отклонения, асимметрии и эксцесса.
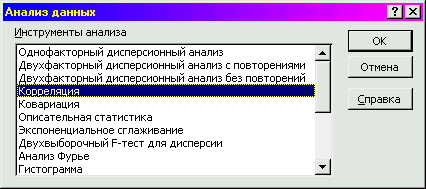
Корреляционный анализ по пирсону
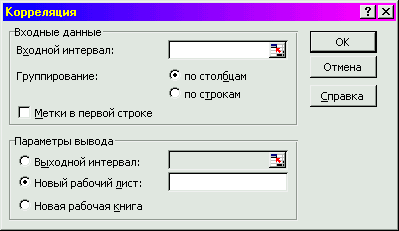
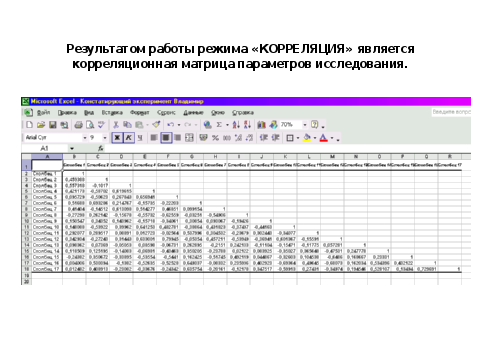
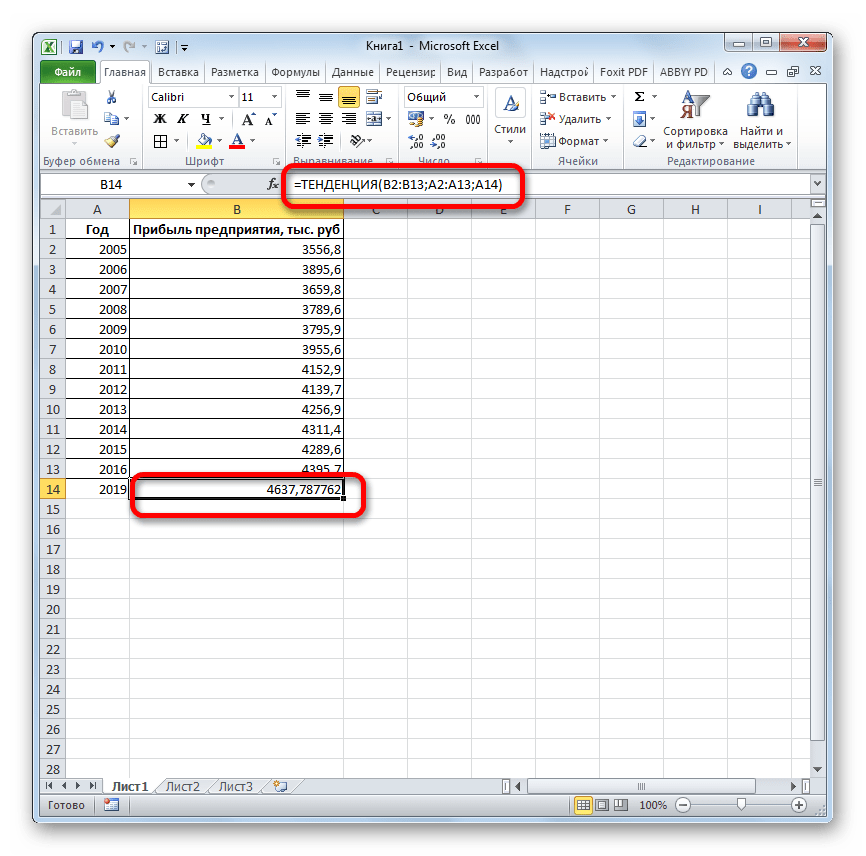
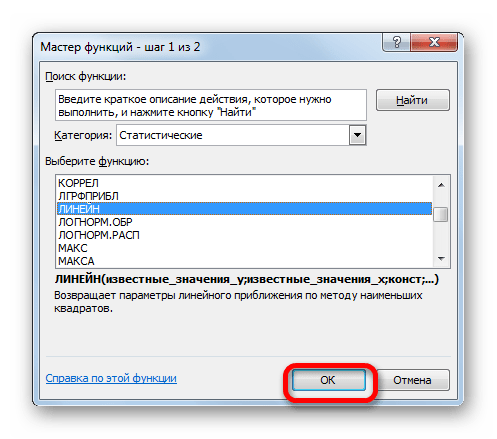
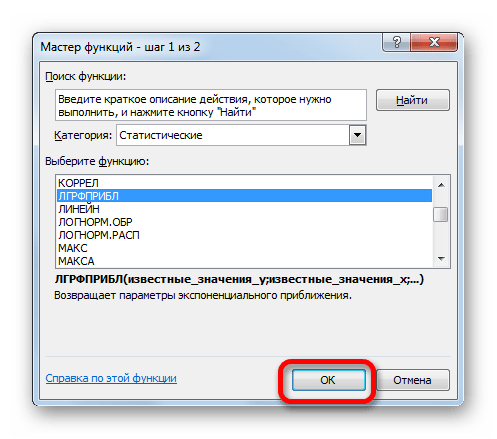
1 этап – в диалоговом окне «АНАЛИЗ ДАННЫХ» выберите режим «КОРРЕЛЯЦИЯ»
2
Области библиографического описания и их основные элементы
Порядок следования области
Знак перед элементом
Пример библиографического описания
Область заглавия и сведений об ответственности
Воспитание? Воспитание… Воспитание!
2. История психологии. От античности к современности
3. Наука радости, или как не попасть на прием к психотерапевту
4. 1000 великих битв, XI — нач. XX в. Но Десять лет, которые потрясли…1991 – 2001
4.1. Основы обшей психологии : в 2 тт.
4.2 Основы обшей психологии : в 2 тт. Т. 1
Первые сведения об ответственности
5. / И.В. Дубровина, М.К.Акимова, Е.М. Борисова и др.
/ Под ред. И.С. Клециной
/ Сост., науч ред., авт. вступ. ст. М.Г. Ярошевский
/ Авторы-составители: к.п.н., доцент Н.В. Киршева, и Н.В. Рябчикова
Сведения об издании
Первые сведения об ответственности, относящиеся к изданию
7. . – Изд. 2-е / перераб. с 1-го изд. П. Агафоншин
Дополнительные сведения об издании
8. – 4-е изд., перераб.
. – 2-е изд., перераб. и доп.
Первые сведения об ответственности, относящиеся к дополнительным сведениям об издании
9. . – 2-е изд., перераб. / Под ред. Д.Я. Райгородского
Область специфических сведений
Для нормативных документов, электронных ресурсов.
Область выходных данных
Первое место издания
Имя издателя, распространителя
Дата издания, распространения
Область физической характеристики
Специфическое обозначение материала и объем
Основное заглавие серии или подсерии
. – (Серия «Золотой фонд психотерапии»)
.– (Библиотека «Первого сентября») (Серия «Я иду на урок)
Первые сведение об ответственности, относящиеся к серии или подсерии
16. . – (Доклады Института Европы / Рос. Акад. Наук)
. – (Серия «Пушкин в ХХ веке / гл. ред. В.С. Непомнящий)
Международный стандартный номер сериального издания, присвоенный данной серии или подсерии (ISSN)
17. . – ISSN 0201-7636
Номер выпуска серии или подсерии
Факультативна. Но приводятся сведения об источнике основного заглавия, системных требованиях к компьютеру, депонированию, режиму доступа.
19. . – Загл, авт. и вых. дан. Установлены по справ.: Подробный словарь русских гравированных портретов / Д.А. Ровинский. СПб., 1888. Т. 3. № 654.
. – Систем. требования: windows 95; Pentium 90 Мhz ; 16Mb RAM
. – Режим доступа: www. un. org
Область стандартного номера (или его альтернативы) и условий доступности
Стандартный номер (или его альтернатива)
20. .- ISBN 5-7975-0063-9
.– ISBN 5-8103-0093-3. – ISBN 5-224-00744-5 (ОЛМА-пресс)
Область заглавия и сведений об ответственности содержит основное заглавие первоисточника, а также иные заглавия (альтернативное, параллельное, другое), прочие относящиеся к заглавию сведения и сведения о лицах и (или) организациях, ответственных за создание документа, являющегося объектом описания.
1. Основное заглавие приводят в том виде, в каком оно дано в источнике информации (на титульном листе, карточке каталога) в той же последовательности и с теми же знаками (пример 1).
2. Если основное заглавие состоит из нескольких предложений, между которыми в источнике информации отсутствуют знаки препинания, в описании эти предложения отделяют друг от друга точкой (пример 2)
3. Если основное заглавие содержит альтернативное заглавие, соединенное с ним союзом «или», и записываемое с прописной буквы, то перед союзом «или» ставят запятую (пример 3).
4. Указанные в источнике информации хронологические и географические данные, связанные по смыслу с основным заглавием, приводят в описании после основного заглавия и отделяют от него запятой, если в источнике перед ними нет других знаков (пример 4).
Сведения от ответственности содержат информацию о лицах и организациях, участвовавших в создании первоисточника, являющегося объектом описания.
Сведения об ответственности записывают в той форме, в какой они указаны в источнике информации – титульном листе, карточке каталога, библиографическом указателе (пример 5). Первым сведениям об ответственности предшествует знак «косая черта». Последующие группы сведений отделяют друг от друга «точкой с запятой». Обязательными являются первые сведения об ответственности.
Область издания содержит информацию об изменениях и особенностях данного издания по отношению к предыдущему изданию того же произведения.
Сведения об издании обычно содержат слово «издание» или «версия», «вариант», «выпуск», «редакция», «репринт». Их приводят в формулировках и в последовательности, имеющихся в источнике информации – титульном листе, карточке каталога, библиографическом указателе.
Порядковый номер записывают арабскими цифрами, добавляя окончание, согласно правилам грамматики соответствующего языка (пример 6).
Первые сведения об ответственности, относящиеся к изданию, записывают в области издания, если они относятся только к конкретному измененному изданию произведения. Им предществует «косая черта» (пример 7).
Дополнительные сведение об издании приводят в описании, если они есть в источнике информации – титульном листе, карточке каталога, библиографическом указателе. Их записывают после предыдущих сведений области издания и отделяют запятой (пример 8).
Первые сведения об ответственности, относящиеся к дополнительным сведениям об издании, записывают после этих сведений по правилам приведения сведения об ответственности (пример 9).
Область выходных данных содержит сведения о месте и времени публикации, распространения и изготовления первоисточника, а также сведения об его издателе, распространителе и изготовителе.
Название места издания, распространения приводят в форме и падеже, указаных в источнике информации – титульном листе, карточке каталога, библиографическом указателе (пример 10). Если указано несколько мест издания, то приводят место, выделенное полиграфическим способом или указанное первым, а опущенные сведения отмечают сокращением [и др.] (пример 11).
Имя (наименование) издателя, распространителя приводят после сведений о месте издания, к которому оно относится, и отделяют двоеточием. Сведения приводят в том виде, как они указаны в источнике информации, сохраняя слова или фразы, указывающие функции (кроме издательской), выполняемый лицом или организацией. Сведения о форме собственности издателя, распространителя (АО, ООО и др.), как правило, опускают (пример 12).
Источник
Инструменты прогнозирования в Microsoft Excel
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть». 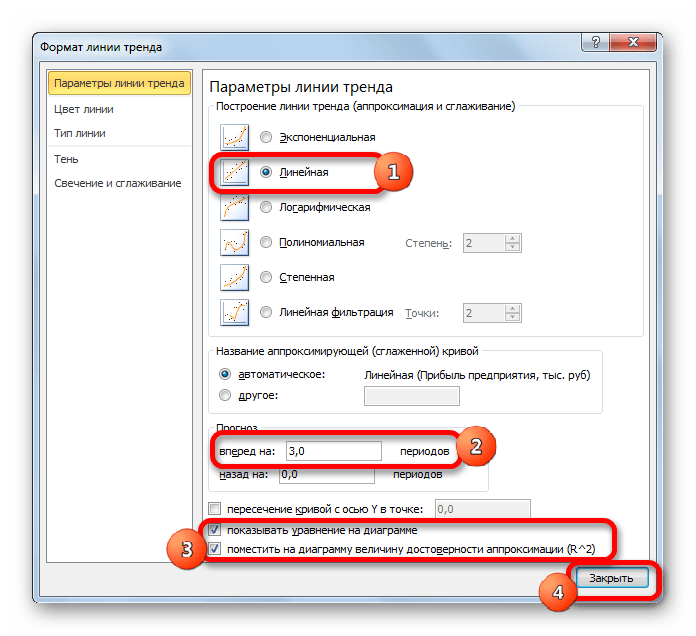
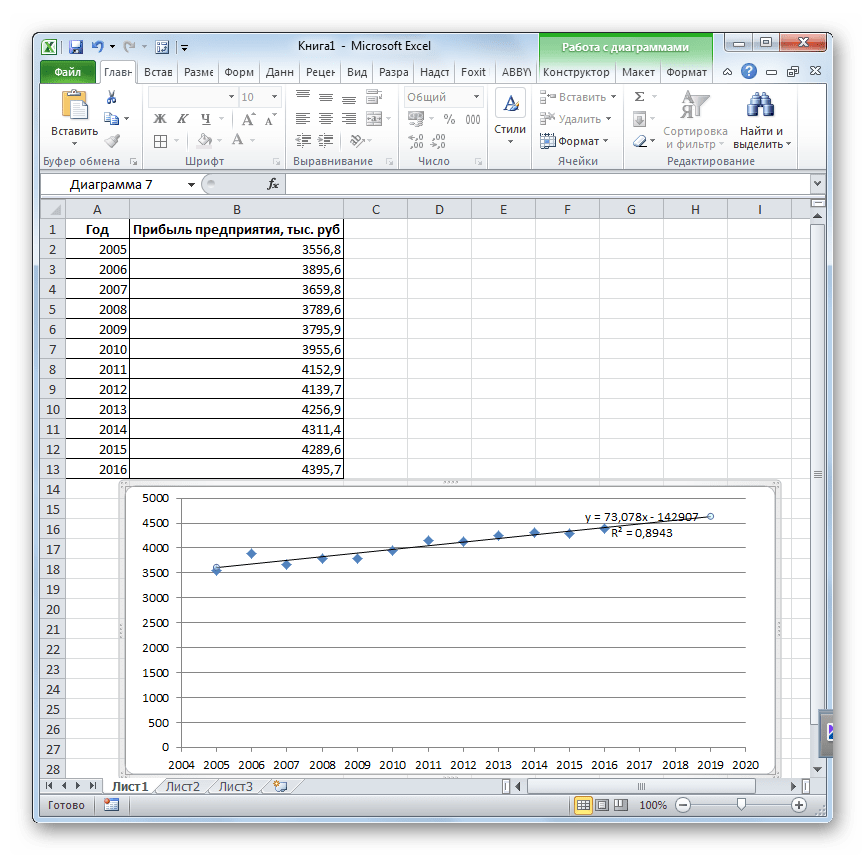
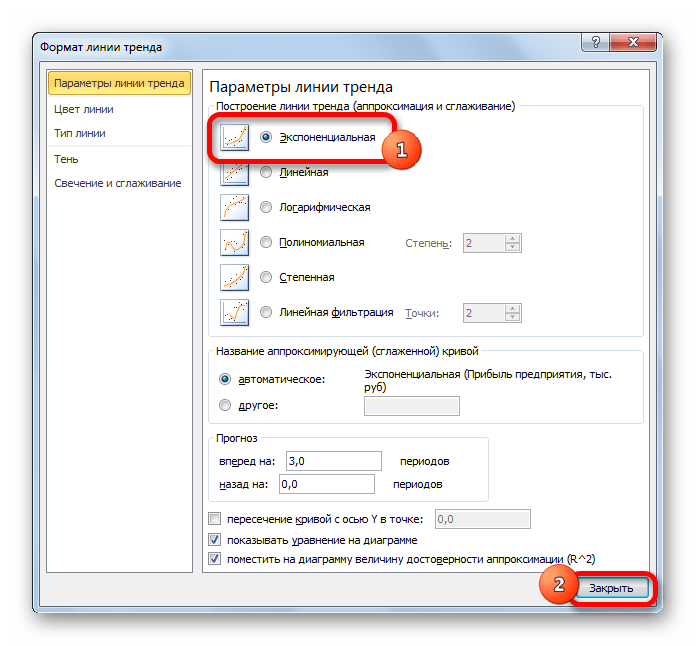
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
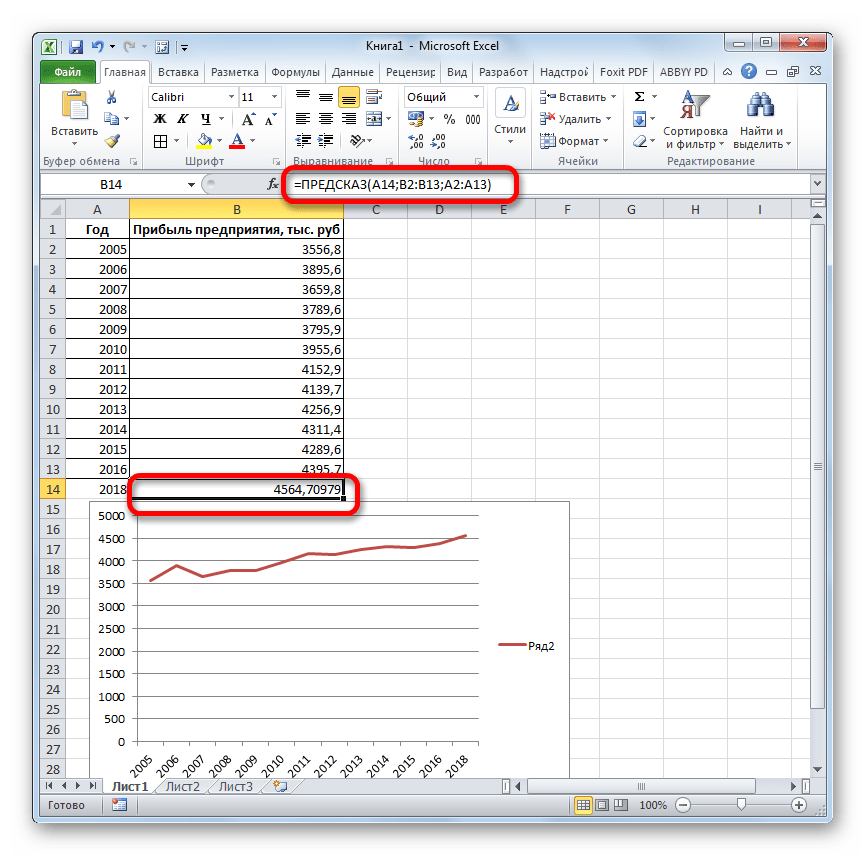
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Источник
-
Помогаю в написании дипломных, курсовых, магистерских работы по психологии, а также рефератов и эссе; контрольных, отчетов по практике и статистических расчетов.
Я профессиональный психолог и автор работ по психологии с многолетним стажем. Выступаю как индивидуальный предприниматель (ИП): заключаю договор, выдаю чеки об оплате.
Помогаю студентам-психологам более 15 лет (этот сайт существует с 2007). Качественно и быстро. Помогу даже с очень трудными темами.
Опишите ситуацию, и я скажу стоимость написания вашей работы.
Тестирование испытуемых для эмпирического исследования
Главные выводы курсовой, дипломной и магистерской работы по психологии основаны на результатах эмпирического исследования. Это исследование представляет собой сбор эмпирических данных, их качественный анализ и статистическую обработку. Эмпирические данные собираются с помощью психодиагностических методик – тестов. Какие же существуют способы тестирования испытуемых и обработки данных?
Таблица исходных данных (сводная таблица результатов психодиагностики)
Для проведения психологического тестирования группы испытуемых студент-психолог может распечатать текст опросников и раздать его испытуемым. Затем собрать заполненные бланки и обработать их по соответствующим ключам. Полученные результаты – показатели по шкалам тестов – заносятся в сводную таблицу результатов или таблицу исходных данных.
Сводная таблица результатов – это таблица, в которой каждая строчка связана с испытуемым, а каждый столбец отражает показатели по какой-то шкале теста.
Вот пример сводной таблицы исходных данных (таблицы психодиагностического обследования) испытуемых:
Таблица 1. Результаты психодиагностического обследования испытуемых
|
№ исп. |
Пол (1-м, 2-ж) |
Группа (1-К, 2-НК, 3-БК) |
Субъекти вная оценка своего здоровья |
Поведенческая компетентность в области здоровья |
Локус контроля в области здоровья |
Позитивный прогноз в отношении здоровья |
Отрица ние |
Подавле ние |
Регрес сия |
|
1 |
2 |
3 |
49 |
38 |
35 |
50 |
91 |
83 |
47 |
|
2 |
2 |
3 |
47 |
51 |
38 |
47 |
70 |
71 |
97 |
|
3 |
2 |
3 |
40 |
52 |
36 |
39 |
91 |
91 |
73 |
|
4 |
2 |
3 |
45 |
54 |
41 |
51 |
97 |
99 |
93 |
|
5 |
2 |
3 |
47 |
49 |
45 |
57 |
70 |
71 |
82 |
|
6 |
2 |
3 |
43 |
47 |
48 |
56 |
70 |
100 |
47 |
|
7 |
2 |
3 |
43 |
38 |
38 |
51 |
70 |
54 |
73 |
|
8 |
2 |
3 |
45 |
41 |
36 |
42 |
8 |
99 |
97 |
|
9 |
2 |
3 |
41 |
52 |
43 |
46 |
91 |
83 |
89 |
|
10 |
2 |
3 |
39 |
52 |
40 |
55 |
8 |
91 |
73 |
|
11 |
1 |
3 |
51 |
48 |
39 |
51 |
8 |
99 |
93 |
|
12 |
1 |
3 |
44 |
51 |
38 |
49 |
83 |
100 |
82 |
|
13 |
1 |
3 |
43 |
38 |
38 |
51 |
70 |
54 |
99 |
|
14 |
1 |
3 |
44 |
51 |
38 |
49 |
33 |
99 |
100 |
|
15 |
1 |
3 |
51 |
48 |
42 |
51 |
52 |
100 |
61 |
|
16 |
1 |
3 |
39 |
38 |
33 |
36 |
91 |
54 |
47 |
|
17 |
1 |
3 |
45 |
48 |
38 |
47 |
91 |
96 |
89 |
|
18 |
1 |
3 |
44 |
51 |
43 |
46 |
52 |
99 |
93 |
|
19 |
1 |
3 |
51 |
42 |
44 |
53 |
33 |
96 |
93 |
|
20 |
2 |
1 |
34 |
47 |
34 |
45 |
52 |
91 |
100 |
Текст опросников можно не распечатывать, а рассылать испытуемым в электронном виде в форме файлов Word. Но далее процедура обработки такая же, как и в случае печатных бланков психологических тестов.
Вот пример бланка, который раздается испытуемым в печатном виде (или рассылается в виде файла Word).
Инструкция: прочитайте каждое из приведённый предложений и зачеркните цифру в соответствующей графе справа в зависимости от того, как вы себя чувствуете в данный момент. Над вопросами долго не задумывайтесь, поскольку правильных и неправильных ответов нет.
|
№ |
Суждение |
Нет, это не так |
Пожалуй, так |
Верно |
Совершенно верно |
|
1 |
Я спокоен |
1 |
2 |
3 |
4 |
|
2 |
Мне ничто не угрожает |
1 |
2 |
3 |
4 |
|
3 |
Я нахожусь в напряжении |
1 |
2 |
3 |
4 |
|
4 |
Я внутренне скован |
1 |
2 |
3 |
4 |
|
5 |
Я чувствую себя свободно |
1 |
2 |
3 |
4 |
|
6 |
Я расстроен |
1 |
2 |
3 |
4 |
|
7 |
Меня волнуют возможные неудачи |
1 |
2 |
3 |
4 |
|
8 |
Я ощущаю душевный покой |
1 |
2 |
3 |
4 |
|
9 |
Я встревожен |
1 |
2 |
3 |
4 |
|
10 |
Я испытываю чувство внутреннего удовлетворения |
1 |
2 |
3 |
4 |
|
11 |
Я уверен в себе |
1 |
2 |
3 |
4 |
|
12 |
Я нервничаю |
1 |
2 |
3 |
4 |
|
13 |
Я не нахожу себе места |
1 |
2 |
3 |
4 |
|
14 |
Я взвинчен |
1 |
2 |
3 |
4 |
|
15 |
Я не чувствую скованности, напряжённости |
1 |
2 |
3 |
4 |
|
16 |
Я доволен |
1 |
2 |
3 |
4 |
|
17 |
Я озабочен |
1 |
2 |
3 |
4 |
|
18 |
Я слишком возбуждён, и мне не по себе |
1 |
2 |
3 |
4 |
|
19 |
Мне радостно |
1 |
2 |
3 |
4 |
|
20 |
Мне приятно |
1 |
2 |
3 |
4 |
Методика Ч.Д.Спилбергера на выявление ситуативной тревожности (адаптирована на русский язык Ю.Л.Ханиным)
Недостатки такого метода психологического тестирования и сбора эмпирических данных в его трудоемкости, так как обработку результатов по ключам приходится делать вручную. Оптимизировать обработку тестов по ключам можно при использовании электронных таблиц Excel.
Психологическое тестирование с помощью электронных таблиц Microsoft Excel
Приведенный выше тест на ситуативную тревожность можно провести таким образом, чтобы можно было обработку результатов тестирования по ключам сделать автоматически. Для этого необходимо перенести психологический тест в таблицу Excel:

Теперь ответы испытуемого, занесенные в таблицу, можно обработать средствами Excel. Для этого потребуются минимальные знания этого инструмента, которыми наверняка владеет каждый студент-психолог.
Ниже приведен пример проведения психологического тестирования с помощью электронных таблиц Microsoft Excel по Методике исследования самоотношения (МИС):

Испытуемому дается не печатный бланк или текстовый файл, а электронная таблица, в которой он отмечает цифрой «1» утверждения, с которыми согласен и с которыми не согласен.
Далее в соответствии с ключами суммируются ответы «да» и «нет» и определяются общие показатели по шкалам. Для суммирования используется стандартная функция Excel: СУММ (число1, число2, …..числоN):

Создав такую форму, ее можно посылать испытуемым много раз. Они будут заполнять ее сверху вниз, и в нижней части таблицы «сами собой» возникнут автоматически рассчитанные результаты респондента по шкалам теста МИС. Далее эти результаты нужно будет перенести в сводную таблицу результатов психодиагностики.
Однако и у этого метода есть свои недостатки. Если испытуемых много, то переносить результаты каждого в сводную таблицу становится довольно утомительной процедурой. Решить эту проблему можно следующим образом.
Для примера рассмотрим проведение психодиагностического обследования по тесту Смысложизненных ориентаций (СЖО) Д.А. Леонтьева с помощью электронных таблиц Excel.

В той таблице в каждой строке приводятся данные по одному испытуемому. Сначала они переводятся в шкалу от -3 до 3, которая не показана в исходном варианте теста, чтобы не указывать респонденту какой полюс шкалы положительный, а какой отрицательный.
Далее данные обрабатываются с учетом обратных шкал. И, наконец, в финальной табличке справа данные суммируются в соответствии с ключами и получаются результаты каждого испытуемого по шкалам.
Достоинство этого метода в том, что нет необходимости переносить результаты каждого испытуемого в сводную таблицу психодиагностики – она формируется сама собой. Фактически таблица справа с результатами по шкалам и представляет собой часть сводной таблицы.
Однако недостаток этого метода в том, что эту таблицу не пошлешь каждому респонденту для заполнения – она не выглядит как тест. Этот метод можно использовать в случае, когда результаты проведенного на печатных бланках тестирования затем переносятся в электронные таблицы Excel.
И все же хотелось, чтобы и психологический тест для испытуемых выглядел презентабельно и результаты его автоматически обрабатывались, создавая таблицу исходных данных (сводную таблицу психодиагностики) для дальнейшей обработки в рамках качественного и статистического анализа психологических данных.
И эта задача может быть решена с помощью современного инструмента от Гугл — Google Form.
Психологическое тестирование и обработка результатов с использованием Google Form
Использование Google Form для психологического тестирования предполагает реализацию следующих этапов:
- Создание Гугл-Формы по соответствующему тесту. То есть, необходимо перенести все вопросы психологического теста и ответы на них в формат Гугл-формы.
- Результаты заполнения формы попадают в таблицу Excel. В этой таблице необходимо перевести текстовые ответы в численные, а также создать шаблон расчета результатов по ключам (см., как это было сделано выше по тесту СЖО).
Этот метод достаточно трудоемкий при первом обращении к психологическому тесту. Однако, когда Гугл-форма для психологического теста создана, она затем может использоваться многократно, что делает процесс тестирования и подсчета результатов психологического тестирования автоматическим. И, что очень важно, респонденты проходят тестирование онлайн в комфортном и современном интерфейсе.
Вот пример Google Form для тестирования по методике диагностики ситуативной тревожности:


Таким образом, использовать Google Form для психологического тестирования и обработки результатов имеет смысл только при проведении более или менее масштабных исследований.
С другой стороны, даже при проведении несложного психологического исследования можно использовать Гугл формы, что позволит освоить современную и эффективную программу.
Надеюсь, эта статья поможет вам самостоятельно написать диплом по психологии. Если возникнет необходимость, обращайтесь, помогу (все виды работ по психологии; статистические расчеты). Заказать
РМО педагогов-психологов г.Лысково и Лысковского района
ТЕХНИКИ В РАБОТЕ ПЕДАГОГА-ПСИХОЛОГА
Мастер-класс 15 мая 2019 года
Муниципальное бюджетное общеобразовательное учреждение
средняя школа №2 г.Лысково
МАСТЕР-КЛАСС
ДЛЯ ПЕДАГОГОВ-ПСИХОЛОГОВ Г.ЛЫСКОВО И
ЛЫСКОВСКОГО РАЙОНА
ПО ТЕМЕ
«Обработке результатов диагностики в программе Excel»
подготовила:
педагог-психолог Шутова И.Ю.
г.Лысково
15 мая 2018
Цель: передать участникам мастер-класса «инновационные продукты», полученные в результате творческой, экспериментальной деятельности педагога-психолога.
Задачи:
- создание условий для профессионального общения, самореализации и стимулирования роста творческого потенциала педагогов-психологов;
- повышение профессионального мастерства и квалификации участников;
- распространение передового педагогического опыта;
- внедрение новых технологий обучения.
Материалы:
- Компьютеры;
- Бумага А4.
Ход мастер-класса
Здравствуйте уважаемые коллеги. Я рада приветствовать вас.
Наша работа будет подвигаться по данному плану:
— Ознакомление с возможностями программы Excel
— Обработка результатов теста в программе Excel
— Помощь участникам в возможности самостоятельно обработать результаты
— Анализ (рефлексия)
Упражнение 1.
«Улыбка»
Психолог: «Давайте подарим, друг другу радость и улыбку, ведь улыбка поднимает всем настроение. (Педагоги-психологи становятся в круг, берутся за руки, улыбаются друг другу).
Вступительная часть
Использование информационно – компьютерных технологий становится неотъемлемой частью образовательного процесса. Работа педагога-психолога не является здесь исключением. При этом, применяемые компьютерные технологии, органично дополняют традиционные методы, в том числе, расширяют возможности взаимодействия психолога с другими участниками образовательного процесса (педагогами, родителями и детьми).
Большие возможности для психолога в плане проведения тестирования и последующей обработки данных имеет программа Excel. Существуют программные продукты, например, «Excel на службе у психолога(автоматическая обработка тестов) v.09.08.24» Это программа автоматической обработки профессиональных психологических тестов в Excel. В нее включено более 40 профессиональных психодиагностических методик. Предназначена для психологов и всех интересующихся практической психодиагностикой. Выбор Excel обусловлен ее доступностью — она по умолчанию входит в стандартный пакет Microsoft Office, а также обладает широким спектром возможностей для работы с массивами данных.
Но у школьного психолога частые случаи, когда необходимо диагностировать целый класс и обработка результатов занимает огромное количество времени. В этом случае я рекомендую создать собственный обработчик, где возможно учесть быстрый подсчет результатов на весь класс и вывести проценты.
На примере опросника школьной мотивации «Оценка школьной мотивации учащихся начальной школы» (методика Н.Г. Лускановой) покажу как быстро обработать результаты в обработчике.
Переходим к практической части.
Для этого нужно создать обработчик для данного опросника в Excel:
Подписываю столбцы и строки необходимых данных.
Чтобы подсчитать сумму нужно в строке форму ввести формулу подсчета:
Для этого нужно выбрать необходимые столбцы и строчки (правильность можно проверить). Клетки начинают выделяться цветом.
Далее вводим данные с опросника и выводим уровень мотивации:
Научиться правильным формулам достаточно легко, вставляя значки и данные, которые хотим получить.
Так мы узнаем уровень мотивации у каждого ученика, данные которого ввели в программу.
Благодаря возможностям программы мы можем подсчитать количество и вывести в процентах. Для этого тоже вводим в строку формул необходимую формулу с данными.
Можно получить проценты по каждому уровню мотивации от общего количества учащихся. Если ввести данные «нет», то можно посчитать процент от количества участников прошедших тестирование. То есть получим более точные данные.
Программа удобна в том, что можно готовые результаты можно вставлять в статистические справки для отчетности.
Совместная работа по созданию обработчика для личного использования в работе.
Анализ проведенной работы
Этот обработчик — готовый протокол для целого класса. Так можно обработать тест числовыми значениями, например, методику исследования словесно-логического мышления (методика разработана Э. Ф. Замбацявичене на основе теста структуры интеллекта Р. Амтхауэра).
Уважаемые коллеги, я вам продемонстрировала возможности использования в работе программы Excel. Данные возможности я использую в своей работе и с уверенностью могу сказать, что работа в данной программе значительно сокращает время обработки результатов тестов, освобождая время для образовательного процесса.
Считаю, что мастер-класса достиг цели и вы научились работать в данной программе при обработке методик.
Упражнение 2.
И в завершении хочу предложить вам такое упражнение.
Положите обе руки к груди и послушайте как стучит сердце: «Тук-тук, тук-тук». От этого становится тепло и приятно и вот это уже не помещается только в вас, поделитесь с коллегами, улыбнитесь им.
Покажите руки. В правую положите все то с чем вы сюда пришли – опыт, багаж знаний. А в левую положите все то, что нового получили на мастер-классе.
Громко хлопнем в ладоши и одновременно скажем: «Ура!»
Мне остается поблагодарить вас за работу и пожелать вам здоровья!
Приложение 1
Стимульный материал методики
1.Тебе нравится в школе?
-не очень
-нравится
-не нравится
2.Утром, когда ты просыпаешься, ты всегда с радостью идешь в школу или тебе часто хочется остаться дома?
-чаще хочется остаться дома
-бывает по-разному
-иду с радостью
3.Если бы учитель сказал, что завтра в школу не обязательно приходить всем ученикам, желающим можно остаться дома, ты бы пошел бы в школу или остался бы дома?
-не знаю
-остался бы дома
-пошел бы в школу
4.Тебе нравится, когда у вас отменяют какие-нибудь уроки?
-не нравится
-бывает по-разному
-нравится
5.Ты хотел бы, чтобы тебе не задавали домашних заданий?
-хотел бы
-не хотел бы
-не знаю
6.Ты хотел бы, чтобы в школе остались одни перемены?
-не знаю
-не хотел бы
-хотел бы
7.Ты часто рассказываешь о школе родителям?
-часто
-редко
-не рассказываю
8.Ты хотел бы, чтобы у тебя был менее строгий учитель?
-точно не знаю
-хотел бы
-не хотел бы
9.У тебя в классе много друзей?
-мало
-много
-нет друзей
10.Тебе нравятся твои одноклассники?
-да
-не очень
-нет
Обработка результатов
Ответы на вопросы анкеты расположены в случайном порядке, поэтому для упрощения оценки может быть использован специальный ключ. В итоге подсчитывается набранное количество баллов.
№ вопроса Оценка за 1 ответ Оценка за 2 ответ Оценка за 3 ответ
1 1 3 0
2 0 1 3
3 1 0 3
4 3 1 0
5 0 3 1
6 1 3 1
7 3 1 0
8 1 0 3
9 1 3 0
10 3 1 0
Интерпретация результатов
1. 25-30 баллов (очень высокий уровень) — высокий уровень школьной мотивации, учебной активности. Такие дети отличаются наличием высоких познавательных мотивов, стремлением наиболее успешно выполнять все предъявляемые школой требования. Они очень четко следуют всем указаниям учителя, добросовестны и ответственны, сильно переживают, если получают неудовлетворительные оценки или замечания педагога.
2. 20-24 балла – (высокий уровень) хорошая школьная мотивация. Подобные показатели имеют большинство учащихся начальных классов, успешно справляющихся с учебной деятельностью. Подобный уровень мотивации является средней нормой.
3. 15 – 19 баллов – (средний уровень) положительное отношение к школе, но школа привлекает больше внеучебными сторонами. Такие дети достаточно благополучно чувствуют себя в школе, однако чаще ходят в школу, чтобы общаться с друзьями, с учителем. Им нравится ощущать себя учениками, иметь красивый портфель, ручки, тетради. Познавательные мотивы у них сформированы в меньшей степени и учебный процесс их мало привлекает.
4. 10 – 14 баллов – (низкий уровень) низкая школьная мотивация. Подобные школьники посещают школу неохотно, предпочитают пропускать занятия. На уроках часто занимаются посторонними делами, играми. Испытывают серьезные затруднения в учебной деятельности. Находятся в состоянии неустойчивой адаптации к школе.
5. Ниже 10 баллов – (очень низкий уровень) негативное отношение к школе, школьная дезадаптация. Такие дети испытывают серьезные трудности в школе: они не справляются с учебной деятельностью, испытывают проблемы в общении с одноклассниками, во взаимоотношениях с учителем. Школа нередко воспринимается ими как враждебная среда, пребывание в которой для них невыносимо. Маленькие дети (5 – 6 лет) часто плачут, просятся домой. В других случаях ученики могут проявлять агрессивность, отказываться выполнить те или иные задания, следовать тем или иным нормам и правилам. Часто у подобных школьников отмечаются нарушения нервно – психического здоровья.