Обработка опытных данных в excel

---

Статьи
Карта сайта
Главная страница

 

Ввод текста помогает оформлять заголовки таблиц, записывать
определенные пояснения. Допустим, нам надо рассчитать объем раствора по его
массе 10 г и плотности 1,25 г/мл, используя простейшую формулу V=m/d. Введем
в ячейки В5, С5, D5 заголовки столбцов будущей таблицы,
обозначения величин m, d и V, и приступим к вводу чисел. В
ячейку В6 введем численное значение массы 10. Заканчиваем ввод, нажимая Enter, и убеждаемся, что тест в ячейке, как правило, смещен к правой границе, а число к левой. Это удобно, так как позволяет замечать ошибки
ввода. В ячейку С6 введем дробное число 1,25. Здесь надо учесть, что в
зависимости от настройки конкретного компьютера для разделения целой и дробной
части числа может использоваться или запятая, или точка. При неправильном вводе
наши символы будут восприниматься как текст,  или даже как дата (янв.25).

Наконец, в ячейке D6 введем формулу, по
которой Excel будет проводить вычисления. Ввод формулы начинается со знака
равенства (=). Затем надо показать программе, где находится первое число в
нашей формуле, масса раствора, дать адрес этой ячейки  — В6. Конечно, можно
набрать этот адрес с клавиатуры, надо только учитывать, что В – это символ
английского алфавита. Поэтому, гораздо проще просто щелкнуть по нужной ячейке и
ее адрес будет введен автоматически (=В6). Далее надо ввести знак
арифметического действия. Эти знаки удобно вводить с правой части клавиатуры,
напоминающей клавиатуру калькулятора. Здесь есть клавиши со знаком сложения
(+), вычитания (-), умножения (*) и деления (/). И, наконец, надо показать
компьютеру, где находится делитель – щелкаем мышкой по ячейке С6 и получаем
окончательный вид формулы (=В6/С6). Нажимаем Enter, и,
если все было набрано правильно, получаем в ячейке D6 результат
(8). Таким образом, формулы возвращают в ячейку результат вычислений, число. Но
если щелкнуть по ячейке и посмотреть на строку формул, мы увидим, что на самом
деле находится в ней.

Иногда формула может возвращать и сообщение об ошибке. Щелкнем
по ячейке В6 и введем вместо числа 10 символы «10 г». В ячейке D6
тут же окажется сообщение #ЗНАЧ!, которое говорит о
неверном значении в одной из ячеек. Действительно, запись «10 г» воспринимается
уже как текст. Чтобы исправить ошибку надо снова вместо «10 г»  ввести число
10. (Для исправления неверных действий можно использовать и кнопку «Отменить»
на панели инструментов). Щелкнем теперь по ячейке С6 и нажмем клавишу “Del”. Этим мы удалим содержимое ячейки, и в соседней ячейке
тут же получим сообщение #ДЕЛ/0! (ошибка деления на 0). Действительно,
на ноль делить нельзя и ошибку надо исправить.

Итак, мы научились вводить числа и формулы, а значит и проводить
простейшие вычисления в Excel. Но как упростить эту процедуру, если таких
вычислений много? Здесь помогают приемы копирования, и автоматического
заполнения ячеек методом «протягивания». Пусть у нас 10 порций раствора массой 10 г, и в ячейки В6, В7 …, В16 надо ввести 10, 10, … и т.д. Щелкнем по ячейке В6, где число 10 уже
введено. В черной рамке выделенной ячейки, внизу справа, есть маленький черный
квадратик. При наведении на него указателя мышки, последний меняет форму. Если
в этот момент «взяться» (нажать левую кнопку мыши) и потянуть вниз, до ячейки
В16, то все десять ячеек окажутся автоматически заполнены нужным числом. Не
труднее заполнить и 100 ячеек!

А если массы растворов отличаются на некоторую постоянную
величину, например 10, 12,5, 15 г и т.д.? В этом случае достаточно ввести два
значения: число 10 в ячейку В6 и число 12,5 в ячейку В7. Теперь надо выделить
эти две ячейки. Для этого щелкаем по первой ячейке и, не отпуская кнопки, ведем
до второй. Теперь обе ячейки обведены жирной рамкой. Снова беремся за черный
квадратик и тянем вниз. Получаем ряд значений от 10 до 35.

Поскольку предполагается, что раствор у нас один и тот же,
оставим колонку С в покое и попробуем методом протягивания скопировать формулу,
которая у нас набрана в ячейке D6. Проделываем уже
описанную операцию: выделяем ячейку, беремся, протягиваем… и получаем во всех
ячейках, кроме первой, ошибку! Разберемся, почему это произошло, для чего
щелкнем по ячейке D7 и посмотрим на строку формул. В
ячейке D6 было написано «=В6/С6», а в ячейке D7 уже «=В7/С7»! То есть, при копировании формул Excel
автоматически меняет адреса ячеек, откуда он берет данные для расчетов. И это
совершенно правильно, когда речь идет о массе раствора. Но плотность раствора у
нас постоянная, как показать программе, что адрес этой ячейки менять не надо?

Для этого мы должны познакомиться с такими понятиями, как
относительный и абсолютный адрес. Те адреса, которые мы использовали,
называются относительными и меняются при копировании. Адрес в абсолютной форме
сопровождается знаками доллара и выглядит так: $C$6. Вот
эту поправку нам и надо внести в формулу в ячейке D6.

Исправлять записи в ячейках удобнее в строке формул. Щелкнем
сначала по ячейке D6, (формула появится в строке
формул), затем в нужном месте строки формул – там появится курсор. Конечно
знаки доллара можно ввести с клавиатуры, но проще, установив курсор на адресе
С6, нажать на клавиатуре клавишу F4. Понажимайте ее
несколько раз и посмотрите, как будет меняться адрес. Он может быть полностью
абсолютным, абсолютным по строчке, по колонке, и полностью относительным.
Добейтесь нужного вида и нажмите Enter. Формула
исправлена, теперь ее снова можно протянуть до ячейки D16.
Если все сделано правильно, вы получите ряд значений от 8 до 28 мл.

Итак, если Вы не только прочитали, но и проделали все, о чем шла
речь выше,  Вы научились многому. Вы умеете вводить текст, числа и формулы,
вносить исправления, устранять ошибки, копировать и заполнять ячейки рядами
данных. Не мешает сохранить результаты своей работы. Процедуры сохранения файла
и его открытия полностью совпадают с работой в Worde и не должны вызвать у Вас затруднений.

Формулы с
функциями.

Но в наших расчетах использовались только простейшие
арифметические действия. Для более сложных расчетов нужно научиться
использовать функции. Этим мы займемся на втором листе нашей книги.

Для перехода на нужный лист достаточно щелкнуть по его ярлычку.
Начнем работу с краткого повторения пройденного: дадим листу 2 имя «Ошибки», в
ячейку А3 введем текст «Данные эксперимента», в ячейки А5 и В5 — заголовки
новой таблицы «№» и «Х». Предполагается что мы проделали серию из 10 опытов,
измеряя некоторую величину Х (здесь не важно, что это, длина побега или объем
раствора). Номера опытов от 1 до 10 легко ввести протягиванием, а вот численные
значения Х надо последовательно ввести (табл.1).

Таблица 1. Примерный вид листа
«Ошибки»

Записи в колонках D и
Е – это подсказки, которые помогут разобраться с тем, какие характеристики мы
будем рассчитывать. Колонка F у
Вас должна быть пока пустой, в нее будем помещать наши формулы.

Обработку результатов начнем с расчета числа опытов n. Казалось бы это очевидное число, но в ходе работы, какой-то
результат мы можем отбросить, или провести еще пару опытов. Желательно, чтобы
нам не пришлось при этом переделывать все формулы. Для определения числа
значений используется специальная функция, которая называется СЧЕТ. Для ввода
формулы с функциями используется Мастер функций, который запускается командой
«Вставка функции» через меню «Вставка» – «Функция» или кнопкой на панели
инструментов с обозначением   f_x. Щелкнем мышкой по ячейке F6,
где должен находиться результат и запустим Мастер функций.

Первый шаг работы (рисунок 1) служит
для выбора нужной функции. Все функции разделены, в зависимости от своего
назначения на несколько категорий (математические, логические и др.). Для
обработки данных эксперимента используются в основном статистические функции.
Поэтому, прежде всего в списке категорий выбираем категорию «Статистические».
Во втором окне появляется список статистических функций. Если щелкнуть по любой
из них, внизу появляется краткое описание функции. Специальной ссылкой можно
вызвать систему помощи Excel, в которой данная функция будет разобрана
подробно, с примерами. Список функций упорядочен по алфавиту, что позволяет без
труда нужную нам функцию СЧЕТ («Подсчитывает количество чисел в списке
аргументов»). Выделив щелчком эту функцию, нажимаем кнопку Ok и переходим к шагу 2.

Второй шаг (рисунок 2) служит для задания аргументов функции. 
Функции СЧЕТ надо указать, какие числа ей надо пересчитывать, или в каких
ячейках находятся эти числа. Диапазон ячеек указывается адресами первой и
последней ячейки, записанными через двоеточие, в нашем случае данные находятся
в ячейках В6:В15. Как и в других случаях эти адреса лучше не вводить, а показать
мышкой. Для этого устанавливаем указатель мышки на первую ячейку, нажимаем
левую кнопку и ведем до последней. Обратите внимание, что окно аргументов можно
перемещать, если оно заслоняет нужную часть экрана. Кроме того, рядом с полем
для ввода есть маленькая кнопка с красной стрелочкой. При щелчке по ней окно
аргументов сворачивается до узкой полоски. Когда мы показываем в основном окне
диапазон ячеек, в окне аргументов появляется запись диапазона адресов, а рядом
с ним – значения чисел из первых ячеек. Предварительное значение функции тоже
показывается после ввода ее аргументов. Это помогает избегать ошибок. Помогает
работе с мастером функций и подсказка под полем для ввода аргументов, в которой
разъясняется их смысл и возможные значения. Заканчивается работа с мастером
функций нажатием кнопки “Ok” или клавиши “Enter”. Если все сделано правильно, в ячейке F6 появится нужное значение “10”.

Следующие два этапа обработки серии опытов проводятся
аналогично. В ячейке F7 c
помощью функции СРЗНАЧ рассчитывается
среднее значение выборки, в ячейке F8 – стандартное
отклонение выборки, с помощью функции СТАНДОТКЛОН.
. Будьте аккуратны при выборе функций
– среди них есть очень похожие по названию. Аргументами этих функций служит все
тот же диапазон ячеек.

Следующая формула сложная, частично она набирается как обычная
формула, начиная с символа ”=”. Указав, где находится делимое S и набрав знак операции (=F8/), вызываем
мастер функций. Функция КОРЕНЬ – математическая, поэтому на первом шаге
выбираем категорию математических функций. Аргументом этой функции служит число
опытов, которое мы рассчитали в ячейке F6. Окончательный
вид формулы “=F8/ КОРЕНЬ(F6)”.

Для расчета доверительного интервала необходимо определить
коэффициент Стьюдента. Он зависит от вероятности ошибки (при обычно задаваемой
надежности 95% вероятность ошибки составляет 5%), и от числа степеней свободы n-1). Для нахождения коэффициента Стьюдента используется
статистическая функция Excel СТЬЮДРАСПОБР (“Стьюдента распределение обратное“).
Особенностью этой функции является то, что первый аргумент, число 5% (или 0,05)
вводится в соответствующее окно с клавиатуры. Для второго указываем адрес
ячейки, где находится значение n,
затем дописываем в окне “-1”. Получаем запись “F6-1”.

Для нахождения
доверительного интервала используется обычная формула умножения. Конечно,
вместо букв там должны стоять адреса ячеек, где находятся коэффициент Стьюдента
и стандартное отклонение среднего. Как правило, значение доверительного
интервала округляется до одной значащей цифры, такой же порядок окружения
должен быть и у среднего. Поэтому окончательный результат можно записать так: с
95%-ной надежностью Х = 14,80±0,05. В заключение посчитаем относительную ошибку определения Х: d = ДИ / Х_ср (формула: “=F11/F7”).
Значение относительной ошибки обычно выражают в процентах, у нас 0,3%.

Если Вы впервые
работаете в Excel, описанная процедура обработки данных эксперимента может
показаться очень сложной.  Но на практике, вводить формулы, с помощью мастера
функций, ничуть не сложнее, чем обычные арифметические. К тому же, один раз
подготовив лист Excel для обработки данных, можно скопировать его, и ввести
результаты новой серии опытов в колонку В. Результаты будут тут же рассчитаны
автоматически.

Изучение
зависимостей.

Часто в исследованиях изучается зависимость некоторой величины
от другой. Характер этих зависимостей стремятся выразить математическими
формулами, коэффициенты которой могут иметь определенный физический смысл.
Наиболее употребительна и проста в обработке линейная зависимость, которую
можно выразить уравнением прямой у = kx + b. При этом коэффициент k показывает
степень влияния х на у, а b – некоторое
начальное значение у. Поскольку значения, полученные в ходе эксперимента,
всегда включают некоторую ошибку,  экспериментальные точки не лежат строго на
прямой. Как же провести по этим разбросанным точкам наилучшую линию. Для этого
используется статистический метод «наименьших квадратов» предлагающий
достаточно сложные функции для нахождения коэффициентов k и b, а также для оценки их
достоверности.

В Excel эта
задача решается при помощи статистических функций НАКЛОН (наклон прямой
относительно оси Х, коэффициент k) и ОТРЕЗОК  (отрезок
отсекаемый прямой на оси Y, коэффициент b). Кроме того, Excel позволяет
построить график зависимости, саму прямую, которая называется линией тренда, а
также вывести уравнение прямой на график.

Для знакомства с этим возможностями перейдем на Лист 3 нашей
книги, назовем его «Зависимость» и введем необходимые исходные данные (таблица
2).

Таблица 2. Примерный вид листа
«Зависимость»

В колонках В и С вводятся данные эксперимента по измерению
величин Х и У, записи в колонке Е играют роль подсказок, колонка F заполняется по мере обработки.
Начнем с ячейки F3.

Ввод формул проводится с помощью мастера функций так, как это
описывалось ранее. Маленькое отличие заключается в том, что у функций НАКЛОН и ОТРЕЗОК два
аргумента: диапазон ячеек со значениями Y и диапазон ячеек со значениями Х.
Щелкаем мышкой сначала по полю для ввода первого аргумента, показываем нужный
диапазон (С3:С13). Затем щелкаем по второму поля и повторяем ввод (В3:В13).
Также рассчитывается и значение функции ОТРЕЗОК в ячейке F4.

Для оценки достоверности можно использовать квадрат коэффициента
корреляции Пирсона (R²). Если он равен 1, то
имеет место полная корреляция с моделью, т.е. точки лежат строго на прямой. В
противоположном случае, если коэффициент  равен 0, то уравнение линейной
зависимости полностью неудачно. Для его нахождения используется статистическая
функция КВПИРСОН. Таким образом, данные
нашего эксперимента с достоверностью 0,98 описываются уравнением у = 1,42х+0,905.

Рассмотрим теперь второй метод обработки и представления
результатов эксперимента в виде графика. Для построения графиков и диаграмм в Excel’e используется
Мастер диаграмм, который можно запустить, используя меню Вставка – Диаграмма,
или кнопки на панели инструментов с условным изображением диаграммы.
Предварительно щелкнем мышкой по любой свободной ячейке нашего листа.

Рисунок 3. 

На первом шаге (рисунок 3) выбирается тип и вид диаграммы. Для
построения графика зависимости одной величины от другой используются точечные
диаграммы, причем лучше (из-за разброса точек) выбирать вид «Точки не
соединенные линиями». Заканчиваем выбор, щелкая по кнопке «Далее».

На втором шаге необходимо указать, где у нас находится
независимая величина Х и зависящая от нее Y (рисунок 4).
Для этого щелкаем по ярлычку вкладки «Ряд» и затем по кнопке «Добавить».

Рисунок 4.

Открываются поля для указания Х и Y. Ввод
значений адресов в эти поля не отличаются от работы с Мастером функций (только
при вводе Y предварительно
сотрите условное значение “={1}”. Если Вы правильно выполните эту часть работы,
на поле вверху уже появится примерный вид графика.

Следующие два шага имеют отношение к оформлению и размещению
графика. На первый раз можно, ничего не меняя, просто нажимать кнопки «Далее» и
«Готово». Полученный черновой вариант графика всегда можно редактировать,
изменять или удалять его отдельные элементы. Обычно для этого щелкают по
нужному элементу графика правой (!) кнопкой мышки. При этом открывается
контекстное меню, в котором выбирают подходящую команду.

Если правой кнопкой мышки щелкнуть по одной из точек графика, то
в контекстном меню можно увидеть команду «Добавить линию тренда». Это и есть
необходимая нам линия. Добавляется она тоже в два шага. На первом выбирается
тип (линейный), на втором – параметры. На вкладке Параметры нам важно поставить
галочки против слов: «показывать уравнение» и «поместить величину
достоверности». Если из теоретических предпосылок понятно, что прямая должна
проходить через начало координат (при нулевой концентрации скорость реакции,
очевидно, равна нулю) поставим галочку и в данном пункте. Примерный вид графика
после добавления линии тренда представлен на рисунке 5. Выведенное уравнение
прямой и величины достоверности совпадает с рассчитанными ранее.

Рисунок 5.

Итак, мы рассмотрели важнейшие приемы работы в Microsoft Excel, необходимые для качественной
обработки данных эксперимента. Разумеется эти приемы не исчерпывают всех
возможностей Excel, и могут развиваться в ходе работы.
Автор статьи с удовольствием ответит на все вопросы, связанные с работой в
данной программе. Желаю успеха!

Задать вопрос.

---

1. Статистический анализ. основные понятия и определения

1.1 Математическая статистика

Математическая статистика – наука,
изучающая методы исследования закономерностей в массовых случайных явлениях и
процессах по данным, полученным из конечного числа наблюдений за ними, с целью
получения вероятностно-статистических моделей случайных явлений. Построенные на
основании этих методов закономерности относятся не к отдельным испытаниям, из
повторения которых складывается данное массовое явление, а представляют
утверждения об общих вероятностных характеристиках данного процесса. Такими
характеристиками могут быть вероятности, плотности распределения вероятностей,
математические ожидания, дисперсии и т. п. Найденные характеристики позволяют
построить вероятностно-статистическую модель изучаемого явления. Применяя к
этой модели методы теории вероятностей, исследователь может решать
технико-экономические задачи, например, определять вероятность безотказной
работы агрегата в течение заданного отрезка времени. Таким образом, теория
вероятностей по вероятностной модели процесса предсказывает его поведение, а
математическая статистика по результатам наблюдений за процессом строит его
вероятностностатистическую модель. В этом состоит тесная взаимосвязь между
данными науками. Очевидно, что для обнаружения закономерностей случайного
массового явления необходимо провести сбор статистических сведений, т. е.
сведений, характеризующих отдельные единицы каких-либо массовых явлений.

В математической статистике
рассматриваются две основные категории задач: оценивание и статистическая
проверка гипотез. Первая задача разделяется на точечное оценивание и
интервальное оценивание параметров распределения. Например, может возникнуть
необходимость по наблюдениям получить точечные оценки параметров М(Х) и D(Х) .
Если мы хотим получить некоторый интервал, с той или иной степенью достоверности
содержащий истинное значение параметра, то это задача интервального оценивания.
Вторая задача – проверка гипотез – заключается в том, что мы делаем
предположение о распределении вероятностей случайной величины (например, о
значении одного или нескольких параметров функции распределения) и решаем,
согласуются ли в некотором смысле эти значения параметров с полученными
результатами наблюдений.

Если интересующая нас совокупность слишком многочисленна,
либо ее элементы малодоступны, а также, если имеются другие причины
(организационные, финансовые, физические и т. п.), не позволяющие изучать сразу
все ее элементы, прибегают к изучению какой-то части этой совокупности. Эта
выбранная для полного исследования группа элементов называется выборкой или выборочной
совокупностью.

Выборка – это группа элементов, выбранная для исследования из
всей совокупности элементов. Задача выборочного метода в том, чтобы сделать
правильные выводы относительно всего собрания объектов, их совокупности.

Конечной целью изучения выборочной совокупности всегда
является получение информации о генеральной совокупности. Поэтому естественно
стремиться сделать выборку так, чтобы она наилучшим образом представляла всю
генеральную совокупность, то есть была бы репрезентативной или представительной.
Для получения репрезентативной выборки необходимо четко определять, что
понимается под генеральной совокупностью. Ее состав и численность зависят от
объектов и целей проводимого исследования.

В тех случаях, когда генеральная совокупность недостаточно
известна, обычно не удается предложить лучшего способа получения
представительной выборки, чем случайный выбор. При этом случайная выборка
формируется случайным отбором: из генеральной совокупности наудачу извлекается
по одному объекту.

В практических задачах закон распределения случайных величин
обычно неизвестен или известен с точностью до некоторых неизвестных параметров.
В частности, невозможно рассчитать точное значение соответствующих
вероятностей, так как нельзя определить количество общих и благоприятных
исходов. Поэтому вводится статистическое определение вероятности. По этому
определению вероятность равна отношению числа испытаний , в которых событие
появилось, к общему количеству произведенных испытаний . Такая вероятность называется
статистической частотой.

В результате на практике сведения о законе распределения
случайной величины получают независимыми многократными повторениями опыта, в
котором измеряются значения интересующей исследователей случайной величины
(варианты). На основе информации из полученной выборки можно построить
приблизительные значения для функции распределения и других характеристик
случайной величины.

Числа, составляющие генеральную совокупность, называются ее
элементами. Закон F(x) распределения случайной величины X называется
генеральным законом распределения, а числовые характеристики X – генеральными
числовыми характеристиками. Так как генеральная совокупность – большая, то
перебрать все ее элементы невозможно, поэтому для изучения генеральной совокупности
из нее делают выборку и по ее свойствам судят о свойствах генеральной
совокупности.

Выборкой называется множество измеренных значений n x ,x
,…,x 1 2 случайной величины X. Выборки разделяются на повторные (с
возвращением) и бесповторные (без возвращения). Требования к выборке. Для того
чтобы сделать правильный вывод о генеральной совокупности по выборке, выборка
должна быть репрезентативной, т. е. правильно представлять генеральную
совокупность. Выборка будет обладать таким свойством, если каждый объект
генеральной совокупности будет иметь один и тот же шанс быть выбранным, в этом
случае выборка является случайной. Число N объектов генеральной совокупности и
число n объектов выборки называют объемами генеральной и выборочной
совокупностей соответственно.

Кумулятивная кривая будет получена, если по оси абсцисс
откладывать интервалы, а по оси ординат – число или долю элементов
совокупности, имеющих значение, меньшее или равное заданному.

При увеличении до бесконечности размера выборки выборочные
функции распределения превращаются в теоретические: гистограмма превращается в
график плотности распределения, а кумулятивная кривая – в график функции
распределения.

В Microsoft Excel для построения выборочных функций распределения используются специальная
функция ЧАСТОТА и процедура Пакета анализа Гистограмма. Функция ЧАСТОТА
вычисляет частоты появления случайной величины в интервалах значений и выводит
их как массив чисел. Функция задается в качестве формулы массива.

Синтаксис: ЧАСТОТА (массив данных; массив карманов), где массив
данных – это массив или ссылка на множество данных, для которых вычисляются
частоты; массив карманов – это массив или ссылка на множество интервалов, в
которые группируются значения аргумента массив данных .

Количество элементов в возвращаемом массиве на единицу больше
числа элементов в массив карманов. Дополнительный элемент в возвращаемом
массиве содержит количество значений, больших, чем максимальное значение в
интервалах.

Процедура Гистограмма используется для вычисления выборочных
и интегральных частот попадания данных в указанные интервалы значений.
Процедура выводит результаты в виде таблицы и гистограммы.

Замена теоретической функции распределения  на ее выборочный аналог  в определении
математического ожидания, дисперсии, стандартного отклонения и т.п. приводят к
выборочному среднему, выборочной дисперсии, выборочному стандартному отклонению
и т.д. Выборочные характеристики являются оценками соответствующих
характеристик генеральной совокупности. Эти оценки должны удовлетворять
определенным требованиям. В соответствии с важнейшими требованиями оценки
должны быть: несмещенными, то есть стремиться к истинному значению
характеристики генеральной совокупности при

неограниченном увеличении количества испытаний; состоятельными,
то есть с ростом размера выборки оценка должна стремиться к значению
соответствующего параметра генеральной совокупности с вероятностью,
приближающейся к 1; эффективными, то есть для выборок равного объема
используемая оценка должна иметь минимальную дисперсию.

Среди выборочных характеристик выделяют показатели,
относящиеся к центру распределения (меры положения), показатели рассеяния
вариант (меры рассеяния) и меры формы распределения. К показателям,
характеризующим центр распределения, относят различные виды средних
(арифметическое, геометрическое и т. п.), а также моду и медиану.

Простейшим показателем, характеризующим центр выборки,
является мода.

Мода – это элемент выборки с наиболее часто встречающимся значением.

Средним значением выборки, или выборочным аналогом
математического ожидания, называется величина

где  – количество элементов в
выборке.

Иначе говоря, среднее значение – это центр выборки, вокруг
которого группируются элементы выборки. При увеличении числа наблюдений среднее
приближается к математическому ожиданию.

Выборочная медиана – это число, которое является серединой
выборки, то есть половина чисел имеет значения большие, чем медиана, а половина
чисел имеет значения меньшие, чем медиана. Для нахождения медианы обычно
выборку ранжируют – располагают элементы в порядке возрастания. Если количество
членов ранжированного ряда нечетное, медианой является значение ряда, которое
расположено посередине, то есть элемент с номером . Если число членов ряда
четное, то медиана равна среднему значению членов ряда с номерами  и .

Основными показателями рассеяния вариант являются интервал,
дисперсия выборки, стандартное отклонение и стандартная ошибка.

Интервал (амплитуда, вариационный размах) – это разница между
максимальным и минимальным значениями элементов выборки. Интервал является
простейшей и наименее надежной мерой вариации или рассеяния элементов в
выборке.

Более точно отражают рассеяние показатели, учитывающие не
только крайние, но и все значения элементов выборки.

Дисперсией выборки, или выборочным аналогом дисперсии,
называется величина

Дисперсия выборки – это параметр, характеризующий степень
разброса элементов выборки относительно среднего значения. Чем больше
дисперсия, тем дальше отклоняются значения элементов выборки от среднего
значения.

Выборочным стандартным отклонением (среднее квадратичное
отклонение) называется величина

Этот параметр также характеризует степень разброса элементов
выборки относительно среднего значения. Чем больше среднее квадратичное
отклонение, тем дальше отклоняются значения элементов выборки от среднего
значения. Параметр аналогичен дисперсии и используется в тех случаях, когда
необходимо, чтобы показатель разброса случайной величины выражался в тех же
единицах, что и среднее значение этой случайной величины.

Стандартная ошибка или ошибка среднего находится из выражения

Стандартная ошибка – это параметр, характеризующий степень
возможного отклонения среднего значения, полученного на исследуемой
ограниченной выборке, от истинного среднего значения, полученного на всей
совокупности элементов. С помощью стандартной ошибки задается так называемый
доверительный интервал. 95-процентный доверительный интервал, равный , обозначает диапазон, в
который с вероятностью  (при достаточно большом
числе наблюдений n > 30) попадает среднее
генеральной совокупности MX[1].

Выборочной квантилью называется решение уравнения

1.2 Использование инструментов
Мастера функций и Пакета анализа Excel при статистической обработке данных

В результате наблюдений или эксперимента получаются наборы
данных, называемые выборками. Для проведения их анализа данные подвергаются статистической
обработке. Первое, что всегда делается при обработке данных, это вычисление
элементарных статистических характеристик выборок по каждому параметру и по
каждой группе. Полезно также вычислить эти характеристики для объединения
родственных групп и суммарно по всем данным.

В Мастере функций Excel имеется ряд специальных функций, предназначенных для вычисления
выборочных характеристик. Прежде всего, это функции, характеризующие центр
распределения .

Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких
массивов (аргументов) чисел. Функция МЕДИАНА позволяет получать медиану
заданной выборки. Функция МОДА вычисляет наиболее часто встречающееся значение.
Функция ДИСП позволяет оценить дисперсию по выборочным данным. Функция
СТАНДОТКЛОН вычисляет стандартное отклонение.

В пакете Excel
помимо Мастера функций имеется набор более мощных инструментов для работы с
несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который
может быть использован для решения задач статистической обработки выборочных
данных .

Для определения характеристик выборки используется процедура
Описательная статистика. Процедура позволяет получить статистический отчет,
содержащий информацию о центральной тенденции и изменчивости входных данных.[2]

1.3 Принятие статистических решений

Статистическая гипотеза – это предположение о виде или
отдельных параметрах распределения вероятностей, которое подлежит проверке на
имеющихся данных.

Проверка статистических гипотез – это процесс формирования решения
о возможности принять или отвергнуть утверждение (гипотезу), основанный на
информации, полученной из анализа выборки. Методы проверки гипотез называются
критериями.

В большинстве случаев рассматривают так называемую нулевую
гипотезу (нуль-гипотезу ), состоящую в том, что все
события произошли случайно, естественным образом. Альтернативная гипотеза () состоит в том, что события
случайным образом произойти не могли, и имело место воздействие некого фактора .

Обычно нулевая гипотеза формулируется таким образом, чтобы на
основании эксперимента или наблюдений ее можно было отвергнуть с заранее
заданной вероятностью ошибки . Эта заранее заданная
вероятность ошибки называется уровнем значимости.

Уровень значимости – максимальное значение вероятности появления
события, при котором событие считается практически невозможным. В статистике
наибольшее распространение получил уровень значимости, равный . Поэтому, если вероятность,
с которой интересующее событие может произойти случайным образом , то принято считать это
событие маловероятным, и если оно все же произошло, то это не было случайным. В
наиболее ответственных случаях, когда требуется особая уверенность в
достоверности полученных результатов, надежности выводов, уровень значимости принимают
равным  или даже .

Величину , равную , называют доверительной
вероятностью (уровнем надежности), то есть вероятностью, признанной достаточной
для того, чтобы уверенно судить о принятом статистическом решении. Соответственно,
в качестве доверительных вероятностей выбирают значения 0,95, 0,99 или 0,999.

Интервал, в котором с заданной доверительной вероятностью  находится оцениваемый
параметр, называется доверительным интервалом. В соответствии с доверительными
вероятностями на практике используются 95-, 99-99,9-процентные доверительные
интервалы. Граничные точки доверительного интервала называют доверительными
пределами.

Выбор того или иного уровня значимости, выше которого результаты
отвергаются как статистически не подтвержденные, в общем случае является
произвольным. Окончательное решение зависит от исследователя, традиций и
накопленного практического опыта в данной области исследований.

Для определения относиться та или иная варианта к данной
статистической совокупности достаточно использовать правило трех сигм. Согласно
этому правилу в пределах  находится 99,7 % всех
вариант. Поэтому если варианта попадает в этот интервал, то она считается
принадлежащей к данной совокупности. Если не попадает, то она может быть
отброшена. Хотя этот метод и предполагает нормальность исходного распределения,
на практике он успешно работает и может быть использован в большинстве других
случаев.

Определения границ доверительного интервала находится по
формуле

где  – среднее значение;

 – табличное значение
распределения Стьюдента с числом степеней свободы  и доверительной вероятностью
.

Наиболее часто проверяется предположение о нормальном
распределении генеральной совокупности, поскольку большинство статистических
процедур ориентировано на выборки, полученные из нормально распределенной
генеральной совокупности.

Для оценки соответствия имеющихся экспериментальных данных
нормальному закону распределения обычно используют графический метод,
выборочные параметры формы распределения и критерии согласия.

Графический метод позволяет давать ориентировочную оценку
расхождения или совпадений распределений.

Наиболее убедительные результаты дает использование критериев
согласия. Критериями согласия называют статистические критерии, предназначенные
для проверки согласия опытных данных и теоретической модели. Здесь нулевая
гипотеза  представляет собой утверждение
о том, что распределение генеральной совокупности, из которой получена выборка,
не отличается от нормального. Среди критериев согласия большое распространение
получил непараметрический критерий  (хи-квадрат). Он основан на
сравнении эмпирических частот интервалов группировки с теоретическими
(ожидаемыми) частотами, рассчитанными по формулам нормального распределения.

Уверенно о нормальности закона распределения можно судить,
если имеется не менее 50 результатов наблюдений. В случаях меньшего числа данных
можно говорить только о том, что данные не противоречат нормальному закону, и в
этом случае обычно используют графические методы оценки соответствия. При
большем числе наблюдений целесообразно совместное использование графических и
статистических (например, тест хи-квадрат или аналогичные) методов оценки,
естественно дополняющих друг друга.

Для применения критерия желательно, чтобы объем выборки  был > 40, выборочные
данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а
в каждом интервале находилось не менее 5 наблюдений (частот).

При этом сравниваться должны именно абсолютные частоты, а не
относительные. Как и любой другой статистический критерий, критерий хи-квадрат
не доказывает справедливость нулевой гипотезы (соответствие эмпирического
распределения нормальному), а лишь может позволить ее отвергнуть с определенной
вероятностью (уровнем значимости).

В Microsoft Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2ТЕСТ
вычисляет вероятность совпадения наблюдаемых (фактических) значений и
теоретических (гипотетических) значений. Если вычисленная вероятность ниже
уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что
наблюдаемые значения не соответствуют нормальному закону распределения. Если
вычисленная вероятность близка к 1, то можно говорить о высокой степени
соответствия экспериментальных данных нормальному закону распределения.

Функция имеет следующий синтаксис: ХИ2ТЕСТ (фактический
интервал; ожидаемый интервал), где фактический интервал – это интервал данных,
которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями; ожидаемый
интервал – это интервал данных, который содержит теоретические (ожидаемые)
значения для соответствующих наблюдаемых [].

Параметрические критерии служат для проверки гипотез о
положении и рассеивании. Из параметрических критериев наибольшей популярностью
при проверке гипотез о равенстве генеральных средних (математических ожиданий)
пользуется t-критерий Стьюдента (t-критерий различия). Он наиболее часто
используется для проверки следующей гипотезы: «Средние двух выборок относятся к
одной и той же совокупности». Критерий позволяет найти вероятность того, что
оба средних относятся к одной и той же совокупности. Если эта вероятность  ниже уровня значимости ( < 0,05), то принято
считать, что выборки относятся к двум разным совокупностям.

При использовании t-критерия можно выделить два случая. В
первом случае его применяют для проверки гипотезы о равенстве генеральных
средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий).
В этом случае есть контрольная группа и опытная группа.

Во втором случае, когда одна и та же группа объектов
порождает числовой материал для проверки гипотез о средних, используется так
называемый парный t-критерий. Выборки при этом
называют зависимыми, связанными.

Для оценки достоверности отличий по критерию Стьюдента принимается
нулевая гипотеза, что средние выборок равны между собой. Затем вычисляется
значение вероятности того, что изучаемые события произошли случайным образом.

В Microsoft Excel для оценки достоверности отличий по критерию Стьюдента используются
специальная функция ТТЕСТ и процедуры Пакета анализа. Эти перечисленные
инструменты вычисляют вероятность, соответствующую критерию Стьюдента, и
используются, чтобы определить, насколько вероятно, что две выборки взяты из
генеральных совокупностей, которые имеют одно и то же среднее.

Функция ТТЕСТ имеет следующий синтаксис: ТТЕСТ (массив1;
массив2; хвосты; тип), где массив1 – это первое множество данных; массив2 – это
второе множество данных; хвосты – число хвостов распределения. Обычно число
хвостов равно 2; тип – это вид исполняемого t-теста. Возможны три варианта выбора: парный тест; двухвыборочный тест с
равными дисперсиями; двухвыборочный тест с неравными дисперсиями [1].

Критерий Фишера используют для проверки гипотезы о
принадлежности двух дисперсий одной генеральной совокупности и, следовательно,
их равенстве. При этом предполагается, что данные независимы и распределены по
нормальному закону. Гипотеза о равенстве дисперсий принимается, если отношение
большей дисперсии к меньшей меньше критического значения распределения Фишера:

Критическое значение Фишера зависит от уровня значимости и
числа степеней свободы для дисперсий в числителе и знаменателе.

В Microsoft Excel для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий
могут быть использованы функция ФТЕСТ (массив1; массив2) и процедура Пакета
анализа Двухвыборочный F-тест для дисперсий.

Важным разделом статистического анализа является
корреляционный анализ, служащий для выявления взаимосвязей между выборками.

Корреляционный анализ состоит в определении степени связи
между двумя случайными величинами  и . В качестве меры такой связи
используется коэффициент корреляции. Он оценивается по выборке объема  связанных пар наблюдений () из совместной генеральной совокупности
 и . Существует несколько типов
коэффициентов корреляции, применение которых зависит от предположений о
совместном распределении величин  и .

Для оценки степени взаимосвязи наибольшее распространение
получил коэффициент линейной корреляции (Пирсона), предполагающий нормальный
закон распределения наблюдений.

Коэффициент корреляции  – параметр, характеризующий
степень линейной взаимосвязи между двумя выборками. Коэффициент корреляции
изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая
пропорциональная зависимость). При значении коэффициента равном 0 линейной
зависимости между двумя выборками нет. Здесь под прямой зависимостью понимают
зависимость, при которой увеличение или уменьшение значения одного признака ведет,
соответственно, к увеличению или уменьшению второго. При обратной зависимости
увеличение одного признака приводит к уменьшению второго и наоборот.

Выборочный коэффициент линейной корреляции между двумя
случайными величинами  и  рассчитывается по формуле

Коэффициент корреляции является безразмерной величиной, и его
значение не зависит от единиц измерения случайных величин  и .

На практике коэффициент корреляции принимает некоторые
промежуточные значения между  и . Для оценки степени
взаимосвязи можно руководствоваться следующими эмпирическими правилами. Если
коэффициент корреляции  по абсолютной величине (без
учета знака) больше, чем , то принято считать, что
между параметрами существует практически линейная зависимость (прямая – при
положительном  и обратная – при
отрицательном ). Если коэффициент
корреляции  лежит в диапазоне от  до , говорят о сильной степени
линейной связи между параметрами. Если , говорят о наличии линейной
связи между параметрами. При обычно считают, что линейную
взаимосвязь между параметрами выявить не удалось.

В Microsoft Excel для вычисления парных коэффициентов линейной корреляции используется
специальная функция КOРРЕЛ. Функция имеет следующий
синтаксис: КОРРЕЛ (массив1; массив2), где массив1 – это диапазон ячеек первой
случайной величины; массив2 – это второй интервал ячеек со значениями второй
случайной величины [3].

1.4 Регрессионный анализ

При исследовании взаимосвязей между выборками помимо
корреляции различают также и регрессию. Регрессия используется для анализа
воздействия на отдельную зависимую переменную значений одной или более
независимых переменных. Соответственно, наряду с корреляционным анализом еще
одним инструментом изучения стохастических зависимостей является регрессионный
анализ. Регрессионный анализ устанавливает формы зависимости между случайной
величиной  (зависимой) и значениями
одной или нескольких переменных величин (независимых), причем значения
последних считаются точно заданными. Такая зависимость обычно определяется
некоторой математической моделью (уравнением регрессии), содержащей несколько
неизвестных параметров. В ходе регрессионного анализа на основании выборочных
данных находятся оценки этих параметров, определяются статистические ошибки
оценок или границы доверительных интервалов и проверяется соответствие
(адекватность) принятой математической модели экспериментальным данным.

В линейном регрессионном анализе связь между случайными
величинами предполагается линейной. В самом простом случае в линейной
регрессионной модели имеются две переменные  и . И требуется по  парам наблюдений (), (),…, () построить (подобрать) прямую
линию, называемую линией регрессии, которая наилучшим образом приближает
наблюдаемые значения. Уравнение этой линии  является регрессионным
уравнением. С помощью регрессионного уравнения можно предсказать ожидаемое
значение зависимой величины , соответствующее заданному
значению независимой переменной .

Таким образом, можно сказать, что линейный регрессионный анализ
заключается в подборе графика и его уравнения для набора наблюдений. В
регрессионном анализе все признаки (переменные), входящие в уравнение, должны
иметь непрерывную, а не дискретную природу.

В случае, когда рассматривается зависимость между одной зависимой
переменной  и несколькими независимыми
переменными , ,…, , говорят о множественной
линейной регрессии. В этом случае регрессионное уравнение имеет вид

где , ,…,  – коэффициенты;

, ,…  – независимые переменные;

 – константа.

Мерой эффективности регрессионной модели является коэффициент
детерминации  (R-квадрат). Он определяет,
с какой точностью полученное регрессионное уравнение описывает (аппроксимирует)
исходные данные.

Значимость регрессионной модели исследуется с помощью F-критерия (Фишера). Если величина F-критерия значима (), то регрессионная модель
является значимой.

Достоверность отличия коэффициентов , , ,…,  от нуля проверяется с
помощью критерия Стьюдента. В случаях, когда , коэффициент может считаться
нулевым, а это означает, что влияние соответствующей независимой переменной на
зависимую переменную недостоверно, и эта независимая переменная может быть
исключена из уравнения.

В Microsoft Excel экспериментальные данные аппроксимируются линейным уравнением до 16
порядка:

где  – зависимая переменная;

,…,  – независимые переменные;

, …,  – искомые коэффициенты
регрессии.

Для получения коэффициентов регрессии используется процедура
Регрессия из Пакета анализа. Кроме того, могут быть использованы функция ЛИНЕЙН
для получения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ для
получения предсказанных значений  в требуемых точках [4].

2. Анализ и обработка экспериментальных данных

2.1 Предварительная статистическая
обработка экспериментальных данных.

В таблице 1 приведены результаты исследования механических
свойств нержавеющей стали 08Х18Н10Т (твёрдости у,) от факторов – параметров
химического состава:

Таблица
1 – Результаты исследования

Для статистической обработки выборочных данных воспользуемся
инструментом Microsoft Excel Пакет анализа. Чтобы определить характеристики выборки используется
процедура Описательная статистика.

Проанализировав данные, получим следующие результаты (рисунок
1)

Рисунок
1 – Результаты анализа

Представим результаты измерений в виде вариационного ряда
(таблица 2)

Таблица 2 – Вариационный ряд

Вычислим доверительные интервалы для среднего арифметического
при -ной доверительной
вероятности (таблица 3), используя процедуру Описательная статистика.[5]

Таблица 3 – Доверительные интервалы

2.2 Проверка гипотезы о нормальном распределении случайной
величины.

Для оценки соответствия имеющихся экспериментальных данных
нормальному закону распределения, воспользуемся графическим методом и критерием
согласия хи-квадрат.

Сформулируем нулевую гипотезу  и альтернативную гипотезу  [1, 3]:

 – «Отличие экспериментальных данных от
нормального закона распределения не существенно»,

 – «Экспериментальные данные не
подчиняются закону нормального распределения».

Если , где  — экспериментальное значение
критерия Пирсона, а  — теоретическое значение
критерия Пирсона, то нуль-гипотеза о нормальном законе распределения
экспериментальных данных принимается с доверительной вероятностью . В противном случае
нуль-гипотеза отвергается и принимается альтернативная гипотеза.

1. Для Углерода

Таблица 4 – Данные для вычисления критерия Пирсона

Интервал Хi-1 — Xi	ni	F (xi)	Pi = F (xi) — F (xi-1)	nPi	ni — nPi	χ2 = (ni — nPi)2/ nPi
(2,9;3]	1	0,001	0,001	0,03	0,97	29,725
(3,1;3,2]	1	0,024	0,018	0,63	-0,63	0,633
(3,2;3,3]	2	0,076	0,052	1,83	-0,83	0,373
(3,3;3,4]	1	0,188	0,112	3,93	-1,93	0,945
(3,4;3,5]	4	0,368	0,180	6,30	-5,30	4,460
(3,5;3,6]	9	0,584	0,216	7,54	-3,54	1,664
(3,6;3,7]	12	0,776	0,192	6,74	2,26	0,760
(3,7;3,8]	4	0,968	0,192	6,72	5,28	4,146
(3,9;4]	1	0,001	0,024	0,83	3,17	12,162

Экспериментальное значение критерия Пирсона определяется
суммированием данных последнего столбца таблицы 4. Теоретическое значение критерия
Пирсона определяется при заданном уровне значимости  и числе степеней свободы  c использованием функции Microsoft Excel ХИ2ОБР(;). Тогда

Т.к. , т.е. , то принимается альтернативная
 гипотеза, т.к. данные не подчиняются нормальному закону распределения. Для построения гистограммы
необходимо предварительно сгруппировать данные и вычислить относительные
частоты (таблица 5).

Таблица
5 – Данные для построения гистограммы

Номер интервала	Интервал	ni	Wi=ni/n	Значения относительной частоты Wi/h
1	(2,9;3]	1	0,029	0,02
2	(3,1;3,2]	1	0,029	0,02
3	(3,2;3,3]	2	0,057	0,04
4	(3,3;3,4]	1	0,029	0,02
5	(3,4;3,5]	4	0,114	0,07
6	(3,5;3,6]	9	0,257	0,16
7	(3,6;3,7]	12	0,343	0,22
8	(3,7;3,8]	4	0,114	0,07
9	(3,9;4]	1	0,029	0,02

Построим гистограмму относительных частот (рисунок 2)

Рисунок
2 – Гистограмма частот

По гистограмме видно, что отличие экспериментальных данных от
нормального закона распределения существенно.

2. Для Марганца

Таблица 6 – Данные для вычисления критерия Пирсона

Интервал Хi-1 — Xi	ni	F (xi)	Pi = F (xi) — F (xi-1)	nPi	ni — nPi	χ2 = (ni — nPi)2/ nPi
(0,2;0,25]	1	0,032	0,017	0,58	0,42	0,303
(0,3;0,35]	4	0,108	0,047	1,64	-1,64	1,640
(0,4;0,45]	5	0,267	0,091	3,18	0,82	0,212
(0,45;0,5]	4	0,377	0,110	3,84	-3,84	3,844
(0,5;0,55]	6	0,498	0,121	4,23	0,77	0,140
(0,55;0,6]	2	0,619	0,121	4,24	-0,24	0,013
(0,6;0,65]	3	0,729	0,110	3,86	2,14	1,183
(0,65;0,7]	2	0,821	0,092	3,20	-1,20	0,453
(0,7;0,75]	2	0,890	0,069	2,42	0,58	0,139

Т.к. , т.е. , то принимается нулевая
гипотеза, следовательно, отличие экспериментальных данных от нормального закона
распределения не существенно.

Построим гистограмму относительных частот (рисунок 3)

Таблица 7 – Данные для построения гистограммы

Номер интервала	Интервал	ni	Wi=ni/n	Значения относительной частоты Wi/h
1	(0,2;0,25]	1	0,029	0,02
2	(0,3;0,35]	4	0,114	0,07
3	(0,4;0,45]	5	0,143	0,09
4	(0,45;0,5]	4	0,114	0,07
Номер интервала	Интервал	ni	Wi=ni/n	Значения относительной частоты Wi/h
5	(0,5;0,55]	6	0,171	0,11
6	(0,55;0,6]	2	0,057	0,04
7	(0,6;0,65]	3	0,086	0,05
8	(0,65;0,7]	2	0,057	0,04
9	(0,7;0,75]	2	0,057	0,04
10	(0,75;0,8]	4	0,114	0,07
11	(0,8;0,85]	2	0,0363	0,02

Рисунок
3 – Гистограмма частот

По гистограмме видно, что отличие экспериментальных данных от
нормального закона распределения не существенно.

3. Для твердости

Таблица 8 – Данные для вычисления критерия Пирсона

Интервал Хi-1 — Xi	ni	F (xi)	Pi = F (xi) — F (xi-1)	nPi	ni — nPi	χ2 = (ni — nPi)2/ nPi
(62;64]	2	0,013	0,020	0,69	1,31	2,512
(64;66]	2	0,033	0,039	1,36	0,64	0,306
(66;68]	4	0,072	0,067	2,33	1,67	1,194
(68;70]	2	0,138	0,100	3,49	-1,49	0,635
(70;72]	4	0,238	0,130	4,54	-0,54	0,065
(72;74]	3	0,368	0,147	5,15	-2,15	0,895
(74;76]	5	0,515	0,145	5,08	-0,08	0,001
(76;78]	5	0,660	0,124	4,36	0,64	0,095
(78;80]	5	0,784	0,093	3,25	1,75	0,937
(80;82]	2	0,877	0,060	2,12	-0,12	0,006
(82;84]	1	0,938	0,034	1,20	-0,20	0,032

Т.к. , т.е. , то принимается нулевая
гипотеза, следовательно, отличие экспериментальных данных от нормального закона
распределения не существенно.

Построим гистограмму относительных частот (рисунок 4)

Таблица 9 – Данные для построения гистограммы

Номер интервала	Интервал	ni	Wi=ni/n	Значения относительной частоты Wi/h
1	(62;64]	2	0,057	0,04
2	(64;66]	2	0,057	0,04
3	(66;68]	4	0,114	0,07
Номер интервала	Интервал	ni	Wi=ni/n	Значения относительной частоты Wi/h
4	(68;70]	2	0,057	0,04
5	(70;72]	4	0,114	0,07
6	(72;74]	3	0,086	0,05
7	(74;76]	5	0,143	0,09
8	(76;78]	5	0,143	0,09
9	(78;80]	5	0,143	0,09
10	(80;82]	2	0,057	0,04
11	(82;84]	1	0,029	0,02

Рисунок
4 – Гистограмма частот

По гистограмме видно, что отличие экспериментальных данных от
нормального закона распределения не существенно.[6]

2.3 Проверка экспериментальных данных на наличие грубой
погрешности.

Для проверки данных применим статистические критерии трех
сигм.

Сформулируем нулевую гипотезу и альтернативную гипотезу :

 – грубой погрешности
(промаха) нет,

 – грубая погрешность
(промах) есть.

При использовании критерия трех сигм, если , то нулевую гипотезу
отвергают и принимают альтернативную.

Таблица
10 – Проверка на промахи

Проанализировав
данные таблицы 10, убедимся, что грубых погрешностей нет.

2.4 Корреляционный и регрессионный
анализ экспериментальных данных.

Для нахождения коэффициентов корреляции воспользуемся
процедурой Корреляция из Пакета анализа [1].

Получим следующие результаты

Рисунок 5 – Коэффициент
корреляции

Из полученных результатов видно, что между твердостью  и
содержанием углерода в стали существует очень слабая обратная зависимость, а
между твердостью и содержанием марганца  в стали существует очень слабая прямая
зависимость.

Проверим значимость коэффициента корреляции.

Сформулируем нулевую гипотезу и альтернативную гипотезу :

 – коэффициент корреляции
равен нулю,

 – коэффициент корреляции не
равен нулю.

Если , где , то нулевая гипотеза на
уровне значимости  отвергается, т.е. связь
между переменными значима.

—статистика находится по формуле

 – табличное значение, при , , .

Для взаимосвязи Твердость-углерод:

Поскольку , нулевую гипотезу принимаем,
т.е. связь между твердостью  и содержанием углерода  в стали незначима.

Для взаимосвязи Твердость  -Марганец:

Поскольку , нулевую гипотезу принимаем,
т.е. связь между твердостью  и содержанием марганца  в стали незначима.

Проведем регрессионный анализ с помощью процедуры Регрессия
из Пакета анализа Microsoft Excel [2].

Для взаимосвязи Твердость – Марганец, получим следующие
результаты

1-
й способ. Функция ЛИНЕЙН.

воспользуемся статистической функцией ЛИНЕЙН.

Рисунок- 6- Функция
ЛИНЕЙН

2    
й
способ (графический). Построение линии тренда

Рисунок-7
Графический способ

3й способ. Инструмент анализа
Регрессия.

Рисунок-8
Регрессия

Анализ результатов. Построена
линейная регрессионная модель

Ан=31,91+56,22

Коэффициент корреляции между наблюдаемыми и предсказанными
моделью значениями R= 0,108

Оценка адекватности построенной модели проведена с помощью
параметра «Значимость F» Значимость F меньше  0,05 поэтому модель может
считаться адекватной с вероятностью 0,95.

Оценка значимости коэффициентов модели проведена по параметру
«Р- значение» Поскольку это значение меньше 0,05, то с вероятностью 0,95 можно
считать, что соответствующие коэффициентов модели значимы.

Для взаимосвязи твердость -углерод, получим следующие
результаты

Рисунок
9 – Полиноминальная модель

По расчётам для полиноминальной модели  наибольшее значение
корреляции имеет полиноминальная модель 6 степени.

2.5 Множественный регрессионный анализ

Проведем множественный регрессионный анализ с помощью
процедуры Регрессия из Пакета анализа Microsoft Excel.

Получим следующий результат

Рисунок
10 – Множественный регрессионный анализ

Рисунок 11 Остаток

 Так как значимость F больше значимости а=0,05 то построенная
регрессия не является значимой. (рисунок 9). Поскольку R-квадрат равен , то точность слабая.

Значения коэффициентов модели указаны в столбце Коэффициенты,
следовательно:  

Выражение для определения предела текучести  в зависимости от
содержания углерода  и кремния в стали будет иметь вид:

Заключение

корреляционный

В технических науках часто приходится сталкиваться с
необходимостью обработки и анализа экспериментальных данных, полученных в
результате наблюдения. В ходе курсовой работы было показано, что необходимым
инструментарием для анализа данных обладает программа Microsoft Excel. С ее помощью были проанализированы результаты исследования зависимости
механических свойств стали 08Х18Н10Т от химического состава. Была выявлена слабая
прямая взаимосвязь между твердостью  и содержанием марганца  в стали. Также
было установлено, что изменение процентного содержания углерода в стали не
влияет на твердость.

Библиографический список

1. Математическая статистика : учеб.-метод. пособие /
авт.-сост. : С. Е. Демин, Е. Л. Демина ; М-во образования и науки РФ ; ФГАОУ ВО
«УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т
(фил.). – Нижний Тагил : НТИ (филиал) УрФУ, 2016. – 284 с.

2.Т.В. Борздова, Основы статистического анализа и
обработки данных с применением Microsoft Excel: учебное пособие /Борздова Т.В. –
Минск: ГИУСТ БГУ, 2011. – 75 с.

3. В.Р. Бараз, Использование MS Excel для анализа статистических
данных: учебное пособие/Бараз В.Р., Пегашин В.Ф. – 2-е изд. – Нижний Тагил: НТИ
(филиал) УрФУ, 2014. – 181 с.

4. В.Е. Гмурман, Теория вероятностей и математическая
статистика: учебное пособие для вузов/Гмурман В.Е. – 9-е изд. – М.: Высшая
школа, 2003. – 479 с.

5. Веременюк В. В., Крушевский Е.А., Мороз О. А./ Статистическая
обработка экспериментальных данных/ Минск БНТУ, 2015-77с.

6. Е .А. Лукерьянова/ Математическая
статистика часть 2/ Курган/ 2018-48с.

Цель работы:Изучение возможностей
пакета MS Excel при
решении задач обработки экспериментальных
данных. Приобретение навыков обработки
результатов эксперимента.

Существует достаточно большой класс
процессов, описание которых основано
на использовании случайных величин. В
MS
Excel
для генерации случайных величин
используют функции:

1) СЛЧИС
()
– в результате ее выполнения на листе
вычислений будет получено равномерно
распределенное случайное число больше
или равные 0 и меньшие 1 (категория
Математические).

Функция
СЛЧИС
()*(b—a)+a
– позволяет
сгенерировать числа из диапазона [a;
b].

Композиция
функций
ЦЕЛОЕ()
и СЛЧИС(): ЦЕЛОЕ(СЛЧИС()*(b—a)+a)
–
позволяет сгенерировать целые числа
из диапазона [a;
b].

2)
СЛУЧМЕЖДУ()
–
в результате будет получено случайное
число, лежащее между произвольными
заданными значениями (категория
Мат.
и тригонометрия).

Процедура
генерации случайных величин используется
для
заполнения диапазона ячеек случайными
числами. Заполнение диапазона (массива)
ячеек происходит с помощью операции
копирования.

Замечание.
При
осуществлении любых операций в ЭТ,
включающих нажатие клавиши Enter,
сгенерированные массивы случайных
значений будут автоматически обновляться
(«перегенерироваться»). Это не очень
удобно. Поэтому имеет смысл после
генерации массива заменить формулы
случайных величин на значения, то есть
зафиксировать значения. Это делается
с помощью команд Копировать
и Правка/Специальная
вставка (выберите
опцию Значения
из раздела Вставка)
и
нажмите ОК.
Заметим, что как правило значения
случайной величины копируются в
тот же
столбец.

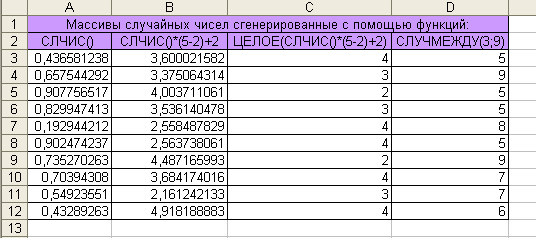
На
рисунке ниже представлен результат
генерации массивов случайных чисел
разными способами. В первом столбце
представлены только значения случайной
величины в промежутке от 0 до 1, во втором
столбце представлен результат генерации
случайных чисел из диапазона [2;5], в
третьем результат генерации целых
случайных чисел из диапазона [2;5], в
четвертом результат генерации случайных
чисел из диапазона [3;9]

Пакет анализа

Пакет анализа— предназначенный для
решения сложных статистических и
инженерных задач. Установим пакета
анализаСервис/Надстройки.

• В меню Сервисвыберите командуАнализ данных.

• Выберите из списка название нужного
  инструмента анализа и нажмите ОК.

• В большинстве случаев в открывшемся
  диалоговом окне нужно просто указать
  интервал исходных данных, интервал для
  вывода результатов и задать некоторые
  параметры.

1) Инструмент Генерация случайных
чисел дает возможность получать
равномерное и неравномерное распределение.

Пример 1:Создать последовательность,
состоящую из 20 действительных случайных
чисел, равномерно распределенных в
диапазоне от 1 до 10.

Решение:В менюСервисвыбираем
пунктАнализ данных, указываем
строкуГенерация случайных чисел.
Заполним рабочие поля диалогового окна
«Генерация случайных чисел».

Ч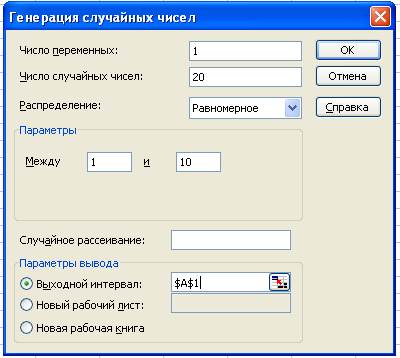исло
переменных.Введите число столбцов
значений, которые необходимо разместить
в выходном диапазоне. Если это число не
введено, то все столбцы в выходном
диапазоне будут заполнены.

Число случайных чисел.Введите число
случайных значений, которое необходимо
вывести для каждой переменной. Каждое
случайное значение будет помещено в
строке выходного диапазона. Если число
случайных чисел не будет введено, все
строки выходного диапазона будут
заполнены.

Распределение. Выберите распределение,
которое необходимо использовать для
генерации случайных переменных.

Параметры.Введите параметры
выбранного распределения.

Выходной
диапазон. Введите
ссылку на левую верхнюю ячейку выходного
диапазона. Размер выходного диапазона
будет определен автоматически, и на
экран будет выведено сообщение в случае
возможного наложения выходного диапазона
на исходные данные.

Если
необходимо получить случайные числа
на новом листе или новой книге – в полях
Новый
лист
и Новая
книга
устанавливаются соответствующие
переключатели.

Нажимаем кнопку ОК, в столбце А
появляются 20 случайных чисел в диапазоне
от 1 до 10.

2) Инструмент Гистограмма позволяет
создавать гистограммы распределения
данных. Область значений измеряемой
величины разбивается на несколько
интервалов, называемых карманами, в
которых в виде столбцов откладывается
количество попавших в этот интервал
измерений, называемой частотой.

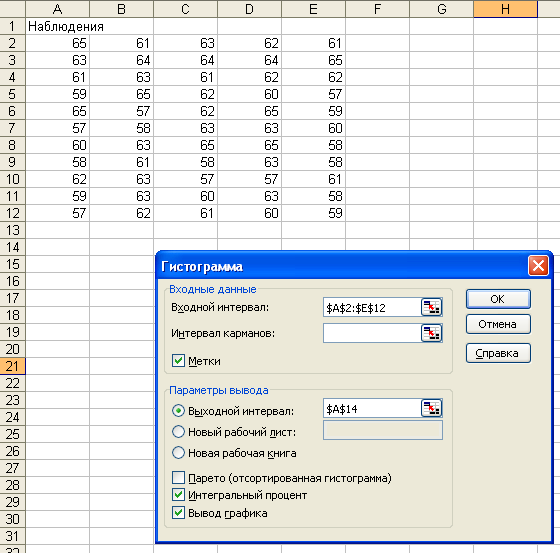
Пример 2:Построить гистограмму
распределение веса студентов в килограммах
для следующей выборки: 65, 61, 63, 62, 61, 63, 64,
64, 64, 65, 61, 63, 61, 62, 62, 59, 65, 62, 60, 57, 65, 57, 62, 65,
59, 57, 58, 63, 63, 60, 60, 63, 65, 65, 58, 58, 61, 58, 63, 58, 62,
63, 57, 57, 61, 59, 63, 60, 63, 58, 57, 62, 61, 60, 59.

Решение: В ячейку А1 введите словоНаблюдения, в диапазон А2:Е12 значения
веса студентов:

65	61	63	62	61
63	64	64	64	65
61	63	61	62	62
59	65	62	60	57
65	57	62	65	59
57	58	63	63	60
60	63	65	65	58
58	61	58	63	58
62	63	57	57	61
59	63	60	63	58
57	62	61	60	59

В меню Сервисвыбираем пунктАнализ
данных, указываемГистограмма. В
появившемся окнеГистограммазаполним рабочие поля:

• во Входной диапазонвведите диапазон
  исследуемых данных;

• в Выходной диапазон– ссылка на
  левую верхнюю ячейку выходного диапазона.
  Установите переключатели в положениеИнтегральный процентиВывод
  графика.

Нажимаем кнопку ОК.

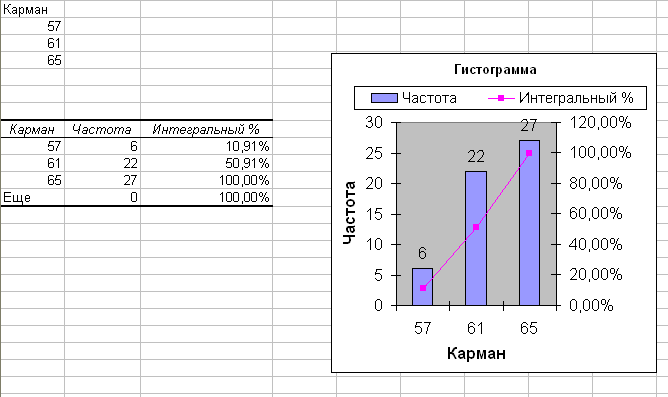
В результате появляется таблица и
диаграмма.

На диаграмме по горизонтальной оси
откладываются граничные значения,
определяющие интервалы (карманы), по
вертикальной оси количество попавших
чисел в каждый интервал (частота).

Одним из параметров диалогового окна
Гистограммаявляется полеИнтервал
карманов(необязательный параметр),
куда может вводиться диапазон ячеек
или необязательный набор граничных
значений, определяющих выбранные
интервалы (карманы). Эти значения должны
быть введены в возрастающем порядке. В
Microsoft Excel вычисляется число попаданий
данных между началом интервала и соседним
большим по порядку. При этом включаются
значения на нижней границе интервала
и не включаются значения на верхней
границе.

Если диапазон карманов не был введен,
то набор интервалов, равномерно
распределенных между минимальным и
максимальным значениями данных, будет
создан автоматически.

Сформируем столбец интервалов группировки
(карманов).

Постоим Гистограмму, указав в полеИнтервал карманов диапазон ячеек,
определяющих выбранные интервалы. В
результате появляется таблица и
диаграмма.

3) Инструмент Описательная статистикаформирует таблицу статистических
данных, ускоряя и упрощая этот процесс
по сравнению с использованием формул.

Соседние файлы в папке Лабораторные_работы

• #
• #
• #

Введение

Теоретическиеметоды исследования в науке дают возможность раскрыть качественные характеристики изучаемых явлений. Эти характеристики будут полнее и глубже, если накопленный эмпирический материал подвергнуть количественной обработке. Однако проблема количественных измерений, в частности, в рамках психолого-педагогических исследований очень сложна. Эта сложность заключается, прежде всего, в субъективно-причинном многообразии педагогической деятельности и ее результатов, в самом объекте измерения, находящемся в состоянии непрерывного движения и изменения. Вместе с тем введение в исследование количественных показателей стало сегодня необходимым и обязательным компонентом получения объективных данных о результатах труда. С этой целью при исследовании проблем психологии применяются методы математической статистики. С их помощью решаются различные задачи: обработка фактического материала, получение новых, дополнительных данных, обоснование научной организации исследования и др.

Правильное применение статистики позволяет экспериментатору:

• строить статистические предсказания;

• обобщать данные эксперимента;

• находить зависимость между экспериментальными данными;

• строго обосновывать экспериментальные планы;

• доказывать правильность и обоснованность используемых методических приемов и методов.

Нельзя забывать, однако, что сами по себе методы статистики – это только инструментарий, помогающий экспериментатору эффективно разбираться в сложном исследуемом материале. Наиболее важным при проведении любого эксперимента является четкая постановка задачи, тщательное планирование эксперимента, построение непротиворечивых гипотез.

Методы математической статистики в руках исследователя могут и должны быть мощным инструментом, позволяющим не только успешно лавировать в море экспериментальных данных, но и, прежде всего, способствовать становлению его объективного мышления.

Актуальность данного исследования означена востребованностью статистической обработки экспериментальных данных в психолого-педагогических исследованиях.

Цель: проведение регрессионного анализа статистических данных психологического эксперимента для выявления уровня враждебности школьников в зависимости от уровней обиды и подозрительности (диагностика состояния враждебности Басса-Дарки).

Объект исследования: процесс статистической обработки данных психологического эксперимента.

Предмет исследования: зависимость уровня враждебности от таких психологических факторов личности как обида и подозрительность.

Задачи:

1. Проанализировать научную, учебную, специальную литературу по теме исследования;

2. Изучить теоретические аспекты разновидностей регрессионного анализа;

3. Выявить методы и средства статистического анализа данных психологического эксперимента;

4. Обработать статистические данные с помощью специальных функций, встроенных в табличный процессор Excel;

5. Провести аппроксимацию данных проведенного эксперимента.

Для решения поставленных задач используются следующие методы:

1. Теоретические:

• анализ литературы;

• систематизация изученного материала;

• обобщение.

1. Эмпирические:

• наблюдение;

• анкетирование(опрос).

Глава 1. Регрессионный анализ экспериментальных данных 1.1. Первичная обработка экспериментальных данных

Современные задачи планирования, управления, прогнозирования невозможно решать, не располагая достоверными статистическими данными и не используя статистические методы обработки этих данных. Стремление объяснить настоящее и заглянуть в будущее всегда было свойственно человечеству, а для решения этих задач применялись различные методы. Статистика при описании случайных явлений использует язык науки – математику. Это значит, что реальные ситуации заменяются вероятностными схемами и анализируются методами теории вероятностей.

Любые статистические данные всегда неполны и неточны, и другими быть не могут. Задача статистики заключается в том, чтобы дать обоснованные выводы о свойствах изучаемого явления, анализируя неполные и неточные данные. Статистика доказала, что умеет справляться с подобными проблемами.

Методы первичной статистической обработки результатов эксперимента применяются при обработке материалов психологических исследований для того, чтобы извлечь из тех количественных данных, которые получены в экспериментах, при опросе и наблюдениях, как можно больше полезной информации. В частности, в обработке данных, получаемых при испытаниях по психологической диагностике, это будет информация об индивидуально-психологических особенностях испытуемых.

Методами статистической обработки результатов эксперимента называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами.

Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок.

Выборочное среднее (среднее арифметическое) как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, можно судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.

Выборочное среднее значение ряда из n числовых значений обозначается и подсчитывается так:

(1.1)

Здесь — это данные (набор чисел), полученные в результате регистрации значений некоторой случайной величины. Этот набор чисел называется выборкой. Величины 1,2…n являются так называемыми индексами. — принятый в математике знак суммирования тех переменных величин, которые находятся справа от этого знака. Числа, стоящие над и под знаком называются пределамисуммирования и указывают наименьшее и наибольшее значения индекса суммирования, между которыми расположены его промежуточные значения.

В том случае, если отдельные значения повторяются, то выборочное среднее вычисляют по формуле:

(1.2)

в таком случае называют взвешенной средней, где — частоты повторяющихся значений.

При вычислении величины средней по таблице чисел используется следующая формула:

(1.3)

где — значения всех переменных, полученных в эксперименте, или все элементы таблицы; при этом индекс jменяется от 1 до p, где p — число столбцов в таблице, а индекс iменяется от 1 до n, где n – число испытуемых или число строк в таблице. Тогда — общая средняя всех элементов в таблице (анализируемой совокупности экспериментальных данных) и в общем случае .

Символическое обозначение удобно для обозначения конкретного элемента таблицы. Символ (двойная сумма) означает, что вначале осуществляется суммирование всех элементов по индексу i– т.е. по строкам, затем полученные суммы по столбцам – по индексу j.

Дисперсия – это среднее арифметическое квадратов отклонений значений переменной от ее среднего значения. Иначе, дисперсия, как статистическая величина, характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных.

(1.4)

где n– объем выборки, i– индекс суммирования, — выборочное среднее.

Расчет дисперсии для таблицы чисел осуществляется по формуле:

(1.5)

где — значения всех переменных, полученных в эксперименте, или все элементы таблицы; — общее среднее арифметическое всех элементов таблицы; N – общее число всех элементов таблицы.

Иногда вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую выборочное отклонение (стандартное):

(1.6)

Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Можно дать второе определение, сказав, что медиана – это величина, по отношению к которой, по крайней мере 50% выборочных значений меньше нее и по крайней мере 50% — больше.

Мода – это количественное значение исследуемого признака, наиболее часто встречающееся в выборке.

Моду находят согласно следующим правилам:

1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет.

2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина, равная 3,5.

3) Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.

Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод).

4) Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой.

Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением.

Обычно полученные в результате наблюдений результаты представляют собой набор чисел (выборку). Просматривая этот набор, как правило, трудно выявить какую-либо закономерность. Поэтому данные подвергают некоторой первичной обработке, целью которой является упрощение дальнейшего анализа.

Дальнейшие действия зависят от того, насколько много в выборке различных чисел. Если величина дискретна и случайна, то различных чисел немного; если же величина непрерывна и случайна, то, скорее всего, все числа окажутся различными.

Дискретный случай

Первый этап обработки выборки – это составление вариационного ряда. Его получают так – среди всех чисел отбирают все различные и располагают в порядке возрастания: , где

Следующий этап обработки выборки – составление дискретной таблицы частот:

		…
		…
		…

Здесь n – число всех измерений, — число измерений, в которых наблюдалось значение . Величины называются частотами, а величины — относительными частотами.

Графической иллюстрацией дискретной таблицы частот является столбиковая диаграмма (рис.1).

Рис.1 Столбиковая диаграмма

Непрерывный случай

Если число различных значений в выборке велико, вычислить частоту каждого их них не имеет большого смысла. Поэтому поступают следующим образом. Весь промежуток изменения значений выборки, от минимального до максимального, разбивают на интервалы. После этого подсчитывают число значений из выборки, попадающих в каждый интервал (частоты), а затем – относительные частоты. В результате получается интервальная таблица частот:

		…
		…
		…

Здесь n – число всех измерений, m – число интервалов, — количество чисел, приходящихся на i-й интервал, — относительная частота попадания в i-й интервал. Интервалы обычно берут одинаковой длины, хотя это и не обязательно.

Графической иллюстрацией интервальной таблицы частот является гистограмма (рис.2). Гистограмма представляет собой ступенчатую линию; основанием i-й ступеньки является интервал , а площадь этой ступеньки равна .

Рис.2 Гистограмма

Таким образом, рассмотрены методы первичной обработки результатов эксперимента, в результате которых имеющиеся «серые» результаты наблюдений преобразовываются для достижения большей наглядности.

1.2. Однофакторный регрессионный анализ

С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, чем методы первичной статистической обработки, и требуют от исследователя хорошей подготовки в области элементарной математики и статистики. Данную группу методов можно разделить на несколько подгрупп:

1. Регрессионный анализ;

2. Методы сравнения между собой двух или нескольких элементарных статистик (средних, дисперсий и т.п.), относящихся к разным выборкам;

3. Методы установления статистических взаимосвязей между переменными, например их корреляции друг с другом;

4. Методы выявления внутренней статистической структуры эмпирических данных (например, факторный анализ).

Регрессионный анализ – это метод математической статистики, позволяющий свести частные, разрозненные данные к их определенной внутренней взаимосвязи, которая по значению одной или нескольких переменных приблизительно оценивает вероятное значение другой переменной.

Регрессионный анализ устанавливает формы зависимости между случайной величиной y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость определяется обычно некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.

Регрессия может быть однофакторной (парной) и многофакторной (множественной). Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, можно использовать графическое изображение. При множественности причинных связей невозможно чётко разграничить одни причинные явления от других. В этом случае наиболее приемлемым способом определения зависимости (уравнения регрессии) является метод перебора различных уравнений, реализуемый с помощью компьютера.

После выбора вида регрессионной модели, используя результаты наблюдений зависимой переменной и факторов, нужно вычислить оценки (приближённые значения) параметров регрессии, а затем проверить значимость и адекватность модели результатам наблюдений.

Порядок проведения регрессионного анализа следующий:

• выбор модели регрессии, что заключает в себе предположение о зависимости функций регрессии от факторов;

• оценка параметров регрессии в выбранной модели методом наименьших квадратов;

• проверка статистических гипотез о регрессии.

Графическое выражение регрессионного уравнения называют линиейрегрессии. Линия регрессии выражает наилучшие предсказания зависимой переменой (y) по независимым переменным (x,z). Эти независимые переменные, а их может быть много, носят название предикторов.

По характеру связи однофакторные уравнения регрессии подразделяются на:

а) линейные: , где x — экзогенная (независимая) переменная, y -эндогенная (зависимая, результативная) переменная, a, b параметры;

б) степенные: ;

в) показательные: и прочие.

Наиболее естественной с точки зрения единого метода оценки неизвестных параметров является модель регрессии, линейная относительно этих параметров:

(2.1)

(2.2)

где — свободные члены, — коэффициенты регрессии, или угловые коэффициенты, определяющие наклон линии регрессии по отношению к осям координат.

Линии регрессии пересекаются в точке , с координатами, соответствующими средним арифметическим значениям корреляционно связанных между собой переменных x и y.

Количественное представление связи (зависимости) между x и y (между yиx) и называется регрессионным анализом. Главная задача регрессионного анализа заключается в нахождении , и определения уровня значимости полученных аналитических выражений (2.1) и (2.2), связывающих между собой переменные x и y.

При этом коэффициенты регрессии показывают, насколько в среднем величина одной переменной изменяется при изменении на единицу меры другой. Коэффициент регрессии в уравнении (2.1) находится по формуле:

(2.3)

а коэффициент из уравнения (2.2) по формуле:

(2.4)

где — коэффициент корреляции между переменными X и Y;

— среднеквадратическое отклонение, подсчитанное для переменной x;

— среднеквадратическое отклонение, подсчитанное для переменной y.

Коэффициенты регрессии можно вычислить также без подсчета среднеквадратических отклонений по следующим формулам:

(2.5)

(2.6)

В том случае, если неизвестен коэффициент корреляции, коэффициенты регрессии можно вычислить по следующим формулам:

(2.7)

(2.8)

Сравнивая формулу для подсчета коэффициента корреляции Пирсона:

(2.9)

где — значения, принимаемые переменной x;

— значения, принимаемые переменной y;

— средняя по x;

— средняя по y.

С формулами (2.7), (2.8) видно, что в числе этих формул стоит одна и та же величина: . Последнее говорит о том, что величины и взаимосвязаны. Более того, зная две из них – всегда можно получить третью. Например, зная величины и , можно легко получить :

(2.10)

Эта формула очень важна, поскольку она позволяет по известным значениям коэффициентов регрессии и определить коэффициент корреляции, и, кроме того, сравнивая вычисления по формулам (2.9) и (2.10), можно поверить правильность расчета данного коэффициента. Как и коэффициент корреляции, коэффициенты регрессии характеризуют только линейную связь и при положительной связи имеют знак плюс, при отрицательной – знак минус.

В свою очередь свободные члены и в уравнениях регрессии вычисляются по формулам:

(2.11)

(2.12)

Вычисления по формулам (2.7), (2.8), (2.11) и (2.12) достаточно сложны, поэтому при расчетах коэффициентов регрессии используют, как правило, более простой метод. Он заключается в решении двух систем уравнений. При решении одной системы находятся величины и , и при решении другой — и .

Общий вид системы уравнений для нахождения величин и таков:

(2.13)

Общий вид системы уравнений для нахождения величин и таков:

(2.14)

В системах уравнений (2.13) и (2.14) используются следующие обозначения:

N – число элементов в переменной xили в переменной y,

— сумма всех элементов переменной x,

— сумма всех элементов переменной y,

— произведение всех элементов переменной yдруг на друга,

— произведение всех элементов переменной xдруг на друга,

— попарное произведение всех элементов переменной xна соответствующие элементы переменной y.

Для применения метода однофакторного регрессионного анализа необходимо соблюдать следующие условия:

1. Сравниваемые переменные x и yдолжны быть измерены в шкале интервалов или отношений.

2. Предполагается, что переменные x и yимеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.

Таким образом, можно сказать, что линейный регрессионный анализ заключается в подборе графика и его уравнения для набора наблюдений. В регрессионном анализе все признаки (переменные), входящие в уравнение, должны иметь непрерывную, а не дискретную природу.

1.3. Многофакторный регрессионный анализ

В общем случае, зависимость между несколькими переменными величинами выражают уравнением множественной регрессии (многофакторной), которая может быть как линейной, так и не линейной. В простейшем случае множественная линейная регрессия выражается уравнением с двумя независимыми переменными величинами x и z и имеет вид:

(3.1)

где y– зависимая переменная, a– свободный член, bи c– параметры уравнения (3.1).

Уравнение (3.1) может решаться относительно зависимой переменной z, тогда x и yявляются независимыми переменными, и уравнение множественной регрессии имеет следующий вид:

(3.2)

Можно решить уравнение (3.1) и относительно X, тогда Zи Yбудут независимыми переменными, и уравнение будет иметь следующий вид:

(3.3)

При проведении конкретных расчетов выбор зависимых и независимых переменных определяется планом эксперимента.

Решение уравнений (3.1), (3.2), (3.3) состоит в том, что находятся величины a, bи c на основе решения системы из трех уравнений.

Для решения уравнения (3.1) система имеет следующий вид:

(3.4)

Для решения уравнения (3.2) система будет выглядеть следующим образом:

(3.5)

Для решения уравнения (3.3) система будет иметь следующий вид:

(3.6)

В общем случае уравнение регрессии представляет собой сложный полином, описывающий зависимость сразу между несколькими переменными. Такое уравнение множественной регрессии имеет вид:

(3.7)

где и т.п. – интересующие психолога независимые переменные, а Y – зависимая переменная.

Для применения метода многофакторного регрессионного анализа необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.

2. Предполагается, что переменные имеют нормальный закон распределения.

3. Число варьирующих признаков в сравниваемых переменных должно быть одинаковым.

Таким образом, качество полученного уравнения регрессии оценивают по степени близости между результатами наблюдений за показателем и предсказанными по уравнению регрессии значениями в заданных точках пространства параметров. Если результаты близки, то задачу регрессионного анализа можно считать решенной. В противном случае следует изменить уравнение регрессии (выбрать другую степень полинома или вообще другой тип уравнения) и повторить расчеты по оценке параметров.

Глава 2. Использование регрессионного анализа в интерпретации результатов методики изучения агрессии Басса-Дарки 2.1. Исследование уровня и рода враждебности школьников

Статистические методы раскрывают связи между изучаемыми яв­лениями. Однако необходимо твердо знать, что, как бы ни была высока вероятность таких связей, они не дают права исследователю признать их причинно-следственными отношениями.

Чтобы подтвердить или отвергнуть существование причинно-след­ственных отношений, исследователю зачастую приходится продумы­вать целые серии экспериментов. Если они будут правильно постро­ены и проведены, то статистика поможет извлечь из результатов этих экспериментов информацию, которая необходима исследователю, что­бы либо обосновать и подтвердить свою гипотезу, либо признать ее недоказанной.

В работе с подростковой аудиторией педагогу и психологу всегда приходится учитывать особенности агрессии у подростков. А для выявления уровня и рода агрессии детей существуют различные методики. Одна из них – диагностика состояния агрессии (опросник Басса-Дарки). Данный опросник состоит из 75 утверждений, на которые испытуемый отвечает «да» или «нет» (Приложение 1).

Создавая свой опросник, дифференцирующий проявления агрессии и враждебности, А. Бассе и А. Дарки выделили следующие виды реакций:

1. Физическая агрессия – использование физической силы против другого лица.

2. Косвенная агрессия – агрессия, окольным путем направленная на другое лицо или ни на кого не направленная.

3. Раздражение – готовность к проявлению негативных чувств при малейшем возбуждении (вспыльчивость, грубость).

4. Негативизм – оппозиционная манера в поведении от пассивного сопротивления до активной борьбы против установившихся обычаев и законов.

5. Обида – зависть и ненависть к окружающим за действительные и вымышленные действия.

6. Подозрительность – в диапазоне от недоверия и осторожности по отношению к людям до убеждения в том, что другие люди планируют и приносят вред.

7. Вербальная агрессия – выражение негативных чувств как через форму (крик, визг), так и через содержание словесных ответов (проклятия, угрозы).

8. Чувство вины – выражает возможное убеждение субъекта в том, что он является плохим человеком, что поступает зло, а также ощущаемые им угрызения совести.

Обработка результатов: Обработка опросника Басса-Дарки производится при помощи индексов различных форм агрессивных и враждебных реакций, которые определяются суммированием полученных ответов. Физическая агрессия, косвенная агрессия, раздражение и вербальная агрессия вместе образуют суммарный индекс агрессивных реакций, а обида и подозрительность – индекс враждебности.

Данная методика была апробирована (в ходе государственной педагогической практики) 28.10.10 г. в 9а классе МАОУ СОШ № 5 г. Тобольска. В исследовании приняли участие 20 учащихся. Результаты опроса (значения параметров) представлены в сводной таблице (Приложение 2).

Для полной реализации сути опросника Басса-Дарки необходимо представить суммарный индекс агрессивных реакций и суммарный индекс враждебности (Приложение 3).

Перед началом регрессионного анализа осуществляется отбор факторов. Сначала отбираются факторы, связанные с изучаемым явлением, на основе данных теоретического исследования (психологическая теория, заключения экспериментатора и т.д.). При этом для построения множественной регрессии отбираются факторы, которые могут быть количественно измерены.

Проблему данного исследования составило рассмотрение и анализ уровня враждебности, вследствие этого регрессионный анализ экспериментальных данных методики Басса-Дарки будет проведен по индексу враждебности (зависимая переменная y), получающийся суммированием выявленных уровней обиды и подозрительности (независимые переменные xи z, соответственно).

2.2. Построение регрессионной модели

Регрессионный анализ экспериментальных данных методики Басса-Дарки будет проведен по индексу враждебности (зависимая переменная y), получающийся суммированием выявленных уровней обиды и подозрительности (независимые переменные xи z, соответственно).

Как будет варьировать индекс враждебности испытуемого, если будут изменяться уровни обиды и подозрительности? Ответ на этот вопрос психолог получит с помощью использования метода множественной регрессии. Данные для анализа представлены в таблице 3, в которой произведены предварительные вычисления.

Таблица 3. Исходные данные

№	Фамилия ученика
1	Бакиева	5	8	13	25	40	65	64	104
2	Гатауллин	1	4	5	1	4	5	16	20
3	Гатин	2	2	4	4	4	8	4	8
4	Долженко	5	4	9	25	20	45	16	36
5	Жарова	4	7	11	16	28	44	49	77
6	Жуйкова	6	3	9	36	18	54	9	27
7	Корикова	5	7	12	25	35	60	49	84
8	Костерина	7	7	14	49	49	98	49	98
9	Курманалиева	4	7	11	16	28	44	49	77
10	Летунов	3	2	5	9	6	15	4	10
11	Мороков	4	5	9	16	20	36	25	45
12	Перовских В.	4	9	13	16	36	52	81	117
13	Перовских М.	4	7	11	16	28	44	49	77
14	Смирнова	4	8	12	16	32	48	64	96
15	Солосина	7	8	15	49	56	105	64	120
16	Тимирова	1	2	3	1	2	3	4	6
17	Трухин	2	4	6	4	8	12	16	24
18	Филиппов	4	6	10	16	24	40	36	60
19	Хабисов	6	3	9	36	18	54	9	27
20	Цыпанов	0	2	2	0	0	0	4	4
Суммы:	78	105	183	376	456	832	621	1117

С помощью решения системы уравнений (3.1) необходимо найти уравнение регрессии y на x, т.е. определить коэффициенты a, bи c, и таким образом ответить на поставленный вопрос.

Чтобы получить и решить уравнение множественной линейной регрессии (3.1), необходимо найти a, bи c. Для этого используется система уравнений (3.4). Благодаря вычислениям, приведенным в таблице 3, известны все необходимые величины сумм. Перепишем систему уравнений (3.4), учитывая N= 20, поскольку в эксперименте участвовало 20 человек, и учитывая данные таблицы 3:

(3.8)

Получили систему линейных уравнений (СЛУ) с тремя неизвестными. Решается данная система несколькими способами: по правилу Крамера, методом Гаусса и с помощью обратной матрицы.

В СЛУ (3.8) число уравнений равно числу неизвестных, поэтому целесообразно для нахождения неизвестных применить метод Крамера. Для начала составляется матрица третьего порядка:

(3.9)

Здесь последний столбец – это столбец свободных членов.

Теорема (правило Крамера). Пусть Δ – определитель матрицы СЛУ, а — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов. Тогда если , то система линейных уравнений имеет единственное решение, определяемое по формулам:

, где j = 1,2,…,n (3.10)

Формулы вычисления неизвестных (3.10) – решения системы линейных уравнений (3.8) – носят название формул Крамера.

Составляется и вычисляется главный определитель матрицы (3.9):

(3.11)

Так как вычисления данного определителя очень громоздкие, то целесообразно осуществлять все расчеты с помощью «Мастера функций» MS Excel. Для этого используется встроенная математическая функция МОПРЕД. Порядок вычисления следующий:

1. введите в упорядоченные ячейки электронной таблице исходные элементы определителя, сохраняя порядок следования элементов;

2. активируйте Мастер функций любым из способов:

а) в главном меню выберите команду Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;

1. в появившемся диалоговом окне «Мастер функций – шаг 1 из 2» в поле Категории выберите Математические, в окне Функция – МОПРЕД. Щелкните по кнопке ОК;

2. в появившемся окне Аргументы функции необходимо указать диапазон ячеек от первого элемента исходного определителя до последнего (например, А1:С3);

3. щелкните по кнопке ОК.

После выполнения данного алгоритма на экране компьютера появится результат – определитель.

Как видно, полученный определитель () отличен от нуля, стало быть, СЛУ (3.8) имеет единственное решение, которое вычисляется по формулам:

, , (3.12)

Чтобы применить формулы (3.12), необходимо составить определители по правилу Крамера (3.10) и произвести их расчеты с помощью «Мастера функций» MS Excel. Все расчеты представлены ниже.

.

Теперь, когда известны все определители, можно применить формулы (3.12):

; ; (3.13)

Решив систему уравнений (3.8), получилось a = — 3,34, b = 1,82, c = 1,02. следовательно, искомое уравнение регрессии y на x (3.1) примет вид:

(3.14)

гдеy– зависимая переменная, –3,34 — свободный член, 1,82 и1,02 – параметры уравнения.

Уравнение (3.14) дает ответ на поставленный ранее вопрос: Как будет варьировать индекс враждебности испытуемого, если будут изменяться уровни обиды и подозрительности? Так, при увеличении величины уровня обиды xна 1 балл, количественная величина индекса враждебности y увеличится на 1,82, при постоянной величине уровня подозрительности z. А при постоянной величине уровня обиды и при увеличении величины уровня подозрительности на 1 балл количественная величина индекса враждебности увеличится в среднем на 1,02 балла.

Полученное уравнение многофакторной регрессии (3.14) имеет еще одно приложение. Так, подставляя в него значения переменных xи z, можно определить ожидаемую величину переменной y (уровня враждебности).

2.3. Анализ регрессионной модели

В предыдущем параграфе была вычислена модель множественной регрессии (3.14): ,

гдеy– значение зависимой переменной,

xи z– значения зависимых переменных,

–3,34 – свободный член,

1,82 и 1,02 – параметры уравнения (коэффициенты при независимых переменных).

Для многофакторной регрессионной модели имеют место следующие предпосылки:

1. Зависимые переменные – величины неслучайные;

2. Математическое ожидание случайной составляющей в любом наблюдении равно нулю: ;

3. Дисперсия случайной составляющей постоянна для всех наблюдений: ;

4. Отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях: .

Факторы, включенные во множественную регрессию (3.14), количественно измерены и не сильно коррелируют друг с другом (корреляция– связь между собой двух и более переменных в одной или нескольких изучаемых группах). Кроме того, каждый фактор тесно связан с результатом.

Многофакторная регрессия представляет регрессию результативного признака с двумя и большим числом независимых переменных вида: .

В уравнении регрессии (3.14) случайная (зависимая) переменная yзависит не только от значений независимых переменных xи z, но и от ряда других факторов, влияющих на y, которые не могут быть проконтролированы. В связи с этим , где e – случайная величина, характеризующая отклонения результативного признака от теоретического, найденного по уравнению регрессии.

При исследовании зависимости результативного признака y в многофакторной модели необходимо решать такие же задачи, что и при однофакторной модели:

• определение вида регрессии;

• оценка параметров;

• определение тесноты связи.

Однако наряду с этими задачами необходимо рассматривать и ряд задач, характерных лишь для многофакторной регрессии.

К таким задачам относится отбор факторов, существенно влияющих на фактор y, при наличии возможностей внутренней взаимосвязи между зависимыми переменными xи z. Такой отбор требует, прежде всего, глубокого теоретического и практического знания качественной стороны рассматриваемых психологических явлений.

Интерпретация результатов

До сих пор мы употребляли абстрактный математический язык. Перевод модели на язык экспериментатора называется интерпретацией модели. Задача интерпретации весьма сложна.

Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации. Величина коэффициента регрессии – количественная мера этого влияния. Чем больше коэффициент, тем сильнее влияет фактор. О характере влияния факторов говорят знаки коэффициентов. Знак плюс свидетельствует о том, что с увеличением зна­чения фактора растет величина параметра оптимизации, а при знаке минус – убывает.

Анализируя сущность уравнения регрессии (3.14), следует отметить следующие положения. Рассмотренный подход не обеспечивает раздельной (независимой) оценки коэффициентов – изменение значения одного коэффициента влечет изменение значений других. Полученные коэффициенты не следует рассматривать как вклад соответствующего параметра в значение показателя. Уравнение регрессии является всего лишь хорошим аналитическим описанием имеющихся экспериментальных данных, а не законом, описывающим взаимосвязи параметров и показателя. Это уравнение применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.

В настоящее время регрессионный анализ широко используется в дифференциальной психологии и психодиагностике. С его помощью можно разрабатывать тесты, устанавливать структуру связей между отдельными психологическими характеристиками, измеряемыми набором тестов или заданиями теста.

Регрессионный анализ используется также для стандартизации тестовых методик, которая проводится на репрезентативной выборке испытуемых.

2.4. Аппроксимация экспериментальных данных

На практике часто приходится сталкиваться с задачей сглаживания экспериментальных зависимостей или задачей аппроксимации. Аппроксимацией называется процесс подбора эмпирической формулы для установленной из опыта функциональной зависимости . Эмпирические формулы служат для аналитического представления опытных данных.

Другими словами, аппроксимация, или приближение – это научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны).

Одна независимая переменная

Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости и, соответственно, вид эмпирической формулы, т.е. решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим. Если нет каких-либо теоретических соображений для подбора вида формулы, обычно выбирают функциональную зависимость из числа наиболее простых, сравнивая их графики с графиком заданной функции. После выбора вида формулы определяют ее параметры. Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных. Во многих случаях, в особенности, если функция задана графиком или таблицей (на дискретном множестве точек), для оценки степени приближения рассматривают разности для точек .

Существуют различные меры близости и, соответственно, способы решения этой задачи. Некоторые из них очень просты, быстро приводят к результату, но результат этот является сильно приближенным, другие более точными, но более сложными. Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов. При этом функция считается наилучшим приближением к , если для нее сумма квадратов отклонений «теоретических» значений , найденных по эмпирической формуле, от соответствующих опытных значений ,

имеет наименьшее значение по сравнению с другими функциями, из числа которых выбирается искомое приближение.

Используя методы дифференциального исчисления, метод наименьших квадратов формулирует аналитические условия достижения суммой квадратов отклонений своего наименьшего значения.

В простейшем случае задача аппроксимации экспериментальных данных выглядит следующим образом.

Пусть экспериментальные данные, полученные практическим путем, которые можно представить парами чисел , зависимость между которыми отражает таблица.

На основе данных требуется подобрать функцию , которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и, по возможности, точно отражала общую тенденцию зависимости междуx и y, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения в каком-то смысле были бы наименьшими.

Выяснить вид функции можно либо из теоретических соображений, либо анализируя расположение точек на координатной плоскости. Расположение экспериментальных точек может иметь самый различный вид, и каждому соответствует конкретный тип функции.

Построение эмпирической функции сводится к вычислению входящих в нее параметров, так чтобы их всех функций такого вида выбрать ту, которая лучше других описывает зависимость между изучаемыми величинами. То есть сумма квадратов разности между табличными значениями функции в некоторых точках и значениями, вычисленными по полученной формуле, должна быть минимальна.

Степень близости аппроксимации экспериментальных данных выбранной функцией оценивается коэффициентом детерминации (). Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных. Таким образом, если есть несколько подходящих вариантов типов аппроксимации функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1).

Количественная мератесноты связи	Качественная характеристикасилы связи
0,1-0,3	Слабая
0,3-0,5	Умеренная
0,5-0,7	Заметная
0,7-0,9	Высокая
0,9-0,99	Весьма высокая

Таблица 4. Показатели тесноты связи

Таким образом, функциональная связь возникает при значении равном 1, а отсутствие связи – 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50%. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

В MS Excel аппроксимация экспериментальных данных осуществляется путем построения графика – линии тренда (x, y – заданные величины).

Тренд – тенденция изменения показателей временного ряда. Тренды могут быть описаны различными функциями. Тип тренда устанавливают на основе данных временного ряда, путем осреднения показателей динамики ряда, на основе статистической проверки гипотезы о постоянстве параметров графика. Возможны следующие варианты функций:

1. Линейная – . Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.

2. Полиномиальная – , где до шестого порядка включительно (), — константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третей степени может дать один или два экстремума, четвертой степени – не более трех экстремумов и т.д.

3. Логарифмическая – , где a и b– константы, lnx– функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.

4. Степенная – , где a и b– константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.

5. Экспоненциальная – , где a и b– константы, e– основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений.

Для осуществления аппроксимации на диаграмме экспериментальных данных необходимо щелчком правой кнопки мыши вызвать всплывающее меню и выбрать пункт Добавить линию тренда. В появившемся диалоговом окне Линия тренда на вкладке Тип выбирается вид аппроксимирующей функции, а на вкладке Параметры устанавливаются флажки в полях показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (). После чего нужно щелкнуть по кнопке ОК. В результате получим на диаграмме аппроксимирующую кривую.

Проделав данную операцию несколько раз, можно представить линейную зависимость индексов с уравнениями линий тренда и коэффициентом детерминации – для анализа полной достоверности результатов исследуемых показателей (рис.3, рис.4).

Рис.3 Зависимость индекса враждебности от индекса обиды

Рис.4 Зависимость индекса враждебности от индекса подозрительности

Как видно, из рис.3,

Несколько независимых переменных

В тех случаях, когда аппроксимируемая переменная yзависит от нескольких независимых переменных , подход с построением линии тренда не дает решения. Здесь могут быть использованы следующие специальные функции MS Excel:

ЛИНЕЙН и ТЕНДЕНЦИЯ для аппроксимации линейных функций вида:

,

ЛГРФПРИБЛ и РОСТ для аппроксимации показательных функций вида:

Функции ЛИНЕЙН и ЛГРФПРИБЛ служат для вычисления неизвестных коэффициентов , в указанных выражениях, а также коэффициентов детерминации (). Обе функции имеют одинаковые параметры:

ЛИНЕЙН (известные значения y; известные значения x; конст; статистика);

ЛГРФПРИБЛ (известные значения y; известные значения x; конст; статистика).

Здесь:

• известные значения y – множество наблюдаемых значений y из казанных выражений;

• известные значения x – множество наблюдаемых значений . Причем, если массив известные значения y имеет один столбец, то каждый столбец массива известные значения x интерпретируется как отдельная переменная, а если массив известные значения y имеет одну строку, то тогда каждая строка массива известные значения xинтерпретируется как отдельная переменная;

• конст – логическое значение, которое указывает, требуется ли, чтобы константа была равна 0 (для функции ЛИНЕЙН) или 1 (для функции ЛГРФПРИБЛ). При этом, если конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то полагается равным 0 или 1;

• статистика – логическое значение, которое указывает, требуется ли вычислять дополнительную статистику по регрессии, если введено значение ИСТИНА, то дополнительные параметры вычисляются, если ЛОЖЬ, то – нет.

Функции ТЕНДЕНЦИЯ и РОСТ позволяют находить точки, лежащие на аппроксимирующих кривых, для значений коэффициентов , найденных функциями ЛИНЕЙН и ЛГРФПРИБЛ.

Обе функции имеют одинаковые аргументы:

ТЕНДЕНЦИЯ (известные значения y; известные значения x; новые значения x; конст);

РОСТ (известные значения y; известные значения x; новые значения x; конст).

Здесь:

• известные значения y – множество значений y;

• известные значения x – множество значений x;

• новые значения x – те значений x, для которых необходимо определить соответствующие аппроксимирующие или предсказанные значения y.Новые значения x должны содержать столбец (или строку) для каждой независимой переменной, как и известные значения x. Если аргумент новые значения x опущен, то предполагается, что он совпадает с аргументом известные значения x;

• конст – логическое значение, которое указывает, требуется ли, чтобы константа была равна 0 (для функции ТЕНДЕНЦИЯ) или 1 (для функции РОСТ). При этом, если конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом, а если конст имеет значение ЛОЖЬ, то полагается равным 0 или 1.

Заключение

Тщательное, скурпулезное проведение эксперимента, несомненно, является главным условием успеха исследования. Это общее правило, и планирование эксперимента не относится к исключениям.

Однако экспериментатору не безразлично, как обработать полученные данные. Необходимо извлечь из них всю информацию и сделать соответствующие выводы. С одной стороны, не извлечь из эксперимента все, что из него следует, — значит пренебречь нелегким трудом экспериментатора. С другой стороны, сделать утверждения, не следующие из эксперимента, — значит создавать иллюзии, заниматься самообманом. Статистические методы обработки результатов эксперимента позволяют не перейти разумной меры риска.

Если данные, полученные в эксперименте, качественного характера, то правильность делаемых на основе их выводов полностью зависит от интуиции, эрудиции и профессионализма исследователя, а также от логики его рассуждений. Если же эти данные количественного типа, то сначала проводят их первичную, а затем вторичную статистическую обработку.

Вторичная статистическая обработка проводится в том случае, если для решения задач или доказательства предложенных гипотез необходимо определить статистические закономерности, скрытые в первичных экспериментальных данных. Приступая к вторичной статистической обработке, исследователь, прежде всего, должен решить, какие из различных вторичных статистик ему следует применить для обработки первичных экспериментальных данных.

Таким образом, реализована цель данной работы, т.е. разработана методика проведения регрессионного анализа статистических данных психологического эксперимента для прогнозирования исследуемых показателей. Это было достигнуто через реализацию всех поставленных задач с помощью теоретических и эмпирических методов. Таких как анализ различной литературы, систематизация полученной информации (знаний) и ее обобщение; наблюдение и анкетирование (опрос).

Математическая статистика – прикладная отрасль математики, основанная на теории вероятностей и предназначенная в самом общем плане для систематизации и анализа эмпирических (опытных) данных, получаемых при изучении повторяющихся и варьирующихся явлений.

Планирование и анализ экспериментов – это раздел математической статистики, включающий систему методов обнаружения и проверки причинных связей между переменными.

Таким образом, математическая статистика – это точная и полезная наука. Но лишь для думающего исследователя, не пренебрегающего необходимостью вникнуть в существо идей и методов теории вероятностей и математической статистики.

В целом же, статистические методы помогают исследователям описывать данные, делать выводы в отношении больших массивов данных и изучать причинные зависимости.

Список использованных источников

1. Дуброва, Т.А. Статистиские методы прогнозирования: Учебное пособие [Текст]/ Т.А. Дуброва. – М.: ЮНИТИ, 2003. – 204с.

2. Ермолаев О.Ю. Математическая статистика для психологов : Учебник [Текст]/ О.Ю. Ермолаев. – М.: Изд-во Флинта Московского психолого-социального института, 2004. – 335с.

3. Калинина, В.Н. Теория вероятностей и математическая статистика: Учебное пособие для вузов [Текст]/ В.Н. Калинина. – М.: Дрофа, 2008. – 471с.

4. Калинина, В.Н. Математическая статистика: Учебник для студентов [Текст]/ В.Н. Калинина, В.Ф. Панкин. – М.: Дрофа, 2002. – 335с.

5. Крамер, Д. Математическая обработка данных в социальных науках: современные методы: Учебное пособие для вузов [Текст]/ Дункан Крамер. – Академия, 2007. – 287с.

6. Красс, М.С. Математика для экономического бакалавриата: Учебник [Текст]/ М.С. Красс, Б.П. Чупрынов. – М.: Дело, 2005. – 574с.

7. Кричевец, А.Н. Математика для психологов: Учебник [Текст]/ А.Н. Кричевец, Е.В. Шикин, А.Г. Дьячков. – М.: Изд-во Флинта Московского психолого-социального института, 2005. – 371с.

8. Могилев, А.В, Информатика: Учебник [Текст]/ А.В. Могилев, Н.И. Пак, Е.К. Хеннер. – М.: Академия, 2003. – 809с.

9. Немов, Р.С. Психодиагностика. Введение в научное психологическое исследование с элементами математической статистики [Текст]/ Р.С. Немов. – М.: ВЛАДОС, 1998. – 632 с.

10. Палий, И.А. Прикладная статистика: Учебное пособие для вузов [Текст]/ И.А. Палий. – М.: Высшая школа, 2004. – 175с.

11. Рубинштейн, С.Л. Основы общей психологии [Текст]/ С.Л. Рубинштейн. – СПб.: Питер, 2008. – 705с.

12. Симонович, С.В. Специальная информатика: Учебное пособие [Текст]/ С.В. Симонович, Г.А. Евсеев, А.Г. Алексеев. – М., 2002. – 479с.

13. Созонова, М.С. Математические методы в психологии: Учебное пособие [Текст]/ М.С. Созонова. – Тобольск: ТГСПА им. Д.И. Менделеева, 2006. – 172с.

14. Фадеев, М.А. Элементарная обработка результатов эксперимента: Учебное пособие [Текст]/ М.А. Фадеев. – СПб, М., Краснодар: Лань, 2008. – 117с.

Приложение 1

Инструкция: опросник Басса-Дарки состоит из 75 утверждений, на которые испытуемый отвечает «да» или «нет».

1. Временами я не могу справиться с желанием причинить вред другим.

2. Иногда я сплетничаю о людях, которых не люблю.

3. Я легко раздражаюсь, но быстро успокаиваюсь.

4. Если меня не попросят по-хорошему, я не выполню просьбы.

5. Я не всегда получаю то, что мне положено.

6. Я знаю, что люди говорят обо мне за моей спиной.

7. Если я не одобряю поведения друзей, то даю им это почувствовать.

8. Если мне случалось обмануть кого-нибудь, я испытывал мучительные угрызения совести.

9. Мне кажется, что я не способен ударить человека.

10. Я никогда не раздражаюсь настолько, чтобы кидаться предметами.

11. Я всегда снисходителен к чужим недостаткам.

12. Если мне не нравится установленное правило, мне хочется нарушить его.

13. Другие умеют (лучше, чем я) почти всегда пользоваться благоприятными обстоятельствами.

14. Я держусь настороженно с людьми, которые относятся ко мне несколько более дружественно, чем я ожидал.

15. Я часто бываю не согласен с людьми.

16. Иногда мне на ум приходят мысли, которых я стыжусь.

17. Если кто-нибудь первым ударит меня, я не отвечу ему.

18. Когда я раздражаюсь, я хлопаю дверьми.

19. Я гораздо более раздражителен, чем кажется окружающим.

20. Если кто-нибудь корчит из себя начальника, я всегда поступаю ему наперекор.

21. Меня немного огорчает моя судьба.

22. Я думаю, что многие люди не любят меня.

23. Я не могу удержаться от спора, если люди не согласны со мной.

24. Люди, увиливающие от работы, должны испытывать чувство вины.

25. Тот, кто оскорбляет меня или мою семью, напрашивается на драку.

26. Я не способен на грубые шутки.

27. Меня охватывает ярость, когда надо мной насмехаются.

28. Когда люди строят из себя начальников, я делаю всё, чтобы они не зазнавались.

29. Почти каждую неделю я вижу кого-нибудь, кто мне не нравится.

30. Довольно многие люди завидуют мне.

31. Я требую, чтобы люди уважали мои права.

32. Меня угнетает то, что я мало делаю для своих родителей.

33. Люди, которые постоянно изводят Вас, стоят того, чтобы их щёлкнули по носу.

34. От злости я иногда бываю мрачен.

35. Если ко мне относятся хуже, чем я того заслуживаю, я не расстраиваюсь.

36. Если кто-то выводит меня из себя, я не обращаю на него внимания.

37. Хотя я и не показываю этого, иногда меня гложет зависть.

38. Иногда мне кажется, что надо мной смеются.

39. Даже если я злюсь, я не прибегаю к «сильным» выражениям.

40. Мне хочется, чтобы мои ошибки были прощены.

41. Я редко даю сдачи, даже если кто-нибудь ударит меня.

42. Когда получается не по-моему, я всегда обижаюсь.

43. Иногда люди раздражают меня просто своим присутствием.

44. Нет людей, которых бы я по-настоящему ненавидел.

45. Мой принцип: «Никогда не доверяй чужакам».

46. Если кто-нибудь раздражает меня, я готов сказать всё, что о нём думаю.

47. Я делаю много такого, о чём впоследствии сожалею.

48. Если я разозлюсь, я могу ударить кого-нибудь.

49. С десяти лет я никогда не проявлял вспышек гнева.

50. Я часто чувствую себя, как пороховая бочка, готовая взорваться.

51. Если бы все знали, что я чувствую, меня бы считали человеком, с которым нелегко ладить.

52. Я всегда думаю о том, какие тайные причины заставляют людей делать что-то приятное для меня.

53. Когда на меня кричат, я начинаю кричать в ответ.

54. Неудачи огорчают меня.

55. Я дерусь не реже и не чаще, чем другие.

56. Я могу вспомнить случай, когда я был настолько зол, что хватал попавшуюся мне под руку вещь и ломал её.

57. Иногда я чувствую, что готов первым начать драку.

58. Иногда я чувствую, что жизнь поступает со мной несправедливо.

59. Раньше я думал, что большинство людей говорит правду, но теперь я в это не верю.

60. Я ругаюсь только от злости.

61. Иногда я поступаю неправильно, меня мучает совесть.

62. Если для защиты своих прав мне надо применять физическую силу, я применяю её.

63. Иногда я выражаю свой гнев тем, что стучупо столу кулаком.

64. Я бываю грубоват по отношению к людям, которые мне не нравятся.

65. У меня нет врагов, которые хотели бы мне навредить.

66. Я не умею поставить человека на место, даже если он того заслуживает.

67. Я часто думаю, что жил неправильно.

68. Я знаю людей, которые способны довести меня до драки.

69. Я не раздражаюсь из-за мелочей.

70. Мне редко приходит в голову, что люди пытаются разозлить или оскорбить меня.

71. Я часто просто угрожаю людям, хотя и не собираюсь приводить угрозы в исполнение.

72. В последнее время я стал занудой.

73. В споре я часто повышаю голос.

74. Обычно я стараюсь скрывать плохое отношение к людям.

75. Я лучше соглашусь с чем-либо, чем стану спорить.

Обработка результатов: Обработка опросника производится при помощи индексов различных форм агрессивных и враждебных реакций, которые определяются суммированием полученных ответов.

1. Физическая агрессия:

Ответы «да» в вопросах №№ 1, 25, 33, 48, 55, 62, 68

Ответы «нет» в вопросах №№ 9, 17, 41 10

2. Косвенная агрессия:

Ответы «да» в вопросах №№ 2, 18, 34, 42, 56, 63

Ответы «нет» в вопросах №№ 10, 26, 49 9

3. Раздражение:

Ответы «да» в вопросах №№ 3, 19, 27, 43, 50, 57, 64, 72

Ответы «нет» в вопросах №№ 11, 35, 69 11

4. Негативизм:

Ответы «да» в вопросах №№ 4, 12, 20, 23, 36 5

5. Обида:

Ответы «да» в вопросах №№ 5, 13, 21, 29, 37, 51, 58

Ответы «нет» — № 44 8

6. Подозрительность:

Ответы «да» в вопросах №№ 6, 14, 22, 30, 38, 45, 52, 59

Ответы «нет» в вопросах — № 65, 70 10

7. Вербальная агрессия:

Ответы «да» в вопросах №№ 7, 15, 23, 31, 46, 53, 60, 71, 73

Ответы «нет» в вопросах №№ 39, 66, 74, 75 13

8. Угрызения совести, чувство вины:

Ответы «да» в вопросах №№ 8, 16, 24, 32, 40, 47, 54, 61, 67 9

Физическая агрессия, косвенная агрессия, раздражение и вербальная агрессия вместе образуют суммарный индекс агрессивных реакций, а обида и подозрительность – индекс враждебности.

Приложение 2

Таблица 1. Набранные индексы по видам реакций, их сумма.

№	Фамилия ученика	1	2	3	4	5	6	7	8	Сумма
1	Бакиева	9	7	6	4	5	8	10	7	56
2	Гатауллин	8	6	3	2	1	4	10	5	34
3	Гатин	7	2	3	2	2	2	7	6	31
4	Долженко	6	2	8	0	5	4	9	5	39
5	Жарова	9	4	7	3	4	7	9	5	48
6	Жуйкова	5	5	7	4	6	3	3	8	41
7	Корикова	9	4	3	4	5	7	7	8	47
8	Костерина	10	9	8	4	7	7	11	9	65
9	Курманалиева	10	7	7	4	4	7	13	8	60
10	Летунов	8	6	6	4	3	2	10	7	46
11	Мороков	9	7	9	4	4	5	10	7	55
12	Перовских В.	10	8	8	4	4	9	11	7	61
13	Перовских М.	8	2	5	2	4	7	9	8	45
14	Смирнова	5	5	9	5	4	8	10	7	53
15	Солосина	4	7	7	1	7	8	9	7	50
16	Тимирова	9	6	4	3	1	2	11	6	42
17	Трухин	7	6	3	4	2	4	12	2	40
18	Филиппов	8	3	5	4	4	6	10	8	48
19	Хабисов	8	3	6	3	6	3	9	5	43
20	Цыпанов	6	0	0	2	0	2	3	3	16
Максимальный набор индексов	10	9	11	5	8	10	13	9	75

1 — физическая агрессия

2 — косвенная агрессия

3 — раздражение

4 — негативизм

5 — обида

6 — подозрительность

7 — вербальная агрессия

8 — угрызение совести, чувство вины

Приложение 3

Таблица 2. Индексы.

№	Фамилия ученика	Индекс агрессии	Индекс враждебности
1	Бакиева	32	13
2	Гатауллин	27	5
3	Гатин	19	4
4	Долженко	25	9
5	Жарова	29	11
6	Жуйкова	20	9
7	Корикова	23	12
8	Костерина	38	14
9	Курманалиева	37	11
10	Летунов	30	5
11	Мороков	35	9
12	Перовских В.	37	13
13	Перовских М.	24	11
14	Смирнова	29	12
15	Солосина	27	15
16	Тимирова	30	3
17	Трухин	28	6
18	Филиппов	26	10
19	Хабисов	26	9
20	Цыпанов	9	2
Максимальный набор индексов	43	18

Содержание

• 1 Использование описательной статистики
  • 1.1 Подключение «Пакета анализа»
  • 1.2 Применение инструмента «Описательная статистика»
  • 1.3 Помогла ли вам эта статья?
  • 1.4 Статистические процедуры Пакета анализа
  • 1.5 Статистические функции библиотеки встроенных функций Excel

Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.

Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

• Медиана;
• Мода;
• Дисперсия;
• Среднее;
• Стандартное отклонение;
• Стандартная ошибка;
• Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

1. Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
2. В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
3. Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Применение инструмента «Описательная статистика»

Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.

1. Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
2. Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
3. После выполнения данных действий непосредственно запускается окно «Описательная статистика».

   В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.

   Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:

   • Выходной интервал;
   • Новый рабочий лист;
   • Новая рабочая книга.

   В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».

   Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.

   Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.

   После того, как все указанные данные внесены, жмем на кнопку «OK».

4. После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
5. После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
   • Асимметричность;
   • Интервал;
   • Минимум;
   • Стандартное отклонение;
   • Дисперсия выборки;
   • Максимум;
   • Сумма;
   • Эксцесс;
   • Среднее;
   • Стандартная ошибка;
   • Медиана;
   • Мода;
   • Счет.

Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.

Урок: Статистические функции в Excel

Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.

Мы рады, что смогли помочь Вам в решении проблемы.

Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

Да Нет

Сортировка данных в Excel

Таблицы Excel можно использовать для создания баз данных, т.е. совокупности определенным образом организованной информации. В таблицах хранят информацию о сотрудниках, клиентах, поставщиках различной продукции, ценах, книгах, фильмах, фотографиях и т.д. Как правило, для таких баз данных используется табличный способ организации. Они содержат большое количество данных, а с большим количеством данных не всегда просто работать. Для этого и необходима обработка данных.

• сортировку списков;
• выборку данных по определенным критериям;
• вычисление промежуточных сумм;
• вычисление средних значений;
• вычисление отклонений от определенного значения;
• построение сводных таблиц.

Как сделать фильтр в Excel

Базы данных очень удобны для хранения информации, но мы создаем их для того, чтобы получать нужную для нас справку, когда возникает подобная необходимость.

Например, нам нужно расписание железнодорожных поездов, которые отправляются в Москву в пятницу после четырех часов дня и т.п.

Поиск нужной информации осуществляется путем отбора строк, удовлетворяющих некоторому критерию. В большинстве случаев критерием отбора является равенство содержимого ячейки определенному значению.

Помимо сравнения на равенство, при отборе записей можно использовать и другие операции сравнения. Например, больше, меньше, больше или равно, меньше или равно. Использование этих операций позволяет сформулировать критерий запроса менее строго. Например, если требуется найти информацию о человеке, фамилия которого начинается с «Ку», то в качестве критерия можно использовать правило «содержимое ячейки Фамилия больше или равно Ку и содержимое ячейки Фамилия меньше Л».

Промежуточные итоги в Excel

Одним из методов обработки данных является подведение итогов. Пусть, например, есть таблица расходов. Для того чтобы узнать, сколько потрачено в каждом месяце, необходимо подвести итог за каждый месяц.

• 1. Выделить диапазон, содержащий данные и заголовки столбцов, в которых данные находятся. В рассматриваемом примере это вся таблица, на фото представлена только ее часть.
• 2. На вкладке Данные -> Структура выбрать команду Промежуточный итог.
• 3. В появившемся диалоговом окне Промежуточные итоги в поле — При каждом изменении в:, требуется задать столбец, при изменении содержимого которого будет вычислена промежуточная сумма. В данном случае это Дата. В поле Операция выбрать операцию из списка, которую нужно выполнить над обрабатываемыми данными. В нашем случае это Сумма. В поле — Добавить итоги по:, установить флажок в том столбце, в котором находятся обрабатываемые данные.

Сводные таблицы Excel 2010

Сводная таблица позволяет выполнить более тонкий анализ данных, чем простое подведение итога. Что такое сводная таблица и как ее построить, рассмотрим на примере.

Пусть есть таблица, в которой находится информация о расходах.

Основными средствами анализа статистических данных в Excel являются статистические процедуры надстройки Пакет анализа (Analysis ToolРак) и статистические функции библиотеки встроенных функций. Основные сведения обо всех этих средствах имеются в электронной справочной системе Excel.

Однако качество описаний статистических процедур и функций, приведенных в этой системе, заставляет желать лучшего. Некоторые из этих описаний не очень понятны, в них имеются неточности, а подчас и просто ошибки (это относится как к англоязычному оригиналу, так и к русскому переводу). Эти недостатки с завидным постоянством повторяются и во многих пособиях по Excel. Найти необходимые пособия в интернете можно быстро если скачать бесплатно Амиго браузер с усовершенствованным поисковым алгоритмом.

Статистические процедуры Пакета анализа

Наиболее развитыми средствами анализа данных являются статистические процедуры Пакета анализа. Они обладают большими возможностями, чем статистические функции. С их помощью можно решать более сложные задачи обработки статистических данных и выполнять более тонкий анализ этих данных.

В Пакет анализа входят следующие статистические процедуры:

1. генерация случайных чисел (Random number generation);
2. выборка (Sampling);
3. гистограмма (Histogram);
4. описательная статистика (Descriptive statistics);
5. ранги персентиль (Rank and percentile);
6. двухвыборочный z-тест для средних (z-Test: Two Sample for Means);
7. двухвыборочный t-тест для средних с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances);
8. двухвыборочный t-тест для средних с различными дисперсиями (t-Test: Two-Sample Assuming Unequal Variances);
9. парный двухвыборочный t-тест для средних (t-Test: Paired Two Sample for Means);
10. двухвыборочный F-тест да я дисперсий (F-Test: Two Sample for Variances);
11. коварнация (Covariance);
12. корреляция (Correlation);
13. рецессия (Regression);
14. однофакторный дисперсионный анализ (ANOVA: Single Factor);
15. двухфакторный дисперсионный анализ без повторений (ANOVA: Two Factor Without Replication);
16. двухфакторный дисперсионный анализ с повторениями (ANOVA: Two Factor With Replication);
17. скользящее среднее (Moving Average);
18. экспоненциальное сглаживание (Exponential Smoothing);
19. анализ Фурье (Fourier Analysis).

Для доступа к процедурам Пакета анализа необходимо в меню Сервис (Tools) щелкнуть указателем мыши на строке Анализ данных (Data Analysis). Откроется диалоговое окно с соответствующим названием, в котором перечислены процедуры статистического анализа данных (рис. 1).

Рис.1. Диалоговое окно Анализ данных

Для того чтобы запустить в работу нужную статистическую процедуру, нужно выделить ее указателем мыши и щелкнуть на кнопке ОК. На экране появится диалоговое окно вызванной процедуры. На рис. 2 для примера показано диалоговое окно процедуры Описательная статистика (Descriptive statistics).

Рис.2. Диалоговое окно процедуры Описательная статистика

Диалоговое окно каждой процедуры содержит элементы управления: поля ввода, раскрывающиеся списки, переключатели, флажки и т. п. Эти элементы позволяют задать нужные параметры используемой процедуры. Некоторые элементы управления имеют специфический характер, присущий одной процедуре или небольшой группе процедур. Назначение таких элементов управления будет рассмотрено при описании соответствующих процедур. Другие элементы управления присутствуют в диалоговых окнах почти всех статистических процедур.

К числу общих для большинства процедур элементов управления относятся:

• поле ввода Входной интервал (Input Range). В это поле вводится ссылка на диапазон, содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом пли группой столбцов (строкой или группой строк);
• переключатель Группирование (Grouped By). В том случае, когда входной диапазон представляет собой столбец или группу столбцов, переключатель устанавливается в положение по столбцам (Columns). Если же входной диапазон представляет собой строку или группу строк, то переключатель устанавливается в положение по строкам (Rows). Более точным названием этого переключателя было бы название Расположение;
• флажок Метки (Labels in First Row). Флажок устанавливается в тех случаях, когда первая строка (первый столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок Метки не устанавливают. При этом Excel автоматически создает и выводит на экран стандартные названия для данных выходного диапазона (Столбец1, Столбец2,… или Строка 1. Строка2,…);
• переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели определяют место вывода таблицы, содержащей результаты реализации статистической процедуры. В группе может быть выбран только одни переключатель.

При выборе переключателя Выходной интервал таблица результатов решения выводится на тот же рабочий лист, на котором находятся исходные данные. Справа от переключателя открывается поле ввода, в которое надо ввести ссылку на левую верхнюю ячейку таблицы результатов. Если возникает опасность наложения таблицы результатов на уже заполненные ячейки, на экране появляется сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых.

В положении Новый рабочий лист открывается новый лист рабочей книги. На этот лист, начиная с ячейки А1, и выводится таблица результатов решения. Справа от переключателя имеется поле ввода, в которое в случае необходимости можно ввести имя нового рабочего листа. При выборе переключателя Новая рабочая книга открывается новая рабочая книга. На первый лист этой новой книги, начиная с ячейки А1, выводится таблица результатов решения.

Следует заметить, что результаты;, получаемые с помощью статистических процедур Пакета анализа, не имеют постоянной связи с исходными данными — в случае изменения исходных данных результаты решения автоматически не изменяются. В том случае, когда необходимо получить результаты, автоматически изменяющиеся вместе с исходными данными, нужно использовать подходящие статистические функции библиотеки встроенных функций.

Эффективным и очень удобным в использовании средством парного регрессионного анализа и анализа временных рядов является процедура Добавить линию тренда (Add Trendline), входящая в комплекс графических средств Excel.

Статистические функции библиотеки встроенных функций Excel

Табличный процессор Excel имеет библиотеку встроенных функции рабочего листа (Worksheet function). Одним из разделов этой библиотеки является раздел Статистические функции. В этот раздел входят 83 функции, предназначенные для решения некоторых наиболее востребованных задач теории вероятностей и математической статистики.

Аргументы статистических функций должны быть числами или ссылками на диапазоны, которые содержат числа Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значениями учитываются.

Когда в качестве какого-либо аргумента встроенной статистической функции введен текст, функция выдает сообщение об ошибке #ЗНАЧ! (#VALUE!). Если в качестве аргумента, который по определению должен быть целым числом, введено число не целое, Excel использует в качестве аргумента целую часть этот числа. Никакие сообщения об этом «несанкционированном округлении» на экран не выводятся.