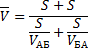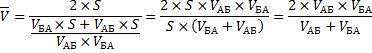Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции С AVERAGE в Microsoft Excel.
Описание
Возвращает среднее арифметическое аргументов. Например, если диапазон A1:A20 содержит числа, формула =СПБ(A1:A20) возвращает среднее из этих чисел.
Синтаксис
СРЗНАЧ(число1;[число2];…)
Аргументы функции СРЗНАЧ описаны ниже.
-
Число1 Обязательный аргумент. Первое число, ссылка на ячейку или диапазон, для которого требуется вычислить среднее значение.
-
Число2… Необязательный. Дополнительные числа, ссылки на ячейки или диапазоны, для которых нужно вычесть среднее значение, не более 255.
Замечания
-
Аргументы могут быть числами, именами или ссылками на диапазоны или ячейки, содержащие числа.
-
Логические значения и текстовые представления чисел, которые непосредственно введите в список аргументов, не учитываются.
-
Если аргумент является ссылкой на диапазон или ячейку, содержащую текст или логические значения, или ссылкой на пустую ячейку, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.
-
Аргументы, являющиеся значениями ошибок или текстом, которые не могут быть преобразованы в числа, вызывают ошибки.
-
Если логические значения и текстовые представления чисел необходимо учитывать в расчетах, используйте функцию СРЗНАЧА.
-
Если требуется вычислить среднее значение только для тех значений, которые удовлетворяют определенным критериям, используйте функцию СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИМН.
Примечание: Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения, описанных ниже.
-
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
-
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При ассиметричном распределении множества чисел они могут отличаться.
Совет: При вычислении средних значений ячеек следует учитывать различие между пустыми ячейками и ячейками, содержащими нулевые значения, особенно если в диалоговом окне Параметры Excel настольного приложения Excel снят флажок Показывать нули в ячейках, которые содержат нулевые значения. Если этот флажок установлен, пустые ячейки игнорируются, но нулевые значения учитываются.
Местонахождение флажка Показывать нули в ячейках, которые содержат нулевые значения
-
Откройте вкладку Файл , а затем нажмите кнопку Параметры и в категории Дополнительно найдите группу Показать параметры для следующего листа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|
10 |
15 |
32 |
|
7 |
||
|
9 |
||
|
27 |
||
|
2 |
||
|
Формула |
Описание |
Результат |
|
=СРЗНАЧ(A2:A6) |
Среднее значение чисел в ячейках A2–A6. |
11 |
|
=СРЗНАЧ(A2:A6;5) |
Среднее значение чисел в ячейках A2–A6 и числа 5. |
10 |
|
=СРЗНАЧ(A2:C2) |
Среднее значение чисел в ячейках A2–C2. |
19 |
Нужна дополнительная помощь?
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
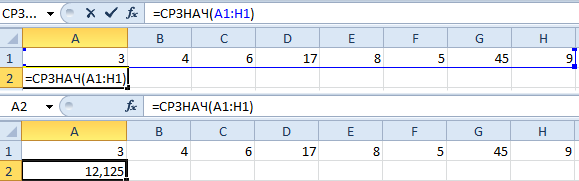
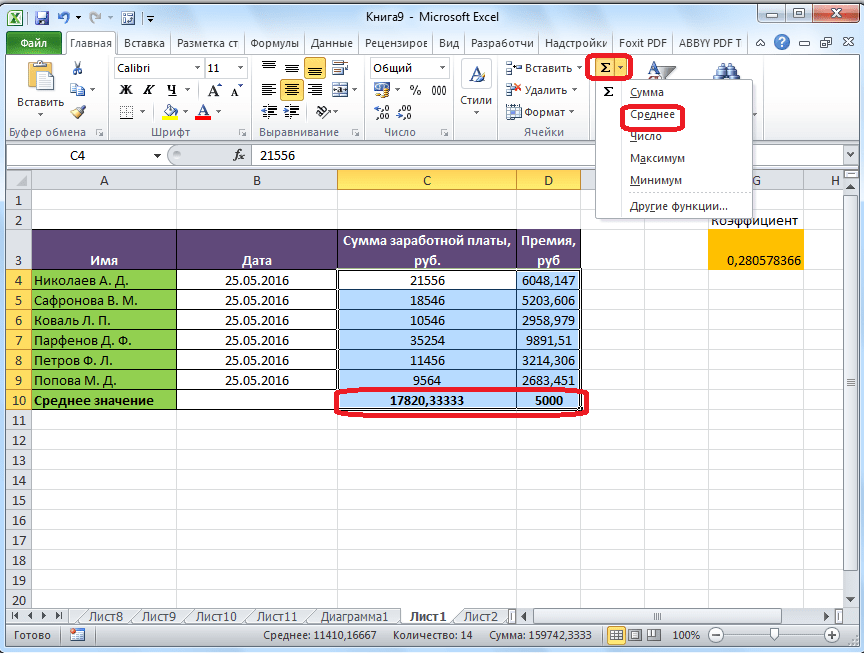
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
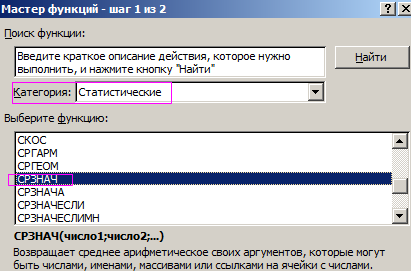
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
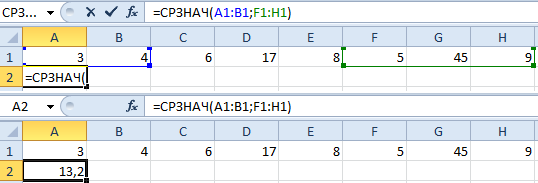
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
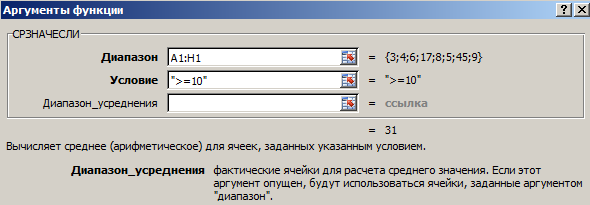
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)
Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:
Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
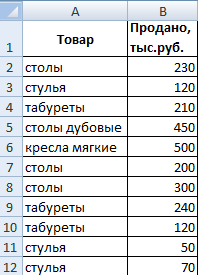
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
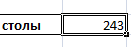
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
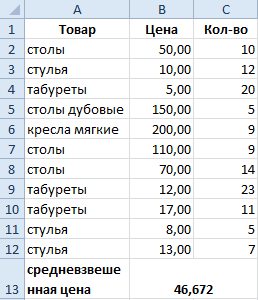
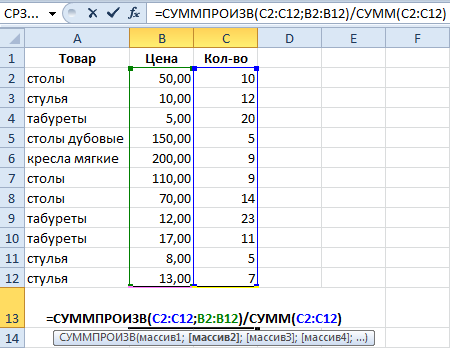
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
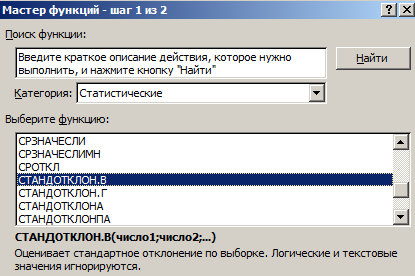
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Содержание
- Стандартный способ вычисления
- Вычисление с помощью Мастера функций
- Панель формул
- Ручной ввод функции
- Расчет среднего значения по условию
- Вопросы и ответы
В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.
Стандартный способ вычисления
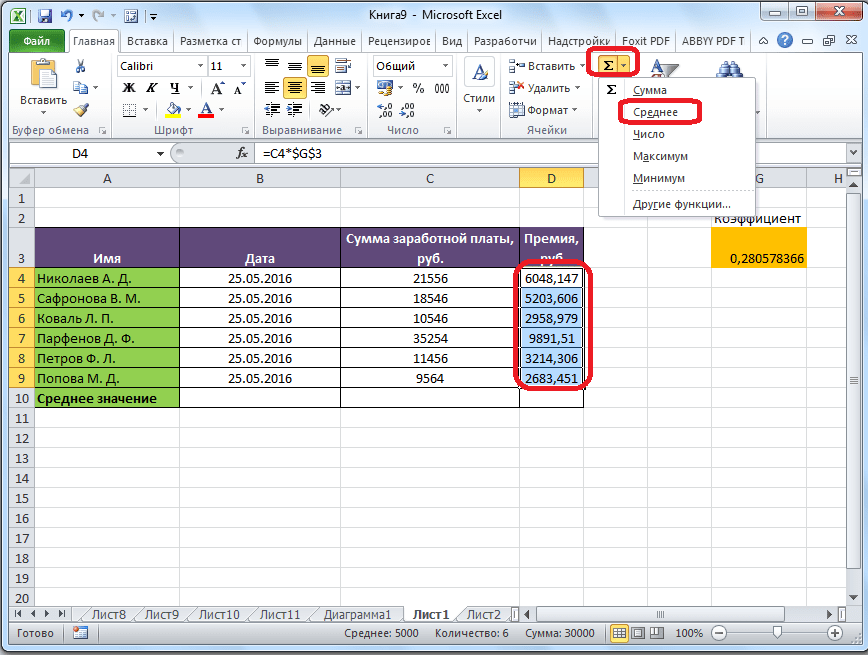
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».
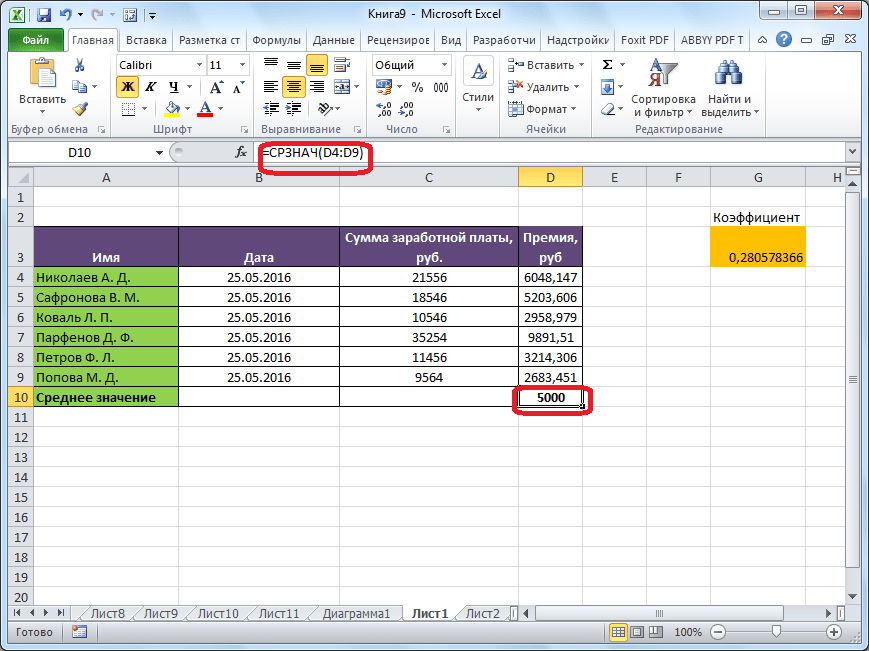
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.
Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.
Вычисление с помощью Мастера функций
Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.
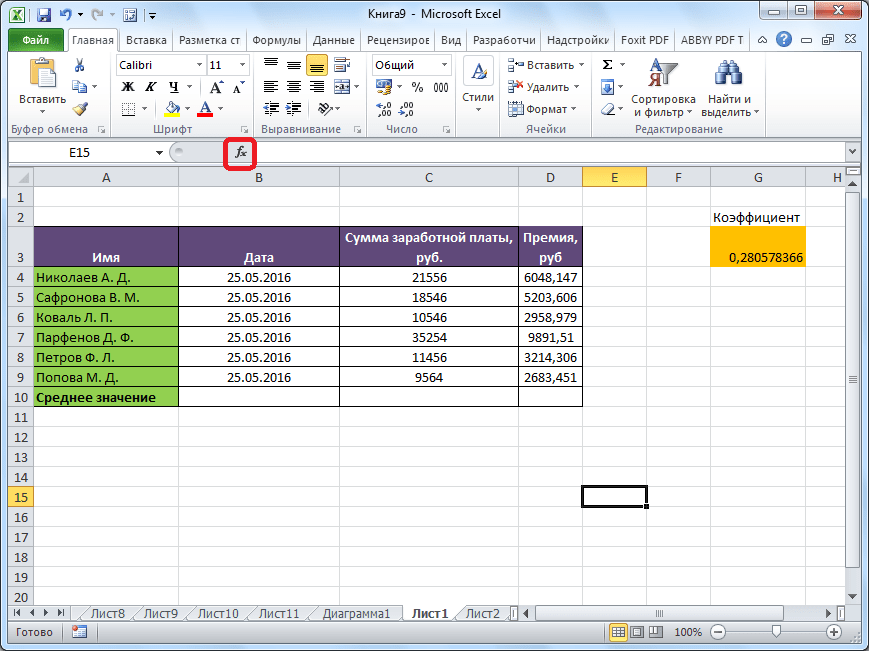
Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.
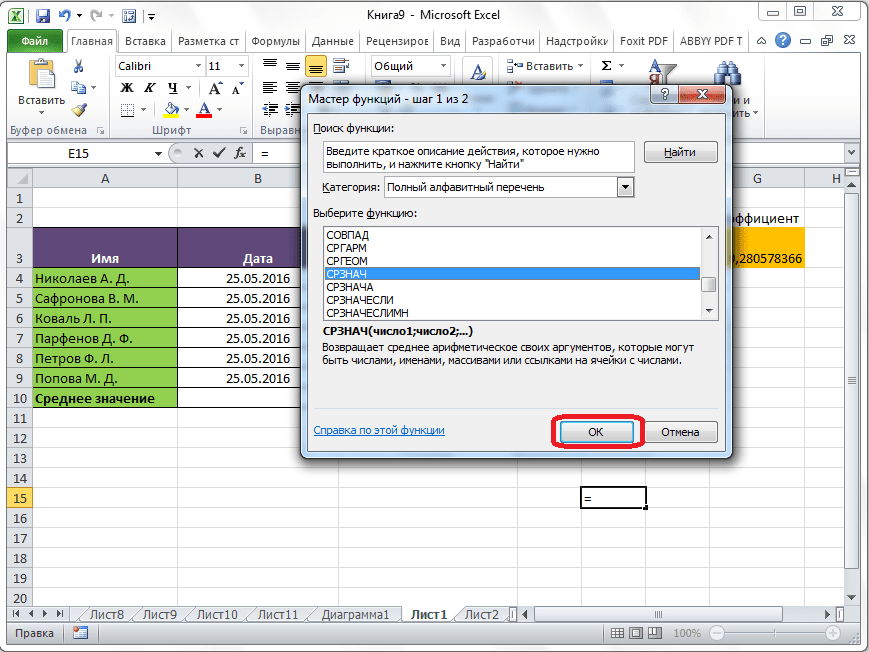
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».
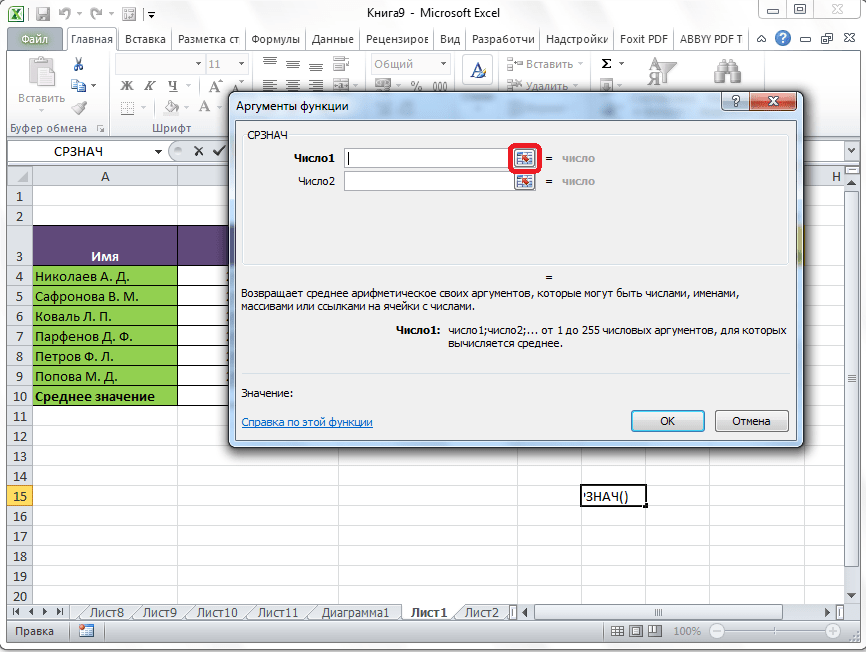
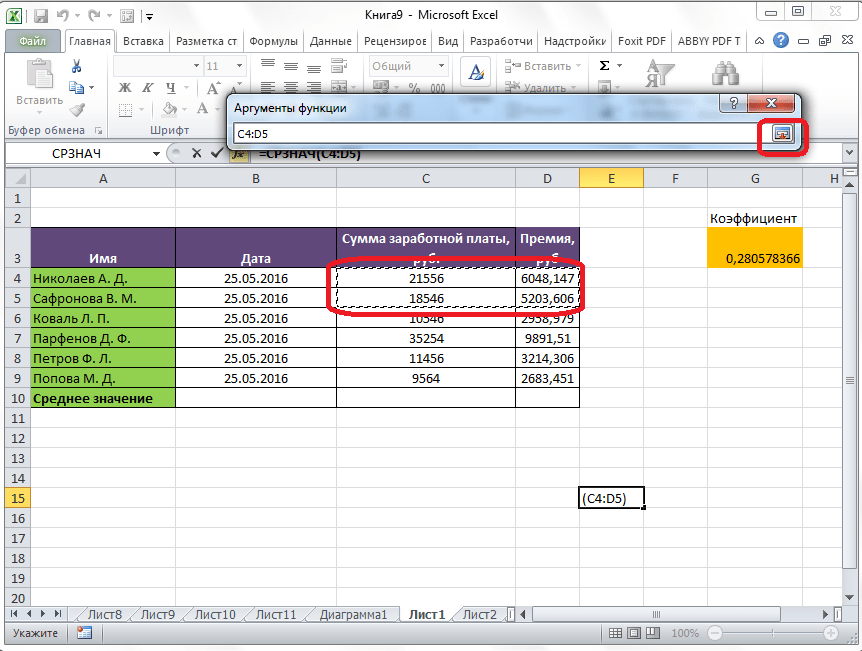
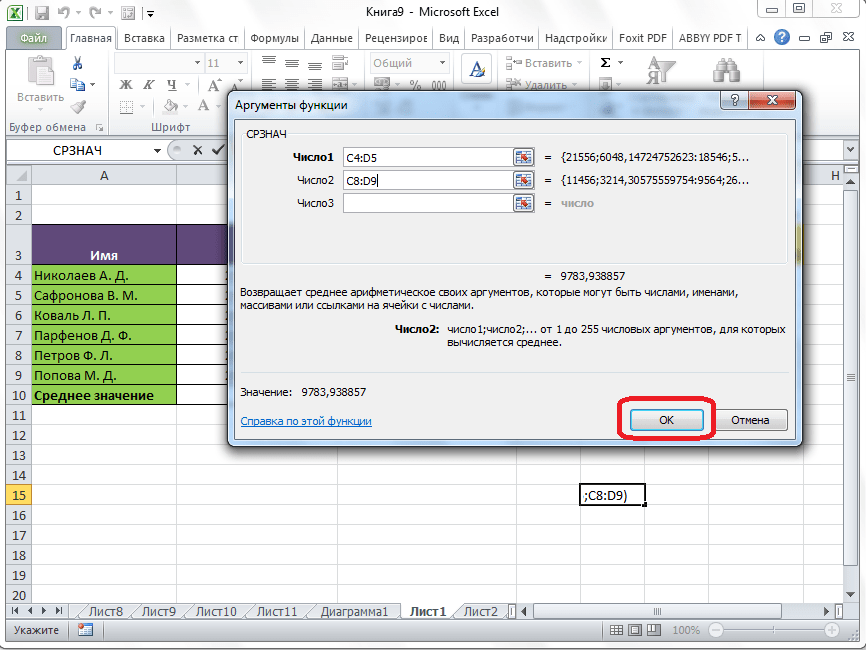
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.
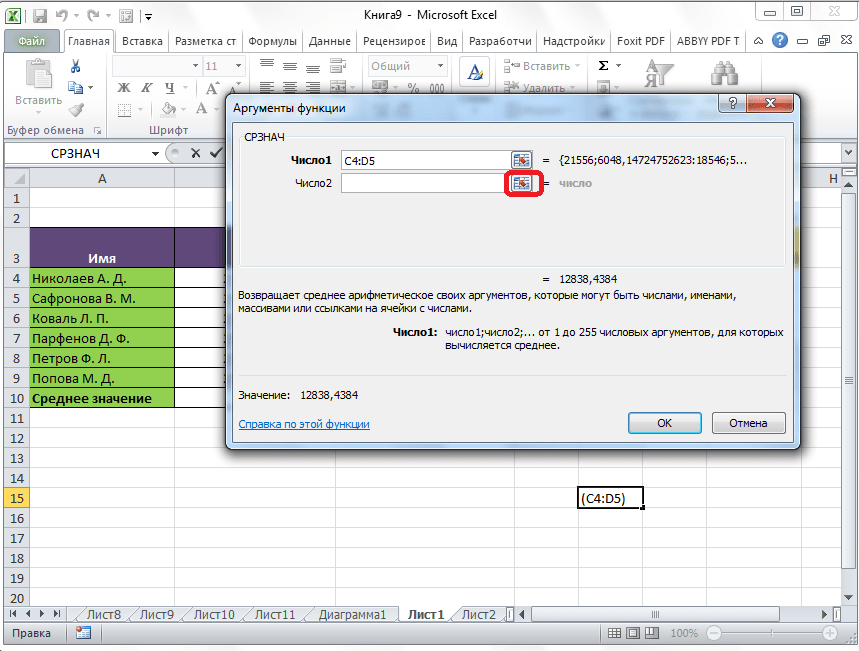
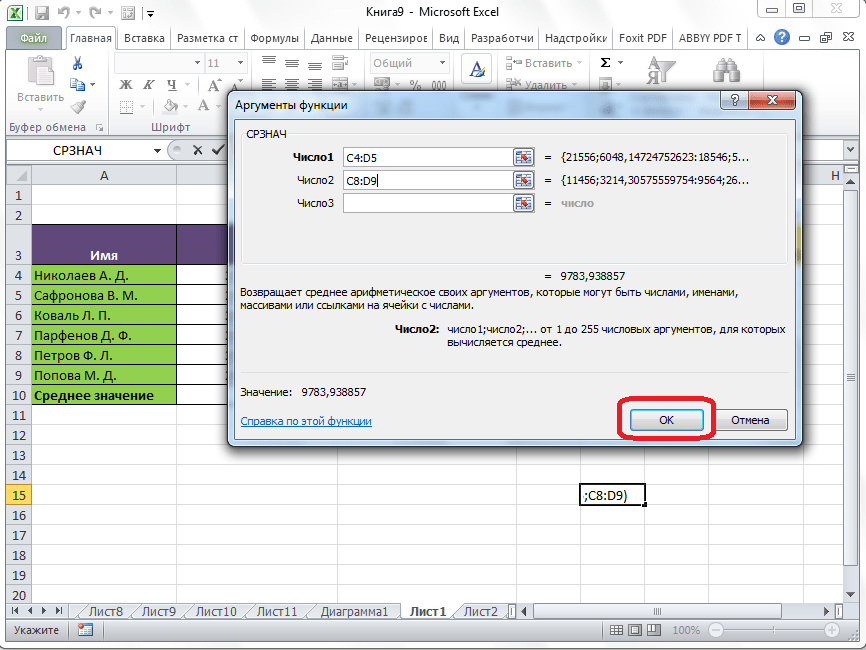
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.
После этого, жмите на кнопку «OK».
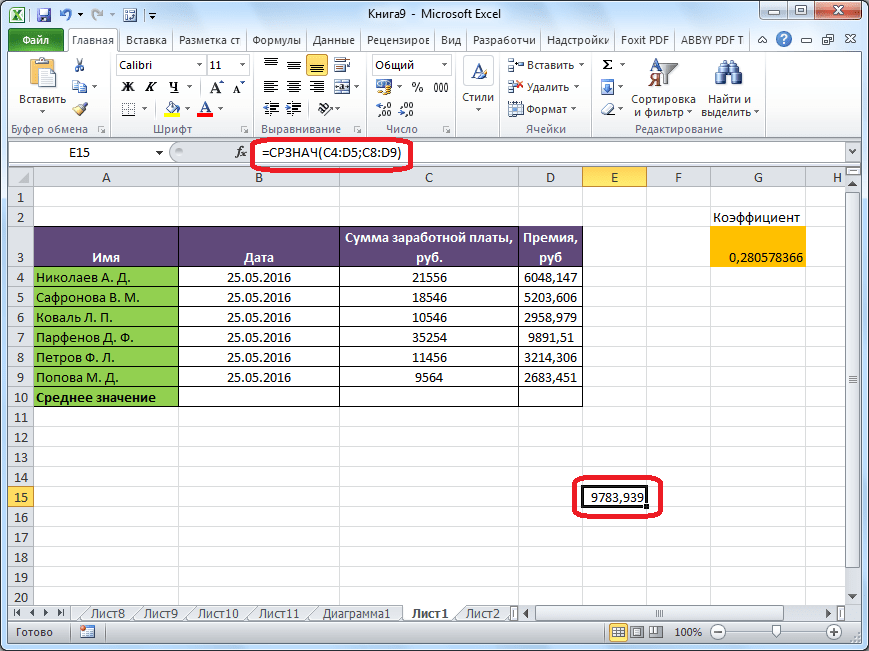
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.
Панель формул
Существует ещё третий способ запустить функцию «СРЗНАЧ». Для этого, переходим во вкладку «Формулы». Выделяем ячейку, в которой будет выводиться результат. После этого, в группе инструментов «Библиотека функций» на ленте жмем на кнопку «Другие функции». Появляется список, в котором нужно последовательно перейти по пунктам «Статистические» и «СРЗНАЧ».
Затем, запускается точно такое же окно аргументов функции, как и при использовании Мастера функций, работу в котором мы подробно описали выше.
Дальнейшие действия точно такие же.
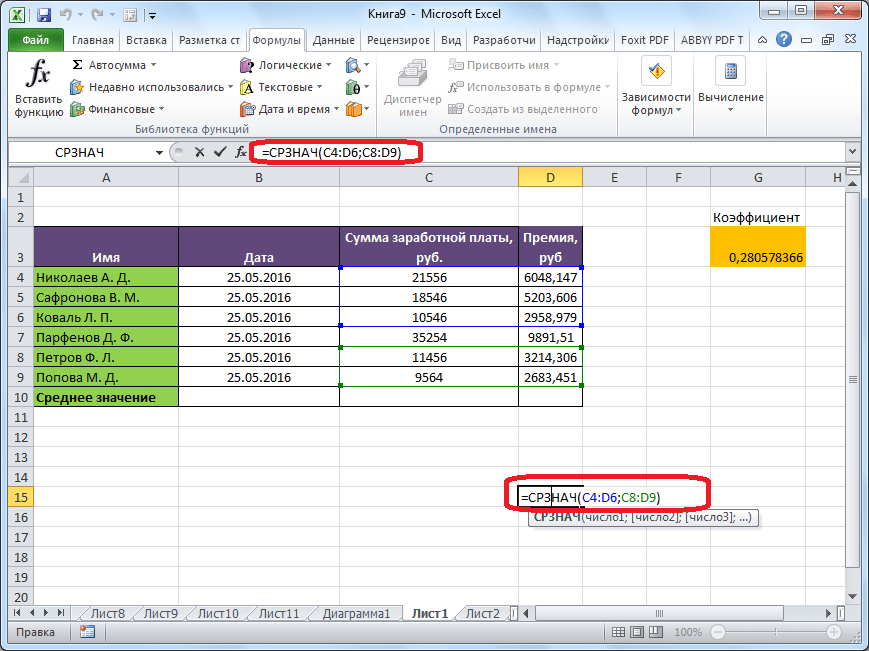
Ручной ввод функции
Но, не забывайте, что всегда при желании можно ввести функцию «СРЗНАЧ» вручную. Она будет иметь следующий шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
Конечно, этот способ не такой удобный, как предыдущие, и требует держать в голове пользователя определенные формулы, но он более гибкий.
Расчет среднего значения по условию
Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.
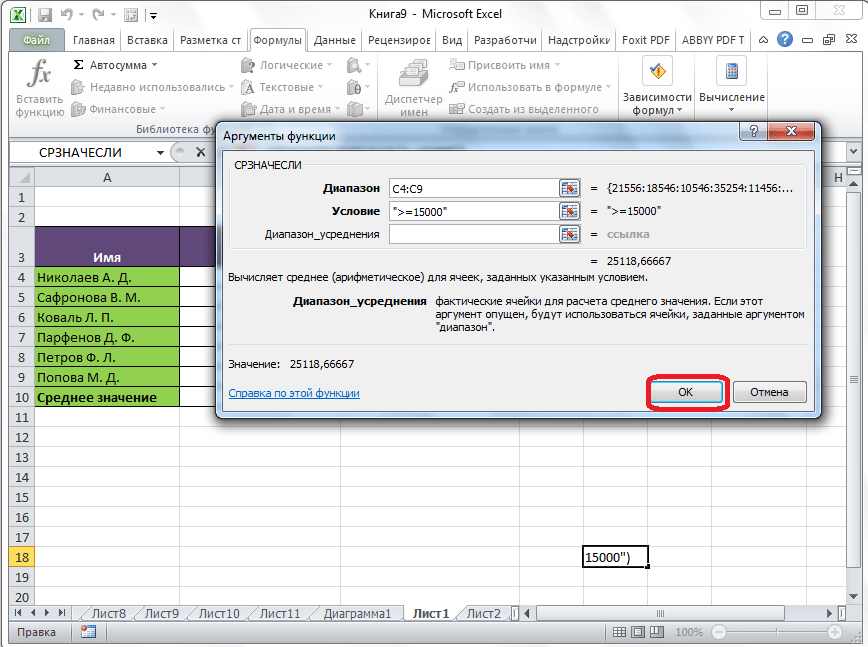
Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».
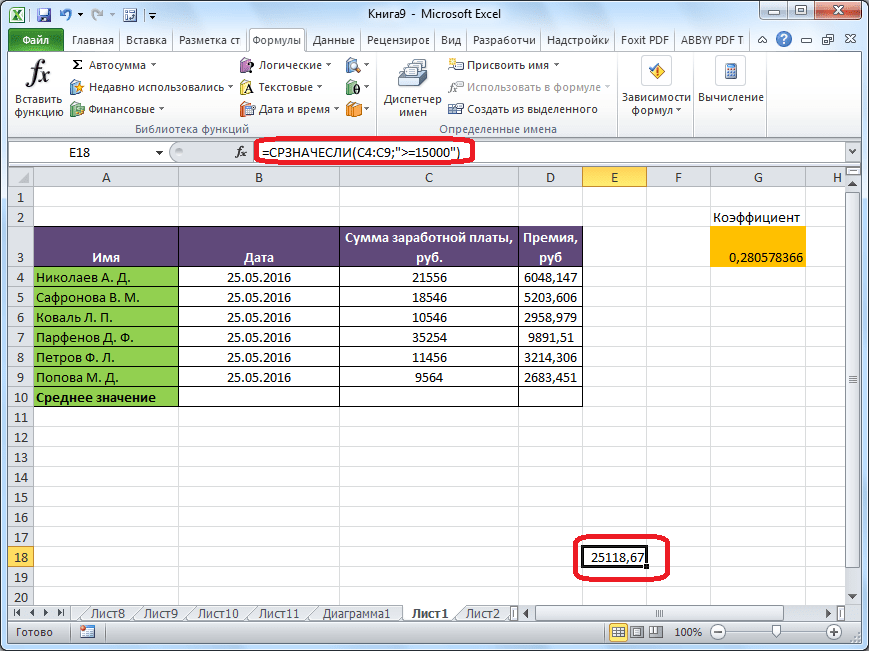
А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.
Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.
Когда все данные введены, жмем на кнопку «OK».
После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.
Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.
Во время работы с числовыми данными в Эксель нередко перед пользователями встает такая задача, как подсчет среднего значения. Математически данное действие выполняется путем деления суммы всех чисел на их количество. А как это сделать в Excel? Давайте разбираться.
Содержание
- Информация в строке состояния
- Расчет среднего значения
-
- Использование арифметического выражения
- Инструменты на ленте
- Использование функции СРЗНАЧ
- Инструменты во вкладке “Формулы”
- Ввод функции в ячейку вручную
- Определение среднего значения по условию
-
- Заключение
Информация в строке состояния
Пожалуй, это самый легкий и быстрый способ определения среднего значения. Для этого достаточно выделить диапазон, содержащий от двух ячеек и более, и среднее значение по ним сразу же отобразится в строке состояния программы.
Если данная информация недоступна, скорее всего, соответствующий пункт выключен в настройках. Чтобы обратно его включить, щелкаем правой кнопкой мыши по строке состояния, в открывшемся списке проверяем наличие флажка напротив строки “Среднее”. Поставить его в случае необходимости можно простым щелчком левой кнопки мыши.
Расчет среднего значения
Когда среднее значение нужно не только определить, но и зафиксировать в отдельной выбранной для этого ячейке, можно использовать несколько методов. Ниже мы подробно рассмотрим каждый из них.
Использование арифметического выражения
Как мы знаем, среднее значение равняется сумме чисел, разделенных на их количество. Данную формулу можно использовать и в Экселе.
- Встаем в нужную ячейку, ставим знак “равно” и пишем арифметическое выражение по следующем принципу:
=(Число1+Число2+Число3...)/Количество_слагаемых.
Примечание: в качестве числа может быть указано как конкретное числовое значение, так и ссылка на ячейку. В нашем случае, давайте попробуем посчитать среднее значение чисел в ячейках B2,C2,D2 и E2.
Конечный вид формулы следующий:=(B2+E2+D2+E2)/4. - Когда все готово, жмем Enter, чтобы получить результат.
Данный метод, безусловно хорош, но удобство его использования существенно ограничено объемом обрабатываемых данных, ведь на перечисление всех чисел или координат ячеек в большом массиве уйдет немало времени, к тому же, в этом случае не исключена вероятность допущения ошибки.
Инструменты на ленте
Данный метод основан на использовании специального инструмента на ленте программы. Вот как это работает:
- Выделяем диапазон ячеек с числовыми данными, для которых мы хотим определить среднее значение.
- Переходим во вкладку “Главная” (если находимся не в ней). В разделе инструментов “Редактирование” находим значок “Автосумма” и щелкаем по небольшой стрелке вниз рядом с ним. В раскрывшемся перечне кликаем по варианту “Среднее”.
- Сразу же под выделенным диапазоном отобразится результат, который и является средним значением по всем отмеченным ячейкам.
- Если мы перейдем в ячейку с результатом, то в строке формул увидим, какая функция была использована программой для расчетов – это оператор СРЗНАЧ, аргументами которого является выделенный нами диапазон ячеек.
Примечание: Если вместо вертикального выделения (столбца целиком или его части) будет выполнено горизонтальное выделение, то результат отобразится не под областью выделения, а справа от нее.
Данный метод, достаточно прост и позволяет быстро получить нужный результат. Однако помимо очевидных плюсов, есть у него и минус. Дело в том, что он позволяет вычислить усредненное значение только по ячейкам, расположенными подряд, причем, только в одном столбце или строке.
Чтобы было нагляднее, разберем следующую ситуацию. Допустим, у нас есть две заполненные данными строки. Мы хотим получить среднее значение сразу по двум строкам, следовательно, выделяем их и применяем рассмотренный инструмент.
В результате, мы получим средние значения под каждым столбцом, что тоже неплохо, если преследовалась именно такая цель.
Но если, все же, требуется определить среднее значение по нескольким строкам/столбцам или разбросанным в разных местах таблицы ячейкам, пригодятся методы, описанные далее.
Альтернативный способ использования “Среднее” на ленте:
- Переходим в первую же свободную ячейку после столбца или строки (в зависимости от структуры данных) и жмем кнопку расчета среднего значения.
- Вместо моментального вывода результата на этот раз программа предложит нам предварительно проверить диапазон ячеек, по которому будет считаться среднее значение, и в случае необходимости скорректировать его координаты.
- По готовности жмем клавишу Enter и получаем результат в заданной ячейке.
Использование функции СРЗНАЧ
С данной функцией мы уже успели познакомиться, когда перешли в ячейку с результатом расчета среднего значения. Теперь давайте научимся полноценно ею пользоваться.
- Встаем в ячейку, куда планируем выводить результат. Кликаем по значку “Вставить функци” (fx) слева от строки формул.
- В открывшемся окне Мастера функций выбираем категорию “Статистические”, в предлагаемом перечне кликаем по строке “СРЗНАЧ”, после чего нажимаем OK.
- На экране отобразится окно с аргументами функции (их максимальное количество – 255). Указываем в качестве значения аргумента “Число1” координаты нужного диапазона. Сделать это можно вручную, напечатав с клавиатуры адреса ячеек. Либо можно сначала кликнуть внутри поля для ввода информации и затем с помощью зажатой левой кнопки мыши выделить требуемый диапазон в таблице. При необходимости (если нужно отметить ячейки и диапазоны ячеек в другом месте таблицы) переходим к заполнению аргумента “Число2” и т.д. По готовности щелкаем OK.
- Получаем результат в выбранной ячейке.
- Среднее значение не всегда может быть “красивым” за счет большого количества знаков после запятой. Если нам такая детализация не нужна, ее всегда можно настроить. Для этого правой кнопкой мыши щелкаем по результирующей ячейке. В открывшемся контекстном меню выбираем пункт “Формат ячеек”.
- Находясь во вкладке “Число” выбираем формат “Числовой” и с правой стороны окна указываем количество десятичных знаков после запятой. В большинстве случаев, двух цифр более, чем достаточно. Также при работе с большими числами можно поставить галочку “Разделитель групп разрядов”. После внесение изменений жмем кнопку OK.
- Все готово. Теперь результат выглядит намного привлекательнее.
Инструменты во вкладке “Формулы”
В программе Excel есть специальная вкладка, отвечающая за работу с формулами. В случае с расчетом среднего значения, она тоже может пригодиться.
- Встаем в ячейку, в которой планируем выполнить расчеты. Переключаемся во вкладку “Формулы”. В разделе инструментов “Библиотека функций” щелкаем по значку “Другие функции”, в раскрывшемся перечне выбираем группу “Статистические”, затем – “СРЗНАЧ”.
- Откроется уже знакомое окно аргументов выбранной функци. Заполняем данные и жмем кнопку OK.
Ввод функции в ячейку вручную
Как и все остальные функции, формулу СРЗНАЧ с нужными аргументами можно сразу же прописать в нужной ячейке.
В общем, синтаксис функции СРЗНАЧ выглядит так:
=СРЗНАЧ(число1;число2;...)
В качестве аргументов могут выступать как ссылки на отельные ячейки (диапазоны ячеек), так и конкретные числовые значения.
=СРЗНАЧ(3;5;22;31;75)
Просто встаем в нужную ячейку и, поставив знак “равно”, пишем формулу, перечислив аргументы через символ “точка с запятой”. Вот, как это выглядит со ссылками на ячейки в нашем случае. Допустим, мы решили включить в подсчет всю первую строку и только три значения из второй:
=СРЗНАЧ(B2;C2;D2;E2;F2;G2;H2;B3;C3;D3)
Когда формула полностью готова, нажимаем клавишу Enter и получаем готовый результат.
Безусловно, такой метод нельзя назвать удобным, но иногда, при небольшом объеме данных, и он вполне может использоваться.
Определение среднего значения по условию
Помимо перечисленных выше методов, в Эксель также предусмотрена возможность расчета среднего значения по заданному пользователем условию. Как следует из описания, участвовать в общем подсчете будут только числа (ячейки с числовыми данными), соответствующие какому-то конкретному условию.
Допустим, нам нужно посчитать среднее значение только по положительным числам, т.е. тем, которые больше нуля. В этом случае, нас выручит функция СРЗНАЧЕСЛИ.
- Встаем в результирующую ячейку и жмем кнопку “Вставить функцию” (fx) слева от строки формул.
- В Мастере функций выбираем категорию “Статистические”, кликаем по оператору “СРЗНАЧЕСЛИ” и жмем ОК.
- Откроются аргументы функции, после заполнения которых кликаем OK:
- в значении аргумента “Диапазон” указываем (вручную или выделив с помощью левой кнопки мыши в самой таблице) требуемую область ячеек;
- в значении аргумента “Условие”, соответственно, задаем наше условие попадания ячеек из отмеченного диапазона в общий расчет. В нашем случае, это выражение “>0”. Вместо конкретного числа, в случае необходимости, в условии можно указать адрес ячейки, содержащей числовое значение.
- поле аргумента “Диапазон_усреднения” можно оставить пустим, так как его обязательное заполнение требуется только при работе с текстовыми данными.
- Среднее значение с учетом заданного нами условия отбора ячеек отобразилось в выдранной ячейке.
Заключение
Таким образом, в Экселе существует немало способов для нахождения среднего значения как по отдельным строкам и столбцам, так и по целым диапазонам ячеек, которые, к тому же, могут быть разбросаны по таблице. А использование того или иного метода определяется удобством и целесообразностью его использования в каждом конкретном случае.
Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.
Средняя арифметическая как оценка математического ожидания
Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.
Формула матожидания имеет следующий вид:
где M(X) – математическое ожидание
xi – это случайные величины
pi – их вероятности.
То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.
Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.
Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.
Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.
где xi – значения переменной,
n – количество значений.
Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).
Свойства средней арифметической (математического ожидания)
Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.
Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).
Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.
M(X+Y+Z) = M(X) + M(Y) + M(Z)
Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.
Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.
M(aX) = aM(X)
К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.
Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).
M(a) = a
Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.
Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
M(XY) = M(X)M(Y)
Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.
Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.
У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.
Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:
После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).
Средняя арифметическая взвешенная
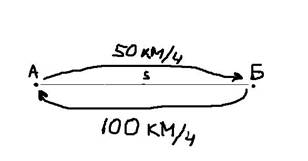
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.
Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:
Теперь преобразуем формулу до удобного вида.
Подставим значения.
Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.
Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.
где x – анализируемый показатель; f – вес.
Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.
Формула средневзвешенного значение в Excel
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.
Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:
=СУММПРОИЗВ(B3:B5;C3:C5)/СУММ(C3:C5)
Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.
Физический смысл средней арифметической
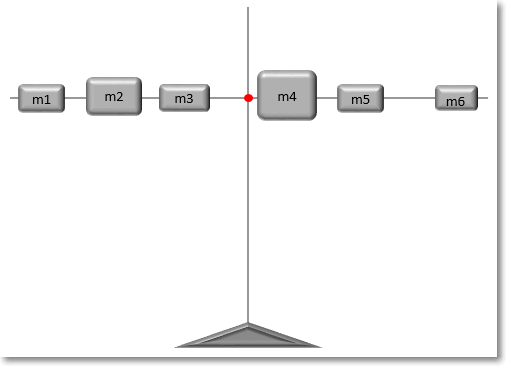
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.
Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (mi), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.
И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.
Поделиться в социальных сетях: