Формула объема в таблице в Excel помогает быстро посчитать объем нужной фигуры, а сделать это можно при помощи инструкции выше.
- Параллелепипед;
- Сфера;
- Пирамида;
- Цилиндр;
- Конус.
Видеоинструкция
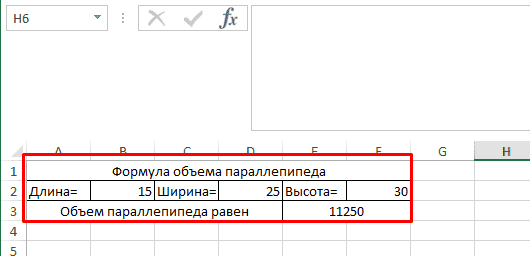
Формула объема параллелепипеда в Excel
Для этого потребуется использовать формулу:
=(Длина)*(Ширину)*(Высоту)
Пример можно скачать ниже:
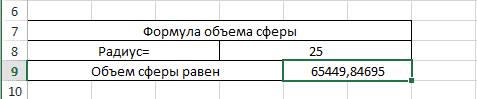
Сфера
Для шара можно воспользоваться конструкцией:
=(4/3)*ПИ()*(D8^3)
Пример:
Пирамида
В этом случае можно воспользоваться:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример:
Цилиндр
Задачу с данной фигурой можно решить через:
=ПИ()*C14*C14*F14
Пример:
Конус
В случае с конусом объем вычисляется через формулу:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример:
Summary
To calculate the volume of a cone, you can use the PI function together with the exponent operator (^). In the example shown, the formula in D5, copied down, is:
=1/3*PI()*B5^2*C5
The formula returns the volume of a cone with the radius given in column B and the height given in column C. Units are indicated generically with «u», and the resulting volume is units cubed (u3).
Generic formula
Explanation
In geometry, the formula for calculating the volume of a cone is:
The formula for calculating the volume of a cone is based on the formula for calculating the volume of a pyramid. Since the base of a cone is a circular, the formula for area of a circle is included.
The Greek letter π («pi») represents the ratio of the circumference of a circle to its diameter. In Excel, π is represented in a formula with the PI function, which returns the number 3.14159265358979, accurate to 15 digits:
=PI() // returns 3.14159265358979
To square a number in Excel, you can use the exponentiation operator (^):
=A1^2
Or, you can use the POWER function:
=POWER(A1,2)
Rewriting the formula for volume of a cone with Excel’s math operators, we get:
=1/3*PI()*B5^2*C5
Or, with the POWER function:
=1/3*PI()*POWER(B5,2)*C5
The result is the same for both formulas. Following Excel’s order of operations, exponentiation will occur before multiplication.
Author
Dave Bruns
Hi — I’m Dave Bruns, and I run Exceljet with my wife, Lisa. Our goal is to help you work faster in Excel. We create short videos, and clear examples of formulas, functions, pivot tables, conditional formatting, and charts.
Your pages offer clear writing and simple explanations that I’m sure are immensely helpful to many. Thanks for making the internet a better place.
Get Training
Quick, clean, and to the point training
Learn Excel with high quality video training. Our videos are quick, clean, and to the point, so you can learn Excel in less time, and easily review key topics when needed. Each video comes with its own practice worksheet.
View Paid Training & Bundles
Help us improve Exceljet
| Раздел функций | Математические |
| Название на английском | PI |
| Похожие функции | СЕГОДНЯ, ТДАТА |
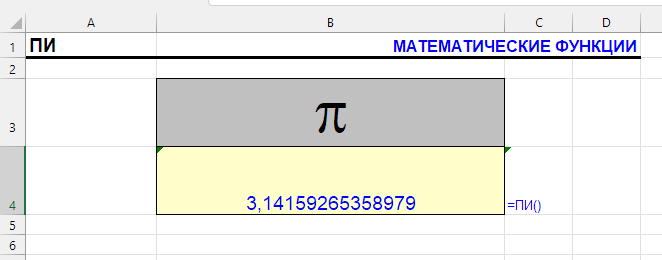
Эта функция возвращает число Пи с точностью в 14 знаков после запятой. Функция не требует ввода аргументов, она отдает значение сама по себе.
Число Пи иррациональное, и нет простых способов его рассчитать, потому и существует подобная функция.
Синтаксис
=ПИ()Примеры формул с функцией ПИ
Число используется в расчете площади и объема фигур, основанных на окружностях и сферах.
Площадь круга
Площадь круга A через радиус r вычисляется по формуле:
A = πr^2
Допустим, радиус находится в ячейке A2, тогда формула площади будет выглядеть так:
Длина окружности
C = 2πr
Если радиус окружности находится в ячейке A2, то формула будет:
Площадь кольца
A = π(R^2 - r^2)
(где R — внешний радиус а r — внутренний). Разместим радиусы в ячейках A2 и B2, формула:
Объём сферы
Для расчёта объёма сферы нужен только её радиус, а геометрическая формула выглядит так:
V = (4/3)πr^3
Введите нужный радиус в ячейку A2 и используйте любую другую ячейку для расчёта объема сферы следующей Excel-формулой:
Площадь поверхности сферы
Математическая формула расчета площади поверхности сферы выглядит так:
A = 4πr^2
А Excel-формула будет такой (r в ячейке A2):
Объём цилиндра
V = πr^2h
Разместите радиус в ячейке A2 и высоту в ячейке B2 и используйте формулу ниже:
Площадь поверхности цилиндра
A = 2πrh + 2πr^2
Здесь r — радиус, а h — высота цилиндра. Соответствующие им ячейки: A2 и B2.
=2*ПИ()*A2*B2+2*ПИ()*A2^2
Объём конуса
V = (1/3)πr^2h
где r — радиус основания, а h — высота конуса.
В формуле ниже это A2 и B2 соответственно:
Площадь поверхности конуса
A = πr(l + r)
где r — радиус основания, а l — длина образующей конуса. Допустим, радиус находится в ячейке A2, а длина образующей конуса — в ячейке B2. Тогда формула будет выглядеть так:
Площадь круга, вписанного в треугольник, по длинам трёх его сторон
Дан треугольник и нам известны длины всех его сторон. Треугольник может быть каким угодно. Внутрь треугольника вписана окружность. Нужно вычислить площадь круга, очерченного ею.
Непростая, но решаемая поэтапно геометрическая задача. Ниже её алгоритм:
Сначала вычисляется полупериметр треугольника (сумма длин сторон, поделённая напополам):
s = (a + b + c)/2
Затем используется формула Герона, чтобы найти площадь А треугольника через полупериметр и длины сторон:
A = √(s(s-a)(s-b)(s-c))
Радиус r вписанной окружности равен отношению площади треугольника к его полупериметру:
r = A/s
Наконец, зная радиус круга, используем формулу площади круга:
А = πr ^ 2
Если собрать все это вместе, формула площади круга, вписанного в треугольник со сторонами, имеющими длины a, b и c, выглядит следующим образом:
А = π((a + b + c)/2((a + b + c)/2-a)((a + b + c)/2-b)((a + b + c)/2-c))
Представим, что длины сторон треугольника a, b и c находятся в ячейках A2, B2 и C2 соответственно:
Тогда итоговая формула будет:
=ПИ()*(A2+B2+C2)/2*((A2+B2+C2)/2-A2)*((A2+B2+C2)/2-B2)*((A2+B2+C2)/2-C2)/((A2+B2+C2)/2)^2
Понравилась статья? Поддержите её автора, купите надстройку для Excel !SEMTools, она поможет вам сэкономить уйму времени при работе в Excel
Общая формула
=1/3*PI()*r^2*h
Резюме
Чтобы вычислить объем конуса, вы можете использовать функцию PI вместе с оператором экспоненты (^). В показанном примере формула в D5, скопированная ниже, имеет следующий вид:
=1/3*PI()*B5^2*C5
Формула возвращает объем конуса с радиусом, указанным в столбце B, и высотой, указанной в столбце C. Единицы измерения обычно обозначаются буквой «u», а результирующий объем является кубическими единицами (u 3 ).
Объяснение
В геометрии формула для расчета объема конуса:
Формула для вычисления объема конуса основана на формуле для вычисления объема пирамиды. Поскольку основание конуса является круглым, формула для площади круга включена.
Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с функцией PI, которая возвращает число 3,14159265358979 с точностью до 15 цифр:
=PI() // returns 3.14159265358979
Чтобы возвести число в квадрат в Excel, вы можете использовать оператор возведения в степень (^):
=A1^2
Или вы можете использовать функцию POWER:
=POWER(A1,2)
Переписывая формулу объема конуса с помощью математических операторов Excel, получаем:
=1/3*PI()*B5^2*C5
Или с помощью функции POWER:
=1/3*PI()*POWER(B5,2)*C5
Результат одинаков для обеих формул. В соответствии с порядком операций в Excel, возведение в степень выполняется перед умножением.

22
#Н/ Д! – неопределенные данные
#ССЫЛКА! – ссылка на несуществующие ячейки
При обнаружении ошибки следует перейти в режим редактирования и исправить формулу. В случае затруднений надо провести синтаксический анализ формулы и ввести ее заново.
Порядок вычислений по формуле: =3+5*COS(B4)-2*A2:
COS(B4)
5*COS(B4)
2*A2
3+ 5*COS(B4)
3+5*COS(B4)-2*A2
2.4.ПРАКТИЧЕСКАЯ РАБОТА
2.4.1.ПРИМЕРЫ
Пример 1. Вычислить объем и площадь поверхности заданного конуса с основанием R и высотой h. Значения R и h заданы. Положить R=1 м , h=3 м. Отчет представить в виде распечатки рабочих листов, содержащих условие задачи, расчетные формулы, расчеты в MS Excel в режиме отображения данных и формул.
РЕШЕНИЕ:
1. Расчетные формулы:
образующая l = 
|
площадь основания конуса |
S0 =π R2 |
|
площадь боковой поверхности |
S1 =π R l |
|
площадь поверхности конуса |
S = S0 + S1 |
объем конуса V = 13 S0 h
2. Создание рабочего листа с заданием и расчетными формулами.
Порядок действий рекомендуется следующий:
−создать новый файл и сохранить его в личной папке под именем Конус.xls;
−в ячейку A1 ввести тему работы; в нижележащие ячейки (например, A3, A4) ввести номер примера и текст задачи;
−в отдельные ячейки A6:A7 и A10:A14 ввести обозначения размеров конуса с пояснениями; ввести данные: значения 1 и 3 для R и h соответственно в
B6, B7;
− выполнить вставку расчетных формул с помощью приложения
MS Equation 3.0.
3. Выполнение расчетов в MS Excel.
В ячейки E10:E14 последовательно ввести формулы: =КОРЕНЬ(B6*B6+B7*B7)
=ПИ()*B7*B7

23
=ПИ()*B7*E10 =E11+E12 =E11*B6/3.
4. Форматирование таблицы.
Установить в таблице шрифт Times New Roman, размер 10. Расположить текст по образцу, используя кнопки вкладки Главная.
Если весь текст не виден в объединенных ячейках, нужно увеличить высоту строки.
Выполнить подчеркивание заголовка, используя команду Формат ячейки|Шрифт|Подчеркивание одностороннее по значению контекстно-
зависимого меню (правая копка мыши).
Фрагмент рабочего листа MS Excel с решением примера 1 представлен на рис. 2.1.
|
A |
B |
C |
D |
E |
F |
Вычисленияпоформуламсиспользованиемвстроенныхматематических 1 функций
2
3Пример1
Вычислитьобъемиплощадьповерхностиконуса, еслизаданыеговысотаирадиус
4основанияc точностьюдочетвертогодесятичногознака
5Пусть
|
6 |
Высотаh= |
3 м |
||||
|
7 |
РадиусR= |
1 м |
||||
|
8 |
||||||
|
9 |
Введемобозначения |
Результаты |
||||
|
10 |
Образующаяконусаl= |
3,1623 |
м |
|||
|
11 |
ПлощадьоснованияконусаS0= |
3,1416 |
м2 |
|||
|
12 |
ПлощадьбоковойповерхностиконусаS1= |
9,9346 |
м2 |
|||
|
13 |
ПлощадьповерхностиконусаS= |
13,0762 |
м2 |
|||
|
14 |
ОбъемконусаV= |
3,1416 |
м3 |
|||
|
15 |
Формулыдлявычисления |
|||||
|
16 |
l = |
h2 + R2 |
||||
|
17 |
S0 = πR2 |
S1 = πRl |
||||
|
18 |
S = S0 + S1 |
|||||
|
19 |
||||||
|
V = |
1 S0 h |
|||||
|
20 |
||||||
|
21 |
3 |
|||||
|
Рис. 2.1. Фрагмент рабочего листа Excel для примера 1 |
||||||
Пример2. Вычислить по заданным формулам величины: f = 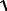
при заданных значениях m = 2; c = −1; t =1,2; b = 0,7

24
РЕШЕНИЕ.
Решение выполним на одном рабочем листе с примером 1. Порядок действий аналогичен предыдущему примеру:
−введем условие задачи с формулами для вычислений;
−введем в отдельные ячейки обозначения и значения исходных данных m, c, t, b (см. рис. 2.2);
−в ячейки для результатов введем формулы:
−=(A33*TAN(C33)+ABS(B33*SIN(C33)))^0,5
−=LOG(A33;2)*COS(D33*C33)*EXP(C33+B33);
−форматируем таблицу.
Фрагмент рабочего листа с решением примера 2 представлен на рис.2.2.
|
A |
B |
C |
D |
||
|
25 |
Пример 2 |
||||
|
26 |
Вычислить по заданным формулам |
||||
|
27 |
|||||
|
28 |
m tgt + c sin t , |
z = log2 m cos bt e |
t+c |
||
|
f = |
|||||
|
29 |
|||||
|
m = 2, c = −1, t =1,2 b = 0,7 |
|||||
|
30 |
Данные |
||||
|
31 |
|||||
|
32 |
m |
c |
t |
b |
|
|
33 |
2 |
-1 |
1,2 |
0,7 |
|
|
34 |
Результаты |
||||
|
35 |
f = |
2,4650 |
|||
|
36 |
z= |
0,8152 |
|||
|
37 |
|||||
|
Рис.2.2. Фрагмент рабочего листа для примера 2 |
При вводе формул, необходим тщательный анализ порядка действий и аккуратный набор всех символов. Возможно, количество ошибок сократится, если применить ряд приемов:
•при вставке ссылки на ячейку нужно щелкнуть мышью по этой ячейке;
•при вставке функции нужно вызвать Мастер функций (вкладка Формулы, кнопка Вставить функцию), который позволяет выполнить вставку функции за два шага: первый шаг – выбор категории функции и выбор функции, второй шаг – задание аргументов функции.
Опишем эту технологию подробнее на примере первой формулы:
•для возведения в степень используем знак операции ^, поэтому основание степени нужно взять в скобки; соответственно, наберем =(
•введем значение m щелчком по ячейке A33 и знак умножения *
•вызовем Мастер функций, при этом появится диалоговое окно первого шага, представленное на рис. 2.3, выберем категорию функций Математические и в появившемся списке функций укажем TAN

25
Рис. 2.3. Диалоговое окно Мастера функций (первый шаг)
• при нажатии OK появится окно второго шага Мастера функций (рис. 2.4). В поле Число введем аргумент щелчком по ячейке со значением t C33. При нажатии OK или клавиши Enter ввод функции заканчивается, заканчивается и ввод формулы в ячейку; для продолжения ввода в эту ячейку нужно нажать кнопку 
Рис. 2.4. Диалоговое окно Мастера функций (второй шаг)
•вставим функцию ABS. При задании аргумента наберем B33* и снова вызовем Мастер функций;
•функция от функции выбирается в списке функций в строке формул. Если требуемой функции нет в списке, нужно выбрать из списка вариант Другие функции, что приведет к повторному вызову Мастера функций. После знака умножения вставим функцию SIN. После задания аргумента нужно щелкнуть в строке формул (нажатие OK или клавиши Enter приведет
кокончанию набора, а предложенный вариант вернет нас к окну внешней функции);

26
• после окончания ввода внешней функции ABS закончим ввод формулы, набрав закрывающую скобку и возведение в степень 0,5 – символы — )^0,5 или )^(1/2). Можно было также использовать функцию КОРЕНЬ, но это привело бы к тройному вложению функций в формуле и усложнению ее набора.
2.4.2. ВАРИАНТЫ ЗАДАНИЙ
Вычислить данные выражения при заданных числовых значениях аргументов. Вычисления выполнить с точностью до третьего десятичного знака.
|
Вариант 1 |
|||||||||||||||||
|
1. |
z = |
0,45 + x3 + (x2 |
−1)2 ; |
x = 3,8 |
|||||||||||||
|
2. |
z = |
7,2 ln |
x −1 |
− et −1 |
; |
x = 0,58; |
t = 0,3 |
||||||||||
|
x 2,4 − t 2 |
|||||||||||||||||
|
3. |
z = |
sin 3(α2 + β) |
; |
α = |
π |
; |
β = 0,4; |
γ = |
π |
||||||||
|
cos( 2,8 γ + α) |
|||||||||||||||||
|
4 |
8 |
||||||||||||||||
|
4. |
z = u +v; где u = |
3 x3 + 2 |
sin 3x; |
v = (1− y)2 /(1−cos2 y); x = 7,3; y = 0,3 |
|||||||||||||
|
0,5 (x2 |
+1) |
||||||||||||||||
|
5. |
l =km−1 +ln(x3 − y) + |
3 |
x + y |
; k =3; |
m =3; x =4,7; y =5,8; z =4,9 |
||||||||||||
|
ctg(z +1) |
|||||||||||||||||
Вариант 2
1. z = 2,58(x3 −1)−ln (x2 +3); , x = 5,1
|
2. |
z = |
e2x −et |
; x =1,3; |
t = 6,2 |
||||||||||
|
lg | x3 −t | |
||||||||||||||
|
3. |
z = |
cos(α2 + β)−sinα |
; |
α = 0,3; β = 2,1 |
||||||||||
|
tg(π +α) |
||||||||||||||
|
4. |
z = uv; |
где u = |
x3 − a3 + a ; |
v = ln|x − a | 8,055; x = 0,2; a = 2,72 |
||||||||||
|
5. |
l = mk +1 −tg(k +1,8)− 1 |
x −1 |
; |
m = 3; |
k = 2; |
x =1,56 |
||||||||
|
1. |
Вариант 3 |
|||||||||||||
|
z = 0,082 x3 + ex+1; x =1,53 |
||||||||||||||
|
2. |
z = [lg(y3 +7,51)− y]/ |
y −8,08 |
; |
y = 6,22 |
||||||||||
|
3. |
z = tg(x2 + y3 ) /[cos2 (x2 |
+ y)−cos x]; x =π / 3; |
y = 0,2 |
|||||||||||
|
4. |
z =uA; |
где |
u = lg2 (x −1); A =9,5 (y0,3 −ex ); x =5,85; y = 21,3 |
|||||||||||
|
5. |
l = k n+2 |
−tg(cos(x + y)); |
k = 2; |
n =1; |
x = 0,33; y = π / 4 |

|
27 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. |
Вариант 4 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
z =x1/ 2 + (3,37 x + 2,03)2 ; |
x = 2,8 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
z = |
cos(w −1) + ln(w2 +3) |
; |
w = 2,65; t = 2,7 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
0,58 t |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
tg 2 (α − β) +cos2 α |
; |
α = π |
; |
β = 0,2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
sin(α + β) |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
z = u t, |
где |
u = |
x1/ 3 |
− a1/ 2 |
; |
t = ln(a1/ 2 + ex ); x =15,73; a = 4,25 |
||||||||||||||||||||||||||||||||||||||||||||
|
5. |
y = hv− f |
+sin 2 (v + f ) − |
v |
; |
h = 3; v = 2,5; f |
= 2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
ln f |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. |
Вариант 5 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
z =x1/ 2 |
+ (3,4 x +12,3)2 ; |
x =12,8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
sin(x −1) +lg(x2 −1) |
; |
x = 3,25; |
t = 2,02 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
0,51t |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
tg (α − β) + cos 2 α |
; |
α = |
π |
; β = 0,05 |
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
sin(α + β) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
z =u t , |
где |
u = |
x1/ 3 −a1/ 2 |
; t =ln(a1/ 2 + x1/ 3 ); |
x =18,08; a =11,75 |
|||||||||||||||||||||||||||||||||||||||||||||
|
5. |
l = k m−n + cos2 (m + n x) − |
m |
; k = 3; m = 5; |
n = 2; |
x = 2,3 |
||||||||||||||||||||||||||||||||||||||||||||||
|
log2 n |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вариант 6 |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
z = 2.198x2 −(x |
2 |
+1)2 ; |
x = 3.75 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
z = |
cos x2 −sin2 y |
; |
x = 0,51; |
y = 0,2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
cos y2 −sin x |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
cos |
α + β |
; α = π |
; |
β = 0,2; |
γ = 0,4 |
||||||||||||||||||||||||||||||||||||||||||||
|
sin γ |
+cosα +tgβ |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
z = u v; |
где u = |
x3 −a3 |
+ a; |
v = 6,5 ln |
x −a |
; x = 0,2; |
a = 2,72 |
|||||||||||||||||||||||||||||||||||||||||||
|
5. |
l = mk −1 −ctg(m − k) − |
1 |
; |
m = 3; k = 2; |
x =1,41 |
||||||||||||||||||||||||||||||||||||||||||||||
|
x −1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. |
Вариант 7 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
z = 0,65(x2 − 2) + x1/ 3 ; |
x =13,58 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
z = (ex−1,2 + e1,2+x ) / ln (0,1t); |
t = 53,5; |
x = 2,5 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
2 |
α + |
sin |
α |
÷sin |
2 |
(α − β); |
α = |
π |
β = |
π |
|||||||||||||||||||||||||||||||||||||||
|
cos |
; |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
cos(α |
3 |
8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
− β) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4. |
c2 |
a −b cos |
a |
; а =1,1; b = 0,5 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
z = u y ; |
где |
u = |
ln |
−7,25 |
; |
с = 2,1; |
y = |
||||||||||||||||||||||||||||||||||||||||||||
|
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||

|
28 |
|||||||
|
5. |
l = |
m2 |
+ k m tg |
z |
; m = 3; k = 2; z = 0,3 |
||
|
sin(z +1) |
|||||||
Вариант 8
|
1. |
z = (8,59 − x1/ 3 ) −(1−ln x); |
x = 0,53 |
|||||||||||||||||||||||||||||||||||||||||
|
2. |
z = [lg( x 2 |
+1) + e x −1 ]/( x 2 |
− t ) ; |
x = 4,8 ; |
t = 3,27 |
||||||||||||||||||||||||||||||||||||||
|
3. |
z = [tg(α − β)2 |
−1]/ cos2 (γ −1); |
α = π / 6; |
β = 0,3; γ = 2,1 |
|||||||||||||||||||||||||||||||||||||||
|
4. |
z = x y ; |
где |
x = 3 |
2,8u 2 |
− a ; y = |
cos 2 (t −1) / sin(t +1) |
; |
u =1,4; a = 0,8; t = 3,8 |
|||||||||||||||||||||||||||||||||||
|
5. |
l = nk + |
4 |
z3 |
x |
; n = 2; |
k = 3; |
z = 7,7; |
x = 0,8 |
|||||||||||||||||||||||||||||||||||
|
+sin |
|||||||||||||||||||||||||||||||||||||||||||
|
ln x |
2 |
||||||||||||||||||||||||||||||||||||||||||
|
Вариант 9 |
|||||||||||||||||||||||||||||||||||||||||||
|
1. |
z = 2,58(x3 −1)−ln(x +1); |
x = 5,1 |
|||||||||||||||||||||||||||||||||||||||||
|
2. |
z = |
e 2 x |
− e 2t |
; |
x = 1,3 ; |
t = 6,2 |
|||||||||||||||||||||||||||||||||||||
|
ln | x − t | |
|||||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
cos(α2 + β)−sin |
2 β |
; α = 0,3; β = 2,1 |
|||||||||||||||||||||||||||||||||||||||
|
tg(π +α + β) |
|||||||||||||||||||||||||||||||||||||||||||
|
4. |
z = u v , где u = |
x3 − a3 |
+ a ; |
v =12,35 ln|x − a |; |
x = 0,82; a = 2,72 |
||||||||||||||||||||||||||||||||||||||
|
5. |
l =mk−1 −tg(m+k)− |
1 |
x −1 |
; |
m=3; |
k =2,5; |
x =2.41 |
||||||||||||||||||||||||||||||||||||
|
Вариант 10 |
|||||||||||||||||||||||||||||||||||||||||||
|
1. |
z = |
(24,6 + x − a2 )2 |
+ln x3 ; x = 0,3; |
a =1,72 |
|||||||||||||||||||||||||||||||||||||||
|
2. |
1 |
+ e x+1 |
|||||||||||||||||||||||||||||||||||||||||
|
z = |
1 − |
/ sin 2 x; |
x =1,32 |
||||||||||||||||||||||||||||||||||||||||
|
e x |
|||||||||||||||||||||||||||||||||||||||||||
|
cos2 α |
0,2 |
π |
|||||||||||||||||||||||||||||||||||||||||
|
3. |
z = |
−1,2 |
/[2,5 −cos |
(α + β)]; |
α = |
; |
β = 0,7 |
||||||||||||||||||||||||||||||||||||
|
1) |
3 |
||||||||||||||||||||||||||||||||||||||||||
|
sin(α − |
|||||||||||||||||||||||||||||||||||||||||||
|
4. |
z = |
u |
где |
u = |
1− y2 |
x |
v = lg y |
1−sin y |
y = 0,5; |
x = π |
|||||||||||||||||||||||||||||||||
|
; |
sin |
; |
; |
||||||||||||||||||||||||||||||||||||||||
|
5. |
v |
1 |
n |
8 |
|||||||||||||||||||||||||||||||||||||||
|
l = k m + |
; |
k = 2; |
m = 3; |
n = 2; |
x = 2,15 |
||||||||||||||||||||||||||||||||||||||
|
1 −sin m |
k + x |
||||||||||||||||||||||||||||||||||||||||||
3.ЛОГИЧЕСКИЕ ФУНКЦИИ MS EXCEL
3.1.ОСНОВНЫЕ ПОНЯТИЯ
Логическое выражение — это высказывание, принимающее значения ИСТИНА или ЛОЖЬ. Логические выражения в MS Excel позволяют выполнять вычисления, зависящие от условий. Условие считается выполненным, если значение соответствующего ему логического выражения — ИСТИНА, и не выполненным, если значение логического выражения — ЛОЖЬ.
29
Логическое выражение может содержать знаки равенств и неравенств и логические функции. Равенства и неравенства применяются к двум операндам (сравниваются две величины).
Пусть, например, в MS Excel требуется проверить истинность неравенств:
x <1,
ln(t + 12) ≥ 2,
a2 +b2 = 4, z ≠ z0 ,
им могут соответствовать логические выражения в MS Excel:
A10 <1,
LN (B3 +1/ 2) >= 2,
A5^2 + A6^2 = 4, C10 <> $A$5.
В данном примере величины, обозначенные буквами, помещены в некоторые ячейки. Ссылка на ячейку $A$5 является абсолютной, показывая постоянство величины z0
Пара символов < > означает — «не равно», смысл остальных символов очевиден. На равенство можно проверить и текстовое значение, причем текст в выражении заключается в кавычки.
Как правило, значение логического выражения меняется в зависимости от конкретных значений входящих в него переменных и может быть использовано в наиболее важной функции категории Логические – функции ЕСЛИ. Другие логические функции НЕ, И, ИЛИ – используются для задания сложных условий. Логические значения ИСТИНА и ЛОЖЬ могут задаваться в MS Excel как функции. Итак, перечислены все логические функции. Далее рассмотрен их синтаксис и примеры применения.
3.2. ЛОГИЧЕСКИЕ ФУНКЦИИ ЕСЛИ, И, ИЛИ, НЕ
Логическая функция ЕСЛИ имеет вид:
ЕСЛИ(x1; x2; x3),
где x1, x2, x3 – аргументы, здесь x1 — логическое выражение, x2, x3 – любые выражения, разрешенные вMS MS Excel; причем вычисляется x2, если x1 имеет значение ИСТИНА, и x3, если x1 имеет значение ЛОЖЬ. Если третий аргумент функции не определен, то ошибки в записи функции нет – в этом случае ей присваивается значение ЛОЖЬ, если условие не выполнено. Если ничего не нужно вычислять при невыполнении условия, следует в качестве третьего аргумента задать пробел как текст.
Примеры: ЕСЛИ(A5>0;LN(A5);-1); ЕСЛИ(B2< >0;1/B2;” ”)
Логическая функция И имеет вид:
И(x1; x2;; …;xn),
где x1; x2;; …;xn – аргументы, являющиеся логическими выражениями. Функция может содержать до 30 аргументов. Функция И

30
принимает значение ИСТИНА, если все ее аргументы истинны, в противном случае она принимает значение ЛОЖЬ.
Логическая функция ИЛИ имеет вид:
ИЛИ(x1; x2, …;xn),
где x1; x2;; …;xn –аргументы, являющиеся логическими выражениями. Функция может содержать до 30 аргументов. Функция ИЛИ принимает значение ИСТИНА, если хотя бы один из ее аргументов есть ИСТИНА, в противном случае она принимает значение ЛОЖЬ.
Логическая функция НЕ имеет вид НЕ(x),
где x – логическое выражение. Ее значение ИСТИНА, если x имеет значение ЛОЖЬ, и наоборот.
3.2.ПРАКТИЧЕСКАЯ РАБОТА
3.2.1.ПРИМЕРЫ
Пример 1. Вычислить величину y при заданном значенииx
3 x2 , если x < 2 y = 4
3 , если x ≥ 2
2x
РЕШЕНИЕ.
В ячейки рабочего листа A1,B1 вводим обозначения x, y
В ячейку A2 вводим значение x
В ячейку B2 вводим формулу:
1-й способ. =ЕСЛИ(A2<2;3*A2*A2/4;3/(2*A2)), которая работает следующим образом – если в ячейке A2 число меньшее 2, то вычисляется выражение 3*A2*A2/4; если содержимое A2 больше или равно 2, то вычисляется 3/(2*A2).
2-й способ. Ввод формулы можно выполнить и с помощью Мастера функций. На первом шаге мастера из категории Логические выбираем функцию ЕСЛИ. На втором шаге заполняем поля аргументов, как показано в окне второго шага Мастера функций (рис. 3.1)
.
Рис. 3.1..Окно второго шага Мастера функций для функции ЕСЛИ

|
31 |
||||||||||||
|
Фрагменты рабочего листа при различных значениях |
x |
могут иметь |
||||||||||
|
вид: |
||||||||||||
|
A |
B |
A |
B |
A |
B |
|||||||
|
1 |
x |
y |
||||||||||
|
1 |
x |
y |
1 |
x |
y |
|||||||
|
а) |
2 |
0,5 |
0,1875 |
b) |
2 |
2 |
0,75 |
c) |
2 |
3 |
0,5 |
|
Рис. 3.2. a) счет по первой формуле; b), c) счет по второй формуле
Для вычисления выражения с большим числом условий часто можно использовать вложенную функцию ЕСЛИ.
Пример 2. Присвоить величине z значение 1, если точка плоскости с координатами x, y лежит внутри круга радиуса 1 с центром в начале координат; значение x2+y2, если точка вне этого круга, но внутри круга радиуса 2; значение 4, если точка лежит вне большего круга.
РЕШЕНИЕ. Данное геометрическое условие выражается формулой.
|
1, |
если x2 + y2 ≤1 |
||
|
2 + y2 , |
если 1 < x2 + y2 < 4 |
||
|
z = x |
|||
|
если |
x2 + y2 ≥ 4 |
||
|
4, |
|||
т. к. x2+y2 является квадратом расстояния точки (x, y) от начала координат. Проведем анализ данного выражения. Если выполнено первое условие, то z = 1. Если оно не выполнено, то выполнено неравенство x2+y2 > 1. При применении функции ЕСЛИ его выполнение соответствует вычислению значения, равного третьему аргументу, но нужно отделить случаи «меньше 4» и «больше или равно 4», поэтому третий аргумент снова
будет функцией ЕСЛИ, с помощью которой мы и проверим условие x2+y2 < 4.
Значения x, y введены в ячейки A2, B2. В ячейку C2 для значения z вводим формулу, начав с вызова функции ЕСЛИ. Чтобы задать третий аргумент снова вызовем функцию ЕСЛИ. Последовательный вид окон внешней и внутренней функции ЕСЛИ представлен на рисунках 3.3-3.5..
Рис. 3.3. Окно внешней функции ЕСЛИ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #