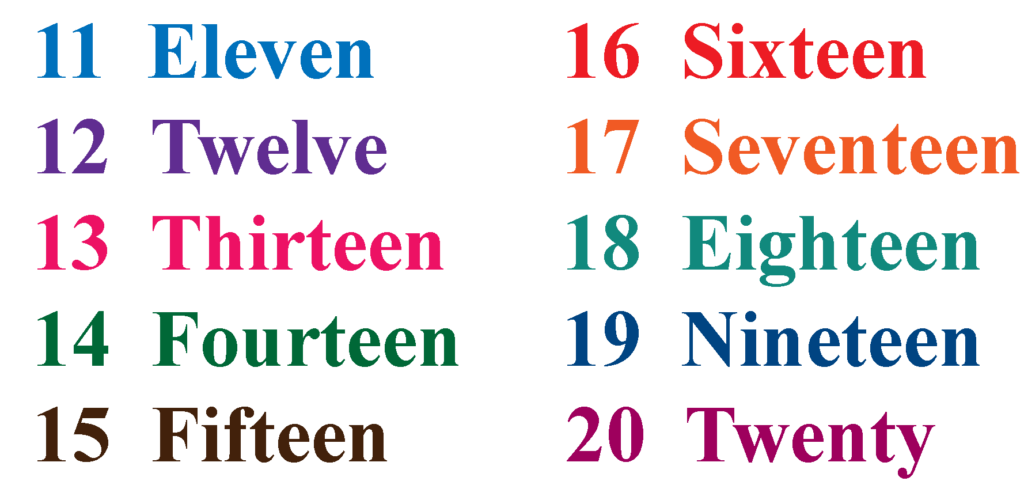Numbers in words means expressing the given numerals in words or spellings. For example, the number 1000 in words is written as one thousand. We can represent all natural numbers in words on the basis of the place value of their digits, such as ones, tens, hundreds, thousands, and so on.
| 1. | What are Number Names? |
| 2. | Number Names 1 to 100 |
| 3. | Numbers in Words in International System |
| 4. | Rules to Write Number Names |
| 5. | Tips to Learn Numbers in Words |
| 6. | FAQs on Numbers in Words |
What are Number Names?
When numbers are expressed in words, we call them number names. Number names help us to learn and identify numbers easily.
- For example, 1 can be written and read in words as one, therefore, the number name for 1 is one.
- 2 is written and read in words as two.
- 3 is written in words as three.
- 4 is written and read in words as four.
- 5 is written and read in words as five.
- 6 is written and read in words as six.
- 7 is written and read in words as seven.
- 8 is written and read in words as eight.
- 9 is written and read in words as nine.
- 10 is written and read in words as ten.
With the help of number names from one to ten, we can write and read higher-value numbers in words.
Numbers in Words in English
To write numbers in words in English we use the place values (ones, tens, hundreds, thousands, lakhs, crores, and so on…) of each digit in the number. With the help of the Indian place value chart, it is easy to find the place value of each digit based on its position and the number can be written in words. Let us understand this with the help of an example.
Example: Write the given number in words: 23456789 according to the Indian place value chart and according to the International place value chart.
Solution:
According to the Indian place value system, 2,34,56,789 is written and read in words as two crores, thirty-four lakh, fifty-six thousand, seven hundred eighty-nine.
According to the International place value chart, 23,456,789 is written and read in words as twenty-three million, four hundred fifty-six thousand, seven hundred eighty-nine.
Number Names 1 to 100
Number names 1 to 100 can be read and understood using the pattern explained below. Observe the pattern to learn numbers in words from 1 to 100 along with their spellings. First let us start with number names from 1 to 20, followed by number names from 21 to 100.
Number Names 1 to 20
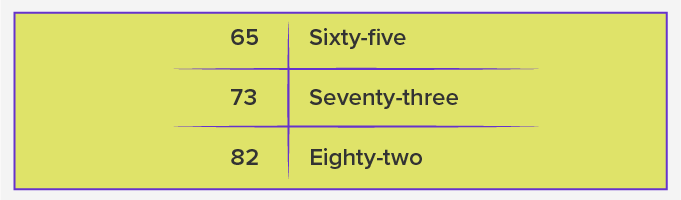
Given below is a chart showing number names from 1 to 20.
1 to 20 Spelling
‘1 to 20 spellings’ means that we need to write the number names from 1 to 20. So, whether we need to write ‘1 to 20 spellings’ or we are asked for ’11 to 20 spellings’, it means that we need to write their number names. The following chart shows the number names from 1 to 20.
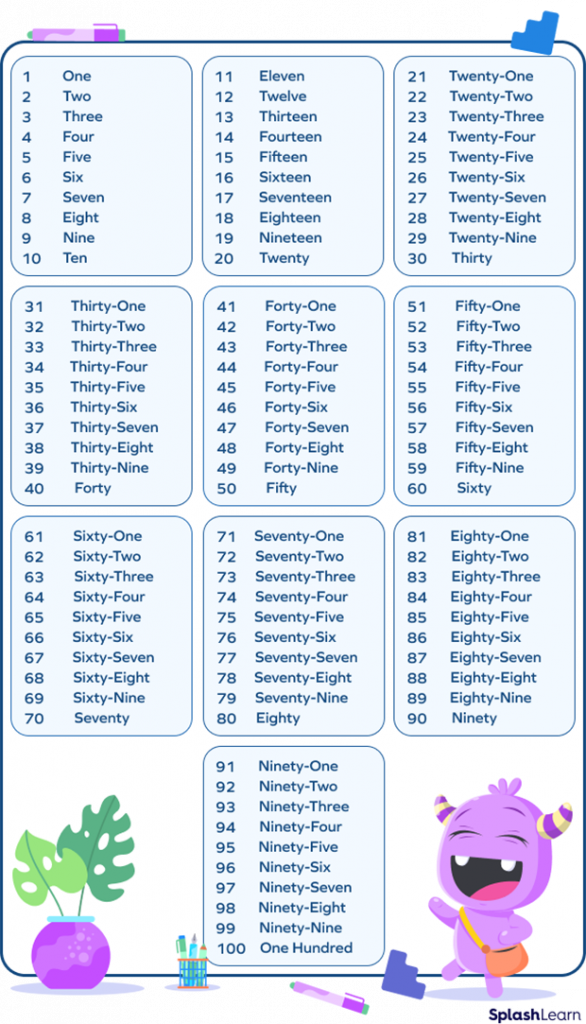
Number Names 21 to 100
Observe the chart given below with number names from number 21 to 100 and learn the counting in words.
Numbers in Words in International System
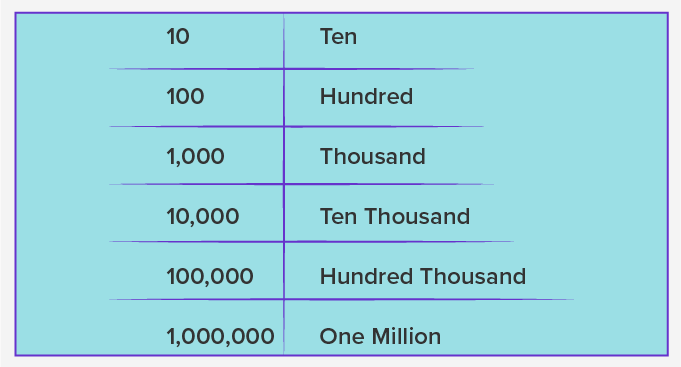
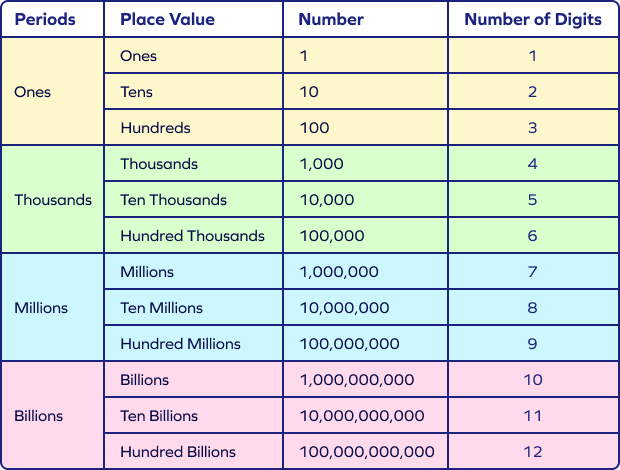
The international system has different place value names for a certain position of a digit in a number. For example, the number 1,000,000 is read as 1 million in words in the international system, whereas, it is read as 10 lakhs in the Indian place value system. In the international system, different periods are formed to read and write large numbers easily. As per the International numeration system, the comma is placed in a number after the hundreds place and then placed after every three digits. The place values in the international system are Ones, Tens, Hundreds, Thousands, Ten Thousand, Hundred Thousands, Millions, and so on.
- 1 million = 1000 thousands
- 1 billion = 1000 millions
For example, the number 7,456,123 is written or read in words as seven million four hundred fifty-six thousand one hundred twenty-three in the international number system.
Rules to Write Number Names
There are certain rules that can be followed while writing the numbers in words. These rules are listed below in detail.
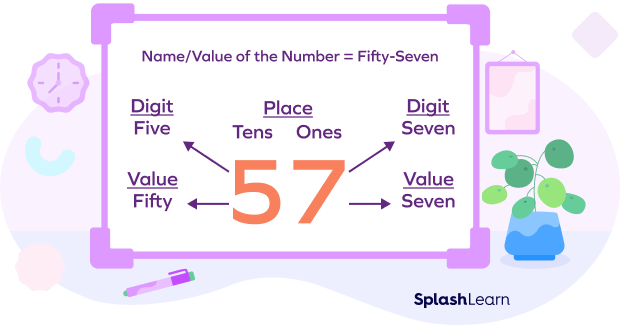
Rule 1: Understanding the place value system: The position of a number plays a very crucial role in writing a number in words. Let us understand how to differentiate between the place values based on the position of 1:
- 1 = ones place
- 10 = tens place
- 100 = hundreds place
- 1000 = thousands place
Rule 2: For numbers between 1-20 we can directly refer to the number names 1 to 20 chart to write their spellings. For example, the number name of 7 is seven, the number name of 15 is fifteen, and so on. After number 20 a generic series or pattern is followed.
Rule 3: The number names for multiples of 100 can be simply written by adding the word ‘hundred’ after the initial word. For example, the number name of 400 is four hundred, the number name for 500 is five hundred, and so on.
Rule 4: To write the number names of more than 2 digit numbers, we write the number in its expanded form. For example, 112 = 100 + 12, and 112 in words is written as one hundred twelve. The expanded form of 153 = 100 + 50 + 3 and 153 in words is written as One hundred fifty-three.
Tips to Learn Number Names
The following tips can be kept in mind to write numbers in words:
- The number names from 1 to 10 can be written directly because each number name is unique, as 1- one, 2-two, 3-three, and so on.
- The number names from 11 to 20 can also be written directly because each number name is unique, as 11 — eleven, 12-twelve, and so on.
- The numbers and spellings of the multiples of 10 can be written as 20- twenty, 30- thirty, 40- forty, 50- fifty, 60- sixty, 70- seventy, 80- eighty, 90- ninety.
- Now, after 20, starting from 21, we follow a different rule. The word form of 20 and 1 can be combined to write 21 as twenty-one, 22 as twenty-two, and so on. Similarly, we can write number names for 31, 41, 51, and so on.
- For large numbers write the number and their word form, like 100 — hundred, 1000 — thousand, and so on.
- The number 101 in words is written as one hundred one and 1001 is written as one thousand one and so on.
Observe the pattern which will help to write and read higher value numbers in words.
- 100 — Hundred
- 200 — Two-Hundred
- 300 — Three-Hundred
- 400 — Four-Hundred
- 500 — Five-Hundred
- 600 — Six-Hundred
- 700 — Seven-Hundred
- 800 — Eight-Hundred
- 900 — Nine-Hundred
- 1000 — One-Thousand or Thousand
Similarly,
- 2000 — Two thousand
- 5000 — Five thousand
- 10,000 — Ten Thousand
- 15,000 — Fifteen Thousand
- 16,000 — Sixteen thousand
- 20,000 — Twenty Thousand
- 25,000 — Twenty-Five Thousand
- 30,000 — Thirty Thousand
- 35,000 — Thirty-Five Thousand
- 40, 000 — Forty Thousand
- 45,000 — Forty-Five Thousand
- 100,000 — One hundred thousand (One Lakh)
- 200, 000 — Two hundred thousand (Two Lakhs)
- 300, 000 — Three hundred thousand (Three Lakhs)
- 400, 000 — Four hundred thousand (Four Lakhs)
- 500, 000 — Five hundred thousand (Five Lakhs)
Important Notes on Number Names
- Read the number from left to right.
- The number 40 in words is written as forty, not fourty.
- To write a number in words, first read the number and write the number name as you say it.
☛Related Articles
Check out these interesting articles to know more about Number Names and their related topics.
- Number names 1 to 10
- Number names 1 to 30
- Number names 1 to 40
- Number names 41 to 50
FAQs on Numbers in Words
What are Number Names in Math?
Number names in math are the infinite cardinal numbers starting from 1 to n written in their word form. To write number names we use the Indian place value system and the International place value system. For example, 798 is written as ‘seven hundred ninety-eight’.
How to Write Numbers in Words in International System?
In the International system of numeration, we use the place values as ones, tens, hundreds, thousands, ten thousand, hundred thousand, one million, ten million, hundred million, and so on, to write number names for large numbers. For example, 567,898 is written as ‘five hundred sixty-seven thousand eight hundred ninety-eight’.
☛ Check:
- Numbers in Words 51 to 60
- Numbers in Words 51 to 100
- Numbers in Words 91 to 100
How to Write 1100 in Words?
The number 1100 in words is written as One thousand one hundred.
☛ Number Names 1 to 50
How to Write Decimal Number Names?
Decimal number names can be written using the following steps. Let us write the number name for 25.578
- First, write the number name for the whole number part. Here, it will be Twenty-five
- Then, write the word ‘and’ for the decimal point. Here, it will be Twenty-five and.
- Now, write the number name for the decimal part, that is, the number to the right side of the decimal point. Here, it will be rewritten as twenty-five and five hundred seventy-eight thousandths. It should be noted that the decimal part is written using the decimal place value chart in which we use the place values like hundredths, thousandths and so on.
How to Write Number Names in International System?
In the international place-value system, we insert commas after every three digits from the right of the number. So while writing numbers in words we can check the place values and write numbers in words. For example, 37,824,500 is written in words as thirty-seven million eight hundred twenty-four thousand five hundred.
How to Write Numbers in Words?
To write a number in words, start from the left-most digit and write it according to its place value For example, 133 is read or written in words as one hundred thirty-three. By knowing the word form of numbers from 1 to 10 we can read and write the numbers easily. The word form of the first ten natural numbers is 1-one, 2-two, 3-three, 4-four, 5-five, 6-six, 7-seven, 8-eight, 9-nine, 10-ten.
☛ Also Read:
- Numbers in Words 100 to 200
- Numbers in Words 1 to 1000
How are Numbers in Words Useful in Real Life?
Numbers in words are useful in reading large numbers. If any document contains large numbers, the numbers in words help readers to read numbers correctly and quickly. While doing cheque payments, it is compulsory to write the numbers in figures as well as in words.
The number name of 40 is forty. It should be noted that 40 is often wrongly spelled as Fourty. However, the correct spelling is forty.
When we are asked to write the spellings from 11 to 20, we need to write the number names from 11 to 20 and we write it in the following way. 11 — Eleven, 12 — Twelve, 13 — Thirteen, 14 — Fourteen, 15 — Fifteen, 16 — Sixteen, 17 — Seventeen, 18 — Eighteen, 19 — Nineteen, 20 — Twenty
Number words are the alphabetical form of numbers. As the name suggests, these are numbers written in words. Word form is writing the numerical/number as you would say it in words.
‘Number words’ or ‘number names’ are simply the names assigned to numbers so that we can identify each number uniquely. When we talk about “math,” what is the first thing that comes to your mind? Numbers! Are you aware that numbers also have names called number names? Yes, like everything else in the world, numbers have names. Let us know the number name definition and the rules to write them.
Related Games
Number Words: Definition
A number word or number name is a way to express numbers in their word form. We can express numbers using their number name form. The spelling of numbers in English is something we should focus on while writing the numbers in word form.
For example, we can write 1 as “one.” So, the number name for 1 is “one.”
Similarly, we can express the number 2 as “two” in its word form.
The number 3 as “three” in its word form, and so on.
For example:
With the help of the number words from one to ten, we can make number words of higher value.
It is important to learn every number word from One to Twenty to learn other number words. Also, the number words from eleven to twenty are very different from other number words.
After learning the number words up to twenty, it is important to learn the number words such as thirty, forty, fifty, sixty until hundred.
Once you know these number words, it is easy to make number words for higher value numbers.
For example:
The above two number words are made from learning the basic number words from one to ten, and the number words for tens value, like sixty, seventy and eighty.
As the numbers increase in value and become larger with three, four, five, six, seven and more digits, the names start to change.
Related Worksheets
Rules to Write Numbers in Word Form
While writing numbers in their number words form, we have to follow certain rules. These rules are as follows:
Rule 1
Always consider place values while writing numbers in the word form.
For example, the digit 2 at the ones place is read as 2. The same digit at the tens place has the value “twenty.” So, 22 can be written as “twenty-two.”
Rule 2
To write numbers between 1–20, refer to the number names chart.
To express numbers beyond 20 in words, you must follow a certain pattern. As per this pattern, the multiples of 10 up to 90 are written as thirty, forty, fifty, sixty, seventy, eighty, and ninety.
Rule 3
For writing multiples of 100 in word form, you can write the digit in the word form and add the word hundred after it.
For example, you can express 200 as two hundred in the word form, 600 as six hundred, and so on.
You can follow the same rule while writing multiples of 1000 in word form. The only difference is that you have to add the word thousand instead of hundred. For example, you can write 3000 as three thousand in the word form.
Rule 4
For writing two-digit or three-digit numbers in word form, you have to write them in their expanded form. Ensure that you take the position of 0 in account.
For example, you can write 107 (expanded into $100 + 0 + 7$) as one hundred seven.
The word form of 125 (expanded into $100 + 20 + 5$) is one hundred twenty-five.
Number Words or Number Names from 1 to 100
Here’s a table containing numbers 1 to 100 and their corresponding word forms:
The Number Words for Higher Values
It becomes easy to convert numbers to number words and number words to number if we know the number words.
For example:
Write the given numbers in words.
Write the given numbers in numerals.
Number Names as per the International Number System
In the international system, the numbers are organized into periods and groups. The periods are categorized as ones, thousands, millions, etc. Each period is grouped into three place values. While writing numbers in this system, we insert a comma or separator after every three digits from the right.
The place value names in the international system are as follows:
- Ones
- Tens
- Hundreds
- Thousands
- Ten Thousands
- Hundred Thousands
- Millions
- Ten Millions
- Hundred Millions
- Billions
- Ten Billions
- Hundred Billions
- Trillions, and so on
Example: Suppose you have to write the word form of the number 6,342,715 in the international system.
6,342,715 is Six Million Three Hundred Forty-two Thousand Seven Hundred Fifteen.
Place Value Chart for International System
Here is the place value chart for the international system:
From this place value chart, we understand:
- 1 million $= 1000$ thousand
- 1 billion $= 1000$ million
Tips and Tricks to Learn Numbers Names
Here are a few tips to help you learn and write numbers in their word forms:
- Write down 1 to 20 as numbers and their spellings.
- Write down the multiples of 10 up to 90 and their spellings.
For example, 10: Ten, 20: Twenty, 30: Thirty, and so on.
- Write down the multiples of 100 and their spellings.
For example, 100: Three hundred, 200: Two hundred, and so on.
- For two-digit numbers beyond 20, expand them and write them in words in their expanded form. For example, you can expand 32 as $30 + 2$ and write “thirty-two.”
- Follow the same technique for large numbers.
For example, you can expand 471 as “$400 + 70 + 1$” and write “four hundred seventy-one” or “four hundred and seventy-one.”
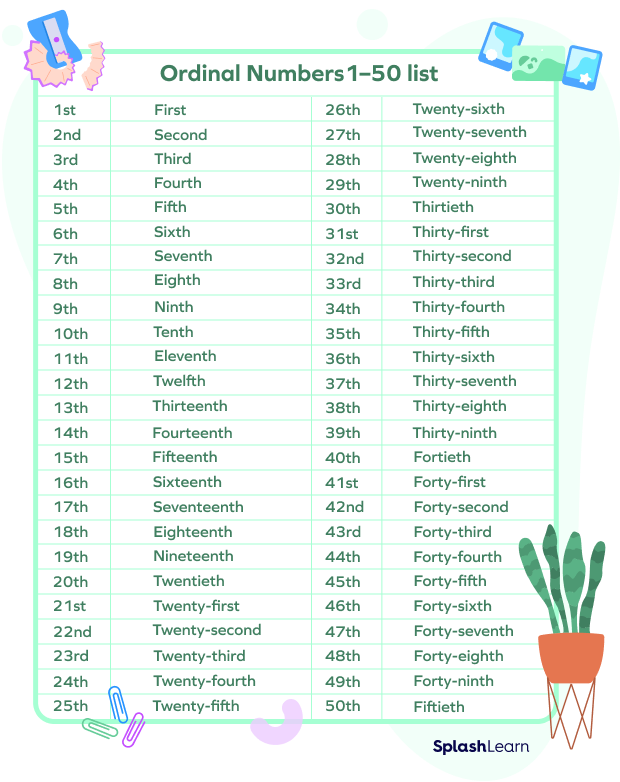
Number Names as per the Ordinal System
An ordinal number expresses the rank or position of something. That is why they are also known as ranking or positioning numbers.
Ordinal numbers are written as 1st, 2nd, 3rd, 4th, and so on.
Here is a chart of the first 50 ordinal numbers and their number names:
Fun Facts
- When writing ordinal numbers in their word form, we use the suffix -th for the numbers 11, 12, and 13; but for all other numbers ending with 1, 2, or 3, we use the suffixes -st, -nd, and -rd, respectively. For example, we express 51 as fifty-first, 52 as fifty-second, and 53 as fifty-third.
- The word form of the number 40 is forty and not fourty.
- When writing numbers between 21 and 99, we use a hyphen $(-)$ in between.
- To write number words, we can write the word form of the numbers as we say them.
Conclusion
Number names offer an easy way to identify and learn numbers. They can help us to understand how the number system functions. Knowing to read and write numbers in words can enable us to identify how numbers relate to one another.
Solved Examples
- Write the number 7575 in words.
Solution:
We can expand 7575 as $7000 + 500 + 70 + 5$.
7575 in word form is “seven thousand five hundred seventy-five.”
- What comes after the given number name: twenty-nine?
Solution:
Twenty-nine $= 29$
The number after 29 is $29 + 1 = 30$
30 in the word form is Thirty.
So, thirty comes after twenty-nine.
- Count the emojis in the given image and write the number in words.
Solution:
$5 + 4 + 3 + 2 + 1 = 15$
The given image has fifteen or 15 smileys.
- Express 2022 in words and also in the ordinal system.
Solution:
$2022 = 2000 + 0 + 20 + 2$
In words, we write it as “two thousand twenty-two.”
Also, 2022 is written as “two thousand twenty-second” in the ordinal system.
- Write the word form of 404.
Solution:
$404 = 400 + 0 + 4$
404 is four hundred four.
Practice Problmes
Fifty-seven
Five & seven
Seventy five
None of the above
Correct answer is: Fifty-seven
We expand 57 as $50 + 7$. So, it would be written as “fifty-seven.”
Sixty-tenth
Seventieth
Seventy
None of the above
Correct answer is: Seventieth
As per the ordinal system, “seventieth” comes after “sixty-ninth.”
4040 is four thousand forty
4004 is four thousand four
4400 is four thousand four hundred
4440 is four thousand forty-four
Correct answer is: 4440 is four thousand forty-four
4440 is four thousand four hundred forty.
$gt$
$=$
$lt$
None of the above
Correct answer is: $lt$
Four hundred sixty-three is 463. Thus, $436 lt 463$.
Fifth and eighth
Fifth and seventh
Fourth and seventh
Sixth and eighth
Correct answer is: Fifth and seventh
By counting the letters in the word “PLACEMENT,” we can see that the letter E appears in the fifth and seventh positions.
Frequently Asked Questions
Do we have to use commas when writing a number in its word form?
No, we don’t use commas when writing a number in its word form.
Does the word zero appear in any number name?
No, we don’t use the word “zero” when writing a number in words.
Can we write decimal numbers in words?
Yes, we can write decimal numbers in words. For example, we can write 42.35 as forty-two point three five.
Are there any real-life applications of writing numbers in words?
Yes, there are real-life applications of writing numbers in words. For example, it is mandatory to write the amount in both figures and words in a bank cheque.
Why is place value important for writing numbers in words?
The place value helps to determine the place of a digit in a number. This is important for reading a number and writing it in words.
Related Articles
- Word Form
- Natural Number
- Number Words
Numbers have names in words. A digit is a single symbol used to make numerals. 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 are the ten digits we use in everyday numerals. In this article, students will learn numbers and their names. Learning numbers with their names will help them to improve their number writing skills quickly. Parents and teachers encourage students to learn numbers and give them support so that they can learn fastly and interestingly.
You can use this page and download this page for free and take a printout of this download so that kids will practice easily. On this page, you will learn numbers and their names from 1 to 50, numbers names(spelling of numbers), example images, some practice questions on writing numbers names in words.
Also, Read:
- Numbers up to 10
- Numbers and Counting up to 10
- Worksheet on Numbers
Numbers and their Names | How do you Write Numbers in Names?
Students who are good at numbers from 1 to 100 at the preschooler stage, can easily learn tables and perform fast mathematical calculations in school. So, Parents start teaching the Number Names at the preschooler stage only. The Number Names in Words are given below in the tabular form so that you can easily learn and remember them.
| 1 | One | 11 | Eleven | 21 | Twenty – one | 31 | Thirty – one | 41 | Forty – one |
| 2 | Two | 12 | Twelve | 22 | Twenty – two | 32 | Thirty – two | 42 | Forty – two |
| 3 | Three | 13 | Thirteen | 23 | Twenty – three | 33 | Thirty – three | 43 | Forty – three |
| 4 | Four | 14 | Fourteen | 24 | Twenty – four | 34 | Thirty – four | 44 | Forty – four |
| 5 | Five | 15 | Fifteen | 25 | Twenty – five | 35 | Thirty – five | 45 | Forty-five |
| 6 | Six | 16 | Sixteen | 26 | Twenty – six | 36 | Thirty – six | 46 | Forty-six |
| 7 | Seven | 17 | Seventeen | 27 | Twenty – seven | 37 | Thirty – seven | 47 | Forty-seven |
| 8 | Eight | 18 | Eighteen | 28 | Twenty – eight | 38 | Thirty – eight | 48 | Forty – eight |
| 9 | Nine | 19 | Nineteen | 29 | Twenty – nine | 39 | Thirty – nine | 49 | Forty – nine |
| 10 | Ten | 20 | Twenty | 30 | Thirty | 40 | Forty | 50 | Fifty |
The image of numbers and their names are given below. The image consists of numbers from 0 to 9 represented in both numbers forms and words form.
Another image of numbers and their names are as shown below, this image consists of numbers from 11 to 20 in numbers from and words form. Students observe the image clear and then start practicing, you can write easily.
Do Check:
- Count the Numbers and Match
- Count and Write Numbers
Practice Questions on Numbers and their Names
Question 1 :
The below figure consists of numbers and missing letters numbers words. Students have to fill the missing letters in numbers names using it pencil.
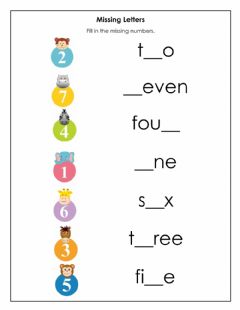
The given figure consists of different numbers and their names but not in sequence order. Students have to match the numbers and their names through a line, draw in between numbers and names using it pencil.
Question 3:
The below image consists of different kinds of pictures, numbers, and numbers names. Students have to count the numbers in pictures, match that number with their number names.

The below-given figure consists of numbers and their names given in the normal form and dotted line, tally marks are just for idea purpose. Using this figure students have to practice and writing these numbers.

Draw a line from the hands to the names of the matching numbers. The given figure consists of hand finger figures and numbers names students draw a line using it pencil.
Question 6:
The below-given figure consists of only number names. Students will write the numbers of their numbers names.
Question 7:
The given figure consists of numbers from 1 to 10 and numbers names letters in reverse words. Students will write the names of the numbers in the correct order.
Question 8:
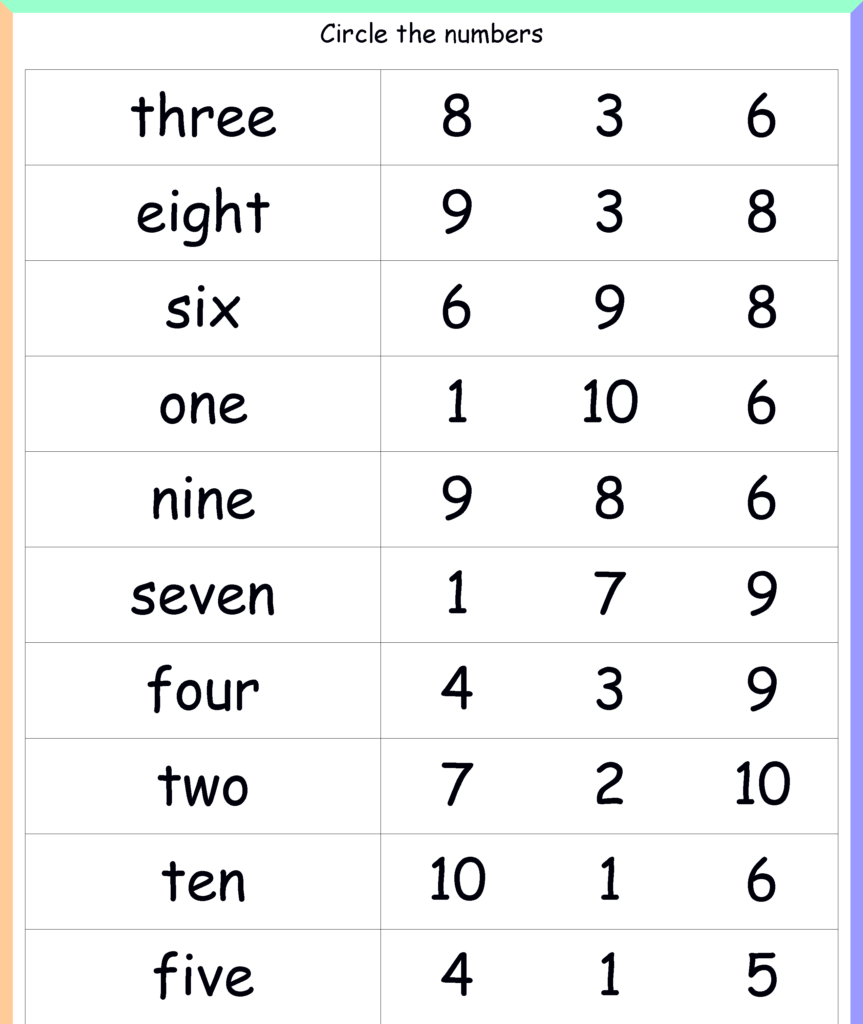
The below figure consists of numbers names and numbers. Students read the number name properly and circle that number in the given number set.
Question 9:
Write the number names in the given figure blank. The figure contains only numbers and blanks students read the number and fill the blank with name using it pencil.
Question 10:
The below figure consists of pictures with their names. Students have to count the picture name letters and write that number and number name in the given boxes.
Make your kids even more interested in Math Activities by taking help from our fun-learning Kindergarten Math Curriculum, Worksheets, Activities, Problems, Fun Games
|
The words for 1 to 10 : 1 — One 2 — Two 3 — Three 4 — Four 5 — Five 6 — Six 7 — Seven 8 — Eight 9 — Nine 10 — Ten |
The words for 11 to 20 : 11 — Eleven 12 — Twelve 13 — Thirteen 14 — Fourteen 15 — Fifteen 16 — Sixteen 17 — Seventeen 18 — Eighteen 19 — Nineteen 20 — Twenty |
After twenty, there is a pattern to the words. The tens place uses the words twenty, thirty, forty, fifty, sixty, seventy, eighty and ninety for 20, 30, 40, 50, 60, 70, 80 and 90.
If the ones place has more than zero, the word is formed by using the ten’s place word, a hyphen, and then the ones place word.
Examples :
38 is thirty-eight
84 is eighty-four
25 is twenty-five
Before going to see example problems naming the numbers, let look into place values.
Example 1 :
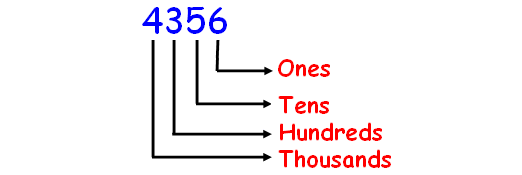
How do you write this number using words?
4,356
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the numbers.
In the given number, we have 4 thousands 3 hundreds 5 tens and 6 ones.
Hence, the name of the number 4356 is
four thousand three hundred fifty-six
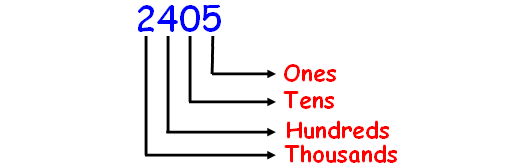
Example 2 :
How do you write this number using words?
2,405
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 2 thousands 4 hundreds 0 tens and 5 ones.
Hence, the name of the number 2405 is
two thousand four hundred five
Example 3 :
How do you write this number using words?
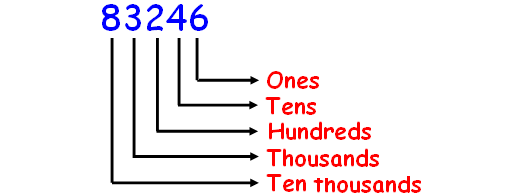
83,246
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 8 ten thousands 3 thousands 2 hundreds 4 tens 6 ones.
Hence, the name of the number 83246 is
eighty three thousands two hundred forty-six
Example 4 :
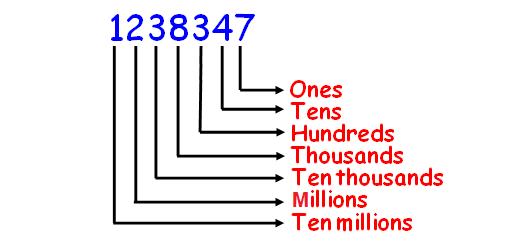
How do you write this number using words?
1,238,347
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
Hence, the name of the number 1238347 is
twelve million thirty-eight thousand three hundred forty-seven
Example 5 :
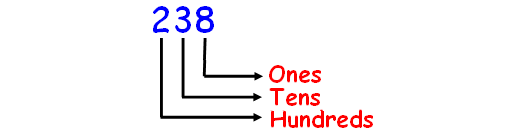
How do you write this number using words?
238
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 2 hundreds 3 tens 8 ones.
Hence, the name of the number 238 is
two hundred thirty-eight
Example 6 :
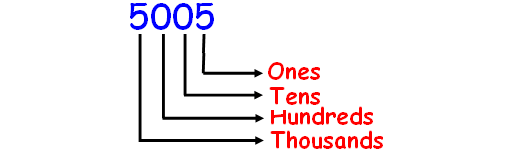
How do you write this number using words?
5005
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 5 thousands 0 hundreds 0 tens 5 ones.
Hence, the name of the number 5005 is
five thousand five
Example 7 :
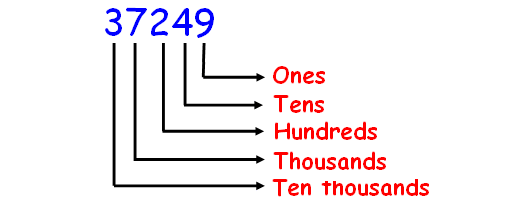
How do you write this number using words?
37249
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 3 ten thousands 7 thousands 2 hundreds 4 tens 9 ones.
Hence, the name of the number 37249 is
thirty seven thousand two hundred forty-nine
Example 8 :
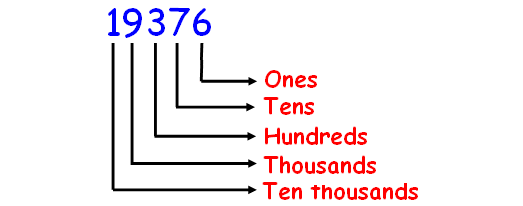
How do you write this number using words?
19376
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 1 ten thousands 9 thousands 3 hundreds 7 tens 6 ones.
Hence, the name of the number 19376 is
nineteen thousand three hundred fifty-six
Example 9 :
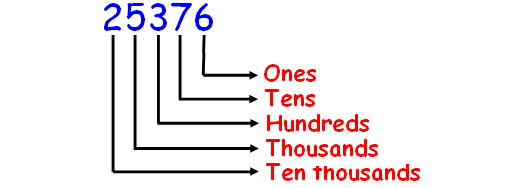
How do you write this number using words?
25376
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 2 ten thousands 5 thousands 3 hundreds 7 tens 6 ones.
Hence, the name of the number 25376 is
twenty five thousand three hundred seventy six
Example 10 :
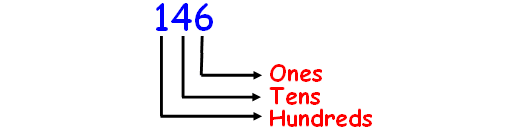
How do you write this number using words?
146
Solution :
Before naming the number, first we have to write their place values. This will help us for naming the number.
In the given number, we have 1 hundred 4 tens 6 ones.
Hence, the name of the number 146 is
one hundred forty-six
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
English number words include numerals and various words derived from them, as well as a large number of words borrowed from other languages.
Cardinal numbers[edit]
Cardinal numbers refer to the size of a group. In English, these words are numerals.
| 0 | zero (nought) | 10 | ten | ||
| 1 | one | 11 | eleven | ||
| 2 | two | 12 | twelve (a dozen) | 20 | twenty |
| 3 | three | 13 | thirteen (a baker’s dozen) | 30 | thirty |
| 4 | four | 14 | fourteen | 40 | forty |
| 5 | five | 15 | fifteen | 50 | fifty |
| 6 | six | 16 | sixteen | 60 | sixty |
| 7 | seven | 17 | seventeen | 70 | seventy |
| 8 | eight | 18 | eighteen | 80 | eighty |
| 9 | nine | 19 | nineteen | 90 | ninety |
If a number is in the range 21 to 99, and the second digit is not zero, the number is typically written as two words separated by a hyphen.
| 21 | twenty-one |
| 25 | twenty-five |
| 32 | thirty-two |
| 58 | fifty-eight |
| 64 | sixty-four |
| 79 | seventy-nine |
| 83 | eighty-three |
| 99 | ninety-nine |
In English, the hundreds are perfectly regular, except that the word hundred remains in its singular form regardless of the number preceding it.
So too are the thousands, with the number of thousands followed by the word «thousand». For the number one thousand it may be written 1 000 or 1000 or 1,000, for larger numbers they are written for example 10 000 or 10,000 for ease of human reading[example needed]. The use of the , as a separator is avoided in some languages[citation needed] as it is used for a decimal placement, for example with money[citation needed]. As a result some style guides[example needed] recommend avoidance of the comma (,) as a separator and only to use the period (.) as a decimal placement. Thus a half would be written 0.5 in decimal, base ten notation, and fifty thousand as 50 000, and not 50.000 nor 50,000 nor 50000. As the English language has no language academy to make usage correct there is still a wide variety of usage, other languages do have language academies which ruled on these matters[example needed], yet their rulings are deprecated by international standards like the SI system or EU recommendations[example needed] which leads to varied usage.
| 1,000 | one thousand |
| 2,000 | two thousand |
| … | … |
| 10,000 | ten thousand or (rarely used) a myriad, which usually means an indefinitely large number. |
| 11,000 | eleven thousand |
| … | … |
| 20,000 | twenty thousand |
| 21,000 | twenty-one thousand |
| 30,000 | thirty thousand |
| 85,000 | eighty-five thousand |
| 100,000 | one hundred thousand or one lakh (Indian English) |
| 999,000 | nine hundred and ninety-nine thousand (inclusively British English, Irish English, Australian English, and New Zealand English) nine hundred ninety-nine thousand (American English) |
| 1,000,000 | one million |
| 10,000,000 | ten million or one crore (Indian English) |
In American usage, four-digit numbers are often named using multiples of «hundred» and combined with tens and ones: «eleven hundred three», «twelve hundred twenty-five», «forty-seven hundred forty-two», or «ninety-nine hundred ninety-nine.» In British usage, this style is common for multiples of 100 between 1,000 and 2,000 (e.g. 1,500 as «fifteen hundred») but not for higher numbers.
Americans may pronounce four-digit numbers with non-zero tens and ones as pairs of two-digit numbers without saying «hundred» and inserting «oh» for zero tens: «twenty-six fifty-nine» or «forty-one oh five». This usage probably evolved from the distinctive usage for years; «nineteen-eighty-one», or from four-digit numbers used in the American telephone numbering system which were originally two letters followed by a number followed by a four-digit number, later by a three-digit number followed by the four-digit number. It is avoided for numbers less than 2500 if the context may mean confusion with time of day: «ten ten» or «twelve oh four».
Intermediate numbers are read differently depending on their use. Their typical naming occurs when the numbers are used for counting. Another way is for when they are used as labels. The second column method is used much more often in American English than British English. The third column is used in British English but rarely in American English (although the use of the second and third columns is not necessarily directly interchangeable between the two regional variants). In other words, British English and American English can seemingly agree, but it depends on a specific situation (in this example, bus numbers).[citation needed]
| Common British vernacular | Common American vernacular | Common British vernacular | |
| «How many marbles do you have?» | «What is your house number?» | «Which bus goes to the High Street?» | |
| 101 | «A hundred and one.» | «One-oh-one.» Here, «oh» is used for the digit zero. |
«One-oh-one.» |
| 109 | «A hundred and nine.» | «One-oh-nine.» | «One-oh-nine.» |
| 110 | «A hundred and ten.» | «One-ten.» | «One-one-oh.» |
| 117 | «A hundred and seventeen.» | «One-seventeen.» | «One-one-seven.» |
| 120 | «A hundred and twenty.» | «One-twenty.» | «One-two-oh», «One-two-zero.» |
| 152 | «A hundred and fifty-two.» | «One-fifty-two.» | «One-five-two.» |
| 208 | «Two hundred and eight.» | «Two-oh-eight.» | «Two-oh-eight.» |
| 394 | «Three hundred and ninety-four.» | «Three-ninety-four.» | «Three-ninety-four.» or «Three-nine-four.» |
Note: When a cheque (or check) is written, the number 100 is always written «one hundred». It is never «a hundred».
In American English, many students are taught[example needed],[citation needed] not to use the word and anywhere in the whole part of a number, so it is not used before the tens and ones. It is instead used as a verbal delimiter when dealing with compound numbers. Thus, instead of «three hundred and seventy-three,» «three hundred seventy-three» would be said. Despite this rule, some Americans use the and in reading numbers containing tens and ones as an alternative variant.
Very large numbers[edit]
For numbers above a million, three main systems name numbers in English (for the use of prefixes such as kilo- for a thousand, mega- for a million, milli- for a thousandth, etc. see SI units):
- the long scale (formerly used in British English but now less so) designates a system of numeric names in which a thousand million is called a milliard, and billion is used for a million million. This system is still used in several other European languages.
- the short scale (always used in American English and almost invariably in British English) designates a system of numeric names in which a thousand million is called a billion, and the word milliard is not used.
- the Indian numbering system, used widely in Indian subcontinent.
Many people have no direct experience of manipulating numbers this large, and many non-American readers may interpret billion as 1012 (even if they are young enough to have been taught otherwise at school); moreover, usage of the «long» billion is standard in some non-English speaking countries. For these reasons, defining the word may be advisable when writing for the public.
| Number notation | Power notation |
Short scale | Long scale | Indian (or South Asian) English |
|---|---|---|---|---|
| 1,000,000 | 106 | one million | one million | ten lakh |
| 1,000,000,000 | 109 | one billion a thousand million |
one milliard a thousand million |
one hundred crore (one arab) |
| 1,000,000,000,000 | 1012 | one trillion a thousand billion |
one billion a million million |
one lakh crore (ten kharab) |
| 1,000,000,000,000,000 | 1015 | one quadrillion a thousand trillion |
one billiard a thousand billion |
ten crore crore (one padm) |
| 1,000,000,000,000,000,000 | 1018 | one quintillion a thousand quadrillion |
one trillion a million billion |
ten thousand crore crore (ten shankh) |
| 1,000,000,000,000,000,000,000 | 1021 | one sextillion a thousand quintillion |
one trilliard a thousand trillion |
one crore crore crore |
The numbers past one trillion in the short scale, in ascending powers of 1000, are as follows: quadrillion, quintillion, sextillion, septillion, octillion, nonillion, decillion, undecillion, duodecillion, tredecillion, quattuordecillion, quindecillion, sexdecillion, septendecillion, octodecillion, novemdecillion and vigintillion (which is 10 to the 63rd power, or a one followed by 63 zeros). The highest number in this series listed in modern dictionaries is centillion, which is 10 to the 303rd power.[1] The interim powers of one thousand between vigintillion and centillion do not have standardized names, nor do any higher powers, but there are many ad hoc extensions in use. The highest number listed in Robert Munafo’s table of such unofficial names[2] is milli-millillion, which was coined as a name for 10 to the 3,000,003rd power.
The googolplex was often cited as the largest named number in English. If a googol is ten to the one hundredth power, then a googolplex is one followed by a googol of zeros (that is, ten to the power of a googol).[3] There is the coinage, of very little use, of ten to the googolplex power, of the word googolplexplex.
The terms arab, kharab, padm and shankh are more commonly found in old books on Indian mathematics.
Here are some approximate composite large numbers in American English:
| Quantity | Written | Pronounced |
|---|---|---|
| 1,200,000 | 1.2 million | one point two million |
| 3,000,000 | 3 million | three million |
| 250,000,000 | 250 million | two hundred fifty million |
| 6,400,000,000 | 6.4 billion | six point four billion |
| 23,380,000,000 | 23.38 billion | twenty-three point three eight billion |
Often, large numbers are written with (preferably non-breaking) half-spaces or thin spaces separating the thousands (and, sometimes, with normal spaces or apostrophes) instead of commas—to ensure that confusion is not caused in countries where a decimal comma is used. Thus, a million is often written 1 000 000.
In some areas, a point (. or ·) may also be used as a thousands separator, but then the decimal separator must be a comma (,). In English the point (.) is used as the decimal separator, and the comma (,) as the thousands separator.
Special names[edit]
Some numbers have special names in addition to their regular names, most depending on context.
- 0:
- zero: formal scientific usage
- nought: mostly British usage, common in science to refer to subscript 0 indicating an initial state
- naught: archaic term for nothingness, which may or may not be equivalent to the number; mostly American usage, old-fashioned spelling of nought
- aught: proscribed but still occasionally used when a digit is 0 (as in «thirty-aught-six», the .30-06 Springfield rifle cartridge and by association guns that fire it). Aughts also refers to the decade of 2000-2009 in American English.
- oh: used when spelling numbers (like telephone, bank account, bus line [British: bus route]) but can cause confusion with the letter o if reading a mix of numbers and letters
- nil: in general sport scores, British usage («The score is two–nil.»)
- nothing: in general sport scores, American usage («The score is two–nothing.»)
- null: to an object or idea related to nothingness. The 0th aleph number (
) is pronounced «aleph-null».
- love: in tennis, badminton, squash and similar sports (origin disputed, said by the Oxford English Dictionary to be from the idea that when one does a thing «for love», that is for no monetary gain, the word «love» implies «nothing». The previously held belief that it originated from French: l’œuf, lit. ‘the egg’, due to its shape, is no longer widely accepted)
- zilch, nada (from Spanish), zip: used informally when stressing nothingness; this is true especially in combination with one another («You know nothing—zero, zip, nada, zilch!»); American usage
- nix: also used as a verb; mostly American usage
- cypher / cipher: archaic, from French chiffre, in turn from Arabic sifr, meaning zero
- goose egg (informal)
- duck (used in cricket when a batsman is dismissed without scoring)
- blank the half of a domino tile with no pips
- 1:
- ace in certain sports and games, as in tennis or golf, indicating success with one stroke, and the face of a die, playing card or domino half with one pip
- birdie in golf denotes one stroke less than par, and bogey, one stroke more than par
- solo
- unit
- linear the degree of a polynomial is 1; also for explicitly denoting the first power of a unit: linear metre
- unity in mathematics
- protagonist first actor in theatre of Ancient Greece, similarly Proto-Isaiah and proton
- 2:
- couple
- brace, from Old French «arms» (the plural of arm), as in «what can be held in two arms».
- pair
- deuce the face of a die, playing card or domino half with two pips
- eagle in golf denotes two strokes less than par
- duo
- quadratic the degree of a polynomial is 2
- also square or squared for denoting the second power of a unit: square metre or metre squared
- penultimate, second from the end
- deuteragonist second actor in theatre of Ancient Greece, similarly Deutero-Isaiah and deuteron
- 3:
- trey the face of a die or playing card with three pips, a three-point field goal in basketball, nickname for the third carrier of the same personal name in a family
- trio
- trips: three-of-a-kind in a poker hand. a player has three cards with the same numerical value
- cubic the degree of a polynomial is 3
- also cube or cubed for denoting the third power of a unit: cubic metre or metre cubed
- albatross in golf denotes three strokes less than par. Sometimes called double eagle
- hat-trick or hat trick: achievement of three feats in sport or other contexts[4]
- antepenultimate third from the end
- tritagonist third actor in theatre of Ancient Greece, similarly Trito-Isaiah and triton
- turkey in bowling, three consecutive strikes
- 4:
- cater: (rare) the face of a die or playing card with four pips
- quartet
- quartic or biquadratic the degree of a polynomial is 4
- quad (short for quadruple or the like) several specialized sets of four, such as four of a kind in poker, a carburetor with four inputs, etc.,
- condor in golf denotes four strokes less than par
- preantepenultimate fourth from the end
- 5:
- cinque or cinq (rare) the face of a die or playing card with five pips
- quintet
- nickel (informal American, from the value of the five-cent US nickel, but applied in non-monetary references)
- quintic the degree of a polynomial is 5
- quint (short for quintuplet or the like) several specialized sets of five, such as quintuplets, etc.
- 6:
- half a dozen
- sice (rare) the face of a die or playing card with six pips
- sextet
- sextic or hectic the degree of a polynomial is 6
- 7:
- septet
- septic or heptic the degree of a polynomial is 7
- 8:
- octet
- 9:
- nonet
- 10:
- dime (informal American, from the value of the ten-cent US dime, but applied in non-monetary references)
- decet
- decade, used for years but also other groups of 10 as in rosary prayers or Braille symbols
- 11: a banker’s dozen
- 12: a dozen (first power of the duodecimal base), used mostly in commerce
- 13: a baker’s dozen
- 20: a score (first power of the vigesimal base), nowadays archaic; famously used in the opening of the Gettysburg Address: «Four score and seven years ago…» The Number of the Beast in the King James Bible is rendered «Six hundred threescore and six». Also in The Book of Common Prayer, Psalm 90 as used in the Burial Service—»The days of our age are threescore years and ten; ….»
- 50: half-century, literally half of a hundred, usually used in cricket scores.
- 55: double-nickel (informal American)
- 60: a shock: historical commercial count, described as «three scores».[5]
- 100:
- A century, also used in cricket scores and in cycling for 100 miles.
- A ton, in Commonwealth English, the speed of 100 mph[6] or 100 km/h.
- A small hundred or short hundred (archaic, see 120 below)
- 120:
- A great hundred or long hundred (twelve tens; as opposed to the small hundred, i.e. 100 or ten tens), also called small gross (ten dozens), both archaic
- Also sometimes referred to as duodecimal hundred, although that could literally also mean 144, which is twelve squared
- 144: a gross (a dozen dozens, second power of the duodecimal base), used mostly in commerce
- 500: a ream
- 1000:
- a grand, colloquially used especially when referring to money, also in fractions and multiples, e.g. half a grand, two grand, etc. Grand can also be shortened to «G» in many cases.
- K, originally from the abbreviation of kilo-, e.g. «He only makes $20K a year.»
- Millennium (plural: millennia), a period of one thousand years.
- kilo- (Greek for «one thousand»), a decimal unit prefix in the Metric system denoting multiplication by «one thousand». For example: 1 kilometre = 1000 metres.
- 1728: a great gross (a dozen gross, third power of the duodecimal base), used historically in commerce
- 10,000: a myriad (a hundred hundred), commonly used in the sense of an indefinite very high number
- 100,000: a lakh (a hundred thousand), in Indian English
- 10,000,000: a crore (a hundred lakh), in Indian English and written as 100,00,000.
- 10100: googol (1 followed by 100 zeros), used in mathematics
- 10googol: googolplex (1 followed by a googol of zeros)
- 10googolplex: googolplexplex (1 followed by a googolplex of zeros)
Combinations of numbers in most sports scores are read as in the following examples:
- 1–0 British English: one-nil; American English: one-nothing, one-zip, or one-zero
- 0–0 British English: nil-nil or nil all; American English: zero-zero or nothing-nothing, (occasionally scoreless or no score)
- 2–2 two-two or two all; American English also twos, two to two, even at two, or two up.
Naming conventions of Tennis scores (and related sports) are different from other sports.
The centuries of Italian culture have names in English borrowed from Italian:
- duecento «(one thousand and) two hundred» for the years 1200 to 1299, or approximately 13th century
- trecento 14th century
- quattrocento 15th century
- cinquecento 16th century
- seicento 17th century
- settecento 18th century
- ottocento 19th century
- novecento 20th century
- ventesimo 21st century
When reading numbers in a sequence, such as a telephone or serial number, British people will usually use the terms double followed by the repeated number. Hence 007 is double oh seven. Exceptions are the emergency telephone number 999, which is always nine nine nine and the apocalyptic «Number of the Beast», which is always six six six. In the US, 911 (the US emergency telephone number) is usually read nine one one, while 9/11 (in reference to the September 11, 2001, attacks) is usually read nine eleven.
Multiplicative adverbs and adjectives[edit]
A few numbers have specialised multiplicative numbers (adverbs), also called adverbial numbers, which express how many times some event happens:
| one time | once |
| two times | twice |
| three times | thrice (largely obsolete) |
Compare these specialist multiplicative numbers to express how many times some thing exists (adjectives):
| × 1 | solitary | singular | one-off |
| × 2 | double | twofold | duplicate |
| × 3 | triple | threefold | triplicate |
| × 4 | quadruple | fourfold | |
| × 5 | quintuple | fivefold | |
| × 6 | sextuple, hextuple | sixfold | |
| × 7 | septuple, heptuple | sevenfold | |
| ×100 | ….. | hundredfold |
English also has some multipliers and distributive numbers, such as singly.
Other examples are given in the Specialist Numbers.
Negative numbers[edit]
The name of a negative number is the name of the corresponding positive number preceded by «minus» or (American English) «negative». Thus −5.2 is «minus five point two» or «negative five point two». For temperatures, North Americans colloquially say «below»—short for «below zero»—so a temperature of −5° is «five below» (in contrast, for example, to «two above» for 2°). This is occasionally used for emphasis when referring to several temperatures or ranges both positive and negative. This is particularly common in Canada where the use of Celsius in weather forecasting means that temperatures can regularly drift above and below zero at certain times of year.
Ordinal numbers[edit]
Ordinal numbers refer to a position in a series. Common ordinals include:
| 0th | zeroth or (rarely) noughth (see below) | 10th | tenth | ||
| 1st | first | 11th | eleventh | ||
| 2nd | second | 12th | twelfth | 20th | twentieth |
| 3rd | third | 13th | thirteenth | 30th | thirtieth |
| 4th | fourth | 14th | fourteenth | 40th | fortieth |
| 5th | fifth | 15th | fifteenth | 50th | fiftieth |
| 6th | sixth | 16th | sixteenth | 60th | sixtieth |
| 7th | seventh | 17th | seventeenth | 70th | seventieth |
| 8th | eighth | 18th | eighteenth | 80th | eightieth |
| 9th | ninth | 19th | nineteenth | 90th | ninetieth |
Zeroth only has a meaning when counting starts with zero, which happens in a mathematical or computer science context. Ordinal numbers predate the invention of zero and positional notation.
Ordinal numbers such as 21st, 33rd, etc., are formed by combining a cardinal ten with an ordinal unit.
| 21st | twenty-first |
| 25th | twenty-fifth |
| 32nd | thirty-second |
| 58th | fifty-eighth |
| 64th | sixty-fourth |
| 79th | seventy-ninth |
| 83rd | eighty-third |
| 99th | ninety-ninth |
Higher ordinals are not often written in words, unless they are round numbers (thousandth, millionth, billionth). They are written with digits and letters as described below. Some rules should be borne in mind.
- The suffixes -th, -st, -nd and -rd are occasionally written superscript above the number itself.
- If the tens digit of a number is 1, then «th» is written after the number. For example: 13th, 19th, 112th, 9,311th.
- If the tens digit is not equal to 1, then the following table could be used:
| If the units digit is: | 0 | 1 | 2 | 3 | 4-9 |
| This is written after the number | th | st | nd | rd | th |
- For example: 2nd, 7th, 20th, 23rd, 52nd, 135th, 301st.
These ordinal abbreviations are actually hybrid contractions of a numeral and a word. 1st is «1» + «st» from «first«. Similarly, «nd» is used for «second» and «rd» for «third«. In the legal field and in some older publications, the ordinal abbreviation for «second» and «third» is simply «d».
- For example: 42d, 33d, 23d.
NB: «D» still often denotes «second» and «third» in the numeric designations of units in the US armed forces, for example, 533d Squadron, and in legal citations for the second and third series of case reporters.
Dates[edit]
There are a number of ways to read years. The following table offers a list of valid pronunciations and alternate pronunciations for any given year of the Gregorian calendar and Julian calendar.
| Year | Most common pronunciation method | Alternative methods |
|---|---|---|
| 1 BC | (The year) One BC | (The year) One BCE[note 1] |
| 1 | The year One | (The year) One CE[note 2] AD One[note 3] |
| 235 | Two thirty-five | Two-three-five Two hundred (and) thirty-five |
| 911 | Nine eleven | Nine-one-one Nine hundred (and) eleven |
| 999 | Nine ninety-nine | Nine-nine-nine Nine hundred (and) ninety-nine |
| 1000 | One thousand | Ten hundred 1K |
| 1004 | One thousand (and) four | Ten oh-four |
| 1010 | Ten ten | One thousand (and) ten |
| 1050 | Ten fifty | One thousand (and) fifty |
| 1225 | Twelve twenty-five | One-two-two-five One thousand, two hundred (and) twenty-five Twelve-two-five |
| 1900 | Nineteen hundred | One thousand, nine hundred Nineteen aught |
| 1901 | Nineteen oh-one | Nineteen hundred (and) one One thousand, nine hundred (and) one Nineteen aught one |
| 1919 | Nineteen nineteen | Nineteen hundred (and) nineteen One thousand, nine hundred (and) nineteen |
| 1999 | Nineteen ninety-nine | Nineteen hundred (and) ninety-nine One thousand, nine hundred (and) ninety-nine |
| 2000 | Two thousand | Twenty hundred Two triple-oh Y2K |
| 2001 | Two thousand (and) one | Twenty oh-one Twenty hundred (and) one Two double-oh-one Two oh-oh-one |
| 2009 | Two thousand (and) nine | Twenty oh-nine Twenty hundred (and) nine Two double-oh-nine Two oh-oh-nine |
| 2010 | Twenty ten[7] | Twenty hundred (and) ten two-oh-one-oh Two thousand (and) ten |
- ^ Before the Common era.
- ^ of the Common era.
- ^ Anno Domini One («In the year One of our Lord») is sometimes written 1 AD.
Twelve thirty-four would be the norm on both sides of the Atlantic for the year 1234. The years 2000 to 2009 are most often read as two thousand, two thousand (and) one and the like by both British and American speakers. For years after 2009, twenty eleven, twenty fourteen, etc. are more common, even in years earlier than 2009 BC/BCE. Likewise, the years after 1009 (until 1099) are also read in the same manner (e.g. 1015 is either ten fifteen or, rarely, one thousand fifteen). Some Britons read years within the 1000s to 9000s BC/BCE in the American manner, that is, 1234 BC is read as twelve (hundred and) thirty-four BC, while 2400 BC can be read as either two thousand four hundred or twenty four hundred BC.
Collective numbers[edit]
Collective numbers are numbers that refer to a group of a specific size. Words like «pair» and «dozen» are common in English, though most are formally derived from Greek and Latin numerals, as follows:
| Group Size | Latin-derived | Colloquial |
|---|---|---|
| 1 | monad | |
| 2 | dyad, duad | pair |
| 3 | triad | |
| 4 | tetrad | |
| 5 | pentad | |
| 6 | hexad | |
| 7 | heptad, hebdomad | |
| 8 | octad, ogdoad | |
| 9 | nonad, ennead | |
| 10 | decad, decade | |
| 11 | hendecad | |
| 12 | dodecad, duodecade | dozen |
| 1000 | chiliad |
Fractions and decimals[edit]
Numbers used to denote the denominator of a fraction are known linguistically as «partitive numerals». In spoken English, ordinal numerals and partitive numerals are identical with a few exceptions. Thus «fifth» can mean the element between fourth and sixth, or the fraction created by dividing the unit into five pieces. When used as a partitive numeral, these forms can be pluralized: one seventh, two sevenths. The sole exceptions to this rule are division by one, two, and sometimes four: «first» and «second» cannot be used for a fraction with a denominator of one or two. Instead, «whole» and «half» (plural «halves») are used. For a fraction with a denominator of four, either «fourth» or «quarter» may be used.
Here are some common English fractions, or partitive numerals:[8]

|
one one-hundredth |

|
two one-hundredths |

|
three one-hundredths |

|
one two-hundredth |

|
two two-hundredths |

|
three two-hundredths |

|
one-sixteenth |
 or 0.1 or 0.1
|
one-tenth |

|
one-eighth |
 or 0.2 or 0.2
|
two-tenths or one-fifth |

|
one-quarter or one-fourth |
 or 0.3 or 0.3
|
three-tenths |

|
one-third |

|
three-eighths |
 or 0.4 or 0.4
|
four-tenths or two-fifths |

|
one-half |
 or 0.6 or 0.6
|
six-tenths or three-fifths |

|
five-eighths |

|
two-thirds |
 or 0.7 or 0.7
|
seven-tenths |

|
three-quarters or three-fourths |
 or 0.8 or 0.8
|
eight-tenths or four-fifths |

|
seven-eighths |
 or 0.9 or 0.9
|
nine-tenths |

|
fifteen-sixteenths |
Alternatively, and for greater numbers, one may say for 1/2 «one over two», for 5/8 «five over eight», and so on. This «over» form is also widely used in mathematics.
Fractions together with an integer are read as follows:
- 1½ is «one and a half»
- 6¼ is «six and a quarter»
- 7⅝ is «seven and five eighths»
A space is required between the whole number and the fraction; however, if a special fraction character is used like «½», then the space can be done without, e.g.
- 9 1/2
- 9½
Numbers with a decimal point may be read as a cardinal number, then «and», then another cardinal number followed by an indication of the significance of the second cardinal number (mainly U.S.); or as a cardinal number, followed by «point», and then by the digits of the fractional part. The indication of significance takes the form of the denominator of the fraction indicating division by the smallest power of ten larger than the second cardinal. This is modified when the first cardinal is zero, in which case neither the zero nor the «and» is pronounced, but the zero is optional in the «point» form of the fraction.
Some American and Canadian schools teach students to pronounce decimaly written fractions (for example, .5) as though they were longhand fractions (five tenths), such as thirteen and seven tenths for 13.7. This formality is often dropped in common speech and is steadily disappearing in instruction in mathematics and science as well as in international American schools. In the U.K., and among most North Americans, 13.7 would be read thirteen point seven.
For example:
- 0.002 is «point zero zero two», «point oh oh two», «nought point zero zero two», etc.; or «two thousandths» (U.S., occasionally)
- 3.1416 is «three point one four one six»
- 99.3 is «ninety-nine point three»; or «ninety-nine and three tenths» (U.S., occasionally).
In English the decimal point was originally printed in the center of the line (0·002), but with the advent of the typewriter it was placed at the bottom of the line, so that a single key could be used as a full stop/period and as a decimal point. In many non-English languages a full-stop/period at the bottom of the line is used as a thousands separator with a comma being used as the decimal point.
Whether or not digits or words are used[edit]
With few exceptions, most grammatical texts rule that the numbers zero to nine inclusive should be «written out» – instead of «1» and «2», one would write «one» and «two».[9]
- Example: «I have two apples.» (Preferred)
- Example: «I have 2 apples.»
After «nine», one can head straight back into the 10, 11, 12, etc., although some write out the numbers until «twelve».
- Example: «I have 28 grapes.» (Preferred)
- Example: «I have twenty-eight grapes.»
Another common usage is to write out any number that can be expressed as one or two words, and use figures otherwise.
- Examples:
- «There are six million dogs.» (Preferred)
- «There are 6,000,000 dogs.»
- «That is one hundred and twenty-five oranges.» (British English)
- «That is one hundred twenty-five oranges.» (US-American English)
- «That is 125 oranges.» (Preferred)
Numbers at the beginning of a sentence should also be written out, or the sentence rephrased.
The above rules are not always followed. In literature, larger numbers might be spelled out. On the other hand, digits might be more commonly used in technical or financial articles, where many figures are discussed. In particular, the two different forms should not be used for figures that serve the same purpose; for example, it is inelegant to write, «Between day twelve and day 15 of the study, the population doubled.»
Empty numbers[edit]
Colloquial English’s small vocabulary of empty numbers can be employed when there is uncertainty as to the precise number to use, but it is desirable to define a general range: specifically, the terms «umpteen», «umpty», and «zillion». These are derived etymologically from the range affixes:
- «-teen» (designating the range as being between 13 and 19 inclusive)
- «-ty» (designating the range as being between 20 and 90 inclusive)
- «-illion» (designating the range as being above 1,000,000; or, more generally, as being extremely large).
The prefix «ump-» is added to the first two suffixes to produce the empty numbers «umpteen» and «umpty»: it is of uncertain origin. A noticeable absence of an empty number is in the hundreds range.
Usage of empty numbers:
- The word «umpteen» may be used as an adjective, as in «I had to go to umpteen stores to find shoes that fit.» It can also be used to modify a larger number, usually «million», as in «Umpteen million people watched the show; but they still cancelled it.»
- «Umpty» is not in common usage. It can appear in the form «umpty-one» (paralleling the usage in such numbers as «twenty-one»), as in «There are umpty-one ways to do it wrong.» «Umpty-ump» is also heard, though «ump» is never used by itself.
- The word «zillion» may be used as an adjective, modifying a noun. The noun phrase normally contains the indefinite article «a», as in «There must be a zillion pages on the World Wide Web.»
- The plural «zillions» designates a number indefinitely larger than «millions» or «billions». In this case, the construction is parallel to the one for «millions» or «billions», with the number used as a plural count noun, followed by a prepositional phrase with «of», as in «There are zillions of grains of sand on the beaches of the world.»
- Empty numbers are sometimes made up, with obvious meaning: «squillions» is obviously an empty, but very large, number; a «squintillionth» would be a very small number.
- Some empty numbers may be modified by actual numbers, such as «four zillion», and are used for jest, exaggeration, or to relate abstractly to actual numbers.
- Empty numbers are colloquial, and primarily used in oral speech or informal contexts. They are inappropriate in formal or scholarly usage.
See also Placeholder name.
See also[edit]
- Indefinite and fictitious numbers
- List of numbers
- Long and short scales
- Names of large numbers
- Natural number
- Number prefixes and their derivatives
References[edit]
- ^ Webster’s Third New International Dictionary, Unabridged, 1993, Merriam-Webster
- ^ «Large Numbers at MROB».
- ^ «Home — Yahoo Answers».
- ^ «Hat trick, n.». Oxford English Dictionary. Oxford University Press. Retrieved 26 December 2014.
- ^ «Shock, n.2». Oxford English Dictionary. Oxford University Press. Retrieved 26 December 2014.
- ^ «the definition of ton».
- ^ «How Do You Say 2010?». NPR.org.
- ^ «What is a partitive numeral?».
- ^ Gary Blake and Robert W. Bly, The Elements of Technical Writing, pg. 22. New York: Macmillan Publishers, 1993. ISBN 0020130856
External links[edit]
- English Numbers — explanations, exercises and number generator (cardinal and ordinal numbers)
Number Names
George Lakoff has pointed out that we do not normally distinguish numbers from what might be more properly be called number names. (Lakoff 1989) The most common number naming systems adopt base-10 and use ten single-digit number names, for instance (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9). They then form other multi-digit number names (21, 1342 etc) from these basic number names, or numerals, using a positional representation. With Arabic numerals this starts with the rightmost numeral being the quantity of units and the next leftward numeral being the quantity of tens and so on.
But many other bases are possible, the next most common probably being base-2 or binary, with just two basic number names (0 and 1). The difference between numbers and number names can therefore perhaps best be understood by realising that the number name ‘3’ in base-10 (3 × 100) represents the same quantity or numerosity as the number name ’11’ in base-2 ((1 × 21 ) + (1 × 20)). That is the base used, as well as the digits or glyphs adopted, can change the way any particular quantity, numerosity or number is represented.
Cardinal numbers measure the size of collections or sets and therefore include the number zero needed to represent the size of an empty collection or set. In English cardinal numbers are nouns.
Ordinal numbers represent position or rank in a sequential, spatial or temporal lists or order and therefore do not include zero, there is no zeroth element in a sequential list. In English ordinal numbers are adjectives.
Number Words
Number names in this sense are different and distinct from number words, the verbal version of numbers, the way numbers are spoken or transliterated, (one, two, three etc.). see Five Finger Exercises
In English, verbal numbers are organised as a hybrid series of additions and multiplications summarised, for the cardinal Arabic number 350172, by the graph below where the plus signs indicate addition and the X signs multiplication.
After Dehaene (1992) Varieties of Numerical Abilities Cognition, 44 1-42
So that ((((three is multiplied by a hundred) and added to fifty) which is then multiplied by a thousand) and added to ((one multiplied by a hundred) added to (seventy added to two)))
This system involves a combination of simple number words; one, two, three etc., some special multiplier words like hundred, thousand etc and the particularly English -ty words like sixty, seventy, eighty and ninety plus the slightly modified twenty, thirty, forty and fifty. And -teen words like thirteen, fourteen etc. plus the unique eleven and twelve.
With Arabic numerals the same cardinal number (350172) is represented positionally; starting with the rightmost numeral being the quantity of units (2) and the next leftward numeral being the quantity of tens (7) etc. Note that Arabic numbers are read, or more accurately generated, from right to left, perhaps betraying their origin.
Chinese number words follow a similar but somewhat simpler, more regular pattern.
Comparison of English and Chinese Number Words

Ordinal Number Words
In English the initial verbal ordinal words are the unique first, second, and third, but typically ordinals have a th suffix added to the cardinal name for the number, so fourth, sixth, seventh, nineth, and tenth plus the slightly modified in spelling terms fif[]th, and eigh[]th. The multiple powers of ten have an ieth suffix replacing the y ending of the cardinal name, so twentieth from twenty, thirtieth from thirty, fortieth from forty etc. Again these are organised as a hybrid series of additions and multiplications.
In English the Arabic version of ordinals borrow their suffices from the end of their verbal equivalents, so we have 1st (from first), 2nd (from second) and 3rd (from third), followed by 4th .. 20th then 21st, 22nd and 23rd etc.
The first three English ordinals have interestingly varied etymologies. First derives from the Old English fyr(e)st and Old Norse fyrst, having the sense of furthest forward, and the German Fürst, a prince, that is furthest forward in rank. Second derives from the Latin sequi follow, secundus following and second via Old French into Middle English. Third derives from Old English thridda via English thrid which was the most common spelling until the 16th century.
A Latinate ordinal system is also used to represent importance and precedence, primary, secondary, tertiary, quaternary etc. which are rarely used beyond the first four. So primary, secondary and tertiary education. This system is also used to indicate a sequence of dependent effects, thus secondary picketing.
In technical and academic practice Greek ordinals are also used as prefixes proto-, deutero-, trite- and tetarto-, thus proto-renaissance, protagonist and deuterium.
Fractions
When speaking of fractions a half is used for 1/2, a quarter for 1/4 and three quarters for 3/4 but a fourth is also used in music. Otherwise ordinals are used as in a third for 1/3, a fifth, a sixth etc. In the more general case a cardinal number is used for the numerator and an ordinal for the denominator, so 2/3 is two thirds and 19/32 is nineteen thirty seconds etc.
Transcoding
Literate English speakers have no problem reading, writing, comprehending or producing all these systems and transcoding between them even though there is evidence, through the study of patients with deficits in one or more of these capacities, of a neurological dissociation between the verbal and written systems (McCloskey 1992)
Bibliography
Dehaene, S. (1992) Varieties of Numerical Abilities Cognition, 44 1-42
Lakoff, G. (1987) Women, Fire, and Dangerous Things University of Chicago, Chicago Page 150
Lakoff, G. and Núñez, R. (2000) Where Mathematics Comes From Basic Books, New York
McCloskey, M. (1992) Cognitive mechanisms in numerical processing: Evidence from acquired dyscalculia, Cognition 44 107-157
Numbers in Words is writing the numbers in alphabetical form instead of digits. There are various systems to write numbers in words. After reading this article, you can write whole numbers in words, and write numbers in word form in standard form. We will primarily focus on the Indian & International number system of writing numbers in words in English, with their Rules, Tricks to remember and write spellings. You can learn to spell numbers in words 1 to 100 with Solved Examples and FAQs.
What is Number in Words?
Alphabetical form of numbers is called writing numbers in words. These are numbers written in words as the name implies. In the English language, the number 100, for example, is written as one hundred. All natural numbers, such as ones, tens, hundreds, thousands, and so on, can be represented in words based on the place value of their digits.
What is a Number Name?
Number name is the method of representing numbers in words. The alphabetical form of numbers is called number words. These are numbers written in words as the name implies. In language, the number 100, for example, is written as one hundred. All natural numbers, such as ones, tens, hundreds, thousands, and so on, can be represented as number names based on the place value of their digits.
Examples: 128 = 100 + 20 + 8. One hundred and twenty-eight is the number name of 128.
412 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 10 + 2 = 400 + 12. As a result, the number 412’s name is Four Hundred and Twelve.
685 = 600 + 80 + 5. = 685 = 600 + 80 + 5. Six hundred eighty-five is the number name for 685.
List of Number Names from 1 to 20
Here is a list of Numbers in Words from 1 – 20. A 1-20 number chart is a great way to teach your youngster numbers and practise one-to-one correspondence. The numbers 1 through 20 are represented in the graphic. Each number has a term for it, as well as a number of visuals that correspond to it.
| List of Numbers in Words from 1 to 20 | ||||
| 1 – One | 2 – Two | 3 – Three | 4 – Four | 5 – Five |
| 6 – Six | 7 – Seven | 8 – Eight | 9 – Nine | 10 – Ten |
| 11 – Eleven | 12 – Twelve | 13 – Thirteen | 14 – Fourteen | 15 – Fifteen |
| 16 – Sixteen | 17 – Seventeen | 18 – Eighteen | 19 – Nineteen | 20 – Twenty |
List of Number Names from 1 to 50
Here’s a list of Numbers in Words from 1 to 50. 1-50 number chart is a great way to teach and learn number names.
| Number In Words 1 – 50 | ||||
| 1 One | 2 Two | 3 Three | 4 Four | 5 Five |
| 6 Six | 7 Seven | 8 Eight | 9 Nine | 10 Ten |
| 11 Eleven | 12 Twelve | 13 Thirteen | 14 Fourteen | 15 Fifteen |
| 16 Sixteen | 17 Seventeen | 18 Eighteen | 19 Nineteen | 20 Twenty |
| 21 Twenty-one | 22 Twenty-two | 23 Twenty-three | 24 Twenty-four | 25 Twenty-five |
| 26 Twenty-six | 27 Twenty-seven | 28 Twenty-eight | 29 Twenty-nine | 30 Thirty |
| 31 Thirty-one | 32 Thirty-two | 33 Thirty-three | 34 Thirty-four | 35 Thirty-five |
| 36 Thirty-six | 37 Thirty-seven | 38 Thirty-eight | 39 Thirty-nine | 40 Forty |
| 41 Forty-one | 42 Forty-two | 43 Forty-three | 44 Forty-four | 45 Forty-five |
| 46 Forty-six | 47 Forty-seven | 48 Forty-eight | 49 Forty-nine | 50 Fifty |
List of Number Names from 1 to 100
Here’s a list of Numbers in Words from 1 – 100. A 1-100 number chart is a great way to teach and learn number names.
| List of Number Names from 1 to 100 | ||||
| 1 one | 2 two | 3 three | 4 four | 5 five |
| 6 six | 7 seven | 8 eight | 9 nine | 10 ten |
| 11 eleven | 12 twelve | 13 thirteen | 14 fourteen | 15 fifteen |
| 16 sixteen | 17 seventeen | 18 eighteen | 19 nineteen | 20 twenty |
| 21 twenty- one | 22 twenty- two | 23 twenty- three | 24 twenty- four | 25 twenty- five |
| 26 twenty- six | 27 twenty- seven | 28 twenty- eight | 29 twenty- nine | 30 thirty |
| 31 thirty- one | 32 thirty- two | 33 thirty- three | 34 thirty- four | 35 thirty- five |
| 36 thirty- six | 37 thirty- seven | 38 thirty- eight | 39 thirty- nine | 40 forty |
| 41 forty- one | 42 forty- two | 43 forty- three | 44 forty- four | 45 forty- five |
| 46 forty- six | 47 forty- seven | 48 forty- eight | 49 forty- nine | 50 fifty |
| 51 fifty- one | 52 fifty- two | 53 fifty- three | 54 fifty- four | 55 fifty- five |
| 56 fifty- six | 57 fifty- seven | 58 fifty- eight | 59 fifty- nine | 60 sixty |
| 61 sixty- one | 62 sixty- two | 63 sixty- three | 64 sixty- four | 65 sixty- five |
| 66 sixty- six | 67 sixty- seven | 68 sixty- eight | 69 sixty- nine | 70 seventy |
| 71 seventy- one | 72 seventy- two | 73 seventy- three | 74 seventy- four | 75 seventy- five |
| 76 seventy- six | 77 seventy- seven | 78 seventy- eight | 79 seventy- nine | 80 eighty |
| 81 eighty- one | 82 eighty- two | 83 eighty- three | 84 eighty- four | 85 eighty- five |
| 86 eighty- six | 87 eighty- seven | 88 eighty- eight | 89 eighty- nine | 90 ninety |
| 91 ninety- one | 92 ninety- two | 93 ninety- three | 94 ninety- four | 95 ninety- five |
| 96 ninety- six | 97 ninety- seven | 98 ninety- eight | 99 ninety- nine | 100 one hundred |
How to write a Number in Words using International System?
It is based on the International Place Value Chart. The steps to write numbers in International System are as follows.
Step 1: First, we begin from the right side and insert commas after every three digits.
Step 2: Each group is assigned a period starting from the right-hand side as ones, thousands, and millions, followed by billions and so on. This becomes the place value of the digits.
Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
Step 4: We add up the amounts in the same period. For example, in 27,000 we have a place value of 2 as twenty thousand and 7 as seven thousand. Together it becomes 20 + 7 i.e. twenty-seven thousand.
Step 5: Now write down the face value of each number starting from the left-hand side.
How to write a Number in Words using Indian System?
It is based on the Indian Place Value Chart. The Indian System is a little different from the International system. But it can be easily learnt below and you can convert numbers to words in Indian rupees.
Step 1: First, we begin from the right side and insert commas. The first group is after three-digit and after that every two digits.
Step 2: Each group is assigned a period starting from the right hand side as ones, thousands, lakhs, crores and so on. This becomes the place value of the digits.
Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
Step 4: We add up the amounts in the same period. For example, in 27,000 we have a place value of 2 as twenty thousand and 7 as seven thousand. Together it becomes 20 + 7 i.e. twenty-seven thousand.
Step 5: Now write down the face value of each number starting from the left-hand side.
Rules of Writing Numbers in Words
- In any Numbering System, we always start on the right side. The number is divided into periods, each of which is read separately.
- Small numbers ranging from one to ten (or one to nine, depending on the style guide) should normally be spelt out in writing.
- Numbers greater than 10 are written as numerals.
- All compound numerals from twenty-one to ninety-nine should be hyphenated.
Tips to Write Numbers in Words
- Using simple Number/Rhyme pictures associated with a storey is the easiest, but the least reliable, approach to recalling numbers.
- A preferable method is to employ a simple peg system, in which you can correlate numerals from the Number/Rhyme System with positions structured using the Alphabet System.
Solved Examples of Numbers in Words
Example 1: Write the numbers in the International and Indian place-value system place commas and the name of the following numbers.
Solution: 721336598 in the Indian system:
Let’s interpret the number by arranging the digits in the Indian place value system from left to right according to their locations as ones, tens, hundreds, thousands, and so on.
The number is written as 72,13,36,598 and read as
Seventy-two crores thirteen lakh thirty-six thousand five hundred and ninety-eight.
721336598 in the International System:
Now, in the international place value system, arrange the digits from left to right according to their locations as ones, tens, hundreds, thousands, and so on, and read and write the number.
The number is written as 721,336,598
Let’s read the number by arranging the digits from left to right.
Seven hundred and twenty-one million, three and thirty-six, hundred thousand five hundred and ninety-eight.
Example 2: Using the International system, write the number; Six million, four hundred and eleven thousand, two hundred and sixty.
Solution: 6,411,260.
Example 3: Using the international system, read the number 7456123.
Solution: 7456123- Seven million Four Hundred Fifty-six thousand one hundred twenty-three.
Example 4: Write the number in words: 12,367,169.
Solution: Twelve million, three hundred and sixty-seven thousand, one hundred and sixty-nine.
Example 5: Write seven hundred forty-three million eight hundred thirteen thousand two hundred fifty-six in the numeral form using the international system.
Solution: 743,813,256.
Hope this article on Number in Words was informative. Get some practice of the same on our free Testbook App. Download Now!
FAQs on Number in Words
Q.1 How do you write numbers in words using the International System?
Ans.1
- Step 1: First, we begin from the right side and insert commas after every three digits.
- Step 2: Each group is assigned a period starting from the right hand side as ones, thousands, and millions, followed by billions and so on. This becomes the place value of the digits.
- Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
- Step 4: We add up the amounts in the same period.
- Step 5: Now write down the face value of each number starting from the left hand side.
Q.2 How do you write numbers in words using the Indian System?
Ans.2
- Step 1: First, we begin from the right side and insert commas. The first group is after three-digit and after that every two digits.
- Step 2: Each group is assigned a period starting from the right-hand side as ones, thousands, lakhs, crores and so on. This becomes the place value of the digits.
- Step 3: Identify the face value of each digit. For example, if a number is 56, the face value of 6 is simply 6, however, if a number is 567, the place value is in the tens place, which is 60.
- Step 4: We add up the amounts in the same period.
- Step 5: Now write down the face value of each number starting from the left-hand side.
For example, in 27,000 we have a place value of 2 as twenty thousand and 7 as seven thousand. Together it becomes 20 + 7 i.e. twenty-seven thousand.
Q.3 What is called 10000000000?
Ans.3 The number: 10000000000 is (10^{13}). I would call it ten million million. You could call it ten trillion. A trillion is a thousand billion.
Q.4 What is number in words?
Ans.4 Alphabetical form of numbers is called writing numbers in words. These are numbers written in words as the name implies.
Q.5 What is a number name?
Ans.5 Number name is the method of representing numbers in words. The alphabetical form of numbers is called number words. These are numbers written in words as the name implies.
Q.6 What are the rules of writing numbers in words?
Ans.6 The rules of writing numbers in words are:
- In any Numbering System, we always start on the right side. The number is divided into periods, each of which is read separately.
- Small numbers ranging from one to ten (or one to nine, depending on the style guide) should normally be spelt out in writing.
- Numbers greater than 10 are written as numerals.
- All compound numerals from twenty-one to ninety-nine should be hyphenated.
-
0
Numbers in words are written using the English alphabet. Numbers can be expressed both in words and figures. For example, 100,000 in words is written as One Lakh or One hundred thousand. Numbers in words can be written for all the natural numbers, based on the place value of digits, such as ones, tens, hundreds, thousands, and so on.
The below table contains numbers names from 1 to 100 in English words. The spelling of numbers from 1 to 100 are given here for students to make them learn.
| 1 | One | 21 | Twenty-one | 41 | Forty-one | 61 | Sixty-one | 81 | Eighty-one |
| 2 | Two | 22 | Twenty-two | 42 | Forty-two | 62 | Sixty-two | 82 | Eighty-two |
| 3 | Three | 23 | Twenty-three | 43 | Forty-three | 63 | Sixty-three | 83 | Eighty-three |
| 4 | Four | 24 | Twenty-four | 44 | Forty-four | 64 | Sixty-four | 84 | Eighty-four |
| 5 | Five | 25 | Twenty-five | 45 | Forty-five | 65 | Sixty-five | 85 | Eighty-five |
| 6 | Six | 26 | Twenty-six | 46 | Forty-six | 66 | Sixty-six | 86 | Eighty-six |
| 7 | Seven | 27 | Twenty-seven | 47 | Forty-seven | 67 | Sixty-seven | 87 | Eighty-seven |
| 8 | Eight | 28 | Twenty-eight | 48 | Forty-eight | 68 | Sixty-eight | 88 | Eighty-eight |
| 9 | Nine | 29 | Twenty-nine | 49 | Forty-nine | 69 | Sixty-nine | 89 | Eighty-nine |
| 10 | Ten | 30 | Thirty | 50 | Fifty | 70 | Seventy | 90 | Ninety |
| 11 | Eleven | 31 | Thirty-one | 51 | Fifty-one | 71 | Seventy-one | 91 | Ninety-One |
| 12 | Twelve | 32 | Thirty-two | 52 | Fifty-two | 72 | Seventy-two | 92 | Ninety-two |
| 13 | Thirteen | 33 | Thirty-three | 53 | Fifty-three | 73 | Seventy-three | 93 | Ninety-three |
| 14 | Fourteen | 34 | Thirty-four | 54 | Fifty-four | 74 | Seventy-four | 94 | Ninety-four |
| 15 | Fifteen | 35 | Thirty-five | 55 | Fifty-five | 75 | Seventy-five | 95 | Ninety-five |
| 16 | Sixteen | 36 | Thirty-six | 56 | Fifty-six | 76 | Seventy-six | 96 | Ninety-six |
| 17 | Seventeen | 37 | Thirty-seven | 57 | Fifty-seven | 77 | Seventy-seven | 97 | Ninety-seven |
| 18 | Eighteen | 38 | Thirty-eight | 58 | Fifty-eight | 78 | Seventy-eight | 98 | Ninety-eight |
| 19 | Nineteen | 39 | Thirty-nine | 59 | Fifty-nine | 79 | Seventy-nine | 99 | Ninety-nine |
| 20 | Twenty | 40 | Forty | 60 | Sixty | 80 | Eighty | 100 | Hundred |
In the same way, students can write the numbers from 101 to 1000 in words.
Numbers in Words (1 to 1000)
Numbers in words from 1 to 100 we have already learned in the above section. Let us see how to write the numbers from 100 to 1000 in words.
| 101 – One hundred one
102 – One hundred two 103 – One hundred three . . . . 110 – One hundred ten |
111 – One hundred eleven
112 – One hundred twelve 113 – One hundred thirteen . . . . 120 – One hundred twenty |
121 – One hundred twenty-one
122 – One hundred twenty-two 123 – One hundred twenty-three . . . . 130 – One hundred thirty |
After 130, we can repeat the pattern similar to the 120 series (i.e. 121 to 129), till 199. Hence, in the same way, we can write all the other numbers from 200 to 1000. Only the numbers that are the multiples of hundreds are written in words as given in the table below.
| Numbers | Words |
| 100 | Hundred |
| 200 | Two-Hundred |
| 300 | Three-Hundred |
| 400 | Four-Hundred |
| 500 | Five-Hundred |
| 600 | Six-Hundred |
| 700 | Seven-Hundred |
| 800 | Eight-Hundred |
| 900 | Nine-Hundred |
| 1000 | One-Thousand or Thousand |
How to Write Numbers in words?
The rules to write the numbers in words are discussed here. To write any number in the form of words, we have to check the place value. Let us learn this by observing the below steps.
- The place value of one’s, a number from 1 to 9 is written in words as, one, two, three, four, five, six, seven, eight and nine.
- The least number which is at tens place is 10, which is written in words as ten.
- The numbers from 11 to 19 are written in words as, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen and nineteen. And the next number is twenty.
- After twenty, the numbers follow the pattern in such a way that they are written in words as thirty, forty, fifty, sixty, seventy, eighty, ninety and so on.
- The preceding numbers are linked with these words and mentioned from one to nine. For example, twenty-one, twenty-two, etc.
For example, if we have to write Rs.40,000 in words, then it will be written as:
Rs.40,000 – Forty thousand rupees only
Numbers in Words in Indian System
The place value names for numbers in the Indian system starts with ones, tens, hundreds, thousands, lakhs, ten-lakhs, one crore, ten-crore and so on. Let us see how the numbers are written in words in the Indian number system.
- 3000 – Three thousand
- 5000 – Five thousand
- 10000 in words – Ten Thousand
- 15000 in words – Fifteen Thousand
- 13000 in words – Thirteen Thousand
- 18000: Eighteen thousand
Similarly,
- 20,000 – Twenty Thousand
- 25,000 – Twenty Five Thousand
- 30,000 – Thirty Thousand
- 35,000 – Thirty-Five Thousand
- 40, 000 – Forty Thousand
- 45,000 – Forty-Five Thousand
For larger numbers:
- 100,000 – One hundred thousand (One Lakh)
- 200, 000 – Two hundred thousand (Two Lakhs)
- 300, 000 – Three hundred thousand (Three Lakhs)
- 400, 000 – Four hundred thousand (Four Lakhs)
- 500, 000 – Five hundred thousand (Five Lakhs)
- 10,00,000 – Ten Lakhs
- 1,00,00,000 – One Crore
Numbers in Words in International System
In the international system, the place value names vary with the Indian number system. For example, 1,000,000 is ten lakhs in the Indian system but in the international system, it is one million. Let us see, how the numbers are written in words in the international system.
| Numbers | Names |
| 1000 | Thousand |
| 10000 | Ten thousand |
| 100,000 | Hundred Thousand |
| 1,000,000 | One Million |
| 10,000,000 | Ten Million |
| 1,000,000,000 | One billion |
Remember:
- 1 million = 1000 thousand
- 1 billion = 1000 millions
3000000 in Words
3000000 in words is 30 lakhs or 3 Million.
3,000,000 represents thirty lakhs in the Indian number system and three million in the international number system.
Tips to Learn Number in Words
To learn numbers spelling or words, follow the below-given tips:
- Write the numbers from 1 to 10 on a sheet of paper and write their spellings
- Memorise all the spellings of 1 to 10, since the basics of all the number names rely on these.
- After 10, 11 – eleven and 12 – twelve, sounds similar.
- Now, remember after 12 we have to write 13 to 19 adding -teen as suffixes, such as thirteen, fourteen and so on.
- After 19, 20 is written as an extended form of two such as twenty, twenty-one, twenty-two, and so on.
- From here, you have to memorise all the multiples of 10, such as 20, 30, 40, 50, and so on.
- In a similar manner, after every multiple of 100, 1000, etc., the number is written in the same format.
Solved Examples on Numbers in Words
Let us know out how to write any given number in words with the help of an example.
Example 1:
Write 33 in words.
Solution:
In number 33, one’s place is occupied with 3, so there are 3 ones, and tens place is also occupied with 3, so there are 3 tens. So 3 tens and 3 ones are equal to 33. Or we can write, 33 as ‘thirty-three’ in words.
Example 2:
Write, 19, 30, 15, 100, 4000, 19000, and 50000 in words.
Solution:
- 19 in words – Nineteen
- 30 in words – Thirty
- 15 in words – Fifteen
- 100 in words – Hundred
- 4000 in words – Four thousand
- 19000 in words – Nineteen thousand
- 50000 in words – Fifty thousand
Example 3:
Write the name of the number 7,155,421,098,910 in word format.
Solution:
On beginning with the first digit that is 7. It is present in the place of a trillion – seven trillion
The next comma to the right side is billion – one hundred fifty-five billion
The next comma to the right side is million – four hundred twenty-one million
The next comma to the right side is thousands – ninety-eight thousand
The comma present on the rightmost side represents – nine hundred and ten
7,155,421,098,910 in word format is seven trillion, one hundred fifty-five billion, four hundred twenty-one million, ninety-eight thousand, nine hundred and ten.
Example 4:
A pupil carried out research and noted that the count of users of mobile phones in the United States in a month in the year 2014 was 327577529. Write the number in word format.
Solution:
On putting the commas, the number is represented by 327,577,529.
Millions comma – three hundred and twenty-seven million
Thousands comma – five hundred and seventy-seven thousand
One’s comma – five hundred and twenty-nine
The count of users of mobile phones in the United States in a month in the year 2014 was three hundred and twenty-seven million, five hundred and seventy-seven thousand, five hundred and twenty-nine (327,577,529).
Example 5:
Write the following numbers using digits.
a] fifty-three million, four hundred one thousand, seven hundred forty-two
b] nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine
Solution:
a] fifty-three million, four hundred one thousand, seven hundred forty-two
The number is 53,401,742.
b] nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine
The number is 9,246,073,189.
Example 6:
Mark the number whose name is:
fifty billion one hundred seventy-nine million seven hundred twelve thousand two hundred two
a] 50,179,712,202
b] 5,017,971,220,200
c] 501,797,122,020
Solution:
The right answer is 50,179,712,202.
Example 7:
Write each number in standard form:
a] The nearest distance between Earth and Mars is approximately 34 million miles.
b] The net weight of an aircraft carrier is 204 million pounds.
Solution:
The above statements are mathematically expressed as follows.
a] The nearest distance between Earth and Mars is approximately 34 million miles.
In the standard form, it is 34,000,000 miles
b] The net weight of an aircraft carrier is 204 million pounds.
In the standard form, it is 204,000,000 pounds
Example 8:
The budget for the state is announced to be 77 billion dollars. Express the budget in standard form.
Solution:
The budget for the state is announced to be 77 billion dollars.
Make a note of the periods or commas, two digits are given in billions.
To express the number in mathematical form, the rest of the numbers are zeros.
77 billion
Millions – 000
Thousands – 000
Ones – 000
The budget announced was about 77,000,000,000 dollars.
Worksheets on Numbers in Words
- Write 114 in words
- Write 500 in words
- Write 786 in words
- Convert 193 to words
- Write the spelling of 876 in English
Related Articles
- Numbers
- Numeral System
- Number Theory
- Roman numerals
- Numbers spelling 1 to 50
Learn from BYJU’S – The Learning App and download its app to get personalized and interesting fun videos.
Frequently Asked Questions on Numbers in Words
Q1
How to write the numbers in words?
Writing numbers in words means writing the spelling of the numbers in alphabetical form. For example, 123 is spelt as one hundred twenty-three. By knowing the word number from 1 to 10 we can spell other numbers as well.
1-one, 2-two, 3-three, 4-four, 5-five, 6-six, 7-seven, 8-eight, 9-nine, 10-ten.
Q2
How to write 1000000 in words?
1,000,000 is written in words as One thousand thousand. It is also spelt as 10 lakhs or 1 million.
Q3
What do you mean by the standard form of numbers?
A standard form of numbers means writing too large numbers or too small numbers in the simplest form or exponent form. It is represented by writing the number in decimal form between 1 to 10, multiplied by powers of 10. For example, 9000000 can be written as:
9000000 = 9 x 106
Q4
How to write Rs. 7000 in words?
Rs.7000 is written as Seven thousand rupees, in words.
Q5
Write 10,20,30,40,50,60,70,80,90 and 100 in words?
Numbers in words are:
10-Ten
20- Twenty
30- Thirty
40- Forty
50- Fifty
60- Sixty
70- Seventy
80-Eighty
90- Ninety
100- Hundred