Ниже представлен фрагмент таблицы в excel - Word и Excel

Всего: 31 1–20 | 21–31

Добавить в вариант

В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения. Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за два фиксированных одногодичных промежутка времени и суммы вкладов с начисленными процентами за соответствующие истекшие периоды времени. Также приведены общие суммы всех вкладов в банке после начисления процентов и доход вкладчиков за истекший двухгодичный период.

	Вклад, р.	4 %	5 %	Сумма начислений за два периода
Осин	2100000	2184000	2293200	193200
Пнев	200000	208000	218400	18400
Чуйкин	50000	52000	54600	4600
Шаталов	2400000	2496000	2620800	220800
Общая сумма	4750000	4940000	5187000	437000

Определите, кто из вкладчиков за истекшее с момента открытия вклада время получил средний ежемесячный доход от вклада более 9000 рублей.

Дан фрагмент электронной таблицы:

	A	B	C
1	2		=A1+1
2	=C1-B1	=(3*B1+C1)/3	=B2+A1

Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

Дан фрагмент электронной таблицы.

	A	B	C
1	5		=A1*2
2	=(B1-A1)/2	=B1-C1	=B2+A1

Какое число должно быть записано в ячейке В1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?

Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

Задания Д10 № 5350

Коле нужно с помощью электронных таблиц построить таблицу сложения чисел от 2 до 5.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 2 до 5. Затем в ячейку Е5 записал формулу сложения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы сложения (см. рис.).

	A	B	C	D	E
1		2	3	4	5
2	2	4	5	6	7
3	3	5	6	7	8
4	4	6	7	8	9
5	5	7	8	9	10

Какая формула была записана в ячейке Е5?

1)  =А$5+$Е1

2)  =А5+Е1

3)  =$А5+$Е1

4)  =$А5+Е$1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 1.

Задания Д10 № 5382

Коле нужно с помощью электронных таблиц построить таблицу умножения чисел от 3 до 6.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 3 до 6. Затем в ячейку Е2 записал формулу умножения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы умножения (см. рис.).

	A	B	C	D	E
1		3	4	5	6
2	3	9	12	15	18
3	4	12	16	20	24
4	5	15	20	25	30
5	6	18	24	30	36

Какая формула была записана в ячейке Е2?

1)  =А$2*$Е1

2)  =А2*Е1

3)  =$А2*$Е1

4)  =$А2*Е$1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 2.

Задания Д10 № 5414

Коле нужно с помощью электронных таблиц построить таблицу двузначных чисел от 60 до 99.

Для этого сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 6 до 9. Затем в ячейку В2 записал формулу двузначного числа (А2  — число десятков; В1  — число единиц), после чего скопировал её во все ячейки диапазона В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы:

	A	B	C	D	E
1		0	1	2	3
2	6	60	61	62	63
3	7	70	71	72	73
4	8	80	81	82	83
5	9	90	91	92	93

Какая формула была записана в ячейке В2?

1)  =$А2*10+В$1

2)  =А$2*10+$В1

3)  =$А2*10+$В1

4)  =А2*10+В1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Дальний Восток. Вариант 4.

Задания Д10 № 5446

Коле нужно с помощью электронных таблиц построить таблицу двузначных чисел от 50 до 89.

Для этого сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 5 до 8. Затем в ячейку В2 записал формулу двузначного числа (А2  — число десятков; В1  — число единиц), после чего скопировал её во все ячейки диапазона В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы.

	A	B	C	D	E
1		0	1	2	3
2	5	50	51	52	53
3	6	60	61	62	63
4	7	70	71	72	73
5	8	80	81	82	83

Какая формула была записана в ячейке В2?

1)  =А$2*10+$В1

2)  =$А2*10+$В1

3)  =А2*10+В1

4)  =$А2*10+В$1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Сибирь. Вариант 1.

Задания Д10 № 5478

Коле нужно с помощью электронных таблиц построить таблицу сложения чисел от 14 до 17.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 14 до 17. Затем в ячейку Е2 записал формулу сложения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы сложения (см. рис.).

	A	B	C	D	E
1		14	15	16	17
2	14	28	29	30	31
3	15	29	30	31	32
4	16	30	31	32	33
5	17	31	32	33	34

Какая формула была записана в ячейке Е2?

1)  =$Е1+А$2

2)  =Е1+А2

3)  =Е$1+А$2

4)  =Е$1+$А2

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 1.

Задания Д10 № 5574

Коле нужно с помощью электронных таблиц построить таблицу значений формулы для значений и от 5 до 8.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 5 до 8. Затем в ячейку В5 записал формулу (А5  — значение x; В1  — значение y), после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы (см. рис.).

	A	B	C	D	E
1		5	6	7	8
2	5	25	28	31	34
3	6	27	30	33	36
4	7	29	32	35	38
5	8	31	34	37	40

Какая формула была записана в ячейке В5?

1)  =А$5*2+$В1*3

2)  =$А5*2+В$1*3

3)  =$А5*2+$В1*3

4)  =А5*2+В1*3

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Сибирь. Вариант 2.

Задания Д10 № 5670

Коле нужно с помощью электронных таблиц построить таблицу умножения чисел от 2 до 5.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 2 до 5. Затем в ячейку Е5 записал формулу умножения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы умножения (см. рис.).

	A	B	C	D	E
1		2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15
4	4	8	12	16	20
5	5	10	15	20	25

Какая формула была записана в ячейке Е5?

1)  =$А5*$Е1

2)  =А5*Е1

3)  =$А5*Е$1

4)  =А$5*$Е1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Сибирь. Вариант 5.

Задания Д10 № 5734

Коле нужно с помощью электронных таблиц построить таблицу значений формулы для значений x и y от 6 до 9.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 6 до 9. Затем в ячейку В5 записал формулу (А5  — значение x В1  — значение y), после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы (см. рис.).

	A	B	C	D	E
1		6	7	8	9
2	6	30	33	36	39
3	7	32	35	38	41
4	8	34	37	40	43
5	9	36	39	42	45

Какая формула была записана в ячейке B5?

1)  =А$5*2+$В1*3

2)  =$А5*2+$В1*3

3)  =А5*2+В1*3

4)  =$А5*2+В$1*3

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 3.

Задания Д10 № 5766

Коле нужно с помощью электронных таблиц построить таблицу двузначных чисел от 30 до 69.

Для этого сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 3 до 6. Затем в ячейку В2 записал формулу двузначного числа (А2  — число десятков; В1  — число единиц), после чего скопировал её во все ячейки диапазона В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы:

	A	B	C	D	E
1		0	1	2	3
2	3	30	31	32	33
3	4	40	41	42	43
4	5	50	51	52	53
5	6	60	61	62	63

Какая формула была записана в ячейке B2?

1)  =$А2*10+$В1

2)  =А2*10+В1

3)  =$А2*10+В$1

4)  =А$2*10+$В1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 4.

Задания Д10 № 5798

Коле нужно с помощью электронных таблиц построить таблицу умножения чисел от 6 до 9.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 6 до 9. Затем в ячейку Е5 записал формулу умножения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы умножения (см. рис.).

	A	B	C	D	E
1		6	7	8	9
2	6	36	42	48	54
3	7	42	49	56	63
4	8	48	56	64	72
5	9	54	63	72	81

Какая формула была записана в ячейке Е5?

1)  =А5*Е1

2)  =А$5*$Е1

3)  =$А5*Е$1

4)  =$А5*$Е1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Урал. Вариант 5.

Задания Д10 № 5830

Коле нужно с помощью электронных таблиц построить таблицу значений формулы для значений x и y от 4 до 7.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 4 до 7. Затем в ячейку В5 записал формулу (А5  — значение x; В1  — значение y), после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы (см. рис.).

	A	B	C	D	E
1		4	5	6	7
2	4	20	23	26	29
3	5	22	25	28	31
4	6	24	27	30	33
5	7	26	29	32	35

Какая формула была записана в ячейке B5?

1)  =$А5*2+В$1*3

2)  =А5*2+В1*3

3)  =$А5*2+$В1*3

4)  =А$5*2+$В1*3

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Центр. Вариант 1.

Задания Д10 № 5862

Коле нужно с помощью электронных таблиц построить таблицу сложения чисел от 15 до 18.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 15 до 18. Затем в ячейку Е2 записал формулу сложения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы сложения (см. рис.).

	A	B	C	D	E
1		15	16	17	18
2	15	30	31	32	33
3	16	31	32	33	34
4	17	32	33	34	35
5	18	33	34	35	36

Какая формула была записана в ячейке Е2?

1)  =Е$1+А$2

2)  =$Е1+А$2

3)  =Е1+А2

4)  =Е$1+$А2

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Центр. Вариант 2.

Задания Д10 № 5926

Коле нужно с помощью электронных таблиц построить таблицу двузначных чисел от 10 до 49.

Для этого сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 0 до 9. Затем в ячейку В2 записал формулу двузначного числа (А2  — число десятков; В1  — число единиц), после чего скопировал её во все ячейки диапазона В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы:

	A	B	C	D	E
1		0	1	2	3
2	1	10	11	12	13
3	2	20	21	22	23
4	3	30	31	32	33
5	4	40	41	42	43

Какая формула была записана в ячейке B2?

1)  =А2*10+В1

2)  =$А2*10+$В1

3)  =А$2*10+$В1

4)  =$А2*10+В$1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Центр. Вариант 4.

Задания Д10 № 5958

Коле нужно с помощью электронных таблиц построить таблицу умножения чисел от 6 до 9.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 6 до 9. Затем в ячейку В2 записал формулу умножения, после чего скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы умножения (см. рис.):

	A	B	C	D	E
1		6	7	8	9
2	6	36	42	48	54
3	7	42	49	56	63
4	8	48	56	64	72
5	9	54	63	72	81

Какая формула была записана в ячейке B2?

1)  =$А2*В$1

2)  =А2*В1

3)  =$А2*$В1

4)  =А$2*$В1

Источник: ЕГЭ по информатике 30.05.2013. Основная волна. Центр. Вариант 5.

Задания Д10 № 5992

Коле нужно с помощью электронных таблиц построить таблицу двузначных чисел от 10 до 49.

Для этого сначала в диапазоне В1:К1 он записал числа от 0 до 9, и в диапазоне А2:А5 он записал числа от 1 до 4. Затем в ячейку В2 записал формулу двузначного числа (А2  — число десятков; В1  — число единиц), после чего скопировал её во все ячейки диапазона B2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы.

	A	B	C	D	E
1		0	1	2	3
2	1	10	11	12	13
3	2	20	21	22	23
4	3	30	31	32	33
5	4	40	41	42	43

Какая формула была записана в ячейке В2?

1)  =$A2*10+$B1

2)  =A$2*10+$B1

3)  =$A2*10+B$1

4)  =A2*10+B1

Источник: Демонстрационная версия ЕГЭ—2014 по информатике.

Задания Д10 № 6254

Коле нужно с помощью электронных таблиц построить таблицу сложения чисел от 6 до 9.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 6 до 9. Затем в ячейку Е5 записал формулу сложения, после чего скопировал её во все ячейки диапазона B2:E5. В итоге на экране получился фрагмент таблицы

сложения (см. рис.).

	A	B	C	D	E
1		6	7	8	9
2	6	12	13	14	15
3	7	13	14	15	16
4	8	14	15	16	17
5	9	15	16	17	18

Какая формула была записана в ячейке Е5?

1)  =$A5+$Е1

2)  =$A5+Е$1

3)  =А5+Е1

4)  =A$5+$Е1

Источник: ЕГЭ по информатике 08.07.2013. Вторая волна. Вариант 501.

Задания Д10 № 6294

Коле нужно с помощью электронных таблиц построить таблицу значений формулы 2х + у для значений х и у от 6 до 9. Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 6 до 9. Затем в ячейку В5 записал формулу (А5  — значение х; В1  — значение у), после чего скопировал её во все ячейки диапазона B2:E5. В итоге на экране получился фрагмент таблицы (см. рис.).

	A	B	C	D	E
1		6	7	8	9
2	6	18	19	20	21
3	7	20	21	22	23
4	8	22	23	24	25
5	9	24	25	26	27

Какая формула была записана в ячейке B5?

1)  =A5*2+B1

2)  =$A5*2+$B1

3)  =$A5*2+B$1

4)  =A$5*2+$B1

Источник: ЕГЭ по информатике 08.07.2013. Вторая волна. Вариант 502.

Всего: 31 1–20 | 21–31

Источник

№1. В ячейке D3 электронной таблицы записана
формула =B$2+$B3. Какой вид приобретет формула, после того как ячейку
D3 скопируют в ячейку E4?

Примечание: знак $ используется для обозначения
абсолютной адресации.

1) =C$2+$B4

2) =A$2+$B1

3) =B$3+$C3

4) =B$1+$A3

Пояснение.

B$2: меняется столбец и не меняется номер строки.

$B3: столбец не меняется, меняется номер строки.

Номер столбца Е больше номера столбца D на 1. Значит
столбец B станет столбцом С.

Номер строки 4 на 1 больше номера строки 3, значит,
строка 3 станет строкой 4.

Окончательный вид =С$2+$B4.

Правильный ответ указан под номером 1.

№2 была скопирована формула. При копировании
адреса ячеек в формуле автоматически изменились, и значение формулы
стало равным 8. В какую ячейку была скопирована формула? В ответе укажите
только одно число – номер строки, в которой расположена ячейка.

	A	B	C	D	E
1	1	2	3	4
2	2	3	4	= B$3 + $C2
3	3	4	5	6
4	4	5	6	7

Примечание.

Знак $ обозначает абсолютную адресацию.

Пояснение.

При копировании формулы из ячейки D2 у первого слагаемого
может изменяться только номер столбца, а у второго — только номер строки.
Таким образом формулы в ячейках E1—E4:

E1 = C$3+$C1 = 8 E2 = C$3+$C2 = 9 E3 = C$3+$C3 =
10 E4 = C$3+$C4 = 11.

Таким образом, формула была скопирована в ячейку
E1.

Ответ: 1.

№3. Саше нужно с помощью электронных таблиц
построить таблицу значений выражения a² + b²,
где a и b — целые числа, a меняется от 1 до 10, а b — от 6 до 15. Для этого
сначала в диапазоне В1:К1 он записал числа от 1 до 10, и в диапазоне
А2:А11 он записал числа от 6 до 15. Затем в ячейку С3 записал формулу
суммы квадратов чисел (А3 — значение b; С1 — значение a), после чего скопировал
её во все ячейки диапазона B2:К11. В итоге получил таблицу сумм квадратов
двузначных чисел. На рисунке ниже представлен фрагмент этой таблицы.

	A	B	C	D	E
1		1	2	3	4
2	6	37	40	45	52
3	7	50	53	58	65
4	8	65	68	73	80
5	9	82	85	90	97

В ячейке С3 была записана одна из следующих формул:

1) =С1^2+A3^2

2) =$С$1^2+$A$3^2

3) =С$1^2+$A3^2

4) =$С1^2+A$3^2

Укажите в ответе номер формулы, которая была записана
в ячейке С3.

Пояснение.

Формула, записанная в ячейку С3, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае, при копировании
формулы в ячейку B2, номер столбца будет автоматически уменьшаться,
появится неверная ссылка, произойдёт ошибка. Кроме того, формула должна
иметь знак абсолютной адресации перед цифрой 1, поскольку в противном
случае, при копировании формулы, например, в ячейку С2, номер строки
будет автоматически уменьшаться, появится неверная ссылка.

Правильный ответ указан под номером 3.

№4. Дан фрагмент электронной таблицы:

	A	B	C
1		3	4
2	=(A1 + B1+2)/(C1 – B1)	=( 2*C1 – 2)/ A1	=B1*C1/(B1 – A1)

Какое целое число должно быть записано в ячейке A1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку?

Пояснение.

По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения в ячейках B2 и C2:

( 2*C1 – 2)/ A1 = B1*C1/(B1 – A1) ⇔ 6/ A1 =
12/(3 – A1) ⇔ A1 = 1 и A1
= 4.

Приравняв выражение в ячейке A2 и ячейке B2, находим
что A1 = 1.

Ответ: 1.

№5. Дан фрагмент электронной таблицы. Из
ячейки B2 в одну из ячеек диапазона A1:A4 была скопирована формула.
При копировании адреса ячеек в формуле автоматически изменились,
и числовое значение в этой ячейке стало равным 8. В какую ячейку была
скопирована формула? В ответе укажите только одно число — номер строки,
в которой расположена ячейка.

	A	B	C	D	E
1		4	3	2	1
2		= D$3 + $C2	4	3	2
3		6	5	4	3
4		7	6	5	4

Примечание. Знак $ обозначает абсолютную адресацию.

Пояснение.

При копировании формулы в в одну из ячеек диапазона
A1:A4 формула примет вид = C$3 + $Cn, где n — номер строки той ячейки в которую
скопировали формулу. Числовое значение в этой ячейке стало равно 8,
следовательно, для того, чтобы выполнялось равенство 5 + Cn = 8, n
должно быть равным 1.

Ответ: 1.

№6. В ячейке F7 электронной таблицы записана
формула =D$12+$D13. Какой вид приобретет формула, после того как ячейку
F7 скопируют в ячейку G8?

Примечание: знак $ используется для обозначения
абсолютной адресации.

1) =C$12+$D11

2) =D$11+$C13

3) =D$13+$E13

4) =E$12+$D14

Пояснение.

D$12: меняется столбец и не меняется номер строки.

$D13: столбец не меняется, меняется номер строки.

Номер столбца G больше номера столбца F на 1. Значит
столбец D станет столбцом Е.

Номер строки 8 на 1 больше номера строки 7, значит,
строка 13 станет строкой 14.

Окончательный вид =Е$12+$D14.

Правильный ответ указан под номером 4.

№7. В ячейке D3 электронной таблицы записана
формула =B$2-$B3. Какой вид приобретет формула, после того как ячейку
D3 скопируют в ячейку С4?

Примечание: знак $ используется для обозначения
абсолютной адресации.

1) =C$2-$B4

2) =A$2-$B4

3) =B$1-$C4

4) =B$1-$B4

Пояснение.

B$2: меняется столбец и не меняется номер строки.

$B3: столбец не меняется, меняется номер строки.

Номер столбца C меньше номера столбца D на 1. Значит
столбец B станет столбцом A.

Номер строки 4 на 1 больше номера строки 3, значит,
строка 3 станет строкой 4.

Окончательный вид =A$2-$B4.

Правильный ответ указан под номером 2.

№8. В ячейке F7 электронной таблицы записана
формула =D$12-$D13. Какой вид приобретет формула, после того как ячейку
F7 скопируют в ячейку E8?

Примечание: знак $ используется для обозначения
абсолютной адресации.

1) =C$12-$C14

2) =D$12-$D13

3) =D$13-$D14

4) =C$12-$D14

Пояснение.

D$12: меняется столбец и не меняется номер строки.

$D13: столбец не меняется, меняется номер строки.

Номер столбца Е меньше номера столбца F на 1. Значит
столбец D станет столбцом С.

Номер строки Е8 на 1 больше номера строки F7, значит,
строка 13 станет строкой 14.

Окончательный вид =С$12-$D14.

Правильный ответ указан под номером 4.

№9. В ячейке B1 записана формула =2*$A1.
Какой вид приобретет формула, после того как ячейку B1 скопируют в
ячейку C2?

1) =2*$B1

2) =2*$A2

3) =3*$A2

4) =3*$B2Н

Пояснение.

Запись $A1 означает , что столбец не меняется, меняется
номер строки.

Номер строки 2 на 1 больше номера строки 1, значит,
при копировании в ячейку C2 строка 1 станет строкой 2.

Окончательный вид =2*$A2.

Правильный ответ указан под номером 2.

№10. В ячейке C2 записана формула
=$E$3+D2. Какой вид приобретет формула, после того как ячейку C2 скопируют
в ячейку B1?

1) =$E$3+C1

2) =$D$3+D2

3) =$E$3+E

4) =$F$4+D2

Пояснение.

Запись $E$3 означает, что столбец не меняется и номер
строки не меняется.

Номер строки 2 уменьшился на 1, значит, при копировании
в ячейку B1 из C2 строка 2 станет строкой 1.

Номер столбца С уменьшился на 1, значит, при копировании
в ячейку B1 из C2 столбец D станет столбцом С.

Окончательный вид =$E$3+С1.

Правильный ответ указан под номером 1.

Определения значения формулы

№1. В электронной таблице значение формулы
=CP3HAЧ(A3:D3) равно 5. Чему равно значение формулы =СУММ(АЗ:СЗ), если значение
ячейки D3 равно 6?

1) 1

2) -1

3) 14

4) 4

Пояснение.

Функция СРЗНАЧ(A3:D3) считает среднее арифметическое
диапазона A3:D3, т. е. сумму значений четырёх ячеек A3, B3, C3, D3,
делённую на 4. Умножим среднее значение на число ячеек и получим сумму
значений ячеек A3 + B3 + C3 + D3 = 5 * 4 = 20.

Теперь вычтем значение ячейки D3 и найдём искомую
сумму: A3 + B3 + C3 = 20 — 6 = 14.

Правильный ответ указан под номером 3.

№2. В электронной таблице значение формулы
=СРЗНАЧ(С2:С5) равно 3. Чему равно значение формулы =СУММ(С2:С4), если значение
ячейки С5 равно 5?

1) 1

2) 7

3) -4

4) 4

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СРЗНАЧ(С2:С5) считает среднее арифметическое
диапазона С2:С5, т. е. сумму значений четырёх ячеек С2, С3, C4, С5,
делённую на 4. Умножим среднее значение на число ячеек и получим сумму
значений ячеек С2 + С3 + C4 + С5 = 3 * 4 = 12

Теперь, вычтем значение ячейки С5 и найдём искомую
сумму: С2 + С3 + C4 = 12 — 5 = 7

Правильный ответ указан под номером 2.

№3. В электронной таблице значение формулы
=СУММ(А5:D5) равно 6. Чему равно значение формулы =СРЗНАЧ(А5:С5), если значение
ячейки D5 равно 9?

1) 1

2) -3

3) 3

4) -1

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СУММ(А5:D5) считает сумму значений ячеек диапазона
A5:D5, т. е. A5 + B5 + C5 + D5 = 6

Функция СРЗНАЧ(А5:С5) считает среднее арифметическое
диапазона А5:С5, т. е. сумму значений трёх ячеек A5, B5, C5, делённую на
3.

Вычтем значение ячейки D5 из первой суммы и найдём
сумму: A5 + B5 + C5 = 6 — 9 = -3.

Теперь разделим ответ на 3 и найдём искомое среднее
значение: СРЗНАЧ(А5:С5) = -3 / 3 = -1.

Правильный ответ указан под номером 4.

№4. В электронной таблице значение формулы
=CУMM(D2:D5) равно 10. Чему равно значение формулы =CP3HAЧ(D2:D4), если значение
ячейки D5 равно −2?

1) 6

2) 2

3) 8

4) 4

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СУММ(D2:D5) считает сумму значений ячеек диапазона
D2:D5, т. е. D2 + D3 + D4 + D5 = 10

Функция СРЗНАЧ(D2:D4) считает среднее арифметическое
диапазона D2:D4, т. е. сумму значений трёх ячеек D2, D3, D4, делённую на
3.

Вычтем значение ячейки D5 из первой суммы и найдём
сумму: D2 + D3 + D4 = 10 — (-2) = 12.

Теперь разделим ответ на 3 и найдём искомое среднее
значение: СРЗНАЧ(D2:D4) = 12 / 3 = 4.

Правильный ответ указан под номером 4.

№5. В электронной таблице значение формулы
=СРЗНАЧ(А4:С4) равно 5. Чему равно значение формулы СУММ(А4:D4), если значение
ячейки D4 равно 6?

1) 1

2) 11

3) 16

4) 21

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СРЗНАЧ(A4:C4) считает среднее арифметическое
диапазона A4:C4, т. е. сумму значений трёх ячеек A4, B4, C4, делённую на
3. Умножим среднее значение на количество ячеек данного диапазона и
найдём: A4 + B4 + C4 = 5 * 3 = 15

Теперь прибавим к полученному резльтату значение
ячейки D4 и найдём искомую сумму:

A4 + B4 + C4 +
D4 = 15 + 6 = 21

Правильный ответ указан под номером 4.

№6. В электронной таблице значение формулы
=СРЗНАЧ(Е2:Е4) равно 3,

чему равно значение формулы =СУММ(Е2:Е5), если значение
ячейки Е5 равно 5?

1) 11

2) 2

3) 8

4) 14

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СРЗНАЧ(Е2:Е4) считает среднее арифметическое
диапазона Е2:Е4, т. е. сумму значений трёх ячеек E2, E3, E4, делённую на
3. Умножим среднее значение на количество ячеек данного диапазона и
найдём: E2 + E3 + E4 = 3 * 3 = 9

Теперь прибавим к полученному резльтату значение
ячейки E5 и найдём искомую сумму:

E2 + E3 + E4 + E5 = 9 + 5 = 14

Правильный ответ указан под номером 4.

№7. В электронной таблице значение формулы
=СУММ(А7:С7) равно 9. Чему равно значение формулы =CPЗHAЧ(A7:D7). если значение
ячейки D7 равно 3?

1) -6

2) 6

3) 3

4) 4

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СУММ(А7:С7) считает сумму значений ячеек А7, B7
и С7, поэтому А7 + B7 + С7 = 9.

Функция СРЗНАЧ(A7:D7) считает среднее арифметическое
диапазона A7:D7, т. е. сумму значений четырёх ячеек А7, B7, С7, D7,
делённую на 4. Поэтому прибавим к первой сумме значение ячейки D7 и
найдём:

А7 + B7 + С7 + D7 = 9 + 3 = 12.

Теперь разделим полученный резльтат на число ячеек и
найдём искомую величину:

СРЗНАЧ(A7:D7) = 12 / 4 = 3.

Правильный ответ указан под номером 3.

№8. В электронной таблице значение формулы
=СУММ(В2:В4) равно 6. Чему равно значение формулы =СРЗНАЧ(В2:В5), если значение
ячейки В5 равно 14?

1) 5

2) 8

3) 10

4) 20

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СУММ(В2:В4) считает сумму значений ячеек B2, B3
и B4, поэтому B2 + B3 + B4 = 6.

Функция СРЗНАЧ(В2:В5) считает среднее арифметическое
диапазона В2:В5, т. е. сумму значений четырёх ячеек B2, B3, B4, B5,
делённую на их количество. Поэтому прибавим к первой сумме значение
ячейки В5 и найдём: B2 + B3 + B4 + В5 = 6 + 14 = 20.

Теперь разделим полученный резльтат на 4 и найдём искомую
величину: СРЗНАЧ(В2:В5) = 20 / 4 = 5.

Правильный ответ указан под номером 1.

№9. В электронной таблице значение формулы
=CPЗHAЧ(A3:D4) равно 5. Чему равно значение формулы =СРЗНАЧ(АЗ:С4), если
значение формулы =CУMM(D3:D4) равно 4?

1) 1

2) 6

3) 3

4) 4

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СУММ(D3:D4) считает сумму значений ячеек D3 и
D4: D3 + D4 = 4.

Функция СРЗНАЧ(A3:D4) считает среднее арифметическое
диапазона A3:D4, т. е. сумму значений восьми ячеек A3, B3, C3, D3, A4,
B4, C4, D4, делённую на их количество. Умножим среднее значение на 8 и
найдём суммму значений этих ячеек: СУММ(A3:D4) = 5 * 8 = 40.

Вычтем из полученной суммы СУММ(A3:D4) значение суммы
D3 + D4 и найдём значение суммы СУММ(A3:C4): оно равно 40 — 4 = 36.

Теперь разделим полученный резльтат на количество
ячеек данной суммы (их здесь 6) и найдём искомую величину: СРЗНАЧ(АЗ:С4)
= 36 / 6 = 6.

Правильный ответ указан под номером 2.

№10. В электронной таблице значение формулы
=CPЗHAЧ(C2:D5) равно 4. Чему равно значение формулы =CУMM(C5:D5), если значение
формулы =CPЗHAЧ(C2:D4) равно 5

1) -6

2) 2

3) -4

4) 4

Пояснение.

*Для лучшего понимания рекомендуется нарисовать
таблицу.

Функция СРЗНАЧ(C2:D5) считает среднее арифметическое
диапазона C2:D5, т. е. сумму значений восьми ячеек С2, D2, C3, D3, C4,
D4, C5, D5, делённую на их количество. Умножим среднее значение на 8 и
найдём суммму значений этих ячеек: СУММ(C2:D5) = 4 * 8 = 32.

Аналогично для CPЗHAЧ(C2:D4), количество ячеек 6:
СУММ(C2:D4) = 5 * 6 = 30.

Вычтем из СУММ(C2:D5) значение СУММ(C2:D4) и найдём значение
суммы С5 + D5: оно равно

32 — 30 = 2.

Правильный ответ указан под номером 2.

Работа с таблицами

№1. В электронной таблице Excel отражены
данные о деятельности страховой компании за 4 месяца. Страховая
компания осуществляет страхование жизни, недвижимости, автомобилей
и финансовых рисков своих клиентов. Суммы полученных по каждому виду
деятельности за эти месяцы страховых взносов (в тысячах рублей)
также вычислены в таблице.

	Страхование	Страхование	Страхование	Страхование
	жизни	автомобилей	фин. рисков	недвижимости
	тыс. р.	тыс. р.	тыс. р.	тыс. р.
Май	10	3	20	11
Июнь	2	4	8	10
Июль	4	6	8	5
Август	6	12	7	4
Сумма	22	25	43	30

Известно, что за эти 4 месяца компании пришлось выплатить
двум клиентам по 20 000 рублей каждому.

Каков общий доход страховой компании в рублях за прошедшие
4 месяца?

1) 120 000

2) 100 000

3) 80 000

4) 60 000

Пояснение.

Найдём сумму значений из строки Сумма: 22 + 25 + 43 + 30
= 120(тыс. р.).

Двум клиентам компания выплатила 2 * 20000 = 40000.
Соответственно общий доход составит:

120000 — 40000 = 80000 руб.

Правильный ответ указан под номером 3.

№2. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промежутка времени и суммы вкладов с начисленными
процентами за соответствующие истекшие периоды времени. Также
приведены общие суммы всех вкладов в банке после начисления процентов
и доход вкладчиков за истекший двухгодичный период.

	Вклад, р.	4 %	5 %	Сумма начислений за два периода
Осин	2100000	2184000	2293200	193200
Пнев	200000	208000	248400	18400
Чуйкин	50000	52000	54600	4600
Шаталов	2400000	2496000	2620800	220800
Общая сумма	4750000	4940000	5187000	437000

Определите, кто из вкладчиков за истекшее с момента
открытия вклада время получил средний ежемесячный доход от вклада
более 9 000 рублей.

1) Осин

2) Пнев

3) Чуйкин

4) Шаталов

Пояснение.

Для определения среднемесячного дохода необходимо
разделить доход каждого на количество месяцев вклада, т. е. на
24 месяца.

Осин: 193200 / 24 = 8 050,

Пнев: 18400 / 24 = 766,7,

Чуйкин: сам доход меньше 9 000, поэтому он не подходит,

Шаталов: 220800 / 24 = 9 200.

Более 9 000 рублей имеет Шаталов.

Правильный ответ указан под номером 4.

№3. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за фиксированные
промежутки времени и суммы вкладов с начисленными процентами за соответствующие
истекшие периоды времени. Также приведены общие суммы всех вкладов в
банке после начисления процентов.

	Вклад, р.	4 %	3 %
Агеев	2100000	2184000	2249520
Агнесян	200000	208000	214240
Сестров	50000	52000	53560
Кучкин	2300000	2392000	2463760
Общая сумма	4650000	4836000	4981080

Определите общую сумму вкладов населения в банке в
рублях после очередного начисления процентов, если процентная ставка
будет составлять 10%.

1) 5 000 000

2) 5 134 567

3) 5 345 678

4) 5 479 188

Пояснение.

Общая сумма вкладов после начисления процентов составила
4 981 080. Увеличение на 10% можно заменить операцией умножения
на 1,1. Тогда общая сумма составит: 4 981 080 · 1,1 = 5 479 188.

Правильный ответ указан под номером 4.

№4. В электронной таблице Excel отражены
данные по продаже некоторого штучного товара в торговых центрах города
за четыре месяца. За каждый месяц в таблице вычислены суммарные продажи
и средняя по городу цена на товар, которая на 2 рубля больше цены поставщика
данного товара.

ТЦ	Январь	Февраль	Март	Апрель
	Продано, шт.	Цена, р.	Продано, шт.	Цена, р.	Продано, шт.	Цена, р.	Продано, шт.	Цена, р.
Эдельвейс	5	14	1	17	5	15	4	15
Покупочка	6	13	2	16	6	11	4	14
Кошелек	2	17	5	14	4	15	1	18
Солнечный	8	12	7	13	7	11	7	13
Продано всего	21		15		22		16
Средняя цена	14		15		13		15

Известно, что весь поступивший от поставщика в текущем
месяце товар реализуется в этом же месяце.

В каком месяце выручка поставщика данного товара
была максимальна?

1) Январь

2) Февраль

3) Март

4) Апрель

Пояснение.

Найдём выручку за продажи в торговых центрах на каждый
месяц. В том месяце, где она максимальна, поставщик также получил наибольшую
прибыль.

Январь: 21 * 14 = 294,

Февраль: 15 * 15 = 225,

Март: 22 * 13 = 286,

Апрель: 16 * 15 = 240.

Наибольшая прибыль в январе.

Правильный ответ указан под номером 1.

№5. В электронной таблице Excel отражены
данные о деятельности страховой компании за 4 месяца. Страховая
компания осуществляет страхование жизни, недвижимости,/автомобилей
и финансовых рисков своих клиентов. Суммы полученных по каждому виду
деятельности за эти месяцы страховых взносов (в тысячах рублей)
также вычислены в таблице.

	Страхование жизни, тыс. р.	Страхование автомобилей, тыс. р.	Страхование фин. рисков, тыс. р.	Страхование недвижимости, тыс, р.
январь	10	4	20	11
февраль	8	4	80	14
март	43	3	8	5
апрель	6	12	7	65
сумма	67	23	115	95

Известно, что за эти 4 месяца компании пришлось выдать
трем клиентам страховые выплаты по 30 000 рублей каждому. Каков общий
доход страховой компании в рублях за прошедшие 4 месяца?

1) 310 000

2) 200 000

3) 210 000

4) 300 000

Пояснение.

Найдём общую сумму: 67 + 23 + 115 + 95 = 300 (тыс. р).

Выплаты клиентам: 30 000 * 3 = 90 000 (р).

Общий доход: 300 000 — 90 000 = 210 000 рублей.

Правильный ответ указан под номером 3.

№6. В электронной таблице Excel приведен
фрагмент банковских расчетов по вкладам населения. Таблица отражает
фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промежутка времени и суммы вкладов с начисленными
процентами за соответствующие истекшие периоды времени. Также
приведены общие суммы всех вкладов в банке после начисления процентов
и доход вкладчиков за истекший двухгодичный период.

	Вклад р.	4 %	5 %	Сумма начислений за два периода
Столков	3200000	3328000	3494400	294400
Чин	3212000	3340480	3507504	295504
Прокопчин	400000	416000	436800	36800
Щеглов	1000000	1040000	1092000	92000
Общая сумма:	7812000	8124480	8530704	718704

Определите, кто из вкладчиков за истекшее с момента
открытия вклада время получил средний ежемесячный доход от вклада
менее 2 000 рублей.

1) Столков

2) Чин

3) Прокопчин

4) Щеглов

Пояснение.

Сумма начислений указана за 2 года, т. е. за 24 месяца.
Чем меньше сумма, тем меньше средний доход. Самая маленькая сумма у Прокопчина.
Проверим 36800 / 24 = 1533,33.

Правильный ответ указан под номером 3.

№7. В 2000 году в РФ создано 7 федеральных
округов. Используя представленную таблицу укажите номер региона с
наименьшей плотностью населения.

Название	Состав	Площадь (тыс.км²)	Население (2002 г.)
1. Северо-Западный	11 регионов − субъектов РФ, центр — г. Санкт-Петербург	1677,9	14158
2. Центральный	18 регионов − субъектов РФ, центр — г. Москва	650,7	36482
3. Приволжский	15 регионов − субъектов РФ, центр — г. Нижний Новгород	1038	31642
4. Южный	13 регионов − субъектов РФ, центр — г. Ростов-на-Дону	589,2	21471
5. Уральский	6 регионов − субъектов РФ, центр — г. Екатеринбург	1788,9	12520
6. Сибирский	16 регионов − субъектов РФ, центр — г. Новосибирск	5114,8	20542
7. Дальневосточный	10 регионов − субъектов РФ, центр — г. Хабаровск	6515,9	7038

1) 4

2) 5

3) 6

4) 7

Пояснение.

Проверим все варианты. Для этого найдём плотность населения
в округах 4—7, поделив население на площадь.

Увидим, что седьмой округ имеет наименьшую плотность населения.

Правильный ответ указан под номером 4.

№8. В 2000 году в РФ создано 7 федеральных
округов. Используя представленную таблицу укажите номер региона с
наибольшей плотностью населения.

Название	Состав	Площадь (тыс.км²)	Население (2002 г.)
1. Северо-Западный	11 регионов − субъектов РФ, центр — г. Санкт-Петербург	1677,9	14158
2. Центральный	18 регионов − субъектов РФ, центр — г. Москва	650,7	36482
3. Приволжский	15 регионов − субъектов РФ, центр — г. Нижний Новгород	1038	31642
4. Южный	13 регионов − субъектов РФ, центр — г. Ростов-на-Дону	589,2	21471
5. Уральский	6 регионов − субъектов РФ, центр — г. Екатеринбург	1788,9	12520
6. Сибирский	16 регионов − субъектов РФ, центр — г. Новосибирск	5114,8	20542
7. Дальневосточный	10 регионов − субъектов РФ, центр — г. Хабаровск	6515,9	7038

1) 1

2) 2

3) 3

4) 4

Пояснение.

Проверим все варианты. Для этого найдём плотность населения
в округах 1—4, поделив население на площадь.

Увидим, что второй окурга имеет наибольшую плотность
населения.

Правильный ответ указан под номером 2.

№9. Коле нужно с помощью электронных таблиц
построить таблицу умножения чисел от 3 до 6.

Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал
числа от 3 до 6. Затем в ячейку Е2 записал формулу умножения, после чего
скопировал её во все ячейки диапазона В2:Е5. В итоге на экране получился
фрагмент таблицы умножения (см. рисунок).

	A	B	C	D	E
1		3	4	5	6
2	3	9	12	15	18
3	4	12	16	20	24
4	5	15	20	25	30
5	6	18	24	30	36

Какая формула была записана в ячейке Е2?

1) =А$2*$Е1

2) =А2*Е1

3) =$А2*$Е1

4) =$А2*Е$1

Пояснение.

Формула, записанная в ячейку Е2, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае, при копировании
формулы в диапазон B2:D2, номер столбца будет автоматически уменьшаться,
появится неверная ссылка. произойдёт ошибка. Кроме того, формула должна
иметь знак абсолютной адресации перед цифрой 1, поскольку в противном
случае, при копировании формулы в диапазон E3:E5, номер строки будет
автоматически увеличиваться, появится неверная ссылка.

Следовательно, ответ 4.

№10. Коле нужно с помощью электронных таблиц
построить таблицу двузначных чисел от 50 до 89.

Для этого сначала в диапазоне В1:К1 он записал числа
от 0 до 9, и в диапазоне А2:А5 он записал числа от 5 до 8. Затем в ячейку
В2 записал формулу двузначного числа (А2 — число десятков;
В1 — число единиц), после чего скопировал её во все ячейки диапазона
В2:К5. В итоге получил таблицу двузначных чисел. На рисунке ниже представлен
фрагмент этой таблицы.

	A	B	C	D	E
1		0	1	2	3
2	5	50	51	52	53
3	6	60	61	62	63
4	7	70	71	72	73
5	8	80	81	82	83

Какая формула была записана в ячейке В2?

1) =А$2*10+$В1

2) =$А2*10+$В1

3) =А2*10+В1

4) =$А2*10+В$1

Пояснение.

Формула, записанная в ячейку В2, должна иметь знак абсолютной
адресации перед буквой А, поскольку в противном случае,при копировании
формулы в диапазон B5:E5, номер столбца будет автоматически увеличиваться,
появится неверная ссылка. Кроме того, формула должна иметь знак абсолютной
адресации перед цифрой 1, поскольку в противном случае, при копировании
формулы в диапазон B3:B5, номер строки будет автоматически увеличиваться,
появится неверная ссылка.

Следовательно, ответ 4.

Составление диаграмм по данным

№1. Сплавляются два вещества, состоящие
из серы, железа, водорода и меди. Массовые доли серы (S), железа (Fe),
водорода (Н) и меди (Си) в каждом веществе приведены на диаграммах.

Определите, какая из диаграмм правильно отражает соотношение
элементов в сплаве.

Пояснение.

Отталкиваемся от железа: в каждом веществе железа
было больше половины, следовательно, и в смеси его будет половина
или более, такой вариант изображён на диаграмме 3.

Правильный ответ: 3.

№2. На диаграмме представлен уровень зарплат
трех членов семьи за два месяца.

Какая из диаграмм правильно отражает суммарный за
два месяца доход каждого члена семьи?

Пояснение.

Визуально видно, что за два месяца папа набирает наибольшую
из всех сумму,

дочка на втором месте (стабильно за оба месяца), и на
третьем месте — мама.

Сразу отсеиваем диаграмму 2 и 3, а вот для 4ой скажем,
что заработок отца во много больше дочери, следовательно остается
диаграмма 1.

Правильный ответ: 1.

№3. Диаграмма отражает количество (в килограммах)
собранного за четыре месяца урожая двух сортов огурцов в парниковом
хозяйстве.

Какая из диаграмм правильно отражает объемы суммарного
за четыре месяца собранного урожая по каждому из сортов?

Пояснение.

1 сорт: 10+20+30+30=90 кг.

2 сорт: 20+40+30+30=120 кг.

2го сорта больше, чем 1го на 120 — 90 = 30 кг или на
30*100/120=25%, что соответствует графику 4.

Правильный ответ: 4.

№4. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение
общего количества участников (из всех трех регионов) по каждому из
предметов тестирования?

Пояснение.

При помощи столбчатых диаграмм можно найти общее количество
учеников:

400+100+200+400+200+200+400+300+200=2400

Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся, тестируемые по различным предметам:

Биология: 12002400=0,5=50%

История: 6002400=0,25=25%

Химия: 6002400,25=25%

Этим данным соответствует первая диаграмма

№5. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение
общего количества участников тестирования по регионам?

Пояснение.

При помощи столбчатых диаграмм можно найти общее количество
учеников:

200+100+200+200+200+200+400+300+200=2000

Круговые диаграммы дают нам представление о долях отдельных
составляющих в общей сумме. Соответственно подсчитаем, какую долю тестируемых
составляют учащиеся из различных регионов:

Татарстан: 5002000=0,25=25%

Чувашия: 6002000=0,30=30%

Якутия: 9002000=0,45=45%

Этим данным соответствует третья диаграмма

№6. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение
количества участников тестирования по химии в регионах?

Пояснение.

Из условия видно, что соотношение для всех регионов
по участникам тестирования по химии одинаково.

Правильный ответ соответствует четвертой диаграмме

№7. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение
количества участников тестирования по истории в регионах?

Пояснение.

При помощи столбчатых диаграмм можно найти общее количество
учеников, принимавших участие в тестировании по истории:

100+200+300=600

Татарстан: 100600=0,17=17%

Чувашия: 200600=0,33=33%

Якутия: 300600=0,5=50%

Этим данным соответствует вторая диаграмма

№8. На диаграмме показано количество
участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение
количества участников тестирования по русскому языку в регионах?

Пояснение.

При помощи столбчатых диаграмм можно найти общее количество
учеников, принимавших участие в тестировании по русскому языку:

200+200+200=600

Башкирия: 200600=0,33=33%

Калмыкия: 200600=0,33=33%

Удмуртия: 200600=0,33=33%

Этим данным соответствует четвёртая диаграмма.

Второй вариант рассуждения

Проанализировав диаграмму, увидим, что тестирование
по русскому языку проходило равное количество учеников во всех трех
регионах. Таким образом, диаграмма под номером 4 правильно отражает
соотношение количества участников тестирования по русскому
языку.

Правильный ответ указан под номером 4.

№9. В таблице представлены средние рыночные
цены для 4–х типов товаров на начало и конец года. Какая из диаграмм наиболее
верно отражает рост цен этих товаров в процентах относительно начала
года?

Пояснение.

Найдем на сколько процентов изменилась цена, для
этого нужно найти изменение цены каждого товара, а затем отнести его к
цене товара в начале года:

1-ый товар:

2-ой товар:

3-ий товар:

4-ый товар:

Анализируя столбчатые диаграммы, приходим к выводу,
что таким данным наиболее точно соответствует 2-ая диаграмма.

№10. На протяжении 3–х минут центральный
процессор компьютера был загружен следующим образом: 1–ю минуту
был загружен на 30%, 2–ю – на 10% и 3–ю – на 60%. Какая из диаграмм соответствует
загруженности процессора на протяжении 3–х минут?

Пояснение.

Для анализа круговых диаграмм необходимо выяснить,
какая доля памяти выделялась программе в течение каждого промежутка
времени. Анализируя круговые диаграммы, видим, что 1-я соответствует
условию задачи.

На второй диаграмме все части равные, что неверно.

На диаграмме 3 третья минута не занимает 60 %. На
четвёртой третья минута также меньше 60 %.

Ответ: 1.

Столбчатая и круговая диаграммы

№1. Все ученики старших классов (с 9-го по
11-й) участвовали в школьной спартакиаде. По результатам соревнований
каждый из них получил от 0 до 3-х баллов. На диаграмме I отражено распределение
учеников по классам, а на диаграмме II — количество учеников, набравших
баллы от 0 до 3-х. На обеих диаграммах каждый ученик учтён только один
раз.

Имеются четыре утверждения:

1 ) Среди учеников 9-го класса есть хотя бы один, набравший
2 или 3 балла.

2 ) Все ученики, набравшие 0 баллов, могут быть 9-классниками.

3 ) Все 10-классники могли набрать ровно по 2 балла.

4 ) Среди набравших 3 балла нет ни одного 10-классника.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего учеников 45 + 30 + 20 + 15 = 110.

Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что

«9 класс»,=50%=55

«11 класс»,

«10 класс» .

Теперь рассмотрим утверждения:

1. Однозначно не следует из анализа обеих диаграмм,
поскольку суммарное количество учеников, набравших 2 или 3 балла
равно 20 + 15 = 35, а учеников девятого класса 55.

2. Могут, так как 0 баллов набрало 45, а 9-классников
55.

3. Не могли, так как 10-классников 37, а ровно по 2 балла
набрало всего 20.

4. Однозначно не следует из анализа обеих диаграмм.

№2. В магазине продаются мячи четырёх цветов
(синие, зелёные, красные и жёлтые) и трёх размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме
II — распределение мячей по цветам.

Имеются четыре утверждения:

1 ) Среди больших мячей должен быть хотя бы один синий.

2 ) Ни один мяч среднего размера не может быть красным.

3 ) Все маленькие мячи могут быть зелёными.

4 ) Все зелёные мячи могут быть маленькими.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего мячей 30+40+35+15=120.

Круговая диаграмма дает нам представление о долях отдельных
составляющих в общей сумме. Из нее мы выясняем, что М=50%=60, Ср=25%=30,
Б=25%=30.

Теперь рассмотрим утверждения:

1. Может, но не обязательно.

2. Может, так как Ср=30, а красных 35.

3. Не могут, так как М=60, а зеленых всего 40.

4. Могут так как зеленых всего 40, а М=60.

№3. В магазине продаются мячи четырёх цветов
(синие, зелёные, красные и жёлтые) и трёх размеров (большие, средние и маленькие).
На диаграмме I отражено количество мячей разного размера, а на диаграмме
II — распределение мячей по цветам.

Имеются четыре утверждения:

1 ) Все маленькие мячи могут быть синими или жёлтыми.

2 ) Среди больших мячей найдётся хотя бы один красный.

3 ) Среди маленьких мячей найдётся хотя бы один зелёный
или красный.

4 ) Все красные мячи могут быть среднего размера.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего мячей 30+40+35+15=120.

Теперь рассмотрим утверждения:

1. Не могут, так как М=60, а синих 30, жёлтых 15.

2. Может, но не обязательно.

3. Найдется, так как неверно «1.»

4. Не могут так как красных 35, а Ср=30.

№4. Заведующая детским садом обнаружила,
что в её саду все дети называются только четырьмя разными именами;
Саша, Валя, Миша и Ира. По цвету волос каждого из них можно чётко отнести
к блондинам, шатенам или брюнетам. На диаграмме I отражено количество
детей каждого имени, а на диаграмме II — распределение детей по цвету
волос.

Имеются четыре утверждения:

1 ) Всех брюнетов могут звать Саша.

2 ) Все Иры могут быть шатенками.

3 ) Среди Миш найдётся хотя бы один блондин.

4 ) Среди Саш нет ни одного шатена.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего детей

40+20+35+25=120

«Бр»,=50%=60

«Бл»,

«Ш» .

Теперь рассмотрим утверждения:

1. Не могут, так «Бр»=60, а Саш 40.

2. Могут, так как «Ш»=45, а Ир 25.

3. Однозначно не следует из анализа обеих диаграмм.

4. Однозначно не следует из анализа обеих диаграмм.

№5. Заведующая детского сада обнаружила,
что в сад ходят дети только четырёх имен: Саши, Вали, Миши и Иры. По цвету
волос каждого из них можно чётко отнести к блондинам, шатенам и брюнетам.
На диаграмме I отражено количество детей каждого имени, а на диаграмме
II — распределение детей по цвету волос.

Имеются четыре утверждения:

1) Всех блондинов зовут Саша.

2) Все Миши могут быть блондинами.

3) Среди Саш может не быть ни одного шатена.

4) Среди брюнетов есть хотя бы один ребёнок по имени Валя
или Ира.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего детей

40+20+35+25=120

«Бр»,=50%=60

«Бл»,

«Ш» .

Теперь рассмотрим утверждения:

1. Однозначно не следует из анализа обеих диаграмм.

2. Не могут, так как «Бл»=20, а Миш 35.

3. Может не быть.

4. Однозначно не следует из анализа обеих диаграмм.

№6. В магазине продаются головные уборы
трёх видов (панамки, шляпы и бейсболки) и четырёх материалов (брезент,
хлопок, шёлк и соломка).На диаграмме 1 отражено количество головных
уборов каждого вида, а на диаграмме II — распределение головных уборов
по материалам.

Имеются четыре утверждения:

A) Все шляпы могут быть из шёлка.

Б) Все панамы могут быть из соломки.

B) Среди головных уборов из соломки найдётся хотя бы
одна панама.

Г) Все бейсболки должны быть из хлопка.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего головных уборов

45+35+20=100

«Х»

«Б»,

«С»,

«Ш» .

Теперь рассмотрим утверждения:

1. Могут, так как шляп 45, а «Ш»=50.

2. Не могут, так как «С»=25, а панам 35.

3. Однозначно не следует из анализа обеих диаграмм.

4. Однозначно не следует из анализа обеих диаграмм.

№7. В магазине продаются головные уборы
трёх видов (панамки, шляпы и бейсболки) и четырёх материалов (брезент,
хлопок, шёлк и соломка).На диаграмме I отражено количество головных
уборов каждого вида, а на диаграмме II — распределение головных уборов
по материалам.

Имеются четыре утверждения:

A) Все соломенные изделия могут быть бейсболками.

Б) Все панамки могут быть из хлопка или брезентовыми.

B) Среди изделий из шёлка может не быть ни одной шляпы.

Г) Среди изделий, сделанных не из соломки, может не
быть ни одной панамы.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

45+35+20=100

«Х»

«Б»,

«С»,

«Ш» .

Теперь рассмотрим утверждения:

1. Не могут, так как «С»=25 а бейсболок 20.

2. Не могут, так как панам 35, а «Б» и
«Х» меньше 20.

3. Может, так как «Ш»=50, а шляп всего 45.

4. Не может.

№8. Молодой человек решил сделать подарок
своей невесте и пришёл в ювелирный магазин. Там он обнаружил кольца
из золота, серебра и платины, каждое из которых было украшено одним
драгоценным камнем (топазом, изумрудом, алмазом или рубином). Он исследовал
соотношение количества колец с разными камнями (результаты отражены
на диаграмме I) и количество колец разных материалов (результаты отражены
на диаграмме II).

Молодой человек сделал четыре предположения:

A) Все кольца с изумрудами могут быть из золота.

Б) Среди серебряных колец найдётся хотя бы одно с изумрудом.

B) Все кольца с рубинами и алмазами могут быть платиновыми.

Г) Все золотые кольца могут быть с алмазами.

Какое из этих предположений следует из анализа обеих
диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что количество колец разных материалов

45+35+20=100

«P» ,=25%*100=25

«A» ,=25%*100=25

«И» .

«Т» .

Теперь рассмотрим утверждения:

1. Могут, так как «И»=33, а золотых 45.

2. Однозначно не следует из анализа обеих диаграмм.

3. Не могут, так как платиновых всего 20, а
«P»+»A»=50.

4. Не могут, так как золотых 45, а «A»=25.

№9. Молодой человек решил сделать подарок
своей невесте и пришёл в ювелирный магазин. Там он обнаружил кольца
из золота, серебра и платины, каждое из которых было украшено одним
драгоценным камнем (топазом, изумрудом, алмазом или рубином). Он исследовал
соотношение количества колец с разными камнями (результаты отражены
на диаграмме I) и количество колец разных материалов (результаты отражены
на диаграмме И).

Молодой человек сделал четыре предположения:

A) Все кольца с изумрудами не могут быть серебряными.

Б) Среди золотых и серебряных колец найдётся хотя бы
одно с рубином.

B) Все золотые кольца могут быть с топазами.

Г) Все рубины находятся в серебряных кольцах.

Какое из этих предположений следует из анализа обеих
диаграмм?

Пояснение.

45+35+20=100

«P» ,=25%*100=25

«A» ,=25%*100=25

«И» .

«Т» .

Теперь рассмотрим утверждения:

1. Могут, так как «И»=33, а серебряных 35.

2. Найдется, так как платиновых всего 20, а
«Р»=25, следовательно, 5 колец либо золотые, либо серебрянные.

3. Не могут, так как золотых 45, а «Т»=17.

4. Однозначно не следует из анализа обеих диаграмм.

№10. Все ученики старших классов (с 9–го по
11–й) участвовали в школьной спартакиаде. По результатам соревнований
каждый из них получил от 0 до 3–х баллов. На диаграмме I отражено распределение
учеников по классам, а на диаграмме II – количество учеников, набравших
баллы от 0 до 3–х. На обеих диаграммах каждый ученик учтён только один
раз.

Имеются четыре утверждения:

А) Среди учеников 9–го класса есть хотя бы один, кто набрал
0 баллов.

Б) Все 11–классники набрали больше 0 баллов.

В) Все ученики 11–го класса могли набрать ровно один
балл.

Г) Среди учеников 10–го класса есть хотя бы один, кто набрал
2 балла.

Какое из этих утверждений следует из анализа обеих диаграмм?

Пояснение.

Столбчатая диаграмма дает нам представление о численных
данных. Из нее мы выясняем, что всего учеников

45+30+20+110

«9 класс»,=50%=55

«11 класс»,

«10 класс» .

Теперь рассмотрим утверждения:

A)Нельзя однозначно утверждать из анализа обеих диаграмм

Б)Нельзя однозначно утверждать из анализа обеих диаграмм

В)Да, могли, т.к. 11-классников 18, а учеников, набравших
один балл 30.

Г)Нельзя однозначно утверждать из анализа обеих диаграмм

Электронные таблицы и диаграммы

№1. Дан фрагмент электронной таблицы:

	A	B	C
1	4	2
2	=2*(A1–C1)	=(2*B1+A1)/4	=C1-1

Какое целое число должно быть записано в ячейке C1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку?

Пояснение.

По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. По данным таблицы найдём значение B2: B2 = (2 * 2 + 4) / 4 =
2.

Выразим С1 из значения С2: С1 = С2 + 1 = B2 + 1 = 2 + 1
= 3.

Ответ: 3.
Источник: Яндекс: Тренировочная работа ЕГЭ по информатике. Вариант 1.

№2. Дан фрагмент электронной таблицы:

	A	B	C
1	4	2
2	=A1+C1	=B1+A1	=3*C1

Пояснение.

В ячейке В2 будет значение 6. Из диаграммы следует,
что значения в ячейках равны между собой. Следовательно, из того, что
6=3*C1 => C1= 2.

№3.

Дан фрагмент электронной таблицы.

	A	B	C
1	2	4
2	= (B1 – A1)/2	= 2 – A1/2	= (C1 – A1)*2 – 4

Какое целое число должно быть записано в ячейке C1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2 : С2 соответствовала рисунку? Известно, что все
значения диапазона, по которым построена диаграмма, имеют один и
тот же знак.

Пояснение.

В ячейке А₂ будет значение 1. В ячейке В₂ будет
значение 1. Из диаграммы следует, что значения в ячейке С₂ в
2 раза больше. Следовательно, из того, что 2 = (C1 – A1)*2 – 4, следует,
что ответ 5.

№4. Дан фрагмент электронной таблицы:

	A	B	C
1	2		=A1+1
2	=C1-B1	=(3*B1+C1)/3	=B2+A1

Какое число должно быть записано в ячейке B1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона ячеек
A2:С2 соответствовала рисунку? Известно, что все значения диапазона,
по которым построена диаграмма, имеют один и тот же знак.

Пояснение.

В ячейке С₁ будет значение 3. С₁ =
3, А₁ = 2, следовательно В₂ = В₁ +
1, С₂ = В₂ + 2 = В₁ + 3. Следовательно,
B₂не равно С₂, то есть, одно из них (судя по диаграмме)
больше другого в 2 раза. Решим эти уравнения последовательно для В₂ =
2С₂ и С₂ = 2В₂. В первом случае В₁ =
-5, А₂ = 8, В₂ = −4, C₂ = −2.
Это не соответствует диаграмме. Во втором случае В₁ =
1, А₂ = В₂ = 2, C₂ = 4. Этот вариант
соответствует диаграмме, следовательно, правильный ответ — 1.

№5. Дан фрагмент электронной таблицы:

	A	B	C
1	2	1
2	=C1-B1*5	=(B1+C1)/A1	=C1-5

Какое число должно быть записано в ячейке С1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек А2:С2 соответствовала рисунку?

Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.

Пояснение.

По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения ячеек А2 и В2, решим уравнение: C1 − B1
* 5 = (B1 + C1) / A1, из него C1 = 11 при А1 равном 2, В1 равном 1.

Ответ: 11.

№6. Дан фрагмент электронной таблицы:

	A	B	C
1	2	1
2	=C1-B1*3	=(B1+C1)/A1	=C1-3

Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.

Пояснение.

По рисунку видно, что значения всех трёх ячеек диапазона
A2:С2 равны. Приравняем значения ячеек А2 и В2, решим уравнение: C1 − B1
* 3 = (B1 + C1) / A1, из него C1 = 7 при А1 равном 2, В1 равном 1.

Ответ: 7.

№7.

Дан фрагмент электронной таблицы.

	A	B	C
1	5		=A1*2
2	=(B1-A1)/2	=B1-C1	=B2+A1

Какое число должно быть записано в ячейке В1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек А2:С2 соответствовала рисунку?

Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.

Пояснение.

В ячейке С₁ будет значение 10. С₁ =
10, А₁ = 5, следовательно, В₂ = В₁ −
10, С₂ = В₂ + 5 = В₁ − 5. Поэтому
B₂ не равно С₂, одно из них, судя по диаграмме,
больше другого в 2 раза.

Решим эти уравнения последовательно для В₂ =
2С₂ и С₂ = 2В₂. В первом случае: В₁ =
−5, А₂ = 8, В₂ = −4, C₂ = 5.
Это не соответствует диаграмме. Во втором случае: В₁ =
15, А₂ = В₂ = 5, C₂ = 10. Этот
вариант соответствует диаграмме, следовательно, правильный ответ
— 15.

№8. Дан фрагмент электронной таблицы

	A	B	C
1	2		=A1*4
2	=b1/A1	=C1/B1	=B2+A1

Какое число должно быть записано в ячейке B1, чтобы построенная
после выполнения вычислений диаграмма по значениям диапазона
ячеек A2:C2 соответствовала рисунку?

Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.

Пояснение.

Посчитаем значения в тех клетках, в которых это возможно.

	A	B	C
1	2		8
2	=B1/2	=8/B1	=8/B1+2

Из диаграммы видно, что две ячейки должны быть равны
друг другу. B2 не равно C2 значит, A2 = B2, а значение в ячейке C2 в два
раза больше.

Таким образом: B1/2 = 8/B1, B1 = 4.

№9. Дан фрагмент электронной таблицы:

	A	B	C
1	5		=A1*2
2	=B1/5	=A1/B1	=B2+C1/10

Известно, что все значения диапазона, по которым построена
диаграмма, имеют один и тот же знак.

Пояснение.

Вычислим значения в тех клетках, в которых это возможно.

	A	B	C
1	5		10
2	=B1/5	=5/B1	=5/B1+1

Из диаграммы видно, что две ячейки должны быть равны
друг другу, а значение в ячейке C2 в два раза больше. Поскольку B2 не
равно C2, имеем B1/5 = 5/B1, B1 = 5 и B1 = −5. Поскольку по условию все значения
диапазона, по которым построена диаграмма, имеют один и тот же знак,
ответ 5.

№10.

Дан фрагмент электронной таблицы:

	A	B	C
1	2		44
2	=С1 − В1В15	=(В1*В1+С1)/А1	=C1−20

Какое целое число должно быть записано в ячейке B1,
чтобы построенная после выполнения вычислений диаграмма по значениям
диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все
значения диапазона А1 :С2 имеют один и тот же знак.

Пояснение.

Преобразуем таблицу:

	A	B	C
1	2		44
2	=44 − В1·В1·5	=В1·В1/2+22	44−20

Из диаграммы следует, что значения в ячейках равны
между собой. Следовательно, из того, что
В1·В1/2 + 22 = 24, В1 = 2, либо
В1 = −2. Все значения диапазона А1 :С2 имеют один и тот же знак,
следовательно, ответ 2.

Источник

1 / 1 / 0

Регистрация: 26.09.2019

Сообщений: 164

23.06.2020, 10:02. Показов 11381. Ответов 8

Представлен фрагмент электронной таблицы MS Excel в режиме отображения формул.
A B C
1 7 11 =мин(А2:С2;B3)
2 =A$1+$B1 6 2
3 5 — =если(С1=B3;C1*B3;C1-B3)

Значение в ячейке C3 после копирования ячейки A2 в ячейку B3 будет равно…

Какой ответ,помогите пожалуйста!
Заранее огромное спасибо!

ᴁ®

3070 / 1736 / 361

Регистрация: 13.12.2016

Сообщений: 5,939

Записей в блоге: 4

23.06.2020, 10:48

Значение в ячейке C3 -1

2633 / 1333 / 255

Регистрация: 25.10.2010

Сообщений: 2,194

23.06.2020, 22:22

-15

ᴁ®

3070 / 1736 / 361

Регистрация: 13.12.2016

Сообщений: 5,939

Записей в блоге: 4

24.06.2020, 10:26

Pelena, -16

Миниатюры

2633 / 1333 / 255

Регистрация: 25.10.2010

Сообщений: 2,194

24.06.2020, 10:45

Не-а) При копировании формулы из А2 в В3 будет 17

ᴁ®

3070 / 1736 / 361

Регистрация: 13.12.2016

Сообщений: 5,939

Записей в блоге: 4

24.06.2020, 11:36

Сообщение от BurnSpark

копирования ячейки A2 в ячейку B3 будет равно

Pelena, тут что-то про формулу сказано?

Добавлено через 1 минуту
к тому-же формула там с абсолютными ссылками….

2633 / 1333 / 255

Регистрация: 25.10.2010

Сообщений: 2,194

24.06.2020, 16:29

Если копируем ячейку, стало быть, копируем её вместе с формулой.

И нет, там смешанные ссылки, а не абсолютные

ᴁ®

3070 / 1736 / 361

Регистрация: 13.12.2016

Сообщений: 5,939

Записей в блоге: 4

24.06.2020, 20:14

Оставлю без ответа. Пусть другие посмотрят….

2640 / 1697 / 694

Регистрация: 04.09.2015

Сообщений: 3,367

24.06.2020, 20:48

Сообщение было отмечено АЕ как решение

Решение

При копировании А2 с формулой =A$1+$B1, в ячейку В3 получаем формулу =B$1+$B2, которая возвращает 17
Ячейка С3=-15
Результат как у Елены (Pelena)

IT_Exp

Эксперт

87844 / 49110 / 22898

Регистрация: 17.06.2006

Сообщений: 92,604

24.06.2020, 20:48

Помогаю со студенческими работами здесь

Как избежать изменений отображения формул
Нужно вставить формулы, в нумерованный список, все нормально когда они не нумерованы, как только их…

режим отображения формул в экселе 2007
Как в экселе 2007 создать лист в режиме отображения формул?

Ошибка отображения формул в пакете Microsoft Office
При открытии файлов расширений Excel, Word, PowerPoint 2003-2013 годов, формулы отображаются…

Связанный выпадающий список для таблицы, где заголовок представлен формулами
Есть таблица, которую я не могу сделать форматированной, так как в заголовках стоят формулы, как по…

Селекторы для отображения сайта в полноэкранном режиме
Вот простой пример. Но почему-то не работает при переходе в полноэкранный режим

<!DOCTYPE html> …

Проблема отображения русского текста в графическом режиме
Столкнулся с проблемой правильного отображения русского текста в графическом режиме.
Установил…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

Источник

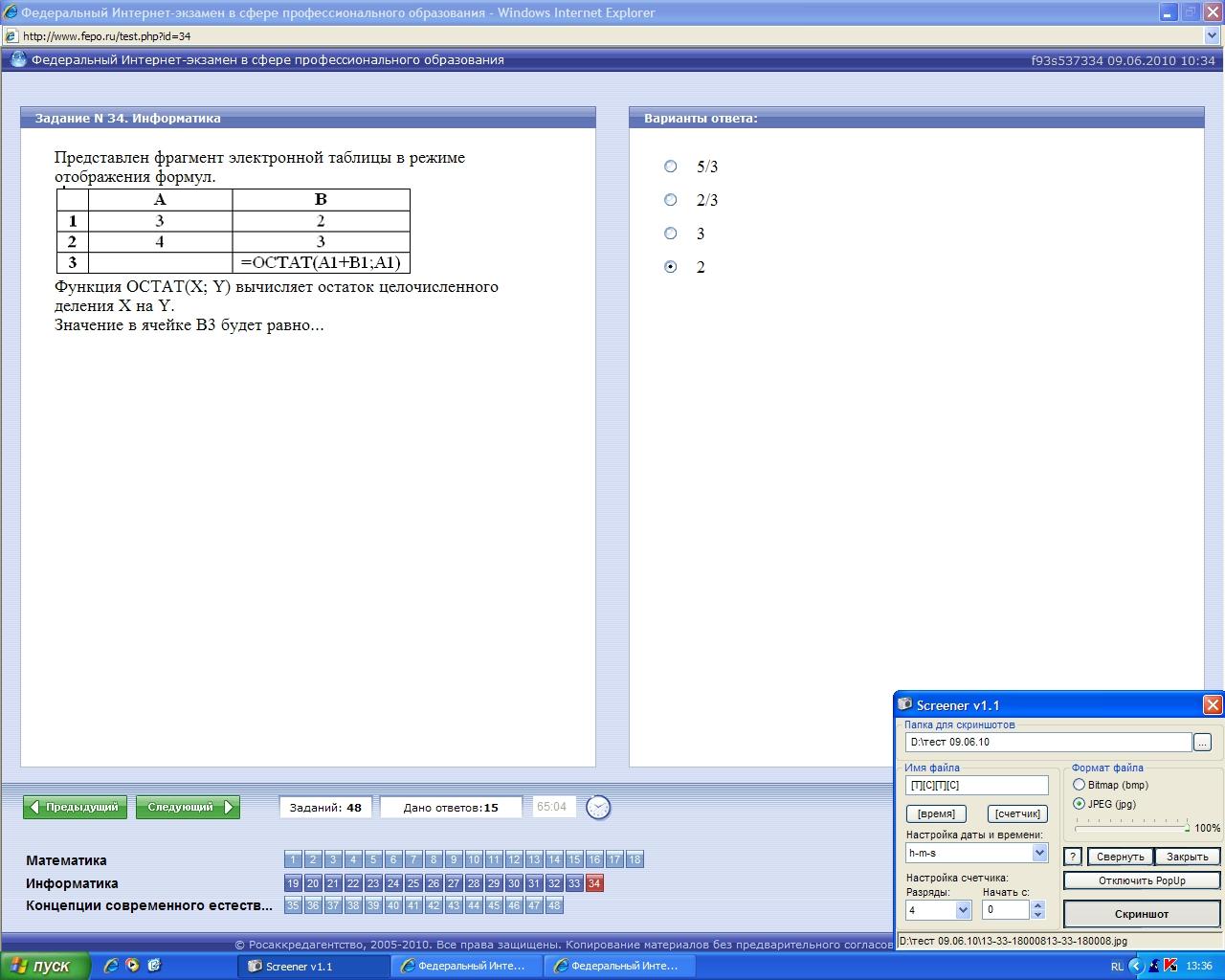
Функция ОСТАТ(X;Y)
вычисляет остаток целочисленного
деления X на Y.

Значение в ячейке В3 будет равно …

5/3

2/3

Пояснение к ответу:

При целочисленном делении числа 5 на
число 3 в остатке получается число 2

2. Ссылка а1 (ms Excel) является …

абсолютной

смешанной

относительной

некорректной

Пояснение к ответу:

Типы ссылок в MSExcel:

A1 – относительная;

$A$1 – абсолютная;

$A1 – смешанная (постоянный
столбец);

A$1 – смешанная (постоянная
строка).

3. При объединении ячеек а1, в1, с1 электронной таблицы ms Excel результирующая ячейка будет иметь значение …

Пояснение к ответу:

Если выделенная в электронной таблице
MSExcelзаполнена значениями, то объединение
ячеек приведет к потере всех значений,
кроме левого верхнего.

4. В электронной таблице MS
Excel знак «$» перед
номером строки в обозначении ячейки
указывает на …

абсолютную адресацию строки

денежный формат числа

начало выделения блока ячеек

начало записи формулы

Пояснение к ответу:

Знак «$»в адресе ячейки обозначает,
какая именно часть адреса будет
зафиксирована при копировании формулы,
т.е. останется абсолютной

Тема: MS Access

1. Результатом запроса к реляционной базе данных (в субд Access), изображенного на рисунке,

будет являться …

группировка и показ сотрудников, не
получивших зарплату

список средних зарплат по всей организации

список номеров отделов

список номеров отделов и средней
зарплаты каждого отдела

Пояснение к ответу:

На рисунке изображен группированный
запрос. В такой запрос обычно включаются
только два поля: по одному из полей
выполняется группировка, по другому
полю выполняется расчет с помощью
специальных функций:

AVG() — среднее значение;
COUNT() – количество значений;
MAX() – максимальное значение;
MIN() – минимальное значение;
SUM() — сумма значений.

2. Представлена база данных «Школа». Запрос для вывода списка учеников 11 классов, 1987 года рождения, имеющих оценки не ниже 4, содержит выражение …

(Оценка >=4) и (Год_рождения=1987) и
(Класс=11)

(Класс > 10) и (Год_рождения =1987) и (Оценка
=5) и (Оценка =4)

(Класс =11) и (Оценка >=4) или (Год_рождения
=1987)

(Класс =11) или (Оценка >=4) или (Год_рождения
=1987)

Пояснение к ответу:

В запросах можно задавать несколько
условий отбора по разным поля, в этом
случае они соединяются операцией «и».

Также можно указать несколько условий
отбора по одному полу, в этом случае
они соединяются операцией «или».

3. В реляционной базе данных запись – это …

отдельная таблица

элемент схемы данных

столбец в таблице

строка в таблице

Пояснение к ответу:

Информация в базе данных MS Access
представляется в виде отдельных таблиц.
При этом каждый столбец таблицы
соответствует полюданных, а
каждая строка –записиданных.

Соседние файлы в папке Экзамен инф и программ

Источник

Автор материалов — Лада Борисовна Есакова.

Microsoft Excel (в дальнейшем просто — Excel) — это программа выполнения расчетов и управления так называемыми электронными таблицами.

Excel позволяет выполнять сложные расчеты, в которых могут использоваться данные, расположенные в разных областях электронной таблицы и связанные между собой определенной зависимостью. Для выполнения таких расчетов в Excel существует возможность вводить различные формулы в ячейки таблицы. Excel выполняет вычисления и отображает результат в ячейке с формулой.

Важной особенностью использования электронной таблицы является автоматический пересчет результатов при изменении значений ячеек. Excel также может строить и обновлять графики, основанные на введенных числах.

Адрес ячейки в электронных таблицах состоит из имени столбца и следующего за ним номера строки, например, C15.

Для написания формул используют адреса ячеек и знаки арифметических операций (+, -, *, /, ^). Формула начинается знаком =.

В Excel предусмотрены стандартные функции, которые могут быть использованы в формулах. Это математические, логические, текстовые, финансовые и другие функции. Однако, на экзамене Вам могут встретиться только самые простые функции: СЧЕТ (количество непустых ячеек), СУММ (сумма), СРЗНАЧ (среднее значение), МИН (минимальное значение), МАКС (максимальное значение).

Диапазон ячеек обозначается следующим образом: A1:D4 (все ячейки прямоугольника от A1 до D4.

Адреса ячеек бывают относительными, абсолютными и смешанными.

Они по-разному ведут себя при копировании формулы из ячейки в ячейку.

Относительная адресация:

Если в ячейке B2 мы напишем формулу =D1+3, то таблица воспримет это как «взять значение ячейки на две правее и на одну выше текущей, и прибавить к нему 3».

Т.е. адрес D1 воспринимается таблицей, как положение относительно ячейки, куда вводится формула. Такой адрес называется относительным. При копировании такой формулы в другую ячейку, таблица автоматически пересчитает адрес относительно нового расположения формулы:

Абсолютная адресация:

Если нам не нужно, чтобы адрес пересчитывался при копировании формулы, мы можем его «закрепить» в формуле — поставить знак $ перед буквой и индексом ячейки: =$D$1+3. Такой адрес называется абсолютным. Такая формула не будет изменяться при копировании:

Смешанная адресация:

Если же мы хотим, чтобы при копировании формулы автоматически пересчитывался, к примеру, только индекс ячейки, а буква оставалась неизменной, мы можем «закрепить» в формуле только букву (или наоборот): =$D1+3. Такой адрес называется смешанным. При копировании формулы будет меняться только индекс в адресе ячейки:

Электронные таблицы. Копирование формул.

Пример 1.

В ячейке C2 записана формула =$E$3+D2. Какой вид приобретет формула, после того как ячейку C2 скопируют в ячейку B1?

1) =$E$3+C1 2) =$D$3+D2 3) =$E$3+E3 4) =$F$4+D2

Решение:

Место расположения формулы меняется с C2 на B1, т.е. формула сдвигается на одну ячейку влево и на одну ячейку вверх (буква «уменьшается» на единицу и индекс уменьшается на единицу). Значит, так же изменятся все относительные адреса, а абсолютные (закрепленные знаком $) останутся неизменными:

=$E$3+С1.

Ответ: 1

Пример 2.

В ячейке В11 электронной таблицы записана формула. Эту формулу скопировали в ячейку А10. В результате значение в ячейке А10 вычисляется по формуле х—Зу, где х — значение в ячейке С22, а у — значение в ячейке D22. Укажите, какая формула могла быть написана в ячейке В11.

1) =C22-3*D22 2) =D$22-3*$D23 3) =C$22-3*D$22 4) =$C22-3*$D22

Решение:

Проанализируем поочередно каждую формулу:

Место расположения формулы меняется с B11 на A10, т.е. буква «уменьшается» на 1 и индекс уменьшается на 1.

Тогда при копировании формулы изменятся следующим образом:

1) =B21-3*C21

2) =C$22-3*$D22

3) =B$22-3*C$22

4) =$C21-3*$D21

Условию задачи соответствует формула 2).

Ответ: 2

Электронные таблицы. Определение значения формулы.

Пример 3.

Дан фрагмент электронной таблицы:

	А	В	С	D
1	1	2	3
2	4	5	6
3	7	8	9

В ячейку D1 введена формула =$А$1*В1+С2, а затем скопирована в ячейку D2. Какое значение в результате появится в ячейке D2?

1) 10 2) 14 3) 16 4) 24

Решение:

Место расположения формулы меняется с D1 на D2, т.е. буква не меняется, а индекс увеличивается на 1.

Значит, формула примет вид: =$А$1*В2+С3. Подставим в формулу числовые значения ячеек:1*5+9=14. Правильный ответ указан под номером 2.

Ответ: 2

Пример 4.

В электронной таблице значение формулы =СРЗНАЧ(A6:C6) равно (-2). Чему равно значение формулы =СУММ(A6:D6), если значение ячейки D6 равно 5?

1) 1 2) -1 3) -3 4) 7

Решение:

По определению среднего значения:

СРЗНАЧ(A6:C6) = СУММ(A6:С6)/3 = -2

Значит, СУММ(A6:С6) = -6

СУММ(A6:D6) = СУММ(A6:С6)+D6 = -6+5 = -1

Ответ: 2

Электронные таблицы и диаграммы.

Пример 5.

Дан фрагмент электронной таблицы в режиме отображения формул.

После выполнения вычислений построили диаграмму по значениям диапазона A1:D1. Укажите полученную диаграмму:

Решение:

Вычислим по формулам значения ячеек A1:D1.

B1 = 3-2 =1

A1 = 2-1 =1

C1 = 1+2 =3

D1 = 1*3 =3

Этим данным соответствует диаграмма 3.

Ответ:3

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №7. Электронные таблицы. Абсолютная и относительная адресация. Графики и диаграммы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.04.2023

Источник