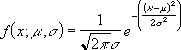Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Синтаксис
НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМ.РАСП описаны ниже.
-
X Обязательный. Значение, для которого строится распределение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если имеется истина, норм. Функция DIST возвращает накопительную функцию распределения; Если этот ложь, возвращается функция плотности вероятности.
Замечания
-
Если число или standard_dev не является числом, то норм. DIST возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, норм. DIST возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если значение «среднее» = 0, «стандартное_откл» = 1 и «интегральная» = ИСТИНА, то функция НОРМ.РАСП возвращает стандартное нормальное распределение, как функция НОРМ.СТ.РАСП.
-
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМ.РАСП(A2;A3;A4;ИСТИНА) |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМ.РАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |
Нужна дополнительная помощь?
Лабораторнаяработа№5 Финансовыефункцииианализ
1. Функции для анализа инвестиций
1.1. Функция ПЗ(ПС)
Функция ПЗ рассчитывает текущую стоимость ряда равных по величине периодических платежей или единовременнойвыплаты. Этафункцияимеетследующийсинтаксис:
=ПЗ(ставка; число периодов; выплата; будущее значение; тип) гдеставка— процентнаяилиучетнаяставка; число периодов — срок вложения; выплата — постоянные периодические вы платы; будущее значение — будущий объем вложениявконцесрокаили0, еслиопущен; тип— число, котороеобозначает, когдадолженпроизводитьсяплатеж: 0 — в концепериода; 1 — вначалепериода.
Предположим, что нам предлагается некой организацией АО ЮЮЮ получать по 1000 рублей ежегодно в течение 5 лет, но при условии, что мы доверим этой замечательной организации 4000 рублей сейчас под 5% годовых. Функциюможнорасписатьтак:
=ПЗ(5%;5;1000)
Вэтой функции не заполнены два аргумента: будущее значение и тип. Будущее значение считается нулем, а тип по умолчанию равен 0, то есть выплаты производятся в конце периода. Возникает вопрос, а как программа узнает, что из пяти аргументов мы взяли только три первых? Да потому, что программа читает аргументы в том порядке, в каком они следуют. Следовательно, в данном случае считаны три первых аргумента, а два последних аргумента не указаны. Эту же формулуможно расписать и по-другому:
=ПЗ(5%;5;1000;;)
Здесьмыпослетретьегоаргументапоставилиточкусзапятой, какэтоипредусмотрено синтаксисом, а четвертый аргумент объявили пустым явнымобразом— поставилитакжеточкусзапятой. Послепятогоаргументаточкасзапятой не предусмотрена, и поэтому аргумент также объявлен пустым (в данном случае действует значение аргумента по умолчанию).
Врезультате расчета мы получим ответ -4 329,48 р. Это означает, что мы можем вложить сумму 4 329,48 р. сейчас, чтобыполучатьпо1000 р. втечение5 лет.
Если АО ЮЮЮ предложит нам другое предложение, например не брать по 1000 р. каждый год, а взять всю суммучерез5 лет. Составимформулурасчета:
=ПЗ(5%;5;;5000)
Вданном случае аргумент выплата не производится, но зато нужен аргумент будущее значение. Поэтому третий аргументзаданпустымявнымобразом, так как если не поставить точку с запятой, то программа будет считать опять с учетом выплаты, а не будущего значения. Ответ будет -3 917,63 р., то есть мы получим даже меньше, чем вкладывали. Поэтомуданноепредложение АО ЮЮЮ мыотклоним.
Рассмотрим еще один вопрос, который будет встречаться практически во всех функциях. При задании ставки мы всевремя задаем число впроцентахипоэтомууказываем символ процента(%). Нопри желанииможноуказывать ставку
ив числовом формате. Для этого нужно ставку в процентах разделить на 100, а символ процента опустить. Итоги, рассчитанные обоимиспособами, неотличаютсядруготдруга. Например, последнююформулуможнопереписатьтак:
=ПЗ(0,05;5;;5000)
1.2. Функция НПЗ (ЧПС)
Возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных и нормы амортизации. Чистый текущий объем вклада — это сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения). Данная функция имеет следующий синтаксис:
=НПЗ(ставка; значение1; значение2; …) Ставка— этоучетнаяставказаодинпериод.
Значение1, значение2,… — этоот1 до29 аргументов, представляющихрасходыидоходы.
Значение1, значение2, … должны быть равномерно распределены по времени и осуществляться в конце каждого периода.
НПЗ использует порядок аргументов значение1, значение2, … для определенияпорядкапоступленийиплатежей. Поэтомунеобходимоубедиться в том, что платежи и поступления введены в правильном порядке.
Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми

представлениями чисел, учитываются. Аргументы, которые являются значениями различных ошибок или текстами или которые не могут быть преобразованы в числа, игнорируются.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, тексты или значения ошибок в массиве или ссылке игнорируются.
Считается, что инвестиция, значение которой вычисляет функция НПЗ, начинается за один период до даты денежного взноса значение 1 и заканчивается с последним денежным взносом в списке. Вычисления функции НПЗ базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции НПЗ, но не включать в список аргументов. Для получения более подробной информации смотрите примеры ниже.
Если n—это количество денежных взносов в списке значений, то формула для функции НПЗ имеет вид:
НПЗ аналогична функции ПЗ (текущее значение). Основное различие между функциями ПЗ и НПЗ заключается в том, что ПЗ допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции НПЗ денежные взносы в функции ПЗ должны быть постоянны на весь период инвестиции. Для получения информации о функциях платежей по ссуде и финансовых функциях смотрите ПЗ.
НПЗ также связана с функцией ВНДОХ (внутренняя скорость оборота). ВНДОХ — это скорость оборота, для которойНПЗравняетсянулю: =НПЗ(ВНДОХ(…); …)=0.
Предположим, что нам предоставляется возможность получать в течение четырех лет каждый год доход по 100 000 рублей, но при условии немедленного разового платежа в размере 300 000 рублей. Ставка равна 10%. Функция будетиметьвид:
=НПЗ( 10%; 100000; 100000; 100000; 100000;)-300000
В ответ получим 16 986,54 р. Это означает, что это предложение выгодно, так как даст нам небольшую прибыль. Этаприбыльбудетдотехпор, покаставканедостигнетвеличины12,59%.
1.3. Функция БЗ
Функция БЗ возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентнойставки. Синтаксис этойфункцииследующий:
=БЗ(ставка; число периодов; выплата; текущее значение; тип) гдеставка— процентнаяилиучетнаяставка; число периодов — срок вложения; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — вначалепериода.
Составим пример. Предположим, что человек, поступая на работу после окончания института, открыл счет в банке, предполагая вносить каждый год по 3000 рублей под 10% годовых. Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды), представляются положительными числами. Рассчитаем, сколько денег будет на счете через 38 лет:
=БЗ(10%;38;-3000;;1)
Нам приходится учитывать все пять аргументов, так как платеж необходимо производить в начале года. В ответе будет 1 201 343,33 р.
1.4. ФункцияППЛАТ(ПЛТ)
Эта функция возвращает величину выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки. Синтаксис этой функции следующий:
=ППЛАТ(ставка; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; число периодов — срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды),
представляются положительными числами.
Для примера рассмотрим следующую ситуацию: человек берет в банке ссуду на 15 лет в размере 1 000 000 рублей под 12 процентов годовых. Рассчитаем, какую сумму человек должен выплачивать ежемесячно:
=ППЛАТ(1%;180;1000000)
Рассмотрим записанное нами значение аргументов: в месяц человек должен выплачивать 1/12 часть ставки, то есть 12%/12 месяцев;. число платежных месяцев равно 15 лет* 12 месяцев в году. Ответ получится такой: человек должен ежемесячно платить -12 001,68 р.. Знак минус (-) означает, что человек должен платить, а не получать.
1.5.Функция ПЛПРОЦ (ПРПЛТ)
Данная функция возвращает платежи по процентам за данный период на основе периодических постоянных выплат и постоянной процентной ставке. Синтаксис этой функции следующий:
=ПЛПРОЦ(ставка; период; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; период — номер периодической выплаты; число периодов
— срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Все аргументы, означающие деньги, которые человек платит (например, депозитные вклады), представляются отрицательными числами; деньги, которые человек получает (например, дивиденды), представляются положительными числами.
Для примера рассмотрим следующую ситуацию: человек берет в банке ссуду на 15 лет в размере 1 000 000 рублей под 12 процентов годовых. В месяц человек должен выплачивать 1/12 часть ставки, то есть 12%/1 2 меся цев; число платежных месяцев равно 15 лет * 12 месяцев в году. Вопрос: какую сумму человек будет платить по процентам в первый и последний платежные месяцы?
=ПЛПРОЦ1 %; 1; 180; 1000000) =ПЛПРОЦ(1%;180;180; 1000000)
Ответ: в первый платежный месяц человек будет платить 10 000 рублей, а в последний — всего 118,83 рубля.
1.6. Функция ОСНПЛАТ (ОСПЛТ)
Функция ОСНПЛАТ возвращает величину выплаты на данный период на основе периодических постоянных платежей и постоянной процентной ставки. Синтаксис этой функции следующий:
=ОСНПЛАТ(ставка; период; число периодов; текущее значение; будущее значение; тип)
где ставка — процентная или учетная ставка; период — номер периодической выплаты; число периодов
— срок вложения; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Составим пример на основе данных, заданных в двух предыдущих разделах. Рассчитаем основные платежи в первый и последний месяцы:
=ОСНПЛАТ(1%;1;180; 1000000) =ОСНПЛАТ(1 %; 180; 180; 1000000)
Ответ: в первый месяц основой платеж будет 2 001,68 рубля, а в последний11 882,85 рубля.
1.7. Функция КПЕР
Функция КПЕР возвращает общее количество периодов выплаты для данного вклада на основе периодических постоянных выплат и постоянной процентной ставки. Синтаксис этой функции следующий:
=КПЕР(ставка; выплата; текущее значение; будущее значение; тип) где ставка — процентная или учетная ставка; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода.
Воспользуемся условиями предыдущих разделов — определим число периодов, которое необходимо для погашения ссуды:
=КПЕР( 1 %;-12000; 1000000)
Ответ: -180,07 месяца. Эта неточность в 0,07 месяца произошла потому, что в предыдущих разделах мы определили, что в месяц нужно платить -12 001,68 рубля. Если нашу формулу немного подправить и сделать так:
=КПЕР(1%;-12001,68; 1000000)
то ответ будет 180 месяцев. Таким образом, мы определили, что путем многократной проверки мы выходим на одни и те же числа при использовании различных функций этой группы.
Если аргумент выплата мал для погашения ссуды при заданной процентной ставке, то функция возвращает сообщение об ошибке. Это означает, что данный кредит не будет выплачен никогда и необходимо или увеличить выплаты, или уменьшить процент ставки.
2. Функции для вычисления скорости оборота 2.1. Функция НОРМА (СТАВКА)
Функция НОРМА возвращает процентную ставку за один период при выплате ренты. Функция НОРМА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность определения ставки превышает 0,0000001, то функция НОРМА возвращает значение ошибки #ЧИСЛО! Синтаксис этой функции следующий:
=НОРМА( число периодов; выплата; текущее значение; будущее значение; тип; прогноз)
где число периодов — срок вложения; выплата — постоянные периодические выплаты; текущее значение — текущий объем вложений или 0, если опущен; будущее значение — будущий объем вложения в конце срока или 0, если опущен; тип — число, которое обозначает, когда должен производиться платеж: 0 — в конце периода; 1 — в начале периода; прогноз — предполагаемая величина нормы. Если значение прогноза опущено, то оно полагается равным по умолчанию 10%. Если функция НОРМА не сходится, следует попытаться использовать различные значения прогноза. Обычнофункция НОРМА сходится, если прогноз имеет значение между 0
и 1.
Предположим, что мы должны получить пять ежегодных выплат по 15 000 рублейприсуммевложения50000 рублей. Формулабудетиметьследующийвид:
=НОРМА(5;15000;-50000)
Функциявозвращает скоростьоборота, котораяравна 15%.
2.2. Функция ВНДОХ (ВСД)
Функция ВНДОХ возвращает внутреннюю скорость оборота для ряда последовательных операций с наличными, представленными числовыми значениями. Объемы операций не обязаны быть регулярными, как в случае ренты. Внутренняя скорость оборота — это процентная ставка дохода, полученного от инвестиции, состоящая из выплат (отрицательные значения) и поступлений (положительные значения), которые происходят в регулярные периоды времени. Синтаксисэтойфункцииследующий:
=ВНДОХ(значения; прогноз)
где значения должны включать по крайней мере одно положительное значение и одно отрицательное значение для того, чтобы можно было вычислить внутреннюю скорость оборота. ВНДОХ использует порядок значений для интерпретации порядка денежных выплат или поступлений. Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются. Прогноз—это величина, о которой предполагается, что она близка к результату ВНДОХ. Microsoft Excel использует метод итераций для вычисления ВНДОХ. Начиная со значения прогноз, функция ВНДОХ выполняет циклические вычисления, пока не получит результат с точностью 0,00001 процента. Если функция ВНДОХ не может получить результат после 20 попыток, то возвращается значение ошибки #ЧИСЛО! В большинстве случаев нет необходимости задавать прогноз для вычислений с помощью функции ВНДОХ. Если прогноз опущен, то он полагается равным 0,1 (10 процентов). Если ВНДОХ выдает значение ошибки #ЧИСЛО! или если результат далек от ожидаемого, необходимо выполнить вычисленияещеразсдругимзначением аргумента прогноз.
Допустим, ваши вложения в проект составляют 50 000 рублей. Предполагается, что доходы в течение трех лет составят 22 000, 24 000, 26 000 рублей. Запишите эти значения в ячейки с Al no A4. Следующая формула вычисляет внутреннюю скоростьоборота инвестиции после трех:
=ВНДОХ(А1:А4)
Ответ— внутренняяскоростьоборотасоставляет20%.
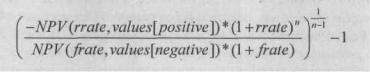
2.3. ФункцияМВСД
ФункцияМВСДвозвращаетмодифицированнуювнутреннююскоростьоборота средств для ряда последовательных периодических операций с наличными. Функция МВСД учитывает как стоимость инвестиции, так и доход, получаемый отреинвестирования. Синтаксисэтойфункцииследующий:
=МВСД(значения; финансовая_ставка; ставка_реинвестирования) Значения — это массив или ссылка на ячейки, содержащие числовые величины. Эти числа представляют ряд денежных выплат (отрицательные значения) и поступлений (положительные значения), происходящие в регулярные периоды времени. Аргумент значения должен содержать по крайней мере одно положительное и одно отрицательное значение для того, чтобы можно было вычислить модифицированную внутреннюю скорость оборота. В противном случае функция МВСД возвращает значение ошибки #ДЕЛ/0! Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются; финансовая_ставка — это норма прибыли, выплачиваемой за деньги, находящиеся в наличном обороте; ставка_реинвестирования — это норма прибыли, получаемой за деньги, находящиеся в наличном обороте при реинвестировании.
МВСД использует порядок расположения чисел в аргументе значения для определения порядка выплат и поступлений. Убедитесь, что значения выплат и поступлений введены в нужной последовательности и с правильными знаками (положительные значения ДЛЯ получаемых денег и отрицательные значения для выплачиваемых). Если n — это количество чисел в аргументе значения, f — это финансовая_ставка, а r — это ставка_реинвестирования, то формула длявычисления функции МВСД будет иметь вид:
Продолжим пример, условия которого заданы в предыдущем разделе. Модифицированная внутренняя скорость оборотазатригодавычисляетсяследующимобразом:
=МВСД(А1:А4;12%;10%)
Ответ: 16%.
3. Функции для вычисления амортизации
3.1. ФункцияAMP (АПЛ)
Функция AMP возвращает величину непосредственной амортизации имущества за один период. Синтаксис этой функции следующий:
=АМР(стоимость; остаток; время_эксплуатации)
где стоимость — первоначальная стоимость имущества; остаток — остаточная стоимость после полной амортизации имущества; время_эксплуатации — количество периодов, за которые имущество амортизируется.
Возьмем следующий пример: предположим, что необходимо рассчитать амортизацию станка с начальной стоимостью 25 000 рублей, время эксплуатации которого 10лет, с остаточной стоимостью 700 рублей. Тогда формула будетследующей:
=АМР(25000;700;10)
Врезультатерасчетабудетопределенаамортизациявразмере2430 рублей.
3.2. Функция ДОБ(ФУО) иДЦОБ (ПУО)
Функция ДОБ возвращает амортизацию имущества на заданный период, используя метод постоянного учета амортизации. Синтаксисэтойфункцииследующий:
=ДОБ(нач_стоимость; остстоимость; времяэксплуатации; период; месяц)
где нач_стоимость — это начальная стоимость имущества; ост_стоимость — это стоимость в конце периода амортизации (иногданазывается остаточнойстоимостью имущества); время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это период, для которого требуется вычислить амортизацию; период должен быть измерен в тех же единицах, что и время_эксплуатации; месяц — это количество месяцев в первом году. Если аргумент месяц опущен, то предполагается, чтоонравен12.
Методпостоянного учетаамортизации вычисляет амортизацию используяфиксированнуюпроцентнуюставку. Функция ДДОБ очень похожа на функцию ДОБ и возвращает величину амортизации имущества для указанного периода, используя метод двукратного учета амортизации или иной явно указанный метод. Синтаксис этой функции
следующий:
=ДДОБ(нач_стоимость; ост_стоимость; время_эксплуатации; период; коэффициент)
где нач_стоимость — это начальная стоимость имущества; ост_стоимость — это остаточная стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества); время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации; коэффициент —это норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, топредполагается, чтоонравен2 (методдвукратногоучетаамортизации).
Всепятьаргументовдолжныбытьположительными числами.
Метод двукратного учета амортизации предполагает ускоренную амортизацию имущества. При этом амортизациямаксимальна в первый период иснижаетсявпоследующиепериоды.
Предположим, что стоимость станка 25 000 рублей, время эксплуатации 10 лет, ликвидная стоимость 700 рублей. Составимформулу:
=ДЦОБ(25000;700;10;1)
Амортизация методом двукратного учета за первый год составит 5000 рублей.
3.3. Функция ПДОБ (ПУО)
Функция ПДОБ возвращает значение амортизации имущества за данный период, включая конкретные периоды, используя метод двойного процента со снижающегося остатка или иной явно указанный метод. ПДОБ представляет методснижающегосяостатка. Синтаксисэтойфункцииследующий:
= ПДОБ(стоимость; остаток; период; начальный_период; конечный_период; коэффициент; без_переключения)
где стоимость — это начальная стоимость имущества; остаток — это остаточная стоимость в конце амортизации (иногда называется ликвидной стоимостью имущества); период — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); начальный_период — это начальный период, для которого вычисляется амортизация, начальный_период должен быть задан в тех же единицах, что и период; конечный_период — это конечный период, для которого вычисляется амортизация, конечный_период должен быть заданвтехжеединицах, чтоипериод.
Коэффициент — это норма снижения балансовой стоимости (амортизации). Если коэффициент опущен, то он полагается равным 2 (метод удвоенного процента со снижающегося остатка). Коэффициент необходимо изменить, если метод удвоенного процента со снижающегося остатка использовать не нужно. Описание метода удвоенного процента со снижающегося остатка смотрите в ДДОБ; без_переключения —это логическое значение, определяющее, следует ли использовать прямую амортизацию в том случае, когда амортизация превышает вычисленную величину амортизации.
Если аргумент без_переключения имеет значение ИСТИНА, то Microsoft Excel не переключается на метод равномерного начисления амортизации, даже если амортизация больше вычисленного снижающегося остатка. Если аргументбез_переключенияимеетзначениеЛОЖЬилиопущен, тоMicrosoft Excel переключаетсянаметодравномерного зачисления амортизации, если амортизация больше вычисленного снижающегося остатка. Все аргументы, за исключением аргументабез_переключения, должныбытьположительнымичислами.
Предположим, чтошвейнаямастерскаяприобрелатришвейныхмашины2 январянаобщуюсумму 25 000 рублей и ликвидной стоимостью через семь лет (7 лет * 4 квартала ежегодно = 28 кварталов) в 500 рублей. Таким образом в первый год эксплуатации все четыре квартала швейных машины работают. Чтобы определить амортизацию имущества заследующийгод(спятогоповосьмойкварталы), создадимформулу:
=ПДОБ(25000;500;28;4;8)
Ответ: амортизация за период с пятого по восьмой кварталы составит 4 768,10 рублей.
3.4. Функция АМГД (АСЧ)
Функция АМГД возвращает годовую амортизацию имущества для указанного периода. Синтаксис этой функции следующий:
АМГД(стоимость; остаточная_стоимость; время_эксплуатации; период)
где стоимость — это начальная стоимость имущества; остаточная_стоимость — это остаточная стоимость в конце периода амортизации; время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации); период — это интервал времени (должен быть измерен в
техжеединицах, чтоивремяполной амортизации).
Если взять условия примера из предыдущего раздела и рассчитать амортизацию за первый год эксплуатации, то можнонаписатьследующуюформулу:
=АМГД(25000;500;7;1)
Сумма амортизации за первый год эксплуатации будет составлять 6 125,00 рублей. Затретийгодсуммаамортизациидолжнабытьрассчитанапотакойформуле: =АМГД(25000;500;7;3)
Ответ: 4 375,00 рублей.
Заседьмойгодамортизация будетсчитатьсяпотакойформуле: =АМГД(25000;500;7;7) ибудетсоставлять875 рублей.
Суммаамортизацииплавно снижается, так какостаточная стоимость машинуменьшается.
.
Purpose
Get values and areas for the normal distribution
Return value
Output of the normal PDF and CDF
Usage notes
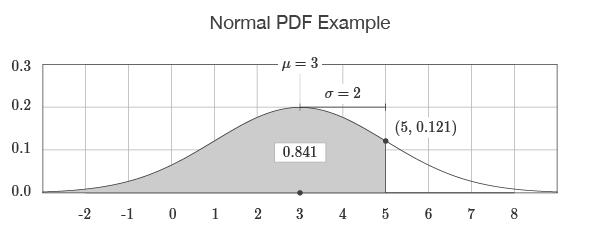
The NORM.DIST function returns values for the normal probability density function (PDF) and the normal cumulative distribution function (CDF). For example, NORM.DIST(5,3,2,TRUE) returns the output 0.841 which corresponds to the area to the left of 5 under the bell-shaped curve described by a mean of 3 and a standard deviation of 2. If the cumulative flag is set to FALSE, as in NORM.DIST(5,3,2,FALSE), the output is 0.121 which corresponds to the point on the curve at 5.
=NORM.DIST(5,3,2,TRUE)=0.841
=NORM.DIST(5,3,2,FALSE)=0.121
The output of the function is visualized by drawing the bell-shaped curve defined by the input to the function. If the cumulative flag is set to TRUE, the return value is equal to the area to the left of the input. If the cumulative flag is set to FALSE, the return value is equal to the value on the curve.
Explanation
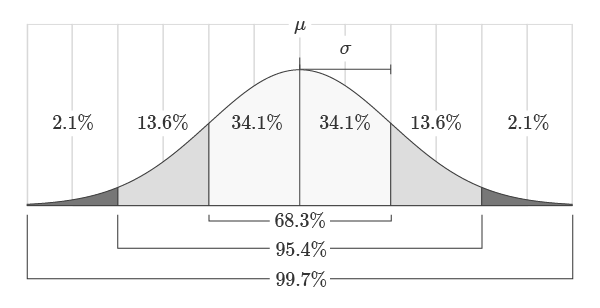
The normal PDF is a bell-shaped probability density function described by two values: the mean and standard deviation. Themean represents the center or «balancing point» of the distribution. The standard deviation represents how spread out around the distribution is around the mean. The area under the normal distribution is always equal to 1 and is proportional to the standard deviation as shown in the figure below. For example, 68.3% of the area will always lie within one standard deviation of the mean.
Probability density functions model problems over continuous ranges. The area under the function represents the probability of an event occurring in that range. For example, the probability of a student scoring exactly 93.41% on a test is very unlikely. Instead, it is reasonable to compute the probability of the student scoring between 90% and 95% on the test. Assuming that the test scores are normally distributed, the probability can be calculated using the output of the cumulative distribution function as shown in the formula below.
=NORM.DIST(95,μ,σ,TRUE)-NORM.DIST(90,μ,σ,TRUE)
In this example, if we substitute a mean of 80 in for μ and a standard deviation of 10 in for σ, then the probability of the student scoring between 90 and 95 out of 100 is 9.18%.
=NORM.DIST(95,80,10,TRUE)-NORM.DIST(90,80,10,TRUE)=0.0918
Images courtesy of wumbo.net.
Вычисление доверительного интервала в Microsoft Excel
Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.
Процедура вычисления
Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.
В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.
Способ 1: функция ДОВЕРИТ.НОРМ
Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.
Его синтаксис выглядит следующим образом:
«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:
«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.
«Размер» — аргумент, определяющий величину выборки.
Все аргументы данного оператора являются обязательными.
Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:
Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.
Граница доверительного интервала определяется при помощи формулы следующего вида:
Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.
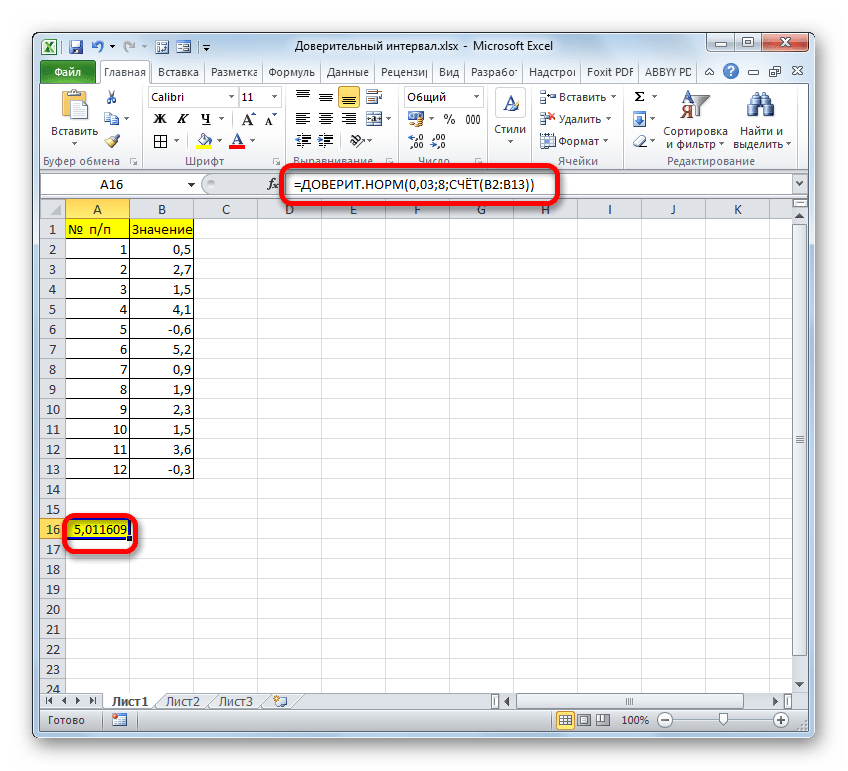
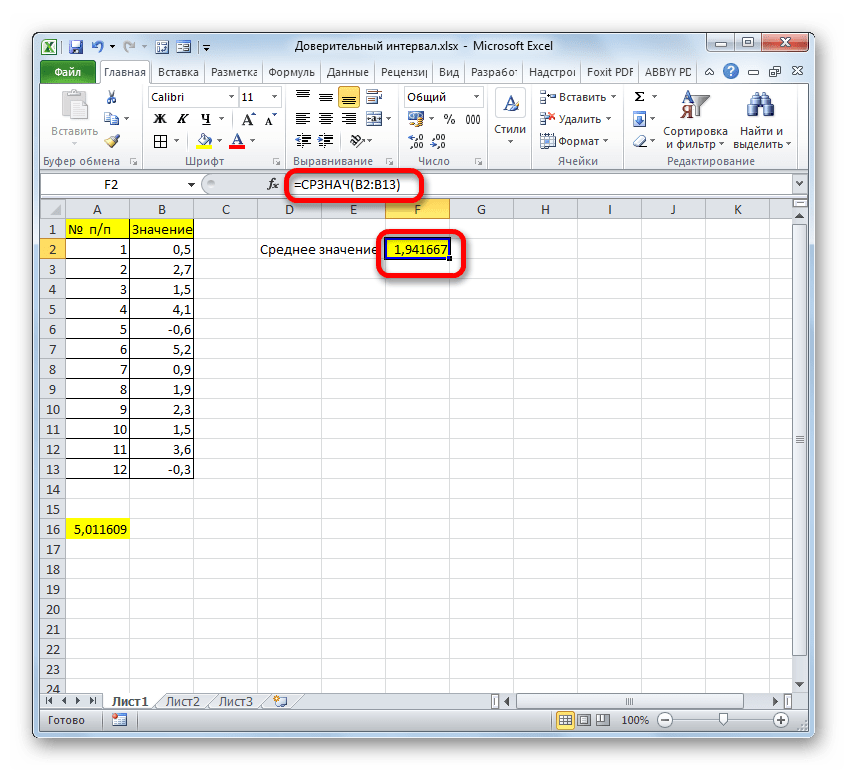
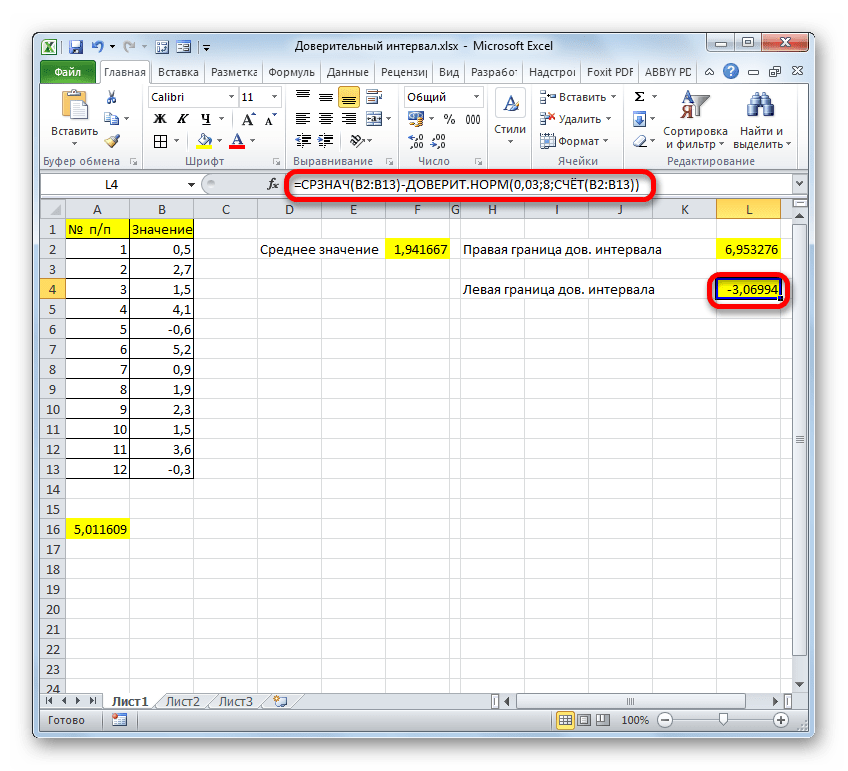
Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.
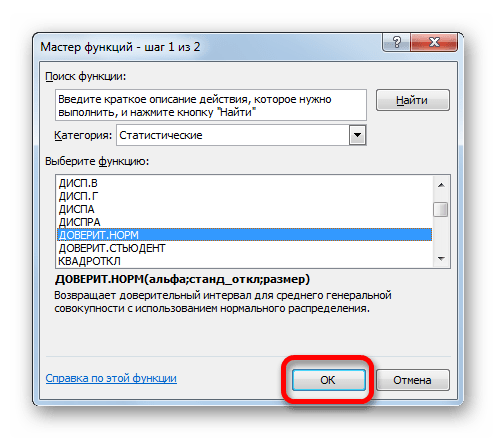
- Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».
Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:
То есть, подставив значение, получаем:
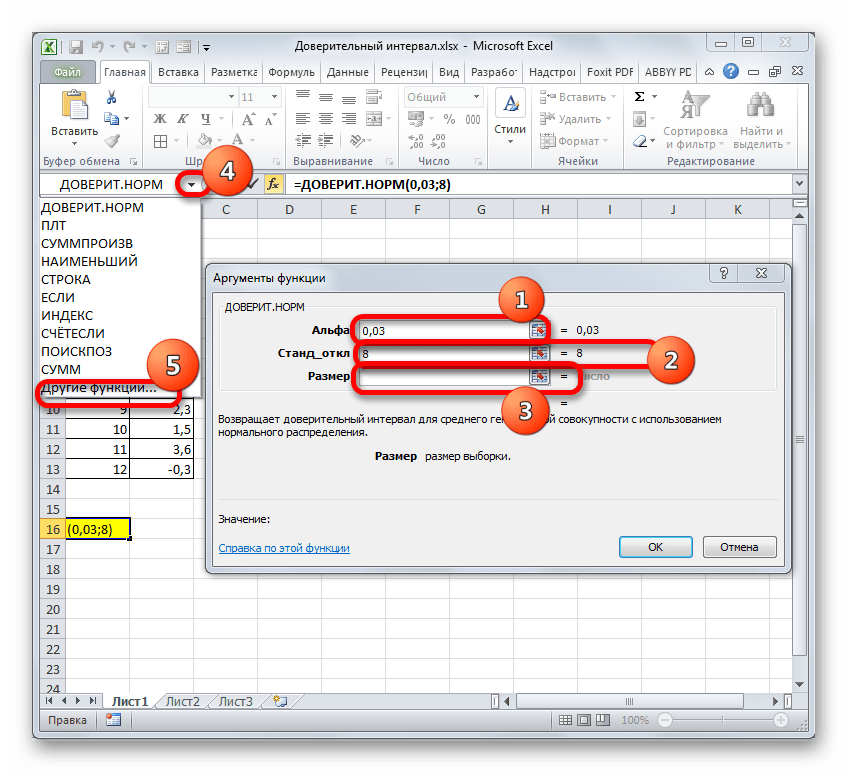
Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.
Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.
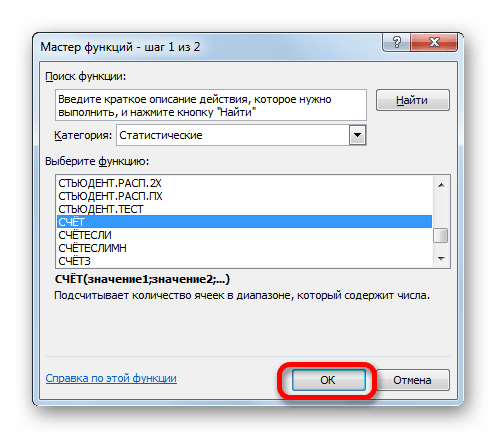
В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.
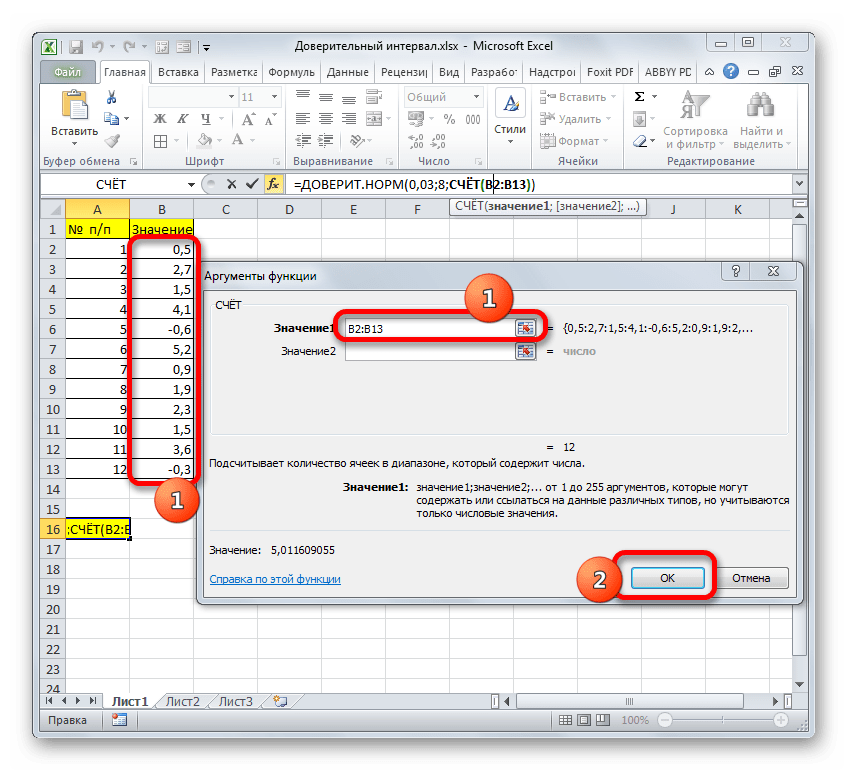
Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.
Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:
Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.
Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
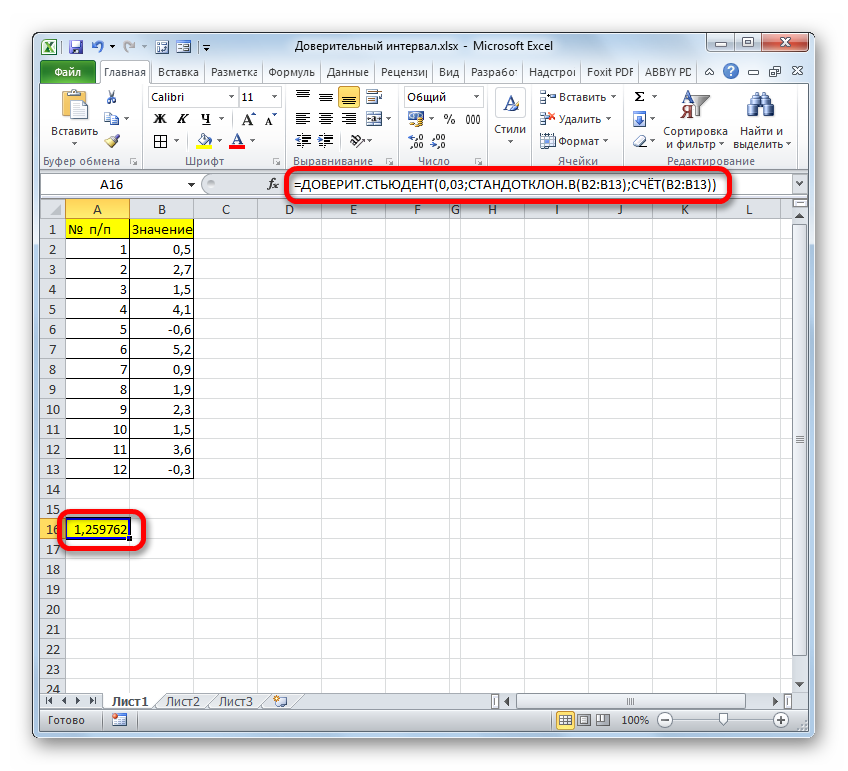
Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:
Как видим, наименования операторов и в этом случае остались неизменными.
Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.
- Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».
В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.
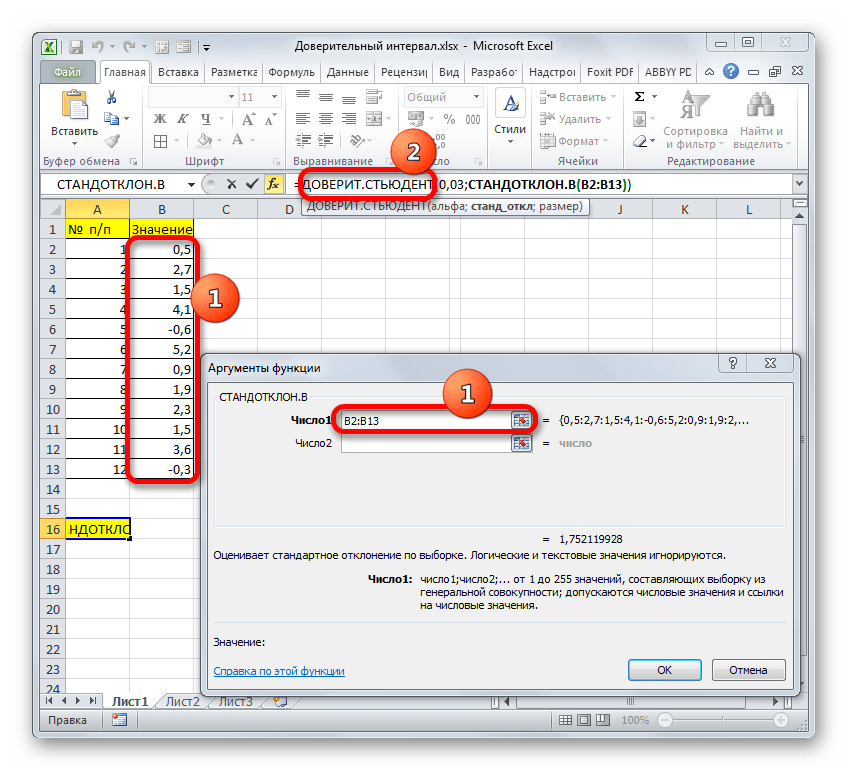
Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.
Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.


Функция СТАНДАРТИЗАЦИЯ в Excel возвращает нормализованное значение (z-оценку) на основе среднего значения и стандартного отклонения.
Возвращаемое значение
Синтаксис
Аргументы
- x — значение для нормализации.
- среднее — Среднее арифметическое распределения.
- standard_dev — стандартное отклонение распределения.
Версия
Примечания по использованию
Функция СТАНДАРТИЗАЦИЯ в Excel возвращает нормализованное значение (z-оценку) на основе среднего значения и стандартного отклонения. Чтобы использовать функцию СТАНДАРТИЗАЦИЯ, рассчитайте среднее значение с помощью функции СРЕДНЕЕ, а стандартное отклонение — с помощью функции СТАНДАРТ.П (см. Ниже).
В показанном примере формула в D5:
О z-показателях / стандартных показателях
Z-оценка или стандартная оценка — это способ стандартизации оценок по той же шкале путем деления отклонения оценки на стандартное отклонение в наборе данных. Результатом является стандартная оценка или z-оценка. Он измеряет количество стандартных отклонений данной точки данных от среднего.
Z-оценка может быть отрицательной или положительной. Отрицательный z-показатель указывает на значение меньше среднего, а положительный z-показатель указывает на значение, превышающее среднее. Среднее значение каждого z-показателя для набора данных равно нулю.
Чтобы вычислить z-оценку, необходимо вычислить среднее значение и стандартное отклонение. Формулы в G4 и G5, соответственно:
Где «точки» — именованный диапазон C5: C12.
Если вы хотите узнать больше о z-показателях и статистическом анализе в Excel, я рекомендую книгу Джозефа Шмуллера «Статистический анализ в Excel для чайников».
Расчет доверительного интервала в Excel
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
- 1-«Альфа» . Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.
- (100-«Альфа»)/100 . Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение: (100-95)/100 . Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05).
- в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
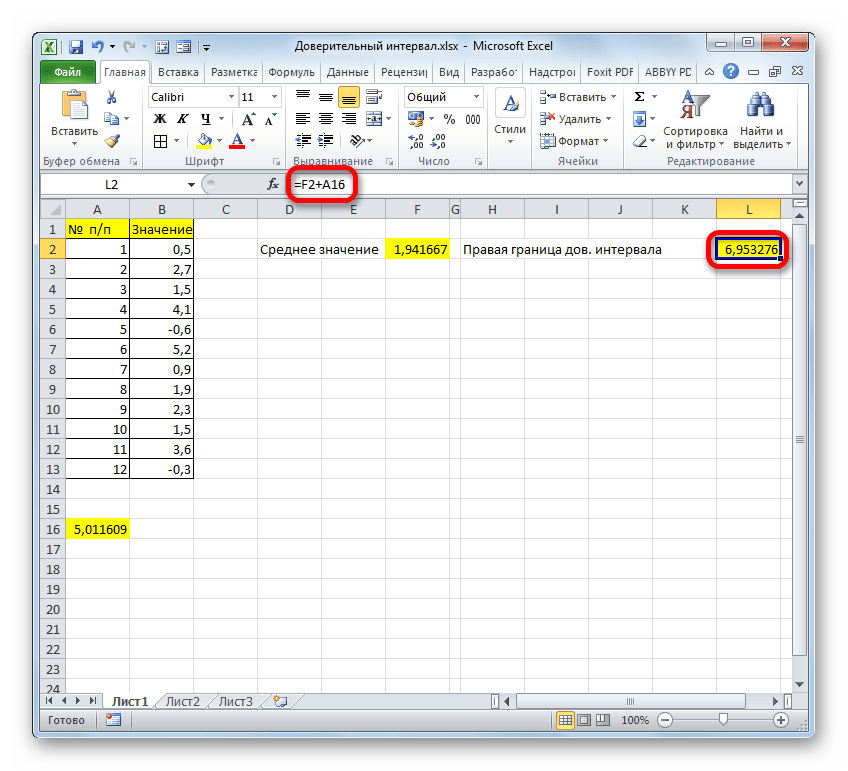
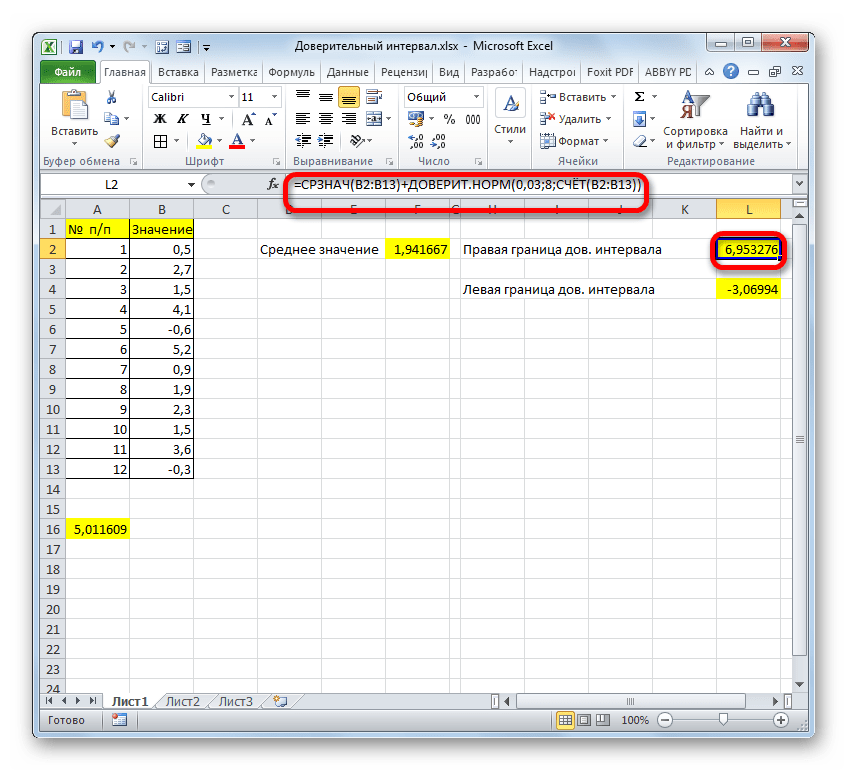
- Для определения правой границы ДИ общая формула будет выглядеть так:
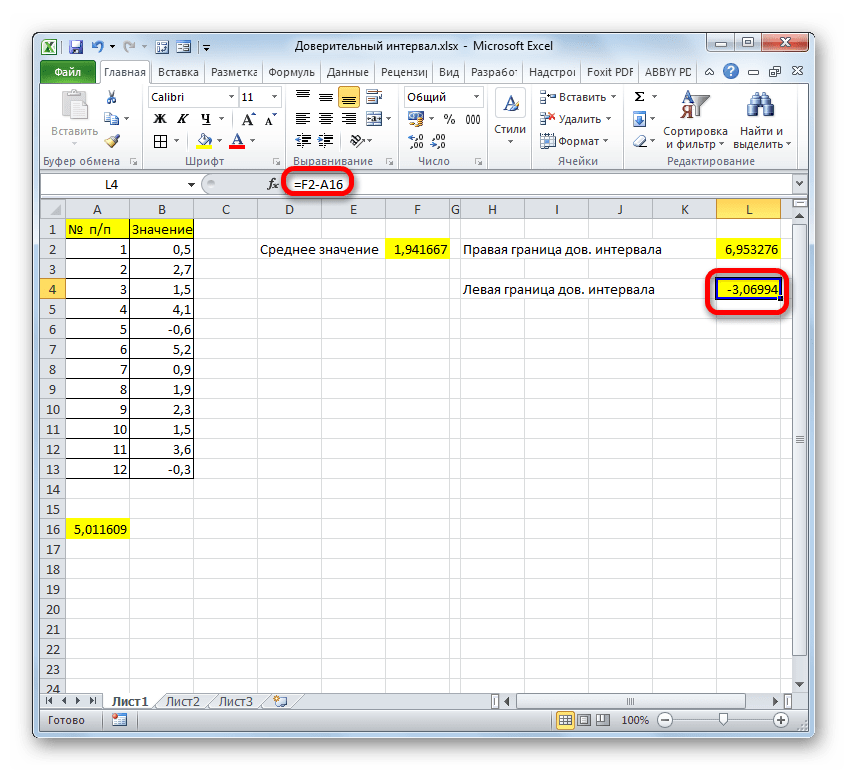
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)) . - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)) .
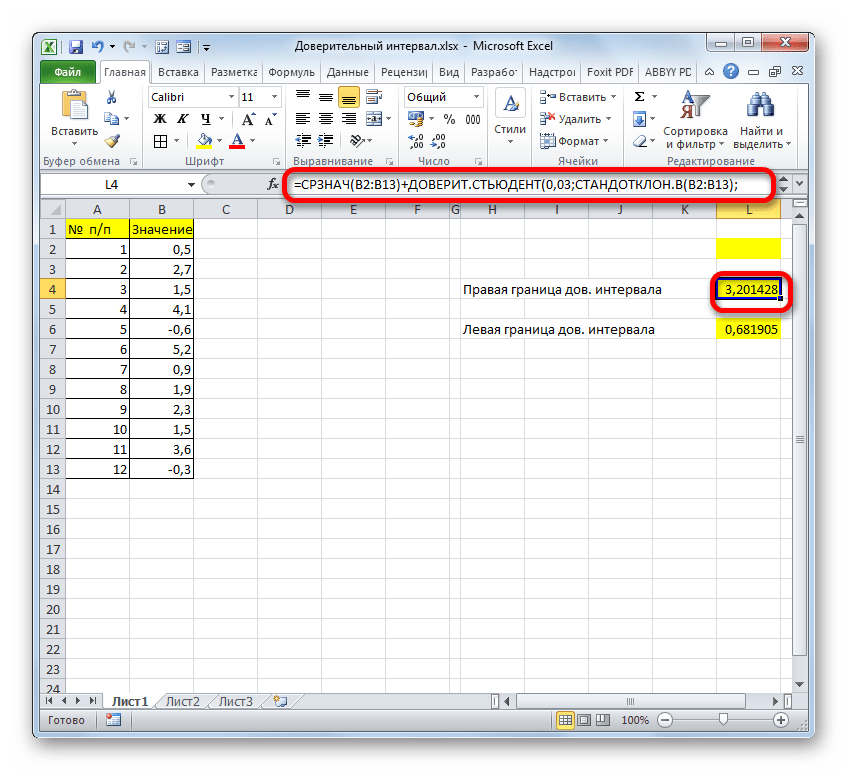
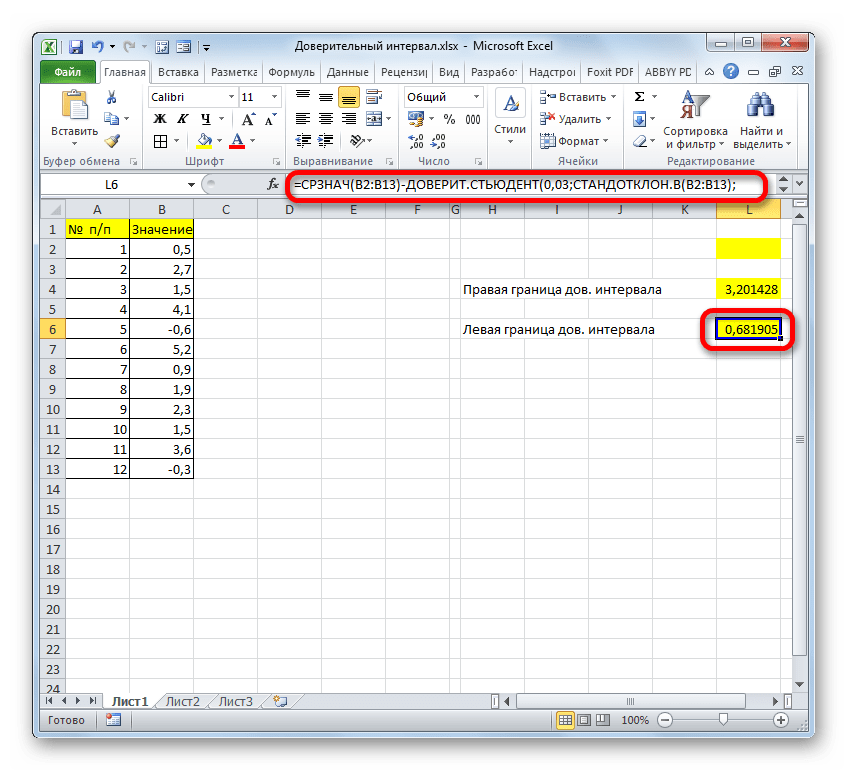
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
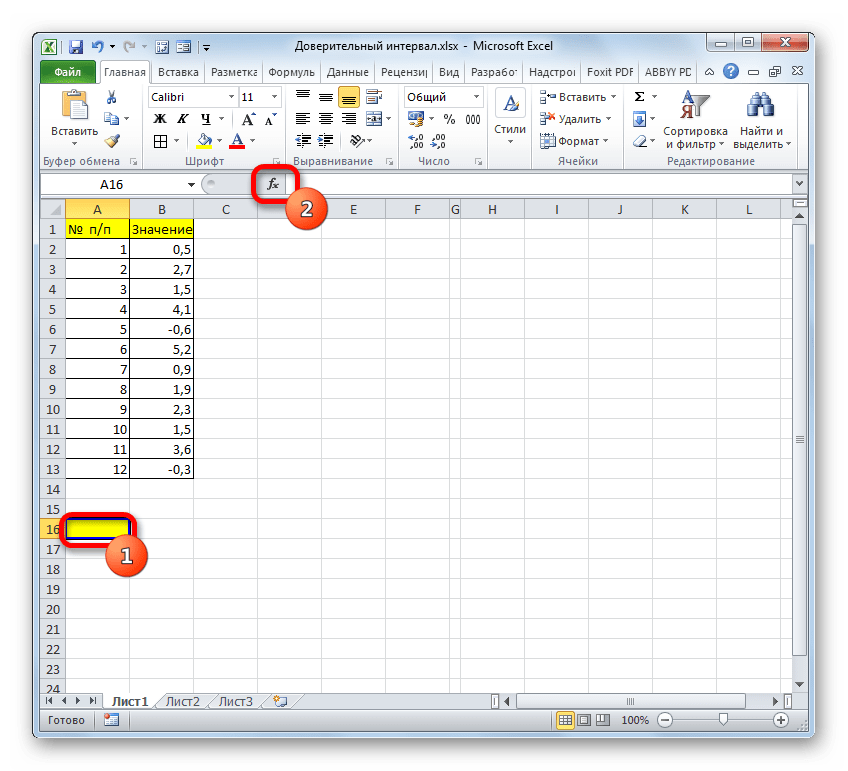
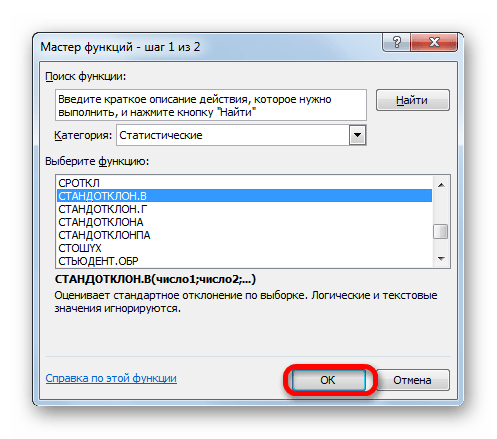
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
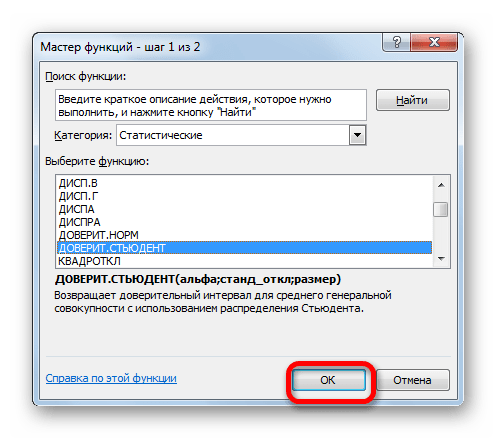
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
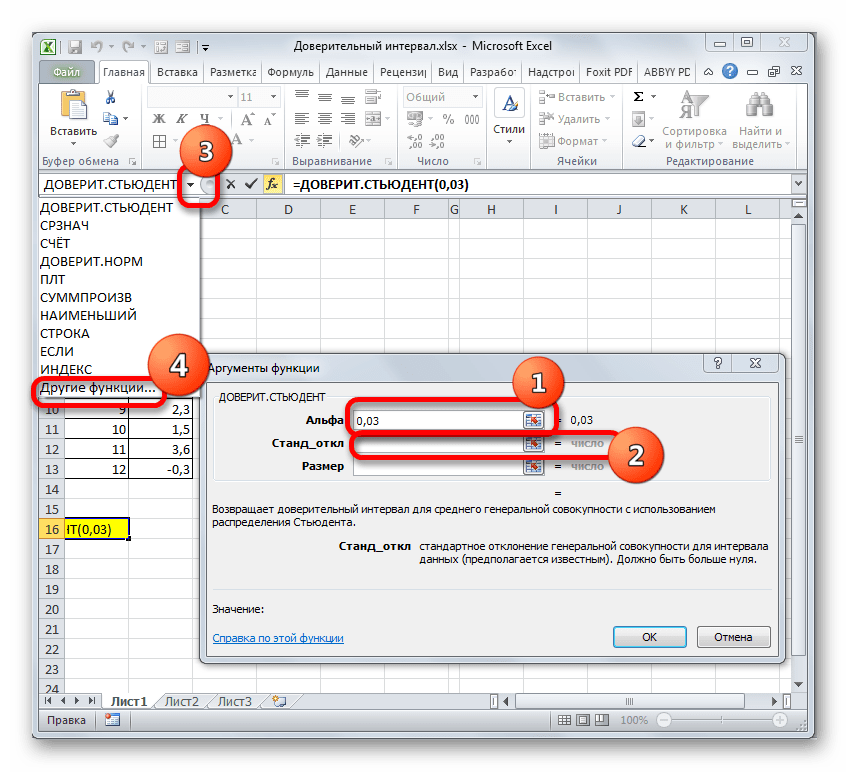
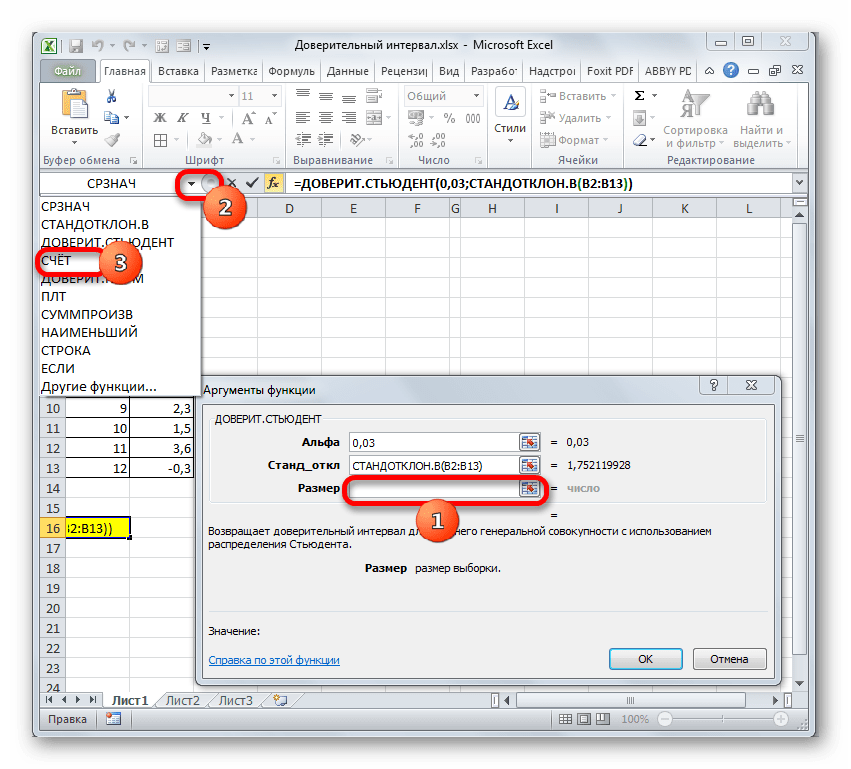
- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
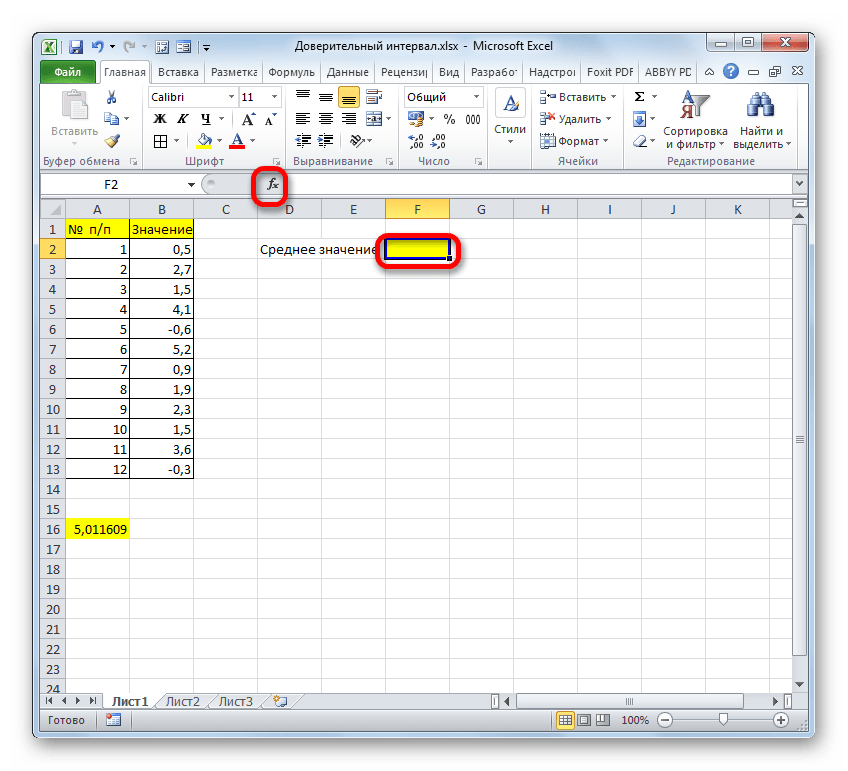
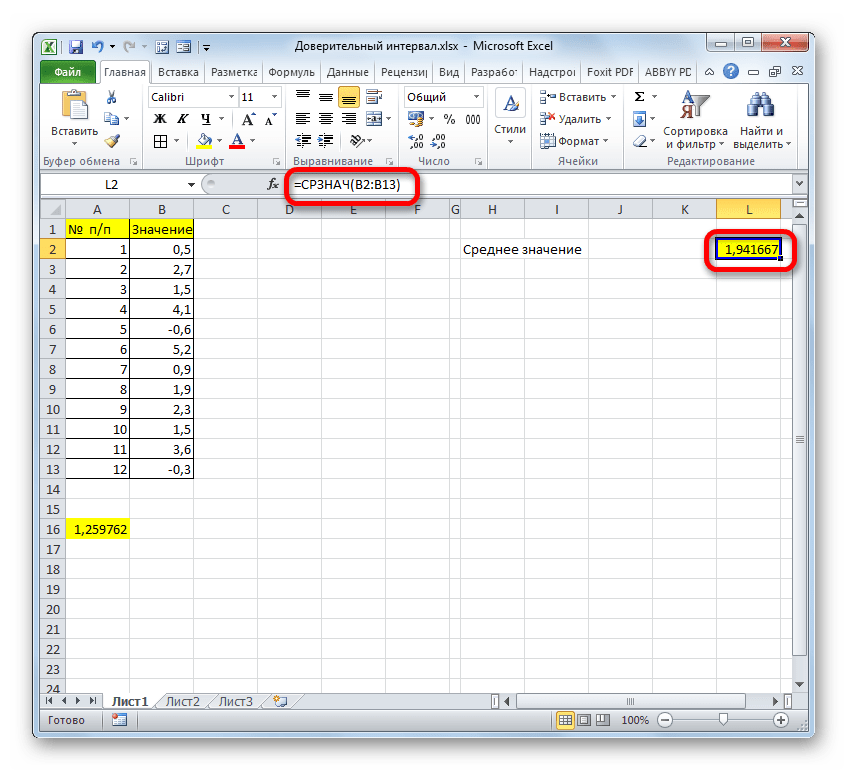
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
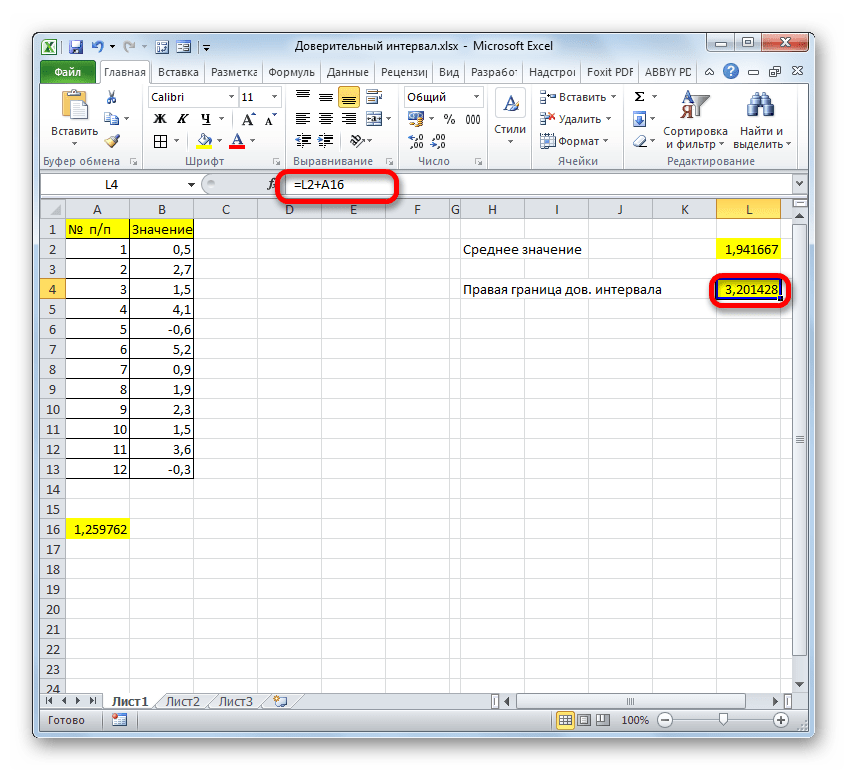
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
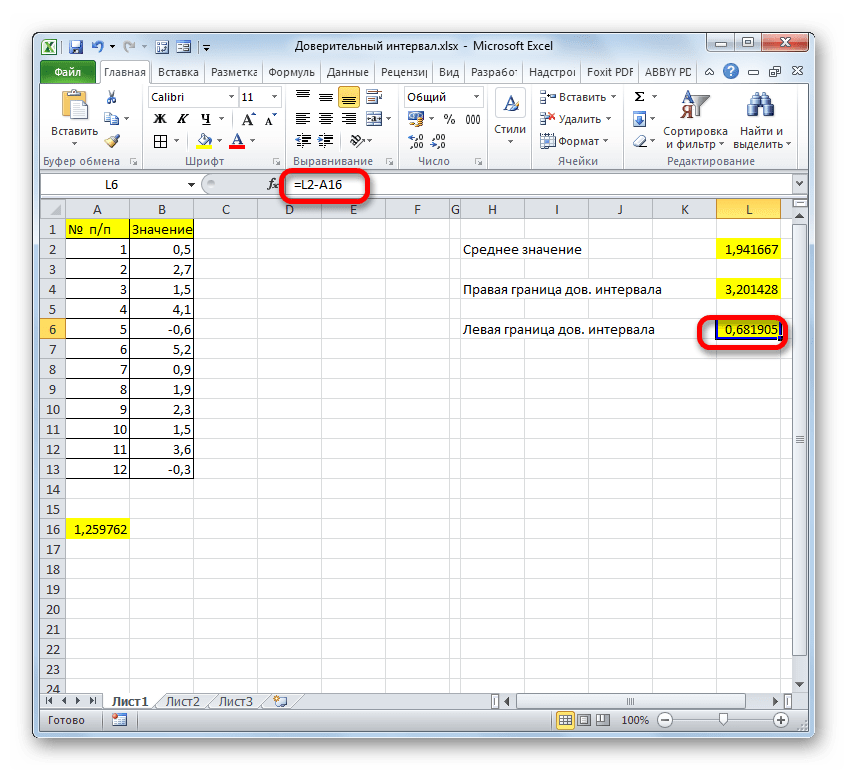
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Содержание
- Вычисление доверительного интервала
- Метод 1: оператор ДОВЕРИТ.НОРМ
- Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
- Заключение
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.(100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
- “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
- “Размер” – объем выборки данных.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
=ДОВЕРИТ(Альфа;Станд_откл;Размер)
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
X+(-)ДОВЕРИТ.НОРМ
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
- Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.
- В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.
- Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
(100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05). - в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
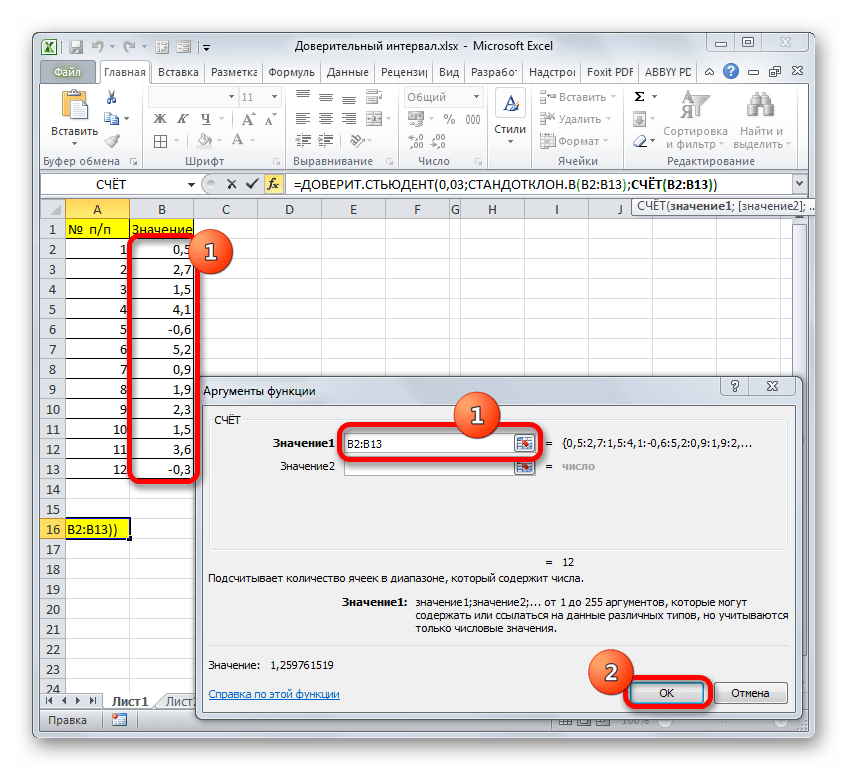
- Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.
- В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.
- На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
Формула функции СЧЕТ пишется так:=СЧЁТ(Значение1;Значение2;...).
Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK. - В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.
- Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
Формула оператора пишется так:=СРЗНАЧ(число1;число2;...).
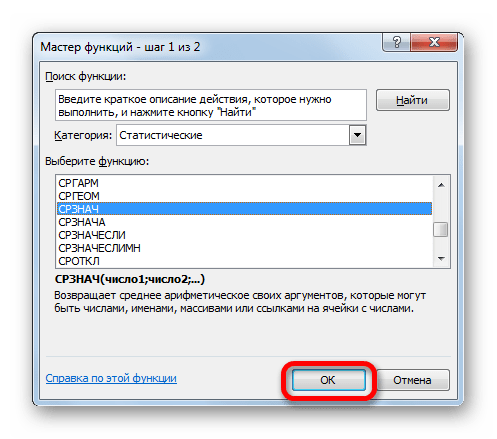
Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”. - В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.
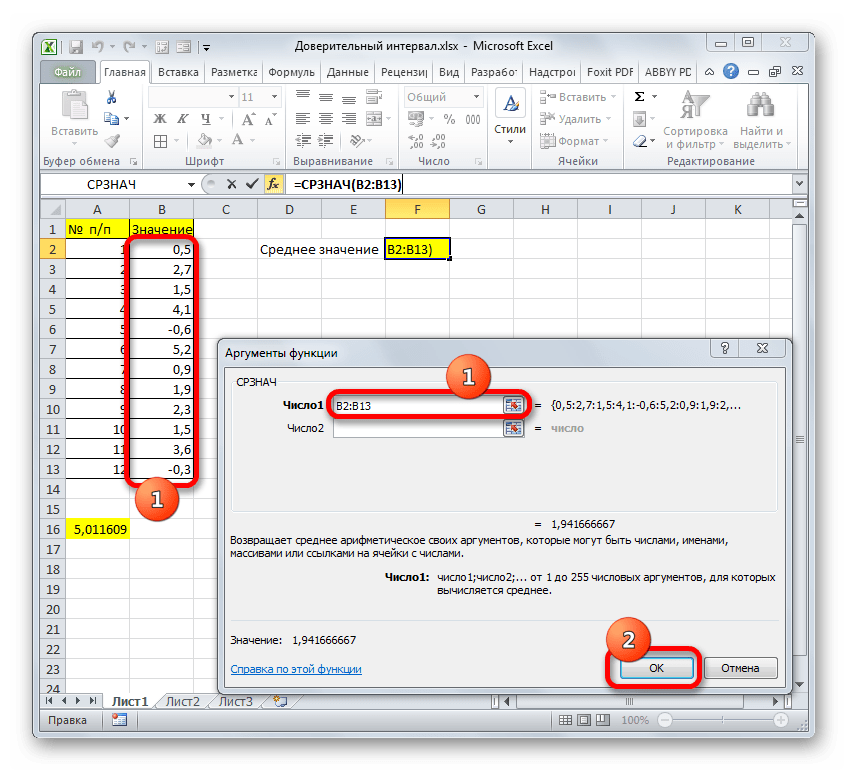
- В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.
- В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.
- Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так:
A14+A16. После ее набора жмем Enter. - В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.
- Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так:
=A16-A14. - После нажатия Enter мы получим результат в заданной ячейке с формулой.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
- Для определения правой границы ДИ общая формула будет выглядеть так:
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)). - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.